Algoritmi di ottimizzazione della popolazione: Algoritmo di Ricerca Gravitazionale (GSA)

Contenuto

1. Introduzione
2. Algoritmo
3. Risultati del test

1. Introduzione

L'algoritmo di Ricerca Gravitazionale (GSA) è stato proposto da E. Rashedi per risolvere i problemi di ottimizzazione, soprattutto quelli non lineari, seguendo i principi della legge gravitazionale di Newton. Nell'algoritmo proposto, le particelle sono considerate come oggetti e le loro prestazioni sono stimate tenendo conto delle loro masse. La gravità è la tendenza delle masse ad accelerare l'una verso l'altra. È una delle quattro forze fondamentali della natura (le altre sono la forza elettromagnetica, la forza nucleare debole e la forza nucleare forte).

Ogni particella dell'universo attrae ogni altra particella. La gravità esiste ovunque. Sebbene sia la forza più debole, è quella più visibile. Grazie alla forza gravitazionale, le persone possono camminare sulla Terra e i pianeti possono orbitare intorno al Sole. La forza gravitazionale di un oggetto è proporzionale alla sua massa. Pertanto, gli oggetti con una massa maggiore hanno più gravità. L'inevitabilità della gravità la distingue da tutte le altre forze della natura. Il comportamento della forza gravitazionale di Newton si chiama azione a distanza. È una legge fisica generale dedotta dall'osservazione empirica attraverso quello che Isaac Newton chiamava ragionamento induttivo. Fa parte della meccanica classica formulata nei Philosophiae Naturalis Principia Mathematica (Principia) di Newton, pubblicati per la prima volta il 5 luglio 1687.

Quando nell'aprile del 1686 Newton presentò il primo libro inedito alla Royal Society, Robert Hooke sostenne che Newton aveva ricevuto da lui la legge del quadrato inverso. Nel linguaggio odierno, la legge dice che ogni punto materiale attrae ogni altro punto materiale con una forza che agisce lungo una linea che interseca due punti.

2. Algoritmo

L'articolo presenta un algoritmo di ottimizzazione basato sulla legge gravitazionale di Newton: "Ogni particella nell'universo attrae ogni altra particella con una forza che è direttamente proporzionale al prodotto delle loro masse e inversamente proporzionale al quadrato della distanza tra loro". Nell'algoritmo proposto, gli agenti di ricerca sono un insieme di masse che interagiscono tra loro in base alla gravitazione newtoniana e alle leggi del moto. Allo stesso tempo, tutti gli agenti possono scambiare informazioni tra loro, ovunque si trovino nello spazio di ricerca, grazie ad una forza di attrazione che dipende dalla massa (calcolata dai valori della funzione obiettivo) e dalla distanza tra loro.

Gli agenti sono trattati come oggetti e la loro fitness è misurata tramite la loro massa. In termini generali (con le impostazioni dell'algoritmo vicine alle leggi fisiche reali), tutti questi oggetti sono attratti l'uno dall'altro dalla forza di gravità, che provoca un movimento globale di tutti gli oggetti verso gli oggetti con una massa maggiore. Pertanto, le masse interagiscono utilizzando una forma diretta di connessione attraverso la forza gravitazionale.

Nel GSA classico, ogni particella ha tre tipi di massa:

a) massa attiva
b) massa passiva
c) massa inerziale

Nella maggior parte dei casi, è conveniente e opportuno utilizzare l'uguaglianza di questi concetti per semplificare i codici e i calcoli e aumentare l'efficienza delle capacità di ricerca dell’algoritmo. Pertanto, nell'algoritmo ci sarà una sola massa, non tre. Le equazioni delle leggi fisiche utilizzate nel GSA sono mostrate nella Figura 1.

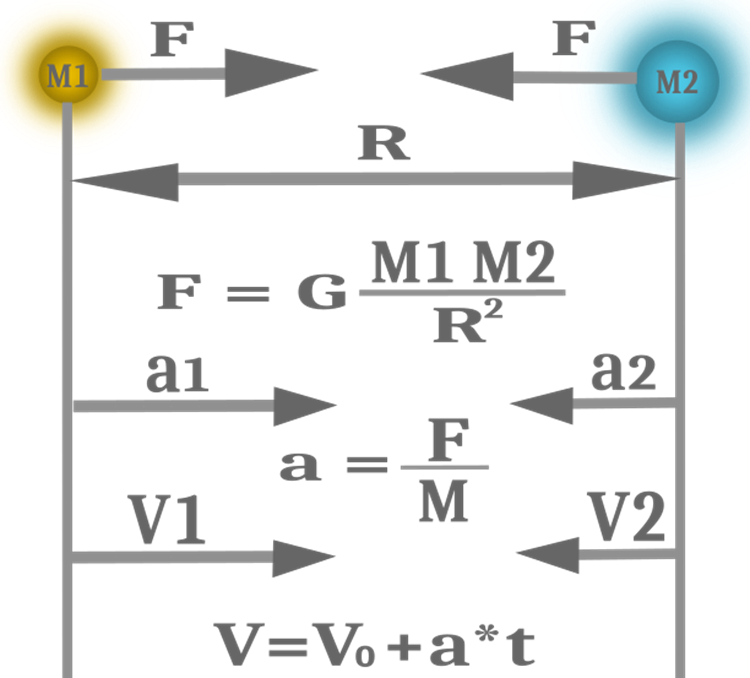
Figura 1. Forza di gravità, accelerazione e velocità

La posizione delle particelle fornisce la soluzione al problema, mentre la funzione di fitness viene utilizzata per calcolare le masse. L'algoritmo prevede due fasi: esplorazione e sfruttamento. Questo algoritmo sfrutta le capacità di intelligenza all'inizio per evitare di rimanere bloccati nell'optimum locale, e successivamente sfrutta le regioni di extrema.

L'algoritmo di ricerca gravitazionale deve trasformare una particella che si muove nello spazio in un oggetto con una certa massa. Questi oggetti si attraggono a causa dell'interazione gravitazionale reciproca e ogni particella nello spazio sarà attratta a causa dell'attrazione reciproca delle particelle che creano accelerazioni. Ogni particella è attratta da altre particelle e si muove nella direzione della forza. Le particelle con una massa piccola si muovono verso quelle con una massa maggiore, ma anche gli oggetti massicci si muovono, ma a una velocità inferiore inversamente proporzionale alla massa. La soluzione ottimale viene trovata dagli oggetti "grandi", che affinano la soluzione muovendosi a bassa velocità rispetto agli oggetti "piccoli" che si muovono più rapidamente. GSA implementa il trasferimento di informazioni attraverso l'interazione tra gli oggetti.

Fasi del GSA:

1. Inizializzazione dell'agente
2. Evoluzione della fitness
3. Calcolo della costante gravitazionale
4. Calcolo delle masse degli agenti

1. Inizializzazione dell'agente.
Tutti gli agenti vengono inizializzati in modo casuale. Ogni agente viene considerato come una soluzione candidata. Affinché l'analisi di stabilità sia significativa e affidabile, è estremamente importante specificare le condizioni iniziali di equilibrio. Infatti, se il "disco" originale di oggetti non è in equilibrio, la sua distensione nei primi passi temporali della simulazione può causare instabilità che sono di scarsa importanza per la nostra comprensione della stabilità delle "galassie a disco". Purtroppo non si conosce una soluzione analitica per la densità, il campo di velocità e la temperatura di un disco gassoso tridimensionale in equilibrio idrostatico nel potenziale esterno dell'alone di materia oscura e/o del disco stellare.

2. Evoluzione della fitness.
L'affidabilità e l'efficacia di GSA dipendono dal bilanciamento tra capacità di ricerca e di sfruttamento. Nelle iterazioni iniziali del processo di ricerca della soluzione, si privilegia l'esplorazione dello spazio di ricerca. Ciò può essere ottenuto consentendo agli agenti di utilizzare passi di grandi dimensioni nelle prime iterazioni. Nelle iterazioni successive, è necessario un affinamento dello spazio di ricerca per evitare la situazione di assenza di optima globale. Pertanto, le soluzioni candidate dovrebbero avere passi di dimensioni ridotte per essere utilizzate nelle iterazioni successive.

3. Calcolo della costante gravitazionale.
La costante gravitazionale (nota anche come costante gravitazionale universale, costante newtoniana di gravitazione o costante gravitazionale di Cavendish), indicata con la lettera G, è una costante fisica empirica coinvolta nel calcolo degli effetti gravitazionali nella legge di gravitazione universale di Isaac Newton e nella teoria della relatività generale di Albert Einstein. Nella legge di Newton, è la costante di proporzionalità che collega la forza gravitazionale tra due corpi con il prodotto delle loro masse e l'inverso del quadrato della loro distanza. Nelle equazioni di campo di Einstein, esso quantifica la relazione tra la geometria dello spaziotempo e il tensore energia-momento.

4. Calcolo delle masse degli agenti.
La massa è la quantità di materia presente nello spazio.

Pseudocodice dell'algoritmo:

1. generare un sistema di oggetti in modo casuale.
2. determinare la fitness di ciascun oggetto.
3. aggiornare i valori della costante gravitazionale, calcolare le masse, l'oggetto migliore e quello peggiore.
4. calcolo delle forze che agiscono su ciascuna coordinata.
5. calcolo delle accelerazioni e delle velocità degli oggetti.
6. aggiornare le posizioni degli oggetti.
7. determinare la fitness di ciascun oggetto.
8. Ripetere da p. 3 fino a quando non viene soddisfatto il criterio di terminazione.

Consideriamo il codice GSA. Per descrivere un oggetto nel sistema di interazione gravitazionale, abbiamo bisogno della struttura S_Object, che descriverà tutte le proprietà fisiche dell'oggetto necessarie per effettuare una ricerca gravitazionale: c [] - coordinate nello spazio di ricerca, v [] - vettore velocità per ciascuna delle coordinate (la dimensione dell'array è il numero di coordinate), M è la massa dell'oggetto (in GSA, la massa è un valore relativo, ovvero un valore calcolato in base al valore di fitness massimo e minimo sull'intero sistema di oggetti), f è il valore di fitness, R[] è la distanza Euclidea dagli altri oggetti (la dimensione dell'array è il numero di oggetti), F [] è il vettore delle forze per ciascuna delle coordinate (la dimensione dell'array è il numero di coordinate).

//——————————————————————————————————————————————————————————————————————————————
struct S_Object
{
  double c  [];   //coordinates
  double v  [];   //velocity
  double M;       //mass
  double f;       //fitness
  double R  [];   //euclidean distance to other objects
  double F  [];   //force vector
};
//——————————————————————————————————————————————————————————————————————————————

Dichiariamo la classe dell'algoritmo di ricerca gravitazionale C_AO_GSA. Delle proprietà fisiche degli oggetti che partecipano all'algoritmo come agenti, è necessaria solo una cosa: le coordinate che rappresentano la soluzione migliore - il valore di fB. La classe dichiara intervalli validi di coordinate dello spazio di ricerca e un passo. Il sistema di oggetti vincolati gravitazionalmente è rappresentato come un array di strutture S_Object. Nell'algoritmo classico, ci sono solo tre parametri esterni: G_constant, a_constant, e_constant, che determinano le proprietà dell'interazione gravitazionale degli oggetti, e il resto delle costanti sono incluse nelle equazioni di calcolo, ma ho ritenuto opportuno spostare queste costanti nei parametri esterni dell'algoritmo, che consentono una regolazione più flessibile delle proprietà dell'algoritmo nel suo complesso. Considererò tutti i parametri in modo più dettagliato più avanti, poiché influenzano notevolmente il comportamento dell'algoritmo.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_GSA
{
  //----------------------------------------------------------------------------
  public: S_Object o       []; //object
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    coordinatesNumberP, //coordinates number
                     const int    objectsNumberP,     //objects number
                     const double PowerOfdistanceP,   //power of distance
                     const double GraviPert_MinP,     //gravitational perturbation Min
                     const double GraviPert_MaxP,     //gravitational perturbation Min
                     const double VelocityPert_MinP,  //Velocity perturbation Min
                     const double VelocityPert_MaxP,  //Velocity perturbation Max
                     const double G_constantP,        //G constant
                     const double a_constantP,        //a constant
                     const double e_constantP,        //e constant
                     const int    maxIterationsP);    //max Iterations

  public: void Moving   (int iter);
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordinatesNumber; //coordinates number
  private: int    objectsNumber;     //objects number
  private: double PowerOfdistance;   //power of distance
  private: double GraviPert_Min;     //gravitational perturbation Min
  private: double GraviPert_Max;     //gravitational perturbation Min
  private: double VelocPert_Min;     //velocity perturbation Min
  private: double VelocPert_Max;     //velocity perturbation Max
  private: double G_constant;        //G constant
  private: double a_constant;        //a constant
  private: double e_constant;        //e constant
  private: int    maxIterations;
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Il metodo pubblico dell'algoritmo Init () serve a passare i parametri esterni dell'algoritmo alle costanti interne per inizializzare le variabili di servizio e assegnare le dimensioni agli array.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GSA::Init (const int    coordinatesNumberP, //coordinates number
                     const int    objectsNumberP,     //objects number
                     const double PowerOfdistanceP,   //power of distance
                     const double GraviPert_MinP,     //gravitational perturbation Min
                     const double GraviPert_MaxP,     //gravitational perturbation Min
                     const double VelocityPert_MinP,  //Velocity perturbation Min
                     const double VelocityPert_MaxP,  //Velocity perturbation Max
                     const double G_constantP,        //G constant
                     const double a_constantP,        //a constant
                     const double e_constantP,        //e constant
                     const int    maxIterationsP)     //max Iterations
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coordinatesNumber = coordinatesNumberP;
  objectsNumber     = objectsNumberP;
  PowerOfdistance   = PowerOfdistanceP;
  GraviPert_Min     = GraviPert_MinP;
  GraviPert_Max     = GraviPert_MaxP;
  VelocPert_Min     = VelocityPert_MinP;
  VelocPert_Max     = VelocityPert_MaxP;
  G_constant        = G_constantP;
  a_constant        = a_constantP;
  e_constant        = e_constantP;
  maxIterations     = maxIterationsP;

  ArrayResize (rangeMax,  coordinatesNumber);
  ArrayResize (rangeMin,  coordinatesNumber);
  ArrayResize (rangeStep, coordinatesNumber);

  ArrayResize (o,  objectsNumber);

  for (int i = 0; i < objectsNumber; i++)
  {
    ArrayResize (o [i].c,  coordinatesNumber);
    ArrayResize (o [i].v,  coordinatesNumber);
    ArrayResize (o [i].R,  objectsNumber);
    ArrayResize (o [i].F,  coordinatesNumber);
    o [i].f  = -DBL_MAX;
  }

  ArrayResize (cB, coordinatesNumber);
}
//——————————————————————————————————————————————————————————————————————————————

Il primo metodo pubblico chiamato ad ogni iterazione dell'iterazione Moving (). Questo metodo contiene tutta la fisica e la logica dell'algoritmo GSA. È piuttosto grande, quindi consideriamolo, suddividendolo in parti. Notare che il metodo prende come parametro l'iterazione corrente, il parametro è coinvolto nel calcolo della costante gravitazionale, regolando il bilanciamento tra ricerca e utilizzo.

Alla prima iterazione, avviene la fase di inizializzazione degli oggetti. Per tutte le coordinate degli oggetti, assegniamo valori casuali nell'intervallo consentito con una distribuzione uniforme, e controlliamo che non ci siano valori fuori intervallo. All'inizio del processo di ottimizzazione, tutti gli oggetti hanno velocità zero, cioè sono immobili nello spazio di ricerca rispetto alle coordinate. Notare che gli oggetti non hanno massa, quindi dovrebbero muoversi alla velocità della luce, ma infrangeremo le leggi della fisica per la prima iterazione, perché questo momento è in qualche modo equivalente al Big Bang. La fitness degli oggetti in questo momento è il più piccolo dei valori possibili di un numero "double". Durante il debug dell'algoritmo, è stato difficile trovare i bug relativi alla massa zero; è possibile vedere la soluzione di seguito.

//----------------------------------------------------------------------------
if (!revision)
{
  fB = -DBL_MAX;

  for (int obj = 0; obj < objectsNumber; obj++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      o [obj].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      o [obj].c [c] = SeInDiSp (o [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      o [obj].v [c] = 0.0;
      o [obj].M     = 0.0;
      o [obj].f     = -DBL_MAX;
    }
  }

  revision = true;
}

Il resto del codice del metodo Moving () si riferisce alla seconda iterazione e a quelle successive, in cui gli oggetti acquistano massa, velocità e accelerazione.

Prima di tutto, dobbiamo calcolare la massa. Come già detto, la massa (un valore scalare positivo per definizione) degli oggetti viene calcolata a partire dai valori della funzione di fitness, quindi è necessario determinare i valori minimi e massimi di fitness prima di calcolare la massa in base ai valori ottenuti. In questo momento, il valore della funzione di fitness è già stato ottenuto nell'iterazione precedente.

//find the minimum and maximum fitness==========================================
for (int obj = 0; obj < objectsNumber; obj++)
{
  if (o [obj].f < Fmin) Fmin = o [obj].f;
  if (o [obj].f > Fmax) Fmax = o [obj].f;
}

A questo punto del codice, la massa viene calcolata utilizzando l'equazione Mo=(Fo-Fmin)/(Fmax-Fmin), dove:

• Mo - massa dell'oggetto
• Fo - fitness dell'oggetto
• Fmax - valore massimo di fitness tra tutti gli oggetti (valore migliore)
• Fmin - valore minimo di fitness tra tutti gli oggetti (valore peggiore)
  

Come si vede dall'equazione, la massa può assumere solo valori positivi nell'intervallo da 0 a 1 compreso. Poiché abbiamo detto in precedenza che la massa non deve essere uguale a zero, altrimenti la velocità sarà uguale alla velocità della luce, limiteremo il limite inferiore della massa a 0,1. Il valore superiore può anche essere uguale a 1. Inoltre, tieni presente che se i valori minimo e massimo della funzione di fitness sono uguali, la massa di tutti gli oggetti sarà uguale per tutti e pari a 1. Ciò corrisponde al caso in cui lo spazio di ricerca è omogeneo nell'area in cui si trovano gli oggetti e tutti gli oggetti sono uguali in termini di qualità della funzione di fitness, così come il movimento in qualsiasi direzione ha la stessa priorità. Sembrerebbe che in questo caso tutti gli oggetti dovrebbero gradualmente muoversi e concentrarsi verso un centro di massa comune, ma ciò non avviene a causa dell'azione non lineare della forza gravitazionale.

//calculating the mass of objects===========================================
for (int obj = 0; obj < objectsNumber; obj++)
{
  Fo = o [obj].f;
  if (Fmax == Fmin) Mo = 1.0;
  else Mo = (Fo - Fmin) / (Fmax - Fmin);
  o [obj].M = Scale (Mo, 0.0, 1.0, 0.1, 1.0, false);
}

Abbiamo calcolato la massa degli oggetti, ora è necessario calcolare un'altra componente dell'equazione R: la distanza euclidea tra ogni oggetto e tutti gli altri oggetti. Il calcolo consiste in due cicli di enumerazione degli oggetti e un ciclo di calcolo per ciascuna delle coordinate. Come ricordiamo, la distanza euclidea è la radice della somma dei quadrati delle differenze delle coordinate.

//calculation of Euclidean distances between all objects====================
for (int obj = 0; obj < objectsNumber; obj++) ArrayInitialize (o [obj].R, 0.0);

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int obj2 = 0; obj2 < objectsNumber; obj2++)
  {
    if (obj != obj2)
    {
      if (o [obj].R [obj2] == 0.0)
      {
        for (int c = 0; c < coordinatesNumber; c++)
        {
          diffDist = o [obj].c [c] - o [obj2].c [c];
          o [obj].R [obj2] += diffDist * diffDist;
        }

        o [obj].R [obj2] = sqrt (o [obj].R [obj2]);
        o [obj2].R [obj] = o [obj].R [obj2];
      }
    }
  }
}

Ora possiamo calcolare i vettori della forza per gli oggetti. Per fare ciò, è necessario passare in rassegna tutti gli oggetti in due cicli e un ciclo per le coordinate, poiché la velocità viene calcolata separatamente per ogni coordinata. È necessario aggiungere una condizione che escluda la coincidenza degli indici degli oggetti, in modo che l'oggetto escluda il calcolo di se stesso nel calcolo della forza. Qui utilizziamo la nota equazione di Newton per calcolare la forza gravitazionale di due oggetti (Figura 1), correggendo la distanza con il rapporto e_costant. Calcoliamo innanzitutto la costante gravitazionale G, che dovrebbe cambiare verso il basso a ogni iterazione, assumendo che l'algoritmo si intensifichi alla fine dell'ottimizzazione.

//calculate the force vector for each object================================
for (int obj = 0; obj < objectsNumber; obj++) ArrayInitialize (o [obj].F, 0.0);

double G = G_constant * exp (-a_constant * (iter / maxIterations));

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int obj2 = 0; obj2 < objectsNumber; obj2++)
  {
    if (obj != obj2)
    {
      for (int c = 0; c < coordinatesNumber; c++)
      {
        diffDist = o [obj2].c [c] - o [obj].c [c];

        if (o [obj].R [obj2] != 0.0)
        {
          o [obj] .F [c] += G * o [obj].M * o [obj2].M * diffDist / (pow (o [obj].R [obj2], PowerOfdistance) + e_constant);
        }
      }
    }
  }
}

Ora dobbiamo solo calcolare la velocità per far sì che gli oggetti inizino a muoversi. Dall'equazione della Figura 1, si evince che il calcolo della velocità implica l'accelerazione, mentre l'accelerazione è uguale alla forza che agisce sul corpo divisa per la massa. L'equazione contiene anche il tempo V=V0+a*t. Nel nostro algoritmo, l'iterazione svolge il ruolo del tempo, quindi la variazione di velocità non è altro che un aumento di velocità in un'iterazione. Il vettore della velocità è già stato calcolato in precedenza. Resta da dividere per la massa. Inoltre, gli autori introducono la perturbazione della forza e la perturbazione della velocità. La perturbazione è un numero casuale uniformemente distribuito compreso tra 0 e 1. Questo aggiunge una componente casuale al movimento degli oggetti, senza la quale il movimento sarebbe strettamente determinato e dipenderebbe solo dalla posizione iniziale dei corpi. Ho ritenuto ragionevole portare gli indicatori di perturbazione nei parametri esterni dell'algoritmo, che consentiranno di regolare il movimento degli oggetti da completamente deterministico a completamente casuale.

//calculation of acceleration and velocity for all objects==================
double a = 0.0; //acceleration

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int c = 0; c < coordinatesNumber; c++)
  {
    r = RNDfromCI (GraviPert_Min, GraviPert_Max);
    a = o [obj].F [c] * r / o [obj].M;
    r = RNDfromCI (GraviPert_Min, GraviPert_Max);
    o [obj].v [c] = o [obj].v [c] * r + a;
    o [obj].c [c] = o [obj].c [c] + o [obj].v [c];

    if (o [obj].c [c] > rangeMax [c]) o [obj].c [c] = rangeMin [c];
    if (o [obj].c [c] < rangeMin [c]) o [obj].c [c] = rangeMax [c];

    o [obj].c [c] = SeInDiSp (o [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

Il secondo metodo Revision (), è obbligatorio per l'esecuzione a ogni iterazione. Il metodo è progettato per determinare il miglior valore di fitness per l'iterazione corrente. Nel ciclo, si passa attraverso tutti gli oggetti e si sostituisce la soluzione globale migliore.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GSA::Revision ()
{
  for (int s = 0; s < objectsNumber; s++)
  {
    if (o [s].f > fB)
    {
      fB = o [s].f;
      ArrayCopy (cB, o [s].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Risultati del test

Passiamo ai risultati dei test. Di seguito sono riportati i risultati del banco di prova con i migliori parametri GSA che sono riuscito a trovare:

2023.02.03 14:12:43.440    Test_AO_GSA (EURUSD,M1)    C_AO_GSA:10;2.0;0.2;0.6;0.0;1.0;2.0;20.0;0.01
2023.02.03 14:12:43.440    Test_AO_GSA (EURUSD,M1)    =============================
2023.02.03 14:12:52.198    Test_AO_GSA (EURUSD,M1)    5 Rastrigin's; Func cicli 10000 risultato: 73.64619475145881
2023.02.03 14:12:52.198    Test_AO_GSA (EURUSD,M1)    Punteggio: 0.91252
2023.02.03 14:13:06.105    Test_AO_GSA (EURUSD,M1)    25 Rastrigin's; Func cicli 10000 risultato: 59.4327218024363
2023.02.03 14:13:06.105    Test_AO_GSA (EURUSD,M1)    Punteggio: 0.73640
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD,M1)    500 Rastrigin's; Func cicli 10000 risultato: 37.550565227034724
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD,M1)    Punteggio: 0.46527
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD,M1)    =============================
2023.02.03 14:14:30.577    Test_AO_GSA (EURUSD,M1)    5 Forest's; Func cicli 10000 risultato: 0.741456333008312
2023.02.03 14:14:30.577    Test_AO_GSA (EURUSD,M1)    Punteggio: 0.41941
2023.02.03 14:14:50.281    Test_AO_GSA (EURUSD,M1)    25 Forest's; Func cicli 10000 risultato: 0.46894018717768426
2023.02.03 14:14:50.282    Test_AO_GSA (EURUSD,M1)    Punteggio: 0.26526
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD,M1)    500 Forest's; Func cicli 10000 risultato: 0.11382493516764165
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD,M1)    Punteggio: 0.06439
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD,M1)    =============================
2023.02.03 14:16:18.195    Test_AO_GSA (EURUSD,M1)    5 Megacity's; Func cicli 10000 risultato: 5.279999999999999
2023.02.03 14:16:18.195    Test_AO_GSA (EURUSD,M1)    Punteggio: 0.44000
2023.02.03 14:16:34.536    Test_AO_GSA (EURUSD,M1)    25 Megacity's; Func cicli 10000 risultato: 2.296
2023.02.03 14:16:34.536    Test_AO_GSA (EURUSD,M1)    Punteggio: 0.19133
2023.02.03 14:17:46.887    Test_AO_GSA (EURUSD,M1)    500 Megacity's; Func cicli 10000 risultato: 0.23399999999999999
2023.02.03 14:17:46.887    Test_AO_GSA (EURUSD,M1)    Punteggio: 0.01950

Parametri dell'algoritmo:

input double PowerOfdistance_P = 2,0; //Potenza della distanza
input double GraviPert_Min_P    = 0.2;  //Perturbazione gravitazionale Minima
input double GraviPert_Max_P    = 0.6;  //Perturbazione gravitazionale Massima
input double VelocityPert_Min_P = 0.0;   //Perturbazione della velocità Minima
input double VelocityPert_Max_P = 1.0;   //Perturbazione della velocità Massima
input double G_constant_P       = 2.0;   //costante G
input double a_constant_P       = 20.0;  //costante a
input double e_constant_P       = 0.01;  //constante e

PowerOfdistance_P - il grado, a cui aumentiamo la distanza tra gli oggetti, influisce sulla formazione di oggetti legati gravitazionalmente. Più alto è il grado nell'equazione, minore è l'impatto degli oggetti sugli altri oggetti.

• GraviPert_Min_P - limite inferiore dell'intervallo di perturbazione gravitazionale.
• GraviPert_Max_P - limite superiore dell'intervallo di perturbazione gravitazionale.
• Nel caso di GraviPert_Min_P = 1,0 e GraviPert_Max_P = 1,0, non vi è alcun disturbo gravitazionale.
• VelocityPert_Min_P - limite inferiore dell'intervallo di perturbazione della velocità.
• VelocityPert_Max_P - limite superiore dell'intervallo di perturbazione della velocità.

Nel caso di VelocityPert_Min_P = 1,0 e VelocityPert_Max_P = 1,0, non c’è alcuna perturbazione della velocità.

• G_constant_P - la costante gravitazionale agisce come un fattore di scala: più alto è il valore, più forti sono le forze gravitazionali e più veloce è la velocità degli oggetti.
• a_constant_P - fattore di correzione per la costante gravitazionale, progettato per ridurre il campo di ricerca durante l'intera ottimizzazione, al fine di affinare gli estremi trovati.
• e_constant_P - fattore di correzione per la distanza tra gli oggetti.

Diamo un'occhiata ai risultati del test di visualizzazione. Il comportamento dell'algoritmo sulle funzioni di prova è molto particolare e interessante. In effetti, l'esperimento mostra il lavoro delle forze gravitazionali. Il movimento degli oggetti e i risultati di ottimizzazione ottenuti sono fortemente influenzati dai parametri esterni dell'algoritmo. Inizialmente, gli oggetti con velocità zero sono distribuiti in modo casuale nello spazio di ricerca e iniziano a muoversi all'iterazione successiva. Le impostazioni utilizzate nei test (le migliori che ho trovato) fanno muovere gli oggetti verso un centro di massa comune.

Non dimenticate che la gravità di ogni oggetto influisce sugli altri oggetti, le cui leggi di moto sono descritte con sufficiente accuratezza nell'algoritmo. Avvicinandosi al centro di massa comune, gli oggetti continuano a muoversi ad alta velocità. Sembra un movimento pulsante di una massa di particelle verso il centro di massa comune e viceversa. Dopo un certo numero di iterazioni, il movimento degli oggetti cambia la sua traiettoria sotto l'influenza del rilievo spaziale della funzione di fitness, che agisce come una disomogeneità gravitazionale che influenza la massa degli oggetti. Come abbiamo detto in precedenza, la massa degli oggetti viene calcolata in base al valore della funzione di fitness. Tuttavia, la funzione Rastrigin, che è simmetrica lungo gli assi, ha un effetto abbastanza uniforme sul movimento degli oggetti e la suddivisione in gruppi non è particolarmente evidente.

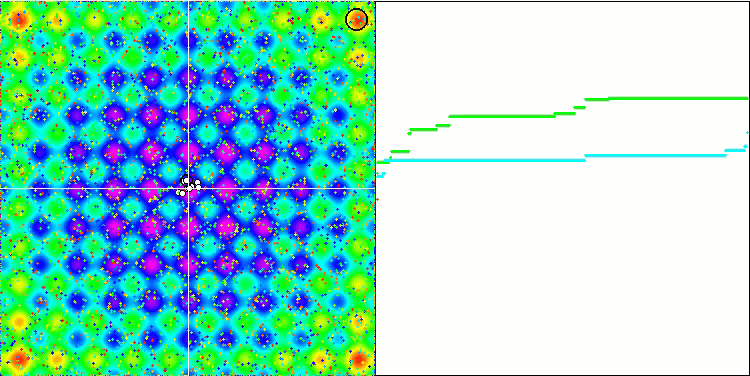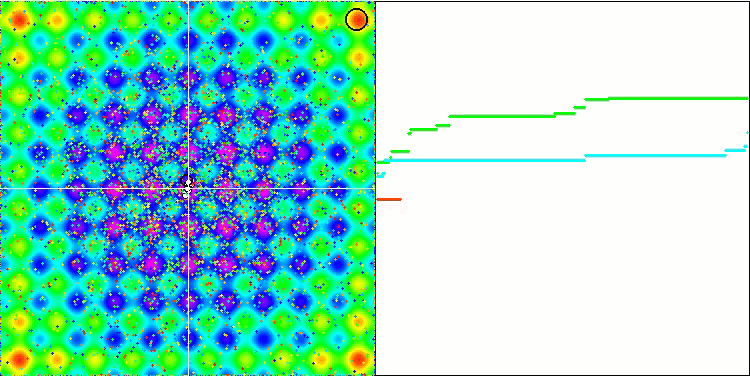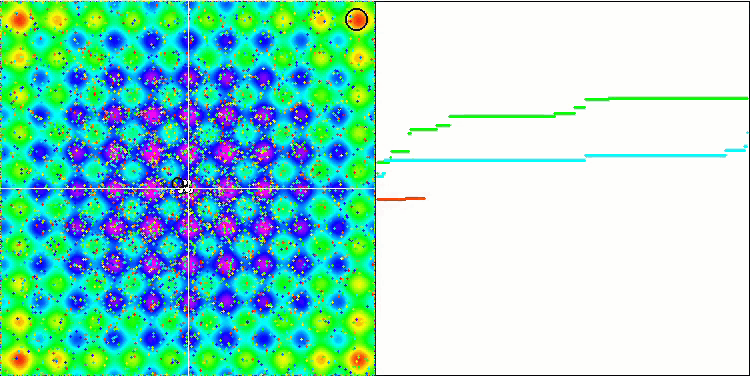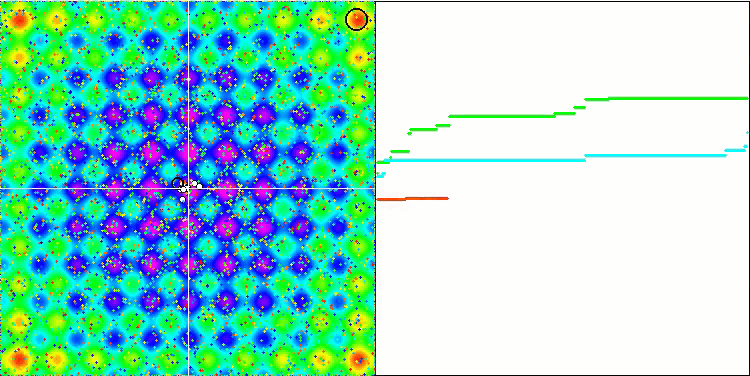
  GSA sulla funzione test Rastrigin.

Un comportamento ancora più interessante è mostrato dagli oggetti nelle funzioni Forest e Megacity. Queste funzioni non sono simmetriche e quindi hanno un effetto non uniforme sull'intero gruppo di oggetti.

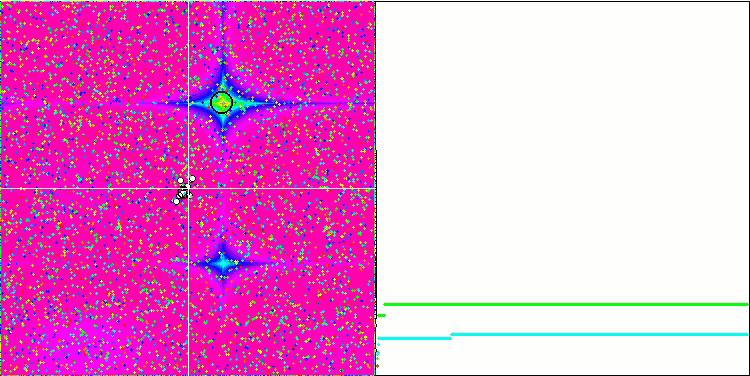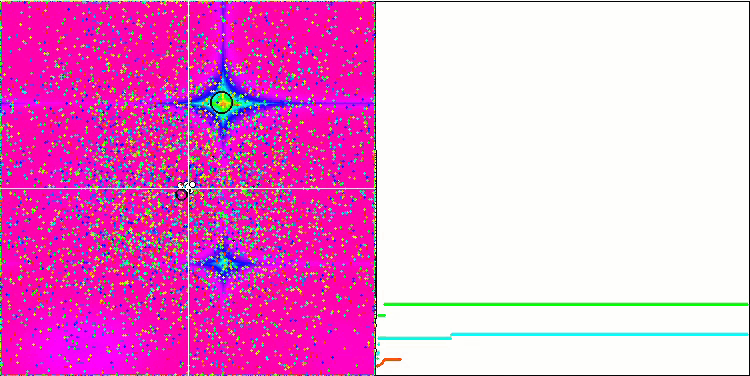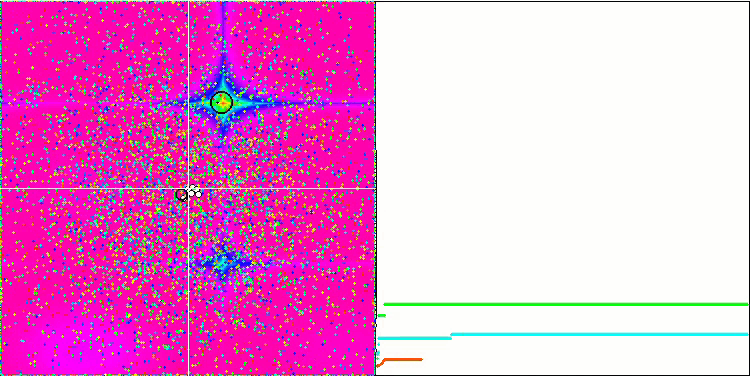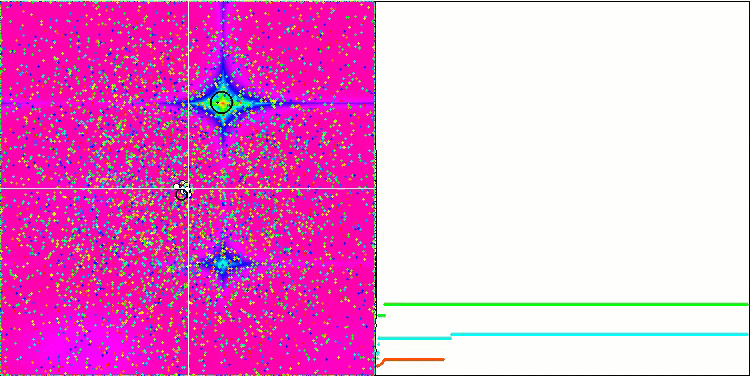
  GSA sulla funzione di test Forest.

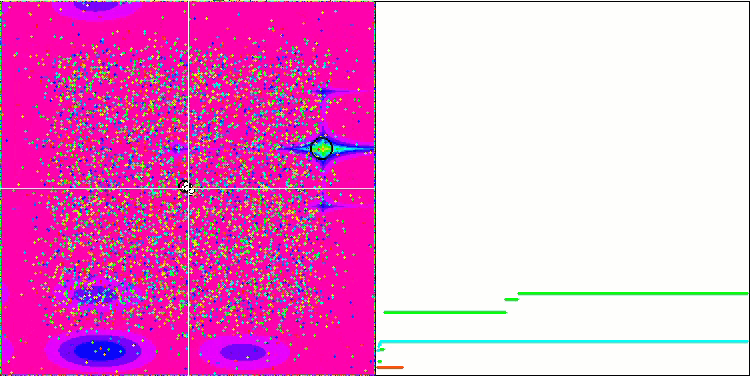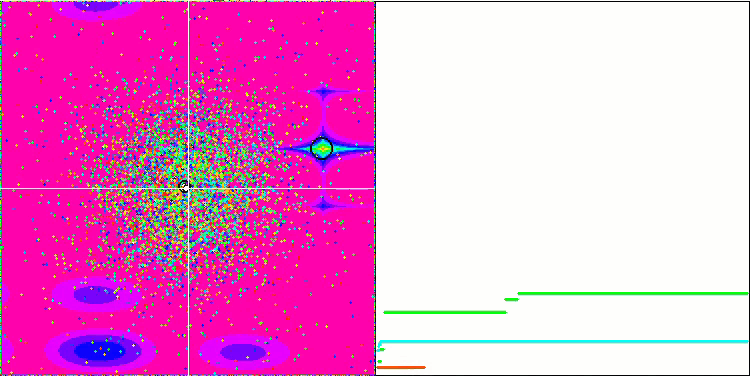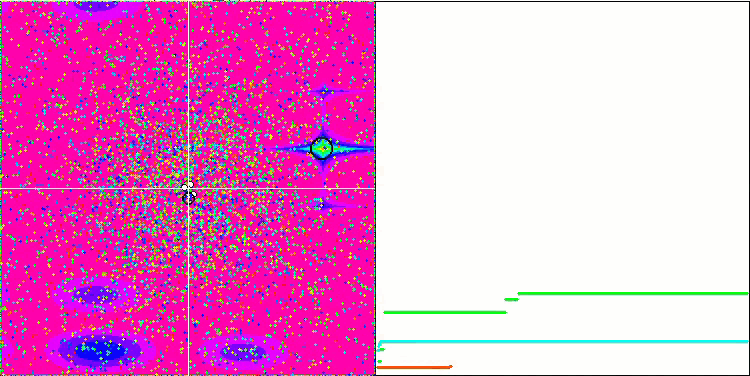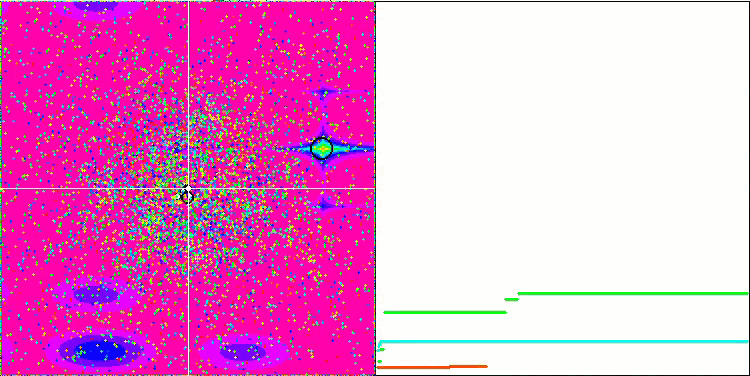
GSA sulla funzione di test Megacity.

Dopo molte sperimentazioni con GSA, mi è venuta l'idea di creare un simulatore di movimento degli oggetti spaziali. Non ha alcun valore pratico, ma dà un'idea delle leggi fisiche che agiscono sui sistemi planetari e stellari. Il simulatore è una versione di GSA con la casualità disabilitata. Inoltre, vengono introdotti tre oggetti che imitano tre stelle (una gigante blu, una stella gialla e una nana bianca). I parametri della massa sono visualizzati separatamente nelle relative impostazioni.

È stata creata una nuova funzione di fitness Universe con uno spazio uniforme appositamente per il simulatore. Il simulatore mostra chiaramente come il grado (parametro) della distanza tra gli oggetti influisca sui loro movimenti reciproci. Nella visualizzazione sottostante, viene applicata una potenza di 3 invece del valore standard 2 della legge di Newton. Risulta chiaro come il grado influisca sulla formazione di sistemi gravitazionalmente legati, come i sistemi stellari a coppie e tripli.

Se nel nostro universo il grado di distanza fosse stato maggiore, allora le galassie si sarebbero formate molto prima rispetto alla realtà. L'animazione mostra chiaramente che gli oggetti accoppiati che circolano intorno a un centro di massa comune sono apparsi già nelle prime iterazioni. Come previsto, il gigante blu ha raccolto il maggior numero di oggetti intorno a sé.

Visualizzazione del simulatore di movimento di oggetti spaziali basato sull'algoritmo GSA

Passiamo all'analisi dei risultati del test GSA. Le caratteristiche originali utilizzate nell'algoritmo non gli hanno permesso di ottenere ottimi risultati nei nostri test. Le numerose variazioni dei parametri che ho provato non hanno migliorato la convergenza dell'algoritmo. L'algoritmo ha mostrato alcuni risultati positivi rispetto agli altri partecipanti al test sulla funzione regolare Rastrigin con 10 variabili e Megacity. In altri test, GSA si posiziona al di sotto della media della tabella, ottenendo l'ottavo posto su dodici.

AO	Descrizione	Rastrigin			Finale Rastrigin	Forest			Finale Forest	Megacity (discreta)			Finale Megacity	Risultato finale
		10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)		10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)		10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)
IWO	Ottimizzazione delle piante infestanti	1.00000	1.00000	0.35295	2.35295	0.79937	0.46349	0.41071	1.67357	0.75912	0.44903	0.94416	2.15231	100.000
ACOm	Ottimizzazione della colonia di formiche M	0.36118	0.26810	0.20182	0.83110	1.00000	1.00000	1.00000	3.00000	1.00000	1.00000	0.15901	2.15901	96.805
COAm	Algoritmo di ottimizzazione a cucù M	0.96423	0.69756	0.30792	1.96971	0.64504	0.34034	0.21362	1.19900	0.67153	0.34273	0.48451	1.49877	74.417
FAm	Algoritmo della lucciola M	0.62430	0.50653	0.20290	1.33373	0.55408	0.42299	0.64360	1.62067	0.21167	0.28416	1.00000	1.49583	70.740
BA	Algoritmo del pipistrello	0.42290	0.95047	1.00000	2.37337	0.17768	0.17477	0.33595	0.68840	0.15329	0.07158	0.49268	0.71755	59.383
ABC	Colonia di api artificiali	0.81573	0.48767	0.24656	1.54996	0.58850	0.21455	0.17249	0.97554	0.47444	0.26681	0.39496	1.13621	57.393
BFO	Ottimizzazione del foraggiamento batterico	0.70129	0.46155	0.13988	1.30272	0.41251	0.26623	0.26695	0.94569	0.42336	0.34491	0.53694	1.30521	55.563
GSA	Algoritmo di ricerca gravitazionale	0.73222	0.67404	0.00000	1.40626	0.31238	0.36416	0.42921	1.10575	0.51095	0.36658	0.00000	0.87753	52.786
FSS	Ricerca del banco di pesci	0.48850	0.37769	0.13383	1.00002	0.78060	0.05013	0.08423	0.91496	0.00000	0.01084	0.23493	0.24577	20.094
PSO	Ottimizzazione dello sciame di particelle	0.21339	0.12224	0.08478	0.42041	0.15345	0.10486	0.28099	0.53930	0.08028	0.02385	0.05550	0.15963	14.358
RND	Casuale	0.17559	0.14524	0.09495	0.41578	0.08623	0.04810	0.06094	0.19527	0.00000	0.00000	0.13960	0.13960	8.117
GWO	Ottimizzazione del lupo grigio	0.00000	0.00000	0.02672	0.02672	0.00000	0.00000	0.00000	0.00000	0.18977	0.04119	0.07252	0.30348	1.000

In generale, l'algoritmo GSA è notevolmente sensibile alla presenza di un gradiente nella funzione da ottimizzare. La scarsa scalabilità non consente di utilizzarlo per compiti seri che contengano molte variabili, quindi non consiglierei l'algoritmo per l'uso con le reti neurali e per l'ottimizzazione dei sistemi di trading. Non ho studiato a fondo le possibilità dell'algoritmo di ricerca gravitazionale. Ulteriori ricerche potrebbero svelare nuove caratteristiche positive sconosciute di questo algoritmo molto interessante e insolito. I principali vantaggi dell'algoritmo sono l'indipendenza dalla migliore soluzione globale attualmente trovata e la capacità di tutti gli agenti di interagire tra loro. 

La Fig. 2 mostra i risultati dei test dell'algoritmo.

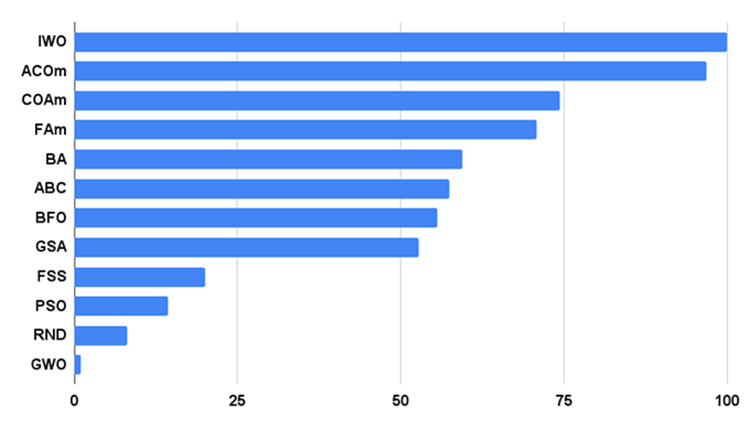
Figure 2. Istogramma dei risultati dei test degli algoritmi

Conclusioni sulle proprietà dell'Algoritmo di Ricerca Gravitazionale (GSA):

Pro:
1. Facile implementazione.
2. Buone prestazioni su funzioni regolari con poche variabili.

Contro:
1. Elevata complessità computazionale.
2. Scarsi risultati sulle funzioni discrete.
3. Scarsa scalabilità.