Matemáticas en el trading: Ratios de Sharpe y Sortino
El rendimiento es la métrica más obvia usada por los inversores y los tráders principiantes a la hora de analizar la efectividad del comercio. Los tráders profesionales utilizan herramientas más fiables para el análisis de estrategias, como los ratios de Sharpe y Sortino. En este artículo, explicaremos con ejemplos sencillos cómo se calculan ambos. Ya hablamos del tema de la evaluación de estrategias comerciales en el artículo anterior "Matemáticas de trading. Cómo estimar los resultados de trade". Recomendamos la lectura de este artículo para refrescar conocimientos o aprender algo nuevo de forma autónoma.
Ratio de Sharpe
Los inversionistas y tráders experimentados saben que para obtener resultados consistentes, debemos comerciar con estrategias múltiples o invertir en varios valores distintos. Este es uno de los conceptos de la inversión inteligente, que implica la creación de un portafolio de inversión. Cada portafolio de valores/estrategias tendrá sus propios parámetros de riesgo y rendimiento, por lo que deberemos compararlos entre sí de alguna forma.
Una de las primeras herramientas para realizar esta comparación es el ratio de Sharpe, que fue desarrollado en 1966 por el futuro premio Nobel William Sharpe. Los principales indicadores que usa esta herramienta son la rentabilidad media, la desviación estándar de la rentabilidad y la rentabilidad libre de riesgo.
La desventaja del ratio de Sharpe es que los datos iniciales para su análisis deben tener una distribución normal. En otras palabras, el gráfico de distribución del rendimiento debe ser simétrico y no debe tener picos o caídas bruscos.
El ratio de Sharpe se calcula utilizando la siguiente fórmula:
Sharpe Ratio = (Return - RiskFree)/Std
donde:
- Return es el valor promedio de los ingresos durante un periodo determinado. Por ejemplo, para un mes, trimestre, año, etcétera.
- RiskFree el valor de los ingresos sin riesgo durante el mismo periodo temporal. Esto puede ser, por ejemplo, el interés sobre un depósito bancario, bonos y otros instrumentos financieros con riesgo mínimo y 100% de fiabilidad.
- Std es la desviación estándar de los rendimientos para el mismo periodo. Cuanto mayor sea el diferencial de los rendimientos, mayor será el riesgo y la volatilidad experimentados por la cuenta/los activos del portafolio/los fondos administrados por el tráder.
Rendimiento
El rendimiento se calcula como el cambio en el coste de los activos durante un cierto intervalo temporal. Para ello, se toman los valores de rendimiento para el periodo en el que se calcula el ratio de Sharpe. Como regla general, el valor del ratio de Sharpe se considera para un año, pero se pueden calcular valores trimestrales, mensuales e incluso diarios. Los rendimientos se calculan usando la fórmula:
Return[i] = (Close[i]-Close[i-1])/Close[i-1]
donde:
- Return[i] — es el rendimiento para el intervalo con índice i;
- Close[i] — es el coste de los activos al final del i-ésimo intervalo;
- Close[i-1] — es el coste de los activos al final del intervalo anterior.
En otras palabras, el rendimiento se puede escribir como el cambio relativo en el coste de los activos durante un intervalo:
Return[i] = Delta[i]/Previous
donde:
- Delta[i] = (Close[i]-Close[i-1]) — es el cambio absoluto en el coste del activo durante el intervalo;
- Previous = Close[i-1] — es el coste de los activos al final del intervalo anterior.
Para calcular el ratio de Sharpe respecto a los valores diarios de un año, deberemos tomar los valores de los rendimientos de cada día durante ese año y calcular el rendimiento promedio diario como la suma de los rendimientos dividida por el número de días incluidos en el cálculo.
Return = Sum(Return[i])/N
donde N es el número de días.
Ingresos libres de riesgo
El concepto de ingresos libres de riesgo es condicional, ya que siempre existe un riesgo. Además, como el ratio de Sharpe se usa para comparar diferentes estrategias/portafolios durante el mismo periodo temporal, resulta más fácil tomar los ingresos libres de riesgo como cero. Es decir
RiskFree = 0
Desviación estándar de los rendimientos
La desviación estándar muestra la dispersión de una variable aleatoria alrededor de la media. Primero, se calcula el valor promedio del rendimiento, y luego se suman las desviaciones al cuadrado de los rendimientos del valor promedio. La cantidad resultante se divide por el número de rendimientos: esta es la varianza. La raíz cuadrada de la varianza es la desviación estándar de los rendimientos.
D = Sum((Return - Return[i])^2 )/N
STD = SQRT(D)
En el artículo mencionado anteriormente se ofrece un ejemplo de cálculo de la desviación estándar.
El cálculo del ratio de Sharpe en cualquier marco temporal y su conversión al valor anual
El cálculo del ratio de Sharpe no ha cambiado desde 1966. Este indicador recibió su nombre moderno después del reconocimiento mundial de su metodología. En ese momento, la valoración de los fondos y portafolios se hacía usando como base los ingresos obtenidos durante varios años. Posteriormente, los cálculos comenzaron a realizarse sobre los datos mensuales, convirtiendo el ratio de Sharpe resultante a un valor anual. De esta forma, se pueden comparar dos fondos/portafolios/estrategias.
El ratio de Sharpe se escala fácilmente en diferentes intervalos y marcos temporales al valor anual. Para conseguirlo, hay que multiplicar el valor resultante por la raíz cuadrada de la razón entre el intervalo anual y el actual. Vamos a mostrar un ejemplo sencillo.
Digamos que estamos calculando el ratio de Sharpe sobre los rendimientos diarios: SharpeDaily. Ahora necesitamos convertir el indicador resultante al valor anual SharpeAnnual. El coeficiente anual es proporcional a la raíz cuadrada de la razón de los periodos; en otras palabras, se calcula el número de intervalos que cabe en un año. Como en un año hay 252 días hábiles, el ratio de Sharpe obtenido de los rendimientos diarios se debe multiplicar por la raíz cuadrada de 252. Este será el valor anual del ratio de Sharpe:
SharpeAnnual = SQRT(252)*SharpeDaily // en un año hay 252 días hábiles
Si realizamos los cálculos en el marco temporal H1, el principio seguirá siendo el mismo: primero convertiremos SharpeHourly a SharpeDaily, y luego obtendremos el ratio de Sharpe anual. Una barra en el marco temporal D1 contiene 24 barras H1, por lo que la fórmula será la siguiente:
SharpeDaily = SQRT(24)*SharpeHourly // D1 contiene 24 barras H1
No todos los instrumentos financieros se comercian las 24 horas del día, pero, a la hora de evaluar las estrategias comerciales en el simulador en el mismo instrumento, esto no importa, ya que las estrategias se comparan en el mismo periodo de prueba y marco temporal.
Valoración de estrategias usando el ratio de Sharpe
Dependiendo de los indicadores de la estrategia/portafolio, el ratio de Sharpe puede adquirir cualquier valor, incluso negativo. Convertir el ratio de Sharpe a un valor anual nos permite interpretarlo de forma clásica: | Valor | Valoración | Descripción |
|---|---|---|
| Sharpe Ratio < 0 | Malo | La estrategia no es rentable, no sirve |
| 0 < Sharpe Ratio < 1.0 | Incierto | El riesgo no se amortiza. Dichas estrategias pueden practicarse si no hay alternativas |
| Sharpe Ratio ≥ 1.0 | Bien | Si el Ratio de Sharpe es superior a uno, significa que el riesgo compensa, el portafolio/estrategia funciona |
| Sharpe Ratio ≥ 3.0 | Muy bien. | Un indicador alto sugiere que la probabilidad de sufrir pérdidas en una operación determinada es muy baja |
Debemos recordar que el ratio de Sharpe es una estadística común. Se trata solo de la rentabilidad con respecto al riesgo. Por consiguiente, al analizar portafolios y estrategias, es importante correlacionar el ratio de Sharpe con los valores recomendados y/o entre sí.
Cálculo del ratio de Sharpe en EURUSD para 2020
El ratio de Sharpe se desarrolló originalmente para evaluar portafolios que siempre contienen muchas acciones. El coste de las acciones cambia todos los días, y el valor del portafolio cambia en consecuencia. Por ello, podemos quitar el cambio en el coste y la rentabilidad en cualquier marco temporal. Vamos a realizar los cálculos con la pareja de divisas EURUSD
y los marcos temporales H1 y D1; luego efectuaremos la conversión al valor anual y la comparación, para comprender si hay diferencias y por qué. Haremos los cálculos usando como base los precios de cierre de las barras durante 2020.
Código en MQL5
//+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- double H1_close[],D1_close[]; double h1_returns[],d1_returns[]; datetime from = D'01.01.2020'; datetime to = D'01.01.2021'; int bars = CopyClose("EURUSD",PERIOD_H1,from,to,H1_close); if(bars == -1) Print("CopyClose(\"EURUSD\",PERIOD_H1,01.01.2020,01.01.2021 failed. Error ",GetLastError()); else { Print("\nCalculamos la desviación media y cuadrática media de los rendimientos en las barras H1"); Print("H1 bars=",ArraySize(H1_close)); GetReturns(H1_close,h1_returns); double average = ArrayMean(h1_returns); PrintFormat("H1 average=%G",average); double std = ArrayStd(h1_returns); PrintFormat("H1 std=%G",std); double sharpe_H1 = average / std; PrintFormat("H1 Sharpe=%G",sharpe_H1); double sharpe_annual_H1 = sharpe_H1 * MathSqrt(ArraySize(h1_returns)); Print("Sharpe_annual(H1)=", sharpe_annual_H1); } bars = CopyClose("EURUSD",PERIOD_D1,from,to,D1_close); if(bars == -1) Print("CopyClose(\"EURUSD\",PERIOD_D1,01.01.2020,01.01.2021 failed. Error ",GetLastError()); else { Print("\nCalculamos la desviación media y cuadrática media de los rendimientos en las barras D1"); Print("D1 bars=",ArraySize(D1_close)); GetReturns(D1_close,d1_returns); double average = ArrayMean(d1_returns); PrintFormat("D1 average=%G",average); double std = ArrayStd(d1_returns); PrintFormat("D1 std=%G",std); double sharpe_D1 = average / std; double sharpe_annual_D1 = sharpe_D1 * MathSqrt(ArraySize(d1_returns)); Print("Sharpe_annual(H1)=", sharpe_annual_D1); } } //+------------------------------------------------------------------+ //| Rellena la matriz de rendimientos returns[] | //+------------------------------------------------------------------+ void GetReturns(const double & values[], double & returns[]) { int size = ArraySize(values); //--- si hay menos de 2 valores, retornaremos una matriz de rendimientos vacía if(size < 2) { ArrayResize(returns,0); PrintFormat("%s: Error. ArraySize(values)=%d",size); return; } else { //--- rellenamos en el ciclo de rendimientos ArrayResize(returns, size - 1); double delta; for(int i = 1; i < size; i++) { returns[i - 1] = 0; if(values[i - 1] != 0) { delta = values[i] - values[i - 1]; returns[i - 1] = delta / values[i - 1]; } } } //--- } //+------------------------------------------------------------------+ //| Calcula el valor medio de los elementos de la matriz | //+------------------------------------------------------------------+ double ArrayMean(const double & array[]) { int size = ArraySize(array); if(size < 1) { PrintFormat("%s: Error, array is empty",__FUNCTION__); return(0); } double mean = 0; for(int i = 0; i < size; i++) mean += array[i]; mean /= size; return(mean); } //+------------------------------------------------------------------+ //| Calcula la desviación estándar de los elementos de la matriz | //+------------------------------------------------------------------+ double ArrayStd(const double & array[]) { int size = ArraySize(array); if(size < 1) { PrintFormat("%s: Error, array is empty",__FUNCTION__); return(0); } double mean = ArrayMean(array); double std = 0; for(int i = 0; i < size; i++) std += (array[i] - mean) * (array[i] - mean); std /= size; std = MathSqrt(std); return(std); } //+------------------------------------------------------------------+ /* Resultado Calculamos la desviación media y cuadrática media de los rendimientos en las barras H1 H1 bars:6226 H1 average=1.44468E-05 H1 std=0.00101979 H1 Sharpe=0.0141664 Sharpe_annual(H1)=1.117708053392263 Calculamos la desviación media y cuadrática media de los rendimientos en las barras D1 D1 bars:260 D1 average=0.000355823 D1 std=0.00470188 Sharpe_annual(H1)=1.2179005039019222 */
Código en Python para realizar los cálculos con ayuda de la biblioteca MetaTrader5
import math from datetime import datetime import MetaTrader5 as mt5 # mostramos los datos sobre el paquete MetaTrader5 print("MetaTrader5 package author: ", mt5.__author__) print("MetaTrader5 package version: ", mt5.__version__) # importamos el módulo pandas para mostrar los datos obtenidos en forma de recuadro import pandas as pd pd.set_option('display.max_columns', 50) # cuántas columnas mostramos pd.set_option('display.width', 1500) # anchura máx. del recuadro a mostrar # importamos el módulo pytz para trabajar con el huso horario import pytz # establecemos la conexión con el terminal MetaTrader 5 if not mt5.initialize(): print("initialize() failed") mt5.shutdown() # establecemos el huso horario en UTC timezone = pytz.timezone("Etc/UTC") # creamos los objetos datetime en el huso horario UTC, para que no se aplique el desplazamiento del huso horario local utc_from = datetime(2020, 1, 1, tzinfo=timezone) utc_to = datetime(2020, 12, 31, hour=23, minute=59, second=59, tzinfo=timezone) # obtenemos las barras de EURUSD H1 en el intervalo 2020.01.01 00:00 - 2020.31.12 13:00 en el huso horario UTC rates_H1 = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_H1, utc_from, utc_to) # obtenemos también las barras de D1 en el intervalo 2020.01.01 00:00 - 2020.31.12 13:00 en el huso horario UTC rates_D1 = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_D1, utc_from, utc_to) # finalizamos la conexión con el terminal MetaTrader 5 y seguimos procesando las barras obtenidas mt5.shutdown() # creamos un DataFrame de los datos obtenidos rates_frame = pd.DataFrame(rates_H1) # añadimos la columna "Rendimiento" rates_frame['return'] = 0.0 # ahora calculamos el rendimiento como return[i] = (close[i] - close[i-1])/close[i-1] prev_close = 0.0 for i, row in rates_frame.iterrows(): close = row['close'] rates_frame.at[i, 'return'] = close / prev_close - 1 if prev_close != 0.0 else 0.0 prev_close = close print("\nCalculamos la desviación media y cuadrática media de los rendimientos en las barras H1") print('H1 rates:', rates_frame.shape[0]) ret_average = rates_frame[1:]['return'].mean() # no tomamos la primera línea con el rendimiento cero print('H1 return average=', ret_average) ret_std = rates_frame[1:]['return'].std(ddof=0) # no tomamos la primera línea con el rendimiento cero print('H1 return std =', ret_std) sharpe_H1 = ret_average / ret_std print('H1 Sharpe = Average/STD = ', sharpe_H1) sharpe_annual_H1 = sharpe_H1 * math.sqrt(rates_H1.shape[0]-1) print('Sharpe_annual(H1) =', sharpe_annual_H1) # ahora calculamos el ratio de Sharpe en el marco temporal D1 rates_daily = pd.DataFrame(rates_D1) # añadimos la columna "Rendimiento" rates_daily['return'] = 0.0 # ahora calculamos el rendimiento prev_return = 0.0 for i, row in rates_daily.iterrows(): close = row['close'] rates_daily.at[i, 'return'] = close / prev_return - 1 if prev_return != 0.0 else 0.0 prev_return = close print("\nCalculamos la desviación media y cuadrática media de los rendimientos en las barras D1") print('D1 rates:', rates_daily.shape[0]) daily_average = rates_daily[1:]['return'].mean() print('D1 return average=', daily_average) daily_std = rates_daily[1:]['return'].std(ddof=0) print('D1 return std =', daily_std) sharpe_daily = daily_average / daily_std print('D1 Sharpe =', sharpe_daily) sharpe_annual_D1 = sharpe_daily * math.sqrt(rates_daily.shape[0]-1) print('Sharpe_annual(D1) =', sharpe_annual_D1) Resultado Calculamos la desviación media y cuadrática media de los rendimientos en las barras H1 H1 rates: 6226 H1 return average= 1.4446773215242986e-05 H1 return std = 0.0010197932969323495 H1 Sharpe = Average/STD = 0.014166373968823358 Sharpe_annual(H1) = 1.117708053392236 Calculamos la desviación media y cuadrática media de los rendimientos en las barras D1 D1 rates: 260 D1 return average= 0.0003558228355051694 D1 return std = 0.004701883757646081 D1 Sharpe = 0.07567665511222807 Sharpe_annual(D1) = 1.2179005039019217
Podemos ver que los resultados de los cálculos en MQL5 y Python coinciden. Los códigos fuente se adjuntan al artículo (CalculateSharpe_2TF).
Al mismo tiempo, el valor anual del ratio de Sharpe obtenido en las barras H1 y D1 difiere entre sí: 1,117708 frente a 1,217900. Vamos a analizar este tema con más detalle.
Cálculo del ratio de Sharpe anual con EURUSD para 2020 en todos los marcos temporales
Calcularemos el ratio de Sharpe anual en todos los marcos temporales de la misma manera. Para ello, recopilaremos en un recuadro los datos obtenidos:
- TF — marco temporal
- Minutes — cuántos minutos hay en el marco temporal
- Rates — número de barras por año en un marco temporal determinado
- Avg — beneficio promedio por barra en un marco temporal, en tanto por ciento (porcentaje promedio de cambio del precio por barra)
- Std — desviación estándar en el marco temporal por barra, en tanto por ciento (volatilidad del precio en porcentaje en este marco temporal)
- SharpeTF — ratio de Sharpe calculado para un marco temporal determinado
- SharpeAnnual — ratio de Sharpe anual, calculado en función de Sharpe en un marco temporal determinado
Vamos a mostrar el bloque de código para el cálculo. El código completo se encuentra en el archivo adjunto CalculateSharpe_All_TF.mq5.
//--- estructura para mostrar las estadísticas en el log struct Stats { string TF; int Minutes; int Rates; double Avg; double Std; double SharpeTF; double SharpeAnnual; }; //--- matriz de estadísticas según los marcos temporales Stats stats[]; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //---matrices para los precios de cierre double H1_close[],D1_close[]; //--- matrices de rendimientos double h1_returns[],d1_returns[]; //--- matriz con los marcos temporales en los que calcularemos el ratio de Sharpe ENUM_TIMEFRAMES timeframes[] = {PERIOD_M1,PERIOD_M2,PERIOD_M3,PERIOD_M4,PERIOD_M5, PERIOD_M6,PERIOD_M10,PERIOD_M12,PERIOD_M15,PERIOD_M20, PERIOD_M30,PERIOD_H1,PERIOD_H2,PERIOD_H3,PERIOD_H4, PERIOD_H6,PERIOD_H8,PERIOD_H12,PERIOD_D1,PERIOD_W1,PERIOD_MN1 }; ArrayResize(stats,ArraySize(timeframes)); //--- parámetros de la solicitud de marcos temporales string symbol = Symbol(); datetime from = D'01.01.2020'; datetime to = D'01.01.2021'; Print(symbol); for(int i = 0; i < ArraySize(timeframes); i++) { //--- obtenemos la matriz de rendimientos en el marco temporal indicado double returns[]; GetReturns(symbol,timeframes[i],from,to,returns); //--- calculamos las estadísticas GetStats(returns,avr,std,sharpe); double sharpe_annual = sharpe * MathSqrt(ArraySize(returns)); PrintFormat("%s aver=%G%% std=%G%% sharpe=%G sharpe_annual=%G", EnumToString(timeframes[i]), avr * 100,std * 100,sharpe,sharpe_annual); //--- rellenamos la estructura de las estadísticas Stats row; string tf_str = EnumToString(timeframes[i]); StringReplace(tf_str,"PERIOD_",""); row.TF = tf_str; row.Minutes = PeriodSeconds(timeframes[i]) / 60; row.Rates = ArraySize(returns); row.Avg = avr; row.Std = std; row.SharpeTF = sharpe; row.SharpeAnnual = sharpe_annual; //--- añadimos la línea de estadísticas para el marco temporal stats[i] = row; } //--- mostramos en el diario las estadísticas de todos los marcos temporales ArrayPrint(stats,8); } /* Resultado [TF] [Minutes] [Rates] [Avg] [Std] [SharpeTF] [SharpeAnnual] [ 0] "M1" 1 373023 0.00000024 0.00168942 0.00168942 1.03182116 [ 1] "M2" 2 186573 0.00000048 0.00239916 0.00239916 1.03629642 [ 2] "M3" 3 124419 0.00000072 0.00296516 0.00296516 1.04590258 [ 3] "M4" 4 93302 0.00000096 0.00341717 0.00341717 1.04378592 [ 4] "M5" 5 74637 0.00000120 0.00379747 0.00379747 1.03746116 [ 5] "M6" 6 62248 0.00000143 0.00420265 0.00420265 1.04854166 [ 6] "M10" 10 37349 0.00000239 0.00542100 0.00542100 1.04765562 [ 7] "M12" 12 31124 0.00000286 0.00601079 0.00601079 1.06042363 [ 8] "M15" 15 24900 0.00000358 0.00671964 0.00671964 1.06034161 [ 9] "M20" 20 18675 0.00000477 0.00778573 0.00778573 1.06397070 [10] "M30" 30 12450 0.00000716 0.00966963 0.00966963 1.07893298 [11] "H1" 60 6225 0.00001445 0.01416637 0.01416637 1.11770805 [12] "H2" 120 3115 0.00002880 0.01978455 0.01978455 1.10421905 [13] "H3" 180 2076 0.00004305 0.02463458 0.02463458 1.12242890 [14] "H4" 240 1558 0.00005746 0.02871564 0.02871564 1.13344977 [15] "H6" 360 1038 0.00008643 0.03496339 0.03496339 1.12645075 [16] "H8" 480 779 0.00011508 0.03992838 0.03992838 1.11442404 [17] "H12" 720 519 0.00017188 0.05364323 0.05364323 1.22207717 [18] "D1" 1440 259 0.00035582 0.07567666 0.07567666 1.21790050 [19] "W1" 10080 51 0.00193306 0.14317328 0.14317328 1.02246174 [20] "MN1" 43200 12 0.00765726 0.43113365 0.43113365 1.49349076 */
Vamos a construir un histograma del ratio de Sharpe con EURUSD para 2020 según los marcos temporales. Podemos ver que en los marcos temporales de minutos de M1 a M30, los cálculos dan un resultado próximo que va de 1.03 a 1.08. Los resultados más inestables se dan en los marcos temporales de H12 a MN1.
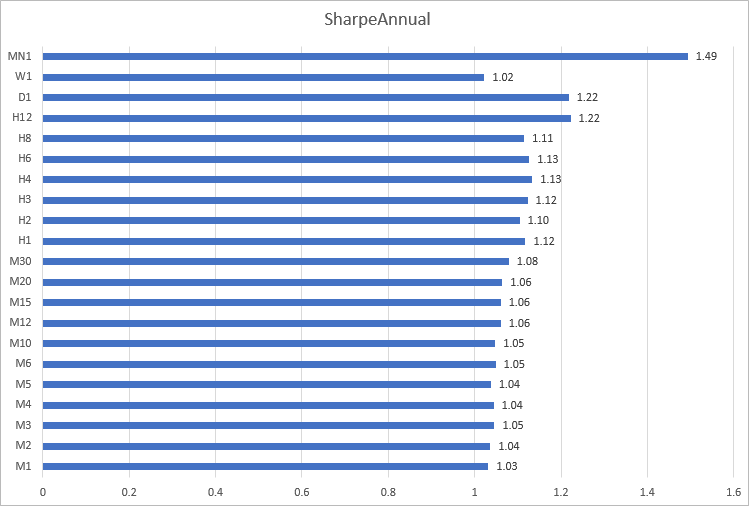
Cálculo del ratio de Sharpe del año 2020 con GBPUSD, USDJPY y USDCHF.
Vamos a realizar los mismos cálculos para otras tres parejas de divisas principales.
En GBPUSD, los valores del ratio de Sharpe han resultado próximos en los marcos temporales de M1 a H12.
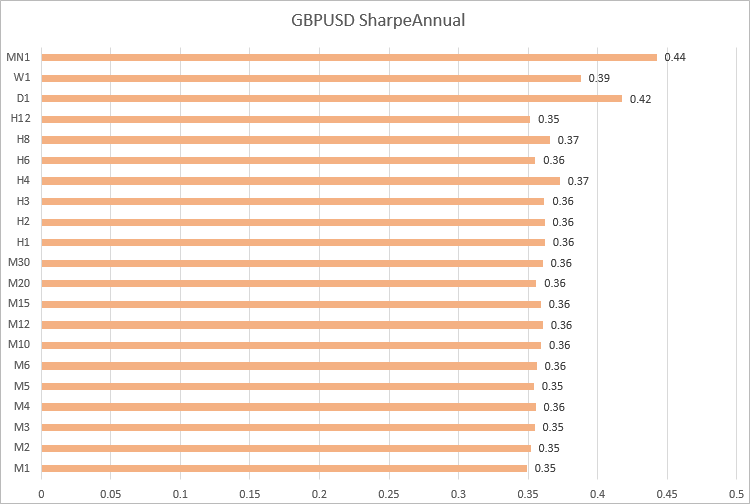
En USDJPY, los valores también han resultado próximos en los marcos temporales de M1 a H12: de -0.56 a -0.60.
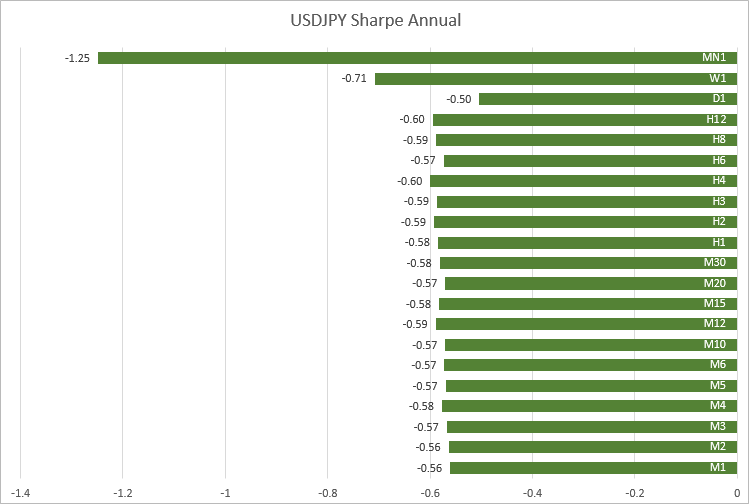
En USDCHF, los valores de cierre en los marcos temporales de M1 a M30 han resultado próximos. A medida que crece el marco temporal, el ratio de Sharpe fluctúa.
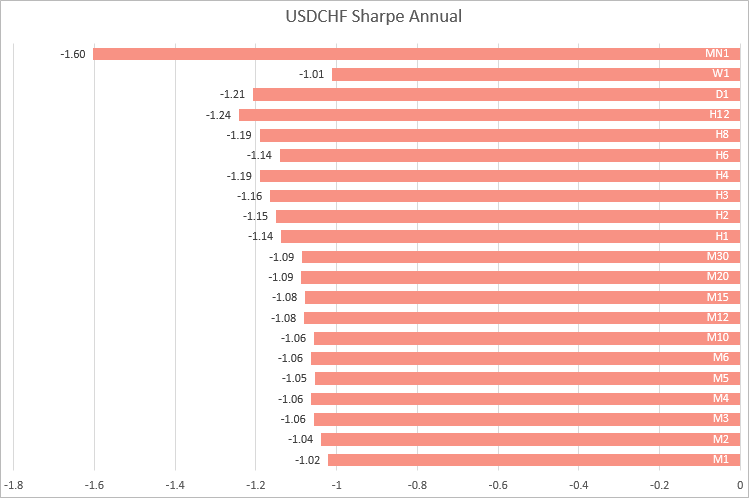
Por consiguiente, usando como ejemplo 4 parejas de divisas principales, podemos concluir que los cálculos más estables del ratio de Sharpe se obtienen en los marcos temporales de M1 a M30. Es decir, para los cálculos, resulta mejor tomar valores de rentabilidad en marcos temporales pequeños, si necesitamos comparar estrategias que funcionan en diferentes símbolos.
Cálculo del ratio de Sharpe anual con EURUSD para 2020 en todos los marcos temporales
Vamos a tomar los rendimientos dentro de cada mes para 2020 y a calcular el valor anual del ratio de Sharpe en los marcos temporales de M1 a H1. El código completo del script CalculateSharpe_Months.mq5 se adjunta al artículo.
//--- estructura para guardar los rendimientos struct Return { double ret; // rendimiento datetime time; // fecha int month; // mes }; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { SharpeMonths sharpe_by_months[]; //--- matriz con los marcos temporales en los que calcularemos el ratio de Sharpe ENUM_TIMEFRAMES timeframes[] = {PERIOD_M1,PERIOD_M2,PERIOD_M3,PERIOD_M4,PERIOD_M5, PERIOD_M6,PERIOD_M10,PERIOD_M12,PERIOD_M15,PERIOD_M20, PERIOD_M30,PERIOD_H1 }; ArrayResize(sharpe_by_months,ArraySize(timeframes)); //--- parámetros de la solicitud de marcos temporales string symbol = Symbol(); datetime from = D'01.01.2020'; datetime to = D'01.01.2021'; Print("Calculate Sharpe Annual on ",symbol, " for 2020 year"); for(int i = 0; i < ArraySize(timeframes); i++) { //--- obtenemos la matriz de rendimientos en el marco temporal indicado Return returns[]; GetReturns(symbol,timeframes[i],from,to,returns); double avr,std,sharpe; //--- calculamos las estadísticas del año GetStats(returns,avr,std,sharpe); string tf_str = EnumToString(timeframes[i]); //--- calculamos el valor anual Sharpe Ratio en cada mes SharpeMonths sharpe_months_on_tf; sharpe_months_on_tf.SetTimeFrame(tf_str); //--- seleccionamos los rendimientos en el mes i for(int m = 1; m <= 12; m++) { Return month_returns[]; GetReturnsByMonth(returns,m,month_returns); //--- calculamos las estadísticas del año double sharpe_annual = CalculateSharpeAnnual(timeframes[i],month_returns); sharpe_months_on_tf.Sharpe(m,sharpe_annual); } //--- añadimos el valor del ratio de Sharpe para los 12 meses en el marco temporal i sharpe_by_months[i] = sharpe_months_on_tf; } //--- mostramos el recuadro de los valores anuales de Sharpe por meses en todos los marcos temporales ArrayPrint(sharpe_by_months,3); } /* Resultado Calculate Sharpe Annual on EURUSD for 2020 year [TF] [Jan] [Feb] [Marc] [Apr] [May] [June] [July] [Aug] [Sept] [Oct] [Nov] [Dec] [ 0] "PERIOD_M1" -2.856 -1.340 0.120 -0.929 2.276 1.534 6.836 2.154 -2.697 -1.194 3.891 4.140 [ 1] "PERIOD_M2" -2.919 -1.348 0.119 -0.931 2.265 1.528 6.854 2.136 -2.717 -1.213 3.845 4.125 [ 2] "PERIOD_M3" -2.965 -1.340 0.118 -0.937 2.276 1.543 6.920 2.159 -2.745 -1.212 3.912 4.121 [ 3] "PERIOD_M4" -2.980 -1.341 0.119 -0.937 2.330 1.548 6.830 2.103 -2.765 -1.219 3.937 4.110 [ 4] "PERIOD_M5" -2.929 -1.312 0.120 -0.935 2.322 1.550 6.860 2.123 -2.729 -1.239 3.971 4.076 [ 5] "PERIOD_M6" -2.945 -1.364 0.119 -0.945 2.273 1.573 6.953 2.144 -2.768 -1.239 3.979 4.082 [ 6] "PERIOD_M10" -3.033 -1.364 0.119 -0.934 2.361 1.584 6.789 2.063 -2.817 -1.249 4.087 4.065 [ 7] "PERIOD_M12" -2.952 -1.358 0.118 -0.956 2.317 1.609 6.996 2.070 -2.933 -1.271 4.115 4.014 [ 8] "PERIOD_M15" -3.053 -1.367 0.118 -0.945 2.377 1.581 7.132 2.078 -2.992 -1.274 4.029 4.047 [ 9] "PERIOD_M20" -2.998 -1.394 0.117 -0.920 2.394 1.532 6.884 2.065 -3.010 -1.326 4.074 4.040 [10] "PERIOD_M30" -3.008 -1.359 0.116 -0.957 2.379 1.585 7.346 2.084 -2.934 -1.323 4.139 4.034 [11] "PERIOD_H1" -2.815 -1.373 0.116 -0.966 2.398 1.601 7.311 2.221 -3.136 -1.374 4.309 4.284 */
Podemos observar que los valores del ratio anual para cada mes están muy próximos en todos los marcos temporales en los que se han realizado los cálculos. Para una mejor presentación, mostraremos los resultados como una superficie 3D usando un gráfico en Excel.
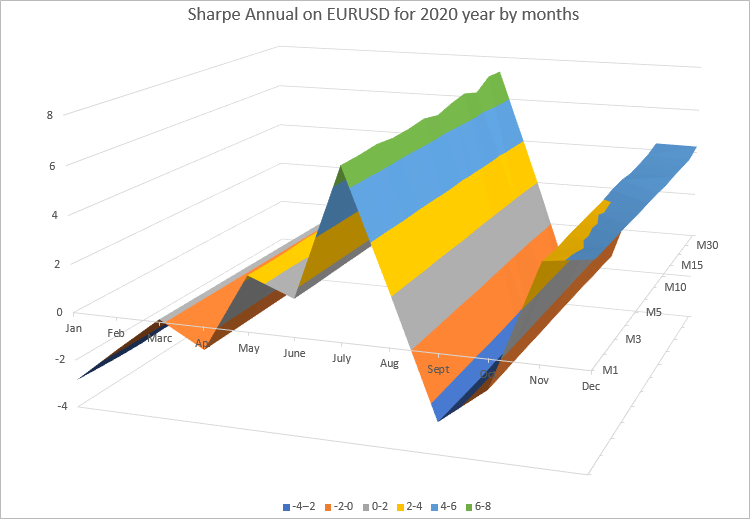
El gráfico muestra claramente que los valores del ratio de Sharpe anual cambian cada mes. Depende de cómo haya cambiado el gráfico EURUSD ese mes. Pero, al mismo tiempo, el valor del ratio de Sharpe anual para cada mes en todos los marcos temporales casi no cambia.
Así, podremos calcular el ratio de Sharpe anual en cualquier marco temporal, mientras que el valor resultante tampoco dependerá del número de barras sobre las que se hayan obtenido los rendimientos. Esto significa que el anterior algoritmo de cálculo puede usarse durante las pruebas, la optimización y el monitoreo en tiempo real. Lo principal es que la matriz de rendimientos no sea demasiado pequeña.
Ratio de Sortino
A la hora de calcular el ratio de Sharpe, se toma como riesgo toda la volatilidad de las cotizaciones, tanto al alza como a la baja en los activos. No obstante, el aumento del coste del portafolio resulta beneficioso para el inversor, y la pérdida solo puede provocar su declive. Por ello, el riesgo real en el ratio está sobreestimado. El ratio de Sortino, desarrollado a principios de la década de los 90 por Frank Sortino, resuelve este problema.
Al igual que sus predecesores, F. Sortino considera el rendimiento futuro como una variable aleatoria igual a su esperanza matemática, y el riesgo como una varianza. El rendimiento y el riesgo se determinan usando como base los valores históricos de las cotizaciones para un periodo determinado. Al igual que en el cálculo del ratio de Sharpe, el rendimiento se divide por el riesgo.
Sortino llamó la atención sobre el hecho de que el riesgo, definido como el diferencial total de los rendimientos (o, en otras palabras, la volatilidad total), depende de cambios tanto positivos como negativos. Sortino reemplazó la varianza total por una semivarianza que tiene en cuenta solo las caídas en los activos. La semivarianza se conoce en varias publicaciones como "volatilidad a la baja", varianza negativa, varianza inferior o desviación estándar de pérdidas.
El ratio de Sortino en realidad se calcula de la misma forma que el ratio de Sharpe, solo que excluyendo los rendimientos positivos del cálculo de la volatilidad. Esto nos permite reducir la medida del riesgo y aumentar el valor del ratio.
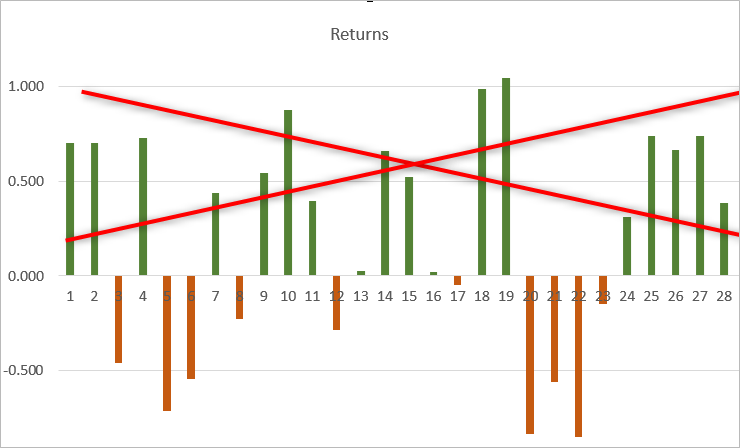
Código de ejemplo para calcular el ratio de Sortino usando como base el cálculo del ratio de Sharpe. Para calcular la "semivarianza", solo tomaremos los rendimientos negativos.
//+------------------------------------------------------------------+ //| Calcula los ratios de Sharpe y Sortino | //+------------------------------------------------------------------+ void GetStats(ENUM_TIMEFRAMES timeframe, const double & returns[], double & avr, double & std, double & sharpe, double & sortino) { avr = ArrayMean(returns); std = ArrayStd(returns); sharpe = (std == 0) ? 0 : avr / std; //--- ahora quitamos los rendimientos positivos y calculamos el ratio de Sortino double negative_only[]; int size = ArraySize(returns); ArrayResize(negative_only,size); ZeroMemory(negative_only); //--- copiamos solo los rendimientos negativos for(int i = 0; i < size; i++) negative_only[i] = (returns[i] > 0) ? 0 : returns[i]; double semistd = ArrayStd(negative_only); sortino = avr / semistd; return; }
El script CalculateSortino_All_TF.mq5, adjunto al artículo, ofrece los siguientes resultados en EURUSD para 2020:
[TF] [Minutes] [Rates] [Avg] [Std] [SharpeAnnual] [SortinoAnnual] [Ratio] [ 0] "M1" 1 373023 0.00000024 0.00014182 1.01769617 1.61605380 1.58795310 [ 1] "M2" 2 186573 0.00000048 0.00019956 1.02194170 1.62401856 1.58914991 [ 2] "M3" 3 124419 0.00000072 0.00024193 1.03126142 1.64332243 1.59350714 [ 3] "M4" 4 93302 0.00000096 0.00028000 1.02924195 1.62618200 1.57998030 [ 4] "M5" 5 74637 0.00000120 0.00031514 1.02303684 1.62286584 1.58632199 [ 5] "M6" 6 62248 0.00000143 0.00034122 1.03354379 1.63789024 1.58473231 [ 6] "M10" 10 37349 0.00000239 0.00044072 1.03266766 1.63461839 1.58290848 [ 7] "M12" 12 31124 0.00000286 0.00047632 1.04525580 1.65215986 1.58062730 [ 8] "M15" 15 24900 0.00000358 0.00053223 1.04515816 1.65256608 1.58116364 [ 9] "M20" 20 18675 0.00000477 0.00061229 1.04873529 1.66191269 1.58468272 [10] "M30" 30 12450 0.00000716 0.00074023 1.06348332 1.68543441 1.58482449 [11] "H1" 60 6225 0.00001445 0.00101979 1.10170316 1.75890688 1.59653431 [12] "H2" 120 3115 0.00002880 0.00145565 1.08797046 1.73062372 1.59068999 [13] "H3" 180 2076 0.00004305 0.00174762 1.10608991 1.77619289 1.60583048 [14] "H4" 240 1558 0.00005746 0.00200116 1.11659184 1.83085734 1.63968362 [15] "H6" 360 1038 0.00008643 0.00247188 1.11005321 1.79507001 1.61710267 [16] "H8" 480 779 0.00011508 0.00288226 1.09784908 1.74255746 1.58724682 [17] "H12" 720 519 0.00017188 0.00320405 1.20428761 2.11045830 1.75245371 [18] "D1" 1440 259 0.00035582 0.00470188 1.20132966 2.04624198 1.70331429 [19] "W1" 10080 51 0.00193306 0.01350157 1.03243721 1.80369984 1.74703102 [20] "MN1" 43200 12 0.00765726 0.01776075 1.49349076 5.00964481 3.35431926
Podemos observar que prácticamente en todos los marcos temporales, el valor anual de Sortino es 1,60 veces superior al ratio de Sharpe. Pero al calcular los resultados comerciales, por supuesto, no habrá un patrón tan claro. Por ello, tiene sentido comparar las estrategias/portafolios usando ambos indicadores.
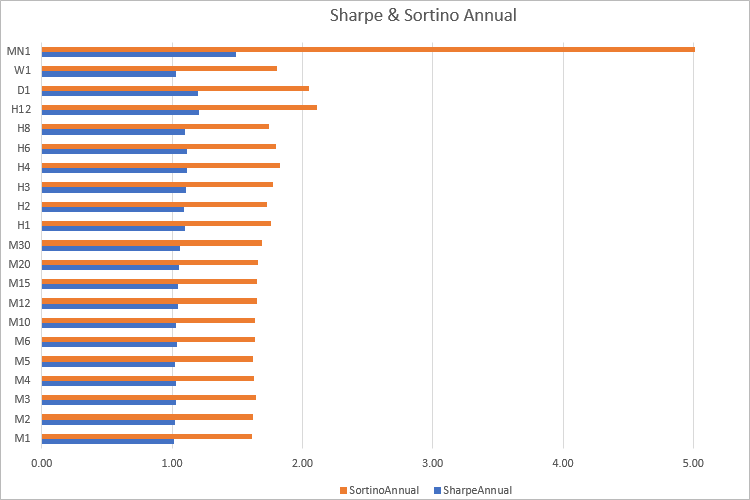
La diferencia entre los dos es que el Ratio de Sharpe muestra principalmente la volatilidad, mientras que el de Sortino realmente muestra el nivel de rendimiento por unidad de riesgo. Sin embargo, no debemos olvidar que todos estos cálculos se realizan usando como base la historia, y el hecho de que los indicadores tengan buenos valores no garantiza beneficios en el futuro.
Ejemplo de cálculo del ratio de Sharpe en el simulador de estrategias de MetaTrader 5
El ratio de Sharpe se desarrolló para valorar portafolios que contienen acciones. El precio de las acciones cambia todos los días, por consiguiente, el tamaño de los activos también cambiará a diario. Las estrategias comerciales por defecto no implican la presencia de posiciones abiertas, por lo que, parte del tiempo, el estado de la cuenta comercial permanecerá sin cambios. Esto significa que, en ausencia de posiciones abiertas, obtendremos un rendimiento cero, y el cálculo del ratio de Sharpe con dichos datos no será fiable. Por lo tanto, solo se deben tener en cuenta las barras en las que ha cambiado el estado de la cuenta comercial. La opción más adecuada sería eliminar los valores de equidad en cada último tick de la barra. Esto permitirá calcular el ratio de Sharpe para cualquier modo de generación de ticks en el simulador de estrategias de MetaTrader 5.
El segundo punto a considerar es que el incremento porcentual de los precios, que suele considerarse como Return[i]=(CloseCurrent-ClosePrevious)/ClosePrevious, tiene cierta desventaja en los cálculos. Es decir: si el precio ha disminuido un 5% y luego ha aumentado un 5%, entonces no obtendremos el valor original. Por lo tanto, en lugar del incremento de precio relativo habitual, los estudios estadísticos suelen usar el logaritmo del incremento de precio. El rendimiento logarítmico no tiene esta desventaja respecto al rendimiento lineal. Se calcula mediante la fórmula:
Log_Return =ln(Current/Previous) = ln(Current) — ln(Previous)
Los rendimientos logarítmicos son cómodos porque se pueden sumar, ya que la suma de los logaritmos es equivalente al producto de los rendimientos relativos.
De esta forma, el algoritmo de cálculo del ratio de Sharpe cambia mínimamente.
//--- calculamos los logaritmos de los incrementos de la matriz de equidad for(int i = 1; i < m_bars_counter; i++) { //--- añadimos solo si la equidad ha cambiado if(m_equities[i] != prev_equity) { log_return = MathLog(m_equities[i] / prev_equity); // algoritmo de incremento aver += log_return; // algoritmo medio de incrementos AddReturn(log_return); // rellenamos la matriz de algoritmos de incrementos counter++; // contador de rendimientos } prev_equity = m_equities[i]; } //--- si no hay valores suficientes para calcular el ratio de Sharpe, retornaremos 0 if(counter <= 1) return(0); //--- valor medio del logaritmo de incremento aver /= counter; //--- calculamos la desviación estándar for(int i = 0; i < counter; i++) std += (m_returns[i] - aver) * (m_returns[i] - aver); std /= counter; std = MathSqrt(std); //--- ratio de Sharpe en el marco temporal actual double sharpe = aver / std;
El código completo de cálculo se implementa como el archivo de inclusión Sharpe.mqh adjunto al artículo. Para calcular el ratio de Sharpe como criterio de optimización personalizado, conecte este archivo a su asesor experto y añada algunas líneas de código. Vamos a mostrar cómo hacerlo usando de ejemplo el asesor "MACD Sample.mq5" del paquete estándar de MetaTrader 5.
#define MACD_MAGIC 1234502 //--- #include <Trade\Trade.mqh> #include <Trade\SymbolInfo.mqh> #include <Trade\PositionInfo.mqh> #include <Trade\AccountInfo.mqh> #include "Sharpe.mqh" //--- input double InpLots = 0.1;// Lots input int InpTakeProfit = 50; // Take Profit (in pips) input int InpTrailingStop = 30; // Trailing Stop Level (in pips) input int InpMACDOpenLevel = 3; // MACD open level (in pips) input int InpMACDCloseLevel = 2; // MACD close level (in pips) input int InpMATrendPeriod = 26; // MA trend period //--- int ExtTimeOut = 10; // time out in seconds between trade operations CReturns returns; .... //+------------------------------------------------------------------+ //| Expert new tick handling function | //+------------------------------------------------------------------+ void OnTick(void) { static datetime limit_time = 0; // last trade processing time + timeout //--- añadimos la equidad actual a la matriz para calcular el ratio de Sharpe MqlTick tick; SymbolInfoTick(_Symbol, tick); returns.OnTick(tick.time, AccountInfoDouble(ACCOUNT_EQUITY)); //--- don't process if timeout if(TimeCurrent() >= limit_time) { //--- check for data if(Bars(Symbol(), Period()) > 2 * InpMATrendPeriod) { //--- change limit time by timeout in seconds if processed if(ExtExpert.Processing()) limit_time = TimeCurrent() + ExtTimeOut; } } } //+------------------------------------------------------------------+ //| Tester function | //+------------------------------------------------------------------+ double OnTester(void) { //--- calculamos el ratio de Sharpe double sharpe = returns.OnTester(); return(sharpe); } //+------------------------------------------------------------------+
Guardaremos el código resultante con el nuevo nombre "MACD Sample Sharpe.mq5"; también se adjunta al artículo.
Ejecutamos la optimización genética con EURUSD M10 para 2020, seleccionando el criterio de optimización personalizado.
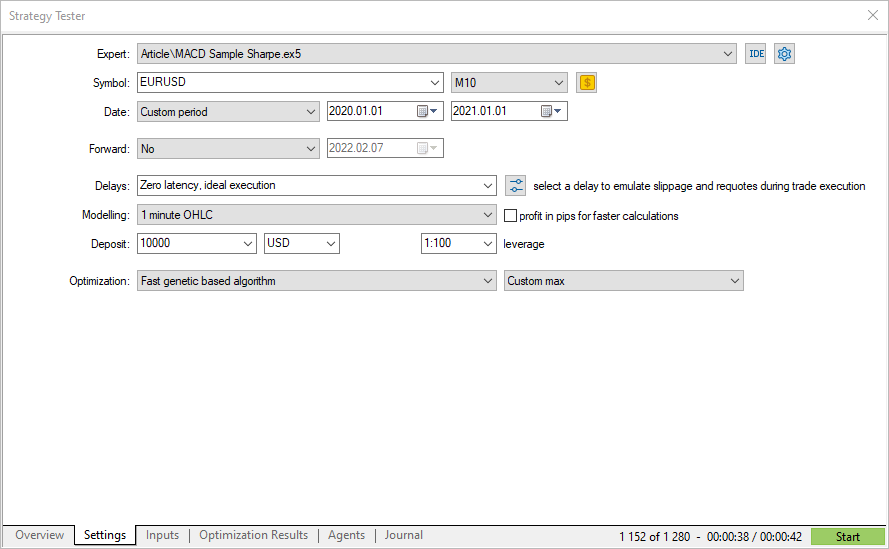
Los valores obtenidos del criterio personalizado coinciden con el ratio de Sharpe calculado por el simulador de estrategias. Ahora conocemos el mecanismo de cálculo y cómo interpretar los valores obtenidos.
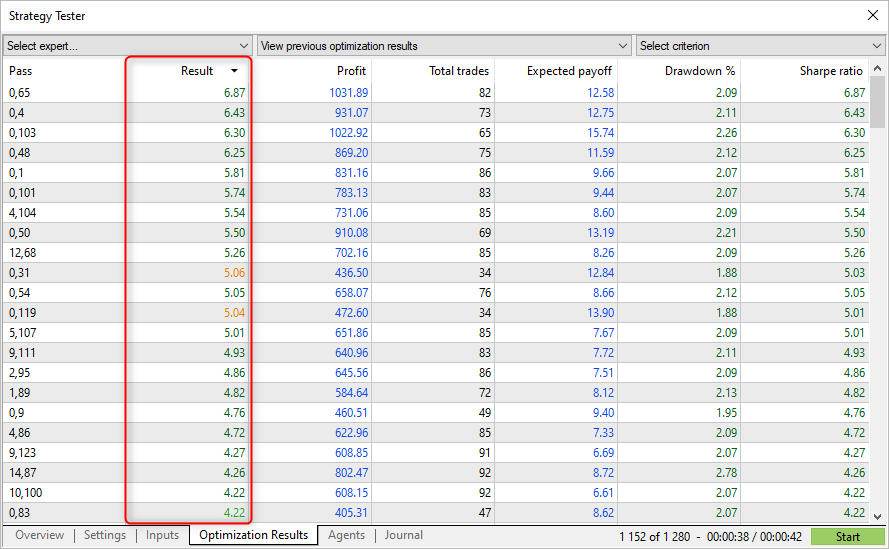
Las pasadas con el ratio de Sharpe máximo no siempre muestran los mayores beneficios en el simulador, pero nos permiten encontrar parámetros con un gráfico de equidad uniforme. En tales gráficos, por regla general, no existe un crecimiento brusco, pero tampoco hay grandes caídas ni reducciones en la equidad.
Por consiguiente, la optimización del ratio de Sharpe permite buscar parámetros más estables en comparación con otros criterios de optimización.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/9171
 Cómo desarrollar sistemas basados en medias móviles
Cómo desarrollar sistemas basados en medias móviles
 Múltiples indicadores en un gráfico (Parte 01): Entendiendo los conceptos
Múltiples indicadores en un gráfico (Parte 01): Entendiendo los conceptos
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso