La matematica nel trading: rapporti di Sharpe e Sortino
Il ritorno sugli investimenti è l'indicatore più ovvio che gli investitori e i trader principianti utilizzano per l'analisi dell'efficienza del trading. I trader professionisti utilizzano strumenti più affidabili per analizzare le strategie, come i rapporti di Sharpe e Sortino, tra gli altri. In questo articolo prenderemo in considerazione semplici esempi per capire come vengono calcolati questi rapporti. Le specifiche della valutazione delle strategie di trading sono state precedentemente considerate nell'articolo "La matematica nel trading. Come stimare i risultati di trading". Si consiglia di leggere l'articolo per aggiornare le conoscenze o per imparare qualcosa di nuovo.
Rapporto di Sharpe
Gli investitori e i trader esperti spesso utilizzano più strategie e investono in asset diversi nel tentativo di ottenere risultati costanti. Questo è uno dei concetti di investimento intelligente che implica la creazione di un portafoglio di investimenti. Ogni portafoglio di titoli/strategie ha i propri parametri di rischio e rendimento, che in qualche modo dovrebbero essere confrontati.
Uno degli strumenti più referenziati per tale confronto è il rapporto di Sharpe, sviluppato nel 1966 dal premio Nobel William F. Sharpe. Il calcolo del rapporto utilizza le metriche di performance di base, tra cui il tasso di rendimento medio, la deviazione standard del rendimento e il rendimento privo di rischio.
Lo svantaggio del rapporto di Sharpe è che i dati di origine utilizzati per l'analisi devono essere distribuiti normalmente. In altre parole, il grafico della distribuzione dei rendimenti dovrebbe essere simmetrico e non dovrebbe avere picchi o cali bruschi.
Il rapporto di Sharpe viene calcolato utilizzando la seguente formula:
Rapporto di Sharpe = (Rendimento - SenzaRischio)/Std
Dove:
- Rendimento — il tasso di rendimento medio per un certo periodo. Ad esempio, per un mese, trimestre, anno, ecc.
- SenzaRischio — tasso di rendimento privo di rischio per lo stesso periodo. Tradizionalmente, questi includono depositi bancari, obbligazioni e altre attività a rischio minimo con affidabilità del 100%.
- Std — deviazione standard dei rendimenti del portafoglio per lo stesso periodo. Maggiore è la deviazione dei rendimenti dal valore atteso, maggiore è il rischio e la volatilità sperimentata dal conto del trader o dalle attività del portafoglio.
Rendimento
Il rendimento è calcolato come variazione del valore delle attività in un certo intervallo. I valori di rendimento vengono utilizzati per lo stesso periodo di tempo per il quale viene calcolato il rapporto di Sharpe. Solitamente viene considerato il rapporto di Sharpe annuale, ma è anche possibile calcolare valori trimestrali, mensili o anche giornalieri. Il rendimento si calcola con la seguente formula:
Rendimento[i] = (Chiusura[i]-Chiusura[i-1])/Chiusura[i-1]
Dove:
- Rendimento[i] — Rendimento nell'intervallo i;
- Chiusura[i] — il valore delle attività alla fine dell'i-esimo intervallo;
- Chiusura[i-1] — il valore degli asset alla fine dell'intervallo precedente.
In altre parole, il rendimento può essere scritto come variazione relativa del valore delle attività nel periodo selezionato:
Rendimento[i] = Delta[i]/Precedente
Dove:
- Delta[i] = (Chiusura[i]-Chiusura[i-1]) — variazione assoluta del valore delle attività nel periodo selezionato;
- Precedente = Chiusura[i-1] — il valore delle attività alla fine dell'intervallo precedente.
Per calcolare il rapporto di Sharpe per un periodo di un anno utilizzando valori giornalieri, dobbiamo utilizzare i valori di rendimento per ogni giorno dell'anno e calcolare il rendimento giornaliero medio come somma dei rendimenti divisa per il numero di giorni del calcolo.
Rendimento = Somma(Rendimento[i])/N
dove N è il numero di giorni.
Rendimento privo di rischio
Il concetto di rendimento privo di rischio è condizionato, poiché c'è sempre un rischio. Poiché il rapporto di Sharpe viene utilizzato per confrontare diverse strategie/portafogli negli stessi intervalli di tempo, nella formula è possibile utilizzare il rendimento zero senza rischio. Cioè,
Senza rischio = 0
Deviazione standard o rendimento
La deviazione standard mostra come le variabili casuali si discostano da un valore medio. Innanzitutto, viene calcolato il valore medio del rendimento, quindi vengono sommate le deviazioni al quadrato dei rendimenti dal valore medio. La somma risultante viene divisa per il numero di rendimenti per ottenere la dispersione. La radice quadrata della dispersione è la deviazione standard.
D = Somma((Rendimento - Rendimento[i])^2 )/N
STD = SQRT(D)
Un esempio di calcolo della deviazione standard è fornito nell'articolo menzionato in precedenza.
Calcolare il rapporto di Sharpe su qualsiasi intervallo di tempo e convertirlo in un valore annuale
Il metodo di calcolo del rapporto di Sharpe non è cambiato dal 1966. La variabile ha ricevuto il suo nome moderno dopo che questa metodologia di calcolo è stata ampiamente riconosciuta. A quel tempo, le valutazioni della performance di fondi e portafogli si basavano sui rendimenti ottenuti in diversi anni. Successivamente, i calcoli sono stati effettuati sui dati mensili, mentre il rapporto di Sharpe risultante è stato mappato in un valore annuale.
Il rapporto di Sharpe può essere facilmente ricondotto da diversi periodi e timeframe a un valore annuale. Questo viene fatto moltiplicando il valore risultante per la radice quadrata del rapporto tra l'intervallo annuale e quello corrente. Consideriamo il seguente esempio.
Supponiamo di aver calcolato il rapporto di Sharpe utilizzando i valori di rendimento giornalieri — SharpeDaily. Il risultato deve essere convertito nel valore annuale SharpeAnnual. Il rapporto annuale è proporzionale alla radice quadrata del rapporto dei periodi, ovvero quanti intervalli giornalieri rientrano in un anno. Poiché ci sono 252 giorni lavorativi in un anno, il rapporto di Sharpe giornaliero basato sul rendimento dovrebbe essere moltiplicato per la radice quadrata di 252. Questo sarà il rapporto di Sharpe annuale:
SharpeAnnual = SQRT(252)*SharpeDaily // 252 giorni lavorativi in un anno
Se il valore viene calcolato in base all'intervallo di tempo H1, utilizziamo lo stesso principio: convertiamo prima SharpeHourly in SharpeDaily, quindi calcoliamo il rapporto di Sharpe annuale. Una barra D1 include 24 barre H1, motivo per cui la formula sarà la seguente:
SharpeDaily = SQRT(24)*SharpeHourly // 24 ore incluse in D1
Non tutti gli strumenti finanziari sono negoziati 24 ore su 24. Ma questo non è importante quando si valutano le strategie di trading nel tester per lo stesso strumento finanziario, poiché il confronto viene eseguito per lo stesso intervallo di test e lo stesso periodo di tempo.
Valutare le strategie utilizzando il rapporto di Sharpe
A seconda della strategia/performance del portafoglio, il rapporto di Sharpe può assumere valori diversi, anche negativi. La conversione del rapporto di Sharpe in un valore annuale ne consente l'interpretazione in modo classico: | Valore | Significato | Descrizione |
|---|---|---|
| Rapporto di Sharpe < 0 | Male | La strategia non è redditizia |
| 0 < Rapporto di Sharpe < 1.0 | Non definito | Il rischio non è ripagato. Tali strategie possono essere prese in considerazione quando non ci sono alternative |
| Rapporto di Sharpe ≥ 1.0 | Bene | Se il rapporto di Sharpe è maggiore di uno, ciò può significare che il rischio viene ripagato e che il portafoglio/la strategia può mostrare risultati positivi |
| Rapporto di Sharpe ≥ 3.0 | Molto bene | Un valore alto indica che la probabilità di ottenere una perdita in ogni singola operazione è molto bassa |
Non dimentichiamo che il coefficiente di Sharpe è una variabile statistica regolare. Riflette il rapporto tra rendimento e rischio. Pertanto, quando si analizzano diversi portafogli e strategie, è importante correlare il rapporto di Sharpe con i valori consigliati o confrontarlo con i valori rilevanti.
Calcolo del rapporto di Sharpe per EURUSD, 2020
Il rapporto di Sharpe è stato originariamente sviluppato per valutare portafogli che di solito sono costituiti da molti titoli. Il valore delle azioni cambia ogni giorno e il valore del portafoglio cambia di conseguenza. Una variazione del valore e dei rendimenti può essere misurata in qualsiasi lasso di tempo. Vediamo i calcoli per EURUSD.
I calcoli verranno eseguiti su due timeframe, H1 e D1. Quindi, convertiremo i risultati in valori annuali e li confronteremo per vedere se c'è una differenza. Per i calcoli utilizzeremo i prezzi di chiusura delle barre del 2020.
Codice in MQL5
//+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- double H1_close[],D1_close[]; double h1_returns[],d1_returns[]; datetime from = D'01.01.2020'; datetime to = D'01.01.2021'; int bars = CopyClose("EURUSD",PERIOD_H1,from,to,H1_close); if(bars == -1) Print("CopyClose(\"EURUSD\",PERIOD_H1,01.01.2020,01.01.2021 failed. Error ",GetLastError()); else { Print("\nCalculate the mean and standard deviation of returns on H1 bars"); Print("H1 bars=",ArraySize(H1_close)); GetReturns(H1_close,h1_returns); double average = ArrayMean(h1_returns); PrintFormat("H1 average=%G",average); double std = ArrayStd(h1_returns); PrintFormat("H1 std=%G",std); double sharpe_H1 = average / std; PrintFormat("H1 Sharpe=%G",sharpe_H1); double sharpe_annual_H1 = sharpe_H1 * MathSqrt(ArraySize(h1_returns)); Print("Sharpe_annual(H1)=", sharpe_annual_H1); } bars = CopyClose("EURUSD",PERIOD_D1,from,to,D1_close); if(bars == -1) Print("CopyClose(\"EURUSD\",PERIOD_D1,01.01.2020,01.01.2021 failed. Error ",GetLastError()); else { Print("\nCalculate the mean and standard deviation of returns on D1 bars"); Print("D1 bars=",ArraySize(D1_close)); GetReturns(D1_close,d1_returns); double average = ArrayMean(d1_returns); PrintFormat("D1 average=%G",average); double std = ArrayStd(d1_returns); PrintFormat("D1 std=%G",std); double sharpe_D1 = average / std; double sharpe_annual_D1 = sharpe_D1 * MathSqrt(ArraySize(d1_returns)); Print("Sharpe_annual(H1)=", sharpe_annual_D1); } } //+------------------------------------------------------------------+ //| Fills the returns[] array of returns | //+------------------------------------------------------------------+ void GetReturns(const double & values[], double & returns[]) { int size = ArraySize(values); //--- if less than 2 values, return an empty array of returns if(size < 2) { ArrayResize(returns,0); PrintFormat("%s: Error. ArraySize(values)=%d",size); return; } else { //--- fill returns in a loop ArrayResize(returns, size - 1); double delta; for(int i = 1; i < size; i++) { returns[i - 1] = 0; if(values[i - 1] != 0) { delta = values[i] - values[i - 1]; returns[i - 1] = delta / values[i - 1]; } } } //--- } //+------------------------------------------------------------------+ //| Calculates the average number of array elements | //+------------------------------------------------------------------+ double ArrayMean(const double & array[]) { int size = ArraySize(array); if(size < 1) { PrintFormat("%s: Error, array is empty",__FUNCTION__); return(0); } double mean = 0; for(int i = 0; i < size; i++) mean += array[i]; mean /= size; return(mean); } //+------------------------------------------------------------------+ //| Calculates the standard deviation of array elements | //+------------------------------------------------------------------+ double ArrayStd(const double & array[]) { int size = ArraySize(array); if(size < 1) { PrintFormat("%s: Error, array is empty",__FUNCTION__); return(0); } double mean = ArrayMean(array); double std = 0; for(int i = 0; i < size; i++) std += (array[i] - mean) * (array[i] - mean); std /= size; std = MathSqrt(std); return(std); } //+------------------------------------------------------------------+ /* Result Calculate the mean and standard deviation of returns on H1 bars H1 bars:6226 H1 average=1.44468E-05 H1 std=0.00101979 H1 Sharpe=0.0141664 Sharpe_annual(H1)=1.117708053392263 Calculate the mean and standard deviation of returns on D1 bars D1 bars:260 D1 average=0.000355823 D1 std=0.00470188 Sharpe_annual(H1)=1.2179005039019222 */
Codice Python per calcolare usando la Libreria MetaTrader 5
import math from datetime import datetime import MetaTrader5 as mt5 # display data on the MetaTrader 5 package print("MetaTrader5 package author: ", mt5.__author__) print("MetaTrader5 package version: ", mt5.__version__) # import the 'pandas' module for displaying data obtained in the tabular form import pandas as pd pd.set_option('display.max_columns', 50) # how many columns to show pd.set_option('display.width', 1500) # max width of the table to show # import pytz module for working with the time zone import pytz # establish connection to the MetaTrader 5 terminal if not mt5.initialize(): print("initialize() failed") mt5.shutdown() # set time zone to UTC timezone = pytz.timezone("Etc/UTC") # create datetime objects in the UTC timezone to avoid the local time zone offset utc_from = datetime(2020, 1, 1, tzinfo=timezone) utc_to = datetime(2020, 12, 31, hour=23, minute=59, second=59, tzinfo=timezone) # get EURUSD H1 bars in the interval 2020.01.01 00:00 - 2020.31.12 13:00 in the UTC timezone rates_H1 = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_H1, utc_from, utc_to) # also get D1 bars in the interval 2020.01.01 00:00 - 2020.31.12 13:00 in the UTC timezone rates_D1 = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_D1, utc_from, utc_to) # shut down connection to the MetaTrader 5 terminal and continue processing obtained bars mt5.shutdown() # create DataFrame out of the obtained data rates_frame = pd.DataFrame(rates_H1) # add the "Return" column rates_frame['return'] = 0.0 # now calculate the returns as return[i] = (close[i] - close[i-1])/close[i-1] prev_close = 0.0 for i, row in rates_frame.iterrows(): close = row['close'] rates_frame.at[i, 'return'] = close / prev_close - 1 if prev_close != 0.0 else 0.0 prev_close = close print("\nCalculate the mean and standard deviation of returns on H1 bars") print('H1 rates:', rates_frame.shape[0]) ret_average = rates_frame[1:]['return'].mean() # skip the first row with zero return print('H1 return average=', ret_average) ret_std = rates_frame[1:]['return'].std(ddof=0) # skip the first row with zero return print('H1 return std =', ret_std) sharpe_H1 = ret_average / ret_std print('H1 Sharpe = Average/STD = ', sharpe_H1) sharpe_annual_H1 = sharpe_H1 * math.sqrt(rates_H1.shape[0]-1) print('Sharpe_annual(H1) =', sharpe_annual_H1) # now calculate the Sharpe ratio on the D1 timeframe rates_daily = pd.DataFrame(rates_D1) # add the "Return" column rates_daily['return'] = 0.0 # calculate returns prev_return = 0.0 for i, row in rates_daily.iterrows(): close = row['close'] rates_daily.at[i, 'return'] = close / prev_return - 1 if prev_return != 0.0 else 0.0 prev_return = close print("\nCalculate the mean and standard deviation of returns on D1 bars") print('D1 rates:', rates_daily.shape[0]) daily_average = rates_daily[1:]['return'].mean() print('D1 return average=', daily_average) daily_std = rates_daily[1:]['return'].std(ddof=0) print('D1 return std =', daily_std) sharpe_daily = daily_average / daily_std print('D1 Sharpe =', sharpe_daily) sharpe_annual_D1 = sharpe_daily * math.sqrt(rates_daily.shape[0]-1) print('Sharpe_annual(D1) =', sharpe_annual_D1) Result Calculate the mean and standard deviation of returns on H1 bars H1 rates: 6226 H1 return average= 1.4446773215242986e-05 H1 return std = 0.0010197932969323495 H1 Sharpe = Average/STD = 0.014166373968823358 Sharpe_annual(H1) = 1.117708053392236 Calculate the mean and standard deviation of returns on D1 bars D1 rates: 260 D1 return average= 0.0003558228355051694 D1 return std = 0.004701883757646081 D1 Sharpe = 0.07567665511222807 Sharpe_annual(D1) = 1.2179005039019217
Come puoi vedere, i risultati del calcolo MQL5 e Python sono gli stessi. I codici sorgente sono allegati di seguito (CalculateSharpe_2TF).
I rapporti di Sharpe annuali calcolati dalle barre H1 e D1 differiscono: 1,117708 e 1,217900, rispettivamente. Proviamo a scoprire il motivo.
Calcolo del rapporto di Sharpe annuale su EURUSD per il 2020 su tutti i timeframe
Ora, calcoliamo il rapporto di Sharpe annuale su tutti i timeframe. Per fare ciò, raccogliamo i dati ottenuti in una tabella:
- TF — timeframe
- Minutes — numero di minuti in un timeframe
- Rates — numero di barre all'anno in questo timeframe
- Avg — rendimento medio per barra sul timeframe in percentuale (percentuale di variazione media del prezzo per barra)
- Std — deviazione standard per barra sul timeframe in percentuale (percentuale di volatilità del prezzo in questo timeframe)
- SharpeTF — Rapporto di Sharpe calcolato in base a un determinato timeframe
- SharpeAnnual — rapporto di Sharpe annuale calcolato in base al rapporto di Sharpe di questo timeframe
Di seguito è riportato il blocco del codice di calcolo. Il codice completo è disponibile nel file CalculateSharpe_All_TF.mq5 allegato all'articolo.
//--- structure to print statistics to log struct Stats { string TF; int Minutes; int Rates; double Avg; double Std; double SharpeTF; double SharpeAnnual; }; //--- array of statistics by timeframes Stats stats[]; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- arrays for close prices double H1_close[],D1_close[]; //--- arrays of returns double h1_returns[],d1_returns[]; //--- arrays of timeframes on which the Sharpe coefficient will be calculated ENUM_TIMEFRAMES timeframes[] = {PERIOD_M1,PERIOD_M2,PERIOD_M3,PERIOD_M4,PERIOD_M5, PERIOD_M6,PERIOD_M10,PERIOD_M12,PERIOD_M15,PERIOD_M20, PERIOD_M30,PERIOD_H1,PERIOD_H2,PERIOD_H3,PERIOD_H4, PERIOD_H6,PERIOD_H8,PERIOD_H12,PERIOD_D1,PERIOD_W1,PERIOD_MN1 }; ArrayResize(stats,ArraySize(timeframes)); //--- timeseries request parameters string symbol = Symbol(); datetime from = D'01.01.2020'; datetime to = D'01.01.2021'; Print(symbol); for(int i = 0; i < ArraySize(timeframes); i++) { //--- get the array of returns on the specified timeframe double returns[]; GetReturns(symbol,timeframes[i],from,to,returns); //--- calculate statistics GetStats(returns,avr,std,sharpe); double sharpe_annual = sharpe * MathSqrt(ArraySize(returns)); PrintFormat("%s aver=%G%% std=%G%% sharpe=%G sharpe_annual=%G", EnumToString(timeframes[i]), avr * 100,std * 100,sharpe,sharpe_annual); //--- fill the statistics structure Stats row; string tf_str = EnumToString(timeframes[i]); StringReplace(tf_str,"PERIOD_",""); row.TF = tf_str; row.Minutes = PeriodSeconds(timeframes[i]) / 60; row.Rates = ArraySize(returns); row.Avg = avr; row.Std = std; row.SharpeTF = sharpe; row.SharpeAnnual = sharpe_annual; //--- add a row for the timeframe statistics stats[i] = row; } //--- print statistics on all timeframes to log ArrayPrint(stats,8); } /* Result [TF] [Minutes] [Rates] [Avg] [Std] [SharpeTF] [SharpeAnnual] [ 0] "M1" 1 373023 0.00000024 0.00168942 0.00168942 1.03182116 [ 1] "M2" 2 186573 0.00000048 0.00239916 0.00239916 1.03629642 [ 2] "M3" 3 124419 0.00000072 0.00296516 0.00296516 1.04590258 [ 3] "M4" 4 93302 0.00000096 0.00341717 0.00341717 1.04378592 [ 4] "M5" 5 74637 0.00000120 0.00379747 0.00379747 1.03746116 [ 5] "M6" 6 62248 0.00000143 0.00420265 0.00420265 1.04854166 [ 6] "M10" 10 37349 0.00000239 0.00542100 0.00542100 1.04765562 [ 7] "M12" 12 31124 0.00000286 0.00601079 0.00601079 1.06042363 [ 8] "M15" 15 24900 0.00000358 0.00671964 0.00671964 1.06034161 [ 9] "M20" 20 18675 0.00000477 0.00778573 0.00778573 1.06397070 [10] "M30" 30 12450 0.00000716 0.00966963 0.00966963 1.07893298 [11] "H1" 60 6225 0.00001445 0.01416637 0.01416637 1.11770805 [12] "H2" 120 3115 0.00002880 0.01978455 0.01978455 1.10421905 [13] "H3" 180 2076 0.00004305 0.02463458 0.02463458 1.12242890 [14] "H4" 240 1558 0.00005746 0.02871564 0.02871564 1.13344977 [15] "H6" 360 1038 0.00008643 0.03496339 0.03496339 1.12645075 [16] "H8" 480 779 0.00011508 0.03992838 0.03992838 1.11442404 [17] "H12" 720 519 0.00017188 0.05364323 0.05364323 1.22207717 [18] "D1" 1440 259 0.00035582 0.07567666 0.07567666 1.21790050 [19] "W1" 10080 51 0.00193306 0.14317328 0.14317328 1.02246174 [20] "MN1" 43200 12 0.00765726 0.43113365 0.43113365 1.49349076 */
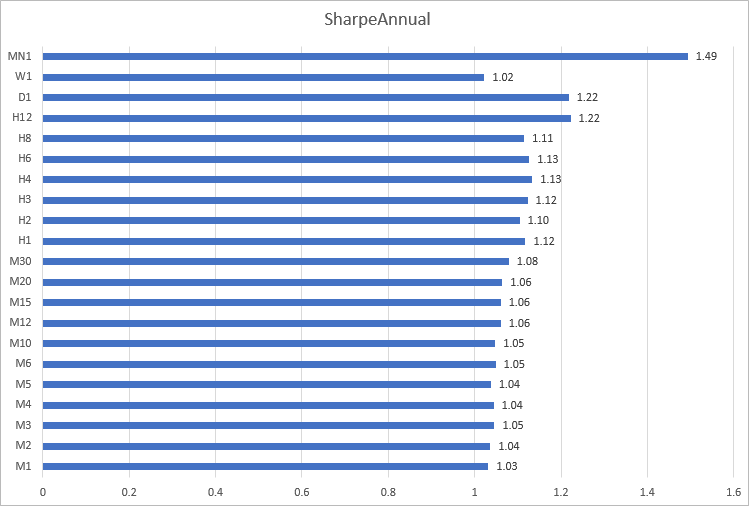
Costruiamo un istogramma del rapporto di Sharpe su EURUSD per il 2020 sui diversi timeframe. Si può notare qui che i calcoli sui timeframe, da M1 a M30, danno risultati ravvicinati: da 1,03 a 1,08. I risultati più incoerenti sono stati ottenuti su intervalli di tempo da H12 a MN1.
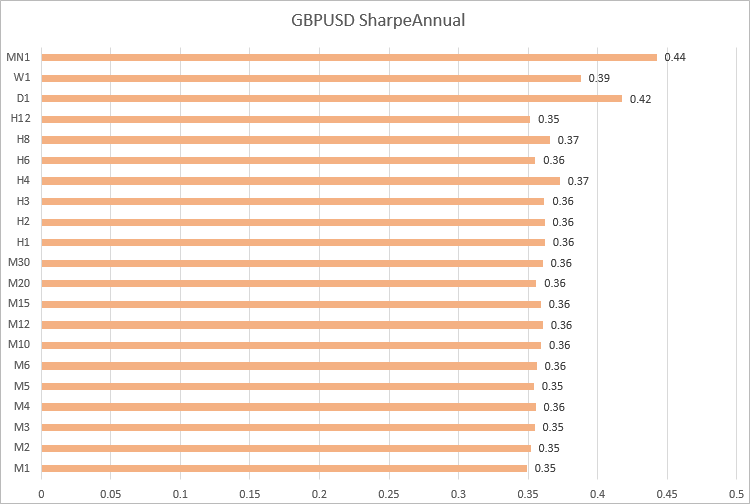
Calcolo del rapporto di Sharpe per GBPUSD, USDJPY e USDCHF per il 2020
LEseguiamo calcoli simili per altre tre coppie di valute.
GBPUSD, i valori del rapporto di Sharpe sono simili su timeframe da M1 a H12.
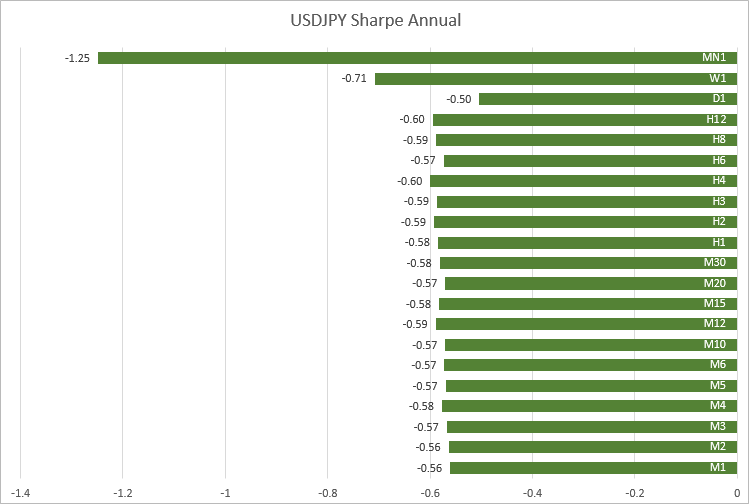
USDJPY, i valori sono vicini anche sui timeframe da M1 a H12: da -0,56 a -0,60.
USDCHF, valori simili sono stati ottenuti sui timeframe da M1 a M30. All'aumentare del tempo, il rapporto di Sharpe fluttua.
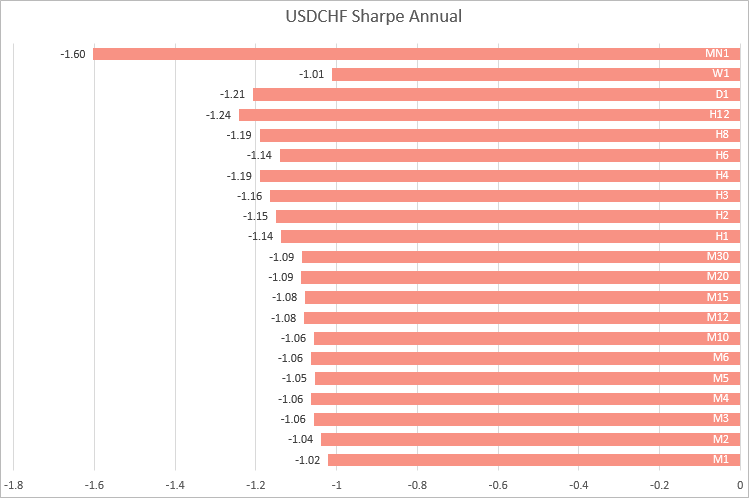
Pertanto, sulla base degli esempi di quattro delle maggiori coppie di valute, possiamo concludere che i calcoli più stabili del rapporto di Sharpe si ottengono su timeframe da M1 a M30. Ciò significa che è meglio calcolare il rapporto utilizzando i rendimenti dei timeframe più bassi, quando si vogliono confrontare strategie che lavorano su simboli diversi.
Calcolo del rapporto di Sharpe annuale su EURUSD per il 2020 in mesi
Usiamo i rendimenti mensili di ogni mese del 2020 e calcoliamo il rapporto di Sharpe annuale su timeframe da M1 a H1. Il codice completo dello script CalculateSharpe_Months.mq5 è allegato all'articolo.
//--- structure to store returns struct Return { double ret; // return datetime time; // date int month; // month }; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { SharpeMonths sharpe_by_months[]; //--- arrays of timeframes on which the Sharpe coefficient will be calculated ENUM_TIMEFRAMES timeframes[] = {PERIOD_M1,PERIOD_M2,PERIOD_M3,PERIOD_M4,PERIOD_M5, PERIOD_M6,PERIOD_M10,PERIOD_M12,PERIOD_M15,PERIOD_M20, PERIOD_M30,PERIOD_H1 }; ArrayResize(sharpe_by_months,ArraySize(timeframes)); //--- timeseries request parameters string symbol = Symbol(); datetime from = D'01.01.2020'; datetime to = D'01.01.2021'; Print("Calculate Sharpe Annual on ",symbol, " for 2020 year"); for(int i = 0; i < ArraySize(timeframes); i++) { //--- get the array of returns on the specified timeframe Return returns[]; GetReturns(symbol,timeframes[i],from,to,returns); double avr,std,sharpe; //--- Calculate statistics for the year GetStats(returns,avr,std,sharpe); string tf_str = EnumToString(timeframes[i]); //--- calculate the annual Sharpe ratio for each month SharpeMonths sharpe_months_on_tf; sharpe_months_on_tf.SetTimeFrame(tf_str); //--- select returns for i-th month for(int m = 1; m <= 12; m++) { Return month_returns[]; GetReturnsByMonth(returns,m,month_returns); //--- Calculate statistics for the year double sharpe_annual = CalculateSharpeAnnual(timeframes[i],month_returns); sharpe_months_on_tf.Sharpe(m,sharpe_annual); } //--- add Sharpe ratio for 12 months on timeframe i sharpe_by_months[i] = sharpe_months_on_tf; } //--- display the table of annual Sharpe values by months on all timeframes ArrayPrint(sharpe_by_months,3); } /* Result Calculate Sharpe Annual on EURUSD for 2020 year [TF] [Jan] [Feb] [Marc] [Apr] [May] [June] [July] [Aug] [Sept] [Oct] [Nov] [Dec] [ 0] "PERIOD_M1" -2.856 -1.340 0.120 -0.929 2.276 1.534 6.836 2.154 -2.697 -1.194 3.891 4.140 [ 1] "PERIOD_M2" -2.919 -1.348 0.119 -0.931 2.265 1.528 6.854 2.136 -2.717 -1.213 3.845 4.125 [ 2] "PERIOD_M3" -2.965 -1.340 0.118 -0.937 2.276 1.543 6.920 2.159 -2.745 -1.212 3.912 4.121 [ 3] "PERIOD_M4" -2.980 -1.341 0.119 -0.937 2.330 1.548 6.830 2.103 -2.765 -1.219 3.937 4.110 [ 4] "PERIOD_M5" -2.929 -1.312 0.120 -0.935 2.322 1.550 6.860 2.123 -2.729 -1.239 3.971 4.076 [ 5] "PERIOD_M6" -2.945 -1.364 0.119 -0.945 2.273 1.573 6.953 2.144 -2.768 -1.239 3.979 4.082 [ 6] "PERIOD_M10" -3.033 -1.364 0.119 -0.934 2.361 1.584 6.789 2.063 -2.817 -1.249 4.087 4.065 [ 7] "PERIOD_M12" -2.952 -1.358 0.118 -0.956 2.317 1.609 6.996 2.070 -2.933 -1.271 4.115 4.014 [ 8] "PERIOD_M15" -3.053 -1.367 0.118 -0.945 2.377 1.581 7.132 2.078 -2.992 -1.274 4.029 4.047 [ 9] "PERIOD_M20" -2.998 -1.394 0.117 -0.920 2.394 1.532 6.884 2.065 -3.010 -1.326 4.074 4.040 [10] "PERIOD_M30" -3.008 -1.359 0.116 -0.957 2.379 1.585 7.346 2.084 -2.934 -1.323 4.139 4.034 [11] "PERIOD_H1" -2.815 -1.373 0.116 -0.966 2.398 1.601 7.311 2.221 -3.136 -1.374 4.309 4.284 */
Si può notare che i valori del rapporto annuale per ogni mese sono molto vicini su tutti i timeframe su cui abbiamo eseguito i calcoli. Per una migliore presentazione, eseguiamo il rendering dei risultati come una superficie 3D utilizzando un diagramma di Excel.
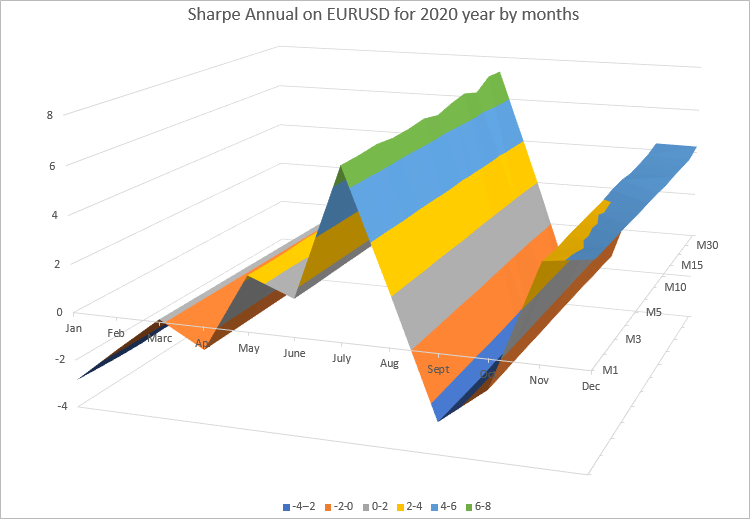
Il diagramma mostra chiaramente che i valori del rapporto di Sharpe annuale cambiano ogni mese. Dipende da come EURUSD variava in questo mese. D'altra parte, il rapporto di Sharpe annuale per ogni mese su tutti i timeframe quasi non cambia.
Pertanto, il rapporto di Sharpe annuale può essere calcolato su qualsiasi timeframe, mentre il valore risultante dipende anche dal numero di barre su cui sono stati ottenuti i rendimenti. Significa che questo algoritmo di calcolo può essere utilizzato per test, ottimizzazione e monitoraggio in tempo reale. L'unico prerequisito è avere una matrice sufficientemente ampia di rendimenti.
Rapporto di Sortino
Nel calcolo del rapporto di Sharpe, il rischio è la piena volatilità delle quotazioni delle attività, sia in aumento che in diminuzione. Ma l'aumento del valore del portafoglio è positivo per l'investitore, mentre la perdita è legata solo alla sua diminuzione. Pertanto, il rischio effettivo nel rapporto è sopravvalutato. Il rapporto di Sortino sviluppato all'inizio degli anni '90 da Frank Sortino affronta questo problema.
Come i suoi predecessori, F. Sortino considera il rendimento futuro come una variabile casuale pari alla sua aspettativa matematica, mentre il rischio è considerato una varianza. Il rendimento e il rischio sono determinati sulla base delle quotazioni storiche in un determinato periodo. Come nel calcolo del rapporto di Sharpe, il rendimento è diviso per il rischio.
Sortino ha osservato che il rischio definito come la varianza totale dei rendimenti (o la piena volatilità) dipende sia da variazioni positive che negative. Sortino ha sostituito la volatilità complessiva totale con la semi-volatilità che considera solo una diminuzione degli asset. La semi-volatilità viene anche definita volatilità dannosa, rischio al ribasso, deviazione al ribasso, volatilità negativa o deviazione standard al ribasso.
Il calcolo del rapporto Sortino è simile a quello di Sharpe, con l'unica differenza che i rendimenti positivi sono esclusi dal calcolo della volatilità. Ciò riduce la misura del rischio e aumenta il peso del rapporto.
Esempio di codice che calcola il rapporto di Sortino in base al rapporto di Sharpe. La semidispersione viene calcolata solo utilizzando rendimenti negativi.
//+------------------------------------------------------------------+ //| Calculates Sharpe and Sortino ratios | //+------------------------------------------------------------------+ void GetStats(ENUM_TIMEFRAMES timeframe, const double & returns[], double & avr, double & std, double & sharpe, double & sortino) { avr = ArrayMean(returns); std = ArrayStd(returns); sharpe = (std == 0) ? 0 : avr / std; //--- now, remove negative returns and calculate the Sortino ratio double negative_only[]; int size = ArraySize(returns); ArrayResize(negative_only,size); ZeroMemory(negative_only); //--- copy only negative returns for(int i = 0; i < size; i++) negative_only[i] = (returns[i] > 0) ? 0 : returns[i]; double semistd = ArrayStd(negative_only); sortino = avr / semistd; return; }
Lo script CalculateSortino_All_TF.mq5 allegato a questo articolo genera i seguenti risultati su EURUSD, per il 2020:
[TF] [Minutes] [Rates] [Avg] [Std] [SharpeAnnual] [SortinoAnnual] [Ratio] [ 0] "M1" 1 373023 0.00000024 0.00014182 1.01769617 1.61605380 1.58795310 [ 1] "M2" 2 186573 0.00000048 0.00019956 1.02194170 1.62401856 1.58914991 [ 2] "M3" 3 124419 0.00000072 0.00024193 1.03126142 1.64332243 1.59350714 [ 3] "M4" 4 93302 0.00000096 0.00028000 1.02924195 1.62618200 1.57998030 [ 4] "M5" 5 74637 0.00000120 0.00031514 1.02303684 1.62286584 1.58632199 [ 5] "M6" 6 62248 0.00000143 0.00034122 1.03354379 1.63789024 1.58473231 [ 6] "M10" 10 37349 0.00000239 0.00044072 1.03266766 1.63461839 1.58290848 [ 7] "M12" 12 31124 0.00000286 0.00047632 1.04525580 1.65215986 1.58062730 [ 8] "M15" 15 24900 0.00000358 0.00053223 1.04515816 1.65256608 1.58116364 [ 9] "M20" 20 18675 0.00000477 0.00061229 1.04873529 1.66191269 1.58468272 [10] "M30" 30 12450 0.00000716 0.00074023 1.06348332 1.68543441 1.58482449 [11] "H1" 60 6225 0.00001445 0.00101979 1.10170316 1.75890688 1.59653431 [12] "H2" 120 3115 0.00002880 0.00145565 1.08797046 1.73062372 1.59068999 [13] "H3" 180 2076 0.00004305 0.00174762 1.10608991 1.77619289 1.60583048 [14] "H4" 240 1558 0.00005746 0.00200116 1.11659184 1.83085734 1.63968362 [15] "H6" 360 1038 0.00008643 0.00247188 1.11005321 1.79507001 1.61710267 [16] "H8" 480 779 0.00011508 0.00288226 1.09784908 1.74255746 1.58724682 [17] "H12" 720 519 0.00017188 0.00320405 1.20428761 2.11045830 1.75245371 [18] "D1" 1440 259 0.00035582 0.00470188 1.20132966 2.04624198 1.70331429 [19] "W1" 10080 51 0.00193306 0.01350157 1.03243721 1.80369984 1.74703102 [20] "MN1" 43200 12 0.00765726 0.01776075 1.49349076 5.00964481 3.35431926
Si può vedere che in quasi tutti i timeframe il valore di Sortino è 1,60 volte il rapporto di Sharpe. Naturalmente, non ci sarà una dipendenza così chiara nel calcolo dei rapporti in base ai risultati di trading. Pertanto, ha senso confrontare strategie/portafogli utilizzando entrambi i rapporti.
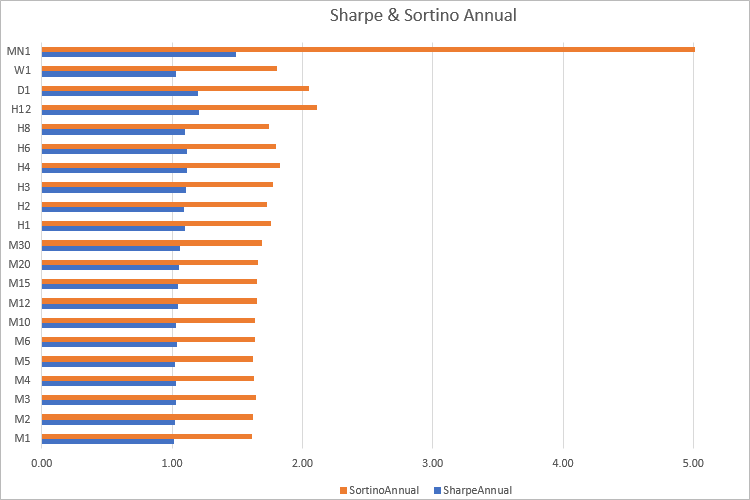
La differenza tra queste due metriche è che il rapporto di Sharpe riflette principalmente la volatilità, mentre il rapporto di Sortino mostra davvero il rapporto o il rendimento per unità di rischio. Non dimentichiamo però che i calcoli vengono eseguiti in base alla storia, quindi buoni risultati non possono garantire profitti futuri.
Esempio di calcolo del rapporto di Sharpe nel Tester di strategia MetaTrader 5
Il rapporto di Sharpe è stato originariamente sviluppato per valutare i portafogli contenenti azioni. I prezzi delle azioni cambiano ogni giorno, e quindi anche il valore degli asset cambia ogni giorno. Per impostazione predefinita, le strategie di trading non implicano l'esistenza di posizioni aperte, quindi per parte del tempo lo stato di un conto di trading rimarrà invariato. Significa che quando non ci sono posizioni aperte, riceveremo valori zero di rendimento, e quindi i calcoli di Sharpe saranno sbagliati per loro. Pertanto, i calcoli utilizzeranno solo le barre su cui è cambiato lo stato del conto di trading. L'opzione più adatta è analizzare i valori azionari sull'ultimo tick di ciascuna barra. Ciò consentirà il calcolo del rapporto di Sharpe con qualsiasi modalità di generazione tick nel tester di strategia MetaTrader 5.
Un altro punto da tenere in considerazione è che l'incremento percentuale del prezzo, che di solito viene calcolato come Rendimento[i]=(ChiusuraCorrente-ChiusuraPrecedente)/ChiusuraPrecedente, presenta un certo svantaggio nei calcoli. È il seguente: se il prezzo scende del 5% e poi cresce del 5%, non otterremo il valore iniziale. Ecco perché, invece del consueto incremento del prezzo relativo, gli studi statistici di solito utilizzano il logaritmo dell'incremento del prezzo. I rendimenti logaritmici (rendimenti logaritmici) non presentano questo svantaggio dei rendimenti lineari. Il valore è calcolato come segue:
Log_Return =ln(Corrente/Precedente) = ln(Corrente) — ln(Precedente)
I rendimenti logaritmici sono convenienti perché possono essere sommati poiché la somma dei logaritmi è equivalente al prodotto dei rendimenti relativi.
Quindi, l'algoritmo di calcolo del rapporto di Sharpe necessita di regolazioni minime.
//--- calculate the logarithms of increments using the equity array for(int i = 1; i < m_bars_counter; i++) { //--- only add if equity has changed if(m_equities[i] != prev_equity) { log_return = MathLog(m_equities[i] / prev_equity); // increment logarithm aver += log_return; // average logarithm of increments AddReturn(log_return); // fill the array of increment logarithms counter++; // counter of returns } prev_equity = m_equities[i]; } //--- if values are not enough for Sharpe calculation, return 0 if(counter <= 1) return(0); //--- average value of the increment logarithm aver /= counter; //--- calculate standard deviation for(int i = 0; i < counter; i++) std += (m_returns[i] - aver) * (m_returns[i] - aver); std /= counter; std = MathSqrt(std); //--- Sharpe ratio on the current timeframe double sharpe = aver / std;
Il codice di calcolo completo è implementato come file inclusivo Sharpe.mqh che è allegato all'articolo. Per calcolare il rapporto di Sharpe come criterio di ottimizzazione personalizzato, collega questo file al tuo Expert Advisor e aggiungi alcune righe di codice. Vediamo come farlo utilizzando il MACD Sample.mq5 EA del pacchetto standard MetaTrader 5 come esempio.
#define MACD_MAGIC 1234502 //--- #include <Trade\Trade.mqh> #include <Trade\SymbolInfo.mqh> #include <Trade\PositionInfo.mqh> #include <Trade\AccountInfo.mqh> #include "Sharpe.mqh" //--- input double InpLots = 0.1;// Lots input int InpTakeProfit = 50; // Take Profit (in pips) input int InpTrailingStop = 30; // Trailing Stop Level (in pips) input int InpMACDOpenLevel = 3; // MACD open level (in pips) input int InpMACDCloseLevel = 2; // MACD close level (in pips) input int InpMATrendPeriod = 26; // MA trend period //--- int ExtTimeOut = 10; // time out in seconds between trade operations CReturns returns; .... //+------------------------------------------------------------------+ //| Expert new tick handling function | //+------------------------------------------------------------------+ void OnTick(void) { static datetime limit_time = 0; // last trade processing time + timeout //--- add current equity to the array to calculate the Sharpe ratio MqlTick tick; SymbolInfoTick(_Symbol, tick); returns.OnTick(tick.time, AccountInfoDouble(ACCOUNT_EQUITY)); //--- don't process if timeout if(TimeCurrent() >= limit_time) { //--- check for data if(Bars(Symbol(), Period()) > 2 * InpMATrendPeriod) { //--- change limit time by timeout in seconds if processed if(ExtExpert.Processing()) limit_time = TimeCurrent() + ExtTimeOut; } } } //+------------------------------------------------------------------+ //| Tester function | //+------------------------------------------------------------------+ double OnTester(void) { //--- calculate Sharpe ratio double sharpe = returns.OnTester(); return(sharpe); } //+------------------------------------------------------------------+
Salva il codice risultante come "MACD Sample Sharpe.mq5" - anche il file pertinente è allegato di seguito.
Eseguiamo un'ottimizzazione genetica per EURUSD M10 2020, selezionando un criterio di ottimizzazione personalizzato.
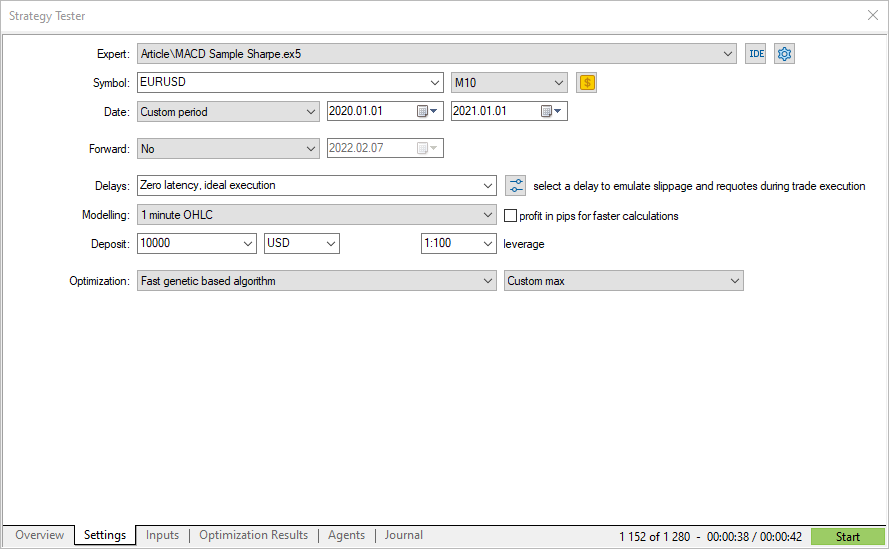
I valori del criterio personalizzato ottenuti coincidono con il rapporto di Sharpe calcolato dal tester della strategia. Ora conosci i meccanismi di calcolo e come interpretare i risultati ottenuti.
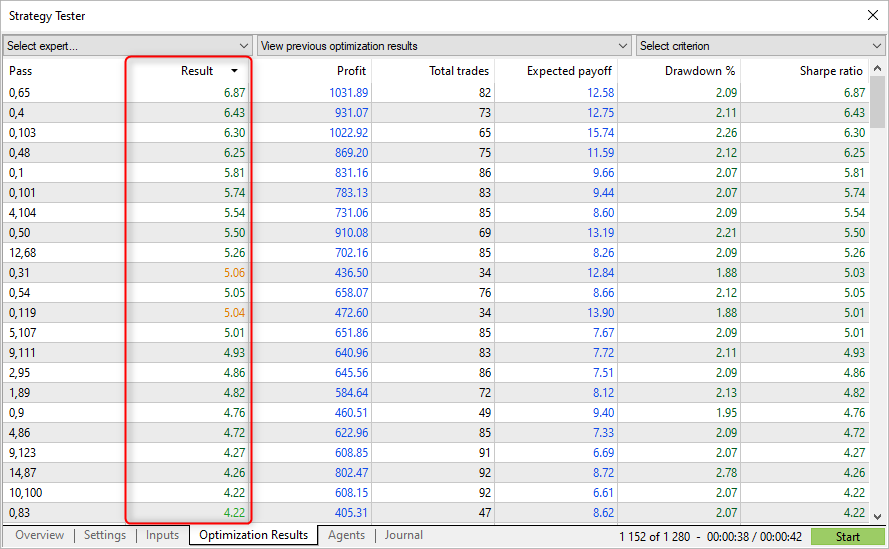
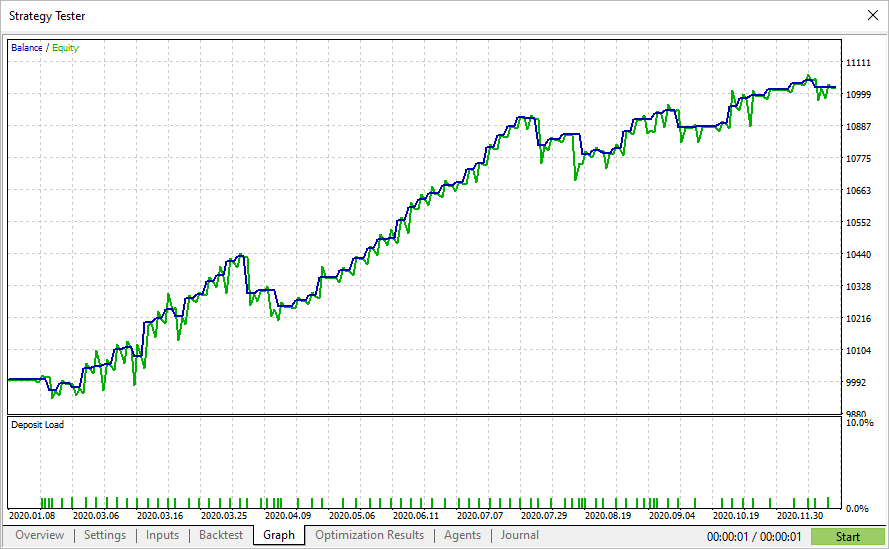
I passaggi con il rapporto di Sharpe più alto non mostrano sempre il profitto più alto nel tester, ma consentono di trovare parametri con un grafico di equità uniforme. Tali grafici di solito non mostrano una forte crescita, ma non ci sono nemmeno grandi cali e drawdown dell'equity.
Significa che utilizzando l'ottimizzazione con il rapporto di Sharpe, è possibile trovare parametri più stabili, rispetto ad altri criteri di ottimizzazione.
Vantaggi e svantaggi
I rapporti di Sharpe e Sortino consentono di determinare se il profitto ricevuto copre o meno il rischio associato. Un altro vantaggio rispetto a misure di rischio alternative è che i calcoli possono essere applicati a tutti i tipi di attività. Ad esempio, puoi confrontare l'oro con l'argento utilizzando il rapporto di Sharpe perché non richiede un benchmark esterno specifico per essere valutato. Pertanto, i rapporti possono essere applicati a singole strategie o titoli, nonché a portafogli di attività o strategie.
Lo svantaggio di questi strumenti è che il calcolo presuppone una distribuzione normale dei rendimenti. In realtà, questo requisito è raramente soddisfatto. Tuttavia, i rapporti di Sharpe e Sortino sono gli strumenti più semplici e comprensibili che consentono il confronto di diverse strategie e portafogli.
Tradotto dal russo da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/ru/articles/9171
 Programmatore migliore (Parte 05): Come diventare uno sviluppatore più veloce
Programmatore migliore (Parte 05): Come diventare uno sviluppatore più veloce
 Programmatore Migliore (Parte 04): Come diventare uno sviluppatore più veloce
Programmatore Migliore (Parte 04): Come diventare uno sviluppatore più veloce
 Programmatore Migliore (Parte 06): 9 abitudini che portano a una codifica efficace
Programmatore Migliore (Parte 06): 9 abitudini che portano a una codifica efficace
 Programmatore migliore (Parte 03): Rinuncia a fare queste 5 cose per diventare un Programmatore MQL5 di successo
Programmatore migliore (Parte 03): Rinuncia a fare queste 5 cose per diventare un Programmatore MQL5 di successo
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso