Ticarette matematik: Sharpe ve Sortino oranları

Yatırım getirisi, yatırımcıların ticaret performansını analiz etmek için kullandıkları en belirgin göstergedir. Profesyonel yatırımcılar, strateji analizi için Sharpe ve Sortino oranları gibi daha güvenilir araçlar kullanır. Bu yazımızda bu oranların nasıl hesaplandığını anlamak için basit örnekleri ele alacağız. Ticaret stratejilerini değerlendirme konusu, daha önceki "Ticarette matematik. Ticaret sonuçları nasıl değerlendirilir?" başlıklı makalede ele alınmıştı. Bilginizi tazelemek veya kendiniz için yeni şeyler öğrenmek adına bu makaleyi okumanızı tavsiye ederiz.

Sharpe oranı

Deneyimli yatırımcılar, tutarlı sonuçlar elde etmek için genellikle birden fazla stratejiyle ve farklı varlıklarla ticaret yapar. Bu, bir yatırım portföyünün oluşturulmasının gerekliliğini vurgulayan akıllı yatırım kavramlarından biridir. Her strateji/varlık portföyünün, bir şekilde kıyaslanmaları gereken kendi risk ve getiri parametreleri vardır.

Bu tür karşılaştırmalar için en çok başvurulan araçlardan biri, Nobel ödüllü William F. Sharpe tarafından 1966 yılında geliştirilen Sharpe oranıdır. Sharpe oranının hesaplamasındaki ana ölçümler ortalama getiri oranı, getirinin standart sapması ve risksiz getiri oranıdır.

Sharpe oranının dezavantajı, analiz için kullanılan kaynak verilerin normal olarak dağıtılması gerektiğidir. Diğer bir deyişle, getiri dağılım grafiği simetrik olmalı, keskin pikler veya dipler içermemelidir.

Sharpe oranı şu formül kullanılarak hesaplanır:

Sharpe Ratio = (Return - RiskFree)/Std

Tanımlamalar:

• Return - belirli bir dönemdeki ortalama getiri oranı. Örneğin, bir ay, bir çeyrek, bir yıl vb.
  
• RiskFree — aynı dönemdeki risksiz getiri oranı. Bu, minimum risk ve %100 güvenilirliğe sahip banka mevduatları, tahviller vb. varlıklar üzerindeki faiz olabilir.
  
• Std - aynı dönemdeki portföy getirilerinin standart sapması. Getirilerdeki fark ne kadar fazla olursa, yatırımcının hesap veya portföy varlıklarının maruz kaldığı risk ve volatilite de o kadar yüksek olur.
  

Getiri

Getiri, belirli bir aralıkta varlıkların değerinde meydana gelen değişim olarak hesaplanır. Sharpe oranının hesaplandığı aynı zaman aralığındaki getiri değerleri kullanılır. Genellikle yıllık Sharpe oranı değerlendirilir, ancak çeyreklik, aylık ve hatta günlük değerleri hesaplamak da mümkündür. Getiri şu formülle hesaplanır:

Return[i] = (Close[i]-Close[i-1])/Close[i-1]

Tanımlamalar:

• Return[i] — i aralığındaki getiri;
• Close[i] — i aralığının sonundaki varlıkların değeri;
• Close[i-1] — önceki aralığın sonundaki varlıkların değeri.

Diğer bir deyişle getiri, belirli bir dönemde varlıkların değerinde meydana gelen göreli değişim olarak da yazılabilir:

Return[i] = Delta[i]/Previous

Tanımlamalar:

• Delta[i] = (Close[i]-Close[i-1]) — ilgili dönemde varlıkların değerinde meydana gelen mutlak değişim;
• Previous = Close[i-1] — önceki aralığın sonundaki varlıkların değeri.
  

Sharpe oranını günlük değerleri kullanarak bir yıllık süre için hesaplamak adına, yıl içindeki her gündeki getirileri hesaplamalıyız; böylece, ortalama günlük getiriyi, hesapladığımız günlük getirilerin toplamını hesaplamadaki gün sayısına bölerek buluruz. 

Return = Sum(Return[i])/N

burada N gün sayısıdır.

Risksiz getiri

Risksiz getiri kavramı koşullara bağlıdır, çünkü her zaman bir risk vardır. Sharpe oranı, aynı zaman aralıklarındaki farklı stratejiler/portföyleri karşılaştırmak için kullanıldığından, risksiz getiriyi sıfır olarak kabul etmek en kolay yoldur. Yani,

RiskFree = 0

Getirinin standart sapması

Standart sapma, rastgele değişkenlerin ortalama değerden nasıl saptığını gösterir. Önce ortalama getiri değeri hesaplanır, ardından getirilerin ortalama değerden sapmalarının kareleri toplanır. Ortaya çıkan toplam, dağılımı elde etmek için getiri sayısına bölünür. Elde edilen dağılımın karekökü de standart sapmadır.

D = Sum((Return - Return[i])^2 )/N

STD = SQRT(D)

Standart sapma hesaplama örneği, daha önce bahsedilen makalede verilmiştir.

Herhangi bir zaman diliminde Sharpe oranının hesaplanması ve yıllık değere dönüştürülmesi

Sharpe oranın hesaplanma yöntemi 1966'dan beri değişmemiştir. Bu değişken, hesaplama metodolojisinin dünya çapında yaygın olarak tanınmasından sonra modern adını almıştır. O zamanlar, fon ve portföy performansı değerlendirmeleri, birkaç yılda elde edilen getiriler temelinde yapılıyordu. Daha sonra aylık veriler üzerinden hesaplamalar yapılmaya ve ortaya çıkan Sharpe oranının yıllık değere dönüştürülmesine başlandı. Bu yöntem, iki fon, portföy veya stratejinin karşılaştırılmasına olanak sağlar.

Sharpe oranı, farklı dönemlerden ve zaman dilimlerinden kolayca yıllık değere ölçeklenebilir. Bu, 'ortaya çıkan sonucun' 'yıllık aralığın mevcut olanla oranının kare köküyle' çarpılmasıyla yapılır. Aşağıdaki örneği ele alalım.

Sharpe oranını günlük getiriler üzerinden hesapladığımızı varsayalım - SharpeDaily. Şimdi ortaya çıkan sonucu SharpeAnnual yıllık değere dönüştürmemiz gerekiyor. Yıllık değer, içerisinde bulundurduğu ilgili dönem sayısının karekökü ile orantılıdır, başka bir deyişle, bir yıla kaç günlük aralık sığar. Bir yılda 252 iş günü olduğu için günlük getirilere dayalı Sharpe oranı 252'nin karekökü ile çarpılmalıdır. Bu, yıllık Sharpe oranı olacaktır:

SharpeAnnual = SQRT(252)*SharpeDaily // bir yılda 252 iş günü

H1 zaman diliminde hesaplarsak, yine aynı prensibi kullanırız - önce SharpeHourly'i SharpeDaily'e dönüştürürüz, ardından yıllık Sharpe oranını hesaplarız. Bir D1 çubuğu 24 H1 çubuğu içerir, bu nedenle formül aşağıdaki gibi olacaktır:

SharpeDaily = SQRT(24)*SharpeHourly   // D1 24 saat içerir

Tüm finansal enstrümanlar günde 24 saat işlem görmez. Ancak, aynı finansal enstrüman için sınayıcıda ticaret stratejileri değerlendirilirken, aynı test aralığı ve aynı zaman dilimi için karşılaştırma yapıldığından, bu önemli değildir.

Sharpe oranını kullanarak stratejileri değerlendirme

Strateji/portföy performansına bağlı olarak Sharpe Ratio, negatif değerler de dahil olmak üzere farklı değerlere sahip olabilir. Sharpe oranının yıllık değere dönüştürülmesi, onu klasik şekilde yorumlamamızı sağlar:

Değer	Anlam	Açıklama
Sharpe oranı < 0	Kötü	Strateji kârsız
0 < Sharpe oranı  < 1.0	Belirsiz	Risk karşılığını vermiyor. Alternatif olmadığında bu tür stratejiler düşünülebilir
Sharpe oranı ≥ 1.0	İyi	Bu, risk karşılığını veriyor ve portföy/strateji pozitif sonuçlar gösterebilir demektir
Sharpe oranı ≥ 3.0	Çok iyi	Yüksek bir değer, her bir işlemde zarar elde etme olasılığının çok düşük olduğunu gösterir

Sharpe katsayısının genel bir istatistiksel değişken olduğunu unutmayın. Sadece getiri ve risk arasındaki oranı yansıtmaktadır. Bu nedenle, farklı portföyleri ve stratejileri analiz ederken, Sharpe oranlarını önerilen değerlerle veya kendi aralarında ilişkilendirmek önemlidir.

2020 için EURUSD'nin Sharpe oranının hesaplanması

Sharpe oranı, başlangıçta genellikle çok sayıda hisse senedinden oluşan portföyleri değerlendirmek için geliştirilmiştir. Hisse senetlerinin değeri her gün değişir ve portföyün değeri de buna göre değişir. Değerdeki ve getirilerdeki değişim herhangi bir zaman diliminde ölçülebilir. EURUSD döviz çifti için hesaplamalar yapalım.

Hesaplamaları H1 ve D1 zaman dilimlerinde yapacağız. Ardından, sonuçları yıllık değerlere dönüştüreceğiz ve bir fark olup olmadığını görmek için karşılaştıracağız. Hesaplamalarda 2020 yılı boyuncaki çubuk kapanış fiyatlarını kullanacağız.

MQL5 kodu

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   double H1_close[],D1_close[];
   double h1_returns[],d1_returns[];
   datetime from = D'01.01.2020';
   datetime to = D'01.01.2021';
   int bars = CopyClose("EURUSD",PERIOD_H1,from,to,H1_close);
   if(bars == -1)
      Print("CopyClose(\"EURUSD\",PERIOD_H1,01.01.2020,01.01.2021 failed. Error ",GetLastError());
   else
     {
      Print("\nCalculate the mean and standard deviation of returns on H1 bars");
      Print("H1 bars=",ArraySize(H1_close));
      GetReturns(H1_close,h1_returns);
      double average = ArrayMean(h1_returns);
      PrintFormat("H1 average=%G",average);
      double std = ArrayStd(h1_returns);
      PrintFormat("H1 std=%G",std);
      double sharpe_H1 = average / std;
      PrintFormat("H1 Sharpe=%G",sharpe_H1);
      double sharpe_annual_H1 = sharpe_H1 * MathSqrt(ArraySize(h1_returns));
      Print("Sharpe_annual(H1)=", sharpe_annual_H1);
     }

   bars = CopyClose("EURUSD",PERIOD_D1,from,to,D1_close);
   if(bars == -1)
      Print("CopyClose(\"EURUSD\",PERIOD_D1,01.01.2020,01.01.2021 failed. Error ",GetLastError());
   else
     {
      Print("\nCalculate the mean and standard deviation of returns on D1 bars");     
      Print("D1 bars=",ArraySize(D1_close));
      GetReturns(D1_close,d1_returns);
      double average = ArrayMean(d1_returns);
      PrintFormat("D1 average=%G",average);
      double std = ArrayStd(d1_returns);
      PrintFormat("D1 std=%G",std);
      double sharpe_D1 = average / std;
      double sharpe_annual_D1 = sharpe_D1 * MathSqrt(ArraySize(d1_returns));
      Print("Sharpe_annual(H1)=", sharpe_annual_D1);
     }
  }

//+------------------------------------------------------------------+
//|  Fills the returns[] array of returns                            |
//+------------------------------------------------------------------+
void GetReturns(const double & values[], double & returns[])
  {
   int size = ArraySize(values);
//--- if less than 2 values, return an empty array of returns
   if(size < 2)
     {
      ArrayResize(returns,0);
      PrintFormat("%s: Error. ArraySize(values)=%d",size);
      return;
     }
   else
     {
      //--- fill returns in a loop
      ArrayResize(returns, size - 1);
      double delta;
      for(int i = 1; i < size; i++)
        {
         returns[i - 1] = 0;
         if(values[i - 1] != 0)
           {
            delta = values[i] - values[i - 1];
            returns[i - 1] = delta / values[i - 1];
           }
        }
     }
//---
  }
//+------------------------------------------------------------------+
//|  Calculates the average number of array elements                 |
//+------------------------------------------------------------------+
double ArrayMean(const double & array[])
  {
   int size = ArraySize(array);
   if(size < 1)
     {
      PrintFormat("%s: Error, array is empty",__FUNCTION__);
      return(0);
     }
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += array[i];
   mean /= size;
   return(mean);
  }
//+------------------------------------------------------------------+
//|  Calculates the standard deviation of array elements             |
//+------------------------------------------------------------------+
double ArrayStd(const double & array[])
  {
   int size = ArraySize(array);
   if(size < 1)
     {
      PrintFormat("%s: Error, array is empty",__FUNCTION__);
      return(0);
     }
   double mean = ArrayMean(array);
   double std = 0;
   for(int i = 0; i < size; i++)
      std += (array[i] - mean) * (array[i] - mean);
   std /= size;
   std = MathSqrt(std);
   return(std);
  }  
//+------------------------------------------------------------------+

/*
Result

Calculate the mean and standard deviation of returns on H1 bars
H1 bars:6226
H1 average=1.44468E-05
H1 std=0.00101979
H1 Sharpe=0.0141664
Sharpe_annual(H1)=1.117708053392263

Calculate the mean and standard deviation of returns on D1 bars
D1 bars:260
D1 average=0.000355823
D1 std=0.00470188
Sharpe_annual(H1)=1.2179005039019222

*/

MetaTrader 5 kütüphanesini kullanarak hesaplamak için Python kodu

import math
from datetime import datetime
import MetaTrader5 as mt5

# display data on the MetaTrader 5 package
print("MetaTrader5 package author: ", mt5.__author__)
print("MetaTrader5 package version: ", mt5.__version__)

# import the 'pandas' module for displaying data obtained in the tabular form
import pandas as pd

pd.set_option('display.max_columns', 50)  # how many columns to show
pd.set_option('display.width', 1500)  # max width of the table to show
# import pytz module for working with the time zone
import pytz

# establish connection to the MetaTrader 5 terminal
if not mt5.initialize():
    print("initialize() failed")
    mt5.shutdown()

# set time zone to UTC
timezone = pytz.timezone("Etc/UTC")
# create datetime objects in the UTC timezone to avoid the local time zone offset
utc_from = datetime(2020, 1, 1, tzinfo=timezone)
utc_to = datetime(2020, 12, 31, hour=23, minute=59, second=59, tzinfo=timezone)
# get EURUSD H1 bars in the interval 2020.01.01 00:00 - 2020.31.12 13:00 in the UTC timezone
rates_H1 = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_H1, utc_from, utc_to)
# also get D1 bars in the interval 2020.01.01 00:00 - 2020.31.12 13:00 in the UTC timezone
rates_D1 = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_D1, utc_from, utc_to)
# shut down connection to the MetaTrader 5 terminal and continue processing obtained bars
mt5.shutdown()

# create DataFrame out of the obtained data
rates_frame = pd.DataFrame(rates_H1)

# add the "Return" column
rates_frame['return'] = 0.0
# now calculate the returns as return[i] = (close[i] - close[i-1])/close[i-1]
prev_close = 0.0
for i, row in rates_frame.iterrows():
    close = row['close']
    rates_frame.at[i, 'return'] = close / prev_close - 1 if prev_close != 0.0 else 0.0
    prev_close = close

print("\nCalculate the mean and standard deviation of returns on H1 bars")
print('H1 rates:', rates_frame.shape[0])
ret_average = rates_frame[1:]['return'].mean()  # skip the first row with zero return
print('H1 return average=', ret_average)
ret_std = rates_frame[1:]['return'].std(ddof=0) # skip the first row with zero return
print('H1 return std =', ret_std)
sharpe_H1 = ret_average / ret_std
print('H1 Sharpe = Average/STD = ', sharpe_H1)

sharpe_annual_H1 = sharpe_H1 * math.sqrt(rates_H1.shape[0]-1)
print('Sharpe_annual(H1) =', sharpe_annual_H1)

# now calculate the Sharpe ratio on the D1 timeframe
rates_daily = pd.DataFrame(rates_D1)

# add the "Return" column
rates_daily['return'] = 0.0
# calculate returns
prev_return = 0.0
for i, row in rates_daily.iterrows():
    close = row['close']
    rates_daily.at[i, 'return'] = close / prev_return - 1 if prev_return != 0.0 else 0.0
    prev_return = close

print("\nCalculate the mean and standard deviation of returns on D1 bars")
print('D1 rates:', rates_daily.shape[0])
daily_average = rates_daily[1:]['return'].mean()
print('D1 return average=', daily_average)
daily_std = rates_daily[1:]['return'].std(ddof=0)
print('D1 return std =', daily_std)
sharpe_daily = daily_average / daily_std
print('D1 Sharpe =', sharpe_daily)

sharpe_annual_D1 = sharpe_daily * math.sqrt(rates_daily.shape[0]-1)
print('Sharpe_annual(D1) =', sharpe_annual_D1)

Result
Calculate the mean and standard deviation of returns on H1 bars

H1 rates: 6226
H1 return average= 1.4446773215242986e-05
H1 return std = 0.0010197932969323495
H1 Sharpe = Average/STD = 0.014166373968823358
Sharpe_annual(H1) = 1.117708053392236

Calculate the mean and standard deviation of returns on D1 bars
D1 rates: 260
D1 return average= 0.0003558228355051694
D1 return std = 0.004701883757646081
D1 Sharpe = 0.07567665511222807
Sharpe_annual(D1) = 1.2179005039019217 

Görüldüğü gibi MQL5 ve Python hesaplama sonuçları aynı. Kaynak kodları aşağıda eklenmiştir (CalculateSharpe_2TF).

H1 ve D1 çubuklarından hesaplanan yıllık Sharpe oranları farklıdır: sırasıyla 1.117708 ve 1.217900. Nedenini bulmaya çalışalım.

Tüm zaman dilimlerinden 2020 için EURUSD'nin yıllık Sharpe oranının hesaplanması

Şimdi tüm zaman dilimlerinden yıllık Sharpe oranını hesaplayalım. Bunu yapmak için elde edilen verileri bir tabloda topluyoruz:

• TF — zaman dilimi
• Minutes — zaman dilimindeki dakika sayısı
• Rates — bir yıldaki zaman dilimi çubuğu sayısı
• Avg — yüzde olarak zaman diliminde çubuk başına ortalama getiri (çubuk başına ortalama fiyat değişimi yüzdesi)
• Std — yüzde olarak zaman diliminde çubuk başına standart sapma (zaman dilimindeki fiyat volatilitesi yüzdesi)
• SharpeTF — zaman diliminde hesaplanan Sharpe oranı
• SharpeAnnual — ilgili zaman diliminin Sharpe oranına göre hesaplanan yıllık Sharpe oranı

Hesaplama kod bloğu aşağıdadır. Kodun tamamı makaleye eklenmiş CalculateSharpe_All_TF.mq5 dosyasında mevcuttur.

//--- structure to print statistics to log
struct Stats
  {
   string            TF;
   int               Minutes;
   int               Rates;
   double            Avg;
   double            Std;
   double            SharpeTF;
   double            SharpeAnnual;
  };
//--- array of statistics by timeframes
Stats stats[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- arrays for close prices
   double H1_close[],D1_close[];
//--- arrays of returns
   double h1_returns[],d1_returns[];
//--- arrays of timeframes on which the Sharpe coefficient will be calculated
   ENUM_TIMEFRAMES timeframes[] = {PERIOD_M1,PERIOD_M2,PERIOD_M3,PERIOD_M4,PERIOD_M5,
                                   PERIOD_M6,PERIOD_M10,PERIOD_M12,PERIOD_M15,PERIOD_M20,
                                   PERIOD_M30,PERIOD_H1,PERIOD_H2,PERIOD_H3,PERIOD_H4,
                                   PERIOD_H6,PERIOD_H8,PERIOD_H12,PERIOD_D1,PERIOD_W1,PERIOD_MN1
                                  };

   ArrayResize(stats,ArraySize(timeframes));
//--- timeseries request parameters
   string symbol = Symbol();
   datetime from = D'01.01.2020';
   datetime to = D'01.01.2021';
   Print(symbol);
   for(int i = 0; i < ArraySize(timeframes); i++)
     {
      //--- get the array of returns on the specified timeframe
      double returns[];
      GetReturns(symbol,timeframes[i],from,to,returns);
      //--- calculate statistics
      GetStats(returns,avr,std,sharpe);
      double sharpe_annual = sharpe * MathSqrt(ArraySize(returns));
      PrintFormat("%s  aver=%G%%   std=%G%%  sharpe=%G  sharpe_annual=%G",
                  EnumToString(timeframes[i]), avr * 100,std * 100,sharpe,sharpe_annual);
      //--- fill the statistics structure
      Stats row;
      string tf_str = EnumToString(timeframes[i]);
      StringReplace(tf_str,"PERIOD_","");
      row.TF = tf_str;
      row.Minutes = PeriodSeconds(timeframes[i]) / 60;
      row.Rates = ArraySize(returns);
      row.Avg = avr;
      row.Std = std;
      row.SharpeTF = sharpe;
      row.SharpeAnnual = sharpe_annual;
      //--- add a row for the timeframe statistics
      stats[i] = row;
     }
//--- print statistics on all timeframes to log
   ArrayPrint(stats,8);
  }

/*
Result

      [TF] [Minutes] [Rates]      [Avg]      [Std] [SharpeTF] [SharpeAnnual]
[ 0] "M1"          1  373023 0.00000024 0.00168942 0.00168942     1.03182116
[ 1] "M2"          2  186573 0.00000048 0.00239916 0.00239916     1.03629642
[ 2] "M3"          3  124419 0.00000072 0.00296516 0.00296516     1.04590258
[ 3] "M4"          4   93302 0.00000096 0.00341717 0.00341717     1.04378592
[ 4] "M5"          5   74637 0.00000120 0.00379747 0.00379747     1.03746116
[ 5] "M6"          6   62248 0.00000143 0.00420265 0.00420265     1.04854166
[ 6] "M10"        10   37349 0.00000239 0.00542100 0.00542100     1.04765562
[ 7] "M12"        12   31124 0.00000286 0.00601079 0.00601079     1.06042363
[ 8] "M15"        15   24900 0.00000358 0.00671964 0.00671964     1.06034161
[ 9] "M20"        20   18675 0.00000477 0.00778573 0.00778573     1.06397070
[10] "M30"        30   12450 0.00000716 0.00966963 0.00966963     1.07893298
[11] "H1"         60    6225 0.00001445 0.01416637 0.01416637     1.11770805
[12] "H2"        120    3115 0.00002880 0.01978455 0.01978455     1.10421905
[13] "H3"        180    2076 0.00004305 0.02463458 0.02463458     1.12242890
[14] "H4"        240    1558 0.00005746 0.02871564 0.02871564     1.13344977
[15] "H6"        360    1038 0.00008643 0.03496339 0.03496339     1.12645075
[16] "H8"        480     779 0.00011508 0.03992838 0.03992838     1.11442404
[17] "H12"       720     519 0.00017188 0.05364323 0.05364323     1.22207717
[18] "D1"       1440     259 0.00035582 0.07567666 0.07567666     1.21790050
[19] "W1"      10080      51 0.00193306 0.14317328 0.14317328     1.02246174
[20] "MN1"     43200      12 0.00765726 0.43113365 0.43113365     1.49349076

*/

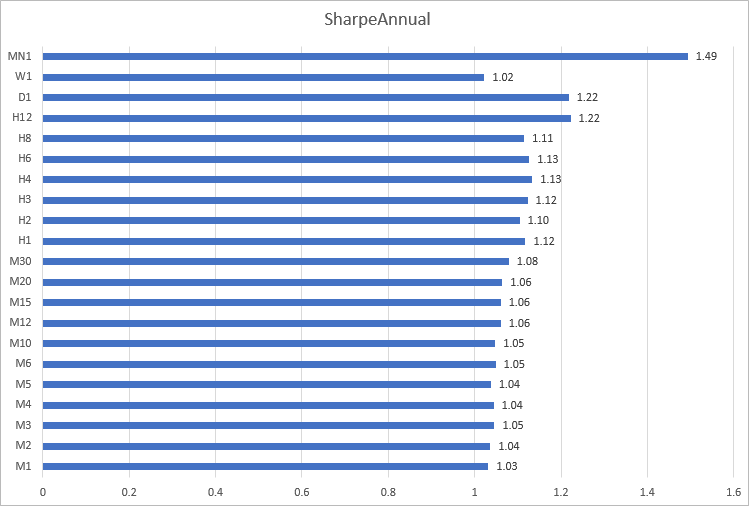
2020 EURUSD Sharpe oranının farklı zaman dilimlerine göre bir histogramını oluşturalım. Burada, M1'den M30'a kadar olan dakika zaman dilimlerindeki hesaplamaların yakın sonuçlar verdiği görülebilir: 1.03'ten 1.08'e. En tutarsız sonuçlar H12'den MN1'e kadar olan zaman dilimlerindedir.

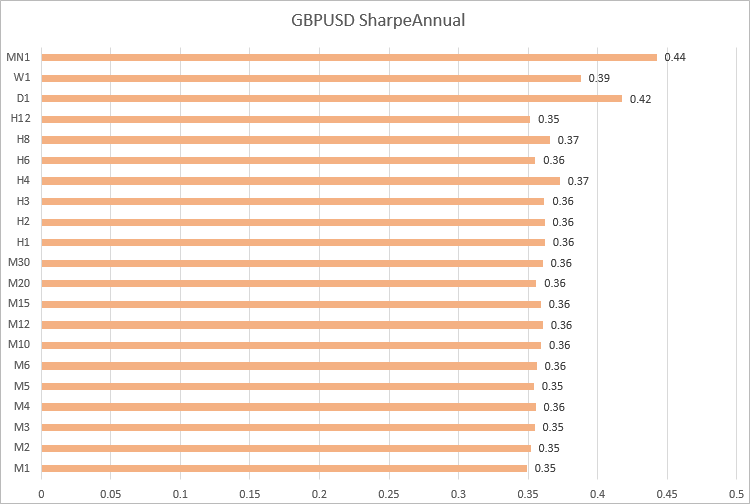
2020 için GBPUSD, USDJPY ve USDCHF'in Sharpe oranlarının hesaplaması

Benzer hesaplamaları üç döviz çifti için daha yapalım.

GBPUSD, Sharpe oranı değerleri M1'den H12'ye kadar olan zaman dilimlerinde yakındır.

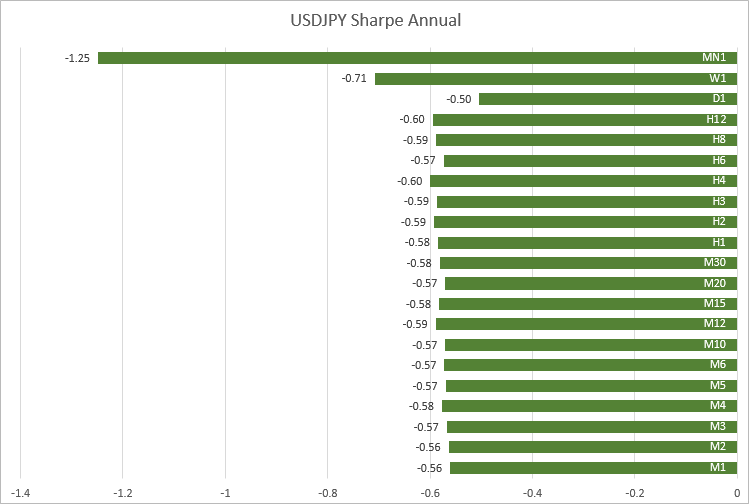
USDJPY, değerler yine M1'den H12'ye kadar olan zaman dilimlerinde yakındır: -0.56'dan -0.60'a.

USDCHF, M1'den M30'a kadar olan zaman dilimlerinde yakın değerler elde edildi. Zaman dilimi arttıkça Sharpe oranı dalgalanıyor.

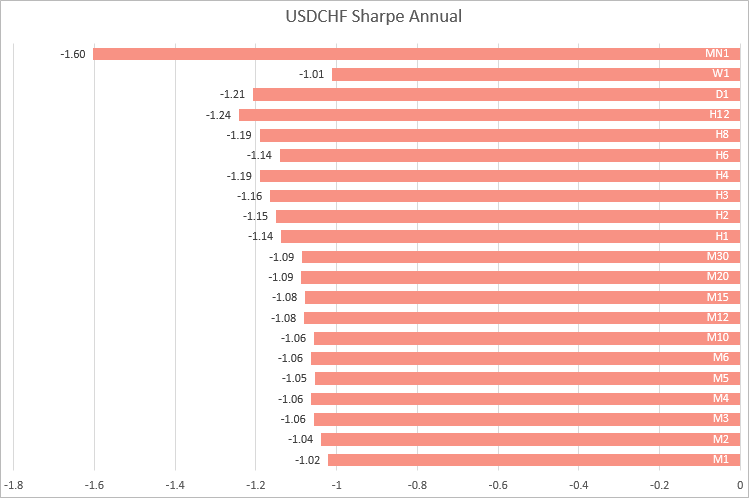
Böylece, dört ana döviz çiftinin örneklerine dayanarak, Sharpe oranının en istikrarlı hesaplamalarının M1'den M30'a kadar olan zaman dilimlerinde elde edildiği sonucuna varabiliriz. Yani, farklı semboller üzerinde çalışan stratejileri karşılaştırmanız gerekiyorsa, daha düşük zaman dilimlerindeki getirileri kullanarak Sharpe oranını hesaplamak daha iyidir.

Aylar üzerinden 2020 için EURUSD'nin yıllık Sharpe oranının hesaplanması

2020'nin her ayının aylık getirilerini kullanalım ve M1'den H1'e kadar olan zaman dilimlerinden yıllık Sharpe Oranını hesaplayalım. Kodun tamamı makaleye eklenmiş CalculateSharpe_Months.mq5 dosyasında mevcuttur.

//--- structure to store returns
struct Return
  {
   double            ret;   // return
   datetime          time;  // date
   int               month; // month
  };
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   SharpeMonths sharpe_by_months[];
//--- arrays of timeframes on which the Sharpe coefficient will be calculated
   ENUM_TIMEFRAMES timeframes[] = {PERIOD_M1,PERIOD_M2,PERIOD_M3,PERIOD_M4,PERIOD_M5,
                                   PERIOD_M6,PERIOD_M10,PERIOD_M12,PERIOD_M15,PERIOD_M20,
                                   PERIOD_M30,PERIOD_H1
                                  };
   ArrayResize(sharpe_by_months,ArraySize(timeframes));
//--- timeseries request parameters
   string symbol = Symbol();
   datetime from = D'01.01.2020';
   datetime to = D'01.01.2021';
   Print("Calculate Sharpe Annual on ",symbol, " for 2020 year");
   for(int i = 0; i < ArraySize(timeframes); i++)
     {
      //--- get the array of returns on the specified timeframe
      Return returns[];
      GetReturns(symbol,timeframes[i],from,to,returns);
      double avr,std,sharpe;
      //--- Calculate statistics for the year
      GetStats(returns,avr,std,sharpe);
      string tf_str = EnumToString(timeframes[i]);
      //--- calculate the annual Sharpe ratio for each month
      SharpeMonths sharpe_months_on_tf;
      sharpe_months_on_tf.SetTimeFrame(tf_str);
      //--- select returns for i-th month
      for(int m = 1; m <= 12; m++)
        {
         Return month_returns[];
         GetReturnsByMonth(returns,m,month_returns);
         //--- Calculate statistics for the year
         double sharpe_annual = CalculateSharpeAnnual(timeframes[i],month_returns);
         sharpe_months_on_tf.Sharpe(m,sharpe_annual);
        }
      //--- add Sharpe ratio for 12 months on timeframe i
      sharpe_by_months[i] = sharpe_months_on_tf;
     }
//--- display the table of annual Sharpe values by months on all timeframes
   ArrayPrint(sharpe_by_months,3);
  }

/*
Result

Calculate Sharpe Annual on EURUSD for 2020 year
             [TF]  [Jan]  [Feb] [Marc]  [Apr] [May] [June] [July] [Aug] [Sept]  [Oct] [Nov] [Dec]
[ 0] "PERIOD_M1"  -2.856 -1.340  0.120 -0.929 2.276  1.534  6.836 2.154 -2.697 -1.194 3.891 4.140
[ 1] "PERIOD_M2"  -2.919 -1.348  0.119 -0.931 2.265  1.528  6.854 2.136 -2.717 -1.213 3.845 4.125
[ 2] "PERIOD_M3"  -2.965 -1.340  0.118 -0.937 2.276  1.543  6.920 2.159 -2.745 -1.212 3.912 4.121
[ 3] "PERIOD_M4"  -2.980 -1.341  0.119 -0.937 2.330  1.548  6.830 2.103 -2.765 -1.219 3.937 4.110
[ 4] "PERIOD_M5"  -2.929 -1.312  0.120 -0.935 2.322  1.550  6.860 2.123 -2.729 -1.239 3.971 4.076
[ 5] "PERIOD_M6"  -2.945 -1.364  0.119 -0.945 2.273  1.573  6.953 2.144 -2.768 -1.239 3.979 4.082
[ 6] "PERIOD_M10" -3.033 -1.364  0.119 -0.934 2.361  1.584  6.789 2.063 -2.817 -1.249 4.087 4.065
[ 7] "PERIOD_M12" -2.952 -1.358  0.118 -0.956 2.317  1.609  6.996 2.070 -2.933 -1.271 4.115 4.014
[ 8] "PERIOD_M15" -3.053 -1.367  0.118 -0.945 2.377  1.581  7.132 2.078 -2.992 -1.274 4.029 4.047
[ 9] "PERIOD_M20" -2.998 -1.394  0.117 -0.920 2.394  1.532  6.884 2.065 -3.010 -1.326 4.074 4.040
[10] "PERIOD_M30" -3.008 -1.359  0.116 -0.957 2.379  1.585  7.346 2.084 -2.934 -1.323 4.139 4.034
[11] "PERIOD_H1"  -2.815 -1.373  0.116 -0.966 2.398  1.601  7.311 2.221 -3.136 -1.374 4.309 4.284

*/

Hesaplama yaptığımız tüm zaman dilimlerinde her ay için yıllık oran değerlerinin çok yakın olduğu görülmektedir. Daha iyi bir sunum için, sonuçları Excel'i kullanarak bir 3D yüzey grafiği şeklinde gösterelim.

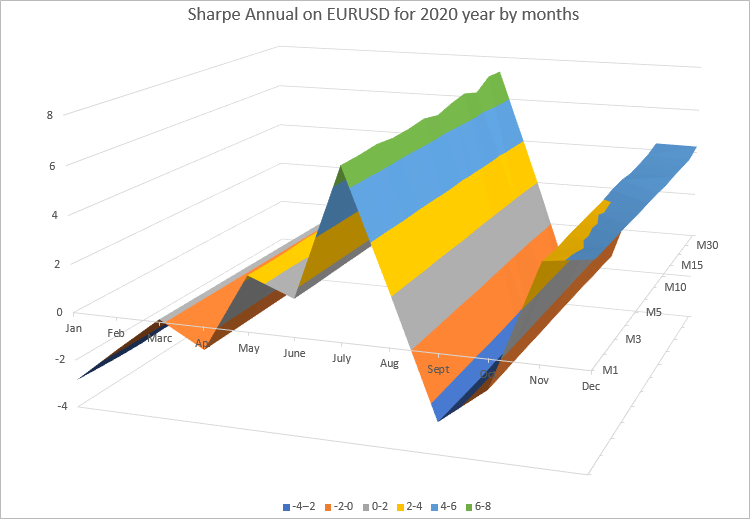
Grafik, yıllık Sharpe oranı değerlerinin her ay değiştiğini açıkça göstermektedir. EURUSD'nin o ay nasıl değiştiğine bağlıdır. Ancak aynı zamanda, her ay için yıllık Sharpe oranının tüm zaman dilimlerindeki değeri neredeyse hiç değişmiyor.

Böylece, yıllık Sharpe oranı herhangi bir zaman diliminde hesaplanabilir ve ayrıca ortaya çıkan değer getirilerin elde edildiği çubukların sayısına da bağlıdır. Bu, bu hesaplama algoritmasının test, optimizasyon ve gerçek zamanlı izleme sırasında kullanılabileceği anlamına gelir. Tek ön koşul, yeterince büyük bir getiri dizisine sahip olmaktır.

Sortino oranı

Sharpe oranı hesaplamasında risk, varlıklarda hem artış hem de azalış olarak fiyatların tam volatilitesidir. Ancak portföy değerindeki artış yatırımcı için iyidir, zarar ise sadece portföy değerindeki düşüşle bağlantılıdır. Bu nedenle, orandaki gerçek risk abartılır. 1990'ların başında Frank Sortino tarafından geliştirilen Sortino oranı bu sorunu çözmektedir.

Kendinden öncekiler gibi, F. Sortino da gelecekteki getiriyi matematiksel beklentisine eşit bir rastgele değişken, riski de bir varyans olarak kabul eder. Getiri ve risk, belirli bir dönem için fiyatların tarihsel değerlerine göre belirlenir. Sharpe oranı hesaplamasında olduğu gibi getiri riske bölünür.

Sortino, getirilerin toplam varyansı (diğer bir deyişle tam volatilite) olarak tanımlanan riskin hem olumlu hem de olumsuz değişimlere bağlı olduğuna dikkat çekmiştir. Sortino, toplam volatiliteyi, yalnızca varlıklardaki düşüşleri dikkate alan yarı volatiliteyle değiştirmiştir. Yarı volatilite aynı zamanda çeşitli yayınlarda zararlı volatilite, aşağı yönlü risk, aşağı yönlü sapma, negatif volatilite veya aşağı yönlü standart sapma olarak da adlandırılır.

Sortino oranı hesaplaması aslında Sharpe oranı hesaplamasına benzerdir, tek fark, pozitif getirilerin volatilite hesaplamasından hariç tutulmasıdır. Bu, risk ölçümünü azaltır ve oran ağırlığını arttırır.

Sharpe oranı hesaplamasına dayalı olarak Sortino oranını hesaplayan kod örneği. Yarı dağılım sadece negatif getiriler kullanılarak hesaplanır.

//+------------------------------------------------------------------+
//|  Calculates Sharpe and Sortino ratios                            |
//+------------------------------------------------------------------+
void GetStats(ENUM_TIMEFRAMES timeframe, const double & returns[], double & avr, double & std, double & sharpe, double & sortino)
  {
   avr = ArrayMean(returns);
   std = ArrayStd(returns);
   sharpe = (std == 0) ? 0 : avr / std;
//--- now, remove negative returns and calculate the Sortino ratio
   double negative_only[];
   int size = ArraySize(returns);
   ArrayResize(negative_only,size);
   ZeroMemory(negative_only);
//--- copy only negative returns
   for(int i = 0; i < size; i++)
      negative_only[i] = (returns[i] > 0) ? 0 : returns[i];
   double semistd = ArrayStd(negative_only);
   sortino = avr / semistd;   
   return;
  }

Makaleye eklenen CalculateSortino_All_TF.mq5 komut dosyası 2020 EURUSD'de şu sonuçları oluşturur:

      [TF] [Minutes] [Rates]      [Avg]      [Std] [SharpeAnnual] [SortinoAnnual]    [Ratio]
[ 0] "M1"          1  373023 0.00000024 0.00014182     1.01769617      1.61605380 1.58795310
[ 1] "M2"          2  186573 0.00000048 0.00019956     1.02194170      1.62401856 1.58914991
[ 2] "M3"          3  124419 0.00000072 0.00024193     1.03126142      1.64332243 1.59350714
[ 3] "M4"          4   93302 0.00000096 0.00028000     1.02924195      1.62618200 1.57998030
[ 4] "M5"          5   74637 0.00000120 0.00031514     1.02303684      1.62286584 1.58632199
[ 5] "M6"          6   62248 0.00000143 0.00034122     1.03354379      1.63789024 1.58473231
[ 6] "M10"        10   37349 0.00000239 0.00044072     1.03266766      1.63461839 1.58290848
[ 7] "M12"        12   31124 0.00000286 0.00047632     1.04525580      1.65215986 1.58062730
[ 8] "M15"        15   24900 0.00000358 0.00053223     1.04515816      1.65256608 1.58116364
[ 9] "M20"        20   18675 0.00000477 0.00061229     1.04873529      1.66191269 1.58468272
[10] "M30"        30   12450 0.00000716 0.00074023     1.06348332      1.68543441 1.58482449
[11] "H1"         60    6225 0.00001445 0.00101979     1.10170316      1.75890688 1.59653431
[12] "H2"        120    3115 0.00002880 0.00145565     1.08797046      1.73062372 1.59068999
[13] "H3"        180    2076 0.00004305 0.00174762     1.10608991      1.77619289 1.60583048
[14] "H4"        240    1558 0.00005746 0.00200116     1.11659184      1.83085734 1.63968362
[15] "H6"        360    1038 0.00008643 0.00247188     1.11005321      1.79507001 1.61710267
[16] "H8"        480     779 0.00011508 0.00288226     1.09784908      1.74255746 1.58724682
[17] "H12"       720     519 0.00017188 0.00320405     1.20428761      2.11045830 1.75245371
[18] "D1"       1440     259 0.00035582 0.00470188     1.20132966      2.04624198 1.70331429
[19] "W1"      10080      51 0.00193306 0.01350157     1.03243721      1.80369984 1.74703102
[20] "MN1"     43200      12 0.00765726 0.01776075     1.49349076      5.00964481 3.35431926

Hemen hemen tüm zaman dilimlerinde yıllık Sortino oranının yıllık Sharpe oranından 1.60 kat daha fazla olduğu görülmektedir. Elbette, ticaret sonuçlarına göre oranlar hesaplanırken bu kadar net bir ilişki olmayacaktır. Bu nedenle, her iki oranı kullanarak stratejileri/portföyleri karşılaştırmak mantıklıdır.

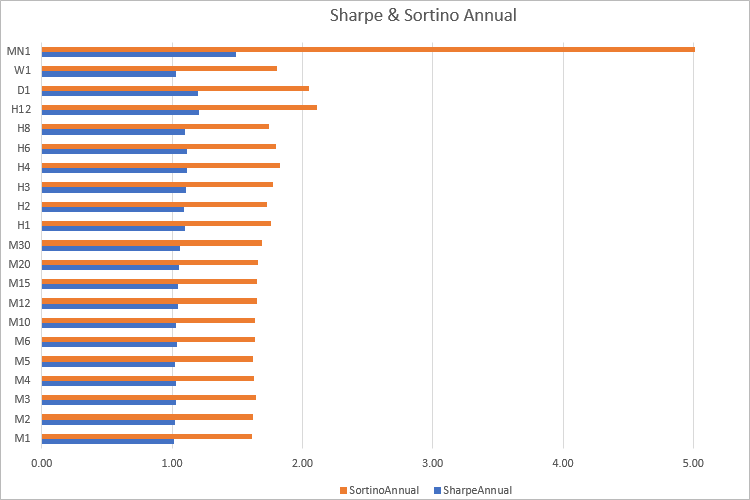
Bu ikisi arasındaki fark, Sharpe oranının esas olarak volatiliteyi yansıtması, Sortino oranınınsa gerçekten birim risk başına getiriyi göstermesidir. Ancak tüm bu hesaplamaların geçmiş üzerinden yapıldığını ve iyi sonuçların gelecekte kârı garanti etmediğini unutmayın.

MetaTrader 5 Strateji Sınayıcıda Sharpe oranı hesaplama örneği

Sharpe oranı, başlangıçta hisse senedi içeren portföyleri değerlendirmek için geliştirilmiştir. Hisse senedi fiyatları her gün değişir ve dolayısıyla varlıkların değeri de her gün değişir. Varsayılan olarak, ticaret stratejileri açık pozisyonların varlığını gerektirmez, bu nedenle zamanın bir bölümünde işlem hesabının durumu değişmeden kalacaktır. Bu, açık pozisyon olmadığında sıfır getiri değerleri alacağımız ve bu nedenle o değerler için Sharpe oranı hesaplamalarının yanlış olacağı anlamına gelir. Dolayısıyla, hesaplamalar yalnızca işlem hesabının durumunun değiştiği çubuklar dikkate alınmalıdır. En uygun seçenek, her çubuğun son tikinde varlık değerlerini analiz etmek olacaktır. Bu, MetaTrader 5 strateji sınayıcıda herhangi bir tik oluşturma moduyla Sharpe oranının hesaplanmasına olanak tanır.

Dikkate alınması gereken bir diğer nokta da, genellikle Return[i]=(CloseCurrent-ClosePrevious)/ClosePrevious şeklinde hesaplanan yüzde fiyat artışının hesaplamalarda belirli bir dezavantaja sahip olmasıdır. Şu şekildedir: eğer fiyat %5 düşer ve ardından %5 artarsa, başlangıç değerine ulaşamayız. Bu nedenle, istatistiksel çalışmalar, olağan göreli fiyat artışı yerine, genellikle fiyat artışı logaritmasını kullanır. Logaritmik getiriler (ya da kısaca log getirilir), doğrusal getirilerin bu dezavantajına sahip değildir. Şu şekilde hesaplanır:

Log_Return =ln(Current/Previous) = ln(Current) — ln(Previous)

Logaritmik getiriler, logaritmaların toplamı göreli getirilerin çarpımına eşdeğer olduğu için, birlikte toplanabilmeleri açısından uygundur.

Böylece, Sharpe oranı hesaplama algoritması minimum ayarlamalar gerektirir.

//--- calculate the logarithms of increments using the equity array
   for(int i = 1; i < m_bars_counter; i++)
     {
      //--- only add if equity has changed
      if(m_equities[i] != prev_equity)
        {
         log_return = MathLog(m_equities[i] / prev_equity); // increment logarithm
         aver += log_return;            // average logarithm of increments
         AddReturn(log_return);         // fill the array of increment logarithms
         counter++;                     // counter of returns
        }
      prev_equity = m_equities[i];
     }
//--- if values are not enough for Sharpe calculation, return 0
   if(counter <= 1)
      return(0);
//--- average value of the increment logarithm
   aver /= counter;
//--- calculate standard deviation
   for(int i = 0; i < counter; i++)
      std += (m_returns[i] - aver) * (m_returns[i] - aver);
   std /= counter;
   std = MathSqrt(std);
//--- Sharpe ratio on the current timeframe
   double sharpe = aver / std;

Kodun tamamı makaleye eklenmiş Sharpe.mqh dosyasında mevcuttur. Sharpe oranını özel bir optimizasyon kriteri olarak hesaplamak için bu dosyayı Uzman Danışmanınıza bağlayın ve birkaç satır kod ekleyin. Örnek olarak MetaTrader 5'in standart paketinden MACD Sample.mq5 Uzman Danışmanını kullanarak nasıl yapılacağını görelim.

#define MACD_MAGIC 1234502
//---
#include <Trade\Trade.mqh>
#include <Trade\SymbolInfo.mqh>
#include <Trade\PositionInfo.mqh>
#include <Trade\AccountInfo.mqh>
#include "Sharpe.mqh"
//---
input double InpLots          = 0.1;// Lots
input int    InpTakeProfit    = 50; // Take Profit (in pips)
input int    InpTrailingStop  = 30; // Trailing Stop Level (in pips)
input int    InpMACDOpenLevel = 3;  // MACD open level (in pips)
input int    InpMACDCloseLevel = 2; // MACD close level (in pips)
input int    InpMATrendPeriod = 26; // MA trend period
//---
int ExtTimeOut = 10; // time out in seconds between trade operations
CReturns   returns;
....
//+------------------------------------------------------------------+
//| Expert new tick handling function                                |
//+------------------------------------------------------------------+
void OnTick(void)
  {
   static datetime limit_time = 0; // last trade processing time + timeout
//--- add current equity to the array to calculate the Sharpe ratio
   MqlTick tick;
   SymbolInfoTick(_Symbol, tick);
   returns.OnTick(tick.time, AccountInfoDouble(ACCOUNT_EQUITY));
//--- don't process if timeout
   if(TimeCurrent() >= limit_time)
     {
      //--- check for data
      if(Bars(Symbol(), Period()) > 2 * InpMATrendPeriod)
        {
         //--- change limit time by timeout in seconds if processed
         if(ExtExpert.Processing())
            limit_time = TimeCurrent() + ExtTimeOut;
        }
     }
  }
//+------------------------------------------------------------------+
//| Tester function                                                  |
//+------------------------------------------------------------------+
double OnTester(void)
  {
//--- calculate Sharpe ratio
   double sharpe = returns.OnTester();
   return(sharpe);
  }
//+------------------------------------------------------------------+

Ortaya çıkan kod da "MACD Sample Sharpe.mq5" dosyası olarak makaleye eklenmiştir.

Özel bir optimizasyon kriteri seçerek EURUSD M10 2020 üzerinde bir genetik optimizasyon çalıştıralım.

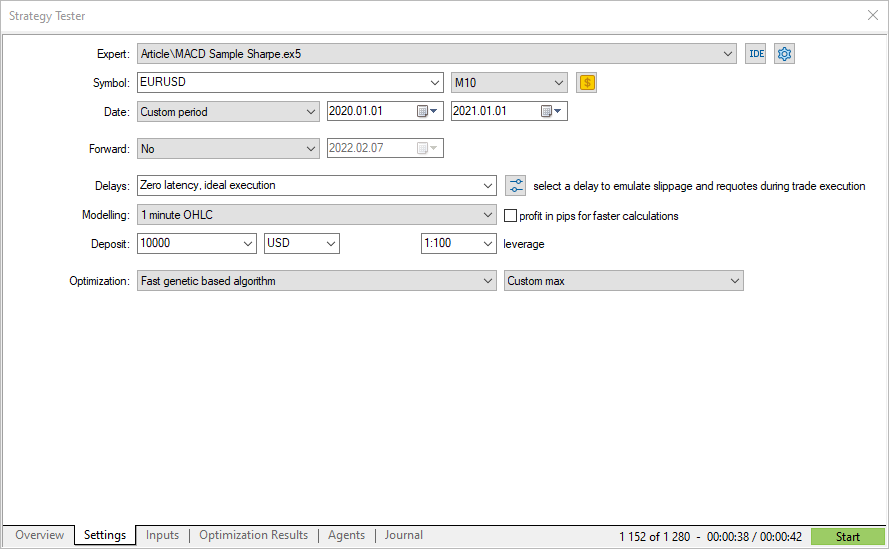
Özel kriterin elde edilen değerleri, strateji sınayıcı tarafından hesaplanan Sharpe oranı ile örtüşmektedir. Artık hesaplama mekanizmalarını ve elde edilen sonuçları nasıl yorumlayacağınızı biliyorsunuz.

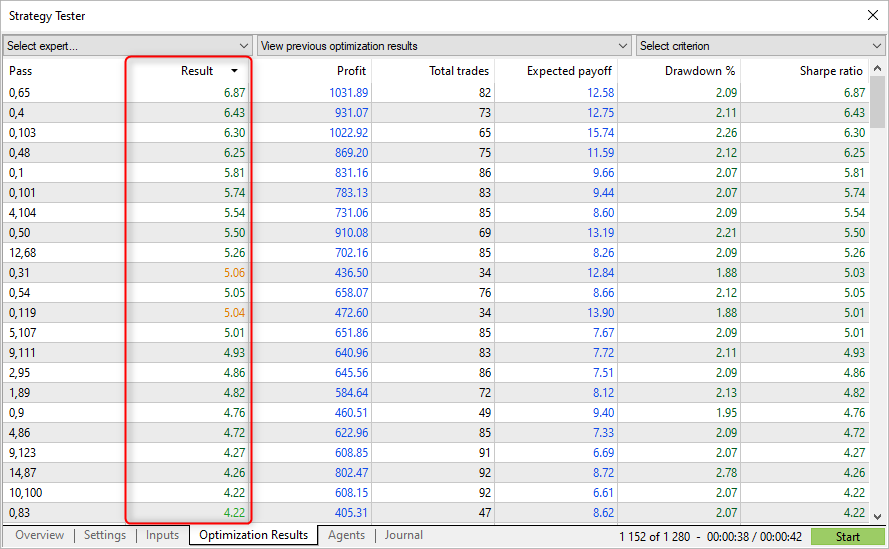
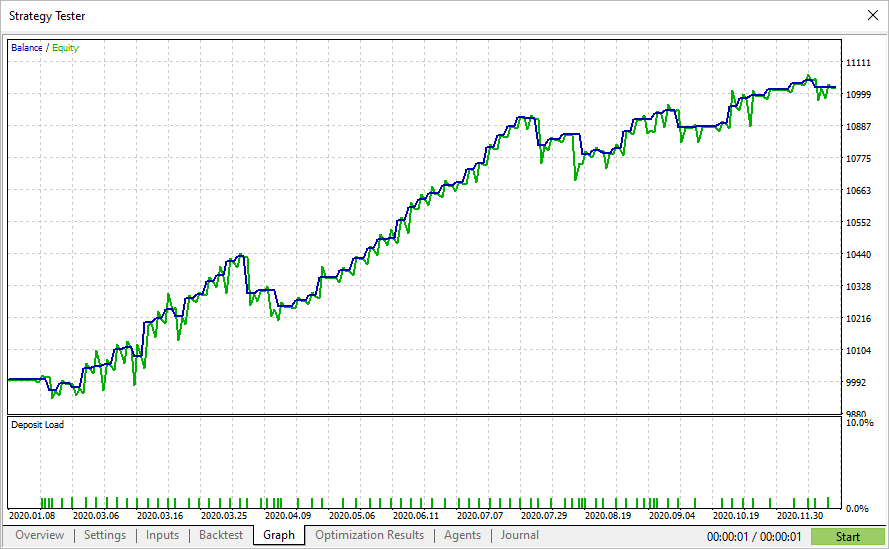
En yüksek Sharpe oranına sahip geçişler, sınayıcıda her zaman en yüksek kârı göstermez, ancak yumuşak varlık grafiğine sahip parametrelerin bulunmasına olanak sağlar. Bu tür grafiklerde genellikle keskin bir büyüme yoktur, ancak aynı zamanda büyük düşüşler ve varlık drawdownları da yoktur.

Yani Sharpe oranı ile optimizasyon kullanarak diğer optimizasyon kriterlerine göre daha kararlı parametreler bulmak mümkündür.

Avantajlar ve dezavantajlar

Sharpe ve Sortino oranları, elde edilen kârın ilgili riski karşılayıp karşılamadığının belirlenmesine olanak sağlar. Alternatif risk ölçütlerine göre bir diğer avanta, hesaplamaların her türlü varlığa uygulanabilmesidir. Örneğin, değerlendirmek için belirli bir harici kıyaslama gerektirmediğinden, Sharpe oranını kullanarak altın ile gümüşü karşılaştırabilirsiniz. Dolayısıyla oranlar, bireysel stratejilere veya menkul kıymetlere, varlık veya strateji portföylerine uygulanabilir.

Bu araçların dezavantajı, hesaplamanın normal bir getiri dağılımı varsaymasıdır. Gerçekte, bu gereksinim nadiren karşılanır. Yine de Sharpe ve Sortino oranları, farklı strateji ve portföylerin karşılaştırılmasına olanak sağlayan en basit ve anlaşılır araçlardır.