Mathematik im Handel: Sharpe- und Sortino-Ratio

Die Kapitalrendite ist der offensichtlichste Indikator, den Anleger und unerfahrene Händler für die Analyse der Handelseffizienz verwenden. Professionelle Händler verwenden zuverlässigere Instrumente zur Analyse von Strategien, wie z.B. die Sharpe- oder die Sortino-Ratio. In diesem Artikel werden wir einfache Beispiele betrachten, um zu verstehen, wie diese Kennziffern berechnet werden. Die Besonderheiten der Bewertung von Handelsstrategien wurden bereits in dem Artikel "Mathematik im Trading. Wie man Handelsergebnisse einschätzt" behandelt. Es wird empfohlen, den Artikel zu lesen, um das Wissen aufzufrischen oder etwas Neues zu lernen.

Sharpe ratio

Erfahrene Anleger und Händler handeln oft mit mehreren Strategien und investieren in verschiedene Vermögenswerte, um konsistente Ergebnisse zu erzielen. Dies ist eines der Konzepte des intelligenten Investierens, das die Erstellung eines Anlageportfolios voraussetzt. Jedes Portfolio von Wertpapieren/Strategien hat seine eigenen Risiko- und Ertragsparameter, die irgendwie verglichen werden sollten.

Eines der meistgenannten Instrumente für einen solchen Vergleich ist die Sharpe-Ratio, die 1966 vom Nobelpreisträger William F. Sharpe entwickelt wurde. Bei der Berechnung der Sharpe-Ratio werden grundlegende Performance-Kennzahlen verwendet, darunter die durchschnittliche Rendite, die Standardabweichung der Rendite und die risikofreie Rendite.

Der Nachteil der Sharpe-Ratio besteht darin, dass die für die Analyse verwendeten Ausgangsdaten normalverteilt sein müssen. Mit anderen Worten, die Grafik der Renditeverteilung sollte symmetrisch sein und keine starken Spitzen oder Rückgänge aufweisen.

Die Sharpe-Ratio wird anhand der folgenden Formel berechnet:

Sharpe-Ratio = (Return - RiskFree)/Std

Wobei:

• Return — die durchschnittliche Rendite für einen bestimmten Zeitraum. Zum Beispiel für einen Monat, ein Quartal, ein Jahr, usw.
  
• RiskFree — eine risikofreie Rendite für denselben Zeitraum. Dazu gehören traditionell Bankeinlagen, Anleihen und andere risikoarme Anlagen mit 100 % Zuverlässigkeit.
  
• Std — Standardabweichung der Portfoliorenditen für denselben Zeitraum. Je stärker die Rendite vom Erwartungswert abweicht, desto höher ist das Risiko und die Volatilität des Kontos oder des Portfolios des Händlers.
  

Renditen

Die Rendite wird als Veränderung des Werts der Vermögenswerte für ein bestimmtes Intervall berechnet. Die Renditewerte werden für denselben Zeitraum verwendet, für den auch die Sharpe-Ratio berechnet wird. In der Regel wird die jährliche Sharpe-Ratio betrachtet, aber es ist auch möglich, vierteljährliche, monatliche oder sogar tägliche Werte zu berechnen. Die Rendite wird nach der folgenden Formel berechnet:

Return[i] = (Close[i]-Close[i-1])/Close[i-1]

Wobei:

• Return[i] — Rendite für das i-te Intervall;
• Close[i] — der Wert der Vermögenswerte am Ende des i-ten Intervalls;
• Close[i-1] — der Wert der Vermögenswerte am Ende des vorhergehenden Intervalls.

Mit anderen Worten, die Rendite lässt sich als relative Veränderung des Werts der Aktiva für den ausgewählten Zeitraum darstellen:

Return[i] = Delta[i]/Previous

Wobei:

• Delta[i] = (Close[i]-Close[i-1]) — absolute Veränderung des Vermögenswerts für den ausgewählten Zeitraum;
• Previous = Close[i-1] — der Wert der Vermögenswerte am Ende des vorherigen Intervalls.
  

Um die Sharpe-Ratio für einen Zeitraum von einem Jahr anhand von Tageswerten zu berechnen, sollten wir die Renditewerte für jeden Tag während des Jahres verwenden und die durchschnittliche tägliche Rendite als Summe der Renditen geteilt durch die Anzahl der Tage in der Berechnung berechnen. 

Rendite = Summe(Rendite[i])/N

wobei N die Anzahl der Tage ist.

Risikofreie Rendite

Das Konzept der risikofreien Rendite ist bedingt, da es immer ein Risiko gibt. Da die Sharpe-Ratio zum Vergleich verschiedener Strategien/Portfolios in denselben Zeitintervallen verwendet wird, kann die risikofreie Rendite Null in die Formel eingesetzt werden. Dies bedeutet,

RiskFree = 0

Standardabweichung oder Rendite

Die Standardabweichung zeigt, wie Zufallsvariablen von einem Mittelwert abweichen. Zunächst wird der durchschnittliche Renditewert berechnet, dann werden die quadrierten Abweichungen der Renditen vom Mittelwert summiert. Die resultierende Summe wird durch die Anzahl der Renditen geteilt, um die Streuung zu erhalten. Die Quadratwurzel der Streuung ist die Standardabweichung.

D = Sum((Return - Return[i])^2 )/N

STD = SQRT(D)

Ein Beispiel für die Berechnung der Standardabweichung finden Sie in dem oben genannten Artikel .

Berechnung der Sharpe-Ratio für einen beliebigen Zeitraum und Umrechnung in einen Jahreswert

Die Methode zur Berechnung der Sharpe-Ratio hat sich seit 1966 nicht geändert. Die Variable erhielt ihren modernen Namen, nachdem diese Berechnungsmethode allgemein anerkannt wurde. Damals basierte die Bewertung der Fonds- und Portfolioperformance auf den über mehrere Jahre erzielten Renditen. Später wurden die Berechnungen auf der Grundlage monatlicher Daten durchgeführt, wobei die sich daraus ergebende Sharpe-Ratio auf einen Jahreswert umgerechnet wurde. Diese Methode ermöglicht den Vergleich von zwei Fonds, Portfolios oder Strategien.

Die Sharpe-Ratio kann leicht von verschiedenen Perioden und Zeiträumen auf einen Jahreswert skaliert werden. Dazu wird der sich ergebende Wert mit der Quadratwurzel des Verhältnisses zwischen dem Jahresintervall und dem aktuellen Intervall multipliziert. Betrachten wir das folgende Beispiel.

Angenommen, wir haben die Sharpe-Ratio anhand der täglichen Renditewerte berechnet — SharpeDaily. Das Ergebnis soll in den Jahreswert SharpeAnnual umgerechnet werden. Das jährliche Verhältnis ist proportional zur Quadratwurzel des Verhältnisses der Perioden, d.h. wie viele Tagesintervalle in ein Jahr passen. Da ein Jahr 252 Arbeitstage hat, muss die Sharpe-Ratio auf Basis der Tagesrendite mit der Quadratwurzel aus 252 multipliziert werden. Dies ergibt die jährliche Sharpe-Ratio:

SharpeAnnual = SQRT(252)*SharpeDaily // 252 Arbeitstage in einem Jahr

Wenn der Wert auf der Grundlage des H1-Zeitrahmens berechnet wird, wenden wir das gleiche Prinzip an — wir konvertieren zunächst SharpeHourly in SharpeDaily und berechnen dann die jährliche Sharpe-Ratio. Ein D1-Balken umfasst 24 H1-Balken, weshalb die Formel wie folgt lautet:

SharpeDaily = SQRT(24)*SharpeHourly // 24 Stunden in einem Tag bzw. D1

Nicht alle Finanzinstrumente werden 24 Stunden am Tag gehandelt. Dies ist jedoch bei der Bewertung von Handelsstrategien im Tester für dasselbe Finanzinstrument nicht von Bedeutung, da der Vergleich für dasselbe Testintervall und denselben Zeitrahmen durchgeführt wird.

Bewertung von Strategien anhand der Sharpe-Ratio

Je nach Strategie-/Portfolioperformance kann die Sharpe-Ratio unterschiedliche, auch negative Werte annehmen. Die Umrechnung der Sharpe-Ratio in einen Jahreswert ermöglicht ihre Interpretation auf klassische Art und Weise:

Wert	Bedeutung	Beschreibung
Sharpe-Ratio < 0	Schlecht	Die Strategie ist nicht profitabel.
0 < Sharpe-Ratio  < 1.0	Unklar	Das Risiko zahlt sich nicht aus. Solche Strategien können in Betracht gezogen werden, wenn es keine Alternativen gibt.
Sharpe-Ratio ≥ 1,0	Gut	Wenn die Sharpe-Ratio größer als Eins ist, kann dies bedeuten, dass sich das Risiko auszahlt und das Portfolio/die Strategie positive Ergebnisse aufweisen kann.
Sharpe-Ratio ≥ 3,0	Sehr gut	Ein hoher Wert bedeutet, dass die Wahrscheinlichkeit, bei jedem einzelnen Geschäft einen Verlust zu erleiden, sehr gering ist.

Vergessen Sie nicht, dass die Sharpe-Ratio eine normale statistische Größe ist. Er spiegelt das Verhältnis zwischen Rendite und Risiko wider. Daher ist es bei der Analyse verschiedener Portfolios und Strategien wichtig, die Sharpe-Ratio mit empfohlenen Werten zu korrelieren oder mit den entsprechenden Werten zu vergleichen.

Berechnung der Sharpe-Ratio für EURUSD, 2020

Die Sharpe-Ratio wurde ursprünglich entwickelt, um Portfolios zu bewerten, die in der Regel aus vielen Aktien bestehen. Der Wert der Aktien ändert sich jeden Tag, und der Wert des Portfolios ändert sich entsprechend. Eine Veränderung des Wertes und der Rendite kann in jedem beliebigen Zeitrahmen gemessen werden. Schauen wir uns die Berechnungen für EURUSD an.

Die Berechnungen werden für zwei Zeitrahmen, H1 und D1, durchgeführt. Anschließend werden wir die Ergebnisse in Jahreswerte umrechnen und vergleichen, um zu sehen, ob es einen Unterschied gibt. Für die Berechnungen werden wir die Schlusskurse der Balken für 2020 verwenden.

Programmcode in MQL5

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   double H1_close[],D1_close[];
   double h1_returns[],d1_returns[];
   datetime from = D'01.01.2020';
   datetime to = D'01.01.2021';
   int bars = CopyClose("EURUSD",PERIOD_H1,from,to,H1_close);
   if(bars == -1)
      Print("CopyClose(\"EURUSD\",PERIOD_H1,01.01.2020,01.01.2021 failed. Error ",GetLastError());
   else
     {
      Print("\nCalculate the mean and standard deviation of returns on H1 bars");
      Print("H1 bars=",ArraySize(H1_close));
      GetReturns(H1_close,h1_returns);
      double average = ArrayMean(h1_returns);
      PrintFormat("H1 average=%G",average);
      double std = ArrayStd(h1_returns);
      PrintFormat("H1 std=%G",std);
      double sharpe_H1 = average / std;
      PrintFormat("H1 Sharpe=%G",sharpe_H1);
      double sharpe_annual_H1 = sharpe_H1 * MathSqrt(ArraySize(h1_returns));
      Print("Sharpe_annual(H1)=", sharpe_annual_H1);
     }

   bars = CopyClose("EURUSD",PERIOD_D1,from,to,D1_close);
   if(bars == -1)
      Print("CopyClose(\"EURUSD\",PERIOD_D1,01.01.2020,01.01.2021 failed. Error ",GetLastError());
   else
     {
      Print("\nCalculate the mean and standard deviation of returns on D1 bars");     
      Print("D1 bars=",ArraySize(D1_close));
      GetReturns(D1_close,d1_returns);
      double average = ArrayMean(d1_returns);
      PrintFormat("D1 average=%G",average);
      double std = ArrayStd(d1_returns);
      PrintFormat("D1 std=%G",std);
      double sharpe_D1 = average / std;
      double sharpe_annual_D1 = sharpe_D1 * MathSqrt(ArraySize(d1_returns));
      Print("Sharpe_annual(H1)=", sharpe_annual_D1);
     }
  }

//+------------------------------------------------------------------+
//|  Fills the returns[] array of returns                            |
//+------------------------------------------------------------------+
void GetReturns(const double & values[], double & returns[])
  {
   int size = ArraySize(values);
//--- if less than 2 values, return an empty array of returns
   if(size < 2)
     {
      ArrayResize(returns,0);
      PrintFormat("%s: Error. ArraySize(values)=%d",size);
      return;
     }
   else
     {
      //--- fill returns in a loop
      ArrayResize(returns, size - 1);
      double delta;
      for(int i = 1; i < size; i++)
        {
         returns[i - 1] = 0;
         if(values[i - 1] != 0)
           {
            delta = values[i] - values[i - 1];
            returns[i - 1] = delta / values[i - 1];
           }
        }
     }
//---
  }
//+------------------------------------------------------------------+
//|  Calculates the average number of array elements                 |
//+------------------------------------------------------------------+
double ArrayMean(const double & array[])
  {
   int size = ArraySize(array);
   if(size < 1)
     {
      PrintFormat("%s: Error, array is empty",__FUNCTION__);
      return(0);
     }
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += array[i];
   mean /= size;
   return(mean);
  }
//+------------------------------------------------------------------+
//|  Calculates the standard deviation of array elements             |
//+------------------------------------------------------------------+
double ArrayStd(const double & array[])
  {
   int size = ArraySize(array);
   if(size < 1)
     {
      PrintFormat("%s: Error, array is empty",__FUNCTION__);
      return(0);
     }
   double mean = ArrayMean(array);
   double std = 0;
   for(int i = 0; i < size; i++)
      std += (array[i] - mean) * (array[i] - mean);
   std /= size;
   std = MathSqrt(std);
   return(std);
  }  
//+------------------------------------------------------------------+

/*
Result

Calculate the mean and standard deviation of returns on H1 bars
H1 bars:6226
H1 average=1.44468E-05
H1 std=0.00101979
H1 Sharpe=0.0141664
Sharpe_annual(H1)=1.117708053392263

Calculate the mean and standard deviation of returns on D1 bars
D1 bars:260
D1 average=0.000355823
D1 std=0.00470188
Sharpe_annual(H1)=1.2179005039019222

*/

Python-Code zur Berechnung mit der MetaTrader 5 Bibliothek

import math
from datetime import datetime
import MetaTrader5 as mt5

# display data on the MetaTrader 5 package
print("MetaTrader5 package author: ", mt5.__author__)
print("MetaTrader5 package version: ", mt5.__version__)

# import the 'pandas' module for displaying data obtained in the tabular form
import pandas as pd

pd.set_option('display.max_columns', 50)  # how many columns to show
pd.set_option('display.width', 1500)  # max width of the table to show
# import pytz module for working with the time zone
import pytz

# establish connection to the MetaTrader 5 terminal
if not mt5.initialize():
    print("initialize() failed")
    mt5.shutdown()

# set time zone to UTC
timezone = pytz.timezone("Etc/UTC")
# create datetime objects in the UTC timezone to avoid the local time zone offset
utc_from = datetime(2020, 1, 1, tzinfo=timezone)
utc_to = datetime(2020, 12, 31, hour=23, minute=59, second=59, tzinfo=timezone)
# get EURUSD H1 bars in the interval 2020.01.01 00:00 - 2020.31.12 13:00 in the UTC timezone
rates_H1 = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_H1, utc_from, utc_to)
# also get D1 bars in the interval 2020.01.01 00:00 - 2020.31.12 13:00 in the UTC timezone
rates_D1 = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_D1, utc_from, utc_to)
# shut down connection to the MetaTrader 5 terminal and continue processing obtained bars
mt5.shutdown()

# create DataFrame out of the obtained data
rates_frame = pd.DataFrame(rates_H1)

# add the "Return" column
rates_frame['return'] = 0.0
# now calculate the returns as return[i] = (close[i] - close[i-1])/close[i-1]
prev_close = 0.0
for i, row in rates_frame.iterrows():
    close = row['close']
    rates_frame.at[i, 'return'] = close / prev_close - 1 if prev_close != 0.0 else 0.0
    prev_close = close

print("\nCalculate the mean and standard deviation of returns on H1 bars")
print('H1 rates:', rates_frame.shape[0])
ret_average = rates_frame[1:]['return'].mean()  # skip the first row with zero return
print('H1 return average=', ret_average)
ret_std = rates_frame[1:]['return'].std(ddof=0) # skip the first row with zero return
print('H1 return std =', ret_std)
sharpe_H1 = ret_average / ret_std
print('H1 Sharpe = Average/STD = ', sharpe_H1)

sharpe_annual_H1 = sharpe_H1 * math.sqrt(rates_H1.shape[0]-1)
print('Sharpe_annual(H1) =', sharpe_annual_H1)

# now calculate the Sharpe ratio on the D1 timeframe
rates_daily = pd.DataFrame(rates_D1)

# add the "Return" column
rates_daily['return'] = 0.0
# calculate returns
prev_return = 0.0
for i, row in rates_daily.iterrows():
    close = row['close']
    rates_daily.at[i, 'return'] = close / prev_return - 1 if prev_return != 0.0 else 0.0
    prev_return = close

print("\nCalculate the mean and standard deviation of returns on D1 bars")
print('D1 rates:', rates_daily.shape[0])
daily_average = rates_daily[1:]['return'].mean()
print('D1 return average=', daily_average)
daily_std = rates_daily[1:]['return'].std(ddof=0)
print('D1 return std =', daily_std)
sharpe_daily = daily_average / daily_std
print('D1 Sharpe =', sharpe_daily)

sharpe_annual_D1 = sharpe_daily * math.sqrt(rates_daily.shape[0]-1)
print('Sharpe_annual(D1) =', sharpe_annual_D1)

Result
Calculate the mean and standard deviation of returns on H1 bars

H1 rates: 6226
H1 return average= 1.4446773215242986e-05
H1 return std = 0.0010197932969323495
H1 Sharpe = Average/STD = 0.014166373968823358
Sharpe_annual(H1) = 1.117708053392236

Calculate the mean and standard deviation of returns on D1 bars
D1 rates: 260
D1 return average= 0.0003558228355051694
D1 return std = 0.004701883757646081
D1 Sharpe = 0.07567665511222807
Sharpe_annual(D1) = 1.2179005039019217 

Wie Sie sehen können, sind die Berechnungsergebnisse von MQL5 und Python identisch. Die Quellcodes sind unten beigefügt (CalculateSharpe_2TF).

Die aus H1- und D1-Balken berechneten jährlichen Sharpe-Ratios unterscheiden sich: 1.117708 und 1.217900, entsprechend. Lassen Sie uns versuchen, den Grund dafür herauszufinden.

Berechnung der jährlichen Sharpe-Ratio für EURUSD für 2020 auf allen Zeitskalen

Lassen Sie uns nun die jährliche Sharpe-Ratio für alle Zeitrahmen berechnen. Zu diesem Zweck sammeln wir die erhaltenen Daten in einer Tabelle:

• TF — Zeitrahmen
• Minutes — Anzahl der Minuten in einem Zeitrahmen
• Rates — Anzahl der Balken pro Jahr in diesem Zeitrahmen
• Avg — durchschnittliche Rendite pro Balken des Zeitrahmens in Prozent (durchschnittliche Preisänderung in Prozent pro Balken)
• Std — Standardabweichung pro Balken auf dem Zeitrahmen in Prozent (prozentuale Preisvolatilität auf diesem Zeitrahmen)
• SharpeTF — Sharpe-Ratio, berechnet für den gegebenen Zeitrahmen
• SharpeAnnual — jährliche Sharpe-Ratio, berechnet auf der Grundlage der Sharpe-Ratio dieses Zeitrahmens

Nachstehend finden Sie den Berechnungscodeblock. Der vollständige Code ist in der Datei CalculateSharpe_All_TF.mq5 verfügbar, die dem Artikel beigefügt ist.

//--- structure to print statistics to log
struct Stats
  {
   string            TF;
   int               Minutes;
   int               Rates;
   double            Avg;
   double            Std;
   double            SharpeTF;
   double            SharpeAnnual;
  };
//--- array of statistics by timeframes
Stats stats[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- arrays for close prices
   double H1_close[],D1_close[];
//--- arrays of returns
   double h1_returns[],d1_returns[];
//--- arrays of timeframes on which the Sharpe coefficient will be calculated
   ENUM_TIMEFRAMES timeframes[] = {PERIOD_M1,PERIOD_M2,PERIOD_M3,PERIOD_M4,PERIOD_M5,
                                   PERIOD_M6,PERIOD_M10,PERIOD_M12,PERIOD_M15,PERIOD_M20,
                                   PERIOD_M30,PERIOD_H1,PERIOD_H2,PERIOD_H3,PERIOD_H4,
                                   PERIOD_H6,PERIOD_H8,PERIOD_H12,PERIOD_D1,PERIOD_W1,PERIOD_MN1
                                  };

   ArrayResize(stats,ArraySize(timeframes));
//--- timeseries request parameters
   string symbol = Symbol();
   datetime from = D'01.01.2020';
   datetime to = D'01.01.2021';
   Print(symbol);
   for(int i = 0; i < ArraySize(timeframes); i++)
     {
      //--- get the array of returns on the specified timeframe
      double returns[];
      GetReturns(symbol,timeframes[i],from,to,returns);
      //--- calculate statistics
      GetStats(returns,avr,std,sharpe);
      double sharpe_annual = sharpe * MathSqrt(ArraySize(returns));
      PrintFormat("%s  aver=%G%%   std=%G%%  sharpe=%G  sharpe_annual=%G",
                  EnumToString(timeframes[i]), avr * 100,std * 100,sharpe,sharpe_annual);
      //--- fill the statistics structure
      Stats row;
      string tf_str = EnumToString(timeframes[i]);
      StringReplace(tf_str,"PERIOD_","");
      row.TF = tf_str;
      row.Minutes = PeriodSeconds(timeframes[i]) / 60;
      row.Rates = ArraySize(returns);
      row.Avg = avr;
      row.Std = std;
      row.SharpeTF = sharpe;
      row.SharpeAnnual = sharpe_annual;
      //--- add a row for the timeframe statistics
      stats[i] = row;
     }
//--- print statistics on all timeframes to log
   ArrayPrint(stats,8);
  }

/*
Result

      [TF] [Minutes] [Rates]      [Avg]      [Std] [SharpeTF] [SharpeAnnual]
[ 0] "M1"          1  373023 0.00000024 0.00168942 0.00168942     1.03182116
[ 1] "M2"          2  186573 0.00000048 0.00239916 0.00239916     1.03629642
[ 2] "M3"          3  124419 0.00000072 0.00296516 0.00296516     1.04590258
[ 3] "M4"          4   93302 0.00000096 0.00341717 0.00341717     1.04378592
[ 4] "M5"          5   74637 0.00000120 0.00379747 0.00379747     1.03746116
[ 5] "M6"          6   62248 0.00000143 0.00420265 0.00420265     1.04854166
[ 6] "M10"        10   37349 0.00000239 0.00542100 0.00542100     1.04765562
[ 7] "M12"        12   31124 0.00000286 0.00601079 0.00601079     1.06042363
[ 8] "M15"        15   24900 0.00000358 0.00671964 0.00671964     1.06034161
[ 9] "M20"        20   18675 0.00000477 0.00778573 0.00778573     1.06397070
[10] "M30"        30   12450 0.00000716 0.00966963 0.00966963     1.07893298
[11] "H1"         60    6225 0.00001445 0.01416637 0.01416637     1.11770805
[12] "H2"        120    3115 0.00002880 0.01978455 0.01978455     1.10421905
[13] "H3"        180    2076 0.00004305 0.02463458 0.02463458     1.12242890
[14] "H4"        240    1558 0.00005746 0.02871564 0.02871564     1.13344977
[15] "H6"        360    1038 0.00008643 0.03496339 0.03496339     1.12645075
[16] "H8"        480     779 0.00011508 0.03992838 0.03992838     1.11442404
[17] "H12"       720     519 0.00017188 0.05364323 0.05364323     1.22207717
[18] "D1"       1440     259 0.00035582 0.07567666 0.07567666     1.21790050
[19] "W1"      10080      51 0.00193306 0.14317328 0.14317328     1.02246174
[20] "MN1"     43200      12 0.00765726 0.43113365 0.43113365     1.49349076

*/

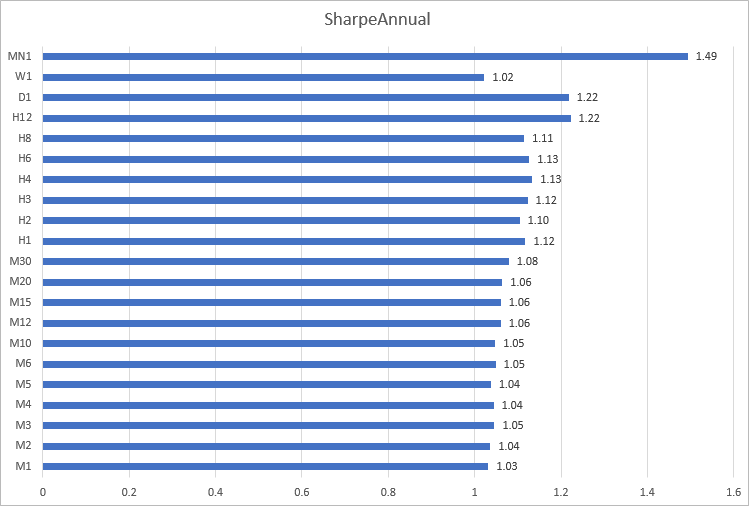
Erstellen wir ein Histogramm der Sharpe-Ratio für EURUSD für das Jahr 2020 auf den verschiedenen Zeitskalen. Hier ist zu erkennen, dass die Berechnungen für den Minuten-Zeitrahmen von M1 bis M30 nahe beieinander liegende Ergebnisse liefern: von 1,03 bis 1,08. Die uneinheitlichsten Ergebnisse wurden für die Zeitrahmen von H12 bis MN1 erzielt.

Berechnung der Sharpe-Ratio für GBPUSD, USDJPY und USDCHF für das Jahr 2020

Lassen Sie uns ähnliche Berechnungen für drei weitere Währungspaare durchführen.

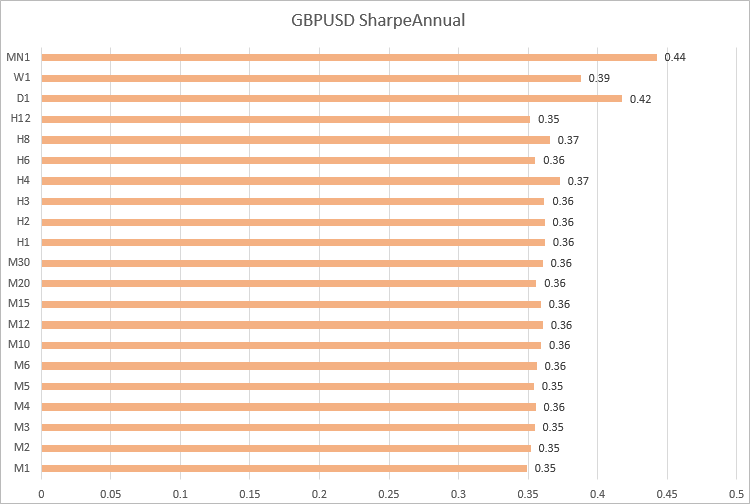
GBPUSD, die Sharpe-Ratio-Werte sind auf Zeitrahmen von M1 bis H12 ähnlich.

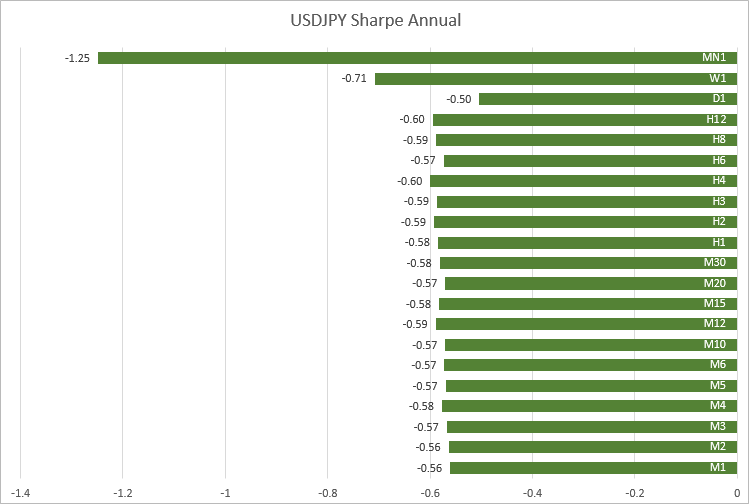
USDJPY, die Werte liegen ebenfalls nahe beieinander für die Zeitrahmen von M1 bis H12: -0,56 bis -0,60.

Für USDCHF wurden ähnliche Werte für Zeitrahmen von M1 bis M30 ermittelt. Mit zunehmendem Zeitrahmen schwankt die Sharpe-Ratio.

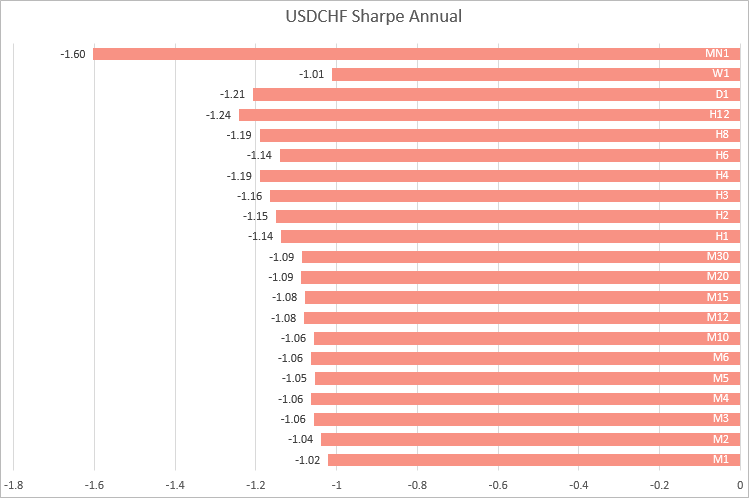
Anhand der Beispiele der vier wichtigsten Währungspaare können wir also feststellen, dass die stabilsten Berechnungen der Sharpe-Ratio auf Zeitrahmen von M1 bis M30 erhalten werden. Das bedeutet, dass es besser ist, die Ratio anhand von Renditen in niedrigeren Zeitrahmen zu berechnen, wenn Sie Strategien vergleichen möchten, die mit verschiedenen Symbolen arbeiten.

Berechnung der jährlichen Sharpe-Ratio auf EURUSD für 2020 nach Monaten

Verwenden wir die monatlichen Renditen der einzelnen Monate des Jahres 2020 und berechnen wir die jährliche Sharpe-Ratio auf Zeitrahmen von M1 bis H1. Der vollständige Code des Skripts CalculateSharpe_Months.mq5 ist dem Artikel beigefügt.

//--- structure to store returns
struct Return
  {
   double            ret;   // return
   datetime          time;  // date
   int               month; // month
  };
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   SharpeMonths sharpe_by_months[];
//--- arrays of timeframes on which the Sharpe coefficient will be calculated
   ENUM_TIMEFRAMES timeframes[] = {PERIOD_M1,PERIOD_M2,PERIOD_M3,PERIOD_M4,PERIOD_M5,
                                   PERIOD_M6,PERIOD_M10,PERIOD_M12,PERIOD_M15,PERIOD_M20,
                                   PERIOD_M30,PERIOD_H1
                                  };
   ArrayResize(sharpe_by_months,ArraySize(timeframes));
//--- timeseries request parameters
   string symbol = Symbol();
   datetime from = D'01.01.2020';
   datetime to = D'01.01.2021';
   Print("Calculate Sharpe Annual on ",symbol, " for 2020 year");
   for(int i = 0; i < ArraySize(timeframes); i++)
     {
      //--- get the array of returns on the specified timeframe
      Return returns[];
      GetReturns(symbol,timeframes[i],from,to,returns);
      double avr,std,sharpe;
      //--- Calculate statistics for the year
      GetStats(returns,avr,std,sharpe);
      string tf_str = EnumToString(timeframes[i]);
      //--- calculate the annual Sharpe ratio for each month
      SharpeMonths sharpe_months_on_tf;
      sharpe_months_on_tf.SetTimeFrame(tf_str);
      //--- select returns for i-th month
      for(int m = 1; m <= 12; m++)
        {
         Return month_returns[];
         GetReturnsByMonth(returns,m,month_returns);
         //--- Calculate statistics for the year
         double sharpe_annual = CalculateSharpeAnnual(timeframes[i],month_returns);
         sharpe_months_on_tf.Sharpe(m,sharpe_annual);
        }
      //--- add Sharpe ratio for 12 months on timeframe i
      sharpe_by_months[i] = sharpe_months_on_tf;
     }
//--- display the table of annual Sharpe values by months on all timeframes
   ArrayPrint(sharpe_by_months,3);
  }

/*
Result

Calculate Sharpe Annual on EURUSD for 2020 year
             [TF]  [Jan]  [Feb] [Marc]  [Apr] [May] [June] [July] [Aug] [Sept]  [Oct] [Nov] [Dec]
[ 0] "PERIOD_M1"  -2.856 -1.340  0.120 -0.929 2.276  1.534  6.836 2.154 -2.697 -1.194 3.891 4.140
[ 1] "PERIOD_M2"  -2.919 -1.348  0.119 -0.931 2.265  1.528  6.854 2.136 -2.717 -1.213 3.845 4.125
[ 2] "PERIOD_M3"  -2.965 -1.340  0.118 -0.937 2.276  1.543  6.920 2.159 -2.745 -1.212 3.912 4.121
[ 3] "PERIOD_M4"  -2.980 -1.341  0.119 -0.937 2.330  1.548  6.830 2.103 -2.765 -1.219 3.937 4.110
[ 4] "PERIOD_M5"  -2.929 -1.312  0.120 -0.935 2.322  1.550  6.860 2.123 -2.729 -1.239 3.971 4.076
[ 5] "PERIOD_M6"  -2.945 -1.364  0.119 -0.945 2.273  1.573  6.953 2.144 -2.768 -1.239 3.979 4.082
[ 6] "PERIOD_M10" -3.033 -1.364  0.119 -0.934 2.361  1.584  6.789 2.063 -2.817 -1.249 4.087 4.065
[ 7] "PERIOD_M12" -2.952 -1.358  0.118 -0.956 2.317  1.609  6.996 2.070 -2.933 -1.271 4.115 4.014
[ 8] "PERIOD_M15" -3.053 -1.367  0.118 -0.945 2.377  1.581  7.132 2.078 -2.992 -1.274 4.029 4.047
[ 9] "PERIOD_M20" -2.998 -1.394  0.117 -0.920 2.394  1.532  6.884 2.065 -3.010 -1.326 4.074 4.040
[10] "PERIOD_M30" -3.008 -1.359  0.116 -0.957 2.379  1.585  7.346 2.084 -2.934 -1.323 4.139 4.034
[11] "PERIOD_H1"  -2.815 -1.373  0.116 -0.966 2.398  1.601  7.311 2.221 -3.136 -1.374 4.309 4.284

*/

Es ist zu erkennen, dass die jährlichen Verhältniswerte für jeden Monat in allen Zeiträumen, für die wir Berechnungen durchgeführt haben, sehr nahe beieinander liegen. Zur besseren Darstellung können wir die Ergebnisse als 3D-Oberfläche in einem Excel-Diagramm darstellen.

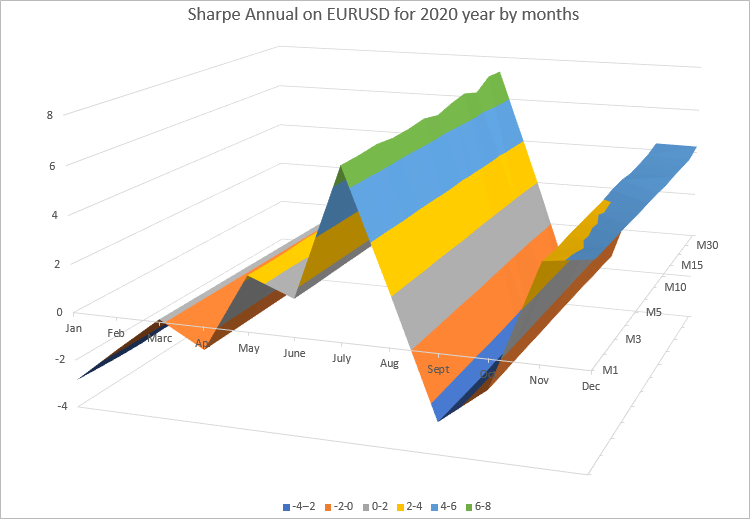
Das Diagramm zeigt deutlich, dass sich die Werte der jährlichen Sharpe-Ratio jeden Monat ändern. Dies hängt davon ab, wie sich EURUSD in diesem Monat entwickelt hat. Auf der anderen Seite ändert sich die jährliche Sharpe-Ratio für jeden Monat in allen Zeitrahmen fast nicht.

Die jährliche Sharpe-Ratio kann also für jeden Zeitrahmen berechnet werden, wobei der resultierende Wert auch von der Anzahl der Balken abhängt, für die Renditen erzielt wurden. Das bedeutet, dass dieser Berechnungsalgorithmus zum Testen, Optimieren und Überwachen in Echtzeit verwendet werden kann. Die einzige Voraussetzung ist, dass eine ausreichend große Anzahl von Renditwerten vorhanden ist.

Sortino-Ratio

Bei der Berechnung der Sharpe-Ratio besteht das Risiko in der vollen Volatilität der Kurse, also sowohl in der Zunahme als auch in der Abnahme des Vermögens. Aber der Anstieg des Portfoliowertes ist gut für den Anleger, während der Verlust nur mit seinem Rückgang verbunden ist. Daher wird das tatsächliche Risiko in der Kennzahl überbewertet. Die in den frühen 1990er Jahren von Frank Sortino entwickelte Sortino-Ratio geht auf dieses Problem ein.

Wie seine Vorgänger betrachtet F. Sortino die künftige Rendite als eine Zufallsvariable, die ihrer mathematischen Erwartung entspricht, während das Risiko als Varianz betrachtet wird. Rendite und Risiko werden auf der Grundlage der historischen Kurse für einen bestimmten Zeitraum ermittelt. Wie bei der Berechnung der Sharpe-Ratio wird die Rendite durch das Risiko geteilt.

Sortino stellte fest, dass das als Gesamtvarianz der Renditen (oder der gesamten Volatilität) definierte Risiko sowohl von positiven als auch negativen Veränderungen abhängt. Sortino ersetzte die gesamte Gesamtvolatilität durch die Semivolatilität, die nur den Rückgang der Vermögenswerte berücksichtigt. Die Semi-Volatilität wird auch als schädliche Volatilität, Abwärtsrisiko, Abwärtsabweichung, negative Volatilität oder Standardabweichung nach unten bezeichnet.

Die Berechnung der Sortino-Ratio ähnelt der von Sharpe, mit dem einzigen Unterschied, dass positive Renditen von der Volatilitätsberechnung ausgeschlossen werden. Dies verringert das Risikomaß und erhöht die Gewichtung der-Ratio.

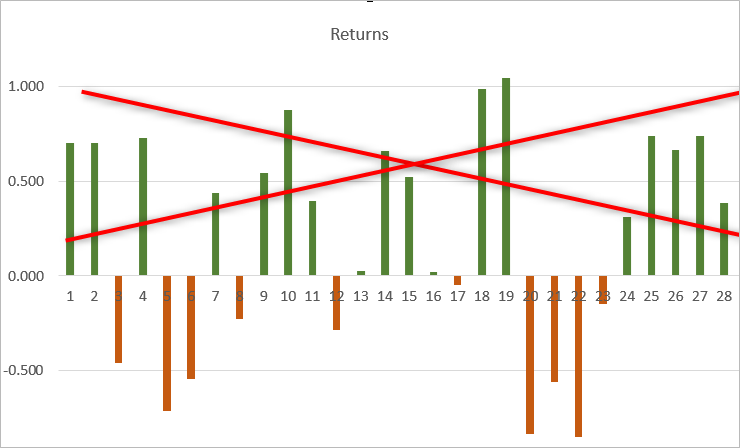
Codebeispiel für die Berechnung der Sortino-Ratio auf der Grundlage der Sharpe-Ratio. Die halbseitige Verteilung wird nur aus negativen Renditen berechnet.

//+------------------------------------------------------------------+
//|  Calculates Sharpe and Sortino ratios                            |
//+------------------------------------------------------------------+
void GetStats(ENUM_TIMEFRAMES timeframe, const double & returns[], double & avr, double & std, double & sharpe, double & sortino)
  {
   avr = ArrayMean(returns);
   std = ArrayStd(returns);
   sharpe = (std == 0) ? 0 : avr / std;
//--- now, remove negative returns and calculate the Sortino ratio
   double negative_only[];
   int size = ArraySize(returns);
   ArrayResize(negative_only,size);
   ZeroMemory(negative_only);
//--- copy only negative returns
   for(int i = 0; i < size; i++)
      negative_only[i] = (returns[i] > 0) ? 0 : returns[i];
   double semistd = ArrayStd(negative_only);
   sortino = avr / semistd;   
   return;
  }

Das diesem Artikel beigefügte Skript CalculateSortino_All_TF.mq5 generiert die folgenden Ergebnisse für EURUSD im Jahr 2020:

      [TF] [Minutes] [Rates]      [Avg]      [Std] [SharpeAnnual] [SortinoAnnual]    [Ratio]
[ 0] "M1"          1  373023 0.00000024 0.00014182     1.01769617      1.61605380 1.58795310
[ 1] "M2"          2  186573 0.00000048 0.00019956     1.02194170      1.62401856 1.58914991
[ 2] "M3"          3  124419 0.00000072 0.00024193     1.03126142      1.64332243 1.59350714
[ 3] "M4"          4   93302 0.00000096 0.00028000     1.02924195      1.62618200 1.57998030
[ 4] "M5"          5   74637 0.00000120 0.00031514     1.02303684      1.62286584 1.58632199
[ 5] "M6"          6   62248 0.00000143 0.00034122     1.03354379      1.63789024 1.58473231
[ 6] "M10"        10   37349 0.00000239 0.00044072     1.03266766      1.63461839 1.58290848
[ 7] "M12"        12   31124 0.00000286 0.00047632     1.04525580      1.65215986 1.58062730
[ 8] "M15"        15   24900 0.00000358 0.00053223     1.04515816      1.65256608 1.58116364
[ 9] "M20"        20   18675 0.00000477 0.00061229     1.04873529      1.66191269 1.58468272
[10] "M30"        30   12450 0.00000716 0.00074023     1.06348332      1.68543441 1.58482449
[11] "H1"         60    6225 0.00001445 0.00101979     1.10170316      1.75890688 1.59653431
[12] "H2"        120    3115 0.00002880 0.00145565     1.08797046      1.73062372 1.59068999
[13] "H3"        180    2076 0.00004305 0.00174762     1.10608991      1.77619289 1.60583048
[14] "H4"        240    1558 0.00005746 0.00200116     1.11659184      1.83085734 1.63968362
[15] "H6"        360    1038 0.00008643 0.00247188     1.11005321      1.79507001 1.61710267
[16] "H8"        480     779 0.00011508 0.00288226     1.09784908      1.74255746 1.58724682
[17] "H12"       720     519 0.00017188 0.00320405     1.20428761      2.11045830 1.75245371
[18] "D1"       1440     259 0.00035582 0.00470188     1.20132966      2.04624198 1.70331429
[19] "W1"      10080      51 0.00193306 0.01350157     1.03243721      1.80369984 1.74703102
[20] "MN1"     43200      12 0.00765726 0.01776075     1.49349076      5.00964481 3.35431926

Es ist zu erkennen, dass der Sortino-Wert in fast allen Zeitrahmen das 1,60-fache der Sharpe-Ratio beträgt. Natürlich gibt es keine so eindeutige Abhängigkeit, wenn die Kennzahlen auf der Grundlage von Handelsergebnissen berechnet werden. Daher ist es sinnvoll, Strategien/Portfolios anhand beider Kennzahlen zu vergleichen.

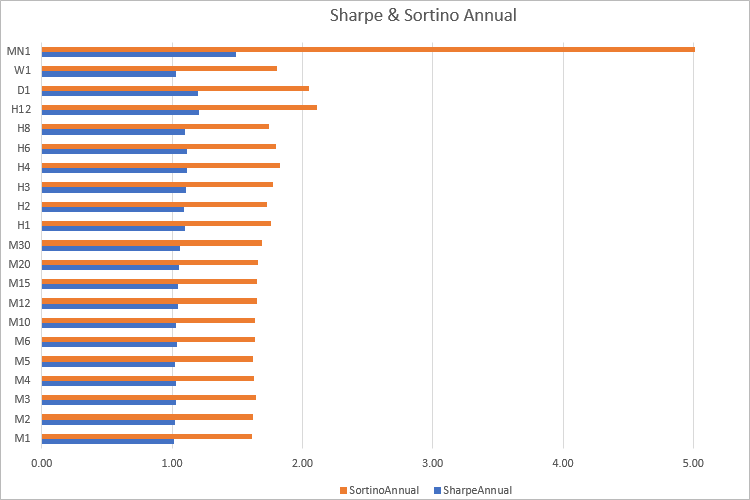
Der Unterschied zwischen diesen beiden Metriken besteht darin, dass die Sharpe-Ratio in erster Linie die Volatilität widerspiegelt, während die Sortino-Ratio wirklich das Verhältnis oder die Rendite pro Risikoeinheit angibt. Vergessen Sie jedoch nicht, dass die Berechnungen auf der Grundlage der Vergangenheit durchgeführt werden, sodass gute Ergebnisse keine Garantie für zukünftige Gewinne sind.

Beispiel für die Berechnung der Sharpe-Ratio im MetaTrader 5 Strategy Tester

Die Sharpe-Ratio wurde ursprünglich entwickelt, um Portfolios mit Aktien zu bewerten. Da sich die Aktienkurse täglich ändern, ändert sich auch der Wert von Vermögenswerten jeden Tag. Standardmäßig setzen Handelsstrategien keine offenen Positionen voraus, sodass der Zustand eines Handelskontos einen Teil der Zeit unverändert bleibt. Das bedeutet, dass wir, wenn keine offenen Positionen vorhanden sind, Null-Rendite-Werte erhalten und die Sharpe-Berechnungen für diese Positionen daher falsch sein werden. Daher werden für die Berechnungen nur die Balken verwendet, bei denen sich der Zustand des Handelskontos geändert hat. Die beste Option ist die Analyse der Aktienwerte zum letzten Tick eines jeden Balkens. Dies ermöglicht die Berechnung der Sharpe-Ratio mit jedem Tickgenerierungsmodus im MetaTrader 5 Strategietester.

Ein weiterer Punkt, der beachtet werden sollte, ist, dass der prozentuale Kursanstieg, der üblicherweise als Return[i]=(CloseCurrent-ClosePrevious)/ClosePrevious berechnet wird, einen gewissen Nachteil bei den Berechnungen hat. Wenn der Kurs um 5 % fällt und dann um 5 % steigt, erhalten wir nicht den Ausgangswert. Aus diesem Grund wird in statistischen Studien statt des üblichen relativen Kursanstiegs in der Regel der Logarithmus des Kursanstiegs verwendet. Logarithmische Renditen haben diesen Nachteil der linearen Renditen nicht. Der Wert wird wie folgt berechnet:

Log_Return =ln(Current/Previous) = ln(Current) — ln(Previous)

Log-Renditen sind praktisch, weil sie addiert werden können, da die Summe der Logarithmen dem Produkt der relativen Renditen entspricht.

Der Algorithmus zur Berechnung der Sharpe-Ratio muss also nur minimal angepasst werden.

//--- calculate the logarithms of increments using the equity array
   for(int i = 1; i < m_bars_counter; i++)
     {
      //--- only add if equity has changed
      if(m_equities[i] != prev_equity)
        {
         log_return = MathLog(m_equities[i] / prev_equity); // increment logarithm
         aver += log_return;            // average logarithm of increments
         AddReturn(log_return);         // fill the array of increment logarithms
         counter++;                     // counter of returns
        }
      prev_equity = m_equities[i];
     }
//--- if values are not enough for Sharpe calculation, return 0
   if(counter <= 1)
      return(0);
//--- average value of the increment logarithm
   aver /= counter;
//--- calculate standard deviation
   for(int i = 0; i < counter; i++)
      std += (m_returns[i] - aver) * (m_returns[i] - aver);
   std /= counter;
   std = MathSqrt(std);
//--- Sharpe ratio on the current timeframe
   double sharpe = aver / std;

Der komplette Berechnungscode ist als Include-Datei Sharpe.mqh implementiert, die dem Artikel beigefügt ist. Um die Sharpe-Ratio als nutzerdefiniertes Optimierungskriterium zu berechnen, verbinden Sie diese Datei mit Ihrem Expert Advisor und fügen ein paar Codezeilen hinzu. Schauen wir uns die Vorgehensweise am Beispiel des MACD Sample.mq5 EA aus dem MetaTrader 5 Standardpaket an.

#define MACD_MAGIC 1234502
//---
#include <Trade\Trade.mqh>
#include <Trade\SymbolInfo.mqh>
#include <Trade\PositionInfo.mqh>
#include <Trade\AccountInfo.mqh>
#include "Sharpe.mqh"
//---
input double InpLots          = 0.1;// Lots
input int    InpTakeProfit    = 50; // Take Profit (in pips)
input int    InpTrailingStop  = 30; // Trailing Stop Level (in pips)
input int    InpMACDOpenLevel = 3;  // MACD open level (in pips)
input int    InpMACDCloseLevel = 2; // MACD close level (in pips)
input int    InpMATrendPeriod = 26; // MA trend period
//---
int ExtTimeOut = 10; // time out in seconds between trade operations
CReturns   returns;
....
//+------------------------------------------------------------------+
//| Expert new tick handling function                                |
//+------------------------------------------------------------------+
void OnTick(void)
  {
   static datetime limit_time = 0; // last trade processing time + timeout
//--- add current equity to the array to calculate the Sharpe ratio
   MqlTick tick;
   SymbolInfoTick(_Symbol, tick);
   returns.OnTick(tick.time, AccountInfoDouble(ACCOUNT_EQUITY));
//--- don't process if timeout
   if(TimeCurrent() >= limit_time)
     {
      //--- check for data
      if(Bars(Symbol(), Period()) > 2 * InpMATrendPeriod)
        {
         //--- change limit time by timeout in seconds if processed
         if(ExtExpert.Processing())
            limit_time = TimeCurrent() + ExtTimeOut;
        }
     }
  }
//+------------------------------------------------------------------+
//| Tester function                                                  |
//+------------------------------------------------------------------+
double OnTester(void)
  {
//--- calculate Sharpe ratio
   double sharpe = returns.OnTester();
   return(sharpe);
  }
//+------------------------------------------------------------------+

Speichern Sie den resultierenden Code als "MACD Sample Sharpe.mq5" — die entsprechende Datei ist ebenfalls unten angehängt.

Führen wir eine genetische Optimierung für EURUSD M10 2020 durch, indem wir ein nutzerdefiniertes Optimierungskriterium auswählen.

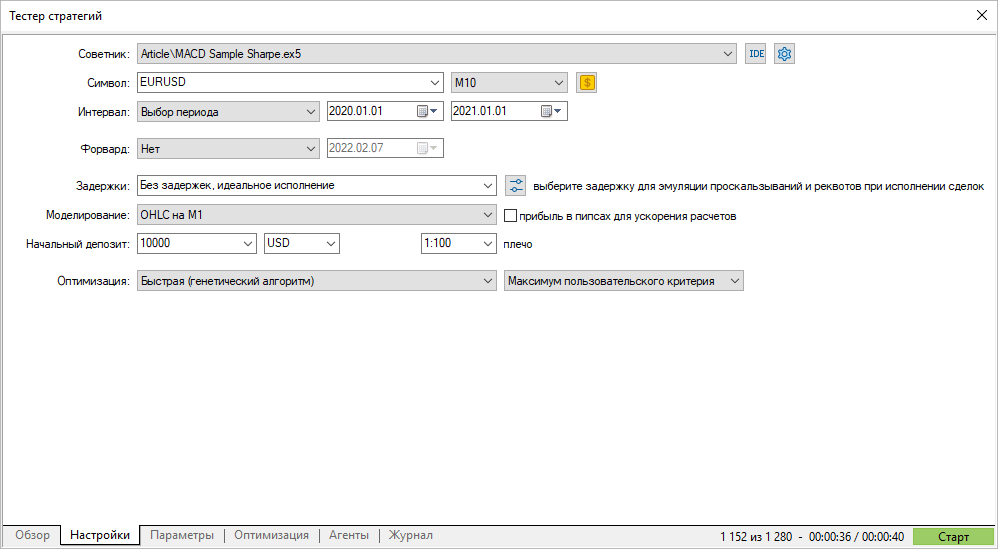
Die erhaltenen Werte des nutzerdefinierten Kriteriums stimmen mit der vom Strategietester berechneten Sharpe-Ratio überein. Sie kennen nun die Berechnungsmechanismen und wissen, wie die Ergebnisse zu interpretieren sind.

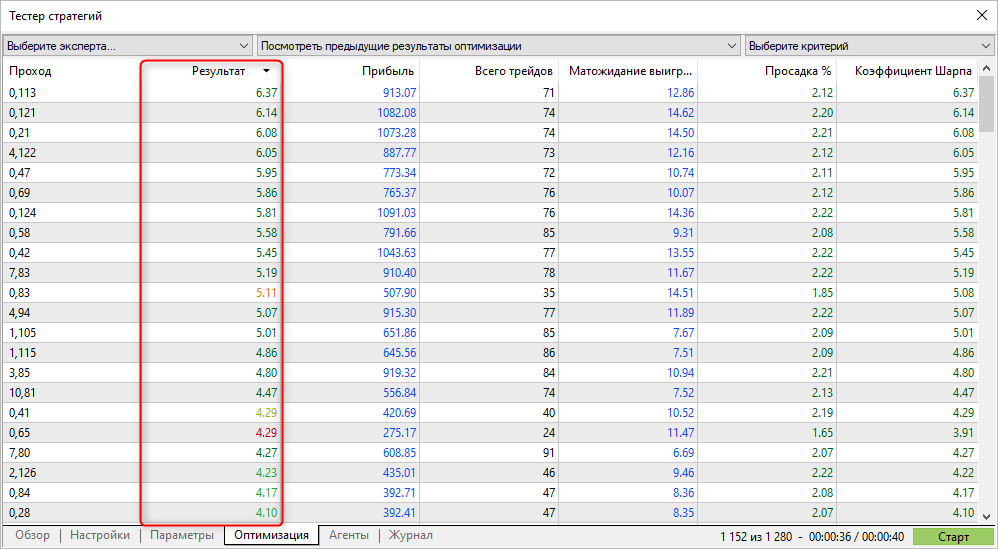
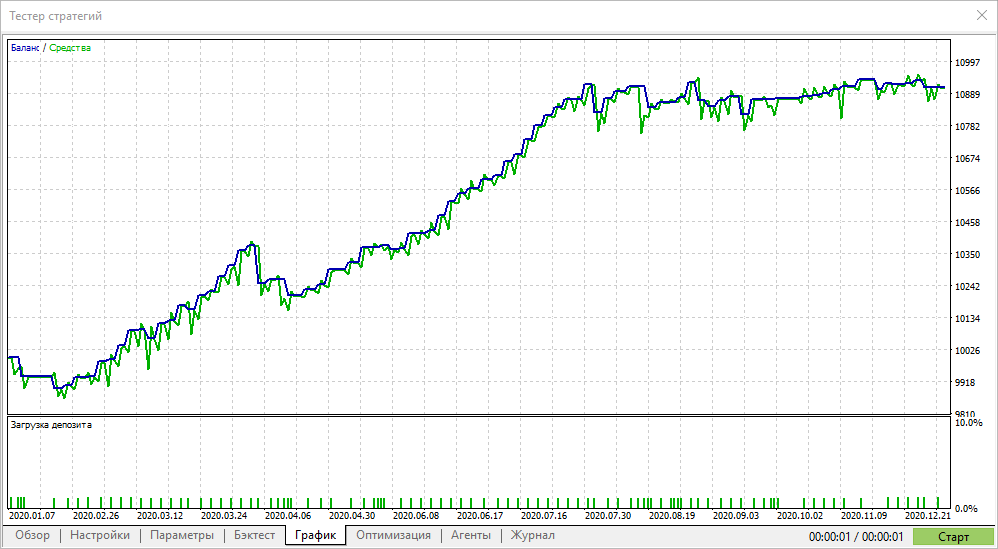
Die Durchläufe mit dem höchsten Sharpe-Ratio zeigen nicht immer den höchsten Gewinn im Tester, aber sie ermöglichen die Suche nach Parametern mit einer glatten Aktienkurve. Solche Graphen zeigen in der Regel kein starkes Wachstum, aber es gibt auch keine großen Einbrüche und Kapitalrückgänge.

Das bedeutet, dass die Optimierung nach der Sharpe-Ratio im Vergleich zu anderen Optimierungskriterien stabilere Parameter finden kann.

>

Vor- und Nachteile

Sharpe- und Sortino-Ratios ermöglichen die Feststellung, ob der erzielte Gewinn das damit verbundene Risiko abdeckt oder nicht. Ein weiterer Vorteil gegenüber alternativen Risikomaßen ist, dass die Berechnungen auf alle Arten von Vermögenswerten angewendet werden können. Beispielsweise kann man mit der Sharpe-Ratio Gold mit Silber vergleichen, da sie keine spezifische externe Benchmark zur Bewertung benötigt. Die Quoten können also sowohl auf einzelne Strategien oder Wertpapiere als auch auf Vermögens- oder Strategieportfolios angewandt werden.

Der Nachteil dieser Instrumente besteht darin, dass bei der Berechnung eine Normalverteilung der Renditen vorausgesetzt wird. In der Realität ist diese Voraussetzung nur selten erfüllt. Dennoch sind die Sharpe- und Sortino-Ratios die einfachsten und verständlichsten Instrumente, die den Vergleich verschiedener Strategien und Portfolios ermöglichen.