Modelos de clasificación de la biblioteca Scikit-learn y su exportación a ONNX
MetaTrader 5
—
Ejemplos
| 15 marzo 2024, 16:57
510
0
El desarrollo de la tecnología ha llevado al surgimiento de un enfoque fundamentalmente nuevo para la construcción de algoritmos de procesamiento de datos. Antes, resolver cada problema individual requería una formalización clara y el desarrollo de los algoritmos correspondientes.
En el aprendizaje automático, la propia computadora aprende a encontrar las mejores formas de procesar datos. Los modelos de aprendizaje automático son capaces de resolver con éxito problemas de clasificación (hay un conjunto fijo de clases, y debemos encontrar la probabilidad de que un conjunto dado de características pertenezca a cada clase) y de regresión (para un conjunto dado de características, debemos estimar el valor numérico de la variable objetivo). A partir de estos vínculos básicos, podemos construir modelos de procesamiento de datos más complejos.
Existen muchas herramientas disponibles en la biblioteca Scikit-learn tanto para clasificación como para regresión. La elección de métodos y modelos específicos depende de las características de los datos, ya que diferentes métodos pueden tener diferente eficiencia y ofrecer resultados distintos según la tarea.
En el comunicado de prensa "ONNX Runtime is now open source" se afirma que ONNX Runtime también ofrece soporte al perfil ONNX-ML:
ONNX Runtime es el primer motor de inferencia disponible públicamente con soporte completo para ONNX 1.2 y superior, incluido el perfil ONNX-ML.
El perfil ONNX-ML es una parte de ONNX creada específicamente para modelos de aprendizaje automático (ML). Está diseñado para describir y representar varios tipos de modelos de ML, como la clasificación, la regresión, la clusterización y otros en una forma cómoda que se pueda usar en diversas plataformas y entornos compatibles con ONNX. El perfil ONNX-ML facilita la comunicación, implementación y ejecución de modelos de aprendizaje automático, haciendo estos más accesibles y portátiles.
En este artículo, analizaremos el uso de todos los modelos de clasificación del paquete Scikit-learn para resolver el problema de la clasificación de los iris de Fisher; asimismo, intentaremos convertir estos al formato ONNX y usar los modelos resultantes en programas MQL5.
También compararemos la precisión de los modelos originales y sus versiones ONNX en el conjunto de datos completo Iris dataset.
Contenido
- 1. Iris de Fisher
- 2. Modelos para la clasificación.
Lista de clasificadores del paquete Scikit-learn
Representación distinta de los datos de salida para los modelos iris.mqh - 2.1. SVC Classifier
2.1.1. Código de creación del modelo SVC Classifier
2.1.2. Código MQL5 para trabajar con el modelo SVC Classifier
2.1.3. Representación ONNX del modelo SVC Classifier - 2.2. LinearSVC Classifier
2.2.1. Código de creación del modelo LinearSVC Classifier
2.2.2. Código MQL5 para trabajar con el modelo LinearSVC Classifier
2.2.3. Representación ONNX del modelo LinearSVC Classifier - 2.3. NuSVC Classifier
2.3.1. Código de creación del modelo NuSVC Classifier
2.3.2. Código MQL5 para trabajar con el modelo NuSVC Classifier
2.3.3. Representación ONNX del modelo NuSVC Classifier - 2.4. Radius Neighbors Classifier
2.4.1. Código de creación del modelo Radius Neighbors Classifier
2.4.2. Código MQL5 para trabajar con el modelo Radius Neighbors Classifier
2.3.3. Representación ONNX del modelo NuSVC Classifier - 2.5. Ridge Classifier
2.5.1. Código de creación del modelo Ridge Classifier
2.5.2. Código MQL5 para trabajar con el modelo Ridge Classifier
2.5.3. Representación ONNX del modelo Ridge Classifier - 2.6. RidgeClassifierCV
2.6.1. Código de creación del modelo RidgeClassifierCV
2.6.2. Código MQL5 para trabajar con el modelo RidgeClassifierCV
2.6.3. Representación ONNX del modelo RidgeClassifierCV - 2.7. Random Forest Classifier
2.7.1. Código de creación del modelo Random Forest Classifier
2.7.2. Código MQL5 para trabajar con el modelo Random Forest Classifier
2.7.3. Representación ONNX del modelo Random Forest Classifier - 2.8. Gradient Boosting Classifier
2.8.1. Código de creación del modelo Gradient Boosting Classifier
2.8.2. Código MQL5 para trabajar con el modelo Gradient Boosting Classifier
2.8.3. Representación ONNX del modelo Gradient Boosting Classifier - 2.9. Adaptive Boosting Classifier
2.9.1. Código de creación del modelo Adaptive Boosting Classifier
2.9.2. Código MQL5 para trabajar con el modelo Adaptive Boosting Classifier
2.9.3. Representación ONNX del modelo Adaptive Boosting Classifier - 2.10. Bootstrap Aggregating Classifier
2.10.1. Código de creación del modelo Bootstrap Aggregating Classifier
2.10.2. Código MQL5 para trabajar con el modelo Bootstrap Aggregating Classifier
2.10.3. Representación ONNX del modelo Bootstrap Aggregating Classifier - 2.11. K-Nearest Neighbors (K-NN) Classifier
2.11.1. Código de creación del modelo K-Nearest Neighbors (K-NN) Classifier
2.11.2. Código MQL5 para trabajar con el modelo K-Nearest Neighbors (K-NN) Classifier
2.11.3. Representación ONNX del modelo K-Nearest Neighbors (K-NN) Classifier - 2.12. Decision Tree Classifier<
2.12.1. Código de creación del modelo Decision Tree Classifier
2.12.2. Código MQL5 para trabajar con el modelo Decision Tree Classifier
2.12.3. Representación ONNX del modelo Decision Tree Classifier - 2.13. Logistic Regression Classifier
2.13.1. Código de creación del modelo Logistic Regression Classifier
2.13.2. Código MQL5 para trabajar con el modelo Logistic Regression Classifier
2.13.3. Representación ONNX del modelo Logistic Regression Classifier - 2.14. LogisticRegressionCV Classifier
2.14.1. Código de creación del modelo LogisticRegressionCV Classifier
2.14.2. Código MQL5 para trabajar con el modelo LogisticRegressionCV Classifier
2.14.3. Representación ONNX del modelo LogisticRegressionCV Classifier - 2.15. Passive-Aggressive (PA) Classifier
2.15.1. Código de creación del modelo Passive-Aggressive (PA) Classifier
2.15.2. Código MQL5 para trabajar con el modelo Passive-Aggressive (PA) Classifier
2.15.3. Representación ONNX del modelo Passive-Aggressive (PA) Classifier - 2.16. Perceptron Classifier
2.16.1. Código de creación del modelo Perceptron Classifier
2.16.2. Código MQL5 para trabajar con el modelo Perceptron Classifier
2.16.3. Representación ONNX del modelo Perceptron Classifier - 2.17. Stochastic Gradient Descent Classifier
2.17.1. Código de creación del modelo Stochastic Gradient Descent Classifier
2.17.2. Código MQL5 para trabajar con el modelo Stochastic Gradient Descent Classifier
2.17.3. Representación ONNX del modelo Stochastic Gradient Descent Classifier - 2.18. Gaussian Naive Bayes (GNB) Classifier
2.18.1. Código de creación del modelo Gaussian Naive Bayes (GNB) Classifier
2.18.2. Código MQL5 para trabajar con el modelo Gaussian Naive Bayes (GNB) Classifier
2.18.3. Representación ONNX del modelo Gaussian Naive Bayes (GNB) Classifier - 2.19. Multinomial Naive Bayes (MNB) Classifier
2.19.1. Código de creación del modelo Multinomial Naive Bayes (MNB) Classifier
2.19.2. Código MQL5 para trabajar con el modelo Multinomial Naive Bayes (MNB) Classifier
2.19.3. Representación ONNX del modelo Multinomial Naive Bayes (MNB) Classifier - 2.20. Complement Naive Bayes (CNB) Classifier
2.20.1. Código de creación del modelo Complement Naive Bayes (CNB) Classifier
2.20.2. Código MQL5 para trabajar con el modelo Complement Naive Bayes (CNB) Classifier
2.20.3. Representación ONNX del modelo Complement Naive Bayes (CNB) Classifier - 2.21. Bernoulli Naive Bayes (BNB) Classifier
2.21.1. Código de creación del modelo Bernoulli Naive Bayes (BNB) Classifier
2.21.2. Código MQL5 para trabajar con el modelo Bernoulli Naive Bayes (BNB) Classifier
2.21.3. Representación ONNX del modelo Bernoulli Naive Bayes (BNB) Classifier - 2.22. Multilayer Perceptron Classifier
2.22.1. Código de creación del modelo Multilayer Perceptron Classifier
2.22.2. Código MQL5 para trabajar con el modelo Multilayer Perceptron Classifier
2.22.3. Representación ONNX del modelo Multilayer Perceptron Classifier - 2.23. Linear Discriminant Analysis (LDA) Classifier
2.23.1. Código de creación del modelo Linear Discriminant Analysis (LDA) Classifier
2.23.2. Código MQL5 para trabajar con el modelo Linear Discriminant Analysis (LDA) Classifier
2.23.3. Representación ONNX del modelo Linear Discriminant Analysis (LDA) Classifier - 2.24. Hist Gradient Boosting
2.24.1. Código para crear el modelo Histogram-Based Gradient Boosting Classifier
2.24.2. Código MQL5 para trabajar con el modelo Histogram-Based Gradient Boosting Classifier
2.24.3. Representación ONNX del modelo Histogram-Based Gradient Boosting Classifier - 2.25. CategoricalNB Classifier
2.25.1. Código para crear el modelo CategoricalNB Classifier
2.23.2. Código MQL5 para trabajar con el modelo CategoricalNB Classifier
2.23.3. Representación ONNX del modelo CategoricalNB Classifier - 2.26. ExtraTreeClassifier
2.26.1. Código de creación del modelo ExtraTreeClassifier
2.26.2. Código MQL5 para trabajar con el modelo ExtraTreeClassifier
2.26.3. Representación ONNX del modelo ExtraTreeClassifier - 2.27. ExtraTreesClassifier
2.27.1. Código de creación del modelo ExtraTreesClassifier
2.27.2. Código MQL5 para trabajar con el modelo ExtraTreesClassifier
2.27.3. Representación ONNX del modelo ExtraTreesClassifier - 2.28. Comparación de la precisión de todos los modelos
2.28.1. Código para calcular todos los modelos y trazar un esquema comparativo de precisión
2.28.2. Código MQL5 para ejecutar todos los modelos ONNX - 2.29. Modelos de clasificación de Sckikit-Learn que no se han podido convertir a ONNX
- 2.29.1. DummyClassifier
2.29.1.1. Código de creación del modelo DummyClassifier - 2.29.2. GaussianProcessClassifier
2.29.2.1. Código de creación del modelo GaussianProcessClassifier - 2.29.3. LabelPropagation Classifier
2.29.3.1. Código de creación del modelo LabelPropagationClassifier - 2.29.4. LabelSpreading Classifier
2.29.4.1. Código de creación del modelo LabelSpreadingClassifier - 2.29.5. NearestCentroid Classifier
2.29.5.1. Código de creación del modelo NearestCentroid Classifier - 2.29.6. Quadratic Discriminant Analysis Classifier
2.29.6.1.Código de creación del modelo Quadratic Discriminant Analysis - Conclusiones
1. Iris de Fisher
El Iris dataset es uno de los conjuntos de datos más famosos y usados en el mundo del aprendizaje automático. Fue introducido por primera vez en 1936 por el estadístico y biólogo R.A. Fisher y desde entonces se ha convertido en un conjunto de datos clásico para problemas de clasificación.
El Iris dataset es un conjunto de mediciones de sépalos y pétalos de tres especies de iris: Iris setosa, Iris virginica e Iris versicolor.
Figura 1. Iris setosa
Figura 2. Iris virginica
Fig. 3. Iris versicolor
El conjunto de datos de Iris consta de 150 especímenes de iris, 50 especímenes de cada una de las tres especies. Cada ejemplar posee cuatro características numéricas (en centímetros):
- Longitud del sépalo
- Anchura del sépalo
- Longitud del pétalo
- Anchura del pétalo
Cada ejemplar posee además una clase correspondiente que indica el tipo de iris (Iris setosa, Iris virginica o Iris versicolor). Este atributo de clasificación hace que el Iris Dataset sea un conjunto de datos ideal para tareas de aprendizaje automático como clasificación y clusterización.
El MetaEditor nos permite trabajar con scripts en Python. Para crear un script de Python, seleccionaremos "Nuevo" en el menú "Archivo" del MetaEditor. Allí aparecerá una ventana de diálogo para seleccionar el objeto a crear (fig. 4).
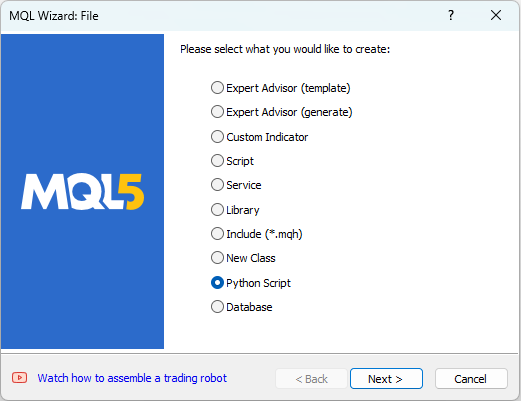
Fig.4. Creamos un script en Python en el MQL5 Wizard - Paso 1
A continuación deberemos especificar el nombre del script, por ejemplo IRIS.py
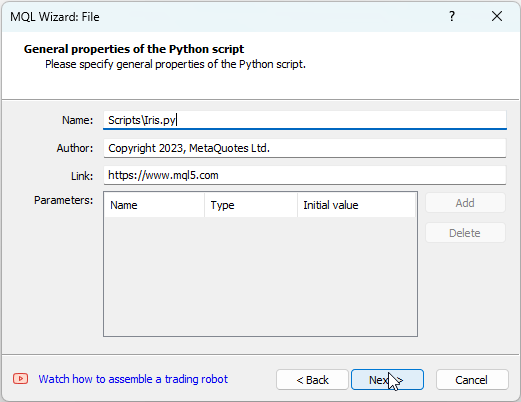
Fig.5. Creamos un script en Python en el MQL5 Wizard - Paso 2 - Nombre del script
Después de esto, podremos especificar qué bibliotecas se utilizarán; en nuestro caso, dejaremos estos campos vacíos.
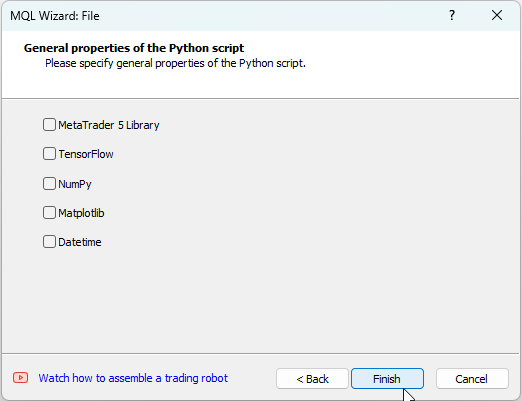
Fig.6. Creamos un script en Python en el MQL5 Wizard - Paso 3
Una forma de comenzar a analizar el conjunto de datos de Iris será visualizar los datos. La representación gráfica nos permitirá comprender mejor la estructura de los datos y las relaciones entre las características.
Por ejemplo, podemos trazar un diagrama de dispersión (scatter plot) para ver cómo se distribuyen los diferentes tipos de iris en el espacio de características.
Código de secuencia de comandos de Python:
# The script shows the scatter plot of the Iris dataset features # Copyright 2023, MetaQuotes Ltd. # https://mql5.com import matplotlib.pyplot as plt from sklearn import datasets # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # extract sepal length and sepal width (the first two features) sepal_length = X[:, 0] sepal_width = X[:, 1] # create a scatter plot plt.figure(figsize=(8, 6)) plt.scatter(sepal_length, sepal_width, c=y, cmap=plt.cm.Set1, edgecolor='k') plt.xlabel('Sepal Length (cm)') plt.ylabel('Sepal Width (cm)') plt.title('Scatter Plot for Sepal Length and Sepal Width') plt.colorbar(label='Iris Species', ticks=[0, 1, 2]) plt.show() # save the scatter plot to a file (optional) # plt.savefig('scatter_plot_sepal_length_width.png') # Extract petal length and petal width (the third and fourth features) petal_length = X[:, 2] petal_width = X[:, 3] # create a scatter plot plt.figure(figsize=(8, 6)) plt.scatter(petal_length, petal_width, c=y, cmap=plt.cm.Set1, edgecolor='k') plt.xlabel('Petal Length (cm)') plt.ylabel('Petal Width (cm)') plt.title('Scatter Plot for Petal Length and Petal Width') plt.colorbar(label='Iris Species', ticks=[0, 1, 2]) plt.show() # save the scatter plot to a file (optional) # plt.savefig('scatter_plot_petal_length_width.png')
Para ejecutar este script, deberemos copiarlo en el MetaEditor (Fig. 7) y hacer clic en "Compilar".
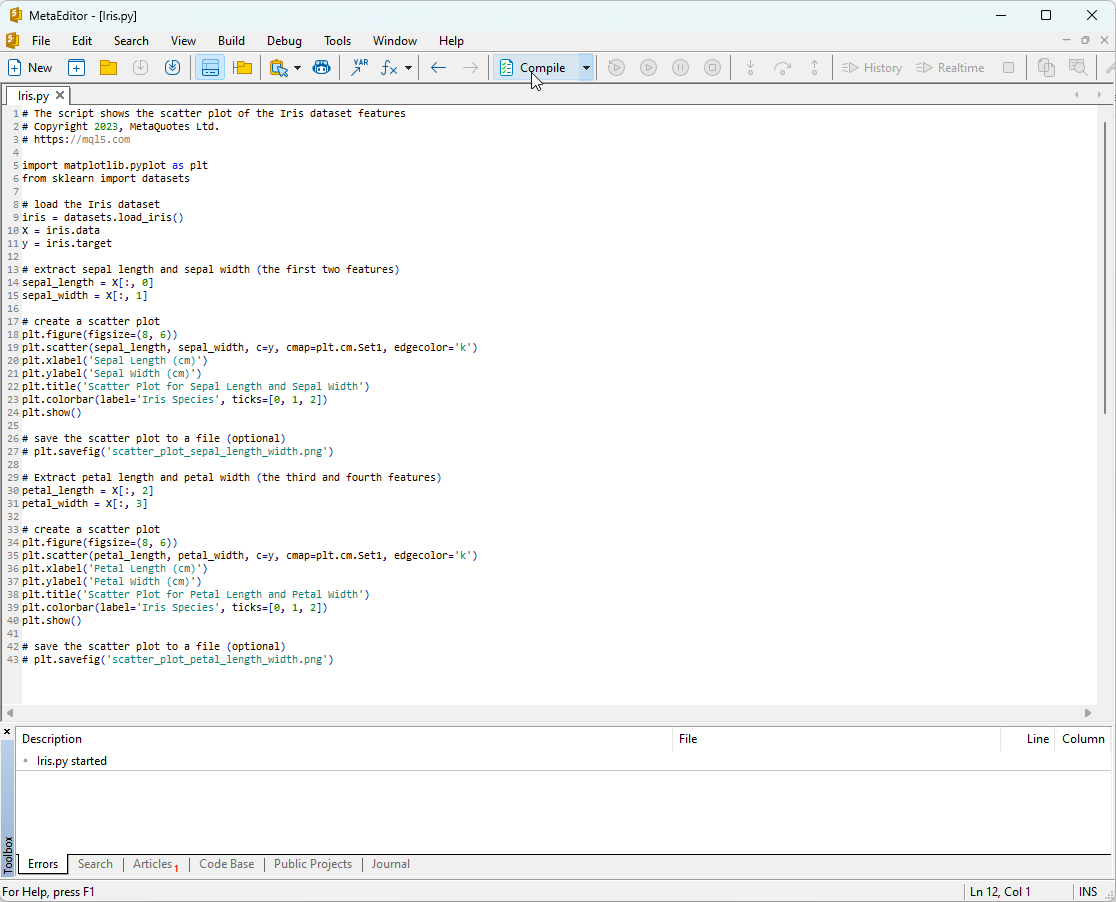
Fig.7. Script IRIS.py en el MetaEditor
Después de esto, aparecerán en pantalla los siguientes gráficos:
Fig.8. Script IRIS.py en el MetaEditor con gráfico de longitud de sépalo/anchura de sépalo
Fig.9. Script IRIS.py en el MetaEditor con gráfico de longitud de pétalo/anchura de pétalo
Veamos las descripciones más de cerca.
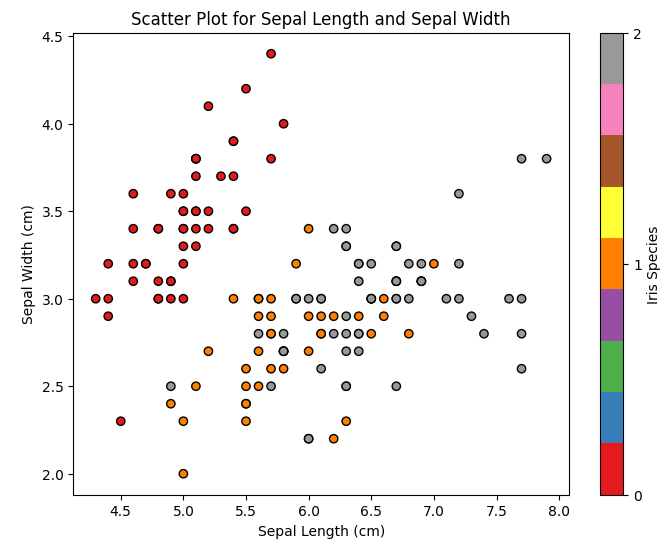
Fig. 10. Gráfico de dispersión Longitud del sépalo versus anchura del sépalo (Scatter Plot Sepal Length vs Sepal Width)
En este diagrama veremos cómo se distribuyen los diferentes tipos de iris según el largo y la anchura del sépalo. Podemos ver que Iris setosa generalmente tiene sépalos más cortos y anchos que las otras dos especies.
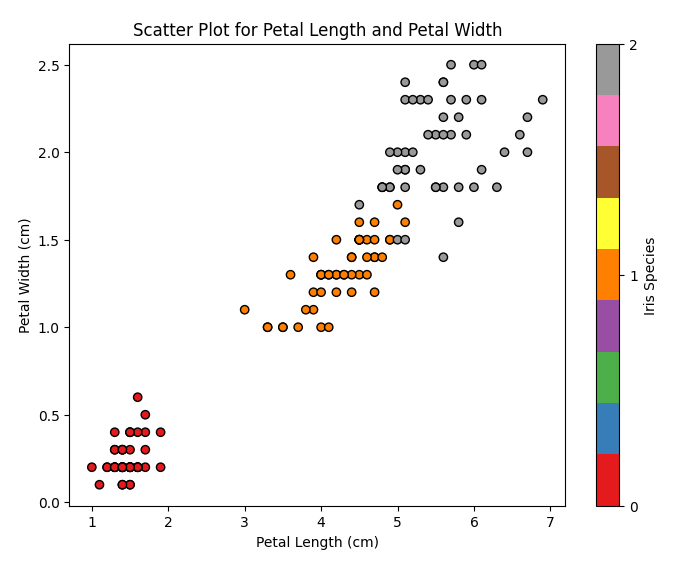
Fig. 11. Diagrama de dispersión longitud del pétalo vs anchura del pétalo (Scatter Plot Petal Length vs Petal Width)
En este diagrama vemos cómo se distribuyen los diferentes tipos de iris según el largo y la anchura del pétalo. Podemos observar que el Iris setosa tiene los pétalos más cortos y estrechos, el Iris virginica los más largos y anchos, y el Iris versicolor se encuentra en medio.
El Iris dataset es ideal para entrenar y probar modelos de aprendizaje automático. Lo utilizaremos para analizar el rendimiento de los modelos de aprendizaje automático en la tarea de clasificación.
2. Modelos para la clasificación
La tarea de clasificación es una de las principales tareas del aprendizaje automático y su objetivo es dividir los datos en diferentes categorías o clases en función de algunos atributos.
Vamos a analizar los principales modelos de aprendizaje automático del paquete scikit-learn.
Lista de clasificadores del paquete Scikit-learn
Podemos utilizar un script para obtener una lista de los clasificadores Scikit-learn disponibles:
# ScikitLearnClassifiers.py # The script lists all the classification algorithms available in scikit-learn # Copyright 2023, MetaQuotes Ltd. # https://mql5.com # print Python version from platform import python_version print("The Python version is ", python_version()) # print scikit-learn version import sklearn print('The scikit-learn version is {}.'.format(sklearn.__version__)) # print scikit-learn classifiers from sklearn.utils import all_estimators classifiers = all_estimators(type_filter='classifier') for index, (name, ClassifierClass) in enumerate(classifiers, start=1): print(f"Classifier {index}: {name}")
Resultado:
Python The Python version is 3.10.0
Python The scikit-learn version is 1.2.2.
Python Classifier 1: AdaBoostClassifier
Python Classifier 2: BaggingClassifier
Python Classifier 3: BernoulliNB
Python Classifier 4: CalibratedClassifierCV
Python Classifier 5: CategoricalNB
Python Classifier 6: ClassifierChain
Python Classifier 7: ComplementNB
Python Classifier 8: DecisionTreeClassifier
Python Classifier 9: DummyClassifier
Python Classifier 10: ExtraTreeClassifier
Python Classifier 11: ExtraTreesClassifier
Python Classifier 12: GaussianNB
Python Classifier 13: GaussianProcessClassifier
Python Classifier 14: GradientBoostingClassifier
Python Classifier 15: HistGradientBoostingClassifier
Python Classifier 16: KNeighborsClassifier
Python Classifier 17: LabelPropagation
Python Classifier 18: LabelSpreading
Python Classifier 19: LinearDiscriminantAnalysis
Python Classifier 20: LinearSVC
Python Classifier 21: LogisticRegression
Python Classifier 22: LogisticRegressionCV
Python Classifier 23: MLPClassifier
Python Classifier 24: MultiOutputClassifier
Python Classifier 25: MultinomialNB
Python Classifier 26: NearestCentroid
Python Classifier 27: NuSVC
Python Classifier 28: OneVsOneClassifier
Python Classifier 29: OneVsRestClassifier
Python Classifier 30: OutputCodeClassifier
Python Classifier 31: PassiveAggressiveClassifier
Python Classifier 32: Perceptron
Python Classifier 33: QuadraticDiscriminantAnalysis
Python Classifier 34: RadiusNeighborsClassifier
Python Classifier 35: RandomForestClassifier
Python Classifier 36: RidgeClassifier
Python Classifier 37: RidgeClassifierCV
Python Classifier 38: SGDClassifier
Python Classifier 39: SVC
Python Classifier 40: StackingClassifier
Python Classifier 41: VotingClassifier
Python The scikit-learn version is 1.2.2.
Python Classifier 1: AdaBoostClassifier
Python Classifier 2: BaggingClassifier
Python Classifier 3: BernoulliNB
Python Classifier 4: CalibratedClassifierCV
Python Classifier 5: CategoricalNB
Python Classifier 6: ClassifierChain
Python Classifier 7: ComplementNB
Python Classifier 8: DecisionTreeClassifier
Python Classifier 9: DummyClassifier
Python Classifier 10: ExtraTreeClassifier
Python Classifier 11: ExtraTreesClassifier
Python Classifier 12: GaussianNB
Python Classifier 13: GaussianProcessClassifier
Python Classifier 14: GradientBoostingClassifier
Python Classifier 15: HistGradientBoostingClassifier
Python Classifier 16: KNeighborsClassifier
Python Classifier 17: LabelPropagation
Python Classifier 18: LabelSpreading
Python Classifier 19: LinearDiscriminantAnalysis
Python Classifier 20: LinearSVC
Python Classifier 21: LogisticRegression
Python Classifier 22: LogisticRegressionCV
Python Classifier 23: MLPClassifier
Python Classifier 24: MultiOutputClassifier
Python Classifier 25: MultinomialNB
Python Classifier 26: NearestCentroid
Python Classifier 27: NuSVC
Python Classifier 28: OneVsOneClassifier
Python Classifier 29: OneVsRestClassifier
Python Classifier 30: OutputCodeClassifier
Python Classifier 31: PassiveAggressiveClassifier
Python Classifier 32: Perceptron
Python Classifier 33: QuadraticDiscriminantAnalysis
Python Classifier 34: RadiusNeighborsClassifier
Python Classifier 35: RandomForestClassifier
Python Classifier 36: RidgeClassifier
Python Classifier 37: RidgeClassifierCV
Python Classifier 38: SGDClassifier
Python Classifier 39: SVC
Python Classifier 40: StackingClassifier
Python Classifier 41: VotingClassifier
Para mayor comodidad, aparecerán resaltados en distintos colores en esta lista de calificadores. Los modelos que requieran clasificadores básicos aparecerán resaltados en amarillo, mientras que los restantes podrán utilizarse de forma independiente.
De cara al futuro, debemos observar que el color verde indicará los modelos que se han exportado correctamente al formato ONNX, mientras que el color rojo indicará los modelos que presentan errores durante la conversión en la versión actual de scikit-learn 1.2.2.
Representación distinta de los datos de salida para los modelos
Hay que tener en cuenta que los distintos modelos representan la información de salida de forma diferente, por lo que hay que tener cuidado al trabajar con modelos convertidos a ONNX.
Para el problema de clasificación del iris de Fisher, los tensores de entrada tienen la misma forma para todos estos modelos:
Information about input tensors in ONNX:
1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Los tensores de salida de los modelos ONNX son distintos.
1. Modelos que no requieren procesamiento posterior
- SVC Classifier;
- LinearSVC Classifier;
- NuSVC Classifier;
- Radius Neighbors Classifier;
- Ridge Classifier;
- Ridge Classifier CV.
Information about output tensors in ONNX:
1. Name: label, Data Type: tensor(int64), Shape: [None]
2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
1. Name: label, Data Type: tensor(int64), Shape: [None]
2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Retornan el resultado (número de clase) explícitamente en la primera etiqueta entera de salida tensor(int64) sin requerir procesamiento posterior.
2. Modelos cuyos resultados requieren un procesamiento posterior:
- Random Forest Classifier;
- Gradient Boosting Classifier;
- AdaBoost Classifier;
- Bagging Classifier;
- K-NN_Classifier;
- Decision Tree Classifier;
- Logistic Regression Classifier;
- Logistic Regression CV Classifier;
- Passive-Aggressive Classifier;
- Perceptron Classifier;
- SGD Classifier;
- Gaussian Naive Bayes Classifier;
- Multinomial Naive Bayes Classifier;
- Complement Naive Bayes Classifier;
- Bernoulli Naive Bayes Classifier;
- Multilayer Perceptron Classifier;
- Linear Discriminant Analysis Classifier;
- Hist Gradient Boosting Classifier;
- Categorical Naive Bayes Classifier;
- ExtraTree Classifier;
- ExtraTrees Classifier.
Information about output tensors in ONNX:
1. Name: output_label, Data Type: tensor(int64), Shape: [None]
2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
1. Name: output_label, Data Type: tensor(int64), Shape: [None]
2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
En la salida retornan una lista de clases y las probabilidades de pertenencia a cada clase.
Para obtener el resultado en estos casos, se requiere un procesamiento posterior como seq(map(int64,tensor(float) (encontrar el elemento con máxima probabilidad).
Por lo tanto, deberemos tener cuidado y considerar estos puntos al trabajar con modelos ONNX. En el script 2.28.2.1 se presenta un ejemplo de procesamiento diferente de resultados.
iris.mqh
Para probar los modelos en el iris dataset completo en MQL5, será necesario formar los datos del conjunto de datos, para ello se utilizará la función PrepareIrisDataset().
Lo más cómodo es poner estas funciones en el archivo iris.mqh
//+------------------------------------------------------------------+ //| Iris.mqh | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" //+------------------------------------------------------------------+ //| Structure for the IRIS Dataset sample | //+------------------------------------------------------------------+ struct sIRISsample { int sample_id; // sample id (1-150) double features[4]; // SepalLengthCm,SepalWidthCm,PetalLengthCm,PetalWidthCm string class_name; // class ("Iris-setosa","Iris-versicolor","Iris-virginica") int class_id; // class id (0,1,2), calculated by function IRISClassID }; //--- Iris dataset sIRISsample ExtIRISDataset[]; int Exttotal=0; //+------------------------------------------------------------------+ //| Returns class id by class name | //+------------------------------------------------------------------+ int IRISClassID(string class_name) { //--- if(class_name=="Iris-setosa") return(0); else if(class_name=="Iris-versicolor") return(1); else if(class_name=="Iris-virginica") return(2); //--- return(-1); } //+------------------------------------------------------------------+ //| AddSample | //+------------------------------------------------------------------+ bool AddSample(const int Id,const double SepalLengthCm,const double SepalWidthCm,const double PetalLengthCm,const double PetalWidthCm, const string Species) { //--- ExtIRISDataset[Exttotal].sample_id=Id; //--- ExtIRISDataset[Exttotal].features[0]=SepalLengthCm; ExtIRISDataset[Exttotal].features[1]=SepalWidthCm; ExtIRISDataset[Exttotal].features[2]=PetalLengthCm; ExtIRISDataset[Exttotal].features[3]=PetalWidthCm; //--- ExtIRISDataset[Exttotal].class_name=Species; ExtIRISDataset[Exttotal].class_id=IRISClassID(Species); //--- Exttotal++; //--- return(true); } //+------------------------------------------------------------------+ //| Prepare Iris Dataset | //+------------------------------------------------------------------+ bool PrepareIrisDataset(sIRISsample &iris_samples[]) { ArrayResize(ExtIRISDataset,150); Exttotal=0; //--- AddSample(1,5.1,3.5,1.4,0.2,"Iris-setosa"); AddSample(2,4.9,3.0,1.4,0.2,"Iris-setosa"); AddSample(3,4.7,3.2,1.3,0.2,"Iris-setosa"); AddSample(4,4.6,3.1,1.5,0.2,"Iris-setosa"); AddSample(5,5.0,3.6,1.4,0.2,"Iris-setosa"); AddSample(6,5.4,3.9,1.7,0.4,"Iris-setosa"); AddSample(7,4.6,3.4,1.4,0.3,"Iris-setosa"); AddSample(8,5.0,3.4,1.5,0.2,"Iris-setosa"); AddSample(9,4.4,2.9,1.4,0.2,"Iris-setosa"); AddSample(10,4.9,3.1,1.5,0.1,"Iris-setosa"); AddSample(11,5.4,3.7,1.5,0.2,"Iris-setosa"); AddSample(12,4.8,3.4,1.6,0.2,"Iris-setosa"); AddSample(13,4.8,3.0,1.4,0.1,"Iris-setosa"); AddSample(14,4.3,3.0,1.1,0.1,"Iris-setosa"); AddSample(15,5.8,4.0,1.2,0.2,"Iris-setosa"); AddSample(16,5.7,4.4,1.5,0.4,"Iris-setosa"); AddSample(17,5.4,3.9,1.3,0.4,"Iris-setosa"); AddSample(18,5.1,3.5,1.4,0.3,"Iris-setosa"); AddSample(19,5.7,3.8,1.7,0.3,"Iris-setosa"); AddSample(20,5.1,3.8,1.5,0.3,"Iris-setosa"); AddSample(21,5.4,3.4,1.7,0.2,"Iris-setosa"); AddSample(22,5.1,3.7,1.5,0.4,"Iris-setosa"); AddSample(23,4.6,3.6,1.0,0.2,"Iris-setosa"); AddSample(24,5.1,3.3,1.7,0.5,"Iris-setosa"); AddSample(25,4.8,3.4,1.9,0.2,"Iris-setosa"); AddSample(26,5.0,3.0,1.6,0.2,"Iris-setosa"); AddSample(27,5.0,3.4,1.6,0.4,"Iris-setosa"); AddSample(28,5.2,3.5,1.5,0.2,"Iris-setosa"); AddSample(29,5.2,3.4,1.4,0.2,"Iris-setosa"); AddSample(30,4.7,3.2,1.6,0.2,"Iris-setosa"); AddSample(31,4.8,3.1,1.6,0.2,"Iris-setosa"); AddSample(32,5.4,3.4,1.5,0.4,"Iris-setosa"); AddSample(33,5.2,4.1,1.5,0.1,"Iris-setosa"); AddSample(34,5.5,4.2,1.4,0.2,"Iris-setosa"); AddSample(35,4.9,3.1,1.5,0.2,"Iris-setosa"); AddSample(36,5.0,3.2,1.2,0.2,"Iris-setosa"); AddSample(37,5.5,3.5,1.3,0.2,"Iris-setosa"); AddSample(38,4.9,3.6,1.4,0.1,"Iris-setosa"); AddSample(39,4.4,3.0,1.3,0.2,"Iris-setosa"); AddSample(40,5.1,3.4,1.5,0.2,"Iris-setosa"); AddSample(41,5.0,3.5,1.3,0.3,"Iris-setosa"); AddSample(42,4.5,2.3,1.3,0.3,"Iris-setosa"); AddSample(43,4.4,3.2,1.3,0.2,"Iris-setosa"); AddSample(44,5.0,3.5,1.6,0.6,"Iris-setosa"); AddSample(45,5.1,3.8,1.9,0.4,"Iris-setosa"); AddSample(46,4.8,3.0,1.4,0.3,"Iris-setosa"); AddSample(47,5.1,3.8,1.6,0.2,"Iris-setosa"); AddSample(48,4.6,3.2,1.4,0.2,"Iris-setosa"); AddSample(49,5.3,3.7,1.5,0.2,"Iris-setosa"); AddSample(50,5.0,3.3,1.4,0.2,"Iris-setosa"); AddSample(51,7.0,3.2,4.7,1.4,"Iris-versicolor"); AddSample(52,6.4,3.2,4.5,1.5,"Iris-versicolor"); AddSample(53,6.9,3.1,4.9,1.5,"Iris-versicolor"); AddSample(54,5.5,2.3,4.0,1.3,"Iris-versicolor"); AddSample(55,6.5,2.8,4.6,1.5,"Iris-versicolor"); AddSample(56,5.7,2.8,4.5,1.3,"Iris-versicolor"); AddSample(57,6.3,3.3,4.7,1.6,"Iris-versicolor"); AddSample(58,4.9,2.4,3.3,1.0,"Iris-versicolor"); AddSample(59,6.6,2.9,4.6,1.3,"Iris-versicolor"); AddSample(60,5.2,2.7,3.9,1.4,"Iris-versicolor"); AddSample(61,5.0,2.0,3.5,1.0,"Iris-versicolor"); AddSample(62,5.9,3.0,4.2,1.5,"Iris-versicolor"); AddSample(63,6.0,2.2,4.0,1.0,"Iris-versicolor"); AddSample(64,6.1,2.9,4.7,1.4,"Iris-versicolor"); AddSample(65,5.6,2.9,3.6,1.3,"Iris-versicolor"); AddSample(66,6.7,3.1,4.4,1.4,"Iris-versicolor"); AddSample(67,5.6,3.0,4.5,1.5,"Iris-versicolor"); AddSample(68,5.8,2.7,4.1,1.0,"Iris-versicolor"); AddSample(69,6.2,2.2,4.5,1.5,"Iris-versicolor"); AddSample(70,5.6,2.5,3.9,1.1,"Iris-versicolor"); AddSample(71,5.9,3.2,4.8,1.8,"Iris-versicolor"); AddSample(72,6.1,2.8,4.0,1.3,"Iris-versicolor"); AddSample(73,6.3,2.5,4.9,1.5,"Iris-versicolor"); AddSample(74,6.1,2.8,4.7,1.2,"Iris-versicolor"); AddSample(75,6.4,2.9,4.3,1.3,"Iris-versicolor"); AddSample(76,6.6,3.0,4.4,1.4,"Iris-versicolor"); AddSample(77,6.8,2.8,4.8,1.4,"Iris-versicolor"); AddSample(78,6.7,3.0,5.0,1.7,"Iris-versicolor"); AddSample(79,6.0,2.9,4.5,1.5,"Iris-versicolor"); AddSample(80,5.7,2.6,3.5,1.0,"Iris-versicolor"); AddSample(81,5.5,2.4,3.8,1.1,"Iris-versicolor"); AddSample(82,5.5,2.4,3.7,1.0,"Iris-versicolor"); AddSample(83,5.8,2.7,3.9,1.2,"Iris-versicolor"); AddSample(84,6.0,2.7,5.1,1.6,"Iris-versicolor"); AddSample(85,5.4,3.0,4.5,1.5,"Iris-versicolor"); AddSample(86,6.0,3.4,4.5,1.6,"Iris-versicolor"); AddSample(87,6.7,3.1,4.7,1.5,"Iris-versicolor"); AddSample(88,6.3,2.3,4.4,1.3,"Iris-versicolor"); AddSample(89,5.6,3.0,4.1,1.3,"Iris-versicolor"); AddSample(90,5.5,2.5,4.0,1.3,"Iris-versicolor"); AddSample(91,5.5,2.6,4.4,1.2,"Iris-versicolor"); AddSample(92,6.1,3.0,4.6,1.4,"Iris-versicolor"); AddSample(93,5.8,2.6,4.0,1.2,"Iris-versicolor"); AddSample(94,5.0,2.3,3.3,1.0,"Iris-versicolor"); AddSample(95,5.6,2.7,4.2,1.3,"Iris-versicolor"); AddSample(96,5.7,3.0,4.2,1.2,"Iris-versicolor"); AddSample(97,5.7,2.9,4.2,1.3,"Iris-versicolor"); AddSample(98,6.2,2.9,4.3,1.3,"Iris-versicolor"); AddSample(99,5.1,2.5,3.0,1.1,"Iris-versicolor"); AddSample(100,5.7,2.8,4.1,1.3,"Iris-versicolor"); AddSample(101,6.3,3.3,6.0,2.5,"Iris-virginica"); AddSample(102,5.8,2.7,5.1,1.9,"Iris-virginica"); AddSample(103,7.1,3.0,5.9,2.1,"Iris-virginica"); AddSample(104,6.3,2.9,5.6,1.8,"Iris-virginica"); AddSample(105,6.5,3.0,5.8,2.2,"Iris-virginica"); AddSample(106,7.6,3.0,6.6,2.1,"Iris-virginica"); AddSample(107,4.9,2.5,4.5,1.7,"Iris-virginica"); AddSample(108,7.3,2.9,6.3,1.8,"Iris-virginica"); AddSample(109,6.7,2.5,5.8,1.8,"Iris-virginica"); AddSample(110,7.2,3.6,6.1,2.5,"Iris-virginica"); AddSample(111,6.5,3.2,5.1,2.0,"Iris-virginica"); AddSample(112,6.4,2.7,5.3,1.9,"Iris-virginica"); AddSample(113,6.8,3.0,5.5,2.1,"Iris-virginica"); AddSample(114,5.7,2.5,5.0,2.0,"Iris-virginica"); AddSample(115,5.8,2.8,5.1,2.4,"Iris-virginica"); AddSample(116,6.4,3.2,5.3,2.3,"Iris-virginica"); AddSample(117,6.5,3.0,5.5,1.8,"Iris-virginica"); AddSample(118,7.7,3.8,6.7,2.2,"Iris-virginica"); AddSample(119,7.7,2.6,6.9,2.3,"Iris-virginica"); AddSample(120,6.0,2.2,5.0,1.5,"Iris-virginica"); AddSample(121,6.9,3.2,5.7,2.3,"Iris-virginica"); AddSample(122,5.6,2.8,4.9,2.0,"Iris-virginica"); AddSample(123,7.7,2.8,6.7,2.0,"Iris-virginica"); AddSample(124,6.3,2.7,4.9,1.8,"Iris-virginica"); AddSample(125,6.7,3.3,5.7,2.1,"Iris-virginica"); AddSample(126,7.2,3.2,6.0,1.8,"Iris-virginica"); AddSample(127,6.2,2.8,4.8,1.8,"Iris-virginica"); AddSample(128,6.1,3.0,4.9,1.8,"Iris-virginica"); AddSample(129,6.4,2.8,5.6,2.1,"Iris-virginica"); AddSample(130,7.2,3.0,5.8,1.6,"Iris-virginica"); AddSample(131,7.4,2.8,6.1,1.9,"Iris-virginica"); AddSample(132,7.9,3.8,6.4,2.0,"Iris-virginica"); AddSample(133,6.4,2.8,5.6,2.2,"Iris-virginica"); AddSample(134,6.3,2.8,5.1,1.5,"Iris-virginica"); AddSample(135,6.1,2.6,5.6,1.4,"Iris-virginica"); AddSample(136,7.7,3.0,6.1,2.3,"Iris-virginica"); AddSample(137,6.3,3.4,5.6,2.4,"Iris-virginica"); AddSample(138,6.4,3.1,5.5,1.8,"Iris-virginica"); AddSample(139,6.0,3.0,4.8,1.8,"Iris-virginica"); AddSample(140,6.9,3.1,5.4,2.1,"Iris-virginica"); AddSample(141,6.7,3.1,5.6,2.4,"Iris-virginica"); AddSample(142,6.9,3.1,5.1,2.3,"Iris-virginica"); AddSample(143,5.8,2.7,5.1,1.9,"Iris-virginica"); AddSample(144,6.8,3.2,5.9,2.3,"Iris-virginica"); AddSample(145,6.7,3.3,5.7,2.5,"Iris-virginica"); AddSample(146,6.7,3.0,5.2,2.3,"Iris-virginica"); AddSample(147,6.3,2.5,5.0,1.9,"Iris-virginica"); AddSample(148,6.5,3.0,5.2,2.0,"Iris-virginica"); AddSample(149,6.2,3.4,5.4,2.3,"Iris-virginica"); AddSample(150,5.9,3.0,5.1,1.8,"Iris-virginica"); //--- ArrayResize(iris_samples,150); for(int i=0; i<Exttotal; i++) { iris_samples[i]=ExtIRISDataset[i]; } //--- return(true); } //+------------------------------------------------------------------+
Nota sobre los métodos de clasificación: SVC, LinearSVC y NuSVC
Compararemos tres métodos de clasificación populares: SVC (Support Vector Classification), LinearSVC (Linear Support Vector Classification) y NuSVC (Nu Support Vector Classification).
Principios de funcionamiento:
- SVC (Support Vector Classification)
Principio de funcionamiento: El SVC es un método de clasificación basado en la maximización de la diferencia entre clases. Busca un hiperplano de separación óptimo que mantenga las clases lo más separadas posible y conserva los vectores de soporte, que son los puntos más cercanos al hiperplano.
Funciones de núcleo: El SVC puede usar varias funciones de núcleo, como la lineal, la función de base radial (RBF), la polinómica y otras. La función de núcleo define la forma en que se transforman los datos para encontrar el hiperplano óptimo. - LinearSVC (Linear Support Vector Classification)
Principio de funcionamiento: LinearSVC es una variante de SVC especializada en la clasificación lineal. Busca el hiperplano de separación lineal óptimo sin usar funciones de núcleo. Esto la hace más rápida y eficaz a la hora de procesar grandes cantidades de datos. - NuSVC (Nu Support Vector Classification)
Principio de funcionamiento: NuSVC también se basa en el método de vectores de soporte, pero introduce un parámetro Nu (nu) que controla la complejidad del modelo y la proporción de vectores de soporte. El valor de Nu está comprendido entre 0 y 1 y determina qué parte de los datos puede usarse para los vectores de soporte y los errores.
Ventajas:
- SVC
Potente algoritmo: El SVC puede realizar tareas de clasificación complejas y trabajar con datos no lineales mediante el uso de funciones de núcleo.
Resistencia a los valores atípicos: El SVC es fiable frente a los valores atípicos en los datos porque utiliza vectores de soporte para construir un hiperplano de separación. - LinearSVC
Alta eficiencia: LinearSVC es más rápido y eficiente al trabajar con grandes cantidades de datos, especialmente cuando hay muchos datos y un hiperplano de separación lineal resulta apropiado para la tarea.
Clasificación lineal: Si el problema se puede dividir bien de forma lineal, LinearSVC puede dar buenos resultados sin necesidad de funciones de núcleo complejas. - NuSVC
Control de la complejidad del modelo: El parámetro Nu de NuSVC permite controlar la complejidad del modelo y el equilibrio entre el ajuste a los datos y la capacidad de generalización.
Resistencia a los valores atípicos: Al igual que el SVC, el NuSVC es resistente a los valores atípicos, lo cual lo hace útil para tareas con datos imprecisos.
Limitaciones:
- SVC
Complejidad computacional: El SVC puede ser lento con grandes cantidades de datos y/o cuando se usan funciones de núcleo complejas.
Sensibilidad a la selección del núcleo: Seleccionar la función de núcleo adecuada puede ser una tarea compleja y afectar en gran medida al rendimiento de un modelo. - LinearSVC
Limitación de la linealidad: LinearSVC se limita a la separación lineal de los datos y puede ofrecer malos resultados en caso de relaciones no lineales entre las características y la variable objetivo. - NuSVC
Ajuste del parámetro Nu: El ajuste del parámetro Nu puede requerir tiempo y experimentación para lograr resultados óptimos.
Dependiendo de las características del problema y de la cantidad de datos, cada uno de estos métodos puede resultar la mejor opción. Es importante realizar experimentos y seleccionar el método que mejor se adapte a los requisitos específicos de la tarea de clasificación.
2.1. SVC Classifier
El método de clasificación Support Vector Classification (SVC) es un potente algoritmo de aprendizaje automático muy utilizado para resolver problemas de clasificación.
Principios de funcionamiento:
- Encontrar el hiperplano de separación óptimo
Principio de funcionamiento: La idea básica del SVC es encontrar el hiperplano de separación óptimo en el espacio de características. Este hiperplano debe separar al máximo los objetos de clases diferentes y debe soportar los vectores de soporte, que son los puntos de datos más cercanos al hiperplano.
Maximización del espacio libre: El SVC trata de maximizar la brecha entre clases, es decir, la distancia desde los vectores de soporte hasta el hiperplano. Esto permite que el método resulte resistente a los valores atípicos y se generalice bien a los nuevos datos. - Uso de funciones de núcleo
Funciones de núcleo: El SVC puede usar varias funciones de núcleo, como la lineal, la función de base radial (RBF), la polinómica y otras. La función de núcleo permite proyectar los datos en un espacio de mayor dimensionalidad en el que el problema se vuelve lineal, aunque no exista separabilidad lineal en el espacio de datos original.
Selección del núcleo: La elección de la función de núcleo adecuada puede afectar en gran medida al rendimiento de un modelo SVC. Un hiperplano lineal no siempre es la solución óptima.
Ventajas:
- Potente algoritmo: Gestión de tareas complejas: El SVC es capaz de resolver problemas de clasificación complejos, incluidos problemas con relaciones no lineales entre las características y la variable objetivo.
- Resistencia a los valores atípicos: El uso de vectores de soporte hace que el método sea robusto frente a valores atípicos en los datos. No depende de toda la muestra, sino solo de los vectores de soporte.
- Flexibilidad en la selección del núcleo. Adaptabilidad de los datos: La posibilidad de usar diferentes funciones de núcleo nos permite adaptar el método SVC a datos específicos y buscar dependencias no lineales.
- Buena capacidad de generalización. Generalización a nuevos datos: El modelo SVC es capaz de generalizarse a nuevos datos, lo cual lo hace útil para tareas de previsión.
Limitaciones:
- Complejidad computacional: Tiempo de entrenamiento: El entrenamiento del SVC puede ser lento, sobre todo cuando se utilizan grandes cantidades de datos o funciones de núcleo complejas.
- Selección del núcleo: Selección de la función de núcleo óptima: La elección de la función de núcleo correcta puede requerir experimentación y depende de las características de los datos.
- Sensibilidad a la escala de características. Normalización de datos: El SVC es sensible a la escala de las características, por lo que se recomienda normalizar o estandarizar los datos antes del entrenamiento.
- Interpretación del modelo. Dificultad de interpretación: Los modelos SVC pueden ser difíciles de interpretar debido al uso de núcleos no lineales y múltiples vectores de soporte.
Dependiendo de la tarea específica y de la cantidad de datos, el método SVC puede ser una potente herramienta para resolver problemas de clasificación. No obstante, es importante tener en cuenta sus limitaciones y ajustar los parámetros para obtener resultados óptimos.
2.1.1. Código de creación del modelo SVC Classifier
Este código demuestra el proceso de entrenamiento del modelo SVC Classifier con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_SVCClassifier.py # The code demonstrates the process of training SVC model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.svm import SVC from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create an SVC Classifier model with a linear kernel svc_model = SVC(kernel='linear', C=1.0) # train the model on the entire dataset svc_model.fit(X, y) # predict classes for the entire dataset y_pred = svc_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of SVC Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(svc_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path +"svc_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of SVC Classifier model in ONNX format:", accuracy_onnx)
Tras ejecutar el script en el MetaEditor utilizando el botón "Compile" en la pestaña Journal, podemos ver los resultados de su trabajo.
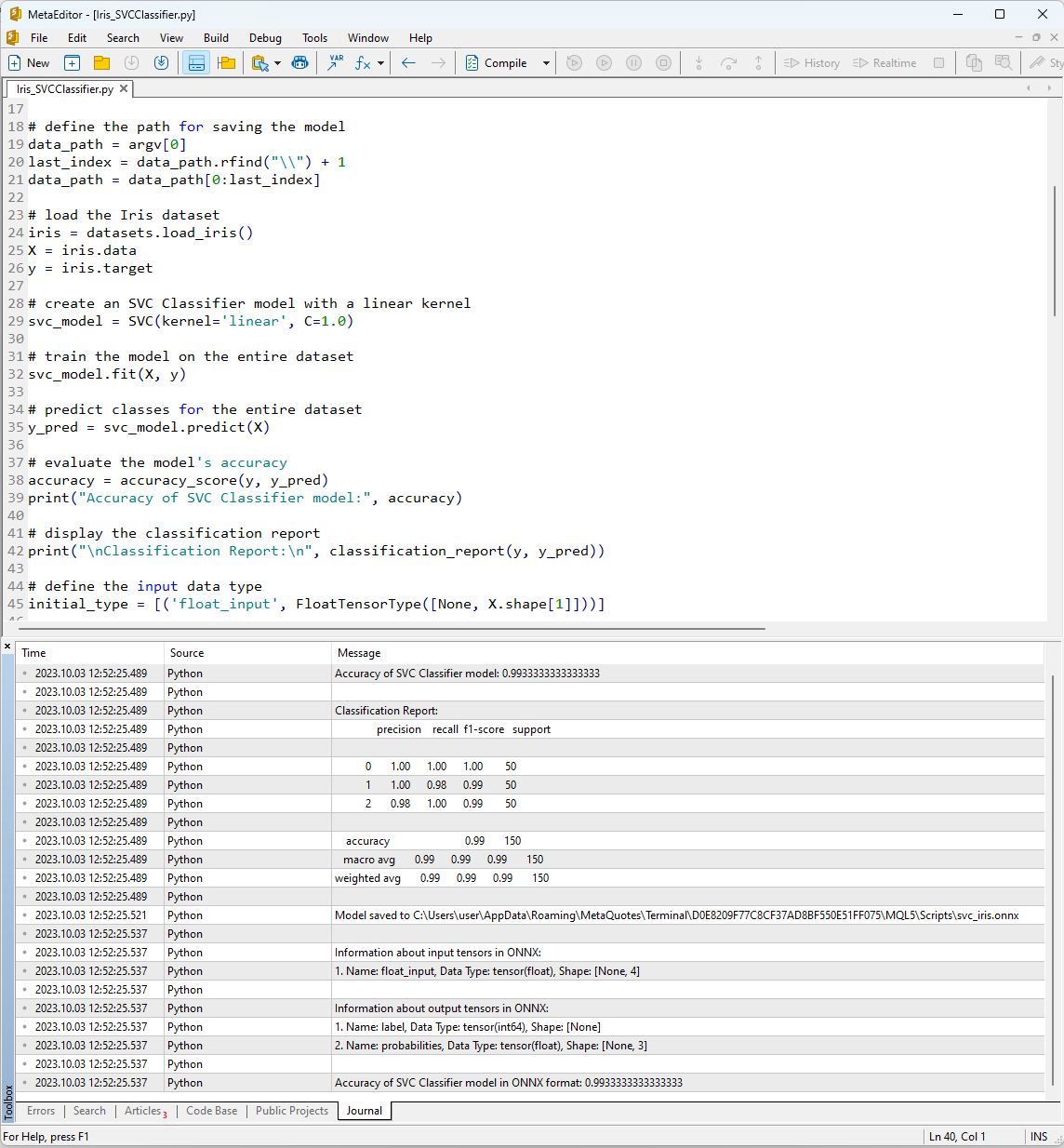
Fig. 12. Resultados del script Iris_SVMClassifier.py en el MetaEditor
Resultados del script Iris_SVCClassifier.py:
Python Accuracy of ExtraTreesClassifier model: 0.9933333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 0.98 0.99 50
Python 2 0.98 1.00 0.99 50
Python
Python accuracy 0.99 150
Python macro avg 0.99 0.99 0.99 150
Python weighted avg 0.99 0.99 0.99 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\svc_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1 0.98 1.00 0.99 50 Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1 0.98 1.00 0.99 50 Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of SVC Classifier model in ONNX format: 0.9933333333333333
Aquí podemos encontrar información sobre la ruta en la que se ha guardado el modelo ONNX, los tipos de parámetros de entrada y salida del modelo ONNX y la precisión de la descripción de los datos del Iris dataset.
La precisión de la descripción del conjunto de datos mediante el clasificador SVM es del 99%; el modelo exportado al formato ONNX muestra una precisión similar.
Ahora vamos a comprobar estos resultados de MQL5 ejecutando el modelo construido para cada una de las 150 muestras de datos. Además, en el script hay un ejemplo de tratamiento de datos por lotes.
2.1.2. Código en MQL5 para trabajar con el modelo SVC Classifier
//+------------------------------------------------------------------+ //| Iris_SVCClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "svc_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- ulong input_shape[]= { batch_size, input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- int output1[]; float output2[][3]; //--- ArrayResize(output1,(int)batch_size); ArrayResize(output2,(int)batch_size); //--- ulong output_shape[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {batch_size,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output1,output2); //--- classes are ready in output1[k]; if(res) { for(int k=0; k<(int)batch_size; k++) model_classes_id[k]=output1[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="SVCClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Los resultados del script se muestran en la pestaña "Experts" del terminal MetaTrader 5.
Iris_SVCClassifier (EURUSD,H1) model:SVCClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_SVCClassifier (EURUSD,H1) model:SVCClassifier correct results: 99.33% Iris_SVCClassifier (EURUSD,H1) model=SVCClassifier all samples accuracy=0.993333 Iris_SVCClassifier (EURUSD,H1) model=SVCClassifier batch test accuracy=1.000000
El modelo SVC ha sido capaz de distinguir correctamente 149 muestras de 150, lo que supone un resultado muy bueno. El modelo solo ha cometido un error de clasificación en el Iris dataset, al predecir la clase 2 (versicolor) en lugar de la clase 1 (virginica) para la muestra nº 84.
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 99,33%, lo cual coincide con la precisión del original.
2.1.3. Representación ONNX del modelo SVC Classifier
El modelo ONNX creado puede visualizarse en el MetaEditor:
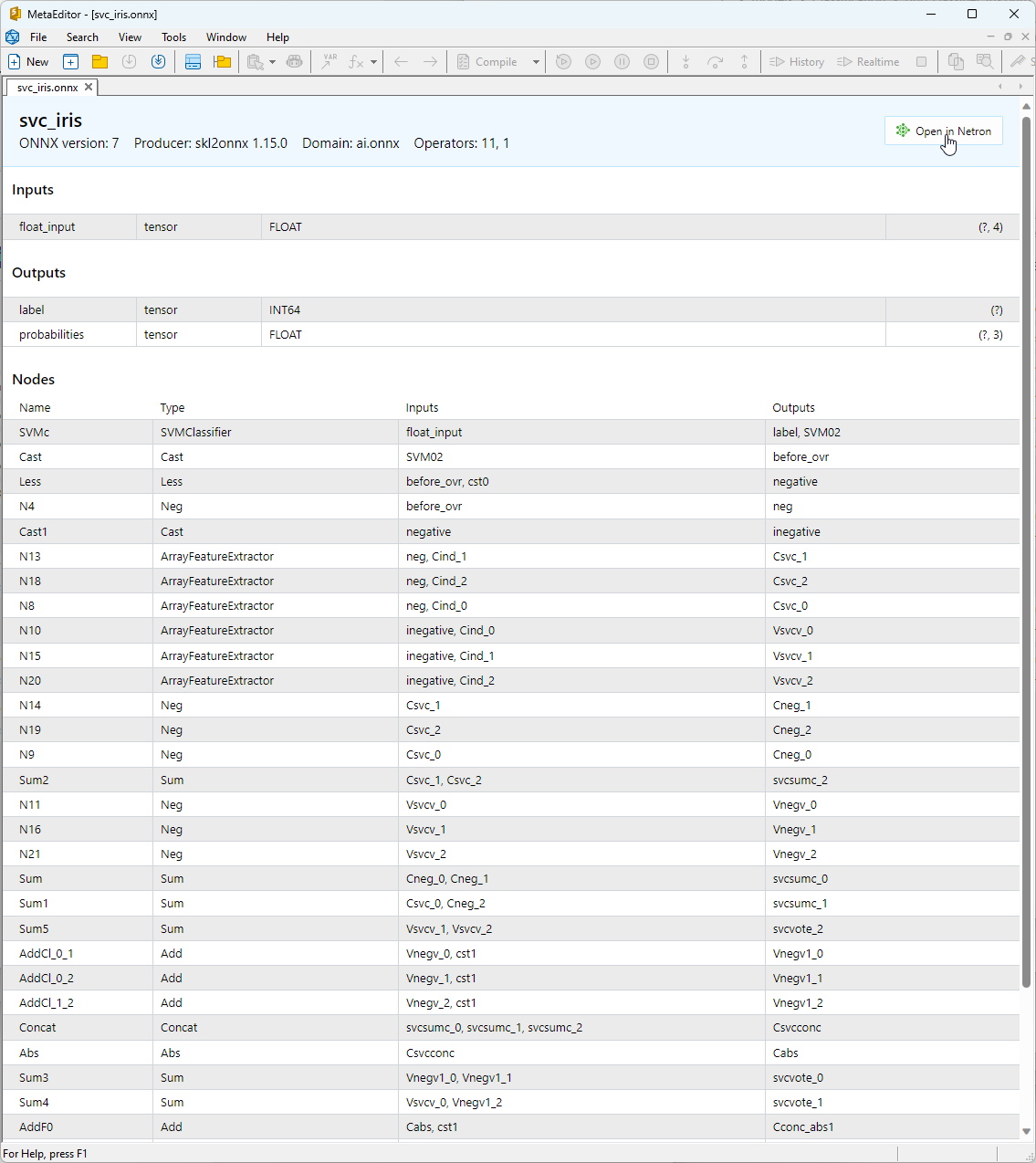
Fig. 13. Modelo ONNX svc_iris.onnx en el MetaEditor
Podemos ver información más detallada sobre la arquitectura del modelo utilizando Netron, para ello en la descripción del modelo en el MetaEditor debemos pulsar el botón "Open in Netron".
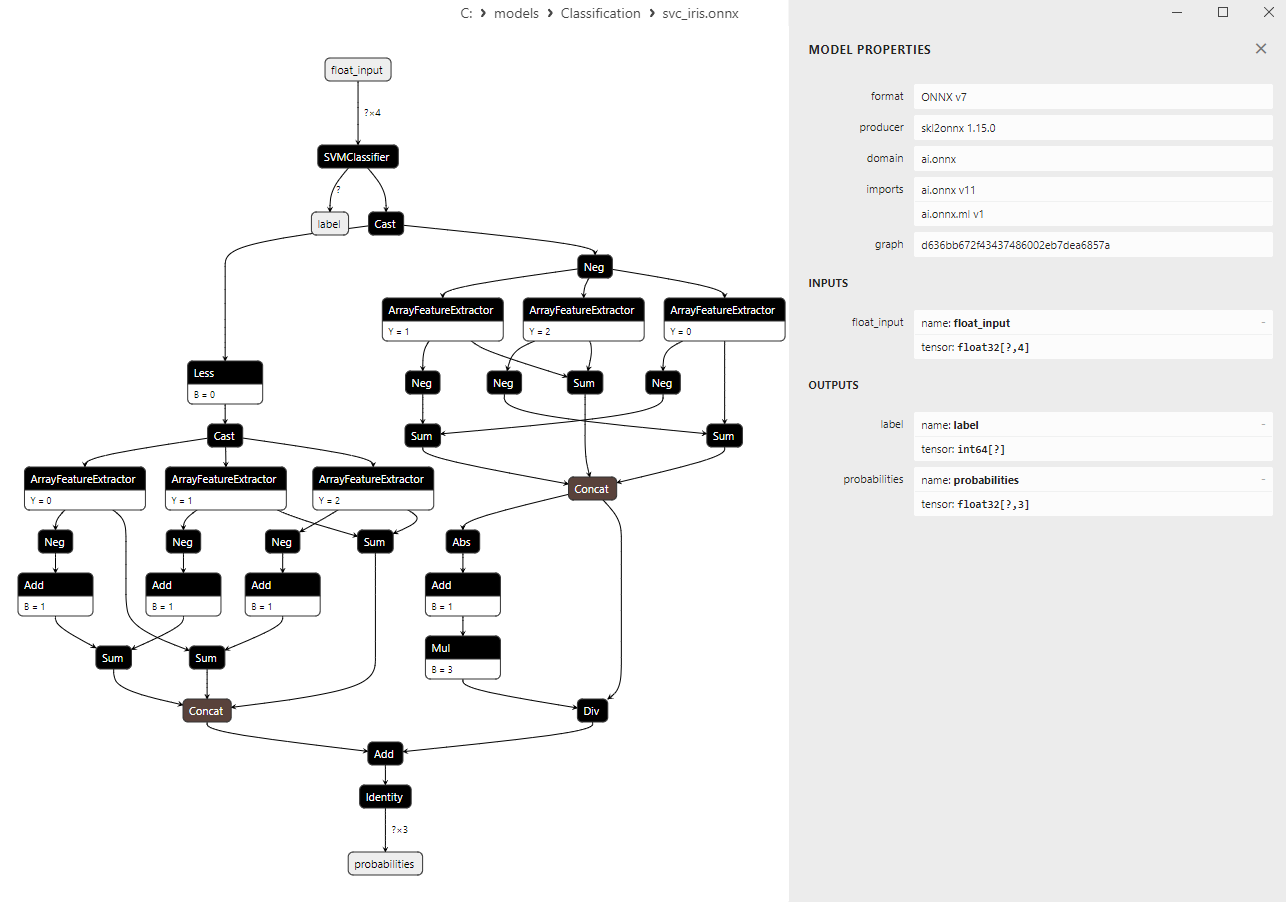
Fig. 14. Modelo ONNX svc_iris.onnx en Netron
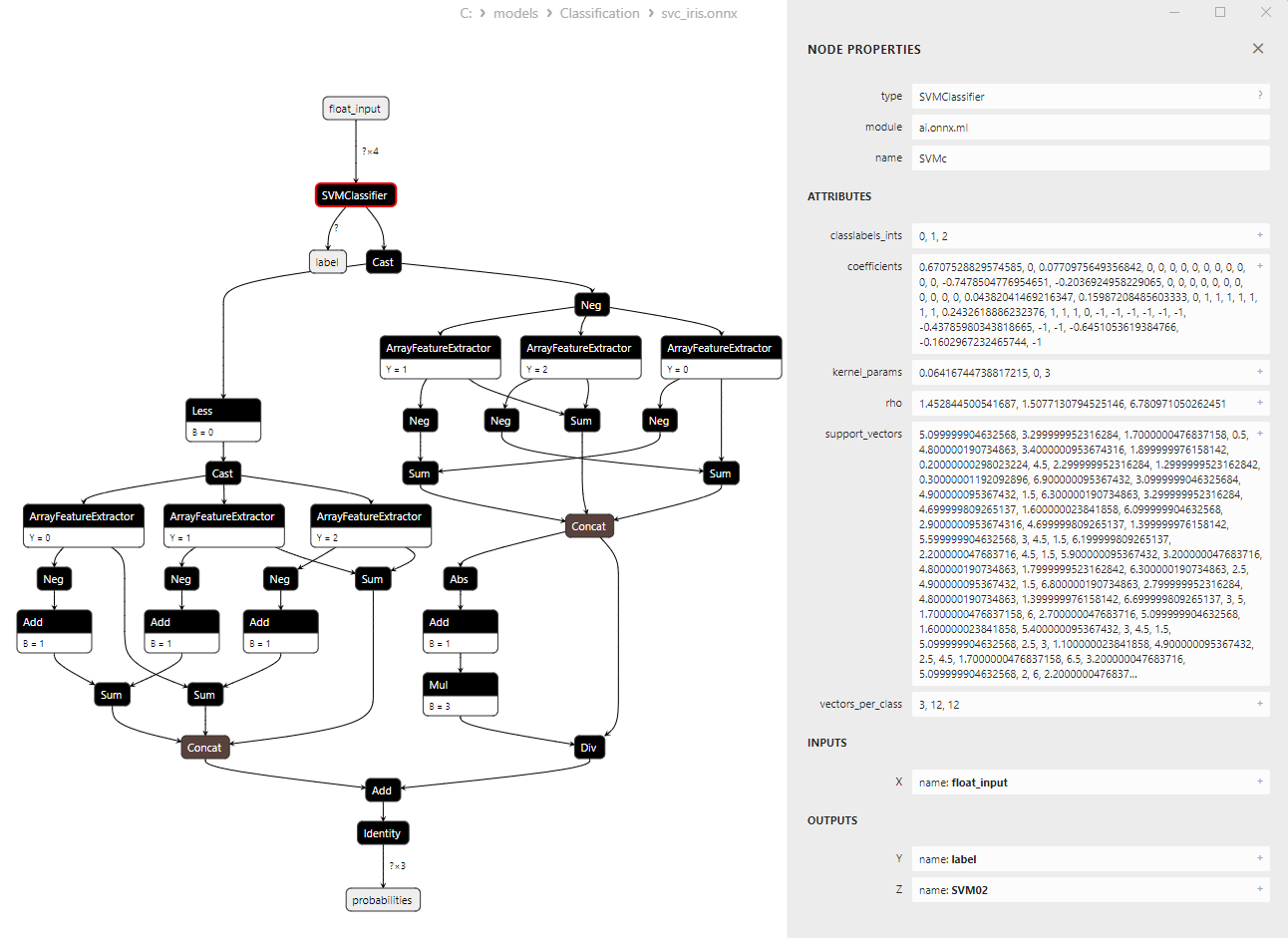
Fig. 15. Modelo ONNX svc_iris.onnx en Netron (parámetros del operador ONNX SVMClassifier)
2.2. LinearSVC Classifier
LinearSVC (Linear Support Vector Classification, método lineal de vectores de soporte) es un potente algoritmo de aprendizaje automático utilizado para tareas de clasificación binarias y multiclase. Se basa en la idea de encontrar el hiperplano que mejor separe los datos.
Principios de LinearSVC:
- Encontrar el hiperplano de separación óptimo La idea básica de LinearSVC consiste en encontrar el hiperplano óptimo que separe al máximo dos clases de datos. Un hiperplano es un plano multidimensional que se define como una ecuación lineal.
- Minimización de márgenes: LinearSVC trata de minimizar los márgenes (distancia de los puntos de datos hasta el hiperplano). Cuanto mayores sean los márgenes, más fiable será el hiperplano para separar las clases.
- Trabajo con datos linealmente inseparables: LinearSVC puede trabajar con datos que no pueden dividirse linealmente en el espacio original, mediante el uso de funciones de núcleo (kernel trick) que permiten proyectar los datos en un espacio de mayor dimensionalidad en el que pueden dividirse linealmente.
Ventajas de LinearSVC:
- Buena capacidad de generalización. LinearSVC tiene una buena capacidad de generalización y puede dar buenos resultados con datos nuevos, no vistos previamente.
- Eficiencia: LinearSVC se ejecuta rápidamente en grandes conjuntos de datos y requiere relativamente pocos recursos informáticos.
- Trabajo con datos linealmente inseparables: Usando características de núcleo, LinearSVC puede resolver problemas de clasificación con datos linealmente indivisibles.
- 6) Escalabilidad: LinearSVC puede usarse eficazmente en tareas con un gran número de características y grandes cantidades de datos.
Limitaciones de LinearSVC:
- Solo hiperplanos de separación lineales: LinearSVC solo construye hiperplanos de separación lineales, lo cual puede no ser suficiente para problemas de clasificación complejos con dependencias no lineales.
- Selección de parámetros: La selección de los parámetros correctos (por ejemplo, el parámetro de regularización) puede requerir de conocimientos expertos o validación cruzada.
- Sensibilidad a los valores atípicos: LinearSVC puede ser sensible a los valores atípicos en los datos, lo que puede afectar a la calidad de la clasificación.
- Interpretación del modelo: Los modelos creados con LinearSVC pueden ser menos interpretables que otros métodos.
LinearSVC es un potente algoritmo de clasificación con una buena capacidad de generalización, alta eficiencia y soporte para manejar datos linealmente indivisibles. Encuentra aplicación en diversos problemas de clasificación, especialmente cuando los datos pueden separarse mediante un hiperplano lineal. No obstante, conviene considerar que para problemas complejos que requieran modelar dependencias no lineales, LinearSVC puede ser una opción menos adecuada, y en tales casos debería considerarse el uso de métodos con superficies de separación más complejas.
2.2.1. Código de creación del modelo LinearSVC Classifier
Este código demuestra el proceso de entrenamiento del modelo LinearSVC Classifier con el Iris dataset, exportándolo al formato ONNX, y efectuando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_LinearSVC.py # The code demonstrates the process of training LinearSVC model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.svm import LinearSVC from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a LinearSVC model linear_svc_model = LinearSVC(C=1.0, max_iter=10000) # train the model on the entire dataset linear_svc_model.fit(X, y) # predict classes for the entire dataset y_pred = linear_svc_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of LinearSVC model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(linear_svc_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "linear_svc_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of LinearSVC model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of LinearSVC model: 0.9666666666666667
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.96 0.94 0.95 50
Python 2 0.94 0.96 0.95 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\linear_svc_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of LinearSVC model in ONNX format: 0.9666666666666667
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.96 0.94 0.95 50
Python 2 0.94 0.96 0.95 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\linear_svc_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of LinearSVC model in ONNX format: 0.9666666666666667
2.2.2. Código en MQL5 para trabajar con el modelo LinearSVC Classifier
//+------------------------------------------------------------------+ //| Iris_LinearSVC.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "linear_svc_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- ulong input_shape[]= { batch_size, input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- int output1[]; float output2[][3]; //--- ArrayResize(output1,(int)batch_size); ArrayResize(output2,(int)batch_size); //--- ulong output_shape[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {batch_size,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output1,output2); //--- classes are ready in output1[k]; if(res) { for(int k=0; k<(int)batch_size; k++) model_classes_id[k]=output1[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="LinearSVC"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_LinearSVC (EURUSD,H1) model:LinearSVC sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_LinearSVC (EURUSD,H1) model:LinearSVC sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_LinearSVC (EURUSD,H1) model:LinearSVC sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_LinearSVC (EURUSD,H1) model:LinearSVC sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_LinearSVC (EURUSD,H1) model:LinearSVC sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_LinearSVC (EURUSD,H1) model:LinearSVC correct results: 96.67% Iris_LinearSVC (EURUSD,H1) model=LinearSVC all samples accuracy=0.966667 Iris_LinearSVC (EURUSD,H1) model=LinearSVC batch test accuracy=1.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 96,67%, lo cual coincide con la precisión del original.
2.2.3. Representación ONNX del modelo LinearSVC Classifier
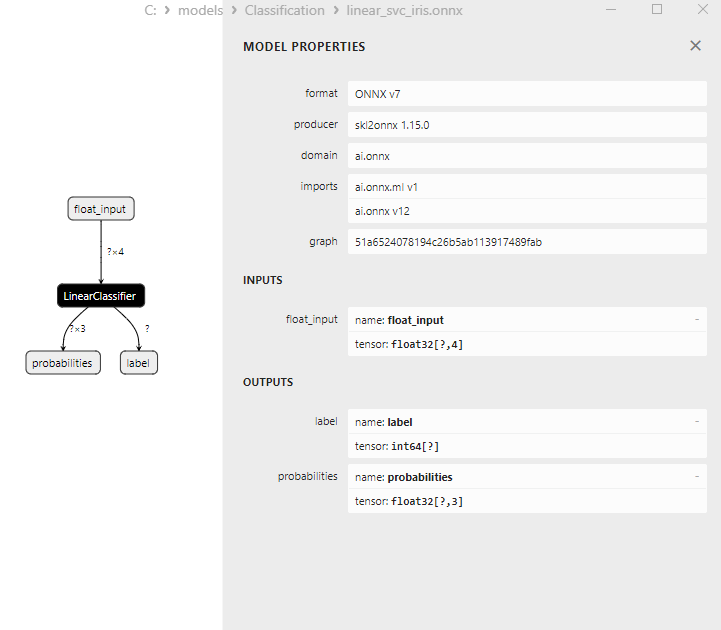
Fig. 16. Representación ONNX del modelo LinearSVC Classifier en Netron
2.3. NuSVC Classifier
El método Nu-Support Vector Classification (NuSVC) es un potente algoritmo de aprendizaje automático basado en el método de vectores de soporte (Support Vector Machine, SVM).
Principios de funcionamiento de NuSVC:
- Método de vectores de soporte (SVM) NuSVC es un tipo de SVM que se usa para resolver problemas de clasificación binarios y multiclase. El principio básico de la SVM es encontrar el hiperplano de separación óptimo que maximice la separación entre clases y tenga la máxima separación entre ellas.
- Parámetro Nu: Uno de los parámetros clave de NuSVC es el parámetro Nu (nu), que controla la complejidad del modelo y determina la proporción de la muestra que puede usarse como vectores de soporte y errores. El valor de Nu está comprendido entre 0 y 1, donde 0,5 significa que aproximadamente la mitad de la muestra se utilizará como vectores de referencia y errores.
- Selección de parámetros: Determinar los valores óptimos del parámetro Nu y otros hiperparámetros puede requerir validación cruzada y encontrar los mejores valores en los datos de entrenamiento.
- Funciones de núcleo: El SVC puede usar varias funciones de núcleo, como la lineal, la función de base radial (RBF), la polinómica y otras. La función de núcleo define el modo en que se transforma el espacio de características para encontrar el hiperplano de separación.
Ventajas de NuSVC:
- Eficiencia en espacios multidimensionales: NuSVC puede trabajar eficientemente en espacios de alta dimensionalidad, lo que lo hace adecuado para tareas con un gran número de características.
- Resistencia a los valores atípicos: SVM y NuSVC en particular son fiables respecto a los valores atípicos en los datos debido al uso de vectores de soporte.
- Control de la complejidad del modelo: El parámetro Nu nos permite controlar la complejidad del modelo y gestionar el equilibrio entre el ajuste a los datos y la capacidad de generalización.
- Buena capacidad de generalización. SVM y NuSVC, en particular, tienen una buena capacidad de generalización, lo cual permite obtener buenos resultados en datos nuevos, no vistos previamente.
Limitaciones de NuSVC:
- Ineficacia con grandes cantidades de datos: NuSVC puede resultar ineficaz en el entrenamiento con grandes cantidades de datos debido a la complejidad computacional.
- Necesidad de seleccionar parámetros: Configurar los parámetros Nu y la función de núcleo puede conllevar tiempo y recursos informáticos.
- Linealidad de la función de núcleo: La eficiencia de NuSVC puede depender en gran medida de la elección de la función del núcleo, y para algunas tareas puede que tengamos que experimentar con diferentes funciones.
- Dificultad de interpretación: SVM y NuSVC ofrecen buenos resultados, pero sus modelos pueden ser difíciles de interpretar, especialmente cuando se utilizan núcleos no lineales.
Nu-Support Vector Classification (NuSVC) es un potente método de clasificación basado en SVM que presenta varias ventajas, como la robustez frente a valores atípicos y su buena capacidad de generalización. No obstante, su eficacia puede depender de la elección de los parámetros y de la función de núcleo, y puede no resultar eficaz en entrenamientos con grandes cantidades de datos. Resulta importante elegir cuidadosamente los parámetros del método y adaptarlo a las tareas específicas de clasificación.
2.3.1. Código de creación del modelo NuSVC Classifier
Este código demuestra el proceso de entrenamiento del modelo NuSVC Classifier con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_NuSVC.py # The code demonstrates the process of training NuSVC model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.svm import NuSVC from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a NuSVC model nusvc_model = NuSVC(nu=0.5, kernel='linear') # train the model on the entire dataset nusvc_model.fit(X, y) # predict classes for the entire dataset y_pred = nusvc_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of NuSVC model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(nusvc_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "nusvc_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of NuSVC model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of NuSVC model: 0.9733333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.96 0.96 0.96 50
Python 2 0.96 0.96 0.96 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\nusvc_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of LinearSVC model in ONNX format: 0.9733333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.96 0.96 0.96 50
Python 2 0.96 0.96 0.96 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\nusvc_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of LinearSVC model in ONNX format: 0.9733333333333334
2.3.2. Código en MQL5 para trabajar con el modelo NuSVC Classifier
//+------------------------------------------------------------------+ //| Iris_NuSVC.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "nusvc_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- ulong input_shape[]= { batch_size, input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- int output1[]; float output2[][3]; //--- ArrayResize(output1,(int)batch_size); ArrayResize(output2,(int)batch_size); //--- ulong output_shape[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {batch_size,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output1,output2); //--- classes are ready in output1[k]; if(res) { for(int k=0; k<(int)batch_size; k++) model_classes_id[k]=output1[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="NuSVC"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_NuSVC (EURUSD,H1) model:NuSVC sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_NuSVC (EURUSD,H1) model:NuSVC sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_NuSVC (EURUSD,H1) model:NuSVC sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_NuSVC (EURUSD,H1) model:NuSVC sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_NuSVC (EURUSD,H1) model:NuSVC correct results: 97.33% Iris_NuSVC (EURUSD,H1) model=NuSVC all samples accuracy=0.973333 Iris_NuSVC (EURUSD,H1) model=NuSVC batch test accuracy=1.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 97,33%, lo cual coincide con la precisión del original.
2.3.3. Representación ONNX del modelo NuSVC Classifier
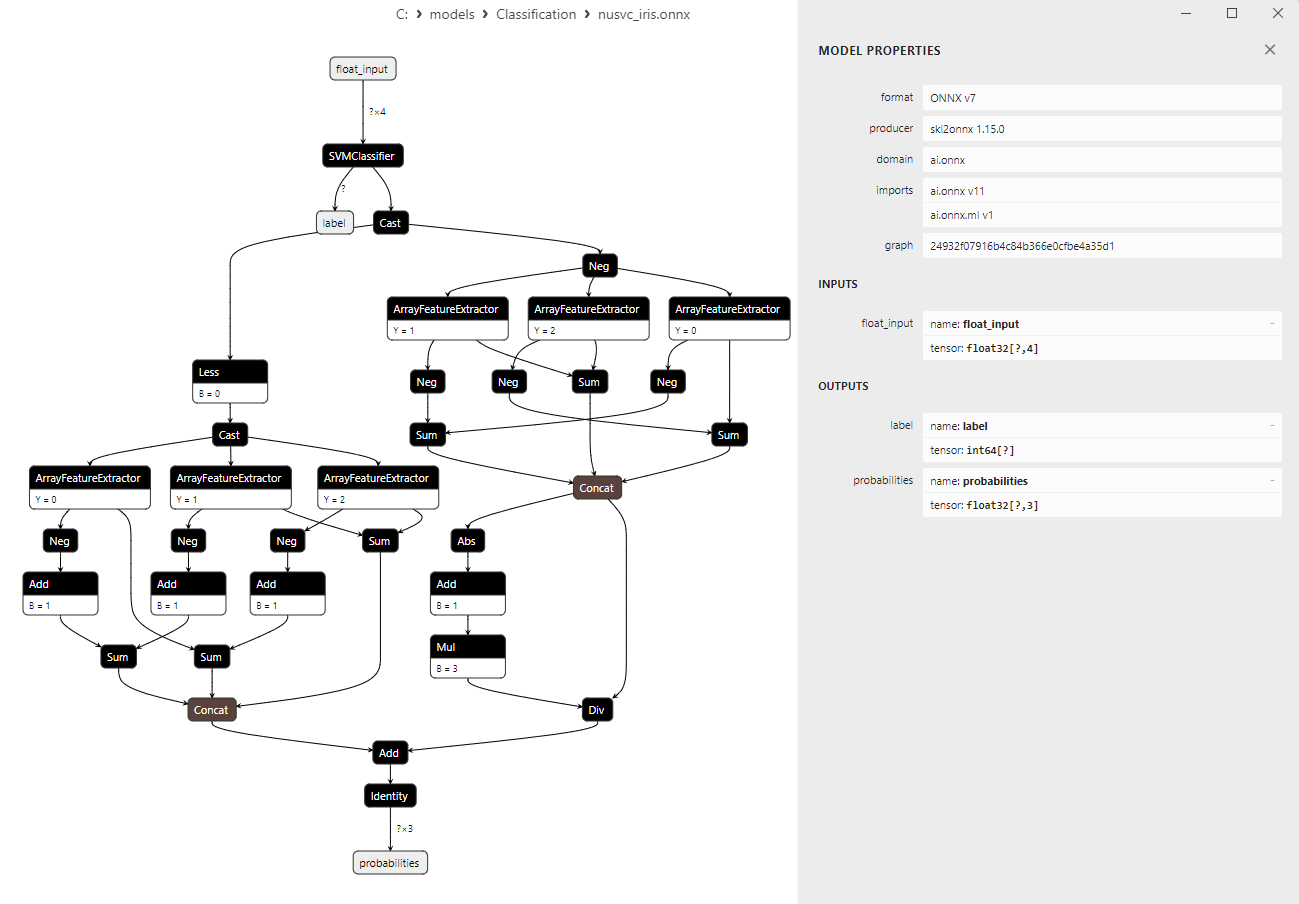
Fig. 17. Representación ONNX del modelo NuSVC Classifier en Netron
2.4. Radius Neighbors Classifier
El Radius Neighbors Classifier es una técnica de aprendizaje automático que también se utiliza para tareas de clasificación y se basa en el principio de proximidad de objetos. A diferencia del clasificador clásico K-Nearest Neighbors (K-NN), en el que se selecciona un número fijo de vecinos más próximos (K), en el clasificador Radius Neighbors los objetos se clasifican según la distancia hasta los vecinos más próximos dentro de un radio determinado.Principios de funcionamiento de Radius Neighbors Classifier:
- Definición de radio: El parámetro principal de Radius Neighbors Classifier es un radio que define la distancia máxima entre un objeto y sus vecinos a partir de la cual se considera que el objeto está cerca de la clase vecina.
- Búsqueda de los vecinos más próximos: Para cada objeto, se calcula la distancia hasta todos los demás objetos del conjunto de entrenamiento. Los objetos que se encuentran dentro del radio establecido se consideran vecinos del objeto dado.
- Votación: El Radius Neighbors Classifier utiliza la votación por mayoría entre los vecinos para determinar la clase de un objeto. Por ejemplo, si la mayoría de los vecinos pertenecen a la clase A, el objeto también se clasificará como clase A.
- Adaptabilidad a la densidad de datos: El Radius Neighbors Classifier resulta adecuado para tareas en las que la densidad de datos en distintas regiones del espacio de características puede ser diferente.
- Capacidad para trabajar con diferentes formas de clases: Este método funciona bien en problemas en los que las clases tienen formas complejas y no lineales.
- Adecuado para datos con valores atípicos: El Radius Neighbors Classifier es más robusto a los valores atípicos que K-NN porque ignora los vecinos fuera del radio.
- Sensibilidad a la selección del radio: Seleccionar el valor óptimo del radio puede ser una tarea nada trivial y requiere personalización.
- Ineficiencia en grandes conjuntos de datos: Con grandes volúmenes de datos, calcular las distancias hasta todos los objetos puede ser costoso desde el punto de vista informático.
- Dependencia de la densidad de datos: Este método puede resultar menos eficaz si los datos tienen una densidad desigual en el espacio de características.
El Radius Neighbors Classifier es una técnica de aprendizaje automático útil en situaciones en las que la proximidad de los objetos es importante y la forma de las clases puede resultar compleja. Puede usarse en diversos campos, como el análisis de imágenes, el procesamiento del lenguaje natural y otros.
2.4.1. Código de creación del modelo Radius Neighbors Classifier
Este código demuestra el proceso de entrenamiento del modelo Radius Neighbors Classifier con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_RadiusNeighborsClassifier.py # The code demonstrates the process of training an Radius Neughbors model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023 MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.neighbors import RadiusNeighborsClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Radius Neighbors Classifier model radius_model = RadiusNeighborsClassifier(radius=1.0) # train the model on the entire dataset radius_model.fit(X, y) # predict classes for the entire dataset y_pred = radius_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Radius Neighbors Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(radius_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "radius_neighbors_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Radius Neighbors Classifier model in ONNX format:", accuracy_onnx)
Resultados del script Iris_RadiusNeighbors.py:
Python Accuracy of Radius Neighbors Classifier model: 0.9733333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.98 0.96 50
Python 2 0.98 0.94 0.96 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\radius_neighbors_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of Radius Neighbors Classifier model in ONNX format: 0.9733333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.98 0.96 50
Python 2 0.98 0.94 0.96 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\radius_neighbors_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of Radius Neighbors Classifier model in ONNX format: 0.9733333333333334
La precisión del modelo original y la precisión del modelo exportado al formato ONNX han resultado iguales.
2.4.2. Código en MQL5 para trabajar con el modelo Radius Neighbors Classifier
//+------------------------------------------------------------------+ //| Iris_RadiusNeighborsClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "radius_neighbors_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- ulong input_shape[]= { batch_size, input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- int output1[]; float output2[][3]; //--- ArrayResize(output1,(int)batch_size); ArrayResize(output2,(int)batch_size); //--- ulong output_shape[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {batch_size,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output1,output2); //--- classes are ready in output1[k]; if(res) { for(int k=0; k<(int)batch_size; k++) model_classes_id[k]=output1[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="RadiusNeighborsClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_RadiusNeighborsClassifier (EURUSD,H1) model:RadiusNeighborsClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_RadiusNeighborsClassifier (EURUSD,H1) model:RadiusNeighborsClassifier sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_RadiusNeighborsClassifier (EURUSD,H1) model:RadiusNeighborsClassifier sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_RadiusNeighborsClassifier (EURUSD,H1) model:RadiusNeighborsClassifier sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_RadiusNeighborsClassifier (EURUSD,H1) model:RadiusNeighborsClassifier correct results: 97.33% Iris_RadiusNeighborsClassifier (EURUSD,H1) model=RadiusNeighborsClassifier all samples accuracy=0.973333 Iris_RadiusNeighborsClassifier (EURUSD,H1) model=RadiusNeighborsClassifier batch test accuracy=1.000000
El modelo Radius Neighbor Classifier ha mostrado una precisión del 97% con 4 errores de clasificación (muestras 78, 107, 127 y 139).
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 97,33%, lo cual coincide con la precisión del original.
2.4.3. Representación ONNX del modelo Radius Neighbors Classifier
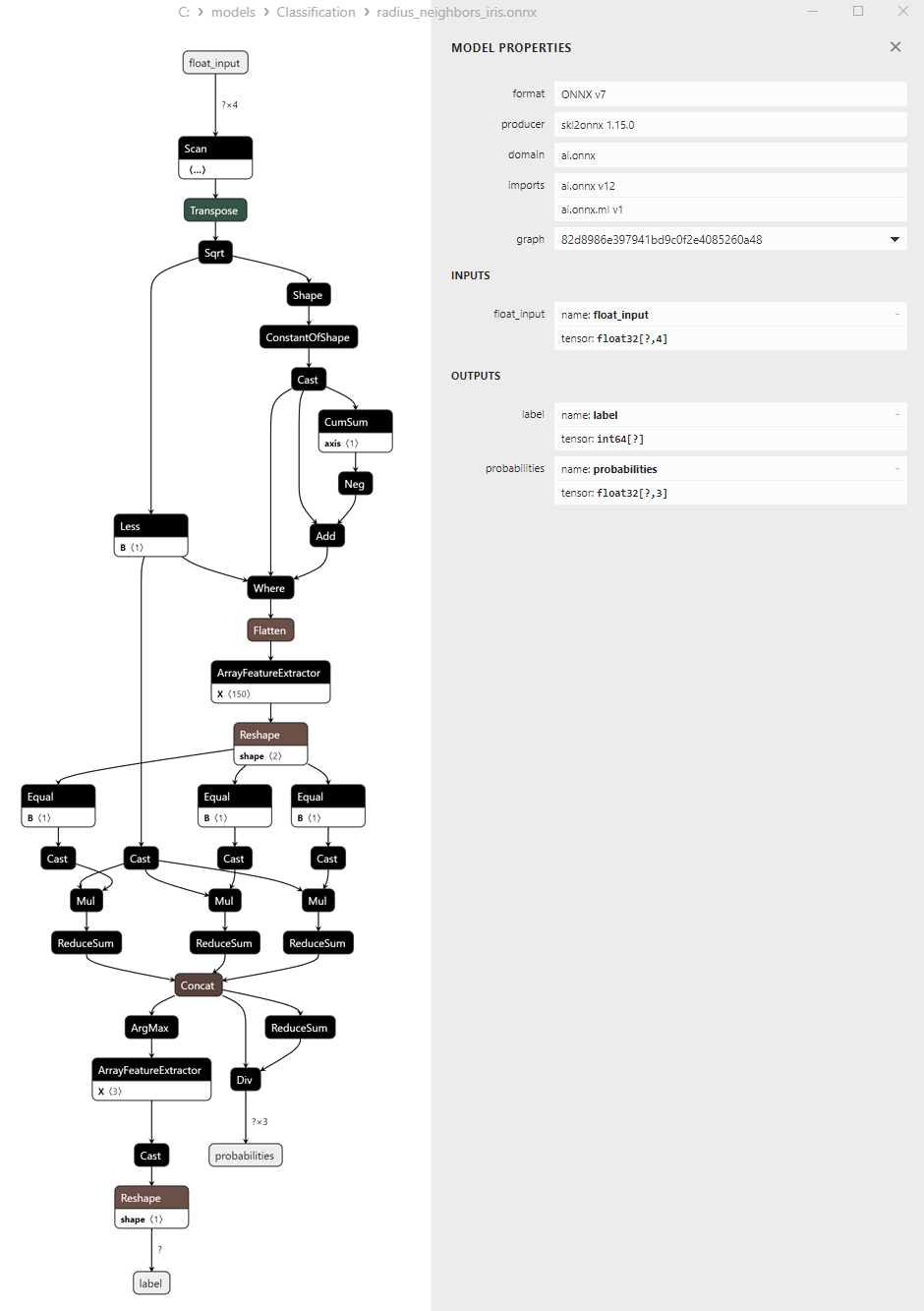
Figura 18. Representación ONNX del modelo Radius Neighbors Classifier en Netron
Nota sobre los métodos RidgeClassifier y RidgeClassifierCV
RidgeClassifier y RidgeClassifierCV son dos métodos de clasificación basados en la regresión de Ridge, pero difieren en la forma de configurar los parámetros y en la selección automática de hiperparámetros:
RidgeClassifier:
- RidgeClassifier es un método de clasificación basado en la regresión lineal de Ridge, que se utiliza para tareas de clasificación binarias y multiclase.
- En el caso de la clasificación multiclase, RidgeClassifier transforma el problema en múltiples tareas binarias (una frente a todas) y construye un modelo para cada una de ellas.
- El parámetro de regularización alpha debe ser ajustado manualmente por el usuario. Esto significa que debemos elegir el valor alpha óptimo mediante experimentación o analizando los resultados con datos de validación.
RidgeClassifierCV:
- RidgeClassifierCV es una extensión de RidgeClassifier que ofrece soporte integrado para la validación cruzada y la selección automática del valor óptimo del parámetro de regularización alpha.
- En lugar de configurar alpha manualmente, podemos transmitir a RidgeClassifierCV una lista de valores alpha para examinar y especificar el método de validación cruzada (por ejemplo, mediante el parámetro cv).
- RidgeClassifierCV seleccionará automáticamente el valor alpha óptimo que ofrezca el mejor rendimiento en la validación cruzada.
Así, la principal diferencia entre ellos es el nivel de automatización de la selección del valor óptimo del parámetro de regularización alpha. RidgeClassifier requiere el ajuste manual de alpha, mientras que RidgeClassifierCV permite la selección automática del valor óptimo de alpha mediante validación cruzada. La selección entre uno u otro depende de nuestras necesidades y de nuestro deseo de automatizar el proceso de personalización de modelos.
2.5. Ridge Classifier
El Ridge Classifier es una variante de la regresión logística que incorpora la regularización L2 (regularización de Tikhonov) al modelo. La regularización L2 añade una penalización a los valores grandes de los coeficientes del modelo, lo cual ayuda a reducir el sobreentrenamiento y mejorar la capacidad de generalización del modelo.Principios de funcionamiento de Ridge Classifier:
- Predicción de la probabilidad: Al igual que la regresión logística, Ridge Classifier modela la probabilidad de que un objeto pertenezca a una clase determinada mediante una función logística (sigmoidal).
- Regularización L2: El Ridge Classifier añade un término de regularización L2 que penaliza los valores grandes de los coeficientes del modelo. Esto se hace para controlar la complejidad del modelo y reducir el sobreentrenamiento.
- Entrenamiento de parámetros: El modelo Ridge Classifier se entrena con el conjunto de datos de entrenamiento para ajustar las ponderaciones (coeficientes) de las características y el parámetro de regularización.
- Reduce el sobreentrenamiento: La regularización L2 ayuda a reducir la tendencia del modelo a sobreajustarse, lo cual resulta especialmente útil cuando los datos son escasos.
- Resistencia a la multicolinealidad: El clasificador Ridge gestiona bien el problema de la multicolinealidad en los datos cuando las características están muy correlacionadas entre sí.
- Sensibilidad a la selección del parámetro de regularización: Como ocurre con otros métodos regularizados, la selección del valor correcto del parámetro de regularización (alpha) requiere ajuste y evaluación.
- Restricción de la clasificación multiclase: El Ridge Classifier se diseñó originalmente para la clasificación binaria, pero puede adaptarse para la clasificación multiclase usando enfoques como One-vs-All.
Ridge Classifier es un potente método de aprendizaje automático que combina las ventajas de la regresión logística con la regularización para combatir el sobreentrenamiento y mejorar la capacidad de generalización del modelo. Tiene aplicaciones en varios campos en los que la clasificación basada en la probabilidad y el control de la complejidad del modelo son importantes.
2.5.1. Código de creación de Ridge Classifier
Este código demuestra el proceso de entrenamiento del modelo Ridge Classifier con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_RidgeClassifier.py # The code demonstrates the process of training Ridge Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import RidgeClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Ridge Classifier model ridge_model = RidgeClassifier() # train the model on the entire dataset ridge_model.fit(X, y) # predict classes for the entire dataset y_pred = ridge_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Ridge Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(ridge_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "ridge_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Ridge Classifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of ExtraTreesClassifier model: 0.8533333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.87 0.66 0.75 50
Python 2 0.73 0.90 0.80 50
Python
Python accuracy 0.85 150
Python macro avg 0.86 0.85 0.85 150
Python weighted avg 0.86 0.85 0.85 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\ridge_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of SVC Classifier model in ONNX format: 0.8533333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.87 0.66 0.75 50
Python 2 0.73 0.90 0.80 50
Python
Python accuracy 0.85 150
Python macro avg 0.86 0.85 0.85 150
Python weighted avg 0.86 0.85 0.85 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\ridge_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of SVC Classifier model in ONNX format: 0.8533333333333334
2.5.2. Código en MQL5 para trabajar con el modelo Ridge Classifier
//+------------------------------------------------------------------+ //| Iris_RidgeClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "ridge_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- ulong input_shape[]= { batch_size, input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- int output1[]; float output2[][3]; //--- ArrayResize(output1,(int)batch_size); ArrayResize(output2,(int)batch_size); //--- ulong output_shape[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {batch_size,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output1,output2); //--- classes are ready in output1[k]; if(res) { for(int k=0; k<(int)batch_size; k++) model_classes_id[k]=output1[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="RidgeClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=51 FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=52 FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=57 FAILED [class=2, true class=1] features=(6.30,3.30,4.70,1.60] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=62 FAILED [class=2, true class=1] features=(5.90,3.00,4.20,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=65 FAILED [class=2, true class=1] features=(5.60,2.90,3.60,1.30] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=66 FAILED [class=2, true class=1] features=(6.70,3.10,4.40,1.40] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=76 FAILED [class=2, true class=1] features=(6.60,3.00,4.40,1.40] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=79 FAILED [class=2, true class=1] features=(6.00,2.90,4.50,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=86 FAILED [class=2, true class=1] features=(6.00,3.40,4.50,1.60] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=87 FAILED [class=2, true class=1] features=(6.70,3.10,4.70,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=89 FAILED [class=2, true class=1] features=(5.60,3.00,4.10,1.30] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=92 FAILED [class=2, true class=1] features=(6.10,3.00,4.60,1.40] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=109 FAILED [class=1, true class=2] features=(6.70,2.50,5.80,1.80] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier correct results: 85.33% Iris_RidgeClassifier (EURUSD,H1) model=RidgeClassifier all samples accuracy=0.853333 Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40) Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50) Iris_RidgeClassifier (EURUSD,H1) model=RidgeClassifier batch test accuracy=0.000000
En el conjunto completo del Iris dataset, el modelo ha mostrado una eficacia del 85,33%, lo que coincide con la precisión del original.
2.5.3. Representación ONNX del modelo Ridge Classifier
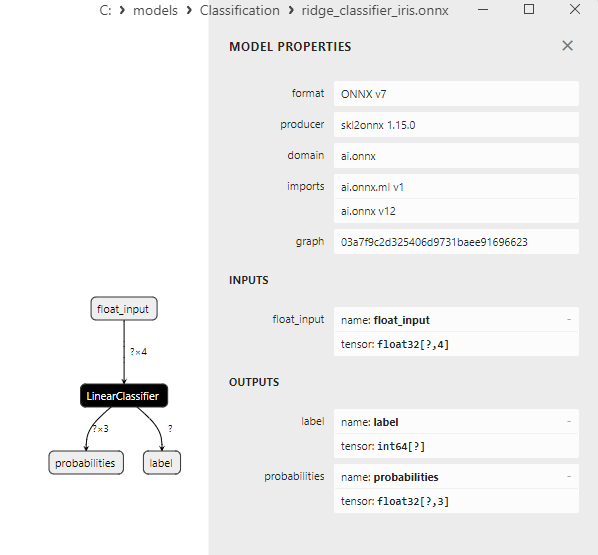
Fig.19. Representación ONNX del modelo Ridge Classifier en Netron
2.6. RidgeClassifierCV
El método de clasificación RidgeClassifierCV es un potente algoritmo de clasificación binaria y multiclase basado en la regresión de Ridge.
Principios de funcionamiento de RidgeClassifierCV:
- Regresión lineal de Ridge: RidgeClassifierCV se basa en la regresión lineal de Ridge. Este método supone una modificación de la regresión lineal a la que se añade la regularización L2. La regularización ayuda a controlar el sobreentrenamiento reduciendo la amplitud de los pesos de las características.
- Clasificación binaria y multiclase: RidgeClassifierCV puede usarse tanto para la clasificación binaria (cuando sólo hay dos clases) como para la clasificación multiclase (cuando hay más de dos clases). Para la clasificación multiclase, el método transforma el problema en varios problemas binarios (uno frente a todos) y construye un modelo para cada uno de ellos.
- Selección automática del parámetro de regularización: Una de las principales ventajas de RidgeClassifierCV es el soporte incorporado para la validación cruzada y la selección automática del valor óptimo del parámetro de regularización alpha. En lugar de seleccionar alpha manualmente, el método prueba diferentes valores de alpha y selecciona el mejor basándose en la validación cruzada.
- Resistencia a la multicolinealidad: La regresión Ridge resuelve bien el problema de la multicolinealidad cuando las características están muy correlacionadas entre sí. La regularización nos permite controlar la contribución de cada característica, haciendo que el modelo resulte robusto frente a datos correlacionados.
Ventajas de RidgeClassifierCV:
- Selección automática de hiperparámetros: Una ventaja importante de RidgeClassifierCV es la capacidad de seleccionar automáticamente el valor alpha óptimo mediante validación cruzada. Esto evita tener que experimentar con distintos valores alpha y aumenta la probabilidad de obtener buenos resultados.
- Resistencia al sobreentrenamiento: La regularización L2 ofrecida por RidgeClassifierCV ayuda a controlar la complejidad del modelo y reduce el riesgo de sobreentrenamiento. Esto resulta especialmente importante en tareas con datos limitados.
- Transparencia e interpretabilidad: RidgeClassifierCV ofrece factores de ponderación interpretables para cada rasgo, lo que permite analizar la contribución de cada rasgo a la predicción e inferir la importancia de las características.
- Eficiencia: El método es muy eficaz y puede aplicarse a grandes cantidades de datos.
Limitaciones de RidgeClassifierCV:
- Linealidad: RidgeClassifierCV asume las relaciones lineales entre las características y la variable objetivo. Si los datos tienen fuertes dependencias no lineales, el método podría no ser lo suficientemente preciso.
- Sensibilidad a la escala de características. El método es sensible a la escala de las características. Resulta recomendable estandarizar o normalizar las características antes de aplicar RidgeClassifierCV.
- Selección del número óptimo de características: RidgeClassifierCV no efectúa una selección automática de características, por lo que debemos decidir manualmente qué características incluir en el modelo.
El método de clasificación RidgeClassifierCV supone una potente herramienta de clasificación binaria y multiclase con selección automática del parámetro de regularización óptimo. Su robustez frente al sobreentrenamiento, su interpretabilidad y eficiencia lo convierten en una elección popular para diversas tareas de clasificación. Sin embargo, resulta importante considerar sus limitaciones, especialmente la suposición de relaciones lineales entre las características y la variable objetivo.
2.6.1. Código de creación del modelo RidgeClassifierCV
Este código demuestra el proceso de entrenamiento del modelo RidgeClassifierCV con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_RidgeClassifierCV.py # The code demonstrates the process of training RidgeClassifierCV model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import RidgeClassifierCV from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a RidgeClassifierCV model ridge_classifier_cv_model = RidgeClassifierCV() # train the model on the entire dataset ridge_classifier_cv_model.fit(X, y) # predict classes for the entire dataset y_pred = ridge_classifier_cv_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of RidgeClassifierCV model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(ridge_classifier_cv_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "ridge_classifier_cv_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of RidgeClassifierCV model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of ExtraTreesClassifier model: 0.8533333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.87 0.66 0.75 50
Python 2 0.73 0.90 0.80 50
Python
Python accuracy 0.85 150
Python macro avg 0.86 0.85 0.85 150
Python weighted avg 0.86 0.85 0.85 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\ridge_classifier_cv_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of SVC Classifier model in ONNX format: 0.8533333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.87 0.66 0.75 50
Python 2 0.73 0.90 0.80 50
Python
Python accuracy 0.85 150
Python macro avg 0.86 0.85 0.85 150
Python weighted avg 0.86 0.85 0.85 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\ridge_classifier_cv_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of SVC Classifier model in ONNX format: 0.8533333333333334
2.6.2. Código en MQL5 para trabajar con el modelo RidgeClassifierCV
//+------------------------------------------------------------------+ //| Iris_RidgeClassifierCV.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "ridge_classifier_cv_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- ulong input_shape[]= { batch_size, input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- int output1[]; float output2[][3]; //--- ArrayResize(output1,(int)batch_size); ArrayResize(output2,(int)batch_size); //--- ulong output_shape[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {batch_size,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output1,output2); //--- classes are ready in output1[k]; if(res) { for(int k=0; k<(int)batch_size; k++) model_classes_id[k]=output1[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="RidgeClassifierCV"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=51 FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=52 FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=57 FAILED [class=2, true class=1] features=(6.30,3.30,4.70,1.60] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=62 FAILED [class=2, true class=1] features=(5.90,3.00,4.20,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=65 FAILED [class=2, true class=1] features=(5.60,2.90,3.60,1.30] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=66 FAILED [class=2, true class=1] features=(6.70,3.10,4.40,1.40] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=76 FAILED [class=2, true class=1] features=(6.60,3.00,4.40,1.40] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=79 FAILED [class=2, true class=1] features=(6.00,2.90,4.50,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=86 FAILED [class=2, true class=1] features=(6.00,3.40,4.50,1.60] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=87 FAILED [class=2, true class=1] features=(6.70,3.10,4.70,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=89 FAILED [class=2, true class=1] features=(5.60,3.00,4.10,1.30] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=92 FAILED [class=2, true class=1] features=(6.10,3.00,4.60,1.40] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=109 FAILED [class=1, true class=2] features=(6.70,2.50,5.80,1.80] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV correct results: 85.33% Iris_RidgeClassifierCV (EURUSD,H1) model=RidgeClassifierCV all samples accuracy=0.853333 Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40) Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50) Iris_RidgeClassifierCV (EURUSD,H1) model=RidgeClassifierCV batch test accuracy=0.000000
El rendimiento del modelo ONNX también coincide plenamente con el del modelo original del paquete Scikit-learn (85,33%).
2.6.3. Representación ONNX del modelo RidgeClassifierCV
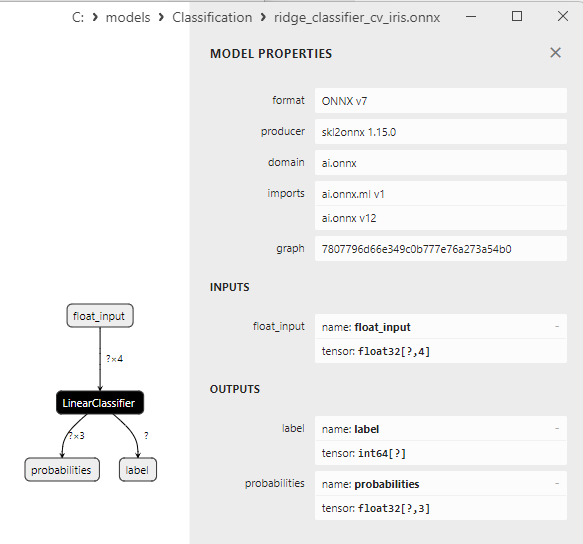
Fig. 20. Representación ONNX del modelo RidgeClassifierCV en Netron
2.7. Random Forest Classifier
Random Forest Classifier es un método de aprendizaje automático basado en conjuntos que se apoya en la construcción de múltiples árboles de decisiones y en la combinación de sus resultados para mejorar la calidad de la clasificación. Este método resulta muy popular por su eficacia y su capacidad para manejar una gran variedad de datos.Principios de Random Forest Classifier:
- Agregación de Bootstrap (Bootstrap Aggregating): Random Forest utiliza una técnica de agregación de Bootstrap que consiste en crear múltiples muestras de bootstrap a partir de los datos de entrenamiento con repetición. Para cada submuestra, se construye un árbol de decisiones distinto.
- Selección aleatoria de características: En la construcción de cada árbol, se selecciona aleatoriamente un subconjunto de características de entre todo el conjunto. Esto fomenta la diversidad arbórea y reduce la correlación entre árboles.
- Votación: Al clasificar un objeto, cada árbol ofrece su propia predicción y la clase que obtiene la mayoría de votos entre todos los árboles se selecciona como predicción final del modelo.
- Gran precisión: Los bosques aleatorios suelen ofrecer una gran precisión de clasificación al promediar los resultados de varios árboles.
- Capacidad para trabajar con datos variados: Funciona bien tanto con atributos numéricos como categóricos, así como con los datos de diversas estructuras.
- Resistencia al sobreentrenamiento: Random Forest lleva incorporada una regularización que lo hace resistente al sobreentrenamiento.
- La importancia de las características: Random Forest puede estimar la importancia de las características, lo cual ayuda a los investigadores e ingenieros de características a comprender mejor los datos.
- Complejidad computacional: El entrenamiento de Random Forest puede llevar mucho tiempo, especialmente cuando el número de árboles y características es grande.
- Dificultad de interpretación: Debido al gran número de árboles y a la selección aleatoria de características, la interpretación del modelo puede resultar difícil.
- No garantiza la tolerancia de los valores atípicos: Random Forest no siempre muestra una buena robustez frente a los valores atípicos en los datos.
El clasificador Random Forest es un potente algoritmo de aprendizaje automático muy usado en diversos campos, como la investigación biomédica, el análisis financiero y el análisis de datos de texto. Resulta muy adecuado para tareas de clasificación y regresión y tiene una gran capacidad de generalización.
2.7.1. Código de creación del modelo Random Forest Classifier
Este código demuestra el proceso de entrenamiento del modelo Random Forest Classifier con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_RandomForestClassifier.py # The code demonstrates the process of training Random Forest Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023,2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.ensemble import RandomForestClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Random Forest Classifier model rf_model = RandomForestClassifier(n_estimators=100, random_state=42) # train the model on the entire dataset rf_model.fit(X, y) # predict classes for the entire dataset y_pred = rf_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Random Forest Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(rf_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "rf_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Random Forest Classifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of ExtraTreesClassifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\rf_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Random Forest Classifier model in ONNX format: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\rf_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Random Forest Classifier model in ONNX format: 1.0
El modelo Random Forest Classifier (y su versión ONNX) resuelve el problema de clasificación de los iris de Fisher con una precisión del 100%.
2.7.2. Código en MQL5 para trabajar con el modelo Random Forest Classifier
//+------------------------------------------------------------------+ //| Iris_RandomForestClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "rf_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shape ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="RandomForestClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_RandomForestClassifier (EURUSD,H1) model:RandomForestClassifier correct results: 100.00% Iris_RandomForestClassifier (EURUSD,H1) model=RandomForestClassifier all samples accuracy=1.000000 Iris_RandomForestClassifier (EURUSD,H1) model=RandomForestClassifier batch test accuracy=1.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 100%, lo cual coincide con la precisión del original.
2.7.3. Representación ONNX del modelo Random Forest Classifier
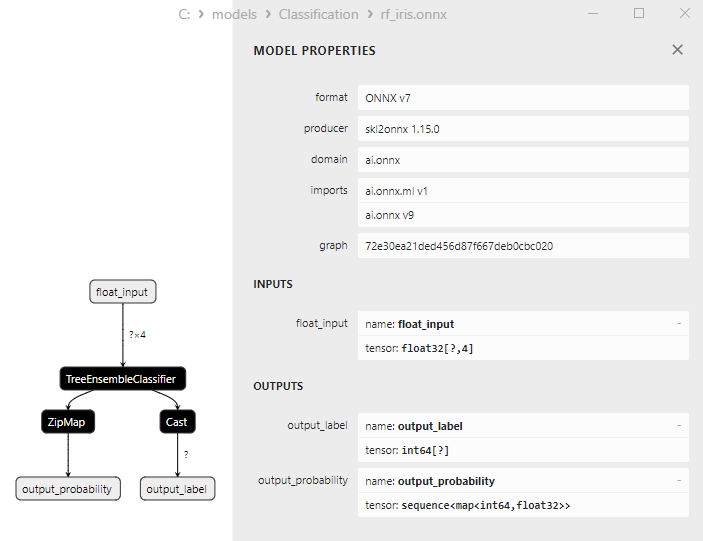
Fig. 21. Representación ONNX del modelo Random Forest Classifier en Netron
2.8. Gradient Boosting Classifier
Gradient Boosting Classifier es una de las técnicas de aprendizaje automático más potentes y encuentra aplicaciones en diversos campos, como el análisis de datos, la visión por computadora, el lenguaje natural y el análisis financiero, debido a su gran precisión y a su capacidad para manejar una gran variedad de datos.
Gradient Boosting Classifier es un método de aprendizaje automático basado en conjuntos que construye una composición de árboles de decisiones para resolver problemas de clasificación. Este método es popular debido a su capacidad para lograr una alta precisión y resistencia al sobreentrenamiento.
Principios de funcionamiento de Gradient Boosting Classifier:
- Conjunto de árboles de decisiones: Gradient Boosting Classifier construye una composición (conjunto) de árboles de decisiones, donde cada árbol intenta mejorar las predicciones del árbol anterior.
- Descenso de gradiente: La agregación de bootstrap de gradiente utiliza el descenso de gradiente para optimizar la función de pérdida. Minimiza el error de clasificación calculando el gradiente de la función de pérdida y actualizando las predicciones con dicho gradiente.
- Ponderación de árboles: Cada árbol de la composición tiene un peso y, finalmente, las predicciones de todos los árboles se combinan considerando sus pesos.
Ventajas de Gradient Boosting Classifier:
- Gran precisión: Gradient Boosting Classifier suele proporcionar una alta precisión de clasificación y es una de las técnicas de aprendizaje automático más potentes.
- Resistencia al sobreentrenamiento: Debido al uso de la regularización y el descenso de gradiente, este método es muy resistente al sobreentrenamiento, especialmente cuando se ajustan los hiperparámetros.
- Capacidad para trabajar con distintos tipos de datos: Gradient Boosting Classifier puede manejar una gran variedad de tipos de datos, incluidas características numéricas y categóricas.
Limitaciones de Gradient Boosting Classifier:
- Complejidad computacional: El entrenamiento de Gradient Boosting Classifier puede ser costoso desde el punto de vista informático, especialmente si se utiliza un gran número de árboles o árboles profundos.
- Dificultad de interpretación: Debido a la complejidad de las composiciones de árboles múltiples, la interpretación de los resultados podría resultar difícil.
- No siempre resulta adecuado para conjuntos de datos pequeños: Gradient Boosting suele requerir una gran cantidad de datos para funcionar con eficacia, y en conjuntos de datos pequeños puede ser propenso al sobreentrenamiento.
Gradient Boosting Classifier es una potente técnica de aprendizaje automático que se utiliza a menudo en concursos de análisis de datos y resuelve con éxito muchos problemas de clasificación. Es capaz de encontrar dependencias no lineales complejas en los datos y tiene una buena capacidad de generalización cuando los hiperparámetros se ajustan adecuadamente.
2.8.1. Código de creación del modelo Gradient Boosting Classifier
Este código demuestra el proceso de entrenamiento del modelo Random Forest Classifier con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_GradientBoostingClassifier.py # The code demonstrates the process of training Gradient Boostring Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.ensemble import GradientBoostingClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Gradient Boosting Classifier model gb_model = GradientBoostingClassifier(n_estimators=100, random_state=42) # train the model on the entire dataset gb_model.fit(X, y) # predict classes for the entire dataset y_pred = gb_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Gradient Boosting Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(gb_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "gb_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Gradient Boosting Classifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of Gradient Boosting Classifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\gb_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Gradient Boosting Classifier model in ONNX format: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\gb_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Gradient Boosting Classifier model in ONNX format: 1.0
El modelo Gradient Boosting Classifier (y su versión ONNX) resuelven el problema de clasificación del iris de Fisher con una precisión del 100%.
2.8.2. Código en MQL5 para trabajar con el modelo Gradient Boosting Classifier
//+------------------------------------------------------------------+ //| Iris_GradientBoostingClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "gb_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="GradientBoostingClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_GradientBoostingClassifier (EURUSD,H1) model:GradientBoostingClassifier correct results: 100.00% Iris_GradientBoostingClassifier (EURUSD,H1) model=GradientBoostingClassifier all samples accuracy=1.000000 Iris_GradientBoostingClassifier (EURUSD,H1) model=GradientBoostingClassifier batch test accuracy=1.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 100%, lo cual coincide con la precisión del original.
2.8.3. Representación ONNX del modelo Gradient Boosting Classifier
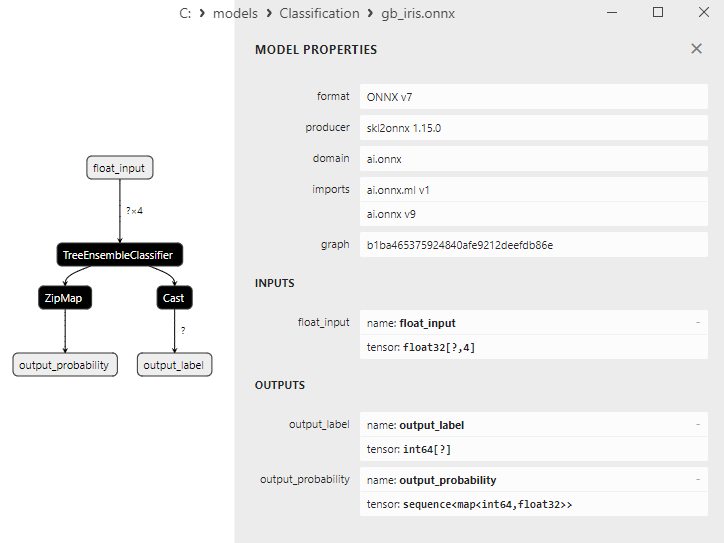
Fig. 22. Representación ONNX del modelo Gradient Boosting Classifier en Netron
2.9. Adaptive Boosting Classifier
AdaBoost (Adaptive Boosting) Classifier es un método de aprendizaje automático basado en conjuntos que se utiliza para mejorar la clasificación combinando los resultados de varios clasificadores débiles (por ejemplo, árboles de decisiones) para crear un algoritmo más potente.Principios de AdaBoost Classifier:
- Conjunto de clasificadores débiles: AdaBoost comienza inicializando cada muestra del conjunto de entrenamiento con pesos, asignándoles los mismos valores iniciales.
- Entrenamiento de clasificadores débiles: A continuación, AdaBoost entrena un clasificador débil (por ejemplo, un árbol de decisiones) en el conjunto de entrenamiento dados los pesos de las muestras. Este clasificador intenta clasificar correctamente las muestras.
- Redistribución de pesos: AdaBoost cambia los pesos de las muestras, aumentando el peso de las muestras mal clasificadas y disminuyendo el peso de las muestras correctamente clasificadas.
- Creación de una composición: AdaBoost repite el proceso de entrenamiento de los clasificadores débiles y la redistribución de pesos repetidamente. A continuación, los resultados de dichos clasificadores débiles se combinan en un compuesto en el que cada clasificador contribuye con respecto a su precisión.
- Gran precisión: AdaBoost suele lograr una alta precisión de clasificación combinando múltiples clasificadores débiles.
- Resistencia al sobreentrenamiento: AdaBoost lleva incorporada una regularización que lo hace resistente al sobreentrenamiento.
- Capacidad para trabajar con distintos clasificadores: AdaBoost puede usar diferentes clasificadores básicos, lo que permite personalizarlo para una tarea específica.
- Sensibilidad a los valores atípicos: AdaBoost puede resultar sensible a los valores atípicos en los datos, ya que pueden tener un gran peso.
- No siempre es adecuado para tareas complejas: En algunas tareas complejas, AdaBoost puede necesitar un gran número de clasificadores básicos para obtener buenos resultados.
- Dependencia de la calidad de los clasificadores básicos: AdaBoost obtiene mejores resultados cuando los clasificadores básicos son mejores que las suposiciones aleatorias.
El clasificador AdaBoost supone un potente algoritmo de aprendizaje automático que se utiliza a menudo en la práctica para resolver problemas de clasificación. Resulta adecuado para problemas binarios y multiclase y puede adaptarse a diversos clasificadores básicos.
2.9.1. Código de creación del modelo Adaptive Boosting Classifier
Este código demuestra el proceso de entrenamiento del modelo Adaptive Boosting Classifier con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_AdaBoostClassifier.py # The code demonstrates the process of training AdaBoost Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.ensemble import AdaBoostClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create an AdaBoost Classifier model adaboost_model = AdaBoostClassifier(n_estimators=50, random_state=42) # train the model on the entire dataset adaboost_model.fit(X, y) # predict classes for the entire dataset y_pred = adaboost_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of AdaBoost Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(adaboost_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "adaboost_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of AdaBoost Classifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of AdaBoost Classifier model: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.92 0.96 0.94 50
Python 2 0.96 0.92 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\adaboost_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of AdaBoost Classifier model in ONNX format: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.92 0.96 0.94 50
Python 2 0.96 0.92 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\adaboost_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of AdaBoost Classifier model in ONNX format: 0.96
2.9.2. Código en MQL5 para trabajar con el modelo Adaptive Boosting Classifier
//+------------------------------------------------------------------+ //| Iris_AdaBoostClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "adaboost_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="AdaBoostClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier correct results: 96.00% Iris_AdaBoostClassifier (EURUSD,H1) model=AdaBoostClassifier all samples accuracy=0.960000 Iris_AdaBoostClassifier (EURUSD,H1) model=AdaBoostClassifier batch test accuracy=1.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 96%, lo cual coincide con la precisión del original.
2.9.3. Representación ONNX del modelo Adaptive Boosting Classifier
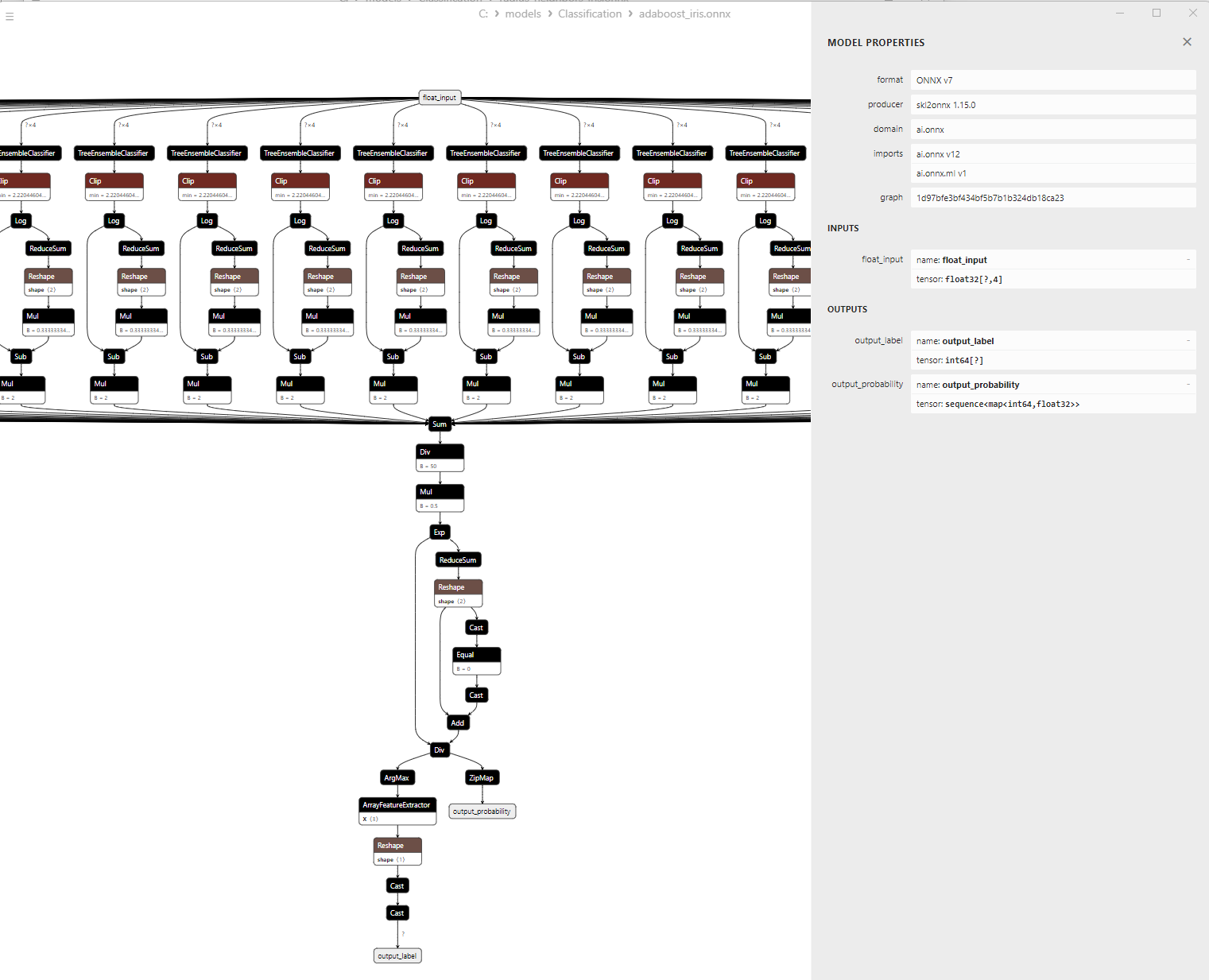
Fig. 23. Representación ONNX del modelo Adaptive Boosting Classifier en Netron
2.10. Bootstrap Aggregating Classifier
Bagging (Bootstrap Aggregating) Classifier es una técnica de aprendizaje automático basada en conjuntos que se basa en la creación de múltiples submuestras (muestras bootstrap) a partir de los datos de entrenamiento y en la construcción de modelos independientes en cada una de ellas, para luego combinar los resultados y mejorar la capacidad de generalización del modelo.Principios de funcionamiento de Bagging Classifier:
- Creación de submuestras: La agregación de bootstrap comienza creando varias submuestras aleatorias (muestras bootstrap) a partir de los datos de entrenamiento con repetición. Esto significa que las mismas muestras pueden aparecer en varias submuestras, mientras que algunas podrían pasar desapercibidas.
- Entrenamiento de modelos básicos: En cada submuestra se entrena un modelo básico distinto (por ejemplo, un árbol de decisiones). Cada modelo se entrena independientemente de los demás.
- Agregación de resultados: Una vez entrenados todos los modelos básicos, se combinan sus resultados de predicción para obtener la predicción final. En el caso de la clasificación binaria, puede hacerse por mayoría.
- Reducción de la varianza: La agregación de bootstrap reduce la varianza del modelo promediando los resultados de varios modelos básicos, lo que puede dar lugar a predicciones más sólidas y fiables.
- Reduce el sobreentrenamiento: Como cada modelo básico se entrena con una submuestra diferente, la agregación de bootstrap puede reducir la propensión del modelo a sobreentrenarse.
- Versatilidad: La agregación de bootstrap puede utilizar diferentes modelos básicos, lo que permite adaptarla a distintos tipos de datos y tareas.
- No mejora el desplazamiento: La agregación de bootstrap tiende a reducir la varianza, pero no el desplazamiento del modelo. Si los modelos básicos son propensos a los desplazamientos (por ejemplo, si no están suficientemente entrenados), la agregación de bootstrap no solucionará este problema.
- No siempre es adecuado para tareas complejas: En algunas tareas complejas, la agregación de bootstrap puede requerir un gran número de modelos básicos para obtener buenos resultados.
Bagging Classifier es un método eficaz de aprendizaje automático que puede mejorar la capacidad de generalización del modelo y reducir el sobreentrenamiento. A menudo se utiliza en combinación con varios modelos básicos para resolver diversos problemas de clasificación y regresión.
2.10.1. Código de creación del modelo Bootstrap Aggregating Classifier
Este código demuestra el proceso de entrenamiento del modelo Bootstrap Aggregating Classifier en el Iris dataset, exportándolo a formato ONNX, y realizando la clasificación utilizando el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_BootstrapAggregatingClassifier.py # The code demonstrates the process of training Bagging Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.ensemble import BaggingClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Bagging Classifier model with a Decision Tree base estimator bagging_model = BaggingClassifier(n_estimators=100, random_state=42) # train the model on the entire dataset bagging_model.fit(X, y) # predict classes for the entire dataset y_pred = bagging_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Bagging Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(bagging_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "bagging_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Bagging Classifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of Bagging Classifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\bagging_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Bagging Classifier model in ONNX format: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\bagging_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Bagging Classifier model in ONNX format: 1.0
El modelo Bootstrap Aggregating Classifier (y su versión ONNX) ha mostrado una precisión del 100% en la clasificación del Iris dataset.
2.10.2. Código MQL5 para trabajar con el modelo Bootstrap Aggregating Classifier
//+------------------------------------------------------------------+ //| Iris_BootstrapAggregatingClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "bagging_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shape ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="BootstrapAggregatingClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_BootstrapAggregatingClassifier (EURUSD,H1) model:BootstrapAggregatingClassifier correct results: 100.00% Iris_BootstrapAggregatingClassifier (EURUSD,H1) model=BootstrapAggregatingClassifier all samples accuracy=1.000000 Iris_BootstrapAggregatingClassifier (EURUSD,H1) model=BootstrapAggregatingClassifier batch test accuracy=1.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 100%, lo cual coincide con la precisión del original.
2.10.3. Representación ONNX del modelo Bootstrap Aggregating Classifier
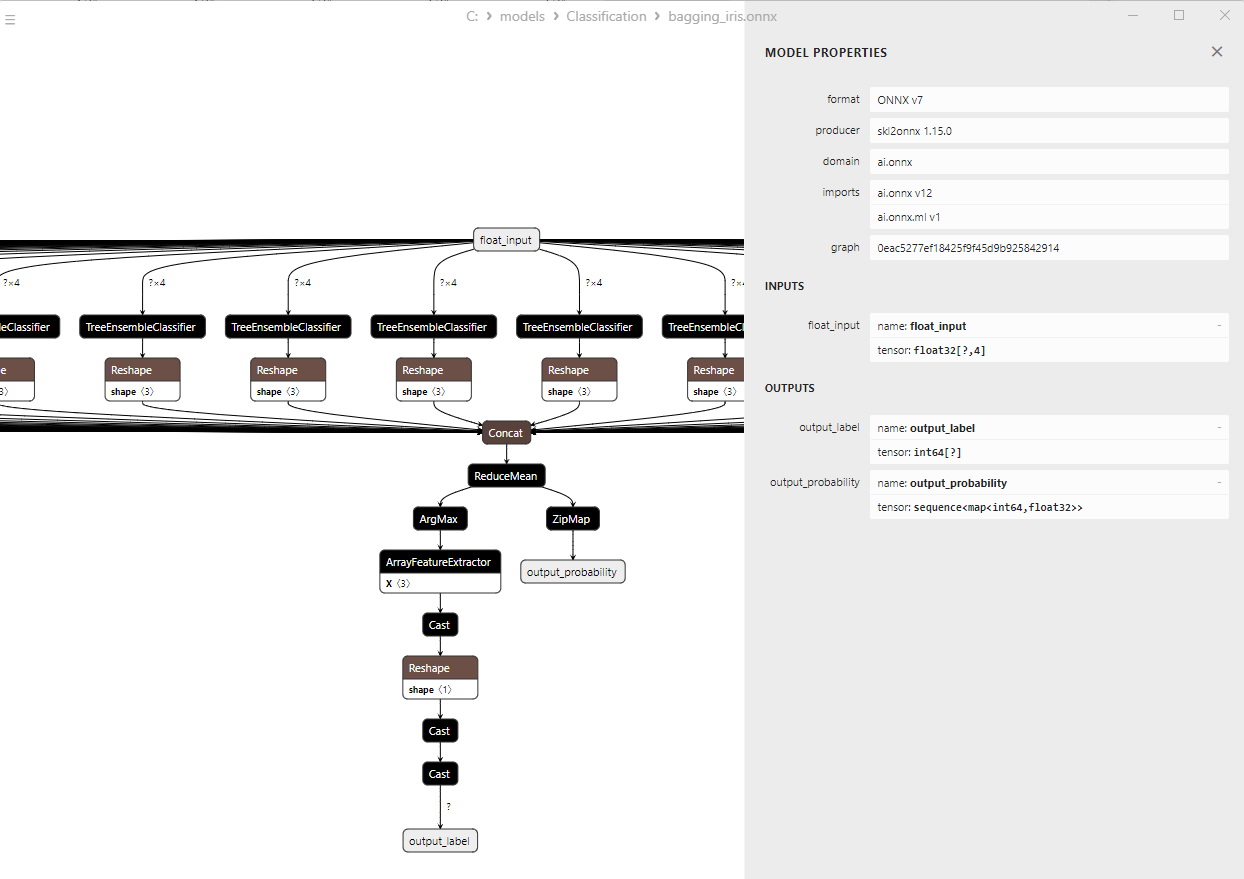
Fig. 24. Representación ONNX del modelo Bootstrap Aggregating Classifier en Netron
2.11. K-Nearest Neighbors (K-NN) Classifier
K-Nearest Neighbors (K-NN) Classifier es una técnica de aprendizaje automático que se utiliza para resolver problemas de clasificación y regresión basados en la proximidad entre objetos de datos. Se basa en el principio de que los objetos cercanos entre sí en un espacio de características multidimensional tienen características similares y, por tanto, pueden tener etiquetas de clase similares.
Principios de K-NN Classifier:
- Definición de proximidad: K-NN Classifier determina la proximidad entre el objeto a clasificar y el resto de objetos del conjunto de entrenamiento. Para ello se suele usar una métrica de distancia como la distancia euclidiana o la distancia Manhattan.
- Selección del número de vecinos: El parámetro K determina el número de vecinos más próximos que se usarán para clasificar el objeto. Normalmente, K se elige según la tarea y los datos.
- Votación: K-NN usa la votación por mayoría entre los K vecinos más próximos para determinar la clase del objeto. Por ejemplo, si la mayoría de los K vecinos pertenecen a la clase A, el objeto también se clasificará como clase A.
Ventajas de K-NN Classifier:
- Sencillez e intuitividad: K-NN es un método sencillo e intuitivo, fácil de comprender y aplicar.
- Capacidad para trabajar con diversos tipos de datos: K-NN puede usarse para diversos tipos de datos, como los numéricos, los categóricos y los textuales.
- Adaptabilidad al cambio de datos: K-NN puede adaptarse rápidamente a los cambios en los datos, lo que lo hace adecuado para tareas con datos dinámicos.
Limitaciones de K-NN Classifier:
- Sensibilidad a la selección de K: Elegir el valor óptimo de K puede resultar una tarea no trivial. Una K demasiado pequeña puede llevar al sobreentrenamiento, y una K demasiado grande puede llevar al subentrenamiento.
- Sensibilidad al escalado: K-NN es sensible al escalado de características, por lo que podría resultar importante la normalización previa de los datos.
- Complejidad computacional: Con una gran cantidad de datos y un gran número de características, calcular las distancias entre todos los pares de objetos puede resultar costoso desde el punto de vista computacional.
- Falta de interpretabilidad: Los resultados de K-NN pueden ser difíciles de interpretar, especialmente si K es grande y existen muchos datos.
K-NN Classifier es un método de aprendizaje automático que puede ser útil en tareas en las que la proximidad del objeto es importante, como las tareas de recomendación, la clasificación de datos de texto y el reconocimiento de patrones. Resulta adecuado para el análisis inicial de datos y la creación rápida de prototipos de modelos.
2.11.1. Código de creación del modelo K-Nearest Neighbors (K-NN) Classifier
Este código demuestra el proceso de entrenamiento del modelo K-Nearest Neighbors (K-NN) Classifier con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_KNearestNeighborsClassifier.py # The code uses the K-Nearest Neighbors (KNN) Classifier for the Iris dataset, converts the model to ONNX format, saves it, and evaluates its accuracy. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.neighbors import KNeighborsClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a K-Nearest Neighbors (KNN) Classifier model knn_model = KNeighborsClassifier(n_neighbors=3) # train the model on the entire dataset knn_model.fit(X, y) # predict classes for the entire dataset y_pred = knn_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of KNN Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(knn_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "knn_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of KNN Classifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of KNN Classifier model: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.94 0.94 50
Python 2 0.94 0.94 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\knn_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1 0.98 1.00 0.99 50 Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1 0.98 1.00 0.99 50 Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of KNN Classifier model in ONNX format: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.94 0.94 50
Python 2 0.94 0.94 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\knn_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1 0.98 1.00 0.99 50 Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1 0.98 1.00 0.99 50 Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of KNN Classifier model in ONNX format: 0.96
2.11.2. Código en MQL5 para trabajar con el modelo K-Nearest Neighbors (K-NN) Classifier
//+------------------------------------------------------------------+ //| Iris_KNearestNeighborsClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "knn_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="KNearestNeighborsClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier correct results: 96.00% Iris_KNearestNeighborsClassifier (EURUSD,H1) model=KNearestNeighborsClassifier all samples accuracy=0.960000 Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50) Iris_KNearestNeighborsClassifier (EURUSD,H1) model=KNearestNeighborsClassifier batch test accuracy=0.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 96%, lo cual coincide con la precisión del original.
2.11.3. Representación ONNX del modelo K-Nearest Neighbors (K-NN) Classifier
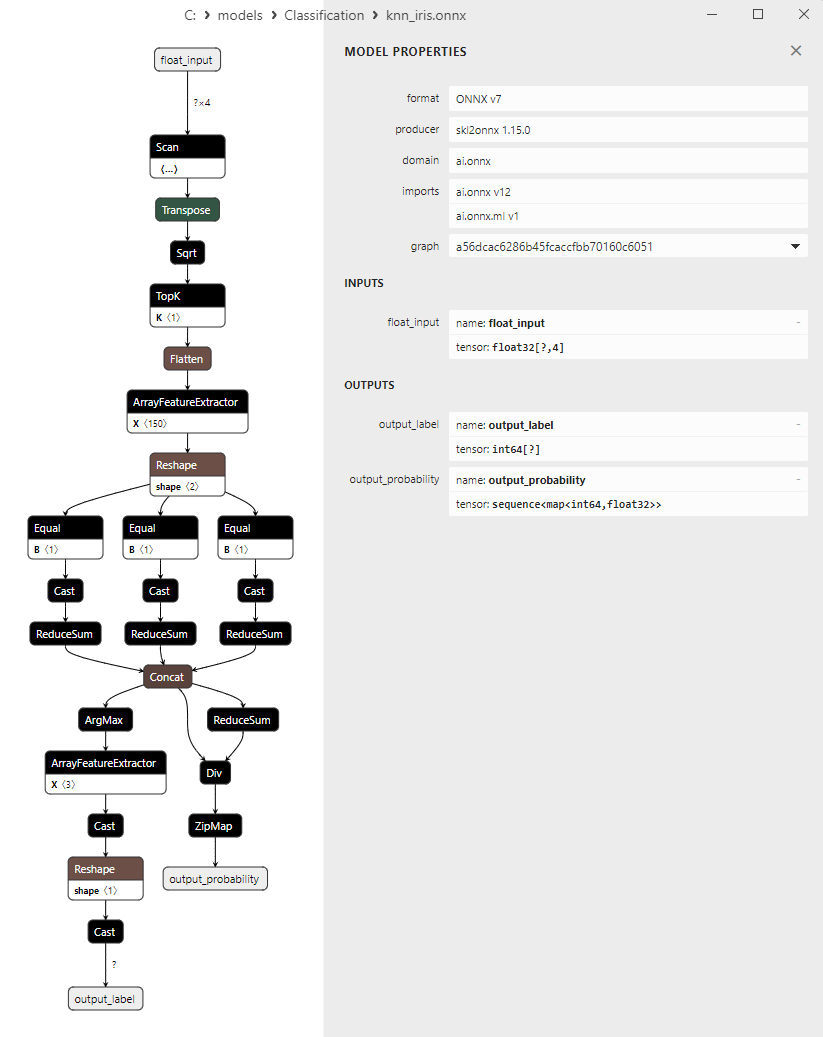
Fig. 25. Representación ONNX del modelo K-Nearest Neighbours en Netron
2.12. Decision Tree Classifier
Decision Tree Classifier es una técnica de aprendizaje automático que se utiliza para tareas de clasificación basadas en la construcción de árboles de decisiones. Este método divide el conjunto de datos en subgrupos más pequeños realizando una serie de pruebas condicionales sobre las características y determina la clase de un objeto según la trayectoria que sigue en el árbol.
Principios de funcionamiento de Decision Tree Classifier
- Construcción de un árbol de decisiones: Inicialmente, todos los datos se representan en la raíz del árbol. Para cada nodo del árbol, los datos se dividen en dos o más subgrupos según los valores de uno de los atributos. Esto se hace para minimizar al máximo la incertidumbre (por ejemplo, la entropía o el índice de Gini) en cada subgrupo.
- Construcción recursiva: El proceso de partición de los datos se efectúa recursivamente hasta alcanzar las hojas del árbol. Las hojas representan clases finitas de objetos.
- Toma de decisiones: Cuando un objeto entra en el árbol, sigue un camino desde la raíz hasta una de las hojas, donde se determina su clase según la mayoría de objetos de esa hoja.
- Facilidad de interpretación: Los árboles de decisiones resultan fáciles de interpretar y visualizar. Las reglas decisivas usadas para la clasificación son claras.
- Trabajo con distintos tipos de datos: El clasificador de árbol de decisiones puede manejar características numéricas y categóricas.
- Identificación de características importantes: Los árboles de decisiones pueden evaluar la importancia de las características, lo cual ayuda a los investigadores e ingenieros de características a comprender los datos.
- Sobreentrenamiento: Los árboles grandes y profundos pueden tender al sobreentrenamiento, lo cual los hace menos generalizables con nuevos datos.
- Sensibilidad al ruido: Los árboles de decisiones pueden ser sensibles al ruido y a los valores atípicos de los datos.
- Construcción codiciosa: Los árboles de decisiones se construyen usando un algoritmo codicioso, que puede llevar a la incapacidad de encontrar una solución globalmente óptima.
- Inestabilidad respecto al cambio de los datos: Incluso pequeños cambios en los datos pueden provocar cambios significativos en la estructura del árbol.
Decision Tree Classifier es un método de aprendizaje automático útil para tareas de clasificación, especialmente en situaciones en las que la interpretabilidad del modelo es importante y es necesario comprender qué características influyen en la decisión. Este método también puede usarse en métodos basados en conjuntos como Random Forest y Gradient Boosting.
2.12.1. Código de creación del modelo Decision Tree Classifier
Este código demuestra el proceso de entrenamiento del modelo Decision Tree Classifier con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_DecisionTreeClassifier.py # The code uses the Decision Tree Classifier for the Iris dataset, converts the model to ONNX format, saves it, and evaluates its accuracy. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.tree import DecisionTreeClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Decision Tree Classifier model decision_tree_model = DecisionTreeClassifier(random_state=42) # train the model on the entire dataset decision_tree_model.fit(X, y) # predict classes for the entire dataset y_pred = decision_tree_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Decision Tree Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(decision_tree_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "decision_tree_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Decision Tree Classifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of ExtraTreesClassifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\decision_tree_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Decision Tree Classifier model in ONNX format: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\decision_tree_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Decision Tree Classifier model in ONNX format: 1.0
El modelo de Decision Tree Classifier (y su versión ONNX) ha mostrado una precisión de clasificación del 100% para todo el conjunto de iris de Fisher.
2.12.2. Código MQL5 para trabajar con el modelo Decision Tree Classifier
//+------------------------------------------------------------------+ //| Iris_DecisionTreeClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "decision_tree_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="DecisionTreeClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_DecisionTreeClassifier (EURUSD,H1) model:DecisionTreeClassifier correct results: 100.00% Iris_DecisionTreeClassifier (EURUSD,H1) model=DecisionTreeClassifier all samples accuracy=1.000000 Iris_DecisionTreeClassifier (EURUSD,H1) model=DecisionTreeClassifier batch test accuracy=1.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 100%, lo cual coincide con la precisión del original.
2.12.3. Representación ONNX del modelo Decision Tree Classifier
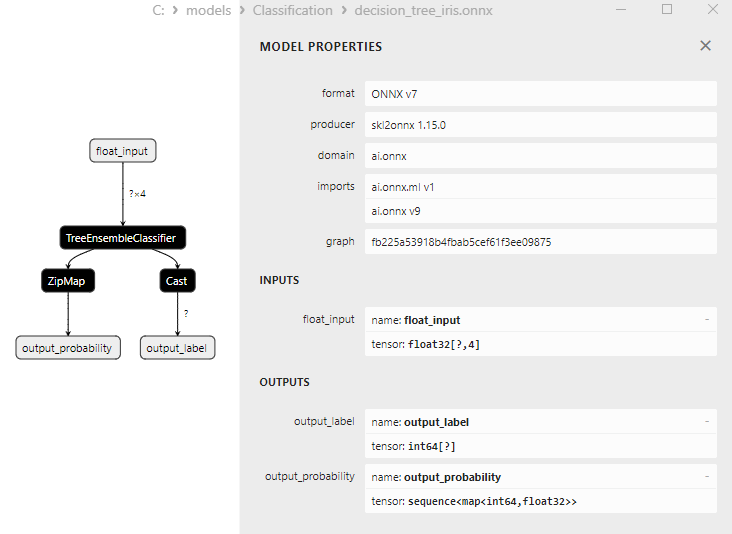
Fig. 26. Representación ONNX del modelo Decision Tree Classifier en Netron
Nota para los modelos LogisticRegression y LogisticRegressionCV
LogisticRegression y LogisticRegressionCV son los dos clasificadores usados para la clasificación binaria mediante regresión logística, pero difieren en la forma de ajustar los parámetros del modelo:
LogisticRegression:
- LogisticRegression es un clasificador que usa una función logística para modelar la probabilidad de pertenecer a una de dos clases (clasificación binaria).
- Proporciona parámetros básicos para el ajuste, como C (regularización inversa), penalty (tipo de regularización, por ejemplo, L1 o L2), solver (algoritmo de optimización) y otros.
- Al usar LogisticRegression, normalmente se eligen los valores y combinaciones de los parámetros y, a continuación, se entrena el modelo con los datos.
LogisticRegressionCV:
- LogisticRegressionCV es una extensión de LogisticRegression que ofrece soporte integrado para la validación cruzada y la selección del valor óptimo del parámetro de regularización C.
- En lugar de seleccionar manualmente C, podemos transmitir a LogisticRegressionCV una lista de valores C para examinar y especificar el método de validación cruzada (por ejemplo, mediante el parámetro cv).
- LogisticRegressionCV seleccionará automáticamente el valor C óptimo que ofrezca el mejor rendimiento en la validación cruzada.
- Esto resulta útil cuando se necesitamos ajustar automáticamente la regularización, especialmente si disponemos de muchos datos o no sabemos qué valor C elegir.
Así pues, la principal diferencia entre ambos es el nivel de automatización en el ajuste de los parámetros C. LogisticRegression requiere el ajuste manual de C, mientras que LogisticRegressionCV permite seleccionar automáticamente el valor óptimo de C usando validación cruzada. La selección entre uno u otro depende de nuestras necesidades y de nuestro deseo de automatizar el proceso de personalización de modelos.
2.13. Logistic Regression Classifier
Logistic Regression Classifier es un método de aprendizaje automático que se utiliza para tareas de clasificación binarias y multiclase. El nombre "regresión" puede inducir a error, pero la regresión logística en realidad predice la probabilidad de que un objeto pertenezca a una de las clases. Después, usando estas probabilidades como base, se toma una decisión final sobre la clasificación del objeto.Principios de funcionamiento de Logistic Regression Classifier
- Predicción de la probabilidad: La regresión logística modela la probabilidad de que un objeto pertenezca a una determinada clase usando una función logística (sigmoidal).
- Definición del límite de decisión: Basándose en las probabilidades predichas, la regresión logística determina un límite de decisión que separa las clases. Si la probabilidad supera un determinado umbral (normalmente 0,5), el objeto se clasifica como perteneciente a una clase, en el caso contrario, a otra.
- Entrenamiento de parámetros: El modelo de regresión logística se entrena con el conjunto de datos de entrenamiento ajustando los pesos (coeficientes) de las características para minimizar la función de pérdida.
- Simplicidad e interpretabilidad: La regresión logística es un modelo sencillo y fácil de interpretar desde el punto de vista de la influencia de las características en la predicción de clases.
- Eficacia con grandes cantidades de datos: La regresión logística puede manejar eficazmente grandes cantidades de datos y aprender de ellos con rapidez.
- Uso en métodos de conjunto: La regresión logística puede usarse como clasificador básico en métodos de conjunto como el apilamiento.
- Linealidad: La regresión logística asume una relación lineal entre las características y el logaritmo de las probabilidades, lo cual puede no ser suficiente para problemas complejos.
- Restricción de la clasificación multiclase: En su forma original, la regresión logística está diseñada para la clasificación binaria, pero existen métodos para ampliarla a la clasificación multiclase, como One-vs-All (One-vs-Rest).
- Sensibilidad a los valores atípicos: La regresión logística puede ser sensible a los valores atípicos en los datos.
La regresión logística es una técnica clásica de aprendizaje automático muy usada en la práctica para tareas de clasificación, especialmente cuando la interpretabilidad del modelo es importante y los datos tienen una estructura lineal o casi lineal. También se usa en estadística y análisis de datos médicos para evaluar la influencia de factores en la probabilidad de sucesos.
2.13.1. Código de creación del modelo Logistic Regression Classifier
Este código demuestra el proceso de entrenamiento del modelo Logistic Regression Classifier con el Iris dataset, exportándolo al formato ONNX, y efectuando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_LogisticRegressionClassifier.py # The code uses the Logistic Regression Classifier for the Iris dataset, converts the model to ONNX format, saves it, and evaluates its accuracy. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Logistic Regression Classifier model logistic_regression_model = LogisticRegression(max_iter=1000, random_state=42) # train the model on the entire dataset logistic_regression_model.fit(X, y) # predict classes for the entire dataset y_pred = logistic_regression_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Logistic Regression Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(logistic_regression_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "logistic_regression_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Logistic Regression Classifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of Logistic Regression Classifier model: 0.9733333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.94 0.96 50
Python 2 0.94 0.98 0.96 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\logistic_regression_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Logistic Regression Classifier model in ONNX format: 0.9733333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.94 0.96 50
Python 2 0.94 0.98 0.96 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\logistic_regression_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Logistic Regression Classifier model in ONNX format: 0.9733333333333334
2.13.2. Código en MQL5 para trabajar con el modelo Logistic Regression Classifier
//+------------------------------------------------------------------+ //| Iris_LogisticRegressionClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "logistic_regression_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="LogisticRegressionClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+Resultado:
Iris_LogisticRegressionClassifier (EURUSD,H1) model:LogisticRegressionClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_LogisticRegressionClassifier (EURUSD,H1) model:LogisticRegressionClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_LogisticRegressionClassifier (EURUSD,H1) model:LogisticRegressionClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_LogisticRegressionClassifier (EURUSD,H1) model:LogisticRegressionClassifier sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_LogisticRegressionClassifier (EURUSD,H1) model:LogisticRegressionClassifier correct results: 97.33% Iris_LogisticRegressionClassifier (EURUSD,H1) model=LogisticRegressionClassifier all samples accuracy=0.973333 Iris_LogisticRegressionClassifier (EURUSD,H1) model=LogisticRegressionClassifier batch test accuracy=1.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 97,33%, lo cual coincide con la precisión del original.
2.13.3. Representación ONNX del modelo Logistic Regression Classifier
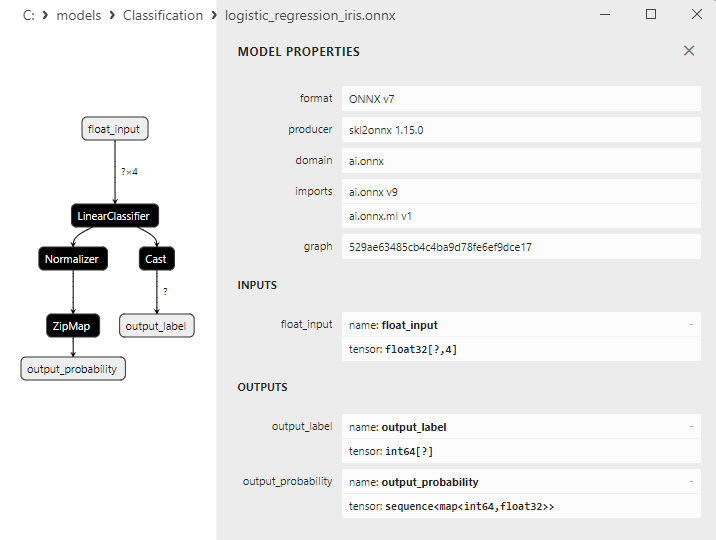
Fig. 27. Representación ONNX del modelo Logistic Regression Classifier en Netron
2.14. LogisticRegressionCV Classifier
LogisticRegressionCV (Logistic Regression con validación cruzada) es un método de clasificación binaria potente y flexible. Este método no solo permite crear modelos de clasificación basados en la regresión logística, sino también ajustar automáticamente los parámetros para obtener el mejor rendimiento.
Principios de funcionamiento de LogisticRegressionCV:
- Regresión logística: El método LogisticRegressionCV se basa en la regresión logística. La regresión logística es una técnica estadística usada para modelizar la probabilidad de que un objeto pertenezca a una de dos clases. Este modelo se aplica cuando la variable dependiente es binaria (dos clases) o cuando puede transformarse en una variable binaria.
- Validación cruzada: La principal ventaja de LogisticRegressionCV es la validación cruzada incorporada. Esto significa que, en lugar de seleccionar manualmente el valor óptimo del parámetro de regularización C, el método prueba automáticamente distintos valores de C y elige el que ofrece el mejor rendimiento en la validación cruzada.
- Selección de C óptimo: LogisticRegressionCV usa una estrategia de validación cruzada para evaluar el rendimiento del modelo con distintos valores de C. C es un parámetro de regularización que controla el grado de regularización del modelo. Un valor pequeño de C implica una regularización fuerte y un valor grande de C implica una regularización débil. La validación cruzada nos permite elegir el valor óptimo de C para equilibrar entre subentrenamiento y sobreentrenamiento.
- Regularización: LogisticRegressionCV también admite distintos tipos de regularización, incluida la regularización L1 (lasso) y L2 (ridge). Este tipo de regularizaciones ayudan a mejorar la capacidad de generalización del modelo y evitan el sobreentrenamiento.
Ventajas de LogisticRegressionCV:
- Ajuste automático de los parámetros: Una de las principales ventajas de LogisticRegressionCV es su capacidad para seleccionar automáticamente el valor óptimo del parámetro C usando validación cruzada. Esto elimina la carga de configurar manualmente el modelo y nos permite centrarnos en los datos y en la tarea que tenemos entre manos.
- Resistencia al sobreentrenamiento: La regularización soportada por LogisticRegressionCV ayuda a gestionar la complejidad del modelo y reducir el riesgo de sobreentrenamiento, especialmente en presencia de pequeñas cantidades de datos.
- Transparencia: La regresión logística es un método con una buena interpretabilidad. Puede analizar la contribución de cada característica a la predicción, lo cual resulta útil para comprender la importancia de las características.
- Alto rendimiento: La regresión logística puede funcionar de forma rápida y eficaz, especialmente con muchos datos.
Limitaciones de LogisticRegressionCV:
- Dependencias lineales: LogisticRegressionCV resulta adecuado para problemas de clasificación lineales y casi lineales. Si la relación entre las características y la variable objetivo es muy poco lineal, es posible que el modelo no sea lo suficientemente preciso.
- Incapacidad para procesar un gran número de características: Cuando el número de características es grande, la regresión logística puede necesitar grandes cantidades de datos o técnicas de reducción de la dimensionalidad para evitar el sobreentrenamiento.
- Dependencia de la representación de los datos: La eficacia de la regresión logística puede depender de cómo se presenten los datos y qué características se seleccionen.
LogisticRegressionCV es una potente herramienta de clasificación binaria con ajuste automático de parámetros y robustez frente al sobreentrenamiento. Resulta especialmente útil cuando necesitamos crear rápidamente un modelo de clasificación con una buena interpretabilidad. No obstante, resulta importante recordar que funciona mejor cuando los datos tienen relaciones lineales o casi lineales.
2.14.1. Código de creación del modelo LogisticRegressionCV Classifier
Este código demuestra el proceso de entrenamiento del modelo LogisticRegressionCV Classifier con el Iris dataset, exportándolo al formato ONNX, y efectuando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_LogisticRegressionCVClassifier.py # The code demonstrates the process of training LogisticRegressionCV model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import LogisticRegressionCV from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a LogisticRegressionCV model logistic_regression_model = LogisticRegressionCV(cv=5, max_iter=1000) # train the model on the entire dataset logistic_regression_model.fit(X, y) # predict classes for the entire dataset y_pred = logistic_regression_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of LogisticRegressionCV model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(logistic_regression_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "logistic_regressioncv_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of LogisticRegressionCV model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of LogisticRegressionCV model: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.96 0.97 50
Python 2 0.96 0.98 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\logistic_regression_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of LogisticRegressionCV model in ONNX format: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.96 0.97 50
Python 2 0.96 0.98 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\logistic_regression_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of LogisticRegressionCV model in ONNX format: 0.98
2.14.2. Código MQL5 para trabajar con el modelo LogisticRegressionCV Classifier
//+------------------------------------------------------------------+ //| Iris_LogisticRegressionCVClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "logistic_regressioncv_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="LogisticRegressionCVClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_LogisticRegressionCVClassifier (EURUSD,H1) model:LogisticRegressionCVClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_LogisticRegressionCVClassifier (EURUSD,H1) model:LogisticRegressionCVClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_LogisticRegressionCVClassifier (EURUSD,H1) model:LogisticRegressionCVClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_LogisticRegressionCVClassifier (EURUSD,H1) model:LogisticRegressionCVClassifier correct results: 98.00% Iris_LogisticRegressionCVClassifier (EURUSD,H1) model=LogisticRegressionCVClassifier all samples accuracy=0.980000 Iris_LogisticRegressionCVClassifier (EURUSD,H1) model=LogisticRegressionCVClassifier batch test accuracy=1.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 98%, lo cual coincide con la precisión del original.
2.14.3. Representación ONNX del modelo LogisticRegressionCV Classifier
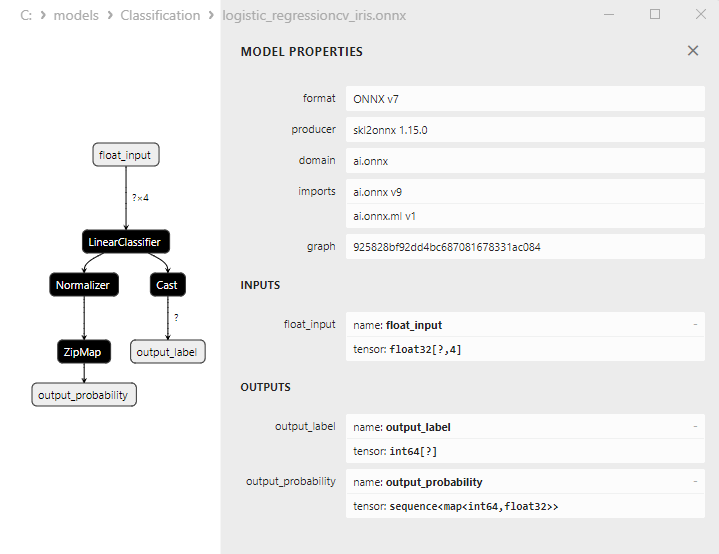
Fig. 28. Representación ONNX del modelo LogisticRegressionCV Classifier en Netron
2.15. Passive-Aggressive (PA) Classifier
Passive-Aggressive (PA) Classifier es una técnica de aprendizaje automático que se utiliza para tareas de clasificación. La idea principal de este método es adaptar los pesos (coeficientes) del modelo durante el entrenamiento para minimizar el error de clasificación. Passive-Aggressive Classifier puede resultar útil en tareas de aprendizaje en línea y en situaciones en las que los datos cambian con el tiempo.Principios de funcionamiento de Passive-Aggressive Classifier:
- Adaptación de pesos: En lugar de actualizar los pesos del modelo en la dirección de la minimización de la función de pérdida, como se hace en el método de descenso de gradiente estocástico, Passive-Aggressive Classifier adapta los pesos en la dirección que minimiza el error de clasificación para el ejemplo actual.
- Conservación de la agresividad: El método tiene un parámetro llamado agresividad (C), que determina cuánto adaptar los pesos del modelo. Valores grandes de C hacen que el método resulte más agresivo en la adaptación, mientras que valores pequeños lo hacen menos agresivo.
- Es adecuado para el aprendizaje online: Passive-Aggressive Classifier puede actualizarse a medida que se dispone de nuevos datos, lo cual lo hace adecuado para tareas de aprendizaje online en las que los datos llegan en forma de flujo.
- Adaptabilidad al cambio de datos: El método se adapta bien a los datos cambiantes porque adapta el modelo a las nuevas circunstancias.
- Sensibilidad a la selección del parámetro de agresividad: La selección del valor óptimo del parámetro C puede requerir un ajuste y depende de las características de los datos.
- No siempre es adecuado para tareas complejas: Passive-Aggressive Classifier puede no ofrecer una gran precisión en tareas complejas en las que es necesario tener en cuenta dependencias complejas entre características.
- Interpretación de los pesos: Los pesos del modelo obtenidos mediante este método pueden ser menos interpretables que los obtenidos mediante regresión lineal o regresión logística.
Passive-Aggressive Classifier es una técnica de aprendizaje automático adecuada para tareas de clasificación con datos cambiantes y para situaciones en las que es importante adaptar rápidamente el modelo a las nuevas circunstancias. Se aplica en diversos campos, como el análisis de datos de texto, la clasificación de imágenes y otras tareas.
2.15.1. Código de creación del modelo Passive-Aggressive (PA) Classifier
Este código demuestra el proceso de entrenamiento del modelo Passive-Aggressive (PA) Classifier con el Iris dataset, exportándolo al formato ONNX, y efectuando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_PassiveAgressiveClassifier.py # The code uses the Passive-Aggressive (PA) Classifier for the Iris dataset, converts the model to ONNX format, saves it, and evaluates its accuracy. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import PassiveAggressiveClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Passive-Aggressive (PA) Classifier model pa_classifier_model = PassiveAggressiveClassifier(max_iter=1000, random_state=42) # train the model on the entire dataset pa_classifier_model.fit(X, y) # predict classes for the entire dataset y_pred = pa_classifier_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Passive-Aggressive (PA) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(pa_classifier_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "pa_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Passive-Aggressive (PA) Classifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of Passive-Aggressive (PA) Classifier model: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.96 0.92 0.94 50
Python 2 0.92 0.96 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\pa_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Passive-Aggressive (PA) Classifier model in ONNX format: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.96 0.92 0.94 50
Python 2 0.92 0.96 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\pa_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Passive-Aggressive (PA) Classifier model in ONNX format: 0.96
2.15.2. Código en MQL5 para trabajar con el modelo Passive-Aggressive (PA) Classifier
//+------------------------------------------------------------------+ //| Iris_PassiveAgressiveClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "pa_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="PassiveAgressiveClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier correct results: 96.00% Iris_PassiveAgressiveClassifier (EURUSD,H1) model=PassiveAgressiveClassifier all samples accuracy=0.960000 Iris_PassiveAgressiveClassifier (EURUSD,H1) model=PassiveAgressiveClassifier batch test accuracy=1.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 96%, lo cual coincide con la precisión del original.
2.15.3. Representación ONNX del modelo Passive-Aggressive (PA) Classifier
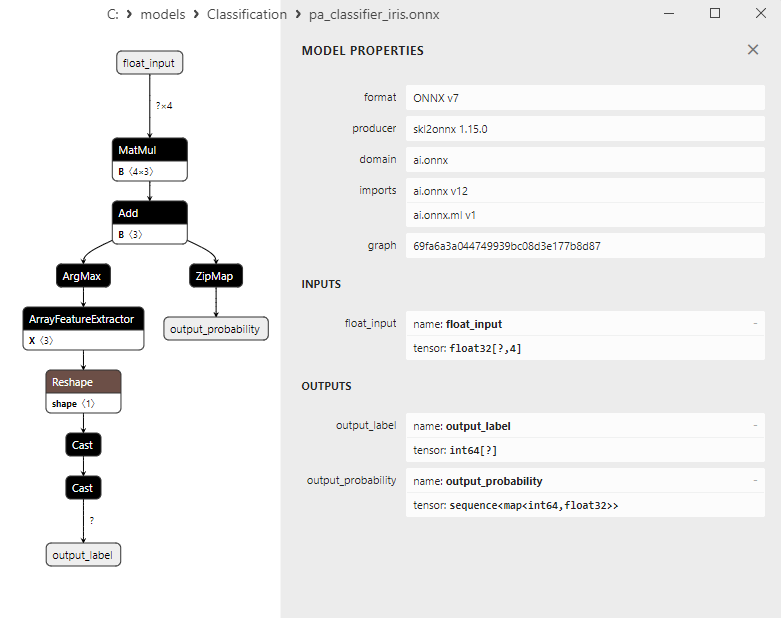
Fig. 29. Representación ONNX del modelo Passive-Aggressive (PA) Classifier en Netron
2.16. Perceptron Classifier
Perceptron Classifier es un clasificador binario lineal que se utiliza para separar dos clases basándose en un hiperplano lineal de separación. Es uno de los métodos de aprendizaje automático más simples y antiguos, y su principio básico consiste en entrenar los pesos (coeficientes) de un modelo para maximizar la corrección de la clasificación en el conjunto de datos de entrenamiento.Principios de funcionamiento de Perceptron Classifier:
- Hiperplano lineal: El perceptrón construye un hiperplano lineal en un espacio de características multidimensional que separa dos clases. Este hiperplano está definido por los pesos (coeficientes) del modelo.
- Entrenamiento de pesos: Inicialmente, los pesos se inicializan aleatoriamente o con ceros. A continuación, para cada objeto del conjunto de entrenamiento, el modelo predice la clase basándose en los pesos actuales y los ajusta en caso de error. El entrenamiento continúa hasta que todos los objetos se clasifiquen correctamente o hasta que se alcance el número máximo de iteraciones.
- Simplicidad: El perceptrón es un algoritmo muy sencillo, fácil de comprender y de aplicar.
- Alta velocidad de aprendizaje: El perceptrón puede aprender rápidamente, especialmente con grandes cantidades de datos, y puede usarse en tareas de aprendizaje online.
- Limitación de la separabilidad lineal: El perceptrón solo funciona bien cuando los datos son linealmente separables. Si los datos no pueden dividirse linealmente, el perceptrón no podrá alcanzar una gran precisión.
- Sensibilidad a la elección de los pesos iniciales: La aproximación inicial de los pesos puede influir en la convergencia del algoritmo. Una mala elección de los pesos iniciales puede provocar una convergencia lenta o incluso una neurona que no divida correctamente las clases.
- Imposibilidad de definir las probabilidades: El perceptrón no ofrece estimaciones de las probabilidades de pertenencia a una clase, lo cual puede ser importante para algunas tareas.
Perceptron Classifier es un algoritmo básico para la clasificación binaria que puede ser útil en problemas sencillos en los que los datos son linealmente separables. También puede servir de base para métodos más complejos, como las redes neuronales multicapa. Debemos recordar que en tareas más sofisticadas en las que los datos tienen una estructura compleja, otros métodos como la regresión logística o el método de vectores de soporte (SVM) pueden proporcionar una mayor precisión de clasificación.
2.16.1. Código de creación del modelo Perceptron Classifier
Este código demuestra el proceso de entrenamiento del modelo Perceptron Classifier con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También estima la precisión tanto del modelo original como del modelo ONNX.# Iris_PerceptronClassifier.py
# Iris_PerceptronClassifier.py # The code demonstrates the process of training Perceptron Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import Perceptron from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Perceptron Classifier model perceptron_model = Perceptron(max_iter=1000, random_state=42) # train the model on the entire dataset perceptron_model.fit(X, y) # predict classes for the entire dataset y_pred = perceptron_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Perceptron Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(perceptron_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "perceptron_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Perceptron Classifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of Perceptron Classifier model: 0.6133333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 0.80 0.89 50
Python 1 0.46 1.00 0.63 50
Python 2 1.00 0.04 0.08 50
Python
Python accuracy 0.61 150
Python macro avg 0.82 0.61 0.53 150
Python weighted avg 0.82 0.61 0.53 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\perceptron_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Perceptron Classifier model in ONNX format: 0.6133333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 0.80 0.89 50
Python 1 0.46 1.00 0.63 50
Python 2 1.00 0.04 0.08 50
Python
Python accuracy 0.61 150
Python macro avg 0.82 0.61 0.53 150
Python weighted avg 0.82 0.61 0.53 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\perceptron_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Perceptron Classifier model in ONNX format: 0.6133333333333333
2.16.2. Código en MQL5 para trabajar con el modelo Perceptron Classifier
//+------------------------------------------------------------------+ //| Iris_PerceptronClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "perceptron_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="PerceptronClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=2 FAILED [class=1, true class=0] features=(4.90,3.00,1.40,0.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=9 FAILED [class=1, true class=0] features=(4.40,2.90,1.40,0.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=10 FAILED [class=1, true class=0] features=(4.90,3.10,1.50,0.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=13 FAILED [class=1, true class=0] features=(4.80,3.00,1.40,0.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=21 FAILED [class=1, true class=0] features=(5.40,3.40,1.70,0.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=26 FAILED [class=1, true class=0] features=(5.00,3.00,1.60,0.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=31 FAILED [class=1, true class=0] features=(4.80,3.10,1.60,0.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=35 FAILED [class=1, true class=0] features=(4.90,3.10,1.50,0.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=42 FAILED [class=1, true class=0] features=(4.50,2.30,1.30,0.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=46 FAILED [class=1, true class=0] features=(4.80,3.00,1.40,0.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=102 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=103 FAILED [class=1, true class=2] features=(7.10,3.00,5.90,2.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=104 FAILED [class=1, true class=2] features=(6.30,2.90,5.60,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=105 FAILED [class=1, true class=2] features=(6.50,3.00,5.80,2.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=106 FAILED [class=1, true class=2] features=(7.60,3.00,6.60,2.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=108 FAILED [class=1, true class=2] features=(7.30,2.90,6.30,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=109 FAILED [class=1, true class=2] features=(6.70,2.50,5.80,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=110 FAILED [class=1, true class=2] features=(7.20,3.60,6.10,2.50] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=111 FAILED [class=1, true class=2] features=(6.50,3.20,5.10,2.00] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=112 FAILED [class=1, true class=2] features=(6.40,2.70,5.30,1.90] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=113 FAILED [class=1, true class=2] features=(6.80,3.00,5.50,2.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=114 FAILED [class=1, true class=2] features=(5.70,2.50,5.00,2.00] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=116 FAILED [class=1, true class=2] features=(6.40,3.20,5.30,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=117 FAILED [class=1, true class=2] features=(6.50,3.00,5.50,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=118 FAILED [class=1, true class=2] features=(7.70,3.80,6.70,2.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=119 FAILED [class=1, true class=2] features=(7.70,2.60,6.90,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=121 FAILED [class=1, true class=2] features=(6.90,3.20,5.70,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=122 FAILED [class=1, true class=2] features=(5.60,2.80,4.90,2.00] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=123 FAILED [class=1, true class=2] features=(7.70,2.80,6.70,2.00] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=124 FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=125 FAILED [class=1, true class=2] features=(6.70,3.30,5.70,2.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=126 FAILED [class=1, true class=2] features=(7.20,3.20,6.00,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=128 FAILED [class=1, true class=2] features=(6.10,3.00,4.90,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=129 FAILED [class=1, true class=2] features=(6.40,2.80,5.60,2.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=131 FAILED [class=1, true class=2] features=(7.40,2.80,6.10,1.90] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=132 FAILED [class=1, true class=2] features=(7.90,3.80,6.40,2.00] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=133 FAILED [class=1, true class=2] features=(6.40,2.80,5.60,2.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=136 FAILED [class=1, true class=2] features=(7.70,3.00,6.10,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=137 FAILED [class=1, true class=2] features=(6.30,3.40,5.60,2.40] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=138 FAILED [class=1, true class=2] features=(6.40,3.10,5.50,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=140 FAILED [class=1, true class=2] features=(6.90,3.10,5.40,2.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=141 FAILED [class=1, true class=2] features=(6.70,3.10,5.60,2.40] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=142 FAILED [class=1, true class=2] features=(6.90,3.10,5.10,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=143 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=144 FAILED [class=1, true class=2] features=(6.80,3.20,5.90,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=145 FAILED [class=1, true class=2] features=(6.70,3.30,5.70,2.50] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=146 FAILED [class=1, true class=2] features=(6.70,3.00,5.20,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=147 FAILED [class=1, true class=2] features=(6.30,2.50,5.00,1.90] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=148 FAILED [class=1, true class=2] features=(6.50,3.00,5.20,2.00] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=149 FAILED [class=1, true class=2] features=(6.20,3.40,5.40,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=150 FAILED [class=1, true class=2] features=(5.90,3.00,5.10,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier correct results: 61.33% Iris_PerceptronClassifier (EURUSD,H1) model=PerceptronClassifier all samples accuracy=0.613333 Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80) Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier FAILED [class=1, true class=0] features=(4.90,3.10,1.50,0.10) Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90) Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier FAILED [class=1, true class=2] features=(7.10,3.00,5.90,2.10) Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier FAILED [class=1, true class=2] features=(6.30,2.90,5.60,1.80) Iris_PerceptronClassifier (EURUSD,H1) model=PerceptronClassifier batch test accuracy=0.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 61.33%, lo cual coincide con la precisión del original.
2.16.3. Representación ONNX del modelo Perceptron Classifier
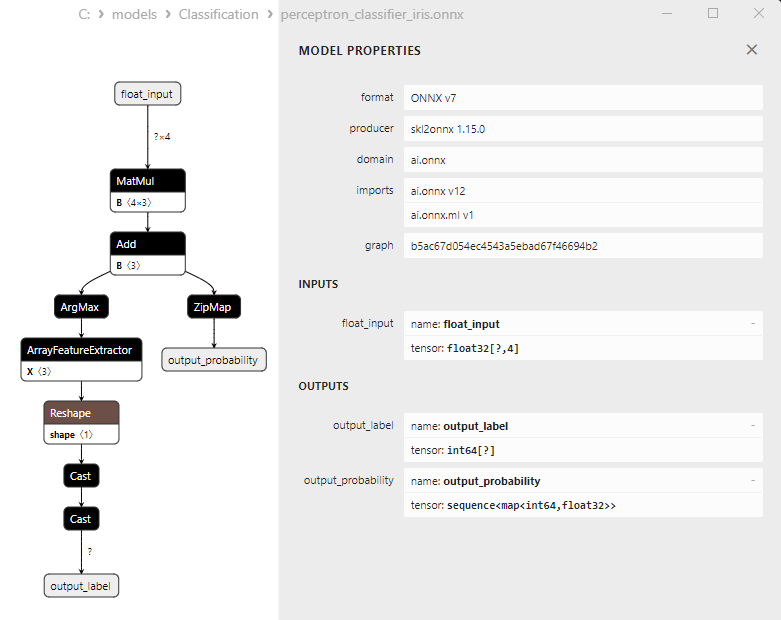
Fig. 30. Representación ONNX del modelo Perceptron Classifier en Netron
2.17. Stochastic Gradient Descent Classifier
SGD Classifier (Stochastic Gradient Descent Classifier) es una técnica de aprendizaje automático que se utiliza para tareas de clasificación. Es un caso especial dentro de los modelos lineales y supone un clasificador lineal que se entrena utilizando el descenso de gradiente estocástico.Principios de funcionamiento de SGD Classifier:
- Hiperplano lineal: El perceptrón construye un hiperplano lineal en un espacio de características multidimensional que separa dos clases. Este hiperplano está definido por los pesos (coeficientes) del modelo.
- Descenso de gradiente estocástico: El método se entrena usando el descenso de gradiente estocástico, lo cual significa que la actualización de los pesos del modelo se realiza en cada objeto del conjunto de entrenamiento (o en un subconjunto seleccionado aleatoriamente) en lugar de en todo el conjunto de datos. Esto hace que el clasificador SGD resulte adecuado para big data y aprendizaje en línea.
- Función de pérdida: SGD Classifier optimiza una función de pérdida, como la función de pérdida logística para tareas de clasificación binaria o la función de pérdida softmax para clasificación multiclase.
- Velocidad de aprendizaje SGD Classifier se entrena rápidamente, especialmente con grandes cantidades de datos, gracias al descenso de gradiente estocástico.
- Es adecuado para el aprendizaje online: El método se adapta bien a las tareas de aprendizaje online, en las que los datos entran en flujos y el modelo debe actualizarse a medida que llegan.
- Sensibilidad de los parámetros: SGD Classifier tiene muchos hiperparámetros, como la velocidad de aprendizaje y el parámetro de regularización, que deben ajustarse con cuidado.
- Inicialización de los pesos: La aproximación inicial de los pesos puede influir en la convergencia y la calidad del modelo.
- Convergencia a mínimos locales: Debido a la naturaleza estocástica del método, SGD Classifier puede converger a mínimos locales de la función de pérdida, lo que puede afectar a la calidad del modelo.
SGD Classifier es un método de aprendizaje automático flexible que puede utilizarse para tareas de clasificación binarias y multiclase, especialmente cuando los datos son numerosos y requieren un procesamiento rápido. Para lograr una alta precisión de clasificación, resulta importante establecer correctamente sus hiperparámetros y controlar la convergencia.
2.17.1. Código de creación del modelo Stochastic Gradient Descent Classifier
Este código demuestra el proceso de entrenamiento del modelo Stochastic Gradient Descent Classifier con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_SGDClassifier.py # The code demonstrates the process of training Stochastic Gradient Descent Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import SGDClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create an SGD Classifier model sgd_model = SGDClassifier(max_iter=1000, random_state=42) # train the model on the entire dataset sgd_model.fit(X, y) # predict classes for the entire dataset y_pred = sgd_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of SGD Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(sgd_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "sgd_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of SGD Classifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of SGD Classifier model: 0.9333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.96 1.00 0.98 50
Python 1 0.88 0.92 0.90 50
Python 2 0.96 0.88 0.92 50
Python
Python accuracy 0.93 150
Python macro avg 0.93 0.93 0.93 150
Python weighted avg 0.93 0.93 0.93 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\perceptron_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1 0.98 1.00 0.99 50 Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1 0.98 1.00 0.99 50 Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of SGD Classifier model in ONNX format: 0.9333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.96 1.00 0.98 50
Python 1 0.88 0.92 0.90 50
Python 2 0.96 0.88 0.92 50
Python
Python accuracy 0.93 150
Python macro avg 0.93 0.93 0.93 150
Python weighted avg 0.93 0.93 0.93 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\perceptron_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1 0.98 1.00 0.99 50 Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1 0.98 1.00 0.99 50 Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of SGD Classifier model in ONNX format: 0.9333333333333333
2.17.2. Código en MQL5 para trabajar con el modelo Stochastic Gradient Descent Classifier
//+------------------------------------------------------------------+ //| Iris_SGDClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "sgd_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="SGDClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=65 FAILED [class=0, true class=1] features=(5.60,2.90,3.60,1.30] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=86 FAILED [class=0, true class=1] features=(6.00,3.40,4.50,1.60] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=124 FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier correct results: 93.33% Iris_SGDClassifier (EURUSD,H1) model=SGDClassifier all samples accuracy=0.933333 Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80) Iris_SGDClassifier (EURUSD,H1) model=SGDClassifier batch test accuracy=0.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 93.33%, lo cual coincide con la precisión del original.
2.17.3. Representación ONNX del modelo Stochastic Gradient Descent Classifier
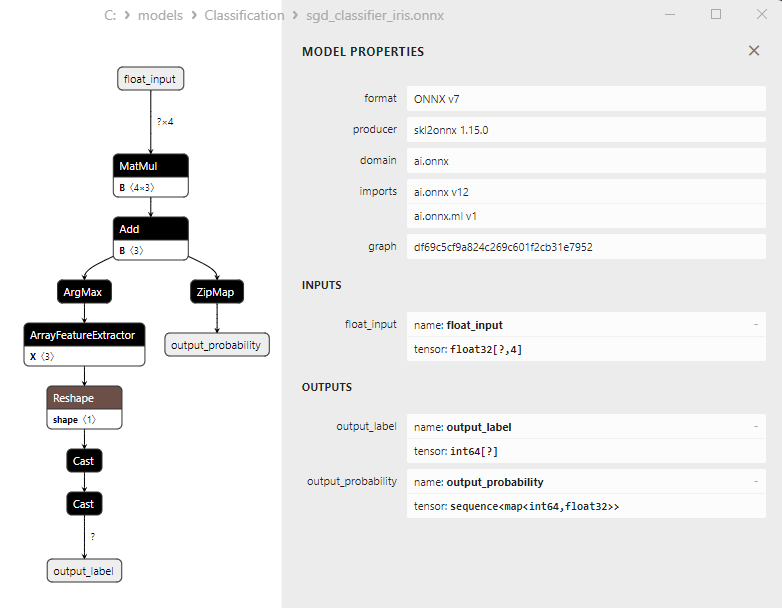
Fig. 31. Representación ONNX del modelo Stochastic Gradient Descent Classifier en Netron
2.18. Gaussian Naive Bayes (GNB) Classifier
Gaussian Naive Bayes (GNB) Classifier es un método de aprendizaje automático basado en un modelo probabilístico bayesiano que se utiliza para tareas de clasificación. Forma parte de la familia de clasificadores bayesianos ingenuos y asume que todas las características son independientes y tienen una distribución normal.Principios de funcionamiento de Gaussian Naive Bayes Classifier:
- Enfoque bayesiano: GNB se basa en un enfoque bayesiano de la clasificación, que utiliza el teorema de Bayes para calcular la probabilidad de que un objeto pertenezca a cada clase.
- Suposición ingenua: La hipótesis principal de GNB es que todas las características son independientes y tienen una distribución normal (gaussiana). Se trata de una suposición ingenua porque, en los datos reales, los rasgos suelen estar correlacionados entre sí.
- Entrenamiento de parámetros: El modelo GNB se entrena con el conjunto de datos de entrenamiento calculando los parámetros de distribución (media y desviación estándar) para cada rasgo de cada clase.
- Facilidad y rapidez de aprendizaje: GNB es un algoritmo muy sencillo y aprende rápidamente incluso con grandes cantidades de datos.
- Eficacia para datos pequeños y medianos: GNB puede ser eficaz para tareas de clasificación con un número pequeño o medio de características, especialmente cuando se cumple bien el supuesto de la distribución normal de las características.
- Suposición ingenua: El supuesto de independencia de las características y de distribución normal puede ser demasiado simplista e incorrecto para los datos reales. Esto puede provocar una disminución de la precisión de la clasificación.
- Sensibilidad a los valores atípicos: GNB puede ser sensible a los valores atípicos en los datos, ya que pueden sesgar significativamente los parámetros de la distribución normal.
- No se tienen en cuenta las dependencias entre rasgos: Debido al supuesto de independencia, GNB no tiene en cuenta las dependencias entre características.
Gaussian Naive Bayes Classifier es una buena opción para tareas de clasificación sencillas, especialmente cuando la suposición de la distribución normal de las características es más o menos válida. No obstante, en problemas más complejos en los que las características están correlacionadas entre sí o la distribución no es normal, otros métodos como el método de vectores soporte (SVM) o el gradient boosting pueden proporcionar resultados más precisos.
2.18.1. Código de creación del modelo Gaussian Naive Bayes (GNB) Classifier
Este código demuestra el proceso de entrenamiento del modelo Gaussian Naive Bayes (GNB) Classifier con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_GaussianNaiveBayesClassifier.py # The code demonstrates the process of training Gaussian Naive Bayes Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.naive_bayes import GaussianNB from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Gaussian Naive Bayes (GNB) Classifier model gnb_model = GaussianNB() # train the model on the entire dataset gnb_model.fit(X, y) # predict classes for the entire dataset y_pred = gnb_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Gaussian Naive Bayes (GNB) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(gnb_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "gnb_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Gaussian Naive Bayes (GNB) Classifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of Gaussian Naive Bayes (GNB) Classifier model: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.94 0.94 50
Python 2 0.94 0.94 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\gnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Gaussian Naive Bayes (GNB) Classifier model in ONNX format: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.94 0.94 50
Python 2 0.94 0.94 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\gnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Gaussian Naive Bayes (GNB) Classifier model in ONNX format: 0.96
2.18.2. Código en MQL5 para trabajar con el modelo Gaussian Naive Bayes (GNB) Classifier
//+------------------------------------------------------------------+ //| Iris_GaussianNaiveBayesClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "gnb_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="GaussianNaiveBayesClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier correct results: 96.00% Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model=GaussianNaiveBayesClassifier all samples accuracy=0.960000 Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model=GaussianNaiveBayesClassifier batch test accuracy=1.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 96%, lo cual coincide con la precisión del original.
2.18.3. Representación ONNX del modelo Gaussian Naive Bayes (GNB) Classifier
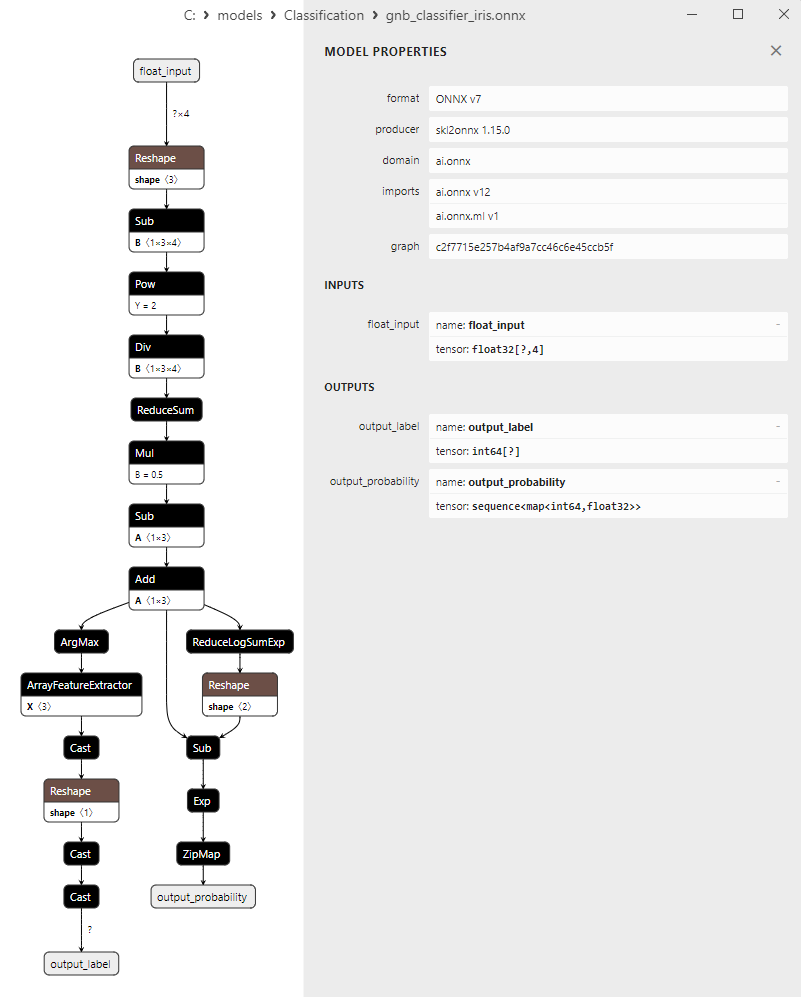
Fig. 32. Representación ONNX del modelo Gaussian Naive Bayes (GNB) Classifier en Netron
2.19. Multinomial Naive Bayes (MNB) Classifier
Multinomial Naive Bayes (MNB) Classifier es un método de aprendizaje automático basado en el modelo probabilístico bayesiano y se utiliza para tareas de clasificación, especialmente en el tratamiento de textos. Supone una variante de los clasificadores bayesianos ingenuos y parte de la base de que las características representan contadores, como el número de palabras de un texto.Principios de funcionamiento de Multinomial Naive Bayes Classifier:
- Enfoque bayesiano: MNB también se basa en un enfoque bayesiano de la clasificación y utiliza el teorema de Bayes para calcular la probabilidad de que un objeto pertenezca a cada clase.
- Supuesto de distribución multinomial: El supuesto básico de MNB es que las características son contadores, como el número de apariciones de las palabras en el texto, y tienen una distribución multinomial. Esta suposición suele ser cierta en el caso de los datos de texto.
- Entrenamiento de parámetros: El modelo MNB se entrena con el conjunto de datos de entrenamiento calculando los parámetros de distribución de cada característica en cada clase.
- Eficacia en el tratamiento de textos: MNB funciona bien en tareas de análisis de datos de texto, como la clasificación de textos o el filtrado de spam, gracias a sus suposiciones sobre contadores de características.
- Facilidad y rapidez de aprendizaje: Al igual que otros clasificadores bayesianos ingenuos, MNB es un algoritmo simple que aprende rápidamente, incluso con grandes cantidades de datos de texto.
- Suposición ingenua: La hipótesis de una distribución multinomial de las características puede ser demasiado simplista e incorrecta para los datos reales, especialmente cuando las características tienen una estructura compleja.
- No se considera el orden de las palabras: MNB no tiene en cuenta el orden de las palabras en el texto, que puede resultar importante en algunas tareas de análisis de texto.
- Sensibilidad a las palabras raras: MNB puede ser sensible a las palabras raras, y una cantidad insuficiente de estas puede reducir la precisión de la clasificación.
Multinomial Naive Bayes Classifier es un método útil para tareas de análisis de texto, especialmente cuando las características están relacionadas con recuentos, como el de palabras en un texto. Se utiliza ampliamente en el procesamiento del lenguaje natural (NLP) para tareas de clasificación de textos, categorización de documentos y otros análisis textuales.
2.19.1. Código de creación del modelo Multinomial Naive Bayes (MNB) Classifier
Este código demuestra el proceso de entrenamiento del modelo Multinomial Naive Bayes (MNB) Classifier con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_MultinomialNaiveBayesClassifier.py # The code demonstrates the process of training Multinomial Naive Bayes (MNB) Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.naive_bayes import MultinomialNB from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Multinomial Naive Bayes (MNB) Classifier model mnb_model = MultinomialNB() # train the model on the entire dataset mnb_model.fit(X, y) # predict classes for the entire dataset y_pred = mnb_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Multinomial Naive Bayes (MNB) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(mnb_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "mnb_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Multinomial Naive Bayes (MNB) Classifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of Multinomial Naive Bayes (MNB) Classifier model: 0.9533333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.92 0.93 50
Python 2 0.92 0.94 0.93 50
Python
Python accuracy 0.95 150
Python macro avg 0.95 0.95 0.95 150
Python weighted avg 0.95 0.95 0.95 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\mnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Multinomial Naive Bayes (MNB) Classifier model in ONNX format: 0.9533333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.92 0.93 50
Python 2 0.92 0.94 0.93 50
Python
Python accuracy 0.95 150
Python macro avg 0.95 0.95 0.95 150
Python weighted avg 0.95 0.95 0.95 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\mnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Multinomial Naive Bayes (MNB) Classifier model in ONNX format: 0.9533333333333334
2.19.2. Código MQL5 para trabajar con el modelo Multinomial Naive Bayes (MNB) Classifier
//+------------------------------------------------------------------+ //| Iris_MultinomialNaiveBayesClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "mnb_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="MultinomialNaiveBayesClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=69 FAILED [class=2, true class=1] features=(6.20,2.20,4.50,1.50] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=132 FAILED [class=1, true class=2] features=(7.90,3.80,6.40,2.00] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier correct results: 95.33% Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model=MultinomialNaiveBayesClassifier all samples accuracy=0.953333 Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50) Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model=MultinomialNaiveBayesClassifier batch test accuracy=0.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 95.33%, lo cual coincide con la precisión del original.
2.19.3. Representación ONNX del modelo Multinomial Naive Bayes (MNB) Classifier
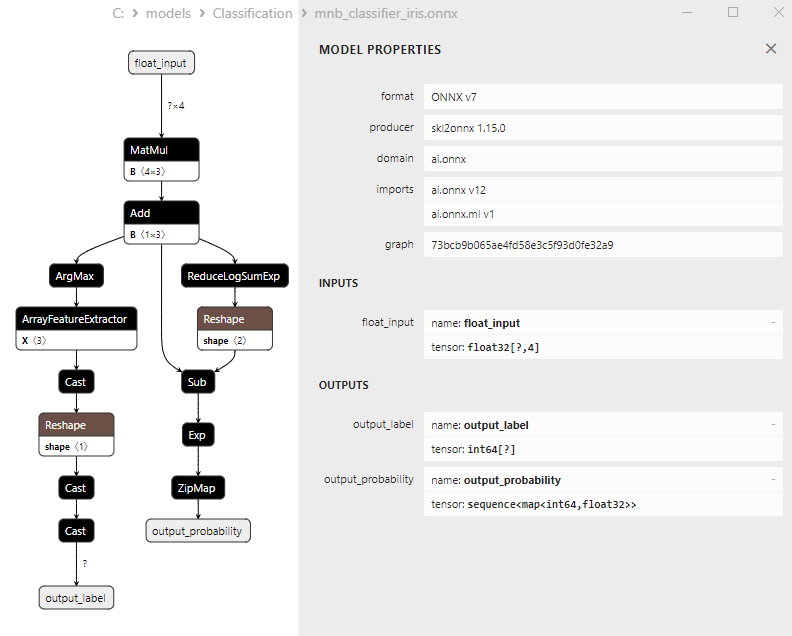
Fig. 33. Representación ONNX del modelo Multinomial Naive Bayes (MNB) Classifier en Netron
2.20. Complement Naive Bayes (CNB) Classifier
Complement Naive Bayes (CNB) Classifier es una variante del clasificador bayesiano ingenuo que se diseñó específicamente para tratar datos desequilibrados, en los que una clase puede ser significativamente más frecuente que otra. Este clasificador es una adaptación del método bayesiano ingenuo clásico que intenta considerar el desequilibrio de clases.Principios de funcionamiento de Complement Naive Bayes Classifier:
- Enfoque bayesiano: Al igual que otros clasificadores bayesianos, CNB se basa en un enfoque bayesiano de la clasificación y utiliza el teorema de Bayes para calcular la probabilidad de que un objeto pertenezca a cada clase.
- Corrección del desequilibrio de clases: El principal objetivo de CNB es corregir el desequilibrio de clases. En lugar de considerar la probabilidad de las características en la clase, como hace el método bayesiano ingenuo estándar, CNB intenta considerar la probabilidad de las características fuera de la clase. Esto resulta especialmente útil cuando una clase está significativamente menos representada que otra.
- Entrenamiento de parámetros: El modelo CNB se entrena en el conjunto de datos de entrenamiento calculando los parámetros de distribución para cada característica fuera de clase.
- Equidad para datos desequilibrados: CNB obtiene buenos resultados en tareas de clasificación con datos desequilibrados en los que las clases aparecen con distinta frecuencia.
- Facilidad y rapidez de aprendizaje: Al igual que otros clasificadores bayesianos ingenuos, CNB es un algoritmo sencillo que aprende rápidamente, incluso con grandes cantidades de datos.
- Sensibilidad a la selección del parámetro de regularización: Como en otros métodos bayesianos, seleccionar el valor correcto del parámetro de regularización puede requerir un ajuste y una estimación.
- Suposición ingenua: Al igual que otros clasificadores bayesianos ingenuos, CNB asume la independencia de las características, lo cual puede resultar demasiado simplista para algunas tareas.
Complement Naive Bayes Classifier es una buena opción para tareas de clasificación con datos desequilibrados, especialmente cuando una clase está significativamente menos representada que otra. Puede resultar especialmente útil en tareas de clasificación de textos en las que las palabras pueden estar muy desequilibradas entre clases, como el análisis del tono en los textos o el filtrado de spam.
2.20.1. Código de creación del modelo Complement Naive Bayes (CNB) Classifier
Este código demuestra el proceso de entrenamiento del modelo Complement Naive Bayes (CNB) Classifier con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_CNBClassifier.py # The code demonstrates the process of training Complement Naive Bayes (CNB) Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.naive_bayes import ComplementNB from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Complement Naive Bayes (CNB) Classifier model cnb_model = ComplementNB() # train the model on the entire dataset cnb_model.fit(X, y) # predict classes for the entire dataset y_pred = cnb_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Complement Naive Bayes (CNB) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(cnb_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "cnb_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Complement Naive Bayes (CNB) Classifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of Complement Naive Bayes (CNB) Classifier model: 0.6666666666666666
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.96 1.00 0.98 50
Python 1 0.00 0.00 0.00 50
Python 2 0.51 1.00 0.68 50
Python
Python accuracy 0.67 150
Python macro avg 0.49 0.67 0.55 150
Python weighted avg 0.49 0.67 0.55 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\cnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Complement Naive Bayes (CNB) Classifier model in ONNX format: 0.6666666666666666
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.96 1.00 0.98 50
Python 1 0.00 0.00 0.00 50
Python 2 0.51 1.00 0.68 50
Python
Python accuracy 0.67 150
Python macro avg 0.49 0.67 0.55 150
Python weighted avg 0.49 0.67 0.55 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\cnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Complement Naive Bayes (CNB) Classifier model in ONNX format: 0.6666666666666666
2.20.2. Código en MQL5 para trabajar con el modelo Complement Naive Bayes (CNB) Classifier
//+------------------------------------------------------------------+ //| Iris_CNBClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "cnb_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="CNBClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=51 FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=52 FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=54 FAILED [class=2, true class=1] features=(5.50,2.30,4.00,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=55 FAILED [class=2, true class=1] features=(6.50,2.80,4.60,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=56 FAILED [class=2, true class=1] features=(5.70,2.80,4.50,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=57 FAILED [class=2, true class=1] features=(6.30,3.30,4.70,1.60] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=58 FAILED [class=2, true class=1] features=(4.90,2.40,3.30,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=59 FAILED [class=2, true class=1] features=(6.60,2.90,4.60,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=60 FAILED [class=2, true class=1] features=(5.20,2.70,3.90,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=61 FAILED [class=2, true class=1] features=(5.00,2.00,3.50,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=62 FAILED [class=2, true class=1] features=(5.90,3.00,4.20,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=63 FAILED [class=2, true class=1] features=(6.00,2.20,4.00,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=64 FAILED [class=2, true class=1] features=(6.10,2.90,4.70,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=65 FAILED [class=2, true class=1] features=(5.60,2.90,3.60,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=66 FAILED [class=2, true class=1] features=(6.70,3.10,4.40,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=68 FAILED [class=2, true class=1] features=(5.80,2.70,4.10,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=69 FAILED [class=2, true class=1] features=(6.20,2.20,4.50,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=70 FAILED [class=2, true class=1] features=(5.60,2.50,3.90,1.10] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=72 FAILED [class=2, true class=1] features=(6.10,2.80,4.00,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=74 FAILED [class=2, true class=1] features=(6.10,2.80,4.70,1.20] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=75 FAILED [class=2, true class=1] features=(6.40,2.90,4.30,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=76 FAILED [class=2, true class=1] features=(6.60,3.00,4.40,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=77 FAILED [class=2, true class=1] features=(6.80,2.80,4.80,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=79 FAILED [class=2, true class=1] features=(6.00,2.90,4.50,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=80 FAILED [class=0, true class=1] features=(5.70,2.60,3.50,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=81 FAILED [class=2, true class=1] features=(5.50,2.40,3.80,1.10] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=82 FAILED [class=2, true class=1] features=(5.50,2.40,3.70,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=83 FAILED [class=2, true class=1] features=(5.80,2.70,3.90,1.20] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=86 FAILED [class=2, true class=1] features=(6.00,3.40,4.50,1.60] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=87 FAILED [class=2, true class=1] features=(6.70,3.10,4.70,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=88 FAILED [class=2, true class=1] features=(6.30,2.30,4.40,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=89 FAILED [class=2, true class=1] features=(5.60,3.00,4.10,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=90 FAILED [class=2, true class=1] features=(5.50,2.50,4.00,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=91 FAILED [class=2, true class=1] features=(5.50,2.60,4.40,1.20] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=92 FAILED [class=2, true class=1] features=(6.10,3.00,4.60,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=93 FAILED [class=2, true class=1] features=(5.80,2.60,4.00,1.20] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=94 FAILED [class=2, true class=1] features=(5.00,2.30,3.30,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=95 FAILED [class=2, true class=1] features=(5.60,2.70,4.20,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=96 FAILED [class=2, true class=1] features=(5.70,3.00,4.20,1.20] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=97 FAILED [class=2, true class=1] features=(5.70,2.90,4.20,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=98 FAILED [class=2, true class=1] features=(6.20,2.90,4.30,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=99 FAILED [class=0, true class=1] features=(5.10,2.50,3.00,1.10] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=100 FAILED [class=2, true class=1] features=(5.70,2.80,4.10,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier correct results: 66.67% Iris_CNBClassifier (EURUSD,H1) model=CNBClassifier all samples accuracy=0.666667 Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50) Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40) Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50) Iris_CNBClassifier (EURUSD,H1) model=CNBClassifier batch test accuracy=0.000000Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 66.67%, lo cual coincide con la precisión del original.
2.20.3. Representación ONNX del modelo Complement Naive Bayes (CNB) Classifier
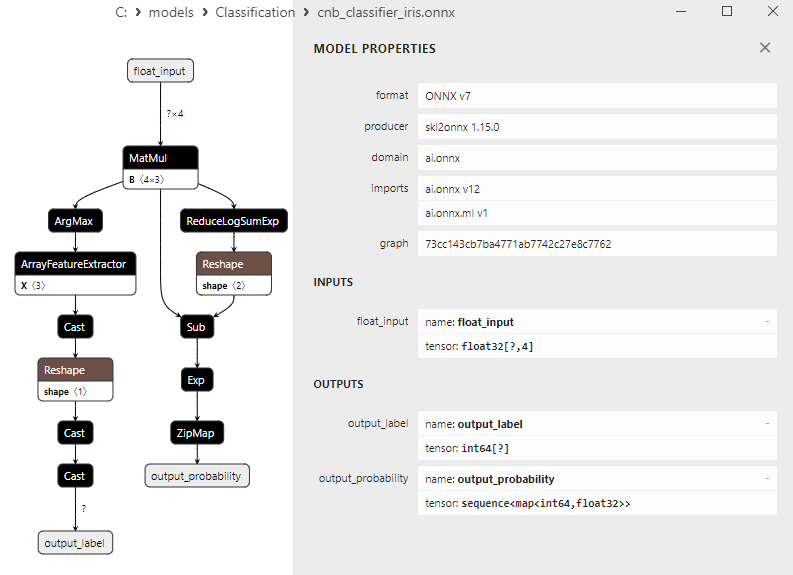
Fig. 34. Representación ONNX del modelo Complement Naive Bayes (CNB) Classifier en Netron
2.21. Bernoulli Naive Bayes (BNB) Classifier
Bernoulli Naive Bayes (BNB) Classifier es otra variante del clasificador bayesiano ingenuo que se utiliza para tareas de clasificación binaria. Este clasificador resulta especialmente útil en situaciones en las que las características se representan mediante datos binarios, como en las tareas de análisis de texto, en las que las características pueden ser la presencia o ausencia de palabras en el texto.
Principios de funcionamiento de Bernoulli Naive Bayes Classifier:
- Enfoque bayesiano: Al igual que otros clasificadores bayesianos, BNB se basa en un enfoque bayesiano de la clasificación y utiliza el teorema de Bayes para calcular la probabilidad de que un objeto pertenezca a cada clase.
- Supuesto de rasgos binarios: El supuesto básico de BNB es que las características son datos binarios, lo cual significa que solo pueden tener dos valores, por ejemplo, 1 y 0, donde 1 denota la presencia de una característica y 0 su ausencia.
- Entrenamiento de parámetros: El modelo BNB se entrena con el conjunto de datos de entrenamiento calculando los parámetros de distribución de cada característica en cada clase.
- Eficacia para datos binarios: BNB funciona bien en tareas en las que las características están representadas por datos binarios, y puede resultar especialmente útil en tareas de análisis de texto o clasificación de eventos.
- Facilidad y rapidez de aprendizaje: Al igual que otros clasificadores bayesianos ingenuos, BNB es un algoritmo simple que aprende rápidamente.
- Limitación a características binarias: BNB no resulta adecuado para tareas en las que las características no son binarias. Si las características tienen más de dos valores, BNB no considera esta información.
- Suposición ingenua: Al igual que otros clasificadores bayesianos ingenuos, BNB asume la independencia de las características, lo cual puede resultar demasiado simplista para algunas tareas.
Bernoulli Naive Bayes Classifier es una buena opción para tareas de clasificación binaria con características binarias, como el análisis de tonos en el texto o la clasificación de spam. Resulta fácil de usar y maneja bien este tipo de datos.
2.21.1. Código de creación del modelo Bernoulli Naive Bayes (BNB) Classifier
Este código demuestra el proceso de entrenamiento del modelo Bernoulli Naive Bayes (BNB) Classifier con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_BNBClassifier.py # The code demonstrates the process of training Bernoulli Naive Bayes (BNB) Classifier on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.naive_bayes import BernoulliNB from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Bernoulli Naive Bayes (BNB) Classifier model bnb_model = BernoulliNB() # train the model on the entire dataset bnb_model.fit(X, y) # predict classes for the entire dataset y_pred = bnb_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Bernoulli Naive Bayes (BNB) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(bnb_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "bnb_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Bernoulli Naive Bayes (BNB) Classifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of Bernoulli Naive Bayes (BNB) Classifier model: 0.3333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.33 1.00 0.50 50
Python 1 0.00 0.00 0.00 50
Python 2 0.00 0.00 0.00 50
Python
Python accuracy 0.33 150
Python macro avg 0.11 0.33 0.17 150
Python weighted avg 0.11 0.33 0.17 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\bnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Bernoulli Naive Bayes (BNB) Classifier model in ONNX format: 0.3333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.33 1.00 0.50 50
Python 1 0.00 0.00 0.00 50
Python 2 0.00 0.00 0.00 50
Python
Python accuracy 0.33 150
Python macro avg 0.11 0.33 0.17 150
Python weighted avg 0.11 0.33 0.17 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\bnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Bernoulli Naive Bayes (BNB) Classifier model in ONNX format: 0.3333333333333333
2.21.2. Código en MQL5 para trabajar con el modelo Bernoulli Naive Bayes (BNB) Classifier
//+------------------------------------------------------------------+ //| Iris_BNBClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "bnb_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="BNBClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=51 FAILED [class=0, true class=1] features=(7.00,3.20,4.70,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=52 FAILED [class=0, true class=1] features=(6.40,3.20,4.50,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=53 FAILED [class=0, true class=1] features=(6.90,3.10,4.90,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=54 FAILED [class=0, true class=1] features=(5.50,2.30,4.00,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=55 FAILED [class=0, true class=1] features=(6.50,2.80,4.60,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=56 FAILED [class=0, true class=1] features=(5.70,2.80,4.50,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=57 FAILED [class=0, true class=1] features=(6.30,3.30,4.70,1.60] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=58 FAILED [class=0, true class=1] features=(4.90,2.40,3.30,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=59 FAILED [class=0, true class=1] features=(6.60,2.90,4.60,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=60 FAILED [class=0, true class=1] features=(5.20,2.70,3.90,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=61 FAILED [class=0, true class=1] features=(5.00,2.00,3.50,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=62 FAILED [class=0, true class=1] features=(5.90,3.00,4.20,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=63 FAILED [class=0, true class=1] features=(6.00,2.20,4.00,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=64 FAILED [class=0, true class=1] features=(6.10,2.90,4.70,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=65 FAILED [class=0, true class=1] features=(5.60,2.90,3.60,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=66 FAILED [class=0, true class=1] features=(6.70,3.10,4.40,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=67 FAILED [class=0, true class=1] features=(5.60,3.00,4.50,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=68 FAILED [class=0, true class=1] features=(5.80,2.70,4.10,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=69 FAILED [class=0, true class=1] features=(6.20,2.20,4.50,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=70 FAILED [class=0, true class=1] features=(5.60,2.50,3.90,1.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=71 FAILED [class=0, true class=1] features=(5.90,3.20,4.80,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=72 FAILED [class=0, true class=1] features=(6.10,2.80,4.00,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=73 FAILED [class=0, true class=1] features=(6.30,2.50,4.90,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=74 FAILED [class=0, true class=1] features=(6.10,2.80,4.70,1.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=75 FAILED [class=0, true class=1] features=(6.40,2.90,4.30,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=76 FAILED [class=0, true class=1] features=(6.60,3.00,4.40,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=77 FAILED [class=0, true class=1] features=(6.80,2.80,4.80,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=78 FAILED [class=0, true class=1] features=(6.70,3.00,5.00,1.70] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=79 FAILED [class=0, true class=1] features=(6.00,2.90,4.50,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=80 FAILED [class=0, true class=1] features=(5.70,2.60,3.50,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=81 FAILED [class=0, true class=1] features=(5.50,2.40,3.80,1.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=82 FAILED [class=0, true class=1] features=(5.50,2.40,3.70,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=83 FAILED [class=0, true class=1] features=(5.80,2.70,3.90,1.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=84 FAILED [class=0, true class=1] features=(6.00,2.70,5.10,1.60] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=85 FAILED [class=0, true class=1] features=(5.40,3.00,4.50,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=86 FAILED [class=0, true class=1] features=(6.00,3.40,4.50,1.60] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=87 FAILED [class=0, true class=1] features=(6.70,3.10,4.70,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=88 FAILED [class=0, true class=1] features=(6.30,2.30,4.40,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=89 FAILED [class=0, true class=1] features=(5.60,3.00,4.10,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=90 FAILED [class=0, true class=1] features=(5.50,2.50,4.00,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=91 FAILED [class=0, true class=1] features=(5.50,2.60,4.40,1.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=92 FAILED [class=0, true class=1] features=(6.10,3.00,4.60,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=93 FAILED [class=0, true class=1] features=(5.80,2.60,4.00,1.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=94 FAILED [class=0, true class=1] features=(5.00,2.30,3.30,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=95 FAILED [class=0, true class=1] features=(5.60,2.70,4.20,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=96 FAILED [class=0, true class=1] features=(5.70,3.00,4.20,1.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=97 FAILED [class=0, true class=1] features=(5.70,2.90,4.20,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=98 FAILED [class=0, true class=1] features=(6.20,2.90,4.30,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=99 FAILED [class=0, true class=1] features=(5.10,2.50,3.00,1.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=100 FAILED [class=0, true class=1] features=(5.70,2.80,4.10,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=101 FAILED [class=0, true class=2] features=(6.30,3.30,6.00,2.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=102 FAILED [class=0, true class=2] features=(5.80,2.70,5.10,1.90] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=103 FAILED [class=0, true class=2] features=(7.10,3.00,5.90,2.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=104 FAILED [class=0, true class=2] features=(6.30,2.90,5.60,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=105 FAILED [class=0, true class=2] features=(6.50,3.00,5.80,2.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=106 FAILED [class=0, true class=2] features=(7.60,3.00,6.60,2.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=107 FAILED [class=0, true class=2] features=(4.90,2.50,4.50,1.70] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=108 FAILED [class=0, true class=2] features=(7.30,2.90,6.30,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=109 FAILED [class=0, true class=2] features=(6.70,2.50,5.80,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=110 FAILED [class=0, true class=2] features=(7.20,3.60,6.10,2.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=111 FAILED [class=0, true class=2] features=(6.50,3.20,5.10,2.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=112 FAILED [class=0, true class=2] features=(6.40,2.70,5.30,1.90] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=113 FAILED [class=0, true class=2] features=(6.80,3.00,5.50,2.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=114 FAILED [class=0, true class=2] features=(5.70,2.50,5.00,2.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=115 FAILED [class=0, true class=2] features=(5.80,2.80,5.10,2.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=116 FAILED [class=0, true class=2] features=(6.40,3.20,5.30,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=117 FAILED [class=0, true class=2] features=(6.50,3.00,5.50,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=118 FAILED [class=0, true class=2] features=(7.70,3.80,6.70,2.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=119 FAILED [class=0, true class=2] features=(7.70,2.60,6.90,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=120 FAILED [class=0, true class=2] features=(6.00,2.20,5.00,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=121 FAILED [class=0, true class=2] features=(6.90,3.20,5.70,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=122 FAILED [class=0, true class=2] features=(5.60,2.80,4.90,2.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=123 FAILED [class=0, true class=2] features=(7.70,2.80,6.70,2.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=124 FAILED [class=0, true class=2] features=(6.30,2.70,4.90,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=125 FAILED [class=0, true class=2] features=(6.70,3.30,5.70,2.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=126 FAILED [class=0, true class=2] features=(7.20,3.20,6.00,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=127 FAILED [class=0, true class=2] features=(6.20,2.80,4.80,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=128 FAILED [class=0, true class=2] features=(6.10,3.00,4.90,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=129 FAILED [class=0, true class=2] features=(6.40,2.80,5.60,2.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=130 FAILED [class=0, true class=2] features=(7.20,3.00,5.80,1.60] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=131 FAILED [class=0, true class=2] features=(7.40,2.80,6.10,1.90] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=132 FAILED [class=0, true class=2] features=(7.90,3.80,6.40,2.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=133 FAILED [class=0, true class=2] features=(6.40,2.80,5.60,2.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=134 FAILED [class=0, true class=2] features=(6.30,2.80,5.10,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=135 FAILED [class=0, true class=2] features=(6.10,2.60,5.60,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=136 FAILED [class=0, true class=2] features=(7.70,3.00,6.10,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=137 FAILED [class=0, true class=2] features=(6.30,3.40,5.60,2.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=138 FAILED [class=0, true class=2] features=(6.40,3.10,5.50,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=139 FAILED [class=0, true class=2] features=(6.00,3.00,4.80,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=140 FAILED [class=0, true class=2] features=(6.90,3.10,5.40,2.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=141 FAILED [class=0, true class=2] features=(6.70,3.10,5.60,2.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=142 FAILED [class=0, true class=2] features=(6.90,3.10,5.10,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=143 FAILED [class=0, true class=2] features=(5.80,2.70,5.10,1.90] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=144 FAILED [class=0, true class=2] features=(6.80,3.20,5.90,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=145 FAILED [class=0, true class=2] features=(6.70,3.30,5.70,2.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=146 FAILED [class=0, true class=2] features=(6.70,3.00,5.20,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=147 FAILED [class=0, true class=2] features=(6.30,2.50,5.00,1.90] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=148 FAILED [class=0, true class=2] features=(6.50,3.00,5.20,2.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=149 FAILED [class=0, true class=2] features=(6.20,3.40,5.40,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=150 FAILED [class=0, true class=2] features=(5.90,3.00,5.10,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier correct results: 33.33% Iris_BNBClassifier (EURUSD,H1) model=BNBClassifier all samples accuracy=0.333333 Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=1] features=(6.30,2.50,4.90,1.50) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=2] features=(6.30,2.70,4.90,1.80) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=1] features=(7.00,3.20,4.70,1.40) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=1] features=(6.40,3.20,4.50,1.50) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=2] features=(6.30,3.30,6.00,2.50) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=2] features=(5.80,2.70,5.10,1.90) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=2] features=(7.10,3.00,5.90,2.10) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=2] features=(6.30,2.90,5.60,1.80) Iris_BNBClassifier (EURUSD,H1) model=BNBClassifier batch test accuracy=0.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 33.33%, lo cual coincide con la precisión del original.
2.21.3. Representación ONNX del modelo Bernoulli Naive Bayes (BNB) Classifier
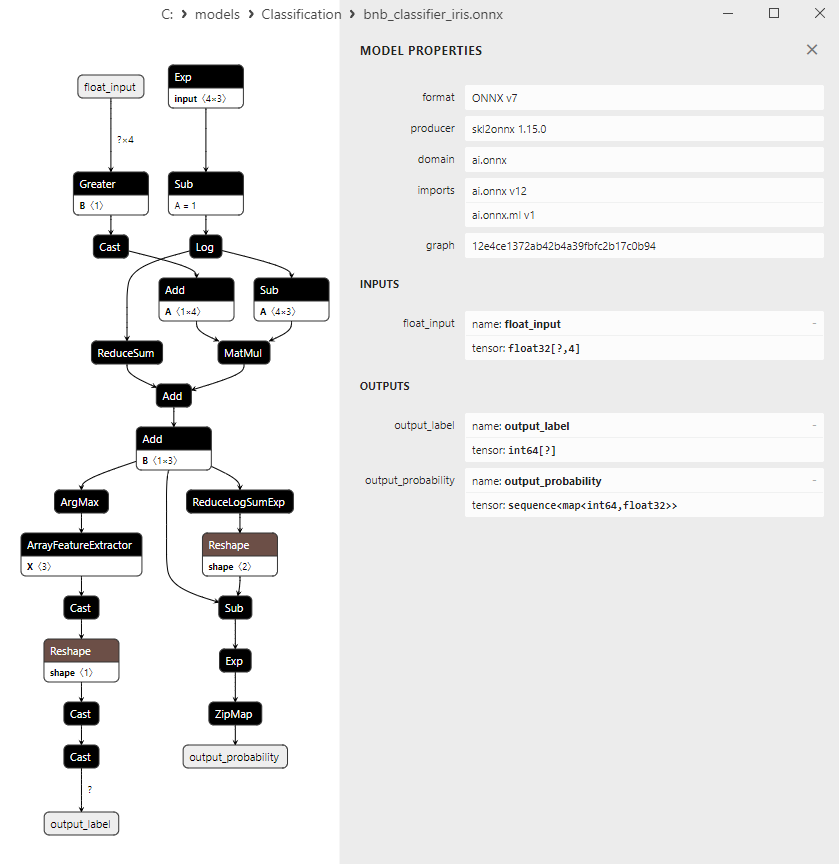
Fig. 35. Representación en ONNX del modelo Bernoulli Naive Bayes (BNB) Classifier en Netron
2.22. Multilayer Perceptron Classifier
MLP Classifier (Multilayer Perceptron Classifier) es una red neuronal multivalor que se utiliza para tareas de clasificación. Se trata de un perceptrón multicapa compuesto por varias capas de neuronas que incluyen una capa de entrada, capas ocultas y una capa de salida. MLP Classifier tiene la capacidad de aprender dependencias no lineales complejas en los datos.
- Arquitectura multicapa: MLP Classifier tiene una arquitectura multicapa que incluye una capa de entrada, una o más capas ocultas y una capa de salida. Cada neurona de las capas está conectada a las neuronas de las capas vecinas con pesos que se deben entrenar.
- Funciones de activación: Dentro de cada neurona, se aplica una función de activación que introduce la no linealidad en el modelo y permite a MLP Classifier modelar dependencias complejas en los datos.
- Aprendizaje por propagación inversa del error: MLP Classifier se entrena usando un método de retropropagación (backpropagation) que minimiza el error entre las predicciones del modelo y las etiquetas de clase verdaderas.
- Capacidad para modelar dependencias complejas: MLP Classifier puede aprender relaciones no lineales complejas en los datos y, por tanto, puede dar buenos resultados en problemas en los que los modelos lineales simples son insuficientes.
- Versatilidad: MLP Classifier puede utilizarse para una amplia gama de tareas de clasificación, incluidas la clasificación multiclase y la clasificación multitarea.
- Sensibilidad a los hiperparámetros: MLP Classifier tiene muchos hiperparámetros como el número de capas ocultas, el número de neuronas en cada capa, la velocidad de aprendizaje y otros. Configurar estos parámetros puede llevar mucho tiempo y consumir muchos recursos.
- Necesidad de una gran cantidad de datos: MLP Classifier requiere una gran cantidad de datos de entrenamiento para evitar el sobreentrenamiento, especialmente cuando el modelo tiene muchos parámetros.
- Tendencia al sobreentrenamiento: Si el modelo tiene demasiados parámetros o pocos datos, puede sobreentrenarse y obtener malos resultados con los nuevos datos.
MLP Classifier es una potente herramienta para tareas de clasificación, especialmente cuando los datos tienen dependencias complejas. A menudo se usa en los campos del aprendizaje automático y el aprendizaje profundo para resolver diversos problemas de clasificación. No obstante, para aplicar con éxito este modelo, resultas importante ajustar adecuadamente sus hiperparámetros y proporcionarle suficientes datos de entrenamiento.
2.22.1. Código de creación del modelo Multilayer Perceptron Classifier
Este código demuestra el proceso de entrenamiento del modelo Multilayer Perceptron Classifier con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_MLPClassifier.py # The code demonstrates the process of training Multilayer Perceptron Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.neural_network import MLPClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Multilayer Perceptron (MLP) Classifier model mlp_model = MLPClassifier(max_iter=1000, random_state=42) # train the model on the entire dataset mlp_model.fit(X, y) # predict classes for the entire dataset y_pred = mlp_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Multilayer Perceptron (MLP) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(mlp_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path +"mlp_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Multilayer Perceptron (MLP) Classifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of Multilayer Perceptron (MLP) Classifier model: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 0.94 0.97 50
Python 2 0.94 1.00 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\mlp_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Multilayer Perceptron (MLP) Classifier model in ONNX format: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 0.94 0.97 50
Python 2 0.94 1.00 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\mlp_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Multilayer Perceptron (MLP) Classifier model in ONNX format: 0.98
2.22.2. Código en MQL5 para trabajar con el modelo Multilayer Perceptron Classifier
//+------------------------------------------------------------------+ //| Iris_MLPClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "mlp_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="MLPClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_MLPClassifier (EURUSD,H1) model:MLPClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_MLPClassifier (EURUSD,H1) model:MLPClassifier sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_MLPClassifier (EURUSD,H1) model:MLPClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_MLPClassifier (EURUSD,H1) model:MLPClassifier correct results: 98.00% Iris_MLPClassifier (EURUSD,H1) model=MLPClassifier all samples accuracy=0.980000 Iris_MLPClassifier (EURUSD,H1) model:MLPClassifier FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50) Iris_MLPClassifier (EURUSD,H1) model=MLPClassifier batch test accuracy=0.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 98%, lo cual coincide con la precisión del original.
2.22.3. Representación ONNX del modelo Multilayer Perceptron Classifier
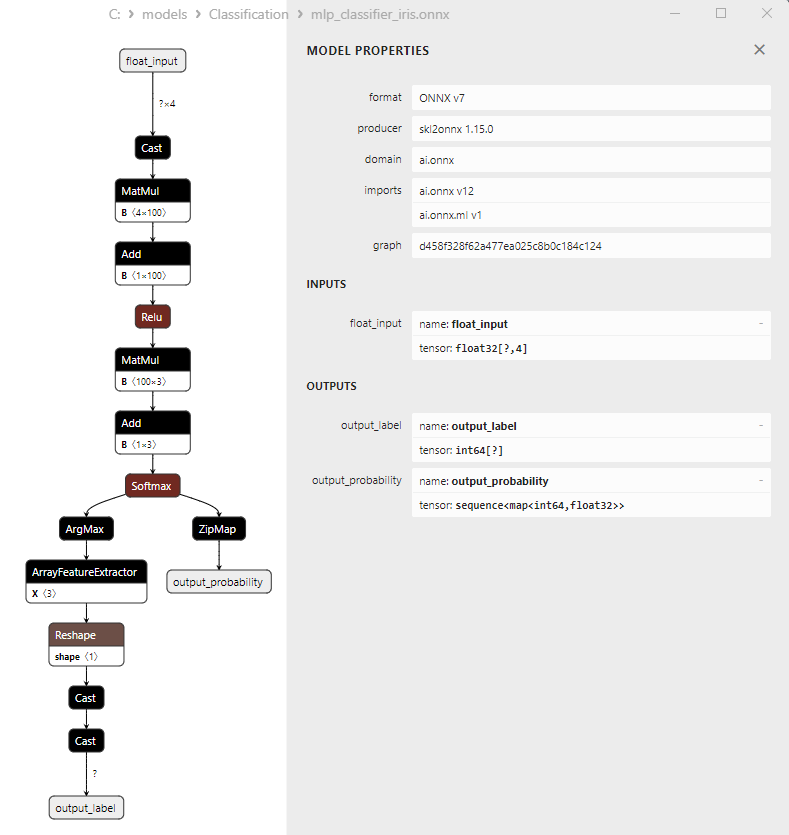
Fig. 36. Representación ONNX del modelo Multilayer Perceptron Classifier en Netron
2.23. Linear Discriminant Analysis (LDA) Classifier
Linear Discriminant Analysis (LDA) Classifier es una técnica de aprendizaje automático que se utiliza para resolver problemas de clasificación. Pertenece a la familia de los métodos de reducción de la dimensionalidad de los datos y de clasificación en un espacio de baja dimensionalidad. LDA construye hiperplanos de forma que se maximice la separación entre clases.Principios de funcionamiento de LDA Classifier:
- Reducción de la dimensionalidad: La idea básica de LDA es reducir la dimensionalidad de los datos. Intenta encontrar un nuevo espacio de características en el que las clases de datos estén lo más separadas posible entre sí.
- Maximización de la separación: LDA construye hiperplanos (combinaciones lineales de características) que maximizan la diferencia entre los valores medios de las características de las distintas clases y minimizan la varianza dentro de cada clase.
- Entrenamiento de parámetros: El modelo LDA se entrena con el conjunto de datos de entrenamiento calculando los parámetros de los hiperplanos y las proyecciones de los datos en el nuevo espacio.
- Mejor separación de clases: LDA puede mejorar enormemente la separación de clases en los datos, especialmente cuando las clases se solapan en gran medida en el espacio de características original.
- Reducción de la dimensionalidad: LDA también puede usarse para reducir la dimensionalidad de los datos, lo cual puede ser útil para la visualización y la reducción de la complejidad computacional del problema.
- Requisito de distribución normal: LDA asume que las características tienen una distribución normal y que las clases tienen las mismas matrices de covarianza. Si no se cumplen estos supuestos, LDA puede producir resultados menos precisos.
- Sensibilidad a los valores atípicos: LDA puede resultar sensible a los valores atípicos en los datos, ya que pueden afectar al cálculo de los parámetros del modelo.
- Dificultades en la clasificación multiclase: LDA se diseñó originalmente para la clasificación binaria, y su aplicación a problemas multiclase requiere la ampliación del método.
LDA Classifier es un método útil para tareas de clasificación y reducción de la dimensionalidad de los datos, especialmente cuando es necesario mejorar la separación de clases. Se usa a menudo en estadística, biología, análisis médico y otros campos para el análisis y la clasificación de datos.
2.23.1. Código de creación del modelo Linear Discriminant Analysis (LDA) Classifier
Este código demuestra el proceso de entrenamiento del modelo Linear Discriminant Analysis (LDA) Classifier con el Iris dataset, exportándolo al formato ONNX, y efectuando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_LDAClassifier.py # The code demonstrates the process of training Linear Discriminant Analysis (LDA) Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.discriminant_analysis import LinearDiscriminantAnalysis from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Linear Discriminant Analysis (LDA) Classifier model lda_model = LinearDiscriminantAnalysis() # train the model on the entire dataset lda_model.fit(X, y) # predict classes for the entire dataset y_pred = lda_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Linear Discriminant Analysis (LDA) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(lda_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path +"lda_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Linear Discriminant Analysis (LDA) Classifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of Linear Discriminant Analysis (LDA) Classifier model: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.96 0.97 50
Python 2 0.96 0.98 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\lda_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Linear Discriminant Analysis (LDA) Classifier model in ONNX format: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.96 0.97 50
Python 2 0.96 0.98 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\lda_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Linear Discriminant Analysis (LDA) Classifier model in ONNX format: 0.98
2.23.2. Código en MQL5 para trabajar con el modelo Linear Discriminant Analysis (LDA) Classifier
//+------------------------------------------------------------------+ //| Iris_LDAClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "lda_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="LDAClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_LDAClassifier (EURUSD,H1) model:LDAClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_LDAClassifier (EURUSD,H1) model:LDAClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_LDAClassifier (EURUSD,H1) model:LDAClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_LDAClassifier (EURUSD,H1) model:LDAClassifier correct results: 98.00% Iris_LDAClassifier (EURUSD,H1) model=LDAClassifier all samples accuracy=0.980000 Iris_LDAClassifier (EURUSD,H1) model=LDAClassifier batch test accuracy=1.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 98%, lo cual coincide con la precisión del original.
2.23.3. Representación ONNX del modelo Linear Discriminant Analysis (LDA) Classifier
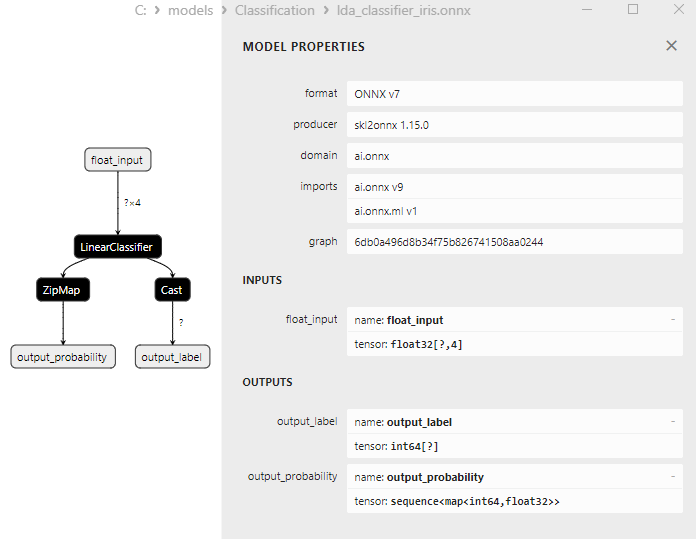
Fig. 37. Representación ONNX del modelo Linear Discriminant Analysis (LDA) Classifier en Netron
2.24. Hist Gradient Boosting
Hist Gradient Boosting Classifier es un algoritmo de aprendizaje automático que pertenece a la familia gradient boosting y está diseñado para tareas de clasificación. Se trata de un método eficaz y potente muy usado en el análisis de datos y el aprendizaje automático.
Principios de funcionamiento de Hist Gradient Boosting Classifier:
- Gradient boosting: Hist Gradient Boosting Classifier se basa en un método de refuerzo de gradiente que construye un conjunto de árboles de decisiones para mejorar la clasificación. Para ello, entrena sucesivamente modelos débiles y corrige los errores de los modelos anteriores.
- Uso de histogramas: La palabra "Hist" en el nombre significa que este algoritmo utiliza histogramas para trabajar eficazmente con los datos. En lugar de una iteración completa de las características, Hist Gradient Boosting construye histogramas de las mismas, lo cual permite calcular rápidamente separaciones en árboles de decisiones.
- Entrenamiento con residuos: Al igual que otros métodos de refuerzo de gradiente, Hist Gradient Boosting entrena cada nuevo árbol con los residuos del modelo anterior para refinar la predicción.
- Gran precisión: Hist Gradient Boosting Classifier suele proporcionar una alta precisión de clasificación, especialmente cuando se utilizan muchos árboles.
- Eficiencia: El uso de histogramas permite al algoritmo procesar eficazmente grandes cantidades de datos y construir rápidamente un conjunto.
- Capacidad para trabajar con datos heterogéneos: El algoritmo es capaz de gestionar datos heterogéneos que incluyen características categóricas y numéricas.
- Sensibilidad al sobreentrenamiento: Si los parámetros no están suficientemente ajustados o se usa un gran número de árboles, Hist Gradient Boosting Classifier puede encontrarse con un problema de sobreentrenamiento.
- Ajuste de parámetros: Al igual que otros algoritmos de Gradient Boosting, Hist Gradient Boosting requiere un ajuste cuidadoso de los parámetros para lograr el mejor rendimiento.
Hist Gradient Boosting Classifier es un potente algoritmo para tareas de clasificación y regresión que ofrece una gran precisión y eficiencia en el procesamiento de datos. Se aplica en muchos campos, tales como el análisis de datos, la bioinformática y las finanzas, entre otros.
2.24.1. Código para crear el modelo Histogram-Based Gradient Boosting Classifier
Este código demuestra el proceso de entrenamiento del modelo Histogram-Based Gradient Boosting Classifier con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_HistGradientBoostingClassifier.py # The code demonstrates the process of training Histogram-Based Gradient Boosting Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.experimental import enable_hist_gradient_boosting from sklearn.ensemble import HistGradientBoostingClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Histogram-Based Gradient Boosting Classifier model hist_gradient_boosting_model = HistGradientBoostingClassifier(random_state=42) # train the model on the entire dataset hist_gradient_boosting_model.fit(X, y) # predict classes for the entire dataset y_pred = hist_gradient_boosting_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Hist Gradient Boosting Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(hist_gradient_boosting_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path +"hist_gradient_boosting_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Hist Gradient Boosting Classifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of Hist Gradient Boosting Classifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\hist_gradient_boosting_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Hist Gradient Boosting Classifier model in ONNX format: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\hist_gradient_boosting_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Hist Gradient Boosting Classifier model in ONNX format: 1.0
2.24.2. Código MQL5 para trabajar con el modelo Histogram-Based Gradient Boosting Classifier
//+------------------------------------------------------------------+ //| Iris_HistGradientBoostingClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "hist_gradient_boosting_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="HistGradientBoostingClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_HistGradientBoostingClassifier (EURUSD,H1) model:HistGradientBoostingClassifier correct results: 100.00% Iris_HistGradientBoostingClassifier (EURUSD,H1) model=HistGradientBoostingClassifier all samples accuracy=1.000000 Iris_HistGradientBoostingClassifier (EURUSD,H1) model=HistGradientBoostingClassifier batch test accuracy=1.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 100%, lo cual coincide con la precisión del original.
2.24.3. Representación ONNX del modelo Histogram-Based Gradient Boosting Classifier
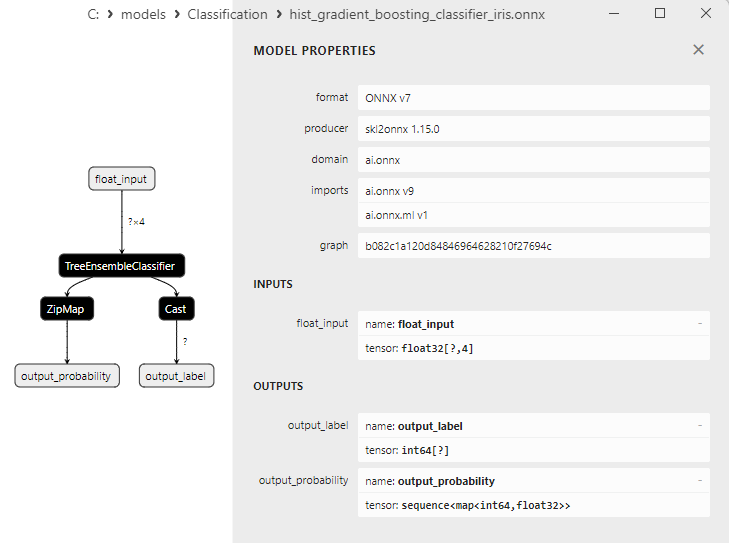
Fig. 38. Representación ONNX del modelo Histogram-Based Gradient Boosting Classifier en Netro
2.25. CategoricalNB Classifier
CategoricalNB es un algoritmo de clasificación basado en el teorema de Bayes. Está diseñado específicamente para conjuntos de datos de características categóricas y se usa ampliamente en la clasificación de textos, la detección de spam y otras aplicaciones de datos discretos.
Principios de funcionamiento de CategoricalNB:
- Clasificador bayesiano ingenuo: CategoricalNB supone un tipo de clasificadores bayesianos ingenuos basados en el teorema de Bayes. Calcula la probabilidad de pertenecer a una clase determinada para un conjunto de características usando las probabilidades condicionales de cada característica dada una clase.
- Características categóricas: A diferencia del clasificador bayesiano ingenuo gaussiano, que asume características continuas con distribución normal, CategoricalNB resulta adecuado para conjuntos de datos con características categóricas. Modela la distribución de probabilidad de cada característica para cada clase.
- Suposición de independencia: La "ingenuidad" en un clasificador bayesiano ingenuo proviene de la suposición de independencia de las características. CategoricalNB asume que las características son condicionalmente independientes dada una clase; aunque este supuesto no siempre se cumple en la práctica, los métodos bayesianos ingenuos pueden producir buenos resultados en muchos conjuntos de datos del mundo real.
Ventajas de CategoricalNB:
- Eficiencia: CategoricalNB resulta eficiente desde el punto de vista computacional y escalable a grandes conjuntos de datos. Requiere una memoria mínima y puede ofrecer predicciones rápidamente.
- Interpretabilidad: La naturaleza probabilística de CategoricalNB facilita su interpretación. Puede ofrece una indicación de qué signos afectan al pronóstico.
- Tratamiento de datos categóricos: CategoricalNB está diseñado concretamente para conjuntos de datos con características categóricas. Puede tratar eficazmente datos de texto y otros tipos de características discretas.
- Rendimiento básico: Con frecuencia sirve como modelo básico sólido para tareas de clasificación de textos y puede superar a algoritmos más complejos en conjuntos de datos pequeños.
Limitaciones de CategoricalNB:
- Suposición de independencia: La suposición de independencia de las características puede no cumplirse en todos los conjuntos de datos. Si las características son muy dependientes, el rendimiento de CategoricalNB podría deteriorarse.
- Sensibilidad al escalado de características: CategoricalNB no requiere escalado de características, ya que trabaja con datos categóricos. No obstante, en algunos casos, normalizar o codificar las características categóricas de diferentes maneras puede afectar a su rendimiento.
- Expresividad limitada: CategoricalNB puede no capturar relaciones complejas en los datos tan bien como otros algoritmos más sofisticados, como los modelos de aprendizaje profundo.
- Procesamiento de omitidos: Se supone que no hay valores omitidos en el conjunto de datos, y los valores omitidos deben procesarse de antemano.
CategoricalNB supone un valioso algoritmo de clasificación especialmente adecuado para conjuntos de datos con características categóricas. Su sencillez, eficacia e interpretabilidad lo convierten en una herramienta útil para diversas tareas de clasificación. A pesar de limitaciones como el supuesto de independencia, sigue siendo una opción popular para la clasificación de textos y otras tareas dominadas por datos discretos. Al trabajar con datos categóricos, considerar CategoricalNB como modelo básico suele ser una opción razonable. No obstante, resulta importante evaluar su rendimiento en comparación con modelos más complejos, especialmente si existen dependencias entre las características de los datos.
2.25.1. Código para crear el modelo CategoricalNB Classifier
Este código demuestra el proceso de entrenamiento del modelo CategoricalNB Classifier con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_CategoricalNBClassifier.py # The code demonstrates the process of training CategoricalNB Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.naive_bayes import CategoricalNB from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a CategoricalNB model categorical_nb_model = CategoricalNB() # train the model on the entire dataset categorical_nb_model.fit(X, y) # predict classes for the entire dataset y_pred = categorical_nb_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of CategoricalNB model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(categorical_nb_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "categorical_nb_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of CategoricalNB model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of CategoricalNB model: 0.9333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.86 0.96 0.91 50
Python 2 0.95 0.84 0.89 50
Python
Python accuracy 0.93 150
Python macro avg 0.94 0.93 0.93 150
Python weighted avg 0.94 0.93 0.93 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\categorical_nb_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of CategoricalNB model in ONNX format: 0.9333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.86 0.96 0.91 50
Python 2 0.95 0.84 0.89 50
Python
Python accuracy 0.93 150
Python macro avg 0.94 0.93 0.93 150
Python weighted avg 0.94 0.93 0.93 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\categorical_nb_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of CategoricalNB model in ONNX format: 0.9333333333333333
2.25.2. Código MQL5 para trabajar con el modelo CategoricalNB Classifier
//+------------------------------------------------------------------+ //| Iris_CategoricalNBClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "categorical_nb_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="CategoricalNBClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+Resultado:
Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=102 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=122 FAILED [class=1, true class=2] features=(5.60,2.80,4.90,2.00] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=124 FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=128 FAILED [class=1, true class=2] features=(6.10,3.00,4.90,1.80] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=143 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier correct results: 93.33% Iris_CategoricalNBClassifier (EURUSD,H1) model=CategoricalNBClassifier all samples accuracy=0.933333 Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80) Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90) Iris_CategoricalNBClassifier (EURUSD,H1) model=CategoricalNBClassifier batch test accuracy=0.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 93.33%, lo cual coincide con la precisión del original.
2.25.3. Representación ONNX del modelo CategoricalNB Classifier
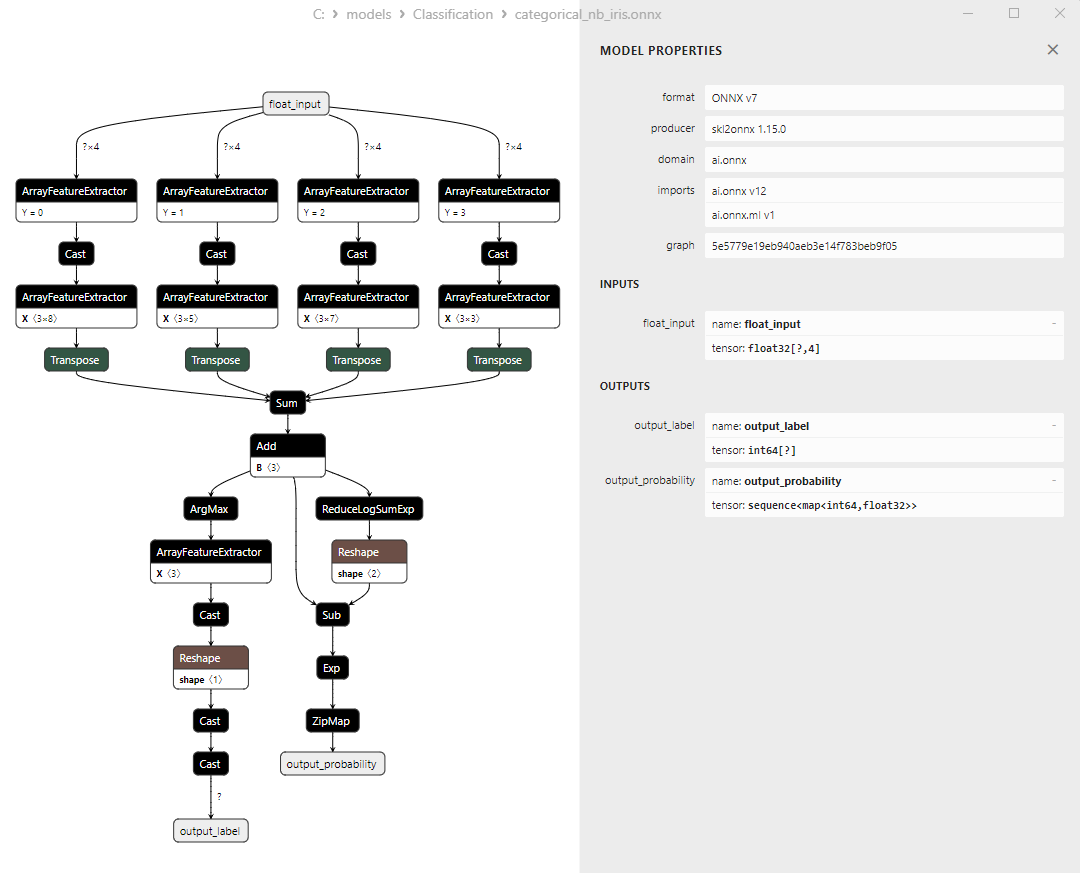
Fig. 39. Representación ONNX del modelo CategoricalNB Classifier en Netron
Nota para los modelos ExtraTreeClassifier y ExtraTreesClassifier
ExtraTreeClassifier y ExtraTreesClassifier son dos clasificadores distintos, y su principal diferencia es cómo funcionan:
ExtraTreeClassifier (Extremely Randomized Trees Classifier):
ExtraTreeClassifier y ExtraTreesClassifier son dos clasificadores distintos, y su principal diferencia es cómo funcionan:
ExtraTreeClassifier (Extremely Randomized Trees Classifier):
- Este clasificador también se conoce como Extremely Randomised Trees o Extra-Trees.
- Se basa en la idea de árboles de decisiones aleatorios.
- En ExtraTreeClassifier, la selección de una partición para cada nodo del árbol se realiza de forma aleatoria, sin búsqueda previa de la mejor partición.
- Esto hace que el clasificador sea menos intensivo computacionalmente que un bosque aleatorio clásico, pues no requiere calcular particiones óptimas para cada nodo.
- ExtraTreeClassifier suele usar umbrales aleatorios para las características y particiones aleatorias, lo cual da lugar a árboles más aleatorios.
- La falta de búsqueda de las mejores particiones hace que ExtraTreeClassifier sea más rápido pero menos preciso que Random Forest.
- ExtraTreesClassifier es también un clasificador basado en el método de los árboles extremadamente aleatorizados.
- La principal diferencia entre ExtraTreesClassifier y ExtraTreeClassifier es que ExtraTreesClassifier realiza particiones aleatorias para seleccionar las mejores particiones en cada nodo del árbol.
- Esto significa que ExtraTreesClassifier aplica un bosque aleatorio con un nivel adicional de aleatoriedad a la hora de seleccionar las particiones óptimas.
- ExtraTreesClassifier suele ser más preciso que ExtraTreeClassifier porque realiza particiones aleatorias para encontrar las mejores características para dividir.
- Sin embargo, ExtraTreesClassifier puede ser más intensivo computacionalmente debido a la necesidad de realizar una búsqueda más amplia de particiones óptimas.
2.26. ExtraTreeClassifier
ExtraTreeClassifier, o Extremely Randomized Trees, es un potente algoritmo de aprendizaje automático que se utiliza en tareas de clasificación y regresión. Este algoritmo se basa en la idea de los árboles de decisiones y ofrece mejoras con respecto a los bosques aleatorios y los árboles de decisiones tradicionales.
Principios de funcionamiento del ExtraTreeClassifier:
- Partición aleatoria de nodos: El principio básico de ExtraTreeClassifier es la selección aleatoria de una partición para cada nodo del árbol. Esto difiere de los árboles de decisiones tradicionales, que seleccionan la mejor característica para particionar. ExtraTreeClassifier realiza la partición sin considerar la mejor partición, lo cual lo hace más aleatorio y resistente al sobreentrenamiento.
- Agregación de resultados: En el proceso de construcción de conjuntos, ExtraTreeClassifier crea muchos árboles aleatorios y añade sus resultados. Esto se hace para aumentar la capacidad de generalización del modelo y reducir la varianza. El conjunto de árboles combate el problema del sobreentrenamiento y mejora la estabilidad de las predicciones.
- Umbrales aleatorios: Al particionar un nodo, ExtraTreeClassifier elige umbrales aleatorios para cada característica, en lugar de los valores óptimos definidos. Esto hace posible una mayor aleatoriedad y estabilidad del modelo.
Ventajas de ExtraTreeClassifier:
- Resistencia al sobreentrenamiento: Debido a la partición aleatoria y a la ausencia de selección de las mejores particiones, ExtraTreeClassifier resulta generalmente menos susceptible al sobreentrenamiento en comparación con los árboles de decisiones normales.
- Alta velocidad de aprendizaje: ExtraTreeClassifier requiere menos recursos informáticos para el entrenamiento que muchos otros algoritmos, como el bosque aleatorio. Esto lo hace rápido y eficaz en tareas que requieren muchos datos.
- Versatilidad: ExtraTreeClassifier puede usarse tanto para tareas de clasificación como de regresión. Esto lo convierte en un algoritmo versátil para distintos tipos de tareas.
Limitaciones de ExtraTreeClassifier:
- Aleatoriedad: El uso de particiones aleatorias puede dar lugar a modelos menos precisos en algunos casos. Resulta importante elegir con cuidado los ajustes del algoritmo.
- Inestabilidad respecto a los valores atípicos: ExtraTreeClassifier puede ser sensible a los valores atípicos en los datos porque construye particiones aleatorias. En algunos casos, esto puede conllevar predicciones inestables.
- Menor interpretabilidad: En comparación con los árboles de decisiones normales, ExtraTreeClassifier es menos interpretable y más difícil de explicar.
ExtraTreeClassifier es un potente algoritmo de aprendizaje automático, fiable ante el sobreentrenamiento, con una alta velocidad de aprendizaje. Puede resultar útil en diversas tareas de clasificación y regresión, especialmente cuando se dispone de recursos informáticos limitados. Sin embargo, debemos considerar la naturaleza aleatoria de este algoritmo y sus limitaciones, como la inestabilidad ante valores atípicos y una menor interpretabilidad. Al utilizar ExtraTreeClassifier, es importante configurar cuidadosamente sus parámetros y ser específico con los datos.
2.26.1. Código de creación del modelo ExtraTreeClassifier
Este código demuestra el proceso de entrenamiento del modelo ExtraTreeClassifier con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_ExtraTreeClassifier.py # The code demonstrates the process of training ExtraTree Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.tree import ExtraTreeClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create an ExtraTreeClassifier model extra_tree_model = ExtraTreeClassifier() # train the model on the entire dataset extra_tree_model.fit(X, y) # predict classes for the entire dataset y_pred = extra_tree_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of ExtraTreeClassifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(extra_tree_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "extra_tree_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of ExtraTreeClassifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of ExtraTreeClassifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\extra_tree_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of ExtraTreeClassifier model in ONNX format: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\extra_tree_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of ExtraTreeClassifier model in ONNX format: 1.0
2.26.2. Código en MQL5 para trabajar con el modelo ExtraTreeClassifier
//+------------------------------------------------------------------+ //| Iris_ExtraTreeClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "extra_tree_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="ExtraTreeClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_ExtraTreeClassifier (EURUSD,H1) model:ExtraTreeClassifier correct results: 100.00% Iris_ExtraTreeClassifier (EURUSD,H1) model=ExtraTreeClassifier all samples accuracy=1.000000 Iris_ExtraTreeClassifier (EURUSD,H1) model=ExtraTreeClassifier batch test accuracy=1.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 100%, lo cual coincide con la precisión del original.
2.26.3. Representación ONNX del modelo ExtraTreeClassifier
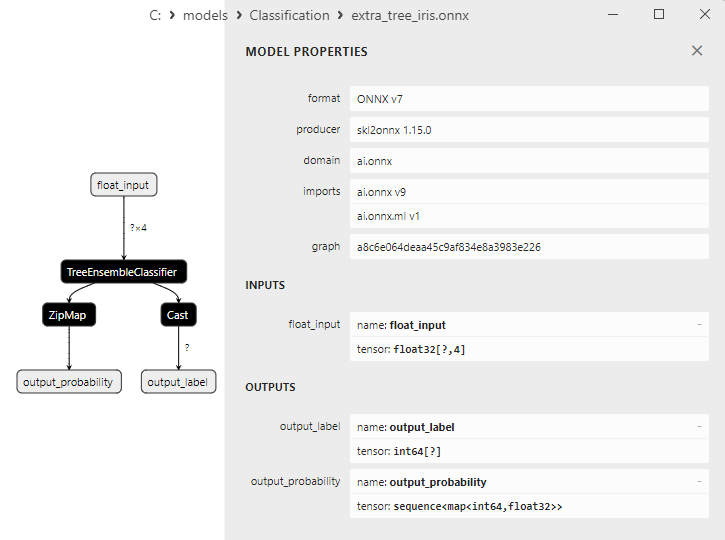
Fig. 40. Representación ONNX del modelo ExtraTreeClassifier en Netron
2.27. ExtraTreesClassifier
ExtraTreesClassifier es un potente algoritmo de aprendizaje automático que se usa para tareas de clasificación. Este algoritmo supone una extensión y mejora de Random Forest (bosque aleatorio) y ofrece una serie de ventajas e inconvenientes.
Principios de funcionamiento de ExtraTreesClassifier:
- Bootstrap de la muestra: De manera similar a un bosque aleatorio, ExtraTreesClassifier utiliza un método bootstrap para crear múltiples submuestras a partir del conjunto de datos de entrenamiento. Esto significa que para cada árbol se crea una submuestra aleatoria con repeticiones a partir de los datos originales.
- Particiones aleatorias: A diferencia del bosque aleatorio, en el que la mejor característica para la partición se selecciona para cada nodo del árbol, ExtraTreesClassifier utiliza características aleatorias y umbrales aleatorios para particionar los nodos. Esto hace que los árboles resulten más aleatorios y reduce el sobreentrenamiento.
- Votación: Tras construir un conjunto de árboles, cada árbol vota por una clase de objeto. Al final, la clase con más votos se convierte en la clase pronosticada.
Ventajas de ExtraTreesClassifier:
- Reduce el sobreentrenamiento: El uso de particiones aleatorias y características aleatorias hace que ExtraTreesClassifier resulte menos susceptible al sobreentrenamiento que los árboles de soluciones tradicionales.
- Alta velocidad de aprendizaje: ExtraTreesClassifier requiere menos recursos computacionales para el entrenamiento en comparación con otros algoritmos como el gradient boosting.
- Resistencia a los valores atípicos: Al usar un conjunto de árboles y particiones aleatorias, ExtraTreesClassifier es generalmente más robusto frente a valores atípicos en los datos.
Limitaciones de ExtraTreesClassifier:
- Dificultad de interpretación: El análisis y la interpretación del modelo ExtraTreesClassifier pueden resultar complejos debido al gran número de particiones y características aleatorias.
- Parámetros para el ajuste: Aunque eficaz, ExtraTreesClassifier puede requerir un ajuste minucioso de los hiperparámetros para lograr un rendimiento óptimo.
- No siempre es el mejor resultado: En algunas tareas, ExtraTreesClassifier puede ser menos preciso que otros algoritmos como el gradient boosting.
ExtraTreesClassifier es un potente algoritmo de clasificación, robusto al sobreentrenamiento, de rápida velocidad de aprendizaje y resistente a los valores atípicos. Puede ser una herramienta útil en tareas de análisis y clasificación de datos, especialmente cuando se dispone de grandes cantidades de datos y se hace necesaria una solución eficaz. No obstante, es importante considerar que un algoritmo no siempre supone la mejor opción, y su eficacia puede depender de la tarea y los datos específicos.
2.27.1. Código de creación del modelo ExtraTreesClassifier
Este código demuestra el proceso de entrenamiento del modelo ExtraTreesClassifier con el Iris dataset, exportándolo al formato ONNX, y realizando una clasificación que usa el modelo ONNX. También evalúa la precisión tanto del modelo original como del modelo ONNX.
# Iris_ExtraTreesClassifier.py # The code demonstrates the process of training ExtraTrees Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.ensemble import ExtraTreesClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create an ExtraTreesClassifier model extra_trees_model = ExtraTreesClassifier() # train the model on the entire dataset extra_trees_model.fit(X, y) # predict classes for the entire dataset y_pred = extra_trees_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of ExtraTreesClassifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(extra_trees_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "extra_trees_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of ExtraTreesClassifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of ExtraTreesClassifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\extra_trees_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of ExtraTreesClassifier model in ONNX format: 1.
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\extra_trees_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of ExtraTreesClassifier model in ONNX format: 1.
2.27.2. Código MQL5 para trabajar con el modelo ExtraTreesClassifier
//+------------------------------------------------------------------+ //| Iris_ExtraTreesClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "extra_trees_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="ExtraTreesClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_ExtraTreesClassifier (EURUSD,H1) model:ExtraTreesClassifier correct results: 100.00% Iris_ExtraTreesClassifier (EURUSD,H1) model=ExtraTreesClassifier all samples accuracy=1.000000 Iris_ExtraTreesClassifier (EURUSD,H1) model=ExtraTreesClassifier batch test accuracy=1.000000
Observe que la precisión del modelo ONNX exportado en el conjunto completo del Iris dataset es del 100%, lo cual coincide con la precisión del original.
2.27.3. Representación ONNX del modelo ExtraTreesClassifier
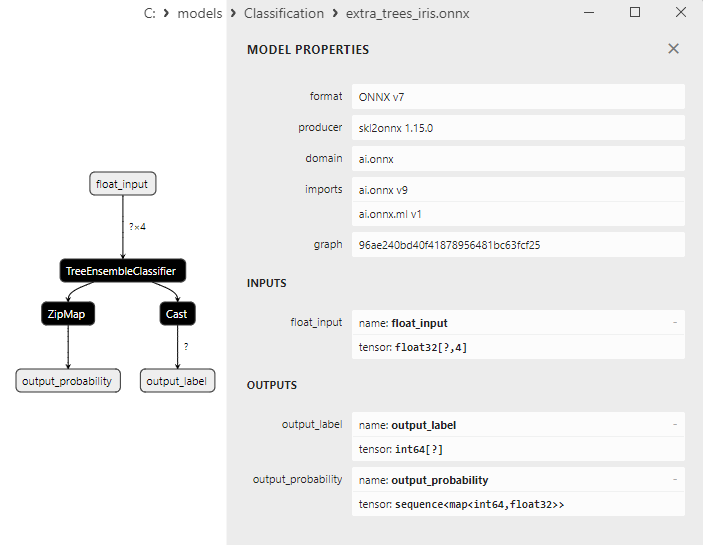
Fig.41. Representación ONNX del modelo ExtraTreesClassifier en Netron
2.28. Comparación de la precisión de todos los modelos.
Ahora veremos todos los modelos juntos y compararemos la calidad de su trabajo. Primero, haremos una comparación usando Python, luego cargaremos y ejecutaremos los modelos ONNX guardados en MetaTrader 5.
2.28.1. Código para calcular todos los modelos y trazar un esquema comparativo de precisión
El script calcula 27 modelos de clasificación del paquete Scikit-learn en el conjunto completo de datos del iris de Fisher, exporta los modelos al formato ONNX, los ejecuta y realiza una comparación de precisión entre los modelos originales y ONNX.
# Iris_AllClassifiers.py # The code demonstrates the process of training 27 Classifier models on the Iris dataset, exports them to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original and the ONNX models. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.metrics import accuracy_score from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np import matplotlib.pyplot as plt from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create and train each classifier model from sklearn.svm import SVC svc_model = SVC() svc_model.fit(X, y) from sklearn.ensemble import RandomForestClassifier random_forest_model = RandomForestClassifier(random_state=42) random_forest_model.fit(X, y) from sklearn.ensemble import GradientBoostingClassifier gradient_boosting_model = GradientBoostingClassifier(random_state=42) gradient_boosting_model.fit(X, y) from sklearn.ensemble import AdaBoostClassifier adaboost_model = AdaBoostClassifier(random_state=42) adaboost_model.fit(X, y) from sklearn.ensemble import BaggingClassifier bagging_model = BaggingClassifier(random_state=42) bagging_model.fit(X, y) from sklearn.neighbors import KNeighborsClassifier knn_model = KNeighborsClassifier() knn_model.fit(X, y) from sklearn.neighbors import RadiusNeighborsClassifier radius_neighbors_model = RadiusNeighborsClassifier(radius=1.0) radius_neighbors_model.fit(X, y) from sklearn.tree import DecisionTreeClassifier decision_tree_model = DecisionTreeClassifier(random_state=42) decision_tree_model.fit(X, y) from sklearn.linear_model import LogisticRegression logistic_regression_model = LogisticRegression(max_iter=1000, random_state=42) logistic_regression_model.fit(X, y) from sklearn.linear_model import RidgeClassifier ridge_classifier_model = RidgeClassifier(random_state=42) ridge_classifier_model.fit(X, y) from sklearn.linear_model import PassiveAggressiveClassifier passive_aggressive_model = PassiveAggressiveClassifier(max_iter=1000, random_state=42) passive_aggressive_model.fit(X, y) from sklearn.linear_model import Perceptron perceptron_model = Perceptron(max_iter=1000, random_state=42) perceptron_model.fit(X, y) from sklearn.linear_model import SGDClassifier sgd_model = SGDClassifier(max_iter=1000, random_state=42) sgd_model.fit(X, y) from sklearn.naive_bayes import GaussianNB gaussian_nb_model = GaussianNB() gaussian_nb_model.fit(X, y) from sklearn.naive_bayes import MultinomialNB multinomial_nb_model = MultinomialNB() multinomial_nb_model.fit(X, y) from sklearn.naive_bayes import ComplementNB complement_nb_model = ComplementNB() complement_nb_model.fit(X, y) from sklearn.naive_bayes import BernoulliNB bernoulli_nb_model = BernoulliNB() bernoulli_nb_model.fit(X, y) from sklearn.naive_bayes import CategoricalNB categorical_nb_model = CategoricalNB() categorical_nb_model.fit(X, y) from sklearn.tree import ExtraTreeClassifier extra_tree_model = ExtraTreeClassifier(random_state=42) extra_tree_model.fit(X, y) from sklearn.ensemble import ExtraTreesClassifier extra_trees_model = ExtraTreesClassifier(random_state=42) extra_trees_model.fit(X, y) from sklearn.svm import LinearSVC # Import LinearSVC linear_svc_model = LinearSVC(random_state=42) linear_svc_model.fit(X, y) from sklearn.svm import NuSVC nu_svc_model = NuSVC() nu_svc_model.fit(X, y) from sklearn.linear_model import LogisticRegressionCV logistic_regression_cv_model = LogisticRegressionCV(cv=5, max_iter=1000, random_state=42) logistic_regression_cv_model.fit(X, y) from sklearn.neural_network import MLPClassifier mlp_model = MLPClassifier(max_iter=1000, random_state=42) mlp_model.fit(X, y) from sklearn.discriminant_analysis import LinearDiscriminantAnalysis lda_model = LinearDiscriminantAnalysis() lda_model.fit(X, y) from sklearn.experimental import enable_hist_gradient_boosting from sklearn.ensemble import HistGradientBoostingClassifier hist_gradient_boosting_model = HistGradientBoostingClassifier(random_state=42) hist_gradient_boosting_model.fit(X, y) from sklearn.linear_model import RidgeClassifierCV ridge_classifier_cv_model = RidgeClassifierCV() ridge_classifier_cv_model.fit(X, y) # define a dictionary to store results results = {} # loop through the models for model_name, classifier_model in [ ('SVC Classifier', svc_model), ('Random Forest Classifier', random_forest_model), ('Gradient Boosting Classifier', gradient_boosting_model), ('AdaBoost Classifier', adaboost_model), ('Bagging Classifier', bagging_model), ('K-NN Classifier', knn_model), ('Radius Neighbors Classifier', radius_neighbors_model), ('Decision Tree Classifier', decision_tree_model), ('Logistic Regression Classifier', logistic_regression_model), ('Ridge Classifier', ridge_classifier_model), ('Ridge ClassifierCV', ridge_classifier_cv_model), ('Passive-Aggressive Classifier', passive_aggressive_model), ('Perceptron Classifier', perceptron_model), ('SGD Classifier', sgd_model), ('Gaussian Naive Bayes Classifier', gaussian_nb_model), ('Multinomial Naive Bayes Classifier', multinomial_nb_model), ('Complement Naive Bayes Classifier', complement_nb_model), ('Bernoulli Naive Bayes Classifier', bernoulli_nb_model), ('Categorical Naive Bayes Classifier', categorical_nb_model), ('Extra Tree Classifier', extra_tree_model), ('Extra Trees Classifier', extra_trees_model), ('LinearSVC Classifier', linear_svc_model), ('NuSVC Classifier', nu_svc_model), ('Logistic RegressionCV Classifier', logistic_regression_cv_model), ('MLP Classifier', mlp_model), ('Linear Discriminant Analysis Classifier', lda_model), ('Hist Gradient Boosting Classifier', hist_gradient_boosting_model) ]: # predict classes for the entire dataset y_pred = classifier_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(classifier_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + f"{model_name.lower().replace(' ', '_')}_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) # store results results[model_name] = { 'accuracy': accuracy, 'accuracy_onnx': accuracy_onnx } # print the accuracy of the original model and the ONNX model #print(f"{model_name} - Original Accuracy: {accuracy}, ONNX Accuracy: {accuracy_onnx}") # sort the models based on accuracy sorted_results = dict(sorted(results.items(), key=lambda item: item[1]['accuracy'], reverse=True)) # print the sorted results print("Sorted Results:") for model_name, metrics in sorted_results.items(): print(f"{model_name} - Original Accuracy: {metrics['accuracy']:.4f}, ONNX Accuracy: {metrics['accuracy_onnx']:.4f}") # create comparison plots for sorted results fig, ax = plt.subplots(figsize=(12, 8)) model_names = list(sorted_results.keys()) accuracies = [sorted_results[model_name]['accuracy'] for model_name in model_names] accuracies_onnx = [sorted_results[model_name]['accuracy_onnx'] for model_name in model_names] bar_width = 0.35 index = range(len(model_names)) bar1 = plt.bar(index, accuracies, bar_width, label='Model Accuracy') bar2 = plt.bar([i + bar_width for i in index], accuracies_onnx, bar_width, label='ONNX Accuracy') plt.xlabel('Models') plt.ylabel('Accuracy') plt.title('Comparison of Model and ONNX Accuracy (Sorted)') plt.xticks([i + bar_width / 2 for i in index], model_names, rotation=90, ha='center') plt.legend() plt.tight_layout() plt.show()
Resultado:
Python Sorted Results: Python Random Forest Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Gradient Boosting Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Bagging Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Decision Tree Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Extra Tree Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Extra Trees Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Hist Gradient Boosting Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Logistic RegressionCV Classifier - Original Accuracy: 0.9800, ONNX Accuracy: 0.9800 Python MLP Classifier - Original Accuracy: 0.9800, ONNX Accuracy: 0.9800 Python Linear Discriminant Analysis Classifier - Original Accuracy: 0.9800, ONNX Accuracy: 0.9800 Python SVC Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 Python Radius Neighbors Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 Python Logistic Regression Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 Python NuSVC Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 Python K-NN Classifier - Original Accuracy: 0.9667, ONNX Accuracy: 0.9667 Python LinearSVC Classifier - Original Accuracy: 0.9667, ONNX Accuracy: 0.9667 Python AdaBoost Classifier - Original Accuracy: 0.9600, ONNX Accuracy: 0.9600 Python Passive-Aggressive Classifier - Original Accuracy: 0.9600, ONNX Accuracy: 0.9600 Python Gaussian Naive Bayes Classifier - Original Accuracy: 0.9600, ONNX Accuracy: 0.9600 Python Multinomial Naive Bayes Classifier - Original Accuracy: 0.9533, ONNX Accuracy: 0.9533 Python SGD Classifier - Original Accuracy: 0.9333, ONNX Accuracy: 0.9333 Python Categorical Naive Bayes Classifier - Original Accuracy: 0.9333, ONNX Accuracy: 0.9333 Python Ridge Classifier - Original Accuracy: 0.8533, ONNX Accuracy: 0.8533 Python Ridge ClassifierCV - Original Accuracy: 0.8533, ONNX Accuracy: 0.8533 Python Complement Naive Bayes Classifier - Original Accuracy: 0.6667, ONNX Accuracy: 0.6667 Python Perceptron Classifier - Original Accuracy: 0.6133, ONNX Accuracy: 0.6133 Python Bernoulli Naive Bayes Classifier - Original Accuracy: 0.3333, ONNX Accuracy: 0.3333El script también mostrará una imagen con los resultados resumidos para los 27 modelos.
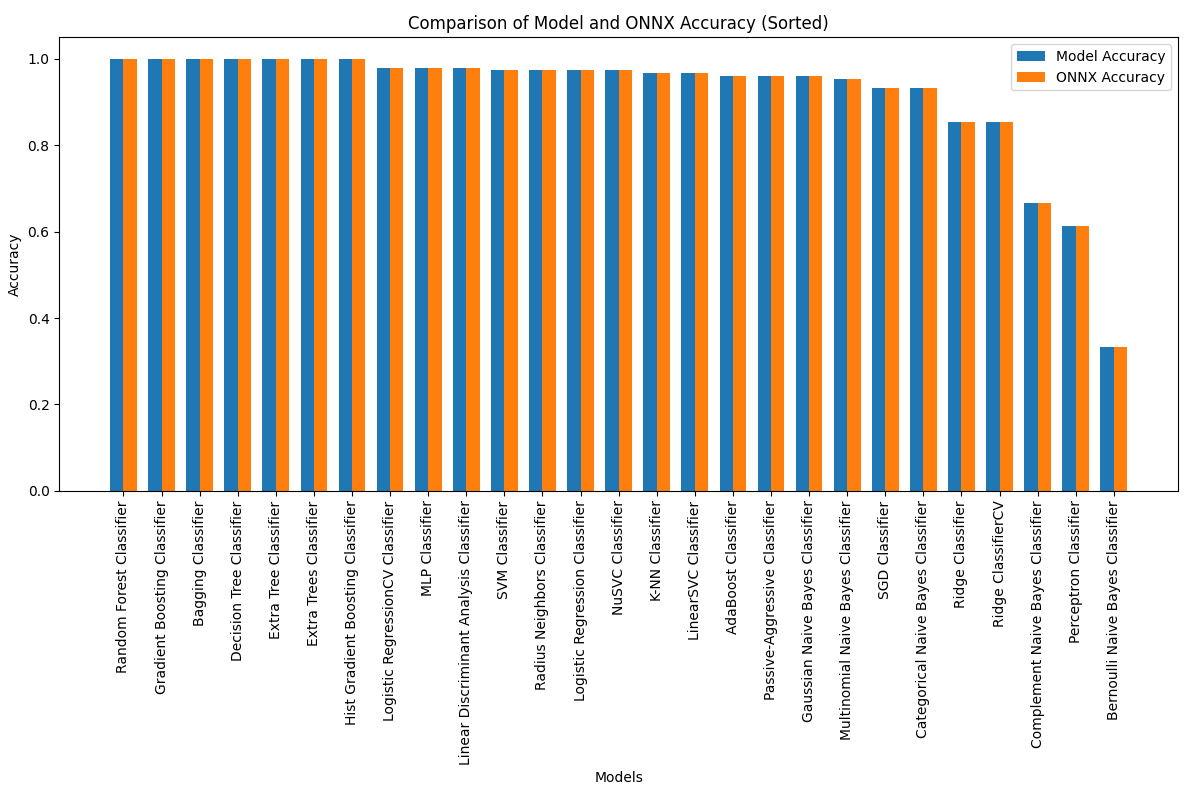
Fig. 42. Comparación de la precisión de 27 modelos de clasificación y sus versiones ONNX para el Iris dataset
Según los resultados de la evaluación de la precisión de los modelos originales y sus versiones ONNX, podemos sacar las siguientes conclusiones:
Los siete modelos han mostrado una precisión perfecta (1,0000) tanto en la versión original como en la ONNX del modelo. Estos modelos incluyen:
- Random Forest Classifier
- Gradient Boosting Classifier
- Bagging Classifier
- Decision Tree Classifier
- Extra Tree Classifier
- Extra Trees Classifier
- Hist Gradient Boosting Classifier
Las representaciones ONNX de estos modelos también mantienen una alta precisión.
Tres modelos (Logistic RegressionCV Classifier, MLP Classifier y Linear Discriminant Analysis Classifier) han logrado una alta precisión en las versiones original y ONNX con una precisión de 0,9800. Estos son modelos que funcionan bien en ambas representaciones.
Varios modelos, incluidos SVC Classifier, Radius Neighbors Classifier, NuSVC Classifier, K-NN Classifier, LinearSVC Classifier, AdaBoost Classifier, Passive-Aggressive Classifier, Gaussian Naive Bayes Classifier, y Multinomial Naive Bayes Classifier, mostraron una buena precisión en las versiones original y ONNX, con una precisión de 0,9733, 0,9667 o 0,9600. Estos modelos también mantienen su precisión en la representación ONNX.
Modelos como SGD Classifier, Categorical Naive Bayes Classifier, Ridge Classifier, Complement Naive Bayes Classifier, Perceptron Classifier y Bernoulli Naive Bayes Classifier muestran una precisión menor. También hacen un buen trabajo para mantener la precisión en ONNX.
Todos los modelos analizados conservan su precisión cuando se exportan al formato ONNX, lo cual indica que ONNX ofrece una forma eficaz de guardar y restaurar modelos de aprendizaje automático. Sin embargo, debemos recordar que la calidad del modelo exportado puede depender del algoritmo específico y de los parámetros del modelo.
2.28.2. Código en MQL5 para ejecutar todos los modelos ONNX
El script ejecutará todos los modelos ONNX guardados por el script desde 2.28.1 en el conjunto de datos completo del iris de Fisher.
//+------------------------------------------------------------------+ //| Iris_AllClassifiers.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" //+------------------------------------------------------------------+ //| TestSampleSequenceMapOutput | //+------------------------------------------------------------------+ bool TestSampleSequenceMapOutput(long model,sIRISsample &iris_sample, int &model_class_id) { //--- model_class_id=-1; float input_data[1][4]; for(int k=0; k<4; k++) { input_data[0][k]=(float)iris_sample.features[k]; } //--- float out1[]; //--- struct Map { ulong key[]; float value[]; } out2[]; //--- bool res=ArrayResize(out1,input_data.Range(0))==input_data.Range(0); //--- if(res) { ulong input_shape[]= { input_data.Range(0), input_data.Range(1) }; ulong output_shape[]= { input_data.Range(0) }; //--- OnnxSetInputShape(model,0,input_shape); OnnxSetOutputShape(model,0,output_shape); //--- res=OnnxRun(model,0,input_data,out1,out2); //--- if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- model_class_id=-1; int max_idx=-1; float max_value=-1; //--- for(uint n=0; n<out2.Size(); n++) { //--- copy to arrays ArrayCopy(output_keys,out2[n].key); ArrayCopy(output_values,out2[n].value); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } } } } //--- return(res); } //+------------------------------------------------------------------+ //| TestSampleTensorOutput | //+------------------------------------------------------------------+ bool TestSampleTensorOutput(long model,sIRISsample &iris_sample, int &model_class_id) { //--- model_class_id=-1; float input_data[1][4]; for(int k=0; k<4; k++) { input_data[0][k]=(float)iris_sample.features[k]; } //--- ulong input_shape[]= { 1, 4}; OnnxSetInputShape(model,0,input_shape); //--- int output1[1]; float output2[1,3]; //--- ulong output_shape[]= {1}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {1,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,0,input_data,output1,output2); //--- result for these models in output1[0]; if(res) model_class_id=output1[0]; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("error in loading iris dataset from iris.csv"); return(false); } /*for(int k=0; k<total_samples; k++) { PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); }*/ //---- string iris_models[]= { "random_forest_classifier_iris.onnx", "gradient_boosting_classifier_iris.onnx", "bagging_classifier_iris.onnx", "decision_tree_classifier_iris.onnx", "extra_tree_classifier_iris.onnx", "extra_trees_classifier_iris.onnx", "hist_gradient_boosting_classifier_iris.onnx", "logistic_regressioncv_classifier_iris.onnx", "mlp_classifier_iris.onnx", "linear_discriminant_analysis_classifier_iris.onnx", "svc_classifier_iris.onnx", "radius_neighbors_classifier_iris.onnx", "logistic_regression_classifier_iris.onnx", "nusvc_classifier_iris.onnx", "k-nn_classifier_iris.onnx", "linearsvc_classifier_iris.onnx", "adaboost_classifier_iris.onnx", "passive-aggressive_classifier_iris.onnx", "gaussian_naive_bayes_classifier_iris.onnx", "multinomial_naive_bayes_classifier_iris.onnx", "sgd_classifier_iris.onnx", "categorical_naive_bayes_classifier_iris.onnx", "ridge_classifier_iris.onnx", "ridge_classifiercv_iris.onnx", "complement_naive_bayes_classifier_iris.onnx", "perceptron_classifier_iris.onnx", "bernoulli_naive_bayes_classifier_iris.onnx" }; //--- test all iris dataset sample by sample for(int i=0; i<ArraySize(iris_models); i++) { //--- load ONNX-model string model_name="IRIS_models\\"+iris_models[i]; //--- long model=OnnxCreate(model_name,0); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- check all samples int correct_results=0; for(int k=0; k<total_samples; k++) { int model_class_id=-1; //--- select data output processor string current_model=iris_models[i]; if(current_model=="svc_classifier_iris.onnx" || current_model=="linearsvc_classifier_iris.onnx" || current_model=="nusvc_classifier_iris.onnx" || current_model=="ridge_classifier_iris.onnx" || current_model=="ridge_classifiercv_iris.onnx" || current_model=="radius_neighbors_classifier_iris.onnx") { TestSampleTensorOutput(model,iris_samples[k],model_class_id); } else { TestSampleSequenceMapOutput(model,iris_samples[k],model_class_id); } //--- if(model_class_id==iris_samples[k].class_id) { correct_results++; //PrintFormat("sample=%d OK [class=%d]",iris_samples[k].sample_id,model_class_id); } else { //PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_class_id,iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } PrintFormat("%d model:%s accuracy: %.4f",i+1,model_name,1.0*correct_results/total_samples); //--- release model OnnxRelease(model); } //--- } return(0); } //+------------------------------------------------------------------+
Resultado:
Iris_AllClassifiers (EURUSD,H1) 1 model:IRIS_models\random_forest_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 2 model:IRIS_models\gradient_boosting_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 3 model:IRIS_models\bagging_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 4 model:IRIS_models\decision_tree_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 5 model:IRIS_models\extra_tree_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 6 model:IRIS_models\extra_trees_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 7 model:IRIS_models\hist_gradient_boosting_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 8 model:IRIS_models\logistic_regressioncv_classifier_iris.onnx accuracy: 0.9800 Iris_AllClassifiers (EURUSD,H1) 9 model:IRIS_models\mlp_classifier_iris.onnx accuracy: 0.9800 Iris_AllClassifiers (EURUSD,H1) 10 model:IRIS_models\linear_discriminant_analysis_classifier_iris.onnx accuracy: 0.9800 Iris_AllClassifiers (EURUSD,H1) 11 model:IRIS_models\svc_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) 12 model:IRIS_models\radius_neighbors_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) 13 model:IRIS_models\logistic_regression_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) 14 model:IRIS_models\nusvc_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) 15 model:IRIS_models\k-nn_classifier_iris.onnx accuracy: 0.9667 Iris_AllClassifiers (EURUSD,H1) 16 model:IRIS_models\linearsvc_classifier_iris.onnx accuracy: 0.9667 Iris_AllClassifiers (EURUSD,H1) 17 model:IRIS_models\adaboost_classifier_iris.onnx accuracy: 0.9600 Iris_AllClassifiers (EURUSD,H1) 18 model:IRIS_models\passive-aggressive_classifier_iris.onnx accuracy: 0.9600 Iris_AllClassifiers (EURUSD,H1) 19 model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx accuracy: 0.9600 Iris_AllClassifiers (EURUSD,H1) 20 model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx accuracy: 0.9533 Iris_AllClassifiers (EURUSD,H1) 21 model:IRIS_models\sgd_classifier_iris.onnx accuracy: 0.9333 Iris_AllClassifiers (EURUSD,H1) 22 model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx accuracy: 0.9333 Iris_AllClassifiers (EURUSD,H1) 23 model:IRIS_models\ridge_classifier_iris.onnx accuracy: 0.8533 Iris_AllClassifiers (EURUSD,H1) 24 model:IRIS_models\ridge_classifiercv_iris.onnx accuracy: 0.8533 Iris_AllClassifiers (EURUSD,H1) ONNX: Removing initializer 'class_log_prior'. It is not used by any node and should be removed from the model. Iris_AllClassifiers (EURUSD,H1) 25 model:IRIS_models\complement_naive_bayes_classifier_iris.onnx accuracy: 0.6667 Iris_AllClassifiers (EURUSD,H1) 26 model:IRIS_models\perceptron_classifier_iris.onnx accuracy: 0.6133 Iris_AllClassifiers (EURUSD,H1) 27 model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx accuracy: 0.3333
Comparando con los resultados del script 2.28.1.1:
Python Random Forest Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 1 model:IRIS_models\random_forest_classifier_iris.onnx accuracy: 1.0000 Python Gradient Boosting Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 2 model:IRIS_models\gradient_boosting_classifier_iris.onnx accuracy: 1.0000 Python Bagging Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 3 model:IRIS_models\bagging_classifier_iris.onnx accuracy: 1.0000 Python Decision Tree Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 4 model:IRIS_models\decision_tree_classifier_iris.onnx accuracy: 1.0000 Python Extra Tree Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 5 model:IRIS_models\extra_tree_classifier_iris.onnx accuracy: 1.0000 Python Extra Trees Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 6 model:IRIS_models\extra_trees_classifier_iris.onnx accuracy: 1.0000 Python Hist Gradient Boosting Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 7 model:IRIS_models\hist_gradient_boosting_classifier_iris.onnx accuracy: 1.0000 Python Logistic RegressionCV Classifier - Original Accuracy: 0.9800, ONNX Accuracy: 0.9800 8 model:IRIS_models\logistic_regressioncv_classifier_iris.onnx accuracy: 0.9800 Python MLP Classifier - Original Accuracy: 0.9800, ONNX Accuracy: 0.9800 9 model:IRIS_models\mlp_classifier_iris.onnx accuracy: 0.9800 Python Linear Discriminant Analysis Classifier - Original Accuracy: 0.9800, ONNX Accuracy: 0.9800 10 model:IRIS_models\linear_discriminant_analysis_classifier_iris.onnx accuracy: 0.9800 Python SVC Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 11 model:IRIS_models\svc_classifier_iris.onnx accuracy: 0.9733 Python Radius Neighbors Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 12 model:IRIS_models\radius_neighbors_classifier_iris.onnx accuracy: 0.9733 Python Logistic Regression Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 13 model:IRIS_models\logistic_regression_classifier_iris.onnx accuracy: 0.9733 Python NuSVC Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 14 model:IRIS_models\nusvc_classifier_iris.onnx accuracy: 0.9733 Python K-NN Classifier - Original Accuracy: 0.9667, ONNX Accuracy: 0.9667 15 model:IRIS_models\k-nn_classifier_iris.onnx accuracy: 0.9667 Python LinearSVC Classifier - Original Accuracy: 0.9667, ONNX Accuracy: 0.9667 16 model:IRIS_models\linearsvc_classifier_iris.onnx accuracy: 0.9667 Python AdaBoost Classifier - Original Accuracy: 0.9600, ONNX Accuracy: 0.9600 17 model:IRIS_models\adaboost_classifier_iris.onnx accuracy: 0.9600 Python Passive-Aggressive Classifier - Original Accuracy: 0.9600, ONNX Accuracy: 0.9600 18 model:IRIS_models\passive-aggressive_classifier_iris.onnx accuracy: 0.9600 Python Gaussian Naive Bayes Classifier - Original Accuracy: 0.9600, ONNX Accuracy: 0.9600 19 model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx accuracy: 0.9600 Python Multinomial Naive Bayes Classifier - Original Accuracy: 0.9533, ONNX Accuracy: 0.9533 20 model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx accuracy: 0.9533 Python SGD Classifier - Original Accuracy: 0.9333, ONNX Accuracy: 0.9333 21 model:IRIS_models\sgd_classifier_iris.onnx accuracy: 0.9333 Python Categorical Naive Bayes Classifier - Original Accuracy: 0.9333, ONNX Accuracy: 0.9333 22 model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx accuracy: 0.9333 Python Ridge Classifier - Original Accuracy: 0.8533, ONNX Accuracy: 0.8533 23 model:IRIS_models\ridge_classifier_iris.onnx accuracy: 0.8533 Python Ridge ClassifierCV - Original Accuracy: 0.8533, ONNX Accuracy: 0.8533 24 model:IRIS_models\ridge_classifiercv_iris.onnx accuracy: 0.8533 Python Complement Naive Bayes Classifier - Original Accuracy: 0.6667, ONNX Accuracy: 0.6667 25 model:IRIS_models\complement_naive_bayes_classifier_iris.onnx accuracy: 0.6667 Python Perceptron Classifier - Original Accuracy: 0.6133, ONNX Accuracy: 0.6133 26 model:IRIS_models\perceptron_classifier_iris.onnx accuracy: 0.6133 Python Bernoulli Naive Bayes Classifier - Original Accuracy: 0.3333, ONNX Accuracy: 0.3333 27 model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx accuracy: 0.3333
Tenga en cuenta que la ejecución de todos los modelos ONNX guardados en MQL5 cumple totalmente con los resultados de 2.28.1.
Así, los modelos examinados convertidos al formato ONNX conservaron su precisión.
Cabe destacar la perfecta precisión de clasificación (accuracy=1,0) del Iris dataset para 7 modelos:
- Random Forest Classifier;
- Gradient Boosting Classifier;
- Bagging Classifier;
- Decision Tree Classifier;
- Extra Tree Classifier;
- Extra Trees Classifier;
- Histogram Gradient Boosting Classifier.
Los 20 modelos restantes presentaban errores de clasificación.
Si no se comenta la línea 208, el script también mostrará las muestras del Iris dataset que fueron clasificadas erróneamente por cada uno de los modelos:
Iris_AllClassifiers (EURUSD,H1) 1 model:IRIS_models\random_forest_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 2 model:IRIS_models\gradient_boosting_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 3 model:IRIS_models\bagging_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 4 model:IRIS_models\decision_tree_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 5 model:IRIS_models\extra_tree_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 6 model:IRIS_models\extra_trees_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 7 model:IRIS_models\hist_gradient_boosting_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regressioncv_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regressioncv_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regressioncv_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) 8 model:IRIS_models\logistic_regressioncv_classifier_iris.onnx accuracy: 0.9800 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\mlp_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\mlp_classifier_iris.onnx sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\mlp_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) 9 model:IRIS_models\mlp_classifier_iris.onnx accuracy: 0.9800 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linear_discriminant_analysis_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linear_discriminant_analysis_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linear_discriminant_analysis_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) 10 model:IRIS_models\linear_discriminant_analysis_classifier_iris.onnx accuracy: 0.9800 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\svc_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\svc_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\svc_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\svc_classifier_iris.onnx sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) 11 model:IRIS_models\svc_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\radius_neighbors_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\radius_neighbors_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\radius_neighbors_classifier_iris.onnx sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\radius_neighbors_classifier_iris.onnx sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) 12 model:IRIS_models\radius_neighbors_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regression_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regression_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regression_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regression_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) 13 model:IRIS_models\logistic_regression_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\nusvc_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\nusvc_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\nusvc_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\nusvc_classifier_iris.onnx sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) 14 model:IRIS_models\nusvc_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\k-nn_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\k-nn_classifier_iris.onnx sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\k-nn_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\k-nn_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\k-nn_classifier_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) 15 model:IRIS_models\k-nn_classifier_iris.onnx accuracy: 0.9667 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linearsvc_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linearsvc_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linearsvc_classifier_iris.onnx sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linearsvc_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linearsvc_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) 16 model:IRIS_models\linearsvc_classifier_iris.onnx accuracy: 0.9667 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\adaboost_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\adaboost_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\adaboost_classifier_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\adaboost_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\adaboost_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\adaboost_classifier_iris.onnx sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AllClassifiers (EURUSD,H1) 17 model:IRIS_models\adaboost_classifier_iris.onnx accuracy: 0.9600 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\passive-aggressive_classifier_iris.onnx sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\passive-aggressive_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\passive-aggressive_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\passive-aggressive_classifier_iris.onnx sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\passive-aggressive_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\passive-aggressive_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) 18 model:IRIS_models\passive-aggressive_classifier_iris.onnx accuracy: 0.9600 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) 19 model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx accuracy: 0.9600 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=69 FAILED [class=2, true class=1] features=(6.20,2.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=132 FAILED [class=1, true class=2] features=(7.90,3.80,6.40,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) 20 model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx accuracy: 0.9533 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=65 FAILED [class=0, true class=1] features=(5.60,2.90,3.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=86 FAILED [class=0, true class=1] features=(6.00,3.40,4.50,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=124 FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AllClassifiers (EURUSD,H1) 21 model:IRIS_models\sgd_classifier_iris.onnx accuracy: 0.9333 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=102 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=122 FAILED [class=1, true class=2] features=(5.60,2.80,4.90,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=124 FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=128 FAILED [class=1, true class=2] features=(6.10,3.00,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=143 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_AllClassifiers (EURUSD,H1) 22 model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx accuracy: 0.9333 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=51 FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=52 FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=57 FAILED [class=2, true class=1] features=(6.30,3.30,4.70,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=62 FAILED [class=2, true class=1] features=(5.90,3.00,4.20,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=65 FAILED [class=2, true class=1] features=(5.60,2.90,3.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=66 FAILED [class=2, true class=1] features=(6.70,3.10,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=76 FAILED [class=2, true class=1] features=(6.60,3.00,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=79 FAILED [class=2, true class=1] features=(6.00,2.90,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=86 FAILED [class=2, true class=1] features=(6.00,3.40,4.50,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=87 FAILED [class=2, true class=1] features=(6.70,3.10,4.70,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=89 FAILED [class=2, true class=1] features=(5.60,3.00,4.10,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=92 FAILED [class=2, true class=1] features=(6.10,3.00,4.60,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=109 FAILED [class=1, true class=2] features=(6.70,2.50,5.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AllClassifiers (EURUSD,H1) 23 model:IRIS_models\ridge_classifier_iris.onnx accuracy: 0.8533 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=51 FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=52 FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=57 FAILED [class=2, true class=1] features=(6.30,3.30,4.70,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=62 FAILED [class=2, true class=1] features=(5.90,3.00,4.20,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=65 FAILED [class=2, true class=1] features=(5.60,2.90,3.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=66 FAILED [class=2, true class=1] features=(6.70,3.10,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=76 FAILED [class=2, true class=1] features=(6.60,3.00,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=79 FAILED [class=2, true class=1] features=(6.00,2.90,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=86 FAILED [class=2, true class=1] features=(6.00,3.40,4.50,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=87 FAILED [class=2, true class=1] features=(6.70,3.10,4.70,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=89 FAILED [class=2, true class=1] features=(5.60,3.00,4.10,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=92 FAILED [class=2, true class=1] features=(6.10,3.00,4.60,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=109 FAILED [class=1, true class=2] features=(6.70,2.50,5.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AllClassifiers (EURUSD,H1) 24 model:IRIS_models\ridge_classifiercv_iris.onnx accuracy: 0.8533 Iris_AllClassifiers (EURUSD,H1) ONNX: Removing initializer 'class_log_prior'. It is not used by any node and should be removed from the model. Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=51 FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=52 FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=54 FAILED [class=2, true class=1] features=(5.50,2.30,4.00,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=55 FAILED [class=2, true class=1] features=(6.50,2.80,4.60,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=56 FAILED [class=2, true class=1] features=(5.70,2.80,4.50,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=57 FAILED [class=2, true class=1] features=(6.30,3.30,4.70,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=58 FAILED [class=2, true class=1] features=(4.90,2.40,3.30,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=59 FAILED [class=2, true class=1] features=(6.60,2.90,4.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=60 FAILED [class=2, true class=1] features=(5.20,2.70,3.90,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=61 FAILED [class=2, true class=1] features=(5.00,2.00,3.50,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=62 FAILED [class=2, true class=1] features=(5.90,3.00,4.20,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=63 FAILED [class=2, true class=1] features=(6.00,2.20,4.00,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=64 FAILED [class=2, true class=1] features=(6.10,2.90,4.70,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=65 FAILED [class=2, true class=1] features=(5.60,2.90,3.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=66 FAILED [class=2, true class=1] features=(6.70,3.10,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=68 FAILED [class=2, true class=1] features=(5.80,2.70,4.10,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=69 FAILED [class=2, true class=1] features=(6.20,2.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=70 FAILED [class=2, true class=1] features=(5.60,2.50,3.90,1.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=72 FAILED [class=2, true class=1] features=(6.10,2.80,4.00,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=74 FAILED [class=2, true class=1] features=(6.10,2.80,4.70,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=75 FAILED [class=2, true class=1] features=(6.40,2.90,4.30,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=76 FAILED [class=2, true class=1] features=(6.60,3.00,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=77 FAILED [class=2, true class=1] features=(6.80,2.80,4.80,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=79 FAILED [class=2, true class=1] features=(6.00,2.90,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=80 FAILED [class=0, true class=1] features=(5.70,2.60,3.50,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=81 FAILED [class=2, true class=1] features=(5.50,2.40,3.80,1.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=82 FAILED [class=2, true class=1] features=(5.50,2.40,3.70,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=83 FAILED [class=2, true class=1] features=(5.80,2.70,3.90,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=86 FAILED [class=2, true class=1] features=(6.00,3.40,4.50,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=87 FAILED [class=2, true class=1] features=(6.70,3.10,4.70,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=88 FAILED [class=2, true class=1] features=(6.30,2.30,4.40,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=89 FAILED [class=2, true class=1] features=(5.60,3.00,4.10,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=90 FAILED [class=2, true class=1] features=(5.50,2.50,4.00,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=91 FAILED [class=2, true class=1] features=(5.50,2.60,4.40,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=92 FAILED [class=2, true class=1] features=(6.10,3.00,4.60,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=93 FAILED [class=2, true class=1] features=(5.80,2.60,4.00,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=94 FAILED [class=2, true class=1] features=(5.00,2.30,3.30,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=95 FAILED [class=2, true class=1] features=(5.60,2.70,4.20,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=96 FAILED [class=2, true class=1] features=(5.70,3.00,4.20,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=97 FAILED [class=2, true class=1] features=(5.70,2.90,4.20,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=98 FAILED [class=2, true class=1] features=(6.20,2.90,4.30,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=99 FAILED [class=0, true class=1] features=(5.10,2.50,3.00,1.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=100 FAILED [class=2, true class=1] features=(5.70,2.80,4.10,1.30] Iris_AllClassifiers (EURUSD,H1) 25 model:IRIS_models\complement_naive_bayes_classifier_iris.onnx accuracy: 0.6667 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=2 FAILED [class=1, true class=0] features=(4.90,3.00,1.40,0.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=9 FAILED [class=1, true class=0] features=(4.40,2.90,1.40,0.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=10 FAILED [class=1, true class=0] features=(4.90,3.10,1.50,0.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=13 FAILED [class=1, true class=0] features=(4.80,3.00,1.40,0.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=21 FAILED [class=1, true class=0] features=(5.40,3.40,1.70,0.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=26 FAILED [class=1, true class=0] features=(5.00,3.00,1.60,0.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=31 FAILED [class=1, true class=0] features=(4.80,3.10,1.60,0.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=35 FAILED [class=1, true class=0] features=(4.90,3.10,1.50,0.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=42 FAILED [class=1, true class=0] features=(4.50,2.30,1.30,0.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=46 FAILED [class=1, true class=0] features=(4.80,3.00,1.40,0.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=102 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=103 FAILED [class=1, true class=2] features=(7.10,3.00,5.90,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=104 FAILED [class=1, true class=2] features=(6.30,2.90,5.60,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=105 FAILED [class=1, true class=2] features=(6.50,3.00,5.80,2.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=106 FAILED [class=1, true class=2] features=(7.60,3.00,6.60,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=108 FAILED [class=1, true class=2] features=(7.30,2.90,6.30,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=109 FAILED [class=1, true class=2] features=(6.70,2.50,5.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=110 FAILED [class=1, true class=2] features=(7.20,3.60,6.10,2.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=111 FAILED [class=1, true class=2] features=(6.50,3.20,5.10,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=112 FAILED [class=1, true class=2] features=(6.40,2.70,5.30,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=113 FAILED [class=1, true class=2] features=(6.80,3.00,5.50,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=114 FAILED [class=1, true class=2] features=(5.70,2.50,5.00,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=116 FAILED [class=1, true class=2] features=(6.40,3.20,5.30,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=117 FAILED [class=1, true class=2] features=(6.50,3.00,5.50,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=118 FAILED [class=1, true class=2] features=(7.70,3.80,6.70,2.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=119 FAILED [class=1, true class=2] features=(7.70,2.60,6.90,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=121 FAILED [class=1, true class=2] features=(6.90,3.20,5.70,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=122 FAILED [class=1, true class=2] features=(5.60,2.80,4.90,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=123 FAILED [class=1, true class=2] features=(7.70,2.80,6.70,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=124 FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=125 FAILED [class=1, true class=2] features=(6.70,3.30,5.70,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=126 FAILED [class=1, true class=2] features=(7.20,3.20,6.00,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=128 FAILED [class=1, true class=2] features=(6.10,3.00,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=129 FAILED [class=1, true class=2] features=(6.40,2.80,5.60,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=131 FAILED [class=1, true class=2] features=(7.40,2.80,6.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=132 FAILED [class=1, true class=2] features=(7.90,3.80,6.40,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=133 FAILED [class=1, true class=2] features=(6.40,2.80,5.60,2.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=136 FAILED [class=1, true class=2] features=(7.70,3.00,6.10,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=137 FAILED [class=1, true class=2] features=(6.30,3.40,5.60,2.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=138 FAILED [class=1, true class=2] features=(6.40,3.10,5.50,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=140 FAILED [class=1, true class=2] features=(6.90,3.10,5.40,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=141 FAILED [class=1, true class=2] features=(6.70,3.10,5.60,2.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=142 FAILED [class=1, true class=2] features=(6.90,3.10,5.10,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=143 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=144 FAILED [class=1, true class=2] features=(6.80,3.20,5.90,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=145 FAILED [class=1, true class=2] features=(6.70,3.30,5.70,2.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=146 FAILED [class=1, true class=2] features=(6.70,3.00,5.20,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=147 FAILED [class=1, true class=2] features=(6.30,2.50,5.00,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=148 FAILED [class=1, true class=2] features=(6.50,3.00,5.20,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=149 FAILED [class=1, true class=2] features=(6.20,3.40,5.40,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=150 FAILED [class=1, true class=2] features=(5.90,3.00,5.10,1.80] Iris_AllClassifiers (EURUSD,H1) 26 model:IRIS_models\perceptron_classifier_iris.onnx accuracy: 0.6133 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=51 FAILED [class=0, true class=1] features=(7.00,3.20,4.70,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=52 FAILED [class=0, true class=1] features=(6.40,3.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=53 FAILED [class=0, true class=1] features=(6.90,3.10,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=54 FAILED [class=0, true class=1] features=(5.50,2.30,4.00,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=55 FAILED [class=0, true class=1] features=(6.50,2.80,4.60,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=56 FAILED [class=0, true class=1] features=(5.70,2.80,4.50,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=57 FAILED [class=0, true class=1] features=(6.30,3.30,4.70,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=58 FAILED [class=0, true class=1] features=(4.90,2.40,3.30,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=59 FAILED [class=0, true class=1] features=(6.60,2.90,4.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=60 FAILED [class=0, true class=1] features=(5.20,2.70,3.90,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=61 FAILED [class=0, true class=1] features=(5.00,2.00,3.50,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=62 FAILED [class=0, true class=1] features=(5.90,3.00,4.20,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=63 FAILED [class=0, true class=1] features=(6.00,2.20,4.00,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=64 FAILED [class=0, true class=1] features=(6.10,2.90,4.70,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=65 FAILED [class=0, true class=1] features=(5.60,2.90,3.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=66 FAILED [class=0, true class=1] features=(6.70,3.10,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=67 FAILED [class=0, true class=1] features=(5.60,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=68 FAILED [class=0, true class=1] features=(5.80,2.70,4.10,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=69 FAILED [class=0, true class=1] features=(6.20,2.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=70 FAILED [class=0, true class=1] features=(5.60,2.50,3.90,1.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=71 FAILED [class=0, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=72 FAILED [class=0, true class=1] features=(6.10,2.80,4.00,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=73 FAILED [class=0, true class=1] features=(6.30,2.50,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=74 FAILED [class=0, true class=1] features=(6.10,2.80,4.70,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=75 FAILED [class=0, true class=1] features=(6.40,2.90,4.30,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=76 FAILED [class=0, true class=1] features=(6.60,3.00,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=77 FAILED [class=0, true class=1] features=(6.80,2.80,4.80,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=78 FAILED [class=0, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=79 FAILED [class=0, true class=1] features=(6.00,2.90,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=80 FAILED [class=0, true class=1] features=(5.70,2.60,3.50,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=81 FAILED [class=0, true class=1] features=(5.50,2.40,3.80,1.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=82 FAILED [class=0, true class=1] features=(5.50,2.40,3.70,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=83 FAILED [class=0, true class=1] features=(5.80,2.70,3.90,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=84 FAILED [class=0, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=85 FAILED [class=0, true class=1] features=(5.40,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=86 FAILED [class=0, true class=1] features=(6.00,3.40,4.50,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=87 FAILED [class=0, true class=1] features=(6.70,3.10,4.70,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=88 FAILED [class=0, true class=1] features=(6.30,2.30,4.40,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=89 FAILED [class=0, true class=1] features=(5.60,3.00,4.10,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=90 FAILED [class=0, true class=1] features=(5.50,2.50,4.00,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=91 FAILED [class=0, true class=1] features=(5.50,2.60,4.40,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=92 FAILED [class=0, true class=1] features=(6.10,3.00,4.60,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=93 FAILED [class=0, true class=1] features=(5.80,2.60,4.00,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=94 FAILED [class=0, true class=1] features=(5.00,2.30,3.30,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=95 FAILED [class=0, true class=1] features=(5.60,2.70,4.20,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=96 FAILED [class=0, true class=1] features=(5.70,3.00,4.20,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=97 FAILED [class=0, true class=1] features=(5.70,2.90,4.20,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=98 FAILED [class=0, true class=1] features=(6.20,2.90,4.30,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=99 FAILED [class=0, true class=1] features=(5.10,2.50,3.00,1.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=100 FAILED [class=0, true class=1] features=(5.70,2.80,4.10,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=101 FAILED [class=0, true class=2] features=(6.30,3.30,6.00,2.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=102 FAILED [class=0, true class=2] features=(5.80,2.70,5.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=103 FAILED [class=0, true class=2] features=(7.10,3.00,5.90,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=104 FAILED [class=0, true class=2] features=(6.30,2.90,5.60,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=105 FAILED [class=0, true class=2] features=(6.50,3.00,5.80,2.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=106 FAILED [class=0, true class=2] features=(7.60,3.00,6.60,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=107 FAILED [class=0, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=108 FAILED [class=0, true class=2] features=(7.30,2.90,6.30,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=109 FAILED [class=0, true class=2] features=(6.70,2.50,5.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=110 FAILED [class=0, true class=2] features=(7.20,3.60,6.10,2.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=111 FAILED [class=0, true class=2] features=(6.50,3.20,5.10,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=112 FAILED [class=0, true class=2] features=(6.40,2.70,5.30,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=113 FAILED [class=0, true class=2] features=(6.80,3.00,5.50,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=114 FAILED [class=0, true class=2] features=(5.70,2.50,5.00,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=115 FAILED [class=0, true class=2] features=(5.80,2.80,5.10,2.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=116 FAILED [class=0, true class=2] features=(6.40,3.20,5.30,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=117 FAILED [class=0, true class=2] features=(6.50,3.00,5.50,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=118 FAILED [class=0, true class=2] features=(7.70,3.80,6.70,2.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=119 FAILED [class=0, true class=2] features=(7.70,2.60,6.90,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=120 FAILED [class=0, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=121 FAILED [class=0, true class=2] features=(6.90,3.20,5.70,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=122 FAILED [class=0, true class=2] features=(5.60,2.80,4.90,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=123 FAILED [class=0, true class=2] features=(7.70,2.80,6.70,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=124 FAILED [class=0, true class=2] features=(6.30,2.70,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=125 FAILED [class=0, true class=2] features=(6.70,3.30,5.70,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=126 FAILED [class=0, true class=2] features=(7.20,3.20,6.00,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=127 FAILED [class=0, true class=2] features=(6.20,2.80,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=128 FAILED [class=0, true class=2] features=(6.10,3.00,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=129 FAILED [class=0, true class=2] features=(6.40,2.80,5.60,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=130 FAILED [class=0, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=131 FAILED [class=0, true class=2] features=(7.40,2.80,6.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=132 FAILED [class=0, true class=2] features=(7.90,3.80,6.40,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=133 FAILED [class=0, true class=2] features=(6.40,2.80,5.60,2.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=134 FAILED [class=0, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=135 FAILED [class=0, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=136 FAILED [class=0, true class=2] features=(7.70,3.00,6.10,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=137 FAILED [class=0, true class=2] features=(6.30,3.40,5.60,2.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=138 FAILED [class=0, true class=2] features=(6.40,3.10,5.50,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=139 FAILED [class=0, true class=2] features=(6.00,3.00,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=140 FAILED [class=0, true class=2] features=(6.90,3.10,5.40,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=141 FAILED [class=0, true class=2] features=(6.70,3.10,5.60,2.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=142 FAILED [class=0, true class=2] features=(6.90,3.10,5.10,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=143 FAILED [class=0, true class=2] features=(5.80,2.70,5.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=144 FAILED [class=0, true class=2] features=(6.80,3.20,5.90,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=145 FAILED [class=0, true class=2] features=(6.70,3.30,5.70,2.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=146 FAILED [class=0, true class=2] features=(6.70,3.00,5.20,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=147 FAILED [class=0, true class=2] features=(6.30,2.50,5.00,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=148 FAILED [class=0, true class=2] features=(6.50,3.00,5.20,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=149 FAILED [class=0, true class=2] features=(6.20,3.40,5.40,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=150 FAILED [class=0, true class=2] features=(5.90,3.00,5.10,1.80] Iris_AllClassifiers (EURUSD,H1) 27 model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx accuracy: 0.3333
2.29. Modelos de clasificación de Sckikit-Learn que no se han podido convertir a ONNX
Algunos modelos de clasificación no podían convertirse al formato ONNX debido a errores en el funcionamiento de convert_sklearn.
2.29.1. DummyClassifier
DummyClassifier es un clasificador de la biblioteca Scikit-learn que se usa como modelo básico simple para la tarea de clasificación. Está diseñado para probar y evaluar el rendimiento de otros modelos de clasificación más sofisticados.
Principio de funcionamiento:
DummyClassifier funciona de forma muy simple: realiza predicciones aleatorias o ingenuas sin tener en cuenta los datos de entrada. Estrategias posibles (la estrategia se selecciona con el parámetro strategy):
- "most_frequent" (La clase más frecuente): Esta estrategia predice siempre la clase que aparece con más frecuencia en el conjunto de datos de entrenamiento. Esto puede ser útil en situaciones en las que las clases están desequilibradas y resulta necesario predecir la clase dominante.
- "stratified" (decisión estratificada): Esta estrategia intenta hacer predicciones que coincidan con la distribución de clases en el conjunto de datos de entrenamiento. Usa la adivinación aleatoria, pero tiene en cuenta las proporciones de clases.
- "uniform" (distribución uniforme): Esta estrategia efectúa predicciones aleatorias con la misma probabilidad para cada clase. Resulta útil si las clases están equilibradas y queremos probar cómo se comportará nuestro modelo de media.
Posibilidades:
- Simplicidad: DummyClassifier es útil para comprobar lo rápido que se puede entrenar un modelo básico y cuál será su resultado. Puede resultar útil para evaluar rápidamente el rendimiento de otros clasificadores.
- Uso en pipeline: Puedes utilizar el DummyClassifier como modelo base en un pipeline junto con otras transformaciones y modelos para comparar y probar.
Limitaciones:
- No considera los datos: DummyClassifier realizará predicciones aleatorias o ingenuas sin considerar los datos reales. Es incapaz de aprender de los datos e identificar patrones.
- No resulta adecuado para tareas complejas: Este clasificador no está diseñado para tareas de clasificación complejas y no suele funcionar bien en tareas con grandes volúmenes de datos y patrones complejos.
- No es informativo: Los resultados obtenidos del DummyClassifier pueden ser poco informativos y no ofrecer información útil sobre el rendimiento del modelo. Resultan más útiles para probar y evaluar el código.
En general, DummyClassifier es una herramienta útil para las pruebas iniciales y la evaluación de modelos de clasificación, pero su uso es limitado en tareas complejas y no puede sustituir a algoritmos de clasificación más avanzados.
2.29.1.1. Código de creación del modelo DummyClassifier
# Iris_DummyClassifier.py
# The code demonstrates the process of training DummyClassifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model.
# It also evaluates the accuracy of both the original model and the ONNX model.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# import necessary libraries
from sklearn import datasets
from sklearn.dummy import DummyClassifier
from sklearn.metrics import accuracy_score, classification_report
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
import onnxruntime as ort
import numpy as np
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# load the Iris dataset
iris = datasets.load_iris()
X = iris.data
y = iris.target
# create a DummyClassifier model with the strategy "most_frequent"
dummy_classifier = DummyClassifier(strategy="most_frequent")
# train the model on the entire dataset
dummy_classifier.fit(X, y)
# predict classes for the entire dataset
y_pred = dummy_classifier.predict(X)
# evaluate the model's accuracy
accuracy = accuracy_score(y, y_pred)
print("Accuracy of DummyClassifier model:", accuracy)
# display the classification report
print("\nClassification Report:\n", classification_report(y, y_pred))
# define the input data type
initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format with float data type
onnx_model = convert_sklearn(dummy_classifier, initial_types=initial_type, target_opset=12)
# save the model to a file
onnx_filename = data_path + "dummy_classifier_iris.onnx"
with open(onnx_filename, "wb") as f:
f.write(onnx_model.SerializeToString())
# print model path
print(f"Model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("\nInformation about input tensors in ONNX:")
para i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("\nInformation about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# convert data to floating-point format (float32)
X_float32 = X.astype(np.float32)
# predict classes for the entire dataset using ONNX
y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0]
# evaluate the accuracy of the ONNX model
accuracy_onnx = accuracy_score(y, y_pred_onnx)
print("\nAccuracy of DummyClassifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of DummyClassifier model: 0.3333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.33 1.00 0.50 50
Python 1 0.00 0.00 0.00 50
Python 2 0.00 0.00 0.00 50
Python
Python accuracy 0.33 150
Python macro avg 0.11 0.33 0.17 150
Python weighted avg 0.11 0.33 0.17 150
Python
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.33 1.00 0.50 50
Python 1 0.00 0.00 0.00 50
Python 2 0.00 0.00 0.00 50
Python
Python accuracy 0.33 150
Python macro avg 0.11 0.33 0.17 150
Python weighted avg 0.11 0.33 0.17 150
Python
El modelo se construyó y operó en Sckit-learn, pero se produjeron errores al convertirlo a ONNX.
La pestaña Errores muestra los mensajes de error de la conversión del modelo al formato ONNX:
onnx_model = convert_sklearn(dummy_classifier, initial_types=initial_type, target_opset=12) Iris_DummyClassifier.py 44 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.dummy.DummyClassifier'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_DummyClassifier.py finished in 2071 ms 19 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.dummy.DummyClassifier'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_DummyClassifier.py finished in 2071 ms 19 1
De esta forma, el modelo DummyClassifier no pudo convertirse a ONNX.
2.29.2. GaussianProcessClassifier
GaussianProcessClassifier es un clasificador que usa un proceso gaussiano para la tarea de clasificación. Pertenece a la familia de modelos que utilizan procesos gaussianos y puede resultar útil en problemas en los que se necesita una estimación probabilística de las clases.
Principio de funcionamiento:
- GaussianProcessClassifier usa un proceso gaussiano para modelar la correspondencia entre el espacio de características y el espacio de estimaciones probabilísticas de las clases.
- Construye un modelo probabilístico para cada clase estimando la probabilidad de que un punto pertenezca a cada clase.
- Al realizar la clasificación, selecciona la clase con mayor probabilidad para un punto dado.
Posibilidades:
- Clasificación probabilística: GaussianProcessClassifier ofrece estimaciones probabilísticas de las clases, que pueden ser útiles, por ejemplo, para evaluar la incertidumbre del modelo.
- Adaptabilidad: Este clasificador es capaz de adaptarse a los datos y actualizar sus predicciones según nuevas observaciones.
- Calibración: El modelo puede calibrarse usando el método de calibración para mejorar las estimaciones de probabilidad.
Limitaciones:
- Complejidad computacional: GaussianProcessClassifier puede ser costoso computacionalmente para grandes cantidades de datos y/o alta dimensionalidad del espacio de características.
- No resulta apto para muestras grandes: Debido a la complejidad computacional, este clasificador puede no ser eficaz para el entrenamiento en muestras grandes.
- Dificultad de interpretación: Los procesos gaussianos pueden ser difíciles de interpretar y comprender, sobre todo para los usuarios sin experiencia en estadística bayesiana.
GaussianProcessClassifier resulta útil en problemas donde la estimación probabilística de clases es importante y cuando el coste computacional puede ser gestionado. De lo contrario, puede haber algoritmos de clasificación más adecuados para tareas de clasificación en big data o con estructuras de datos simples.
2.29.2.1. Código de creación del modelo GaussianProcessClassifier# Iris_GaussianProcessClassifier.py
# The code demonstrates the process of training Iris_GaussianProcess Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model.
# It also evaluates the accuracy of both the original model and the ONNX model.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# import necessary libraries
from sklearn import datasets
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF
from sklearn.metrics import accuracy_score, classification_report
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
import onnxruntime as ort
import numpy as np
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# load the Iris dataset
iris = datasets.load_iris()
X = iris.data
y = iris.target
# create a GaussianProcessClassifier model with an RBF kernel
kernel = 1.0 * RBF(1.0)
gpc_model = GaussianProcessClassifier(kernel=kernel)
# train the model on the entire dataset
gpc_model.fit(X, y)
# predict classes for the entire dataset
y_pred = gpc_model.predict(X)
# evaluate the model's accuracy
accuracy = accuracy_score(y, y_pred)
print("Accuracy of GaussianProcessClassifier model:", accuracy)
# display the classification report
print("\nClassification Report:\n", classification_report(y, y_pred))
# define the input data type
initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format with float data type
onnx_model = convert_sklearn(gpc_model, initial_types=initial_type, target_opset=12)
# save the model to a file
onnx_filename = data_path + "gpc_iris.onnx"
with open(onnx_filename, "wb") as f:
f.write(onnx_model.SerializeToString())
# print the path to the model
print(f"Model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("\nInformation about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("\nInformation about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# convert data to floating-point format (float32)
X_float32 = X.astype(np.float32)
# predict classes for the entire dataset using ONNX
y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0]
# evaluate the accuracy of the ONNX model
accuracy_onnx = accuracy_score(y, y_pred_onnx)
print("\nAccuracy of GaussianProcessClassifier model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of GaussianProcessClassifier model: 0.9866666666666667
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.98 0.98 50
Python 2 0.98 0.98 0.98 50
Python
Python accuracy 0.99 150
Python macro avg 0.99 0.99 0.99 150
Python weighted avg 0.99 0.99 0.99 150
Python
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.98 0.98 50
Python 2 0.98 0.98 0.98 50
Python
Python accuracy 0.99 150
Python macro avg 0.99 0.99 0.99 150
Python weighted avg 0.99 0.99 0.99 150
Python
Errores en la pestaña Errors:
onnx_model = convert_sklearn(gpc_model, initial_types=tipo_inicial, target_opset=12) Iris_GaussianProcessClassifier.py 46 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_converter(operator, container, verbose=verbose) _topology.py 1349 1
conv(self.scopes[0], operator, container) _topology.py 1132 1
return self._fct(*args) _registration.py 27 1
raise NotImplementedError("Only binary classification is iplemented.") gaussian_process.py 247 1
NotImplementedError: Only binary classification is iplemented. gaussian_process.py 247 1
Iris_GaussianProcessClassifier.py finished in 4004 ms 9 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_converter(operator, container, verbose=verbose) _topology.py 1349 1
conv(self.scopes[0], operator, container) _topology.py 1132 1
return self._fct(*args) _registration.py 27 1
raise NotImplementedError("Only binary classification is iplemented.") gaussian_process.py 247 1
NotImplementedError: Only binary classification is iplemented. gaussian_process.py 247 1
Iris_GaussianProcessClassifier.py finished in 4004 ms 9 1
Así, el modelo GaussianProcessClassifier tampoco pudo convertirse a ONNX.
2.29.3. LabelPropagation Classifier
LabelPropagation es un método de aprendizaje semisupervisado (semisupervised) usado para tareas de clasificación. La idea básica de este método es propagar etiquetas (clases) de objetos etiquetados a objetos no etiquetados en una estructura de datos de grafos.
Proceso de trabajo de LabelPropagation:
- Comienza construyendo un grafo en el que los nodos representan objetos de datos, mientras que las aristas entre nodos reflejan la similitud o proximidad entre objetos.
- Colocación inicial de etiquetas: Los objetos etiquetados reciben su etiqueta, mientras que los no etiquetados comienzan con una etiqueta indefinida.
- Las etiquetas están repartidas por todo el grafo: Las etiquetas de los objetos etiquetados se propagan a los objetos no etiquetados, teniendo en cuenta la similitud entre los objetos. Esta similitud puede determinarse de varias formas, por ejemplo, basándose en los vecinos más próximos en el grafo.
- Proceso iterativo: Las etiquetas pueden cambiar a lo largo de múltiples iteraciones, cuando cada iteración actualiza las etiquetas de los objetos sin etiquetar basándose en las etiquetas actuales y en las similitudes entre los objetos.
- Estabilización: El proceso continúa hasta que las etiquetas se estabilizan o se cumple un determinado criterio de parada.
Ventajas de LabelPropagation:
- Usa información de datos no etiquetados (marcados): LabelPropagation permite usar la información entre objetos no etiquetados para mejorar la calidad de la clasificación. Esto resulta especialmente útil cuando los datos etiquetados son insuficientes.
- Resistencia al ruido: El método funciona bien con datos que contienen ruido porque considera la similitud entre los objetos y no se basa únicamente en la partición.
Limitaciones de LabelPropagation:
- Dependencia de la selección del grafo: La calidad de la clasificación LabelPropagation puede depender en gran medida de la selección del grafo y del modo en que se determina la similitud entre los objetos. Una selección incorrecta de los parámetros puede dar lugar a malos resultados.
- Complejidad computacional: Dependiendo del tamaño y la complejidad de los datos, así como de los parámetros del método, LabelPropagation puede requerir grandes recursos computacionales.
- Posibilidad de sobreentrenamiento: Si hay demasiadas aristas ruidosas o etiquetas incorrectas en el grafo, el método puede sobreentrenarse.
- No siempre converge: En raras ocasiones, LabelPropagation puede no converger a etiquetas estables, y esto puede requerir una limitación del número de iteraciones u otros ajustes.
LabelPropagation es un método potente, pero requiere un ajuste cuidadoso de los parámetros y un análisis de la estructura gráfica de los datos para obtener buenos resultados.
2.29.3.1. Código de creación del modelo LabelPropagationClassifier
# Iris_LabelPropagationClassifier.py
# The code demonstrates the process of training LabelPropagation Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model.
# It also evaluates the accuracy of both the original model and the ONNX model.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# import necessary libraries
from sklearn import datasets
from sklearn.semi_supervised import LabelPropagation
from sklearn.metrics import accuracy_score, classification_report
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
import onnxruntime as ort
import numpy as np
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# load the Iris dataset
iris = datasets.load_iris()
X = iris.data
y = iris.target
# create a LabelPropagation model
lp_model = LabelPropagation()
# train the model on the entire dataset
lp_model.fit(X, y)
# predict classes for the entire dataset
y_pred = lp_model.predict(X)
# evaluate the model's accuracy
accuracy = accuracy_score(y, y_pred)
print("Accuracy of LabelPropagation model:", accuracy)
# display the classification report
print("\nClassification Report:\n", classification_report(y, y_pred))
# define the input data type
initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format with float data type
onnx_model = convert_sklearn(lp_model, initial_types=initial_type, target_opset=12)
# save the model to a file
onnx_filename = data_path + "lp_iris.onnx"
with open(onnx_filename, "wb") as f:
f.write(onnx_model.SerializeToString())
# print the path to the model
print(f"Model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("\nInformation about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("\nInformation about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# convert data to floating-point format (float32)
X_float32 = X.astype(np.float32)
# predict classes for the entire dataset using ONNX
y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0]
# evaluate the accuracy of the ONNX model
accuracy_onnx = accuracy_score(y, y_pred_onnx)
print("\nAccuracy of LabelPropagation model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of LabelPropagation model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
El modelo se construyó, pero se produjeron errores al convertirlo al formato ONNX.
Errores en la pestaña Errors:
onnx_model = convert_sklearn(lp_model, initial_types=initial_type, target_opset=12) Iris_LabelPropagation.py 44 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.semi_supervised._label_propagation.LabelPropagation'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_LabelPropagation.py finished in 2064 ms 19 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.semi_supervised._label_propagation.LabelPropagation'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_LabelPropagation.py finished in 2064 ms 19 1
Así, el modelo LabelPropagation Classifier tampoco se convirtió a ONNX.
2.29.4. LabelSpreading Classifier
LabelSpreading es un método de aprendizaje semisupervisado (semisupervised) usado para tareas de clasificación. Se basa en la idea de propagar etiquetas (clases) de objetos etiquetados a objetos no etiquetados en una estructura de datos gráficos similar a LabelPropagation. No obstante, LabelSpreading incluye una estabilización y regularización adicionales del proceso de difusión de etiquetas.
Proceso de trabajo de LabelSpreading:
- Comienza construyendo un grafo en el que los nodos representan objetos de datos, mientras que las aristas entre nodos reflejan la similitud o proximidad entre objetos.
- Colocación inicial de etiquetas: Los objetos etiquetados reciben su etiqueta, mientras que los no etiquetados comienzan con una etiqueta indefinida.
- Las etiquetas están repartidas por todo el grafo: Las etiquetas de los objetos etiquetados se propagan a los objetos no etiquetados, teniendo en cuenta la similitud entre los objetos.
- Regularización y estabilización: LabelSpreading incorpora regularización para ayudar a estabilizar el proceso de propagación de etiquetas y reducir el sobreentrenamiento. Esto se consigue considerando no solo la similitud entre objetos, sino también la diferencia entre las etiquetas de los objetos vecinos.
- Proceso iterativo: Las etiquetas pueden cambiar a lo largo de múltiples iteraciones, en las que cada iteración actualiza las etiquetas de los objetos no etiquetados basándose en las etiquetas actuales y en la regularización.
- Estabilización: El proceso continúa hasta que las etiquetas se estabilizan o se cumple un determinado criterio de parada.
Ventajas de LabelSpreading:
- Usa información de datos no etiquetados (marcados): LabelSpreading nos permite usar la información entre objetos no etiquetados para mejorar la calidad de la clasificación.
- Regularización: La presencia de regularización en LabelSpreading ayuda a reducir el sobreentrenamiento y a hacer más robusto el proceso de propagación de etiquetas.
Limitaciones de LabelSpreading:
- Dependencia de la selección del grafo: Como en el caso de LabelPropagation, la calidad de la clasificación LabelSpreading puede depender en gran medida de la selección de los parámetros del grafo y del método.
- Complejidad computacional: En función del tamaño y la complejidad de los datos, así como de los parámetros del método, LabelSpreading puede necesitar grandes recursos informáticos.
- No siempre converge: En raras ocasiones, LabelSpreading puede no converger a etiquetas estables, lo cual puede requerir limitar el número de iteraciones u otros ajustes.
LabelSpreading es un método que también necesita un ajuste cuidadoso y puede ser una potente herramienta para utilizar datos no etiquetados en tareas de clasificación.
2.29.4.1. Código de creación del modelo LabelSpreadingClassifier
# Iris_LabelSpreadingClassifier.py
# The code demonstrates the process of training LabelSpreading Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model.
# It also evaluates the accuracy of both the original model and the ONNX model.
# Copyright 2023, MetaQuotes Ltd.
# import necessary libraries
from sklearn import datasets
from sklearn.semi_supervised import LabelSpreading
from sklearn.metrics import accuracy_score, classification_report
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
import onnxruntime as ort
import numpy as np
import sys
# get the script path
script_path = sys.argv[0]
last_index = script_path.rfind("\\") + 1
data_path = script_path[0:last_index]
# load the Iris dataset
iris = datasets.load_iris()
X = iris.data
y = iris.target
# create a LabelSpreading model
ls_model = LabelSpreading()
# train the model on the entire dataset
ls_model.fit(X, y)
# predict classes for the entire dataset
y_pred = ls_model.predict(X)
# evaluate the model's accuracy
accuracy = accuracy_score(y, y_pred)
print("Accuracy of LabelSpreading model:", accuracy)
# display the classification report
print("\nClassification Report:\n", classification_report(y, y_pred))
# define the input data type
initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format with float data type
onnx_model = convert_sklearn(ls_model, initial_types=initial_type, target_opset=12)
# save the model to a file
onnx_filename = data_path + "ls_iris.onnx"
with open(onnx_filename, "wb") as f:
f.write(onnx_model.SerializeToString())
# print the path to the model
print(f"Model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("\nInformation about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("\nInformation about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# convert data to floating-point format (float32)
X_float32 = X.astype(np.float32)
# predict classes for the entire dataset using ONNX
y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0]
# evaluate the accuracy of the ONNX model
accuracy_onnx = accuracy_score(y, y_pred_onnx)
print("\nAccuracy of LabelSpreading model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of LabelSpreading model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
La pestaña Errors muestra información sobre los errores de conversión de ONNX.
onnx_model = convert_sklearn(ls_model, initial_types=tipo_inicial, target_opset=12) Iris_LabelSpreading.py 45 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.semi_supervised._label_propagation.LabelSpreading'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_LabelSpreading.py finished in 2032 ms 19 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.semi_supervised._label_propagation.LabelSpreading'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_LabelSpreading.py finished in 2032 ms 19 1
Así, el modelo LabelPropagation Classifier tampoco se convirtió a ONNX.
2.29.5. NearestCentroid Classifier
NearestCentroid es un método de clasificación que se basa en la idea de determinar el centroide de cada clase y clasificar los objetos según el centroide más cercano. Este método resulta adecuado para problemas multiclase y funciona bien en conjuntos de datos con clases linealmente separables.
Proceso de trabajo de NearestCentroid:
- Para cada clase, se calcula un centroide, que es la media de las características de todos los objetos pertenecientes a esa clase. Esto puede lograrse calculando el valor medio de cada característica para los objetos de una clase determinada.
- Al clasificar un nuevo objeto, se calcula su centroide más cercano entre los centroides de todas las clases.
- El nuevo objeto pertenece a la clase cuyo centroide resultó estar más próximo a él en el espacio métrico.
Ventajas de NearestCentroid:
- Sencillez y rapidez: NearestCentroid es un método de baja complejidad computacional que funciona con rapidez en grandes conjuntos de datos.
- Adecuado para clases linealmente separables: El método funciona bien en problemas en los que las clases son linealmente separables o casi linealmente separables.
- Eficacia en problemas multiclase: NearestCentroid resulta adecuado para tareas multiclase y puede utilizarse como clasificador básico en conjuntos.
Limitaciones de NearestCentroid:
- Sensibilidad a los valores atípicos: El método NearestCentroid es sensible a los valores atípicos en los datos porque el centroide puede estar muy desplazado por la presencia de valores atípicos.
- Desplazamiento espacial: Si las clases de los datos tienen varianzas y formas distintas, el método NearestCentroid puede funcionar con menos eficacia.
- Se requiere un supuesto de promedios: El método supone que las clases tienen aproximadamente los mismos valores medios de características, lo cual puede no ser siempre el caso en los datos reales.
- No resulta adecuado para problemas no lineales: NearestCentroid no resulta adecuado para problemas con límites de separación no lineales entre clases.
NearestCentroid es un método de clasificación simple e interpretable que puede ser útil en determinados escenarios, especialmente cuando las clases son linealmente separables y no hay valores atípicos en los datos.
2.29.5.1. Código de creación del modelo NearestCentroid Classifier
# Iris_NearestCentroidClassifier.py
# The code demonstrates the process of training NearestCentroid Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model.
# It also evaluates the accuracy of both the original model and the ONNX model.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# import necessary libraries
from sklearn import datasets
from sklearn.neighbors import NearestCentroid
from sklearn.metrics import accuracy_score, classification_report
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
import onnxruntime as ort
import numpy as np
import sys
# get the script path
script_path = sys.argv[0]
last_index = script_path.rfind("\\") + 1
data_path = script_path[0:last_index]
# load the Iris dataset
iris = datasets.load_iris()
X = iris.data
y = iris.target
# create a NearestCentroid model
nc_model = NearestCentroid()
# train the model on the entire dataset
nc_model.fit(X, y)
# predict classes for the entire dataset
y_pred = nc_model.predict(X)
# evaluate the model's accuracy
accuracy = accuracy_score(y, y_pred)
print("Accuracy of NearestCentroid model:", accuracy)
# display the classification report
print("\nClassification Report:\n", classification_report(y, y_pred))
# define the input data type
initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format with float data type
onnx_model = convert_sklearn(nc_model, initial_types=initial_type, target_opset=12)
# save the model to a file
onnx_filename = data_path + "nc_iris.onnx"
with open(onnx_filename, "wb") as f:
f.write(onnx_model.SerializeToString())
# print the path to the model
print(f"Model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("\nInformation about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("\nInformation about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# convert data to floating-point format (float32)
X_float32 = X.astype(np.float32)
# predict classes for the entire dataset using ONNX
y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0]
# evaluate the accuracy of the ONNX model
accuracy_onnx = accuracy_score(y, y_pred_onnx)
print("\nAccuracy of NearestCentroid model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of NearestCentroid model: 0.9266666666666666
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.87 0.92 0.89 50
Python 2 0.91 0.86 0.89 50
Python
Python accuracy 0.93 150
Python macro avg 0.93 0.93 0.93 150
Python weighted avg 0.93 0.93 0.93 150
Python
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.87 0.92 0.89 50
Python 2 0.91 0.86 0.89 50
Python
Python accuracy 0.93 150
Python macro avg 0.93 0.93 0.93 150
Python weighted avg 0.93 0.93 0.93 150
Python
Errores en la pestaña Errors:
onnx_model = convert_sklearn(nc_model, initial_types=initial_type, target_opset=12) Iris_NearestCentroid.py 45 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.neighbors._nearest_centroid.NearestCentroid'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_NearestCentroid.py finished in 2131 ms 19 1
El modelo NearestCentroid Classifier tampoco se convirtió a ONNX. onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.neighbors._nearest_centroid.NearestCentroid'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_NearestCentroid.py finished in 2131 ms 19 1
2.29.6. Quadratic Discriminant Analysis Classifier
Quadratic Discriminant Analysis (QDA) es un método de clasificación que utiliza un modelo probabilístico para dividir los datos en clases. Supone una generalización del análisis discriminante lineal (LDA) y permite considerar la covarianza de las características dentro de cada clase. La idea básica de QDA consiste en modelar la distribución de características para cada clase y luego utilizar dicha distribución para clasificar nuevos objetos.
Proceso de trabajo de QDA:
- Para cada clase, se calculan los parámetros de distribución, como el valor medio y la matriz de covarianza de las características. Estos parámetros se estiman a partir de los datos de entrenamiento de cada clase.
- Partiendo de los parámetros obtenidos, podemos calcular las densidades de probabilidad para cada clase utilizando una distribución normal multivariante (o función de distribución cuadrática).
- Al clasificar un nuevo objeto, se calculan los valores de las densidades de probabilidad de cada clase y el objeto se asigna a la clase con mayor probabilidad.
Ventajas de Quadratic Discriminant Analysis (QDA):
- Considera la covarianza de los rasgos: QDA es más flexible que LDA porque permite diferentes matrices de covarianza para diferentes clases, lo cual lo hace más adaptable a diferentes estructuras de datos.
- Adecuado para límites de separación no lineales: QDA es capaz de modelar límites de separación complejos y no lineales entre clases.
- Resistencia a los datos desequilibrados: QDA puede funcionar bien cuando las clases están desequilibradas.
Limitaciones de Quadratic Discriminant Analysis (QDA):
- Complejidad computacional: QDA requiere la estimación de parámetros para cada clase, incluidas las matrices de covarianza, lo cual puede resultar costoso desde el punto de vista informático en grandes conjuntos de datos.
- Pocos datos: QDA puede ser menos eficaz cuando los datos son escasos y la estimación de los parámetros es menos precisa.
- Supuesto de distribución normal: QDA asume que los datos tienen una distribución normal, lo cual puede no ser cierto para algunos tipos de datos.
- Posible sobreentrenamiento: Si los datos de entrenamiento son insuficientes o si existe una fuerte covarianza entre las características, QDA puede enfrentarse a un problema de sobreentrenamiento.
Quadratic Discriminant Analysis (QDA) es un potente método de clasificación adecuado para distintos tipos de datos y que puede tener en cuenta la covarianza de las características dentro de las clases. No obstante, también tiene limitaciones que deben tenerse en cuenta al utilizarlo.
2.29.6.1.Código de creación del modelo Quadratic Discriminant Analysis
# Iris_QuadraticDiscriminantAnalysisClassifier.py
# The code demonstrates the process of training Quadratic Discriminant Analysis Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model.
# It also evaluates the accuracy of both the original model and the ONNX model.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# import necessary libraries
from sklearn import datasets
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
from sklearn.metrics import accuracy_score, classification_report
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
import onnxruntime as ort
import numpy as np
import sys
# get the script path
script_path = sys.argv[0]
last_index = script_path.rfind("\\") + 1
data_path = script_path[0:last_index]
# load the Iris dataset
iris = datasets.load_iris()
X = iris.data
y = iris.target
# create a QuadraticDiscriminantAnalysis model
qda_model = QuadraticDiscriminantAnalysis()
# train the model on the entire dataset
qda_model.fit(X, y)
# predict classes for the entire dataset
y_pred = qda_model.predict(X)
# evaluate the model's accuracy
accuracy = accuracy_score(y, y_pred)
print("Accuracy of Quadratic Discriminant Analysis model:", accuracy)
# display the classification report
print("\nClassification Report:\n", classification_report(y, y_pred))
# define the input data type
initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format with float data type
onnx_model = convert_sklearn(qda_model, initial_types=initial_type, target_opset=12)
# save the model to a file
onnx_filename = data_path + "qda_iris.onnx"
with open(onnx_filename, "wb") as f:
f.write(onnx_model.SerializeToString())
# print the path to the model
print(f"Model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("\nInformation about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("\nInformation about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# convert data to floating-point format (float32)
X_float32 = X.astype(np.float32)
# predict classes for the entire dataset using ONNX
y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0]
# evaluate the accuracy of the ONNX model
accuracy_onnx = accuracy_score(y, y_pred_onnx)
print("\nAccuracy of Quadratic Discriminant Analysis model in ONNX format:", accuracy_onnx)
Resultado:
Python Accuracy of Quadratic Discriminant Analysis model: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.96 0.97 50
Python 2 0.96 0.98 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\qda_iris.onnx
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.96 0.97 50
Python 2 0.96 0.98 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\qda_iris.onnx
Esta vez, el modelo se guardó en ONNX, pero los errores se muestran en la pestaña Errors al ejecutarse:
onnx_session = ort.InferenceSession(onnx_filename) Iris_QuadraticDiscriminantAnalysisClassifier.py 55 1
self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1
sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1
onnxruntime.capi.onnxruntime_pybind11_state.InvalidGraph: [ONNXRuntimeError] : 10 : INVALID_GRAPH : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\qda_iris.onnx failed:This is an invalid mode onnxruntime_inference_collection.py 424 1
Iris_QuadraticDiscriminantAnalysisClassifier.py finished in 2063 ms 5 1
self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1
sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1
onnxruntime.capi.onnxruntime_pybind11_state.InvalidGraph: [ONNXRuntimeError] : 10 : INVALID_GRAPH : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\qda_iris.onnx failed:This is an invalid mode onnxruntime_inference_collection.py 424 1
Iris_QuadraticDiscriminantAnalysisClassifier.py finished in 2063 ms 5 1
La conversión del modelo Quadratic Discriminant Analysis Classifier a ONNX falló.
Conclusiones
Utilizando el Iris dataset como ejemplo, se investigaron 33 modelos de clasificación disponibles en la biblioteca Scikit-learn versión 1.2.2.
1. De este conjunto, 6 modelos tuvieron dificultades para convertirse al formato ONNX:
- DummyClassifier: Dummy Classifier (clasificador ficticio);
- GaussianProcessClassifier: Gaussian Process Classifier (clasificador de procesos gaussianos);
- LabelPropagation : Label Propagation Classifier (Clasificador por propagación de etiquetas);
- LabelSpreading : Label Spreading Classifier (Clasificador por propagación de etiquetas);
- NearestCentroid: Nearest Centroid Classifier (Clasificador de centroide más próximo);
- QuadraticDiscriminantAnalysis: Quadratic Discriminant Analysis Classifier (Clasificador de análisis discriminante cuadrático).
Aparentemente, estos modelos resultan más complejos en cuanto a su estructura y/o lógica, y adaptarlos para su ejecución en el formato ONNX puede requerir un esfuerzo adicional. También es posible que usen estructuras de datos o algoritmos específicos que no sean totalmente compatibles o adecuados para el formato ONNX.
2. Los 27 modelos restantes se convirtieron con éxito al formato ONNX y mostraron su capacidad de mantener la precisión, lo que pone de manifiesto la eficacia de ONNX como herramienta para preservar y recuperar modelos de aprendizaje automático. Esto permite transferir fácilmente modelos entre distintos entornos y usarlos en diferentes aplicaciones manteniendo la calidad de sus prestaciones.
Lista completa de modelos convertidos con éxito al formato ONNX:
- SVC: Support Vector Classifier (Clasificador de vectores de soporte);
- LinearSVC: Linear Support Vector Classifier (Clasificador lineal de vectores de soporte);
- NuSVC: Nu Support Vector Classifier (Clasificador de vectores de soporte con parámetro Nu);
- AdaBoostClassifier: Adaptive Boosting Classifier (Clasificador de boosting adaptativo);
- BaggingClassifier: Bootstrap Aggregating Classifier (Clasificador de agregación de bootstrap);
- BernoulliNB: Bernoulli Naive Bayes (Clasificador bayesiano ingenuo con hipótesis de distribución Bernoulli);
- CategoricalNB: Categorical Naive Bayes (Clasificador bayesiano ingenuo para datos categóricos);
- ComplementNB: Complement Naive Bayes (Clasificador bayesiano ingenuo complementario);
- DecisionTreeClassifier: Decision Tree Classifier (Clasificador de árbol de decisiones);
- ExtraTreeClassifier: Extra Tree Classifier (Clasificador basado en árbol extra);
- ExtraTreesClassifier: Extra Tree Classifier (Clasificador basado en árboles extra);
- GaussianNB: Gaussian Naive Bayes (Clasificador bayesiano ingenuo con suposición de distribución gaussiana);
- GradientBoostingClassifier: Gradient Boosting Classifier (Clasificador de aumento de gradiente);
- HistGradientBoostingClassifier: Histogram-Based Gradient Boosting Classifier (Clasificador de aumento de gradiente basado en histogramas);
- KNeighborsClassifier: k-Nearest Neighbors Classifier (Clasificador de k-vecinos más próximos);
- LinearDiscriminantAnalysis: Linear Discriminant Analysis (Análisis discriminante lineal);
- LogisticRegression: Logistic Regression Classifier (Clasificador de regresión logística);
- LogisticRegressionCV: Logistic Regression Classifier with Cross-Validation (Clasificador de regresión logística con validación cruzada);
- MLPClassifier: Multi-Layer Perceptron Classifier (Clasificador de perceptrón multicapa);
- MultinomialNB: Multinomial Naive Bayes (Clasificador bayesiano ingenuo con suposición de distribución multinomial);
- PassiveAggressiveClassifier: Passive-Aggressive Classifier (Clasificador pasivo-agresivo);
- Perceptron: Perceptron (Perceptrón);
- RadiusNeighborsClassifier: Radius Neighbors Classifier (Clasificador basado en radio de vecinos);
- RandomForestClassifier: Random Forest Classifier (Clasificador de bosque aleatorio);
- RidgeClassifier: Ridge Classifier (Clasificador basado en la regresión de Ridge);
- RidgeClassifierCV: Ridge Classifier with Cross-Validation (Clasificador de Ridge con validación cruzada;
- SGDClassifier: Stochastic Gradient Descent Classifier (Clasificador por descenso de gradiente estocástico)
3. Además, el estudio destacó los modelos que demostraron un rendimiento sobresaliente en la tarea de clasificación del Iris dataset. Modelos de clasificación como Random Forest Classifier, Gradient Boosting Classifier, Bagging Classifier, Decision Tree Classifier, Extra Tree Classifier, Extra Trees Classifier y Hist Gradient Boosting Classifier lograron una precisión perfecta en las predicciones. Esto significa que son capaces de determinar con gran precisión la clase a la que pertenece cada espécimen del Iris dataset.
Estos resultados pueden resultar especialmente útiles a la hora de seleccionar el mejor modelo para una determinada tarea de clasificación. Los modelos que han alcanzado una precisión perfecta con el Iris dataset pueden ser una opción ideal si su tarea implica analizar o clasificar dichos datos.
Así pues, el estudio realizado subraya la importancia de elegir correctamente el modelo para una tarea concreta y nos permite identificar las opciones más prometedoras para futuras investigaciones y aplicaciones en tareas prácticas.
Conclusión
En este trabajo se analizaron 33 modelos de clasificación usando como ejemplo el Iris dataset con la ayuda de la biblioteca Scikit-learn versión 1.2.2.
De todos los modelos examinados, 6 resultaron difíciles de convertir al formato ONNX. Estos modelos incluyen Dummy Classifier, Gaussian Process Classifier, Label Propagation Classifier, Label Spreading Classifier, Nearest Centroid Classifier y Quadratic Discriminant Analysis Classifier. Es probable que su compleja estructura o lógica requiera una adaptación adicional para una conversión satisfactoria al formato ONNX.
Los 27 modelos restantes se convirtieron con éxito al formato ONNX y demostraron que mantenían su precisión. Esto confirma que ONNX es una herramienta eficaz para almacenar y restaurar modelos de aprendizaje automático, garantizando su portabilidad y preservando la calidad de su rendimiento.
Modelos de clasificación como Random Forest Classifier, Gradient Boosting Classifier, Bagging Classifier, Decision Tree Classifier, Extra Tree Classifier, Extra Trees Classifier y Hist Gradient Boosting Classifier lograron una precisión perfecta en las predicciones. Estos modelos pueden resultar especialmente atractivos para tareas de clasificación en las que una gran precisión desempeña un papel fundamental.
Este estudio pone de relieve la importancia de seleccionar adecuadamente el modelo para tareas específicas y demuestra las ventajas de utilizar ONNX para preservar y aplicar modelos de aprendizaje automático a tareas de clasificación.
Todos los scripts del artículo también estarán disponibles en el proyecto público MQL5\Shared Projects\Scikit.Classification.ONNX.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/13451
Archivos adjuntos |
Scikit-learn-ClassificationModels-ONNX.zip
(220.05 KB)
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Pasar a la discusión en el foro de los operadores
Dominando ONNX: Un punto de inflexión para los tráders de MQL5
Sumérjase en el mundo de ONNX, un potente formato abierto para compartir modelos de aprendizaje automático. Descubra cómo el uso de ONNX puede revolucionar el trading algorítmico en MQL5, permitiendo a los tráders integrar sin problemas modelos avanzados de IA y llevar sus estrategias al siguiente nivel. Descubra los secretos de la compatibilidad multiplataforma y aprenda a liberar todo el potencial de ONNX en sus operaciones MQL5. Mejore sus operaciones con esta guía detallada de ONNX.
Redes neuronales: así de sencillo (Parte 59): Dicotomía de control (DoC)
En el artículo anterior nos familiarizamos con el transformador de decisión. Sin embargo, el complejo entorno estocástico del mercado de divisas no nos permitió aprovechar plenamente el potencial del método presentado. Hoy veremos un algoritmo que tiene como objetivo mejorar el rendimiento de los algoritmos en entornos estocásticos.
Trabajamos con fechas y horas en MQL5
Resulta esencial que los tráders y desarrolladores de herramientas comerciales comprendan cómo manejar las fechas y horas de manera adecuada y eficaz. En este artículo, veremos cómo podemos manejar fechas y horas al crear herramientas comerciales efectivas.
Algoritmos de optimización de la población: Búsqueda por difusión estocástica (Stochastic Diffusion Search, SDS)
En este artículo veremos la búsqueda por difusión estocástica, o SDS, que es un algoritmo de optimización muy potente y eficiente basado en los principios del paseo aleatorio. El algoritmo puede encontrar soluciones óptimas en espacios multidimensionales complejos, con una alta tasa de convergencia y la capacidad de evitar extremos locales.
Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese