MetaTrader 5 / 例
English Русский Deutsch Português
preview
ブレインストーム最適化アルゴリズム(第1部）：クラスタリング

ブレインストーム最適化アルゴリズム(第1部）：クラスタリング

MetaTrader 5 — 例 | 11 9月 2024, 10:15
35 0
Andrey Dik
Andrey Dik

内容

1. はじめに
2.  アルゴリズムの説明
3. K-Means


1. はじめに

ブレインストーム最適化(BSO: Brain Storm Optimization)は、ブレインストーミングという現象に着想を得た、エキサイティングで革新的な集団最適化アルゴリズムの1つです。この最適化手法は、集合知と集団行動の原理を利用して複雑な問題を解決するための効果的なアプローチです。BSOは、グループディスカッションで起こるような新しいアイデアや解決策を生み出すプロセスをシミュレートしており、様々な分野で最適な解決策を見出すためのユニークで有望なツールとなっています。この記事では、BSOの基本原理、その利点、適用分野について見ていきます。

母集団基本の手法は、複雑な最適化問題を解くための重要なツールです。しかし、複数の最適解を見つける必要があるマルチモーダル問題の文脈では、既存のアプローチには限界があります。本稿では、ブレインストーム最適化法と呼ばれる新しい最適化法を紹介します。

ニッチング法やクラスタリング法などの既存のアプローチは、一般的に母集団を部分集団に分割して複数の解を探索します。しかし、これらの方法は、部分集団の数を事前に決定する必要があり、特に最適解の数が事前にわからない場合には困難であるという問題を抱えています。BSOは、ターゲット空間を、個体がクラスタ化され、その座標に基づいて更新される空間に変換することで、この欠点を補います。1つの大域的最適解を求める既存の方法とは異なり、提案するBSO法は、いくつかの「有意義な」解に探索プロセスを向けるのです。

BSO法とそのマルチモーダル最適化問題への適用性について詳しく見てみましょう。ブレインストーム最適化(BSO)アルゴリズムは、2015年にShiらによって開発されました。これは、問題解決のために人々が集まってアイデアを出し合い、共有するブレインストーミングの自然なプロセスにヒントを得たものです。

ハイポ分散ブレインストーム最適化(Hypo Variance Brain Storm Optimization)のように、対象関数の推定がガウス分散ではなくハイポ分散またはサブ分散に基づくアルゴリズムのバリエーションがいくつかあります。グローバルベストブレインストーム最適化(Global-best Brain Storm Optimization)のような他のバリエーションもあります。このバリエーションには、変数基本の更新と適応度基本のグループ化と組み合わせた、母集団の現在の状態によってトリガーされる再初期化スキームが含まれます。

BSOアルゴリズムの各個体は、最適化されるべき問題の解を示すだけでなく、問題ランドスケープを明らかにするデータポイントでもあります。コレクティブインテリジェンスとデータ分析技術を組み合わせることで、どちらか一方だけでは達成できない利益を得ることができます。


2. アルゴリズム

BSOアルゴリズムはこのプロセスをモデル化することで機能し、候補解の集団（「個体」または「アイデア」と呼ばれる）は最適解に収束するように反復的に更新されます。アルゴリズムは以下の主要な段階から構成されます。

1. 初期化

- アルゴリズムは、個体の初期集団を生成することから始まり、各個体は最適化問題の潜在的な解を表します。
- 各個体は、解の特性を定義する解変数のセットで表されます。

2. ブレインストーミング

- この段階では、アルゴリズムがブレインストーミングをシミュレートし、個体が自分のアイデアと他の個体のアイデアを組み合わせたり修正したりすることによって、新しいアイデア（すなわち新しい解決策の候補）を生成します。
- ブレインストーミングは、新しいアイデアがどのように生み出されるかを決定する一連のルールによって導かれます。これらのルールは、人間のブレインストーミングから着想を得ており、以下のようなものがあります。
  • 新しいアイデアのランダム生成
  • 異なる個体のアイデアの組み合わせ
  • 既存のアイデアの修正

3.評価

- 新しく生成されたアイデア（すなわち新しい解の候補）は、最適化問題の目的関数を使って評価されます。
- 目的関数は、各候補解の品質または適合度を測定し、アルゴリズムはこの関数を最小化（または最大化）する解を見つけようとします。

4.選択

- 評価ステップの後、アルゴリズムは、次の反復のために保持するために、母集団から最良の個体を選択します。
- 選択は個体の適応度値に基づいておこなわれ、適応度値の高い個体が選択される確率が高くなります。

5.完了

- アルゴリズムは、最大反復回数や目標解の品質達成などの終了基準が満たされるまで、ブレインストーミング、評価、選択の各段階を反復し続けます。

他の母集団最適化手法と異なるBSOの特徴的な手法とアルゴリズムの特徴を挙げてみましょう。

1. クラスタリング：個体は、探索空間における位置の類似性に基づいてクラスタにグループ化されます。これはK-Meansクラスタリングアルゴリズムを使用して実装されています。
2. コンバージェンス：この段階で、各クラスタ内の個体はクラスタ重心の周りにグループ化されます。これは、参加者が集まってアイデアを話し合うブレインストーミングの段階をシミュレートしたものです。
3. 発散：この段階で、新しい個体が生まれます。新しい個体は、クラスタ内の1つか2つの個体に基づいて生成することができます。このプロセスは、参加者が既成概念にとらわれず、新しいアイデアを考え出すブレインストーミングの段階を模倣したものです。
4.選択：新しい個体が生成された後、それらはメインの親グループに入れられ、その後グループが並び替えられます。従って、次のイテレーションでは、更新され改善されたアイデアを扱うことになります。
5.変異：アイデアを組み合わせて新しいアイデアを生み出した後、新たに生まれたアイデアはすべて突然変異を起こし、母集団にさらなる多様性を加え、早すぎる収束を防ぎます。

BSOアルゴリズムのロジックを擬似コードで示してみましょう。

1. パラメータの初期化と初期集団の生成
2. 集団内の各個体の適応度を計算する
3. 停止基準が満たされるまで
    4. 集団内の各個体の適応度を計算する
    5.集団内の最良の個体を決定する
    6. 母集団をクラスタに分割し、クラスタ内の最適解をクラスタの中心とする
    7. 母集団内の新しい個体ごとに
        |7.1. pReplaceの確率が満たされた場合
        |    |ランダムに選択されたクラスタの新しいシフトされた中心が生成される（クラスタの中心がシフトされる）
        |7.2. pOneの確率が満たされた場合
        |    |ランダムなクラスタを選択する
        |    |pOne_center確率が満たされた場合
        |    |    |7.2.a クラスタの中心を選択する
        |    |それ以外の場合
        |         |7.2.b クラスタからランダムに個体を選ぶ
        |7.3 それ以外の場合
        |         |2つのクラスタを選択する
        |         |Two_centerの確率が満たされた場合
        |             |7.3.a 2つのクラスタ中心を結合することによって新しい個体が形成される
        |         |それ以外の場合
        |             |7.3.b 選択された各クラスタから選択された2つの個体の位置を結合して新しい個体を作成する（異なるクラスタ）
        |7.4 変異：新しい個体の位置にランダムなガウス偏差を加える
        |7.5 新しい個体が探索空間の外に出た場合、それを探索空間に戻す
    8. 現在の母集団を新しい個体で更新する
    9. 停止基準が満たされるまでステップ4に戻る
10. 母集団の中で最良の個体を解として返す
11. BSO操作終了


擬似コードのステップ7の操作を見てみましょう。

実際、最初の操作7.1では新しい個体は作成されませんが、クラスタの中心が移動され、その後アルゴリズムの他の操作で新しい個体が作成されます。変位は、外部パラメータで指定された元の位置からの距離で、各座標ごとに正規分布でランダムに発生します。

操作7.2は、クラスタ中心か、ステップ7.4で突然変異を起こし、新しい個体を作成する選択されたクラスタ内の個体のいずれかを選択します。

操作7.3は、無作為に選んだ2つのクラスタの中心か、選んだクラスタから選んだ2つの個体のどちらかを結合して、新しい個体を作るように設計されています。クラスタは別個であるべきですが、空でないクラスタが1つしかない場合（クラスタが空の場合もある）、結合操作はこの1つの空でないクラスタ内の選択された2個体に対して実行されます。この操作は、アイデアクラスタ間の意見交換を目的としています。

結合操作は以下の式で表されます。


ここで
Xf：結合後の新しい個体
v：0から1の乱数
X1とX2：結合される2つのランダムな個体（または2つのクラスタ中心）

結合式の意味は、2つのアイデアの間のランダムな位置にアイデアが生まれるということです。

突然変異の操作は以下の式で表されます。


ここで
Xm：突然変異後の新しい個体
Xs：変異させる個体の選択
n(µ, σ)：平均µ、分散σのガウス乱数、
ξ：数式で表される突然変異率。

突然変異率はは以下の式で表されます。


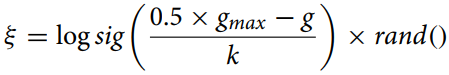
ここで
gmax：反復の最大回数
g：現在の反復回数
k：補正比率

この式（突然変異率）は、突然変異パラメータを適応的に変化させる最適化アルゴリズムにおいて、個体間の縮小距離を計算するために使用されます。logsig()関数は、スムーズな非線形の値の減少を提供し、randによる乗算は、早すぎる収束を避け、母集団の多様性を維持するのに有用な確率的要素を追加します。

ブレインストーム最適化(BSO)アルゴリズムにおけるk補正比は、ξ比の経時変化率をコントロールする上で重要な役割を果たします。kの値は、特定の問題とデータによって異なり、経験的に計算されるか、ハイパーパラメータのチューニング方法を使用します。

一般的に、kは、アルゴリズムにおける探索と搾取のバランスが取れるように選択されるべきです。kが大きすぎると、ξの変化が非常に遅くなり、アルゴリズムが早期に収束してしまう可能性があります。kが小さすぎると、ξの変化が非常に速くなり、探索空間の過剰探索や収束の遅れにつながります。

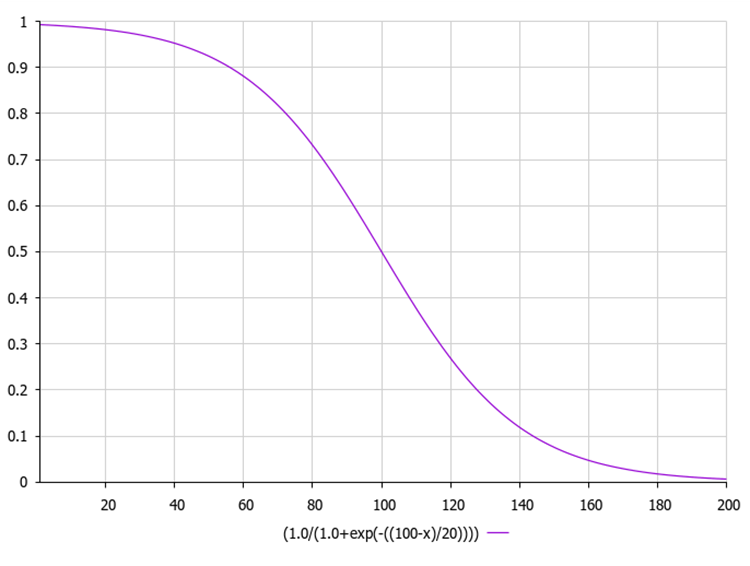
対数シグモイド関数はロジスティック関数としても知られ、一般にσ(x)または sig(x)と表記されます。これは以下の式で計算されます。


ここで
exp(-x)：指数-xのべき乗
1 / (1 + exp(-x))：0から1の範囲の出力値

下図はシグモイド関数のグラフです。不均等な関数削減は、初期の反復で探索をおこない、後の反復で洗練をおこなうことを可能にします。

以下は、指数を使って計算されたシグモイド関数とともに、突然変異率を計算するコード例です。

このコードでは、関数sigmoidが入力数値xのシグモイド値を計算し、関数xiが上式に従ってξの値を計算します。ここでgmaxは最大反復回数、gは現在の反復回数、kは補正率です。MathRand関数は0から32,767の間の乱数を生成するので、それを32,767.0で割って0から1の間の乱数を得ます。次に、この乱数のシグモイド値を計算します。この値はxi関数によって返されます。

double sigmoid(double x) 
{
    return 1.0 / (1.0 + MathExp(-x));
}

double xi(int gmax, int g, double k) 
{
    double randNum = MathRand() / 32767.0; // Generate a random number from 0 to 1
    return sigmoid (0.5 * (gmax - g) / k) * randNum;
}


3. KMeansクラスタリング法

BSOアルゴリズムは、k平均クラスタ分析を使用して、アイデアを別個のグループに分離します。グループ討論の参加者の行動をシミュレートし、探索効率を向上させるために、反復に入力するための現在のn個の解の集合をm個のカテゴリに分割します。

ここでは、K-Meansアルゴリズムを実装し、一般的なクラスタリング手法であるS_Cluster構造体を使用した個別のクラスタについて説明します。

この構造体を見てみましょう。

  • centroid[]：クラスタの重心を表す配列
  • f：重心の適応度値
  • count：クラスタ内のポイント数
  • ideasList[]：アイデアのリスト

Init関数は、centroid配列とideasList配列のサイズを変更し、fの初期値を設定することにより、構造体を初期化します。

//——————————————————————————————————————————————————————————————————————————————
struct S_Cluster
{
    double centroid [];  //cluster centroid
    double f;            //centroid fitness
    int    count;        //number of points in the cluster
    int    ideasList []; //list of ideas

    void Init (int coords)
    {
      ArrayResize (centroid, coords);
      f = -DBL_MAX;
      ArrayResize (ideasList, 0, 100);
    }
};
//——————————————————————————————————————————————————————————————————————————————

C_BSO_KMeansクラスは、BSO最適化アルゴリズムでエージェントをクラスタリングするためのK-Meansアルゴリズムの実装です。各メソッドが何をするのかを説明しましょう。

  1. KMeansInit：メソッドは、データからランダムなエージェントを選択してクラスタ重心を初期化します。各クラスタについて、ランダムなエージェントが選択され、その座標がクラスタの重心にコピーされます。
  2. VectorDistance：このメソッドは、2つのベクトル間のユークリッド距離を計算します。2つのベクトルを引数にとり、そのユークリッド距離を返します。
  3. KMeans：このメソッドは、データクラスタリングのためのK-Meansアルゴリズムの基本ロジックを実装しています。引数としてデータとクラスタ配列を取ります。
K-Meansは、操作中に以下のステップを実行します。
  • データ点を最も近い重心に割り当てます。
  • 各クラスタに割り当てられた点の平均に基づいて重心を更新します。
  • 重心が変化しなくなるか、最大反復回数に達するまで、これら2つのステップを繰り返します。

K平均クラスタリング法における重心とは、クラスタの中心を指します。K-Meansの文脈では、重心は与えられたクラスタに属するすべてのデータ点の算術平均です。
K-Meansアルゴリズムの各反復では、重心が再計算され、その後、データポイントは、選択されたメトリックに従って、新しい重心のどちらが近いかに従って、再びクラスタにグループ化されます。
このように、重心はK-Meansにおいて重要な役割を果たし、クラスタの形と位置を決定します。

このクラスはBSO最適化アルゴリズムの重要な部分であり、探索プロセスを改善するためにエージェントのクラスタリングを提供します。K-Meansアルゴリズムは、変化がなくなるか、反復の最大回数に達するまで、ポイントを繰り返しクラスタに割り当て、重心を再計算します。

//——————————————————————————————————————————————————————————————————————————————
class C_BSO_KMeans
{
  public: //--------------------------------------------------------------------

  void KMeansInit (S_BSO_Agent &data [], int dataSizeClust, S_Clusters &clust [])
  {
    for (int i = 0; i < ArraySize (clust); i++)
    {
      int ind = MathRand () % dataSizeClust;
      ArrayCopy (clust [i].centroid, data [ind].c, 0, 0, WHOLE_ARRAY);
    }
  }

  double VectorDistance (double &v1 [], double &v2 [])
  {
    double distance = 0.0;
    for (int i = 0; i < ArraySize (v1); i++)
    {
      distance += (v1 [i] - v2 [i]) * (v1 [i] - v2 [i]);
    }
    return MathSqrt (distance);
  }

  void KMeans (S_BSO_Agent &data [], int dataSizeClust, S_Clusters &clust [])
  {
    bool changed   = true;
    int  nClusters = ArraySize (clust);
    int  cnt       = 0;

    while (changed && cnt < 100)
    {
      cnt++;
      changed = false;

      //Assigning data points to the nearest centroid
      for (int d = 0; d < dataSizeClust; d++)
      {
        int    closest_centroid = -1;
        double closest_distance = DBL_MAX;

        if (data [d].f != -DBL_MAX)
        {
          for (int cl = 0; cl < nClusters; cl++)
          {
            double distance = VectorDistance (data [d].c, clust [cl].centroid);

            if (distance < closest_distance)
            {
              closest_distance = distance;
              closest_centroid = cl;
            }
          }

          if (data [d].label != closest_centroid)
          {
            data [d].label = closest_centroid;
            changed = true;
          }
        }
        else
        {
          data [d].label = -1;
        }
      }


      //Updating centroids
      double sum_c [];
      ArrayResize (sum_c, ArraySize (data [0].c));

      for (int cl = 0; cl < nClusters; cl++)
      {
        ArrayInitialize (sum_c, 0.0);

        clust [cl].count = 0;
        ArrayResize (clust [cl].ideasList, 0);

        for (int d = 0; d < dataSizeClust; d++)
        {
          if (data [d].label == cl)
          {
            for (int k = 0; k < ArraySize (data [d].c); k++)
            {
              sum_c [k] += data [d].c [k];
            }

            clust [cl].count++;
            ArrayResize (clust [cl].ideasList, clust [cl].count);
            clust [cl].ideasList [clust [cl].count - 1] = d;
          }
        }

        if (clust [cl].count > 0)
        {
          for (int k = 0; k < ArraySize (sum_c); k++)
          {
            clust [cl].centroid [k] = sum_c [k] / clust [cl].count;
          }
        }
      }
    }
  }
};
//——————————————————————————————————————————————————————————————————————————————

ブレインストーム最適化(BSO)アルゴリズムでは、個体の適応度はその個体が表す解の品質として定義されます。最適化問題では、適応度は最適化される関数の値に等しくなります。

具体的なクラスタリング方法は異なるかもしれません。一般的なアプローチの1つはK-Meansを使うことで、クラスタ重心はランダムに初期化され、各点からそのクラスタ重心までの距離の二乗和を最小化するように繰り返し更新されます。

適応度はクラスタリングにおいて重要な役割を果たしますが、クラスタ形成に影響を与える要因はそれだけではありません。意思決定空間における個体間の距離など、他の側面も重要な役割を果たすかもしれません。これはアルゴリズムが母集団の多様性を維持し、不適切な解への早期収束を防ぐのに役立ちます。

K-Meansアルゴリズムが収束するのに必要な反復回数は、重心の初期状態、データの分布、クラスタ数など様々な要因に大きく依存します。しかし一般的に、K-Meansは通常数十から数百回の反復で収束します。

また、K-Meansは点から最も近い重心までの距離の二乗和を最小化しますが、これは特定のタスクやデータ内のクラスタの形状によっては必ずしも最適とは限らないことも考慮する価値があります。場合によっては、他のクラスタリングアルゴリズムの方が適切なこともあります。

K-Means++は、2007年にDavid ArthurとSergei Vassilvitskiiによって提案されたK-Meansアルゴリズムの改良版です。K-Means++と標準的なK-Meansの主な違いは、重心の初期化方法です。K-Means++は、初期重心をランダムに選択する代わりに、重心間の距離を最大化するように選択します。これはクラスタリングの質を向上させ、アルゴリズムの収束を早めるのに役立ちます。

以下はK-Means++の主な初期化ステップです。

  1. データ点から最初の重心をランダムに選択します。
  2. 各データ点について、最も近い、以前に選択した重心までの距離を計算します。
  3. ある点を重心として選択する確率が、最も近い、以前に選択された重心からの距離に正比例するように、データ点から次の重心を選択する（つまり、最も近い重心への距離が最大である点が、次の重心として選択される可能性が最も高い）。
  4. k個の重心が選択されるまで、ステップ2と3を繰り返します。

重心を初期化した後、K-Means++は標準的なものと同じように動作を続ける。この初期化方法はクラスタリングの質を向上させ、アルゴリズムの収束を早めるのに役立ちます。しかし、この方法は計算コストが高い。

各点の座標が1000個ある場合、K-Means++アルゴリズムは高次元空間での距離を計算しなければならないため、計算オーバーヘッドが増えることになります。しかし、K-Means++の方が収束が速く、クラスタ品質が良いことが多いので、K-Means++が有効である可能性がある（この仮定を確認するためには実験が必要である）。

高次元のデータ（1000座標など）を扱う場合、「次元の呪い」に関連する新たな問題が生じる可能性があります。このため、点間の距離が意味を持たなくなり、クラスタリングが困難になることがあります。このような場合、K-MeansやK-Means++を適用する前に、PCA（主成分分析）のような次元削減法を使用することが有効な場合があります。これはデータの次元を減らし、クラスタリングをより効率的にするのに役立ちます。

データの次元削減は、特に多数の座標や特徴を扱う場合、データ処理における重要なステップです。これにより、データを簡素化し、計算コストを削減し、クラスタリングアルゴリズムの性能を向上させることができます。ここでは、クラスタリングでよく使われる次元削減法をいくつか紹介します。

  1. 主成分分析（PCA）。この方法は、多くの変数を持つデータセットを、最大限の情報を保持しながら、より少ない変数を持つデータセットに変換します。
  2. 多次元尺度構成法（MDS）。この方法は、元の高次元空間と同様に点間の距離を保持する低次元構造を見つけようとするものです。
  3. t-分散確率的近傍埋め込み(t-SNE)。これは非線形次元削減法で、特に高次元データの可視化に適しています。
  4. オートエンコーダ。これは、データの次元を減らすために使用されるニューラルネットワークです。入力データをコンパクトな表現にエンコードすることを学習し、その表現をデコードして元のデータに戻すことで機能します。
  5. 独立成分分析（ICA）。これは、データセットを元のデータよりも情報量の多い独立成分に変換する統計的手法です。コンポーネントは、データの構造や重要な側面をよりよく反映することができます。例えば、隠れた要素を可視化したり、分類問題でクラスをよりよく分離したりすることができます。
  6. 線形判別分析（LDA）。この方法は、2つ以上のクラスをうまく分離する特徴の線形結合を見つけるために使用されます。

そのため、K-Means++は、特に高次元データの場合、初期化ステップで計算量が多くなるかもしれないが、それでも場合によっては価値があるかもしれません。しかし、あなたの特定の問題やデータセットに何が最適かを判断するために、さまざまなアプローチを試して比較する価値は常にあります。

K-Means++法をさらに試してみたい方のために、このアルゴリズムの初期化法を以下に示します（残りのコードは従来のK-Meansコードと変わらない）。

以下のコードは、K-Means++アルゴリズムの初期化を実装したものです。この関数は、S_BSO_Agent構造体で表現されるデータポイントの配列、データサイズ（dataSizeClust）、およびS_Cluster構造体で表現されるクラスタの配列を受け取ります。この方法では、最初の重心をデータ点からランダムに初期化します。次に、後続の各重心について、アルゴリズムは各データ点から最も近い重心までの距離を計算し、距離に比例する確率で次の重心を選択します。これは、0と全距離の合計の間の乱数rを生成し、すべてのデータポイントをループし、"rが現在のポイントの距離以下になるまで、各ポイントの距離によってrを減少させることによっておこなわれます。この場合、現在の点が次の重心として選ばれます。このプロセスは、すべての重心が初期化されるまで繰り返されます。

全体として、K-Means++初期化が実装されており、これは標準K-Meansアルゴリズムの初期化の改良版です。重心は、重心とデータ点間の潜在的な二乗距離の和を最小化するように選択され、より効率的で安定したクラスタリングにつながります。

void KMeansPlusPlusInit (S_BSO_Agent &data [], int dataSizeClust, S_Cluster &clust [])
{
  // Choose the first centroid randomly
  int ind = MathRand () % dataSizeClust;
  ArrayCopy (clust [0].centroid, data [ind].c, 0, 0, WHOLE_ARRAY);

  for (int i = 1; i < ArraySize (clust); i++)
  {
    double sum = 0;
      
    // Compute the distance from each data point to the nearest centroid
    for (int j = 0; j < dataSizeClust; j++)
    {
      double minDist = DBL_MAX;
       
      for (int k = 0; k < i; k++)
      {
        double dist = VectorDistance (data [j].c, clust [k].centroid);
          
        if (dist < minDist)
        {
            minDist = dist;
        }
      }
        
      data [j].minDist = minDist;
      sum += minDist;
    }

    // Choose the next centroid with a probability proportional to the distance
    double r = MathRand () * sum;
      
    for (int j = 0; j < dataSizeClust; j++)
    {
      if (r <= data [j].minDist)
      {
        ArrayCopy (clust [i].centroid, data [j].c, 0, 0, WHOLE_ARRAY);
        break;
      }
      r -= data [j].minDist;
    }
  }
}


続編をお楽しみに...

この記事では、BSOアルゴリズムの論理構造、クラスタリング手法、最適化問題の次元を減らす方法を検討しました。次回は、BSOアルゴリズムの研究を完了し、そのパフォーマンスを要約します。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/14707

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
多通貨エキスパートアドバイザーの開発（第8回）：新しいバーの負荷テストと処理 多通貨エキスパートアドバイザーの開発（第8回）：新しいバーの負荷テストと処理
進歩に伴い、1つのEAでより多くの取引戦略インスタンスを同時に実行するようになりました。リソースの限界に達する前に、どのくらいのインスタンスが利用可能かを検討することが重要です。
ニューラルネットワークが簡単に（第83回）：「Conformer」Spatio-Temporal Continuous Attention Transformerアルゴリズム ニューラルネットワークが簡単に（第83回）：「Conformer」Spatio-Temporal Continuous Attention Transformerアルゴリズム
この記事では、天気予報を目的に開発されたConformerアルゴリズムについて紹介します。天気の変動性や予測の難しさは、金融市場の動きとしばしば比較されます。Conformerは、Attentionモデルと常微分方程式の利点を組み合わせた高度な手法です。
ブレインストーム最適化アルゴリズム(第2部）：マルチモーダリティ ブレインストーム最適化アルゴリズム(第2部）：マルチモーダリティ
記事の第2部では、BSOアルゴリズムの実用的な実装に移り、テスト関数のテストを実施し、BSOの効率を他の最適化手法と比較します。
リプレイシステムの開発（第45回）：Chart Tradeプロジェクト(IV) リプレイシステムの開発（第45回）：Chart Tradeプロジェクト(IV)
この記事の主な目的は、C_ChartFloatingRADクラスの紹介と説明です。Chart Trade指標は、非常に興味深い方法で機能しています。チャート上のオブジェクトの数はまだ少ないものの、期待通りの機能を実現しています。指標の値は編集可能ですが、その実現方法については疑問が残るかもしれません。この記事を読めば、これらの疑問が解消されるでしょう。