Redes neuronales: así de sencillo (Parte 85): Predicción multidimensional de series temporales

Introducción

La previsión de series temporales es, de una forma u otra, uno de los elementos más importantes para construir una estrategia de negociación eficaz. Al fin y al cabo, cuando realizamos una transacción comercial en una u otra dirección, partimos de nuestra propia visión (previsión) del próximo movimiento del precio. Avances recientes en modelos de aprendizaje profundo, especialmente modelos basados en arquitecturas del Transformer, han demostrado un progreso significativo en este ámbito y ofrecen un gran potencial para resolver problemas multifacéticos relacionados con la previsión de series temporales a largo plazo.

Sin embargo, se nos plantea la cuestión de la eficacia del uso de la arquitectura del Transformer para la previsión de series temporales. La mayoría de los modelos basados en el Transformer que hemos considerado anteriormente utilizaban el mecanismo de Self-Attention para captar las dependencias a largo plazo de los distintos pasos temporales de la secuencia analizada. No obstante, algunos trabajos sostienen que la mayoría de los modelos de Transformer existentes basados en la atención intertemporal no exploran adecuadamente las dependencias intertemporales. Y, a veces, el modelo lineal simple supera a algunos de ellos.

Los autores abordaron de forma constructiva esta cuestión en el artículo Self-Attention "Client: Cross-variable Linear Integrated Enhanced Transformer for Multivariate Long-Term Time Series Forecasting". Para evaluar la magnitud del problema, realizaron un experimento exhaustivo con una serie de enmascaramientos de parte de la serie histórica, sustituyendo de forma aleatoria datos individuales por "0". Los modelos más sensibles a la dependencia temporal mostraron una gran degradación de su rendimiento en ausencia de datos históricos correctos. Así, la disminución del rendimiento supone un indicador de la capacidad del modelo para mostrar patrones temporales. Como resultado del experimento, se observó que el rendimiento de los modelos de Transformer basados en la atención cruzada no se degrada significativamente a medida que aumenta la escala del enmascaramiento de datos. Para algunos de estos modelos, el rendimiento de predicción permanece esencialmente inalterado incluso sustituyendo el 80% de los datos históricos por "0" de forma aleatoria. Esto puede indicar que los resultados de las previsiones de dichos modelos no son sensibles a los cambios en las series temporales analizadas.

Mi opinión personal respecto a los resultados del análisis presentado no es inequívoca. Obviamente, la falta de sensibilidad del modelo a los cambios en las series temporales analizadas es, por decirlo suavemente, alarmante. Y, considerando que analizamos el modelo como una "caja negra", resulta difícil saber qué parte de los datos tiene en cuenta el modelo y qué parte ignora.

Por otra parte, en condiciones de estocasticidad de los mercados financieros, las series temporales analizadas contienen bastante ruido, que naturalmente debe filtrarse. En tal contexto, ignorar las fluctuaciones insignificantes o los valores atípicos que no son propios del entorno considerado nos ayudará a identificar la parte más significativa de la serie temporal analizada.

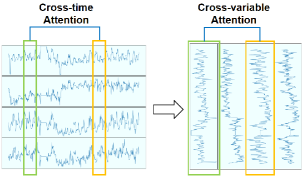
Además, los autores del artículo observaron que, en algunas series temporales multidimensionales, distintas variables muestran patrones relacionados a lo largo del tiempo. Esto sugiere que los mecanismos de atención pueden usarse para analizar dependencias entre variables en lugar de entre pasos temporales. Esta suposición nos permitirá cambiar la dirección del mecanismo de Self-Attention.

Aunque el Transformer propuesto por los autores del articulo modela bien la no linealidad y capta las dependencias entre variables, podría no funcionar bien a la hora de extraer las tendencias de las series analizadas. Sin embargo, los modelos lineales son perfectamente capaces de llevar a cabo esa tarea. Con el objetivo de combinar lo mejor de ambos mundos, los autores del artículo proponen un método de Transformer mejorado linealmente integrado con análisis de variables cruzadas para el pronóstico multidimensional de series de tiempo a largo plazo (Cross-variable Linear Integrated Enhanced Transformer — Client). El algoritmo propuesto combina la capacidad de los modelos lineales para extraer tendencias con la potencia expresiva del Transformer ampliado.

1. Algoritmo Client

La idea principal de Client consiste en pasar de centrarse en el tiempo a analizar las dependencias entre variables e integrar un módulo lineal en el modelo para aprovechar mejor las dependencias de las variables y la información sobre tendencias, respectivamente.

Los autores del método Client abordan de forma creativa la tarea de previsión de series temporales. Por un lado, en el algoritmo propuesto nos encontramos con planteamientos que ya nos son familiares. Por otro lado, rechaza métodos aparentemente establecidos. Al mismo tiempo, la inclusión o exclusión de cada bloque individual en el algoritmo irá acompañada de una serie de pruebas que demostrarán la idoneidad de la decisión tomada en cuanto al rendimiento del modelo.

Para resolver el problema del desplazamiento de distribución, los autores del método usan la normalización reversible con estructura simétrica (RevIN), que presentamos en el artículo anterior. Se usa para eliminar primero la información estadística de las series temporales de los datos de origen. Y tras el procesamiento por parte del modelo y la obtención de valores de previsión, se restaura en ellos la información estadística de las series temporales iniciales, lo que en general permite aumentar la estabilidad del entrenamiento del modelo y la calidad de los valores de previsión de las series temporales.

Para permitir un análisis más profundo de variables y no de pasos temporales, los autores del método sugieren transponer los datos de origen.

Los datos así preparados se introducen en el Codificador Transformer, que consta de varias capas de Self-Attention (MHA) multicabeza y bloques FeedForward (FFN).

Aquí debemos señalar que los datos de origen se introducen en la entrada del codificador sin pasar por la ya conocida capa de incorporación. Las pruebas realizadas por los autores del método demuestran que no es eficaz porque el nivel adicional de transformación de los datos distorsiona la información temporal y provoca una disminución del rendimiento del modelo. Además, se ha eliminado el bloque de codificación de posiciones porque no existe secuencia temporal entre las distintas variables.

Tras extraer las características en el Codificador, la secuencia temporal pasa a la capa de proyección, que genera valores predichos para cada variable.

La capa de proyección propuesta sustituye al descodificador del Transformer clásico. En su artículo, los autores de Client descubrieron que la adición del Decodificador provoca una disminución del rendimiento global del modelo.

Paralelamente al bloque de atención, se integra un módulo lineal en el modelo Client, que se utiliza para examinar la información sobre las tendencias de las series temporales de canales independientes de variables individuales.

Los valores predichos del bloque de atención y del módulo lineal se suman con pesos entrenados aplicados a los resultados del módulo lineal.

A la salida del modelo, los resultados se transponen de nuevo para ajustarlos a la secuencia de los datos de origen. Y luego se recupera la información estadística de la serie temporal.

Así, el método Client utiliza un módulo lineal para recopilar información sobre las tendencias y un módulo Transformer ampliado para recopilar información no lineal y dependencias entre variables. A continuación le presentamos la visualización del método por parte del autor.

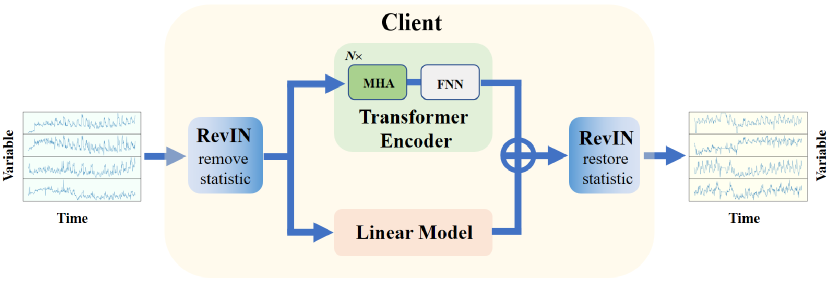
2. Implementación con MQL5

Tras repasar los aspectos teóricos del método Client, pasaremos a la parte práctica de nuestro artículo, donde implementaremos nuestra visión de los enfoques propuestos utilizando herramientas MQL5.

2.1 Creando una nueva capa neuronal

En primer lugar, crearemos una nueva clase CNeuronClientOCL que combinará la mayoría de los enfoques propuestos. Esta clase, como la mayoría de las clases creadas anteriormente, la crearemos heredando de nuestra clase básica de la capa neuronal CNeuronBaseOCL.

class CNeuronClientOCL  :  public CNeuronBaseOCL
  {
protected:
   //--- Attention
   CNeuronMLMHAttentionOCL cTransformerEncoder;
   CNeuronConvOCL    cProjection;
   //--- Linear model
   CNeuronConvOCL    cLinearModel[];
   //---
   CNeuronBaseOCL    cInput;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);

public:
                     CNeuronClientOCL(void) {};
                    ~CNeuronClientOCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint heads,
                          uint at_layers, uint count, uint &mlp[],
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronClientOCL;   }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual void      SetOpenCL(COpenCLMy *obj);
   virtual void      TrainMode(bool flag);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
  };

Crearemos un bloque de atención partiendo de 2 objetos:

• cTransformerEncoder, un objeto de la clase CNeuronMLMHAttentionOCL que permite crear un bloque de Codificador de Transformer multicabeza a partir de un número determinado de capas consecutivas;
• cProjection, una capa de proyección. Aquí utilizaremos la capa de convolución para crear previsiones independientes para variables individuales, mientras que la profundidad de predicción determinará el número de filtros de la capa.

Para crear un módulo lineal, crearemos un array dinámico de capas de convolución cLinearModel[], que nos permitirá generar predicciones independientes sobre variables individuales.

Nótese que en esta implementación hemos decidido sacar de la clase las capas de normalización reversible y transposición de datos. Esto se debe a que el bloque Client puede integrarse en una arquitectura más compleja. Como consecuencia, el borrado y la recuperación de la información estadística podrán realizarse lejos de este bloque.

Sin embargo, la transposición de datos también podrá realizarse fuera del bloque Client. Además, en algunos casos, será posible crear la secuencia necesaria de datos de entrada en la fase de preparación.

El conjunto de métodos de nuestra nueva clase es bastante estándar y nada original.

Primero declararemos como estáticos todos los objetos internos, lo cual nos permitirá dejar vacíos el constructor y el destructor de la clase. Este enfoque nos permitirá poner menos énfasis en los problemas de limpieza de memoria, trasladando esta funcionalidad al sistema.

La inicialización de todos los objetos internos se realizará en el método Init. En los parámetros de este método transmitiremos al objeto de clase toda la información necesaria para organizar la arquitectura requerida.

Y aquí deberemos prestar atención al hecho de que en el cuerpo de la clase se crearán 2 hilos paralelos:

• El bloque de Transformer;
• El módulo lineal.

Ambos módulos tendrán arquitecturas independientes complejas y muy diferentes, aunque trabajarán con el mismo conjunto de datos. Por lo tanto, necesitaremos un mecanismo para transmitir la arquitectura de ambos módulos al objeto. Para el bloque Transformer, utilizaremos el planteamiento de 5 variables elaborado anteriormente:

• window - tamaño del vector 1 del elemento de la secuencia;
• window_key - tamaño del vector de representación interna de 1 elemento de la secuencia;
• heads - número de cabezas de atención;
• count - número de elementos de la secuencia;
• at_layers - número de capas del bloque del Codificador.

Para describir la arquitectura del módulo lineal, utilizaremos el array numérico mlp[]. El número de elementos del array indicará el número de capas que se crearán, mientras que el valor de cada elemento indicará el tamaño del vector de descripción de un elemento de la secuencia a la salida de la capa. El módulo lineal trabajará con la misma secuencia de datos que la unidad de atención. Por ello tanto, el número de elementos de la secuencia se utilizará igual.

Aquí deberemos prestar atención al hecho de que los autores del método Client proponen analizar las dependencias entre variables. Por consiguiente, en este caso, el tamaño del vector de descripción del primer elemento de la secuencia será igual a la profundidad de la historia analizada, mientras que el número de elementos de la secuencia será igual al número de variables analizadas. Y los datos de origen deberán transponerse de la forma correspondiente antes de introducirlos en la entrada del objeto de nuestra nueva clase CNeuronClientOCL.

Con este enfoque, especificaremos la profundidad de la predicción de los datos en el último elemento del array mlp[].

Una vez definida la lógica de transferencia de datos, implementaremos el enfoque propuesto en el código. En los parámetros del método Init, especificaremos las variables anteriormente presentadas y las complementaremos con elementos de la clase básica.

bool CNeuronClientOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                            uint window, uint window_key, uint heads,
                            uint at_layers, uint count, uint &mlp[],
                            ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   uint mlp_layers = mlp.Size();
   if(mlp_layers == 0)
      return false;

En el cuerpo del método, primero comprobaremos el tamaño del array de descripción de la arquitectura del módulo lineal mlp[]. Deberá contener al menos un elemento que indique la profundidad de la predicción de los datos. Si el array está vacía, el método finalizará con el resultado false.

El siguiente paso consistirá en inicializar los objetos de clase. En primer lugar, modificaremos el array dinámico del módulo lineal.

   if(ArrayResize(cLinearModel, mlp_layers + 1) != (mlp_layers + 1))
      return false;

Tenga en cuenta que el tamaño del array deberá ser 1 elemento mayor que la arquitectura de capa de línea resultante. Hablaremos de las razones de este movimiento un poco más adelante.

A continuación, llamaremos al método homónimo de la clase padre, que inicializará todos los objetos heredados.

   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, mlp[mlp_layers - 1] * count, optimization_type, batch))
      return false;

Luego llamaremos al método de inicialización del Codificador Transformer.

   if(!cTransformerEncoder.Init(0, 0, OpenCL, window, window_key, heads, count, at_layers, optimization, iBatch))
      return false;

Y una capa auxiliar de almacenamiento temporal de datos de origen.

   if(!cInput.Init(0, 1, open_cl, window * count, optimization_type, batch))
      return false;

Después crearemos un ciclo en el que inicializaremos las capas del módulo lineal.

   uint w = window;
   for(uint i = 0; i < mlp_layers; i++)
     {
      if(!cLinearModel[i].Init(0, i + 2, OpenCL, w, w, mlp[i], count, optimization, iBatch))
         return false;
      cLinearModel[i].SetActivationFunction(LReLU);
      w = mlp[i];
     }

Aquí debemos recordar que los autores del método Client proponen aplicar coeficientes entrenables a los resultados del módulo lineal. Y tenemos que decir que hallaron un método poco ortodoxo de crear multiplicadores entrenables. Así que hemos decidido sustituirlos por una capa de convolución con un número de filtros, un tamaño de ventana y un paso de convolución iguales a "1". Lo añadiremos al último elemento (el que hemos agregado antes) del array del módulo lineal.

   if(!cLinearModel[mlp_layers].Init(0, mlp_layers + 2, OpenCL, 1, 1, 1, w * count, optimization, iBatch))
      return false;

Una cosa más: Durante la normalización de los datos de origen, los llevaremos a una media de "0" y una varianza de "1". Por consiguiente, los valores previstos también deberían seguir esta distribución. Usaremos la tangente hiperbólica (tanh) como función de activación para restringir los valores predichos.

Del mismo modo, iniciaremos también la capa de proyección del bloque de atención.

   cLinearModel[mlp_layers].SetActivationFunction(TANH);
   if(!cProjection.Init(0, mlp_layers + 3, OpenCL, window, window, w, count, optimization, iBatch))
      return false;
   cProjection.SetActivationFunction(TANH);

Como podemos ver, ambos bloques de predicción de datos de salida se activan mediante una tangente hiperbólica. Para que la transferencia del gradiente de error sea correcta, especificaremos una función de activación similar para toda la capa.

   SetActivationFunction(TANH);

Como además tenemos previsto sumar simplemente los valores de los 2 módulos, podemos distribuir todo el gradiente de error a ambos módulos en la pasada inversa. Para eliminar operaciones innecesarias de copiado de datos, implementaremos el intercambio de los búferes de datos de almacenamiento del gradiente de error en las capas internas.

   if(!SetGradient(cProjection.getGradient()))
      return false;
   if(!cLinearModel[mlp_layers].SetGradient(Gradient))
      return false;
//---
   return true;
  }

Al mismo tiempo, no nos olvidaremos de controlar el proceso de las operaciones en cada fase. Y tras inicializar con éxito todos los objetos anidados, retornaremos el resultado lógico de las operaciones al programa que realiza la llamada.

Después de inicializar los objetos de clase anidados, procederemos a organizar el algoritmo de pasada directa en el método CNeuronClientOCL::feedForward. Ya hemos hablado de los principios básicos de la transferencia de datos al inicializar objetos. Veamos ahora la aplicación de los planteamientos propuestos.

En los parámetros, el método obtendrá un puntero al objeto de la capa neuronal precedente. Y en el cuerpo del método, llamaremos directamente al método de pasada directa de nuestro bloque de atención por capas.

bool CNeuronClientOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cTransformerEncoder.FeedForward(NeuronOCL))
      return false;

A continuación, realizaremos una proyección de los valores pronosticados a la profundidad de planificación requerida.

   if(!cProjection.FeedForward(GetPointer(cTransformerEncoder)))
      return false;

Para evitar copiar la cantidad de datos de origen al completo en la capa interna, solo copiaremos el puntero al búfer de datos correspondiente.

   if(cInput.getOutputIndex() != NeuronOCL.getOutputIndex())
      cInput.getOutput().BufferSet(NeuronOCL.getOutputIndex());

Y organizaremos el ciclo de pasada directa del módulo lineal.

   uint total = cLinearModel.Size();
   CNeuronBaseOCL *neuron = NeuronOCL;
   for(uint i = 0; i < total; i++)
     {
      if(!cLinearModel[i].FeedForward(neuron))
         return false;
      neuron = GetPointer(cLinearModel[i]);
     }

En esta fase, dispondremos de proyecciones de los valores previstos de ambos módulos. En este caso, las predicciones del módulo lineal ya han sido ajustadas según los coeficientes de entrenamiento. Solo tendremos que sumar los datos de ambos hilos.

   if(!SumAndNormilize(neuron.getOutput(), cProjection.getOutput(), Output, 1, false, 0, 0, 0, 
0.5 ))
      return false;
//---
   return true;
  }

Del mismo modo, pero en orden inverso, la distribución del gradiente de error a través de los objetos anidados hasta la capa precedente se organizará según su influencia en el resultado final. Podemos observar esto en el método CNeuronClientOCL::calcInputGradients.

Recuerde que al intercambiar los búferes de datos, el gradiente de error de la capa siguiente se escribirá directamente en las búferes de objetos de ambos módulos. Por lo tanto, omitiremos la operación innecesaria de distribuir el gradiente de error entre el Transformer y el módulo lineal. Y pasaremos directamente a la distribución del gradiente de error en los módulos especificados. Primero bajaremos el gradiente de error a través del bloque de atención.

bool CNeuronClientOCL::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(!cTransformerEncoder.calcHiddenGradients(cProjection.AsObject()))
      return false;
   if(!prevLayer.calcHiddenGradients(cTransformerEncoder.AsObject()))
      return false;

Y luego en un ciclo inverso a través del módulo lineal.

   CNeuronBaseOCL *neuron = NULL;
   int total = (int)cLinearModel.Size() - 1;
   for(int i = total; i >= 0; i--)
     {
      neuron = (i > 0 ? cLinearModel[i - 1] : cInput).AsObject();
      if(!neuron.calcHiddenGradients(cLinearModel[i].AsObject()))
         return false;
     }

Observe que el Transformer escribe el gradiente de error en el búfer de la capa anterior. Y el modelo lineal, en el búfer de la capa interior.

Antes de que el método finalice, sumaremos los gradientes de error de ambos hilos.

   if(!SumAndNormilize(neuron.getGradient(), prevLayer.getGradient(), prevLayer.getGradient(), 1, false))
      return false;
//---
   return true;
  }

Los otros métodos de esta clase se construirán según el mismo esquema. Nos limitaremos a llamar uno a uno los métodos de los objetos internos homónimos. Pero en el marco de este artículo no nos detendremos en la descripción de su algoritmo. Le propongo familiarizarse con ellos por sí mismo. Encontrará el código completo de la clase y todos sus métodos en el archivo adjunto. Allí también verá el código completo de todos los programas utilizados en la elaboración del artículo.

2.2 Arquitectura del modelo

Más arriba hemos creado una nueva clase CNeuronClientOCL que implementa la mayoría de los enfoques propuestos por los autores del método Client. Sin embargo, hemos dejado que algunos de los requisitos del método se implementen directamente en la arquitectura del modelo.

Hemos propuesto el método Client para resolver problemas de previsión de series temporales. Y ahora vamos a usarlo en nuestro Codificador.

Aquí deberemos entender que en la estructura de nuestros modelos, el codificador se utiliza para preparar una representación concisa del estado del entorno. El modelo del Actor utilizará esta representación para generar una acción óptima en un estado individual basada en la política de comportamiento entrenada. Obviamente, para aprender las mejores políticas de comportamiento, necesitaremos una representación concisa, correcta e informativa del estado del entorno.

El concepto "representación concisa, correcta e informativa del estado del entorno" suena bastante abstracto y vago. Y resulta lógico suponer que, como estamos entrenando la política del Actor para que realice acciones óptimas que generen el máximo beneficio posible en las condiciones del movimiento de precios próximo más probable, la representación comprimida deberá contener la máxima información posible sobre el movimiento de precios próximo más probable. Además, deberemos evaluar los riesgos y la probabilidad de que el precio se mueva en sentido contrario, así como la posible magnitud de dicho movimiento. En un paradigma así, parece apropiado entrenar al Codificador para que prediga los movimientos futuros de los precios. Y entonces el estado oculto del Codificador contendrá la máxima información posible sobre el próximo movimiento de precios. Por ello, en la arquitectura de nuestro Codificador utilizaremos enfoques basados en el método Client.

La arquitectura del Codificador se presenta en el método CreateEncoderDescriptions. En los parámetros, el método recibirá el puntero a un array dinámico único en el que se almacenará la arquitectura del modelo.

bool CreateEncoderDescriptions(CArrayObj *encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }

En el cuerpo del método comprobaremos el puntero recibido y, si es necesario, crearemos una nueva instancia del objeto de array dinámico.

Como de costumbre, suministraremos a la entrada del modelo una descripción "bruta" del estado del entorno. Para registrar los datos de origen, crearemos una capa básica de red neuronal con un tamaño lo suficientemente grande como para aceptar los datos de origen.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Aquí, al igual que antes, el tamaño de la capa vendrá determinado por el producto de 2 constantes:

• HistoryBars - profundidad de la historia analizada de los estados del entorno (barras);
• BarDescr - tamaño del vector de descripción de una barra de estado del entorno.

No obstante, deberemos considerar un pequeño detalle: Antes, en cada iteración suministrábamos a la entrada del modelo información sobre solo 1 última barra cerrada del movimiento del precio. Y toda la profundidad necesaria de la historia analizada se acumulaba como Incorporaciones en la pila de la capa interna de nuestro modelo. Ahora bien, los autores del método Client afirman que la capa adicional de incorporación distorsiona la información de la serie temporal y recomiendan eliminarla. Como consecuencia, ampliaremos la capa de datos de origen del modelo para pasar a ella toda la profundidad de la historia analizada.

Debemos decir que hemos aumentado el valor de la constante HistoryBars a 120. Estos nos permitirá analizar los datos históricos de la última semana en el marco temporal H1.

#define        HistoryBars             120           //Depth of history

A continuación, al igual que antes, estableceremos una capa de normalización por lotes en la que los datos de origen se llevarán a una forma comparable eliminando de ellos la información estadística de las series temporales.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1000;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Asimismo, recordaremos el identificador de esta capa. Al fin y al cabo, en la salida del modelo tendremos que retornar la información estadística de la serie temporal a los valores predichos.

Al preparar los datos de origen, podremos entrenarlos como una secuencia de datos de indicadores individuales (variables en el contexto del método Client). O como una secuencia de descripciones de pasos temporales (barras), como se ha hecho antes. En el marco de este trabajo hemos decidido no modificar el bloque de preparación inicial de los datos. Esto nos permitirá utilizar asesores expertos de interacción con el entorno creados previamente con modificaciones mínimas.

Pero una implementación de este tipo requerirá una capa de transposición de datos, que añadiremos en el siguiente paso.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   prev_count = descr.count = HistoryBars;
   int prev_wout = descr.window = BarDescr;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Y tras la capa de transposición, añadiremos una instancia de nuestra nueva capa, el bloque Client.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronClientOCL;
   descr.count = prev_wout;
   descr.window = prev_count;
   descr.step = 4;
   descr.window_out = EmbeddingSize;
   descr.layers = 5;
     {
      int temp[] = {1024, 1024, 1024, NForecast};
      ArrayCopy(descr.windows, temp);
     }
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Aquí especificaremos el número de variables analizadas (constante BarDescr) como el tamaño de la secuencia analizada. El tamaño del vector de descripción de un elemento de la secuencia será igual a la profundidad de la historia analizada (constante HistoryBars). En el bloque del Transformer, utilizaremos 4 cabezas de atención y crearemos 5 capas de este tipo.

Asimismo, crearemos un módulo lineal de 4 capas: 3 capas ocultas con un tamaño igual a 1024, y una última capa igual al horizonte de planificación (constante NForecast).

A continuación, realizaremos una transposición inversa de los datos.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   prev_count = descr.count = BarDescr;
   prev_wout = descr.window = NForecast;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Y reconstruiremos la información estadística que contienen.

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   prev_count = descr.count = prev_count * prev_wout;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers = 1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

También debemos decir unas palabras sobre la arquitectura del Actor. Está tomada casi íntegramente del artículo anterior. Pero incluso aquí hay un matiz a considerar, del que hablaremos un poco más adelante. 

La arquitectura de los modelos del Actor y el Crítico se presenta en el método CreateDescriptions. En los parámetros del método, obtendremos los punteros a 2 arrays dinámicos para registrar la arquitectura de los modelos.

bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic)
  {
//---
   CLayerDescription *descr;
//---
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!critic)
     {
      critic = new CArrayObj();
      if(!critic)
         return false;
     }

En el cuerpo del método comprobaremos los punteros obtenidos y, de ser necesario, crearemos nuevos ejemplares de objetos de arrays dinámicos.

Como antes, introduciremos la descripción del estado actual de la cuenta y las posiciones abiertas en el modelo del Actor.

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = AccountDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

A continuación, formaremos una incorporación del estado de la cuenta.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = EmbeddingSize;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Y añadiremos 3 capas consecutivas de atención cruzada, en las que analizaremos las dependencias entre el estado actual de la cuenta y la representación comprimida de futuros estados del entorno generada por el Codificador.

//--- layer 2-4
   for(int i = 0; i < 3; i++)
     {
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronCrossAttenOCL;
        {
         int temp[] = {1, BarDescr};
         ArrayCopy(descr.units, temp);
        }
        {
         int temp[] = {EmbeddingSize, NForecast};
         ArrayCopy(descr.windows, temp);
        }
      descr.window_out = 16;
      descr.step = 4;
      descr.activation = None;
      descr.optimization = ADAM;
      if(!actor.Add(descr))
        {
         delete descr;
         return false;
        }
     }

Aquí debemos señalar que, siguiendo el espíritu del método Client, para el análisis cruzado hemos tomado los datos del estado oculto del Codificador antes de transponer nuevamente los datos, lo cual nos permitirá analizar las dependencias del estado actual de la cuenta con los valores previstos de las variables individuales. Esto se reflejará en el cambio de los valores de los arrays descr.units y descr.windows.

A continuación, al igual que antes, vendrá el bloque de decisión con la estocasticidad añadida de la política del Actor.

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 2 * NActions;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronVAEOCL;
   descr.count = NActions;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Hemos introducido cambios similares en el modelo del Crítico. Como recordará, los modelos Actor y Crítico tienen una arquitectura similar, solo que en la entrada del modelo del Crítico sustituiremos la descripción del estado de la cuenta por un vector de acciones, y en la salida del modelo, el vector de acciones se sustituirá por un vector de recompensas. Las descripciones arquitectónicas completas de todos los modelos usados figuran en el anexo. Allí también verá el código completo de todos los programas utilizados en la elaboración del artículo.

Además, cambiaremos el valor de la constante de puntero a la capa oculta del Codificador para la extracción de datos.

#define        LatentLayer             3

Los trabajos realizados para armonizar las arquitecturas de los modelos y modificar las constantes usadas nos han permitido utilizar prácticamente sin cambios los asesores de interacción con el entorno creados anteriormente. Lo único que hemos tenido que hacer es compilarlos nuevamente para adaptarlos a las constantes y la arquitectura del modelo modificadas. Sin embargo, este no es el caso de los asesores de entrenamiento de modelos.

2.3 Asesor de entrenamiento del modelo de predicción

El modelo de previsión de las condiciones del entorno se entrenará con el asesor experto "...\Experts\Client\StudyEncoder.mq5". En general, la estructura del EA se tomará de artículos anteriores, así que no nos detendremos a analizar de todos sus métodos. Consideraremos únicamente la propia etapa de entrenamiento del modelo, que se llevará a cabo en el método Train.

void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);
//---
   vector<float> result, target;
   bool Stop = false;
//---
   uint ticks = GetTickCount();

En el cuerpo del método, primero generamos un vector de probabilidades para seleccionar las trayectorias del búfer de repetición de experiencias según sus rendimientos reales. Las pasadas rentables tendrán más probabilidades de ser utilizadas en el proceso de entrenamiento. De este modo, desplazaremos el enfoque del entrenamiento hacia las trayectorias con rendimientos máximos.

Una vez realizado el trabajo preparatorio, organizaremos un ciclo de entrenamiento para el modelo. A diferencia de otros artículos recientes, aquí utilizaremos un ciclo simple en lugar de un sistema de ciclos anidados como antes. Esto es posible gracias a la renuncia a los elementos recurrentes (pila de incorporación) en la arquitectura del modelo.

   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++)
     {
      int tr = SampleTrajectory(probability);
      int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast));
      if(i <= 0)
        {
         iter--;
         continue;
        }

En el cuerpo del ciclo, muestrearemos una trayectoria desde el búfer de repetición de experiencias y el estado del entorno en ella.

Luego extraeremos la descripción del estado del entorno muestreado del búfer de reproducción de experiencias y transferiremos los valores resultantes al búfer de datos.

      bState.AssignArray(Buffer[tr].States[i].state);

Esta información bastará para hacer una pasada directa del Codificador.

      //--- State Encoder
      if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

A continuación, tendremos que preparar el vector de valores objetivo. A efectos del presente artículo, el horizonte de planificación será mucho más corto que la profundidad de la historia analizada, lo que simplificará enormemente nuestra tarea de preparar los valores objetivo. Simplemente extraeremos una descripción del estado del entorno del búfer de repetición de experiencias, con una separación respecto al horizonte de planificación. Y luego tomaremos los primeros elementos del tensor en el volumen requerido.

      //--- Collect target data
      if(!bState.AssignArray(Buffer[tr].States[i + NForecast].state))
         continue;
      if(!bState.Resize(BarDescr * NForecast))
         continue;

Sin embargo, si utilizamos un horizonte de planificación superior a la profundidad de la historia analizada, la recopilación de los valores objetivo requerirá la creación de un ciclo con iteración de los estados del búfer de reproducción de experiencias para el horizonte de planificación.

Tras entrenar el tensor de valores objetivo, realizaremos una pasada inversa del codificador con el fin de optimizar los parámetros del modelo entrenado para minimizar el error de predicción de los datos.

      if(!Encoder.backProp(GetPointer(bState), (CBufferFloat*)NULL))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Y luego solo tendremos que informar al usuario sobre el progreso del proceso de entrenamiento y pasar a la siguiente iteración del ciclo.

      if(GetTickCount() - ticks > 500)
        {
         double percent = double(iter) * 100.0 / (Iterations);
         string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Encoder", percent, 
                                                                       Encoder.getRecentAverageError());
         Comment(str);
         ticks = GetTickCount();
        }
     }

Tendremos que supervisar obligatoriamente el proceso de las operaciones en cada paso. Y una vez completadas con éxito todas las iteraciones de entrenamiento del modelo, borraremos el campo de comentarios del gráfico.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Encoder", Encoder.getRecentAverageError());
   ExpertRemove();
//---
  }

Después registraremos los resultados del entrenamiento del modelo. E iniciaremos el proceso de finalización del asesor.

2.4 Asesor para el entrenamiento de la política del Actor

También hemos hecho algunas modificaciones en el asesor de política del Actor "...\Experts\Client\Study.mq5". Al igual que en la EA anterior, nos centraremos únicamente en el método de entrenamiento del modelo.

void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);
//---
   vector<float> result, target;
   bool Stop = false;
//---
   uint ticks = GetTickCount();

En el cuerpo del método, primero generaremos un vector de probabilidades de selección de trayectorias y realizaremos otros trabajos preparatorios. En esta parte, podemos notar la repetición exacta del algoritmo del asesor experto anterior.

A continuación, organizaremos de forma similar un ciclo de entrenamiento del modelo en el que muestrearemos una trayectoria a partir del búfer de repetición de experiencias y el estado del entorno en ella.

Después cargaremos la descripción seleccionada del estado del entorno y realizaremos una pasada directa del Codificador.

      bState.AssignArray(Buffer[tr].States[i].state);
      //--- State Encoder
      if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Con esto completaremos el "copiado" del algoritmo del asesor experto anterior. Tras generar una representación comprimida del entorno, primero realizaremos la optimización de los parámetros del Crítico. Aquí, primero cargaremos las acciones del Actor realizadas mientras interactuaba con el entorno en el estado dado y realizaremos una pasada directa del Crítico.

      //--- Critic
      bActions.AssignArray(Buffer[tr].States[i].action);
      if(bActions.GetIndex() >= 0)
         bActions.BufferWrite();
      if(!Critic.feedForward((CBufferFloat*)GetPointer(bActions), 1, false, GetPointer(Encoder), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

A continuación, recuperaremos del búfer de repetición de experiencias la recompensa real del entorno recibida por las acciones del Actor dado.

      result.Assign(Buffer[tr].States[i + 1].rewards);
      target.Assign(Buffer[tr].States[i + 2].rewards);
      result = result - target * DiscFactor;
      Result.AssignArray(result);

 Y optimizaremos los parámetros del Crítico para minimizar el error de evaluación de acciones del Actor.

      Critic.TrainMode(true);
      if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Después vendrá un bloque de 2 etapas de entrenamiento de la política del Actor. Aquí, primero extraeremos la descripción del estado de la cuenta correspondiente al estado del entorno seleccionado y la transferimos al búfer de datos.

      //--- Policy
      float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0];
      float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];
      bAccount.Clear();
      bAccount.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance);
      bAccount.Add(Buffer[tr].States[i].account[1] / PrevBalance);
      bAccount.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity);
      bAccount.Add(Buffer[tr].States[i].account[2]);
      bAccount.Add(Buffer[tr].States[i].account[3]);
      bAccount.Add(Buffer[tr].States[i].account[4] / PrevBalance);
      bAccount.Add(Buffer[tr].States[i].account[5] / PrevBalance);
      bAccount.Add(Buffer[tr].States[i].account[6] / PrevBalance);

A continuación, añadiremos los armónicos de la marca temporal al búfer.

      double time = (double)Buffer[tr].States[i].account[7];
      double x = time / (double)(D'2024.01.01' - D'2023.01.01');
      bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_MN1);
      bAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_W1);
      bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_D1);
      bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      if(bAccount.GetIndex() >= 0)
         bAccount.BufferWrite();

Y luego realizaremos una pasada directa del Actor para generar el vector de acciones.

      //--- Actor
      if(!Actor.feedForward((CBufferFloat*)GetPointer(bAccount), 1, false, GetPointer(Encoder), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Como ya hemos mencionado, el entrenamiento de política del Actor se realizará en 2 etapas. Primero ajustaremos la política del Actor para mantener sus acciones dentro de la distribución de nuestra muestra de entrenamiento. Para ello, minimizaremos el error entre el vector de acciones generado por el Actor y las acciones reales del búfer de reproducción de experiencias.

      if(!Actor.backProp(GetPointer(bActions), GetPointer(Encoder), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

En la segunda etapa, ajustaremos la política del Actor según la evaluación de las acciones generadas por el Crítico. En primer lugar, realizaremos una evaluación de las acciones.

      if(!Critic.feedForward((CNet *)GetPointer(Actor), -1, (CNet*)GetPointer(Encoder), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Y entonces desactivaremos el modo de entrenamiento del Crítico y pasaremos a través de este el gradiente de desviación de la estimación de las acciones respecto a lo que es realmente posible en el estado actual.

      Critic.TrainMode(false);
      if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder), LatentLayer) ||
         !Actor.backPropGradient((CNet *)GetPointer(Encoder), LatentLayer, -1, true))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Aquí partiremos del supuesto de que la política del Actor solo debería mejorar durante el proceso de entrenamiento, y de que la recompensa recibida no debería ser peor que la que se obtiene realmente al interactuar con el entorno.

Tras actualizar los parámetros de los modelos, informaremos al usuario del progreso del proceso de entrenamiento y pasaremos a la siguiente iteración del ciclo.

      if(GetTickCount() - ticks > 500)
        {
         double percent = double(iter) * 100.0 / (Iterations);
         string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", percent, 
                                                                       Actor.getRecentAverageError());
         str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Critic", percent, 
                                                                       Critic.getRecentAverageError());
         Comment(str);
         ticks = GetTickCount();
        }
     }

Al mismo tiempo, no nos olvidaremos de controlar el proceso de las operaciones en cada paso.

Y una vez completadas con éxito todas las iteraciones del proceso de entrenamiento del modelo, borraremos el campo de comentarios del gráfico.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic", Critic.getRecentAverageError());
   ExpertRemove();
//---
  }

Luego enviaremos los resultados del entrenamiento del modelo al registro del terminal e iniciaremos la finalización del asesor experto.

El código completo de todos los programas utilizados en la elaboración del artículo figura en el anexo.

3. Simulación

En este artículo, nos hemos familiarizado con el método de previsión multidimensional de las series temporales de Client y hemos implementado nuestra visión de los enfoques propuestos usando MQL5. Ahora pasaremos a la fase final de nuestro trabajo: comprobar los resultados. En esta fase entrenaremos los modelos con datos históricos reales de EURUSD con el marco temporal H1 para 2023. Después de eso, comprobaremos los resultados del modelo entrenado en el simulador de estrategias MetaTrader 5 con los datos históricos de enero de 2024, manteniendo el instrumento y el marco temporal utilizado para el entrenamiento del modelo.

Aquí cabe señalar que si descartamos la capa de incorporación y aumentamos el número de barras de la descripción 1 de la condición del entorno, no podremos utilizar la muestra de entrenamiento del artículo anterior.  Por lo tanto, tendremos que volver a montarla. Pero como este proceso repite por entero el algoritmo descrito en el artículo anterior, no nos detendremos ahora en su descripción detallada.

Tras recoger la muestra de entrenamiento inicial, primero entrenaremos el modelo de previsión de series temporales. Y aquí hemos tenido la primera sorpresa desagradable: la calidad de las previsiones ha resultado ser bastante baja. Probablemente la gran cantidad de ruido en los datos de origen y la mayor atención del modelo a los detalles de las series temporales hayan jugado en nuestra contra.

Pero vamos a rendirnos, continuaremos el experimento. Veamos si el modelo del Actor puede adaptarse a tales predicciones. Realizaremos varias iteraciones de entrenamiento del Actor y de actualización de la muestra de entrenamiento. Pero, ¡ay! No hemos sido capaces de entrenar un modelo capaz de generar beneficios en la muestra de entrenamiento, y mucho menos en la muestra de prueba. La línea de balance tiende inexorablemente hacia abajo. Y el valor del factor de beneficio ha fluctuado en torno a 0,5.

Es probable que este resultado solo sea típico de nuestra aplicación. Pero el hecho sigue saltando a la vista. El modelo aplicado es incapaz de ofrecer la calidad deseada de previsión de series temporales en un entorno altamente estocástico.

Conclusión

En este artículo, hemos presentado un algoritmo Client bastante interesante y complejo, que combina un modelo lineal para estudiar las tendencias lineales y un modelo de Transformer con análisis de dependencia entre variables individuales para estudiar la información no lineal. Al mismo tiempo, los autores del método excluyen de su modelo la atención entre estados del entorno separados en el tiempo. El modelo de Transformer mejorado propuesto también simplifica los niveles de incorporación y codificación posicional mientras que el módulo decodificador es sustituido por una capa de proyección, lo cual, según los autores del método, mejora notablemente la eficacia de la predicción. Además, los resultados experimentales presentados en el artículo del autor demuestran que, para las tareas de previsión de series temporales, el análisis de las dependencias entre variables en el Transformer resulta más importante que el análisis de las dependencias entre estados del entorno separados por el tiempo.

Sin embargo, nuestros resultados muestran que los enfoques propuestos no resultan eficaces en condiciones de mayor estocasticidad de los mercados financieros.

Al mismo tiempo, querríamos recordarles que este artículo presenta los resultados de las pruebas de nuestra aplicación sobre los enfoques propuestos, y los resultados obtenidos solo pueden ser relevantes para una aplicación determinada. En otras condiciones, puede que se obtengan resultados exactamente opuestos.

El objetivo del presente artículo es únicamente familiarizar al lector con el método Client y mostrar una de las variantes de aplicación de los planteamientos propuestos. En ningún caso evaluamos el algoritmo propuesto por los autores, sino que solo intentamos aplicar los enfoques propuestos para resolver nuestros propios problemas.

Enlaces

Client: Cross-variable Linear Integrated Enhanced Transformer for Multivariate Long-Term Time Series Forecasting

Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de cobros de ejemplo Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	StudyEncoder.mq5	Asesor	Asesor de entrenamiento del Codificador
5	Test.mq5	Asesor	Asesor para la prueba de modelos
6	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
7	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
8	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL