Datenwissenschaft und maschinelles Lernen (Teil 20): Algorithmische Handelseinblicke, eine Gegenüberstellung von LDA und PCA in MQL5

-- Je mehr man hat, desto weniger sieht man!

Was ist die lineare Diskriminanzanalyse (LDA)?

LDA ist ein überwachter Algorithmus für maschinelles Lernen, der darauf abzielt, eine lineare Kombination von Merkmalen zu finden, die die Klassen in einem Datensatz am besten trennt.

Genau wie die Hauptkomponentenanalyse (PCA) ist sie ein Algorithmus zur Dimensionsreduktion. Diese Algorithmen sind eine gängige Wahl für die Dimensionsreduktion, in diesem Artikel werden wir sie vergleichen und beobachten, in welcher Situation jeder Algorithmus am besten funktioniert. Wir haben die PCA bereits in den vorherigen Artikeln dieser Serie besprochen. Beginnen wir mit der Beobachtung, worum es bei dem PCA-Algorithmus geht, denn wir werden ihn größtenteils besprechen, und schließlich werden wir ihre Leistungen auf einem einfachen Datensatz und im Strategietester vergleichen, stellen Sie sicher, dass Sie bis zum Ende bleiben, um großartige Datenwissenschaft zu erleben.

Zielsetzung/Theorie:

Zu den Zielen der linearen Diskriminanzanalyse (LDA) gehören:

• Maximierung der Trennbarkeit von Klassen: LDA zielt darauf ab, lineare Kombinationen von Merkmalen zu finden, die die Trennung zwischen den Klassen in den Daten maximieren. Durch die Projektion der Daten auf diese Unterscheidungsdimensionen trägt LDA dazu bei, die Unterscheidung zwischen verschiedenen Klassen zu verbessern und die Klassifizierung effektiver zu gestalten.
• Reduzierung der Dimensionen: LDA reduziert die Dimensionen des Merkmalsraums durch Projektion der Daten auf einen niedrigdimensionalen Unterraum. Diese Dimensionsreduzierung wird erreicht, indem so viele klassenunterscheidende Informationen wie möglich erhalten bleiben. Der reduzierte Merkmalsraum kann zu einfacheren Modellen, schnellerer Berechnung und besserer Generalisierungsleistung führen.
• Minimierung der Variabilität innerhalb einer Klasse: LDA zielt darauf ab, die klasseninterne Streuung oder Variabilität zu minimieren, indem sichergestellt wird, dass Datenpunkte, die zur selben Klasse gehören, im transformierten Raum eng zusammen geclustert werden. Durch die Verringerung der Variabilität innerhalb einer Klasse trägt LDA dazu bei, die Trennbarkeit zwischen den Klassen zu verbessern und die Robustheit des Klassifizierungsmodells zu erhöhen.
• Maximierung der Variabilität zwischen den Klassen: Umgekehrt versucht LDA, die Streuung oder Variabilität zwischen den Klassen zu maximieren, indem der Abstand zwischen den Klassenmitteln im transformierten Raum maximiert wird. Durch die Maximierung der Variabilität zwischen den Klassen bei gleichzeitiger Minimierung der Variabilität innerhalb der Klassen erzielt LDA eine bessere Unterscheidung zwischen den Klassen, was zu genaueren Klassifizierungsergebnissen führt.
• Handhabung der Mehrklassen-Klassifikation: LDA kann Mehrklassen-Klassifizierungsprobleme behandeln, bei denen es mehr als zwei Klassen gibt. Durch die gleichzeitige Berücksichtigung der Beziehungen zwischen allen Klassen findet LDA einen gemeinsamen Unterraum, der alle Klassen optimal trennt, was zu effektiven Klassifikationsgrenzen in hochdimensionalen Merkmalsräumen führt.

Annahmen:

Die lineare Diskriminanzanalyse geht von mehreren Annahmen aus, z. B. von einem Datensatz mit Tausenden von Proteinen.

1. Die Messungen sind unabhängig voneinander 
2. Die Daten sind innerhalb der Merkmale normal verteilt
3. Die Klassen im Datensatz haben die gleiche Kovarianzmatrix

Schritte des linearen Diskriminierungsalgorithmus:

01: Berechnung der klasseninternen Streumatrix (SW):

Berechnung der Streumatrizen für jede Klasse.

  matrix SW, SB; //within and between scatter matrices 
  SW.Init(num_features, num_features);
  SB.Init(num_features, num_features);
  
  for (ulong i=0; i<num_classes; i++)
   {
     matrix class_samples = {};
      for (ulong j=0, count=0; j<x.Rows(); j++)
         {
           if (y[j] == classes[i]) //Collect a matrix for samples belonging to a particular class
            {
               count++;
               class_samples.Resize(count, num_features);
               class_samples.Row(x.Row(j), count-1);
            }
         }

         
     matrix diff = Base::subtract(class_samples, class_means.Row(i)); //Each row subtracted to the mean
     if (diff.Rows()==0 && diff.Cols()==0) //if the subtracted matrix is zero stop the program for possible bugs or errors
      {
        DebugBreak();
        return x_centered;
      }
     
     SW += diff.Transpose().MatMul(diff); //Find within scatter matrix 
     
     vector mean_diff = class_means.Row(i) - x_centered.Mean(0);
     SB += class_samples.Rows() * mean_diff.Outer(mean_diff); //compute between scatter matrix 
   }

Addieren dieser einzelnen Streumatrizen, um die klasseninterne Streumatrix zu erhalten.

02: Berechnung der Streumatrix zwischen den Klassen (SB):

Berechnung des Mittelwertvektors für jede Klasse.

  matrix SW, SB; //within and between scatter matrices 
  SW.Init(num_features, num_features);
  SB.Init(num_features, num_features);
  
  for (ulong i=0; i<num_classes; i++)
   {

     matrix class_samples = {};
      for (ulong j=0, count=0; j<x.Rows(); j++)
         {
           if (y[j] == classes[i]) //Collect a matrix for samples belonging to a particular class
            {
               count++;
               class_samples.Resize(count, num_features);
               class_samples.Row(x.Row(j), count-1);
            }
         }
         
     matrix diff = Base::subtract(class_samples, class_means.Row(i)); //Each row subtracted to the mean
     if (diff.Rows()==0 && diff.Cols()==0) //if the subtracted matrix is zero stop the program for possible bugs or errors
      {
        DebugBreak();
        return x_centered;
      }
     
     SW += diff.Transpose().MatMul(diff); //Find within scatter matrix 
     
     vector mean_diff = class_means.Row(i) - x_centered.Mean(0);
     SB += class_samples.Rows() * mean_diff.Outer(mean_diff); //compute between scatter matrix 
   }

Berechnung der Streumatrix zwischen den Klassen.

     SB += class_samples.Rows() * mean_diff.Outer(mean_diff); //compute between scatter matrix 

03: Berechnung von Eigenwerten und Eigenvektoren:

Lösen des verallgemeinerten Eigenwertproblems mit SW und SB für den Erhalt der Eigenwerte und die entsprechenden Eigenvektoren.

  matrix eigen_vectors;
  vector eigen_values;
  
  matrix SBSW = SW.Inv().MatMul(SB);
  
  SBSW += this.m_regparam * MatrixExtend::eye((uint)SBSW.Rows());
  
  if (!SBSW.Eig(eigen_vectors, eigen_values))
    {
      Print("%s Failed to calculate eigen values and vectors Err=%d",__FUNCTION__,GetLastError());
      DebugBreak();
      
      matrix empty = {};
      return empty;
    }

Wählen der Unterscheidungsmerkmale:

Sortieren der Eigenwerte in absteigender Reihenfolge.

   vector args = MatrixExtend::ArgSort(eigen_values);
   MatrixExtend::Reverse(args);
   
   eigen_values = Base::Sort(eigen_values, args);
   eigen_vectors = Base::Sort(eigen_vectors, args);   

Auswahl der obersten k Eigenvektoren, um die Transformationsmatrix zu bilden.

   this.m_components = extract_components(eigen_values);

Da sowohl die lineare Diskriminanzanalyse als auch die Hauptkomponentenanalyse dem gleichen Zweck der Dimensionsreduktion dienen, können wir ähnliche Techniken verwenden, um Komponenten wie die Varianz und den Scree-Test zu extrahieren, genau wie die, die wir im PCA-Artikel verwendet haben.

Wir können unsere LDA-Klasse so erweitern, dass sie in der Lage ist, Komponenten für sich selbst zu extrahieren, wenn die Anzahl NULL von Komponenten standardmäßig ausgewählt ist.

  if (this.m_components == NULL)
    this.m_components = extract_components(eigen_values);
  else //plot the scree plot 
    extract_components(eigen_values);

Projizieren der Daten auf einen neuen Merkmalsraum:

Multiplizieren der Originaldaten mit den ausgewählten Eigenvektoren, um den neuen Merkmalsraum zu erhalten.

  this.projection_matrix = Base::Slice(eigen_vectors, this.m_components);
    
  return x_centered.MatMul(projection_matrix.Transpose());

Der gesamte Code wird innerhalb der Funktion fit_transform ausgeführt, die für das Training und die Vorbereitung des Algorithmus der linearen Diskriminanzanalyse zuständig ist. Damit unsere Klasse in der Lage ist, neue/unbekannte Daten zu verarbeiten, müssen wir die Funktionen für weitere Transformationen hinzufügen.

matrix CLDA::transform(const matrix &x)
 {
   if (this.projection_matrix.Rows() == 0)
    {
      printf("%s fit_transform method must be called befor transform",__FUNCTION__);
      matrix empty = {};
      return empty; 
    }
  matrix x_centered = Base::subtract(x, this.mean);
  
  return x_centered.MatMul(this.projection_matrix.Transpose());  
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
vector CLDA::transform(const vector &x)
 {
   matrix m = MatrixExtend::VectorToMatrix(x, this.num_features); 
   
   if (m.Rows()==0)
    {
      vector empty={};
      return empty; //return nothing since there is a failure in converting vector to matrix
    }
   
   m = transform(m);
   return MatrixExtend::MatrixToVector(m);
 }

LDA-Klassenübersicht:

Unsere gesamte LDA-Klasse sieht nun wie folgt aus:

enum lda_criterion //selecting best components criteria selection
  {
    CRITERION_VARIANCE,
    CRITERION_KAISER,
    CRITERION_SCREE_PLOT
  };

class CLDA
  {  
CPlots   plt;

protected:
   uint m_components;
   lda_criterion m_criterion;
   
   matrix projection_matrix;
   ulong num_features;
   double m_regparam;
   vector mean;
   
   uint CLDA::extract_components(vector &eigen_values, double threshold=0.95);
   
public:
                     CLDA(uint k=NULL, lda_criterion CRITERION_=CRITERION_SCREE_PLOT, double reg_param =1e-6);
                    ~CLDA(void);
                    
                     matrix fit_transform(const matrix &x, const vector &y);
                     matrix transform(const matrix &x);
                     vector transform(const vector &x);
  };

Der reg_param, der für den Regularisierungsparameter steht, ist weniger wichtig, da er nur dazu dient, die SW- und SB-Matrizen zu regularisieren, um die Berechnung der Eigenwerte und Vektoren weniger fehleranfällig zu machen.

   SW += this.m_regparam * MatrixExtend::eye((uint)num_features);
   SB += this.m_regparam * MatrixExtend::eye((uint)num_features);

Anwendung der linearen Diskriminanzanalyse auf einen Datensatz:

Wenden wir unsere LDA-Klasse auf den beliebten Iris-Daten an und beobachten, was sie kann.

   string headers;
   matrix data = MatrixExtend::ReadCsv("iris.csv",headers); //Read csv

Bedenken wir, dass es sich hierbei um eine überwachte, maschinelle Lerntechnik handelt, was bedeutet, dass wir die unabhängigen und die Zielvariablen getrennt erfassen und einem Modell übergeben müssen.

   matrix x;
   vector y;
   MatrixExtend::XandYSplitMatrices(data, x, y);   

#include <MALE5\Dimensionality Reduction\LDA.mqh>

CLDA *lda;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---

   string headers;
   matrix data = MatrixExtend::ReadCsv("iris.csv",headers); //Read csv
   
   matrix x;
   vector y;
   MatrixExtend::XandYSplitMatrices(data, x, y);
   
   Print("Original X\n",x);
   
   lda = new CLDA();
   matrix transformed_x = lda.fit_transform(x, y);
   
   Print("Transformed X\n",transformed_x);
   
   return(INIT_SUCCEEDED);
  }

Ausdruck:

HH      0       10:18:21.210    LDA Test (EURUSD,H1)    Original X
IQ      0       10:18:21.210    LDA Test (EURUSD,H1)    [[5.1,3.5,1.4,0.2]
HF      0       10:18:21.210    LDA Test (EURUSD,H1)     [4.9,3,1.4,0.2]
...
...
ES      0       10:18:21.211    LDA Test (EURUSD,H1)     [6.5,3,5.2,2]
ML      0       10:18:21.211    LDA Test (EURUSD,H1)     [6.2,3.4,5.4,2.3]
EI      0       10:18:21.211    LDA Test (EURUSD,H1)     [5.9,3,5.1,1.8]]
IL      0       10:18:21.243    LDA Test (EURUSD,H1)    
DD      0       10:18:21.243    LDA Test (EURUSD,H1)    Transformed X
DM      0       10:18:21.243    LDA Test (EURUSD,H1)    [[-1.058063221542643,2.676898315513957]
JD      0       10:18:21.243    LDA Test (EURUSD,H1)     [-1.060778666796316,2.532150351483708]
DM      0       10:18:21.243    LDA Test (EURUSD,H1)     [-0.9139922886488467,2.777963946569435]
...
...
IK      0       10:18:21.244    LDA Test (EURUSD,H1)     [1.527279343196588,-2.300606221030168]
QN      0       10:18:21.244    LDA Test (EURUSD,H1)     [0.9614855249192527,-1.439559895222919]
EF      0       10:18:21.244    LDA Test (EURUSD,H1)     [0.6420061576026481,-2.511057690832021…]

Auf dem Bild wurde auch ein schönes Geröllfeld angezeigt:

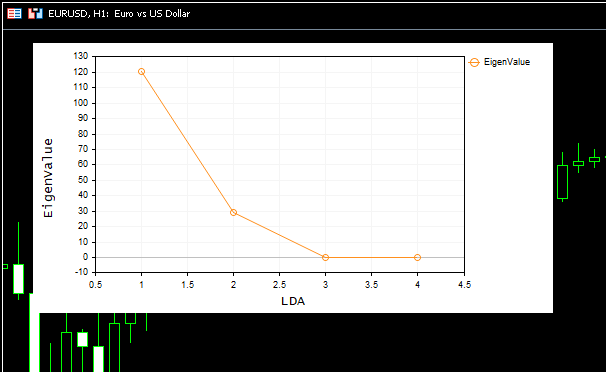
Aus dem Screeplot können wir ersehen, dass die beste Anzahl von Komponenten am Ellbogenpunkt liegt, nämlich bei 2, und das ist genau die Anzahl von Komponenten, die unsere Klasse zurückgegeben hat, großartig. Nun wollen wir die zurückgegebenen Komponenten visualisieren, um zu sehen, ob sie unterscheidbar sind. Wie wir alle wissen, besteht der Zweck der Dimensionsreduktion darin, die minimale Anzahl von Komponenten zu erhalten, die die gesamte Varianz in den ursprünglichen Daten erklärt, einfach gesagt eine vereinfachte Version unserer Daten.

Ich beschloss, die Komponenten aus unserem EA in einer csv-Datei zu speichern und sie mit Python auf diesem Notebook darzustellen https://www.kaggle.com/code/omegajoctan/lda-vs-pca-components-iris-data

  MatrixExtend::WriteCsv("iris-data lda-components.csv",transformed_x);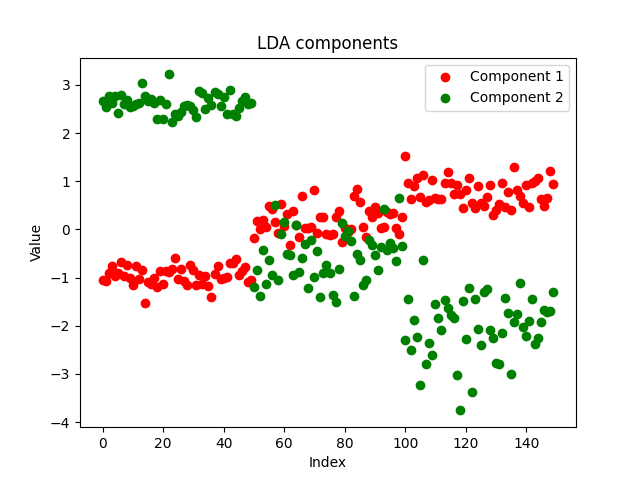

Die Komponenten sehen sauber aus, was auf eine erfolgreiche Implementierung hindeutet. Nun wollen wir sehen, wie die PCA-Komponenten aussehen:

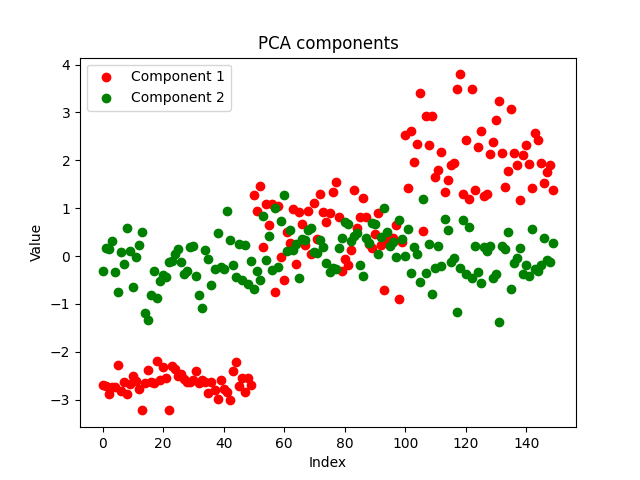
Beide Methoden haben die Daten gut getrennt. Wir können nicht sagen, welches Modell besser abschneidet, wenn wir uns das Diagramm anschauen, sondern wir verwenden dasselbe Modell mit denselben Parametern für denselben Datensatz und beobachten die Genauigkeit beider Modelle sowohl beim Training als auch beim Out-of-Sample-Test.

LDA vs. PCA bei Trainings-Test:

Verwendung des Entscheidungsbaummodells mit denselben Parametern für zwei getrennte Daten, die mit LDA- bzw. PCA-Algorithmen gewonnen wurden.

#include <MALE5\Dimensionality Reduction\LDA.mqh>
#include <MALE5\Dimensionality Reduction\PCA.mqh>
#include <MALE5\Decision Tree\tree.mqh>
#include <MALE5\Metrics.mqh>

CLDA *lda;
CPCA *pca;
CDecisionTreeClassifier *classifier_tree;

input int random_state_ = 42;
input double training_sample_size = 0.7;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---

   string headers;
   matrix data = MatrixExtend::ReadCsv("iris.csv",headers); //Read csv
  
   Print("<<<<<<<< LDA Applied >>>>>>>>>");
   
   matrix x_train, x_test;
   vector y_train, y_test;
   
   MatrixExtend::TrainTestSplitMatrices(data,x_train,y_train,x_test,y_test,training_sample_size,random_state_);
   
   lda = new CLDA(NULL);
   
   matrix x_transformed = lda.fit_transform(x_train, y_train); //Transform the training data
   
   classifier_tree = new CDecisionTreeClassifier();
   classifier_tree.fit(x_transformed, y_train); //Train the model using the transformed data
   
   vector preds = classifier_tree.predict(x_transformed); //Make predictions using the transformed data
   
   Print("Train accuracy: ",Metrics::confusion_matrix(y_train, preds).accuracy);
   
   x_transformed = lda.transform(x_test);
   preds = classifier_tree.predict(x_transformed);
   
   Print("Test accuracy: ",Metrics::confusion_matrix(y_test, preds).accuracy);
   
   delete (classifier_tree);
   delete (lda);
   
//---
   
   Print("<<<<<<<< PCA Applied >>>>>>>>>");
   
   pca = new CPCA(NULL);
   
   x_transformed = pca.fit_transform(x_train);
   
   classifier_tree = new CDecisionTreeClassifier();
   classifier_tree.fit(x_transformed, y_train);
   
   preds = classifier_tree.predict(x_transformed); //Make predictions using the transformed data
   
   Print("Train accuracy: ",Metrics::confusion_matrix(y_train, preds).accuracy);
   
   x_transformed = pca.transform(x_test);
   preds = classifier_tree.predict(x_transformed);
   
   Print("Test accuracy: ",Metrics::confusion_matrix(y_test, preds).accuracy);
   
   delete (classifier_tree);
   delete(pca);

   return(INIT_SUCCEEDED);
  }

LDA-Ergebnisse:

GM      0       18:23:18.285    LDA Test (EURUSD,H1)    <<<<<<<< LDA Applied >>>>>>>>>
MR      0       18:23:18.302    LDA Test (EURUSD,H1)    
JP      0       18:23:18.344    LDA Test (EURUSD,H1)    Confusion Matrix
FK      0       18:23:18.344    LDA Test (EURUSD,H1)    [[39,0,0]
CR      0       18:23:18.344    LDA Test (EURUSD,H1)     [0,30,5]
QF      0       18:23:18.344    LDA Test (EURUSD,H1)     [0,2,29]]
IS      0       18:23:18.344    LDA Test (EURUSD,H1)    
OM      0       18:23:18.344    LDA Test (EURUSD,H1)    Classification Report
KF      0       18:23:18.344    LDA Test (EURUSD,H1)    
QQ      0       18:23:18.344    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
FF      0       18:23:18.344    LDA Test (EURUSD,H1)    1.0    1.00     1.00     1.00       1.00     39.0
GI      0       18:23:18.344    LDA Test (EURUSD,H1)    2.0    0.94     0.86     0.97       0.90     35.0
ML      0       18:23:18.344    LDA Test (EURUSD,H1)    3.0    0.85     0.94     0.93       0.89     31.0
OS      0       18:23:18.344    LDA Test (EURUSD,H1)    
FN      0       18:23:18.344    LDA Test (EURUSD,H1)    Accuracy                                   0.93
JO      0       18:23:18.344    LDA Test (EURUSD,H1)    Average   0.93    0.93    0.97      0.93    105.0
KJ      0       18:23:18.344    LDA Test (EURUSD,H1)    W Avg     0.94    0.93    0.97      0.93    105.0
EQ      0       18:23:18.344    LDA Test (EURUSD,H1)    Train accuracy: 0.933
JH      0       18:23:18.344    LDA Test (EURUSD,H1)    Confusion Matrix
LS      0       18:23:18.344    LDA Test (EURUSD,H1)    [[11,0,0]
IJ      0       18:23:18.344    LDA Test (EURUSD,H1)     [0,13,2]
RN      0       18:23:18.344    LDA Test (EURUSD,H1)     [0,1,18]]
IK      0       18:23:18.344    LDA Test (EURUSD,H1)    
OE      0       18:23:18.344    LDA Test (EURUSD,H1)    Classification Report
KN      0       18:23:18.344    LDA Test (EURUSD,H1)    
QI      0       18:23:18.344    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
LN      0       18:23:18.344    LDA Test (EURUSD,H1)    1.0    1.00     1.00     1.00       1.00     11.0
CQ      0       18:23:18.344    LDA Test (EURUSD,H1)    2.0    0.93     0.87     0.97       0.90     15.0
QD      0       18:23:18.344    LDA Test (EURUSD,H1)    3.0    0.90     0.95     0.92       0.92     19.0
OK      0       18:23:18.344    LDA Test (EURUSD,H1)    
FF      0       18:23:18.344    LDA Test (EURUSD,H1)    Accuracy                                   0.93
GD      0       18:23:18.344    LDA Test (EURUSD,H1)    Average   0.94    0.94    0.96      0.94    45.0
HQ      0       18:23:18.344    LDA Test (EURUSD,H1)    W Avg     0.93    0.93    0.96      0.93    45.0
CF      0       18:23:18.344    LDA Test (EURUSD,H1)    Test accuracy: 0.933

LDA hat ein stabiles Modell mit einer Genauigkeit von 93 % sowohl beim Training als auch bei den Tests hervorgebracht, schauen wir uns die PCA an:

PCA-Ergebnisse:

MM      0       18:26:40.994    LDA Test (EURUSD,H1)    <<<<<<<< PCA Applied >>>>>>>>>

LS      0       18:26:41.071    LDA Test (EURUSD,H1)    Confusion Matrix
LJ      0       18:26:41.071    LDA Test (EURUSD,H1)    [[39,0,0]
ER      0       18:26:41.071    LDA Test (EURUSD,H1)     [0,34,1]
OE      0       18:26:41.071    LDA Test (EURUSD,H1)     [0,4,27]]
KD      0       18:26:41.071    LDA Test (EURUSD,H1)    
IL      0       18:26:41.071    LDA Test (EURUSD,H1)    Classification Report
MG      0       18:26:41.071    LDA Test (EURUSD,H1)    
CR      0       18:26:41.071    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
DE      0       18:26:41.071    LDA Test (EURUSD,H1)    1.0    1.00     1.00     1.00       1.00     39.0
EH      0       18:26:41.071    LDA Test (EURUSD,H1)    2.0    0.89     0.97     0.94       0.93     35.0
KL      0       18:26:41.071    LDA Test (EURUSD,H1)    3.0    0.96     0.87     0.99       0.92     31.0
ID      0       18:26:41.071    LDA Test (EURUSD,H1)    
NO      0       18:26:41.071    LDA Test (EURUSD,H1)    Accuracy                                   0.95
CH      0       18:26:41.071    LDA Test (EURUSD,H1)    Average   0.95    0.95    0.98      0.95    105.0
KK      0       18:26:41.071    LDA Test (EURUSD,H1)    W Avg     0.95    0.95    0.98      0.95    105.0
NR      0       18:26:41.071    LDA Test (EURUSD,H1)    Train accuracy: 0.952
LK      0       18:26:41.071    LDA Test (EURUSD,H1)    Confusion Matrix
FR      0       18:26:41.071    LDA Test (EURUSD,H1)    [[11,0,0]
FJ      0       18:26:41.072    LDA Test (EURUSD,H1)     [0,14,1]
MM      0       18:26:41.072    LDA Test (EURUSD,H1)     [0,3,16]]
NL      0       18:26:41.072    LDA Test (EURUSD,H1)    
HD      0       18:26:41.072    LDA Test (EURUSD,H1)    Classification Report
LO      0       18:26:41.072    LDA Test (EURUSD,H1)    
FJ      0       18:26:41.072    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
KM      0       18:26:41.072    LDA Test (EURUSD,H1)    1.0    1.00     1.00     1.00       1.00     11.0
EP      0       18:26:41.072    LDA Test (EURUSD,H1)    2.0    0.82     0.93     0.90       0.88     15.0
HD      0       18:26:41.072    LDA Test (EURUSD,H1)    3.0    0.94     0.84     0.96       0.89     19.0
HL      0       18:26:41.072    LDA Test (EURUSD,H1)    
OG      0       18:26:41.072    LDA Test (EURUSD,H1)    Accuracy                                   0.91
PS      0       18:26:41.072    LDA Test (EURUSD,H1)    Average   0.92    0.93    0.95      0.92    45.0
IP      0       18:26:41.072    LDA Test (EURUSD,H1)    W Avg     0.92    0.91    0.95      0.91    45.0
PE      0       18:26:41.072    LDA Test (EURUSD,H1)    Test accuracy: 0.911

Die PCA lieferte ein genaueres Modell mit einer Genauigkeit von 95 % beim Training und 91,1 % beim Test.

Vorteile der linearen Diskriminanzanalyse (LDA):

Die lineare Diskriminanzanalyse (LDA) bietet mehrere Vorteile, die sie zu einer weit verbreiteten Technik bei Klassifizierungs- und Dimensionsreduktionsaufgaben machen:

• Sie hilft bei der Reduzierung der Dimensionen. LDA reduziert die Dimensionen des Merkmalsraums, indem es die ursprünglichen Merkmale in einen niedrigdimensionalen Raum transformiert. Diese Reduktion kann zu einfacheren Modellen führen, den Fluch der Dimensionen mindern und die Effizienz der Berechnungen verbessern.
• Sie bewahrt unterscheidungsrelevante Informationen der Klasse. LDA zielt darauf ab, lineare Kombinationen von Merkmalen zu finden, die die Trennung zwischen den Klassen maximieren. Durch die Konzentration auf die diskriminierende Information, die zwischen den Klassen unterscheidet, stellt LDA sicher, dass die transformierten Merkmale wichtige klassenbezogene Muster und Strukturen beibehalten.
• Sie extrahiert und klassifiziert die Merkmale in einem Schritt. LDA führt gleichzeitig eine Merkmalsextraktion und eine Klassifizierung durch. Sie lernt eine Transformation der ursprünglichen Merkmale, die die Klassentrennbarkeit maximiert, und ist daher von Natur aus für Klassifizierungsaufgaben geeignet. Dieser integrierte Ansatz kann zu effizienteren und besser interpretierbaren Modellen führen.
• Sie ist robust gegenüber Überanpassungen. LDA ist im Vergleich zu anderen Klassifizierungsalgorithmen weniger anfällig für eine Überanpassung, insbesondere wenn die Anzahl der Stichproben im Verhältnis zur Anzahl der Merkmale klein ist. Durch die Verringerung der Dimensionen des Merkmalsraums und die Konzentration auf die unterscheidungskräftigsten Merkmale kann LDA gut auf ungesehene Daten verallgemeinert werden.
• Sie ermöglicht die Klassifizierung in mehrere Klassen. LDA lässt sich natürlich auch auf Mehrklassen-Klassifizierungsprobleme mit mehr als zwei Klassen anwenden. Sie berücksichtigt die Beziehungen zwischen allen Klassen gleichzeitig, was zu effektiven Trenngrenzen in hochdimensionalen Merkmalsräumen führt.
• Effiziente Berechnungen. LDA beinhaltet die Lösung von Eigenwertproblemen und Matrixmultiplikationen, die rechnerisch effizient sind und mit integrierten MQL5-Methoden implementiert werden können. Dadurch eignet sich LDA für große Datensätze und Echtzeitanwendungen.
• Leicht zu interpretieren. Die aus LDA gewonnenen transformierten Merkmale sind interpretierbar und können analysiert werden, um die zugrunde liegenden Muster in den Daten zu verstehen. Die von LDA gelernten Linearkombinationen von Merkmalen können Einblicke in die diskriminierenden Faktoren geben, die die Klassifizierungsentscheidung beeinflussen.
• Ihre Annahmen werden häufig erfüllt. LDA geht davon aus, dass die Daten innerhalb jeder Klasse normalverteilt sind und die Kovarianzmatrizen gleich sind. Auch wenn diese Annahmen in der Praxis nicht immer zutreffen, kann LDA auch dann noch gute Ergebnisse liefern, wenn die Annahmen annähernd erfüllt sind.

Die lineare Diskriminanzanalyse (LDA) hat zwar mehrere Vorteile, aber auch einige Einschränkungen und Nachteile:

Nachteile der linearen Diskriminanzanalyse (LDA):

• Sie geht von einer Gaußschen Verteilung innerhalb der Merkmale aus. LDA geht davon aus, dass die Daten innerhalb jeder Klasse normalverteilt sind und die Kovarianzmatrizen gleich sind. Wenn diese Annahme verletzt wird, kann LDA suboptimale Ergebnisse liefern oder sogar nicht konvergieren. In der Praxis können reale Daten nicht-normale Verteilungen aufweisen, was die Wirksamkeit von LDA einschränken kann.
• Sie kann empfindlich auf Ausreißer reagieren. LDA ist empfindlich gegenüber Ausreißern, insbesondere wenn die Kovarianzmatrizen aus begrenzten Daten geschätzt werden. Ausreißer können die Schätzung von Kovarianzmatrizen und die sich daraus ergebenden Unterscheidungsrichtungen erheblich beeinträchtigen, was zu verzerrten oder unzuverlässigen Klassifizierungsergebnissen führen kann.
• Sie ist weniger flexibel bei der Modellierung nicht-linearer Beziehungen. Denn es wird davon ausgegangen, dass die Entscheidungsgrenzen zwischen den Klassen linear sind. Wenn die zugrundeliegenden Beziehungen zwischen Merkmalen und Klassen nichtlinear sind, kann LDA diese komplexen Muster möglicherweise nicht effektiv erfassen. In solchen Fällen können nichtlineare Verfahren zur Dimensionsreduktion oder nichtlineare Klassifikatoren besser geeignet sein.
• Der Fluch der Dimensionen ist real. Wenn die Anzahl der Merkmale viel größer ist als die Anzahl der Stichproben, kann die LDA unter dem Fluch der Dimensionen leiden. In hochdimensionalen Merkmalsräumen wird die Schätzung von Kovarianzmatrizen weniger zuverlässig, und die diskriminanten Richtungen erfassen die tatsächliche zugrunde liegende Struktur der Daten möglicherweise nicht effektiv.
• Begrenzte Leistung bei unausgewogenen Klassen. LDA kann bei unausgewogenen Klassenverteilungen, bei denen eine oder mehrere Klassen deutlich weniger Stichproben haben als andere, schlecht abschneiden. In solchen Fällen kann die Klasse mit weniger Stichproben bei der Schätzung der Klassenmittelwerte und Kovarianzmatrizen schlecht vertreten sein, was zu verzerrten Klassifizierungsergebnissen führt.
• Sie kann kaum nichtnumerische Daten verarbeiten. LDA arbeitet in der Regel mit numerischen Daten und ist möglicherweise nicht direkt auf Datensätze anwendbar, die kategoriale oder nicht-numerische Variablen enthalten. Vorverarbeitungsschritte wie die Kodierung kategorischer Variablen oder die Umwandlung nichtnumerischer Daten in numerische Darstellungen können erforderlich sein, was zu zusätzlicher Komplexität und potenziellem Informationsverlust führen kann.

LDA vs. PCA in der Handelsumgebung:

Um diese Techniken zur Dimensionsreduzierung in der Handelsumgebung zu nutzen, müssen wir eine Funktion zum Trainieren und Testen des Papiermodells erstellen. Dann können wir das trainierte Modell verwenden, um Vorhersagen für den Strategietester zu treffen, die uns helfen, ihre Leistung zu analysieren.

Wir werden die 5 Indikatoren in unserem Datensatz verwenden, den wir mit beiden Methoden schrumpfen möchten:

int OnInit()
  {
  
//--- Trend following indicators

    indicator_handle[0] = iAMA(Symbol(), PERIOD_CURRENT, 9 , 2 , 30, 0, PRICE_OPEN);
    indicator_handle[1] = iADX(Symbol(), PERIOD_CURRENT, 14);
    indicator_handle[2] = iADXWilder(Symbol(), PERIOD_CURRENT, 14);
    indicator_handle[3] = iBands(Symbol(), PERIOD_CURRENT, 20, 0, 2.0, PRICE_OPEN);
    indicator_handle[4] = iDEMA(Symbol(), PERIOD_CURRENT, 14, 0, PRICE_OPEN);
 }

Da diese Algorithmen aufgrund ihrer Beschaffenheit nicht darauf programmiert sind, zu lernen und aussagekräftige Handelssignale zu liefern, werden wir die Entscheidungsbaum-KI verwenden, um Vorhersagen über die transformierten Daten sowohl in Trainings- als auch in Testsituationen zu treffen.

void TrainTest()
 {
   vector buffer = {};
   for (int i=0; i<ArraySize(indicator_handle); i++)
    {
      buffer.CopyIndicatorBuffer(indicator_handle[i], 0, 0, bars); //copy indicator buffer
      dataset.Col(buffer, i); //add the indicator buffer values to the dataset matrix 
    }

//---
  
   vector y(bars);
   MqlRates rates[];
   CopyRates(Symbol(), PERIOD_CURRENT,0,bars, rates);
   for (int i=0; i<bars; i++) //Creating the target variable 
     {
       if (rates[i].close > rates[i].open) //if bullish candle assign 1 to the y variable else assign the 0 class
        y[i] = 1;
       else
        y[0] = 0;
     }  
     
//---
   
   dataset.Col(y, dataset.Cols()-1); //add the y variable to the last column
   
//---

   matrix x_train, x_test;
   vector y_train, y_test;
      
   MatrixExtend::TrainTestSplitMatrices(dataset,x_train,y_train,x_test,y_test,training_sample_size,random_state_);
   
   matrix x_transformed = {};
   switch(dimension_reduction)
     {
      case  LDA:
         
         lda = new CLDA(NULL);
         
         x_transformed = lda.fit_transform(x_train, y_train); //Transform the training data   
         
        break;
      case PCA:
      
         pca = new CPCA(NULL);
         
         x_transformed = pca.fit_transform(x_train);
         
        break;
     }
     
   
   classifier_tree = new CDecisionTreeClassifier();
   classifier_tree.fit(x_transformed, y_train); //Train the model using the transformed data
   
   vector preds = classifier_tree.predict(x_transformed); //Make predictions using the transformed data
   
   Print("Train accuracy: ",Metrics::confusion_matrix(y_train, preds).accuracy);
   
   switch(dimension_reduction)
     {
      case  LDA:
        
        x_transformed = lda.transform(x_test); //Transform the testing data   
        
        break;
        
      case PCA:
        
        x_transformed = pca.transform(x_test); 
        
        break;
     }
   preds = classifier_tree.predict(x_transformed);
   
   Print("Test accuracy: ",Metrics::confusion_matrix(y_test, preds).accuracy);
   
 }

Sobald die Daten trainiert sind, müssen sie getestet werden. Im Folgenden werden die Ergebnisse für beide Methoden dargestellt, beginnend mit LDA: 

JK      0       01:00:24.440    LDA Test (EURUSD,H1)    
GK      0       01:00:37.442    LDA Test (EURUSD,H1)    Confusion Matrix
QR      0       01:00:37.442    LDA Test (EURUSD,H1)    [[60,266]
FF      0       01:00:37.442    LDA Test (EURUSD,H1)     [46,328]]
DR      0       01:00:37.442    LDA Test (EURUSD,H1)    
RN      0       01:00:37.442    LDA Test (EURUSD,H1)    Classification Report
FE      0       01:00:37.442    LDA Test (EURUSD,H1)    
LP      0       01:00:37.442    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
HD      0       01:00:37.442    LDA Test (EURUSD,H1)    0.0    0.57     0.18     0.88       0.28     326.0
FI      0       01:00:37.442    LDA Test (EURUSD,H1)    1.0    0.55     0.88     0.18       0.68     374.0
RM      0       01:00:37.442    LDA Test (EURUSD,H1)    
QH      0       01:00:37.442    LDA Test (EURUSD,H1)    Accuracy                                   0.55
KQ      0       01:00:37.442    LDA Test (EURUSD,H1)    Average   0.56    0.53    0.53      0.48    700.0
HP      0       01:00:37.442    LDA Test (EURUSD,H1)    W Avg     0.56    0.55    0.51      0.49    700.0
KK      0       01:00:37.442    LDA Test (EURUSD,H1)    Train accuracy: 0.554
DR      0       01:00:37.443    LDA Test (EURUSD,H1)    Confusion Matrix
CD      0       01:00:37.443    LDA Test (EURUSD,H1)    [[20,126]
LO      0       01:00:37.443    LDA Test (EURUSD,H1)     [12,142]]
OK      0       01:00:37.443    LDA Test (EURUSD,H1)    
ME      0       01:00:37.443    LDA Test (EURUSD,H1)    Classification Report
QN      0       01:00:37.443    LDA Test (EURUSD,H1)    
GI      0       01:00:37.443    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
JM      0       01:00:37.443    LDA Test (EURUSD,H1)    0.0    0.62     0.14     0.92       0.22     146.0
KR      0       01:00:37.443    LDA Test (EURUSD,H1)    1.0    0.53     0.92     0.14       0.67     154.0
MF      0       01:00:37.443    LDA Test (EURUSD,H1)    
MQ      0       01:00:37.443    LDA Test (EURUSD,H1)    Accuracy                                   0.54
MJ      0       01:00:37.443    LDA Test (EURUSD,H1)    Average   0.58    0.53    0.53      0.45    300.0
OI      0       01:00:37.443    LDA Test (EURUSD,H1)    W Avg     0.58    0.54    0.52      0.45    300.0
QP      0       01:00:37.443    LDA Test (EURUSD,H1)    Test accuracy: 0.54

Die PCA schnitt beim Training besser ab, fiel aber beim Testen etwas ab:

GE      0       01:01:57.202    LDA Test (EURUSD,H1)    
MS      0       01:01:57.202    LDA Test (EURUSD,H1)    Classification Report
IH      0       01:01:57.202    LDA Test (EURUSD,H1)    
OS      0       01:01:57.202    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
KG      0       01:01:57.202    LDA Test (EURUSD,H1)    0.0    0.62     0.28     0.85       0.39     326.0
GL      0       01:01:57.202    LDA Test (EURUSD,H1)    1.0    0.58     0.85     0.28       0.69     374.0
MP      0       01:01:57.202    LDA Test (EURUSD,H1)    
JK      0       01:01:57.202    LDA Test (EURUSD,H1)    Accuracy                                   0.59
HL      0       01:01:57.202    LDA Test (EURUSD,H1)    Average   0.60    0.57    0.57      0.54    700.0
CG      0       01:01:57.202    LDA Test (EURUSD,H1)    W Avg     0.60    0.59    0.55      0.55    700.0
EF      0       01:01:57.202    LDA Test (EURUSD,H1)    Train accuracy: 0.586
HO      0       01:01:57.202    LDA Test (EURUSD,H1)    Confusion Matrix
GG      0       01:01:57.202    LDA Test (EURUSD,H1)    [[26,120]
GJ      0       01:01:57.202    LDA Test (EURUSD,H1)     [29,125]]
KN      0       01:01:57.202    LDA Test (EURUSD,H1)    
QJ      0       01:01:57.202    LDA Test (EURUSD,H1)    Classification Report
MQ      0       01:01:57.202    LDA Test (EURUSD,H1)    
CL      0       01:01:57.202    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
QP      0       01:01:57.202    LDA Test (EURUSD,H1)    0.0    0.47     0.18     0.81       0.26     146.0
GE      0       01:01:57.202    LDA Test (EURUSD,H1)    1.0    0.51     0.81     0.18       0.63     154.0
QI      0       01:01:57.202    LDA Test (EURUSD,H1)    
MD      0       01:01:57.202    LDA Test (EURUSD,H1)    Accuracy                                   0.50
RE      0       01:01:57.202    LDA Test (EURUSD,H1)    Average   0.49    0.49    0.49      0.44    300.0
IL      0       01:01:57.202    LDA Test (EURUSD,H1)    W Avg     0.49    0.50    0.49      0.45    300.0
PP      0       01:01:57.202    LDA Test (EURUSD,H1)    Test accuracy: 0.503

Schließlich können wir aus den Signalen, die das Entscheidungsbaummodell liefert, eine einfache Handelsstrategie erstellen.

void OnTick()
  {
//---

   if (!train_once) //call the function to train the model once on the program lifetime
    {
      TrainTest();
      train_once = true; 
    }

//--- 
   
   vector inputs(indicator_handle.Size());
   vector buffer;
   
   for (uint i=0; i<indicator_handle.Size(); i++)
     {
       buffer.CopyIndicatorBuffer(indicator_handle[i], 0, 0, 1); //copy the current indicator value
       inputs[i] = buffer[0]; //add its value to the inputs vector 
     }

//---
    
    SymbolInfoTick(Symbol(), ticks);
      
     if (isnewBar(PERIOD_CURRENT)) // We want to trade on the bar opening 
      {
        vector transformed_inputs = {};
         switch(dimension_reduction) //transform every new data to fit the dimensions selected during training
           {
            case  LDA:
               transformed_inputs = lda.transform(inputs); //Transform the new data   
              break;
            case PCA:
               transformed_inputs = pca.transform(inputs);
              break;
           }
     
        int signal = (int)classifier_tree.predict(transformed_inputs);
        double min_lot = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN);
        SymbolInfoTick(Symbol(), ticks);
        
         if (signal == -1)
           {
              if (!PosExists(MAGICNUMBER, POSITION_TYPE_SELL)) // If a sell trade doesnt exist
                m_trade.Sell(min_lot, Symbol(), ticks.bid, ticks.bid+stoploss*Point(), ticks.bid - takeprofit*Point());
           }
         else
           {
             if (!PosExists(MAGICNUMBER, POSITION_TYPE_BUY))  // If a buy trade doesnt exist
               m_trade.Buy(min_lot, Symbol(), ticks.ask, ticks.ask-stoploss*Point(), ticks.ask + takeprofit*Point());
           }
      }
  }

Ich habe einen Test im Modus Offene Preise von 2023 Januar bis 2024 Februar mit beiden Methoden für die einfache Strategie durchgeführt:

Lineare Diskriminanzanalyse (LDA):

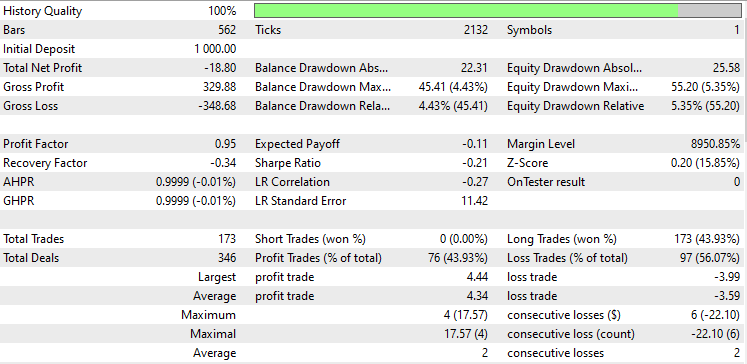
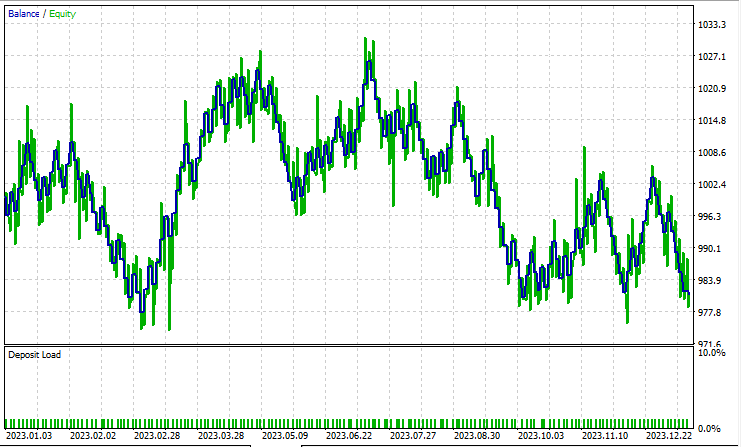
Ein Test zur Hauptkomponentenanalyse (PCA):

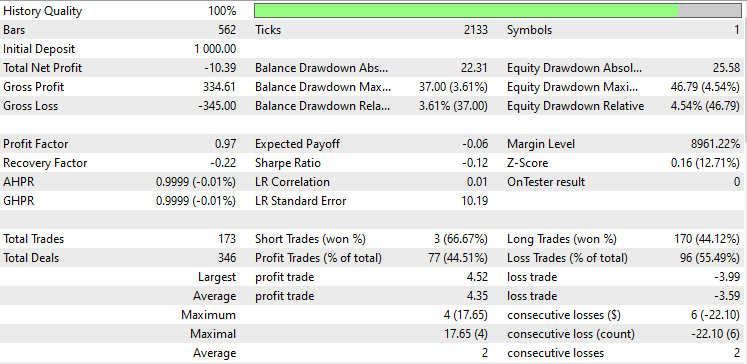
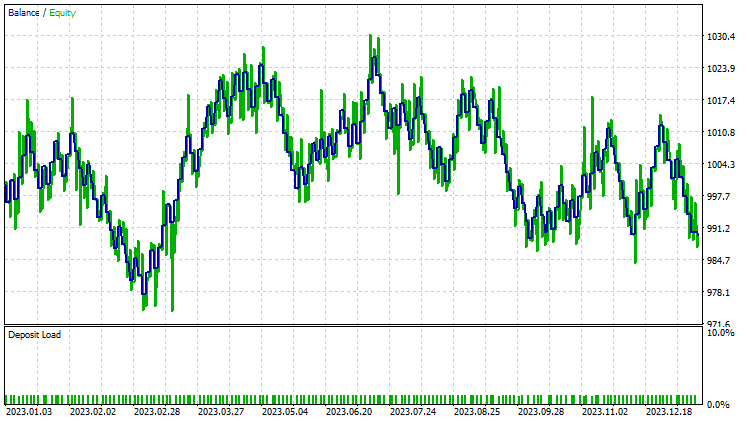
Während der Strategietester etwas ist, das jeder MQL5-Händler aus dem Blickwinkel eines Datenwissenschaftlers betrachtet, ist er für diese Dimensionsreduktionstechniken weniger relevant, da ihre primäre Aufgabe darin besteht, die Variablen zu vereinfachen, insbesondere bei der Arbeit mit großen Daten. Ich muss auch erklären, dass wenn dieser EA im Strategie-Tester läuft, mir einige Unstimmigkeiten bei den Berechnungen durch Fehler, die in Matrizen und Vektor-Methoden unerforscht sind, begegnet bin. Bitte führen Sie das Programm mehrmals aus, bis Sie sinnvolle Ergebnis erhalten, wenn Sie Fehler und Hindernisse auf dem Weg begegnen.

Wenn Sie diese Artikelserie gelesen haben, fragen Sie sich vielleicht , warum wir die transformierten Daten, die wir mit diesen beiden Techniken erhalten haben, nicht skalierten, wie wir es im vorherigen Artikel getan haben.

Ob die Daten aus PCA oder LDA für ein maschinelles Lernmodell normalisiert werden müssen, hängt von den spezifischen Merkmalen Ihres Datensatzes, dem verwendeten Algorithmus und Ihren Zielen ab. Im Folgenden finden Sie einige Punkte, die Sie beachten sollten:

• Die PCA-Transformation: Beiden arbeiten mit der Kovarianzmatrix der ursprünglichen Merkmale und finden orthogonale Komponenten (Hauptkomponenten), die die maximale Varianz in den Daten erfassen. Die aus diesen beiden Methoden gewonnenen transformierten Daten bestehen aus diesen Hauptkomponenten.
• Normalisierung vor PCA oder LDA: Es ist gängige Praxis, die ursprünglichen Merkmale vor der Durchführung von PCA oder LDA zu normalisieren, insbesondere wenn die Merkmale unterschiedliche Skalen oder Einheiten haben. Die Normalisierung stellt sicher, dass alle Merkmale gleichmäßig zur Kovarianzmatrix beitragen und verhindert, dass Merkmale mit größeren Skalen die Hauptkomponenten dominieren.
• Die Normalisierung nach PCA oder LDA: Ob Sie die transformierten Daten aus der PCA normalisieren müssen, hängt von den spezifischen Anforderungen Ihres Algorithmus für maschinelles Lernen und den Eigenschaften der transformierten Merkmale ab. Einige Algorithmen, wie z. B. die logistische Regression oder Nächste-Nachbarn-Klassifikation, reagieren empfindlich auf Unterschiede in den Merkmalsskalen und können von normalisierten Merkmalen profitieren, selbst nach PCA oder LDA.

• Andere Algorithmen, wie z. B. die von uns eingesetzten Entscheidungsbäume oder Random-Forest, reagieren weniger empfindlich auf die Skalierung von Merkmalen und erfordern möglicherweise keine Normalisierung nach der PCA.

• Auswirkung der Normalisierung auf die Interpretierbarkeit: Die Normalisierung nach der PCA kann die Interpretierbarkeit der Hauptkomponenten beeinträchtigen. Wenn Sie daran interessiert sind, die Beiträge der ursprünglichen Merkmale zu den Hauptkomponenten zu verstehen, kann die Normalisierung der transformierten Daten diese Beziehungen verschleiern.
• Auswirkungen auf die Leistung: Experimentieren Sie mit normalisierten und nicht normalisierten transformierten Daten, um die Auswirkungen auf die Modellleistung zu bewerten. In einigen Fällen kann die Normalisierung zu einer besseren Konvergenz, einer verbesserten Generalisierung oder einem schnelleren Training führen, während sie in anderen Fällen wenig oder gar keine Auswirkungen hat.

Verfolgen Sie die Entwicklung von Modellen für maschinelles Lernen und vieles mehr in dieser Artikelserie auf diesem GitHub Repo.

Anhänge:

Datei	Beschreibung/Verwendung
tree.mqh	Enthält das Entscheidungsbaum-Klassifikatormodell
MatrixExtend.mqh	Hat zusätzliche Funktionen für Matrixmanipulationen.
metrics.mqh	Enthält Funktionen und Code zur Messung der Leistung von ML-Modellen.
preprocessing.mqh	Die Bibliothek für die Vorverarbeitung von rohen Eingabedaten, um sie für die Verwendung von Modellen des maschinellen Lernens geeignet zu machen.
base.mqh	Die Basisbibliothek für pca und lda enthält einige Funktionen, die das Kodieren dieser beiden Bibliotheken vereinfachen
pca.mqh	Bibliothek zur Hauptkomponentenanalyse
lda.mqh	Bibliothek zur linearen Diskriminanzanalyse
plots.mqh	Bibliothek zum Zeichnen von Vektoren und Matrizen
lda vs pca script.mq5	Skript für die Darstellung der Algorithmen pca und lda
LDA Test.mq5	Der Haupt-EA zum Testen des Großteils des Codes
iris.csv	Der verbreitete Iris-Datensatz