Ciência de dados e aprendizado de máquina (Parte 20): Escolha entre LDA e PCA em tarefas de algotrading no MQL5

-- Quanto mais se tem, menos se percebe.

O que é a Análise Discriminante Linear (Linear Discriminant Analysis, LDA)?

O LDA é um algoritmo de aprendizado de máquina supervisionado cuja meta é encontrar uma combinação linear de características que melhor separe as classes em um conjunto de dados.

Assim como a Análise de Componentes Principais (PCA), é um algoritmo de redução de dimensionalidade. Esses algoritmos são frequentemente usados para redução de dimensionalidade. Neste artigo, vamos compará-los e ver em que situação cada um dos algoritmos funciona melhor. Já discutimos o PCA em artigos anteriores desta série. Vamos começar nos familiarizando com o algoritmo LDA, pois a maior parte do artigo será dedicada a este algoritmo e à sua comparação com o PCA. Vamos comparar o desempenho desses dois algoritmos em um conjunto de dados simples e no testador de estratégias.

Objetivos/teoria

Para que é usado o método de análise discriminante linear:

• Melhoria da separabilidade das classes: LDA busca encontrar combinações lineares de características que maximizem a separação entre as classes nos dados. Ao projetar os dados nesses eixos discriminantes, o LDA ajuda a aumentar as diferenças entre as classes, tornando a classificação mais eficiente.
• Redução de dimensionalidade: LDA reduz a dimensionalidade do espaço de características, projetando os dados em um subespaço de menor dimensionalidade. Ao fazer isso, durante a redução de dimensionalidade, é mantida a maior quantidade possível de informação sobre as diferenças entre as classes. Reduzir o espaço de características pode simplificar modelos, acelerar cálculos e aumentar o desempenho.
• Minimização da variabilidade intraclasse: LDA busca minimizar a dispersão ou variabilidade dentro da classe, garantindo que os pontos de dados pertencentes a uma classe estejam bem agrupados no espaço transformado. Por conta da variabilidade intraclasse, o LDA ajuda a melhorar a separação entre as classes e a aumentar a confiabilidade do modelo de classificação.
• Aumento da distância entre classes: Por outro lado, LDA busca maximizar as diferenças entre as classes estabelecendo a maior distância possível entre as classes no espaço transformado. Assim, o algoritmo LDA permite fazer distinções mais claras entre as classes e tornar a classificação mais precisa.
• Capacidades de classificação multiclasse: LDA é adequado para agrupar características em mais de duas classes. Considerando as relações entre todas as classes ao mesmo tempo, o algoritmo encontra um subespaço comum que otimamente separa todas as classes. Com isso, obtemos fronteiras de classificação eficazes em espaços de características multidimensionais.

Pressupostos:

O método de análise discriminante linear faz vários pressupostos. Assim, presume-se que

1. As medições são independentes umas das outras.
   
2. Os dados são distribuídos normalmente dentro dos objetos.
3. As classes no conjunto de dados têm a mesma matriz de covariância.

Etapas do algoritmo LDA

1. Cálculo da matriz de dispersão dentro da classe (SW):

Calculamos a matriz de dispersão para cada classe.

  matrix SW, SB; //within and between scatter matrices 
  SW.Init(num_features, num_features);
  SB.Init(num_features, num_features);
  
  for (ulong i=0; i<num_classes; i++)
   {
     matrix class_samples = {};
      for (ulong j=0, count=0; j<x.Rows(); j++)
         {
           if (y[j] == classes[i]) //Collect a matrix for samples belonging to a particular class
            {
               count++;
               class_samples.Resize(count, num_features);
               class_samples.Row(x.Row(j), count-1);
            }
         }

         
     matrix diff = Base::subtract(class_samples, class_means.Row(i)); //Each row subtracted to the mean
     if (diff.Rows()==0 && diff.Cols()==0) //if the subtracted matrix is zero stop the program for possible bugs or errors
      {
        DebugBreak();
        return x_centered;
      }
     
     SW += diff.Transpose().MatMul(diff); //Find within scatter matrix 
     
     vector mean_diff = class_means.Row(i) - x_centered.Mean(0);
     SB += class_samples.Rows() * mean_diff.Outer(mean_diff); //compute between scatter matrix 
   }

Somamos essas matrizes de dispersão individuais para obter a matriz de dispersão dentro da classe.

2. Cálculo da matriz de dispersão entre classes (SB):

Encontramos o vetor médio para cada classe.

  matrix SW, SB; //within and between scatter matrices 
  SW.Init(num_features, num_features);
  SB.Init(num_features, num_features);
  
  for (ulong i=0; i<num_classes; i++)
   {

     matrix class_samples = {};
      for (ulong j=0, count=0; j<x.Rows(); j++)
         {
           if (y[j] == classes[i]) //Collect a matrix for samples belonging to a particular class
            {
               count++;
               class_samples.Resize(count, num_features);
               class_samples.Row(x.Row(j), count-1);
            }
         }
         
     matrix diff = Base::subtract(class_samples, class_means.Row(i)); //Each row subtracted to the mean
     if (diff.Rows()==0 && diff.Cols()==0) //if the subtracted matrix is zero stop the program for possible bugs or errors
      {
        DebugBreak();
        return x_centered;
      }
     
     SW += diff.Transpose().MatMul(diff); //Find within scatter matrix 
     
     vector mean_diff = class_means.Row(i) - x_centered.Mean(0);
     SB += class_samples.Rows() * mean_diff.Outer(mean_diff); //compute between scatter matrix 
   }

Calculamos a matriz de dispersão entre classes.

     SB += class_samples.Rows() * mean_diff.Outer(mean_diff); //compute between scatter matrix 

3. Cálculo dos autovalores e autovetores

Resolvemos o problema generalizado de autovalores envolvendo SW e SB, obtendo autovalores e os correspondentes autovetores.

  matrix eigen_vectors;
  vector eigen_values;
  
  matrix SBSW = SW.Inv().MatMul(SB);
  
  SBSW += this.m_regparam * MatrixExtend::eye((uint)SBSW.Rows());
  
  if (!SBSW.Eig(eigen_vectors, eigen_values))
    {
      Print("%s Failed to calculate eigen values and vectors Err=%d",__FUNCTION__,GetLastError());
      DebugBreak();
      
      matrix empty = {};
      return empty;
    }

Escolha das características distintivas:

Classificamos os autovalores em ordem decrescente.

   vector args = MatrixExtend::ArgSort(eigen_values);
   MatrixExtend::Reverse(args);
   
   eigen_values = Base::Sort(eigen_values, args);
   eigen_vectors = Base::Sort(eigen_vectors, args);   

Escolhemos os k melhores autovetores para formar a matriz de transformação.

   this.m_components = extract_components(eigen_values);

Como tanto a análise discriminante linear (LDA) quanto a análise de componentes principais (PCA) servem ao mesmo propósito, que é reduzir a dimensionalidade — podemos usar métodos semelhantes para extrair componentes, como a variância e o gráfico Scree Plot de autovalores. Usamos esses mesmos métodos no artigo sobre PCA.

Podemos expandir nossa classe de algoritmo LDA para que possa extrair componentes para si mesma, quando o número de componentes for NULL por padrão.

  if (this.m_components == NULL)
    this.m_components = extract_components(eigen_values);
  else //plot the scree plot 
    extract_components(eigen_values);

Projeção dos dados no novo espaço de características

Multiplicamos os dados brutos pelos autovetores escolhidos para obter o novo espaço de características.

  this.projection_matrix = Base::Slice(eigen_vectors, this.m_components);
    
  return x_centered.MatMul(projection_matrix.Transpose());

Todo esse código é executado dentro da função fit_transform. Esta função é responsável por treinar e preparar o algoritmo de análise discriminante linear. Para que nossa classe possa processar novos dados invisíveis, precisamos adicionar funções para transformações futuras.

matrix CLDA::transform(const matrix &x)
 {
   if (this.projection_matrix.Rows() == 0)
    {
      printf("%s fit_transform method must be called befor transform",__FUNCTION__);
      matrix empty = {};
      return empty; 
    }
  matrix x_centered = Base::subtract(x, this.mean);
  
  return x_centered.MatMul(this.projection_matrix.Transpose());  
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
vector CLDA::transform(const vector &x)
 {
   matrix m = MatrixExtend::VectorToMatrix(x, this.num_features); 
   
   if (m.Rows()==0)
    {
      vector empty={};
      return empty; //return nothing since there is a failure in converting vector to matrix
    }
   
   m = transform(m);
   return MatrixExtend::MatrixToVector(m);
 }

Visão geral da classe LDA

A classe geral do algoritmo LDA agora fica assim:

enum lda_criterion //selecting best components criteria selection
  {
    CRITERION_VARIANCE,
    CRITERION_KAISER,
    CRITERION_SCREE_PLOT
  };

class CLDA
  {  
CPlots   plt;

protected:
   uint m_components;
   lda_criterion m_criterion;
   
   matrix projection_matrix;
   ulong num_features;
   double m_regparam;
   vector mean;
   
   uint CLDA::extract_components(vector &eigen_values, double threshold=0.95);
   
public:
                     CLDA(uint k=NULL, lda_criterion CRITERION_=CRITERION_SCREE_PLOT, double reg_param =1e-6);
                    ~CLDA(void);
                    
                     matrix fit_transform(const matrix &x, const vector &y);
                     matrix transform(const matrix &x);
                     vector transform(const vector &x);
  };

O parâmetro de regularização reg_param tem um valor menor, pois é usado apenas para regularizar as matrizes SW e SB. Isso evita erros ao calcular autovalores e autovetores.

   SW += this.m_regparam * MatrixExtend::eye((uint)num_features);
   SB += this.m_regparam * MatrixExtend::eye((uint)num_features);

Usando a análise discriminante linear na amostra

Aplicamos nossa classe LDA em uma amostra popular de dados Iris-csv e veremos o que ela faz.

   string headers;
   matrix data = MatrixExtend::ReadCsv("iris.csv",headers); //Read csv

Lembre-se de que este é um método de aprendizado supervisionado. Isso significa que precisamos coletar variáveis independentes e dependentes separadamente e passá-las para o modelo.

   matrix x;
   vector y;
   MatrixExtend::XandYSplitMatrices(data, x, y);   

#include <MALE5\Dimensionality Reduction\LDA.mqh>

CLDA *lda;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---

   string headers;
   matrix data = MatrixExtend::ReadCsv("iris.csv",headers); //Read csv
   
   matrix x;
   vector y;
   MatrixExtend::XandYSplitMatrices(data, x, y);
   
   Print("Original X\n",x);
   
   lda = new CLDA();
   matrix transformed_x = lda.fit_transform(x, y);
   
   Print("Transformed X\n",transformed_x);
   
   return(INIT_SUCCEEDED);
  }

Resultado

HH      0       10:18:21.210    LDA Test (EURUSD,H1)    Original X
IQ      0       10:18:21.210    LDA Test (EURUSD,H1)    [[5.1,3.5,1.4,0.2]
HF      0       10:18:21.210    LDA Test (EURUSD,H1)     [4.9,3,1.4,0.2]
...
...
ES      0       10:18:21.211    LDA Test (EURUSD,H1)     [6.5,3,5.2,2]
ML      0       10:18:21.211    LDA Test (EURUSD,H1)     [6.2,3.4,5.4,2.3]
EI      0       10:18:21.211    LDA Test (EURUSD,H1)     [5.9,3,5.1,1.8]]
IL      0       10:18:21.243    LDA Test (EURUSD,H1)    
DD      0       10:18:21.243    LDA Test (EURUSD,H1)    Transformed X
DM      0       10:18:21.243    LDA Test (EURUSD,H1)    [[-1.058063221542643,2.676898315513957]
JD      0       10:18:21.243    LDA Test (EURUSD,H1)     [-1.060778666796316,2.532150351483708]
DM      0       10:18:21.243    LDA Test (EURUSD,H1)     [-0.9139922886488467,2.777963946569435]
...
...
IK      0       10:18:21.244    LDA Test (EURUSD,H1)     [1.527279343196588,-2.300606221030168]
QN      0       10:18:21.244    LDA Test (EURUSD,H1)     [0.9614855249192527,-1.439559895222919]
EF      0       10:18:21.244    LDA Test (EURUSD,H1)     [0.6420061576026481,-2.511057690832021…]

O gráfico resultante ficou bonito:

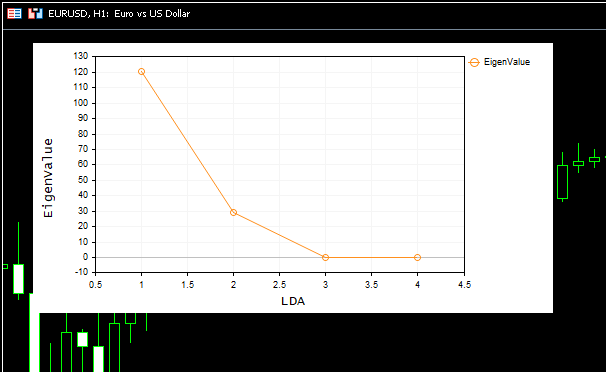
No gráfico Scree Plot, pode-se ver que o melhor número de componentes está no ponto de inflexão 2, e este é exatamente o número de componentes retornado pela nossa classe. Agora, vamos visualizar os componentes retornados. Vamos ver se eles são distintivos, pois o objetivo da redução de dimensionalidade é obter o menor número de componentes que explique todas as diferenças nos dados brutos. Simplificando, esta é uma versão simplificada de nossos dados.

Decidi salvar os componentes do nosso EA em um arquivo CSV e plotá-los com Python, usando https://www.kaggle.com/code/omegajoctan/lda-vs-pca-comComponents-iris-data

  MatrixExtend::WriteCsv("iris-data lda-components.csv",transformed_x);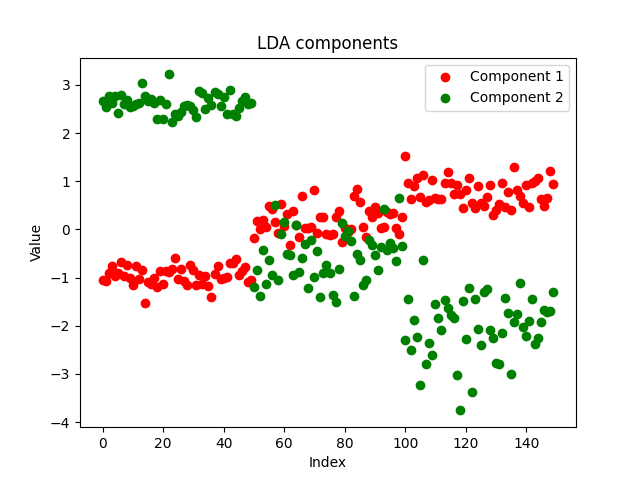

Os componentes parecem limpos, o que prova a implementação bem-sucedida. Agora vamos ver como ficam os componentes do PCA:

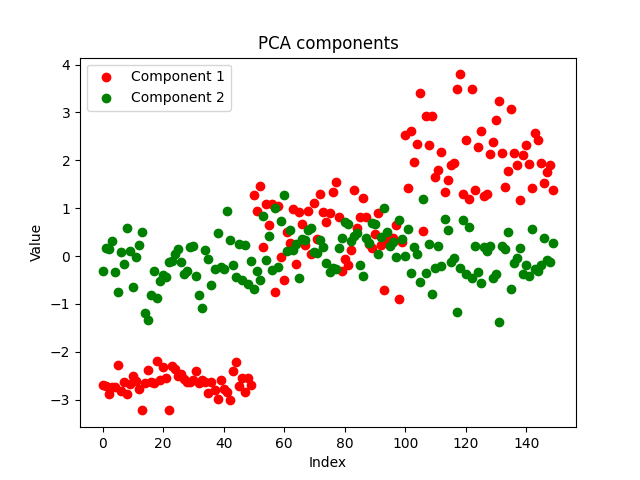
Ambos os métodos separaram bem os dados. Não podemos dizer qual deles funciona melhor apenas olhando para o gráfico. Vamos usar o mesmo modelo com os mesmos parâmetros para o mesmo conjunto de dados e verificar a precisão de ambos os modelos tanto durante o treinamento quanto o teste.

Comparação da eficiência dos algoritmos LDA e PCA no treinamento e teste

Usamos modelos de árvore de decisão com os mesmos parâmetros para os dados separados obtidos pelos algoritmos LDA e PCA, respectivamente.

#include <MALE5\Dimensionality Reduction\LDA.mqh>
#include <MALE5\Dimensionality Reduction\PCA.mqh>
#include <MALE5\Decision Tree\tree.mqh>
#include <MALE5\Metrics.mqh>

CLDA *lda;
CPCA *pca;
CDecisionTreeClassifier *classifier_tree;

input int random_state_ = 42;
input double training_sample_size = 0.7;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---

   string headers;
   matrix data = MatrixExtend::ReadCsv("iris.csv",headers); //Read csv
  
   Print("<<<<<<<< LDA Applied >>>>>>>>>");
   
   matrix x_train, x_test;
   vector y_train, y_test;
   
   MatrixExtend::TrainTestSplitMatrices(data,x_train,y_train,x_test,y_test,training_sample_size,random_state_);
   
   lda = new CLDA(NULL);
   
   matrix x_transformed = lda.fit_transform(x_train, y_train); //Transform the training data
   
   classifier_tree = new CDecisionTreeClassifier();
   classifier_tree.fit(x_transformed, y_train); //Train the model using the transformed data
   
   vector preds = classifier_tree.predict(x_transformed); //Make predictions using the transformed data
   
   Print("Train accuracy: ",Metrics::confusion_matrix(y_train, preds).accuracy);
   
   x_transformed = lda.transform(x_test);
   preds = classifier_tree.predict(x_transformed);
   
   Print("Test accuracy: ",Metrics::confusion_matrix(y_test, preds).accuracy);
   
   delete (classifier_tree);
   delete (lda);
   
//---
   
   Print("<<<<<<<< PCA Applied >>>>>>>>>");
   
   pca = new CPCA(NULL);
   
   x_transformed = pca.fit_transform(x_train);
   
   classifier_tree = new CDecisionTreeClassifier();
   classifier_tree.fit(x_transformed, y_train);
   
   preds = classifier_tree.predict(x_transformed); //Make predictions using the transformed data
   
   Print("Train accuracy: ",Metrics::confusion_matrix(y_train, preds).accuracy);
   
   x_transformed = pca.transform(x_test);
   preds = classifier_tree.predict(x_transformed);
   
   Print("Test accuracy: ",Metrics::confusion_matrix(y_test, preds).accuracy);
   
   delete (classifier_tree);
   delete(pca);

   return(INIT_SUCCEEDED);
  }

Resultados do algoritmo LDA:

GM      0       18:23:18.285    LDA Test (EURUSD,H1)    <<<<<<<< LDA Applied >>>>>>>>>
MR      0       18:23:18.302    LDA Test (EURUSD,H1)    
JP      0       18:23:18.344    LDA Test (EURUSD,H1)    Confusion Matrix
FK      0       18:23:18.344    LDA Test (EURUSD,H1)    [[39,0,0]
CR      0       18:23:18.344    LDA Test (EURUSD,H1)     [0,30,5]
QF      0       18:23:18.344    LDA Test (EURUSD,H1)     [0,2,29]]
IS      0       18:23:18.344    LDA Test (EURUSD,H1)    
OM      0       18:23:18.344    LDA Test (EURUSD,H1)    Classification Report
KF      0       18:23:18.344    LDA Test (EURUSD,H1)    
QQ      0       18:23:18.344    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
FF      0       18:23:18.344    LDA Test (EURUSD,H1)    1.0    1.00     1.00     1.00       1.00     39.0
GI      0       18:23:18.344    LDA Test (EURUSD,H1)    2.0    0.94     0.86     0.97       0.90     35.0
ML      0       18:23:18.344    LDA Test (EURUSD,H1)    3.0    0.85     0.94     0.93       0.89     31.0
OS      0       18:23:18.344    LDA Test (EURUSD,H1)    
FN      0       18:23:18.344    LDA Test (EURUSD,H1)    Accuracy                                   0.93
JO      0       18:23:18.344    LDA Test (EURUSD,H1)    Average   0.93    0.93    0.97      0.93    105.0
KJ      0       18:23:18.344    LDA Test (EURUSD,H1)    W Avg     0.94    0.93    0.97      0.93    105.0
EQ      0       18:23:18.344    LDA Test (EURUSD,H1)    Train accuracy: 0.933
JH      0       18:23:18.344    LDA Test (EURUSD,H1)    Confusion Matrix
LS      0       18:23:18.344    LDA Test (EURUSD,H1)    [[11,0,0]
IJ      0       18:23:18.344    LDA Test (EURUSD,H1)     [0,13,2]
RN      0       18:23:18.344    LDA Test (EURUSD,H1)     [0,1,18]]
IK      0       18:23:18.344    LDA Test (EURUSD,H1)    
OE      0       18:23:18.344    LDA Test (EURUSD,H1)    Classification Report
KN      0       18:23:18.344    LDA Test (EURUSD,H1)    
QI      0       18:23:18.344    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
LN      0       18:23:18.344    LDA Test (EURUSD,H1)    1.0    1.00     1.00     1.00       1.00     11.0
CQ      0       18:23:18.344    LDA Test (EURUSD,H1)    2.0    0.93     0.87     0.97       0.90     15.0
QD      0       18:23:18.344    LDA Test (EURUSD,H1)    3.0    0.90     0.95     0.92       0.92     19.0
OK      0       18:23:18.344    LDA Test (EURUSD,H1)    
FF      0       18:23:18.344    LDA Test (EURUSD,H1)    Accuracy                                   0.93
GD      0       18:23:18.344    LDA Test (EURUSD,H1)    Average   0.94    0.94    0.96      0.94    45.0
HQ      0       18:23:18.344    LDA Test (EURUSD,H1)    W Avg     0.93    0.93    0.96      0.93    45.0
CF      0       18:23:18.344    LDA Test (EURUSD,H1)    Test accuracy: 0.933

O LDA criou um modelo estável com precisão de 93% tanto durante o treinamento quanto o teste. Agora vejamos o desempenho do PCA:

Resultados do algoritmo PCA:

MM      0       18:26:40.994    LDA Test (EURUSD,H1)    <<<<<<<< PCA Applied >>>>>>>>>

LS      0       18:26:41.071    LDA Test (EURUSD,H1)    Confusion Matrix
LJ      0       18:26:41.071    LDA Test (EURUSD,H1)    [[39,0,0]
ER      0       18:26:41.071    LDA Test (EURUSD,H1)     [0,34,1]
OE      0       18:26:41.071    LDA Test (EURUSD,H1)     [0,4,27]]
KD      0       18:26:41.071    LDA Test (EURUSD,H1)    
IL      0       18:26:41.071    LDA Test (EURUSD,H1)    Classification Report
MG      0       18:26:41.071    LDA Test (EURUSD,H1)    
CR      0       18:26:41.071    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
DE      0       18:26:41.071    LDA Test (EURUSD,H1)    1.0    1.00     1.00     1.00       1.00     39.0
EH      0       18:26:41.071    LDA Test (EURUSD,H1)    2.0    0.89     0.97     0.94       0.93     35.0
KL      0       18:26:41.071    LDA Test (EURUSD,H1)    3.0    0.96     0.87     0.99       0.92     31.0
ID      0       18:26:41.071    LDA Test (EURUSD,H1)    
NO      0       18:26:41.071    LDA Test (EURUSD,H1)    Accuracy                                   0.95
CH      0       18:26:41.071    LDA Test (EURUSD,H1)    Average   0.95    0.95    0.98      0.95    105.0
KK      0       18:26:41.071    LDA Test (EURUSD,H1)    W Avg     0.95    0.95    0.98      0.95    105.0
NR      0       18:26:41.071    LDA Test (EURUSD,H1)    Train accuracy: 0.952
LK      0       18:26:41.071    LDA Test (EURUSD,H1)    Confusion Matrix
FR      0       18:26:41.071    LDA Test (EURUSD,H1)    [[11,0,0]
FJ      0       18:26:41.072    LDA Test (EURUSD,H1)     [0,14,1]
MM      0       18:26:41.072    LDA Test (EURUSD,H1)     [0,3,16]]
NL      0       18:26:41.072    LDA Test (EURUSD,H1)    
HD      0       18:26:41.072    LDA Test (EURUSD,H1)    Classification Report
LO      0       18:26:41.072    LDA Test (EURUSD,H1)    
FJ      0       18:26:41.072    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
KM      0       18:26:41.072    LDA Test (EURUSD,H1)    1.0    1.00     1.00     1.00       1.00     11.0
EP      0       18:26:41.072    LDA Test (EURUSD,H1)    2.0    0.82     0.93     0.90       0.88     15.0
HD      0       18:26:41.072    LDA Test (EURUSD,H1)    3.0    0.94     0.84     0.96       0.89     19.0
HL      0       18:26:41.072    LDA Test (EURUSD,H1)    
OG      0       18:26:41.072    LDA Test (EURUSD,H1)    Accuracy                                   0.91
PS      0       18:26:41.072    LDA Test (EURUSD,H1)    Average   0.92    0.93    0.95      0.92    45.0
IP      0       18:26:41.072    LDA Test (EURUSD,H1)    W Avg     0.92    0.91    0.95      0.91    45.0
PE      0       18:26:41.072    LDA Test (EURUSD,H1)    Test accuracy: 0.911

O algoritmo PCA gerou um modelo ainda mais preciso, alcançando uma precisão de 95% no treinamento e 91,1% no teste.

Vantagens da análise discriminante linear (LDA):

O LDA tem várias vantagens, o que torna o algoritmo frequentemente usado em tarefas de classificação e redução de dimensionalidade:

• Reduz eficazmente a dimensionalidade. O LDA reduz a dimensionalidade do espaço de características, transformando as características originais em um espaço de menor dimensionalidade. Essa redução de dimensionalidade permite obter modelos mais simples, "combate a maldição" da dimensionalidade e aumenta a eficiência computacional.
• Preserva informações sobre as diferenças entre classes. O método LDA busca encontrar combinações lineares de características que maximizem a separação entre as classes. O método foca nas diferenças entre as classes para preservar padrões e estruturas importantes de classes específicas.
• Extrai características e as classifica em um único passo. O método LDA realiza simultaneamente a extração e classificação das características. Ele aprende a transformação das características originais e melhora a separabilidade das classes, tornando-o inerentemente adequado para tarefas de classificação. Essa abordagem abrangente permite a criação de modelos mais eficientes e interpretáveis.
• Resistente ao sobreajuste. O método LDA é menos propenso ao sobreajuste em comparação com outros algoritmos de classificação, especialmente quando o número de amostras é pequeno em relação ao número de características. Ao reduzir a dimensionalidade do espaço de características e focar nas características mais distintivas, o método pode generalizar bem para dados não vistos.
• Adequado para classificação multiclasse. O método é bem aplicável a tarefas de classificação envolvendo mais de duas classes. Ele considera as relações entre todas as classes ao mesmo tempo, resultando em fronteiras de separação eficientes em espaços de características multidimensionais.
• Eficiência computacional. Dentro do método, resolvem-se tarefas de busca de autovalores e multiplicação de matrizes — cálculos eficientes que podem ser convenientemente implementados usando métodos embutidos do MQL5. Graças a isso, o algoritmo LDA é adequado para grandes conjuntos de dados e aplicações em tempo real.
• Fácil de interpretar. Os recursos transformados obtidos através do LDA são fáceis de interpretar e analisar, permitindo um melhor entendimento dos padrões subjacentes nos dados. As combinações lineares de características obtidas com o método LDA podem fornecer insights sobre os fatores discriminantes que influenciam a decisão de classificação.
• Suas suposições frequentemente se justificam. O método LDA assume que os dados são normalmente distribuídos dentro de cada classe com matrizes de covariância iguais. Embora isso nem sempre se confirme na prática, o LDA ainda pode funcionar bem, mesmo que tal suposição seja apenas parcialmente verdadeira.

Embora a análise discriminante linear (LDA) tenha várias vantagens, ela também apresenta algumas limitações e desvantagens:

Desvantagens do método de análise discriminante linear (LDA):

• Ele assume uma distribuição gaussiana dentro dos objetos. O método LDA pressupõe que os dados dentro de cada classe são normalmente distribuídos com matrizes de covariância iguais. Se essa suposição não se confirmar, o método pode produzir resultados subótimos ou até mesmo não convergir. Na prática, os dados reais podem ter distribuição não normal, o que pode limitar a eficácia do método.
• Sensibilidade a valores atípicos. O método é sensível a valores atípicos, especialmente quando as matrizes de covariância são estimadas com base em dados limitados. Os valores atípicos podem influenciar significativamente a estimativa das matrizes de covariância e das direções discriminantes resultantes, o que pode levar a resultados de classificação tendenciosos ou não confiáveis.
• Menos flexível na modelagem de relações não lineares. O método assume que os limites de decisão entre as classes são lineares. Se as relações entre as características e as classes forem não lineares, o método pode não capturar eficientemente esses padrões complexos. Nesses casos, métodos de redução de dimensionalidade não lineares ou classificadores não lineares podem ser mais apropriados.
• A maldição da dimensionalidade é real. Quando o número de características é muito maior que o número de amostras, o LDA pode sofrer com a maldição da dimensionalidade. Em espaços de características de alta dimensão, a estimativa das matrizes de covariância torna-se menos confiável, e as direções discriminantes refletem pior a verdadeira estrutura subjacente dos dados.
• Resultados limitados ao trabalhar com classes desbalanceadas. O método funciona pior em distribuições desbalanceadas de classes, quando uma ou mais classes têm significativamente menos amostras do que outras. Nesses casos, a classe com menos amostras pode ser mal representada ao estimar as médias das classes e as matrizes de covariância, dando resultados de classificação enviesados.
• Dificuldade em lidar com dados não numéricos. O método LDA geralmente trabalha com dados numéricos e é difícil aplicá-lo diretamente a conjuntos de dados que contenham variáveis categóricas ou não numéricas. Isso pode exigir pré-processamento, como a codificação de variáveis categóricas ou a conversão de dados não numéricos em representações numéricas, o que pode introduzir dificuldades adicionais e resultar na potencial perda de informação.

LDA versus PCA no ambiente de trading

Para usar os métodos de redução de dimensionalidade no ambiente de trading, precisamos criar uma função para treinar e testar o modelo, após o que poderemos usar o modelo treinado para previsão no testador de estratégias, o que nos ajudará a analisar sua eficácia.

Usaremos 5 indicadores em nosso conjunto de dados, que serão reduzidos usando ambos os métodos:

int OnInit()
  {
  
//--- Trend following indicators

    indicator_handle[0] = iAMA(Symbol(), PERIOD_CURRENT, 9 , 2 , 30, 0, PRICE_OPEN);
    indicator_handle[1] = iADX(Symbol(), PERIOD_CURRENT, 14);
    indicator_handle[2] = iADXWilder(Symbol(), PERIOD_CURRENT, 14);
    indicator_handle[3] = iBands(Symbol(), PERIOD_CURRENT, 20, 0, 2.0, PRICE_OPEN);
    indicator_handle[4] = iDEMA(Symbol(), PERIOD_CURRENT, 14, 0, PRICE_OPEN);
 }

Como esses algoritmos não foram programados para aprender e exibir sinais de trading significativos devido à sua natureza, usaremos uma árvore de decisão para fazer previsões com base nos dados transformados, tanto no treinamento quanto no teste.

void TrainTest()
 {
   vector buffer = {};
   for (int i=0; i<ArraySize(indicator_handle); i++)
    {
      buffer.CopyIndicatorBuffer(indicator_handle[i], 0, 0, bars); //copy indicator buffer
      dataset.Col(buffer, i); //add the indicator buffer values to the dataset matrix 
    }

//---
  
   vector y(bars);
   MqlRates rates[];
   CopyRates(Symbol(), PERIOD_CURRENT,0,bars, rates);
   for (int i=0; i<bars; i++) //Creating the target variable 
     {
       if (rates[i].close > rates[i].open) //if bullish candle assign 1 to the y variable else assign the 0 class
        y[i] = 1;
       else
        y[0] = 0;
     }  
     
//---
   
   dataset.Col(y, dataset.Cols()-1); //add the y variable to the last column
   
//---

   matrix x_train, x_test;
   vector y_train, y_test;
      
   MatrixExtend::TrainTestSplitMatrices(dataset,x_train,y_train,x_test,y_test,training_sample_size,random_state_);
   
   matrix x_transformed = {};
   switch(dimension_reduction)
     {
      case  LDA:
         
         lda = new CLDA(NULL);
         
         x_transformed = lda.fit_transform(x_train, y_train); //Transform the training data   
         
        break;
      case PCA:
      
         pca = new CPCA(NULL);
         
         x_transformed = pca.fit_transform(x_train);
         
        break;
     }
     
   
   classifier_tree = new CDecisionTreeClassifier();
   classifier_tree.fit(x_transformed, y_train); //Train the model using the transformed data
   
   vector preds = classifier_tree.predict(x_transformed); //Make predictions using the transformed data
   
   Print("Train accuracy: ",Metrics::confusion_matrix(y_train, preds).accuracy);
   
   switch(dimension_reduction)
     {
      case  LDA:
        
        x_transformed = lda.transform(x_test); //Transform the testing data   
        
        break;
        
      case PCA:
        
        x_transformed = pca.transform(x_test); 
        
        break;
     }
   preds = classifier_tree.predict(x_transformed);
   
   Print("Test accuracy: ",Metrics::confusion_matrix(y_test, preds).accuracy);
   
 }

Depois de treinar os dados, eles precisam ser testados. Abaixo estão os resultados de ambos os métodos. Primeiro vem o LDA: 

JK      0       01:00:24.440    LDA Test (EURUSD,H1)    
GK      0       01:00:37.442    LDA Test (EURUSD,H1)    Confusion Matrix
QR      0       01:00:37.442    LDA Test (EURUSD,H1)    [[60,266]
FF      0       01:00:37.442    LDA Test (EURUSD,H1)     [46,328]]
DR      0       01:00:37.442    LDA Test (EURUSD,H1)    
RN      0       01:00:37.442    LDA Test (EURUSD,H1)    Classification Report
FE      0       01:00:37.442    LDA Test (EURUSD,H1)    
LP      0       01:00:37.442    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
HD      0       01:00:37.442    LDA Test (EURUSD,H1)    0.0    0.57     0.18     0.88       0.28     326.0
FI      0       01:00:37.442    LDA Test (EURUSD,H1)    1.0    0.55     0.88     0.18       0.68     374.0
RM      0       01:00:37.442    LDA Test (EURUSD,H1)    
QH      0       01:00:37.442    LDA Test (EURUSD,H1)    Accuracy                                   0.55
KQ      0       01:00:37.442    LDA Test (EURUSD,H1)    Average   0.56    0.53    0.53      0.48    700.0
HP      0       01:00:37.442    LDA Test (EURUSD,H1)    W Avg     0.56    0.55    0.51      0.49    700.0
KK      0       01:00:37.442    LDA Test (EURUSD,H1)    Train accuracy: 0.554
DR      0       01:00:37.443    LDA Test (EURUSD,H1)    Confusion Matrix
CD      0       01:00:37.443    LDA Test (EURUSD,H1)    [[20,126]
LO      0       01:00:37.443    LDA Test (EURUSD,H1)     [12,142]]
OK      0       01:00:37.443    LDA Test (EURUSD,H1)    
ME      0       01:00:37.443    LDA Test (EURUSD,H1)    Classification Report
QN      0       01:00:37.443    LDA Test (EURUSD,H1)    
GI      0       01:00:37.443    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
JM      0       01:00:37.443    LDA Test (EURUSD,H1)    0.0    0.62     0.14     0.92       0.22     146.0
KR      0       01:00:37.443    LDA Test (EURUSD,H1)    1.0    0.53     0.92     0.14       0.67     154.0
MF      0       01:00:37.443    LDA Test (EURUSD,H1)    
MQ      0       01:00:37.443    LDA Test (EURUSD,H1)    Accuracy                                   0.54
MJ      0       01:00:37.443    LDA Test (EURUSD,H1)    Average   0.58    0.53    0.53      0.45    300.0
OI      0       01:00:37.443    LDA Test (EURUSD,H1)    W Avg     0.58    0.54    0.52      0.45    300.0
QP      0       01:00:37.443    LDA Test (EURUSD,H1)    Test accuracy: 0.54

O PCA mostrou melhores resultados durante o treinamento e um pouco piores nos testes:

GE      0       01:01:57.202    LDA Test (EURUSD,H1)    
MS      0       01:01:57.202    LDA Test (EURUSD,H1)    Classification Report
IH      0       01:01:57.202    LDA Test (EURUSD,H1)    
OS      0       01:01:57.202    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
KG      0       01:01:57.202    LDA Test (EURUSD,H1)    0.0    0.62     0.28     0.85       0.39     326.0
GL      0       01:01:57.202    LDA Test (EURUSD,H1)    1.0    0.58     0.85     0.28       0.69     374.0
MP      0       01:01:57.202    LDA Test (EURUSD,H1)    
JK      0       01:01:57.202    LDA Test (EURUSD,H1)    Accuracy                                   0.59
HL      0       01:01:57.202    LDA Test (EURUSD,H1)    Average   0.60    0.57    0.57      0.54    700.0
CG      0       01:01:57.202    LDA Test (EURUSD,H1)    W Avg     0.60    0.59    0.55      0.55    700.0
EF      0       01:01:57.202    LDA Test (EURUSD,H1)    Train accuracy: 0.586
HO      0       01:01:57.202    LDA Test (EURUSD,H1)    Confusion Matrix
GG      0       01:01:57.202    LDA Test (EURUSD,H1)    [[26,120]
GJ      0       01:01:57.202    LDA Test (EURUSD,H1)     [29,125]]
KN      0       01:01:57.202    LDA Test (EURUSD,H1)    
QJ      0       01:01:57.202    LDA Test (EURUSD,H1)    Classification Report
MQ      0       01:01:57.202    LDA Test (EURUSD,H1)    
CL      0       01:01:57.202    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
QP      0       01:01:57.202    LDA Test (EURUSD,H1)    0.0    0.47     0.18     0.81       0.26     146.0
GE      0       01:01:57.202    LDA Test (EURUSD,H1)    1.0    0.51     0.81     0.18       0.63     154.0
QI      0       01:01:57.202    LDA Test (EURUSD,H1)    
MD      0       01:01:57.202    LDA Test (EURUSD,H1)    Accuracy                                   0.50
RE      0       01:01:57.202    LDA Test (EURUSD,H1)    Average   0.49    0.49    0.49      0.44    300.0
IL      0       01:01:57.202    LDA Test (EURUSD,H1)    W Avg     0.49    0.50    0.49      0.45    300.0
PP      0       01:01:57.202    LDA Test (EURUSD,H1)    Test accuracy: 0.503

Finalmente, podemos criar uma estratégia de trading simples baseada nos sinais fornecidos pelo modelo de árvore de decisão.

void OnTick()
  {
//---

   if (!train_once) //call the function to train the model once on the program lifetime
    {
      TrainTest();
      train_once = true; 
    }

//--- 
   
   vector inputs(indicator_handle.Size());
   vector buffer;
   
   for (uint i=0; i<indicator_handle.Size(); i++)
     {
       buffer.CopyIndicatorBuffer(indicator_handle[i], 0, 0, 1); //copy the current indicator value
       inputs[i] = buffer[0]; //add its value to the inputs vector 
     }

//---
    
    SymbolInfoTick(Symbol(), ticks);
      
     if (isnewBar(PERIOD_CURRENT)) // We want to trade on the bar opening 
      {
        vector transformed_inputs = {};
         switch(dimension_reduction) //transform every new data to fit the dimensions selected during training
           {
            case  LDA:
               transformed_inputs = lda.transform(inputs); //Transform the new data   
              break;
            case PCA:
               transformed_inputs = pca.transform(inputs);
              break;
           }
     
        int signal = (int)classifier_tree.predict(transformed_inputs);
        double min_lot = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN);
        SymbolInfoTick(Symbol(), ticks);
        
         if (signal == -1)
           {
              if (!PosExists(MAGICNUMBER, POSITION_TYPE_SELL)) // If a sell trade doesnt exist
                m_trade.Sell(min_lot, Symbol(), ticks.bid, ticks.bid+stoploss*Point(), ticks.bid - takeprofit*Point());
           }
         else
           {
             if (!PosExists(MAGICNUMBER, POSITION_TYPE_BUY))  // If a buy trade doesnt exist
               m_trade.Buy(min_lot, Symbol(), ticks.ask, ticks.ask-stoploss*Point(), ticks.ask + takeprofit*Point());
           }
      }
  }

Testei no modo de preços de abertura de janeiro de 2023 a fevereiro de 2024. Ambos os métodos funcionaram em uma estratégia simples:

Análise Discriminante Linear (LDA):

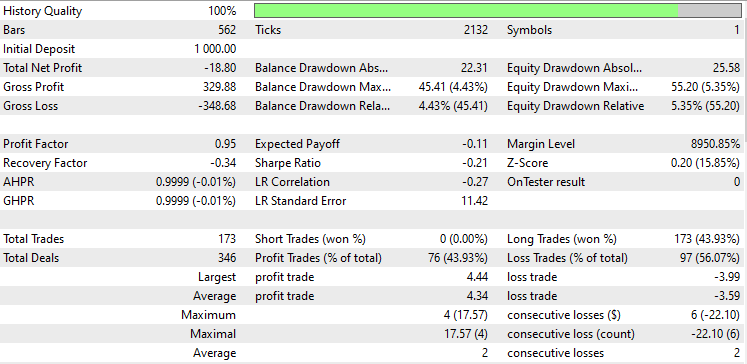
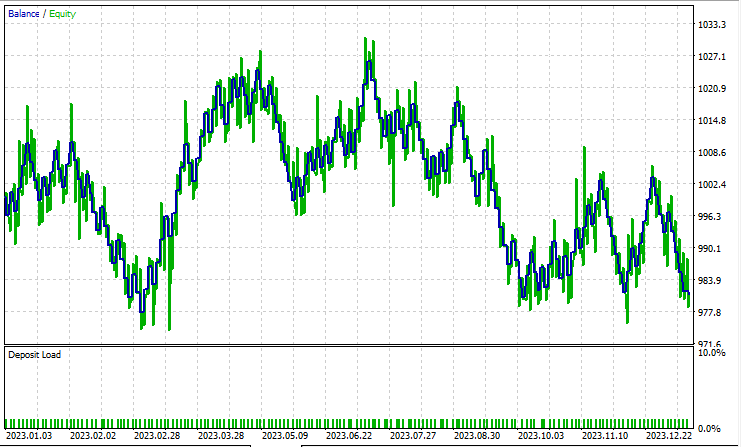
Teste com Análise de Componentes Principais (PCA):

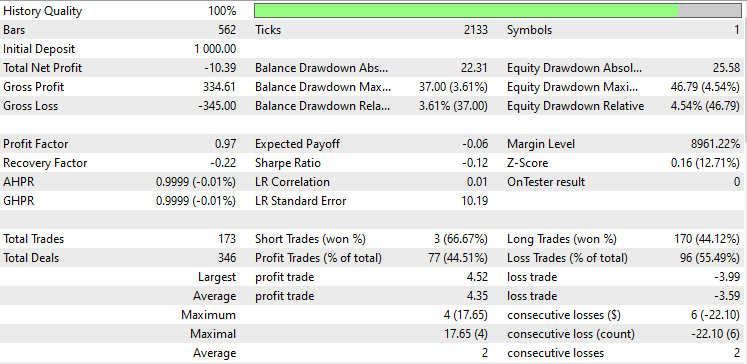
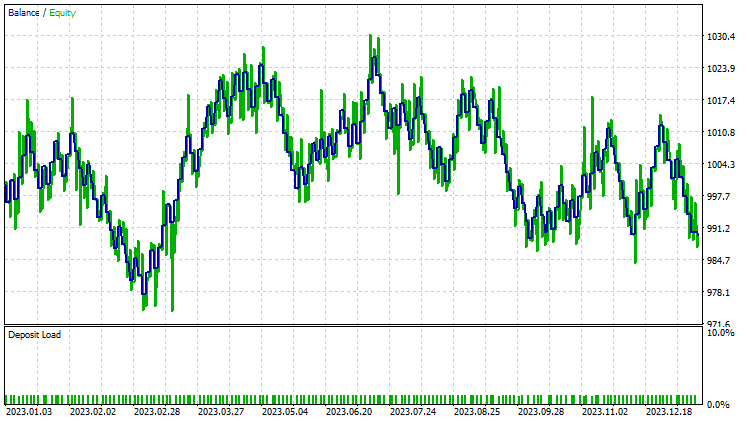
Os resultados são quase idênticos: o modelo com LDA teve uma perda de 8 dólares a mais do que o PCA. Em termos de trabalho com dados, o testador de estratégias é menos relevante para métodos de redução de dimensionalidade, pois seu objetivo principal é simplificar as variáveis, especialmente ao lidar com grandes volumes de dados. Além disso, ao executar esse EA no testador de estratégias, encontrei algumas inconsistências nos cálculos, causadas por erros inesperados nos métodos matriciais e vetoriais. Recomendo executar o programa várias vezes até obter um resultado significativo, caso encontre erros.

Se você acompanhou esta série de artigos, talvez esteja se perguntando por que não escalamos os dados transformados obtidos com esses dois métodos, como fizemos no artigo anterior.

A necessidade de normalizar os dados dos algoritmos PCA ou LDA para o modelo de aprendizado de máquina depende das características específicas do seu conjunto de dados, do algoritmo usado e dos objetivos. O que considerar:

• Transformação — os métodos trabalham com a matriz de covariância dos recursos originais e encontram componentes ortogonais (componentes principais) que transmitem a máxima variância dos dados. Os dados transformados obtidos por esses métodos consistem nesses componentes principais.
• Normalização antes de usar PCA ou LDA. Frequentemente, normalizam-se os objetos originais antes de executar o método PCA ou LDA, especialmente se os objetos tiverem diferentes escalas ou unidades de medida. A normalização garante que todas as características contribuam igualmente para a matriz de covariância e evita que características com escalas maiores dominem os componentes principais.
• Normalização após métodos PCA ou LDA. A necessidade de normalizar os dados transformados depende dos requisitos específicos do seu algoritmo de aprendizado de máquina e das características dos recursos transformados. Algoritmos como regressão logística ou k-vizinhos mais próximos são sensíveis às diferenças nas escalas dos recursos e podem se beneficiar da normalização dos recursos, mesmo após métodos PCA ou LDA.

• Outros algoritmos, como as árvores de decisão que usamos, são menos sensíveis às escalas dos recursos e podem funcionar sem a normalização dos dados após a redução de dimensionalidade.

• Impacto da normalização na interpretabilidade. A normalização após métodos LDA e PCA pode afetar a interpretabilidade dos componentes principais. Se for necessário entender a contribuição dos recursos originais para os componentes principais, a normalização dos dados transformados pode ocultar essas relações.
• Impacto no desempenho. Experimente tanto com dados transformados normalizados quanto não normalizados para avaliar o impacto no desempenho do modelo. Em alguns casos, a normalização pode levar a uma melhor convergência, aprimorar a generalização ou acelerar o treinamento, enquanto em outros casos pode não ter praticamente nenhum efeito.

Você pode acompanhar o desenvolvimento deste modelo de aprendizado de máquina e muito mais desta série de artigos no meu https://github.com/MegaJoctan/MALE5.

Conteúdo do anexo:

Arquivo	Descrição/propósito
tree.mqh	Modelo do classificador de árvore de decisão.
MatrixExtend.mqh	Funções adicionais para trabalhar com matrizes.
metrics.mqh	Funções e código para medir o desempenho dos modelos de aprendizado de máquina.
preprocessing.mqh	Biblioteca para pré-processamento de dados brutos, tornando-os adequados para uso em modelos de aprendizado de máquina.
base.mqh	Biblioteca base para usar métodos PCA e LDA, contém funções que simplificam a escrita de código.
pca.mqh	Biblioteca do método de Análise de Componentes Principais (PCA).
lda.mqh	Biblioteca do método de Análise Discriminante Linear (LDA).
plots.mqh	Biblioteca para plotar vetores e matrizes.
lda vs pca script.mq5	Script para demonstrar os algoritmos PCA e LDA.
LDA Test.mq5	Expert Advisor principal para testar a maior parte do código.
iris.csv	Conjunto de dados para testar o modelo Iris.