Aprendizaje automático y Data Science (Parte 20): Elección entre LDA y PCA en tareas de trading algorítmico en MQL5

-- Cuanto más tienes, menos te das cuenta.

¿Qué es el análisis discriminante lineal (LDA)?

El LDA es un algoritmo de aprendizaje automático supervisado generalizable cuyo objetivo es encontrar una combinación lineal de características que separe mejor las clases en un conjunto de datos.

Al igual que el Análisis de Componentes Principales (PCA), es un algoritmo de reducción de la dimensionalidad. Estos algoritmos se usan a menudo para reducir la dimensionalidad. En este artículo, los compararemos y veremos en qué situación funciona mejor cada uno de ellos. Ya hemos hablado del PCA en artículos anteriores de esta serie. Empezaremos con una introducción al algoritmo LDA, ya que el cuerpo principal del artículo estará dedicado a este algoritmo y a su comparación con el PCA. Compararemos el rendimiento de estos dos algoritmos usando un conjunto de datos sencillo y el simulador de estrategias.

Objetivos/teoría

Para qué sirve el método de análisis discriminante lineal:

• Mejora de la separabilidad de las clases: El LDA trata de encontrar combinaciones lineales de características con las que se produzca la máxima separación entre clases en los datos. Proyectando los datos sobre estas dimensiones discriminativas, el LDA ayuda a amplificar las diferencias entre clases, lo cual hace más eficaz la clasificación.
• Reducción de la dimensionalidad: El LDA reduce la dimensionalidad del espacio de características proyectando los datos en un subespacio de dimensionalidad menor. Al reducir la dimensionalidad, se conserva tanta información sobre las diferencias de clase como resulte posible. Reducir el espacio de características puede dar lugar a modelos más simples, cálculos más rápidos y un mayor rendimiento.
• Minimización de la variabilidad intraclase: El LDA trata de minimizar la dispersión o variabilidad dentro de una clase garantizando que los puntos de datos que pertenecen a la misma clase se agrupen estrechamente en el espacio transformado. Gracias a la variabilidad intraclase, el LDA ayuda a mejorar la separación entre clases y a aumentar la fiabilidad del modelo de clasificación.
• Aumento de la distancia entre clases: Por el contrario, el LDA intenta maximizar la distinción entre clases estableciendo la máxima distancia posible entre clases en el espacio transformado. De esta forma, el algoritmo LDA puede establecer distinciones más claras entre las clases y hacer que la clasificación resulte más precisa.
• Capacidades de clasificación multiclase: El LDA es adecuado para agrupar características en más de dos clases. Dadas las relaciones entre todas las clases simultáneamente, el algoritmo encuentra un subespacio común que separe de forma óptima todas las clases. Haciendo esto, obtendremos límites de clasificación eficientes en espacios de características multidimensionales.

Supuestos:

El método de análisis discriminante lineal parte de varios supuestos. Por lo tanto, se supone que

1. Las mediciones resultan independientes entre sí.
   
2. Los datos suelen estar distribuidos dentro de los objetos.
3. Las clases del conjunto de datos tienen la misma matriz de covarianza.

Pasos del algoritmo LDA

1. Cálculo de la matriz de dispersión dentro de la clase (SW):

Calculamos la matriz de dispersión para cada clase.

  matrix SW, SB; //within and between scatter matrices 
  SW.Init(num_features, num_features);
  SB.Init(num_features, num_features);
  
  for (ulong i=0; i<num_classes; i++)
   {
     matrix class_samples = {};
      for (ulong j=0, count=0; j<x.Rows(); j++)
         {
           if (y[j] == classes[i]) //Collect a matrix for samples belonging to a particular class
            {
               count++;
               class_samples.Resize(count, num_features);
               class_samples.Row(x.Row(j), count-1);
            }
         }

         
     matrix diff = Base::subtract(class_samples, class_means.Row(i)); //Each row subtracted to the mean
     if (diff.Rows()==0 && diff.Cols()==0) //if the subtracted matrix is zero stop the program for possible bugs or errors
      {
        DebugBreak();
        return x_centered;
      }
     
     SW += diff.Transpose().MatMul(diff); //Find within scatter matrix 
     
     vector mean_diff = class_means.Row(i) - x_centered.Mean(0);
     SB += class_samples.Rows() * mean_diff.Outer(mean_diff); //compute between scatter matrix 
   }

Sumamos estas matrices de dispersión individuales para obtener la matriz de dispersión dentro de una clase.

2. Cálculo de la matriz de dispersión entre clases (SB):

Encontramos el vector medio para cada clase.

  matrix SW, SB; //within and between scatter matrices 
  SW.Init(num_features, num_features);
  SB.Init(num_features, num_features);
  
  for (ulong i=0; i<num_classes; i++)
   {

     matrix class_samples = {};
      for (ulong j=0, count=0; j<x.Rows(); j++)
         {
           if (y[j] == classes[i]) //Collect a matrix for samples belonging to a particular class
            {
               count++;
               class_samples.Resize(count, num_features);
               class_samples.Row(x.Row(j), count-1);
            }
         }
         
     matrix diff = Base::subtract(class_samples, class_means.Row(i)); //Each row subtracted to the mean
     if (diff.Rows()==0 && diff.Cols()==0) //if the subtracted matrix is zero stop the program for possible bugs or errors
      {
        DebugBreak();
        return x_centered;
      }
     
     SW += diff.Transpose().MatMul(diff); //Find within scatter matrix 
     
     vector mean_diff = class_means.Row(i) - x_centered.Mean(0);
     SB += class_samples.Rows() * mean_diff.Outer(mean_diff); //compute between scatter matrix 
   }

Calculamos la matriz de dispersión entre clases.

     SB += class_samples.Rows() * mean_diff.Outer(mean_diff); //compute between scatter matrix 

3. Cálculo de valores y vectores propios

Resolveremos el problema generalizado de los valores propios incluyendo SW y SB, y obteniendo los valores propios y sus correspondientes vectores propios.

  matrix eigen_vectors;
  vector eigen_values;
  
  matrix SBSW = SW.Inv().MatMul(SB);
  
  SBSW += this.m_regparam * MatrixExtend::eye((uint)SBSW.Rows());
  
  if (!SBSW.Eig(eigen_vectors, eigen_values))
    {
      Print("%s Failed to calculate eigen values and vectors Err=%d",__FUNCTION__,GetLastError());
      DebugBreak();
      
      matrix empty = {};
      return empty;
    }

Selección de características distintivas:

Clasificamos los valores propios en orden descendente.

   vector args = MatrixExtend::ArgSort(eigen_values);
   MatrixExtend::Reverse(args);
   
   eigen_values = Base::Sort(eigen_values, args);
   eigen_vectors = Base::Sort(eigen_vectors, args);   

Seleccionamos los k mejores vectores propios para formar la matriz de transformación.

   this.m_components = extract_components(eigen_values);

Como tanto el análisis discriminante lineal LDA como el análisis de componentes principales PCA sirven al mismo propósito de reducción de dimensionalidad, podemos utilizar métodos similares para extraer los componentes, como la varianza y el gráfico de valores propios Scree Plot. Son los mismos que usamos en el artículo sobre el PCA.

Podemos ampliar nuestra clase de algoritmo LDA para que pueda extraer componentes para sí misma cuando el número por defecto de componentes es NULL.

  if (this.m_components == NULL)
    this.m_components = extract_components(eigen_values);
  else //plot the scree plot 
    extract_components(eigen_values);

Proyección de datos en un nuevo espacio de objetos

Multiplicamos los datos originales por los vectores propios seleccionados para obtener un nuevo espacio de características.

  this.projection_matrix = Base::Slice(eigen_vectors, this.m_components);
    
  return x_centered.MatMul(projection_matrix.Transpose());

Todo este código se ejecutará dentro de la función fit_transform. Esta función se encarga de entrenar y preparar el algoritmo de análisis discriminante lineal. Para que nuestra clase pueda procesar los datos nuevos/no vistos, necesitaremos añadir funciones para las transformaciones posteriores.

matrix CLDA::transform(const matrix &x)
 {
   if (this.projection_matrix.Rows() == 0)
    {
      printf("%s fit_transform method must be called befor transform",__FUNCTION__);
      matrix empty = {};
      return empty; 
    }
  matrix x_centered = Base::subtract(x, this.mean);
  
  return x_centered.MatMul(this.projection_matrix.Transpose());  
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
vector CLDA::transform(const vector &x)
 {
   matrix m = MatrixExtend::VectorToMatrix(x, this.num_features); 
   
   if (m.Rows()==0)
    {
      vector empty={};
      return empty; //return nothing since there is a failure in converting vector to matrix
    }
   
   m = transform(m);
   return MatrixExtend::MatrixToVector(m);
 }

Visión general de la clase LDA

La clase general del algoritmo LDA tendrá ahora este aspecto:

enum lda_criterion //selecting best components criteria selection
  {
    CRITERION_VARIANCE,
    CRITERION_KAISER,
    CRITERION_SCREE_PLOT
  };

class CLDA
  {  
CPlots   plt;

protected:
   uint m_components;
   lda_criterion m_criterion;
   
   matrix projection_matrix;
   ulong num_features;
   double m_regparam;
   vector mean;
   
   uint CLDA::extract_components(vector &eigen_values, double threshold=0.95);
   
public:
                     CLDA(uint k=NULL, lda_criterion CRITERION_=CRITERION_SCREE_PLOT, double reg_param =1e-6);
                    ~CLDA(void);
                    
                     matrix fit_transform(const matrix &x, const vector &y);
                     matrix transform(const matrix &x);
                     vector transform(const vector &x);
  };

El parámetro de regularización reg_param tiene un valor menor porque solo se utiliza para regularizar las matrices SW y SB. Así se evitan errores en el cálculo de los valores propios y los vectores.

   SW += this.m_regparam * MatrixExtend::eye((uint)num_features);
   SB += this.m_regparam * MatrixExtend::eye((uint)num_features);

Análisis discriminante lineal de la muestra

Vamos a aplicar nuestra clase LDA a una muestra de datos popular Iris-csv y a ver qué hace.

   string headers;
   matrix data = MatrixExtend::ReadCsv("iris.csv",headers); //Read csv

Recuerde que se trata de un método de aprendizaje supervisado. Esto significa que deberemos recoger las variables independientes y objetivo por separado y transmitirlas al modelo.

   matrix x;
   vector y;
   MatrixExtend::XandYSplitMatrices(data, x, y);   

#include <MALE5\Dimensionality Reduction\LDA.mqh>

CLDA *lda;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---

   string headers;
   matrix data = MatrixExtend::ReadCsv("iris.csv",headers); //Read csv
   
   matrix x;
   vector y;
   MatrixExtend::XandYSplitMatrices(data, x, y);
   
   Print("Original X\n",x);
   
   lda = new CLDA();
   matrix transformed_x = lda.fit_transform(x, y);
   
   Print("Transformed X\n",transformed_x);
   
   return(INIT_SUCCEEDED);
  }

Resultado

HH      0       10:18:21.210    LDA Test (EURUSD,H1)    Original X
IQ      0       10:18:21.210    LDA Test (EURUSD,H1)    [[5.1,3.5,1.4,0.2]
HF      0       10:18:21.210    LDA Test (EURUSD,H1)     [4.9,3,1.4,0.2]
...
...
ES      0       10:18:21.211    LDA Test (EURUSD,H1)     [6.5,3,5.2,2]
ML      0       10:18:21.211    LDA Test (EURUSD,H1)     [6.2,3.4,5.4,2.3]
EI      0       10:18:21.211    LDA Test (EURUSD,H1)     [5.9,3,5.1,1.8]]
IL      0       10:18:21.243    LDA Test (EURUSD,H1)    
DD      0       10:18:21.243    LDA Test (EURUSD,H1)    Transformed X
DM      0       10:18:21.243    LDA Test (EURUSD,H1)    [[-1.058063221542643,2.676898315513957]
JD      0       10:18:21.243    LDA Test (EURUSD,H1)     [-1.060778666796316,2.532150351483708]
DM      0       10:18:21.243    LDA Test (EURUSD,H1)     [-0.9139922886488467,2.777963946569435]
...
...
IK      0       10:18:21.244    LDA Test (EURUSD,H1)     [1.527279343196588,-2.300606221030168]
QN      0       10:18:21.244    LDA Test (EURUSD,H1)     [0.9614855249192527,-1.439559895222919]
EF      0       10:18:21.244    LDA Test (EURUSD,H1)     [0.6420061576026481,-2.511057690832021…]

Hemos obtenido un gráfico precioso:

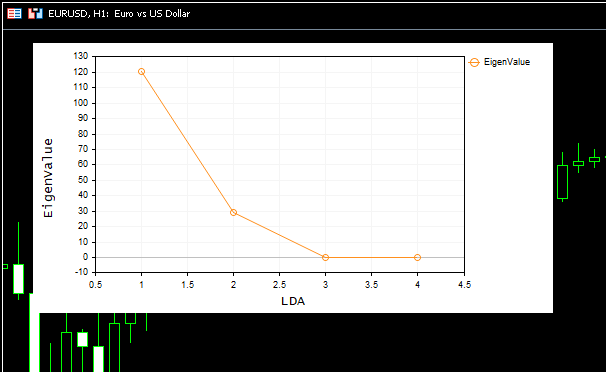
El Scree Plot muestra que el mejor número de componentes se encuentra en el punto de flexión 2, y este es exactamente el número de componentes que ha retornado nuestra clase. Ahora vamos a visualizar los componentes retornados. Veamos si son distintivos, pues el objetivo de la reducción de la dimensionalidad consiste en obtener el número mínimo de componentes que explica toda la variación de los datos brutos. En pocas palabras, supone una versión simplificada de nuestros datos.

Hemos decidido guardar los componentes de nuestro asesor en un archivo csv y construirlos con Python usando https://www.kaggle.com/code/omegajoctan/lda-vs-pca-comComponents-iris-data

  MatrixExtend::WriteCsv("iris-data lda-components.csv",transformed_x);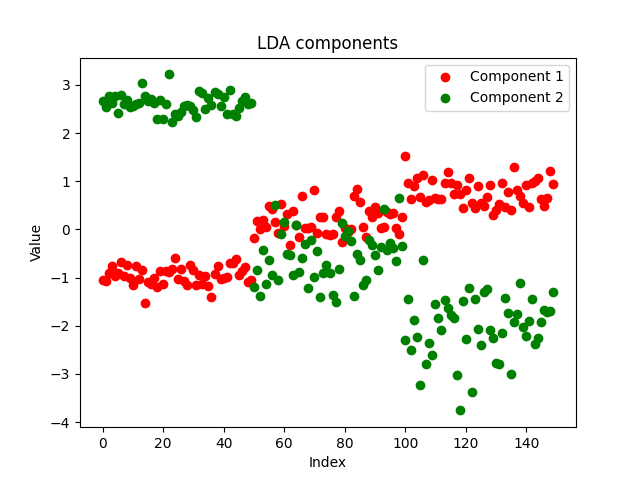

Los componentes tienen un aspecto bastante aseado, lo cual demuestra el éxito de la aplicación. Veamos ahora cómo son los componentes del PCA:

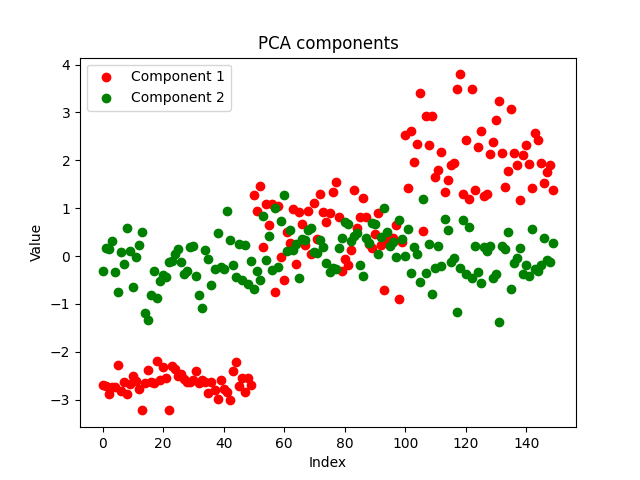
Ambos métodos han separado bien los datos. No podemos decir cuál funciona mejor simplemente mirando el gráfico. Utilizaremos el mismo modelo con los mismos parámetros para el mismo conjunto de datos y comprobaremos la precisión de ambos modelos tanto en el entrenamiento como en las pruebas.

Comparación del rendimiento de los algoritmos LDA y PCA en el entrenamiento y la prueba

Usaremos modelos de árboles de decisión con los mismos parámetros para los datos individuales obtenidos mediante los algoritmos LDA y PCA, respectivamente.

#include <MALE5\Dimensionality Reduction\LDA.mqh>
#include <MALE5\Dimensionality Reduction\PCA.mqh>
#include <MALE5\Decision Tree\tree.mqh>
#include <MALE5\Metrics.mqh>

CLDA *lda;
CPCA *pca;
CDecisionTreeClassifier *classifier_tree;

input int random_state_ = 42;
input double training_sample_size = 0.7;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---

   string headers;
   matrix data = MatrixExtend::ReadCsv("iris.csv",headers); //Read csv
  
   Print("<<<<<<<< LDA Applied >>>>>>>>>");
   
   matrix x_train, x_test;
   vector y_train, y_test;
   
   MatrixExtend::TrainTestSplitMatrices(data,x_train,y_train,x_test,y_test,training_sample_size,random_state_);
   
   lda = new CLDA(NULL);
   
   matrix x_transformed = lda.fit_transform(x_train, y_train); //Transform the training data
   
   classifier_tree = new CDecisionTreeClassifier();
   classifier_tree.fit(x_transformed, y_train); //Train the model using the transformed data
   
   vector preds = classifier_tree.predict(x_transformed); //Make predictions using the transformed data
   
   Print("Train accuracy: ",Metrics::confusion_matrix(y_train, preds).accuracy);
   
   x_transformed = lda.transform(x_test);
   preds = classifier_tree.predict(x_transformed);
   
   Print("Test accuracy: ",Metrics::confusion_matrix(y_test, preds).accuracy);
   
   delete (classifier_tree);
   delete (lda);
   
//---
   
   Print("<<<<<<<< PCA Applied >>>>>>>>>");
   
   pca = new CPCA(NULL);
   
   x_transformed = pca.fit_transform(x_train);
   
   classifier_tree = new CDecisionTreeClassifier();
   classifier_tree.fit(x_transformed, y_train);
   
   preds = classifier_tree.predict(x_transformed); //Make predictions using the transformed data
   
   Print("Train accuracy: ",Metrics::confusion_matrix(y_train, preds).accuracy);
   
   x_transformed = pca.transform(x_test);
   preds = classifier_tree.predict(x_transformed);
   
   Print("Test accuracy: ",Metrics::confusion_matrix(y_test, preds).accuracy);
   
   delete (classifier_tree);
   delete(pca);

   return(INIT_SUCCEEDED);
  }

Resultados del algoritmo LDA:

GM      0       18:23:18.285    LDA Test (EURUSD,H1)    <<<<<<<< LDA Applied >>>>>>>>>
MR      0       18:23:18.302    LDA Test (EURUSD,H1)    
JP      0       18:23:18.344    LDA Test (EURUSD,H1)    Confusion Matrix
FK      0       18:23:18.344    LDA Test (EURUSD,H1)    [[39,0,0]
CR      0       18:23:18.344    LDA Test (EURUSD,H1)     [0,30,5]
QF      0       18:23:18.344    LDA Test (EURUSD,H1)     [0,2,29]]
IS      0       18:23:18.344    LDA Test (EURUSD,H1)    
OM      0       18:23:18.344    LDA Test (EURUSD,H1)    Classification Report
KF      0       18:23:18.344    LDA Test (EURUSD,H1)    
QQ      0       18:23:18.344    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
FF      0       18:23:18.344    LDA Test (EURUSD,H1)    1.0    1.00     1.00     1.00       1.00     39.0
GI      0       18:23:18.344    LDA Test (EURUSD,H1)    2.0    0.94     0.86     0.97       0.90     35.0
ML      0       18:23:18.344    LDA Test (EURUSD,H1)    3.0    0.85     0.94     0.93       0.89     31.0
OS      0       18:23:18.344    LDA Test (EURUSD,H1)    
FN      0       18:23:18.344    LDA Test (EURUSD,H1)    Accuracy                                   0.93
JO      0       18:23:18.344    LDA Test (EURUSD,H1)    Average   0.93    0.93    0.97      0.93    105.0
KJ      0       18:23:18.344    LDA Test (EURUSD,H1)    W Avg     0.94    0.93    0.97      0.93    105.0
EQ      0       18:23:18.344    LDA Test (EURUSD,H1)    Train accuracy: 0.933
JH      0       18:23:18.344    LDA Test (EURUSD,H1)    Confusion Matrix
LS      0       18:23:18.344    LDA Test (EURUSD,H1)    [[11,0,0]
IJ      0       18:23:18.344    LDA Test (EURUSD,H1)     [0,13,2]
RN      0       18:23:18.344    LDA Test (EURUSD,H1)     [0,1,18]]
IK      0       18:23:18.344    LDA Test (EURUSD,H1)    
OE      0       18:23:18.344    LDA Test (EURUSD,H1)    Classification Report
KN      0       18:23:18.344    LDA Test (EURUSD,H1)    
QI      0       18:23:18.344    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
LN      0       18:23:18.344    LDA Test (EURUSD,H1)    1.0    1.00     1.00     1.00       1.00     11.0
CQ      0       18:23:18.344    LDA Test (EURUSD,H1)    2.0    0.93     0.87     0.97       0.90     15.0
QD      0       18:23:18.344    LDA Test (EURUSD,H1)    3.0    0.90     0.95     0.92       0.92     19.0
OK      0       18:23:18.344    LDA Test (EURUSD,H1)    
FF      0       18:23:18.344    LDA Test (EURUSD,H1)    Accuracy                                   0.93
GD      0       18:23:18.344    LDA Test (EURUSD,H1)    Average   0.94    0.94    0.96      0.94    45.0
HQ      0       18:23:18.344    LDA Test (EURUSD,H1)    W Avg     0.93    0.93    0.96      0.93    45.0
CF      0       18:23:18.344    LDA Test (EURUSD,H1)    Test accuracy: 0.933

El LDA ha creado un modelo estable con una precisión del 93% tanto en el entrenamiento como en las pruebas. Veamos ahora el funcionamiento del PCA:

Resultados del algoritmo PCA:

MM      0       18:26:40.994    LDA Test (EURUSD,H1)    <<<<<<<< PCA Applied >>>>>>>>>

LS      0       18:26:41.071    LDA Test (EURUSD,H1)    Confusion Matrix
LJ      0       18:26:41.071    LDA Test (EURUSD,H1)    [[39,0,0]
ER      0       18:26:41.071    LDA Test (EURUSD,H1)     [0,34,1]
OE      0       18:26:41.071    LDA Test (EURUSD,H1)     [0,4,27]]
KD      0       18:26:41.071    LDA Test (EURUSD,H1)    
IL      0       18:26:41.071    LDA Test (EURUSD,H1)    Classification Report
MG      0       18:26:41.071    LDA Test (EURUSD,H1)    
CR      0       18:26:41.071    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
DE      0       18:26:41.071    LDA Test (EURUSD,H1)    1.0    1.00     1.00     1.00       1.00     39.0
EH      0       18:26:41.071    LDA Test (EURUSD,H1)    2.0    0.89     0.97     0.94       0.93     35.0
KL      0       18:26:41.071    LDA Test (EURUSD,H1)    3.0    0.96     0.87     0.99       0.92     31.0
ID      0       18:26:41.071    LDA Test (EURUSD,H1)    
NO      0       18:26:41.071    LDA Test (EURUSD,H1)    Accuracy                                   0.95
CH      0       18:26:41.071    LDA Test (EURUSD,H1)    Average   0.95    0.95    0.98      0.95    105.0
KK      0       18:26:41.071    LDA Test (EURUSD,H1)    W Avg     0.95    0.95    0.98      0.95    105.0
NR      0       18:26:41.071    LDA Test (EURUSD,H1)    Train accuracy: 0.952
LK      0       18:26:41.071    LDA Test (EURUSD,H1)    Confusion Matrix
FR      0       18:26:41.071    LDA Test (EURUSD,H1)    [[11,0,0]
FJ      0       18:26:41.072    LDA Test (EURUSD,H1)     [0,14,1]
MM      0       18:26:41.072    LDA Test (EURUSD,H1)     [0,3,16]]
NL      0       18:26:41.072    LDA Test (EURUSD,H1)    
HD      0       18:26:41.072    LDA Test (EURUSD,H1)    Classification Report
LO      0       18:26:41.072    LDA Test (EURUSD,H1)    
FJ      0       18:26:41.072    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
KM      0       18:26:41.072    LDA Test (EURUSD,H1)    1.0    1.00     1.00     1.00       1.00     11.0
EP      0       18:26:41.072    LDA Test (EURUSD,H1)    2.0    0.82     0.93     0.90       0.88     15.0
HD      0       18:26:41.072    LDA Test (EURUSD,H1)    3.0    0.94     0.84     0.96       0.89     19.0
HL      0       18:26:41.072    LDA Test (EURUSD,H1)    
OG      0       18:26:41.072    LDA Test (EURUSD,H1)    Accuracy                                   0.91
PS      0       18:26:41.072    LDA Test (EURUSD,H1)    Average   0.92    0.93    0.95      0.92    45.0
IP      0       18:26:41.072    LDA Test (EURUSD,H1)    W Avg     0.92    0.91    0.95      0.91    45.0
PE      0       18:26:41.072    LDA Test (EURUSD,H1)    Test accuracy: 0.911

El algoritmo PCA ha dado como resultado un modelo aún más preciso, con un 95% de exactitud en el entrenamiento y un 91,1% en las pruebas.

Ventajas del análisis discriminante lineal (LDA):

El LDA tiene varias ventajas, por lo que el algoritmo se usa a menudo en tareas de clasificación y reducción de la dimensionalidad:

• Reduce eficazmente la dimensionalidad. El LDA reduce la dimensionalidad del espacio de objetos convirtiendo los objetos originales en un espacio de menor dimensionalidad. Dicha reducción de la dimensionalidad permite conseguir modelos más simples, combate la maldición de la dimensionalidad y mejora la eficiencia computacional.
• Conserva la información sobre las diferencias entre clases. El método LDA intenta encontrar combinaciones lineales de características con las que se produzca la máxima separación entre clases. El método se centra en las diferencias entre clases para conservar patrones y estructuras importantes de clases específicas.
• Extrae características y las clasifica en un solo paso. El método LDA efectúa simultáneamente la extracción de características y la clasificación. Asimismo, aprende la transformación de las características originales y mejora la separabilidad de las clases, por lo que resulta intrínsecamente adecuado para tareas de clasificación. Este enfoque integrado nos permite obtener modelos más eficaces e interpretables.
• Resistente al sobreentrenamiento. El método LDA resulta menos propenso al sobreentrenamiento que otros algoritmos de clasificación, especialmente cuando el número de muestras es pequeño en comparación con el número de características. Reduciendo la dimensionalidad del espacio de características y centrándose en las más distintivas, el método puede generalizar bien los datos no vistos.
• Adecuado para la clasificación multiclase. El método resulta altamente aplicable a los problemas de clasificación en los que intervienen más de dos clases. Considera simultáneamente las relaciones entre todas las clases, lo cual da lugar a límites de separación eficaces en espacios de objetos multidimensionales.
• Eficiencia computacional. Dentro del método, se resuelven las tareas de búsqueda de los valores propios y la multiplicación de matrices: estos son cálculos eficientes que se pueden implementar de forma cómoda utilizando los métodos incorporados de MQL5. Esto hace que el algoritmo LDA resulte adecuado para grandes conjuntos de datos y aplicaciones en tiempo real.
• Fácil de interpretar. Las características transformadas obtenidas con la ayuda del LDA pueden interpretarse y analizarse fácilmente para permitir una mejor comprensión de los patrones subyacentes en los datos. Las combinaciones lineales de características obtenidas mediante el método LDA pueden ofrecer información sobre los factores discriminatorios que afectan a la decisión de clasificación.
• Sus suposiciones suelen estar justificadas. El método LDA asume que los datos se distribuyen normalmente dentro de cada clase con matrices de covarianza iguales. Si bien esto no siempre está justificado en la práctica, el LDA puede seguir funcionando bien aunque se cumpla parcialmente esta suposición.

Aunque el análisis discriminante lineal (LDA) tiene varias ventajas, también presenta ciertas limitaciones y desventajas:

Desventajas del método de LDA:

• Supone una distribución gaussiana dentro de los objetos. El método LDA asume que los datos dentro de cada clase se distribuyen normalmente con matrices de covarianza iguales. Si esta suposición no resulta justificada, el método puede producir resultados subóptimos o incluso no converger. En la práctica, los datos reales pueden tener una distribución no normal, lo cual puede limitar la eficacia del método.
• Sensibilidad a los valores atípicos. El método es sensible a los valores atípicos, especialmente cuando las matrices de covarianza se estiman partiendo de datos limitados. Los valores atípicos pueden influir significativamente en la estimación de las matrices de covarianza y en las direcciones discriminantes resultantes, lo cual puede dar lugar a resultados de clasificación sesgados o poco fiables.
• Menos flexible a la hora de modelizar relaciones no lineales. El método presupone que los límites de decisión entre clases son lineales. No obstante, si las relaciones entre las características y las clases no son lineales, el método no podrá captar eficazmente patrones tan complejos. En dichos casos, los métodos no lineales de reducción de la dimensionalidad o los clasificadores no lineales pueden resultar más apropiados.
• La maldición de la dimensionalidad es real. Cuando el número de características supera holgadamente el número de muestras, el LDA puede sufrir la maldición de la dimensionalidad. En los espacios de características multivariantes, la estimación de las matrices de covarianza es menos fiable y las direcciones discriminantes reflejan peor la verdadera estructura subyacente de los datos.
• Resultados limitados al trabajar con clases desequilibradas. El método funciona peor con distribuciones de clases desequilibradas, en las que una o más clases poseen muchas menos muestras que otras. En estos casos, una clase con menos muestras puede estar mal representada al estimar los promedios de clase y las matrices de covarianza, lo cual provoca un desplazamiento en los resultados de la clasificación.
• Tiene dificultades para procesar datos no numéricos. El método LDA suele trabajar con datos numéricos y resulta difícil aplicarlo directamente a conjuntos de datos que contienen variables categóricas o no numéricas. Esto puede requerir un procesamiento previo, como la codificación de variables categóricas o la conversión de datos no numéricos en representaciones numéricas, lo cual puede suponer una complejidad adicional y una posible pérdida de información.

El LDA frente al PCA en un entorno comercial

Para utilizar estas técnicas de reducción de la dimensionalidad en un entorno comercial, necesitaremos crear una función para entrenar y probar el modelo, hecho lo cual, podremos utilizar el modelo entrenado para realizar previsiones en el simulador de estrategias, lo cual nos ayudará a analizar su rendimiento.

Usaremos 5 indicadores en nuestro conjunto de datos, que reduciremos utilizando estos dos métodos:

int OnInit()
  {
  
//--- Trend following indicators

    indicator_handle[0] = iAMA(Symbol(), PERIOD_CURRENT, 9 , 2 , 30, 0, PRICE_OPEN);
    indicator_handle[1] = iADX(Symbol(), PERIOD_CURRENT, 14);
    indicator_handle[2] = iADXWilder(Symbol(), PERIOD_CURRENT, 14);
    indicator_handle[3] = iBands(Symbol(), PERIOD_CURRENT, 20, 0, 2.0, PRICE_OPEN);
    indicator_handle[4] = iDEMA(Symbol(), PERIOD_CURRENT, 14, 0, PRICE_OPEN);
 }

Como estos algoritmos no han sido programados para aprender y mostrar señales comerciales significativas debido a su naturaleza, utilizaremos un árbol de decisión para realizar predicciones basadas en los datos transformados tanto en el entrenamiento como en las pruebas.

void TrainTest()
 {
   vector buffer = {};
   for (int i=0; i<ArraySize(indicator_handle); i++)
    {
      buffer.CopyIndicatorBuffer(indicator_handle[i], 0, 0, bars); //copy indicator buffer
      dataset.Col(buffer, i); //add the indicator buffer values to the dataset matrix 
    }

//---
  
   vector y(bars);
   MqlRates rates[];
   CopyRates(Symbol(), PERIOD_CURRENT,0,bars, rates);
   for (int i=0; i<bars; i++) //Creating the target variable 
     {
       if (rates[i].close > rates[i].open) //if bullish candle assign 1 to the y variable else assign the 0 class
        y[i] = 1;
       else
        y[0] = 0;
     }  
     
//---
   
   dataset.Col(y, dataset.Cols()-1); //add the y variable to the last column
   
//---

   matrix x_train, x_test;
   vector y_train, y_test;
      
   MatrixExtend::TrainTestSplitMatrices(dataset,x_train,y_train,x_test,y_test,training_sample_size,random_state_);
   
   matrix x_transformed = {};
   switch(dimension_reduction)
     {
      case  LDA:
         
         lda = new CLDA(NULL);
         
         x_transformed = lda.fit_transform(x_train, y_train); //Transform the training data   
         
        break;
      case PCA:
      
         pca = new CPCA(NULL);
         
         x_transformed = pca.fit_transform(x_train);
         
        break;
     }
     
   
   classifier_tree = new CDecisionTreeClassifier();
   classifier_tree.fit(x_transformed, y_train); //Train the model using the transformed data
   
   vector preds = classifier_tree.predict(x_transformed); //Make predictions using the transformed data
   
   Print("Train accuracy: ",Metrics::confusion_matrix(y_train, preds).accuracy);
   
   switch(dimension_reduction)
     {
      case  LDA:
        
        x_transformed = lda.transform(x_test); //Transform the testing data   
        
        break;
        
      case PCA:
        
        x_transformed = pca.transform(x_test); 
        
        break;
     }
   preds = classifier_tree.predict(x_transformed);
   
   Print("Test accuracy: ",Metrics::confusion_matrix(y_test, preds).accuracy);
   
 }

Una vez entrenados los datos, deberemos probarlos. Más abajo, le resumimos los resultados de ambos métodos. En primer lugar, el LDA: 

JK      0       01:00:24.440    LDA Test (EURUSD,H1)    
GK      0       01:00:37.442    LDA Test (EURUSD,H1)    Confusion Matrix
QR      0       01:00:37.442    LDA Test (EURUSD,H1)    [[60,266]
FF      0       01:00:37.442    LDA Test (EURUSD,H1)     [46,328]]
DR      0       01:00:37.442    LDA Test (EURUSD,H1)    
RN      0       01:00:37.442    LDA Test (EURUSD,H1)    Classification Report
FE      0       01:00:37.442    LDA Test (EURUSD,H1)    
LP      0       01:00:37.442    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
HD      0       01:00:37.442    LDA Test (EURUSD,H1)    0.0    0.57     0.18     0.88       0.28     326.0
FI      0       01:00:37.442    LDA Test (EURUSD,H1)    1.0    0.55     0.88     0.18       0.68     374.0
RM      0       01:00:37.442    LDA Test (EURUSD,H1)    
QH      0       01:00:37.442    LDA Test (EURUSD,H1)    Accuracy                                   0.55
KQ      0       01:00:37.442    LDA Test (EURUSD,H1)    Average   0.56    0.53    0.53      0.48    700.0
HP      0       01:00:37.442    LDA Test (EURUSD,H1)    W Avg     0.56    0.55    0.51      0.49    700.0
KK      0       01:00:37.442    LDA Test (EURUSD,H1)    Train accuracy: 0.554
DR      0       01:00:37.443    LDA Test (EURUSD,H1)    Confusion Matrix
CD      0       01:00:37.443    LDA Test (EURUSD,H1)    [[20,126]
LO      0       01:00:37.443    LDA Test (EURUSD,H1)     [12,142]]
OK      0       01:00:37.443    LDA Test (EURUSD,H1)    
ME      0       01:00:37.443    LDA Test (EURUSD,H1)    Classification Report
QN      0       01:00:37.443    LDA Test (EURUSD,H1)    
GI      0       01:00:37.443    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
JM      0       01:00:37.443    LDA Test (EURUSD,H1)    0.0    0.62     0.14     0.92       0.22     146.0
KR      0       01:00:37.443    LDA Test (EURUSD,H1)    1.0    0.53     0.92     0.14       0.67     154.0
MF      0       01:00:37.443    LDA Test (EURUSD,H1)    
MQ      0       01:00:37.443    LDA Test (EURUSD,H1)    Accuracy                                   0.54
MJ      0       01:00:37.443    LDA Test (EURUSD,H1)    Average   0.58    0.53    0.53      0.45    300.0
OI      0       01:00:37.443    LDA Test (EURUSD,H1)    W Avg     0.58    0.54    0.52      0.45    300.0
QP      0       01:00:37.443    LDA Test (EURUSD,H1)    Test accuracy: 0.54

El PCA ha funcionado mejor durante el entrenamiento y ligeramente peor durante las pruebas:

GE      0       01:01:57.202    LDA Test (EURUSD,H1)    
MS      0       01:01:57.202    LDA Test (EURUSD,H1)    Classification Report
IH      0       01:01:57.202    LDA Test (EURUSD,H1)    
OS      0       01:01:57.202    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
KG      0       01:01:57.202    LDA Test (EURUSD,H1)    0.0    0.62     0.28     0.85       0.39     326.0
GL      0       01:01:57.202    LDA Test (EURUSD,H1)    1.0    0.58     0.85     0.28       0.69     374.0
MP      0       01:01:57.202    LDA Test (EURUSD,H1)    
JK      0       01:01:57.202    LDA Test (EURUSD,H1)    Accuracy                                   0.59
HL      0       01:01:57.202    LDA Test (EURUSD,H1)    Average   0.60    0.57    0.57      0.54    700.0
CG      0       01:01:57.202    LDA Test (EURUSD,H1)    W Avg     0.60    0.59    0.55      0.55    700.0
EF      0       01:01:57.202    LDA Test (EURUSD,H1)    Train accuracy: 0.586
HO      0       01:01:57.202    LDA Test (EURUSD,H1)    Confusion Matrix
GG      0       01:01:57.202    LDA Test (EURUSD,H1)    [[26,120]
GJ      0       01:01:57.202    LDA Test (EURUSD,H1)     [29,125]]
KN      0       01:01:57.202    LDA Test (EURUSD,H1)    
QJ      0       01:01:57.202    LDA Test (EURUSD,H1)    Classification Report
MQ      0       01:01:57.202    LDA Test (EURUSD,H1)    
CL      0       01:01:57.202    LDA Test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
QP      0       01:01:57.202    LDA Test (EURUSD,H1)    0.0    0.47     0.18     0.81       0.26     146.0
GE      0       01:01:57.202    LDA Test (EURUSD,H1)    1.0    0.51     0.81     0.18       0.63     154.0
QI      0       01:01:57.202    LDA Test (EURUSD,H1)    
MD      0       01:01:57.202    LDA Test (EURUSD,H1)    Accuracy                                   0.50
RE      0       01:01:57.202    LDA Test (EURUSD,H1)    Average   0.49    0.49    0.49      0.44    300.0
IL      0       01:01:57.202    LDA Test (EURUSD,H1)    W Avg     0.49    0.50    0.49      0.45    300.0
PP      0       01:01:57.202    LDA Test (EURUSD,H1)    Test accuracy: 0.503

Por último, podemos crear una estrategia comercial sencilla basada en las señales ofrecidas por el modelo de árbol de decisión.

void OnTick()
  {
//---

   if (!train_once) //call the function to train the model once on the program lifetime
    {
      TrainTest();
      train_once = true; 
    }

//--- 
   
   vector inputs(indicator_handle.Size());
   vector buffer;
   
   for (uint i=0; i<indicator_handle.Size(); i++)
     {
       buffer.CopyIndicatorBuffer(indicator_handle[i], 0, 0, 1); //copy the current indicator value
       inputs[i] = buffer[0]; //add its value to the inputs vector 
     }

//---
    
    SymbolInfoTick(Symbol(), ticks);
      
     if (isnewBar(PERIOD_CURRENT)) // We want to trade on the bar opening 
      {
        vector transformed_inputs = {};
         switch(dimension_reduction) //transform every new data to fit the dimensions selected during training
           {
            case  LDA:
               transformed_inputs = lda.transform(inputs); //Transform the new data   
              break;
            case PCA:
               transformed_inputs = pca.transform(inputs);
              break;
           }
     
        int signal = (int)classifier_tree.predict(transformed_inputs);
        double min_lot = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN);
        SymbolInfoTick(Symbol(), ticks);
        
         if (signal == -1)
           {
              if (!PosExists(MAGICNUMBER, POSITION_TYPE_SELL)) // If a sell trade doesnt exist
                m_trade.Sell(min_lot, Symbol(), ticks.bid, ticks.bid+stoploss*Point(), ticks.bid - takeprofit*Point());
           }
         else
           {
             if (!PosExists(MAGICNUMBER, POSITION_TYPE_BUY))  // If a buy trade doesnt exist
               m_trade.Buy(min_lot, Symbol(), ticks.ask, ticks.ask-stoploss*Point(), ticks.ask + takeprofit*Point());
           }
      }
  }

Hemos realizado la prueba en el modo de precios de apertura desde enero de 2023 hasta febrero de 2024. Ambos métodos han operado con una estrategia sencilla:

Análisis discriminante lineal (LDA):

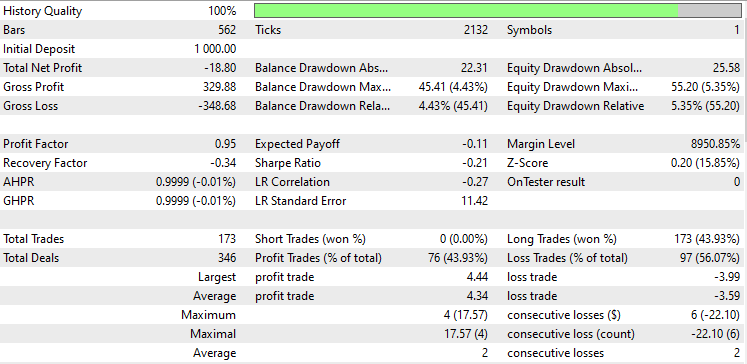
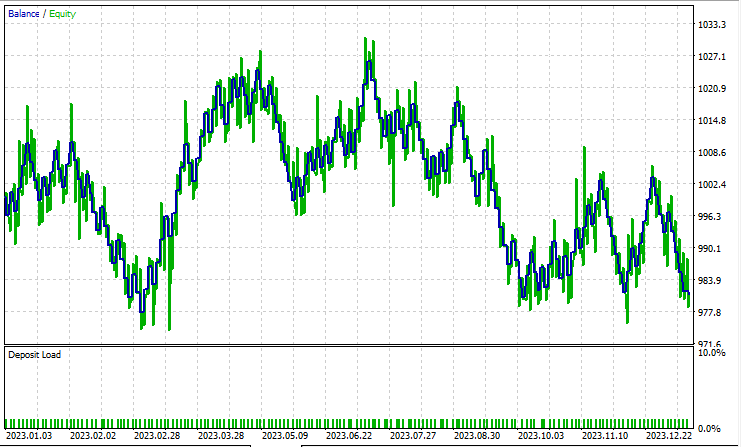
Pruebas con el PCA:

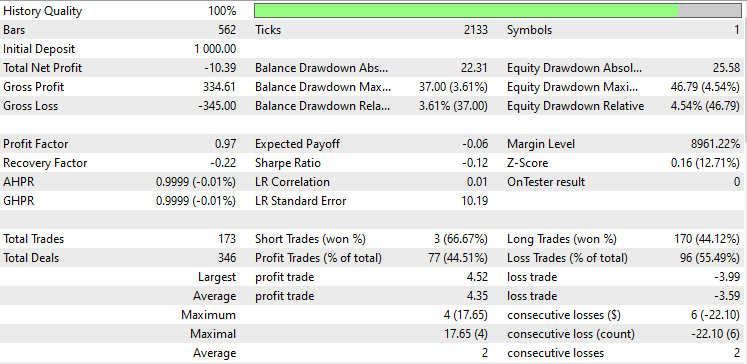
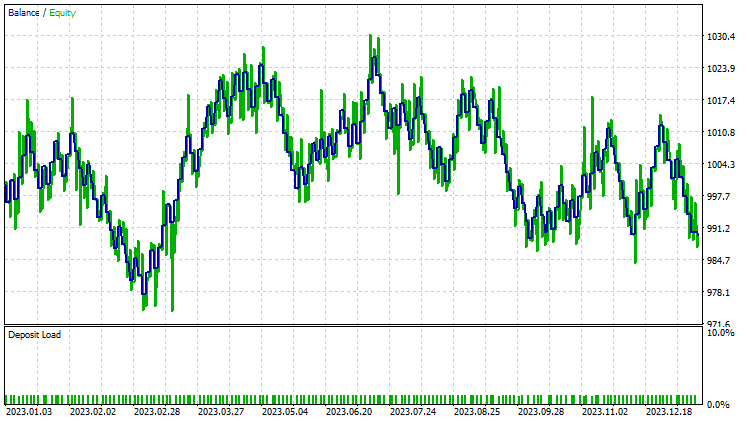
Los resultados son casi idénticos: el modelo de LDA ha dado unas pérdidas de 8 dólares más que el PCA. En cuanto al trabajo con los datos, el simulador de estrategias resulta menos relevante para las técnicas de reducción de dimensionalidad, ya que su principal objetivo es la simplificación de variables, especialmente cuando se trata de grandes volúmenes de datos. Además, al ejecutar este asesor en el simulador de estrategias, hemos hallado algunas inconsistencias en los cálculos causadas por errores inesperados en los métodos de matrices y vectores. Le recomiendo que ejecute el programa varias veces hasta obtener un resultado significativo, por si de repente se encuentra con errores.

Si ha estado siguiendo esta serie de artículos, puede que se pregunte por qué no hemos escalado los datos transformados de estos dos métodos como hicimos en el artículo anterior.

La necesidad de normalizar los datos de los algoritmos PCA o LDA para un modelo de aprendizaje automático depende de las características concretas de su muestra, del algoritmo utilizado y de sus objetivos. Qué debemos considerar:

• Transformación: los métodos trabajan con la matriz de covarianza de las características originales y encuentran los componentes ortogonales (componentes principales) que transmiten la varianza máxima de los datos. Los datos transformados obtenidos por estos métodos constan de dichos componentes principales.
• Normalización al uso de PCA o LDA. Es habitual normalizar los objetos originales antes de aplicar el método PCA o LDA, sobre todo si los objetos poseen escalas o unidades diferentes. La normalización garantiza que todas las características contribuyan por igual a la matriz de covarianza y evita que las características con escalas mayores dominen los componentes principales.
• Normalización tras los métodos PCA o LDA. La necesidad de normalizar los datos transformados dependerá de los requisitos específicos de su algoritmo de aprendizaje automático y de las características de las funciones transformadas. Algunos algoritmos, como la regresión logística o los k vecinos más próximos, son sensibles a las diferencias en las escalas de las características, por lo que puede resultar útil normalizar las características incluso después de aplicar los métodos PCA o LDA.

• Otros algoritmos, como los árboles de decisión que usamos, son menos sensibles a las escalas de las características y pueden funcionar sin normalizar los datos tras la reducción de la dimensionalidad.

• Efecto de la normalización en la interpretabilidad. La normalización tras los métodos LDA y PCA puede influir en la interpretabilidad de los componentes principales. Si necesitamos comprender la contribución de las características originales a los componentes principales, la normalización de los datos transformados puede ocultar estas relaciones.
• Impacto en el rendimiento. Experimente con datos transformados normalizados y no normalizados para valorar el impacto en el rendimiento del modelo. En algunos casos, la normalización puede conducir a una mejor convergencia, una mejor generalización o un aprendizaje más rápido, mientras que en otros casos puede tener escaso efecto o ninguno en absoluto.

Podrá seguir el desarrollo de este modelo de aprendizaje automático y mucho más en esta serie de artículos en mi repositorio en GitHub.

Contenidos del anexo:

Archivo	Descripción/uso
tree.mqh	Modelo clasificador de árbol de decisión.
MatrixExtend.mqh	Funciones adicionales para trabajar con matrices.
metrics.mqh	Funciones y código para medir el rendimiento de los modelos de aprendizaje automático.
preprocessing.mqh	Biblioteca para preprocesar datos de entrada sin procesar con el fin de adecuarlos para su uso en los modelos de aprendizaje automático.
base.mqh	Biblioteca básica para usar los métodos PCA y LDA, contiene funciones para simplificar la escritura de código.
pca.mqh	Biblioteca del método de análisis de componentes principales PCA
lda.mqh	Biblioteca del método de análisis discriminante lineal LDA
plots.mqh	Biblioteca para construir vectores y matrices
lda vs pca script.mq5	Script para demostrar los algoritmos pca y lda
LDA Test.mq5	Asesor principal para probar la mayor parte del código
iris.csv	Conjunto de datos para comprobar el modelo iris