适应性社会行为优化（ASBO）：两阶段演变

目录

1. 概述
2. 算法的实现
3. 测试结果

1.概述

在前一篇文章中，我们讨论了 Schwefel 概念的一个例子，其中包括正态分布、自适应变异率的使用以及通过适应度值确定最近邻的函数。现在，我们的研究进入了一个新阶段，我们将分两个阶段完成算法的数学模型 - ASBO（适应性社会行为优化）的形成。我们将在我们已经熟悉的测试函数上对这一令人兴奋的模型进行全面测试，并就其效率得出结论。在这篇文章中，我们将揭示社会行为在生物体优化领域的新应用，并展示独特的结果，这将有助于我们更好地理解和使用集体行为的原理来解决复杂的问题。

2.算法的实现

让我们先来编写一个 ABSO 算法的伪代码（所用公式如下所示）：

输入：PZ 种群大小、M 种群数量和 P' 每个种群的历时数。f (x)- 目标函数。

初始化：

1.创建 M 个种群 ，每个种群的大小为 PZ
2.对于每个种群：

• 随机初始化 xi 解决方案
• 计算每个解决方案的 f (xi) 目标函数值
• 将 Gb 全局领导者定义为 f (xi) 最大的解
• 对于每个 xi 解，定义一组最近邻 Nc
• 初始化个人最佳决策 Sb = xi
• 在 [-1.0; 1.0] 范围内随机初始化自适应参数 Cg、Cs 和 Cn
  

第 1 阶段：独立处理种群问题。
3.对于 M 个种群 中的每一个：

•  对于每个 xi 解决方案
  

• 根据公式 (3) 和 (4) 应用自适应突变来更新 Cg、Cs 和 Cn 的比例
  
• 根据公式 (1) 计算 ΔX(i + 1) 位置的变化
• 根据公式 (2) 更新位置 xi
• 计算新值 f (xi)
• 如果 f (xi) > f (Sb)，则更新个体最佳解决方案 Sb
• 如果 f (xi) > f (Gb)，则更新全局领导者 Gb

• 重复，直到达到 P' 个轮次（epoch）

4.保存最终种群、f (xi) 值以及 Cg、Cs 和 Cn 参数

第 2 阶段：处理合并的种群。
5.在所有最终种群中，为 f (xi) 选择 PZ 最佳解
6.为这些 PZ 解决方案使用保存的 Cg、Cs 和 Cn 参数
7.对规模为 PZ 的合并种群采用 ASBO 算法
8.重复步骤 6 到 7，直至达到停止标准

结论：全局最佳值 Gb

关键公式：

• ΔX(i + 1) = Cg * R1 * (Gb - xi) + Cs * R2 * (Sb - xi) + Cn * R3 * (Nc - xi) (1)
• x (i + 1) = xi + ΔX (i + 1) (2)
• p'i (j) = pi (j) + σi (j) * N (0, 1) (3)
• σ'i (j) = σi (j) * exp (τ' * N (0, 1) + τ * Nj (0, 1)) (4)

其中，

• Gb - 全局领导者
• Sb - 个人最佳解决方案
• Nc - 按适应性划分的邻居组的中心点
  
• R1、 R2、 R3 - [0, 1]范围内的随机数
• Cg、Cs、Cn - 适应性参数
• N (0, 1)- 正态分布中的随机数
• Nj (0,1)- 每 j 次测量的正态分布随机数
• τ、τ' - 自适应突变的比例因子

所展示的伪代码表明，该算法实现了社会模型发展的两阶段演变。算法的逻辑可以分阶段简要描述：

1.第一阶段：

• 取相同 PZ 大小的 M 个种群。
• 在固定的 P' 迭代次数内，对这 M 个种群中的每一个独立应用 ASBO 算法。
• 在该阶段结束时，为所有最终群体中的每个个体保存适应度函数和自适应突变参数的值。

2.第二阶段：

• 从第一阶段的所有最终种群中选出适应度函数值最佳的 P.Z. 个个体。
• 它们保存的自适应突变参数适用于这些 PZ 个最佳个体。
• ASBO 算法适用于 PZ 大小的新种群，以获得最终解决方案。

两阶段进化的意义：

1.由于几个种群的独立进化，第一阶段提供了多种解决方案，并更好地定位了全局最优区域。
2.第二阶段使用来自第一阶段的种群的最佳解及其自适应参数，以加速收敛到全局最优值。

因此，从理论上讲，两阶段进化允许将第一阶段的全局搜索与第二阶段的更有效的局部优化相结合，这最终可能会提高整个算法的性能。

多种群两阶段 ASBO 算法的传统版本涉及在第一阶段并行和独立地使用多个种群。在第二阶段，从种群中提取最佳解决方案，并创建新的种群。然而，将我们的单一模板用于所有种群算法会引发如何处理多个种群的问题。

第一种解决方案可能是将一个正常种群，比如 50 个个体，分成几个种群，比如 5 个。在这种情况下，5 个种群中的每个种群将包含 10 个个体。我们可以用通常的方式对待多个种群，就像它们是一个整体一样。然而，在第二阶段，出现了一个问题：我们需要从这 5 个种群中选取最佳解决方案，并将其放入一个新的种群中。但我们将无法获得所需的数量，因为我们必须将它们全部放入，这实际上意味着创建原始种群的副本。

这个问题的第二个解决方案是创建 5 个种群，其大小等于我们的种群大小，即 50 个个体。对于这些种群中的每一个，都分配了固定数量的轮次（epoch），例如 20 个。在这种情况下，在第一阶段，我们将按顺序处理这 5 个种群，每个种群有固定数量的轮次，即 5*20 =100 个轮次。第二阶段将使用剩余的 100 个轮次（总共 200 个轮次）。在第二阶段，我们将把这 5 个种群合并成一个 250 个个体的大种群，对它们进行分类，并从中挑选出最好的 50 个个体，创建一个新种群。接下来，我们将根据公式，以常规方式对这些新种群进行操作。这与原始算法完全一致，同时我们坚持使用种群算法的概念。我们以前不得不在其他算法中应用创新方法，如 Nelder-Mead、化学 CRO、进化算法等，以确保所有算法都是兼容的，可以无缝互换。

现在，让我们开始编写代码。

实现 S_ASBO_Agent 结构，该结构将描述多种群两阶段 ASBO 算法中的搜索代理。该结构定义了变量和 Init 方法，用于初始化代理。

变量:

• c- 坐标数组
• cBest - 最佳坐标数组
• f - 适应度数值
• fBest - 最佳适应度数值
• Cg、Cs、Cn - 适应性参数
• u -C_AO_Utilities 类对象

Init 方法初始化代理：

• 接受 coords 坐标数以及 rangeMin 和 rangeMax 数组，分别代表每个坐标的最小值和最大值。
• 根据 coords 坐标数为 c 和 cBest 数组分配内存。
• 将初始值 fBest 设为 -DBL_MAX。
• 为 Cg、Cs 和 Cn 适应性参数生成随机值。
• 用 rangeMin 和 rangeMax 之间范围内的随机值填充 c 数组。
• 将 c 中的值赋值给 cBest 数组。
  

//——————————————————————————————————————————————————————————————————————————————
struct S_ASBO_Agent
{
    double c     [];   //coordinates
    double cBest [];   //best coordinates
    double f;          //fitness
    double fBest;      //best fitness

    double Cg, Cs, Cn; //adaptive parameters
    C_AO_Utilities u;

    void Init (int coords, double &rangeMin [], double &rangeMax [])
    {
      ArrayResize (c,     coords);
      ArrayResize (cBest, coords);
      fBest = -DBL_MAX;
      Cg = u.RNDprobab ();
      Cs = u.RNDprobab ();
      Cn = u.RNDprobab ();

      for (int i = 0; i < coords; i++)
      {
        c     [i] = u.RNDfromCI (rangeMin [i], rangeMax [i]);
        cBest [i] = c [i];
      }

    }
};
//——————————————————————————————————————————————————————————————————————————————

要依次处理多个种群，使用种的群数组会比较方便。为此，我们将编写只包含一个字段的 S_ASBO_Population 结构：

• agent - S_ASBO_Agent 类型的对象数组，代表种群中的代理。

//——————————————————————————————————————————————————————————————————————————————
struct S_ASBO_Population
{
    S_ASBO_Agent agent [];
};
//——————————————————————————————————————————————————————————————————————————————

声明 C_AO_ASBO类 - C_AO 类的后代。该类包含许多用于处理优化的方法和变量：

1.构造函数和析构函数：

• 构造函数初始化算法参数，如种群大小、种群数量、每个种群的轮次数量，以及算法描述的引用。
• 析构函数为空。
  

2.可供选择的方案有：

• SetParams - 从 params 数组中设置算法参数。
• Init - 使用给定参数初始化算法：搜索范围、搜索步长和轮次数。
• Moving - 在搜索空间中移动代理。
• Revision - 修订搜索空间中的代理，更新全局最佳解决方案。

3.变量:

• numPop,epochsForPop - 种群数量和每个种群的轮次数。
• epochs,epochNow,currPop,isPhase2,popEpochs,tau,tau_prime - 算法中使用的附加变量。
• allAgentsForSortPhase2,allAgentsTemp,agentsPhase2,agentsTemp - 算法中使用的代理数组。
• pop - 种群数组。
  

4.辅助方法：

• AdaptiveMutation - 为代理执行自适应突变。
• UpdatePosition - 更新代理的位置。
• FindNeighborCenter - 查找代理的邻居中心。
• Sorting - 代理排序。

因此，C_AO_ASBO 类是 ASBO 算法的实现，它使用各种方法和操作来移动和修改搜索空间中的代理。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ASBO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ASBO () { }
  C_AO_ASBO ()
  {
    ao_name = "ASBO";
    ao_desc = "Adaptive Social Behavior Optimization";
    ao_link = "https://www.mql5.com/ru/articles/15283";

    popSize       = 50;   //population size
    numPop        = 5;    //number of populations
    epochsForPop  = 10;   //number of epochs for each population

    ArrayResize (params, 3);

    params [0].name = "popSize";      params [0].val = popSize;
    params [1].name = "numPop";       params [1].val = numPop;
    params [2].name = "epochsForPop"; params [2].val = epochsForPop;
  }

  void SetParams ()
  {
    popSize      = (int)params [0].val;
    numPop       = (int)params [1].val;
    epochsForPop = (int)params [2].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int numPop;       //number of populations
  int epochsForPop; //number of epochs for each population

  private: //-------------------------------------------------------------------
  int  epochs;
  int  epochNow;
  int  currPop;
  bool isPhase2;
  int  popEpochs;

  double tau;
  double tau_prime;

  S_ASBO_Agent      allAgentsForSortPhase2 [];
  S_ASBO_Agent      allAgentsTemp          [];
  S_ASBO_Agent      agentsPhase2           [];
  S_ASBO_Agent      agentsTemp             [];
  S_ASBO_Population pop                    []; //M populations

  void   AdaptiveMutation   (S_ASBO_Agent &agent);
  void   UpdatePosition     (int ind, S_ASBO_Agent &ag []);
  void   FindNeighborCenter (int ind, S_ASBO_Agent &ag [], double &center []);
  void   Sorting (S_ASBO_Agent &p [], S_ASBO_Agent &pTemp [], int size);
};
//——————————————————————————————————————————————————————————————————————————————

Init 方法执行 C_AO_ASBO 类的一项重要功能，即在开始优化之前初始化 ASBO 算法所需的参数和数据结构。Init 方法中的基本初始化步骤：

1.检查并初始化基本参数：

• 该方法调用 StandardInit 来初始化基本参数，如最小和最大搜索范围以及搜索步长。如果初始化失败，该方法将返回 false。

2.初始化附加变量：

• 设置 epochs、epochNow、currPop、isPhase2 和 popEpochs 变量的值。
• tau 和 tau_prime 变量的值是根据 coords 搜索空间的维度计算得出的。

3.创建和初始化种群和代理：

• 创建 pop 数组用于存储种群，并对每个种群进行初始化。对于种群中的每个代理，都会调用 Init 将其坐标初始化到指定范围内。
• agentsPhase2 数组是为第二阶段的代理创建的，其初始化与 populations 类似。
• 创建 allAgentsForSortPhase2 和 allAgentsTemp 数组，用于在排序过程中临时存储代理，并对每个代理进行初始化。

4.返回结果：

•    如果初始化成功，该方法返回 true。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ASBO::Init (const double &rangeMinP  [], //minimum search range
                      const double &rangeMaxP  [], //maximum search range
                      const double &rangeStepP [], //step search
                      const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs    = epochsP;
  epochNow  = 0;
  currPop   = 0;
  isPhase2  = false;
  popEpochs = 0;

  tau       = 1.0 / MathSqrt (2.0 * coords);
  tau_prime = 1.0 / MathSqrt (2.0 * MathSqrt (coords));

  ArrayResize (pop, numPop);
  for (int i = 0; i < numPop; i++)
  {
    ArrayResize (pop [i].agent, popSize);

    for (int j = 0; j < popSize; j++) pop [i].agent [j].Init (coords, rangeMin, rangeMax);
  }

  ArrayResize (agentsPhase2, popSize);
  ArrayResize (agentsTemp,   popSize);
  for (int i = 0; i < popSize; i++) agentsPhase2 [i].Init (coords, rangeMin, rangeMax);

  ArrayResize (allAgentsForSortPhase2, popSize * numPop);
  ArrayResize (allAgentsTemp,          popSize * numPop);

  for (int i = 0; i < popSize * numPop; i++)
  {
    allAgentsForSortPhase2 [i].Init (coords, rangeMin, rangeMax);
    allAgentsTemp          [i].Init (coords, rangeMin, rangeMax);
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ASBO 类的 Moving 方法代表了 ASBO 算法中代理移动的基本过程，包括阶段之间的转换和每个阶段适当操作的执行。Moving 方法的主要步骤：

1.增加 epochNow 值：

• epochNow 变量的值增加了 1，反映了优化新轮次的开始。

2.第 1 阶段：

• 如果算法不在第 2 阶段，则进行如下处理：
• 如果当前种群的轮次数已达到 epochsForPop 的上限，则 popEpochs 计数器会被重置，currPop 计数器会被增加，fB 值也会被重置。
• 如果达到 numPop 个种群的最大数量，算法就会进入第二阶段。在这种情况下，所有种群的代理都会合并到一个数组中并进行排序。最好的代理将被复制到 agentsPhase2 数组中。
• 否则，将对当前种群中的每个代理进行自适应突变和位置更新操作，以及复制坐标。

3.第 2 阶段：

• 在第 2 阶段，还会对 agentsPhase2 数组中的每个代理进行自适应突变和位置更新操作，以及坐标复制。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::Moving ()
{
  epochNow++;

  //Phase 1----------------------------------------------------------------------
  if (!isPhase2)
  {
    if (popEpochs >= epochsForPop)
    {
      popEpochs = 0;
      currPop++;

      fB = -DBL_MAX;
    }

    if (currPop >= numPop)
    {
      isPhase2 = true;

      int cnt = 0;
      for (int i = 0; i < numPop; i++)
      {
        for (int j = 0; j < popSize; j++)
        {
          allAgentsForSortPhase2 [cnt] = pop [i].agent [j];
          cnt++;
        }
      }

      u.Sorting (allAgentsForSortPhase2, allAgentsTemp, popSize * numPop);

      for (int j = 0; j < popSize; j++) agentsPhase2 [j] = allAgentsForSortPhase2 [j];
    }
    else
    {
      for (int i = 1; i < popSize; i++)
      {
        AdaptiveMutation (pop [currPop].agent [i]);
        UpdatePosition   (i, pop [currPop].agent);

        ArrayCopy (a [i].c, pop [currPop].agent [i].c);
      }

      popEpochs++;
      return;
    }
  }

  //Phase 2----------------------------------------------------------------------
  for (int i = 1; i < popSize; i++)
  {
    AdaptiveMutation (agentsPhase2 [i]);
    UpdatePosition   (i, agentsPhase2);

    ArrayCopy (a [i].c, agentsPhase2 [i].c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ASBO 类的 Revision 方法表示修订优化结果的过程，包括更新 fB 值和更新 ASBO 算法每个阶段的优化结果。代码的主要组成部分：

1.变量及其初始化：

• int ind = -1; - 用于存储 f 函数最佳值元素索引的变量。
• fB - 变量，代表当前阶段找到的 "f" 函数的最佳值。

2.寻找最佳代理：

• 在第一个 for 循环中，遍历 popSize 大小的 a 数组中的所有代理（代表决策的对象）。
• 如果当前代理的 f 函数大于当前最佳 fB 值，则更新 fB 和 ind 索引。

3.复制数据：

• 如果找到了具有 ind != -1 函数最佳值的代理，cB 数组（代表最佳解决方案参数）就会用 a 数组中的值进行更新。

4.第 1 阶段：

• 如果 currPop 当前种群小于 numPop 种群总数，则更新当前种群代理的 f 函数值。
• 如果 a 数组中的 f 代理值超过了 fBest 的最佳值，则更新 fBest，并将相应的特征复制到 cBest。
• 然后使用 u.Sorting 方法对当前种群中的代理进行排序。

5.第 2 阶段：

• 如果当前种群数量等于或大于种群总数，则会对 agentsPhase2 数组执行类似操作。
• 更新 f 函数的值，检查并更新 fBest 最佳值，并进行排序。

一般逻辑：

• Revision 方法主要执行两个步骤：寻找最佳代理和根据当前阶段（阶段 1 或阶段 2）更新代理数据。
• 主要目标是跟踪和更新优化过程中发现的最佳解决方案，并对代理进行分类，以备日后使用。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  //phase 1
  if (currPop < numPop)
  {
    for (int i = 0; i < popSize; i++)
    {
      pop [currPop].agent [i].f = a [i].f;

      if (a [i].f > pop [currPop].agent [i].fBest)
      {
        pop [currPop].agent [i].fBest = a [i].f;
        ArrayCopy (pop [currPop].agent [i].cBest, a [i].c, 0, 0, WHOLE_ARRAY);
      }
    }

    u.Sorting (pop [currPop].agent, agentsTemp, popSize);
  }
  //phase 2
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      agentsPhase2 [i].f = a [i].f;

      if (a [i].f > agentsPhase2 [i].fBest)
      {
        agentsPhase2 [i].fBest = a [i].f;
        ArrayCopy (agentsPhase2 [i].cBest, a [i].c, 0, 0, WHOLE_ARRAY);
      }
    }

    u.Sorting (agentsPhase2, agentsTemp, popSize);
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ASBO 类的 AdaptiveMutation 方法表示 ASBO 算法中 ag 代理比率的自适应突变，包括使用高斯分布和根据随机变量计算新比率值。AdaptiveMutation 方法的主要步骤：

1.比率的适应性突变：

• ag 代理的 Cg、Cs 和 Cn 比率采用高斯分布发生变化。
• 对于每个比率，使用两个高斯随机变量之和的指数函数计算出一个新值，每个新值乘以相应的 tau_prime 和 tau 比率。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::AdaptiveMutation (S_ASBO_Agent &ag)
{
  ag.Cg *= MathExp (tau_prime * u.GaussDistribution (0, -1, 1, 1) + tau * u.GaussDistribution (0, -1, 1, 8));
  ag.Cs *= MathExp (tau_prime * u.GaussDistribution (0, -1, 1, 1) + tau * u.GaussDistribution (0, -1, 1, 8));
  ag.Cn *= MathExp (tau_prime * u.GaussDistribution (0, -1, 1, 1) + tau * u.GaussDistribution (0, -1, 1, 8));
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ASBO 类的 UpdatePosition 方法表示在 ASBO 算法中更新代理位置，包括根据各种因素计算位置变化和在指定范围内更新位置。UpdatePosition 方法的主要步骤：

1.计算位置变化：

• 使用各种比率和数值，如 cB、cBest、deltaX、rangeMin、 rangeMax 和 rangeStep，计算 ag [ind] 代理在每个维度 j 上的位置变化。

2.代理位置的更新：

• 对于每 j 维度，通过添加 deltaX [j] 和随后在指定范围内对数值进行修正，计算出新的代理位置 ag[ind].c[j]。

代码注释部分1)- 原始版本，3)- 我的版本没有考虑 Cg、Cs 和 Cn，而是使用了正态分布。"2)" 是我的选择。在三者中，它的效果最好。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::UpdatePosition (int ind, S_ASBO_Agent &ag [])
{
  double deltaX [];
  ArrayResize (deltaX, coords);

  FindNeighborCenter (ind, ag, deltaX);

  for (int j = 0; j < coords; j++)
  {
    /*
    //1)
    deltaX [j] = ag [ind].Cg * u.RNDfromCI (-1, 1) * (cB             [j] - ag [ind].c [j]) +
                 ag [ind].Cs * u.RNDfromCI (-1, 1) * (ag [ind].cBest [j] - ag [ind].c [j]) +
                 ag [ind].Cn * u.RNDfromCI (-1, 1) * (deltaX         [j] - ag [ind].c [j]);
    */
    
    //2)
    deltaX [j] = ag [ind].Cg * (cB             [j] - ag [ind].c [j]) +
                 ag [ind].Cs * (ag [ind].cBest [j] - ag [ind].c [j]) +
                 ag [ind].Cn * (deltaX         [j] - ag [ind].c [j]);


    /*
    //3)
    deltaX [j] = u.GaussDistribution (0, -1, 1, 8) * (cB             [j] - ag [ind].c [j]) +
                 u.GaussDistribution (0, -1, 1, 8) * (ag [ind].cBest [j] - ag [ind].c [j]) +
                 u.GaussDistribution (0, -1, 1, 8) * (deltaX         [j] - ag [ind].c [j]);
    */

    ag [ind].c [j] += deltaX [j];
    ag [ind].c [j] = u.SeInDiSp (ag [ind].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

3.测试结果

ASBO 算法的打印输出显示了一些有趣的特征，使其真正独一无二。其主要特点之一是具有出色的可扩展性，这使得该算法能够高效处理高维问题。尤其值得注意的是，在使用 1000 个参数测试 Forest 函数和 Megacity 函数时取得的结果。在这些情况下，ASBO 的表现令人印象深刻，可与评级表中领先算法的结果相媲美。这些成就不仅凸显了该算法的效率，还显示了它在需要高质量优化的各种领域的应用潜力。

ASBO|Adaptive Social Behavior Optimization|50.0|5.0|10.0|
=============================
5 Hilly's; Func runs:10000; result：0.7633114189858913
25 Hilly's；Func runs：10000; result：0.4925279738997658
500 Hilly's；Func runs：10000; result：0.3261850685263711
=============================
5 Forest's; Func runs：10000; result：0.7954558091769679
25 Forest's; Func runs：10000; result：0.4003462752027551
500 Forest's; Func runs：10000; result：0.26096981234192485
=============================
5 Megacity's; Func runs:10000; result：0.2646153846153846
25 Megacity's; Func runs:10000; result：0.1716923076923077
500 Megacity's；Func runs：10000; result：0.18200000000000044
=============================
All score:3.65710 (40.63%)

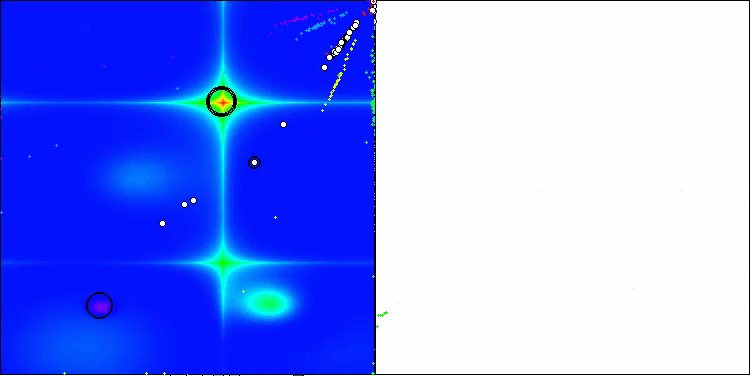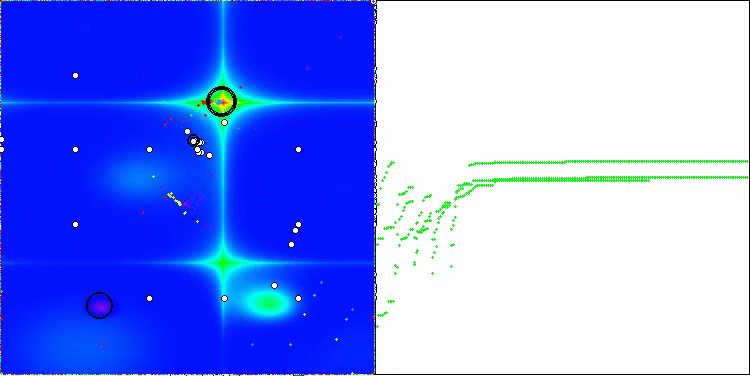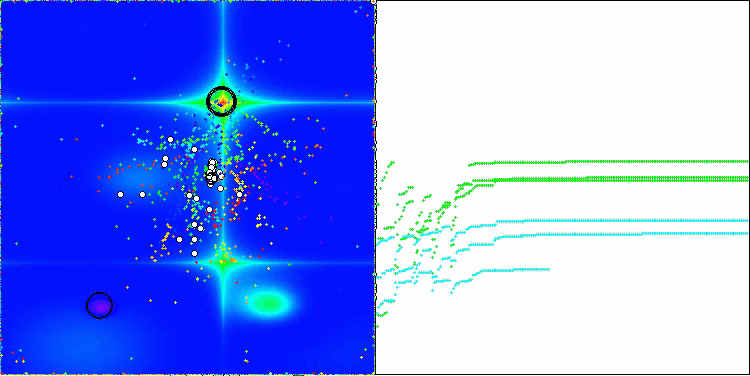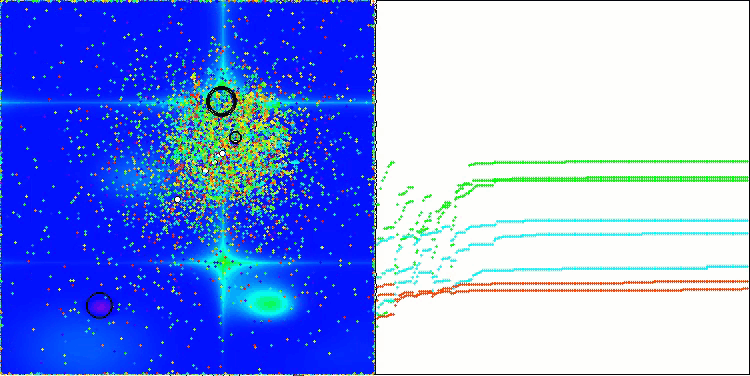
ASBO 算法结果的可视化显示了一些值得关注的有趣特征。从算法运行的一开始，人们就可以看到它是如何成功地识别出至关重要的解区域的，这证明了它有效探索参数空间的能力。

收敛图显示了线中的特征断裂，这是由第一阶段中几个种群的顺序操作引起的。这些差距表明，每个群体都通过探索空间的不同部分为优化做出了贡献。然而，在第二阶段，该图采用实心形式，这意味着在第一阶段之后收集到的所有群体的最佳解决方案被组合在一起。这种统一使算法能够专注于提炼有前景的领域。

因此，可视化不仅说明了算法的动态性，还突出了其自适应和协作机制。

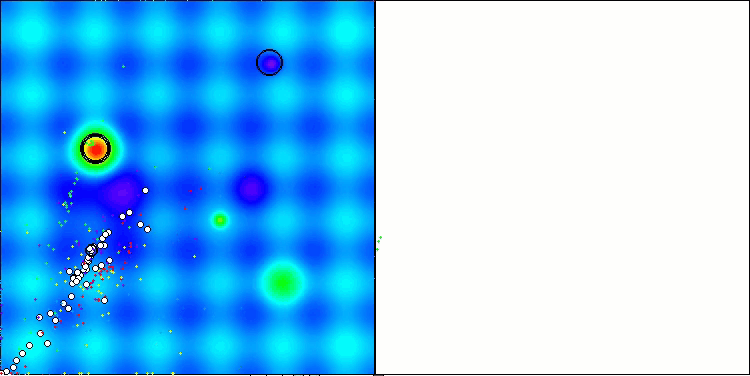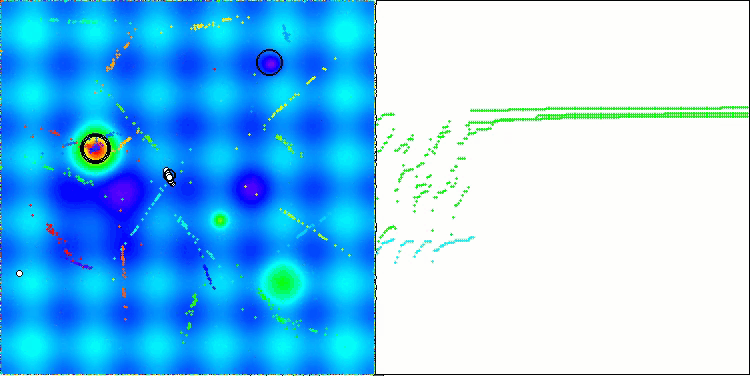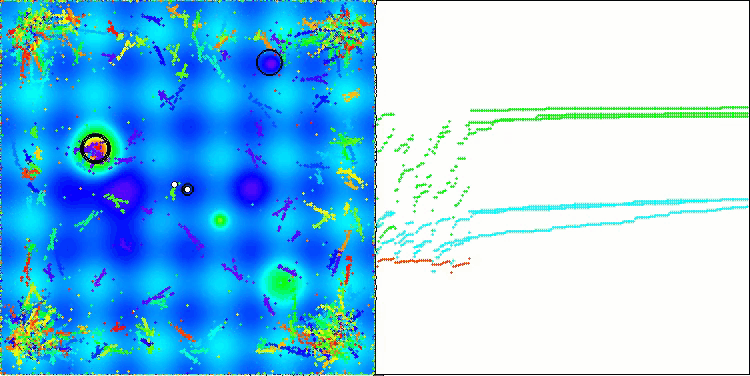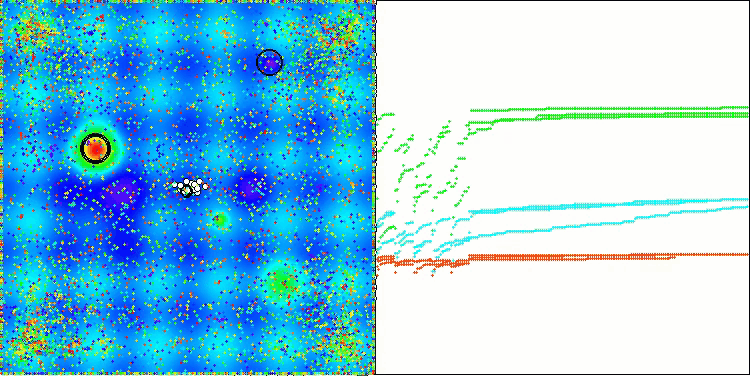
  Hilly 测试函数上的 ASBO

关于 Forest 测试函数上的 ASBO

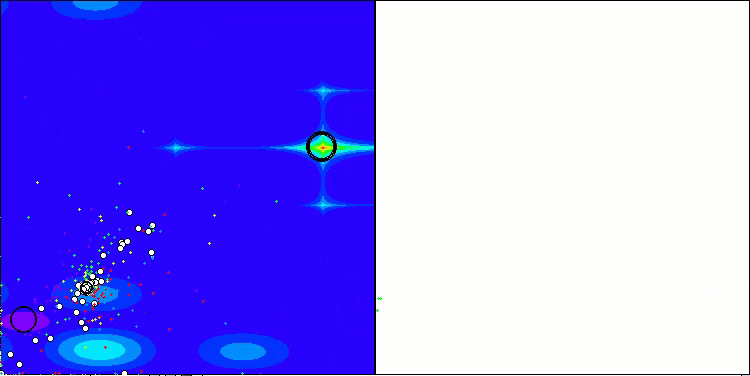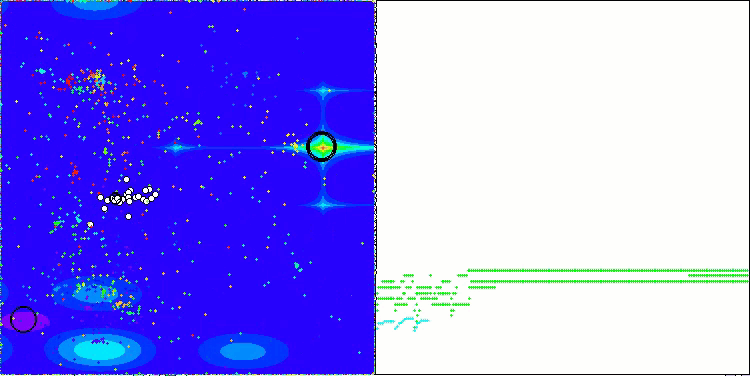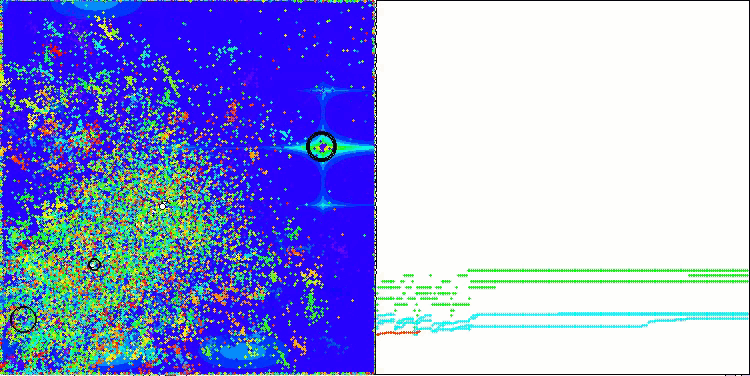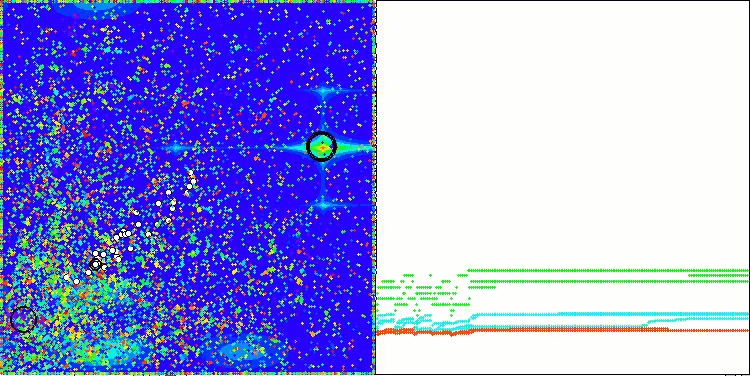
关于Megacity 测试函数上的 ASBO

根据所进行的研究结果，该算法自信地位于评分表的中间位置。

#	AO	描述	Hilly			Hilly 最终	Forest			Forest 最终	Megacity (discrete)			Megacity 最终	最终结果	最大值的百分比
			10 p（5 F）	50 p（25 F）	1000 p（500 F）		10 p（5 F）	50 p（25 F）	1000 p（500 F）		10 p（5 F）	50 p（25 F）	1000 p（500 F）
1	ANS	跨邻里搜索（across neighbourhood search）	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	代码锁定算法（code lock algorithm）	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	(P+O)ES	(P+O) 演进战略（(P+O) evolution strategies）	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
4	CTA	彗尾算法（comet tail algorithm）	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
5	SDSm	随机扩散搜索 M（stochastic diffusion search M）	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
6	ESG	社会群体演变（evolution of social groups）	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
7	SIA	模拟各向同性退火（simulated isotropic annealing）	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
8	ACS	人工协同搜索（artificial cooperative search）	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
9	TSEA	龟甲进化算法（turtle shell evolution algorithm）	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
10	DE	差分进化（differential evolution）	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
11	CRO	化学反应优化（chemical reaction optimization）	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
12	BSA	鸟群算法（bird swarm algorithm）	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
13	HS	和声搜索（harmony search）	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
14	SSG	树苗播种和生长（saplings sowing and growing）	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
15	(PO)ES	(PO) 进化策略（(PO) evolution strategies）	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
16	BSO	头脑风暴优化（brain storm optimization）	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
17	WOAm	Wale 优化算法 M（wale optimization algorithm M）	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
18	AEFA	人工电场算法（artificial electric field algorithm）	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
19	ACOm	蚁群优化M（ant colony optimization M）	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
20	BFO-GA	细菌觅食优化 - ga（bacterial foraging optimization - ga）	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
21	ASBO	适应性社会行为优化（adaptive social behavior optimization）	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
22	MEC	思维进化计算（mind evolutionary computation）	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
23	IWO	入侵性杂草优化（invasive weed optimization）	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
24	Micro-AIS	微型人工免疫系统（micro artificial immune system）	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
25	COAm	布谷鸟优化算法 M（cuckoo optimization algorithm M）	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
26	SDOm	螺旋动力学优化 M（spiral dynamics optimization M）	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
27	NMm	Nelder-Mead 方法 M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
28	FAm	萤火虫算法 M（firefly algorithm M）	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
29	GSA	重力搜索算法（gravitational search algorithm）	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
30	BFO	细菌觅食优化（bacterial foraging optimization）	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
31	ABC	人工蜂群（artificial bee colony）	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
32	BA	蝙蝠算法（bat algorithm）	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
33	SA	模拟退火（simulated annealing）	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
34	IWDm	智能水滴 M（intelligent water drops M）	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
35	PSO	粒子群优化（particle swarm optimisation）	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
36	Boids	Boids 算法	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
37	MA	猴子算法（monkey algorithm）	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
38	SFL	混合蛙跳（shuffled frog-leaping）	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
39	FSS	鱼群搜索（fish school search）	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
40	RND	随机（random）	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37
41	GWO	灰狼优化器（grey wolf optimizer）	0.59169	0.36561	0.29595	1.25326	0.24499	0.09047	0.03612	0.37158	0.27667	0.08567	0.02170	0.38403	2.009	22.32
42	CSS	带电系统搜索（charged system search）	0.44252	0.35454	0.35201	1.14907	0.24140	0.11345	0.06814	0.42299	0.18333	0.06300	0.02322	0.26955	1.842	20.46
43	EM	类电磁算法（electroMagnetism-like algorithm）	0.46250	0.34594	0.32285	1.13129	0.21245	0.09783	0.10057	0.41085	0.15667	0.06033	0.02712	0.24412	1.786	19.85

总结

该算法因其独创性和非标准行为而脱颖而出，这使其可视化独特，不同于任何先前已知的方法。这引起了人们对其内部机制的关注和兴趣。

尽管在解决小维问题时总体结果和收敛性平均，但该算法在处理更复杂的问题和在大搜索空间内时表现出了真正的潜力。它使用在第一阶段按顺序运行的多个种群，这就提出了将有限数量的轮次划分为独立种群的预先计算是否明智的问题。在第一阶段仅使用一个种群进行的实验显示出明显较差的结果，这证实了预先收集周围搜索空间信息的有用性。这使得算法能够更有效地使用领先的个体 — 这是搜索第二阶段最成功的解决方案。

此外，该算法具有进一步研究的巨大潜力。我认为它的功能尚未完全实现，需要更多的实验和分析来了解如何最好地利用其算法优势。

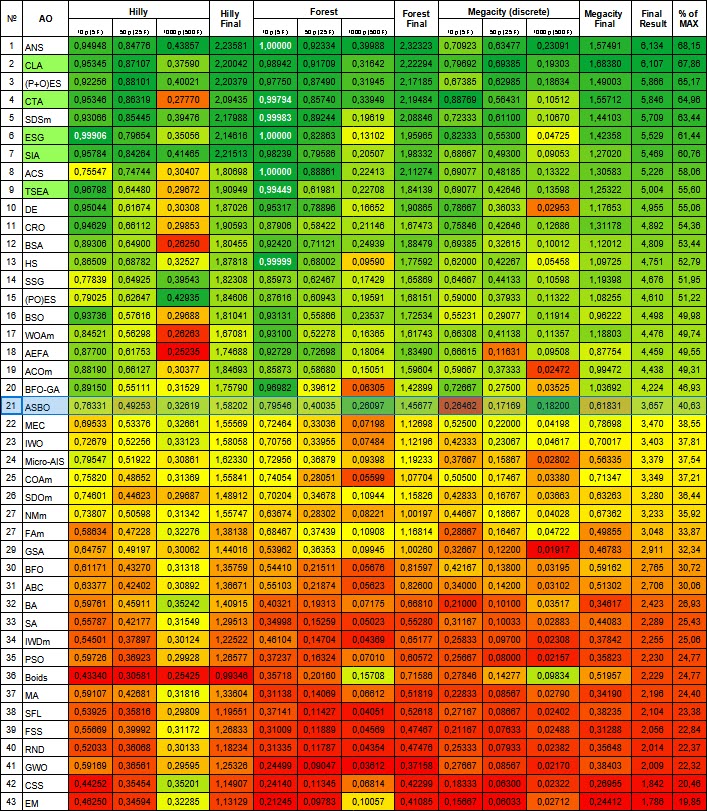
图 2.根据相关测试对算法进行颜色渐变 大于或等于 0.99 的结果用白色标出。 绿色标注的名字是我自己的算法

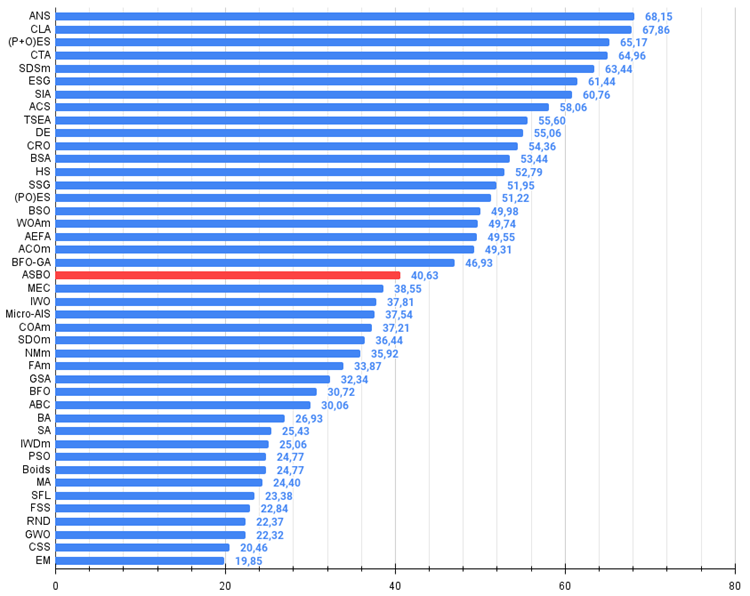
图 3.算法测试结果直方图（从 0 到 100，越多越好、

其中 100 是最大可能的理论结果，归档中有一个计算评级表的脚本）。

ASBO 算法的优缺点：

优点：

1. 外部参数数量少。
   
2. 在复杂的高维问题上取得了良好的效果。
   

缺点：

1. 低维问题的低收敛性。
   

这篇文章附有一个归档，其中包含当前版本的算法代码。文章作者不对规范算法描述的绝对准确性负责。为提高搜索能力，已对其中多项功能进行了修改。文章中提出的结论和判断都是基于实验结果。

• github：https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• 代码库：https://www.mql5.com/ru/code/49355

总结已完成工作的中期成果

在研究过程中，我们探讨了四十多种优化算法，每种算法都代表了解决复杂问题的独特方法。这个过程不仅充满乐趣，而且极富教育意义，揭示了优化领域方法的丰富性和多样性。

重新创建和修改算法。对于所考虑的绝大多数算法，没有广泛可用的源代码。这促使我采取了一种创造性的方法：代码完全基于作者从各种出版物中获得的文本描述进行重新创建。这种方法不仅使我们能够更好地理解每种算法的操作原理，而且使它们能够适应我们的特定需求。
少数开源算法通常不适用于解决优化问题。这需要进行重大修改，使其具有通用性，并易于应用于各种任务。

创新和改进。一些算法，如 ACO（用于解决图上问题的蚁群算法），其作者最初并不打算处理连续空间中的问题，需要修改以扩大其应用范围。其他算法对其搜索策略进行了改进，提高了效率。这些修改后的版本在它们的名字中被赋予了“m”后缀，反映了它们的演变。此外，我们还详细研究了处理种群、生成新解决方案和选择方法的许多不同方法。

为了展示优化的新想法和方法，我开发了五种以上的新专有算法，并在文章中独家介绍。

应用和进一步研究。所提出的任何算法都可以应用于解决优化问题，而不需要额外的修订或修改。这使得它们对广泛的研究人员和从业者来说非常方便。

对于那些寻求在特定的个人任务中取得最佳结果的人，提供了比较表格和直方图，以研究每种算法的个人属性。这为更精细的调整和优化提供了机会，以满足特定的要求。

这两种方法 — 使用现成的算法，以及对它们的深入研究和适应 — 都是可行的。了解不同算法的搜索策略中的微妙之处和技术，为研究人员实现出色的结果开辟了新的视野。

我衷心祝愿所有读者在找到最佳解决方案和实现目标方面取得成功。愿您在优化和算法交易领域的旅程令人兴奋和成功！