MetaTrader 5 / 示例
English Русский Español Deutsch 日本語 Português 한국어 Français Italiano Türkçe
preview
种群优化算法：蝙蝠算法（BA）

种群优化算法：蝙蝠算法（BA）

MetaTrader 5 — 示例 | 18 五月 2023, 10:20
1 205 0
Andrey Dik
Andrey Dik

内容

1. 概述
2. 算法描述
3. 测试结果


1. 概述

蝙蝠是种神奇的动物。 科学家认为，最早的蝙蝠出现在 65-100 亿年前，曾与恐龙并肩生活。 蝙蝠是唯一有翅膀的哺乳动物。 蝙蝠的种类拥有 1300 多种。 除了极地高寒地区之外，它们几乎无处不在。 白天间，它们躲在避难所里。 为了在黑暗的洞穴中导航，并在天黑后狩猎，蝙蝠依靠回声定位，该系统允许它们依靠声波检测物体。 它们通过发出高频声波的回声定位，该声波向前移动，直到它击中物体，并被反射回来。 回声定位是一种声纳：蝙蝠发出响亮而短促的脉冲声波。 当声波到达物体时，回声会在短时间内反射回到蝙蝠的耳朵，这就是蝙蝠在空间中定位自己，并判定猎物位置的方式。 

蝙蝠算法（BA）是杨（Yang）在 2010 年推出的一种启发式算法，它模仿蝙蝠的回声定位行为进行全局优化。 元启发式通常受到自然和物理过程的启发，现在被用作解决许多复杂优化问题的最强大的技术之一。 优化是从许多有效选项中选取最佳元素成为一组特定准则，这在计算效率和全局优化的可能性方面展现出许多不同的优点和缺点。

特征优化通过提供的“目标”函数，依据输入的参数，为建模和解决许多特定问题提供了一个正式的框架。 目标是找到组合参数的值，并返回最佳值。 这个框架足够抽象，因此可以将各种问题解释为“特征优化”问题。


然而，传统的特征优化仅能解决一些小问题，而在实践中这些往往不顶用。 故此，科学家们正在将注意力转向自然界，其为解决这些问题提供了丰富的模型。 通过对自然生物系统进行建模，提出了许多智能群体优化算法，可以非常规方法解决应用问题。 它们因其优异的性能而广泛用于各种优化问题。 BA 是一种新颖的现代种群算法，它使用人造蝙蝠作为搜索代理者，模拟真实蝙蝠的自然声波脉冲音量和发射频率，来执行搜索过程。


2. 算法说明

在基本的蝙蝠算法中，每个蝙蝠都被视为一个“无质量和无大小”的粒子，代表解空间中的有效解。 对于不同的适应度函数，每只蝙蝠都有对应的特征值，通过对比特征值来判定当前的最优个体。 然后更新声波的频率、速度、脉冲发射速度、和种群中每只蝙蝠的体积，继续迭代演化，逼近当前最优解，最终找到全局最优解。 该算法更新每只蝙蝠的频率、速度和位置。

标准算法需要五个基本参数：频率、音量、纹波、以及音量和纹波的比率。 频率用于平衡历史最佳位置对当前位置的影响。 当搜索频率范围较大时，单只蝙蝠就能远离群体的历史位置进行搜索，反之亦然。

与前面考虑的参数相比，该算法有很多参数：

input double MIN_FREQ_P          = 0.0;
input double MAX_FREQ_P         = 1.0;
input double MIN_LOUDNESS_P  = 0.0;
input double MAX_LOUDNESS_P = 1.5;
input double MIN_PULSE_P        = 0.0;
input double MAX_PULSE_P        = 1.0;
input double ALPHA_P               = 0.3;
input double GAMMA_P              = 0.3;

在实现 BA 算法时，我遇到了这样一个事实，即在众多来源中，各篇文章的作者以完全不同的方式描述算法。 区别仅在于关键点描述中所用的术语，和基本算法特征，因此我将讲述自己如何理解它。 回声定位的基本物理原理可以在用在算法当中，但有明显的保留和约定。 我们假设蝙蝠所用的频率范围从 MinFreq 到 MaxFreq 的声波脉冲。 频率会影响蝙蝠的速度。 还用到了音量概念的条件，这会影响蝙蝠从当前位置的局部搜索状态到最佳解附近的全局搜索状态的转换。 在整个优化过程中，脉动频率增加，而声波的音量减小。

BA 算法伪代码（图例 1）：

1. 蝙蝠种群初始化。
2. 生成频率、速度和新解。
3. 搜索局部解。
4. 更新全局解。
5. 降低音量，提升脉动频率。
6. 重复步骤 2，直到满足停止条件。

示意图

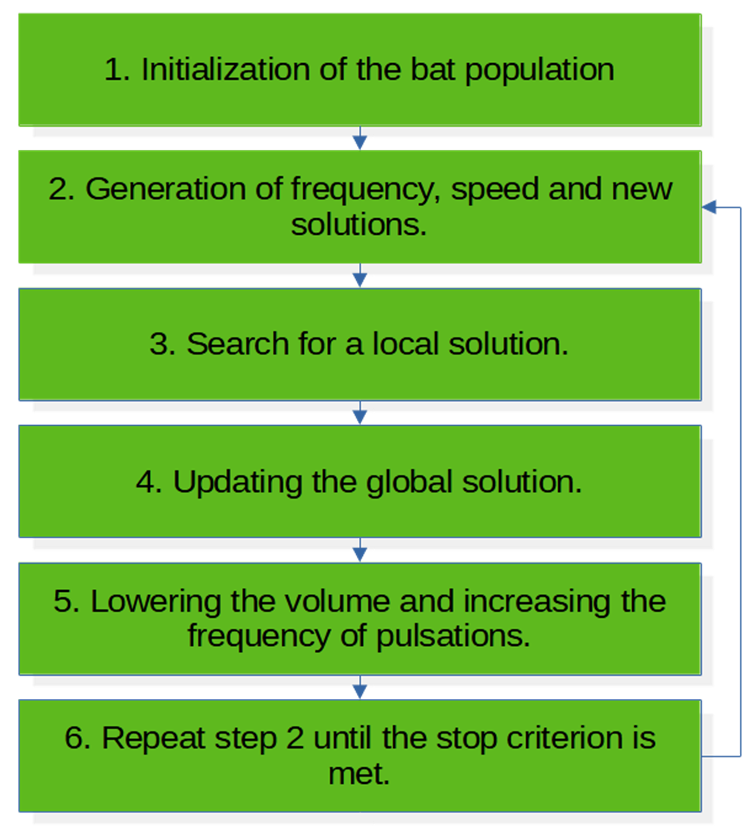
图例 1. BA 算法框图

我们开始讲述代码。 为了讲述“蝙蝠”搜索代理者，我们需要一个结构，在其中是每次迭代时的状态完整描述所需的所有特征。 position [] 数组用于存储空间中的最佳位置坐标，而 auxPosition [] 数组用于当前“操作”坐标。 speed [] 数组在按照坐标计算速度矢量时是必需的。 frequency - 声音脉冲的频率，initPulseRate - 初始脉冲速率（从优化一开始每个蝙蝠都是单独的），pulseRate - 当前迭代时的脉冲速率，loudness - 声波脉冲的音量，fitness - 最后一次移动后的适应度函数值，fitnessBest - 代理者所有迭代的适应度函数的最佳值。  

//——————————————————————————————————————————————————————————————————————————————
struct S_Bat
{
  double position    [];
  double auxPosition [];
  double speed       [];
  double frequency;
  double initPulseRate;
  double pulseRate;
  double loudness;
  double fitness;
  double fitnessBest;
};
//——————————————————————————————————————————————————————————————————————————————

蝙蝠算法类包含搜索代理者所需的结构数组、欲探索空间的边界和步长、算法找到的最佳坐标、适应度函数的最佳值、和存储算法参数的常量，以及公开的初始化方法、算法进行操作所需的两个公开方法、和特定于算法的私密方法。 

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BA
{
  //============================================================================
  public: S_Bat  bats      []; //bats
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    paramsP,
                     const int    batsNumberP,
                     const double min_FREQ_P,
                     const double max_FREQ_P,
                     const double min_LOUDNESS_P,
                     const double max_LOUDNESS_P,
                     const double min_PULSE_P,
                     const double max_PULSE_P,
                     const double alpha_P,
                     const double gamma_P,
                     const int    maxIterP);

  public: void Flight (int epoch);
  public: void Preparation ();

  //============================================================================
  private: void Walk               (S_Bat &bat);
  private: void AproxBest          (S_Bat &bat, double averageLoudness);
  private: void AcceptNewSolutions (S_Bat &bat);
  private: int  currentIteration;
  private: int  maxIter;

  private: double MIN_FREQ;
  private: double MAX_FREQ;

  private: double MIN_LOUDNESS;
  private: double MAX_LOUDNESS;

  private: double MIN_PULSE;
  private: double MAX_PULSE;

  private: double ALPHA;
  private: double GAMMA;

  private: int    params;
  private: int    batsNumber;

  private: bool   firstFlight;

  private: double SeInDiSp  (double In, double inMin, double inMax, double step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

在算法设置参数的 Init() 公开方法中，为数组分配内存，将变量重置为最小值以存储最佳拟合，并重置初始迭代的标志。 一般来说，这种方法并不复杂，而且很特别。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::Init (const int    paramsP,
                    const int    batsNumberP,
                    const double min_FREQ_P,
                    const double max_FREQ_P,
                    const double min_LOUDNESS_P,
                    const double max_LOUDNESS_P,
                    const double min_PULSE_P,
                    const double max_PULSE_P,
                    const double alpha_P,
                    const double gamma_P,
                    const int    maxIterP)
{
  MathSrand (GetTickCount ());

  fB = -DBL_MAX;

  params       = paramsP;
  batsNumber   = batsNumberP;
  MIN_FREQ     = min_FREQ_P;
  MAX_FREQ     = max_FREQ_P;
  MIN_LOUDNESS = min_LOUDNESS_P;
  MAX_LOUDNESS = max_LOUDNESS_P;
  MIN_PULSE    = min_PULSE_P;
  MAX_PULSE    = max_PULSE_P;
  ALPHA        = alpha_P;
  GAMMA        = gamma_P;
  maxIter      = maxIterP;

  ArrayResize (rangeMax,  params);
  ArrayResize (rangeMin,  params);
  ArrayResize (rangeStep, params);

  firstFlight = false;

  ArrayResize (bats, batsNumber);

  for (int i = 0; i < batsNumber; i++)
  {
    ArrayResize (bats [i].position,    params);
    ArrayResize (bats [i].auxPosition, params);
    ArrayResize (bats [i].speed,       params);

    bats [i].fitness  = -DBL_MAX;
  }

  ArrayResize (cB, params);
}
//——————————————————————————————————————————————————————————————————————————————

每次迭代时调用的第一个方法是 Flight()。 它集中了搜索逻辑的主框架，其余细节则置于此优化算法的特定辅助私密方法当中。 在第一次迭代之初，firstFlight 标志被重置（重置发生在 Init() 方法的初始化期间）。这意味着我们需要为每只蝙蝠分配一个初始状态，这是搜索空间中的一个随机位置:

  • 零速，
  • 按参数指定范围，为声波脉冲随机数分配单独频率，
  • 取参数范围内随机数定义单独脉动的初始频率
  • 并在参数范围内定义声波脉冲的音量。

如您所见，每只人造蝙蝠都有一组单独的声波信号特征，这令它们更像自然界中的真实蝙蝠。 在整个种群中，可能包括数十万只，母体可以通过婴儿发出的独特声波特征找到幼崽。

如果启用了 firstFlight 标志，则需要执行基本操作来移动蝙蝠。 该算法的一个有趣特征在于整个种群的平均声波音量的概念。 通常，在所有迭代中，声波音量都会通过 “alpha” 系数降低。 这里有两种类型的蝙蝠运动：Walk () - 计算每个坐标分量的速度矢量的单个运动，和最佳解附近的局部运动。

随着下一次迭代，脉动的强度降低，这会影响邻域探索的强度。 因此，探索及其动态变化会贯穿整个优化过程之中。 接下来，我们将看到当前的迭代如何影响蝙蝠的行为。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::Flight (int epoch)
{
  currentIteration = epoch;

  //============================================================================
  if (!firstFlight)
  {
    fB = -DBL_MAX;

    //--------------------------------------------------------------------------
    for (int b = 0; b < batsNumber; b++)
    {
      for (int p = 0; p < params; p++)
      {
        bats [b].position    [p] = RNDfromCI (rangeMin [p], rangeMax [p]);
        bats [b].position    [p] = SeInDiSp (bats [b].position [p], rangeMin [p], rangeMax [p], rangeStep [p]);
        bats [b].auxPosition [p] = bats [b].position    [p];
        bats [b].speed       [p] = 0.0;
        bats [b].frequency       = RNDfromCI (MIN_FREQ, MAX_FREQ);
        bats [b].initPulseRate   = RNDfromCI (MIN_PULSE, MAX_PULSE / 2);
        bats [b].pulseRate       = bats [b].initPulseRate;
        bats [b].loudness        = RNDfromCI (MAX_LOUDNESS / 2, MAX_LOUDNESS);
        bats [b].fitness         = -DBL_MAX;
        bats [b].fitnessBest     = -DBL_MAX;
      }
    }

    firstFlight = true;
  }
  //============================================================================
  else
  {
    double avgLoudness = 0;

    for (int b = 0; b < batsNumber; b++)
    {
      avgLoudness += bats [b].loudness;
    }

    avgLoudness /= batsNumber;

    for (int b = 0; b < batsNumber; b++)
    {
      Walk (bats [b]);

      if (RNDfromCI (MIN_PULSE, MAX_PULSE) > bats [b].pulseRate)
      {
        AproxBest (bats [b], avgLoudness);
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

每次迭代时必需调用的第二个公开方法 - Preparation() 是更新全局最佳解所必需的。 在这里，我们可以看到如何使用“音量”的概念。 鉴于每次迭代时，每只蝙蝠的音量都会按照一个因子（“alpha” 算法调整参数）降低，因此局部研究的概率随着全局解研究的强度而降低。 换言之，更新每只蝙蝠最佳位置的概率随着每次迭代而降低。 这是算法中最难以理解的时刻之一，至少对我来说是这样。 然而，该算法的作者实现了这一点，这意味着这是必要的。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::Preparation ()
{
  //----------------------------------------------------------------------------
  for (int b = 0; b < batsNumber; b++)
  {
    if (bats [b].fitness > fB)
    {
      fB = bats [b].fitness;
      ArrayCopy (cB, bats [b].auxPosition, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  for (int b = 0; b < batsNumber; b++)
  {
    if (RNDfromCI (MIN_LOUDNESS, MAX_LOUDNESS) < bats [b].loudness && bats [b].fitness >= bats [b].fitnessBest)
    {
      AcceptNewSolutions (bats [b]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

私密的 Walk() 方法确保每只蝙蝠相对于其当前最佳位置独立移动，给出目前为止的全局最佳解。 该方法使用声波脉冲的频率，其值在 [MIN_FREQ;MAX_FREQ] 范围内变化。 需要频率来计算搜索代理者的移动速度，这是频率与最佳蝙蝠位置和最佳全局解之差的乘积。 之后，将速度值逐个添加到蝙蝠的当前最佳解之中。 因此，我们的操作与物理量不成比例，但我们能怎样做呢？ 这只是对真实物理对象的近似值。 在这种情况下，必须忽略合理性。 计算新位置后，应调用 SeInDiSp() 方法检查坐标是否超出范围。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::Walk (S_Bat &bat)
{
  for (int j = 0; j < params; ++j)
  {
    bat.frequency       = MIN_FREQ + (MAX_FREQ - MIN_FREQ) * RNDfromCI (0.0, 1.0);
    bat.speed       [j] = bat.speed [j] + (bat.position [j] - cB [j]) * bat.frequency;
    bat.auxPosition [j] = bat.position [j] + bat.speed [j];

    bat.auxPosition [j] = SeInDiSp (bat.auxPosition [j], rangeMin [j], rangeMax [j], rangeStep [j]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

第二个私密方法 AproxBest() 负责相对于全局最佳解移动蝙蝠，提供额外的坐标细化。 对于我自己，不太理解这个动作的物理含义，它的组成以整个蝙蝠种群的平均音量的形式逐个向量添加到增量坐标中，并乘以 [-1.0; 1.0] 范围内的随机数。 我尝试通过定义域的有效值向量将值减少到正在优化的函数的维度，但测试结果比作者的算法版本更差，所以我让一切都保持原样，但我确信 BA 算法的效率还可以提高， 但这需要额外的研究，不过这并非本文案的目标。 计算坐标后，使用 SeInDiSp （） 方法检查值是否超出范围。 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::AproxBest (S_Bat &bat, double averageLoudness)
{
  for (int j = 0; j < params; ++j)
  {
    bat.auxPosition [j] = cB [j] + averageLoudness * RNDfromCI (-1.0, 1.0);
    bat.auxPosition [j] = SeInDiSp (bat.auxPosition [j], rangeMin [j], rangeMax [j], rangeStep [j]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

另一个特殊的私密方法是 AcceptNewSolutions()，当满足每只蝙蝠的声波脉冲频率的测试条件时，就会调用该方法。 接受新的最佳独立解，以及于此处重新计算单独音量和单独脉动频率。 在此，我们可以看到迭代的序数如何参与脉动频率的计算。

在算法逻辑的这一点上，我采取了一些自由度，并改变了逻辑，令结果独立于总迭代次数的维度，最终略微提高了算法的效率。 在原始版本中，迭代次数直接参与计算脉冲频率的非线性公式。 BA 已经有很多约定。 在这种情况下，我不能再熟视无睹。 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::AcceptNewSolutions (S_Bat &bat)
{
  ArrayCopy(bat.position, bat.auxPosition, 0, 0, WHOLE_ARRAY);
  bat.fitnessBest = bat.fitness;
  bat.loudness    = ALPHA * bat.loudness;
  double iter     = Scale (currentIteration, 1, maxIter, 0.0, 10.0, false);
  bat.pulseRate   = bat.initPulseRate *(1.0 - exp(-GAMMA * iter));
}
//——————————————————————————————————————————————————————————————————————————————

脉动频率对当前迭代次数（图例中 x）和 GAMMA 设置参数的依赖性如图例 2 所示。

gamma

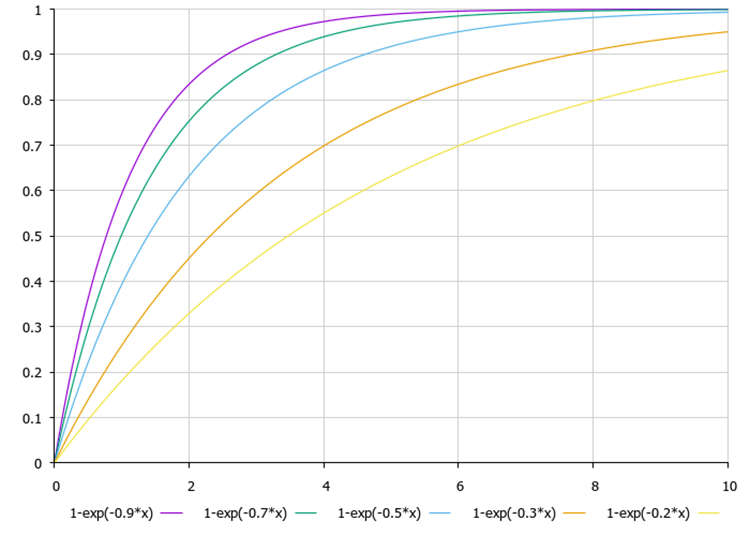
图例 2. 脉动频率对当前迭代次数和 GAMMA 设置参数的依赖性，值为 0.9, 0.7, 0.5, 0.3, 0.2

3. 测试结果

在上一篇文章中，我提到了修订计算测试算法评级方法的计划。 首先，由于大多数算法可以轻松处理两个变量的测试函数，并且结果之间的差异几乎无法区分，因此我决定在所有测试函数里增加前两个测试的变量数字。 现在变量的数字将是 10, 50 和 1000。

其次，Skin 测试函数已被广泛使用的 Rastrigin 函数所取代（图例 3）。 此函数像 Skin 一样平滑。 它拥有许多局部极值的复杂表面，四个点处有一个全局最大值，坐标轴中心有一个全局最小值。

第三，我决定将测试结果规范化为表中所有算法中的一系列值，其中最佳结果为 1.0，最差结果为 0.0。 这令我们能够均匀地评估测试结果，同时根据测试中每种优化算法的结果考虑函数的复杂性。

之后，汇总算法的测试结果。 最大结果的值分配为 100（参考最大结果），而最小值为 1。 这令我们能够直接拿算法相互比较，并参考测试函数的复杂性。 现在，在 Print() 中打印的结果分别保存在每个算法的测试脚本的源文件之中。 计算测试分数的脚本附在文后。 在后续文章中会更新它，并添加正在研究的新算法结果。



rastrigin

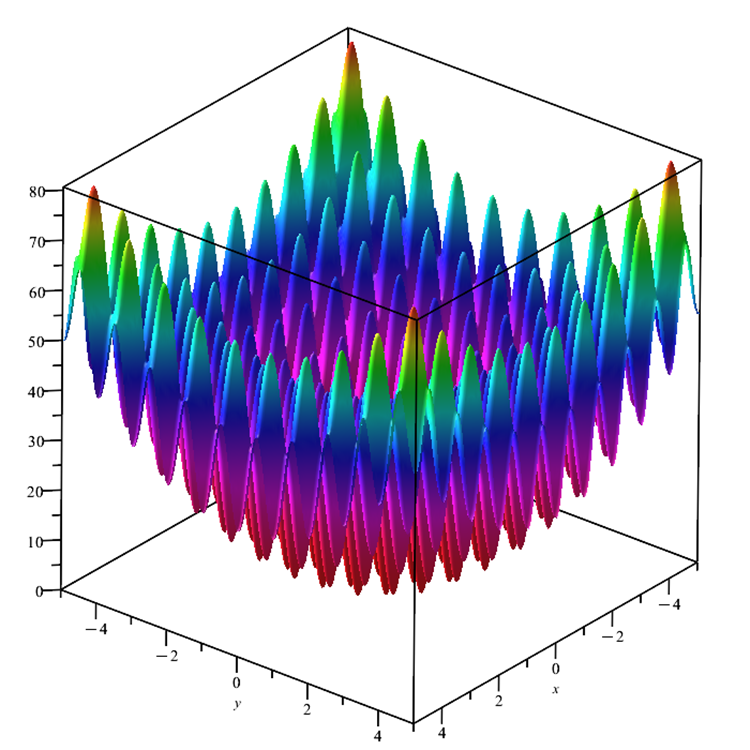
图例 3. Rastrigin 测试函数

测试台结果如下所示： 

2022.12.28 17:13:46.384    Test_AO_BA (EURUSD,M1)    C_AO_BA:50;0.0;1.0;0.0;1.5;0.0;1.0;0.3;0.3
2022.12.28 17:13:46.384    Test_AO_BA (EURUSD,M1)    =============================
2022.12.28 17:13:48.451    Test_AO_BA (EURUSD,M1)    5 Rastrigin's; Func runs 10000 result: 66.63334336098077
2022.12.28 17:13:48.451    Test_AO_BA (EURUSD,M1)    Score: 0.82562
2022.12.28 17:13:52.630    Test_AO_BA (EURUSD,M1)    25 Rastrigin's; Func runs 10000 result: 65.51391114042588
2022.12.28 17:13:52.630    Test_AO_BA (EURUSD,M1)    Score: 0.81175
2022.12.28 17:14:27.234    Test_AO_BA (EURUSD,M1)    500 Rastrigin's; Func runs 10000 result: 59.84512760590815
2022.12.28 17:14:27.234    Test_AO_BA (EURUSD,M1)    Score: 0.74151
2022.12.28 17:14:27.234    Test_AO_BA (EURUSD,M1)    =============================
2022.12.28 17:14:32.280    Test_AO_BA (EURUSD,M1)    5 Forest's; Func runs 10000 result: 0.5861602092218606
2022.12.28 17:14:32.280    Test_AO_BA (EURUSD,M1)    Score: 0.33156
2022.12.28 17:14:39.204    Test_AO_BA (EURUSD,M1)    25 Forest's; Func runs 10000 result: 0.2895682720055589
2022.12.28 17:14:39.204    Test_AO_BA (EURUSD,M1)    Score: 0.16379
2022.12.28 17:15:14.716    Test_AO_BA (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.09867854051596259
2022.12.28 17:15:14.716    Test_AO_BA (EURUSD,M1)    Score: 0.05582
2022.12.28 17:15:14.716    Test_AO_BA (EURUSD,M1)    =============================
2022.12.28 17:15:20.843    Test_AO_BA (EURUSD,M1)    5 Megacity's; Func runs 10000 result: 3.3199999999999994
2022.12.28 17:15:20.843    Test_AO_BA (EURUSD,M1)    Score: 0.27667
2022.12.28 17:15:26.624    Test_AO_BA (EURUSD,M1)    25 Megacity's; Func runs 10000 result: 1.2079999999999997
2022.12.28 17:15:26.624    Test_AO_BA (EURUSD,M1)    Score: 0.10067
2022.12.28 17:16:05.013    Test_AO_BA (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.40759999999999996
2022.12.28 17:16:05.013    Test_AO_BA (EURUSD,M1)    Score: 0.03397

蝙蝠算法在平滑 Rastrigin 函数上展现出令人印象深刻的结果。 有趣的是，随着函数中变量数字的增加，结果的稳定性（可重复性）增加，这表明 BA 在平滑函数上具有出色的可扩展性。 特别是，BA 在所有测试有 50 个和 1000 个变量的参与者中被证明是 Rastrigin 函数中最好的，这样我们能够推荐蝙蝠算法来处理复杂的平滑函数和神经网络。 在 Forest 和 Megacity 函数上，蝙蝠算法的结果较平庸，显示出陷入局部极值的趋势。 坐标被本地化为群组，并非显示朝向全局最优的变化和走势的动态。 我认为，发生这种情况是因为该算法对于所研究函数的表面梯度很敏感。 在缺乏梯度的情况下，算法会快速停在适应度函数值无显著增量的局部区域附近。 甚至，BA 算法缺乏允许“跃迁”到新的未知区域的机制，类似于 COA（Levy 飞行）中实施的机制。

我还应该提到 BA 的大量设置。 不仅有许多参数（自由度），而且每个参数都极大地影响搜索属性的性质和整体收敛率。 一些参数可以在平滑函数上给出完美的结果，而一些参数可以在离散函数和裂隙函数上给出完美的结果。 找到一些通用参数，令其能够很好地应对不同类型的测试函数是一项艰巨的任务。 本文介绍了蝙蝠算法的源代码，其中包含对我来说似乎最优化的参数。 一般来说，我不建议那些在使用优化算法方面经验不足的用户使用 BA，因为优化结果可能会有很大差异。  

rastrigin

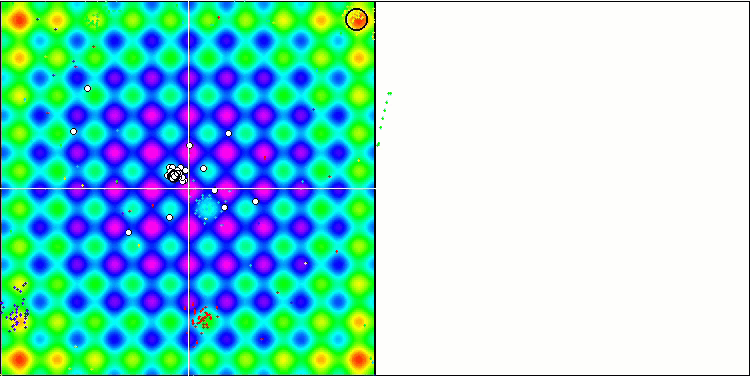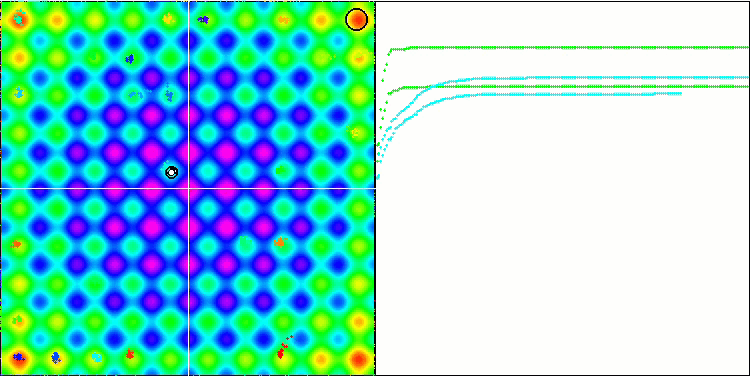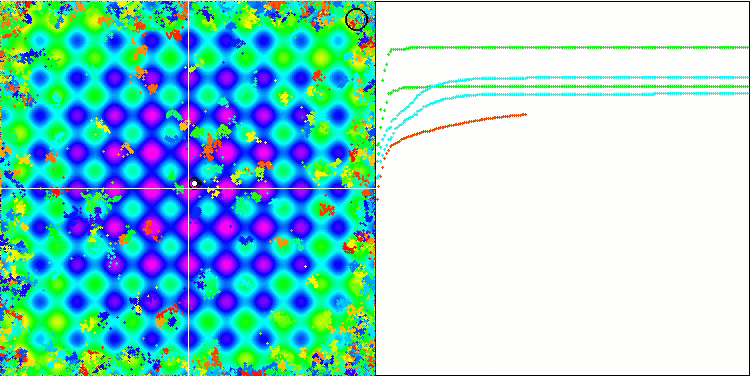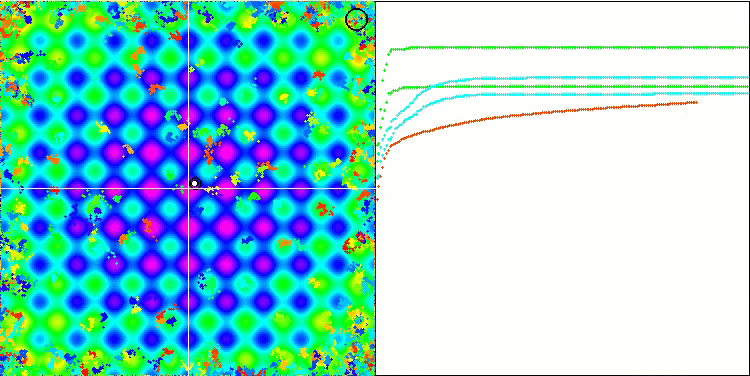
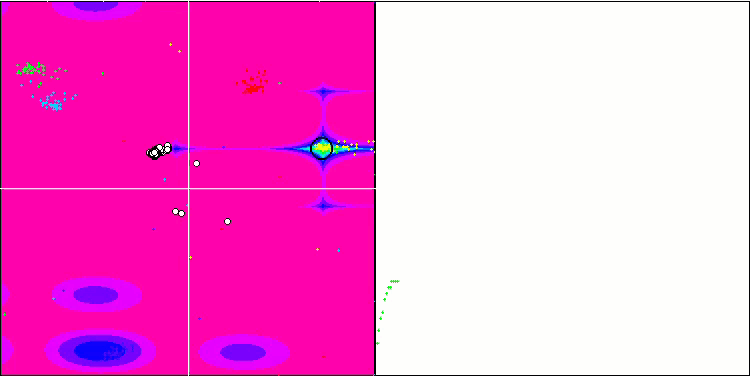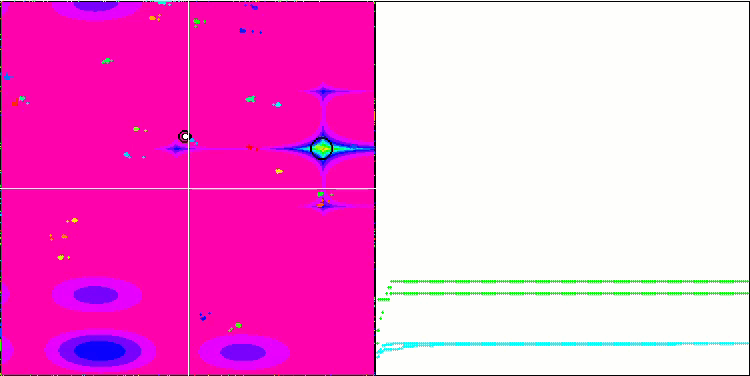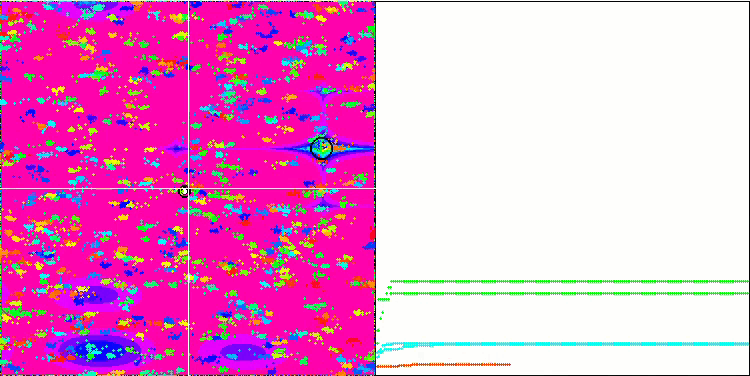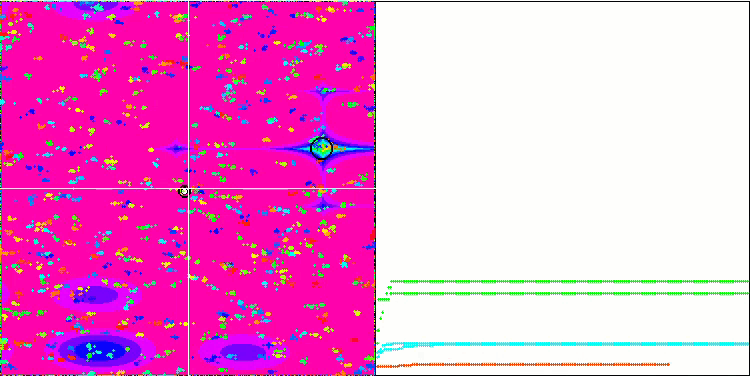
  Rastrigin 测试函数上的 BA

forest

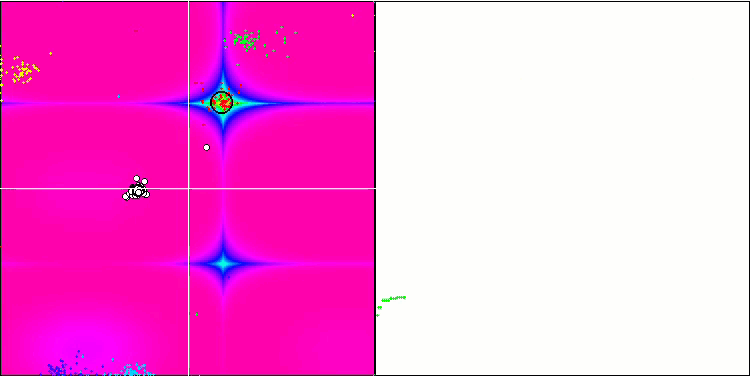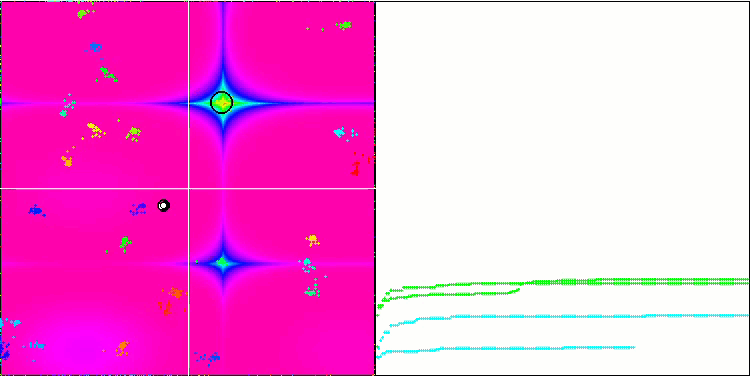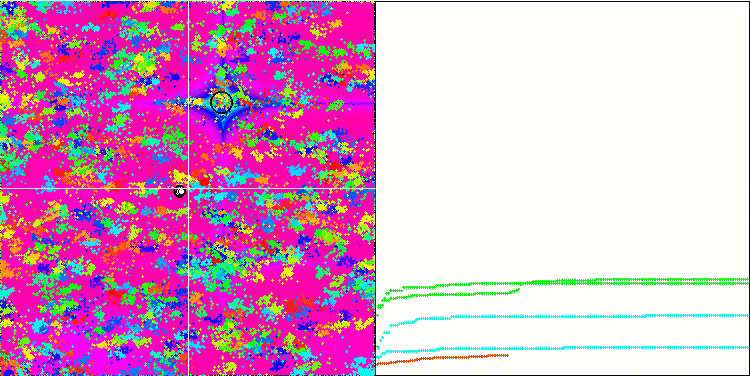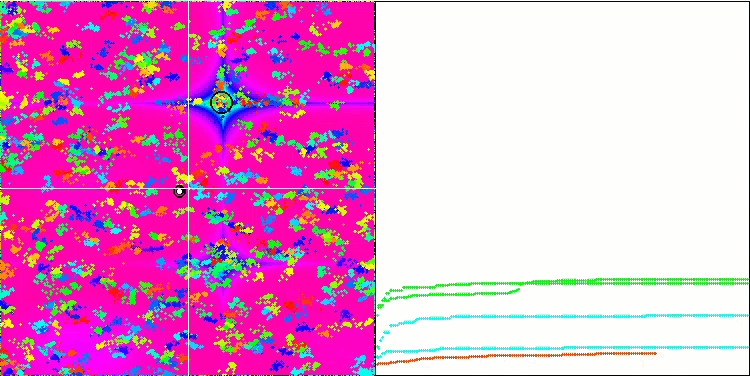
Forest 测试函数上的 BA。

megacity

Megacity 测试函数上的 BA。

在专注于测试函数可视化的同时，可以了解蝙蝠算法的特征。 特别是，在处理所有测试函数时，该算法的特点是在非常小的局部区域中对坐标进行分组。 而对于平滑函数，即使适应度函数的梯度略有变化，此函数也可以移动；但在离散函数上，此函数被证明是一个缺点，因为算法会在平坦的高原上卡住。

脚本计算优化算法分数获得的结果：

2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_RND=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.18210 | 0.15281 | 0.07011 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.08623 | 0.04810 | 0.06094 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.00000 | 0.00000 | 0.08904 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.6893397068905002
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_PSO=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.22131 | 0.12861 | 0.05966 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.15345 | 0.10486 | 0.28099 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.08028 | 0.02385 | 0.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    1.053004072893302
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_ACOm=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.37458 | 0.28208 | 0.17991 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    1.00000 | 1.00000 | 1.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    1.00000 | 1.00000 | 0.10959 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    5.946151922377553
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_ABC=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.84599 | 0.51308 | 0.22588 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.58850 | 0.21455 | 0.17249 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.47444 | 0.26681 | 0.35941 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    3.661160435265267
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_GWO=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.00000 | 0.00000 | 0.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.00000 | 0.00000 | 0.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.18977 | 0.04119 | 0.01802 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.24898721240154956
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_COAm=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    1.00000 | 0.73390 | 0.28892 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.64504 | 0.34034 | 0.21362 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.67153 | 0.34273 | 0.45422 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    4.690306586791184
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_FSS=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.50663 | 0.39737 | 0.11006 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.07806 | 0.05013 | 0.08423 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.00000 | 0.01084 | 0.18998 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    1.4272897567648186
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_FAm=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.64746 | 0.53292 | 0.18102 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.55408 | 0.42299 | 0.64360 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.21167 | 0.28416 | 1.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    4.477897116029613
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_BA=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.43859 | 1.00000 | 1.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.17768 | 0.17477 | 0.33595 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.15329 | 0.07158 | 0.46287 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    3.8147314003892507
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    ================
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    ================
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    ================
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.24898721240154956 | 5.946151922377553
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_RND: 8.652
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_PSO: 14.971
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_ACOm: 100.000
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_ABC: 60.294
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_GWO: 1.000
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_COAm: 78.177
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_FSS: 21.475
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_FAm: 74.486
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_BA: 62.962

我们来看看最终的评级表。 如上所述，算法的估算特征的计算方法已经有所变化，因此算法得到了新的位置。 一些经典算法已从表中删除，只剩下其修改后的版本，这些算法在测试中表现出更高的性能。 现在，测试结果不像以前那样是绝对的（测试函数值的绝对归一化结果），而是基于相互比较算法的结果的相对结果。

该表显示 ACOm（蚁群优化）目前处于领先地位。 该算法在九次测试中的五次中显示出最佳结果，因此最终结果为 100 分。 COAm 是杜鹃鸟优化算法的修改版本，排在第二位。 事实证明，该算法在平滑 Rastrigin 函数上是最好的，并且与其它测试参与者相比，在其它测试中也显示出良好的结果。 修改后的萤火虫算法 FAm 排名第三。 它在 Megacity 离散函数上显示出最佳结果。 仅有 FSS 在此测试中显示出相同的结果。

算法

说明

Rastrigin

Rastrigin 最终

Forest

Forest 最终

Megacity (离散)

Megacity 最终

最终结果

10 参数 (5 F)

50 参数 (25 F)

1000 参数 (500 F)

10 参数 (5 F)

50 参数 (25 F)

1000 参数 (500 F)

10 参数 (5 F)

50 参数 (25 F)

1000 参数 (500 F)

ACOm

蚁群优化 M

0.37458

0.28208

0.17991

0.83657

1.00000

1.00000

1.00000

3.00000

1.00000

1.00000

0.10959

2.10959

100.000

COAm

杜鹃优化算法 M

1.00000

0.73390

0.28892

2.02282

0.64504

0.34034

0.21362

1.19900

0.67153

0.34273

0.45422

1.46848

78.177

FAm

萤火虫算法 M

0.64746

0.53292

0.18102

1.36140

0.55408

0.42299

0.64360

1.62067

0.21167

0.28416

1.00000

1.49583

74.486

BA

蝙蝠算法

0.43859

1.00000

1.00000

2.43859

0.17768

0.17477

0.33595

0.68840

0.15329

0.07158

0.46287

0.68774

62.962

ABC

人工蜂群

0.84599

0.51308

0.22588

1.58495

0.58850

0.21455

0.17249

0.97554

0.47444

0.26681

0.35941

1.10066

60.294

FSS

鱼群搜索

0.64746

0.53292

0.18102

1.36140

0.55408

0.42299

0.64360

1.62067

0.21167

0.28416

1.00000

1.49583

21.475

PSO

粒子群优化

0.22131

0.12861

0.05966

0.40958

0.15345

0.10486

0.28099

0.53930

0.08028

0.02385

0.00000

0.10413

14.971

RND

随机

0.18210

0.15281

0.07011

0.40502

0.08623

0.04810

0.06094

0.19527

0.00000

0.00000

0.08904

0.08904

8.652

GWO

灰狼优化器

0.00000

0.00000

0.00000

0.00000

0.00000

0.00000

0.00000

0.00000

0.18977

0.04119

0.01802

0.24898

1.000


算法测试结果直方图如图例 4 所示

评级

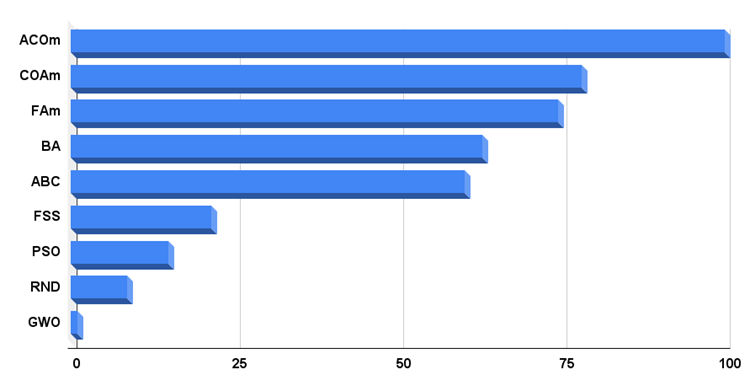
图例 4. 测试算法最终结果的直方图

关于蝙蝠算法（BA）属性的结论：

优点:
1. 高速。
2. 算法能与平滑函数配合良好。
3. 可扩展性。

缺点:
1. 太多设置。
2. 离散函数的结果平庸。


本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/11915

附加的文件 |
下载ZIP
9_The_world_of_AO_gBAs.zip (68.81 KB)
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论
神经网络实验（第 3 部分）：实际应用 神经网络实验（第 3 部分）：实际应用
在本系列文章中，我会采用实验和非标准方法来开发一个可盈利的交易系统，并检查神经网络是否对交易者有任何帮助。 若在交易中运用神经网络，MetaTrader 5 则可作为近乎自给自足的工具。
学习如何基于鳄嘴（Gator）振荡器设计交易系统 学习如何基于鳄嘴（Gator）振荡器设计交易系统
这是我们关于学习如何基于流行技术指标设计交易系统系列的一篇新文章，将介绍鳄嘴（Gator）振荡器技术指标，以及如何通过简单的策略创建交易系统。
种群优化算法：入侵杂草优化（IWO） 种群优化算法：入侵杂草优化（IWO）
在各种条件下杂草的惊人生存能力已演化成强大优化算法的思路。 IWO 是以前审阅过的算法中最好的算法之一。
您应该知道的 MQL5 向导技术（第 05 部分）：马尔可夫（Markov）链 您应该知道的 MQL5 向导技术（第 05 部分）：马尔可夫（Markov）链
马尔可夫（Markov）链是一个强大的数学工具，能够针对包括金融在内的各个领域的时间序列数据进行建模和预测。 在金融时间序列建模和预测中，马尔可夫链通常用于模拟金融资产随时间的演变，例如股票价格或汇率。 马尔可夫链模型的主要优点之一是其简单性和易用性。