Adaptive Social Behavior Optimization (ASBO): Zweiphasige Entwicklung

Inhalt

1. Einführung
2. Implementierung des Algorithmus
3. Testergebnisse

1. Einführung

Im vorangegangenen Artikel haben wir ein Beispiel für Schwefels Konzept besprochen, das eine Normalverteilung, die Verwendung von selbstanpassenden Mutationsraten und eine Funktion zur Bestimmung der nächsten Nachbarn anhand ihres Fitnesswerts umfasst. Unser Weg führt uns nun in eine neue Phase der Forschung, in der wir in einen zweistufigen Prozess eintauchen und die Bildung des Algorithmus als mathematisches Modell - ASBO (Adaptive Social Behavior Optimization) - abschließen werden. Wir werden dieses spannende Modell an den uns bereits bekannten Testfunktionen umfassend testen und Rückschlüsse auf seine Effizienz ziehen. In diesem Artikel werden wir neue Anwendungen des Sozialverhaltens lebender Organismen im Bereich der Optimierung aufdecken und einzigartige Ergebnisse präsentieren, die uns helfen werden, die Prinzipien des kollektiven Verhaltens besser zu verstehen und zur Lösung komplexer Probleme zu nutzen.

2. Implementierung des Algorithmus

Beginnen wir mit der Bildung eines Pseudocodes des ABSO-Algorithmus (die verwendeten Gleichungen sind unten aufgeführt):

Eingaben: PZ population size, M number of populations and P' number of epochs per population. f (x) - objective function.

Initialisierung:

1. Erstelle M Populationen mit der Größe von PZ
2. Für jede Population:

• Initialisiere xi zufällige Lösungen
• Berechne die Werte der Zielfunktion f(xi) für jede Lösung
• Definiere den globalen Spitzenreiter Gb als die Lösung mit dem höchsten f(xi)
• Definiere für jede Lösung xi eine Gruppe von nächsten Nachbarn Nc
• Initialisiere die beste, persönliche Entscheidungen Sb = xi
• Initialisiere die adaptiven Parameter Cg, Cs und Cn nach dem Zufallsprinzip innerhalb des Bereichs [-1,0; 1,0]
  

Phase 1: Unabhängiger Umgang mit Populationen.
3. Für jede der Populationen M:

•  Für jede Lösung xi:
  

• Wende die selbstanpassenden Mutation zur Aktualisierung der Verhältnisse von Cg, Cs und Cn gemäß den Gleichungen (3) und (4) an.
  
• Berechne die Änderung der Position ΔX(i + 1) nach Gleichung (1).
• Aktualisiere die Position xi gemäß Gleichung (2).
• Berechne den neuen Wert f(xi).
• Aktualisiere die beste, persönliche Lösung Sb, wenn f(xi) > f(Sb)
• Aktualisiere den globalen Führenden Gb, wenn f(xi) > f(Gb)

• Wiederhole den Vorgang, bis P' Epochen erreicht werden.

4. Die endgültigen Populationen, die Werte von f(xi) sowie die Parameter Cg, Cs und Cn werden gespeichert.

Phase 2: Behandlung der kombinierten Population.
5. Aus allen endgültigen Populationen wählen wir die besten Lösungen PZ für f(xi) aus.
6. Wir verwenden die gespeicherten Parameter Cg, Cs und Cn für diese Lösungen PZ.
7. Auf die kombinierte Grundgesamtheit mit der Größe von PZ wenden wir des ASBO-Algorithmus an
8. Wir wiederholen die Schritte 6-7, bis das Stoppkriterium erreicht ist.

Schlussfolgerung: Globales Optimum Gb

Schlüsselgleichungen:

• ΔX (i + 1) = Cg * R1 * (Gb - xi) + Cs * R2 * (Sb - xi) + Cn * R3 * (Nc - xi)  (1)
• x (i + 1) = xi + ΔX (i + 1)                                                                           (2)
• p'i (j) = pi (j) + σi (j) * N (0, 1)                                                                  (3)
• σ'i (j) = σi (j) * exp (τ' * N (0, 1) + τ * Nj (0, 1))                                        (4)

Wobei:

• Gb - der global Führender
• Sb - die beste, persönliche Lösung
• Nc - das Zentrum der Gruppe der Nachbarn nach Fitness
  
• R1, R2, R3 - Zufallszahlen im Bereich [0, 1]
• Cg, Cs, Cn - adaptive Parameter
• N(0, 1) - eine Zufallszahl aus einer Normalverteilung
• Nj(0,1) - eine Zufallszahl aus einer Normalverteilung für jede Messung j
• τ, τ' - die Skalierungsfaktoren für die selbstanpassende Mutation

Der vorgestellte Pseudocode zeigt, dass der Algorithmus eine zweistufige Evolution der Entwicklung des Sozialmodells implementiert. Die Logik des Algorithmus kann kurz in Phasen beschrieben werden:

1. Erste Phase:

• Nimm M Populationen mit jeweils der gleichen Größe PZ.
• Wende den ASBO-Algorithmus auf jede der Populationen M einzeln innerhalb einer festen Anzahl von P' Iterationen an.
• Speichere am Ende dieser Phase die Werte der Fitnessfunktionen und der adaptiven Mutationsparameter von jedem Individuum aus allen endgültigen Populationen.

2. Zweite Phase:

• Aus allen endgültigen Populationen der ersten Phase werden die P.Z. der besten Individuen in Bezug auf den Wert der Fitnessfunktion ausgewählt.
• Ihre gespeicherten adaptiven Mutationsparameter werden auf diese besten PZ-Individuen angewendet.
• Der ASBO-Algorithmus wird auf die neue Population der Größe PZ angewendet, um die endgültige Lösung zu erhalten.

Die Bedeutung der zweiphasigen Evolution:

1. Die erste Phase bietet eine Vielfalt von Lösungen und eine bessere Lokalisierung der Region des globalen Optimums aufgrund der unabhängigen Entwicklung mehrerer Populationen.
2. In der zweiten Phase werden die besten Lösungen der Populationen aus der ersten Phase und ihre adaptiven Parameter für eine beschleunigte Konvergenz zum globalen Optimum verwendet.

Die Zweiphasen-Evolution ermöglicht es also theoretisch, die globale Suche in der ersten Phase mit einer effizienteren lokalen Optimierung in der zweiten Phase zu kombinieren, was letztlich vermutlich die Leistung des Algorithmus als Ganzes verbessert.

Bei der herkömmlichen Version des zweiphasigen ASBO-Algorithmus mit mehreren Populationen werden in der ersten Phase mehrere Populationen parallel und unabhängig voneinander verwendet. In der zweiten Phase werden die besten Lösungen aus den Populationen entnommen und eine neue Population wird erstellt. Die Verwendung einer einzigen Vorlage für alle Populationsalgorithmen wirft jedoch die Frage auf, wie man mit mehreren Populationen umgeht.

Die erste Lösung könnte darin bestehen, eine normale Population, beispielsweise 50 Individuen, in mehrere Populationen, beispielsweise 5, aufzuteilen. In diesem Fall wird jede der 5 Populationen 10 Individuen enthalten. Wir können mehrere Populationen auf die übliche Weise behandeln, als wären sie eine einzige Population. In der zweiten Phase stellt sich jedoch ein Problem: Wir müssen die besten Lösungen aus diesen 5 Populationen nehmen und sie in eine neue Population einfügen. Aber wir werden nicht in der Lage sein, die erforderliche Anzahl zu erhalten, weil wir sie alle aufnehmen müssten, was effektiv bedeuten würde, eine Kopie der ursprünglichen Population zu erstellen.

Die zweite Lösung für dieses Problem besteht darin, 5 Populationen zu schaffen, deren Größe der Größe unserer Population entspricht, d. h. 50 Individuen. Für jede dieser Populationen wird eine feste Anzahl von Epochen zugewiesen, z. B. 20. In diesem Fall werden wir in der ersten Phase diese 5 Populationen nacheinander mit einer festen Anzahl von Epochen für jede Population bearbeiten, d. h. es werden 5 * 20 = 100 Epochen ausgegeben. In der zweiten Phase werden die restlichen 100 Epochen (von insgesamt 200 Epochen) verwendet. In dieser zweiten Phase werden wir diese 5 Populationen zu einer großen Population von 250 Individuen zusammenfassen, sie sortieren und die besten 50 Individuen daraus auswählen, um eine neue Population zu schaffen. Als Nächstes führen wir die Operationen mit dieser neuen Population auf die übliche Weise gemäß den Gleichungen durch. Dies steht in völliger Übereinstimmung mit dem ursprünglichen Algorithmus, während wir an unserem Konzept der Arbeit mit Populationsalgorithmen festhalten. Wir mussten bereits bei anderen Algorithmen wie Nelder-Mead, Chemical CRO, evolutionären Algorithmen und anderen innovative Ansätze anwenden, um sicherzustellen, dass alle Algorithmen kompatibel sind und nahtlos ausgetauscht werden können.

Kommen wir nun zum Schreiben des Codes.

Wir implementieren die Struktur S_ASBO_Agent, die den Suchagenten im zweiphasigen ASBO-Algorithmus mit mehreren Populationen beschreiben wird. Die Struktur definiert Variablen und die Methode Init, die den Agenten initialisiert.

Variablen:

• c - Array von Koordinaten
• cBest - Array der besten Koordinaten
• f - Fitnesswert
• fBest - bester Fitnesswert
• Cg, Cs, Cn - adaptive Parameter
• u - Objekt der Klasse C_AO_Utilities

Die Methode Init initialisiert den Agenten:

• Sie akzeptiert die Anzahl der Koordinaten sowie die Arrays rangeMin und rangeMax, die die Mindest- und Höchstwerte für jede Koordinate angeben.
• Sie weist Speicherplatz für die Arrays c und cBest mit der Anzahl der Koordinaten zu.
• Sie setzt den Anfangswert fBest auf -DBL_MAX.
• Sie erzeugt Zufallswerte für die adaptiven Parameter Cg, Cs und Cn.
• Sie füllt das Array c mit Zufallswerten im Bereich zwischen rangeMin und rangeMax auf.
• Sie weist dem Array cBest die Werte von c zu.
  

//——————————————————————————————————————————————————————————————————————————————
struct S_ASBO_Agent
{
    double c     [];   //coordinates
    double cBest [];   //best coordinates
    double f;          //fitness
    double fBest;      //best fitness

    double Cg, Cs, Cn; //adaptive parameters
    C_AO_Utilities u;

    void Init (int coords, double &rangeMin [], double &rangeMax [])
    {
      ArrayResize (c,     coords);
      ArrayResize (cBest, coords);
      fBest = -DBL_MAX;
      Cg = u.RNDprobab ();
      Cs = u.RNDprobab ();
      Cn = u.RNDprobab ();

      for (int i = 0; i < coords; i++)
      {
        c     [i] = u.RNDfromCI (rangeMin [i], rangeMax [i]);
        cBest [i] = c [i];
      }

    }
};
//——————————————————————————————————————————————————————————————————————————————

Um mit mehreren Populationen nacheinander zu arbeiten, ist es sinnvoll, eine Reihe von Populationen zu verwenden. Um dies zu erreichen, schreiben wir die Struktur S_ASBO_Population, die nur ein Feld enthält:

• agent - Array von Objekten des Typs S_ASBO_Agent, die Agenten in der Grundgesamtheit darstellen.

//——————————————————————————————————————————————————————————————————————————————
struct S_ASBO_Population
{
    S_ASBO_Agent agent [];
};
//——————————————————————————————————————————————————————————————————————————————

Wir deklarieren die Klasse C_AO_ASBO - abgeleitet von der Klasse C_AO. Die Klasse enthält eine Reihe von Methoden und Variablen zur Handhabung der Optimierung:

1. Konstruktor und Destruktor:

• Der Konstruktor initialisiert die Algorithmusparameter wie Populationsgröße, Anzahl der Populationen, Anzahl der Epochen für jede Population und Verweise auf die Algorithmusbeschreibung.
• Der Destruktor ist leer.
  

2. Die verfügbaren Optionen sind:

• SetParams - setzt Algorithmusparameter aus dem Array params.
• Init - initialisiert den Algorithmus mit den angegebenen Parametern: Suchbereich, Suchschritt und Anzahl der Epochen.
• Moving - verschiebt Agenten im Suchraum.
• Revision - Überarbeitung der Agenten im Suchraum und Aktualisierung der besten globalen Lösung.

3. Variablen:

• numPop, epochsForPop - Anzahl der Populationen und Epochen für jede Population.
• epochs, epochNow, currPop, isPhase2, popEpochs, tau, tau_prime - zusätzliche Variablen für den Algorithmus.
• allAgentsForSortPhase2, allAgentsTemp, agentsPhase2, agentsTemp - Arrays der im Algorithmus verwendeten Agenten.
• pop - Array der Population.
  

4. Hilfsmethoden:

• AdaptiveMutation - führt eine adaptive Mutation für den Agenten durch.
• UpdatePosition - aktualisiert die Position des Agenten.
• FindNeighborCenter - findet das Zentrum der Nachbarn für den Agenten.
• Sorting - Sortiert die Agenten.

Die Klasse C_AO_ASBO ist also eine Implementierung des ASBO-Algorithmus, die verschiedene Methoden und Operationen verwendet, um Agenten im Suchraum zu bewegen und zu überarbeiten.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ASBO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ASBO () { }
  C_AO_ASBO ()
  {
    ao_name = "ASBO";
    ao_desc = "Adaptive Social Behavior Optimization";
    ao_link = "https://www.mql5.com/ru/articles/15283";

    popSize       = 50;   //population size
    numPop        = 5;    //number of populations
    epochsForPop  = 10;   //number of epochs for each population

    ArrayResize (params, 3);

    params [0].name = "popSize";      params [0].val = popSize;
    params [1].name = "numPop";       params [1].val = numPop;
    params [2].name = "epochsForPop"; params [2].val = epochsForPop;
  }

  void SetParams ()
  {
    popSize      = (int)params [0].val;
    numPop       = (int)params [1].val;
    epochsForPop = (int)params [2].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int numPop;       //number of populations
  int epochsForPop; //number of epochs for each population

  private: //-------------------------------------------------------------------
  int  epochs;
  int  epochNow;
  int  currPop;
  bool isPhase2;
  int  popEpochs;

  double tau;
  double tau_prime;

  S_ASBO_Agent      allAgentsForSortPhase2 [];
  S_ASBO_Agent      allAgentsTemp          [];
  S_ASBO_Agent      agentsPhase2           [];
  S_ASBO_Agent      agentsTemp             [];
  S_ASBO_Population pop                    []; //M populations

  void   AdaptiveMutation   (S_ASBO_Agent &agent);
  void   UpdatePosition     (int ind, S_ASBO_Agent &ag []);
  void   FindNeighborCenter (int ind, S_ASBO_Agent &ag [], double &center []);
  void   Sorting (S_ASBO_Agent &p [], S_ASBO_Agent &pTemp [], int size);
};
//——————————————————————————————————————————————————————————————————————————————

Die Init-Methode erfüllt eine wichtige Funktion der Klasse C_AO_ASBO, indem sie die für den ASBO-Algorithmus erforderlichen Parameter und Datenstrukturen initialisiert, bevor die Optimierung beginnt. Grundlegende Initialisierungsschritte in der Init-Methode:

1. Überprüfung und Initialisierung der Basisparameter:

• Die Methode ruft StandardInit auf, um grundlegende Parameter wie den minimalen und maximalen Suchbereich und den Suchschritt zu initialisieren. Wenn die Initialisierung fehlschlägt, gibt die Methode false zurück.

2. Initialisierung zusätzlicher Variablen:

• Die Werte der Variablen epochs, epochNow, currPop, isPhase2 und popEpochs werden gesetzt.
• Die Werte der Variablen tau und tau_prime werden auf der Grundlage der Dimensionalität des Koordinatensuchraums berechnet.

3. Erstellung und Initialisierung der Populationen und Agenten:

• Das Array Pop wird für die Speicherung der Populationen erstellt und jede Population wird initialisiert. Für jeden Agenten in der Population wird Init aufgerufen, um seine Koordinaten im angegebenen Bereich zu initialisieren.
• Das Array agentsPhase2 wird für Phase-2-Agenten erstellt und ähnlich wie die Populationen initialisiert.
• Die Arrays allAgentsForSortPhase2 und allAgentsTemp werden für die temporäre Speicherung von Bearbeitern während des Sortiervorgangs erstellt, und jeder Bearbeiter wird initialisiert.

4. Rückgabe des Ergebnisses:

•    Die Methode gibt true zurück, wenn die Initialisierung erfolgreich war.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ASBO::Init (const double &rangeMinP  [], //minimum search range
                      const double &rangeMaxP  [], //maximum search range
                      const double &rangeStepP [], //step search
                      const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs    = epochsP;
  epochNow  = 0;
  currPop   = 0;
  isPhase2  = false;
  popEpochs = 0;

  tau       = 1.0 / MathSqrt (2.0 * coords);
  tau_prime = 1.0 / MathSqrt (2.0 * MathSqrt (coords));

  ArrayResize (pop, numPop);
  for (int i = 0; i < numPop; i++)
  {
    ArrayResize (pop [i].agent, popSize);

    for (int j = 0; j < popSize; j++) pop [i].agent [j].Init (coords, rangeMin, rangeMax);
  }

  ArrayResize (agentsPhase2, popSize);
  ArrayResize (agentsTemp,   popSize);
  for (int i = 0; i < popSize; i++) agentsPhase2 [i].Init (coords, rangeMin, rangeMax);

  ArrayResize (allAgentsForSortPhase2, popSize * numPop);
  ArrayResize (allAgentsTemp,          popSize * numPop);

  for (int i = 0; i < popSize * numPop; i++)
  {
    allAgentsForSortPhase2 [i].Init (coords, rangeMin, rangeMax);
    allAgentsTemp          [i].Init (coords, rangeMin, rangeMax);
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode Moving der Klasse C_AO_ASBO stellt den grundlegenden Prozess der Agentenbewegung innerhalb des ASBO-Algorithmus dar, einschließlich des Übergangs zwischen Phasen und der Ausführung der entsprechenden Operationen für jede Phase. Die wichtigsten Schritte der Methode Moving:

1. Sie erhöht den Wert von epochNow:

• Der Wert der Variable epochNow wird um 1 erhöht, was den Beginn einer neuen Ära der Optimierung widerspiegelt.

2. Phase 1:

• Befindet sich der Algorithmus nicht in Phase 2, so wird Folgendes getan:
• Wenn die Anzahl der Epochen für die aktuelle Population die Grenze von epochsForPop erreicht hat, wird der Zähler popEpochs zurückgesetzt, der Zähler currPop erhöht und der Wert fB ebenfalls zurückgesetzt.
• Wenn die maximale Anzahl von numPop Populationen erreicht ist, geht der Algorithmus zu Phase 2 über. In diesem Fall werden die Agenten aus allen Populationen in einem einzigen Feld zusammengefasst und sortiert. Die besten Bearbeiter werden in das Array agentsPhase2 kopiert.
• Andernfalls werden für jeden Agenten der aktuellen Population adaptive Mutations- und Positionsaktualisierungsoperationen sowie das Kopieren von Koordinaten durchgeführt.

3. Phase 2:

• In Phase 2 werden auch adaptive Mutations- und Positionsaktualisierungsoperationen sowie das Kopieren von Koordinaten für jeden Agenten im Array agentsPhase2 durchgeführt.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::Moving ()
{
  epochNow++;

  //Phase 1----------------------------------------------------------------------
  if (!isPhase2)
  {
    if (popEpochs >= epochsForPop)
    {
      popEpochs = 0;
      currPop++;

      fB = -DBL_MAX;
    }

    if (currPop >= numPop)
    {
      isPhase2 = true;

      int cnt = 0;
      for (int i = 0; i < numPop; i++)
      {
        for (int j = 0; j < popSize; j++)
        {
          allAgentsForSortPhase2 [cnt] = pop [i].agent [j];
          cnt++;
        }
      }

      u.Sorting (allAgentsForSortPhase2, allAgentsTemp, popSize * numPop);

      for (int j = 0; j < popSize; j++) agentsPhase2 [j] = allAgentsForSortPhase2 [j];
    }
    else
    {
      for (int i = 1; i < popSize; i++)
      {
        AdaptiveMutation (pop [currPop].agent [i]);
        UpdatePosition   (i, pop [currPop].agent);

        ArrayCopy (a [i].c, pop [currPop].agent [i].c);
      }

      popEpochs++;
      return;
    }
  }

  //Phase 2----------------------------------------------------------------------
  for (int i = 1; i < popSize; i++)
  {
    AdaptiveMutation (agentsPhase2 [i]);
    UpdatePosition   (i, agentsPhase2);

    ArrayCopy (a [i].c, agentsPhase2 [i].c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode Revision der Klasse C_AO_ASBO stellt den Prozess der Überarbeitung der Optimierungsergebnisse dar, einschließlich der Aktualisierung des Wertes von fB und der Aktualisierung der Optimierungsergebnisse für jede Phase des Algorithmus ASBO. Die wichtigsten Bestandteile des Codes:

1. Variablen und ihre Initialisierung:

• int ind = -1; — Variable zum Speichern des Index des Elements mit dem besten Wert der Funktion f.
• fB — Variable, die den besten Wert der in der aktuellen Phase gefundenen Funktion „f“ darstellt.

2. Auf der Suche nach dem besten Vermittler:

• In der ersten for-Schleife werden alle Agenten (Objekte, die Entscheidungen darstellen) in einem Array der Größe popSize durchlaufen.
• Wenn die Funktion f des aktuellen Bearbeiters größer ist als der aktuell beste Wert fB, werden fB und den Index ind aktualisiert.

3. Kopieren der Daten:

• Wenn ein Agent mit dem besten Funktionswert, ind != -1, gefunden wurde, wird das Array cB (das die besten Lösungsparameter darstellt) mit Werten aus dem Array a aktualisiert.

4. Phase 1:

• Wenn die aktuelle Population currPop kleiner ist als die Gesamtzahl der Populationen numPop, werden die Werte der Funktion f für die Agenten der aktuellen Population aktualisiert.
• Wenn der Wert des Agenten f im Array a seinen besten Wert von fBest übersteigt, wird fBest aktualisiert und die entsprechenden Merkmale werden in cBest kopiert.
• Dann werden die Agenten der aktuellen Population mit der Methode u.Sorting sortiert.

5. Phase 2:

• Wenn die aktuelle Population gleich oder größer ist als die Gesamtzahl der Populationen, werden ähnliche Aktionen für das Array agentsPhase2 durchgeführt.
• Die Werte der Funktion f werden aktualisiert, die besten fBest-Werte werden überprüft und aktualisiert, und die Sortierung wird durchgeführt.

Allgemeine Logik:

• Die Methode Revision führt zwei Hauptschritte durch: die Suche nach dem besten Agenten und die Aktualisierung der Daten für die Agenten in Abhängigkeit von der aktuellen Phase (Phase 1 oder Phase 2).
• Das Hauptziel besteht darin, die besten Lösungen, die während der Optimierung gefunden wurden, zu verfolgen und zu aktualisieren und die Sortierung der Agenten für eine spätere Verwendung beizubehalten.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  //phase 1
  if (currPop < numPop)
  {
    for (int i = 0; i < popSize; i++)
    {
      pop [currPop].agent [i].f = a [i].f;

      if (a [i].f > pop [currPop].agent [i].fBest)
      {
        pop [currPop].agent [i].fBest = a [i].f;
        ArrayCopy (pop [currPop].agent [i].cBest, a [i].c, 0, 0, WHOLE_ARRAY);
      }
    }

    u.Sorting (pop [currPop].agent, agentsTemp, popSize);
  }
  //phase 2
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      agentsPhase2 [i].f = a [i].f;

      if (a [i].f > agentsPhase2 [i].fBest)
      {
        agentsPhase2 [i].fBest = a [i].f;
        ArrayCopy (agentsPhase2 [i].cBest, a [i].c, 0, 0, WHOLE_ARRAY);
      }
    }

    u.Sorting (agentsPhase2, agentsTemp, popSize);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode AdaptiveMutation der Klasse C_AO_ASBO steht für die adaptive Mutation der Agentenquoten im Rahmen des Algorithmus ASBO, einschließlich der Verwendung der Gauß-Verteilung und der Berechnung neuer Quotenwerte auf der Grundlage von Zufallsvariablen. Die wichtigsten Schritte der AdaptiveMutation-Methode:

1. Adaptive Mutation von Verhältnissen:

• Die Verhältnisse Cg, Cs und Cn des Ag-Agens verändern sich unter Verwendung der Gaußschen Verteilung.
• Für jedes Verhältnis wird ein neuer Wert anhand der Exponentialfunktion der Summe zweier Gaußscher Zufallsvariablen berechnet, die jeweils mit dem entsprechenden Verhältnis tau_prime und tau multipliziert werden.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::AdaptiveMutation (S_ASBO_Agent &ag)
{
  ag.Cg *= MathExp (tau_prime * u.GaussDistribution (0, -1, 1, 1) + tau * u.GaussDistribution (0, -1, 1, 8));
  ag.Cs *= MathExp (tau_prime * u.GaussDistribution (0, -1, 1, 1) + tau * u.GaussDistribution (0, -1, 1, 8));
  ag.Cn *= MathExp (tau_prime * u.GaussDistribution (0, -1, 1, 1) + tau * u.GaussDistribution (0, -1, 1, 8));
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode UpdatePosition der Klasse C_AO_ASBO steht für die Aktualisierung der Agentenposition innerhalb des Algorithmus ASBO, einschließlich der Berechnung der Positionsänderung auf der Grundlage verschiedener Faktoren und der Aktualisierung der Position innerhalb bestimmter Bereiche. Die wichtigsten Schritte der Methode UpdatePosition:

1. Berechnung der Positionsveränderung:

• Wir berechnen die Veränderung der Agentenposition ag [ind] in jeder Dimension j unter Verwendung verschiedener Verhältnisse und Werte, wie cB, cBest, deltaX, rangeMin, rangeMax und rangeStep.

2. Aktualisierung der Position des Agenten:

• Für jede Dimension j wird eine neue Agentenposition ag [ind].c [j] durch Addition von deltaX [j] und anschließende Korrektur des Wertes innerhalb der angegebenen Bereiche berechnet.

Der kommentierte Teil des Codes 1) - Originalversion, 3) - meine Version ohne Berücksichtigung von Cg, Cs und Cn, stattdessen wurde die Normalverteilung verwendet. Meine Option ist „2)“. Sie zeigte die besten Ergebnisse von allen drei.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::UpdatePosition (int ind, S_ASBO_Agent &ag [])
{
  double deltaX [];
  ArrayResize (deltaX, coords);

  FindNeighborCenter (ind, ag, deltaX);

  for (int j = 0; j < coords; j++)
  {
    /*
    //1)
    deltaX [j] = ag [ind].Cg * u.RNDfromCI (-1, 1) * (cB             [j] - ag [ind].c [j]) +
                 ag [ind].Cs * u.RNDfromCI (-1, 1) * (ag [ind].cBest [j] - ag [ind].c [j]) +
                 ag [ind].Cn * u.RNDfromCI (-1, 1) * (deltaX         [j] - ag [ind].c [j]);
    */
    
    //2)
    deltaX [j] = ag [ind].Cg * (cB             [j] - ag [ind].c [j]) +
                 ag [ind].Cs * (ag [ind].cBest [j] - ag [ind].c [j]) +
                 ag [ind].Cn * (deltaX         [j] - ag [ind].c [j]);


    /*
    //3)
    deltaX [j] = u.GaussDistribution (0, -1, 1, 8) * (cB             [j] - ag [ind].c [j]) +
                 u.GaussDistribution (0, -1, 1, 8) * (ag [ind].cBest [j] - ag [ind].c [j]) +
                 u.GaussDistribution (0, -1, 1, 8) * (deltaX         [j] - ag [ind].c [j]);
    */

    ag [ind].c [j] += deltaX [j];
    ag [ind].c [j] = u.SeInDiSp (ag [ind].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Testergebnisse

Ein Ausdruck des ASBO-Algorithmus zeigt eine Reihe interessanter Merkmale, die ihn wirklich einzigartig machen. Eines seiner wichtigsten Merkmale ist seine hervorragende Skalierbarkeit. Dadurch kann der Algorithmus hochdimensionale Probleme effizient behandeln. Besonders bemerkenswert sind die Ergebnisse, die beim Testen der Funktionen Forest und Megacity mit 1000 Parametern erzielt wurden. In diesen Fällen zeigt ASBO eine beeindruckende Leistung, die mit den Ergebnissen der führenden Algorithmen in der Bewertungstabelle vergleichbar ist. Diese Erfolge unterstreichen nicht nur die Effizienz des Algorithmus, sondern auch sein Potenzial für die Anwendung in einer Vielzahl von Bereichen, die eine hochwertige Optimierung erfordern.

ASBO|Adaptive Optimierung des Sozialverhaltens|50.0|5.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.7633114189858913
25 Hilly's; Func runs: 10000; result: 0.4925279738997658
500 Hilly's; Func runs: 10000; result: 0.3261850685263711
=============================
5 Forest's; Func runs: 10000; result: 0.7954558091769679
25 Forest's; Func runs: 10000; result: 0.4003462752027551
500 Forest's; Func runs: 10000; result: 0.26096981234192485
=============================
5 Megacity's; Func runs: 10000; result: 0.2646153846153846
25 Megacity's; Func runs: 10000; result: 0.1716923076923077
500 Megacity's; Func runs: 10000; result: 0.18200000000000044
=============================
All score: 3.65710 (40.63%)

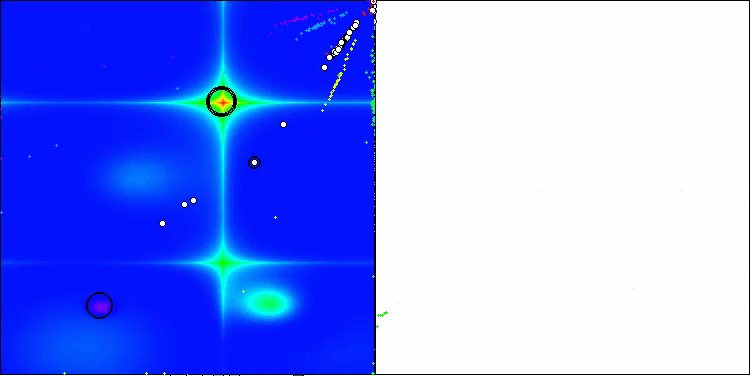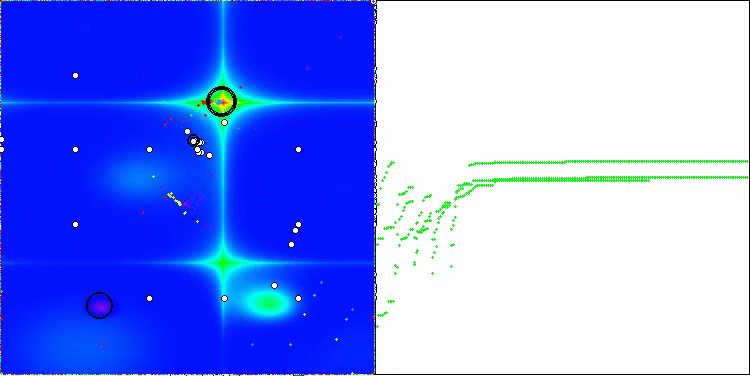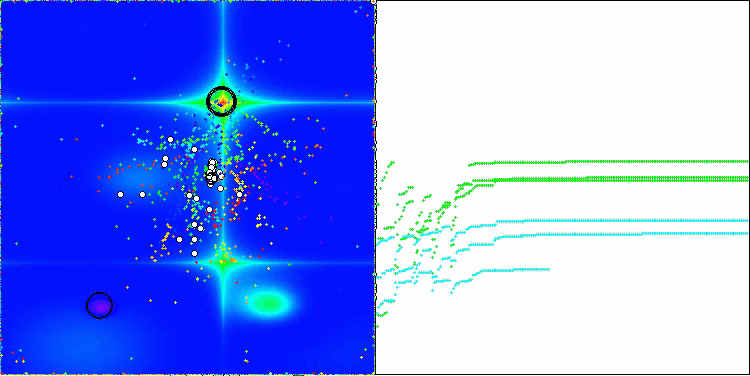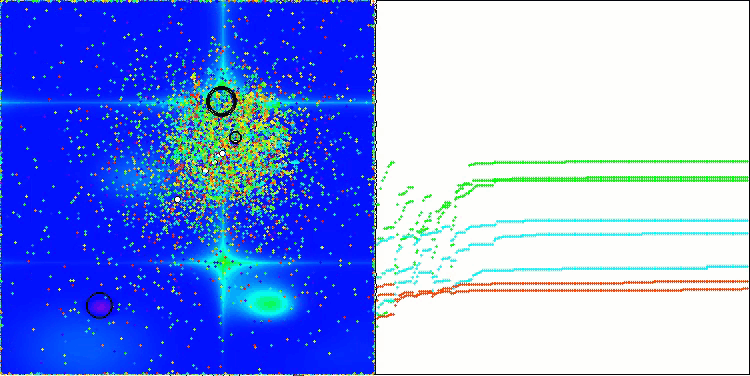
Die Visualisierung der Ergebnisse des ASBO-Algorithmus zeigt eine Reihe interessanter Merkmale, die Beachtung verdienen. Schon zu Beginn der Arbeit des Algorithmus kann man sehen, wie er erfolgreich kritische Lösungsregionen identifiziert, was seine Fähigkeit, den Parameterraum effizient zu erkunden, unter Beweis stellt.

Das Konvergenzdiagramm zeigt charakteristische Brüche in der Linie, die durch das Aufeinanderfolgen mehrerer Populationen in der ersten Phase verursacht werden. Diese Lücken zeigen, dass jede Population zur Optimierung beiträgt, indem sie verschiedene Teile des Raums erkundet. In der zweiten Phase nimmt das Diagramm jedoch eine feste Form an, was bedeutet, dass die besten Lösungen aus allen nach der ersten Phase gesammelten Populationen kombiniert werden. Diese Vereinheitlichung ermöglicht es dem Algorithmus, sich auf die Verfeinerung vielversprechender Bereiche zu konzentrieren.

So veranschaulicht die Visualisierung nicht nur die Dynamik des Algorithmus, sondern verdeutlicht auch seine adaptiven und kooperativen Mechanismen.

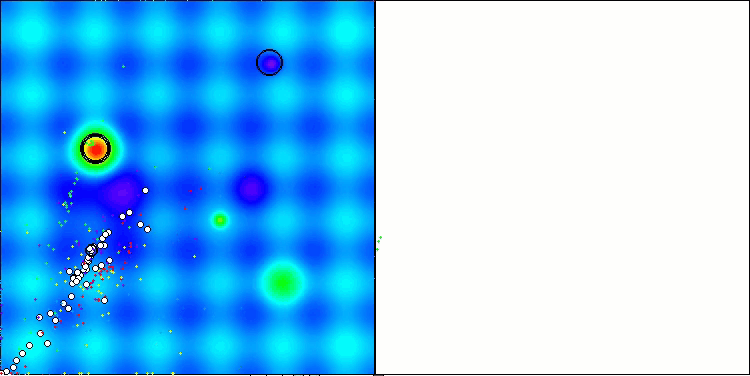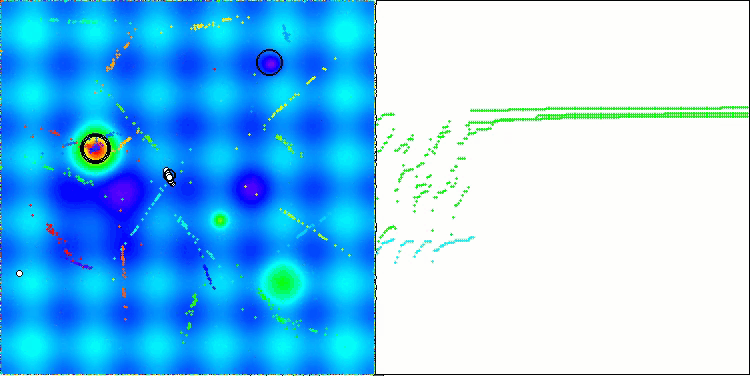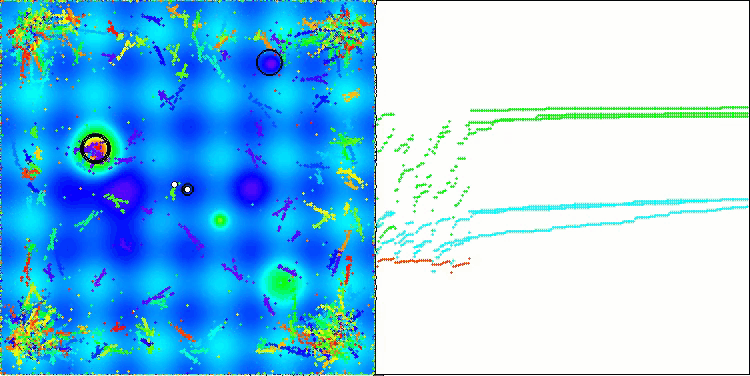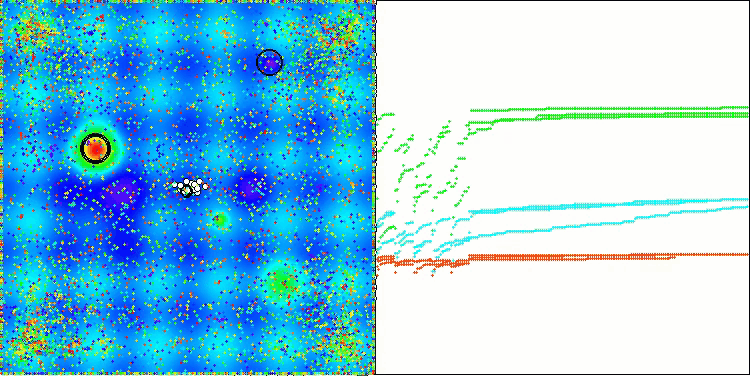
  ASBO mit der Testfunktion Hilly

AASBO mit der Testfunktion Forest

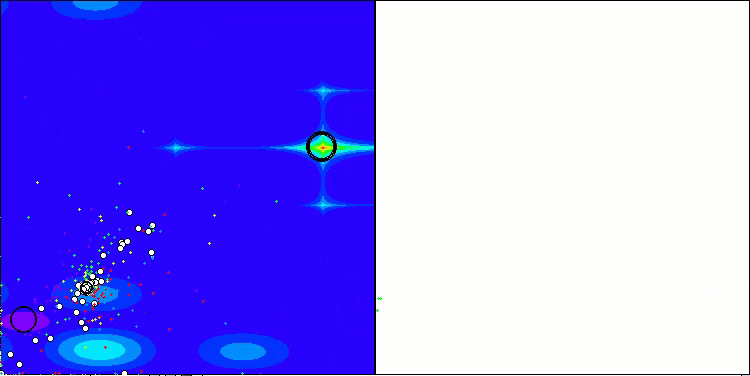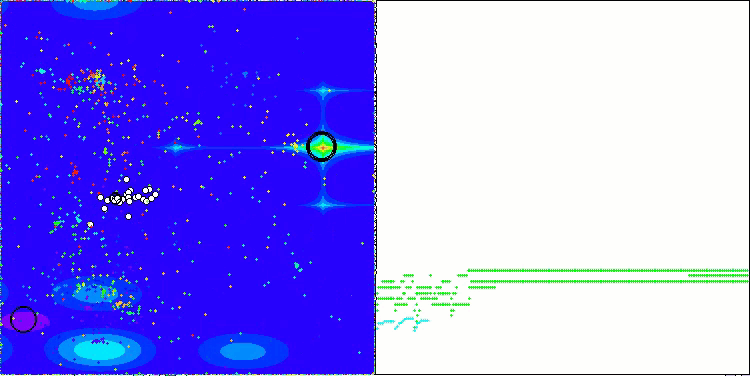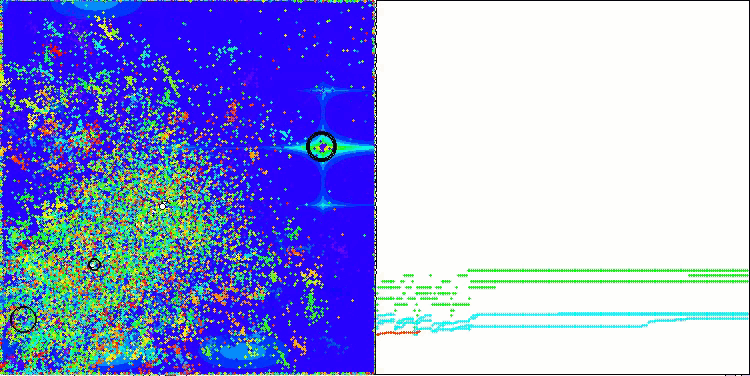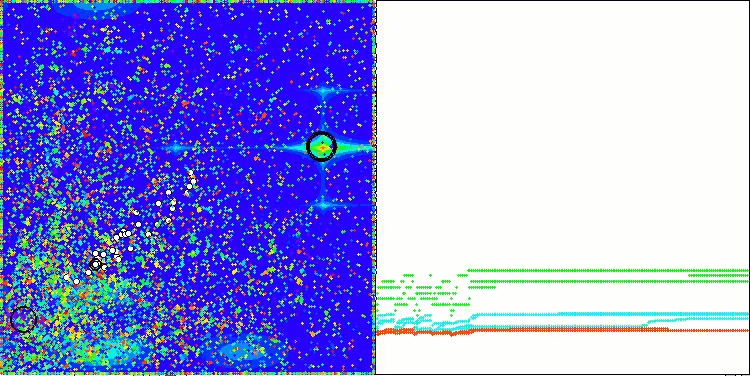
ASBO mit der Testfunktion Megacity

Auf der Grundlage der Ergebnisse der durchgeführten Untersuchungen nimmt der Algorithmus einen sicheren Platz in der Mitte der Bewertungstabelle ein.

#	AO	Beschreibung	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	Nachbarschaftsübergreifende Suche	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	Zahlenschloss-Algorithmus	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	(P+O)ES	(P+O) Entwicklungsstrategien	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
4	CTA	Kometenschweif-Algorithmus	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
5	SDSm	stochastische Diffusionssuche M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
6	ESG	Entwicklung der sozialen Gruppen	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
7	SIA	Simuliertes isotropes Abkühlen	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
8	ACS	künstliche, kooperative Suche	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
9	TSEA	Schildkrötenpanzer-Evolutionsalgorithmus	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
10	DE	differentielle Evolution	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
11	CRO	Optimierung chemischer Reaktionen	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
12	BSA	Vogelschwarm-Algorithmus	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
13	HS	Harmoniesuche	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
14	SSG	Setzen, Säen und Wachsen	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
15	(PO)ES	(PO) Entwicklungsstrategien	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
16	BSO	Brainstorming-Optimierung	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
17	WOAm	Wal-Optimierungsalgorithmus M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
18	AEFA	Algorithmus für künstliche elektrische Felder	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
19	ACOm	Ameisen-Kolonie-Optimierung M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
20	BFO-GA	Optimierung der bakteriellen Futtersuche - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
21	ASBO	Optimierung des adaptiven Sozialverhaltens	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
22	MEC	Evolutionäre Berechnung des Geistes	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
23	IWO	Optimierung mit invasiven Unkräutern	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
24	Micro-AIS	Künstliches Mikro-Immunsystem	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
25	COAm	Kuckuck-Optimierungsalgorithmus M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
26	SDOm	Optimierung der Spiraldynamik M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
27	NMm	Nelder-Mead-Verfahren M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
28	FAm	Firefly-Algorithmus M	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
29	GSA	Algorithmus für die Schwerkraftsuche	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
30	BFO	Optimierung der bakteriellen Futtersuche	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
31	ABC	Künstliches Bienenvolk (Artificial Bee Colony, ABC)	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
32	BA	Fledermaus-Algorithmus	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
33	SA	simuliertes Abkühlen	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
34	IWDm	intelligente Wassertropfen M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
35	PSO	Partikelschwarmoptimierung	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
36	Gebote	Boids-Algorithmus	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
37	MA	Affen-Algorithmus	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
38	SFL	schlurfender Froschsprung	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
39	FSS	Fischschulsuche	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
40	RND	zufällig	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37
41	GWO	Grauer-Wolf-Optimierung	0.59169	0.36561	0.29595	1.25326	0.24499	0.09047	0.03612	0.37158	0.27667	0.08567	0.02170	0.38403	2.009	22.32
42	CSS	Suche geladener Systeme	0.44252	0.35454	0.35201	1.14907	0.24140	0.11345	0.06814	0.42299	0.18333	0.06300	0.02322	0.26955	1.842	20.46
43	EM	elektromagnetismusähnlicher Algorithmus	0.46250	0.34594	0.32285	1.13129	0.21245	0.09783	0.10057	0.41085	0.15667	0.06033	0.02712	0.24412	1.786	19.85

Zusammenfassung

Der Algorithmus zeichnet sich durch seine Originalität und sein nicht standardisiertes Verhalten aus, was seine Visualisierung einzigartig macht und von allen bisher bekannten Methoden unterscheidet. Das erregt Aufmerksamkeit und weckt das Interesse an den internen Mechanismen.

Trotz der durchschnittlichen Gesamtergebnisse und der Konvergenz bei der Lösung kleindimensionaler Probleme zeigt der Algorithmus sein wahres Potenzial bei der Arbeit mit komplexeren Problemen und in einem großen Suchraum. Es verwendet mehrere Populationen, die in der ersten Phase nacheinander durchlaufen werden, was die Frage aufwirft, ob es sinnvoll ist, eine begrenzte Anzahl von Epochen in Vorberechnungen unabhängiger Populationen aufzuteilen. Experimente, die in der ersten Phase mit nur einer Population durchgeführt wurden, zeigen deutlich schlechtere Ergebnisse, was die Nützlichkeit der Vorab-Informationssammlung über den umgebenden Suchraum bestätigt. Auf diese Weise kann der Algorithmus die führenden Individuen - die erfolgreichsten Lösungen - in der zweiten Phase der Suche effektiver nutzen.

Außerdem hat der Algorithmus ein großes Potenzial für weitere Forschung. Ich bin der Meinung, dass seine Möglichkeiten noch nicht voll ausgeschöpft sind und mehr Experimente und Analysen erforderlich sind, um zu verstehen, wie man seine algorithmischen Vorteile am besten nutzen kann.

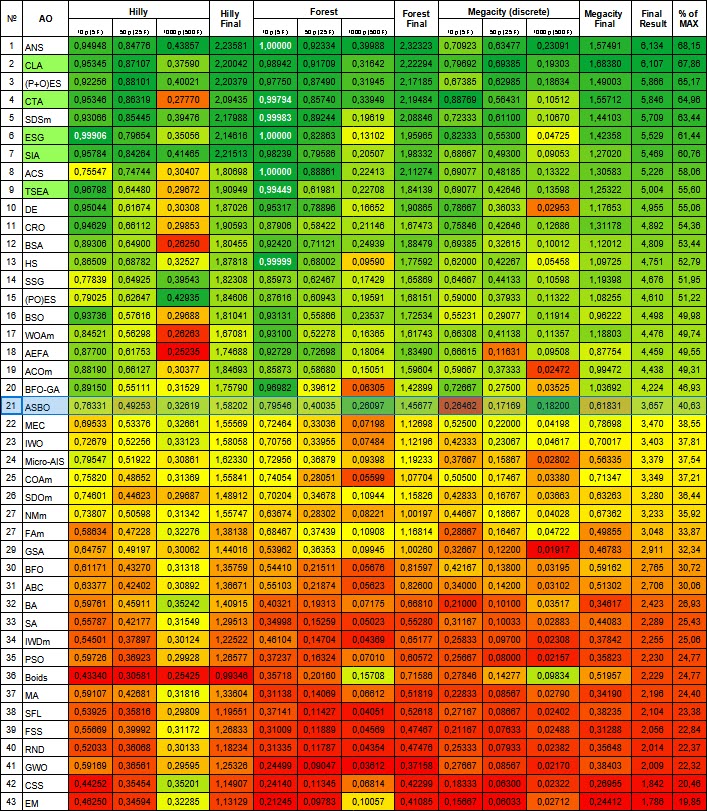
Abbildung 2. Farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben. Die grün hervorgehobenen Namen sind meine eigenen Algorithmen

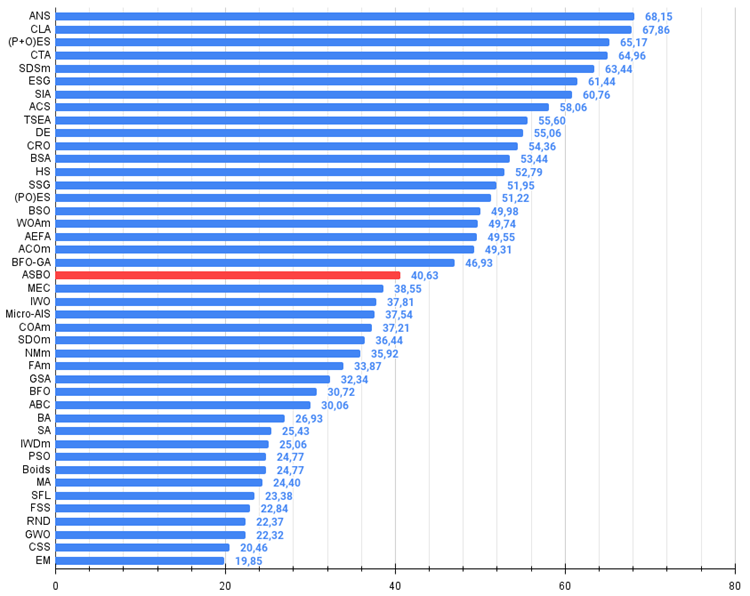
Abbildung 3. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, je mehr, desto besser,

wobei 100 das maximal mögliche, theoretische Ergebnis ist; das Archiv enthält ein Skript zur Berechnung der Bewertungstabelle)

Vor- und Nachteile des ASBO-Algorithmus:

Vorteile:

1. Eine kleine Anzahl externer Parameter.
   
2. Gute Ergebnisse bei komplexen, hochdimensionalen Problemen.
   

Nachteile

1. Geringe Konvergenz bei niedrigdimensionalen Problemen.
   

Der Artikel wird von einem Archiv mit den aktuellen Versionen der Algorithmuscodes begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/ru/code/49355

Zusammenfassung der Zwischenergebnisse der durchgeführten Arbeiten

Während unserer Forschung haben wir mehr als vierzig Optimierungsalgorithmen untersucht, von denen jeder einen einzigartigen Ansatz zur Lösung komplexer Probleme darstellt. Dieser Prozess hat nicht nur Spaß gemacht, sondern war auch äußerst lehrreich und hat den Reichtum und die Vielfalt der Methoden auf dem Gebiet der Optimierung gezeigt.

Neuerstellung und Änderung von Algorithmen. Für die überwiegende Mehrheit der betrachteten Algorithmen gab es keinen allgemein verfügbaren Quellcode. Dies veranlasste mich zu einem kreativen Ansatz: Der Code wurde ausschließlich auf der Grundlage der Textbeschreibungen der Autoren aus verschiedenen Veröffentlichungen neu erstellt. Dieser Ansatz ermöglichte es uns nicht nur, die Funktionsweise der einzelnen Algorithmen besser zu verstehen, sondern auch, sie an unsere spezifischen Bedürfnisse anzupassen.
Die wenigen quelloffenen Algorithmen waren für die Lösung von Optimierungsproblemen im Allgemeinen nicht geeignet. Dies erforderte erhebliche Änderungen, um sie universell einsetzbar und für eine Vielzahl von Aufgaben geeignet zu machen.

Innovationen und Verbesserungen. Einige Algorithmen, wie z. B. ACO (Ameisenkolonie-Algorithmen zur Lösung von Problemen auf Graphen), waren von ihren Autoren ursprünglich nicht für die Bearbeitung von Problemen im kontinuierlichen Raum vorgesehen und mussten geändert werden, um ihren Anwendungsbereich zu erweitern. Bei anderen Algorithmen wurden Verbesserungen an der Suchstrategie vorgenommen, um ihre Effizienz zu steigern. Diese modifizierten Versionen erhielten das Postfix „m“ in ihrem Namen, was ihre Entwicklung widerspiegelt. Darüber hinaus haben wir uns viele verschiedene Methoden für den Umgang mit Populationen, die Generierung neuer Lösungen und Auswahlmethoden im Detail angesehen.

Zur Demonstration neuer Ideen und Optimierungsansätze wurden mehr als fünf meiner neuen proprietären Algorithmen entwickelt und exklusiv in Artikeln vorgestellt.

Anwendung und weitere Studien. Jeder der vorgestellten Algorithmen kann zur Lösung von Optimierungsproblemen eingesetzt werden, ohne dass eine zusätzliche Überarbeitung oder Modifizierung erforderlich ist. Dadurch sind sie für ein breites Spektrum von Forschern und Praktikern zugänglich und geeignet.

Für diejenigen, die die besten Ergebnisse bei bestimmten Einzelaufgaben erzielen wollen, werden Vergleichstabellen und Histogramme bereitgestellt, um die individuellen Eigenschaften der einzelnen Algorithmen zu untersuchen. Dies eröffnet Möglichkeiten für eine feinere Abstimmung und Optimierung, um spezifische Anforderungen zu erfüllen.

Beide Ansätze - sowohl die Verwendung fertiger Algorithmen als auch deren eingehende Untersuchung und Anpassung - sind praktikabel. Das Verständnis der Feinheiten und Techniken in den Suchstrategien verschiedener Algorithmen eröffnet den Forschern neue Horizonte, um hervorragende Ergebnisse zu erzielen.

Ich wünsche allen Lesern viel Erfolg beim Finden der besten Lösungen und beim Erreichen ihrer Ziele. Möge Ihre Reise in die Welt der Optimierung und des algorithmischen Handels spannend und erfolgreich sein!