周期与外汇

引言

周期性是我们世界的主要性质之一。周期让人们能够安排自己的生活。知晓周期的顺序，我们就能预测未来。例如，我可以自信地说，2025 年是从 1 月 1 日开始的。

外汇周期可能与各种因素有关：经济新闻、一天中的时间、一周的几天、一年的月份以及季节。研究这些周期可以帮助交易者预测未来的价格走势，并做出更明智的交易决策。

周期可以在相当出人意料的领域中被发现。甚至对周期和波浪在外汇中的兴趣本身也具有周期性：

• 文章 “在 MQL5 中实现艾略特波浪自动分析”— 2011
• 文章 “沃尔夫波浪”— 2017
• 文章 “利用外汇市场的季节性”— 2023
• 文章 “为 EA 使用 Python 进行季节性过滤和深度学习 ONNX 模型的时间周期”— 2024

正如你所看到的，文章每6年发布一次。只有最后一篇文章打破了这个周期。但也许还有其他解释可以说明这种偏离？

让我们尝试回答两个问题。价格走势中是否存在周期？如果存在，如何在交易中利用它？

寻找周期

在交易中，周期可以与重复出现的市场趋势或模式相关联。例如，价格可能在一个给定的通道内波动。而这种行为可能会持续相当长的时间。

我们可以使用频谱分析、三角多项式、周期图、自相关函数和周期检测算法来从时间序列中提取周期成分。

我们也可以使用简单移动平均线来找到周期。这种方法是最简单且最直观的。假设我们有一个周期为 N 的时间序列。如果我们对该序列应用相同周期的简单移动平均线（SMA），我们将得到一个平均值水平，周期波动围绕该水平发生。使用其他周期的简单移动平均线（SMA），可以得到与原始周期不同的振荡过程。但尽管存在这些差异，使用这些平均值仍有可能恢复原始周期的参数。

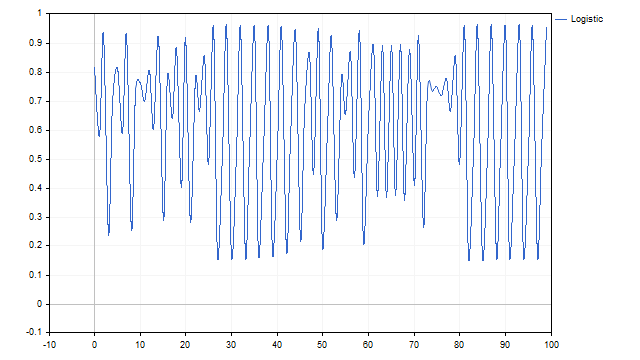
一些时间序列可能是不同时间框架的周期之和。在这种情况下，移动平均线也能很好地处理。该算法非常简单。首先，我们从原始序列中减去最大周期的平均值。从结果余数中减去下一个平均值，并继续此操作，直到最终只剩下零。我们需要更多的简单移动平均线（SMA）。

移动平均线同样可以轻松处理周期 + 趋势时间序列模型。在这种情况下，简单移动平均线（SMA）将同时作为周期和趋势检测器。

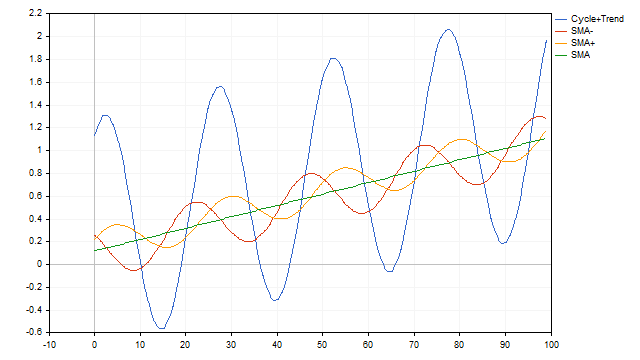
到目前为止，我们一直将移动平均应用于确定性时间序列——周期和趋势函数是明确定义的，并且随着时间的推移不会改变。让我们在原始时间序列中加入一些随机性，看看简单移动平均线（SMA）如何处理这种情况。我们将周期的振幅设为100%。假设振幅可以在正负10%的范围内随机变化。趋势的速度可以在0到1%之间变化。并且我们再加入10%的白噪声。简单移动平均线（SMA）成功地应对了这一任务。

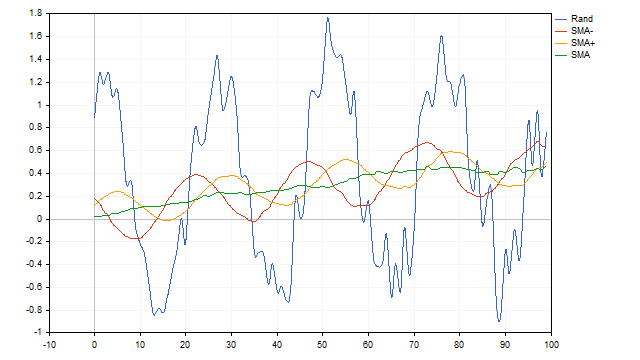
似乎我们已经找到了完美的指标。不幸的是，简单移动平均线（SMA）的缺点可能超过了它的优点。移动平均线无法识别仅由正半波或负半波组成的周期。此外，该指标分辨率较低。简单来说，如果噪声超过一定限度，它将无法分离出有用信号。

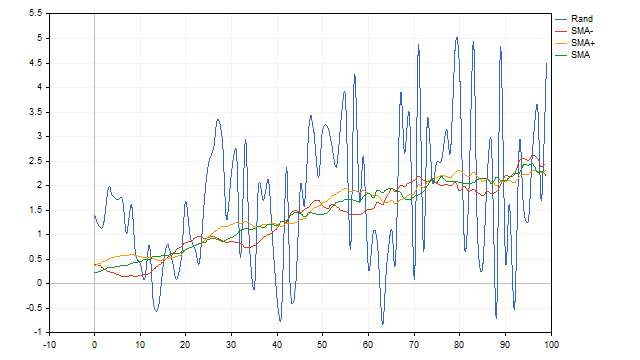
另一个小缺点是，在使用简单移动平均线之前，最好预先知道我们需要选择哪个周期。在这里，我们面临两个问题：

• 我们研究的时间序列中是否存在周期？
• 如果存在周期，我们如何知道它的参数？

为了回答这些问题，我们可以使用点映射。

看看这幅图你能说出它代表了什么吗？

这可能是一个由几个周期叠加构成的图表。或者，它可能是戴立克的阴谋的一部分。

所以，我们有一个一维时间序列，其值为 Z[i]。基于此，我将构建一个二维图表，该图表上每个点的坐标将根据以下规则设置（索引与时间序列相同）：

X[i] = Z[i];

Y[i] = Z[i-1].

这种转换的目的是，我想展示原始时间序列中两个相邻值之间的关系。例如，这个晦涩的图表展现如下。

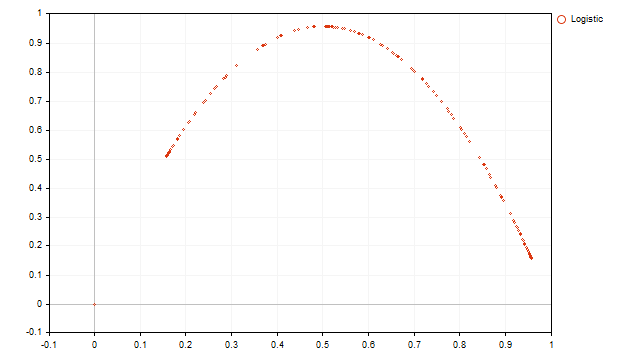
我们可以看到一个普通的抛物线。了解抛物线的性质后，我们可以制定原始时间序列的方程：

为了找到方程的比例，我们可以使用最小二乘法。结果，我们将得到一个逻辑映射，它被用来生成原始时间序列的值。

点图方法可以应用于任何时间序列，但它并不总是给出时间序列的清晰和精确的表示。

例如，让我们研究一下伪随机数生成器。它的图表看起来是这样的：

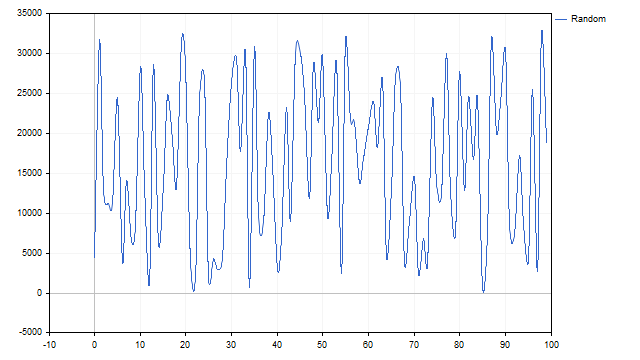
几个周期的叠加清晰可见。现在我们将弄清楚这一切。构建一个点阵图显示获得的值。

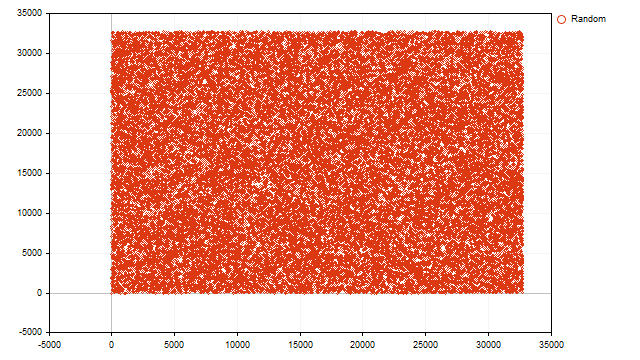
所有点均匀地填满整个平面。从这一点我们可以得出结论：伪随机数生成器的当前值不依赖于前一个值，所有匹配都是随机的。

循环过程的显示看起来是周期性的：

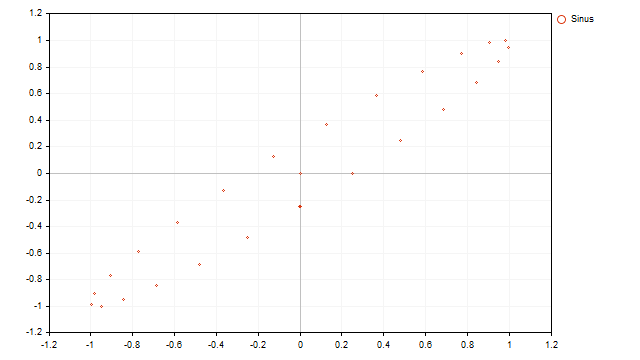
现在让我们看看实际价格的点图显示是什么样的：

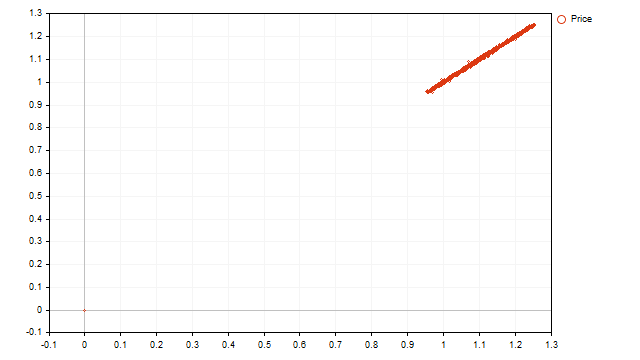
我们看到一个上升的线性趋势，没有周期。然而，现在就陷入绝望还为时过早。看着这张图，我们可以得出以下结论：

• 趋势是决定价格运动的主要因素；
• 趋势的强度足够大，可以掩盖周期性过程。

结论是显而易见的——我们需要更多方法来识别周期。

周期与随机性

1927 年，尤金·斯卢茨基发表了文章“随机原因的相加作为周期过程的来源”。在这项工作中，他出色地证明了周期性和波动过程可以作为随机变量相互作用（例如，相加）的结果而出现。

让我们在金融时间序列上测试这个理论是如何运作的。我们将不同符号的价格作为初始随机变量。在这种情况下，我们将做如下操作：对于当前货币对，我们取当前K线的价格，对于所有后续品种，我们取前1根K线的价格。因此，随机变量的方程大致如下：

因此，得到的随机变量将依赖于许多不同品种的先前价格值。让我们通过基于这些值构建移动平均线来加强这种依赖性。

可以看到存在波动过程。但我们想知道它们是否是周期性的？如果有周期，它的参数是什么？

为了回答这些问题，我们可以使用有限差分。通过从当前值中减去时间序列的前一个值来获得一阶差分：

通过减去一阶差分来获得二阶有限差分。

这个差分很有趣，因为如果满足某些条件，它可能表明过程的周期性。假设我们正在处理某种周期。设 a 为角度的初始值，s 为其变化步长。那么时间序列的最后三个点可以设置为：

使用三角恒等式来找到这些值的二阶差分：

这是离散谐波振荡器的方程。请注意，这里的振子是指一个振荡系统，而不是一个指标。

将这个方程应用到价格上并不容易。在方程的左侧，我们可以直接使用任何实际值，但在右侧，我们将不得不做一些改变。

为了分离出波动，我们首先需要找到围绕哪个位置水平发生。我们将其标记为 MA。然后方程将如下所示：

在左侧，MA 会相互抵消，但在右侧，它们将保留。

计算这个价格水平有几种方法。例如，我们可以先从原始时间序列中移除趋势，或者找到序列中所有值的平均值。这两种方法都有一个共同的缺点——它们非常依赖于历史数据，对市场当前变化的响应较弱。为了克服这个缺点，我将使用自适应指标的计算算法。在这种情况下，MA 水平将根据当前市场情况调整。最终，我们将得到一个指标，允许我们跟踪移动平均线波动的水平。在示例中我使用了简单移动平均线（SMA），但在实践中你可以使用任何价格平均方法。

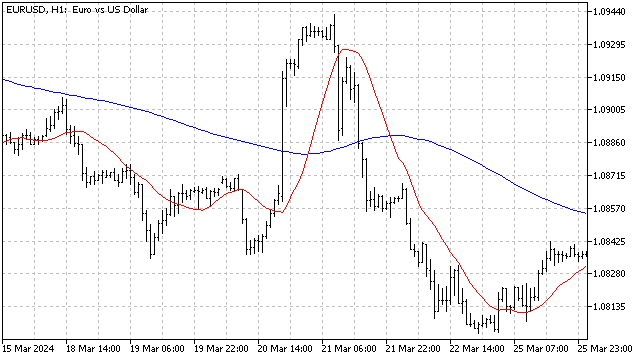
不幸的是，谐波振荡器在使用时存在一些缺点，必须加以考虑。它对正弦信号的工作效果很好。但即使是正弦波的混合也可能导致困难——振荡器根本无法选择最重要的周期。

大多数缺点都可以通过二阶差分来解决。它的形式保持不变。但我们可以通过改变这个差分的成员之间的距离来调整。例如，我打开了一张 H1 时间框架的图表。我假设价格走势中可能存在一个日周期（周期为 24）。那么我将使用如下所示的二阶差分：

如果价格走势中存在周期或多个周期，那么二阶差分将为零。这些周期的出现形式并不重要。重要的是它们能够相对正确地重复出现。此外，二阶差分还可以轻松应对趋势。唯一的要求是，这个趋势的长度不应少于周期的两倍。

这种方法如何在实践中应用？假设价格走势中存在一个稳定的周期，但有一些随机偏差。那么，如果我们计算最近几个（在我的例子中是24个）差值的总和，随机误差会相互抵消。也就是说，如果周期和/或趋势是稳定的，差值的总和将在零附近波动。如果市场上出现任何干扰（新趋势的开始、新周期的启动或旧周期的结束），差值的总和将开始显著偏离。而且，这些偏离可能具有周期性。由此我们可以得出结论：周期的干扰可能具有周期性。这就像一个薛定谔的市场。

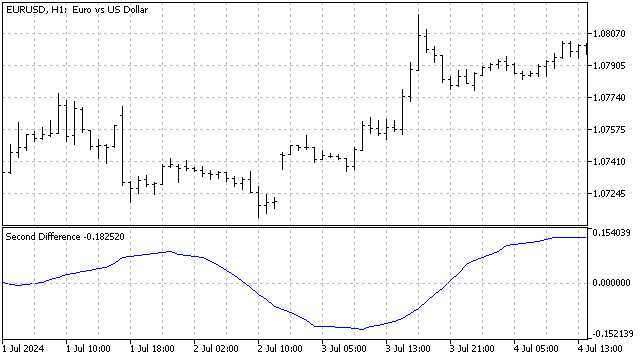
总的来说，使用有限差分在市场分析中可以非常有用。它们可以单独使用，相互结合，也可以与其他指标配对。最终，你可以得到一些新的有趣的工具，用于研究价格走势。

其他差分方式

在分析时间序列时，没有必要使用经典的差分。我们可以根据任务构建差分。为此，我们可以应用在构建小波时使用的原则。 

让我们取一个数字来表示初始波。最简单和最明显的选择是取1。我们在该数字的左右两边放置0。我们将得到一个这样的字符串：“0, 1, 0”。现在，从第二个数字开始，我们从左到右依次从右边的数字中减去左边的数字。

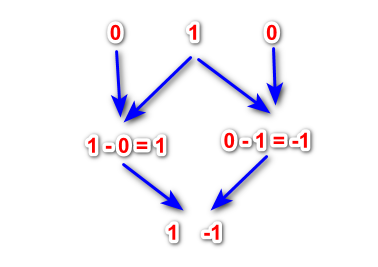
这样我们就得到了一个一级小波。在得到的比率的左右两边放置零，然后再次进行减法运算。这个操作可以一直进行，直到我们达到所需的小波级别。这些差分具有一些经典小波的特性，可以在金融时间序列分析中使用。

任何一组数字都可以作为初始波，例如1, 2, 1或1, 1, 1。在这种情况下，原始波的比率不应相对于波的中心对称。如果初始波表示为3, 2, 1，也不会有什么问题。我们也可以使用负数。

由于所有获得的差分的总和等于0，它们即是现成的振荡器。

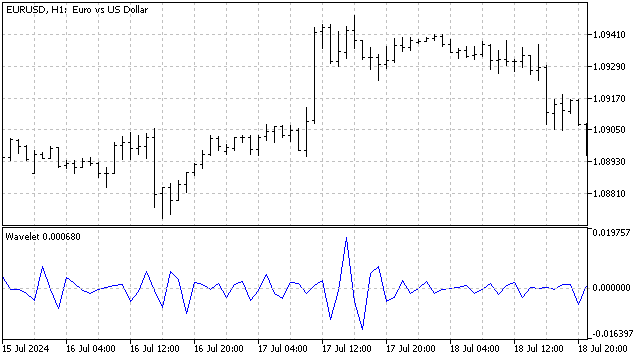
这种差分的缺点是，我们甚至无法想象使用某个初始波时结果将会是什么。

这种差分的主要优点是，我们可以借助它们恢复原始信号。例如，我们知道一阶和二阶差分的值。如果我们从当前时间序列的值中减去一阶差分，我们将得到该序列的前一个值。知道这两个值和二阶差分后，我们就可以得到序列的下一个值，依此类推。

这个特性使我们能够在历史数据中寻找相似的区域。如果不同级别之间的差分大致相等，那么我们就有了相似的价格走势。

结论

重要的是要记住，市场通常不会遵循可预测的周期。即使我们观察到某种周期，也总是存在模式可能会改变的风险。存在波动，但它们的行为需要进一步深入研究。不管怎样，理解市场周期可以成为任何交易者武器库中的有用工具。通过研究周期，我们可以找到技术分析的新方法和手段。

文章附带以下程序：

名称	类型	特征
点阵图	脚本	显示类型 逻辑 随机 Integrated - 整合序列 Price - 真实价格 Linear - 线性趋势 Sinus - 周期 SinusTrend - 周期 + 趋势 Sinus3 - 三个周期的总和 脚本运行完成后，图像将保存在“文件”文件夹中。
Slutsky周期	指标	处理市场观察中所有可用的交易品种。
Slutsky MA	指标	iPeriod - 指标周期 平滑
二阶差分	指标	Sampling - 采样频率
小波脚本	脚本	显示小波比率 InpWave - 原始波的比率列表。Ratios - 以逗号分隔的整数 Lvl - 所需的小波级别
小波	指标	使用小波作为振荡器 InpWave - 原始波的比率列表。Ratios - 以逗号分隔的整数 Lvl - 所需的小波级别