种群优化算法：入侵杂草优化（IWO）

内容

1. 概述
2. 算法描述
3. 测试结果

1. 概述

入侵杂草元启发式算法是一种基于种群的优化算法，通过模拟杂草菌落的兼容性和随机性，来寻找优化函数的整体最优值。
杂草优化算法是指受自然启发的种群算法，反映出杂草在有限时间内，为生存而斗争，于有限区域内的行为。

杂草是顽强的草种，它们的侵略性生长对农作物构成严重威胁。 它们非常有韧性，能够适应环境变化。 考虑到它们的特性，我们有一个强大的优化算法。 该算法试图模拟自然界中杂草群落的稳健性、适应性和随机性。

是什么让杂草如此特别？ 杂草往往是先行者，通过各种机制到处传播。 因此，它们很少被划归到濒危物种的类别。
以下是杂草在自然界中适应和生存的八种方式的简要描述：

1. 通用基因型。 这些研究已揭示出杂草的进化变化是对气候变化的反应。

2. 生命周期策略，繁衍能力。 杂草表现出广泛的生命周期策略。 随着耕作管理系统的变化，以前在给定的种植系统中不是主要问题的杂草变得更有韧性。 例如，减少耕作系统导致具有不同生命周期策略的多年生杂草的出现。 此外，气候变化开始为杂草物种或基因型创造新的生态位，这些物种或基因型的生活史更能适应不断变化的条件。 为了应对二氧化碳排放量的增加，杂草变得更高、更大、更强壮，这意味着它们可以产生更多的种子，并且由于空气动力学特性，它们可以将种子传播到距高大植物更远的地方。 它们的繁衍能力是巨大的。 例如，玉米播种蓟产生多达 19000 颗种子。

3. 迅速进化（发芽、朴实生长、竞争力、育种系统、种子繁衍、和传播特点）。 种子传播能力的增强，随之而来的散播和朴平淡无奇的成长为生存提供了机会。 杂草对土壤条件极端不挑剔，并且能够稳定地承受温度和湿度的急剧波动。

4. 表观遗传学。 除了快速进化外，许多入侵物种还具有通过改变其基因表达来快速响应不断变化的环境因素的能力。 在不断变化的环境中，植株需要灵活善变，从而承受光照、温度、水分可用性、和土壤盐分水平波动等压力。 为了灵活起见，植株能够自行进行表观遗传修饰。

5. 杂交。 杂交草种通常展现出杂交活力，也称为优势。 与两个亲本物种相比，后代显示出改善的生物学功能。 典型地，杂交活力表现出更积极的成长，并具有更高的传播到新领域、并在入侵领土内竞争的能力。

6. 对除草剂的抗性和耐受性。 在过去的几十年里，大多数杂草对于除草剂的耐药性急剧增加。

7. 杂草伴随着人类活动共同进化。 人类往往施用除草剂和除草等控制措施，而杂草已经形成了抗性机制。 与栽培植株相比，它们在耕作过程中受到的外部损害较小。 与之对比，这些损害通常甚至对无性繁殖杂草的繁殖有用（例如，通过部分根或根茎繁殖的杂草）。
8. 与“温室”栽培植株相比，日益频繁的气候变化为杂草提供了更可行的机会。 杂草对农业造成很大危害。 由于对生长条件的要求较低，它们在生长和发育方面超过了栽培植株。 杂草吸收水分、养分和阳光，令农作物急剧降低产量，农田作物难以收获和脱粒，并降低产品质量。

2. 算法说明

入侵杂草算法的灵感来自自然界中杂草的生长过程。 这种方法是由 Mehrabian 和 Lucas 在 2006 年引入的。 很自然地，杂草生长越旺盛，这种强壮的生长对有用的植物构成了严重威胁。 杂草的一个重要特征是其抗性，和在自然界中的高适应性，这是 IWO 优化算法的基础。 该算法可作为高效优化方法的基础。

IWO 是一种连续随机数值算法，模仿杂草的定植行为。 首先，初始种子种群随机分布在整个搜索空间当中。 这些杂草最终会生长，并执行算法的进一个步骤。 该算法由七个步骤组成，可以用伪代码表示为：

1. 随机播种
2. 计算 FF
3. 来自杂草的播种
4. 计算 FF
5. 将子杂草与亲本杂草合并
6. 所有杂草进行分类
7. 重复步骤 3。 直到满足停止条件

框图表示算法在一次迭代中的操作。 IWO 从种子初始化过程开始操作。 种子随机均匀地散布在搜索空间的“领域”上。 之后，我们假设种子发芽，并已长为成年植株，这应该通过适应度函数进行评估。

下一步，了解每种植株的适应性，我们可以让杂草通过种子繁衍，其中种子的数量与适应性成正比。 之后，我们将发芽的种子与亲本植株相结合，并对其进行分类。 通常来讲，入侵性杂草算法可考虑易于编码、修改，并与第三方应用程序结合使用。

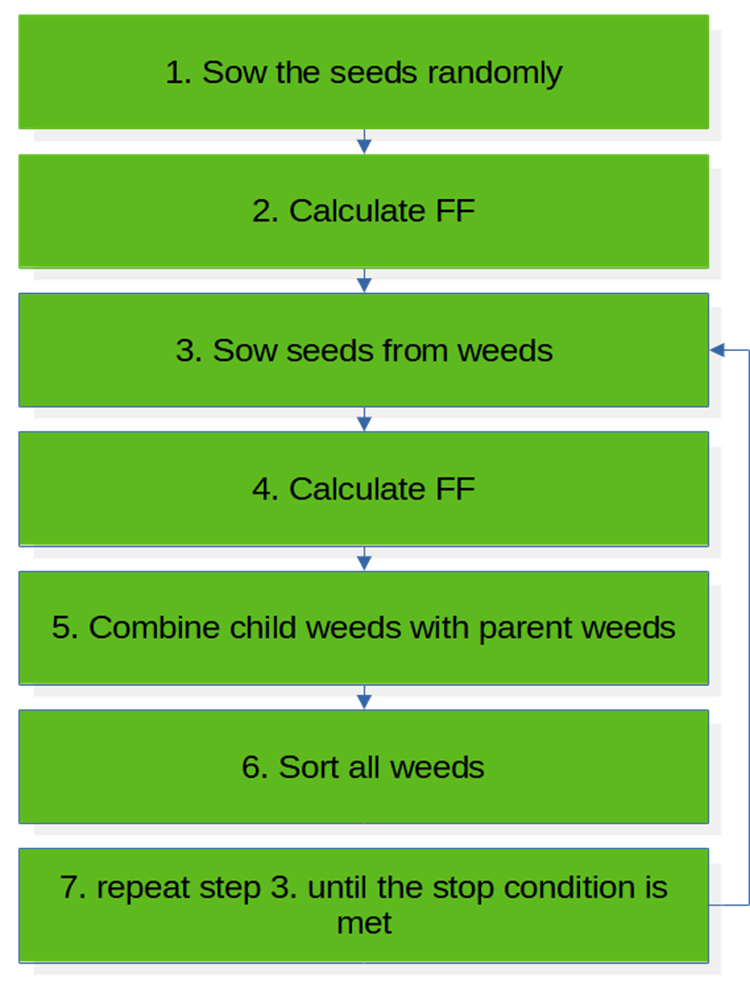
图例 1. IWO 算法框图

我们继续研究杂草算法的特性。 它具有杂草的许多极端生存适应性。 与遗传、蜜蜂和其它一些算法相对比，杂草菌落的一个显著特征是保证菌落的所有植株无一例外地得到播种。 即使是适应性最差的植株，这样一来也可以留下后代，因为最差的植株趋向全局极端的概率也始终是非零的。

正如我已经说过的，每种杂草都会在从最小可能到最大可能的数量（算法的外部参数）的范围内产生种子。 自然而然地，在这种情况下，当每棵植株至少留下一颗或多颗种子时，子植株将比亲本植株更多 — 这个特性在代码中得到了有趣的实现，将在下面讨论。 图例 2 直观显示了该算法。 亲本植株根据其适应性成比例地散布种子。

故此，1 号最好的植株播下了 6 颗种子，而 6 号的植株只播下了一粒种子（保底的种子）。 发芽的种子产生新植株，随后与亲本一起分类。 这是对生存的模仿。 从整个排序组中，选择新的亲本植株，并在下一次迭代中重复生命周期。 该算法具有的机制，能解决“人口过剩”，以及散播能力实施不彻底等问题。

例如，我们取种子数，其中一个算法参数是 50，亲本植株的数量是 5，最小种子数是 1，而最大种子数是 6。 在本例中，5 * 6 = 30，小于 50。 从这个例子中我们可以看到，播种的可能性并没有完全实施。 在这种情况下，保留后代的权利将传递到链表中的下一代，直到所有亲本植株达到允许的最大后代数量。 当到达链表末尾时，权利转到链表中的第一个，且允许留下超过限量的后代。 

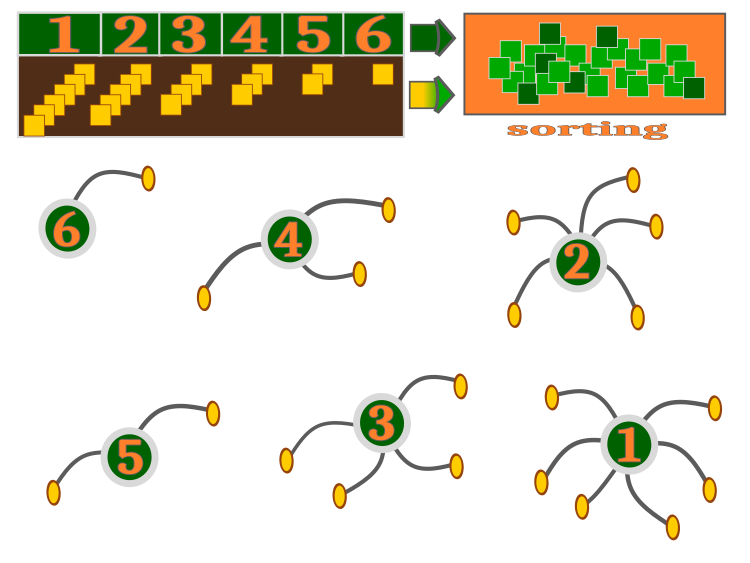
图例 2. IWO 算法操作。 后代的数量与亲本的适应度成正比

接下来要注意的是种子散播。 算法中的种子散播是与迭代次数成比例的线性递减函数。 外部散播参数是种子散播的下限和上限。 因此，随着迭代次数的增加，播种半径减小，发现的极值得到细化。 根据算法作者的建议，应该采用正态散播分布，但我简化了计算，并应用了立方函数。 迭代次数的离散函数如图例 3 所示。

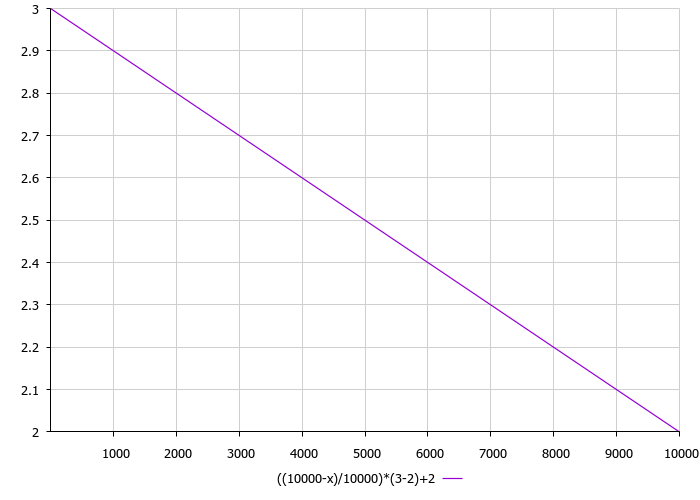
图例 3. 离散对迭代次数的依赖性，其中 3 是最大极限，2 是最小极限

我们继续讨论 IWO 代码。 代码执行简单快捷。

该算法最简单的单元（代理者）是“杂草”。 它还将描述杂草的种子。 这可令我们取用相同类型的数据进行后续排序。 该结构由一个坐标数组、一个存储适应度函数值的变量、和一个种子（后代）数量的计数器组成。 该计数器将令我们能够控制每种植株的最小和最大允许种子数量。

//——————————————————————————————————————————————————————————————————————————————
struct S_Weed
{
  double c []; //coordinates
  double f;    //fitness
  int    s;    //number of seeds
};
//——————————————————————————————————————————————————————————————————————————————

我们需要一个结构来实现选择亲本的概率函数，即与它们的健康状况成比例。 在这种情况下，可以应用轮盘赌原理，我们已在蜂群算法中看到了这一点。 'start' 和 'end' 变量负责概率域的开始和结束。

//——————————————————————————————————————————————————————————————————————————————
struct S_WeedFitness
{
  double start;
  double end;
};
//——————————————————————————————————————————————————————————————————————————————

我们来声明杂草算法类。 在其中，声明我们需要的所有必要变量 — 需优化参数的边界和步长，描述杂草的数组，以及种子数组，最佳全局坐标数组，和算法实现的适应度函数的最佳值。 我们还需要第一次迭代的 “sowing” 标志，和算法参数的常量变量。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_IWO
{
  //============================================================================
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: S_Weed weeds     []; //weeds
  public: S_Weed weedsT    []; //temp weeds
  public: S_Weed seeds     []; //seeds
  public: double cB        []; //best coordinates
  public: double fB;           //fitness of the best coordinates

  public: void Init (const int    coordinatesP,      //Number of coordinates
                     const int    numberSeedsP,      //Number of seeds
                     const int    numberWeedsP,      //Number of weeds
                     const int    maxNumberSeedsP,   //Maximum number of seeds per weed
                     const int    minNumberSeedsP,   //Minimum number of seeds per weed
                     const double maxDispersionP,    //Maximum dispersion
                     const double minDispersionP,    //Minimum dispersion
                     const int    maxIterationP);    //Maximum iterations

  public: void Sowing      (int iter);
  public: void Germination ();

  //============================================================================
  private: void   Sorting        ();
  private: double SeInDiSp       (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI      (double Min, double Max);
  private: double Scale          (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool Revers);

  private: double vec [];            //Vector
  private: int    ind [];
  private: double val [];
  private: S_WeedFitness wf [];      //Weed fitness
  private: bool   sowing;            //Sowing
  private: int    coordinates;       //Coordinates number
  private: int    numberSeeds;       //Number of seeds
  private: int    numberWeeds;       //Number of weeds
  private: int    totalNumWeeds;     //Total number of weeds
  private: int    maxNumberSeeds;    //Maximum number of seeds
  private: int    minNumberSeeds;    //Minimum number of seeds
  private: double maxDispersion;     //Maximum dispersion
  private: double minDispersion;     //Minimum dispersion
  private: int    maxIteration;      //Maximum iterations
};
//——————————————————————————————————————————————————————————————————————————————

在初始化函数的 open 方法中，为常量变量赋值，检查算法的输入参数是否都为有效值，因此亲本植株的最小可能值的乘积不能超过种子总数。 需要亲本植株和种子的总和来判定要执行排序的数组。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_IWO::Init (const int    coordinatesP,      //Number of coordinates
                     const int    numberSeedsP,      //Number of seeds
                     const int    numberWeedsP,      //Number of weeds
                     const int    maxNumberSeedsP,   //Maximum number of seeds per weed
                     const int    minNumberSeedsP,   //Minimum number of seeds per weed
                     const double maxDispersionP,    //Maximum dispersion
                     const double minDispersionP,    //Minimum dispersion
                     const int    maxIterationP)     //Maximum iterations
{
  MathSrand (GetTickCount ());
  sowing = false;
  fB     = -DBL_MAX;

  coordinates    = coordinatesP;
  numberSeeds    = numberSeedsP;
  numberWeeds    = numberWeedsP;
  maxNumberSeeds = maxNumberSeedsP;
  minNumberSeeds = minNumberSeedsP;
  maxDispersion  = maxDispersionP;
  minDispersion  = minDispersionP;
  maxIteration   = maxIterationP;


  if (minNumberSeeds < 1) minNumberSeeds = 1;
  if (numberWeeds * minNumberSeeds > numberSeeds) numberWeeds = numberSeeds / minNumberSeeds;
  else numberWeeds = numberWeedsP;

  totalNumWeeds  = numberWeeds + numberSeeds;

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);
  ArrayResize (vec,       coordinates);
  ArrayResize (cB,        coordinates);

  ArrayResize (weeds,  totalNumWeeds);
  ArrayResize (weedsT, totalNumWeeds);
  ArrayResize (seeds,  numberSeeds);

  for (int i = 0; i < numberWeeds; i++)
  {
    ArrayResize (weeds  [i].c, coordinates);
    ArrayResize (weedsT [i].c, coordinates);
    weeds [i].f = -DBL_MAX;
    weeds [i].s = 0;
  }
  for (int i = 0; i < numberSeeds; i++)
  {
    ArrayResize (seeds [i].c, coordinates);
    seeds [i].s = 0;
  }

  ArrayResize (ind, totalNumWeeds);
  ArrayResize (val, totalNumWeeds);

  ArrayResize (wf, numberWeeds);
}
//——————————————————————————————————————————————————————————————————————————————

在 Sowing () 每次迭代中调用的第一个公开方法。 它包含算法的主要逻辑。 为了便于理解，我将该方法划分为几个部分。

当算法处于第一次迭代时，有必要在整个搜索空间中播下种子。 这通常是随机和均匀地完成的。 在优化参数的可接受数值范围内生成随机数后，检查获得的数值是否超出范围，并设置算法参数定义的离散性。 在此，我们还将分配一个分布向量，在代码后面播种时将需要它。 将种子适应度值初始化为最小双精度值，并重置种子计数器（将成为植株的种子会用到种子计数器）。

//the first sowing of seeds---------------------------------------------------
if (!sowing)
{
  fB = -DBL_MAX;

  for (int s = 0; s < numberSeeds; s++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      seeds [s].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      seeds [s].c [c] = SeInDiSp (seeds [s].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);

      vec [c] = rangeMax [c] - rangeMin [c];
    }

    seeds [s].f = -DBL_MAX;
    seeds [s].s = 0;
  }

  sowing = true;
  return;
}

在这段代码中，散播是根据当前迭代计算的。 我前面提到的每种亲本杂草的保底最小种子数在这里实现。 保底的最小种子数量将由两个循环提供，在第一个循环中，我们将整理亲本植株；在第二个循环中，我们将实际生成新种子，同时增加种子计数器。 如您所见，创建新后代的意义是利用立方函数的分布递增一个随机数，并将先前计算的离散度加入到亲本坐标。 检查新坐标的获取值，以便获取可接受的数值，并分配离散性。

//guaranteed sowing of seeds by each weed-------------------------------------
int    pos = 0;
double r   = 0.0;
double dispersion = ((maxIteration - iter) / (double)maxIteration) * (maxDispersion - minDispersion) + minDispersion;

for (int w = 0; w < numberWeeds; w++)
{
  weeds [w].s = 0;

  for (int s = 0; s < minNumberSeeds; s++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      r = RNDfromCI (-1.0, 1.0);
      r = r * r * r;

      seeds [pos].c [c] = weeds [w].c [c] + r * vec [c] * dispersion;
      seeds [pos].c [c] = SeInDiSp (seeds [pos].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }

    pos++;
    weeds [w].s++;
  }
}

使用此代码，我们将根据轮盘原则为每个亲本植株提供与适应度成比例的概率域。 当这里的种子数量遵循随机定律时，上面的代码为每种植株提供了保底数量的种子；因此杂草的适应性越强，它可以留下的种子就越多，反之亦然。 植株的适应性越差，它产生的种子就越少。

//============================================================================
//sowing seeds in proportion to the fitness of weeds--------------------------

//the distribution of the probability field is proportional to the fitness of weeds
wf [0].start = weeds [0].f;
wf [0].end   = wf [0].start + (weeds [0].f - weeds [numberWeeds - 1].f);

for (int f = 1; f < numberWeeds; f++)
{
  if (f != numberWeeds - 1)
  {
    wf [f].start = wf [f - 1].end;
    wf [f].end   = wf [f].start + (weeds [f].f - weeds [numberWeeds - 1].f);
  }
  else
  {
    wf [f].start = wf [f - 1].end;
    wf [f].end   = wf [f].start + (weeds [f - 1].f - weeds [f].f) * 0.1;
  }
}

根据获得的概率域，我们选择有权利留下后代的亲本植株。 如果种子计数器已达到允许的最大值，则权利传递到排序链表中的下一个计数器。 如果到达链表的末尾，则权力不会传递到下一个，而是传递到链表中的第一个。 然后根据上述规则依据计算出的散播形成子植株。

bool seedingLimit = false;
int  weedsPos = 0;

for (int s = pos; s < numberSeeds; s++)
{
  r = RNDfromCI (wf [0].start, wf [numberWeeds - 1].end);

  for (int f = 0; f < numberWeeds; f++)
  {
    if (wf [f].start <= r && r < wf [f].end)
    {       
      weedsPos = f;
      break;
    }
  }

  if (weeds [weedsPos].s >= maxNumberSeeds)
  {
    seedingLimit = false;
    while (!seedingLimit)
    {
      weedsPos++;
      if (weedsPos >= numberWeeds)
      {
        weedsPos = 0;
        seedingLimit = true;
      }
      else
      {
        if (weeds [weedsPos].s < maxNumberSeeds)
        {
          seedingLimit = true;
        }
      }
    }
  }

  for (int c = 0; c < coordinates; c++)
  {
    r = RNDfromCI (-1.0, 1.0);
    r = r * r * r;

    seeds [s].c [c] = weeds [weedsPos].c [c] + r * vec [c] * dispersion;
    seeds [s].c [c] = SeInDiSp (seeds [s].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }

  seeds [s].s = 0;
  weeds [weedsPos].s++;
}

第二个 open 方法是每次迭代时执行的必需方法，并且在计算每个子杂草的适应度函数后是必需的。 在应用排序之前，将发芽的种子放在公开数组之中，亲本植株位于链表的末尾，从而替换上一代，其中可能包括上一次迭代的后代和亲本。 如此，我们销毁适应性较弱的杂草，就像自然界中发生的那样。 之后，应用排序。 结果列表中的第一种杂草如果真的更好，则值得更新全局达成的最佳解。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_IWO::Germination ()
{
  for (int s = 0; s < numberSeeds; s++)
  {
    weeds [numberWeeds + s] = seeds [s];
  }

  Sorting ();

  if (weeds [0].f > fB) fB = weeds [0].f;
}
//——————————————————————————————————————————————————————————————————————————————

3. 测试结果

测试台结果如下所示：

2023.01.13 18:12:29.880    Test_AO_IWO (EURUSD,M1)    C_AO_IWO:50;12;5;2;0.2;0.01
2023.01.13 18:12:29.880    Test_AO_IWO (EURUSD,M1)    =============================
2023.01.13 18:12:32.251    Test_AO_IWO (EURUSD,M1)    5 Rastrigin's; Func runs 10000 result: 79.71791976868334
2023.01.13 18:12:32.251    Test_AO_IWO (EURUSD,M1)    Score: 0.98775
2023.01.13 18:12:36.564    Test_AO_IWO (EURUSD,M1)    25 Rastrigin's; Func runs 10000 result: 66.60305588198622
2023.01.13 18:12:36.564    Test_AO_IWO (EURUSD,M1)    Score: 0.82525
2023.01.13 18:13:14.024    Test_AO_IWO (EURUSD,M1)    500 Rastrigin's; Func runs 10000 result: 45.4191288396659
2023.01.13 18:13:14.024    Test_AO_IWO (EURUSD,M1)    Score: 0.56277
2023.01.13 18:13:14.024    Test_AO_IWO (EURUSD,M1)    =============================
2023.01.13 18:13:16.678    Test_AO_IWO (EURUSD,M1)    5 Forest's; Func runs 10000 result: 1.302934874807614
2023.01.13 18:13:16.678    Test_AO_IWO (EURUSD,M1)    Score: 0.73701
2023.01.13 18:13:22.113    Test_AO_IWO (EURUSD,M1)    25 Forest's; Func runs 10000 result: 0.5630336066477166
2023.01.13 18:13:22.113    Test_AO_IWO (EURUSD,M1)    Score: 0.31848
2023.01.13 18:14:05.092    Test_AO_IWO (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.11082098547471195
2023.01.13 18:14:05.092    Test_AO_IWO (EURUSD,M1)    Score: 0.06269
2023.01.13 18:14:05.092    Test_AO_IWO (EURUSD,M1)    =============================
2023.01.13 18:14:09.102    Test_AO_IWO (EURUSD,M1)    5 Megacity's; Func runs 10000 result: 6.640000000000001
2023.01.13 18:14:09.102    Test_AO_IWO (EURUSD,M1)    Score: 0.55333
2023.01.13 18:14:15.191    Test_AO_IWO (EURUSD,M1)    25 Megacity's; Func runs 10000 result: 2.6
2023.01.13 18:14:15.191    Test_AO_IWO (EURUSD,M1)    Score: 0.21667
2023.01.13 18:14:55.886    Test_AO_IWO (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.5668
2023.01.13 18:14:55.886    Test_AO_IWO (EURUSD,M1)    Score: 0.04723

快速一瞥就足以注意到算法在测试函数上的高结果。 人们明显倾向于处理平滑函数，尽管到目前为止，没有一种研究过的算法在离散函数上的收敛性优于平滑函数，这可以通过所有算法的 Forest 和 Megacity 函数的复杂性来解释，无一例外。 我们最终可能会得到一些测试算法，这些算法将比平滑函数更好地解决离散函数。

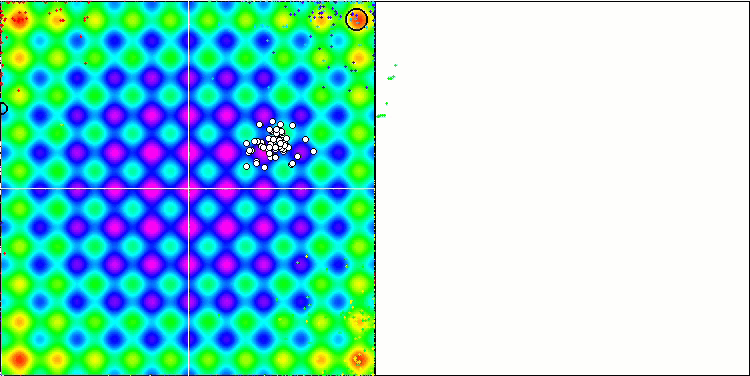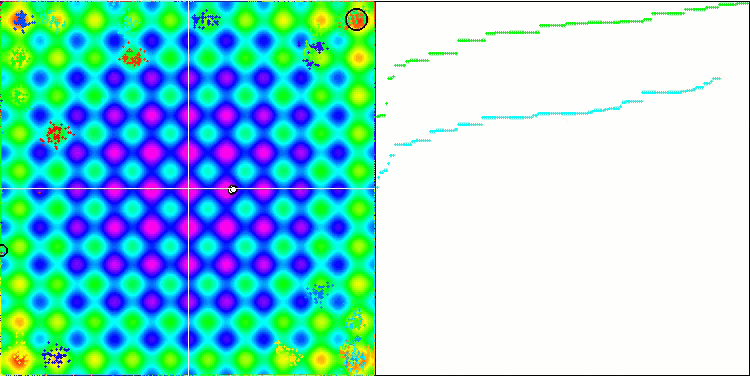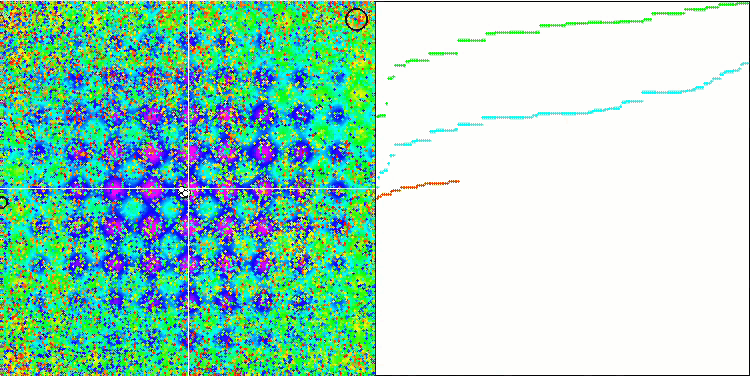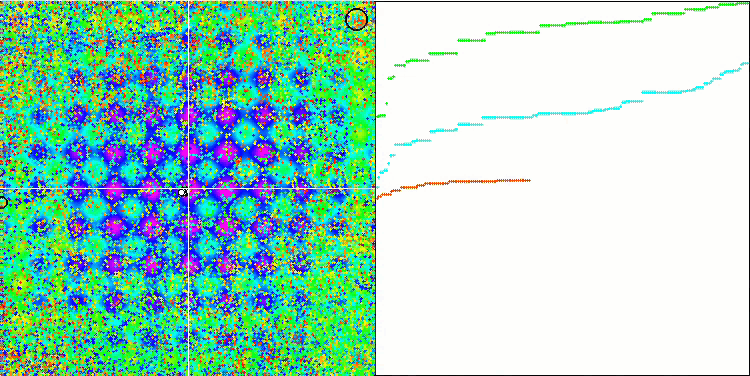
  Rastrigin 测试函数上的 IWO

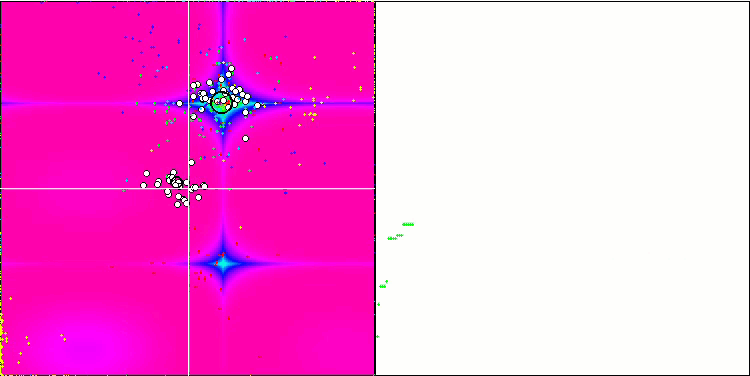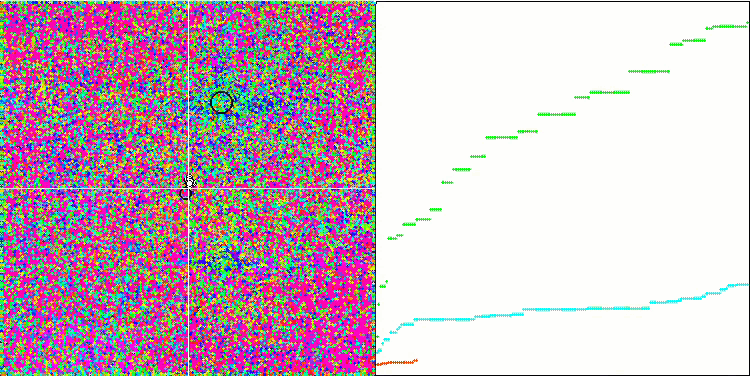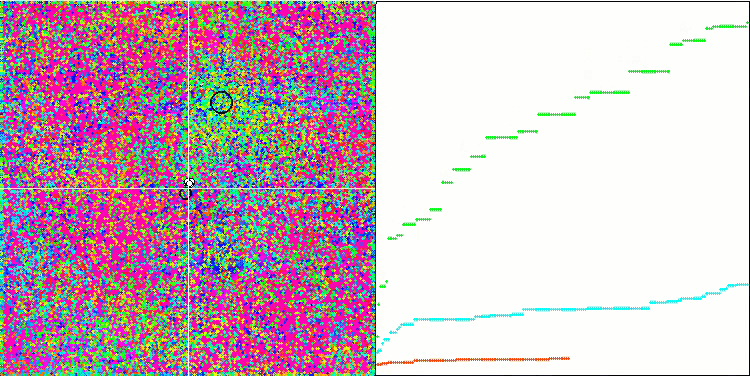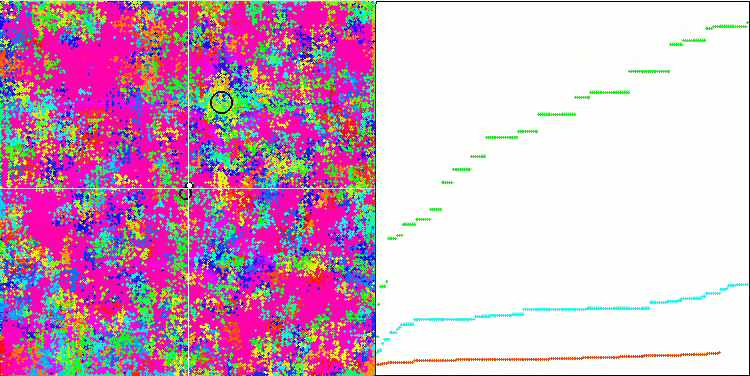
Forest 测试函数上的 IWO。

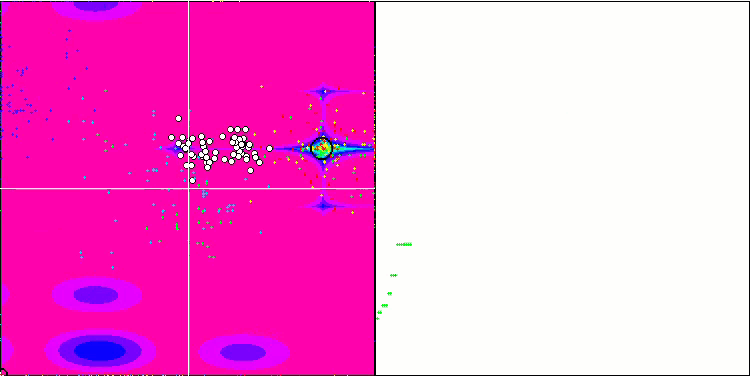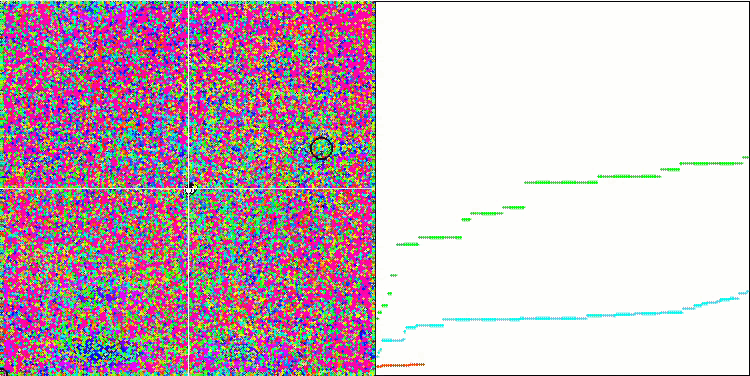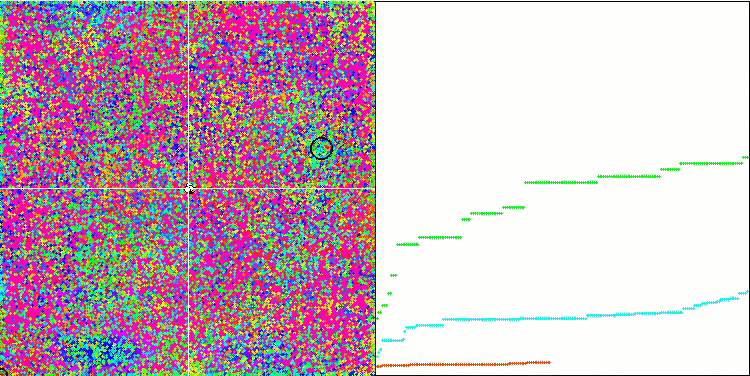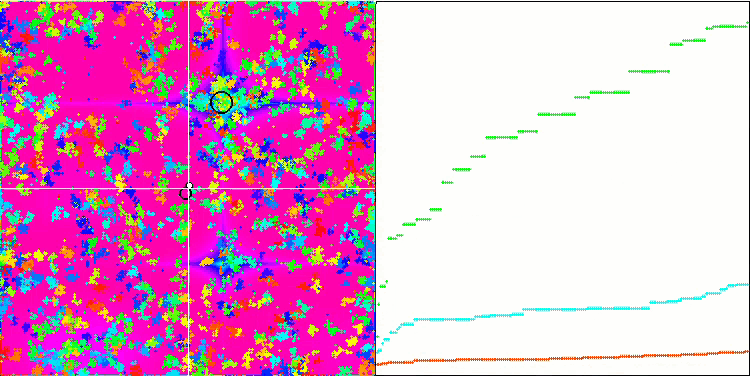
Megacity 测试函数上的 IWO。

入侵杂草算法在大多数测试中展现出令人印象深刻的结果，特别是在含有 10 和 50 个参数的平滑 Rastrigin 函数上。 仅在含有 1000 个参数的测试中，它的性能略有下降，这通常表明在平滑函数上具有良好的性能。 这令我能够为复杂的平滑函数和神经网络推荐该算法。 在 Forest 函数上，该算法在含有 10 个参数的第一个测试中显示出良好的结果，但仍表现出总体平均结果。 在 Megacity 离散函数上，入侵杂草算法的表现高于平均水平，特别是在 1000 个变量的测试中展现出优秀的可扩展性，仅次于萤火虫算法，但在含有 10 和 50 个参数的测试中明显优于它。

尽管入侵杂草算法具有相当多的参数，但这不应被视为缺点，因为参数非常直观，并且可以轻松配置。 此外，算法的微调通常只影响离散函数的测试结果，而平滑函数的结果仍然很好。

在测试函数的可视化中，算法隔离和探索搜索空间某些部分的能力清晰可见，就像在蜜蜂算法，和其它一些算法中发生的那样。 尽管一些出版物指出该算法容易卡顿，并且搜索功能较弱。 尽管该算法没有参考全局极值，也没有“跳跃”出局部陷阱的机制，但 IWO 以某种方式设法在 Forest 和 Megacity.等复杂函数上充分发挥作用。 在处理离散函数时，更多优化参数，结果越稳定。

由于种子离散随每次迭代线性降低，因此极值细化在优化结束时进一步增加。 在我看来，这并不是整体优化，因为算法的探索能力随着时间的推移分布不均匀，我们可以在测试函数的可视化中注意到这是恒定的白噪声。 此外，搜索的不均匀性可以通过测试台窗口右侧的收敛图来判断。 在优化开始时观察到一些收敛加速，这几乎是所有算法的典型特征。 在锐化开始后，大多数优化的收敛速度会变慢。 我们可以看到，仅在接近尾声时，收敛才显著加速。 散播的动态变化是进一步详细研究和实验的原因。 因为我们可以看到，如果迭代次数更多，收敛可以延续。 然而，为了维护客观性和实际有效性而进行的比较测试存在局限性。 

我们来到最终评级表的讨论。 该表显示 IWO 目前处于领先地位。 该算法在九个测试中的两项中显示出最好的结果，而在其余测试中，结果远好于平均水平，因此最终结果是 100 分。 修订后的蚁群算法（ACOm）排在第二位。 在 9 项测试中的 5 项中，它仍然保持最佳。

算法	说明	Rastrigin			Rastrigin 最终	Forest			Forest 最终	Megacity (离散)			Megacity 最终	最终结果
		10 参数 (5 F)	50 参数 (25 F)	1000 参数 (500 F)		10 参数 (5 F)	50 参数 (25 F)	1000 参数 (500 F)		10 参数 (5 F)	50 参数 (25 F)	1000 参数 (500 F)
IWO	入侵杂草优化	1.00000	1.00000	0.33519	2.33519	0.79937	0.46349	0.41071	1.67357	0.75912	0.44903	0.94088	2.14903	100.000
ACOm	蚁群优化 M	0.36118	0.26810	0.17991	0.80919	1.00000	1.00000	1.00000	3.00000	1.00000	1.00000	0.10959	2.10959	95.996
COAm	杜鹃优化算法 M	0.96423	0.69756	0.28892	1.95071	0.64504	0.34034	0.21362	1.19900	0.67153	0.34273	0.45422	1.46848	74.204
FAm	萤火虫算法 M	0.62430	0.50653	0.18102	1.31185	0.55408	0.42299	0.64360	1.62067	0.21167	0.28416	1.00000	1.49583	71.024
BA	蝙蝠算法	0.42290	0.95047	1.00000	2.37337	0.17768	0.17477	0.33595	0.68840	0.15329	0.07158	0.46287	0.68774	59.650
ABC	人工蜂群	0.81573	0.48767	0.22588	1.52928	0.58850	0.21455	0.17249	0.97554	0.47444	0.26681	0.35941	1.10066	57.237
FSS	鱼群搜索	0.48850	0.37769	0.11006	0.97625	0.07806	0.05013	0.08423	0.21242	0.00000	0.01084	0.18998	0.20082	20.109
PSO	粒子群优化	0.21339	0.12224	0.05966	0.39529	0.15345	0.10486	0.28099	0.53930	0.08028	0.02385	0.00000	0.10413	14.232
RND	随机	0.17559	0.14524	0.07011	0.39094	0.08623	0.04810	0.06094	0.19527	0.00000	0.00000	0.08904	0.08904	8.142
GWO	灰狼优化器	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	0.18977	0.04119	0.01802	0.24898	1.000

入侵杂草算法非常适合全局搜索。 该算法展现出良好的性能，尽管没有使用种群中的最佳成员，并且没有机制可以防止局部极端情况下的潜在卡顿。 研究和开发算法之间没有平衡，但这并没有对算法的准确性和速度产生负面影响。 该算法目前尚有其它缺点。 在整个优化过程中搜索性能参差不齐的现象表明，如果上述问题能够得到解决，IWO 的性能可能会更高。

算法测试结果直方图如图例 4 所示

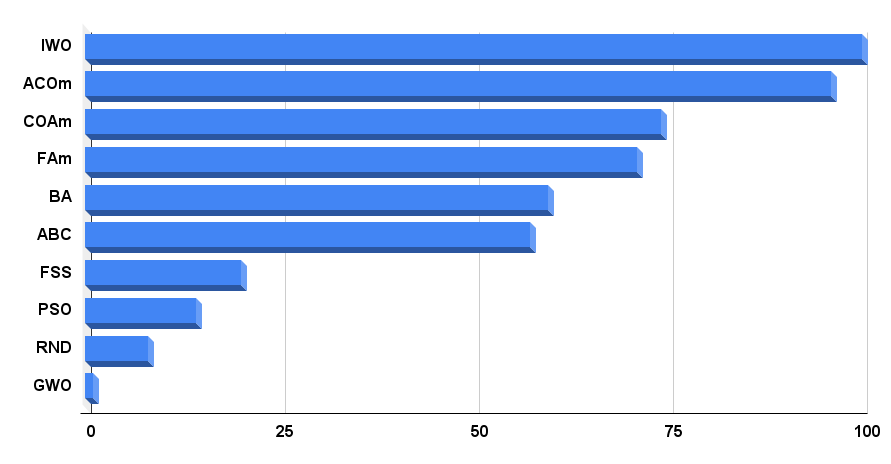
图例 4. 测试算法最终结果的直方图

关于入侵性杂草优化（IWO）算法性质的结论：

优点:
1. 高速。
2. 该算法适用于各种类型的函数，包括平滑和离散。
3. 良好的扩展性。

缺点:
1. 参数太多（尽管它们是不言自明的）。