
Алгоритм атомарного орбитального поиска — Atomic Orbital Search (AOS)
Содержание
Введение
Современные подходы к решению сложных задач оптимизации все чаще черпают вдохновение из принципов физики, особенно из области квантовой механики. В данной статье мы представляем алгоритм AOS (Atomic Orbital Search), который основан на концепциях атомной орбитальной модели. Алгоритм был предложен Махди Азизи в 2021 году. Этот алгоритм является новым метаэвристическим методом. Модель описывает поведение электронов не как строго определенные траектории, а как волновые функции, создающие облака вероятности вокруг атомного ядра, благодаря научным разработкам выдающегося физика Эрвина Шредера.Атомная орбиталь, являющаяся результатом квантового описания, представляет собой область, где вероятность нахождения электрона максимальна. В этой модели электроны движутся в воображаемых слоях, которые определяются радиусами и квантовыми числами, отражающими уровни энергии. Слои с более высокими значениями n соответствуют большим радиусам и, соответственно, более высоким уровням энергии. Это поведение электронов, подверженное возбуждениям от взаимодействий с другими частицами и воздействием фотонов, создает динамическую и изменчивую среду, в которой электроны могут испускать или поглощать энергию, перемещаясь между различными орбиталями.
Алгоритм AOS использует эти физические принципы для моделирования процесса поиска решений в задачах оптимизации. Он учитывает вероятностные распределения и динамику взаимодействий, что позволяет эффективно исследовать пространство решений. В частности, алгоритм рассматривает обновления положений кандидатов решений (электронов) в зависимости от их энергий, что в свою очередь влияет на вероятность нахождения в определенных слоях. Это позволяет AOS не только находить оптимальные решения, но и адаптироваться к изменениям в окружающей среде.
В данной статье мы подробно рассмотрим математическую модель AOS, включая шаги обновления положений кандидатов решений, а также механизмы, регулирующие поглощение и выброс энергии. Таким образом, AOS не только представляет собой интересный подход к оптимизации, но и открывает новые горизонты для применения квантовых принципов в вычислительных задачах.
Реализация алгоритма
Алгоритм AOS основан на принципах атомной орбитальной модели, в которой рассматриваются выброс и поглощение энергии атомами, а также конфигурация плотности электронов. В начале работы алгоритма задается несколько кандидатов решений, обозначаемых как X, которые рассматриваются как электроны, находящиеся вокруг ядра атома. Эти кандидаты формируют облако электронов, а пространство поиска представлено в виде сферического объема, разделенного на концентрические слои. Кандидаты решений можно записать в общем виде так:
X = [x1, x2 ..., xj ..., xm], где xi — это i-й кандидат решения, m — общее количество кандидатов.
Начальные позиции кандидатов решений инициализируются случайным образом. Каждый электрон имеет уровень энергии, определяемой целевой функцией, которую необходимо минимизировать. Таким образом, электроны с низкими уровнями энергии соответствуют кандидатам с лучшими значениями целевой функции, а электроны с высокими уровнями энергии — кандидатам с худшими значениями. Вектор значений целевой функции записывается как:
E = [E1, E2, ..., Ei, ..., Em], где Ei — уровень энергии i-го кандидата.
Воображаемые слои вокруг ядра моделируются с помощью случайного целого числа n, которое может быть от 1 до количества слоев L. Слой с наименьшим радиусом L0 представляет ядро, а остальные слои Li — расположение электронов (в AOS в слое "ядро" так же могут быть электроны). Распределение кандидатов решений по слоям осуществляется с использованием функции плотности вероятности (PDF), которая определяет вероятность нахождения значения переменной в заданном диапазоне. В алгоритме используется логнормальное распределение, что позволяет моделировать реальное волновое поведение электронов. Кандидаты решений распределяются по различным слоям, где вектор Xk, содержащий кандидатов в n слоях, записывается как:
Xk = [Xk1, Xk2, ..., Xki, ..., Xkp], где k — номер слоя, p — количество кандидатов в слое.
В соответствии с атомной орбитальной моделью, электроны принимаются в основном состоянии уровня энергии. Связующее состояние и связующая энергия для каждого слоя рассчитываются как:
BS_k = (1/p) * Σ(Xki),
BE_k = (1/p) * Σ(Eki).
Общий уровень энергии атома определяется как:
BS = (1/m) * Σ(Xi),
BE = (1/m) * Σ(Ei).
Электроны могут изменять свое местоположение и перемещаться между слоями под воздействием фотонов и других взаимодействий. Обновление положения кандидатов решений в алгоритме AOS происходит на основе вероятности взаимодействия, представленной случайно сгенерированным числом ϕ, которое распределено в диапазоне [0,1]. Если ϕ ≥ PR (параметр скорости фотонов), то возможны испускание или поглощение энергии.
Если Eki ≥ BEk, то происходит испускание энергии: Xki[t+1] = Xkit + αi × (βi × LE − γi × BS) / k.
Если Eki < BEk, то происходит поглощение энергии: Xki[t+1] = Xkit + αi × (βi × LEk − γi × BSk).
Если ϕ < PR, то рассматриваются перемещения в магнитные поля или взаимодействия с другими частицами: Xki[t+1] = Xkit + ri, где ri - случайное приращение в диапазоне от min до max соответсвующего оптимизируемого параметра задачи.
Если говорить проще, то в AOS популяцию кандидатных решений можно образно представить как молекулу, где атомы соответствуют координатам в пространстве поиска, а электроны в этих атомах — конкретным решениям. Таким образом, если популяция состоит из 50 кандидатных решений, то в каждом атоме будет распределено по слоям, согласно логнормальному распределению, 50 электронов.
В описании алгоритма автор не указывает, как определяется диаметр внешнего слоя атома, подразумевая, что ядро атома расположено в центре по отношению к слоям. Это означает, что атом вместе со слоями перемещается в заданных границах задачи. Чтобы придать алгоритму большую гибкость, условимся, что диаметр внешнего слоя будет соответствовать диапазону [min; max] для соответствующей координаты в пространстве поиска, а центр ядра атома будет находиться в точке лучшего глобального решения по данной координате. Визуально модель атома в AOS можно представить на рисунке 1.
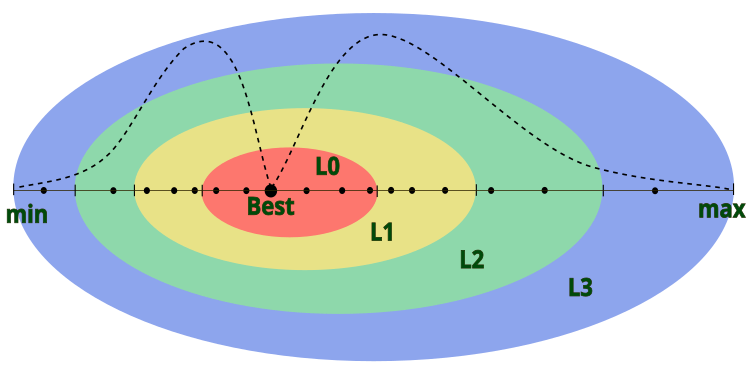
Рисунок 1. Модель атома в алгоритме AOS, где точками обозначены электроны, а пунктирной линией - логнормальное распределение электронов
Псевдокод алгоритма атомарного орбитального поиска (AOS):
1. Инициализация
1.1 Начальные позиции (Xi)
Создается популяция из m кандидатов решения
Каждый кандидат получает случайную позицию в пространстве поиска
1.2 Вычисление начальной пригодности (Ei)
Для каждого кандидата вычисляется значение целевой функции
Это значение представляет энергию частицы
Чем ниже энергия, тем лучше решение
1.3 Определение параметров атома
BS (Binding State) состояние связи атома, представляет текущее среднее положение всех частиц
BE (Binding Energy) энергия связи, представляет среднюю энергию всех частиц
LE (Lowest Energy) частица с наименьшей энергией (лучшее решение)
2. Создание структуры слоев
2.1 Генерация случайного количества слоев [1; n] для каждого атома
Определяется количество воображаемых орбиталей
Каждая орбиталь представляет собой уровень поиска с разной интенсивностью
2.2 Распределение частиц
Частицы распределяются по слоям согласно функции плотности вероятности (PDF)
Внутренние слои обычно содержат лучшие решения
Внешние слои используются для исследования пространства
2.3 Процесс поиска для каждого слоя (k)
3.1 Параметры слоя
BSk состояние связи для конкретного слоя
BEk энергия связи слоя
LEk частица с наименьшей энергией в слое
3.2 Обновление позиций частиц
Для каждой частицы i в слое k:
3.3 Генерация управляющих параметров:
φ: определяет тип движения
α: коэффициент масштабирования
β: коэффициент притяжения к лучшему решению
γ: коэффициент отталкивания от среднего состояния
PR: вероятность фотонного перемещения
3.4 Выбор типа движения:
если φ ≥ PR:
если Eki ≥ BEk:
// Глобальное исследование
Xi[t+1] = Xit + αi × (βi × LE - γi × BS) / k
иначе:
// Локальное исследование
Xi[t+1] = Xit + αi × (βi × LEk - γi × BSk)
иначе:
// Случайное перемещение
Xki[t+1] = Xkit + ri
4. Вычисление пригодности (Ei)
5. Обновление глобальных параметров
6. Повторить с 1.3 до выполнения критерия останова
Для расчета вероятности распределения электронов вокруг ядра (наилучшего решения), можно использовать генерацию чисел для различных распределений. Автор предпочитает логнормальное распределение, что требует его реализации в коде. Напишем код генератора. Для алгоритма необходимо сделать не просто логнормальное распределение, а смещенное асимметрично относительно центра (ядра), как показано на рисунке 1. Реализуем функцию "LognormalDistribution" в коллекцию библиотеки функций для алгоритмов оптимизации, которая генерирует случайное число, распределенное по логнормальному закону в заданных границах со смещением.
Функция принимает следующие параметры:
1. center - центральное значение распределения.
2. min_value - минимальное значение, которое может быть сгенерировано.
3. max_value - максимальное значение, которое может быть сгенерировано.
4. peakDisplCoeff - коэффициент смещения пика относительно центра распределения (по умолчанию равен 0.2).
Описание работы функции:
1. Проверка границ:
Если "min_value" больше или равно "max_value", функция возвращает "max_value".
Если "max_value" меньше или равно "min_value", функция возвращает "min_value".
2. Случайное число "random" генерируется в диапазоне от 0 до 1.
3. Коррекция центра:
Если "center" меньше "min_value", он устанавливается в "min_value", и "random" устанавливается в 1.
Если "center" больше "max_value", он устанавливается в "max_value", и "random" устанавливается в 0.
4. Вычисляются значения "peak_left" и "peak_right", которые определяют положение пиков распределения.
5. Генерация значения:
Если "random" меньше 0.5, выполняется расчет для левой части распределения:
Рассчитываются параметры "mu_left" и "sigma_left".
Генерируются случайные числа "u1" и "u2" для метода Бокса-Мюллера.
Применяется метод Бокса-Мюллера для получения нормального распределенного значения "z".
Вычисляется результат для левой части.
Если "random" больше или равно 0.5, выполняется аналогичный процесс для правой части распределения, используя параметры "mu_right" и "sigma_right".
6. Если сгенерированное значение "result" выходит за пределы "min_value" и "max_value", вызывается функция "RNDfromCI", чтобы "закинуть" значение в допустимый диапазон, тем самым предотвращая накопление вероятностей на границах генерируемых случайных чисел.
//------------------------------------------------------------------------------ //The lognormal distribution of the species: min|------P---C---P------|max double C_AO_Utilities :: LognormalDistribution (double center, double min_value, double max_value, double peakDisplCoeff = 0.2) { // Проверка правой границы if (min_value >= max_value) { return max_value; } // Проверка левой границы if (max_value <= min_value) { return min_value; } // Генерация случайного числа от 0 до 1 double random = MathRand () / 32767.0; // Коррекция центра, если он выходит за границы if (center < min_value) { center = min_value; random = 1; } if (center > max_value) { center = max_value; random = 0; } // Расчет положения пиков double peak_left = center - (center - min_value) * peakDisplCoeff; double peak_right = center + (max_value - center) * peakDisplCoeff; double result = 0.0; if (random < 0.5) // Левая часть распределения { // Расчет параметров для левой части double diff_center_peak = MathMax (center - peak_left, DBL_EPSILON); double diff_center_min = MathMax (center - min_value, DBL_EPSILON); double mu_left = MathLog (diff_center_peak); double sigma_left = MathSqrt (2.0 * MathLog (MathMax (diff_center_min / diff_center_peak, DBL_EPSILON)) / 9.0); // Генерация случайных чисел для метода Бокса-Мюллера double u1 = MathRand () / 32767.0; double u2 = MathRand () / 32767.0; // Защита от нулевых значений u1 = MathMax (u1, DBL_EPSILON); // Применение метода Бокса-Мюллера double z = MathSqrt (-2.0 * MathLog (u1)) * MathCos (2.0 * M_PI * u2); // Расчет результата для левой части result = center - MathExp (mu_left + sigma_left * z); } else // Правая часть распределения { // Расчет параметров для правой части double diff_peak_center = MathMax (peak_right - center, DBL_EPSILON); double diff_max_center = MathMax (max_value - center, DBL_EPSILON); double mu_right = MathLog (diff_peak_center); double sigma_right = MathSqrt (2.0 * MathLog (MathMax (diff_max_center / diff_peak_center, DBL_EPSILON)) / 9.0); // Генерация случайных чисел для метода Бокса-Мюллера double u1 = MathRand () / 32767.0; double u2 = MathRand () / 32767.0; // Защита от нулевых значений u1 = MathMax (u1, DBL_EPSILON); // Применение метода Бокса-Мюллера double z = MathSqrt (-2.0 * MathLog (u1)) * MathCos (2.0 * M_PI * u2); // Расчет результата для правой части result = center + MathExp (mu_right + sigma_right * z); } // Проверка и коррекция результата, если он выходит за границы if (result < min_value || result > max_value) return RNDfromCI (min_value, max_value); return result; }
Напишем скрипт для визуальной проверки получаемого распределения. Вот что делает проверочный скрипт (остальной код приводить не будем — класс по работе с канвасом для тестового стенда можно найти в архиве к статье):
1. Создается объект "Canvas" для рисования графики.
2. Инициализируются параметры канваса: ширина "W", высота "H" и отступы "O".
3. Создаются массивы "CountL" и "CountR" для подсчета значений слева и справа от входного параметра "Inp_P", инициализируемые нулями.
4. Создается графический элемент (канвас) с заданными размерами и цветом фона.
Логнормальное распределение описывает случайные величины, логарифм которых имеет нормальное распределение. В коде оно используется для генерации значений, визуализируемых на графике.
5. В цикле "for" генерируются "N" значений с помощью функции "U.LognormalDistribution()". Каждое значение сравнивается с "Inp_P": если меньше, увеличивается счетчик "CountL[i]", если больше - "CountR[i]".
6. Перед генерацией массивы "CountL" и "CountR" инициализируются нулями.
7. Подсчитываются минимальные и максимальные значения в массивах для определения диапазона графиков.
8. Вычисляются координаты для рисования графиков, включая центр канваса и шаги для левой и правой частей.
9. Рисуются точки на канвасе, представляющие количество значений в диапазонах, с цветом, определяемым частотой выпадения.
10. Обновляется канвас для отображения изменений.
// Функция, вызываемая при старте void OnStart () { CCanvas Canvas; // Объект для работы с графикой (канвас) // Параметры канваса int W = 750; // Ширина канваса int H = 400; // Высота канваса int O = 10; // Отступы от границ канваса // Массивы для хранения подсчета значений int CountL []; // Подсчет значений слева от входного параметра int CountR []; // Подсчет значений справа от входного параметра // Инициализация массивов ArrayResize (CountL, Size_P); // Изменяем размер массива CountL ArrayInitialize (CountL, 0); // Инициализируем массив CountL нулями ArrayResize (CountR, Size_P); // Изменяем размер массива CountR ArrayInitialize (CountR, 0); // Инициализируем массив CountR нулями // Создание канваса string canvasName = "Test_Probability_Distribution_Canvas"; // Имя канваса if (!Canvas.CreateBitmapLabel(canvasName, 5, 30, W, H, COLOR_FORMAT_ARGB_RAW)) { Print ("Error creating Canvas: ", GetLastError()); // Вывод ошибки, если создание не удалось return; } // Настройка свойств канваса ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN, false); // Сделать канвас видимым ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true); // Сделать канвас выбираемым // Очистка канваса и рисование границы Canvas.Erase (COLOR2RGB(clrWhite)); // Заполнение белым цветом Canvas.Rectangle (1, 1, W - 1, H - 1, COLOR2RGB(clrBlack)); // Рисование черной рамки int ind = 0; // Индекс для подсчета double X = 0.0; // Переменная для хранения значений // Основной цикл для генерации значений for (int i = 0; i < CNT_P; i++) { // Генерация логнормального распределения X = U.LognormalDistribution (Inp_P, Min_P, Max_P, PeakDisplCoeff_P); // Определение, в какую сторону от входного параметра попадает значение if (X < Inp_P) { // Считаем индекс для левой части ind = (int) U.Scale(X, Min_P, Inp_P, 0, Size_P, true); if (ind >= Size_P) ind = Size_P - 1; // Ограничиваем индекс if (ind < 0) ind = 0; // Ограничиваем индекс CountL [ind] += 1; // Увеличиваем счетчик для левой части } else { // Считаем индекс для правой части ind = (int) U.Scale (X, Inp_P, Max_P, 0, Size_P, false); if (ind >= Size_P) ind = Size_P - 1; // Ограничиваем индекс if (ind < 0) ind = 0; // Ограничиваем индекс CountR [ind] += 1; // Увеличиваем счетчик для правой части } } // Определение минимальных и максимальных значений для графика int minCNT = CNT_P; // Начальное значение для минимального счетчика int maxCNT = 0; // Начальное значение для максимального счетчика // Поиск минимальных и максимальных значений в счетчиках for (int i = 0; i < Size_P; i++) { if (CountL [i] > maxCNT) maxCNT = CountL [i]; // Обновление максимального значения для левой части if (CountR [i] > maxCNT) maxCNT = CountR [i]; // Обновление максимального значения для правой части if (CountL [i] < minCNT) minCNT = CountL [i]; // Обновление минимального значения для левой части if (CountR [i] < minCNT) minCNT = CountR [i]; // Обновление минимального значения для правой части } // Переменные для рисования графиков int x = 0.0; // Координата X для рисования int y = 0.0; // Координата Y для рисования color clrF; // Цвет для рисования int centre = 0; // Центр канваса int stepL = 0; // Шаг для левой части int stH_L = 0; // Высота для левой части int stepR = 0; // Шаг для правой части int stH_R = 0; // Высота для правой части // Определение центра канваса centre = (int) U.Scale(Inp_P, Min_P, Max_P, O, W - O - 1, false); // Вычисление шагов и высот для левой части stepL = (centre - O) / Size_P; stH_L = stepL / 2; if (stH_L == 0) stH_L = 1; // Убедимся, что высота не 0 // Вычисление шагов и высот для правой части stepR = (W - O - centre) / Size_P; stH_R = stepR / 2; if (stH_R == 0) stH_R = 1; // Убедимся, что высота не 0 // Рисование графиков для левой и правой частей for (int i = 0; i < Size_P; i++) { // Рисование для левой части x = (int) U.Scale (i, 0, Size_P - 1, O, centre - stH_L, true); // Вычисление координаты X y = (int) U.Scale (CountL [i], 0, maxCNT, O, H - O - 1, true); // Вычисление координаты Y clrF = DoubleToColor(CountL [i], minCNT, maxCNT, 0, 255); // Определение цвета по значению // Рисование точек для левой части Canvas.Circle (x, y, 2, COLOR2RGB (clrF)); // Рисуем маленький круг Canvas.Circle (x, y, 3, COLOR2RGB (clrF)); // Рисуем круг большего размера // Рисование для правой части x = (int) U.Scale (i, 0, Size_P - 1, centre + stH_R, W - O - 1, false); // Вычисление координаты X y = (int) U.Scale (CountR[i], 0, maxCNT, O, H - O - 1, true); // Вычисление координаты Y clrF = DoubleToColor (CountR [i], minCNT, maxCNT, 0, 255); // Определение цвета по значению // Рисование точек для правой части Canvas.Circle (x, y, 2, COLOR2RGB (clrF)); // Рисуем маленький круг Canvas.Circle (x, y, 3, COLOR2RGB (clrF)); // Рисуем круг большего размера } Canvas.Update (); // Обновление канваса для отображения изменений}
Запустим скрипт и получим на чарте картинку, как на рисунке 2.
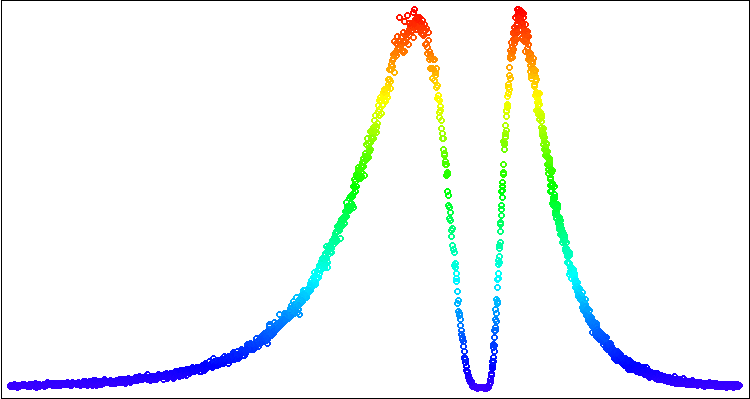
Рисунок 2. Визуализация построения асимметричного логнормального распределения с помощью стандартной библиотеки Canvas
После того, как мы подробно разобрали теорию всех этапов алгоритма, переходим непосредственно к реализации кода. В то время как алгоритм AOS как метод минимизации задачи, мы поправим логику таким образом, чтобы он работал на максимизацию. Давайте напишем структуру "S_Layer", которая будет моделировать слой атома и содержать информацию о количестве частиц, находящихся в этом слое. Она будет включать в себя как числовые характеристики, так и метод для инициализации. Поля структуры:
- pc — счетчик частиц, находящихся в данном слое атома, который позволяет отслеживать, сколько частиц (электронов) находится в конкретном слое.
- BSk — состояние связи в слое, отражает уровень взаимодействия между частицами в слое.
- BEk — энергия связи в слое, показывает, насколько сильно частицы в слое связаны друг с другом.
- LEk — минимальная энергия в слое и используется для определения наименьшего уровня энергии, который может быть достигнут частицами в данном конкретном слое.
Метод "Init" предназначен для инициализации полей структуры значениями по умолчанию и позволяет легко многократно при необходимости сбросить состояние слоя.
//—————————————————————————————————————————————————————————————————————————————— struct S_Layer { int pc; // счетчик частиц double BSk; // состояние связи double BEk; // энергия связи double LEk; // минимальная энергия void Init () { pc = 0; BSk = 0.0; BEk = 0.0; LEk = 0.0; } }; //——————————————————————————————————————————————————————————————————————————————
Далее рассмотрим структуру "S_Atom" и ее метод "Init". "S_Atom" — это структура, которая представляет собой атом, состоящий из нескольких слоев. Каждый слой моделируется с помощью массива "layers []" структуры "S_Layer", которая была описана ранее. Поля структуры:
- Init — метод инициализации массива слоев атома, а также инициализации каждого слоя в этом массиве.
- layersNumb — это целочисленный параметр указывает на количество слоев, которые будут созданы для данного атома.
//—————————————————————————————————————————————————————————————————————————————— struct S_Atom { S_Layer layers []; // массив слоев атома void Init (int layersNumb) { ArrayResize (layers, layersNumb); for (int i = 0; i < layersNumb; i++) layers [i].Init (); } }; //——————————————————————————————————————————————————————————————————————————————
Следующая структура "S_Electron" и ее метод "Init". Структура представляет собой электрон — член популяции решений, который содержит информацию о своем положении в соответствующем слое атома. Поля "layerID []" — массив целых чисел хранит идентификаторы слоев, к которым принадлежит электрон. Каждый идентификатор соответствует определенному слою в атоме, что позволяет отслеживать, на каком уровне находится электрон.
//—————————————————————————————————————————————————————————————————————————————— struct S_Electron { int layerID []; // массив идентификаторов слоев для электрона void Init (int coords) { ArrayResize (layerID, coords); } }; //——————————————————————————————————————————————————————————————————————————————
Класс алгоритма AOS "C_AO_AOS" наследуется от базового класса "C_AO" и подразумевает наличие общей функциональности, связанной с атомными орбитами.
Параметры класса:
- popSize — размер популяции в алгоритме.
- maxLayers — максимальное количество слоев, которое может быть использовано в атомной модели.
- photonEmissions — количество фотонных излучений, которые будут использованы в процессе оптимизации.
- PR — коэффициент перехода фотонов, определяет вероятность перехода между состояниями.
- peakPosition — позиция пика в логнормальном распределении.
Методы класса:
1. SetParams () — устанавливает параметры алгоритма, считывая значения из массива "params".
2. Init () — инициализирует алгоритм с заданными параметрами поиска: минимальные и максимальные диапазоны, шаг поиска и количество эпох.
3. Moving () — метод для перемещения частиц в пространстве поиска.
4. Revision () — метод отвечает за пересмотр лучших решений, найденных в процессе оптимизации.
Приватные поля класса:
- atomStage — текущая стадия атома определяет, на каком этапе находятся процессы в атоме.
- currentLayers [] — массив хранит информацию о текущем количестве слоев для каждого атома (на каждой эпохе количество слоев в каждом атоме — случайное число в диапазоне [1; maxLayers].
- S_Atom atoms [] — массив атомов, размер которого соответствует количеству координат, используемых в алгоритме.
- S_Electron electrons [] — массив электронов, соответствующий размеру популяции.
- BS [] — массив хранит состояния связей между электронами по всей популяции.
Приватные методы класса:
1. GetOrbitBandID () — получает идентификатор орбитальной полосы для заданных параметров, таких как количество слоев и диапазоны.2. DistributeParticles() — метод для распределения частиц в пространстве поиска.
3. LayersGenerationInAtoms () — генерирует количество слоев в атомах.
4. UpdateElectronsIDs () — обновляет идентификаторы слоев для электронов.
5. CalcLayerParams () — рассчитывает параметры слоев и включает в себя определение энергетических уровней и связей.
6. UpdateElectrons () — обновляет положение электронов.
//—————————————————————————————————————————————————————————————————————————————— // Класс реализующий алгоритм атомарной оптимизации (Atomic Orbital Search) class C_AO_AOS : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_AOS () { } C_AO_AOS () { ao_name = "AOS"; ao_desc = "Atomic Orbital Search"; ao_link = "https://www.mql5.com/ru/articles/16276"; popSize = 50; // размер популяции maxLayers = 5; // максимальное количество слоев photonEmissions = 1; // количество излучений фотонов PR = 0.1; // коэффициент перехода фотонов peakPosition = 0.05; // позиция пика в логнормальном распределении ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "maxLayers"; params [1].val = maxLayers; params [2].name = "photonEmissions"; params [2].val = photonEmissions; params [3].name = "photonRate"; params [3].val = PR; params [4].name = "peakPsition"; params [4].val = peakPosition; } // Установка параметров алгоритма void SetParams () { popSize = (int)params [0].val; maxLayers = (int)params [1].val; photonEmissions = (int)params [2].val; PR = params [3].val; peakPosition = params [4].val; } // Инициализация алгоритма с заданными параметрами поиска bool Init (const double &rangeMinP [], // минимальный диапазон поиска const double &rangeMaxP [], // максимальный диапазон поиска const double &rangeStepP [], // шаг поиска const int epochsP = 0); // количество эпох void Moving (); // Метод перемещения частиц void Revision (); // Метод пересмотра лучших решений //---------------------------------------------------------------------------- int maxLayers; // максимальное количество слоев int photonEmissions; // количество излучений фотонов double PR; // коэффициент перехода фотонов double peakPosition; // позиция пика в логнормальном распределении private: //------------------------------------------------------------------- int atomStage; // текущая стадия атома int currentLayers []; // текущее количество слоев для соответствующего атома (координаты) S_Atom atoms []; // атомы, размер соответствует количеству координат S_Electron electrons []; // электроны, соответствует размеру популяции double BS []; // состояния связей // Получение орбитальной полосы для заданных параметров int GetOrbitBandID (int layersNumb, double min, double max, double center, double p); // Распределение частиц в пространстве поиска void DistributeParticles (); // Генерация слоев в атомах void LayersGenerationInAtoms (); // Обновление идентификаторов электронов void UpdateElectronsIDs (); // Расчет параметров слоев void CalcLayerParams (); // Обновление положения электронов void UpdateElectrons (); }; //——————————————————————————————————————————————————————————————————————————————
Посмотрим, что происходит в методе "Init" класса алгоритма AOS.
1. Стандартная инициализация: метод начинает с вызова "StandardInit", выполняет общие этапы инициализации, такие как установка диапазонов для координат.
2. Инициализация переменных:
- atomStage — устанавливается в "0", что означает, что алгоритм начинает с начальной стадии.
- ArrayResize (currentLayers, coords) — изменяет размер массива "currentLayers" в соответствии с количеством координат "coords".
- ArrayResize (atoms, coords) — изменяет размер массива "atoms", создавая для каждого атома (координаты) отдельный объект. Для каждого атома вызывается метод "Init (maxLayers)", который инициализирует его с максимальным количеством слоев.
- ArrayResize (electrons, popSize) — изменяет размер массива "electrons" в соответствии с размером популяции "popSize". Для каждого электрона создается массив "layerID", который соответствует количеству координат.
- ArrayResize (BS, coords) — изменяет размер массива "BS", который, хранит состояния для каждой координаты.
4. Если все операции инициализации прошли успешно, метод возвращает "true".
//—————————————————————————————————————————————————————————————————————————————— // Инициализация алгоритма bool C_AO_AOS::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- atomStage = 0; ArrayResize (currentLayers, coords); ArrayResize (atoms, coords); for (int i = 0; i < coords; i++) atoms [i].Init (maxLayers); ArrayResize (electrons, popSize); for (int i = 0; i < popSize; i++) ArrayResize (electrons [i].layerID, coords); ArrayResize (BS, coords); return true; } //——————————————————————————————————————————————————————————————————————————————
Метод перемещения частиц. Опишем метод "Moving":
1. Начальное случайное позиционирование:
- Если переменная "revision" равна "false", это означает, что алгоритм еще не начал свою работу. В этом случае происходит случайное позиционирование частиц.
- Далее вложенный цикл "for" проходит по всем электронам (размер популяции) и для каждой координаты генерирует случайное значение с использованием метода "u.RNDfromCI", который берет значение из диапазона, заданного "rangeMin" и "rangeMax". Затем это значение корректируется с помощью метода "u.SeInDiSp", который устанавливает значение в соответствии с заданным шагом (step).
2. Выполнение соответствующего этапа эволюции атомов:
- Если "revision" равен "true", это означает, что алгоритм уже инициализирован, и можно выполнять его основные этапы. В зависимости от текущей стадии "atomStage", вызываются разные методы:
- Если "atomStage" равен "0", вызывается "DistributeParticles ()", который отвечает за распределение частиц в пространстве в соответствии с асимметричным логнормальным распределением.
- В противном случае, вызываются методы, которые генерируют слои в атомах, обновляют идентификаторы электронов, рассчитывают параметры слоев и обновляют положение электронов.
3. После выполнения всех необходимых операций "atomStage" увеличивается на "1". Если "atomStage" превышает значение "photonEmissions", оно сбрасывается на "0", что позволяет циклически повторять этапы алгоритма.
//—————————————————————————————————————————————————————————————————————————————— // Метод перемещения частиц void C_AO_AOS::Moving () { // Начальное случайное позиционирование if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Выполнение соответствующего этапа алгоритма if (atomStage == 0) { DistributeParticles (); } else { LayersGenerationInAtoms (); UpdateElectronsIDs (); CalcLayerParams (); UpdateElectrons (); } // Переход к следующей стадии atomStage++; if (atomStage > photonEmissions) atomStage = 0; } //——————————————————————————————————————————————————————————————————————————————
Переходим к разбору специфичных методов. Метод "GetOrbitBandID" класса "C_AO_AOS" предназначен для определения орбитальной полосы для частицы на основе ее положения относительно заданного центра. Он принимает количество слоев, минимальное и максимальное значения, центр и позицию частицы "p".
1. Рассчитывает ширину полос слева и справа от центра.
2. Если позиция частицы "p" меньше центра, то ищет, в какой из левых полос она находится.
3. Если больше — ищет в правых полосах.
4. Если равна центру, возвращает номер 0 (центр).
Таким образом, функция возвращает индекс соответствующей орбитальной полосы для заданной позиции.
//—————————————————————————————————————————————————————————————————————————————— // Определение орбитальной полосы для частицы int C_AO_AOS::GetOrbitBandID (int layersNumb, double min, double max, double center, double p) { // Расчет ширины полос слева и справа от центра double leftWidth = (center - min) / layersNumb; double rightWidth = (max - center) / layersNumb; // Определение номера полосы if (p < center) { // Объект находится слева от центра for (int i = 1; i <= layersNumb; i++) { if (p >= center - i * leftWidth) return i - 1; } return layersNumb - 1; // Если объект находится в крайней левой полосе } else if (p > center) { // Объект находится справа от центра for (int i = 1; i <= layersNumb; i++) { if (p <= center + i * rightWidth) return i - 1; } return layersNumb - 1; // Если объект находится в крайней правой полосе } else { // Объект находится в центре return 0; } } //——————————————————————————————————————————————————————————————————————————————
Метод "DistributeParticles" класса "C_AO_AOS" отвечает за распределение частиц в пространстве поиска. Метод распределяет частицы в пространстве поиска с использованием логнормального распределения.
Для каждой частицы (в цикле по "popSize") и для каждой координаты (в цикле по "coords"):
- Генерирует позицию частицы с помощью логнормального распределения, используя заданные параметры ("cB", "rangeMin", "rangeMax", "peakPosition").
- Применяет функцию "SeInDiSp" для корректировки значения позиции частицы в пределах заданного диапазона с учетом шага.
//—————————————————————————————————————————————————————————————————————————————— // Распределение частиц в пространстве поиска void C_AO_AOS::DistributeParticles () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Используем логнормальное распределение для позиционирования частиц a [i].c [c] = u.LognormalDistribution (cB [c], rangeMin [c], rangeMax [c], peakPosition); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Метод "UpdateElectronsIDs" класса "C_AO_AOS", который обновляет идентификаторы слоев для электронов в зависимости от их координат и заданных параметров.
//—————————————————————————————————————————————————————————————————————————————— // Обновление идентификаторов слоев для каждого электрона void C_AO_AOS::UpdateElectronsIDs () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { electrons [i].layerID [c] = GetOrbitBandID (currentLayers [c], rangeMin [c], rangeMax [c], cB [c], a [i].c [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Метод "CalcLayerParams" класса "C_AO_AOS" предназначен для расчета параметров для каждого слоя атомов в системе. Основные компоненты метода:
1. Инициализация переменной: "energy" — переменная для хранения максимальной энергии, которая будет обновляться в процессе обработки электронов.
2. Цикл проходит по всем атомам (координатам) в системе. Индекс "c" указывает на текущий атом.
3. Для каждого атома вызывается метод "Init", который инициализирует параметры для максимального количества слоев, заданного переменной "maxLayers".
4. Цикл по слоям: внутренний цикл, который проходит по всем слоям, связанным с текущим атомом, "currentLayers [c]" указывает на количество слоев для атома "c".
5. Обработка электронов: еще один внутренний цикл проходит по всем электронам "e" в популяции, где проверяется, принадлежит ли текущий электрон слою "L" для атома "c".
6. Обновление параметров слоя:
- Если электрон принадлежит слою, увеличивается счетчик частиц в слое.
- Значения энергии "BEk" и состояния "BSk" обновляются для слоя в зависимости от свойств электрона.
- Если энергия электрона "a [e].f" больше текущей максимальной энергии "energy" слоя, то обновляются значения максимальной энергии "energy" и состояния "LEk".
7. Расчет средних значений для слоя: если счетчик частиц "pc" не равен нулю, вычисляются средние значения для энергии и состояния.
8. Расчет общего состояния связей: аналогично подсчитывается состояние связей для каждого атома "BS", но для популяции электронов в целом.
//—————————————————————————————————————————————————————————————————————————————— // Расчет параметров для каждого слоя void C_AO_AOS::CalcLayerParams () { double energy; // Обработка каждой координаты (атома) for (int c = 0; c < coords; c++) { atoms [c].Init (maxLayers); // Обработка каждого слоя for (int L = 0; L < currentLayers [c]; L++) { energy = -DBL_MAX; // Обработка каждого электрона for (int e = 0; e < popSize; e++) { if (electrons [e].layerID [c] == L) { atoms [c].layers [L].pc++; atoms [c].layers [L].BEk = a [e].f; atoms [c].layers [L].BSk = a [e].c [c]; if (a [e].f > energy) { energy = a [e].f; atoms [c].layers [L].LEk = a [e].c [c]; } } } // Расчет средних значений для слоя if (atoms [c].layers [L].pc != 0) { atoms [c].layers [L].BEk /= atoms [c].layers [L].pc; atoms [c].layers [L].BSk /= atoms [c].layers [L].pc; } } } // Расчет общего состояния связей ArrayInitialize (BS, 0); for (int c = 0; c < coords; c++) { for (int e = 0; e < popSize; e++) { BS [c] += a [e].c [c]; } BS [c] /= popSize; } } //——————————————————————————————————————————————————————————————————————————————
Метод "UpdateElectrons" класса "C_AO_AOS" отвечает за обновление положения электронов в системе.
1. Инициализация параметров: определяются коэффициенты скорости, веса лучшего решения, веса среднего состояния и вероятность перехода.
2. Для каждой частицы и каждой координаты:
- Генерируется случайная вероятность "φ".
- Если "φ" меньше порогового значения "PR", происходит случайное рассеивание, и новая позиция выбирается случайно, в пределах заданного диапазона.
- В противном случае:
- Получается идентификатор слоя "lID" для текущей частицы.
- Генерируются случайные значения для коэффициентов.
- Если текущая энергия частицы меньше средней энергии слоя, происходит движение в сторону глобального оптимума.
- Если нет, происходит движение в сторону локального оптимума слоя.
- В конце новая позиция ограничивается в пределах заданного диапазона с учетом шага.
//—————————————————————————————————————————————————————————————————————————————— // Обновление положения электронов void C_AO_AOS::UpdateElectrons () { double α; // коэффициент скорости double β; // коэффициент веса лучшего решения double γ; // коэффициент веса среднего состояния double φ; // вероятность перехода double newPos; // новая позиция double LE; // лучшая энергия double BSk; // состояние связи int lID; // идентификатор слоя // Обработка каждой частицы for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { φ = u.RNDprobab (); if (φ < PR) { // Случайное рассеивание newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]); } else { lID = electrons [p].layerID [c]; α = u.RNDfromCI (-1.0, 1.0); β = u.RNDprobab (); γ = u.RNDprobab (); // Если текущая энергия частицы меньше средней энергии слоя if (a [p].f < atoms [c].layers [lID].BEk) { // Движение в сторону глобального оптимума---------------------------- LE = cB [c]; newPos = a [p].c [c]+ α * (β * LE - γ * BS [c]) / currentLayers [c]; } else { // Движение в сторону локального оптимума слоя LE = atoms [c].layers [lID].LEk; BSk = atoms [c].layers [lID].BSk; newPos = a [p].c [c] + α * (β * LE - γ * BSk); } } // Ограничение новой позиции в пределах диапазона поиска с учетом шага a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Метод "Revision" класса "C_AO_AOS" предназначен для пересмотра и обновления лучших решений (или оптимальных состояний) в процессе итерации. Шаги метода:
1. Инициализация переменной "bestIndex", которая будет использоваться для хранения индекса лучшего решения.
2. Поиск лучшего решения. Условие для проверки, является ли значение функции (или оценка) текущего решения "a [i].f" больше, чем текущее значение глобального лучшего решения "fB". Если это условие истинно, то обновляется значение глобального лучшего решения на текущее значение и сохраняется индекс текущего решения, как лучший.
3. Если лучшее решение найдено, то копируются координаты лучшего решения "a[bestIndex].c" в массив "cB".
//—————————————————————————————————————————————————————————————————————————————— // Метод пересмотра лучших решений void C_AO_AOS::Revision () { int bestIndex = -1; // Поиск лучшего решения в текущей итерации for (int i = 0; i < popSize; i++) { // Обновление глобального лучшего решения if (a [i].f > fB) { fB = a [i].f; bestIndex = i; } } // Обновление лучших координат если найдено лучшее решение if (bestIndex != -1) ArrayCopy (cB, a [bestIndex].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
Результаты тестов
Запустим тестовый стенд и получим такие результаты работы AOS:
AOS|Atomic Orbital Search|50.0|5.0|1.0|0.1|0.05|
=============================
5 Hilly's; Func runs: 10000; result: 0.6521321213930082
25 Hilly's; Func runs: 10000; result: 0.39883708808831186
500 Hilly's; Func runs: 10000; result: 0.2602779698842558
=============================
5 Forest's; Func runs: 10000; result: 0.5165008091396371
25 Forest's; Func runs: 10000; result: 0.30233740723010416
500 Forest's; Func runs: 10000; result: 0.1926906342754638
=============================
5 Megacity's; Func runs: 10000; result: 0.39384615384615385
25 Megacity's; Func runs: 10000; result: 0.1892307692307692
500 Megacity's; Func runs: 10000; result: 0.09903076923077013
=============================
All score: 3.00488 (33.39%)
На визуализации работы алгоритма AOS можно заметить интересное поведение, характерные области "кучкования" на орбиталях атомов, но точность сходимости не очень высокая.
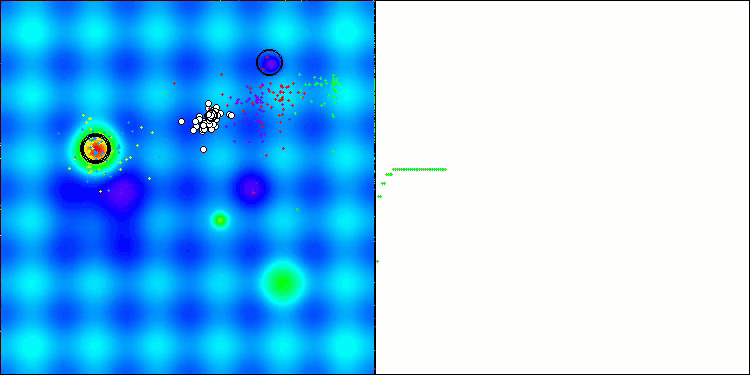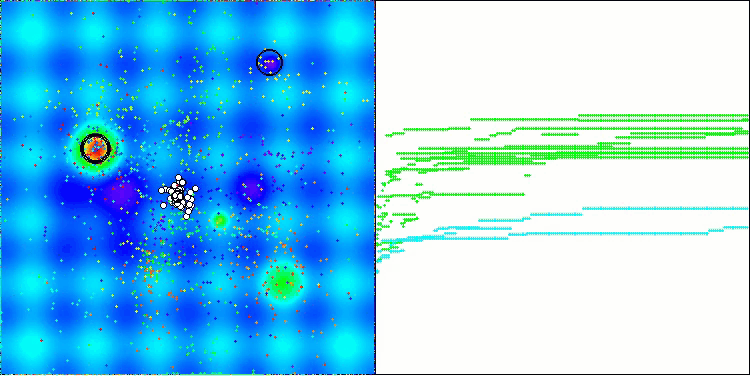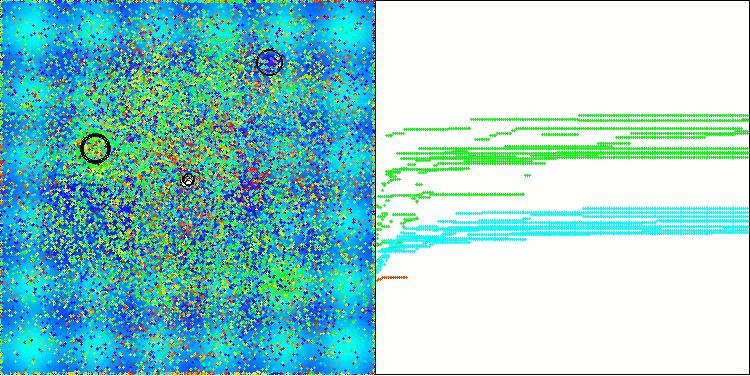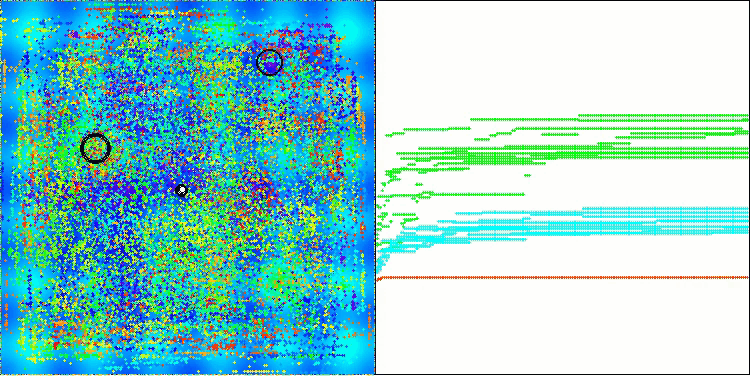
AOS на тестовой функции Hilly
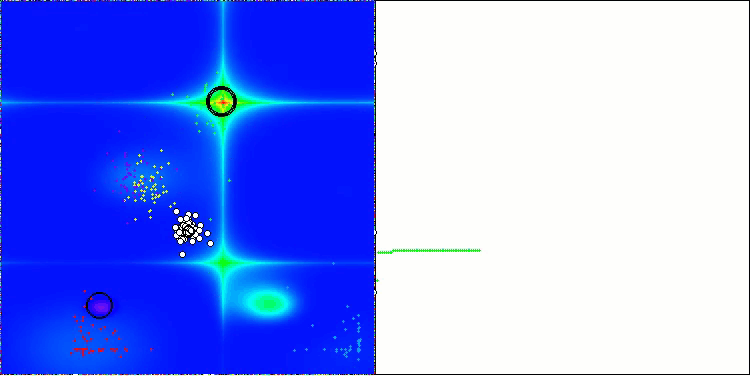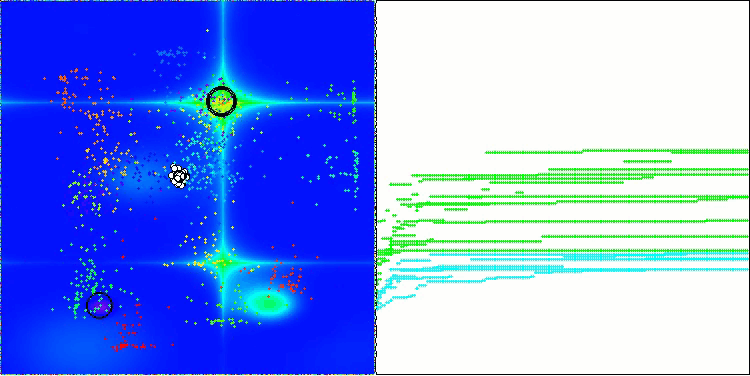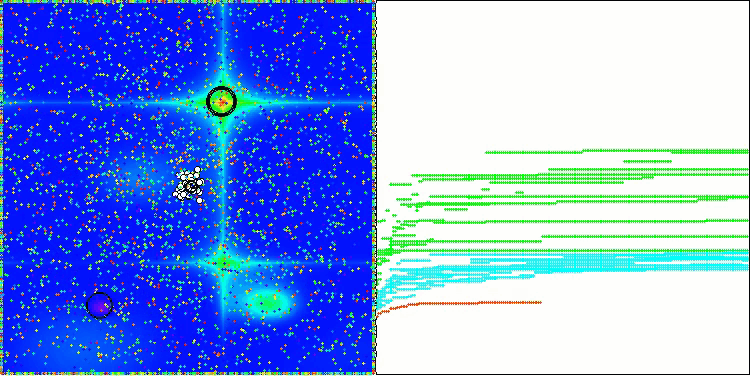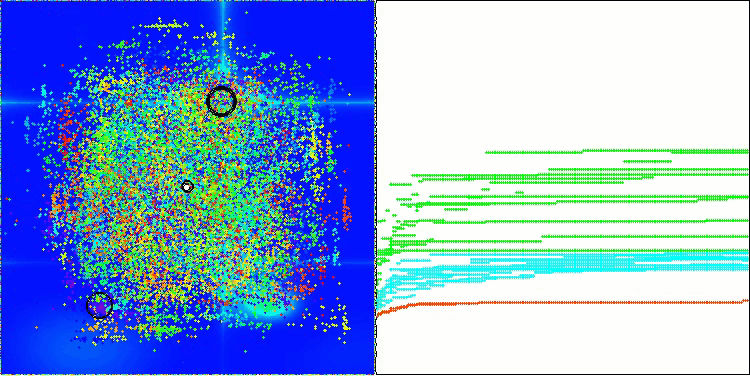
AOS на тестовой функции Forest
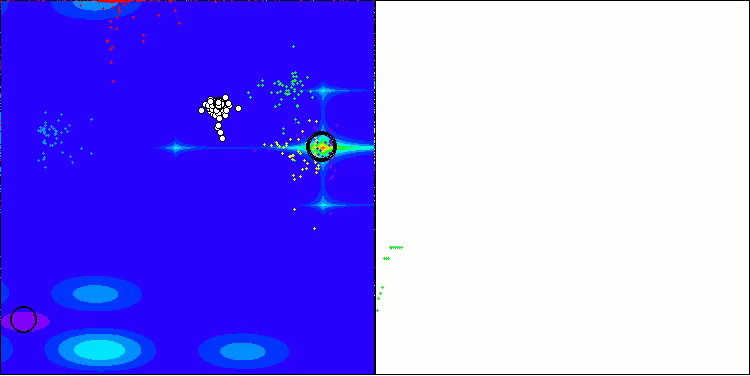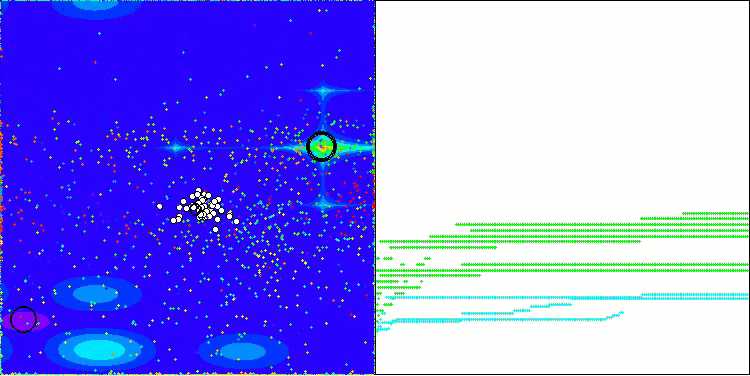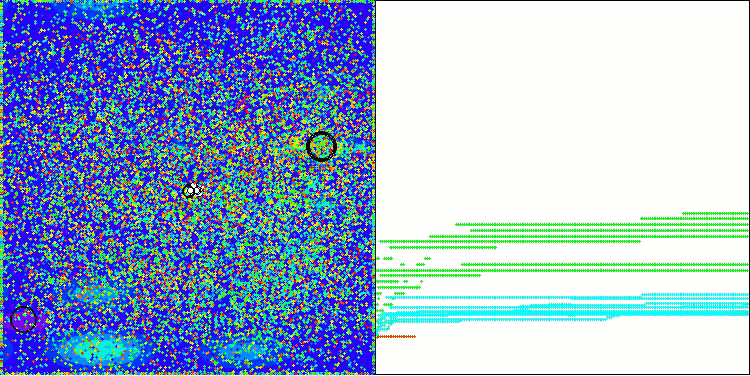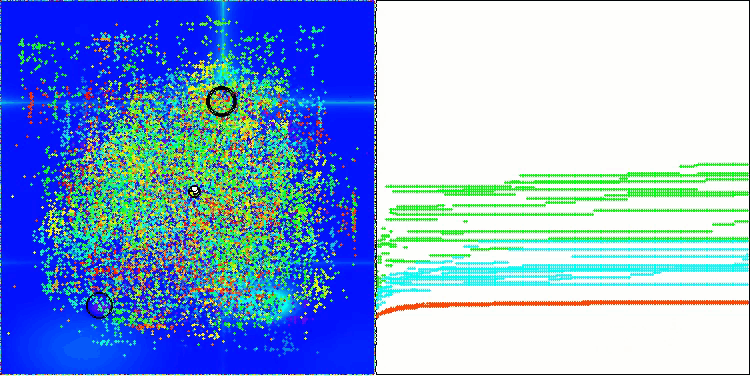
AOS на тестовой функции Megacity
По результатам тестирования алгоритм AOS разместился на 39-м месте рейтинговой таблицы.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 8 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 10 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 11 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 12 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 13 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 14 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 15 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 16 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 17 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 18 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 19 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 20 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 21 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 22 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 23 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 24 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 25 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 26 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 27 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 28 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 29 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 30 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 31 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 32 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 33 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 34 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 35 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 36 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 37 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 38 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 39 | AOS | atomic orbital search | 0,65213 | 0,39884 | 0,26028 | 1,31125 | 0,51650 | 0,30234 | 0,19269 | 1,01153 | 0,39385 | 0,18923 | 0,09903 | 0,68211 | 3,005 | 33,39 |
| 40 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 41 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 42 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 43 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 44 | AAA | algae adaptive algorithm | 0,50007 | 0,32040 | 0,25525 | 1,07572 | 0,37021 | 0,22284 | 0,16785 | 0,76089 | 0,27846 | 0,14800 | 0,09755 | 0,52402 | 2,361 | 26,23 |
| 45 | SA | simulated annealing | 0,55787 | 0,42177 | 0,31549 | 1,29513 | 0,34998 | 0,15259 | 0,05023 | 0,55280 | 0,31167 | 0,10033 | 0,02883 | 0,44083 | 2,289 | 25,43 |
Выводы
Мы рассмотрели интересный алгоритм атомарного орбитального поиска, в котором применены новаторские подходы к глобальному поиску и локальному уточнению результатов. Благодаря динамичным орбитальным слоям атомов, электроны сбалансировано перемещаются в поисках стабильного атомарного состояния. Алгоритм показывает ограниченные возможности на гладких функциях, но демонстрирует неплохие результаты при увеличении размерности задачи, даже на дискретной функции Megacity.
Этот алгоритм является примером перспективной идеи, однако его эффективность страдает из-за некоторых мелких, но значительных нюансов. В следующей статье мы рассмотрим мою модификацию AOS и проанализируем, на что на самом деле способна эта замечательная концепция орбитального поиска.
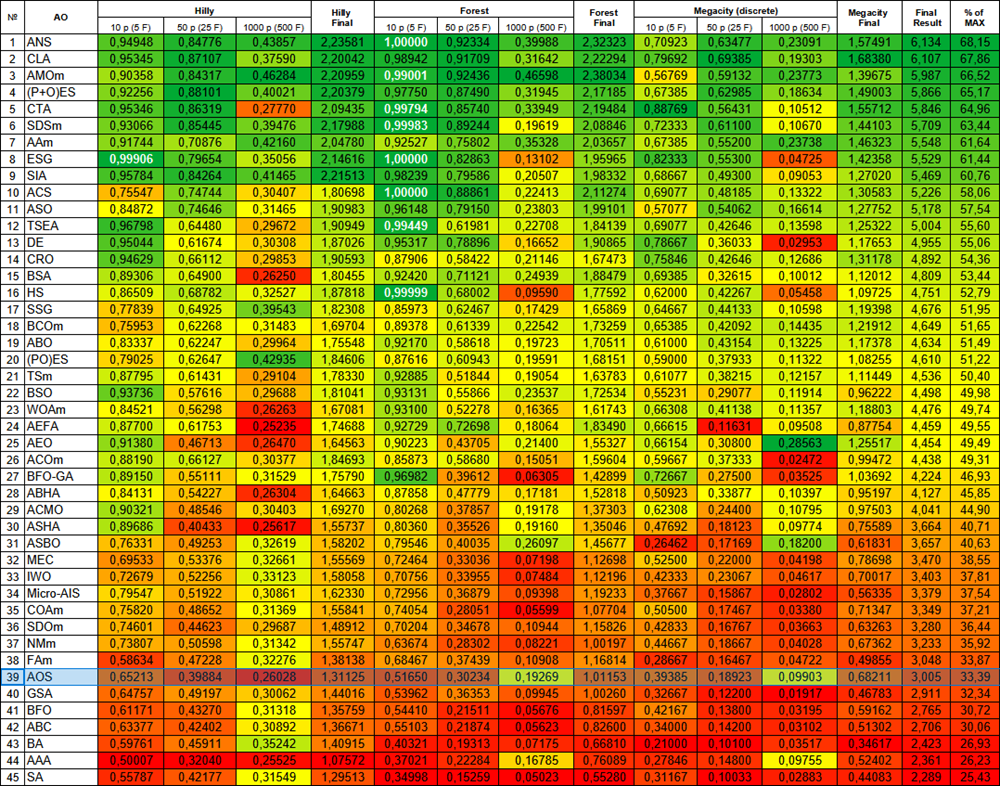
Рисунок 3. Цветовая градация алгоритмов по соответствующим тестам. Белым цветом подсвечены результаты больше или равные 0.99
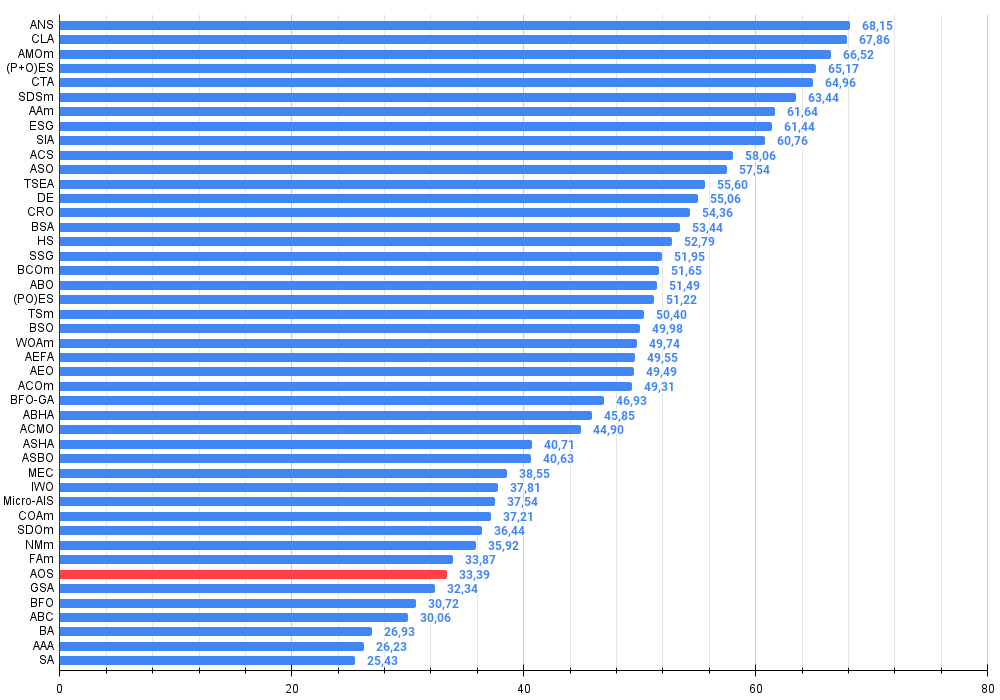
Рисунок 4. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше,
где 100 - максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма AOS:
Плюсы:
- Перспективная база для улучшений алгоритма.
- Небольшое количество внешних параметров.
Минусы:
- Медленный из-за частой генерации случайных чисел.
- Достаточно сложная реализация.
- Низкая точность сходимости.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | AO_AOS_AtomicOrbitalSearch.mqh | Включаемый файл | Класс алгоритма AOS |
| 9 | Test_AO_AOS.mq5 | Скрипт | Испытательный стенд для AOS |
 Быстрый тестер торговых стратегий на Python с использованием Numba
Быстрый тестер торговых стратегий на Python с использованием Numba
 Построение модели для ограничения диапазона сигналов по тренду (Часть 4): Настройка стиля отображения для каждой трендовой волны
Построение модели для ограничения диапазона сигналов по тренду (Часть 4): Настройка стиля отображения для каждой трендовой волны
 Торговый инструментарий MQL5 (Часть 1): Разработка EX5-библиотеки для управления позициями
Торговый инструментарий MQL5 (Часть 1): Разработка EX5-библиотеки для управления позициями
 Нейросети в трейдинге: Гиперболическая модель латентной диффузии (Окончание)
Нейросети в трейдинге: Гиперболическая модель латентной диффузии (Окончание)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования