Применение локализованного отбора признаков на Python и MQL5

Введение

При анализе финансового рынка индикаторы часто демонстрируют разную эффективность по мере изменения базовых условий. Например, изменчивая волатильность может сделать ранее надежные индикаторы неэффективными по мере изменения рыночных режимов. Эта изменчивость объясняет широкое распространение используемых трейдерами индикаторов, поскольку ни один индикатор не может стабильно работать во всех рыночных условиях. С точки зрения машинного обучения это требует гибкого метода отбора признаков, который может учитывать такое динамическое поведение.

Многие распространенные алгоритмы отбора признаков определяют приоритетность признаков, обладающих прогностической способностью во всем пространстве признаков. Этим признакам часто отдается предпочтение, даже если их взаимосвязи с целевой переменной нелинейны или находятся под влиянием других признаков. Однако это глобальное предубеждение может быть проблематичным, поскольку современные нелинейные модели могут извлекать ценную информацию из признаков с сильными локальными прогностическими возможностями или из тех, чьи связи с целевой переменной смещаются в определенных областях пространства признаков.

В настоящей статье мы исследуем алгоритм выбора признаков, представленный в статье Наргеса Арманфарда (Narges Armanfard), Джеймса П. Рейли (James P. Reilly) и Маджида Комейли (Majid Komeili) "Выбор локальных признаков для классификации данных» (“Local Feature Selection for Data Classification»). Данный метод направлен на выявление прогностических признаков, которые часто упускаются из вида традиционными методами отбора из-за своей ограниченной глобальной применимости. Начнем с общего обзора алгоритма, за которым последует его реализация на Python для создания моделей классификаторов, пригодных для экспорта в MetaTrader 5.

Локальный отбор признаков

Успешное машинное обучение зависит от выбора информативных признаков, способствующих решению проблемы. В контролируемой классификации признаки должны эффективно различать категории данных. Однако идентификация этих информативных признаков может оказаться сложной задачей, поскольку неинформативные признаки могут создавать шум и снижать эффективность работы модели. В результате отбор признаков часто является важным начальным шагом в построении прогнозных моделей.

В отличие от традиционных методов, которые ищут единое оптимальное подмножество признаков для всех данных, локальный отбор признаков (LFS) определяет оптимальные подмножества для конкретных локальных областей. Такая адаптивность может быть особенно полезна при обработке нестационарных данных. Кроме того, LFS включает в себя классификатор, учитывающий различные подмножества признаков, используемые в разных выборках. Это достигается за счет кластеризации по классам, отбирая признаки, которые минимизируют внутриклассовые расстояния и максимизируют межклассовые.

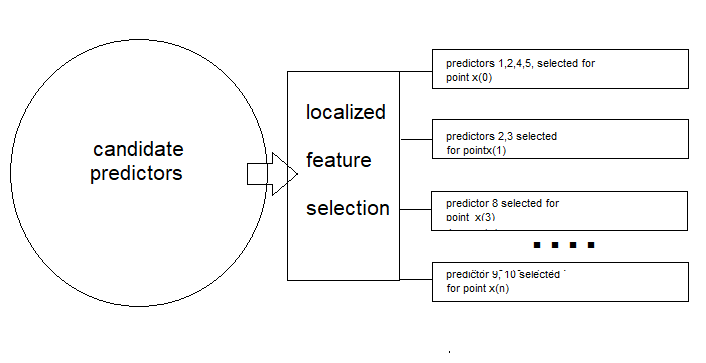
Данный подход определяет локально оптимальное подпространство признаков в перекрывающихся областях, обеспечивая представленность каждого образца во множественных пространствах признаков. Для лучшего понимания данной концепции рассмотрим сценарий, в котором телекоммуникационная компания стремится спрогнозировать отток клиентов, выявляя клиентов, которые, скорее всего, закроют свои счета. Компания собирает различные характеристики клиентов, в том числе:

• Период пребывания клиентом: Как долго клиент пребывает с компанией?
• Ежемесячный счет: Сколько клиент платит каждый месяц?
• Вес и рост клиента.
• Количество звонков, совершённых в службу поддержки клиентов: Как часто клиент обращается в службу поддержки?

Представьте, что вы выбираете двух постоянных клиентов, пользующихся услугами компании уже много лет. По каждому из описанных признаков различия между этими постоянными клиентами, скорее всего, будут минимальными, поскольку они принадлежат к одному классу. Теперь сравним это с разницей между постоянным клиентом и клиентом, отменившим подписку вскоре после регистрации. Хотя их вес и рост могут незначительно отличаться друг от друга, другие важные предикторы, вероятно, будут демонстрировать значительные различия.

Очевидно, что постоянный клиент пользуется услугами компании гораздо дольше, может с большей готовностью выбрать более дорогой пакет подписки и, скорее всего, обратится в службу поддержки при возникновении проблем, а не откажется от подписки в случае неудовлетворенности качеством услуг. В то же время такие показатели, как вес и рост, оставались бы близкими к среднестатистическим показателям по населению и не внесли бы существенного вклада в различение этих типов клиентов.

Анализ значений отдельных признаков в парах с использованием евклидова расстояния показывает, что наиболее релевантные предикторы будут иметь наибольшее межклассовое расстояние между клиентами, в то время как наименее релевантные предикторы будут демонстрировать наименьшее межклассовое расстояние. Это упрощает выбор эффективных предикторов: мы назначаем приоритет парам с низким внутриклассовым расстоянием и высоким межклассовым расстоянием.

Хотя такой подход кажется эффективным, он не учитывает локальные различия в данных. Чтобы решить эту проблему, мы должны рассмотреть, насколько различается прогностическая способность в различных областях признаков. Представьте себе набор данных с двумя классами, где один класс разделен на два различных подмножества. Диаграмма рассеяния двух признаков из этого набора данных показывает, что первое подмножество может быть хорошо отделено от класса 1 с помощью переменной x1, но не x2. И наоборот, второе подмножество может быть хорошо разделено с помощью x2, но не x1.

Если мы рассмотрим только разделение между классами, алгоритм может ошибочно выбрать как x1, так и x2, даже если только один из них действительно эффективен в каждом подмножестве. Это происходит потому, что алгоритм может назначать приоритет общему большому расстоянию между двумя подмножествами по сравнению с меньшими, более релевантными расстояниями внутри каждого подмножества. Чтобы решить эту проблему, авторы цитируемой статьи ввели схему взвешивания расстояний. Присваивая более высокие веса наблюдаемым парам, находящимся ближе друг к другу, и более низкие - парам, находящимся дальше друг от друга, алгоритм может уменьшить влияние выбросов внутри класса. При этом учитывается как принадлежность к классу, так и глобальное распределение расстояний.

Таким образом, алгоритм LFS, описанный в цитируемой статье, состоит из двух основных элементов. Первый - это процесс отбора признаков, при котором для каждого образца выбирается подмножество признаков. Второй элемент включает в себя локализованный механизм, который измеряет сходство тестовой выборки с определенным классом, используемым для целей логического вывода.

Отбор признаков

В данном разделе мы опишем процедуру обучения, используемую методом LFS, шаг за шагом, с небольшой математикой. Начнем с ожидаемой структуры обучающих данных. Реализация локализованного отбора признаков выполняется на наборе данных с N-обучающими выборками, классифицированными по Z-меткам классов и сопровождаемыми M-признаками или предикторами-кандидатами.

Обучающие данные могут быть представлены в виде матрицы X, где строки соответствуют выборкам, а столбцы представляют различные предикторы-кандидаты. Таким образом, матрица X содержит N-строки и M-столбцы. Каждая выборка обозначается как X(i), что относится к i-й строке матрицы. Метки классов хранятся в отдельном векторе-столбце Y, причем каждая метка сопоставляется с соответствующей выборкой (рядом) в матрице.

Конечная цель применения метода LFS состоит в том, чтобы определить для каждой обучающей выборки X(i) двоичный вектор F(i) размером M, указывающий какие потенциальные предикторы наиболее релевантны для определения соответствующей метки класса. Матрица F будет иметь те же размеры, что и X.

Используя евклидово расстояние, алгоритм стремится минимизировать среднее расстояние между текущей выборкой и другими выборками с такой же меткой класса, одновременно увеличивая среднее расстояние между текущей выборкой и выборками с разными метками класса. Кроме того, расстояния должны быть взвешены в пользу выборок, расположенных по соседству с текущей выборкой, для чего вводится вектор-столбец весов W. Поскольку веса (W) и двоичный вектор F(i) изначально недоступны, для оценки оптимальных значений векторов W и F(i) используется итеративная процедура.

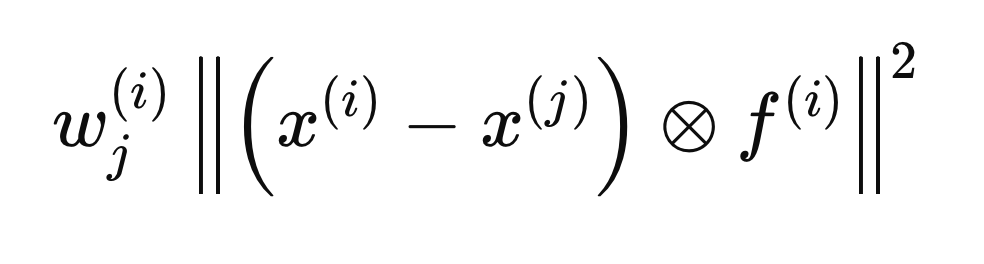
Вычисление внутриклассовых и межклассовых расстояний

Каждый шаг, описанный в следующих разделах, относится к вычислениям, выполняемым для одной выборки, X(i), для определения оптимального вектора F(i). Процесс начинается с инициализации всех записей вектора F до нуля и установки начальных весов равными 1. Далее, вычисляем внутриклассовые и межклассовые расстояния относительно X(i). Включение вектора F(i) в расчеты расстояния гарантирует, что будут учитываться только те переменные, которые считаются релевантными (равные 1). Для математического удобства евклидовы расстояния возведены в квадрат, что приводит к следующему уравнению расстояния.

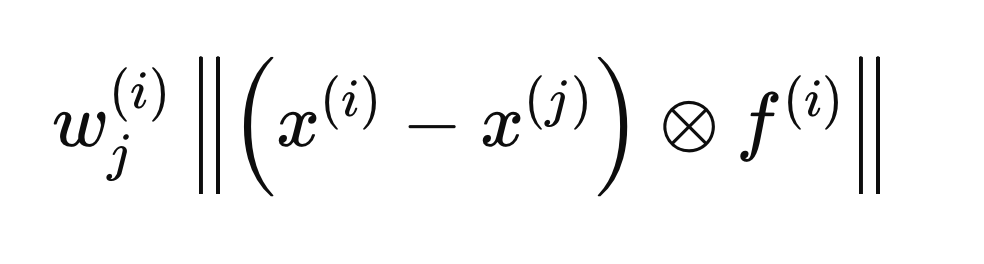
Кружок с заключенной в него буквой "x" обозначает оператора поэлементного умножения. Внутриклассовые и межклассовые расстояния вычисляются с использованием приведенной выше формулы, но с разными j элементами (строками) X. Внутриклассовое расстояние вычисляется с использованием j элементов, которые имеют ту же метку класса, что и X(i),

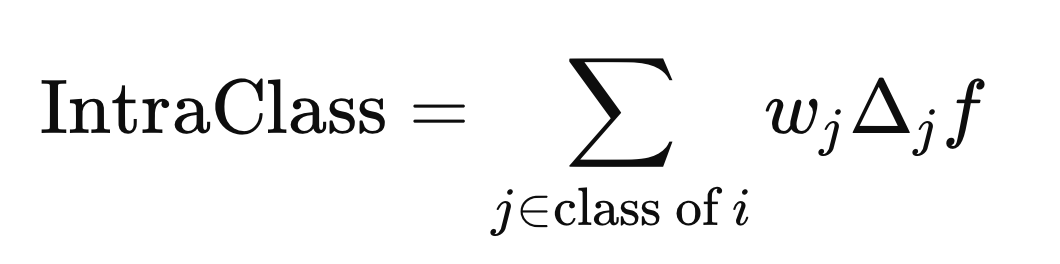
в то время как расстояние между классами вычисляется с использованием j элементов с любой меткой класса, отличной от Y(i).

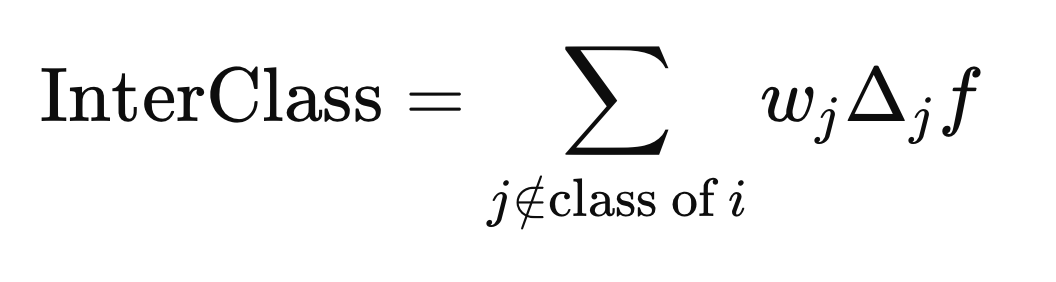
Расчет весов

Для выборки X(i) мы вычисляем вектор весов (W) длиной N, так что если X(j) находится далеко от X(i), её вес должен быть небольшим, и наоборот, если он находится рядом, вес должен быть больше. При взвешивании не следует браковать выборки только потому, что они имеют маркировку другого класса. Поскольку F(i) еще не является оптимальным, переменные, выбранные для определения базиса окрестностей, все еще неизвестны. В цитируемой статье эта проблема решается путем усреднения весов, вычисленных на предыдущих итерациях уточнения веса.

Когда вектор F включается для определения расстояния между двумя выборками, он рассматривается в метрическом пространстве, определяемом параметром F(i). Расчет оптимальных весов выполняется путем определения расстояний с точки зрения другого метрического пространства, которое мы будем называть как F(z), как указано в приведенной ниже формуле.

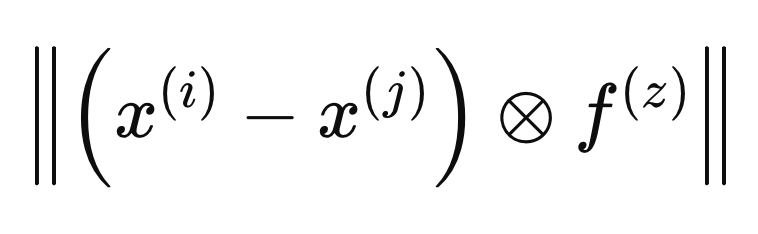
Чтобы гарантировать, что веса не будут отбраковывать выборки просто за то, что они принадлежат к другому классу, мы вычисляем минимальное расстояние между X(i) и всеми другими выборками того же класса в метрическом пространстве, определяемом F(z).

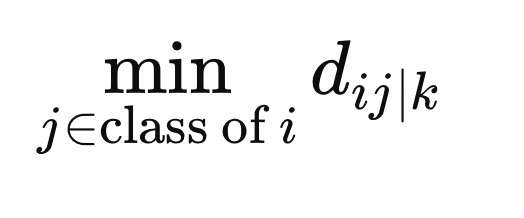
Кроме того, мы вычисляем минимальное расстояние от выборок с отличной меткой класса до X(i).

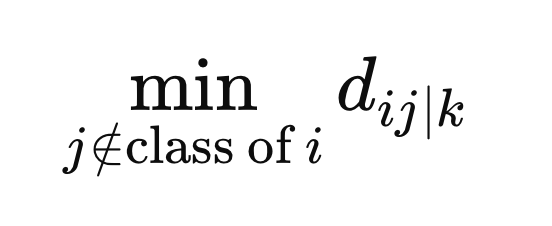
Это окончательные значения, необходимые для определения весов. Веса вычисляются как среднее значение по всем метрическим пространствам, определяемое отрицательной экспонентой разницы между расстоянием и минимальным расстоянием для конкретного метрического пространства, z.

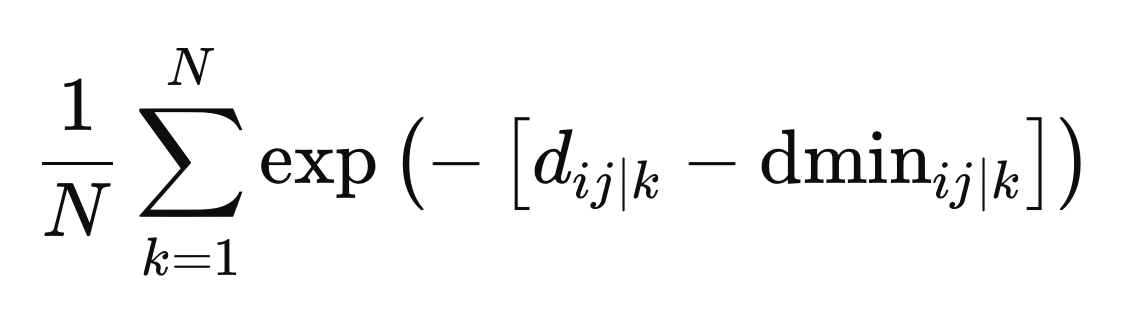
Противоречивые цели

На данном этапе мы получили оптимальные веса, что позволило нам решить задачу поиска правильного баланса между межклассовым и внутриклассовым разделением. Это предполагает согласование двух противоречащих друг другу целей: минимизация внутриклассового разделения (сделать сходство точек данных внутри одного класса максимально возможным) и максимизация межклассового разделения (сделать различные классы максимально различимыми). Идеальное достижение обеих целей с помощью одного и того же набора предикторов обычно неосуществимо.

Эффективным подходом является метод эпсилон-ограничений, который позволяет найти компромисс между этими противоречивыми целями. Этот метод работает путем сначала решения одной из задач оптимизации (обычно задачи максимизации), а затем решения задачи минимизации с дополнительным ограничением, заключающимся в том, что максимизируемая функция остается выше определенного порога.

Сначала мы максимизируем межклассовое разделение и записываем максимальное значение данной функции, обозначаемое как эпсилон (ϵ), которое представляет собой максимально возможное межклассовое разделение. Затем мы минимизируем внутриклассовое разделение для различных значений параметра β (в диапазоне от 0 до 1) с ограничением, что межклассовое разделение для минимизируемого решения должно оставаться больше или равным βϵ.

Параметр β служит компромиссным фактором, балансирующим между двумя целями: при значении β, равном 1, межклассовое разделение приобретает первостепенное значение, в то время как при значении β, равном 0, основное внимание полностью переключается на минимизацию внутриклассового разделения. На обе задачи оптимизации накладываются четыре ограничения:

• Все элементы F должны быть в диапазоне от 0 до 1 включительно.
• Сумма элементов вектора F должна быть меньше или равна заданному пользователем гиперпараметру, который определяет максимальное количество предикторов, которые могут быть активированы.
• Сумма элементов вектора F должна быть больше или равна единице, гарантируя активацию по крайней мере одного предиктора для каждой выборки.
  

Для внутриклассовой минимизации существует дополнительное ограничение, унаследованное от начальной операции максимизации: значение максимизации функции должно быть по меньшей мере равно произведению β и θ.

Используемые функции и ограничения являются линейными, что указывает на то, что задачи оптимизации являются задачами линейного программирования. Стандартные задачи линейного программирования направлены на максимизацию целевой функции с учетом ограничений, определяющих пороговые значения, которые не должны быть превышены.

Линейное программирование предполагает оптимизацию линейной целевой функции с учетом линейных ограничений. Целевая функция, обычно обозначаемая как "z", представляет собой линейную комбинацию переменных решения. Ограничения выражаются в виде линейных неравенств или равенств, ограничивающих значения переменных решения. Помимо заданных пользователем ограничений, существуют неявные ограничения на неотрицательность переменных решения и ограничения на неотрицательность правых частей неравенств.

В то время как стандартная форма предполагает неотрицательные переменные решения и неравенства "меньше или равно", эти ограничения могут быть ослаблены с помощью преобразований. Умножив обе части неравенства на -1, мы можем получить неравенства "больше или равно" и отрицательные правые части. Кроме того, неположительные коэффициенты, связанные с переменными решения, можно преобразовать в положительные коэффициенты путем создания новых переменных.

Метод внутренней точки является эффективным алгоритмом для решения задач линейного программирования, особенно при решении крупномасштабных задач оптимизации. В нашей реализации на Python будет использоваться данный метод для эффективного поиска оптимального решения. Как только сходимость будет достигнута, мы получим оптимальный вектор F(i). Однако важно отметить, что эти значения приведены не в требуемом формате (либо 1, либо 0). Это исправляется на заключительном этапе метода LFS.

Бета-тесты

Проблема с вычисленным вектором F(i) заключается в том, что он состоит из действительных значений, а не из двоичных значений. Цель процедуры LFS - определить наиболее релевантные переменные для каждой выборки, которая представлена двоичной F-матрицей, где значения равны либо 0, либо 1. Значение 0 указывает на то, что соответствующая переменная считается несущественной или пропущена.

Для преобразования действительных значений вектора F(i) в двоичные значения, мы используем метод Монте-Карло для нахождения наилучшего двоичного эквивалента. Это включает в себя повторение процесса заданное пользователем количество раз, что является ключевым гиперпараметром метода LFS. Для каждой итерации мы начинаем с двоичного вектора, где каждому предиктору-кандидату изначально присваивается значение 1, используя непрерывные значения F(i) в качестве вероятностей для каждого предиктора. Затем мы проверяем, удовлетворяет ли двоичный вектор ограничениям процедуры минимизации, и вычисляем значение его целевой функции. Двоичный вектор с минимальным значением целевой функции выбирается в качестве конечного вектора F(i).

Последующая обработка для отбора признаков

LFS независимо отбирает оптимальных предикторов-кандидатов для каждой выборки, что делает непрактичным представление единого окончательного набора данных. Чтобы решить эту проблему мы подсчитываем частоту включения каждого предиктора в оптимальные подмножества. Это позволяет пользователям устанавливать пороговое значение и определять наиболее часто встречающиеся предикторы как наиболее релевантные. Важно отметить, что значимость предиктора в рамках этого набора не подразумевает его индивидуальной ценности; его ценность может заключаться в его взаимодействии с другими предикторами.

Это ключевое преимущество LFS: его способность точно определять предикторы, которые могут быть незначительными по отдельности, но ценными в сочетании с другими. Данный этап предварительной обработки важен для современных моделей прогнозирования, которые превосходно распознают сложные взаимосвязи между переменными. Устраняя нерелевантные предикторы, LFS упрощает процесс моделирования и повышает эффективность модели.

Реализация на Python: LFSpy

В настоящем разделе мы рассмотрим практическое применение алгоритма LFS, прежде всего концентрируясь на его использовании в качестве метода выбора признаков и кратко обсудив его возможности классификации данных. Все демонстрации будут проводиться на Python с использованием пакета LFSpy, который реализует как аспекты отбора функций, так и аспекты классификации данных алгоритма LFS. Пакет доступен по адресу PyPI, где можно найти подробную информацию о нем.

Сначала установите пакет LFSpy.

pip install LFSpy

Затем импортируйте локальный класс LocalFeatureSelection из LFSpy.

from LFSpy import LocalFeatureSelection

Экземпляр LocalFeatureSelection можно создать путем вызова параметрического конструктора.

lfs = LocalFeatureSelection(alpha=8,tau=2,n_beta=20,nrrp=2000)

Конструктор поддерживает следующие опциональные параметры:

Название параметра	Тип данных	Описание
alpha	целое число	Максимальное количество выбранных предикторов из всех предикторов-кандидатов. Значение по умолчанию — 19.
gamma	двойное число	Уровень допуска, определяющий соотношение выборок с разными метками класса к выборкам с одинаковой меткой класса в пределах локальной области. Значение по умолчанию — 0,2.
tau	целое число	Количество итераций по всему набору данных (эквивалентно количеству эпох в традиционном машинном обучении). Значение по умолчанию равно 2, и рекомендуется установить это значение в виде однозначного числа, обычно не более 5.
sigma	двойное число	Управляет взвешиванием наблюдений в зависимости от их удаленности. Значение, превышающее 1, уменьшает взвешивание. Значение по умолчанию равно 1.
n_beta	целое число	Количество бета-значений, проверенных при преобразовании непрерывных векторов F в их двоичные эквиваленты.
nrrp	целое число	Количество итераций для бета-тестирования. Это значение должно быть не менее 500, увеличиваясь с размером обучающего набора данных. Значение по умолчанию равно 2000.
knn	целое число	Применяется, в частности, к задачам классификации. Определяет количество ближайших соседей для выполнения сравнения для категоризации. Значение по умолчанию составляет 1.

После инициализации экземпляра класса LFSpy мы используем метод fit(), по крайней мере, с двумя входными параметрами: двумерной матрицей обучающих выборок, состоящей из предикторов-кандидатов, и одномерным массивом соответствующих меток классов.

lfs.fit(xtrain,ytrain)

Как только модель настроена, вызов fstat возвращает матрицу включения F, состоящую из единиц и нулей для обозначения выбранных признаков. Обратите внимание, что эта матрица перемещена относительно ориентации обучающих выборок.

fstar = lfs.fstar

Метод predict() используется для классификации тестовых выборок на основе изученной модели и возвращает метки классов, соответствующие тестовым данным.

predicted_classes = lfs.predict(test_samples)

Метод score() вычисляет точность модели путем сравнения ожидаемых меток классов с известными метками. Он возвращает долю тестовых выборок, которые были корректно классифицированы.

accuracy = lfs.score(test_data,test_labels)

Примеры LFSpy

Для первой практической демонстрации мы генерируем несколько тысяч равномерно распределенных случайных величин в интервале [-1,1][-1,1]. Эти переменные упорядочены в матрицу с заданным количеством столбцов. Затем мы создаем вектор меток {0, 1}, соответствующих каждой строке, в зависимости от того, являются ли значения в двух произвольных столбцах отрицательными или положительными. Цель этой демонстрации - определить, может ли метод LFS идентифицировать наиболее релевантные предикторы в данном наборе данных. Мы оцениваем результаты путем суммирования количества раз, когда выбирался каждый предиктор (обозначается единицей) в бинарной матрице включения F. Ниже приведен код, реализующий этот тест.

import numpy as np
import pandas as pd
from LFSpy import LocalFeatureSelection
from timeit import default_timer as timer

#number of random numbers to generate
datalen = 500 

#number of features the dataset will have
datavars = 5

#set random number seed
rng_seed = 125
rng = np.random.default_rng(rng_seed)

#generate the numbers
data = rng.uniform(-1.0,1.0,size=datalen)

#shape our dataset
data = data.reshape([datalen//datavars,datavars])

#set up container for class labels
class_labels = np.zeros(shape=data.shape[0],dtype=np.uint8)

#set the class labels
for i in range(data.shape[0]):
    class_labels[i] = 1 if (data[i,1] > 0.0 and data[i,2] > 0.0) or (data[i,1] < 0.0 and data[i,2] < 0.0) else 0

#partition our training data
xtrain = data
ytrain = class_labels

#initialize the LFS object
lfs = LocalFeatureSelection(rr_seed=rng_seed,alpha=8,tau=2,n_beta=20,nrrp=2000)

#start timer
start = timer()

#train the model
lfs.fit(xtrain,ytrain)

#output training duration
print("Training done in ", timer()-start , " seconds. ")

#get the inclusion matrix
fstar = lfs.fstar

#add up all ones for each row of the inclusion matrix
ibins = fstar.sum(axis=1)

#calculate the percent of times a candidate was selected
original_crits = 100.0 * ibins.astype(np.float64)/np.float64(ytrain.shape[0])

#output the results
print("------------------------------> Percent of times selected <------------------------------" )
for i in range(original_crits.shape[0]):
   print( f" Variable at column {i}, selected {original_crits[i]} %")

Результат выполнения LFSdemo.py

Training done in  45.84896759999992  seconds. 
Python  ------------------------------> Percent of times selected <------------------------------
Python   Variable at column 0, selected 19.0 %
Python   Variable at column 1, selected 81.0 %
Python   Variable at column 2, selected 87.0 %
Python   Variable at column 3, selected 20.0 %
Python   Variable at column 4, selected 18.0 %

Интересно, что одна из соответствующих переменных выбиралась несколько чаще, чем другая, несмотря на их идентичную роль в прогнозировании класса. Это говорит о том, что на процесс отбора могут влиять тонкие нюансы в данных. Очевидно, что обе переменные последовательно выбирались чаще, чем нерелевантные предикторы, что указывает на их значимость при определении класса. Относительно медленное выполнение алгоритма, вероятно, связано с его однопоточным характером, что потенциально снижает его производительность при работе с большими наборами данных.

LFS для классификации данных

Учитывая локальный характер LFS, построение классификатора на его основе требует больше усилий по сравнению с традиционными глобально ориентированными методами отбора признаков. В упомянутом документе обсуждается предлагаемая архитектура классификатора, в которую мы здесь не будем углубляться. Заинтересованным читателям рекомендуется ознакомиться с цитируемой статьей для получения более подробной информации. В настоящем разделе сосредоточимся на реализации.

Метод predict() класса LocalFeatureSelection оценивает сходство классов. Он принимает тестовые данные, соответствующие структуре обучающих данных, и возвращает прогнозные метки классов на основе паттернов, изученных обученной моделью LFS. В следующей демонстрации кода мы расширим предыдущий скрипт для создания модели классификатора LFS, экспортируем ее в формат JSON, загрузим с помощью скрипта MQL5 и классифицируем набор данных, не являющийся выборкой. Код, используемый для экспорта модели LFS, содержится в JsonModel.py. Этот файл определяет функцию lfspy2json(), которая преобразует состояние и параметры модели LocalFeatureSelection в файл JSON. Это позволяет сохранять модель в формате, который легко читается и используется в MQL5-коде, что облегчает интеграцию с MetaTrader 5. Полный код можно увидеть ниже.

# Copyright 2024, MetaQuotes Ltd.
# https://www.mql5.com

from LFSpy import LocalFeatureSelection
import json 

MQL5_FILES_FOLDER = "MQL5\\FILES"
MQL5_COMMON_FOLDER = "FILES"

def lfspy2json(lfs_model:LocalFeatureSelection, filename:str):
    """
    function export a LFSpy model to json format 
    readable from MQL5 code.
    
    param: lfs_model should be an instance of LocalFeatureSelection
    param: filename or path to file where lfs_model
    parameters will be written to
    
    """
    if not isinstance(lfs_model,LocalFeatureSelection):
        raise TypeError(f'invalid type supplied, "lfs_model" should be an instance of LocalFeatureSelection')
    if len(filename) < 1 or not isinstance(filename,str):
        raise TypeError(f'invalid filename supplied')
    jm  = {
            "alpha":lfs_model.alpha,
            "gamma":lfs_model.gamma,
            "tau":lfs_model.tau,
            "sigma":lfs_model.sigma, 
            "n_beta":lfs_model.n_beta,
            "nrrp":lfs_model.nrrp,
            "knn":lfs_model.knn,
            "rr_seed":lfs_model.rr_seed,
            "num_observations":lfs_model.training_data.shape[1],
            "num_features":lfs_model.training_data.shape[0],
            "training_data":lfs_model.training_data.tolist(),
            "training_labels":lfs_model.training_labels.tolist(),
            "fstar":lfs_model.fstar.tolist()
          }
          
    
    with open(filename,'w') as file:
        json.dump(jm,file,indent=None,separators=(',', ':')) 
    return 

Функция принимает признак LocalFeatureSelection и имя файла в качестве входных данных. Она сериализует параметры модели в виде объекта JSON и сохраняет их под указанным именем файла. Модуль также определяет две константы, MQL5_FILES_FOLDER и MQL5_COMMON_FOLDER, которые представляют пути в каталогах к доступным папкам в стандартной установке MetaTrader 5. Это только одна часть решения для интеграции с MetaTrader 5. Другая часть реализована в MQL5-коде, который представлен в lfspy.mqh. Этот включенный файл содержит определение класса Clfspy, который облегчает загрузку модели LFS, сохраненной в формате JSON, для целей логического вывода. Полный код представлен ниже.

//+------------------------------------------------------------------+
//|                                                        lfspy.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<JAson.mqh>
#include<Files/FileTxt.mqh>
#include<np.mqh>
//+------------------------------------------------------------------+
//|structure of model parameters                                     |
//+------------------------------------------------------------------+
struct LFS_PARAMS
  {
   int               alpha;
   int               tau;
   int               n_beta;
   int               nrrp;
   int               knn;
   int               rr_seed;
   int               sigma;
   ulong             num_features;
   double            gamma;
  };
//+------------------------------------------------------------------+
//|  class encapsulates LFSpy model                                  |
//+------------------------------------------------------------------+
class Clfspy
  {
private:
   bool              loaded;
   LFS_PARAMS        model_params;
   matrix train_data,
          fstar;
   vector            train_labels;
   //+------------------------------------------------------------------+
   //|  helper function for parsing model from file                     |
   //+------------------------------------------------------------------+
   bool              fromJSON(CJAVal &jsonmodel)
     {

      model_params.alpha = (int)jsonmodel["alpha"].ToInt();
      model_params.tau = (int)jsonmodel["tau"].ToInt();
      model_params.sigma = (int)jsonmodel["sigma"].ToInt();
      model_params.n_beta = (int)jsonmodel["n_beta"].ToInt();
      model_params.nrrp = (int)jsonmodel["nrrp"].ToInt();
      model_params.knn = (int)jsonmodel["knn"].ToInt();
      model_params.rr_seed = (int)jsonmodel["rr_seed"].ToInt();
      model_params.gamma = jsonmodel["gamma"].ToDbl();

      ulong observations = (ulong)jsonmodel["num_observations"].ToInt();
      model_params.num_features = (ulong)jsonmodel["num_features"].ToInt();

      if(!train_data.Resize(model_params.num_features,observations) || !train_labels.Resize(observations) ||
         !fstar.Resize(model_params.num_features,observations))
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }


      for(int i=0; i<int(model_params.num_features); i++)
        {
         for(int j = 0; j<int(observations); j++)
           {
            if(i==0)
               train_labels[j] = jsonmodel["training_labels"][j].ToDbl();
            train_data[i][j] = jsonmodel["training_data"][i][j].ToDbl();
            fstar[i][j] = jsonmodel["fstar"][i][j].ToDbl();
           }
        }

      return true;
     }
   //+------------------------------------------------------------------+
   //| helper classification function                                   |
   //+------------------------------------------------------------------+
   matrix            classification(matrix &testing_data)
     {
      int N = int(train_labels.Size());
      int H = int(testing_data.Cols());

      matrix out(H,2);

      for(int i = 0; i<H; i++)
        {
         vector column = testing_data.Col(i);
         vector result = class_sim(column,train_data,train_labels,fstar,model_params.gamma,model_params.knn);
         if(!out.Row(result,i))
           {
            Print(__FUNCTION__, " row insertion failure ", GetLastError());
            return matrix::Zeros(1,1);
           }
        }

      return out;
     }
   //+------------------------------------------------------------------+
   //| internal feature classification function                         |
   //+------------------------------------------------------------------+
   vector            class_sim(vector &test,matrix &patterns,vector& targets, matrix &f_star, double gamma, int knn)
     {
      int N = int(targets.Size());
      int n_nt_cls_1 = (int)targets.Sum();
      int n_nt_cls_2 = N - n_nt_cls_1;
      int M = int(patterns.Rows());
      int NC1 = 0;
      int NC2 = 0;
      vector S = vector::Zeros(N);

      S.Fill(double("inf"));

      vector NoNNC1knn = vector::Zeros(N);
      vector NoNNC2knn = vector::Zeros(N);
      vector NoNNC1 = vector::Zeros(N);
      vector NoNNC2 = vector::Zeros(N);
      vector radious = vector::Zeros(N);
      double r = 0;
      int k = 0;
      for(int i = 0; i<N; i++)
        {
         vector fs = f_star.Col(i);
         matrix xpatterns = patterns * np::repeat_vector_as_rows_cols(fs,patterns.Cols(),false);
         vector testpr = test * fs;
         vector mtestpr = (-1.0 * testpr);
         matrix testprmat = np::repeat_vector_as_rows_cols(mtestpr,xpatterns.Cols(),false);
         vector dist = MathAbs(sqrt((pow(testprmat + xpatterns,2.0)).Sum(0)));
         vector min1 = dist;
         np::sort(min1);
         vector min_uniq = np::unique(min1);
         int m = -1;
         int no_nereser = 0;
         vector NN(dist.Size());
         while(no_nereser<int(knn))
           {
            m+=1;
            double a1  = min_uniq[m];
            for(ulong j = 0; j<dist.Size(); j++)
               NN[j]=(dist[j]<=a1)?1.0:0.0;
            no_nereser = (int)NN.Sum();
           }
         vector bitNN = np::bitwiseAnd(NN,targets);
         vector Not = np::bitwiseNot(targets);
         NoNNC1knn[i] = bitNN.Sum();
         bitNN = np::bitwiseAnd(NN,Not);
         NoNNC2knn[i] = bitNN.Sum();
         vector A(fs.Size());
         for(ulong v =0; v<A.Size(); v++)
            A[v] = (fs[v]==0.0)?1.0:0.0;
         vector f1(patterns.Cols());
         vector f2(patterns.Cols());
         if(A.Sum()<double(M))
           {
            for(ulong v =0; v<A.Size(); v++)
               A[v] = (A[v]==1.0)?0.0:1.0;
            matrix amask = matrix::Ones(patterns.Rows(), patterns.Cols());
            amask *= np::repeat_vector_as_rows_cols(A,patterns.Cols(),false);
            matrix patternsp = patterns*amask;
            vector testp = test*(amask.Col(0));
            vector testa = patternsp.Col(i) - testp;
            vector col = patternsp.Col(i);
            matrix colmat = np::repeat_vector_as_rows_cols(col,patternsp.Cols(),false);
            double Dist_test = MathAbs(sqrt((pow(col - testp,2.0)).Sum()));
            vector Dist_pat  = MathAbs(sqrt((pow(patternsp - colmat,2.0)).Sum(0)));
            vector eerep = Dist_pat;
            np::sort(eerep);
            int remove = 0;
            if(targets[i] == 1.0)
              {
               vector unq = np::unique(eerep);
               k = -1;
               NC1+=1;
               if(remove!=1)
                 {
                  int Next = 1;
                  while(Next == 1)
                    {
                     k+=1;
                     r = unq[k];
                     for(ulong j = 0; j<Dist_pat.Size(); j++)
                       {
                        if(Dist_pat[j] == r)
                           f1[j] = 1.0;
                        else
                           f1[j] = 0.0;
                        if(Dist_pat[j]<=r)
                           f2[j] = 1.0;
                        else
                           f2[j] = 0.0;
                       }
                     vector f2t = np::bitwiseAnd(f2,targets);
                     vector tn = np::bitwiseNot(targets);
                     vector f2tn = np::bitwiseAnd(f2,tn);
                     double nocls1clst = f2t.Sum() - 1.0;
                     double nocls2clst = f2tn.Sum();
                     if(gamma *(nocls1clst/double(n_nt_cls_1-1)) < (nocls2clst/(double(n_nt_cls_2))))
                       {
                        Next = 0 ;
                        if((k-1) == 0)
                           r = unq[k];
                        else
                           r = 0.5 * (unq[k-1] + unq[k]);
                        if(r==0.0)
                           r = pow(10.0,-6.0);
                        r = 1.0*r;
                        for(ulong j = 0; j<Dist_pat.Size(); j++)
                          {
                           if(Dist_pat[j]<=r)
                              f2[j] = 1.0;
                           else
                              f2[j] = 0.0;
                          }
                        f2t = np::bitwiseAnd(f2,targets);
                        f2tn = np::bitwiseAnd(f2,tn);
                        nocls1clst = f2t.Sum() - 1.0;
                        nocls2clst = f2tn.Sum();
                       }
                    }
                  if(Dist_test<r)
                    {
                     patternsp = patterns * np::repeat_vector_as_rows_cols(fs,patterns.Cols(),false);
                     testp = test * fs;
                     dist = MathAbs(sqrt((pow(patternsp - np::repeat_vector_as_rows_cols(testp,patternsp.Cols(),false),2.0)).Sum(0)));
                     min1 = dist;
                     np::sort(min1);
                     min_uniq = np::unique(min1);
                     m = -1;
                     no_nereser = 0;
                     while(no_nereser<int(knn))
                       {
                        m+=1;
                        double a1  = min_uniq[m];
                        for(ulong j = 0; j<dist.Size(); j++)
                           NN[j]=(dist[j]<a1)?1.0:0.0;
                        no_nereser = (int)NN.Sum();
                       }
                     bitNN = np::bitwiseAnd(NN,targets);
                     Not = np::bitwiseNot(targets);
                     NoNNC1[i] = bitNN.Sum();
                     bitNN = np::bitwiseAnd(NN,Not);
                     NoNNC2[i] = bitNN.Sum();
                     if(NoNNC1[i]>NoNNC2[i])
                        S[i] = 1.0;
                    }
                 }
              }
            if(targets[i] == 0.0)
              {
               vector unq = np::unique(eerep);
               k=-1;
               NC2+=1;
               int Next;
               if(remove!=1)
                 {
                  Next =1;
                  while(Next==1)
                    {
                     k+=1;
                     r = unq[k];
                     for(ulong j = 0; j<Dist_pat.Size(); j++)
                       {
                        if(Dist_pat[j] == r)
                           f1[j] = 1.0;
                        else
                           f1[j] = 0.0;
                        if(Dist_pat[j]<=r)
                           f2[j] = 1.0;
                        else
                           f2[j] = 0.0;
                       }
                     vector f2t = np::bitwiseAnd(f2,targets);
                     vector tn = np::bitwiseNot(targets);
                     vector f2tn = np::bitwiseAnd(f2,tn);
                     double nocls1clst = f2t.Sum() ;
                     double nocls2clst = f2tn.Sum() -1.0;
                     if(gamma *(nocls2clst/double(n_nt_cls_2-1)) < (nocls1clst/(double(n_nt_cls_1))))
                       {
                        Next = 0 ;
                        if((k-1) == 0)
                           r = unq[k];
                        else
                           r = 0.5 * (unq[k-1] + unq[k]);
                        if(r==0.0)
                           r = pow(10.0,-6.0);
                        r = 1.0*r;
                        for(ulong j = 0; j<Dist_pat.Size(); j++)
                          {
                           if(Dist_pat[j]<=r)
                              f2[j] = 1.0;
                           else
                              f2[j] = 0.0;
                          }
                        f2t = np::bitwiseAnd(f2,targets);
                        f2tn = np::bitwiseAnd(f2,tn);
                        nocls1clst = f2t.Sum();
                        nocls2clst = f2tn.Sum() -1.0;
                       }
                    }
                  if(Dist_test<r)
                    {
                     patternsp = patterns * np::repeat_vector_as_rows_cols(fs,patterns.Cols(),false);
                     testp = test * fs;
                     dist = MathAbs(sqrt((pow(patternsp - np::repeat_vector_as_rows_cols(testp,patternsp.Cols(),false),2.0)).Sum(0)));
                     min1 = dist;
                     np::sort(min1);
                     min_uniq = np::unique(min1);
                     m = -1;
                     no_nereser = 0;
                     while(no_nereser<int(knn))
                       {
                        m+=1;
                        double a1  = min_uniq[m];
                        for(ulong j = 0; j<dist.Size(); j++)
                           NN[j]=(dist[j]<a1)?1.0:0.0;
                        no_nereser = (int)NN.Sum();
                       }
                     bitNN = np::bitwiseAnd(NN,targets);
                     Not = np::bitwiseNot(targets);
                     NoNNC1[i] = bitNN.Sum();
                     bitNN = np::bitwiseAnd(NN,Not);
                     NoNNC2[i] = bitNN.Sum();
                     if(NoNNC2[i]>NoNNC1[i])
                        S[i] = 1.0;
                    }
                 }
              }
           }
         radious[i] = r;
        }
      vector q1 = vector::Zeros(N);
      vector q2 = vector::Zeros(N);
      for(int i = 0; i<N; i++)
        {
         if(NoNNC1[i] > NoNNC2knn[i])
            q1[i] = 1.0;
         if(NoNNC2[i] > NoNNC1knn[i])
            q2[i] = 1.0;
        }

      vector ntargs = np::bitwiseNot(targets);
      vector c1 = np::bitwiseAnd(q1,targets);
      vector c2 = np::bitwiseAnd(q2,ntargs);

      double sc1 = c1.Sum()/NC1;
      double sc2 = c2.Sum()/NC2;

      if(sc1==0.0 && sc2==0.0)
        {
         q1.Fill(0.0);
         q2.Fill(0.0);

         for(int i = 0; i<N; i++)
           {
            if(NoNNC1knn[i] > NoNNC2knn[i])
               q1[i] = 1.0;
            if(NoNNC2knn[i] > NoNNC1knn[i])
               q2[i] = 1.0;

            if(!targets[i])
               ntargs[i] = 1.0;
            else
               ntargs[i] = 0.0;
           }

         c1 = np::bitwiseAnd(q1,targets);
         c2 = np::bitwiseAnd(q2,ntargs);

         sc1 = c1.Sum()/NC1;
         sc2 = c2.Sum()/NC2;
        }

      vector out(2);

      out[0] = sc1;
      out[1] = sc2;

      return out;
     }
public:
   //+------------------------------------------------------------------+
   //|    constructor                                                   |
   //+------------------------------------------------------------------+
                     Clfspy(void)
     {
      loaded = false;
     }
   //+------------------------------------------------------------------+
   //|  destructor                                                      |
   //+------------------------------------------------------------------+
                    ~Clfspy(void)
     {
     }
   //+------------------------------------------------------------------+
   //|  load a LFSpy trained model from file                            |
   //+------------------------------------------------------------------+
   bool              load(const string file_name, bool FILE_IN_COMMON_DIRECTORY = false)
     {
      loaded = false;
      CFileTxt modelFile;
      CJAVal js;
      ResetLastError();
      if(modelFile.Open(file_name,FILE_IN_COMMON_DIRECTORY?FILE_READ|FILE_COMMON:FILE_READ,0)==INVALID_HANDLE)
        {
         Print(__FUNCTION__," failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         if(!js.Deserialize(modelFile.ReadString()))
           {
            Print("failed to read from ",file_name,".Error -",::GetLastError());
            return false;
           }
         loaded = fromJSON(js);
        }
      return loaded;
     }
   //+------------------------------------------------------------------+
   //|   make a prediction based specific inputs                        |
   //+------------------------------------------------------------------+
   vector            predict(matrix &inputs)
     {
      if(!loaded)
        {
         Print(__FUNCTION__, " No model available, Load a model first before calling this method ");
         return vector::Zeros(1);
        }

      if(inputs.Cols()!=train_data.Rows())
        {
         Print(__FUNCTION__, " input matrix does np::bitwiseNot match with shape of expected model inputs (columns)");
         return vector::Zeros(1);
        }

      matrix testdata = inputs.Transpose();

      matrix probs = classification(testdata);
      vector classes = vector::Zeros(probs.Rows());

      for(ulong i = 0; i<classes.Size(); i++)
         if(probs[i][0] > probs[i][1])
            classes[i] = 1.0;

      return classes;

     }
   //+------------------------------------------------------------------+
   //| get the parameters of the loaded model                           |
   //+------------------------------------------------------------------+
   LFS_PARAMS        getmodelparams(void)
     {
      return model_params;
     }


  };
//+------------------------------------------------------------------+

В этом классе есть два основных метода, которые должны понимать пользователи:

• Метод load() принимает имя файла в качестве входных данных, которое должно указывать на экспортированную модель LFS.
• Метод predict() принимает матрицу с требуемым количеством столбцов и возвращает вектор меток классов, соответствующий количеству рядов во входной матрице.
  

Посмотрим как все это работает на практике. Начинаем с кода на Python. Файл LFSmodelExportDemo.py подготавливает наборы данных в выборке и за ее пределами с помощью случайно сгенерированных чисел. Данные за пределами выборки сохраняются в виде CSV-файла. Модель LFS обучается с использованием данных в выборке, затем сериализуется и сохраняется в формате JSON. Мы тестируем модель на данных вне выборки и записываем результаты, чтобы позже сравнить их с аналогичным тестом, проведенным в MetaTrader 5. Ниже представлен код на Python.

# Copyright 2024, MetaQuotes Ltd.
# https://www.mql5.com
# imports
import MetaTrader5 as mt5
import numpy as np
import pandas as pd
from JsonModel import lfspy2json, LocalFeatureSelection, MQL5_COMMON_FOLDER, MQL5_FILES_FOLDER
from os import path
from sklearn.metrics import accuracy_score, classification_report

#initialize MT5 terminal
if not mt5.initialize():
    print("MT5 initialization failed ")
    mt5.shutdown()
    exit() # stop the script if mt5 not initialized
  
#we want to get the path to the MT5 file sandbox
#initialize TerminalInfo instance    
terminal_info = mt5.terminal_info()

#model file name
filename = "lfsmodel.json"

#build the full path
modelfilepath = path.join(terminal_info.data_path,MQL5_FILES_FOLDER,filename)

#number of random numbers to generate
datalen = 1000

#number of features the dataset will have
datavars = 5

#set random number seed
rng_seed = 125
rng = np.random.default_rng(rng_seed)

#generate the numbers
data = rng.uniform(-1.0,1.0,size=datalen)

#shape our dataset
data = data.reshape([datalen//datavars,datavars])

#set up container for class labels
class_labels = np.zeros(shape=data.shape[0],dtype=np.uint8)

#set the class labels
for i in range(data.shape[0]):
    class_labels[i] = 1 if (data[i,1] > 0.0 and data[i,2] > 0.0) or (data[i,1] < 0.0 and data[i,2] < 0.0) else 0

#partition our data
train_size = 100
xtrain = data[:train_size,:]
ytrain = class_labels[:train_size]

#load testing data (out of sample)
test_data = data[train_size:,:]
test_labels = class_labels[train_size:]

#here we prepare the out of sample data for export using pandas
#the data will be exported in a single csv file
colnames = [ f"var_{str(col+1)}" for col in range(test_data.shape[1])]
testdata = pd.DataFrame(test_data,columns=colnames)

#the last column will be the target labels
testdata["c_labels"]=test_labels

#display first 5 samples
print("Out of sample dataframe head \n", testdata.head())
#display last 5 samples
print("Out of sample dataframe tail \n", testdata.tail())

#build the full path of the csv file
testdatafilepath=path.join(terminal_info.data_path,MQL5_FILES_FOLDER,"testdata.csv")

#try save the file
try:
    testdata.to_csv(testdatafilepath)
except Exception as e:
    print(" Error saving iris test data ")
    print(e) 
else:
    print(" test data successfully saved to csv file ")  

#initialize the LFS object
lfs = LocalFeatureSelection(rr_seed=rng_seed,alpha=8,tau=2,n_beta=20,nrrp=2000)

#train the model
lfs.fit(xtrain,ytrain)

#get the inclusion matrix
fstar = lfs.fstar

#add up all ones for each row of the inclusion matrix
bins = fstar.sum(axis=1)

#calculate the percent of times a candidate was selected
percents = 100.0 * bins.astype(np.float64)/np.float64(ytrain.shape[0])
index = np.argsort(percents)[::-1]

#output the results
print("------------------------------> Percent of times selected <------------------------------" )
for i in range(percents.shape[0]):
   print(f" Variable  {colnames[index[i]]}, selected {percents[index[i]]} %")


#conduct out of sample test of trained model
accuracy = lfs.score(test_data,test_labels)
print(f" Out of sample accuracy is {accuracy*100.0} %")


#export the model
try:
    lfspy2json(lfs,modelfilepath)
except Exception as e:
    print(" Error saving lfs model ")
    print(e)
else:
   print("lfs model saved to \n ", modelfilepath)

Далее мы переключаем внимание на скрипт MetaTrader 5, LFSmodelImportDemo.mq5. Здесь мы считываем данные вне выборки, полученные с помощью скрипта на Python, и загружаем обученную модель. Затем набор данных вне выборки тестируется, а результаты сравниваются с результатами, полученными в результате тестирования на Python. Код на MQL5 представлен ниже.

//+------------------------------------------------------------------+
//|                                           LFSmodelImportDemo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<lfspy.mqh>
//script inputs
input string OutOfSampleDataFile = "testdata.csv";
input bool   OutOfSampleDataInCommonFolder = false;
input string LFSModelFileName = "lfsmodel.json";
input bool   LFSModelInCommonFolder = false;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   matrix testdata = np::readcsv(OutOfSampleDataFile,OutOfSampleDataInCommonFolder);
   
   if(testdata.Rows()<1)
    {
     Print(" failed to read csv file ");
     return;
    }
    
   
   vector testlabels = testdata.Col(testdata.Cols()-1);
   testdata = np::sliceMatrixCols(testdata,1,testdata.Cols()-1);
   
  
   Clfspy lfsmodel;
   
   if(!lfsmodel.load(LFSModelFileName,LFSModelInCommonFolder))
    {
     Print(" failed to load the iris lfs model ");
     return;
    }
    
   vector y_pred = lfsmodel.predict(testdata);
   
   vector check = MathAbs(testlabels-y_pred);
   
   Print("Accuracy is " , (1.0 - (check.Sum()/double(check.Size()))) * 100.0, " %");
  }
//+------------------------------------------------------------------+

Результат выполнения скрипта на Python LFSmodelExportDemo.py.

Python  Out of sample dataframe head 
Python         var_1     var_2     var_3     var_4     var_5  c_labels
Python  0  0.337773 -0.210114 -0.706754  0.940513  0.434695         1
Python  1 -0.009701 -0.119561 -0.904122 -0.409922  0.619245         1
Python  2  0.442703  0.295811  0.692888  0.618308  0.682659         1
Python  3  0.694853  0.244405 -0.414633 -0.965176  0.929655         0
Python  4  0.120284  0.247607 -0.477527 -0.993267  0.317743         0
Python  Out of sample dataframe tail 
Python          var_1     var_2     var_3     var_4     var_5  c_labels
Python  95  0.988951  0.559262 -0.959583  0.353533 -0.570316         0
Python  96  0.088504  0.250962 -0.876172  0.309089 -0.158381         0
Python  97 -0.215093 -0.267556  0.634200  0.644492  0.938260         0
Python  98  0.639926  0.526517  0.561968  0.129514  0.089443         1
Python  99 -0.772519 -0.462499  0.085293  0.423162  0.391327         0
Python  test data successfully saved to csv file 

Python  ------------------------------> Percent of times selected <------------------------------
Python   Variable  var_3, selected 87.0 %
Python   Variable  var_2, selected 81.0 %
Python   Variable  var_4, selected 20.0 %
Python   Variable  var_1, selected 19.0 %
Python   Variable  var_5, selected 18.0 %
Python   Out of sample accuracy is 92.0 %
Python  lfs model saved to 
Python    C:\Users\Zwelithini\AppData\Roaming\MetaQuotes\Terminal\FB9A56D617EDDDFE29EE54EBEFFE96C1\MQL5\FILES\lfsmodel.json

Результаты работы скрипта на MQL5 - LFSmodelImportDemo.mq5.

LFSmodelImportDemo (BTCUSD,D1)  Accuracy is 92.0 %

Сравнивая результаты, мы видим, что выходные данные обеих программ совпадают, что указывает на то, что метод экспорта модели работает так, как ожидалось.

Заключение

Локальный отбор признаков предлагает инновационный подход к отбору признаков, особенно подходящий для динамичных сред, таких как финансовые рынки. Выявляя локально значимые признаки, LFS преодолевает ограничения традиционных методов, основанных на едином глобальном наборе признаков. Адаптивность алгоритма к различным паттернам данных, его способность управлять нелинейными взаимосвязями и способность балансировать между противоречивыми целями делают его ценным инструментом для построения моделей машинного обучения. Хотя пакет LFSpy обеспечивает практическую реализацию LFS, существует потенциал для дальнейшей оптимизации его вычислительной эффективности, особенно для крупномасштабных наборов данных. В заключение, LFS представляет собой многообещающий подход к задачам классификации в областях, характеризующихся сложными и постоянно меняющимися данными.

Название файла	Описание
Mql5/include/np.mqh	Включает в себя файл, содержащий общие определения для различных матричных и векторных служебных функций.
Mql5/include/lfspy.mqh	Включаемый файл, содержащий определение класса Clfspy, обеспечивающего функциональность вывода модели LFS в программах MetaTrader 5.
Mql5/scripts/JsonModel.py	Локальный модуль на Python, содержащий определение функции, позволяющей экспортировать модель LFS в формате JSON.
Mql5/scripts/LFSdemo.py	Скрипт на Python, демонстрирующий, как использовать класс LocalFeatureSelection для выбора признаков с использованием случайных величин
Mql5/scripts/LFSmodelExportDemo.py	Скрипт на Python, демонстрирующий, как экспортировать модель LFS для использования в MetaTrader 5.
Mql5/scripts/LFSmodelImportDemo.mq5	Скрипт на MQL5, показывающий, как загрузить и использовать экспортированную модель LFS в программе MetaTrader 5.