
Нейросети в трейдинге: Гиперболическая модель латентной диффузии (Окончание)
Введение
Гиперболическое геометрическое пространство способно представлять дискретные древовидные или иерархические структуры, которые находят применение в разнообразных задачах обучения графов. Оно также обладает значительным потенциалом для решения проблемы структурной анизотропии неевклидовых пространств в процессах латентной диффузии графов. Гиперболическая геометрия объединяет угловые и радиальные измерения полярных координат, обеспечивая геометрические измерения с физической семантикой и интерпретируемостью.
И в этом контексте, фреймворк HypDiff представляет собой усовершенствованный метод создания гиперболического гауссова шума, который решает проблему аддитивного сбоя гауссовых распределений в гиперболическом пространстве. Авторы фреймворка ввели геометрические ограничения углового подобия, применяемые в процессе анизотропной диффузии для сохранения локальной структуры графов.
Авторская визуализация фреймворка представлена ниже.
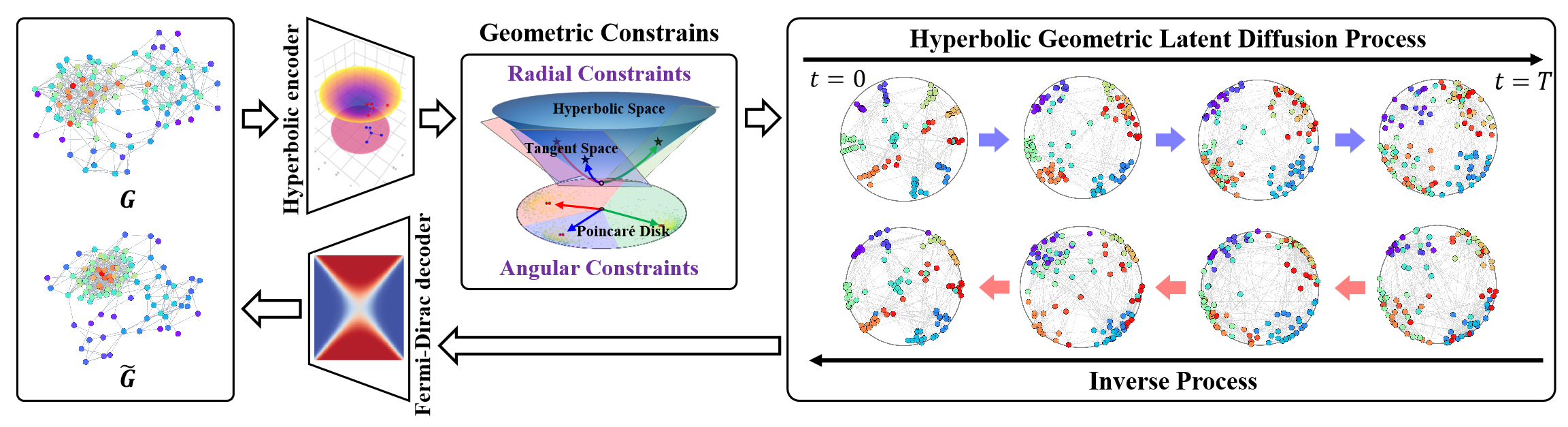
В предыдущей статье мы начали работу по реализации предложенных подходов средствами MQL5. Однако объем работы достаточно велик. И мы смогли рассмотреть лишь блоки реализации на стороне OpenCL-программы. В данной статье мы продолжим начатую работу. И доведем до логического завершения реализацию фреймворка HypDiff. Однако в своей реализации мы сделаем некоторые отступления от авторского алгоритма, которые обсудим в процессе построения алгоритмов.
1. Проекция данных в гиперболическое пространство
Свою работу на стороне OpenCL-программы мы начинали с построения кернелов прямого и обратного проходов проекции исходных данных в гиперболическое пространства (HyperProjection и HyperProjectionGrad соответственно). Реализацию подходов фреймворка HypDiff на стороне основной программы мы так же начнем с построения алгоритмов данного функционала. Для этого мы создадим новый класс CNeuronHyperProjection, структура которого представлена ниже.
class CNeuronHyperProjection : public CNeuronBaseOCL { protected: uint iWindow; uint iUnits; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) { return true; } public: CNeuronHyperProjection(void) : iWindow(-1), iUnits(-1) {}; ~CNeuronHyperProjection(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronHyperProjection; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); };
В представленной структуре мы видим объявление двух внутренних переменных для записи констант, определяющих архитектуру объекта, и уже привычный набор переопределяемых методов. Но обратите внимание, что метод обновления параметров модели updateInputWeights представлен положительной "заглушкой". И это не случайно. Ведь реализованные нами кернелы прямого и обратного проходов проекции данных выполняют явно прописанный алгоритм, лишенный обучаемых параметров. Однако наличие метода обновления параметров необходимо для корректной работы нашей модели. И мы вынуждены переопределить указанный метод с постоянным возвратом положительного результата.
Отсутствие объявлений новых внутренних объектов позволяет нам оставить пустыми конструктор и деструктор класса. А инициализация унаследованных объектов и объявленных внутренних переменных осуществляется в методе Init.
Алгоритм метода инициализации довольно прост. В параметрах метода мы, как обычно, получаем основные константы, позволяющие однозначно идентифицировать архитектуру создаваемого объекта.
bool CNeuronHyperProjection::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, (window + 1)*units_count, optimization_type, batch)) return false; iWindow = window; iUnits = units_count; //--- return true; }
А в теле метода мы сразу вызываем одноименный метод родительского класса, передав ему необходимую часть полученных параметров. Как вы знаете, в теле родительского класса уже реализованы алгоритмы контроля полученных параметров и инициализации унаследованных объектов. И нам достаточно лишь проверить логический результат выполнения метода родительского класса. После чего сохраняем полученные от внешней программы константы архитектуры объекта во внутренних переменных.
И все. Мы не объявляли новых внутренних объектов, а унаследованные инициализированы в методе родительского класса. Нам остается лишь вернуть логический результат выполнения операций вызывающей программе и завершить работу метода.
С методами прямого и обратного проходов данного класса я предлагаю вам ознакомиться самостоятельно. Оба они являются лишь "обертками" для вызова соответствующих кернелов OpenCL-программы. Подобные методы были уже много раз описаны в рамках нашей серии статей. И я думаю, что реализация их алгоритмов у вас не вызовет вопросов. С полным кодом данного класса и всех его методов вы можете ознакомиться во вложении.
2. Проекция на касательные плоскости
После проекции исходных данных в гиперболическое пространство, фреймворком HypDiff предусмотрено построение Энкодера генерации гиперболических эбедингов узлов. Этот функционал мы планируем покрыть уже имеющимися в нашей библиотеке средствами. Полученные эмбединги проецируются на касательные плоскости, соответствующие k центроидам. Алгоритмы проекции на касательные и обратного распределения градиентов мы уже реализовали на стороне OpenCL-программы в кернелах LogMap и LogMapGrad, соответственно. Но вопрос центроидов остается открытым.
Здесь надо сказать, что авторы фреймворка HypDiff определяли центроиды из обучающей выборки на стадии подготовки данных. К сожалению, такой подход для нас неприемлем. И дело не только в трудоемкости процесса. Такой подход не подходит для анализа в условиях динамичного рынка финансовых инструментов. Ведь в рамках технического анализа ценового движения порой большее внимание уделяется формирующимся паттернам, чем конкретным значениям стоимости инструмента. И для похожих рыночных ситуаций, зафиксированных на разных временных интервалах, могут быть актуальны различные центроиды. Из этого можно сделать вывод о необходимости создания динамической модели адаптации или генерации центроидов и их параметров. В своей реализации мы решили пойти по пути создания модели генерации центроидов на основе эмбедингов исходных данных. И было принято решение об объединении процессов генерации центроидов и проекции данных на соответствующие касательные плоскости в рамках класса CNeuronHyperboloids. Его структура представлена ниже.
class CNeuronHyperboloids : public CNeuronBaseOCL { protected: uint iWindows; uint iUnits; uint iCentroids; //--- CLayer cHyperCentroids; CLayer cHyperCurvatures; //--- int iProducts; int iDistances; int iNormes; //--- virtual bool LogMap(CNeuronBaseOCL *featers, CNeuronBaseOCL *centroids, CNeuronBaseOCL *curvatures, CNeuronBaseOCL *outputs); virtual bool LogMapGrad(CNeuronBaseOCL *featers, CNeuronBaseOCL *centroids, CNeuronBaseOCL *curvatures, CNeuronBaseOCL *outputs); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronHyperboloids(void) : iWindows(0), iUnits(0), iCentroids(0), iProducts(-1), iDistances(-1), iNormes(-1) {}; ~CNeuronHyperboloids(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, uint centroids, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronHyperboloids; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); virtual void TrainMode(bool flag); };
В представленной структуре нового класса можно заметить объявление 2 динамических массивов и 6 переменных, разделенных на 2 группы.
Динамические массивы предназначены для записи указателей на объекты нейронных слоев двух вложенных моделей. Да, в своей реализации мы решили разделить на 2 модели функционал генерации параметров центроидов. Первая модель отвечает за генерацию координат центроидов в гиперболическом пространстве. А вторая вернет параметры кривизны пространства в соответствующих точках.
Деление внутренних переменных на 2 группы так же имеет логическое объяснение. В одной группе мы объединили параметры архитектуры создаваемого объекта, которые мы будем получать от внешней программы. А во второй блок вынесены переменные для записи указателей на буфера записи промежуточных значений, которые мы создадим только в контексте OpenCL без копирования данных в оперативную память устройства.
Все внутренние объекты мы объявили статично, что позволяет нам оставить пустыми конструктор и деструктор класса. А инициализация всех унаследованных и объявленных объектов осуществляется в методе Init.
bool CNeuronHyperboloids::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, uint centroids, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window*units_count*centroids, optimization_type, batch)) return false;
В параметрах метода мы, как обычно, получаем ряд констант, позволяющих однозначно интерпретировать архитектуру создаваемого объекта. В данном случае это:
- units_count — количество элементов в анализируемой последовательности;
- window — размер вектора эмбединга одного элемента анализируемой последовательности;
- centroids — количество центроидов, которые генерирует модель для всестороннего анализа исходных данных.
В теле метода мы, по уже отработанной схеме, вызываем одноименный метод родительского класса для инициализации унаследованных объектов и переменных. И здесь стоит обратить внимание, что, в отличие от авторского алгоритма HypDiff, в своей реализации мы не разделяем элементы исходной последовательности по принадлежности к тому или иному центроиду. Вместо этого, с целью предоставления модели максимально возможного объема информации, мы генерируем проекции всей последовательности на все касательные плоскости. Что естественным образом увеличивает объем тензора результатов, пропорционально количеству генерируемых центроидов. Поэтому, при вызове метода инициализации родительского класса, мы указываем произведение всех трех полученных от внешней программы констант в качестве размера создаваемого слоя.
А после успешного выполнения операций метода родительского класса, о чем мы узнаем по логическому результату его работы, сохраним полученные константы во внутренних переменных.
iWindows = window; iUnits = units_count; iCentroids = centroids;
На следующем шаге мы подготовим наши динамические массивы для записи указателей на объекты моделей генерации параметров центроидов.
cHyperCentroids.Clear(); cHyperCurvatures.Clear(); cHyperCentroids.SetOpenCL(OpenCL); cHyperCurvatures.SetOpenCL(OpenCL);
И перейдем к непосредственной работе по инициализации объектов модели. Первой мы инициализируем модель генерации координат центроидов.
Здесь мы предполагаем построить линейную модель, которая, проанализировав набор исходных данных, вернет нам пакет координат для актуальных центроидов. Однако использование полносвязных слоев для этих целей ведет к созданию большого количества обучаемых параметров и повышению количества вычислений. Использование сверточных слоев позволит нам сократить как количество обучаемых параметров, так и объем вычислений. При этом вполне логичным выглядит применение сверточных слоев в рамках отдельных унитарных последовательностей. Для реализации такого подхода нам понадобится предварительно транспонировать полученные исходные данные.
CNeuronTransposeOCL *transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, 0, OpenCL, iUnits, iWindows, optimization, iBatch) || !cHyperCentroids.Add(transp)) { delete transp; return false; } transp.SetActivationFunction(None);
А затем добавим сверточный слой понижения размерности унитарных последовательностей.
CNeuronConvOCL *conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, 1, OpenCL, iUnits, iUnits, iCentroids, iWindows, 1, optimization, iBatch) || !cHyperCentroids.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(TANH);
Здесь мы используем один набор параметров для всех унитарных последовательностей. А на выходе слоя воспользуемся гиперболическим тангенсом в качестве функции активации для создания нелинейности.
Далее мы добавим ещё один сверточный слой без функции активации, но на этот раз он содержит уже отдельные обучаемые параметры для каждой унитарной последовательности.
conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, 2, OpenCL, iCentroids, iCentroids, iCentroids, 1, iWindows, optimization, iBatch) || !cHyperCentroids.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(None);
Таким образом, два последовательных сверточных слоя позволяют нам создать по уникальной MLP для каждого унитарного ряда исходной последовательности. Каждая такая MLP даст нам по одной координате для необходимого количества центроидов. Иными словами, мы создали по MLP для каждого измерения координатного пространства, которые в совокупности генерируют нам координаты заданного количества центроидов.
И теперь нам остается вернуть полученные координаты центроидов в исходное представление. Для этого мы добавим ещё один слой транспонирования данных.
transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, 3, OpenCL, iWindows, iCentroids, optimization, iBatch) || !cHyperCentroids.Add(transp)) { delete transp; return false; } transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
Далее мы переходим к созданию объектов второй модели, которая укажет нам параметры кривизны гиперболического пространства в точках центроидов. Определять параметры кривизны мы будем уже на основании сгенерированных координат центроидов. И здесь вполне логично, что параметр кривизны зависит только от конкретных координат. Ведь мы предполагаем, что представление об используемом гиперболическом пространстве модель получит в процессе обучения и отразит его в своих обучаемых параметрах. Поэтому в модели определения параметров кривизны мы уже не используем слоев транспонирования. Мы просто создаем из 2 последовательных сверточных слоев уникальную MLP для каждого центроида.
conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, 4, OpenCL, iWindows, iWindows, iWindows, iCentroids, 1, optimization, iBatch) || !cHyperCurvatures.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(TANH); //--- conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, 5, OpenCL, iWindows, iWindows, 1, 1, iCentroids, optimization, iBatch) || !cHyperCurvatures.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(None);
Здесь мы так же используем гиперболический тангенс для создания нелинейности между слоями модели.
На этом этапе мы завершаем работу по инициализации объектов моделей для генерации параметров центроидов. И нам остается подготовить объекты, необходимые для обслуживания кернелов проекции данных на касательные плоскости и распределения градиентов ошибки. Здесь я хочу напомнить, что при построении алгоритмов указанных кернелов, мы говорили о создании буферов временного хранения результатов промежуточных операций. Это 3 буфера данных, каждый из которых содержит по одному элементу для пар "Центроид — Элемент последовательности".
Данные буфера данных используются только для передачи информации из кернела прямого прохода в кернел распределения градиента ошибки. А значит, их создание оправдано только в рамках OpenCL-контекста. Иными словами, создание указанных буферов в оперативной памяти устройства и операции копирования данных между памятью OpenCL-контекста и основной — будет излишним. Также нет необходимости записывать эти данные при сохранении параметров модели, так как они обновляются при каждом прямом проходе. Поэтому на стороне основной программы мы создаем лишь переменные для хранения указателей на указанные буфера данных.
Но нам все же необходимо создать их на стороне OpenCL-контекста. Для этого мы сначала определяем необходимый размер буферов данных. Как уже было сказано выше, все 3 буфера имеют одинаковый размер.
uint size = iCentroids * iUnits * sizeof(float); iProducts = OpenCL.AddBuffer(size, CL_MEM_READ_WRITE); if(iProducts < 0) return false; iDistances = OpenCL.AddBuffer(size, CL_MEM_READ_WRITE); if(iDistances < 0) return false; iNormes = OpenCL.AddBuffer(size, CL_MEM_READ_WRITE); if(iNormes < 0) return false; //--- return true; }
После этого создадим буфера данных в памяти OpenCL-контеста с сохранением полученных указателей в соответствующих переменных. При этом не забываем проверить действительность полученного указателя.
А после инициализации всех объектов, мы возвращаем логический результат выполнения операций вызывающей программе и завершаем работу метода.
Следующим этапом нашей работы является построение алгоритмов прямого прохода нашего класса CNeuronHyperboloids. Здесь следует сказать, что методы LogMap и LogMapGrad являются обертками для вызова одноименных кернелов. И мы оставим их для самостоятельного изучения.
Рассмотрим метод прямого прохода feedForward. В параметрах данного метода мы получаем указатель объект нейронного слоя, который содержит тензор исходных данных.
bool CNeuronHyperboloids::feedForward(CNeuronBaseOCL *NeuronOCL) { CNeuronBaseOCL *prev = NeuronOCL; CNeuronBaseOCL *centroids = NULL; CNeuronBaseOCL *curvatures = NULL;
И в теле метода мы проведем сначала небольшую подготовительную работу: объявим локальные переменные для временного хранения указателей на объекты внутренних нейронных слоев. Одному из них мы передадим полученный указатель на объект исходных данных. Два других пока оставим пустыми.
Обратите внимание, что на данном этапе мы не проверяем актуальность полученного указателя на объект исходных данных. Мы не планируем осуществлять прямое обращение к буферам данного объекта в рамках операций текущего метода. Поэтому такой контроль будет излишен.
Далее нам предстоит сгенерировать координаты центроидов для текущего набора исходных данных. С этой целью мы организуем цикл перебора объектов соответствующей внутренней модели.
//--- Centroids for(int i = 0; i < cHyperCentroids.Total(); i++) { centroids = cHyperCentroids[i]; if(!centroids || !centroids.FeedForward(prev)) return false; prev = centroids; }
В теле цикла мы поочередно берем указатели на объекты нейронных слоев и проверяем их актуальность. После чего вызываем одноименный метод прямого прохода извлеченного объекта с передачей ему в качестве исходных данных указателя из соответствующей локальной переменной. После успешного выполнения метода прямого прохода внутреннего слоя, он становится источником исходных данных для последующего слоя модели. Следовательно, мы запишем его указатель в локальную переменную исходных данных.
Обратите внимание, что изначально в локальной переменной был записан указатель на объект исходных данных, полученный от внешней программы. Следовательно, на первой итерации нашего цикла мы использовали его в качестве исходных данных. А значит, проверка актуальности указателя на объект, полученный от внешней программы, была осуществлена в рамках выполнения операций метода прямого прохода слоя внутренней модели. Таким образом, осуществлены все точки контроля и соблюден поток информации от объекта исходных данных.
Аналогичный цикл мы организуем и для определения параметров кривизны гиперпространства в точках центроидов. И здесь стоит обратить внимание, что после завершения итераций предыдущего цикла локальные переменные prev и centroids содержат указатель на один и тот же объект последнего слоя модели генерации координат центроидов. А так как мы планировали определять параметры кривизны по координатам центроидов, то можем смело работать дальше с переменной prev.
//--- Curvatures for(int i = 0; i < cHyperCurvatures.Total(); i++) { curvatures = cHyperCurvatures[i]; if(!curvatures || !curvatures.FeedForward(prev)) return false; prev = curvatures; }
И после успешного получения всех необходимых параметров центроидов, мы можем осуществить проекцию исходных данных на соответствующие касательные плоскости. Для этого мы вызовем метод-обертку созданного в предыдущей статье кернела LogMap.
if(!LogMap(NeuronOCL, centroids, curvatures, AsObject())) return false; //--- return true; }
Обратите внимание, что в качестве объекта-получателя результатов мы передаем указатель на текущий объект. Это позволит нам сохранить результаты выполнения операций в буферах интерфейсов нашего класса, которым и будут обращаться последующие нейронные слои нашей модели.
Нам остается лишь вернуть логический результат выполнения операций вызывающей программе и завершить работу метода прямого прохода.
После построения методов прямого прохода, мы переходим к работе над алгоритмами обратного прохода. И здесь я предлагаю рассмотреть алгоритм метода распределения градиента ошибки calcInputGradients. А метод обновления параметров модели updateInputWeights оставить для самостоятельного изучения.
Как обычно, в параметрах метода распределения градиента ошибки calcInputGradients мы получаем указатель на объект предшествующего слоя, в буфер которого нам и предстоит передать градиент ошибки, в соответствии с влиянием исходных данных на конечный результат работы модели.
bool CNeuronHyperboloids::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!prevLayer) return false;
И на этот раз мы сразу проверяем корректность полученного указателя. Ведь в случае получения некорректного указателя, все дальнейшие операции сразу теряют смысл.
Также, как и в случае прямого прохода, мы объявляем локальные переменные для временного хранения указателей на объекты внутренних моделей. Только на этот раз мы сразу извлечем указатели на последние слои внутренних моделей.
CObject *next = NULL; CNeuronBaseOCL *centroids = cHyperCentroids[-1]; CNeuronBaseOCL *curvatures = cHyperCurvatures[-1];
После чего вызовем метод-обертку кернела распределения градиента через операции проекции исходных данных на касательные плоскости.
if(!LogMapGrad(prevLayer, centroids, curvatures, AsObject())) return false;
И распределяем градиент ошибки по внутренней модели определения кривизны гиперпространства в точках центроидов, создав цикл обратного перебора нейронных слоев модели.
//--- Curvatures for(int i = cHyperCurvatures.Total() - 2; i >= 0; i--) { next = curvatures; curvatures = cHyperCurvatures[i]; if(!curvatures || !curvatures.calcHiddenGradients(next)) return false; }
И далее нам необходимо передать градиент ошибки от модели определения кривизны к модели генерации координат центроидов. Но здесь мы замечаем, что в буфере последнего слоя модели генерации координат центроидов уже есть градиент ошибки от операций проекции данных на касательные плоскости. И нам желательно сохранить имеющиеся значения. Как обычно, в таких случаях мы прибегаем к подмене указателей на буфера данных. Вначале мы сохраним текущей указатель на буфер градиентов ошибки последнего слоя модели генерации координат центроидов в локальной переменной и, при необходимости, скорректируем значения на производную функции активации нейронного слоя.
CBufferFloat *temp = centroids.getGradient(); if(centroids.Activation()!=None) if(!DeActivation(centroids.getOutput(),temp,temp,centroids.Activation())) return false; if(!centroids.SetGradient(centroids.getPrevOutput(), false) || !centroids.calcHiddenGradients(curvatures.AsObject()) || !SumAndNormilize(temp, centroids.getGradient(), temp, iWindows, false, 0, 0, 0, 1) || !centroids.SetGradient(temp, false) ) return false;
Затем временно заменим его на неиспользуемый буфер соответствующего размера. Вызовем метод распределения градиента ошибки для последнего слоя модели генерации координат центроидов, передав ей в качестве последующего объекта первый слой модели определения кривизны гиперпространства в точках центроидов. Суммируем значения двух буферов данных и вернем их указатели в исходное состояние. Не забываем при этом контролировать процесс выполнения каждой описанной операции.
Теперь, имея суммарный градиент ошибки в буфере последнего слоя модели определения координат центроидов, мы можем организовать цикл обратного перебора нейронных слоев модели. В рамках данного цикла организуем распределения градиента ошибки между слоями модели в зависимости от их вклада в конечный результат.
//--- Centroids for(int i = cHyperCentroids.Total() - 2; i >= 0; i--) { next = centroids; centroids = cHyperCentroids[i]; if(!centroids || !centroids.calcHiddenGradients(next)) return false; }
После чего нам остается лишь передать градиент ошибки на уровень исходных данных. Но тут мы опять сталкиваемся с вопросом сохранения ранее накопленного градиента ошибки. И мы повторяем ранее описанный фокус с подменой буферов данных, только на это раз для объекта исходных данных.
temp = prevLayer.getGradient(); if(prevLayer.Activation()!=None) if(!DeActivation(prevLayer.getOutput(),temp,temp,prevLayer.Activation())) return false; if(!prevLayer.SetGradient(prevLayer.getPrevOutput(), false) || !prevLayer.calcHiddenGradients(centroids.AsObject()) || !SumAndNormilize(temp, prevLayer.getGradient(), temp, iWindows, false, 0, 0, 0, 1) || !prevLayer.SetGradient(temp, false) ) return false; //--- return true; }
Нам остается лишь вернуть логический результат выполнения операций вызывающей программе и завершить работу метода.
На этом мы завершаем рассмотрение алгоритмов построения методов нашего класса CNeuronHyperboloids. С полным кодом данного класса и всех его методов вы можете самостоятельно ознакомиться во вложении.
3. Собираем фреймворк HypDiff
Мы завершили работу по построению отдельных новых блоков фреймворка HypDiff и подошли к моменту построения единого объекта верхнеуровневой реализация фреймворка. Для этого мы создадим новый класс CNeuronHypDiff, структура которого представлена ниже.
class CNeuronHypDiff : public CNeuronRMAT { public: CNeuronHypDiff(void) {}; ~CNeuronHypDiff(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint layers, uint centroids, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronHypDiff; } //--- virtual uint GetWindow(void) const override { CNeuronRMAT* neuron = cLayers[1]; return (!neuron ? 0 : neuron.GetWindow() - 1); } virtual uint GetUnits(void) const override { CNeuronRMAT* neuron = cLayers[1]; return (!neuron ? 0 : neuron.GetUnits()); } };
Как можно заметить в представленной выше структуре нового класса, основной функционал мы наследуем от объекта CNeuronRMAT. Указанный объект обладает функционалом организации работы небольшой линейной модели, чего нам вполне достаточно для реализации фреймворка HypDiff. Поэтому на данном этапе нам достаточно переопределить метод инициализации объекта, указав в нем корректную архитектуру вложенной модели. А все другие процессы уже покрываются методами родительского класса.
В параметрах метода инициализации объекта мы получаем основные константы, позволяющие однозначно интерпретировать архитектуру создаваемого объекта.
bool CNeuronHypDiff::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint layers, uint centroids, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
И в теле метода мы сразу вызываем одноименный метод базового объекта нейронных слоев в рамках которого реализована инициализация основных интерфейсов. Мы намеренно не используем на данном этапе метод инициализации прямого родительского класса, так как архитектура создаваемой внутренней модели сильно отличается.
Затем мы подготовим унаследованный динамический массив хранение указателей на внутренние объекты.
cLayers.Clear(); cLayers.SetOpenCL(OpenCL); int layer = 0;
И перейдем к непосредственному процессу построения внутренней архитектуры фреймворка HypDiff.
Поступающие на вход модели исходные данные вначале проецируются в гиперболическое пространство. Для этого мы добавляем объект выше созданного класса CNeuronHyperProjection.
//--- Projection CNeuronHyperProjection *lorenz = new CNeuronHyperProjection(); if(!lorenz || !lorenz.Init(0, layer, OpenCL, window, units_count, optimization, iBatch) || !cLayers.Add(lorenz)) { delete lorenz; return false; } layer++;
Далее фреймворком HypDiff предусмотрен гиперболический энкодер, который предназначен для генерации эмбедингов узлов анализируемого графа. Авторы фреймворка использовали здесь графовые нейронные модели совместно со сверточными слоями. В своей реализации мы заменим графовые нейронные сети на Transformer с относительным кодированием.
//--- Encoder CNeuronRMAT *rmat = new CNeuronRMAT(); if(!rmat || !rmat.Init(0, layer, OpenCL, window + 1, window_key, units_count, heads, layers, optimization, iBatch) || !cLayers.Add(rmat)) { delete rmat; return false; } layer++; //--- CNeuronConvOCL *conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer, OpenCL, window + 1, window + 1, 2 * window, units_count, 1, optimization, iBatch) || !cLayers.Add(conv)) { delete conv; return false; } layer++; conv.SetActivationFunction(TANH); //--- conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer, OpenCL, 2 * window, 2 * window, 3, units_count, 1, optimization, iBatch) || !cLayers.Add(conv)) { delete conv; return false; } layer++;
Здесь следует обратить внимание, что далее, при проекции полученных эмбедингов на касательные плоскости, мы сильно увеличиваем объем обрабатываемой информации, осуществляя проекции на все касательные плоскости полного объема информации. И чтобы немного компенсировать негативное влияние такого подхода, мы сжимаем размер эмбединга каждого узла.
Полученные эмбединги исходных данных нам предстоит спроецировать на касательные плоскости центроидов. Функционал генерации центроидов и проекции исходных данных на соответствующие касательные мы уже организовали в классе CNeuronHyperboloids. И теперь нам достаточно добавить экземпляр такого объекта в нашу линейную модель.
//--- LogMap projecction CNeuronHyperboloids *logmap = new CNeuronHyperboloids(); if(!logmap || !logmap.Init(0, layer, OpenCL, 3, units_count, centroids, optimization, iBatch) || !cLayers.Add(logmap)) { delete logmap; return false; } layer++;
На выходе мы получаем проекции исходных данных на несколько плоскостей. И теперь мы можем к ним применить алгоритм направленной диффузии, изначально разработанный для евклидовых моделей. В своей реализации мы использовали объект CNeuronDiffusion.
//--- Diffusion model CNeuronDiffusion *diff = new CNeuronDiffusion(); if(!diff || !diff.Init(0, layer, OpenCL, 3, window_key, heads, units_count*centroids, 2, layers, optimization, iBatch) || !cLayers.Add(diff)) { delete diff; return false; } layer++;
Здесь стоит обратить внимание на тот момент, что мы не стали объединять различные проекции одного элемента последовательности в единую сущность. Напротив, в нашей реализации модель направленной диффузии рассматривает каждую проекцию как отдельный объект. Тем самым мы предлагаем модели научиться сопоставлять отдельные проекции одной последовательности и формировать из них объемное представление об анализируемых данных.
Ещё один неявный момент, о котором следует сказать, — это добавляемый шум. Мы не стали усложнять модель в попытках сопоставления шума различных проекций одного элемента последовательности. Ведь сам процесс добавления шума подразумевает "размытие" исходных в некоторой их окрестности. А различное добавления шума в разных проекциях делает это "размытие" объемным.
На выходе диффузионной модели мы ожидаем получить представление исходных данных в различных проекциях очищенное от шума. И тут начинаются наши наиболее кардинальные отступления от авторского фреймворка. Авторы HypDiff осуществляли обратную проекцию данных в гиперболическое пространство и с помощью декодера Ферми-Дирака получали исходное представление графа. Нашей же целью является получение информативного латентного представления исходных данных для последующей их передачи в модель Актера и обучения прибыльной политики поведения нашего агента. Поэтому мы воспользуемся слоем пулинга на основе зависимостей для получения общего представления о каждом элементе последовательности.
//--- Pooling CNeuronMHAttentionPooling *pooling = new CNeuronMHAttentionPooling(); if(!pooling || !pooling.Init(0, layer, OpenCL, 3, units_count, centroids, optimization, iBatch) || !cLayers.Add(pooling)) { delete pooling; return false; } layer++;
И изменим размер тензора результатов до уровня исходных данных.
//--- Resize to source size conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer, OpenCL, 3, 3, window, units_count, 1, optimization, iBatch) || !cLayers.Add(conv)) { delete conv; return false; }
Теперь нам остается осуществить подмену указателей буферов данных интерфейсов на соответствующие буфера последнего слоя нашей модели. И завершить работу метода инициализации нашего класса.
//--- if(!SetOutput(conv.getOutput(), true) || !SetGradient(conv.getGradient(), true)) return false; //--- return true; }
На этом мы завершаем работу по реализации собственного видения подходов фреймворка HypDiff средствами MQL5. Полный код всех представленных в статье классов и их методов вы можете найти во вложении. Там же вы найдете код программ взаимодействия с окружающей средой и обучения моделей, которые были перенесены без изменений из предыдущих работ.
И несколько слов об архитектуре обучаемых моделей. Архитектура моделей Актера и Критика осталась без изменений. Однако, мы внесли небольшие правки в модель Энкодера состояния окружающей среды. Подаваемые на вход модели исходные данные, как и ранее, проходят первичную обработку в слое пакетной нормализации.
bool CreateEncoderDescriptions(CArrayObj *&encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } //--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
После чего они сразу передаются в нашу модель гиперболической латентной диффузии.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronHypDiff; descr.count = HistoryBars; descr.window = BarDescr; descr.window_out = BarDescr; descr.layers=2; descr.step=10; // centroids { int temp[] = {4}; // Heads if(ArrayCopy(descr.heads, temp) < (int)temp.Size()) return false; } descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Описанный выше алгоритм модели гиперболической латентной диффузии представляет собой довольно сложный и комплексный процесс. Поэтому мы исключили дальнейшую обработку данных. И использовали лишь один полносвязный слой для приведения данных к необходимому размеру тензора, который подается на вход модели Актера.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
На этом мы завершаем работу по реализации подходов фреймворка HypDiff и переходим к наиболее волнительному этапу — практической оценке результатов выполненной на реальных исторических данных.
4. Тестирование
Мы реализовали фреймворк HypDiff средствами MQL5 и теперь переходим к завершающему этапу — обучению моделей и оценке полученной политики поведения Актера. Мы следуем алгоритму обучения, описанному в предыдущих работах, и одновременно обучаем три модели: Энкодер состояния счета, Актер и Критик. Энкодер анализирует рыночную ситуацию. Актер принимает торговые решения на основе изученной политики. А Критик оценивает действия Актера и указывает направления для корректировки его политики.
Обучение проводится на реальных исторических данных за весь 2023 год финансового инструмента EURUSD, таймфрейм H1. Параметры всех анализируемых индикаторов используются по умолчанию.
Процесс обучения носит итерационный характер и включает в себя регулярное обновление обучающей выборки.
Для проверки эффективности обученной политики используются реальные исторические данные за первый квартал 2024 года. Результаты тестирования представлены ниже.
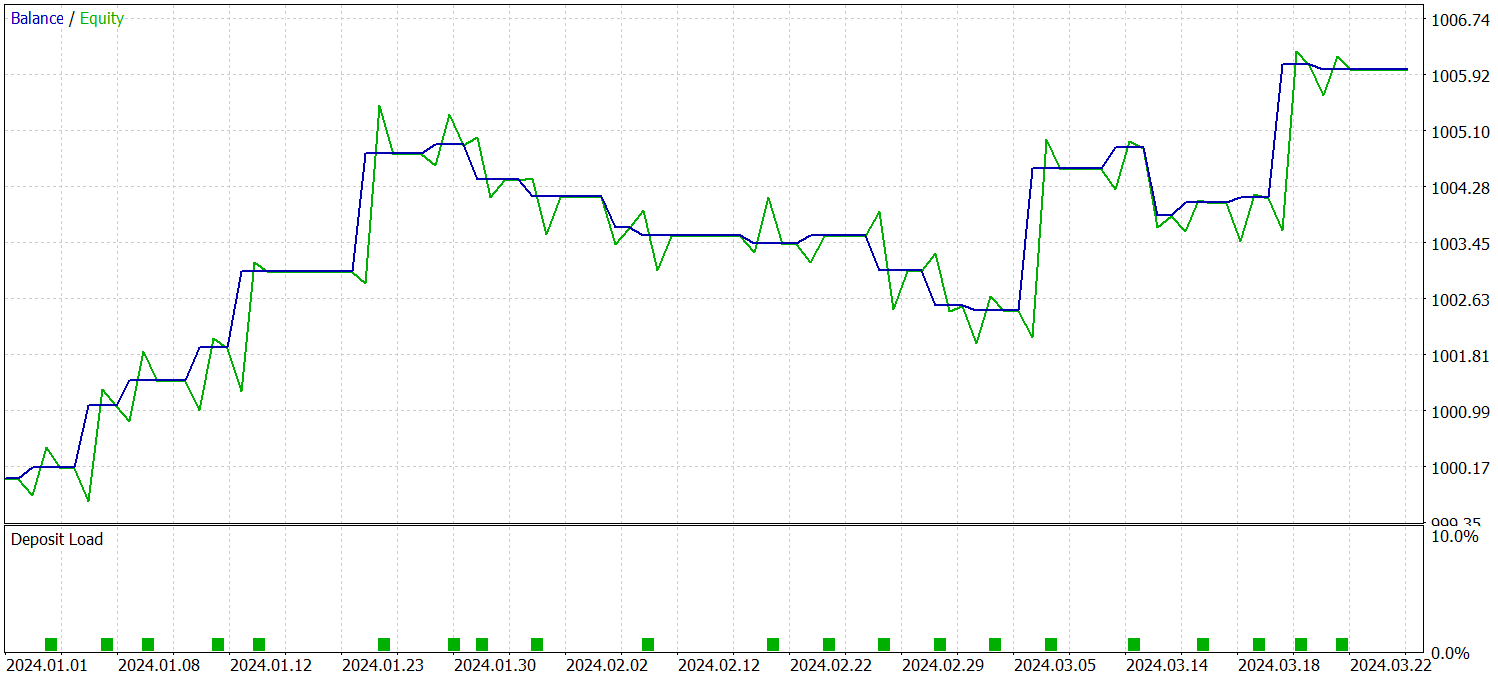

Как можно заметить из представленных данных, модель смогла получить прибыль за период тестирования. Всего за 3 месяца было совершено 23 торговых операции, что конечно мало. Более 56% из них было закрыто с прибылью. При этом, как максимальная так и средняя прибыльная сделка в 2 раза превышают аналогичный показатель убыточных операций.
Однако гораздо больший интерес вызывает детальное рассмотрение операций. Из 3 месяцев тестирования модель смогла получить прибыль только в 2 из них. Февраль месяц оказался полностью провальным. При этом из 8 сделок, совершенных в январе 2024 года, только последняя была убыточной. Что вполне подтверждает ранее высказанную теорию о снижении репрезентативности обучающей выборки в один год за рамками первого месяца эксплуатации модели.
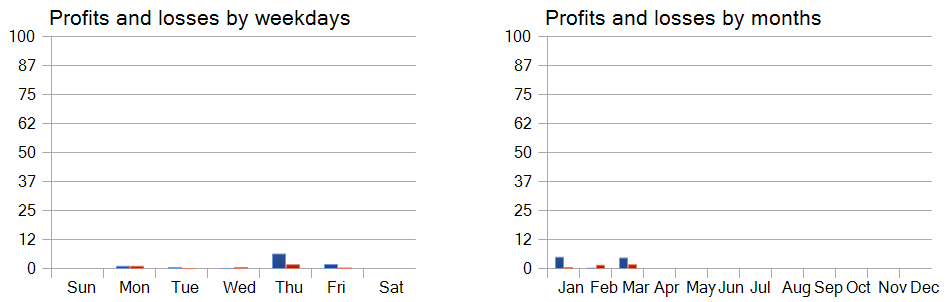
А рассмотрение доходности торговых операций по дням недели позволяет сделать вывод о явном приоритете работы модели в четверг и пятницу.
Заключение
Применение гиперболической геометрии помогает преодолеть проблемы, возникающие из-за конфликта между дискретной природой графовых данных и непрерывной моделью диффузии. Фреймворк HypDiff предлагает усовершенствованный метод генерации гиперболического гауссового шума, который решает проблему аддитивных сбоев гауссовых распределений в гиперболическом пространстве. Для сохранения локальной структуры в процессе анизотропной диффузии вводятся геометрические ограничения на угловое подобие.
В практической части нашей работы мы реализовали свое видение предложенных подходов средствами MQL5. Обучили модели с использованием предложенных подходов на реальных исторических данных. И провели тестирование обученной политики поведения Актера за рамками обучающей выборки. Полученные результаты свидетельствуют о существующем потенциале предложенных подходов и указывают на возможные пути повышения эффективности работы модели.
Ссылки
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Research.mq5 | Советник | Советник сбора примеров |
| 2 | ResearchRealORL.mq5 | Советник | Советник сбора примеров методом Real-ORL |
| 3 | Study.mq5 | Советник | Советник обучения Моделей |
| 4 | Test.mq5 | Советник | Советник для тестирования модели |
| 5 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы |
| 6 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 7 | NeuroNet.cl | Библиотека | Библиотека кода программы OpenCL |
 Построение модели для ограничения диапазона сигналов по тренду (Часть 4): Настройка стиля отображения для каждой трендовой волны
Построение модели для ограничения диапазона сигналов по тренду (Часть 4): Настройка стиля отображения для каждой трендовой волны
 Пошаговая инструкция для торговли по стратегии Break of Structure (BoS)
Пошаговая инструкция для торговли по стратегии Break of Structure (BoS)
 Алгоритм атомарного орбитального поиска — Atomic Orbital Search (AOS)
Алгоритм атомарного орбитального поиска — Atomic Orbital Search (AOS)
 Интеграция скрытых марковских моделей в MetaTrader 5
Интеграция скрытых марковских моделей в MetaTrader 5
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования