Возможности Мастера MQL5, которые вам нужно знать (Часть 19): Байесовский вывод

Введение

Продолжим изучение возможностей Мастера MQL5 и рассмотрим байесовский вывод - статистический метод, который обрабатывает и обновляет вероятности с каждым новым поступлением информации. Очевидно, что спектр возможных применений у него широкий, однако для нас, трейдеров, важнее всего его роль в прогнозировании временных рядов. Временные ряды, доступные трейдерам для анализа, в первую очередь представляют собой цены торгуемых ценных бумаг, но, как мы увидим в этой статье, эти ряды можно "расширить", чтобы также учесть альтернативные данные, такие как история торговли ценными бумагами.

Теоретически байесовский вывод должен повышать рыночную адаптивность любой торговой системы, поскольку переоценка любой гипотезы является неизбежной. Это должно привести к меньшей подгонке кривой при тестировании на исторических данных и последующем анализе данных с использованием реальных счетов. Но это теория. На практике же ее реализация может разрушить любую здравую идею, поэтому в этой статье мы постараемся рассмотреть несколько возможных реализаций байесовского вывода.

Мы дадим определение байесовского вывода и рассмотрим примеры его использования в классе пользовательских сигналов, в классе управления капиталом и в классе трейлинг-стопа. Также мы рассмотрим отчеты о тестировании стратегий и, наконец, дадим заключение.

Определение

Байесовский вывод (Bayesian Inference, BI) выражается формулой P(H|E) = [P(E|H) * P(H)] / P(E),  где:

• H обозначает гипотезу, а
• E - доказательства, такие что:
• P(H) - априорная вероятность гипотезы, тогда как
• P(E) — это вероятность доказательства, также известная как предельная вероятность.
• P(H|E) и P(E|H) - соответствующие условные вероятности вышеперечисленного. Их также называют апостериорной вероятностью и правдоподобием соответственно.

Приведенная выше формула, хотя и проста и понятна, представляет собой разновидность проблемы курицы и яйца, а именно, как нам найти: P(E|H). Это потому, что из приведенной выше формулы следует, что ее решение:

P(E|H) = [P(H|E) * P(E)] / P(H).

Выражение можно также переписать как P(E|H) = [P(E∩H)] / P(H). Это позволит нам применять обходные пути вручную, как будет показано ниже.

Класс сигналов

Класс сигналов обычно определяет позицию, которую должен открыть советник, - длинную или короткую. Это делается путем сложения весовых коэффициентов индикаторов, а суммарное значение всегда находится в диапазоне от 0 до 100. При использовании BI мы сталкиваемся с широким выбором временных рядов, однако в этой статье для класса сигналов будут представлены только примеры с временными рядами изменения цены закрытия.

Чтобы использовать этот временной ряд или любой другой тип, нам сначала нужно найти "систематический" способ классификации значений временного ряда или их кластеризации. Этот очевидный шаг важен, поскольку он не только нормализует наши данные временного ряда, но и позволяет нам правильно идентифицировать их при обработке их вероятности.

Кластеризация проводится без учителя, и мы используем ее в элементарном виде, назначая кластер каждой точке данных в зависимости от типа изменения цены. Всем положительным значениям назначается кластер, нулевым значениям — свой собственный кластер, а отрицательным — свой собственный. Ранее в рамках данной серии статей мы рассматривали альтернативные подходы к кластеризации. Читатель может поэкспериментировать с ними. Однако в этой статье, поскольку кластеризация не является основной темой, мы рассмотрели нечто весьма элементарное.

Даже при использовании этого базового подхода к кластеризации становится ясно, что мы можем лучше "идентифицировать" точки данных и, следовательно, оценивать их вероятности. Поскольку мы имеем дело с данными с плавающей точкой, без такого подхода каждая точка данных была бы уникальной, что по сути означало бы уникальный тип кластера, а это явно противоречит нашей цели получения и вычисления значений вероятности. Наш простой подход реализован в коде ниже:

//+------------------------------------------------------------------+
//| Function to assign cluster for each data point                   |
//+------------------------------------------------------------------+
void CSignalBAYES::SetCluster(matrix &Series)
{  for(int i = 0; i < int(Series.Rows()); i++)
   {  if(Series[i][0] < 0.0)
      {  Series[i][1] = 0.0;
      }
      else if(Series[i][0] == 0.0)
      {  Series[i][1] = 1.0;
      }
      else if(Series[i][0] > 0.0)
      {  Series[i][1] = 2.0;
      }
   }
}

После того, как мы "идентифицировали" точки данных, мы приступаем к вычислению апостериорной вероятности, как определено в приведенной выше формуле. Однако для этого нам понадобится определенный тип кластера, который послужит нашей гипотезой. Этот кластер обязательно будет уникальным для длинных и коротких позиций, поэтому у нас есть специальные входные параметры для каждой позиции, которые служат индексами, определяющими тип кластера, который следует использовать в каждом случае. Они обозначены как m_cluster_long и m_cluster_short соответственно.

Таким образом, для получения апостериорной вероятности в качестве входных данных потребуется этот кластерный индекс вместе с "идентифицированным" или кластеризованным временным рядом. Наша функция, которая вычисляет апостериорную вероятность, получает вероятность появления кластера типов позиций с учетом текущего типа кластера. Поскольку мы предоставляем ряд последних точек данных, каждая из которых имеет свой кластерный индекс в матричном формате, по сути, мы имеем точку данных с нулевым индексом в качестве текущего кластера.

Чтобы разрешить нашу потенциальную ситуацию "курица или яйцо", упомянутую выше, мы работаем следующим образом - P(E|H).

Из основных принципов. Поскольку H представлен соответствующим индексом положения, доказательство E является текущим кластером или типом кластера с индексом ноль во входном ряду. Итак, наша апостериорная вероятность — это определение вероятности того, что тип кластера данной позиции идет следующим, учитывая, что появилось последнее доказательство (кластер с индексом 0).

Чтобы найти обратное P(E|H), мы повторно просматриваем входной ряд и перечисляем случаев, когда индекс положения H встречался с последующим нулевым индексом E (доказательство). Это также вероятность, поэтому мы сначала перечислим пространство, то есть найдем вхождения H, а затем внутри этого пространства найдем, сколько раз индекс доказательства следовал подряд.

Это явно означает, что наш входной ряд имеет достаточную длину с учетом количества рассматриваемых типов кластеров. В нашем очень простом примере у нас есть 3 типа кластеров (на самом деле 2, учитывая, что нулевое изменение цены, скорее всего, произойдет редко). Это может работать с входным рядом менее 50. Однако если выбрать более основательный подход к кластеризации, при котором используются пять, шесть или более типов кластеров, то размер входного ряда по умолчанию должен быть достаточно большим, чтобы охватить возникновение всех этих типов кластеров для работы нашей апостериорной функции. Ниже приведен листинг апостериорной функции:

//+------------------------------------------------------------------+
//| Function to calculate the posterior probability for each cluster |
//+------------------------------------------------------------------+
double CSignalBAYES::GetPosterior(int Type, matrix &Series)
{  double _eh_sum = 0.0, _eh = 0.0, _e = 0.0, _h = 0.0;
   for(int i = 0; i < int(Series.Rows()); i++)
   {  if(Type == Series[i][1])
      {  _h += 1.0;
         if(i != 0)
         {  _eh_sum += 1.0;
            if(Series[i][1] == Series[i - 1][1])
            {  _eh += 1.0;
            }
         }
      }
      if(i != 0 && Series[0][1] == Series[i][1])
      {  _e += 1.0;
      }
   }
   _h /= double(Series.Rows() - 1);
   _e /= double(Series.Rows() - 1);
   if(_eh_sum > 0.0)
   {  _eh /= _eh_sum;
   }
   double _posterior = 0.0;
   if(_e > 0.0)
   {  _posterior += ((_eh * _h) / _e);
   }
   return(_posterior);
}

Как только мы получим нашу апостериорную вероятность, она будет представлять собой вероятность того, что оптимальный тип кластера позиции (будь то m_cluster_long или m_cluster_short) возникнет с учетом текущего типа кластера (то есть свидетельства или типа кластера для точки данных с нулевым индексом). Это будет значение в диапазоне от 0,0 до 1,0. Для того чтобы соответствующая гипотеза, будь то для длинных или коротких позиций, была вероятной, возвращаемое значение в идеале должно быть больше 0,5, однако вы можете изучите особые ситуации, в которых немного меньшее значение может дать интересные результаты.

Однако десятичное значение необходимо нормализовать до стандартного диапазона 0–100, который выводится функциями условий для длинного и короткого входов. Для этого просто умножаем его на 100,0. Ниже приведен типовой листинг условий длинного и короткого входов:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalBAYES::LongCondition(void)
{  int result = 0;
   vector _s_new, _s_old, _s;
   _s_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_series_size);
   _s_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_series_size);
   _s = _s_new - _s_old;
   matrix _series;
   _series.Init(_s.Size(), 2);
   for(int i = 0; i < int(_s.Size()); i++)
   {  _series[i][0] = _s[i];
   }
   SetCluster(_series);
   double _cond = GetPosterior(m_long_cluster, _series);
   _cond *= 100.0;
   //printf(__FUNCSIG__ + " cond: %.2f", _cond);
   //return(result);
   if(_cond > 50.0)
   {  result = int(2.0 * (_cond - 50.0));
   }
   return(result);
}

С помощью этого класса сигналов его можно легко встроить в любой советник с помощью Мастера MQL5, используя руководства, приведенные здесь и здесь для пользователей, не знакомых с Мастером MQL5.

Класс управления капиталом

Мы можем реализовать пользовательский класс управления капиталом (money management, MM), использующий BI. И снова, для начала нам нужно будет выбрать подходящий временной ряд, на котором мы будем основывать наш анализ, но, как упоминалось во введении, для ММ мы выберем исторические показатели торговли. Таким образом, поскольку собранный нашим Мастером советник будет торговать только одним символом, вся торговая история, доступная для выбора, по запросу будет применима к советнику.

Используя временные ряды торговой истории в качестве основы для анализа, мы будем следовать примеру одного из встроенных и "оптимизированных по размеру" классов управления капиталом, в котором размер объема торговли уменьшается пропорционально недавнему числу последовательных убытков. Однако в нашем случае мы уменьшим размер лота, если вероятность нашего предпочтительного индекса кластера (гипотезы) упадет ниже другого оптимизируемого параметра - m_condition.

Итак, по сути, мы пытаемся установить идеальный индекс кластера, при котором мы можем использовать обычный размер лота пропорционально свободной марже. Индекс кластера является идентификатором типа кривой капитала (поскольку торгуется только один символ), при котором мы можем свободно масштабировать размер лота пропорционально свободной марже. Ссылка на "тип кривой эквити" немного широка, поскольку наша кластеризация следует простому формату, который мы приняли в классе сигналов, а здесь конкретно указывается тип результата торговли, то есть выигрыш или проигрыш (результаты с нулевой прибылью присваиваются индексу, но вряд ли будут существенно отражены в анализе).

Это означает, например, что если благоприятный результат торговли для масштабирования размера лота со свободной маржей является прибыльным результатом торговли, то мы будем изучать последовательность предыдущих результатов торговли и пытаться установить вероятность получения еще одного прибыльного результата торговли в свете имеющихся доказательств (результат торговли при нулевом индексе входного ряда).

Это требует еще одного оптимизируемого параметра в форме порогового значения вероятности, который измеряет вероятность повторения целевых благоприятных условий таким образом, что если апостериорный результат не достигает этого порогового значения, то размер позиции уменьшается пропорционально количеству подсчитанных потерь, как это происходит в исходном классе управления капиталом "оптимизированного размера". Ниже приведен листинг функции оптимизации:

//+------------------------------------------------------------------+
//| Optimizing lot size for open.                                    |
//+------------------------------------------------------------------+
double CMoneyBAYES::Optimize(int Type, double lots)
{  double lot = lots;
//--- calculate number of losses orders without a break
   if(m_decrease_factor > 0)
   {  //--- select history for access
      HistorySelect(0, TimeCurrent());
      //---
      int       orders = HistoryDealsTotal(); // total history deals
      int       losses=0;                    // number of consequent losing orders
      //--
      int      size=0;
      matrix series;
      series.Init(fmin(m_series_size,orders), 2);
      series.Fill(0.0);
      //--
      CDealInfo deal;
      //---
      for(int i = orders - 1; i >= 0; i--)
      {  deal.Ticket(HistoryDealGetTicket(i));
         if(deal.Ticket() == 0)
         {  Print("CMoneySizeOptimized::Optimize: HistoryDealGetTicket failed, no trade history");
            break;
         }
         //--- check symbol
         if(deal.Symbol() != m_symbol.Name())
            continue;
         //--- check profit
         double profit = deal.Profit();
         //--
         series[size][0] = profit;
         size++;
         //--
         if(size >= m_series_size)
            break;
         if(profit<0.0)
            losses++;
      }
      //--
      series.Resize(size,2);
      SetCluster(series);
      double _cond = GetPosterior(Type, series);
      //--
      //---
      if(_cond < m_condition)
         lot = NormalizeDouble(lot - lot * losses / m_decrease_factor, 2);
   }
//--- normalize and check limits


...

//---

...

//---

...

//---
   return(lot);
}

Все остальные параметры коэффициента уменьшения и процента инвестированной маржи остаются такими же, как и в исходном классе ММ, "оптимизированного по размеру".

Для сравнения с BI мы могли бы рассмотреть критерий Келли, который учитывает выигрышные результаты и соотношение риска и вознаграждения, но с долгосрочной точки зрения и, возможно, не обновляя критерии распределения на основе недавних или промежуточных показателей. Формула имеет вид K = W – ((1 - W) / R)

где:

• K - процентное распределение
• W - процент выигрышей
• R - профит-фактор
  

Сообщается, что этот подход был принят инвестиционными гуру из-за его долгосрочной перспективы при распределении капитала, однако можно утверждать, что долгосрочный подход должен применяться к позиционированию, а не к распределению. В вопросах торговых операций часто используются долгосрочные прогнозы, однако там, где есть риск, краткосрочная перспектива, как правило, имеет большее значение, поэтому ее реализация является отдельной темой.

Таким образом, преимущества BI по сравнению с критерием Келли (KC) можно суммировать с помощью того аргумента, что KC предполагает постоянное преимущество на рынках, что может быть верно в случаях, когда у вас очень длинный горизонт. Игнорирование стоимости сделок и проскальзывания — еще один аргумент против критерия Келли, и хотя оба эти фактора можно игнорировать в долгосрочной перспективе, справедливо будет сказать, что большинство рынков устроено так, что позволяет кому-то торговать с использованием чужого капитала. Это по сути подразумевает, что к краткосрочным отклонениям необходимо относиться с большой долей чувствительности, поскольку они могут определить, по-прежнему ли трейдер или инвестор управляет капиталом.

Класс трейлинг-стопа

Наконец, рассмотрим реализацию пользовательского трейлинг-стопа, который также использует BI. Для этого нам придется сосредоточиться на диапазоне ценовых баров, поскольку это всегда хороший показатель волатильности — ключевого показателя, влияющего на то, насколько следует скорректировать уровень стоп-лосса для открытых позиций. Мы использовали изменения значений временных рядов, тогда как для сигнала мы применили изменения цен закрытия, а для ММ - торговый результат (прибыль в отличие от уровня эквити на счете), который также фактически является изменением уровня эквити на счете. Изменения, примененные к нашему элементарному методу кластеризации, дают нам очень простой, но работоспособный набор индексов, которые полезны для группировки точек данных с плавающей точкой.

Аналогичный подход для класса трейлинга советника будет сосредоточен на изменениях в диапазоне ценовых баров от высоких до низких. Наша гипотеза при таком подходе заключается в том, что мы ищем индекс кластера (m_long_cluster или m_short_cluster - оба могут быть одинаковыми в данной ситуации трейлинга) - такой, что когда вероятность его следования во временном ряду возрастает, нам необходимо переместить наш стоп-лосс на величину, пропорциональную текущему диапазону ценового бара.

Мы использовали отдельные входные параметры для длинных и коротких позиций, но в принципе мы могли бы использовать только один для регулировки стоп-лосса как по длинным, так и по коротким позициям. Ниже приведен листинг для длинных позиций:

//+------------------------------------------------------------------+
//| Checking trailing stop and/or profit for long position.          |
//+------------------------------------------------------------------+
bool CTrailingBAYES::CheckTrailingStopLong(CPositionInfo *position,double &sl,double &tp)
  {
//--- check

...

//---
 
...

//---
   sl=EMPTY_VALUE;
   tp=EMPTY_VALUE;
   //
   
   vector _h_new, _h_old, _l_new, _l_old, _s;
   _h_new.CopyRates(m_symbol.Name(), m_period, COPY_RATES_HIGH, 0, m_series_size);
   _h_old.CopyRates(m_symbol.Name(), m_period, COPY_RATES_HIGH, 1, m_series_size);
   _l_new.CopyRates(m_symbol.Name(), m_period, COPY_RATES_LOW, 0, m_series_size);
   _l_old.CopyRates(m_symbol.Name(), m_period, COPY_RATES_LOW, 1, m_series_size);
   _s = (_h_new - _l_new) - (_h_old - _l_old);
   matrix _series;
   _series.Init(_s.Size(), 2);
   for(int i = 0; i < int(_s.Size()); i++)
   {  _series[i][0] = _s[i];
   }
   SetCluster(_series);
   double _cond = GetPosterior(m_long_cluster, _series);
   //
   delta=0.5*(_h_new[0] - _l_new[0]);
   if(_cond>0.5&&price-base>delta)
     {
      sl=price-delta;
     }
//---
   return(sl!=EMPTY_VALUE);
  }

В разделе тестирования и отчетов ниже приведено сравнение с альтернативными классами трейлинг-стопа, в частности, с теми, что встроены в библиотеку MQL5.

Тестирование и отчеты

Мы проводим тесты на EURJPY H4 за 2022 год. Поскольку мы разработали 3 отдельных пользовательских класса, которые можно использовать в советниках, собранных в Мастере, мы последовательно соберем 3 отдельных советника, причем первый будет иметь только класс сигнала, в то время как управление капиталом использует фиксированные лоты и не использует трейлинг-стоп. Второй будет иметь тот же класс сигнала, но с добавлением класса управления капиталом, который мы реализовали выше, без трейлинг-стопа. Третий советник будет иметь все 3 класса, реализованных выше. Инструкции по сборке классов с помощью Мастера доступны здесь.

Если мы запустим тесты на всех трех советниках, то получим следующие отчеты и кривые эквити:

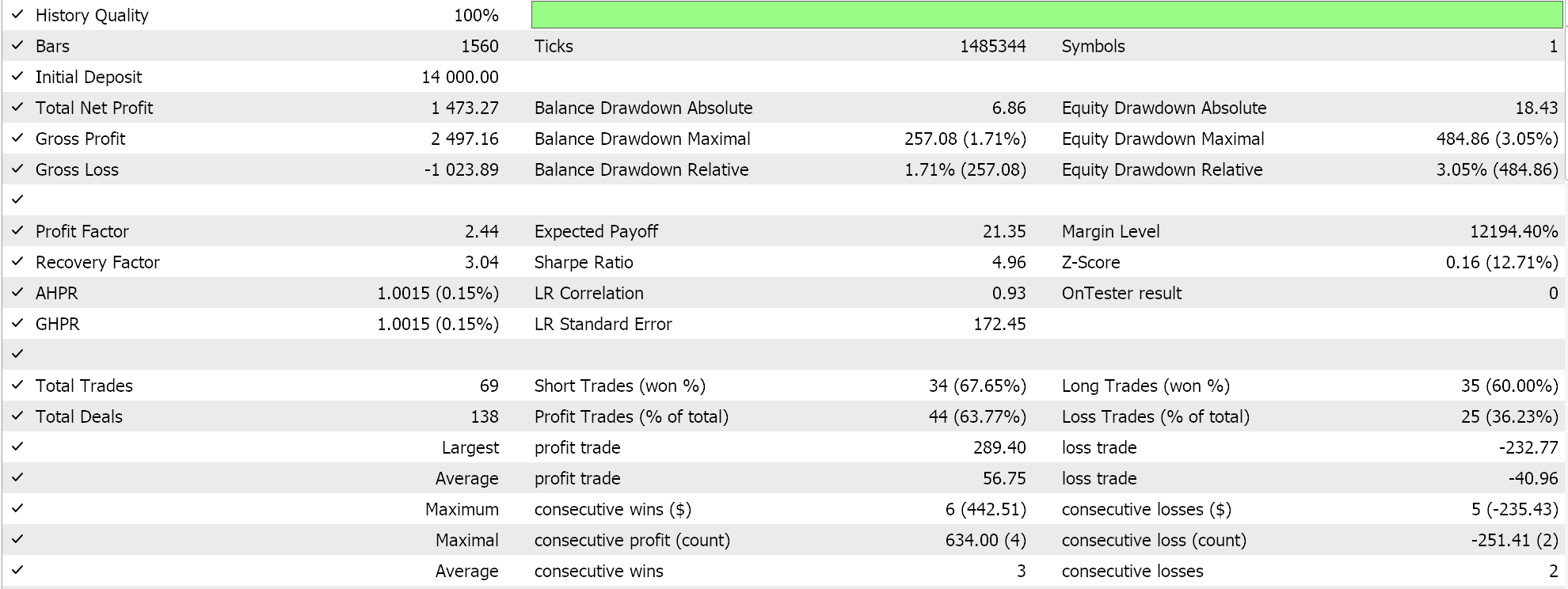
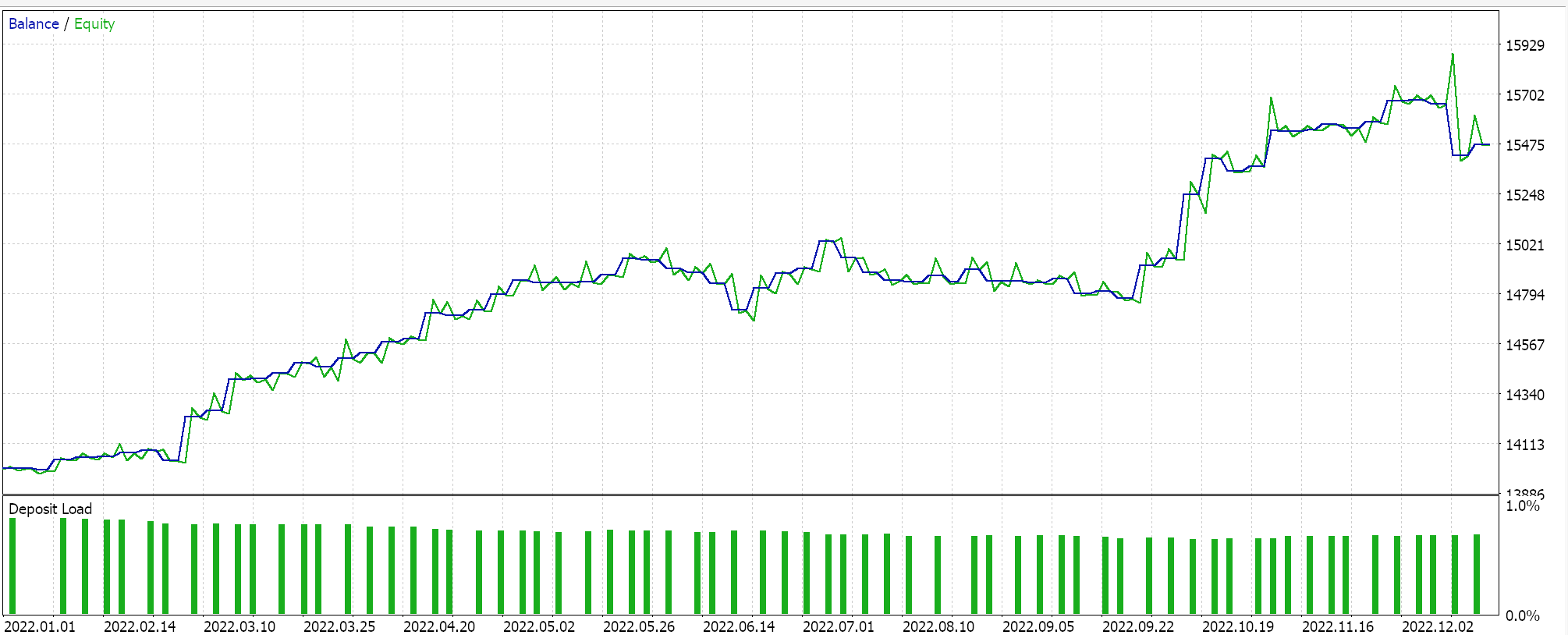
Отчет и кривая эквити советника только с классом сигнала BI.

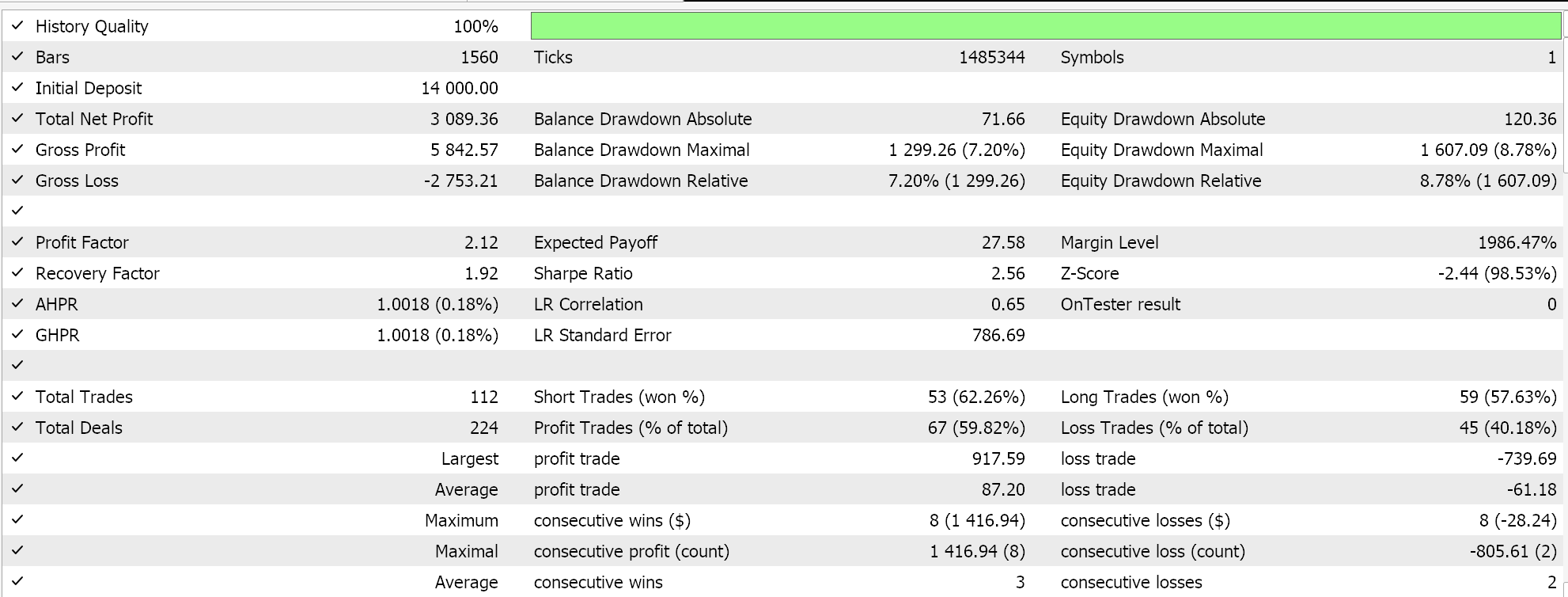
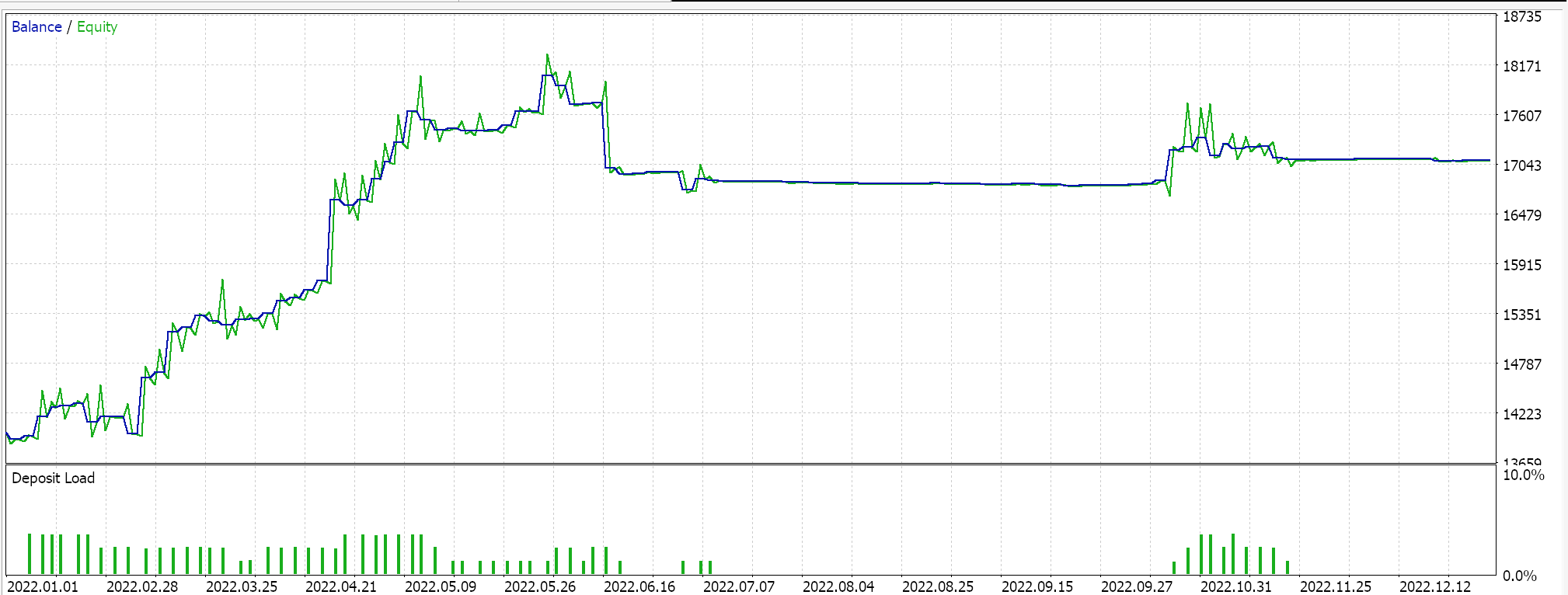
Отчет и кривая эквити советника с классом сигнала BI и классом MM.

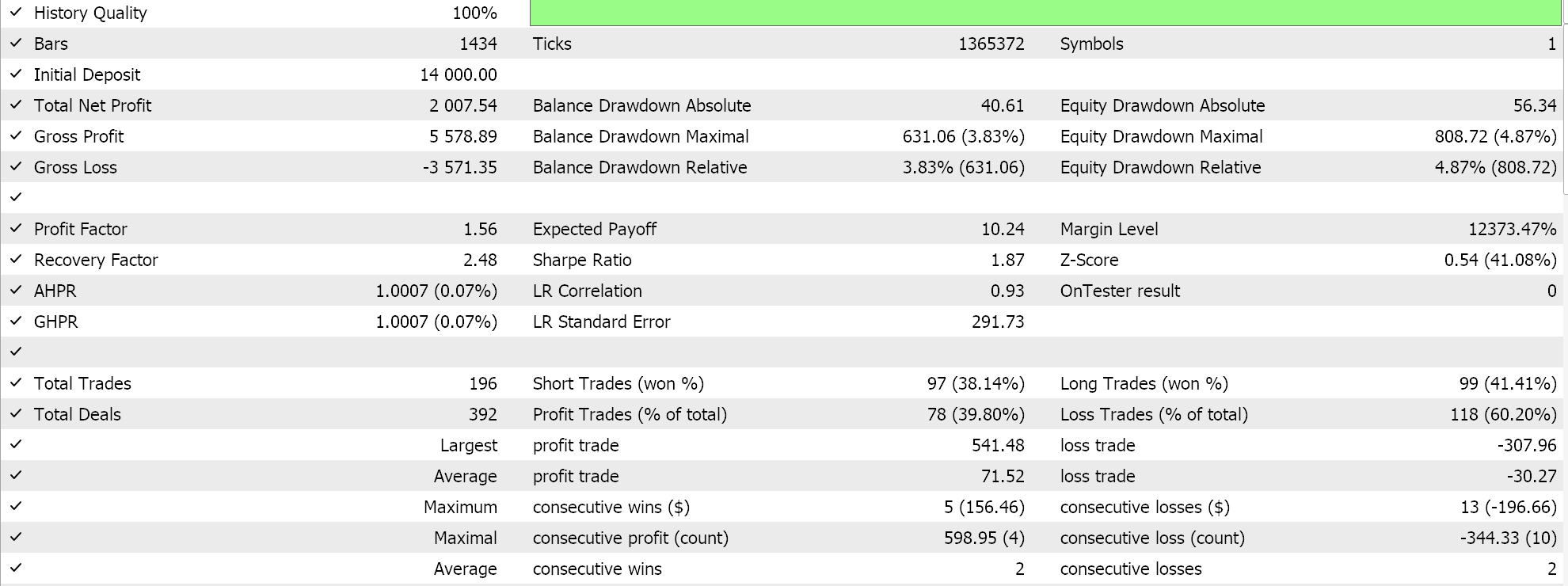
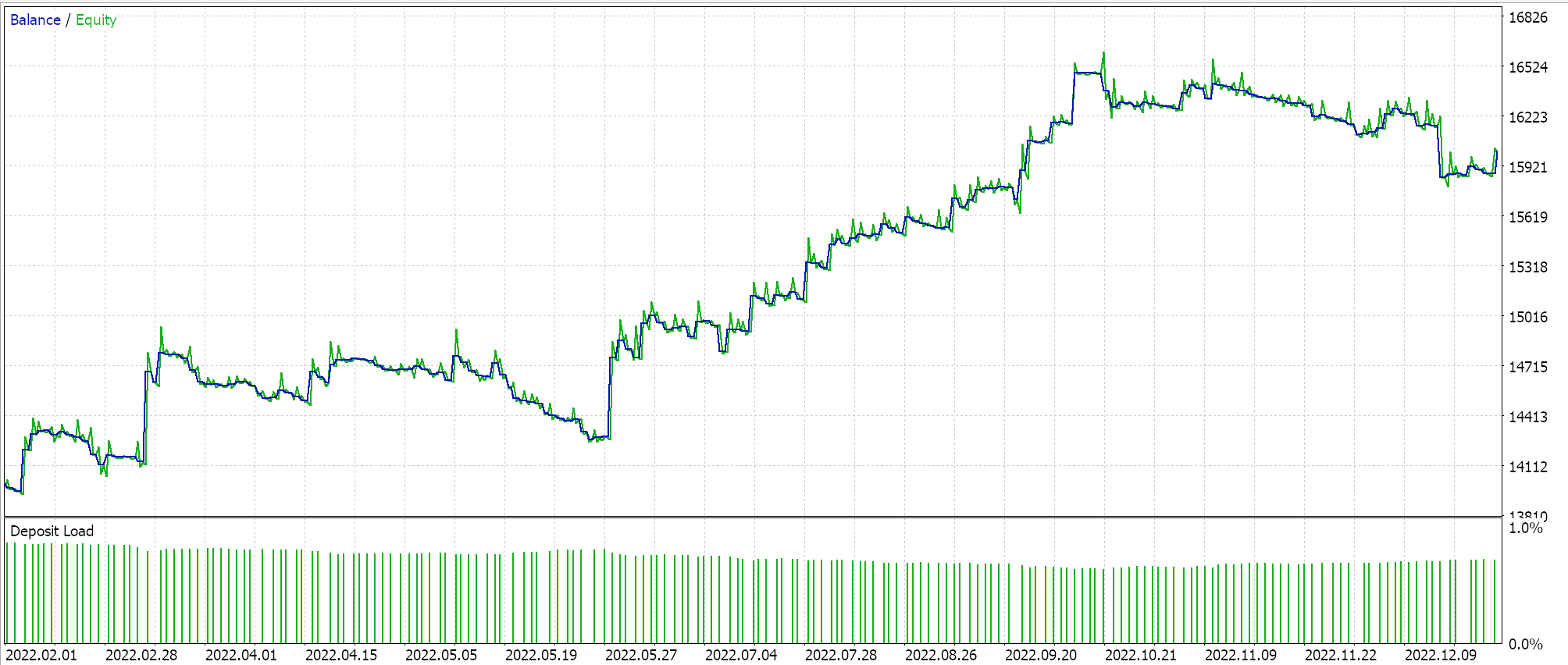
Отчет и кривая эквити советника с классами сигнала BI, ММ и трейлинга.

Похоже, что по мере дальнейшей адаптации BI от сигнального класса через MM к трейлинг-классу общая производительность имеет тенденцию к положительной корреляции. Тестирование проводилось на реальных тиках, но, как всегда, в идеале необходимо независимое тестирование в течение более длительных периодов времени. В качестве контроля мы можем оптимизировать три отдельных советника, использующих библиотечные классы. Во всех этих тестовых прогонах я не использую целевые цены выхода и полагаюсь только на сигналы открытия и закрытия для контроля выходов. Я выбрал класс сигнала Awesome Oscillator, класс управления капиталом с оптимизированным размером и трейлинг-классы скользящих средних для использования в "контрольных" советниках. Аналогичные тестовые прогоны, описанные выше, дают следующие результаты:

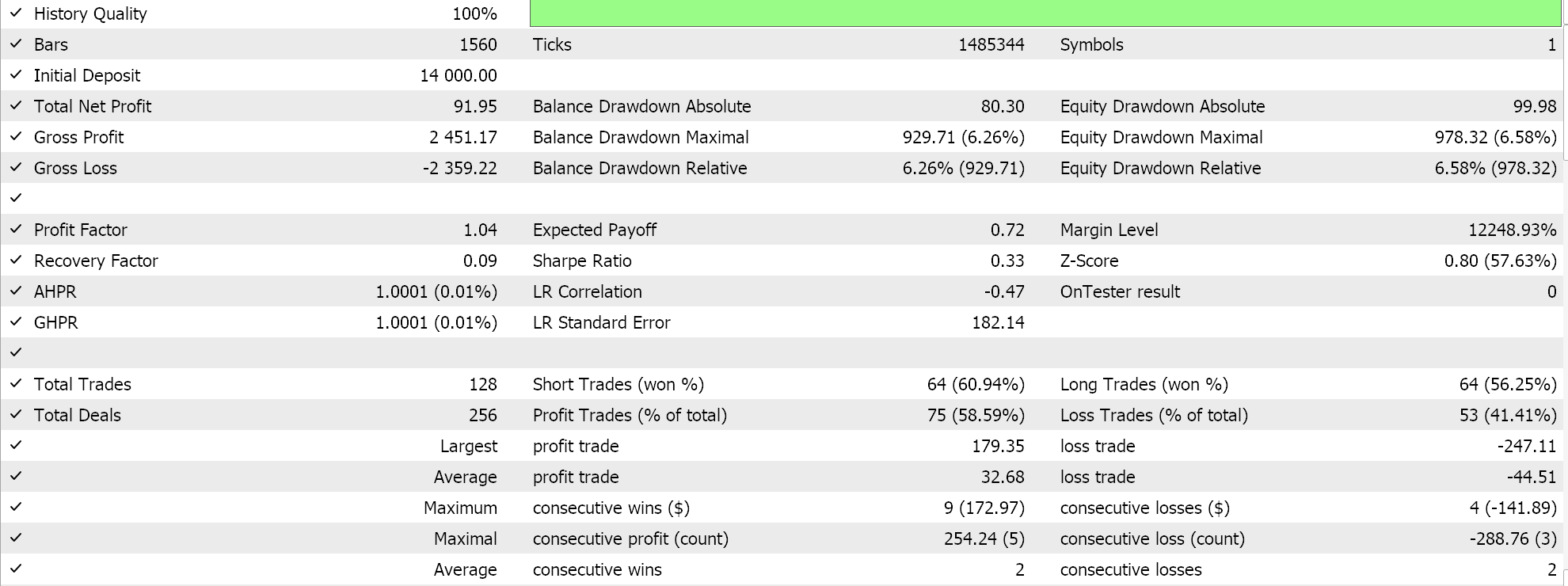
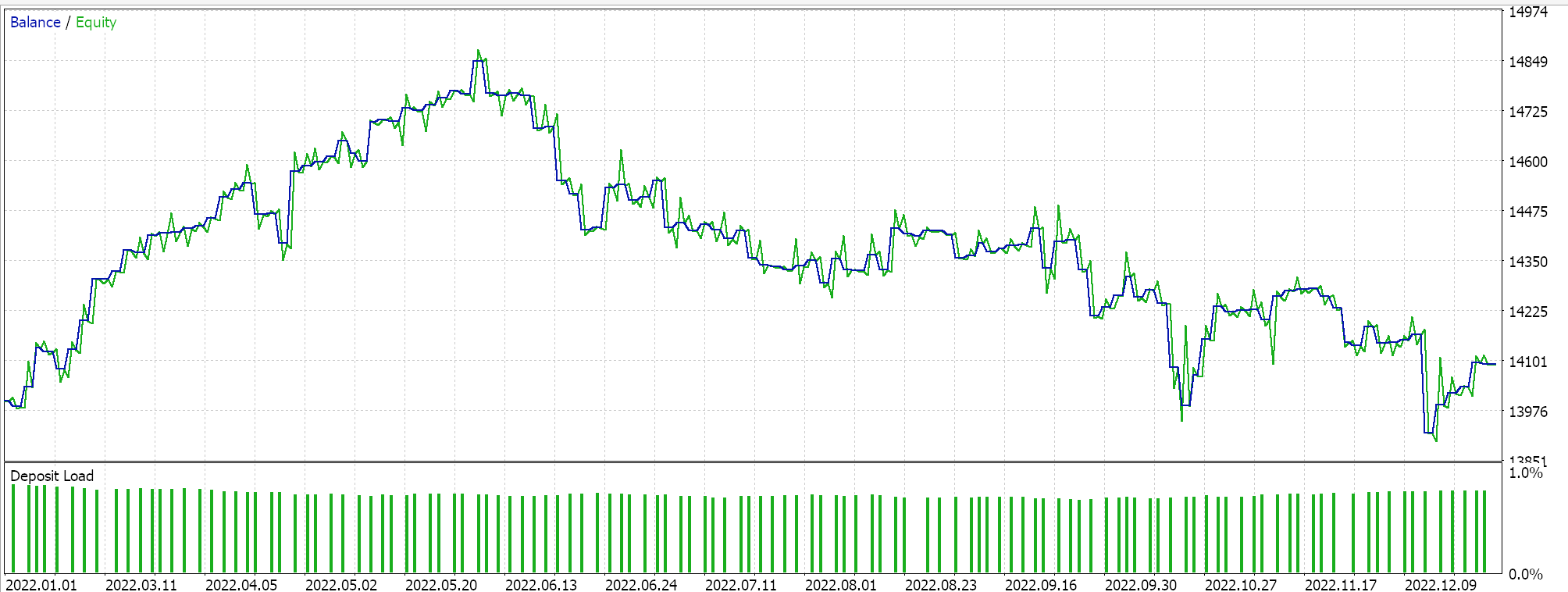
Отчет и кривая эквити советника только с классом Awesome Oscillator.

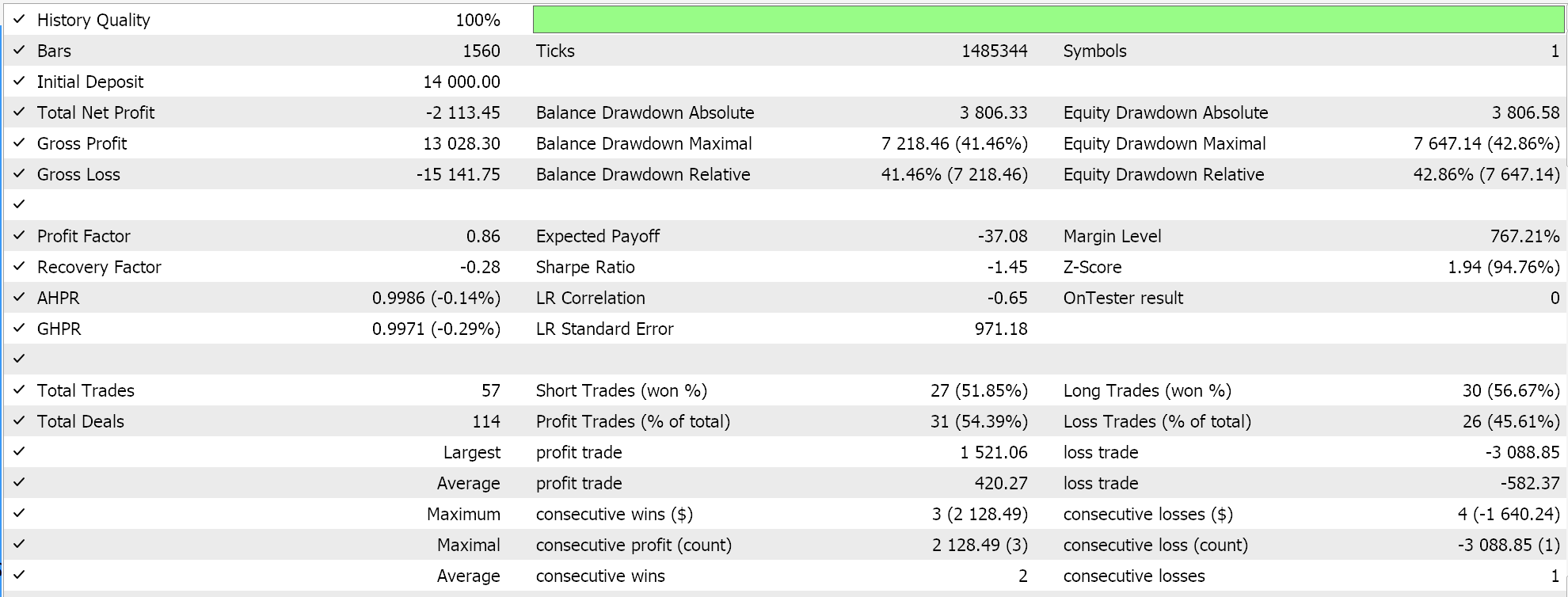
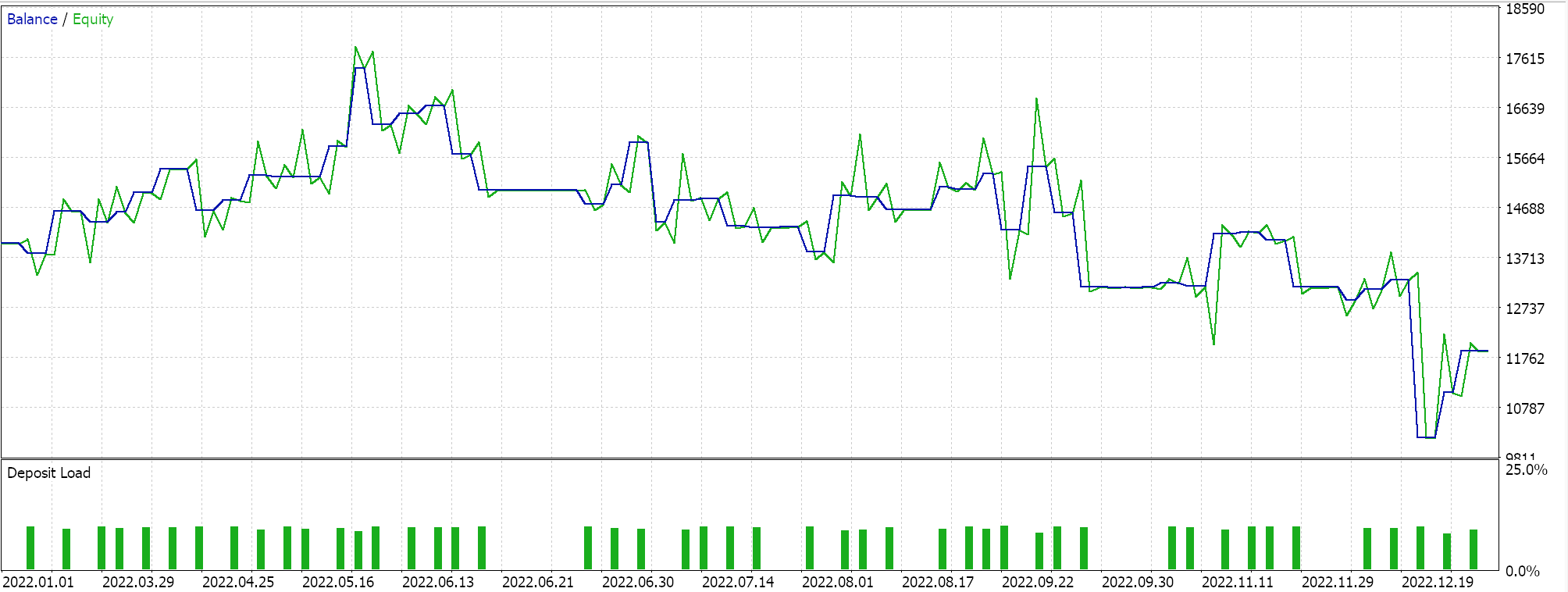
Отчет и кривая эквити управляющего советника с двумя выбранными классами.

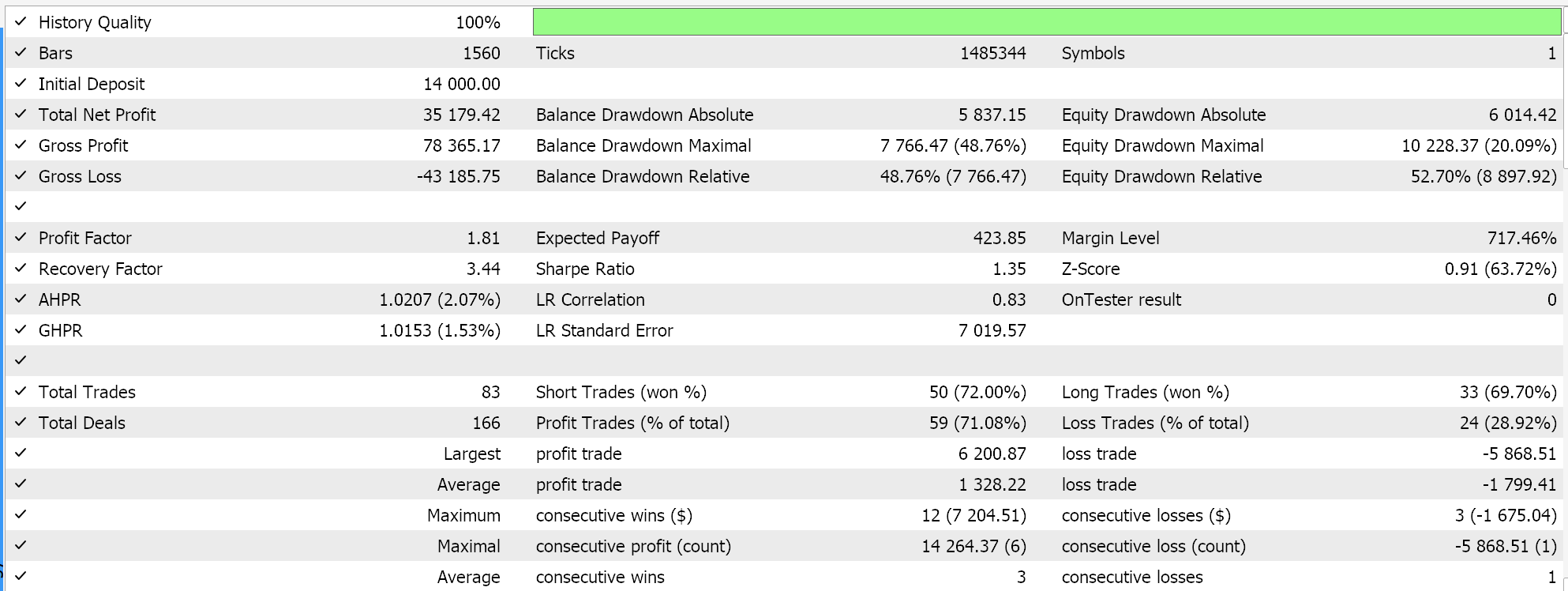
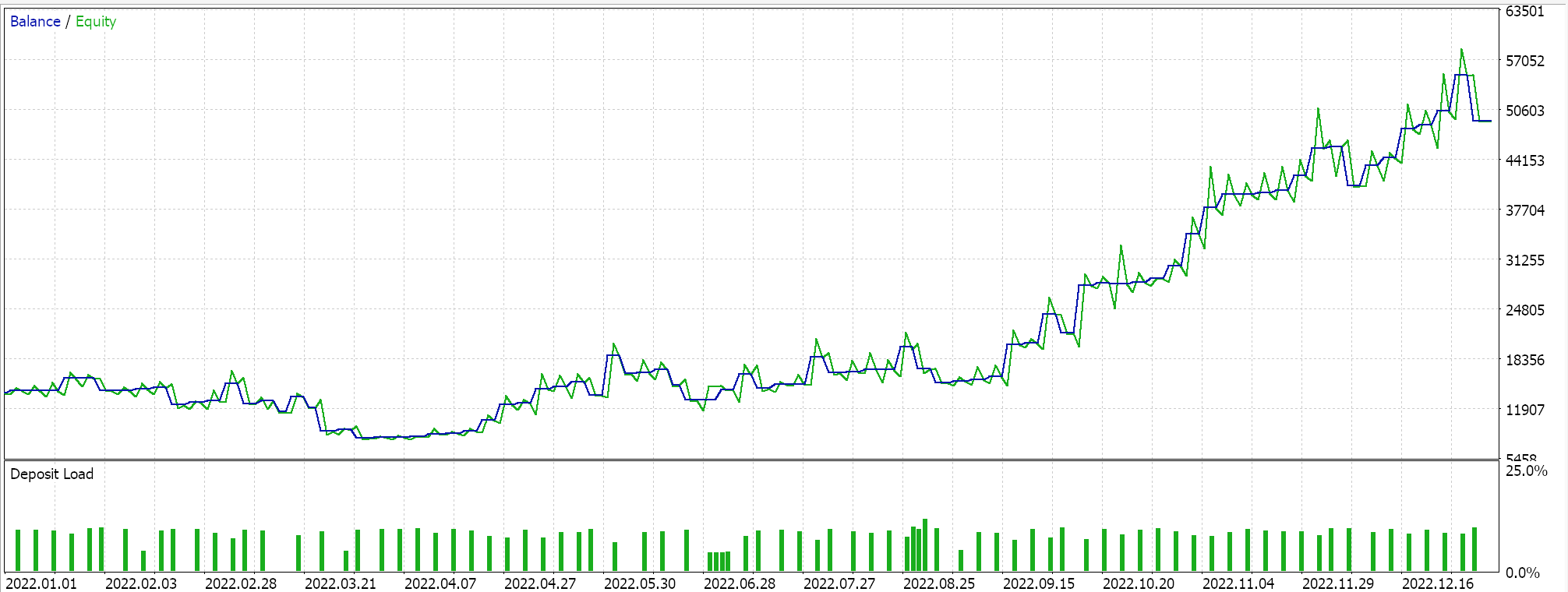
Отчет и кривая эквити управляющего советника со всеми тремя выбранными классами.

Результаты хуже, чем у советника BI, за исключением третьего запуска. Наш выбор альтернативных классов сигналов, ММ и трейлинга также во многом повлиял на этот "результат", однако общая цель состояла в том, чтобы установить, есть ли существенные различия в производительности между советником BI и тем, что доступно в библиотеке MQL5. Ответ на этот вопрос очевиден.

Заключение

Мы протестировали байесовский вывод в построении простого советника, включив его основные идеи в три различных класса советников, собранных с помощью Мастера MQL5. Наш подход здесь был строго вводным и не охватывал существенных вопросов, в частности использования более сложных кластерных алгоритмов или даже многомерных наборов данных. Все это эти темы можно исследовать и они могут дать преимущество, если их правильно протестировать на достаточно больших исторических периодах и на тиковых данных хорошего качества. С помощью байесовского вывода можно протестировать довольно много торговых идей. При этом советники, собранные в Мастере, остаются надежными инструментами для их тестирования и прототипирования.