Возможности Мастера MQL5, которые вам нужно знать (Часть 12): Полином Ньютона

Введение

Анализ временных рядов играет важную роль не только как часть фундаментального анализа. На очень ликвидных рынках, таких как форекс, он может быть основным фактором принятия решений. Традиционные технические индикаторы имеют тенденцию сильно отставать от рынка, что привело к появлению альтернатив. Возможно, наиболее популярными из них на данный момент являются нейронные сети. Но что насчет полиномиальной интерполяции?

Она представляет некоторые преимущества, главным образом потому, что их легко понять и реализовать, поскольку интерполяция явно представляет взаимосвязь между прошлыми наблюдениями и будущими прогнозами в простом уравнении. Это помогает понять, как прошлые данные влияют на будущие значения, что, в свою очередь, приводит к разработке широких концепций и возможных теорий поведения изучаемых временных рядов.

Кроме того, возможность адаптации как к линейным, так и к квадратичным отношениям делает ее гибкой для различных временных рядов и, возможно, более подходящей для трейдеров, работающих с различными типами рынков (например, флет против тренда или волатильность против спокойного рынка).

Более того, интерполяция обычно не требует больших вычислительных ресурсов и относительно проста по сравнению с альтернативными подходами, такими как нейронные сети. Фактически, модели, рассмотренные в этой статье, не имеют никаких требований к памяти, чего нельзя сказать о нейронной сети, которая, в зависимости от ее архитектуры, требует места для хранения большого количества оптимальных весов и смещений после каждого сеанса обучения.

Формально интерполяционный полином Ньютона N(x) определяется уравнением:

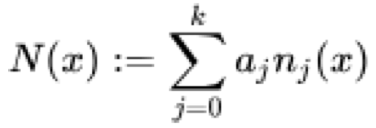
где все x j уникальны в ряду, a j - сумма разделенных разностей, в то время как n j (x) - сумма произведений базовых коэффициентов для x, что можно формально представить так:

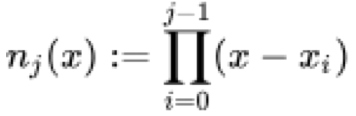
Формулы разделенных разностей и базовых коэффициентов можно легко найти независимо, однако давайте попробуем раскрыть их определения в менее строгом виде.

Разделенные разности — это повторяющийся процесс деления, при котором коэффициенты для x устанавливаются в каждом показателе степени до тех пор, пока все показатели x не будут исчерпаны из предоставленного набора данных. Чтобы проиллюстрировать это, давайте рассмотрим приведенный ниже пример из трех точек данных:

(1,2), (3,4) и (5,6)

Для использования разделенной разницы все значения x должны быть уникальными. Количество предоставленных точек данных определяет максимальную степень x в получаемом полиноме Ньютона. Например, если бы у нас было только две точки, наше уравнение было бы линейным:

y = mx + c.

Подразумевается, что максимальная степень равна единице. Таким образом, в нашем примере с тремя точками наивысший показатель степени равен 2, что означает, что нам нужно получить 3 разных коэффициента для нашего производного полинома.

Получение каждого из этих трех коэффициентов представляет собой пошаговый итеративный процесс, пока мы не доберемся до третьего. В приведенных выше ссылках есть формулы, но, вероятно, лучший способ понять весь процесс — использовать таблицу, подобную показанной ниже:

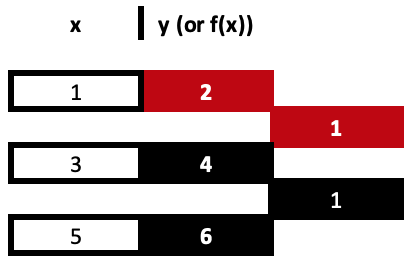
Итак, наш первый столбец разделенных разностей получается в результате деления разницы между значениями y и изменением соответствующих значений x. Помните, что все значения x должны быть уникальными. Эти вычисления очень просты и понятны, однако их легко проследить по таблице, как показано выше, а не по типичным формулам, указанным в общих ссылках. Оба подхода приводят к одному и тому же результату.

= (4 - 2) / (3 - 1)

Получаем наш первый коэффициент, равный 1.

= (6 - 4) / (5 - 3)

Дает нам второй аналогичный коэффициент. Коэффициенты выделены красным.

В нашем примере с тремя точками данных окончательное значение получит разности y от только что вычисленных значений. Но его знаменатели x будут двумя крайними значениями в ряду x, поскольку их разность будет делителем, поэтому наша таблица будет выглядеть следующим образом:

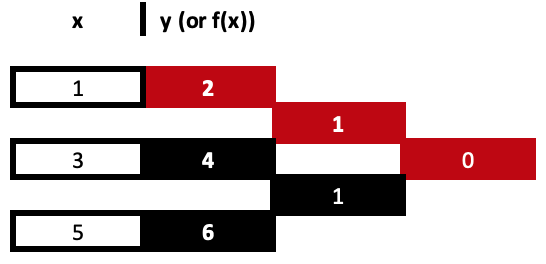
В нашей заполненной таблице выше у нас есть 3 производных значения, но только 2 из них используются для получения коэффициентов. Это приводит нас к суммам произведений "базовых полиномов". Как бы причудливо это ни звучало, на самом деле они даже проще чем разделенные разности. Чтобы проиллюстрировать это на основе наших производных коэффициентов из таблицы выше, наше уравнение для трех точек будет иметь следующий вид:

y = 2 + 1*(x – 1) + 0*(x – 1)*(x – 3)

что сводится к:

y = x + 1

Добавленные скобки — это все, что составляет базовые полиномы. Значение x n представляет собой соответствующее значение x для каждой точки выборки данных. Вернемся к коэффициентам. Как правило, мы используем только верхние значения таблицы в качестве префикса значений в скобках. По мере того, как мы продвигаемся вправо, получая более короткие столбцы в таблице, верхние значения выступают в качестве префиксов более длинных последовательностей в скобках до тех пор, пока не будут рассмотрены все имеющиеся точки данных. Как уже упоминалось, чем больше точек данных нужно интерполировать, тем больше показателей степени x и, следовательно, тем больше столбцов мы будем иметь в нашей производной таблице.

Прежде чем перейти к реализации, давайте приведем еще один пример. Предположим, у нас есть 7 точек данных для цен на ценные бумаги, где значения x — это просто индекс ценового бара, как показано ниже:

0	1,25590
1	1,26370
2	1,25890
3	1,25395
4	1,25785
5	1,26565
6	1,26175

Наша таблица, которая распространяет значения коэффициентов, будет расширена на 8 столбцов следующим образом:

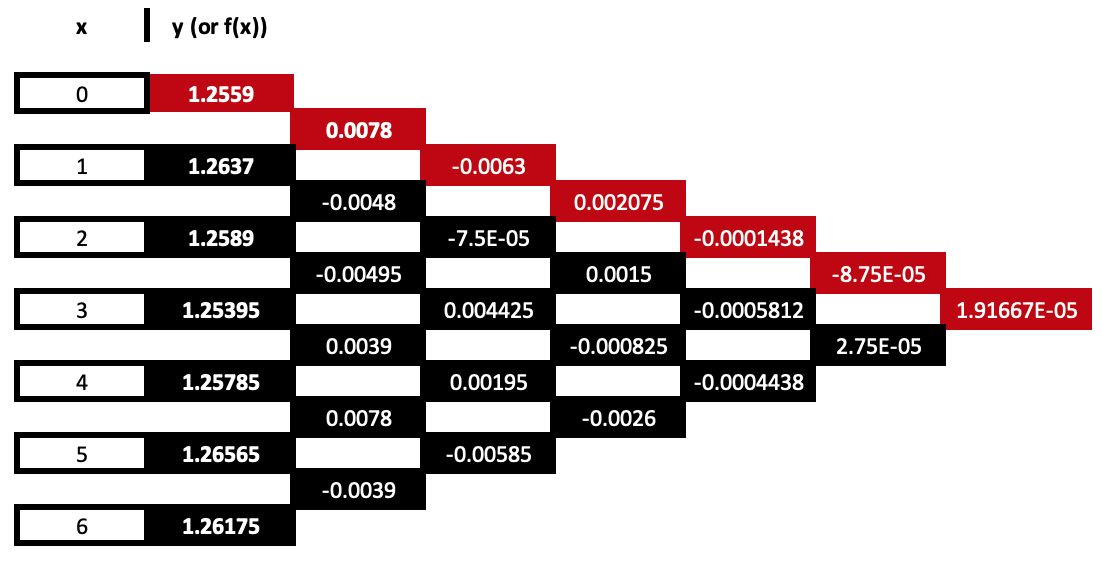
С учетом приведенных коэффициентов (выделены красным), уравнение будет выглядеть следующим образом:

y = 1.2559 + 0.0078*(x – 0) – 0.0063*(x – 0)*(x – 1) + …

Уравнение доходит до степени 6, учитывая семь точек данных, и его ключевая функция может состоять в прогнозировании следующего значения путем ввода в уравнение нового индекса x. Если выборочные данные были "заданы как серия", то следующий индекс будет равен -1, в противном случае он будет равен 8.

Реализация в MQL5

Реализация средствами MQL5 может быть достигнута с минимальным написанием кода, хотя мне не удалось найти какие-либо библиотеки, которые позволяли бы реализовать эти идеи, например, из уже готовых экземпляров классов.

Однако для этого нам нужно сделать две вещи. Во-первых, нам нужна функция для расчета коэффициентов x для нашего уравнения с учетом нашего набора выборочных данных. Во-вторых, нам также нужна функция для обработки прогнозируемого значения с использованием нашего уравнения, представленного со значением x. Все это звучит довольно просто, но, учитывая, что мы хотим добиться масштабируемости, необходимо учитывать несколько нюансов на этапе обработки.

Что здесь понимается под "масштабируемостью"? Это функции, которые могут использовать разделенные разности для получения коэффициентов для наборов данных, размер которых не определен заранее. Это может показаться очевидным, но давайте рассмотрим наш первый пример с тремя точками данных. Его реализация на MQL5 для получения коэффициентов приведена ниже.

Приведенный ниже листинг содержит уравнения для получения разделенной разности для двух пар в выборочных данных, повторяя эту процедуру для получения последнего значения. Теперь, если бы у нас была выборка из 4 точек данных, то для интерполяции ее уравнения потребовалась бы другая функция, поскольку нам нужно сделать больше шагов, чем показано в примере с 3 точками выше.

Итак, если бы у нас была масштабируемая функция, она была бы способна обрабатывать наборы данных размера n и выводить коэффициенты n-1. Это показано в следующем листинге:

//+------------------------------------------------------------------+
//| INPUT PARAMETERS                                                 |
//|     X   -   vector with x values of sampled data                 |
//|     Y   -   vector with y values of sampled data                 |
//| OUTPUT PARAMETERS                                                |
//|     W   -   vector with coefficients.                            |                                          |
//+------------------------------------------------------------------+
void Cnewton::Set(vector &W, vector &X, vector &Y)
{  vector _w[];
   ArrayResize(_w, int(X.Size() - 1));
   int _x_scale = 1;
   int _y_scale = int(X.Size() - 1);
   for(int i = 0; i < int(X.Size() - 1); i++)
   {  _w[i].Init(_y_scale);
      for(int ii = 0; ii < _y_scale; ii++)
      {  if(X[ii + _x_scale] != X[ii])
         {  if(i == 0)
            {  _w[i][ii] = (Y[ii + 1] - Y[ii]) / (X[ii + _x_scale] - X[ii]);
            }
            else if(i > 0)
            {  _w[i][ii] = (_w[i - 1][ii + 1] - _w[i - 1][ii]) / (X[ii + _x_scale] - X[ii]);
            }
         }
         else
         {  printf(__FUNCSIG__ + " ERR!, identical X value: " + DoubleToString(X[ii + _x_scale]) + ", at: " + IntegerToString(ii + _x_scale) + ", and: " + IntegerToString(ii));
            return;
         }
      }
      _x_scale++;
      _y_scale--;
      W[i + 1] = _w[i][0];
      if(_y_scale <= 0)
      {  break;
      }
   }
}

Эта функция работает с использованием двух вложенных циклов for и двух целых чисел, которые отслеживают индексы для значений x и y. Возможно, это не самый эффективный способ реализации, но он работает. В него можно вносить улучшения в зависимости от варианта использования.

Функция для обработки следующего y с учетом входного сигнала x и всех коэффициентов наших уравнений также представлена ниже:

//+------------------------------------------------------------------+
//| INPUT PARAMETERS                                                 |
//|     W   -   vector with pre-computed coefficients                |
//|     X   -   vector with x values of sampled data                 |
//|     XX  -   query x value with unknown y                         |
//| OUTPUT PARAMETERS                                                |
//|     YY  -   solution for unknown y.                              |  
//+------------------------------------------------------------------+
void Cnewton::Get(vector &W, vector &X, double &XX, double &YY)
{  YY = W[0];
   for(int i = 1; i < int(W.Size()); i++)
   {  double _y = W[i];
      for(int ii = 0; ii < i; ii++)
      {  _y *= (XX - X[ii]);
      }
      YY += _y;
   }
}

Она выглядит проще, чем наша предыдущая функция, хотя также имеет вложенный цикл. Всё, что мы делаем, — это отслеживаем коэффициенты, которые получили в функции набора, и присваиваем им соответствующий базовый полином Ньютона.

Области применения

В этой статье мы рассмотрим, как метод можно использовать в качестве сигнала и трейлинг-стопа, а также в управлении капиталом. Прежде чем начать писать код, обычно рекомендуется подготовить класс привязки с двумя функциями, реализующими интерполяцию. Код класса приведен выше. Для класса у нас будет следующий интерфейс:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cnewton
{
private:

public:
                     Cnewton();
                    ~Cnewton();
   void              Set(vector &W, vector &X, vector &Y);
   void              Get(vector &W, vector &X, double &XX, double &YY);
};

Сигнал

Стандартные файлы классов сигналов советников, представленные в библиотеке MQL5, как всегда служат полезным руководством в собственных разработках. В нашем случае первым очевидным выбором входных выборочных данных для генерации полинома будут необработанные цены закрытия ценных бумаг. Чтобы сгенерировать полином на основе цен закрытия, мы сначала заполняем векторы x и y индексами ценовых баров и фактическими ценами закрытия соответственно. Эти два вектора являются ключевыми входными данными нашей функции set, которая отвечает за получение коэффициентов. Мы просто используем индексы ценовых баров для x в нашем сигнале, но можно использовать альтернативы, такие как дневные или недельные сессии, при условии, конечно, что ни одна из них не повторяется в выборке данных, т.е. все они появляются только один раз, например, если в ваш торговый день проведено 4 сессии, вы можете предоставить не более 4 точек данных, а индексы сессий 0, 1, 2 и 3 могут появляться в наборе данных только один раз.

После заполнения наших векторов x и y вызов функции set должен предоставить предварительные коэффициенты нашему полиномиальному уравнению. Если мы запустим это уравнение с коэффициентами и следующим значением x с помощью функции get, мы получим проекцию того, каким будет следующее значение y. Поскольку наши входные значения y в функции set были ценами закрытия, мы будем искать следующую цену закрытия. Соответствующий код приведен ниже:

   double _xx = -1.0;//m_length + 1.0,
   double _yy = 0.0;
   __N.Get(_w, _xx, _yy);

Помимо получения следующей прогнозируемой цены закрытия, функции открытия проверки класса сигналов советника обычно выводят целое число в диапазоне от 0 до 100 как признак того, насколько сильным является сигнал на покупку или продажу. Поэтому в нашем случае нам нужно найти способ представить прогнозируемую цену закрытия в виде простого целого числа, которое помещается в этот диапазон.

Чтобы получить эту нормализацию, прогнозируемое изменение цены закрытия выражается в процентах от текущего диапазона высоких и низких цен. Затем этот процент выражается целым числом в диапазоне от 0 до 100. Это означает, что отрицательные изменения цены закрытия в функции "проверки открытия длинной позиции" автоматически будут равны нулю, как и положительные изменения прогноза в функции "проверки открытия короткой позиции".

   m_high.Refresh(-1);
   m_low.Refresh(-1);
   m_close.Refresh(-1);
   int _i = StartIndex();
   double _h = m_high.GetData(m_high.MaxIndex(_i,m_length));
   double _l = m_low.GetData(m_low.MinIndex(_i,m_length));
   double _c = m_close.GetData(0);
//
   if(_yy > _c)
   {  _result = int(round(((_yy - _c) / (fmax(_h, fmax(_yy, _c)) - fmin(fmin(_yy, _c), _l))) * 100.0));
   }

При составлении прогнозов с помощью полиномиального уравнения единственная переменная, которую мы используем, — это продолжительность периода ретроспективного анализа (который устанавливает размер выборочных данных). Это переменная m_length. При запуске оптимизации только для этого параметра на символе EURJPY H1 в 2023 году мы получим следующие отчеты.

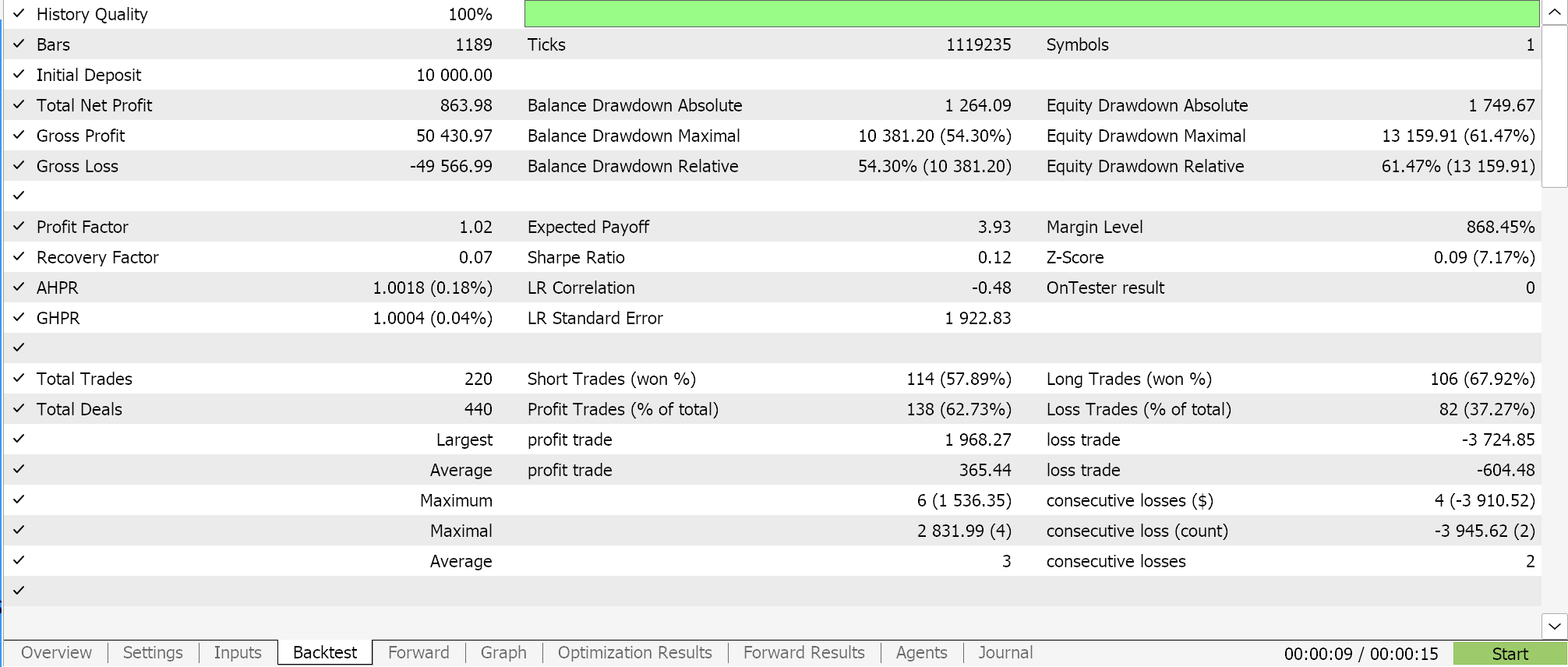
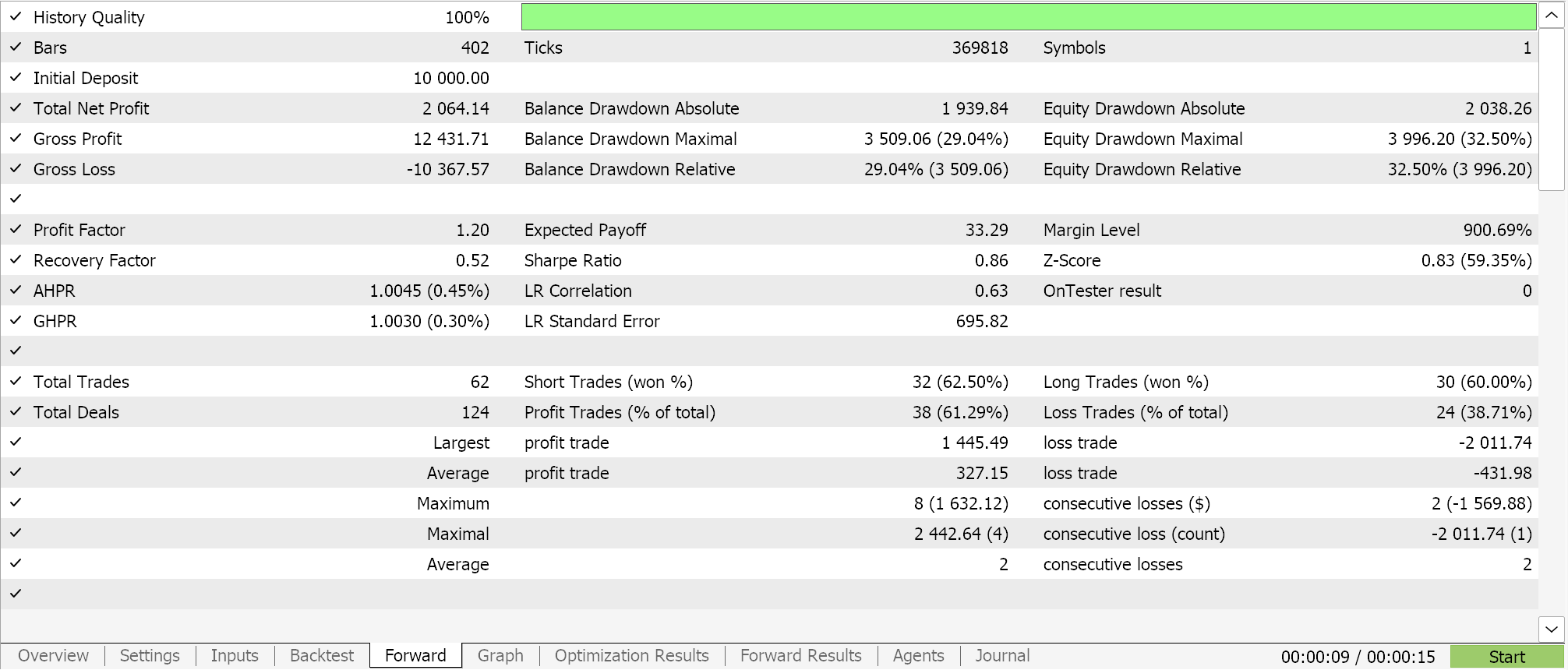
Полный анализ за весь год дает нам следующую картину по эквити:

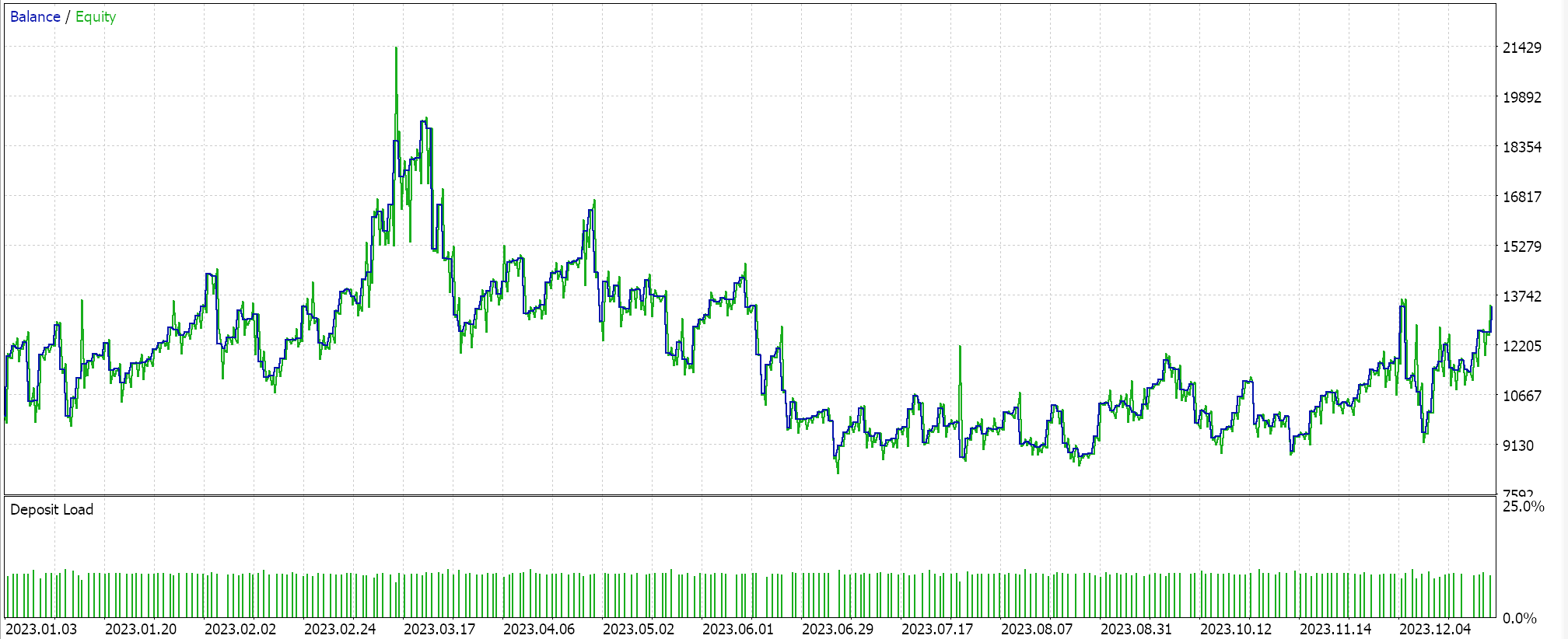
Трейлинг-стоп

Помимо класса сигнала советника, мы можем собрать советник с помощью мастера, выбрав также метод установки и настройки трейлинг-стопа открытых позиций. В библиотеке предусмотрены методы, использующие Parabolic Sar и скользящие средние, и в целом их количество намного меньше, чем в библиотеке сигналов. Если мы хотим улучшить этот подсчет, добавив класс, использующий полином Ньютона, тогда, возможно, нашими выборочными данными должны быть диапазоны ценовых баров.

Таким образом, если мы выполним те же шаги, которые мы предприняли выше при прогнозировании следующей цены закрытия, при этом основным изменением будут данные вектора y, который в данном случае теперь будет диапазоном ценовых баров, тогда наш источник будет следующим:

//+------------------------------------------------------------------+
//| Checking trailing stop and/or profit for long position.          |
//+------------------------------------------------------------------+
bool CTrailingNP::CheckTrailingStopLong(CPositionInfo *position, double &sl, double &tp)
{
//--- check

   ...

//---
   m_high.Refresh(-1);
   m_low.Refresh(-1);
   vector _x, _y;
   _x.Init(m_length);
   _y.Init(m_length);
   for(int i = 0; i < m_length; i++)
   {  _x[i] = i;
      _y[i] = (m_high.GetData(StartIndex()+i)-m_low.GetData(StartIndex()+i));
   }
   vector _w;
   _w.Init(m_length);
   _w[0] = _y[0];
   __N.Set(_w, _x, _y);
   double _xx = -1.0;
   double _yy = 0.0;
   __N.Get(_w, _x, _xx, _yy);
//---

   ...

//---
   return(sl != EMPTY_VALUE);
}

Часть этого диапазона прогнозируемых баров затем используется для установки размера стоп-лосса позиции. Используемая пропорция представляет собой оптимизируемый параметр m_stop_level, и перед установкой нового стоп-лосса мы добавляем к этой дельте минимальное расстояние стопа, чтобы избежать ошибок брокера. Эта нормализация показана в коде ниже:

//+------------------------------------------------------------------+
//| Checking trailing stop and/or profit for long position.          |
//+------------------------------------------------------------------+
bool CTrailingNP::CheckTrailingStopLong(CPositionInfo *position, double &sl, double &tp)
{
//--- check
   
   ...

//---
   sl = EMPTY_VALUE;
   tp = EMPTY_VALUE;
   delta = (m_stop_level * _yy) + (m_symbol.Point() * m_symbol.StopsLevel());
//---
   if(price - base > delta)
   {  sl = price - delta;
   }
//---
   return(sl != EMPTY_VALUE);
}

Если мы соберем советник с помощью Мастера MQL5, использующего класс сигналов библиотеки Awesome Oscillator, и попробуем оптимизировать только для идеальной полиномиальной длины, для того же символа, таймфрейма и 1-летнего периода, что и выше, мы получим следующий отчет при наилучшем исходе:

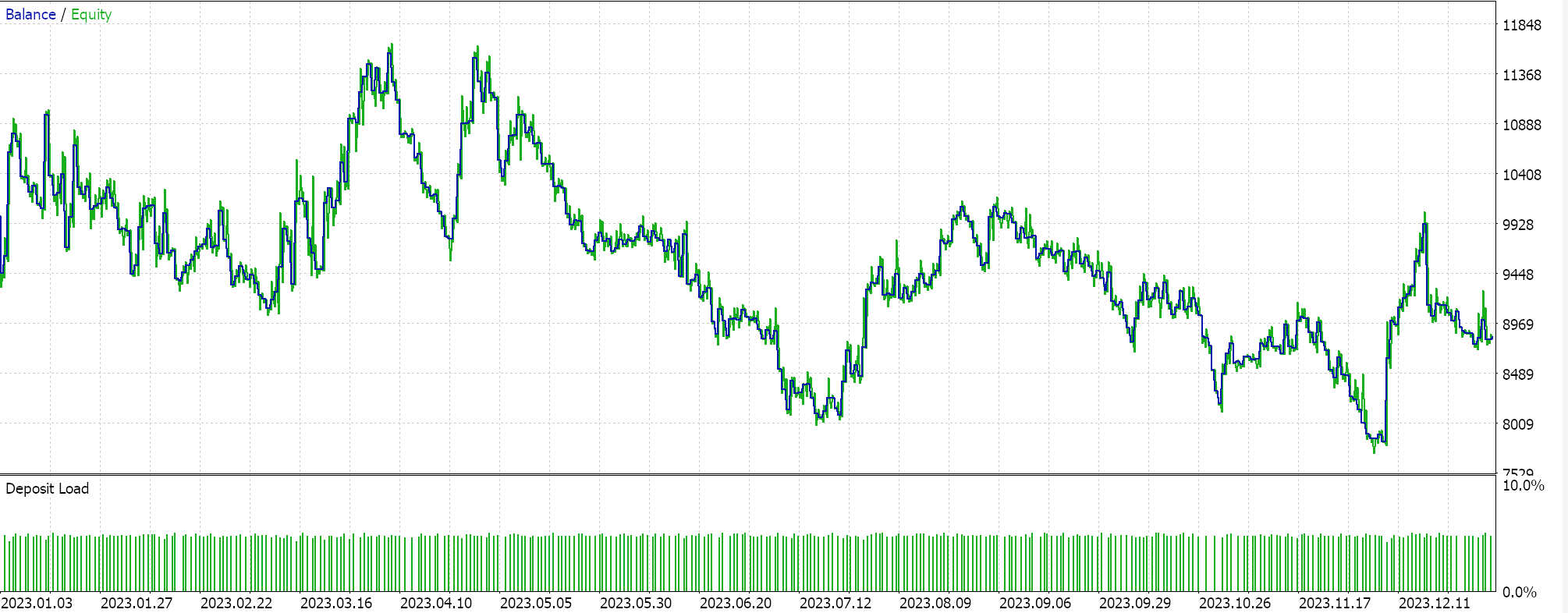
Результаты в лучшем случае неудовлетворительны. Интересно, что если мы запустим тот же советник, но с трейлинг-стопом на основе скользящей средней, результаты "улучшатся":

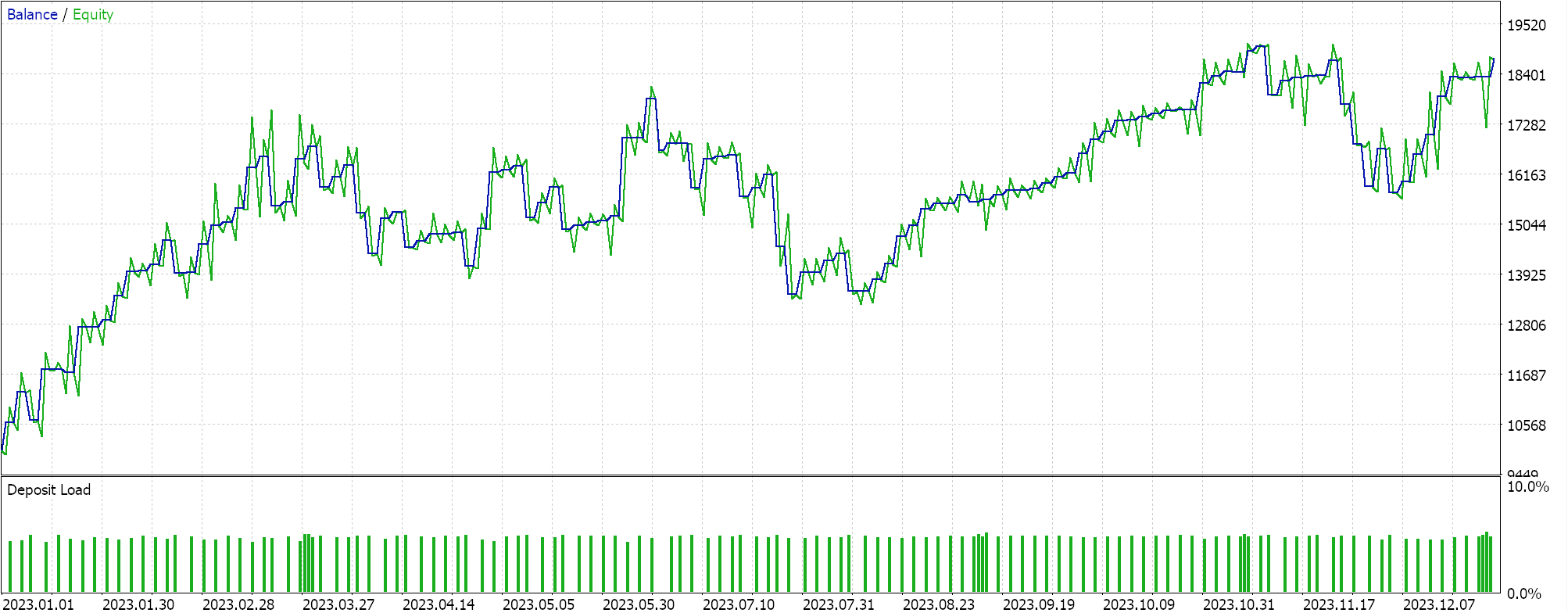
Эти результаты можно объяснить оптимизацией большего количества параметров, а не одного, как при работе с полиномом. Сочетание с другим сигналом может дать радикально разные результаты. Тем не менее, для целей контрольного эксперимента эти отчеты могут служить руководством по потенциалу полинома Ньютона в управлении стоп-лоссами.

Управление капиталом

Наконец, рассмотрим, как полиномы Ньютона могут помочь в определении размера позиции с помощью третьего типа встроенных классов Мастера - CExpertMoney. Так как наш полином может здесь помочь? Конечно, существует много направлений, в которых полином может найти наилучшее применение, однако мы будем рассматривать изменения в диапазоне баров как индикатор волатильности и, следовательно, как руководство к тому, как нам следует корректировать размер позиции с фиксированной маржей. Наш простой тезис будет заключаться в том, что если мы прогнозируем увеличение диапазона ценовых баров, то мы пропорционально уменьшаем размер нашей позиции, однако, если диапазон не увеличивается, мы ничего не делаем. У нас не будет роста из-за прогнозируемого падения волатильности.

Исходный код приведен ниже. Из него удалены отрывки, не относящиеся к управлению капиталом.

//+------------------------------------------------------------------+
//| Optimizing lot size for open.                                    |
//+------------------------------------------------------------------+
double CMoneySizeOptimized::Optimize(double lots)
{  double lot = lots;
//--- 0 factor means no optimization
   if(m_decrease_factor > 0)
   {  m_high.Refresh(-1);
      m_low.Refresh(-1);
      vector _x, _y;
      _x.Init(m_length);
      _y.Init(m_length);
      for(int i = 0; i < m_length; i++)
      {  _x[i] = i;
         _y[i] = (m_high.GetData(StartIndex() + i) - m_low.GetData(StartIndex() + i)) - (m_high.GetData(StartIndex() + i + 1) - m_low.GetData(StartIndex() + i + 1));
      }
      vector _w;
      _w.Init(m_length);
      _w[0] = _y[0];
      __N.Set(_w, _x, _y);
      double _xx = -1.0;
      double _yy = 0.0;
      __N.Get(_w, _x, _xx, _yy);
      //---
      if(_yy > 0.0)
      {  double _range = (m_high.GetData(StartIndex()) - m_low.GetData(StartIndex()));
         _range += (m_decrease_factor*m_symbol.Point());
         _range += _yy;
         lot = NormalizeDouble(lot*(1.0-(_yy/_range)), 2);
      }
   }
//--- normalize and check limits

...

//---
   return(lot);
}

Если мы запустим оптимизацию ТОЛЬКО для периода ретроспективного анализа полинома для советника, который использует тот же класс сигналов, что и для трейлинга для того же символа и таймфрейма за тот же период, мы получим следующие отчеты:

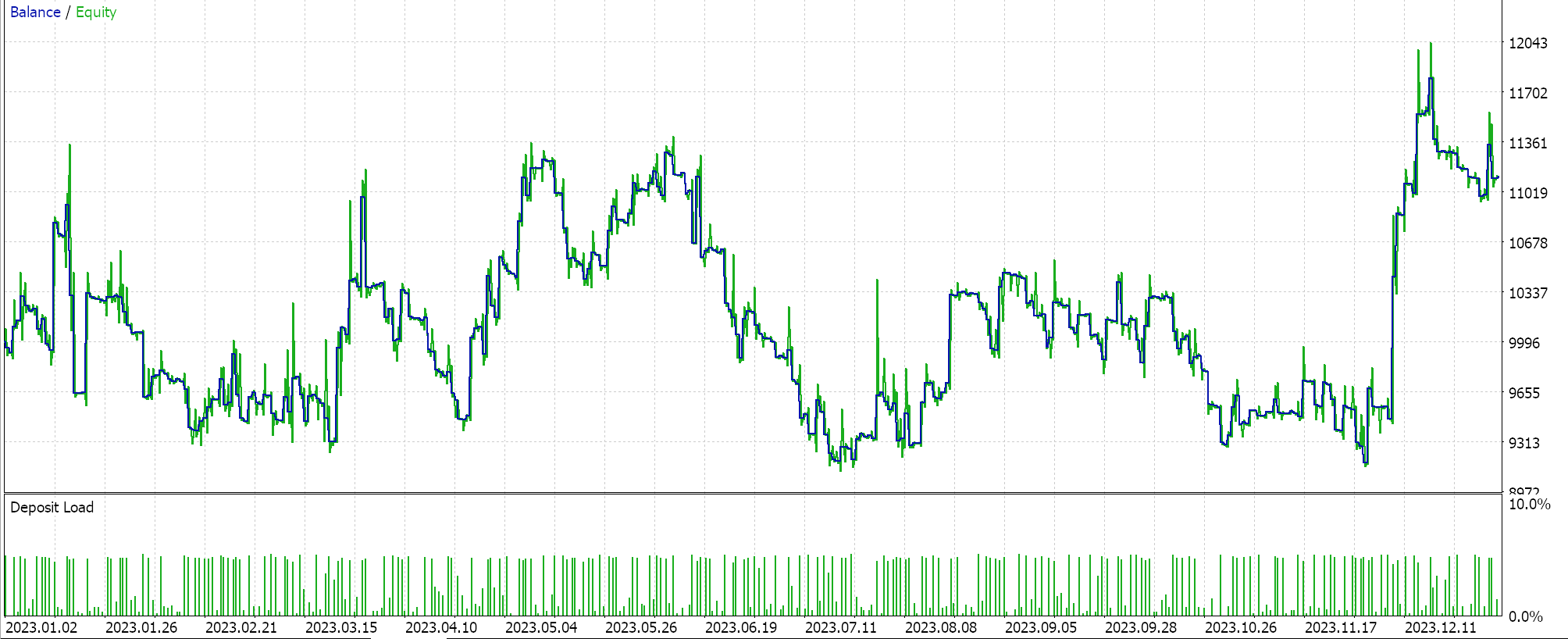
В Мастере этого советника не был выбран метод трейлинг-стопа, и, по сути, он использует необработанные сигналы Awesome Oscillator, при этом единственное изменение заключается только в уменьшении размера позиции, если прогнозируется волатильность.

В качестве контроля мы используем встроенный класс управления капиталом, оптимизированный по размеру на советнике с аналогичным сигналом и без трейлинг-стопа. Советник позволяет корректировать только понижающий коэффициент, образующий знаменатель, на дробное значение, уменьшающее размер позиции пропорционально потерям, понесенным советником. Если мы проведем тесты с лучшими настройками, мы получим следующие отчеты.

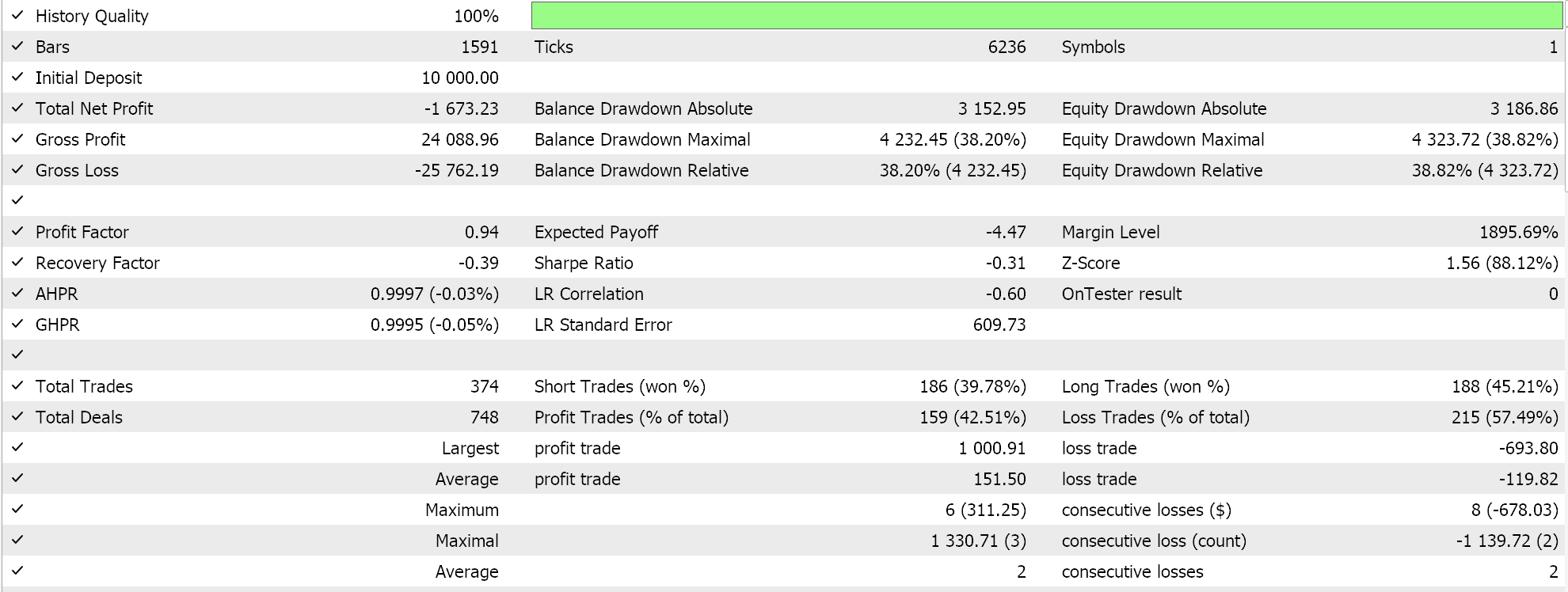
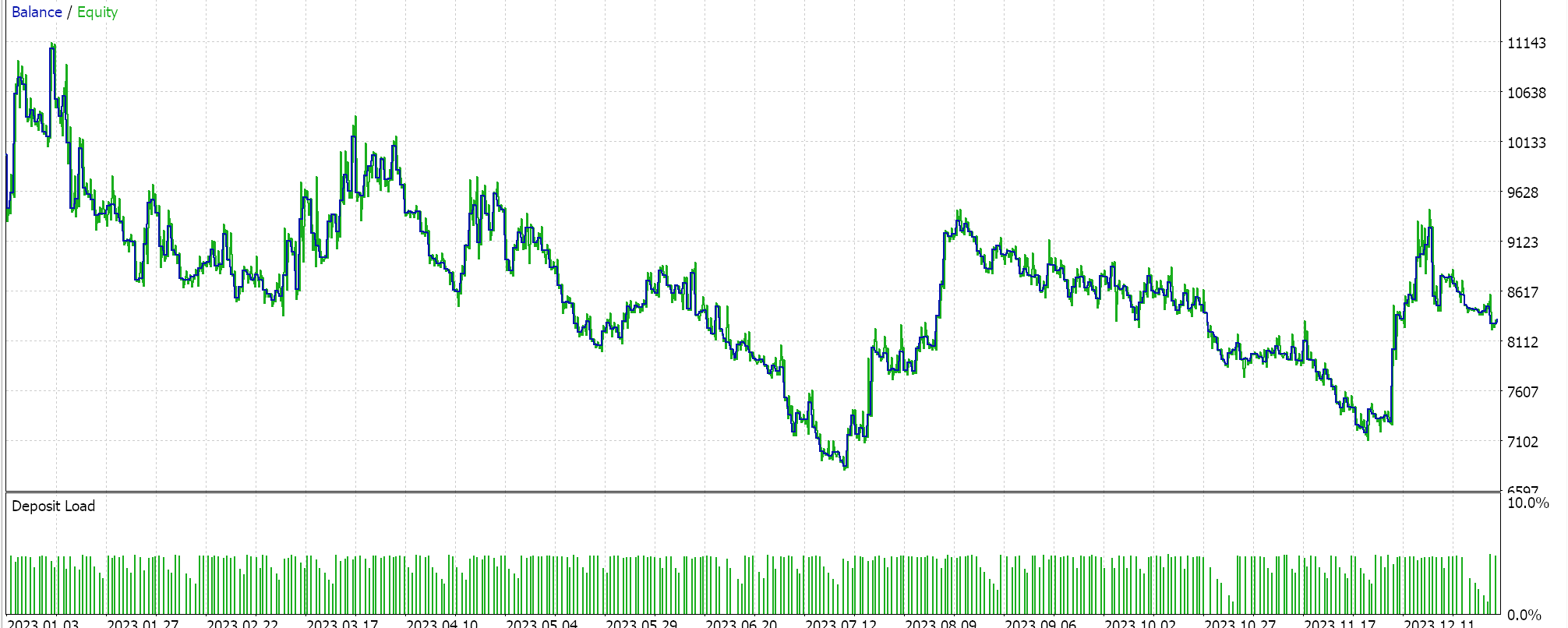
Результаты явно не так хороши по сравнению с теми, что мы получили при управлении капиталом, основанном на полиноме Ньютона. Как мы видели на примере завершающих классов, это само по себе не является приговором советникам, оптимизированным по размеру позиции. Для наших сравнительных целей управление капиталом, основанное на полиноме Ньютона, в том виде, в котором мы это реализовали, является лучшей альтернативой.

Заключение

Мы рассмотрели полином Ньютона — метод, который выводит полиномиальное уравнение на основе набора из нескольких точек данных. Полином, цифровая стена, рассмотренная в прошлой статье, а также ранее рассмотренная ограниченная машина Больцмана представляют собой идеи, которые можно использовать многочисленными способами, в том числе и неописанными в этой серии.

Статья не выступает против устоявшихся и проверенных методов анализа рынка, но, учитывая, что мы находимся в ситуации, когда всё - от биткоина до акций, облигаций и даже товаров - во многом коррелирует, мы можем говорить о системных закономерностях. Во времена легких денег легко упустить преимущество, поэтому эту серию можно рассматривать как средство популяризации новых и зачастую не самых распространенных подходов, которые могут обеспечить некоторую столь необходимую страховку, когда мы все идем в неизведанное.

У полиномов Ньютона действительно есть ограничения, как показано в отчетах тестирования выше. Они связаны в первую очередь с их неспособностью отфильтровывать белый шум, что означает, что у них есть потенциал для хорошей работы в сочетании с другими индикаторами, которые решают эту проблему. Мастер MQL5 позволяет объединять несколько сигналов в один советник, поэтому можно использовать фильтр или даже несколько фильтров для получения лучшего сигнала советника. Модули трейлинг-класса и управления капиталом не позволяют этого сделать, поэтому необходимо провести дополнительное тестирование, чтобы определить, какие классы трейлинга и управления капиталом лучше всего работают с сигналом.

Неспособность фильтровать белый шум можно объяснить тенденцией полиномов к чрезмерному подбору выборочных данных путем улавливания всех колебаний вместо обработки основных закономерностей. Это часто называют шумом запоминания, который приводит к снижению производительности при обработке данных за пределами выборки. Финансовые временные ряды, как правило, также имеют изменяющиеся статистические свойства (среднее значение, дисперсия…) и нелинейную динамику, где резкие изменения цен могут быть нормой. Полиномы Ньютона, основанные на гладких полиномиальных кривых, с трудом справляются с такими сложностями. Наконец, как уже упоминалось выше, их неспособность учитывать экономические настроения и фундаментальные показатели означает, что их следует сочетать с соответствующими финансовыми индикаторами.