
Uso do filtro de Kalman na previsão da tendência
Introdução
Nos gráficos de moedas ou ações, nós sempre observamos flutuações do preço que se diferenciam pela sua frequência e amplitude. Nossa tarefa consiste em identificar as principais tendências durante esses movimentos curtos e longos. Há quem, para fazer isso, trace linhas de tendência no gráfico, há quem use indicadores. Em ambos os casos, o nosso objetivo é filtrar o verdadeiro movimento do preço do ruído causado pela influência de fatores secundários que têm um impacto de curto prazo sobre o preço. Neste artigo proponho apartar o ruído de fundo usando o filtro de Kalman.
A ideia de usar filtros digitais em negociação não é nova. Inclusive, eu já falei sobre o uso de filtros passa-baixos. Mas, como dizem, o céu é o limite, e, em busca das melhores estratégias, consideraremos uma outra opção, para, no final, comparar os resultados.
1. Princípio de funcionamento do filtro de Kalman
Bem, o que é o filtro de Kalman e por que devemos prestar atenção a ele? Wikipedia dá a seguinte definição:
Em estatística, o filtro de Kalman é um método matemático criado por Rudolf Kalman. Seu propósito é utilizar medições de grandezas realizadas ao longo do tempo (contaminadas com ruído e outras incertezas) e gerar resultados que tendam a se aproximar dos valores reais das grandezas medidas e valores associados.
Ou seja, inicialmente, esta ferramenta foi projetada para trabalhar com dados contaminados com ruído. Ela é capaz de trabalhar com dados incompletos. Finalmente, uma outra vantagem é o fato de ser usada para sistemas dinâmicos (eles estão relacionados com nosso gráfico de preços).
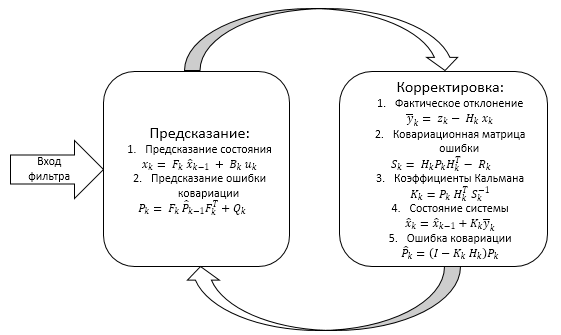
O funcionamento do filtro é dividido em duas etapas:
- Extrapolação (predição)
- Correção
1.1. Extrapolação é a predição dos valores do sistema
A primeira etapa de funcionamento do filtro é baseada num modelo do processo analisado. É de acordo com ele que se constrói a predição do estado do sistema.
![]() (1.1)
(1.1)
Onde:
- xk, valor extrapolado do sistema dinâmico na etapa k,
- Fk, matriz do modelo de dependência entre o estado real e o anterior,
- x^k-1, estado anterior do sistema (valor do filtro na etapa anterior),
- Bk, matriz de efeito das entradas de controle sobre o sistema,
- uk, ação de controle (entrada de controle) sobre o sistema.
Como ação de controle pode ser tomado, por exemplo, um fator de notícias. Mas, na prática, normalmente, a ação de controle é desconhecida e ignorada, no entanto, seu efeito é ruído.
Em seguida, é feita a predição para o erro de covariância do sistema:
![]() (1.2)
(1.2)
Onde:
- Pk, matriz de covariância extrapolada do vetor de estado de nosso sistema dinâmico,
- Fk, matriz do modelo de dependência entre o estado real e o anterior,
- P^k-1, matriz de covariância do vetor de estado corrigida na etapa anterior,
- Qk, matriz de covariância do ruído processo.
1.2. Correção dos valores do sistema
A segunda etapa do funcionamento do filtro começa com a medição do estado real do sistema zk. Aqui, o valor medido real do estado do sistema é especificado levando em conta o estado atual do sistema e os erros de medição. No nosso caso, os erros de medição fazem referência ao impacto do ruído sobre o sistema dinâmico.
Até agora, temos dois valores diferentes que representam o estado do processo dinâmico. Trata-se do valor extrapolado do sistema dinâmico, calculado por nós na primeira fase, e do valor medido real. Com uma certa probabilidade, cada um desses valores caracteriza o verdadeiro estado do nosso processo, que, portanto, está em algum lugar entre eles dois. Assim, nosso objetivo é determinar até que ponto confiamos num valor em particular. É com este intuito que se realiza a iteração da segunda etapa do filtro de Kalman.
Com base nos dados disponíveis, determinamos o desvio entre o estado real do sistema e o valor extrapolado.
![]() (2.1)
(2.1)
Aqui:
- yk, desvio do estado real do sistema na etapa k,
- zk, estado real do sistema na etapa k,
- Hk, matriz de medidas que mostra a dependência entre o estado real do sistema e os dados calculados (na prática muitas vezes tem um valor único),
- xk, valor extrapolado do sistema dinâmico na etapa k.
Na seguinte etapa, calcula-se a matriz de covariância para o vetor de erro:
![]() (2.2)
(2.2)
Aqui:
- Sk, matriz de covariância do vetor de erro na etapa k,
- Hk, matriz de medidas que mostra a dependência entre o estado real do sistema e os dados calculados,
- Pk, matriz de covariância extrapolada do vetor de estado de nosso sistema dinâmico,
- Rk, matriz de covariância do ruído das medidas.
Em seguida, é definido o valor dos ganhos, que representam o grau de confiança nos valores teóricos e empíricos.
![]() (2.3)
(2.3)
Aqui:
- Kk, matriz de ganho de Kalman,
- Pk, matriz de covariância extrapolada do vetor de estado de nosso sistema dinâmico,
- Hk, matriz de medidas que mostra a dependência entre o estado real do sistema e os dados calculados,
- Sk, matriz de covariância do vetor de erro na etapa k.
Agora, com base nos ganhos de Kalman obtidos, corregemos o valor do estado de nosso sistema e a matriz de covariância da estimativa do vetor de estado.
![]() (2.4)
(2.4)
Onde:
- x^k e x^k-1 , valores de correção nas etapas 1 e 2,
- Kk, matriz de ganho de Kalman,
- yk, desvio do estado real do sistema na etapa k.
![]() (2.5)
(2.5)
Onde:
- P^k, matriz de covariância corrigida do vetor de estado de nosso sistema dinâmico,
- I, matriz de identidade,
- Kk, matriz de ganho de Kalman,
- Hk, matriz de medidas que mostra a dependência entre o estado real do sistema e os dados calculados,
- Pk, matriz de covariância extrapolada do vetor de estado de nosso sistema dinâmico.
Em resumo, temos o esquema abaixo
2. Aplicação prática do filtro de Kalman
Bem, já temos uma ideia sobre como funciona o filtro de Kalman. Debrucemo-nos sobre sua implementação. A visualização matricial das fórmulas, descrita acima, toma em consideração que recebemos dados de várias fontes. Eu proponho construir o filtro sobre os preços de fechamento das barras e, assim, simplificar a representação da matriz.
2.1. Inicialização de dados de origem
Antes de começar a escrever o código, definimos os dados de origem.
Como mencionado acima, a base do filtro de Kalman é o modelo do processo dinâmico, modelo esse que ajuda a prever o seguinte estado do processo em causa. Inicialmente, este filtro era projetado para trabalhar com sistemas lineares em que o estado atual do sistema era facilmente definido través do coeficiente anterior. No nosso caso, a questão se torna um pouco mais difícil, uma vez que não estamos lidando com um sistema dinâmico linear, onde o coeficiente muda em etapas. Além disso, não temos ideia sobre a dependência entre os dois estados vizinhos do sistema. O problema parece ser insolúvel. Porém, tentemos contornar o assunto usando os modelos auto-regressivos já discutidos nos artigos [1],[2],[3].
Bem, vamos a isso. Primeiro, declaramos a classe CKalman, ela contém as variáveis necessárias
class CKalman { private: //--- uint ci_HistoryBars; //Bars for analysis uint ci_Shift; //Shift of autoregression calculation string cs_Symbol; //Symbol ENUM_TIMEFRAMES ce_Timeframe; //Timeframe double cda_AR[]; //Autoregression coefficients int ci_IP; //Number of autoregression coefficients datetime cdt_LastCalculated; //Time of LastCalculation; bool cb_AR_Flag; //Flag of autoregression calculation //--- Values of Kalman's filter double cd_X; // X double cda_F[]; // F array double cd_P; // P double cd_Q; // Q double cd_y; // y double cd_S; // S double cd_R; // R double cd_K; // K public: CKalman(uint bars=6240, uint shift=0, string symbol=NULL, ENUM_TIMEFRAMES period=PERIOD_H1); ~CKalman(); void Clear_AR_Flag(void) { cb_AR_Flag=false; } };
Na função de inicialização da classe, atribuímos valores iniciais às variáveis.
CKalman::CKalman(uint bars, uint shift, string symbol, ENUM_TIMEFRAMES period) { ci_HistoryBars = bars; cs_Symbol = (symbol==NULL ? _Symbol : symbol); ce_Timeframe = period; cb_AR_Flag = false; ci_Shift = shift; cd_P = 1; cd_K = 0.9; }
Para construir o modelo auto-regressivo, eu utilizei o algoritmo do artigo [1]. Para fazer isso, adicionamos à classe duas funções private.
bool Autoregression(void); bool LevinsonRecursion(const double &R[],double &A[],double &K[]);
A função LevinsonRecursion é transferida sem alterações, no entanto, por outra parte, eu modifiquei a função Autoregression ligeiramente, por isso vamos vê-la em detalhes. No início da função, nós verificamos a disponibilidade do histórico necessário para a análise, e, se ele não for suficiente, será retornado false.
bool CKalman::Autoregression(void) { //--- check for insufficient data if(Bars(cs_Symbol,ce_Timeframe)<(int)ci_HistoryBars) return false;
Carregamos o histórico necessário na matriz e preenchemos a matriz de coeficientes reais de dependência entre o estado atual do sistema e o anterior.
//--- double cda_QuotesCenter[]; //Data to calculate //--- make all prices available double close[]; int NumTS=CopyClose(cs_Symbol,ce_Timeframe,ci_Shift+1,ci_HistoryBars+1,close)-1; if(NumTS<=0) return false; ArraySetAsSeries(close,true); if(ArraySize(cda_QuotesCenter)!=NumTS) { if(ArrayResize(cda_QuotesCenter,NumTS)<NumTS) return false; } for(int i=0;i<NumTS;i++) cda_QuotesCenter[i]=close[i]/close[i+1]; // Calculate coefficients
Após o trabalho preliminar, definimos o número de coeficientes do modelo auto-regressivo e calculamos seus valores.
ci_IP=(int)MathRound(50*MathLog10(NumTS)); if(ci_IP>NumTS*0.7) ci_IP=(int)MathRound(NumTS*0.7); // Autoregressive model order double cor[],tdat[]; if(ci_IP<=0 || ArrayResize(cor,ci_IP)<ci_IP || ArrayResize(cda_AR,ci_IP)<ci_IP || ArrayResize(tdat,ci_IP)<ci_IP) return false; double a=0; for(int i=0;i<NumTS;i++) a+=cda_QuotesCenter[i]*cda_QuotesCenter[i]; for(int i=1;i<=ci_IP;i++) { double c=0; for(int k=i;k<NumTS;k++) c+=cda_QuotesCenter[k]*cda_QuotesCenter[k-i]; cor[i-1]=c/a; // Autocorrelation } if(!LevinsonRecursion(cor,cda_AR,tdat)) // Levinson-Durbin recursion return false;
Convertemos a soma de coeficiente de auto-regressão obtida em "1" e definimos o sinalizador do cálculo realizado como true.
double sum=0; for(int i=0;i<ci_IP;i++) { sum+=cda_AR[i]; } if(sum==0) return false; double k=1/sum; for(int i=0;i<ci_IP;i++) cda_AR[i]*=k;cb_AR_Flag=true;
Em seguida, inicializamos as variáveis necessárias para o filtro. Como covariância do ruído das medições, tomamos o desvio padrão dos valores close para o período analisado.
cd_R=MathStandardDeviation(close);
Para determinar a covariância do ruído do processo, primeiro, calculamos a matriz de valores do modelo autorregressivo e tomamos o desvio padrão dos valores do modelo.
double auto_reg[]; ArrayResize(auto_reg,NumTS-ci_IP); for(int i=(NumTS-ci_IP)-2;i>=0;i--) { auto_reg[i]=0; for(int c=0;c<ci_IP;c++) { auto_reg[i]+=cda_AR[c]*cda_QuotesCenter[i+c]; } } cd_Q=MathStandardDeviation(auto_reg);
Copiamos os coeficientes reais de dependência entre o estado atual do sistema e o anterior e, em seguida, colamo-los na matriz cda_F, pois, mais tarde, vamos usá-los no cálculo dos novos coeficientes.
ArrayFree(cda_F); if(ArrayResize(cda_F,(ci_IP+1))<=0) return false; ArrayCopy(cda_F,cda_QuotesCenter,0,NumTS-ci_IP,ci_IP+1);
Para o valor inicial de nosso sistema, tomamos a média aritmética dos últimos 10 valores.
cd_X=MathMean(close,0,10);
2.2. Predição do movimento do preço
Uma vez que recebemos todos os dados iniciais para o filtro, podemos prosseguir com sua implementação. Como mencionado acima, a primeira etapa de funcionamento do filtro consiste na extrapolação do estado do sistema num passo à frente. Criamos a função public Forecast, na qual serão implementadas as funções 1.1. e 1.2.
double Forecast(void);
No início da função, verificamos se já foi calculado o modelo de regressão. Se necessário, chamamos a função para calculá-la. Se, durante o recálculo do modelo, ocorrer um erro, será retornado EMPTY_VALUE,
double CKalman::Forecast() { if(!cb_AR_Flag) { ArrayFree(cda_AR); if(Autoregression()) { return EMPTY_VALUE; } }
Em seguida, calculamos o coeficiente de dependência entre o estado atual do sistema e o anterior e, logo a seguir, armazenamo-lo na célula "0" da matriz cda_F, cujos valores deslocaremos uma célula, antecipadamente.
Shift(cda_F); cda_F[0]=0; for(int i=0;i<ci_IP;i++) cda_F[0]+=cda_F[i+1]*cda_AR[i];
Depois disso, recalculamos o estado do sistema a a probabilidade de erro.
cd_X=cd_X*cda_F[0]; cd_P=MathPow(cda_F[0],2)*cd_P+cd_Q;
No final, a função retorna o estado previsto do sistema. No nosso caso, prevê-se o preço de fechamento de uma nova barra.
return cd_X;
}
2.3. Correção do estado do sistema
Na próxima etapa, após obtermos o valor real do fechamento da barra, ajustamos o estado do sistema. Para fazer isso, criar a função pública Correction. Para seus parâmetros, redirecionaremos o valor real - obtido - do estado do sistema, isto é, o preço de fechamento da última barra.
double Correction(double z);
Nesta função, implementa-se a parte teórica 1.2. deste artigo. Seu código completo pode ser encontrado em anexo. Quando conclui seu trabalho, a função retorna o valor corregido do estado do sistema.
3. Demonstração do filtro de Kalman na prática
Experimentemos o funcionamento de nossa classe no filtro de Kalman na prática. Para esse efeito, na base da classe, criamos um pequeno indicador. Ele chamará a função de correção de estado do sistema, na abertura de uma nova vela, e, em seguida, invocará a função de predição, a fim de prever o preço de fechamento da barra atual. Não se intimide com a mudança na ordem da chamada das funções da classe, uma vez que chamaremos a função de correção do estado para a barra (fechada) anterior e invocaremos a predição do preço de fechamento para a atual (barra recém aberta), cujo preço de fechamento é desconhecido para nós.
No indicador haverá 2 buffers. No primeiro, serão apresentados os valores do estado do sistema previstos, no segundo, os corrigidos. Criei deliberadamente dois buffers, de modo que o indicador não se redesenhasse e fosse possível ver a escala da correção do sistema, na segunda etapa de funcionamento do filtro. O código do indicador é simples, ele se encontra no anexo. Aqui eu apresento os seus resultados.
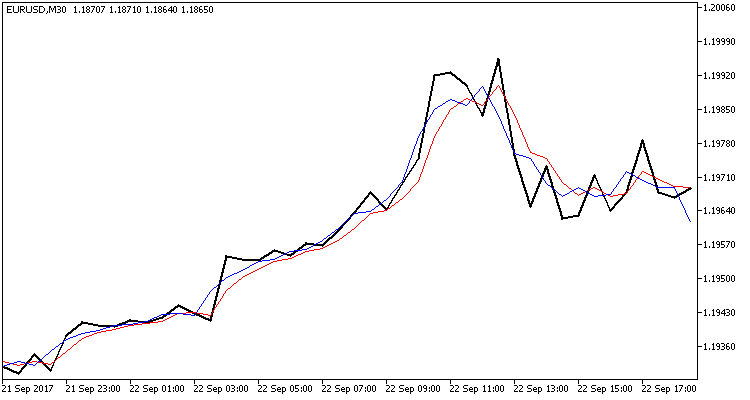
O gráfico mostra três linhas quebradas:
- Preta, preço atual de fechamento das barras;
- Vermelha, predição do preço de fechamento;
- Azul, estado do sistema corrigido pelo filtro de Kalman.
Como você pode ver, ambas as linhas estão perto dos preços de fechamento reais e, com uma boa probabilidade, indicam pontos de viragem. Eu gostaria de salientar mais uma vez que o indicador não é redesenhado e a linha vermelha é plotada na abertura da barra, quando o preço de fechamento é ainda desconhecido.
Tal gráfico mostra a consistência no funcionamento do filtro utilizado e a capacidade de construir um sistema de negociação usando o mesmo.
4. Criamos o módulo de sinais de negociação para o gerador de experts MQL5
Ao olhar para o gráfico apresentado acima, podemos ver que a linha vermelha (predição do estado do sistema) é mais suave em comparação com a linha preta (preço real). Além disso, a linha azul (estado corrigido do sistema) sempre se encontra entra as outras duas. Em outras palavras, o fato de a linha azul estar acima da vermelho indica uma tendência de alta. E, vice-versa, a linha azul abaixo da vermelha indica uma uma tendência de baixa. Assim, o cruzamento entre as linhas azul e vermelha é o sinal de mudança da tendência.
Para testar esta estratégia, criamos o módulo de sinais de negociação para o gerador de experts MQL5. O método de criação de módulos de sinais de negociação já têm sido discutido nos artigos [1], [4], [5]. Em resumo, estes são os momentos relacionados com nossa estratégia.
Primeiro, criamos o módulo de classe CSignalKalman, herdado do CExpertSignal. Como nossa estratégia se baseia no uso do filtro de Kalman, precisamos declarar, em nossa classe, uma instância da classe CKalman criada acima. Como declaramos a instância da classe CKalman no módulo, devemos inicializá-la no módulo. Por sua vez, par fazer isso, precisamos carregar no módulo os parâmetros iniciais. No código, a solução destes problemas é a seguinte:
//+---------------------------------------------------------------------------+ // wizard description start //+---------------------------------------------------------------------------+ //| Description of the class | //| Title=Signals of Kalman's filter degign by DNG | //| Type=SignalAdvanced | //| Name=Signals of Kalman's filter degign by DNG | //| ShortName=Kalman_Filter | //| Class=CSignalKalman | //| Page=https://www.mql5.com/pt/articles/3886 | //| Parameter=TimeFrame,ENUM_TIMEFRAMES,PERIOD_H1,Timeframe | //| Parameter=HistoryBars,uint,3000,Bars in history to analysis | //| Parameter=ShiftPeriod,uint,0,Period for shift | //+---------------------------------------------------------------------------+ // wizard description end //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ class CSignalKalman: public CExpertSignal { private: ENUM_TIMEFRAMES ce_Timeframe; //Timeframe uint ci_HistoryBars; //Bars in history to analysis uint ci_ShiftPeriod; //Period for shift CKalman *Kalman; //Class of Kalman's filter //--- datetime cdt_LastCalcIndicators; double cd_forecast; // Forecast value double cd_corretion; // Corrected value //--- bool CalculateIndicators(void); public: CSignalKalman(); ~CSignalKalman(); //--- void TimeFrame(ENUM_TIMEFRAMES value); void HistoryBars(uint value); void ShiftPeriod(uint value); //--- method of verification of settings virtual bool ValidationSettings(void); //--- method of creating the indicator and timeseries virtual bool InitIndicators(CIndicators *indicators); //--- methods of checking if the market models are formed virtual int LongCondition(void); virtual int ShortCondition(void); };
Na função de inicialização da classe, atribuímos os valores padrão às variáveis e inicializamos a classe do filtro de Kalman.
CSignalKalman::CSignalKalman(void): ci_HistoryBars(3000), ci_ShiftPeriod(0), cdt_LastCalcIndicators(0) { ce_Timeframe=m_period; if(CheckPointer(m_symbol)!=POINTER_INVALID) Kalman=new CKalman(ci_HistoryBars,ci_ShiftPeriod,m_symbol.Name(),ce_Timeframe); }
Calcularemos o estado do sistema com ajuda do filtro na função private CalculateIndicators. No início da função, verificamos se foram calculados os valores do filtro na barra atual. Se o valor for recalculado, sairemos da função.
bool CSignalKalman::CalculateIndicators(void) { //--- Check time of last calculation datetime current=(datetime)SeriesInfoInteger(m_symbol.Name(),ce_Timeframe,SERIES_LASTBAR_DATE); if(current==cdt_LastCalcIndicators) return true; // Exit if data alredy calculated on this bar
Logo, verificamos o estado mais recente do sistema. Se não for definido, redefinimos o sinalizador do cálculo do modelo autorregressivo na classe CKalman, de modo que, ao chamar novamente a classe, o modelo seja recalculado novamente.
if(cd_corretion==QNaN) { if(CheckPointer(Kalman)==POINTER_INVALID) { Kalman=new CKalman(ci_HistoryBars,ci_ShiftPeriod,m_symbol.Name(),ce_Timeframe); if(CheckPointer(Kalman)==POINTER_INVALID) { return false; } } else Kalman.Clear_AR_Flag(); }
Na próxima etapa, verificaremos quantas barras se formaram após a última chamada de função. Se o intervalo for muito grande, também redefiniremos o sinalizador do cálculo do modelo autorregressivo.
int shift=StartIndex(); int bars=Bars(m_symbol.Name(),ce_Timeframe,current,cdt_LastCalcIndicators); if(bars>(int)fmax(ci_ShiftPeriod,1)) { bars=(int)fmax(ci_ShiftPeriod,1); Kalman.Clear_AR_Flag(); }
Em seguida, recalcularemos os valores do estado do sistema para todas as barras que não foram contadas.
double close[]; if(m_close.GetData(shift,bars+1,close)<=0) { return false; } for(uint i=bars;i>0;i--) { cd_forecast=Kalman.Forecast(); cd_corretion=Kalman.Correction(close[i]); }
Após o recálculo, verificamos o estado do sistema e salvamos o tempo da última chamada de função. Se a operação for concluída com sucesso, a função retornará true.
if(cd_forecast==EMPTY_VALUE || cd_forecast==0 || cd_corretion==EMPTY_VALUE || cd_corretion==0) return false; cdt_LastCalcIndicators=current; //--- return true; }
Funções de tomada de decisão (LongCondition e ShortCondition) têm uma estrutura completamente idêntica à condição espelhada de abertura de transação. Consideraremos o código da função no exemplo da função ShortCondition.
Primeiro, executamos a função para recalcular os valores do filtro. Se o recálculo dos valores do filtro for mal-sucedida, saímos da função e retornamos 0.
int CSignalKalman::ShortCondition(void) { if(!CalculateIndicators()) return 0;
Se o recálculo dos valores do filtro for bem sucedido, compararemos o valor previsto e o valor corrigido. Se o valor previsto é maior do que o corrigido, a função retorna um valor ponderado. Caso contrário, será retornado "0".
int result=0; //--- if(cd_corretion<cd_forecast) result=80; return result; }
O módulo é construído sobre o princípio dos "lados opostos", é por isso que não vamos escrever as funções de fechamento de posições.
O código de todas as funções pode ser encontrado no arquivo anexado ao artigo.
5. Teste do expert advisor
Uma descrição em detalhes sobre a criação do expert com uso do módulo de sinais de negociação é apresentada no artigo [1], portanto, ignoraremos este passo. Leve em conta que, para testar a qualidade dos sinais, o expert advisor foi desenvolvido apenas em um módulo de negociação, criado acima, com lote estático e sem uso de trailing-stop.
O teste do expert advisor foi realizado em dados históricos para agosto de 2017, EURUSD, timeframe H1. Para calcular o modelo autorregressivo, foram usados os dados históricos de 3 000 barras, o que é quase 6 meses. O teste foi realizado sem usar stop-loss e take-profit, o que permitiu ver o impacto de só os sinais do filtro de Kalman sobre a negociação.
Os resultados do teste mostraram 49,33% de trades rentáveis. Além disso, o lucro máximo e médio dos trades rentáveis ultrapassa os valores correspondentes dos trades desfavoráveis. Em geral, isto deu lucro para o período de teste; o fator de lucro foi de 1,56. Capturas de tela do teste se encontram abaixo.
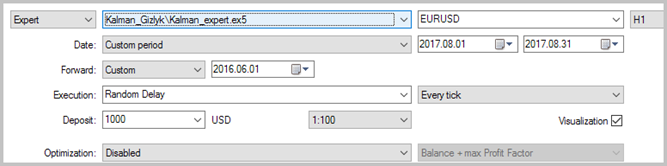
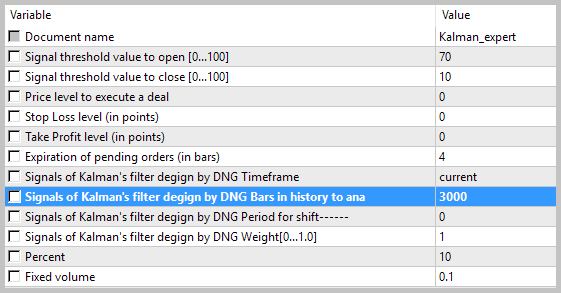
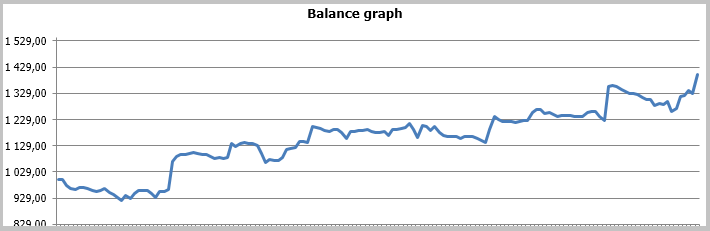
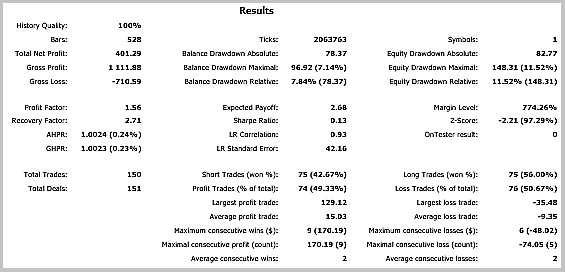
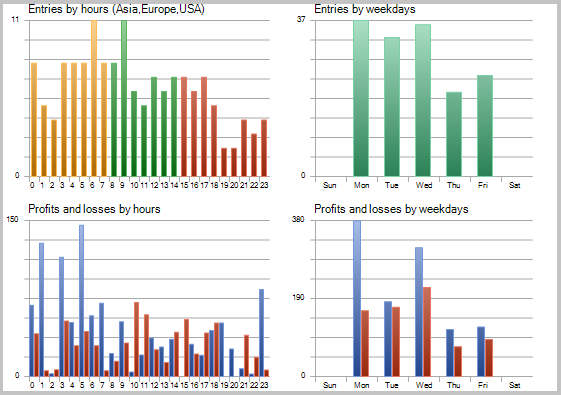
Se observarmos bem os trades no gráfico de preços, veremos 2 gargalos nesta estratégia:
- trades mal-sucedidos durante movimentos laterais;
- saída demorada da posição de abertura.
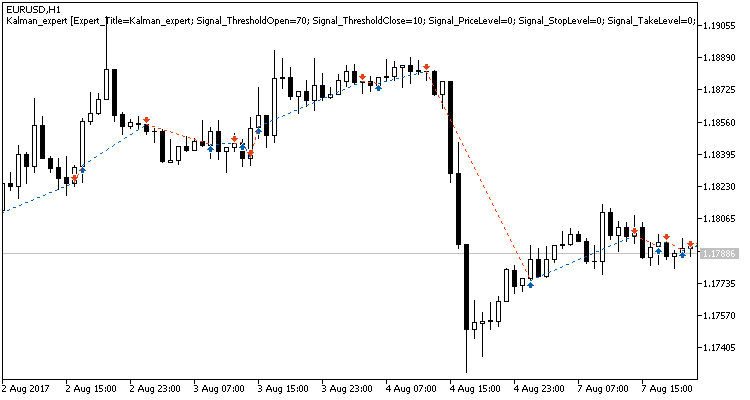
Estas áreas problemáticas foram observados durante o teste do expert advisor na estratégia acompanhamento adaptativo do mercado, nela também foram propostas algumas soluções. Mas, em contraste com a estratégia anterior, o expert advisor com filtro de Kalman mostrou um resultado positivo. Eu acho que a estratégia proposta neste artigo tem chances de ser bem-sucedida se for complementada com um filtro que defina movimentos laterais (de correção). Na verdade, a rentabilidade da estratégia pode vir a melhorar se for usada apenas durante certas horas. Além disso, nesse sentido, vale a pena experimentar sinais de saída da posição, o que permitirá não perder o lucro obtido durante fortes reversões do preço.
Fim do artigo
Examinamos o princípio de funcionamento do filtro de Kalman e construímos com base nele um indicador e um expert advisor. O teste revelou o carácter promissório desta estratégia, porém, ao mesmo tempo, destacou uma série de gargalos que precisam ser abordados.
Também, observe que o artigo só fornece informações gerais e um exemplo para construção de um expert advisor que, sob nenhuma circunstância, é um "Santo Graal" para usar em negociação real.
Desejo a todos uma abordagem séria à negociação o bons trades!
Referências
- Examinemos na prática o método adaptativo de acompanhamento do mercado.
- Análise das principais características da série temporal.
- Extrapolação AR de preço - indicadores para MetaTrader 5
- Assistente MQL5: Como criar um módulo de sinais de negociação
- Crie o seu próprio robô de negociação em 6 passos!
- Assistente MQL5: nova versão
Programas utilizados no artigo:
| # |
Nome |
Tipo |
Descrição |
|---|---|---|---|
| 1 | Kalman.mqh | Biblioteca de classes | Classe do filtro de Kalman |
| 2 | SignalKalman.mqh | Biblioteca de classes | Módulo de sinais de negociação sobre o filtro de Kalman |
| 3 | Kalman_indy.mq5 | Indicador | Indicador do filtro de Kalman |
| 4 | Kalman_expert.mq5 | Expert Advisor | Expert Advisor usando o filtro de Kalman |
| 5 | Kalman_test.zip | Arquivo | O arquivo contém os resultados dos testes do EA no testador de estratégias. |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/3886
 Expert Advisor Multiplataforma: As classes CExpertAdvisor e CExpertAdvisors
Expert Advisor Multiplataforma: As classes CExpertAdvisor e CExpertAdvisors
 Comparação de diferentes tipos de médias móveis durante a negociação
Comparação de diferentes tipos de médias móveis durante a negociação
 Mini-emulador do mercado ou Testador de estratégias manual
Mini-emulador do mercado ou Testador de estratégias manual
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Novo artigo Uso do filtro de Kalman na previsão da tendência foi publicado:
Autor: Dmitriy Gizlyk
Awesome, do you offer the EA?
Hi Dmitriy. First, congrats for your work!
A question, the indicator just work in EURUSD? I tried in another pairs and CFDs, the lines are streights and far from the prices.
Awesome for EURUSD
Bad for USDJPY
And BAD for Brasilian Index