カルマンフィルタを用いた価格方向予測

MetaTrader 5 — トレーディングシステム | 27 12月 2017, 14:15

5 553

イントロダクション

通貨と株価のチャートは、常に周波数と振幅が異なり、変動があります。今回のタスクは、短い動きと長い動きに基づいて主なトレンドを決定することです。チャート上の近似曲線を描く人もいれば、また他のインジケーターを使用する人もいます。どちらの場合も、目的は価格に短期的な影響を与えるマイナーな要因の影響によって引き起こされるノイズから、真の価格の動きを分離することです。この記事では、相場のノイズからの本当の動きを分離するためにカルマンフィルタを使用してます。

トレードでデジタルフィルタを使用するという考え方は、新しいものではありません。例えば、すでにローパスフィルタを説明しています。しかし、完璧なものなどないので、もう一つの戦略を検討し、結果を比較してみましょう。

1. カルマンフィルタ原理

では、カルマンフィルタとは何か、なにが良いのでしょうか。ウィキペディアからフィルタの定義を示します。

カルマンフィルタは、統計的なノイズやその他の誤りを含む、時系列で観測された一連の測定値を使用するアルゴリズムです。

これは、そもそもフィルタがノイズの多いデータで動作するように設計されたことを意味します。また、不完全なデータを処理することもできます。もう一つの利点は、動的なシステムで適用されます。価格は、そのようなシステムに属します。

フィルタアルゴリズムは、2段階のプロセスで動作します。

外挿法 (予測)
更新 (訂正)

1.1. システム値の外挿、予測

フィルタ操作アルゴリズムの最初のフェーズでは、分析対象のプロセスの基になるモデルを利用します。このモデルに基づいて、ワンステップフォワード予測が形成されます。

(1.1)

ただし:

xkは、k 番目のステップでの動的システムの外挿値です。
Fkは、前の状態における現在のシステム状態の依存性を示す状態遷移モデルであり、
x ^k-1は、システムの以前の状態 (前のステップでのフィルタ値) です。
Bkは制御エントリーモデルで、システムに対する制御の影響を示し、
ukは、システム上の制御ベクトルです。

コントロールの効果は、たとえばニュースファクターになります。ただし、実際には効果は不明であり、その影響はノイズを指しますが、省略されます。

次に、システムの共分散エラーが予測されます。

(1.2)

ただし:

Pkは、動的システム状態ベクトルの外挿共分散行列であり、
Fkは、前の状態における現在のシステム状態の依存性を示す状態遷移モデルであり、
P ^k-1は、前のステップで更新された状態ベクトルの共分散行列であり、
Qkは、プロセスの共分散ノイズマトリックスです。

1.2. システム値の更新

フィルタアルゴリズムの2番目のステップは、実際のシステム状態 zkの測定から始まります。システムの実際の測定値は、本当のシステム状態と測定誤差を考慮して指定されます。今回のケースでは、測定誤差は、動的システム上のノイズです。

この時点で、1つの動的プロセスの状態を表す2つの異なる値があります。最初のステップで計算された動的システムの外挿値と実測値が含まれます。この2つの値の間のどこかにあるプロセスの真の状態を特徴付けます。したがって、今回の目標は、その値が信頼されている範囲、すなわち、信頼できる値を決定することです。この目的のために、カルマンフィルタの第2フェーズの繰り返しが実行されます。

使用可能なデータを使用して、外挿値から実際のシステム状態の偏差を決定します。

(2.1)

ただし:

ykは、外挿後の k 番目のステップでのシステムの実際の状態の偏差です。
zkは、k 番目のステップでのシステムの実際の状態です。
Hkは、計算されたデータの実際のシステム状態の依存性を表示する測定マトリックスです (実際には1つの値をとります)。
xkは、k 番目のステップでの動的システムの外挿値です。

次のステップでは、エラーベクトルの共分散行列が計算されます。

(2.2)

ただし:

Skは、k 番目のステップでのエラーベクトルの共分散行列であり、
Hkは、計算されたデータの実際のシステム状態の依存性を表示する測定行列であり、
Pkは、動的システム状態ベクトルの外挿共分散行列であり、
Rkは、測定ノイズの共分散行列です。

その後、最適なゲインが決定されます。ゲインは、計算および経験的値の信頼性を反映します。

(2.3)

ただし:

kkは、カルマンゲイン値の行列であり、
Pkは、動的システム状態ベクトルの外挿共分散行列であり、
Hkは、計算されたデータの実際のシステム状態の依存性を表示する測定行列であり、
Skは、k 番目のステップでのエラーベクトルの共分散行列です。

ここでは、カルマンゲインを使用して、状態ベクトル推定のシステム状態値と共分散行列を更新します。

(2.4)

ただし:

x ^kおよび x ^ k-1 は、k 番目と k-1 ステップで更新された値です。
kkは、カルマンゲイン値の行列であり、
ykは、外挿後の k 番目のステップでのシステムの実際の状態の偏差です。

(2.5)

ただし:

P ^kは、動的システム状態ベクトルの更新された共分散行列であり、
Iはid 行列です。
kkは、カルマンゲイン値の行列であり、
Hkは、計算されたデータの実際のシステム状態の依存性を表示する測定行列であり、
Pkは、動的システム状態ベクトルの外挿共分散行列です。

上記すべてを以下のスキームとしてまとめることができる

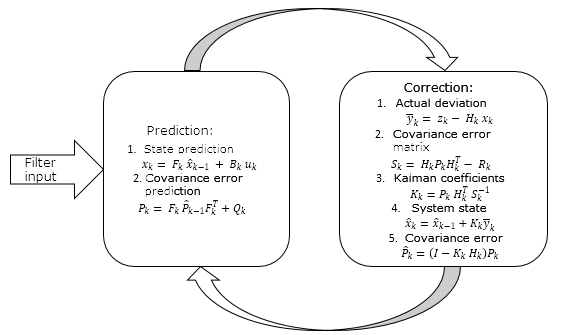
2. カルマンフィルタの実用化

カルマンフィルタがどのように動作するかのアイデアがあります。実装に移りましょう。フィルタの上記の行列表現は、複数のソースからのデータを受信することができます。足の近くの価格でフィルタを構築し、離散的なデータにマトリックス表現を簡素化することをお勧めします。

2.1. エントリーデータの初期化

コードの記述を開始する前に、エントリーデータを定義しておきます。

前述のように、カルマンフィルタの基礎は、プロセスの次の状態を予測するために使用される動的なプロセスモデルです。フィルタは当初、線形システムで使用することを目的としており、前の状態に係数を適用することで、現在の状態を容易に定義することができます。今回のケースは、もう少し難しいです。ダイナミックシステムは、非線形であり、比率はステップごとに異なります。また、システムの近隣の状態間の関係については考慮の余地がありません。一見このタスクが困難に見えます。ここではトリッキーなソリューションで解決しましょう。記事 [1]、[2]、[3] に記載されている自己回帰モデルを使用します。

やってみましょう。まず、このクラス内で CKalman クラスと必要な変数を宣言します。

class CKalman
  {
private:
//---
   uint              ci_HistoryBars;               //分析の足
   uint              ci_Shift;                     //回帰計算のシフト
   string            cs_Symbol;                    //シンボル
   ENUM_TIMEFRAMES   ce_Timeframe;                 //タイムフレーム
   double            cda_AR[];                     //回帰係数
   int               ci_IP;                        //回帰係数の数
   datetime          cdt_LastCalculated;           //LastCalculation の時間;
   
   bool              cb_AR_Flag;                   //回帰計算のフラグ
//カルマンフィルタの---値
   double            cd_X;                         //X
   double            cda_F[];                      //F 配列
   double            cd_P;                         //P
   double            cd_Q;                         //Q
   double            cd_y;                         //y
   double            cd_S;                         //S
   double            cd_R;                         //R
   double            cd_K;                         //K
   
public:
                     CKalman(uint bars=6240, uint shift=0, string symbol=NULL, ENUM_TIMEFRAMES period=PERIOD_H1);
                    ~CKalman();
   void              Clear_AR_Flag(void)  {  cb_AR_Flag=false; }
  };

クラス初期化関数の変数に初期値を割り当てます。

CKalman::CKalman(uint bars, uint shift, string symbol, ENUM_TIMEFRAMES period)
  {
   ci_HistoryBars =  bars;
   cs_Symbol      =  (symbol==NULL ? _Symbol : symbol);
   ce_Timeframe   =  period;
   cb_AR_Flag     =  false;
   ci_Shift       =  shift;
   cd_P           =  1;
   cd_K           =  0.9;
  }

記事 [1] のアルゴリズムを使用して自己回帰モデルを作成しました。この目的のために、2つのプライベート関数をクラスに追加する必要があります。

   bool              Autoregression(void);
   bool              LevinsonRecursion(const double &R[],double &A[],double &K[]);

LevinsonRecursion 関数はそのまま使用します。回帰関数は少し変更されているので、この関数について詳しく考えてみましょう。関数の冒頭で、解析に必要な履歴データの可用性を確認します。十分な履歴データがない場合は、false が返されます。

bool CKalman::Autoregression(void)
  {
   //---不足しているデータを確認する
   if(Bars(cs_Symbol,ce_Timeframe)<(int)ci_HistoryBars)
      return false;

ここでは、必要な履歴データを読み込んで、実際の状態遷移モデル係数の配列をエントリーします。

//---
   double   cda_QuotesCenter[];                          //計算するデータ

//---すべての価格を利用可能にする
   double close[];
   int NumTS=CopyClose(cs_Symbol,ce_Timeframe,ci_Shift+1,ci_HistoryBars+1,close)-1;
   if(NumTS<=0)
      return false;
   ArraySetAsSeries(close,true);
   if(ArraySize(cda_QuotesCenter)!=NumTS)
     {
      if(ArrayResize(cda_QuotesCenter,NumTS)<NumTS)
         return false;
     }
   for(int i=0;i<NumTS;i++)
      cda_QuotesCenter[i]=close[i]/close[i+1];           //係数の計算

準備タスクの後、自己回帰モデルの係数の数を決定し、その値を計算します。

   ci_IP=(int)MathRound(50*MathLog10(NumTS));
   if(ci_IP>NumTS*0.7)
      ci_IP=(int)MathRound(NumTS*0.7);                         //自己回帰モデルのオーダー
  
   double cor[],tdat[];
   if(ci_IP<=0 || ArrayResize(cor,ci_IP)<ci_IP || ArrayResize(cda_AR,ci_IP)<ci_IP || ArrayResize(tdat,ci_IP)<ci_IP)
      return false;
   double a=0;
   for(int i=0;i<NumTS;i++)
      a+=cda_QuotesCenter[i]*cda_QuotesCenter[i];    
   for(int i=1;i<=ci_IP;i++)
     {  
      double c=0;
      for(int k=i;k<NumTS;k++)
         c+=cda_QuotesCenter[k]*cda_QuotesCenter[k-i];
      cor[i-1]=c/a;                                            //自己相関
     } 
  
   if(!LevinsonRecursion(cor,cda_AR,tdat))                     //レビン-ダー再帰
      return false;

ここで、自己回帰係数の合計を ' 1 ' に減らし、計算パフォーマンスのフラグを ' true ' に設定します。

   double sum=0;
   for(int i=0;i<ci_IP;i++)
     {
      sum+=cda_AR[i];
     }
   if(sum==0)
      return false;
  
   double k=1/sum;
   for(int i=0;i<ci_IP;i++)
      cda_AR[i]*=k;

   cb_AR_Flag=true;

次に、フィルタに必要な変数を初期化します。計算ノイズの共分散については、解析期間のClose値の偏差の２乗平均平方根値を使用します。

   cd_R=MathStandardDeviation(close);

プロセスノイズの共分散の値を決定するために、まず自己回帰モデルの値の配列を計算し、モデル値の２乗平均平方根偏差を求めます。

   double auto_reg[];
   ArrayResize(auto_reg,NumTS-ci_IP);
   for(int i=(NumTS-ci_IP)-2;i>=0;i--)
     {
      auto_reg[i]=0;
      for(int c=0;c<ci_IP;c++)
        {
         auto_reg[i]+=cda_AR[c]*cda_QuotesCenter[i+c];
        }
     }
   cd_Q=MathStandardDeviation(auto_reg);

次に、実際の状態遷移係数を cda_F 配列にコピーし、さらに新しい係数の計算に使用することができます。

   ArrayFree(cda_F);
   if(ArrayResize(cda_F,(ci_IP+1))<=0)
      return false;
   ArrayCopy(cda_F,cda_QuotesCenter,0,NumTS-ci_IP,ci_IP+1);

システムの初期値については、最後の10の値の算術平均を使用してみましょう。

   cd_X=MathMean(close,0,10);

2.2. 価格移動予測

フィルタ操作に必要な初期データをすべて受信した後、実装に進むことができます。カルマンフィルタ操作の最初のステップは、ワンステップフォワードシステム状態予測です。関数1.1を実装する予測パブリック関数を作成してみましょう。 1.2も同様に作成します。

double            Forecast(void);

関数の先頭で、回帰モデルが既に計算されているかどうかを確認します。その計算関数は必要に応じて呼び出す必要があります。再計算エラーが発生した場合に EMPTY_VALUE が返されます。

double CKalman::Forecast()
  {
   if(!cb_AR_Flag)
     {
      ArrayFree(cda_AR);
      if(Autoregression())
        {
         return EMPTY_VALUE;
        }
     }

その後、状態遷移係数を計算し、cda_F 配列の "0" セルに保存すると、その値は1つのセルによってシフトされます。

   Shift(cda_F);
   cda_F[0]=0;
   for(int i=0;i<ci_IP;i++)
      cda_F[0]+=cda_F[i+1]*cda_AR[i];

次に、システムの状態とエラーの確率を再計算します。

   cd_X=cd_X*cda_F[0];
   cd_P=MathPow(cda_F[0],2)*cd_P+cd_Q;

この関数は、最後に予測されたシステム状態を返します。今回のケースでは、新しい足の終値です。

   return cd_X;
  }

2.3. システム状態の修正

次のフェーズでは、実際の足の終値を受け取った後、システム状態を修正します。この目的のため、公開修正関数を作成してみましょう。この関数のパラメータでは、実際のシステム状態の値、すなわち実際の足の終値を渡します。

double            Correction(double z);

この関数は、記事理論的なセクション 1.2で実装されています。フルコードは、添付ファイルで利用可能です。操作の終了時に、この関数はシステム状態の更新された (修正済み) 値を返します。

3. カルマンフィルタの実用的なデモンストレーション

このカルマンフィルタベースのクラスが実際にどのように動作するかをテストしてみましょう。このクラスに基づいてインジケーターを作成してみましょう。新しいローソク足が開くと、インジケーターはシステム更新関数を呼び出し、現在の足の終値を予測する関数を呼び出します。このクラスは、前の足の更新 (修正) 関数と、終値がまだ不明な現在の足の予測を呼び出すため、逆順で呼び出されます。

このインジケーターには2つのバッファがあります。システム状態の予測値が最初のバッファに追加され、更新された値が2つ目のバッファに追加されます。 2つのバッファを意図的に使用して、インジケーターが再描画されないようにし、2番目のフィルター操作フェーズでシステムが更新 (修正) される仕組みを確認しました。インジケーターコードは簡単で、以下の添付ファイルでご利用いただけます。インジケータ操作の結果を次に示します。

チャート上のカルマンフィルタ

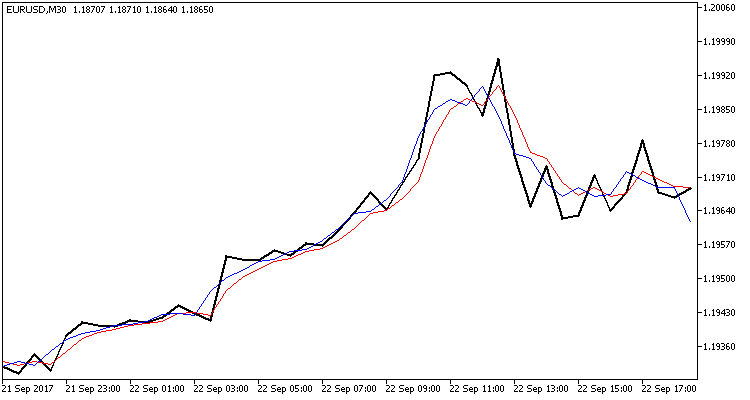
チャートには、次の3つの破線が表示されます。

黒い線は、実際の足の終値を示します
赤色の線は予測値を示します。
青色の線は、カルマンフィルタによって更新されたシステム状態です。

ご覧の通り、両方のラインは、実際の終値に近いと良い確率で反転ポイントを示しています。インジケーターが値を再描画しないことに注意してください。赤い線は、終値がまだ知られていないときに、足の始値に描画されます。

このフィルタの一貫性と、このフィルタを使用したトレーディングシステムの作成の可能性について説明します。

4. MQL5 ウィザード用のトレーディングシグナルモジュールの作成

赤いシステムの状態予測ラインは、実際の価格を示す黒い線よりもスムーズなことが上記のチャートからわかります。修正されたシステム状態を示す青色の線は、常に間にあります。言い換えれば、赤い線上の青い線は強気のトレンドを示しています。逆に、赤線の下の青線は、弱気のトレンドの徴候です。青線と赤線のクロスは、トレンドチェンジシグナルです。

この戦略をテストするには、MQL5 ウィザード用のトレーディングシグナルのモジュールを作成しましょう。トレーディングシグナルモジュールの作成については、このサイトで利用できるさまざまな記事で説明されています: [1]、[4]、[5]。ここでは、戦略に関連するポイントについて説明します。

まず、CExpertSignal から継承される CSignalKalman モジュールクラスを作成します。今回の戦略は、カルマンフィルタに基づいているので、クラスの上に作成された CKalman クラスのインスタンスを宣言する必要があります。モジュール内で CKalman クラスインスタンスを宣言するため、モジュール内でも初期化されます。そのため、初期パラメータをモジュールに渡す必要があります。上記のタスクがコードに実装されているメソッドです。

//+---------------------------------------------------------------------------+
// wizard description start
//+---------------------------------------------------------------------------+
//| Description of the class                                                  |
//| Title=Signals of Kalman's filter design by DNG                            |
//| Type=SignalAdvanced                                                       |
//| Name=Signals of Kalman's filter design by DNG                             |
//| ShortName=Kalman_Filter                                                   |
//| Class=CSignalKalman                                                       |
//| Page=https://www.mql5.com/ru/articles/3886                                |
//| Parameter=TimeFrame,ENUM_TIMEFRAMES,PERIOD_H1,Timeframe                   |
//| Parameter=HistoryBars,uint,3000,Bars in history to analysis               |
//| Parameter=ShiftPeriod,uint,0,Period for shift                             |
//+---------------------------------------------------------------------------+
// wizard description end
//+------------------------------------------------------------------+
//                                                                 |
//+------------------------------------------------------------------+
class CSignalKalman: public CExpertSignal
  {
private:
   ENUM_TIMEFRAMES   ce_Timeframe;        //タイムフレーム
   uint              ci_HistoryBars;      //分析へのヒストリーの棒
   uint              ci_ShiftPeriod;      //シフト期間
   CKalman          *Kalman;              //カルマンフィルタのクラス
   //---
   datetime          cdt_LastCalcIndicators;
   
   double            cd_forecast;         //予測値
   double            cd_corretion;        //修正値
   //---
   bool              CalculateIndicators(void);
       
public:
                     CSignalKalman();
                    ~CSignalKalman();
   //---
   void              TimeFrame(ENUM_TIMEFRAMES value);
   void              HistoryBars(uint value);
   void              ShiftPeriod(uint value);
   //---設定の検証メソッド
   virtual bool      ValidationSettings(void);
   //---インジケーターと時系列の作成メソッド
   virtual bool      InitIndicators(CIndicators *indicators);
   //相場モデルが形成されているかどうかを確認するメソッド
   virtual int       LongCondition(void);
   virtual int       ShortCondition(void);
  };

クラス初期化関数では、変数にデフォルト値を割り当て、カルマンフィルタクラスを初期化します。

CSignalKalman::CSignalKalman(void):    ci_HistoryBars(3000),
                                       ci_ShiftPeriod(0),
                                       cdt_LastCalcIndicators(0)
  {
   ce_Timeframe=m_period;
   
   if(CheckPointer(m_symbol)!=POINTER_INVALID)
      Kalman=new CKalman(ci_HistoryBars,ci_ShiftPeriod,m_symbol.Name(),ce_Timeframe);
  }

フィルタを使用したシステム状態の計算は、CalculateIndicators 関数で実行されます。関数の先頭には、フィルタ値が現在の足で計算されているかどうかを確認する必要があります。値が既に再計算されている場合は、関数を終了します。

boolCSignalKalman:: CalculateIndicators (void)
  {
   //---最後の計算の時刻を確認する
   datetime current=(datetime)SeriesInfoInteger(m_symbol.Name(),ce_Timeframe,SERIES_LASTBAR_DATE);
   if(current==cdt_LastCalcIndicators)
      return true;                  //この足でデータが既に計算されている場合は終了

次に、最後のシステム状態を確認します。定義されていない場合は、CKalman クラスの自己回帰モデル計算フラグをリセットします (この場合、クラスの次の呼び出し時にモデルが再計算されます)。

   if(cd_corretion==QNaN)
     {
      if(CheckPointer(Kalman)==POINTER_INVALID)
        {
         Kalman=new CKalman(ci_HistoryBars,ci_ShiftPeriod,m_symbol.Name(),ce_Timeframe);
         if(CheckPointer(Kalman)==POINTER_INVALID)
           {
            return false;
           }
        }
      else
         Kalman.Clear_AR_Flag();
     }

次のステップでは、以前の関数呼び出し以降に出現した足の数を確認する必要があります。間隔が大きすぎる場合は、自己回帰モデルの計算フラグをリセットします。

   int shift=StartIndex();
   int bars=Bars(m_symbol.Name(),ce_Timeframe,current,cdt_LastCalcIndicators);
   if(bars>(int)fmax(ci_ShiftPeriod,1))
     {
      bars=(int)fmax(ci_ShiftPeriod,1);
      Kalman.Clear_AR_Flag();
     }

次に、すべての未経産の足のシステム状態値を再計算します。

   double close[];
   if(m_close.GetData(shift,bars+1,close)<=0)
     {
      return false;
     }
  
   for(uint i=bars;i>0;i--)
     {
      cd_forecast=Kalman.Forecast();
      cd_corretion=Kalman.Correction(close[i]);
     }

再計算後、システム状態を確認し、最後の関数の呼び出し時間を保存します。操作が正常に完了した場合、この関数は true を返します。

   if(cd_forecast==EMPTY_VALUE || cd_forecast==0 || cd_corretion==EMPTY_VALUE || cd_corretion==0)
      return false;
  
   cdt_LastCalcIndicators=current;
  //---
   return true;
  }

意思決定関数 (LongCondition および ShortCondition) の構造は完全に同一であり、トレード開始の反対の条件を使用します。 ShortCondition 関数コードの例を次に示します。

まず、フィルタ値再計算関数を開始します。値の再計算が失敗した場合は、関数を終了して0を返します。

intCSignalKalman:: ShortCondition (void)
  {
   if(!CalculateIndicators())
      return 0;

フィルタ値が正常に再計算された場合は、予測値と修正した数値を比較します。予測値が修正された数値より大きい場合、関数は重み値を返します。それ以外の場合は0が返されます。

   int result=0;
   //--- 
   if(cd_corretion<cd_forecast)
      result=80;
   return result;
  }

モジュールは、"反転" の原則に基づいて構築されているので、ポジションのクローズ関数を実装していません。

すべての関数のコードは、添付ファイルにあります。

5. EAのテスト

シグナルモジュールに基づくエキスパートアドバイザの作成の詳細については、記事 [1] に記載されているので、ここの手順を省略します。テストにおける目的では、EA は上記の1つのトレーディングモジュールのみに基づいており、固定ロットで、トレーリングストップを使用せずに実行されることに注意してください。

このEAは、Н1の時間枠で、2017年８月の EURUSD のヒストリカルデータを使用してテストされました。 3000足の履歴データ、すなわちほぼ6ヶ月間で、自己回帰モデルの計算に使用されました。 EA はテイクプロフィット・ストップロスなしでテストされ、トレードのカルマンフィルタの明確な影響を見ました。

収益性の高いトレードが 49.33% となりました。平均の勝ちトレードの利益は、負けトレードの値を超えています。一般的に、EA のテストでは、選択した期間の利益を示し、利益率は1.56 でした。以下はテストのスクリーンショットです。

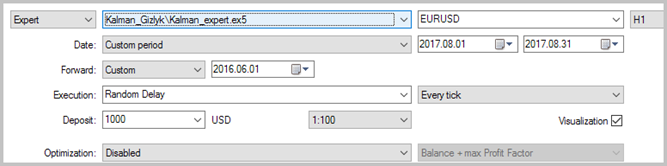
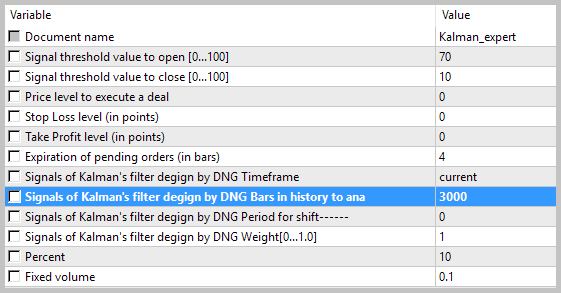
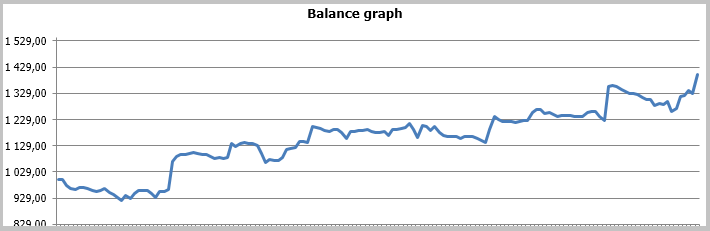
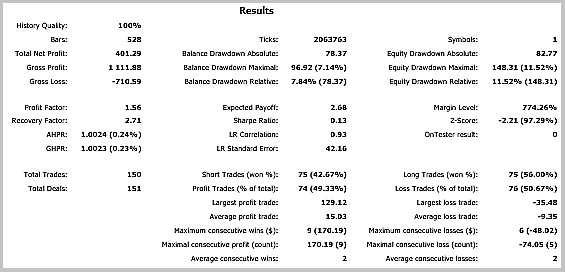
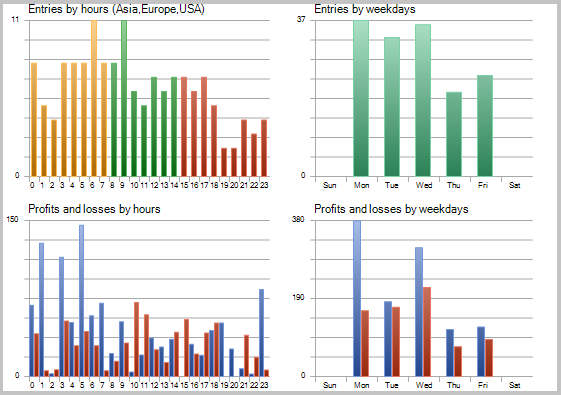
チャート上のトレードの詳細な分析は、この戦術の次の2つの弱点を明らかにしています。

レンジ相場における一連の負けトレード
オープンポジションからの決済の遅延

価格表のテスト結果

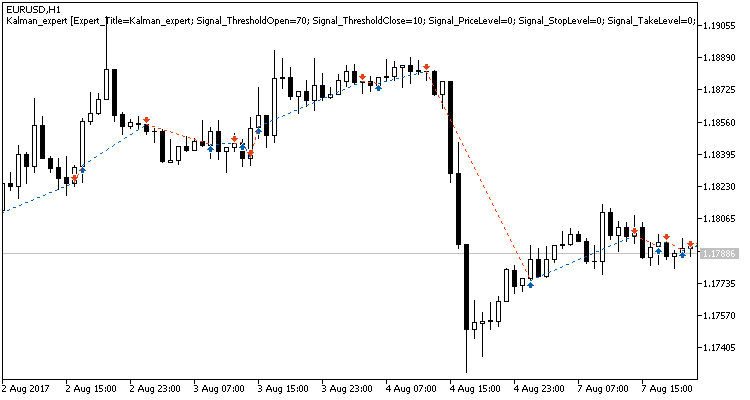
また、アダプティブ・マーケット・フォロー戦略を使用してEAをテストする際にも、同じ問題点が明らかになりました。問題を解決するためのオプションは、前述の記事で示唆されています。しかし、以前の戦略とは異なり、カルマンフィルタベースの EA はポジティブな結果を示しました。私の意見では、この記事で説明した戦略は、レンジを決定するための追加のフィルタを補えば成功すると思います。この結果は、タイムフィルタを利用しても、おそらく改善されるでしょう。結果を改善するもう一つの選択は、シャープな逆の動きをする場合に、利益が失われることを防ぐために、ポジションの決済シグナルを加えることです。

結論

カルマンフィルタの原理を分析し, その基礎となるインジケーターとEAを作成しました。テスト結果は有望であり、対処する必要があるボトルネックが明らかになりました。

この記事は、実際のトレードで使用するための "聖杯" ではなく、あくまで一般的な情報とEAを作成する例を提供していることに注意してください。

熟慮されたアプローチと収益性の高いトレードを構築することを切に願っています。

URL リンク

この記事で使用されるプログラム:

#	Name	Type	Description
1	Kalman.mqh	クラスライブラリ	カルマンフィルタクラス
2	SignalKalman.mqh	クラスライブラリ	カルマンフィルタを用いたトレーディングシグナルモジュール
3	Kalman_indy.mq5	Indicator	カルマンフィルタインジケーター
4	Kalman_expert.mq5	EA	カルマンフィルタを利用した戦略に基づくEA
5	Kalman_test.zip	Archive	アーカイブには、EA をストラテジーテスタで実行して得られたテスト結果があります。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/3886

添付されたファイル |

ZIPをダウンロード

Kalman_test.zip (95.5 KB)

MQL5.zip (290.55 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

通貨ペアバスケットをトレードするときに発生するパターンのテストパート2

通貨ペアバスケットをトレードするときに発生するパターンをテストし、トレード通貨ペアバスケットの記事で説明したメソッドを試していきます。実際には、移動平均のクロスの複合 WPR チャートのパターンを使用できるかどうかを検討してみましょう。もし使用できる場合は、適切な使用メソッドを検討する必要があります。

インジケーターへのエントリの解決

トレーダーにはさまざまな事態が発生します。多くの場合、勝ちトレードは、負けトレードと照らし合わせながら、戦略を再構成することができます。どちらの場合でも、既知のインジケーターとトレードを比較します。この記事では、インジケーターを使ったトレードの比較方法を考察します。

MQL5 ウィザードの NRTR に基づく NRTR インジケーターとトレーディングモジュール

この記事では、NRTR インジケーターを分析し、このインジケーターに基づいてトレードシステムを作成します。追加のトレンド確認インジケーターと NRTR の組み合わせに基づいて戦略を作成する際に使用することができるトレードシグナルのモジュールを開発します。

取引における様々な移動平均の比較

7種類の移動平均（MA）が検討されており、それに対応する取引戦略が開発されています。単一の取引戦略における様々なMAのテストと比較が行われ、与えられた移動平均の適用の比較パフォーマンス特性が提供されています。