Treinamento de perceptron multicamadas com o algoritmo de Levenberg-Marquardt

MetaTrader 5 — Negociação | 22 abril 2025, 08:55

Introdução

O objetivo deste artigo é oferecer aos traders praticantes um algoritmo muito eficiente para o treinamento de redes neurais, que é uma variante do método de otimização de Newton conhecida como algoritmo de Levenberg-Marquardt. Este é um dos algoritmos mais rápidos para treinar redes neurais com propagação para frente, rivalizando apenas com o algoritmo de Broyden-Fletcher-Goldfarb-Shanno (L-BFGS).

Métodos estocásticos de otimização, como a descida do gradiente estocástica (SGD) e Adam, são bastante adequados para treinamento offline, quando o retreinamento da rede neural ocorre em intervalos longos. No entanto, se o trader que utiliza redes neurais deseja que o modelo se adapte rapidamente às condições de mercado em constante mudança, é necessário treiná-lo novamente a cada nova barra, ou em intervalos curtos. Nesses casos, são mais indicados algoritmos que utilizam não só a informação do gradiente da função de perda, mas também informações adicionais das segundas derivadas parciais, o que permite encontrar um mínimo local da função de perda em poucas épocas de treinamento.

Até onde sei, não há nenhuma implementação do algoritmo de Levenberg-Marquardt em MQL5 disponível publicamente. Está na hora de preencher essa lacuna e, ao mesmo tempo, revisar brevemente os algoritmos de otimização mais conhecidos e simples, como a descida do gradiente, a descida do gradiente com impulso (momentum) e a descida do gradiente estocástica. Ao final do artigo, faremos um pequeno teste de eficácia do algoritmo de Levenberg-Marquardt em comparação com os algoritmos da biblioteca scikit-learn para aprendizado de máquina.

Conjunto de dados

Em todos os exemplos a seguir, para simplificar a explicação, são utilizados dados sintéticos. A única variável preditora utilizada é o tempo, e a variável-alvo, que queremos prever com a rede neural, é a função:

1 + sin(pi/4*time) + NormDistr(0,sigma)

Essa função é composta por uma parte determinística, representada por um componente periódico em forma de seno, e uma parte estocástica, representada por ruído branco gaussiano. Ao todo, são 81 pontos de dados. Abaixo está apresentado o gráfico dessa função e sua aproximação por um perceptron de três camadas.

SyntheticData

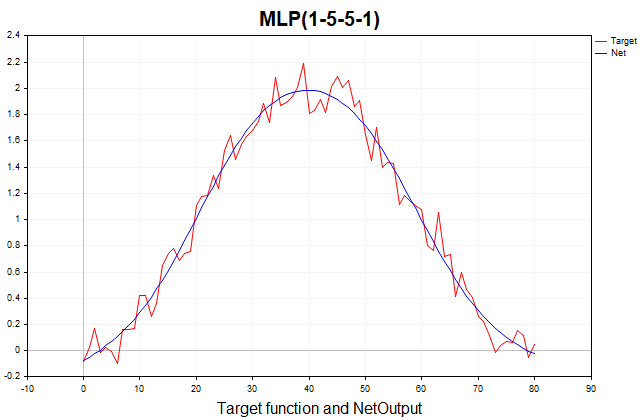
Figura (1) Função-alvo e sua aproximação por um perceptron de três camadas

Descida do gradiente

Começaremos com a implementação da descida do gradiente padrão, por ser o método mais simples de treinamento de redes neurais. Para isso, utilizei como base um excelente exemplo do guia MQL5 (Matrizes e Vetores / Aprendizado de Máquina). Adicionei a possibilidade de escolher a função de ativação para a última camada da rede e tornei a implementação da descida do gradiente mais genérica, capaz de treinar não apenas com a função de perda quadrática, como é implicitamente assumido no exemplo do guia, mas com todas as funções de perda disponíveis no MQL5. A função de perda ocupa um papel central no treinamento de redes neurais, e às vezes vale a pena experimentar diferentes funções, não se limitando apenas à perda quadrática. A seguir, está a fórmula geral para calcular o erro da camada de saída (delta):

delta last layer

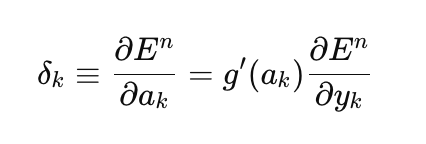
onde:

delta_k — erro da camada de saída,
E — função de perda,
g'(a_k) — derivada da função de ativação,
a_k — pré-ativação da última camada,
y_k — valor previsto pela rede.

//--- Производная функции потерь по предсказанному значению       
matrix DerivLoss_wrt_y = result_.LossGradient(target,loss_func);  
matrix deriv_act;
  if(!result_.Derivative(deriv_act, ac_func_last)) 
     return false;      
 matrix  loss = deriv_act*DerivLoss_wrt_y;  // loss = delta_k

As derivadas parciais da função de perda em relação ao valor previsto pela rede são calculadas pela função LossGradient, e a derivada da função de ativação é calculada pela função Derivative. No exemplo do guia, o erro da camada de saída é representado pela diferença entre o valor alvo e o valor previsto pela rede, multiplicada por 2.

matrix loss = (target - result_)*2;

Na literatura de aprendizado de máquina, o erro de cada camada da rede normalmente é chamado de delta (D2, D1, etc.), e não de loss (veja, por exemplo, Bishop (1995)). A partir de agora, vou usar essa notação no código.

Certo, como esse resultado foi obtido? Aqui, assume-se implicitamente que a função de perda é a soma dos quadrados das diferenças entre o valor alvo e o previsto, e não o erro quadrático médio (MSE), que é normalizado pelo tamanho do conjunto de treinamento. A derivada dessa função de perda é justamente (target - result)*2. Como a função de ativação identidade é usada na última camada da rede, cuja derivada é igual a um, chegamos a esse resultado. Portanto, para utilizar funções de perda e funções de ativação arbitrárias na saída da rede, é preciso usar a fórmula geral mencionada acima.

Vamos agora treinar nossa rede com a função de perda de erro quadrático médio. Para melhor visualização, o gráfico foi exibido em escala logarítmica.

Loss SD

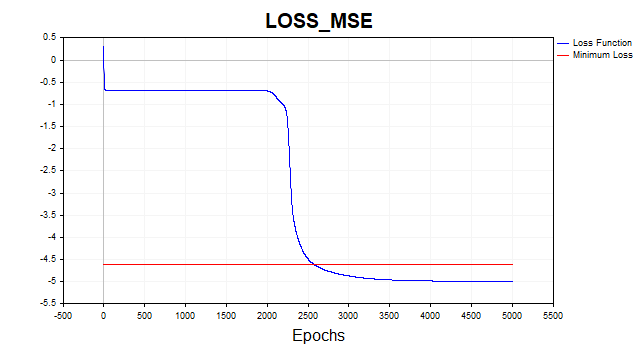
Figura 2 Função de perda MSE, descida do gradiente

Em média, o algoritmo de descida do gradiente precisa de 1.500 a 2.000 épocas (ou seja, passagens por todo o conjunto de dados de treinamento) para atingir o limiar mínimo da função de perda. Neste exemplo, utilizei duas camadas ocultas com cinco neurônios em cada uma.

A linha vermelha no gráfico indica o limiar mínimo da função de perda. Esse valor é definido como a variância do ruído branco gaussiano. Aqui, utilizei ruído com variância igual a 0,01 (0,1 sigma * 0,1 sigma).

E se permitirmos que o modelo da rede neural aprenda além desse limiar mínimo? Nesse caso, enfrentamos um fenômeno indesejado conhecido como sobreajuste da rede. Não faz sentido tentar reduzir o erro da função de perda no conjunto de dados de treinamento para um valor inferior ao limiar mínimo, pois isso compromete a capacidade preditiva do modelo no conjunto de teste. Aqui lidamos com o fato de que não é possível prever uma série com mais precisão do que aquela permitida pela dispersão estatística dessa série. Se interrompermos o treinamento antes de atingir o nível mínimo, enfrentamos outro problema: a rede ficará subajustada. Ou seja, será uma rede que não conseguiu captar completamente o componente previsível da série.

Como você pode ver, a descida do gradiente exige um número bastante elevado de iterações para alcançar um conjunto ideal de parâmetros. E isso em um caso com um conjunto de dados tão simples quanto o nosso. Para problemas práticos reais, o tempo de treinamento com descida do gradiente acaba sendo inviável. Uma das maneiras mais simples de melhorar a convergência e a velocidade da descida do gradiente é o método do momentum (impulso).

Descida do gradiente com impulso

A ideia por trás da descida do gradiente com impulso é suavizar a trajetória dos parâmetros da rede durante o treinamento, utilizando uma média exponencial simples dos parâmetros. Da mesma forma que usamos médias para suavizar séries temporais de preços de instrumentos financeiros com o objetivo de identificar a tendência principal, também podemos suavizar a trajetória do vetor de parâmetros que caminha em direção ao ponto de mínimo local da nossa função de perda. Para visualizar melhor esse processo, observe o gráfico que mostra como os valores de dois parâmetros variaram desde o início do treinamento até o ponto de mínimo da função de perda. A Fig. 3 demonstra a trajetória sem o uso do impulso.

SD without Momentum

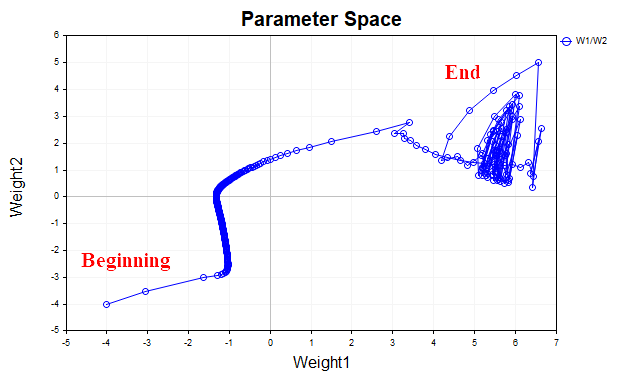
Fig. 3 Descida do gradiente sem impulso

Percebemos que, à medida que se aproxima do mínimo, o vetor de parâmetros começa a oscilar de forma caótica, impedindo que o ponto ótimo seja alcançado. Para eliminar esse comportamento, é necessário reduzir o coeficiente da taxa de aprendizado. Nesse caso, o algoritmo pode até começar a convergir, mas o tempo necessário para encontrar a solução pode aumentar significativamente.

A Fig. 4 mostra a trajetória do vetor de parâmetros com o uso de impulso (com valor = 0,9). Desta vez, a trajetória está mais suavizada, e conseguimos alcançar tranquilamente o ponto ótimo. E agora, inclusive, é possível aumentar o coeficiente da taxa de aprendizado. Essa é justamente a ideia central por trás da descida do gradiente com impulso: acelerar o processo de convergência.

SD with Momentum

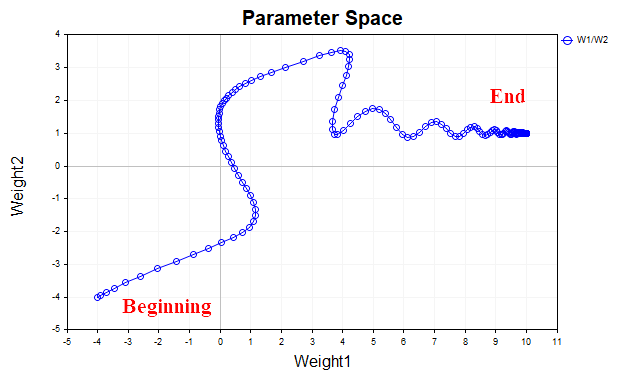
Fig.(4) Descida do gradiente, momentum (0,9)

O script Momentum_SD implementa o algoritmo de descida do gradiente com impulso. Nele, decidi remover uma das camadas ocultas e separar os pesos e os vieses da rede para facilitar a visualização. Agora temos apenas uma camada oculta, com 20 neurônios, em vez de duas camadas ocultas com 5 neurônios cada, como no exemplo anterior.

//+------------------------------------------------------------------+
//|                                                  Momentum_SD.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <Graphics\Graphic.mqh>
#include <Math\Stat\Math.mqh>
#include <Math\Stat\Normal.mqh>
enum Plots
  {
   LossFunction_plot,  
   target_netpredict_plot
  };
  
matrix weights1, weights2,bias1,bias2;                      // network parameter matrices
matrix dW1,db1,dW2,db2;                                     // weight increment matrices
matrix n1,n2,act1,act2;                                     // neural layer output matrices
input int    layer1                  = 20;                  // neurons Layer 1
input int    Epochs                  = 1000;                // Epochs
input double lr                      = 0.1;                 // learning rate coefficient
input double sigma_                  = 0.1;                 // standard deviation synthetic data
input double gamma_                  = 0.9;                 // momentum 
input Plots  plot_                   = LossFunction_plot;   // display graph
input bool   plot_log                = false;               // Plot Log graph
input ENUM_ACTIVATION_FUNCTION ac_func      = AF_TANH;      // Activation Layer1
input ENUM_ACTIVATION_FUNCTION ac_func_last = AF_LINEAR;    // Activation Layer2
input ENUM_LOSS_FUNCTION       loss_func    = LOSS_MSE;     // Loss function

double LossPlot[],target_Plot[],NetOutput[];
matrix ones_;
int Sample_,Features; 

//+------------------------------------------------------------------+
//| Функция запуска скрипта                                          |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- генерируем обучающую выборку
   matrix data, target;
   Func(data,target);
   StandartScaler(data);
   Sample_= (int)data.Rows();
   Features = (int)data.Cols();
   ArrayResize(target_Plot,Sample_);
   for(int i=0; i< (int)target.Rows(); i++)
     {
      target_Plot[i] =target[i,0];
     }
   ones_ = matrix::Ones(1,Sample_);  
      
   ulong start=GetMicrosecondCount(); 
//--- обучаем модель
   if(!Train(data, target, Epochs))
      return;
   ulong end = (GetMicrosecondCount()-start)/1000;  
   Print("Learning time = " + (string)end + " msc");
//--- генерируем тестовую выборку
    Func(data,target);
    StandartScaler(data);
//--- тестирование модели
   Test(data, target);
//--- отображаем графики  
   PlotGraphic(15,plot_log);
  }
//+------------------------------------------------------------------+
//| Метод обучения модели                                            |
//+------------------------------------------------------------------+
bool Train(matrix &data, matrix &target, const int epochs)
  {
//--- создаем модель
   if(!CreateNet())
      return false;
   ArrayResize(LossPlot,Epochs);
//--- обучаем модель
   for(int ep = 0; ep < epochs; ep++)
     {
      //--- прямой проход
      if(!FeedForward(data))
         return false;
      PrintFormat("Epoch %d, loss %.5f", ep, act2.Loss(target, loss_func));
      LossPlot[ep] = act2.Loss(target, loss_func);
      //--- обратный проход и обновление матриц весов
      if(!Backprop(data, target))
         return false;
     }
//---
   double rmse=act2.RegressionMetric(target.Transpose(),REGRESSION_RMSE);
   PrintFormat("rmse %.3f / sigma %.2f ",rmse,sigma_);
   ArrayResize(NetOutput,Sample_);
   for(int i=0; i< (int)act2.Cols(); i++)
     {
      NetOutput[i]  =act2.Transpose()[i,0];
     }
//--- возвращаем результат
   return true;
  }
//+------------------------------------------------------------------+
//| Метод создания модели                                            |
//+------------------------------------------------------------------+
bool CreateNet()
  {
//--- инициализируем матрицы весов
   if(!weights1.Init(layer1,Features)  || !weights2.Init(1,layer1)) 
      return false;
//--- инициализируем матрицы смещений
   if(!bias1.Init(layer1,1)  || !bias2.Init(1,1))  
      return false;
//--- инициализируем матрицы приращений параметров
   dW1.Init(layer1,Features);
   dW2.Init(1, layer1);
   db1.Init(layer1,1);
   db2.Init(1,1);
   dW1.Fill(0);
   dW2.Fill(0);
   db1.Fill(0);
   db2.Fill(0);
//--- заполняем матрицы параметров случайными значениями
   weights1.Random(-0.1, 0.1);
   weights2.Random(-0.1, 0.1);
   bias1.Random(-0.1,0.1);
   bias2.Random(-0.1,0.1);
//--- возвращаем результат
   return true;
  }
//+------------------------------------------------------------------+
//| Метод прямого прохода                                            |
//+------------------------------------------------------------------+
bool FeedForward(matrix &data)
  { 
//--- вычисляем первый нейронный слой
//--- n1 предактивация первого слоя
   n1 = weights1.MatMul(data.Transpose()) + bias1.MatMul(ones_);
//--- вычисляем функцию активации первого слоя act1
   n1.Activation(act1, ac_func);
//--- вычисляем второй нейронный слой
//--- n2 предактивация второго слоя
   n2 = weights2.MatMul(act1) + bias2.MatMul(ones_);
//--- вычисляем функцию активации второго слоя act2
   n2.Activation(act2, ac_func_last);
//--- возвращаем результат
   return true;
  }
//+------------------------------------------------------------------+
//| Метод обратного прохода                                          |
//+------------------------------------------------------------------+
bool Backprop(matrix &data, matrix &target)
  {
//--- Производная функции потерь по предсказанному значению
   matrix DerivLoss_wrt_y = act2.LossGradient(target.Transpose(),loss_func);
   matrix deriv_act2;
   n2.Derivative(deriv_act2, ac_func_last);
//--- D2   
   matrix  D2 = deriv_act2*DerivLoss_wrt_y; // ошибка(delta) выходного слоя сети
//--- D1
   matrix deriv_act1;
   n1.Derivative(deriv_act1, ac_func);
   matrix D1 = weights2.Transpose().MatMul(D2);
   D1 = D1*deriv_act1; // ошибка (delta) первого слоя сети
//--- обновляем параметры  сети
   matrix  ones = matrix::Ones(data.Rows(),1);
   dW1 = gamma_*dW1 + (1-gamma_)*(D1.MatMul(data)) * lr;
   db1 = gamma_*db1 + (1-gamma_)*(D1.MatMul(ones)) * lr;
   dW2 = gamma_*dW2 + (1-gamma_)*(D2.MatMul(act1.Transpose())) * lr;
   db2 = gamma_*db2 + (1-gamma_)*(D2.MatMul(ones)) * lr;
   weights1 =  weights1 - dW1;
   weights2 =  weights2 - dW2;
   bias1    =  bias1    - db1;
   bias2    =  bias2    - db2;
//--- возвращаем результат
   return true;
  }

Graças a esse impulso, consegui aumentar a taxa de aprendizado de 0,1 para 0,5. Agora o algoritmo converge em 150 a 200 iterações, em vez de 500, como ocorria anteriormente.

Loss SD with Momentum

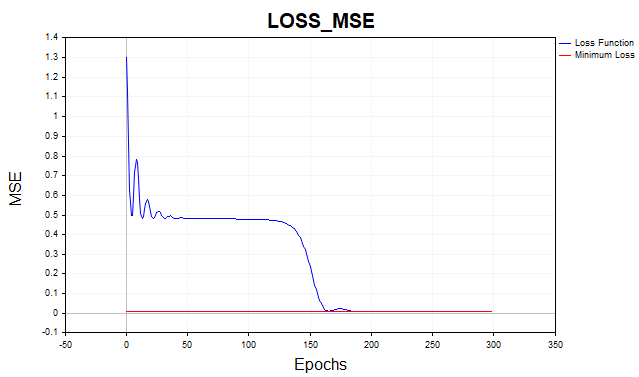
Fig.(5) Função de perda MSE, MLP(1-20-1) SD_Momentum

Descida do gradiente estocástica

O Momentum é ótimo, mas quando o conjunto de dados não é composto por 81 pontos, como no nosso exemplo, e sim por dezenas de milhares de amostras, então já faz sentido falar sobre um algoritmo bem estabelecido (e simples) como o SGD. O que ele é, exatamente? É a mesma descida do gradiente, mas o gradiente é calculado não com base em todo o conjunto de dados de treinamento, e sim sobre uma parte muito pequena desse conjunto (mini-batch), ou até mesmo sobre um único ponto de dado. Depois disso, os pesos da rede são atualizados, um novo ponto de dado é escolhido aleatoriamente e o processo se repete até que o algoritmo convirja. É por isso que o algoritmo se chama estocástico — na descida do gradiente tradicional, os pesos da rede só eram atualizados após o cálculo do gradiente em todo o conjunto de dados, o que é chamado de método em (batch method).

Vamos implementar a versão do SGD onde o mini-lote consiste de apenas um ponto de dado.

Loss SGD

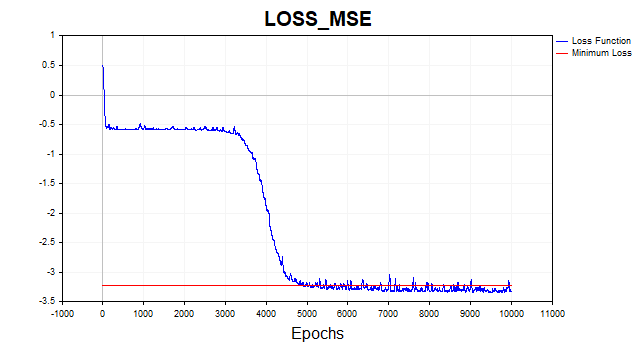
Fig.(6) Função de perda em escala logarítmica, SGD

O algoritmo SGD (com batch_size = 1) converge até o limite mínimo em cerca de 4 a 6 mil iterações, mas é importante lembrar que estamos usando apenas um exemplo de treino, dentre os 81 disponíveis, para atualizar o vetor de parâmetros. Sendo assim, o algoritmo neste conjunto de dados converge em aproximadamente 50 a 75 épocas. Nada mal em comparação com o algoritmo anterior, não é mesmo? Aqui também usei impulso, mas como estamos trabalhando com um único ponto de dado, ele não tem um impacto muito grande sobre a velocidade de convergência.

Algoritmo de Levenberg-Marquardt

Este bom e velho algoritmo está, por algum motivo, completamente esquecido hoje em dia, embora, se sua rede tiver apenas algumas centenas de parâmetros, não exista concorrência à sua altura, exceto pelo L-BFGS.

Mas, há um ponto importante. O algoritmo de Levenberg-Marquardt foi projetado para minimizar funções que são somas de quadrados de outras funções não lineares. Por isso, ao utilizarmos esse método, estaremos limitados apenas à função de perda quadrática ou ao erro quadrático médio. Considerando todas as outras condições iguais, essa função de perda dá conta do recado, portanto esse não é um problema sério, mas é importante saber que não conseguiremos treinar a rede com esse algoritmo usando outras funções de perda.

Vamos agora entender em detalhes como esse algoritmo surgiu. Começamos pelo método de Newton:

Newton’s method

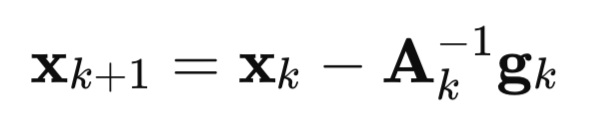
onde:

A – é a matriz inversa do hessiano da função de perda F(x),

g – é o gradiente da função de perda F(x),

x – é o vetor de parâmetros.

Agora, vamos observar nossa função de perda quadrática:

SSE

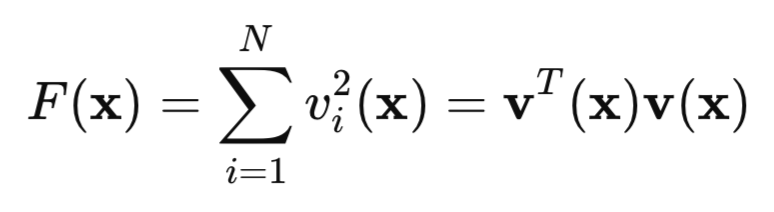
aqui, v representa o erro da rede (valor previsto menos o alvo), e x é o vetor de parâmetros da rede, que inclui todos os pesos e vieses de cada camada.

Vamos calcular o gradiente dessa função de perda:

gradient SSE Loss function

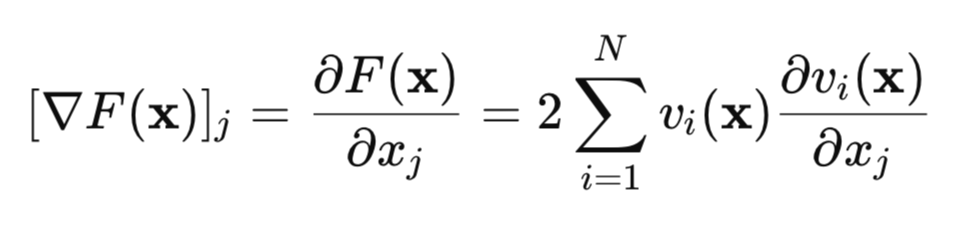
Na forma matricial, isso pode ser representado assim:

matrix notation gradient

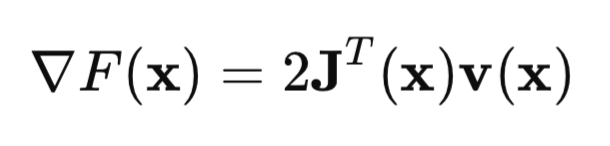
O ponto-chave aqui é a matriz Jacobiana:

Jacobian

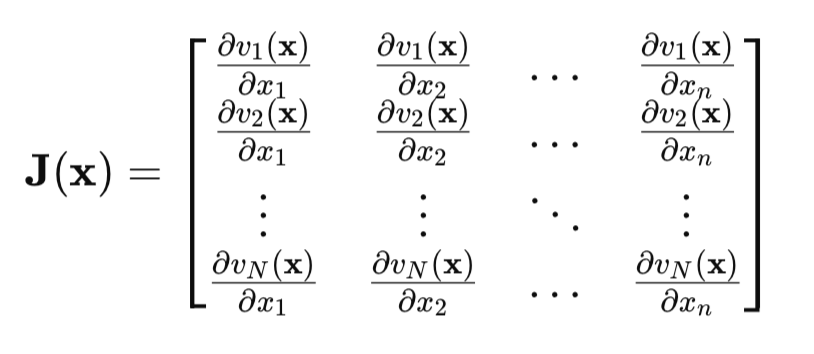
Na matriz Jacobiana, cada linha contém todas as derivadas parciais do erro da rede em relação a todos os parâmetros. Cada linha corresponde a um exemplo do conjunto de treinamento.

Agora vejamos a matriz hessiana. Essa é a matriz das segundas derivadas parciais da função de perda. Calcular o hessiano é uma tarefa complexa e custosa, por isso usamos uma aproximação do hessiano pela matriz Jacobiana:

Hessian

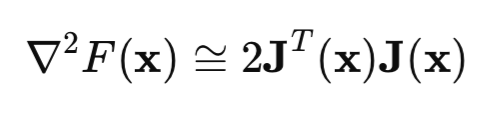
Se substituirmos as fórmulas do hessiano e do gradiente na fórmula do método de Newton, obtemos o método de Gauss-Newton:

Mas o problema do método de Gauss-Newton é que a matriz [J'J] pode não ser invertível. Então, para resolver esse problema, adiciona-se a essa matriz a matriz identidade multiplicada por um escalar positivo mu*I. É justamente aí que obtemos o algoritmo de Levenberg-Marquardt:

Levenberg-Marquardt method

A particularidade desse algoritmo é que, quando o parâmetro mu assume valores positivos grandes, o algoritmo se comporta como a descida do gradiente tradicional, que vimos no início do artigo. Se o parâmetro mu tende a zero, retornamos ao método de Gauss-Newton.

Geralmente, o treinamento começa com um valor pequeno de mu, se o valor da função de perda não diminuir, então o parâmetro mu é aumentado (por exemplo, multiplicado por 10). Isso nos aproxima do método de descida do gradiente, e mais cedo ou mais tarde a função de perda começa a diminuir. Se a função de perda diminuir, reduzimos o valor do parâmetro mu, e ativamos o método de Gauss-Newton para acelerar a convergência até o ponto de mínimo. Essa é a ideia principal do método de Levenberg-Marquardt: alternar continuamente entre a descida do gradiente e o método de Gauss-Newton.

A implementação do processo de propagação reversa no algoritmo de Levenberg-Marquardt tem suas particularidades. Como os elementos da matriz Jacobiana representam as derivadas parciais dos erros da rede, e não dos quadrados desses erros, a fórmula para calcular o delta da última camada da rede, apresentada no início do artigo, fica mais simples. Agora, o delta é simplesmente igual à derivada da função de ativação da última camada. Esse resultado surge quando calculamos a derivada do erro da rede (y – target) em relação a y, que, evidentemente, é igual a um.

Aqui está, então, o código da rede neural com comentários detalhados.

//+------------------------------------------------------------------+
//|                                                           LM.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <Graphics\Graphic.mqh>
#include <Math\Stat\Math.mqh>
#include <Math\Stat\Normal.mqh>
enum Plots
  {
   LossFunction_plot,
   mu_plot,
   gradient_plot,
   target_netpredict_plot
  };

matrix weights1,weights2,bias1,bias2;                    // network parameter matrices
matrix n1,n2,act1,act2,new_n1,new_n2,new_act1,new_act2;  // neural layer output matrices
input int    layer1     = 20;                            // neurons Layer 1
input int    Epochs     = 10;                            // Epochs
input double Initial_mu = 0.001;                         // mu
input double Incr_Rate  = 10;                            // increase mu
input double Decr_Rate  = 0.1;                           // decrease mu
input double Min_grad   = 0.000001;                      // min gradient norm
input double Loss_goal  = 0.001;                         // Loss goal
input double sigma_     = 0.1;                           // standard deviation synthetic data
input Plots  plot_      = LossFunction_plot;             // display graph
input bool   plot_log   = false;                         // logarithmic function graph 
input ENUM_ACTIVATION_FUNCTION ac_func      = AF_TANH;   // first layer activation function
input ENUM_ACTIVATION_FUNCTION ac_func_last = AF_LINEAR; // last layer activation function
input ENUM_LOSS_FUNCTION       loss_func    = LOSS_MSE;  // Loss function

double LossPlot[],NetOutput[],mu_Plot[],gradient_Plot[],target_Plot[];
matrix ones_;
double old_error,gradient_NormP2;
double mu_ = Initial_mu;
bool break_forloop = false;
int Sample_,Features;

//+------------------------------------------------------------------+
//| Функция запуска скрипта                                          |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- генерируем обучающую выборку
   matrix data, target;
   Func(data,target);
   StandartScaler(data);
   Sample_= (int)data.Rows();
   Features = (int)data.Cols();
   ArrayResize(target_Plot,Sample_);
   for(int i=0; i< (int)target.Rows(); i++)
     {
      target_Plot[i] =target[i,0];
     }

   ones_ = matrix::Ones(1,Sample_);
//--- обучаем модель
   ulong start=GetMicrosecondCount();
   Train(data, target, Epochs);
   ulong end = (GetMicrosecondCount()-start)/1000 ;
   Print("Learning time = " + (string)end + " msc");
   int NumberParameters = layer1*(Features+1) + 1*(layer1+1);
   Print("Number Parameters of NN = ",NumberParameters);

//--- генерируем тестовую выборку
   Func(data,target);
   StandartScaler(data);
//--- тестирование модели
   Test(data,target);
   
//--- отображаем графики
   PlotGraphic(15,plot_log);
  }
//+------------------------------------------------------------------+
//| Метод обучения модели                                            |
//+------------------------------------------------------------------+
bool Train(matrix &data, matrix &target, const int epochs)
  {
//--- создаем модель
   if(!CreateNet())
      return false;
//--- обучаем модель
   for(int ep = 0; ep < epochs; ep++)
     {
      //--- прямой проход
      if(!FeedForward(data))
         return false;
      PrintFormat("Epoch %d, loss %.5f", ep, act2.Loss(target, loss_func));
      //--- массивы для графиков
      ArrayResize(LossPlot,ep+1,10000);
      ArrayResize(mu_Plot,ep+1,10000);
      ArrayResize(gradient_Plot,ep+1,10000);
      LossPlot[ep]       = act2.Loss(target, loss_func);
      mu_Plot [ep]       = mu_;
      gradient_Plot[ep]  = gradient_NormP2;
      //--- Прекращаем обучение если достигнуто целевое значение функции потерь
      if(break_forloop == true){break;}
      //--- обратный проход и обновление матриц весов
      if(!Backprop(data, target))
         return false;
     }
//--- Евклидова норма градиента, параметр mu, метрика RMSE
   Print("gradient_normP2 =  ", gradient_NormP2);
   Print(" mu_ = ", mu_);
   double rmse=act2.RegressionMetric(target.Transpose(),REGRESSION_RMSE);
   PrintFormat("rmse %.3f / sigma %.2f ",rmse,sigma_);
//--- массив выхода сети для графика
   ArrayResize(NetOutput,Sample_);
   for(int i=0; i< (int)act2.Transpose().Rows(); i++)
     {
      NetOutput[i]  = act2.Transpose()[i,0];
     }
//--- возвращаем результат
   return true;
  }
//+------------------------------------------------------------------+
//| Метод создания модели                                            |
//+------------------------------------------------------------------+
bool CreateNet()
  {
//--- инициализируем матрицы весов
   if(!weights1.Init(layer1,Features) || !weights2.Init(1,layer1))
      return false;
//--- инициализируем матрицы смещений
   if(!bias1.Init(layer1,1)  || !bias2.Init(1,1))
      return false;
//--- заполняем матрицы весов случайными значениями
   weights1.Random(-0.1, 0.1);
   weights2.Random(-0.1, 0.1);
   bias1.Random(-0.1, 0.1);
   bias2.Random(-0.1, 0.1);   
//--- возвращаем результат
   return true;
  }
//+------------------------------------------------------------------+
//| Метод прямого прохода                                            |
//+------------------------------------------------------------------+
bool FeedForward(matrix &data)
  {
//--- вычисляем первый нейронный слой
//--- n1 предактивация первого слоя
   n1 = weights1.MatMul(data.Transpose()) + bias1.MatMul(ones_);
//--- вычисляем функцию активации первого слоя act1
   n1.Activation(act1, ac_func);
//--- вычисляем второй нейронный слой
//--- n2 предактивация второго слоя
   n2 = weights2.MatMul(act1) + bias2.MatMul(ones_);
//--- вычисляем функцию активации второго слоя act2
   n2.Activation(act2, ac_func_last);
//--- возвращаем результат
   return true;
  }
//+------------------------------------------------------------------+
//| Метод обратного прохода                                          |
//+------------------------------------------------------------------+
bool Backprop(matrix &data, matrix &target)
  {
//--- текущее значение функции потерь
   old_error = act2.Loss(target, loss_func);
//--- ошибка сети (квадратичная функция потерь)
   matrix loss = act2.Transpose() - target ;
//--- производная функции активации последнего слоя
   matrix D2;
   n2.Derivative(D2, ac_func_last);
//--- производная функции активации первого слоя
   matrix deriv_act1;
   n1.Derivative(deriv_act1, ac_func);
//--- ошибка первого слоя сети
   matrix D1 = weights2.Transpose().MatMul(D2);
   D1 = deriv_act1 * D1;
//--- первые частные производные ошибок сети по весам первого слоя
   matrix jac1;
   partjacobian(data.Transpose(),D1,jac1);
//--- первые частные производные ошибок сети по весам второго слоя
   matrix jac2;
   partjacobian(act1,D2,jac2);
//--- Якобиан
   matrix j1_D1 = Matrixconcatenate(jac1,D1.Transpose(),1);
   matrix j2_D2 = Matrixconcatenate(jac2,D2.Transpose(),1);
   matrix jac   = Matrixconcatenate(j1_D1,j2_D2,1);
// --- Градиент функции потерь
   matrix je = (jac.Transpose().MatMul(loss));
//--- Евклидова норма градиента нормируемая на обьем выборки
   gradient_NormP2 = je.Norm(MATRIX_NORM_FROBENIUS)/Sample_;
   if(gradient_NormP2 < Min_grad)
     {
      Print("Локальный минимум.Градиент меньше заданного значения.");
      break_forloop = true; // прекращаем обучение
      return true;
     }
//--- Гессиан
   matrix Hessian = (jac.Transpose().MatMul(jac));
   matrix I=matrix::Eye(Hessian.Rows(), Hessian.Rows());
//---
   break_forloop = true;
   while(mu_ <= 1e10 && mu_ > 1e-20)
     {
      matrix H_I = (Hessian + mu_*I);
      //--- решение через Solve
      vector v_je = je.Col(0);
      vector Updatelinsolve = -1* H_I.Solve(v_je);
      matrix Update = matrix::Zeros(Hessian.Rows(),1);
      Update.Col(Updatelinsolve,0); // приращение вектора параметров
      
      //--- неэффективное вычисление обратной матрицы
      //   matrix Update = H_I.Inv();
      //   Update = -1*Update.MatMul(je);
      //---

      //--- cохраняем текущие параметры 
      matrix  Prev_weights1 = weights1;
      matrix  Prev_bias1    = bias1;
      matrix  Prev_weights2 = weights2;
      matrix  Prev_bias2    = bias2;
      //---

      //--- обновляем параметры 
      //--- первый слой
      matrix updWeight1 = matrix::Zeros(layer1,Features);
      int count =0;
      for(int j=0; j <Features; j++)
        {
         for(int i=0 ; i <layer1; i++)
           {
            updWeight1[i,j] = Update[count,0];
            count = count+1;
           }
        }

      matrix updbias1 = matrix::Zeros(layer1,1);
      for(int i =0 ; i <layer1; i++)
        {
         updbias1[i,0] = Update[count,0];
         count = count +1;
        }
        
      weights1 = weights1 + updWeight1;
      bias1 = bias1 + updbias1;

      //--- второй слой
      matrix updWeight2 = matrix::Zeros(1,layer1);
      for(int i =0 ; i <layer1; i++)
        {
         updWeight2[0,i] = Update[count,0];
         count = count +1;
        }
      matrix updbias2 = matrix::Zeros(1,1);
      updbias2[0,0] = Update[count,0];

      weights2 = weights2 + updWeight2;
      bias2 = bias2 + updbias2;

      //--- вычисляем функцию потерь для новых параметров
      new_n1 = weights1.MatMul(data.Transpose()) + bias1.MatMul(ones_);
      new_n1.Activation(new_act1, ac_func);
      new_n2 = weights2.MatMul(new_act1) + bias2.MatMul(ones_);
      new_n2.Activation(new_act2, ac_func_last);
      //--- функция потерь с учетом новых параметров
      double new_error = new_act2.Loss(target, loss_func);
      //--- если функция потерь меньше заданного порога завершаем обучение
      if(new_error < Loss_goal)
        {
         break_forloop = true;
         Print("Обучение завершено. Достигнуто желаемое значение функции потерь");
         return true;
        }
      break_forloop = false;
      //---корректируем параметр mu
      if(new_error >= old_error)
        {
         weights1 = Prev_weights1;
         bias1    = Prev_bias1;
         weights2 = Prev_weights2;
         bias2    =  Prev_bias2;
         mu_ = mu_*Incr_Rate;
        }
      else
        {
         mu_ = mu_*Decr_Rate;
         break; 
        }

     }
//--- возвращаем результат
   return true;
  }

O algoritmo converge quando a norma do gradiente fica abaixo de um valor predefinido ou quando se atinge o nível desejado da função de perda. O algoritmo é interrompido se o parâmetro mu se tornar menor ou maior que um valor limite, ou após completar um número pré-estabelecido de épocas.

LM parameters

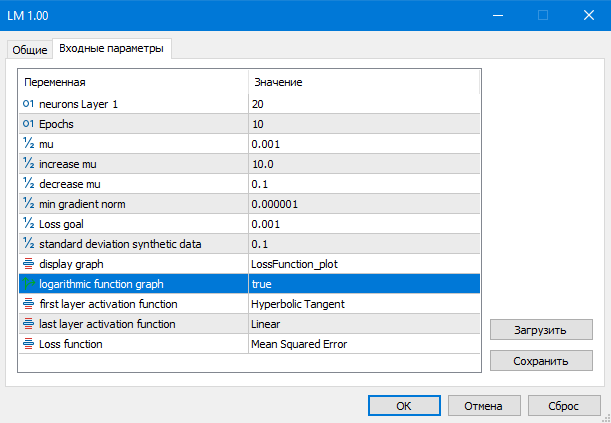
Fig.(7) Parâmetros do script LM

Vamos agora ver o resultado de toda essa ginástica matemática:

Loss LM

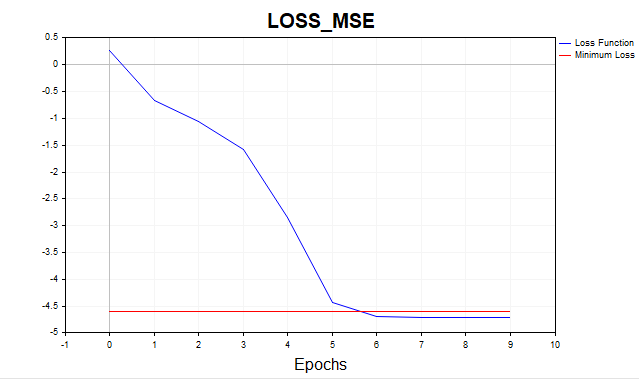
Fig.(8) Função de perda em escala logarítmica, LM

Agora sim, estamos falando de resultado: o algoritmo atingiu o limite mínimo em apenas seis iterações. E se tivéssemos treinado a rede por mil épocas? Teríamos um caso típico de overfitting, como mostra claramente a figura a seguir. A rede simplesmente começa a memorizar o ruído gaussiano.

Overfitting LM

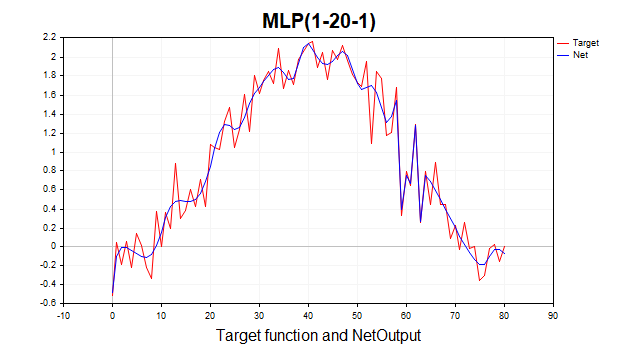
Fig.(9) Overfitting típico, LM, 1000 épocas

Vamos analisar as métricas no conjunto de treino e no conjunto de teste.

performance LM

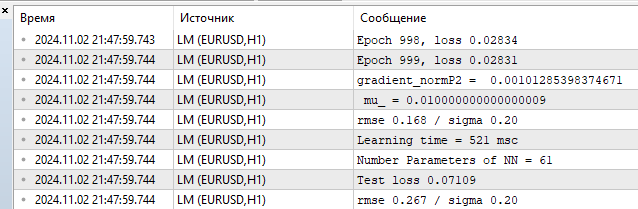
Fig.(10) Estatísticas de desempenho, LM, 1000 épocas

Vemos um RMSE de 0,168 frente a um limite inferior de 0,20 e, em seguida, a penalidade imediata pelo overfitting no teste: 0,267.

Testes com conjuntos de dados maiores e comparação com a biblioteca Python sklearn

Chegou a hora de testar nosso algoritmo em um exemplo mais realista. Agora, utilizei dois atributos com 1.000 pontos de dados cada. Esses dados poderão ser baixados junto com o script LM_BigData, disponível no final do artigo. A concorrência do LM será formada pelos algoritmos SGD, Adam e L-BFGS da biblioteca Python.

Aqui está o script de teste em Python

# Eugene
# https://www.mql5.com

import numpy as np
import time 
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.neural_network import MLPRegressor

# здесь ваш путь к данным
df = pd.read_csv(r'C:\Users\Evgeniy\AppData\Local\Programs\Python\Python39\Data.csv',delimiter=';')
X = df.to_numpy()
df1 = pd.read_csv(r'C:\Users\Evgeniy\AppData\Local\Programs\Python\Python39\Target.csv')
y = df1.to_numpy()
y = y.reshape(-1)

start = time.time() 

'''
clf = MLPRegressor(solver='sgd', alpha=0.0, 
                    hidden_layer_sizes=(20),
                    activation='tanh',
                    max_iter=700,batch_size=10,
                    learning_rate_init=0.01,momentum=0.9,
                    shuffle = False,n_iter_no_change = 2000, tol = 0.000001)
'''

'''
clf = MLPRegressor(solver='adam', alpha=0.0, 
                    hidden_layer_sizes=(20),
                    activation='tanh',
                    max_iter=3000,batch_size=100,                                    
                    learning_rate_init=0.01,
                    n_iter_no_change = 2000, tol = 0.000001)
'''

#'''
clf = MLPRegressor(solver='lbfgs', alpha=0.0, 
                    hidden_layer_sizes=(100),
                    activation='tanh',max_iter=300,
                    tol = 0.000001)
#'''                    
                       
clf.fit(X, y)
end = time.time() - start          # время обучения

print("learning time  =",end*1000) 
print("solver = ",clf.solver);      
print("loss = ",clf.loss_*2)
print("iter = ",clf.n_iter_)
#print("n_layers_ = ",clf.n_layers_)
#print("n_outputs_ = ",clf.n_outputs_)
#print("out_activation_ = ",clf.out_activation_)

coef = clf.coefs_
#print("coefs_ = ",coef)
inter = clf.intercepts_  
#print("intercepts_ = ",inter) 
plt.plot(np.log(pd.DataFrame(clf.loss_curve_)))
plt.title(clf.solver)
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.show()

Para garantir uma comparação justa entre os algoritmos, multipliquei a função de perda no Python por 2, já que nessa biblioteca ela é calculada assim:

return ((y_true - y_pred) ** 2).mean() / 2

Ou seja, os desenvolvedores ainda dividem o MSE por 2. Abaixo, são apresentados os resultados típicos dos otimizadores. Procurei ajustar os melhores hiperparâmetros possíveis para esses algoritmos. Infelizmente, essa biblioteca não oferece a opção de inicializar os valores dos parâmetros iniciais, de modo que todos os algoritmos comecem do mesmo ponto no espaço de parâmetros. Também não é possível definir um limiar-alvo para a função de perda. Para o LM, o objetivo da função de perda foi fixado em 0,01; para os algoritmos do Python, tentei definir um número de iterações que os levasse a aproximadamente esse mesmo nível.

Resultados do teste com MLP de uma camada oculta e 20 neurônios:

1) Descida do gradiente estocástica

loss mse – 0,00278
tempo de treinamento – 11459 msc

SGD Loss Python

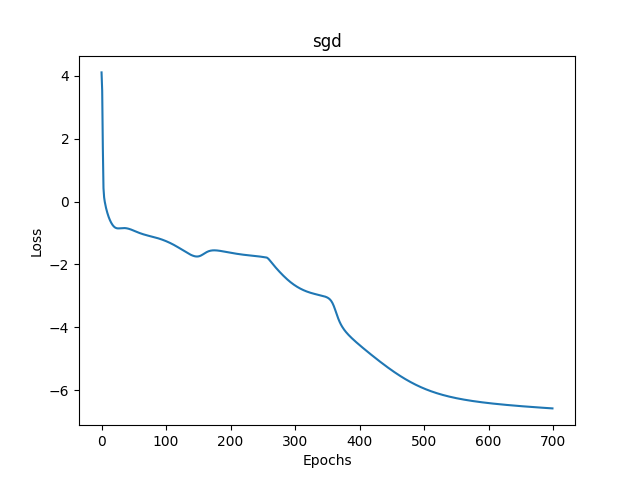
Fig.(11) SGD, 20 neurônios, loss = 0,00278

2) Adam

loss mse – 0,03363
tempo de treinamento – 8581 msc

Adam loss

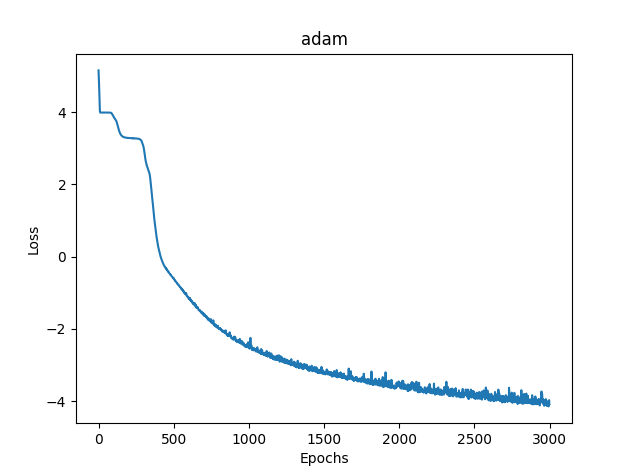
Fig.(12) Adam, 20 neurônios, loss = 0,03363

3) L-BFGS

loss mse – 0,02770
tempo de treinamento – 277 msc

Infelizmente, para o L-BFGS não é possível exibir o gráfico da função de perda.

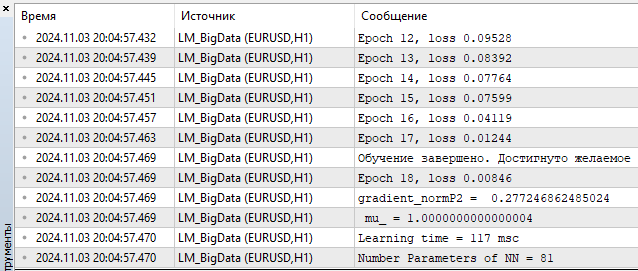
4) LM MQL5

loss – 0,00846
tempo de treinamento — 117 msc

LM Loss

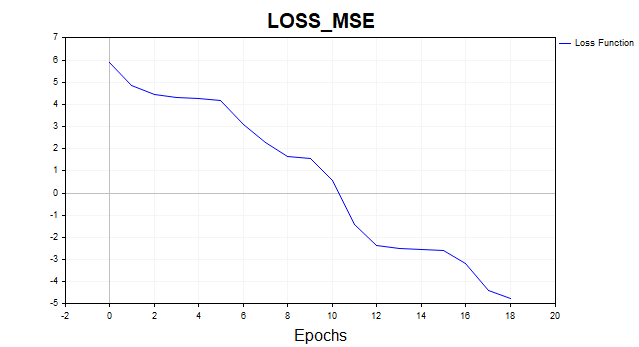
Fig.(13) LM, 20 neurônios, loss = 0,00846

performance LM

Pois bem, na minha opinião, o resultado ficou muito bom, já que o algoritmo compete tranquilamente com o L-BFGS e, como dá pra ver, ainda consegue levar vantagem. Mas nada é perfeito: conforme o número de parâmetros cresce, o método de Levenberg-Marquardt começa a perder desempenho em relação ao L-BFGS.

100 neurônios L-BFGS:

loss mse – 0,00847
tempo de treinamento – 671 msc

100 neurônios LM:

loss mse – 0,00206
tempo de treinamento – 1253 msc

100 neurônios correspondem a 401 parâmetros na rede. Fica a seu critério, caro leitor, julgar se isso é muito ou pouco, na minha humilde opinião, já é mais do que suficiente. Até 100 neurônios, o LM leva vantagem.

Considerações finais

Neste artigo discutimos e implementamos os algoritmos básicos e mais simples de treinamento de redes neurais:

descida do gradiente
descida do gradiente com impulso
descida do gradiente estocástica

Além disso, abordamos brevemente as questões de convergência e sobreajuste em redes neurais.

O mais importante, porém, é que desenvolvemos um algoritmo de Levenberg-Marquardt extremamente rápido, ideal para o treinamento online de redes pequenas.

Realizamos uma comparação de desempenho entre os algoritmos de treinamento de redes neurais utilizados na biblioteca de aprendizado de máquina scikit-learn, e o mais rápido deles foi justamente o nosso algoritmo, desde que o número de parâmetros da rede neural não ultrapasse 400 ou 100 neurônios na camada oculta. A partir daí, com o aumento no número de neurônios, o L-BFGS começa a dominar.

Foi criado um script separado para cada algoritmo, com comentários detalhados:

#	Nome	Tipo	Descrição
1	SD.mq5	Script	Descida do gradiente
2	Momentum_SD.mq5	Script	Descida do gradiente com impulso
3	SGD.mq5	Script	Descida do gradiente estocástica
4	LM.mq5	Script	Algoritmo de Levenberg-Marquardt
5	LM_BigData.mq5	Script	Algoritmo LM, teste com atributos bidimensionais
6	SklearnMLP.py	Script	Script de teste dos algoritmos em Python
7	FileCSV.mqh	Include	Leitura de arquivos de texto com dados
8	Data.csv, Target.csv	Csv	Atributos e alvo para o script em Python
9	X1.txt, X2.txt, Target.txt	Txt	Atributos e alvo para o script LM_BigData.mq5

Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/16296

Arquivos anexados |

Baixar como ZIP

SD.mq5 (26.11 KB)

SGD.mq5 (26.08 KB)

Momentum_SD.mq5 (22.58 KB)

LM.mq5 (36.08 KB)

LM_BigData.mq5 (36 KB)

FileCSV.mqh (10.46 KB)

X1.txt (19.26 KB)

X2.txt (19.26 KB)

Target.txt (17.62 KB)

Data.csv (37.56 KB)

Target.csv (17.62 KB)

SklearnMLP.py (1.94 KB)

Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.

Outros artigos do autor

Ir para discussão

Recursos do SQLite em MQL5: Exemplo de painel interativo com estatísticas de trading por símbolo e magic

Neste artigo, vamos criar um indicador que exibe, em um painel interativo, estatísticas de trading da conta divididas por símbolos e estratégias de negociação. Escreveremos o código com base em exemplos da Documentação e do artigo sobre trabalho com bancos de dados.

Redes neurais em trading: Modelo hiperbólico de difusão latente (HypDiff)

Esse artigo analisa formas de codificar dados brutos no espaço latente hiperbólico por meio de processos de difusão anisotrópicos. Isso ajuda a preservar com mais precisão as características topológicas da situação atual do mercado e melhora a qualidade de sua análise.

Métodos de otimização da biblioteca Alglib (Parte II)

Neste artigo, continuaremos a análise dos métodos de otimização restantes da biblioteca ALGLIB, com foco especial em seus testes em funções complexas e multidimensionais. Isso nos permitirá não apenas avaliar a eficiência de cada algoritmo, mas também identificar seus pontos fortes e fracos em diferentes condições.

Redes neurais em trading: Modelos de difusão direcionada (DDM)

Apresentamos os modelos de difusão direcionada, que utilizam ruídos anisotrópicos e direcionais, dependentes dos dados, no processo de propagação para frente, para capturar representações de grafos significativas.