Нейросети в трейдинге: Модели направленной диффузии (DDM)
Введение
Неконтролируемое обучение представлениям с помощью диффузионных моделей стало важной областью исследований в области компьютерного зрения. Результаты экспериментов, проведенных различными исследователями, подтверждают эффективность диффузионных моделей в обучении значимым визуальным представлениям. Восстановление данных, искаженных определенными уровнями шума, обеспечивает подходящую базу для изучения моделью сложных визуальных концепций, а повышение приоритета одних уровней шума над другими во время обучения улучшает производительность диффузионных моделей.
Авторы работы "Directional diffusion models for graph representation learning" предложили использовать диффузионные модели для неконтролируемого обучения представления графов. Однако на практике столкнулись с ограничением ванильных диффузионных моделей. Проведенные ими эксперименты показали, что данные в графах могут обладать отчетливыми анизотропными и направленными структурами, которые менее заметны на изображениях. Стандартные модели диффузии с изотропным процессом прямой диффузии приведут к быстрому снижению внутренних отношений сигнал/шум (Signal-to-Noise Ratio — SNR), что сделает их менее эффективными в изучении анизотропных структур. Поэтому были предложены новые подходы, которые позволили эффективно захватывать такие анизотропные структуры. Такими являются модели направленной диффузии, которые могут эффективно смягчить проблему быстрого снижения отношения сигнал/шум. Предложенный фреймворк включает в себя генерацию зависимого от данных и направленного шума в процесс прямой диффузии. Промежуточные активации, полученные от шумопоглощающей модели, эффективно захватывают полезную семантическую и топологическую информацию, необходимую для последующих задач.
Как следствие, модели направленной диффузии предлагают многообещающий генеративный подход к обучению представления графов. Результаты экспериментов, проведенных авторами метода, демонстрируют превосходную производительность моделей по сравнению с контрастным обучением и генеративными подходами. Примечательно, что для задач классификации графов модели направленной диффузии даже превосходят базовые модели с контролируемым обучением, подчеркивая огромный потенциал моделей диффузии в области обучения представления графов.
Применение диффузионных моделей в контексте трейдинга открывает перспективы для улучшения методов представления и анализа рыночных данных. Потенциально полезными могут быть модели направленной диффузии, учитывающие анизотропные структуры данных. Поскольку финансовые рынки часто характеризуются асимметричными и направленными движениями, модели с направленным шумом могут более эффективно распознавать структурные паттерны на трендовом и коррекционном движении. Это позволит выделить скрытые зависимости и сезонные закономерности.
1. Алгоритм DDM
Существуют заметные различия в структурных свойствах данных между графами и изображениями. В ванильном процессе прямой диффузии изотропный гауссовский шум последовательно добавляется к исходным данным до тех пор, пока он не превратит анализируемую последовательность в белый шум. Этот процесс имеет смысл, когда данные следуют изотропным распределениям, так как он постепенно преобразует точку данных в шум и генерирует зашумленные данные с широким диапазоном SNR. Однако в случае анизотропных распределений данных добавление изотропного шума может быстро загрязнить структуру данных, что приведет к быстрому снижению SNR до нуля.
Следовательно, шумоподавление моделей не способно обучать значимые и дискриминирующие представления признаков, которые могут быть эффективно использованы для решения последующих задач. Напротив, при использовании моделей направленной диффузии, которые включают в себя процесс, зависящий от данных и направленной прямой диффузии, отношение сигнал/шум снижается более медленными темпами. Это более медленное снижение позволяет извлекать мелкозернистые представления признаков с различными SNR, сохраняя важную информацию об анизотропных структурах. Полученную информацию можно использовать для решения последующих задач классификации графов и узлов.
Процесс генерации направленного шума включает в себя преобразование исходного изотропного гауссова шума в анизотропный путем включения двух дополнительных ограничений. Эти два ограничения играют решающую роль в улучшении моделей диффузии.
Пусть Gt = (A, Xt) является рабочим решением на t-м шаге прямой диффузии, где 𝐗t = {xt,1, xt,2, …, xt,N} представляет изучаемые признаки.
![]()
![]()
![]()
где x0,i — вектор необработанных признаков узла i, μ ∈ ℛ и σ ∈ ℛ обозначают тензоры средних значений и стандартных отклонений размерности d признаков по всем N узлам соответственно, и ⊙ обозначает поэлементное умножение. Во время обучения в мини-пакете μ и σ рассчитываются для графов внутри пакета. Параметр ɑt представляет собой график фиксированных отклонений и параметризуется убывающей последовательностью {β ∈ (0, 1)}.
В отличие от ванильного процесса диффузии, модели направленной диффузии включают два дополнительных ограничения. Одно предопределяет преобразование независимого от данных гауссова шума в анизотропный и пакетно-зависимый шум. В этом ограничении каждая координата вектора шума имеет то же эмпирическое среднее значение и эмпирическое стандартное отклонение, что и соответствующая координата в данных. Это ограничивает процесс диффузии локальной окрестностью пакета, предотвращая чрезмерное отклонение и поддерживая локальную когерентность. Другое ограничение вводится как угловое направление, которое вращает шум ε в ту же гиперплоскость объекта x0,i, сохраняя направленность исходного объекта. Это ограничение помогает поддерживать внутреннюю структуру данных в процессе прямой диффузии.
Эти два ограничения работают в тандеме, гарантируя, что процесс прямой диффузии учитывает базовую структуру данных и предотвращает быстрое размывание сигналов. В результате, отношение сигнал/шум медленно затухает, что позволяет моделям направленной диффузии эффективно извлекать значимые представления признаков в различных масштабах SNR. Это, в свою очередь, улучшает выполнение задач на последующих этапах, обеспечивая более надежные и информативные представления.
Авторы метода следуют той же стратегии обучения, что и в ванильных диффузионных моделях, и обучают шумопоглощающую модель fθ для приближения процесса обратной диффузии. Поскольку обратный ход прямого процесса с направленным шумом не может быть выражен в замкнутом виде, то было предложено модели шумоподавления fθ напрямую прогнозировать исходную последовательность.
Авторская визуализация фреймворка Directional diffusion models представлена ниже.
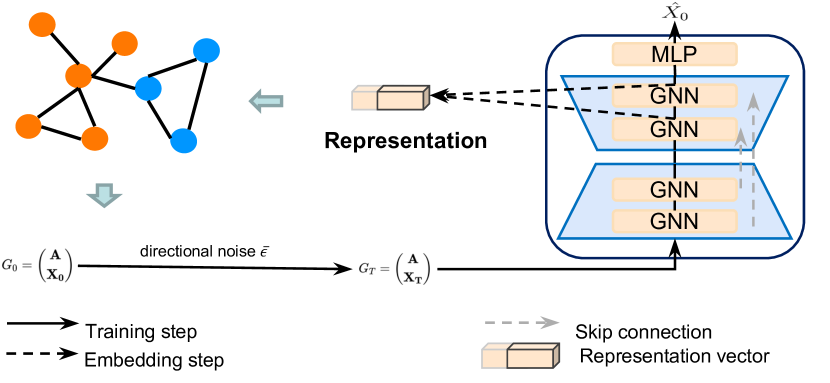
2. Реализация средствами MQL5
После рассмотрения теоретических аспектов фреймворка Directional diffusion models, мы переходим к практической части нашей статьи, в которой рассмотрим один из вариантов реализации предложенных подходов средствами MQL5.
Свою работу мы разделим на 2 блока. На первом этапе мы добавим к анализируемым данным направленный шум, а затем реализуем фреймворк в рамках одного класса.
2.1 Добавление направленного шума
И перед тем, как приступить к работе, давайте обсудим алгоритм действий генерации направленного шума. Прежде всего нам понадобится шум из нормального распределения. Его мы можем легко получить средствами стандартных библиотек MQL5.
Далее, согласно предложенному авторами фреймворка алгоритму, нам необходимо преобразовать его в анизотропный, зависимый от исходных данных шум. Для этого нам потребуется среднее значение и дисперсия по каждому признаку. Если хорошо подумать, то подобную задачу мы уже решали при построении слоя пакетной нормализации CNeuronBatchNormOCL. Здесь следует вспомнить, что алгоритм пакетной нормализации приводит исходные данные к нулевому среднему и единичной дисперсии. Однако на этапе смещения и масштабирования происходит изменения распределения данных. И, наверное, мы могли бы взять эту информацию из слоя нормализации исходных данных. Тем более мы уже реализовывали процедуру получения параметров исходного распределения при построении класса обратной нормализации CNeuronRevINDenormOCL. Но такой подход ограничивает нас в использовании данного фреймворка.
Поэтому мы пошли немного дальше. И решили объединить добавление направленного шума с нормализацией данных. И здесь появляется вопрос: в какой точке добавить шум?
Действительно, мы можем добавить шум ДО нормализации исходных данных. Но в таком случае мы исказим сам процесс нормализации. Ведь добавление шума изменяет распределение данных. Следовательно, при нормализации с определенными ранее средним и дисперсией на выходе мы получим смещенное распределение. А это не желательно.
Второй вариант, добавить шум на выходе слоя нормализации. В этом случае нам необходимо скорректировать гауссовский шум на коэффициенты масштабирования и смещения. Но если вы посмотрите на приведенные выше формулы авторского алгоритма, то можно заметить, что при корректировке направления шума он сместится в сторону нашего коэффициента смещения. Следовательно, при росте коэффициента смещения мы получаем смещенный "однобокий" шум. Что также не желательно.
Взвесив все за и против, мы пошли иным путем и добавили шум меду нормализацией данных и этапом смещения с масштабированием. При этом мы исключаем этап преобразования шума, так как после нормализации ожидаем получить данные с нулевой средней и единичной дисперсией. Именно с таким распределением мы генерировали шум. А на этап масштабирования и смещения мы подаем уже зашумленные данные, что позволит модели выучить корректные коэффициенты.
С принципами реализации определились. И теперь мы можем перейти к практической работе. Данный алгоритм мы реализуем на стороне контекста OpenCL. Для этого мы создадим новый кернел BatchFeedForwardAddNoise. Сразу скажем, что алгоритм данного кернела во многом заимствован из кернела прямого прохода слоя пакетной нормализации. Тем не менее мы добавляем буфер данных гауссовского шума и коэффициент отклонений ɑ.
__kernel void BatchFeedForwardAddNoise(__global const float *inputs, __global float *options, __global const float *noise, __global float *output, const int batch, const int optimization, const int activation, const float alpha) { if(batch <= 1) return; int n = get_global_id(0); int shift = n * (optimization == 0 ? 7 : 9);
В теле метода мы сначала проверяем размер пакета нормализации, который должен быть больше "1". А затем определяем смещение в буферах данных на основании идентификатора текущего потока.
Далее мы проконтролируем наличие действительных чисел в буфере параметров нормализации. Некорректные элементы заменим нулевыми значениями.
for(int i = 0; i < (optimization == 0 ? 7 : 9); i++) { float opt = options[shift + i]; if(isnan(opt) || isinf(opt)) options[shift + i] = 0; }
Затем мы выполняем нормализацию исходных данных в полном соответствии с алгоритмом базового кернела.
float inp = inputs[n]; float mean = (batch > 1 ? (options[shift] * ((float)batch - 1.0f) + inp) / ((float)batch) : inp); float delt = inp - mean; float variance = options[shift + 1] * ((float)batch - 1.0f) + pow(delt, 2); if(batch > 0) variance /= (float)batch; float nx = (variance > 0 ? delt / sqrt(variance) : 0);
На данном этапе мы получаем нормализованные исходные данные с нулевой средней и единичной дисперсией. И в этот момент мы добавляем шум, предварительно скорректировав его направление.
float noisex = sqrt(alpha) * nx + sqrt(1-alpha) * fabs(noise[n]) * sign(nx);
А далее мы выполняем алгоритм масштабирования и смещения с сохранением результатов в соответствующих буферах данных, аналогично реализации донорского кернела. Только на этот раз мы применяем масштабирование и смещение к зашумленным значениям.
float gamma = options[shift + 3]; if(gamma == 0 || isinf(gamma) || isnan(gamma)) { options[shift + 3] = 1; gamma = 1; } float betta = options[shift + 4]; if(isinf(betta) || isnan(betta)) { options[shift + 4] = 0; betta = 0; } //--- options[shift] = mean; options[shift + 1] = variance; options[shift + 2] = nx; output[n] = Activation(gamma * noisex + betta, activation); }
Алгоритм прямого прохода мы реализовали. А как же с обратным проходом. Здесь надо сказать, что для выполнения операций обратного прохода мы решили использовать полностью реализацию алгоритмов слоя пакетной нормализации. Дело в том, что шум мы не обучаем. Следовательно, градиент ошибки полностью передается на исходные данные. Использование нами коэффициента ɑ лишь создает некоторое размытие области с центром, близким к исходным данным. Поэтому мы можем пренебречь данным коэффициентом и в полном объеме передать градиент ошибки на уровень исходных данных в соответствии с алгоритмом слоя пакетной нормализации.
Таким образом мы завершаем работу на стороне OpenCL-программы. С полным её кодом вы можете ознакомиться во вложении. А мы переходим к работе на стороне основной программы, где создадим новый класс CNeuronBatchNormWithNoise. Как несложно догадаться, основной функционал мы наследуем от класса пакетной нормализации. Здесь же мы переопределяем только метод прямого прохода. Структура нового класса представлена ниже.
class CNeuronBatchNormWithNoise : public CNeuronBatchNormOCL { protected: CBufferFloat cNoise; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); public: CNeuronBatchNormWithNoise(void) {}; ~CNeuronBatchNormWithNoise(void) {}; //--- virtual int Type(void) const { return defNeuronBatchNormWithNoise; } };
Как вы могли заметить, мы постарались максимально упростить работу над нашим новым классом CNeuronBatchNormWithNoise. Тем не менее, для организации требуемого функционала нам понадобится буфер для передачи шума, который мы будем генерировать на стороне основной программы, в контекст OpenCL. Однако мы не стали переопределять ни метод инициализации объекта, ни методы работы с файлами. Ведь нам нет смысла сохранять случайный шум. Поэтому мы всю работу вынесли в метод прямого прохода feedForward, в параметрах которого мы получаем указатель на объект исходных данных.
bool CNeuronBatchNormWithNoise::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!bTrain) return CNeuronBatchNormOCL::feedForward(NeuronOCL);
Здесь стоит обратить внимание, что добавлять шум мы будем только в процессе обучения модели. Это позволит выучить значимые структуры исходных данных. В процессе же эксплуатации мы хотим использовать обученную модель в качестве фильтра, восстанавливая из реальных данных, содержащих некую долю шумовых значений, значимые структуры данных. Поэтому в процессе эксплуатации мы просто выполняем нормализацию данных средствами родительского класса.
Дальнейший код выполняется только в процессе обучения модели. Мы сначала проверяем актуальность полученного указателя на объект исходных данных.
if(!OpenCL || !NeuronOCL) return false;
А затем сохраняем его во внутренней переменной.
PrevLayer = NeuronOCL;
После чего проверяем размер пакета нормализации. И если он не более 1, то мы просто синхронизируем функции активации и завершаем работу метода с положительным результатом. Ведь в таком случае результат работы алгоритма нормализации будет равен исходным данным. А чтобы не выполнять лишнюю работу, мы просто передадим последующему слою полученные исходные данные.
if(iBatchSize <= 1) { activation = (ENUM_ACTIVATION)NeuronOCL.Activation(); return true; }
В случае успешного прохождения всех вышеописанных точек контроля, мы сначала генерируем шум из нормального распределения.
double random[]; if(!Math::MathRandomNormal(0, 1, Neurons(), random)) return false;
После чего нам необходимо передать его в контекст OpenCL. Но мы не стали переопределять метод инициализации объекта. Поэтому мы сначала проверяем наш буфер данных на наличие достаточного количества элементов и ранее созданного буфера в контексте.
if(cNoise.Total() != Neurons() || cNoise.GetOpenCL() != OpenCL) { cNoise.BufferFree(); if(!cNoise.AssignArray(random)) return false; if(!cNoise.BufferCreate(OpenCL)) return false; }
При получении отрицательного значения в одной из точек контроля мы изменяем размер буфера и создаем новый указатель в контексте OpenCL.
В противном случае мы просто копируем данные в буфер и переносим их в память контекста OpenCL.
else { if(!cNoise.AssignArray(random)) return false; if(!cNoise.BufferWrite()) return false; }
Далее мы скорректируем фактический размер пакета и случайным образом определи уровень зашумленности исходных данных.
iBatchCount = MathMin(iBatchCount, iBatchSize); float noise_alpha = float(1.0 - MathRand() / 32767.0 * 0.01);
И теперь, когда мы подготовили все необходимы данные нам остается их передать в параметры нашему выше созданному кернелу.
uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = Neurons(); int kernel = def_k_BatchFeedForwardAddNoise; ResetLastError(); if(!OpenCL.SetArgumentBuffer(kernel, def_k_normwithnoise_inputs, NeuronOCL.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(kernel, def_k_normwithnoise_noise, cNoise.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(kernel, def_k_normwithnoise_options, BatchOptions.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(kernel, def_k_normwithnoise_output, Output.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(kernel, def_k_normwithnoise_activation, int(activation))) { printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(kernel, def_k_normwithnoise_alpha, noise_alpha)) { printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(kernel, def_k_normwithnoise_batch, iBatchCount)) { printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(kernel, def_k_normwithnoise_optimization, int(optimization))) { printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), GetLastError(), __LINE__); return false; } //--- if(!OpenCL.Execute(kernel, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), GetLastError(), __LINE__); return false; } iBatchCount++; //--- return true; }
И поставить кернел в очередь выполнения. При этом мы контролируем процесс выполнения операций на каждом шаге. А после их завершения возвращаем логический результат выполнения операций внешней программе.
На этом мы завершаем работу с нашим новым классом CNeuronBatchNormWithNoise. Его полный код представлен во вложении.
2.2 Класс фреймворка DDM
Выше мы реализовали объект добавления направленного шума к исходным данным. И теперь переходим к построению фреймворка Directional diffusion models в нашей интерпретации.
Сразу обратим внимание, что мы используем структуру подходов, предложенных авторами фреймворка. Но допускаем некоторые отступления в контексте решения наших задач. В своей реализации мы также используем U-образную архитектуру, предложенную авторами метода, но заменяем графовые нейронные сети (GNN) на блоки энкодера Трансформера. Кроме того, авторы метода подают уже зашумленные данные на вход модели, мы же добавляем шумы в самой модели. Но обо всем по порядку.
Для реализации нашего решения мы создаем новый класс CNeuronDiffusion. В качестве родительского объекта мы используем U-образный Трансформер. Структура нового класса представлена ниже.
class CNeuronDiffusion : public CNeuronUShapeAttention { protected: CNeuronBatchNormWithNoise cAddNoise; CNeuronBaseOCL cResidual; CNeuronRevINDenormOCL cRevIn; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronDiffusion(void) {}; ~CNeuronDiffusion(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint layers, uint inside_bloks, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronDiffusion; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
В представленной структуре класса мы видим объявление трех объектов, с назначением которых познакомимся в процессе реализации методов класса. Для построения основной архитектуры модели фильтрации шумов мы воспользуемся унаследованными объектами.
Все новые объекты объявлены статично, что позволяет нам оставить пустыми конструктор и деструктор класса. Инициализация всех объектов осуществляется в методе Init.
В параметрах метода мы получаем основные константы, определяющие архитектуру создаваемого объекта. Надо сказать, что в данном случае мы полностью перенесли без изменений структуру параметров метода родительского класса.
bool CNeuronDiffusion::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint layers, uint inside_bloks, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
Однако, в процессе построения новых алгоритмов мы немного изменим последовательность использования унаследованных объектов. Поэтому в теле метода мы вызываем одноименный метод базового класса, в котором инициализируются только основные интерфейсы.
Далее мы инициализируем объект нормализации исходных данных с добавлением шума. Именно этот объект мы будем использовать для первичной обработки исходных данных.
if(!cAddNoise.Init(0, 0, OpenCL, window * units_count, iBatch, optimization)) return false;
Затем мы выстраиваем структуру U-образного Трансформер. Здесь мы сначала используем блок многоголового внимания.
if(!cAttention[0].Init(0, 1, OpenCL, window, window_key, heads, units_count, layers, optimization, iBatch)) return false;
А за ним добавляем сверточный слой понижения размерности.
if(!cMergeSplit[0].Init(0, 2, OpenCL, 2 * window, 2 * window, window, (units_count + 1) / 2, optimization, iBatch)) return false;
И рекуррентно формируем объекты шеи.
if(inside_bloks > 0) { CNeuronDiffusion *temp = new CNeuronDiffusion(); if(!temp) return false; if(!temp.Init(0, 3, OpenCL, window, window_key, heads, (units_count + 1) / 2, layers, inside_bloks - 1, optimization, iBatch)) { delete temp; return false; } cNeck = temp; } else { CNeuronConvOCL *temp = new CNeuronConvOCL(); if(!temp) return false; if(!temp.Init(0, 3, OpenCL, window, window, window, (units_count + 1) / 2, optimization, iBatch)) { delete temp; return false; } cNeck = temp; }
Здесь следует обратить внимание, что мы несколько усложнили архитектуру модели. А вместе с ней и задачу, решаемую моделью. Дело в том, что в качестве объекта шеи мы рекуррентно добавляем аналогичные объекты направленной диффузии. А это значит, что каждый новый слой добавляет шум в исходные данные. Следовательно, модель учится работать и восстанавливать данные из данных с большой долей шума.
Такой подход не противоречит идеи диффузионных моделей, которые по сути являются генеративными моделями. И создавались для итерационной генерации данных из шума. Однако возможно и использование объектов родительского класса в шее модели.
Далее мы добавляем второй блок внимания нашей модели шумоподавления.
if(!cAttention[1].Init(0, 4, OpenCL, window, window_key, heads, (units_count + 1) / 2, layers, optimization, iBatch)) return false;
И сверточный слой восстановления размерности до уровня исходных данных.
if(!cMergeSplit[1].Init(0, 5, OpenCL, window, window, 2 * window, (units_count + 1) / 2, optimization, iBatch)) return false;
Согласно архитектуре U-образного Трансформер, полученный результат мы дополняем данными остаточных связей. Для их записи мы создадим базовый нейронный слой.
if(!cResidual.Init(0, 6, OpenCL, Neurons(), optimization, iBatch)) return false; if(!cResidual.SetGradient(cMergeSplit[1].getGradient(), true)) return false;
После чего синхронизируем буфера градиентов слоя остаточных связей и восстановления размерности.
Далее мы добавляем слой обратной нормализации, который не упоминается авторами фреймворка, но следует из логики его работы.
if(!cRevIn.Init(0, 7, OpenCL, Neurons(), 0, cAddNoise.AsObject())) return false;
Дело в том, что в авторской версии фреймворка не используется нормализация данных. Считается, что используются подготовленные данные графов, которые обрабатываются графовыми сетями. И на выходе модели ожидается получение исходных данных, свободных от шума. И в процессе обучения минимизируется ошибка восстановления данных. Мы же в своем решении использовали нормализацию данных. Следовательно, для сопоставления результатов с истинными значениями, нам необходимо вернуть данным исходное распределение. Эту работу и выполняет слой обратной нормализации.
Теперь нам остается осуществить подмену указателей на буфера данных для исключения излишних операций копирования и вернуть логический результат выполнения операций вызывающей программе.
if(!SetOutput(cRevIn.getOutput(), true)) return false; //--- return true; }
Но обратите внимание, что в данном случае мы осуществляем подмену указателя только на буфер результатов. При этом оставляем нетронутым буфер градиентов ошибки. О причинах такого решения мы поговорим в процессе рассмотрения алгоритмов методов обратного прохода.
А пока мы переходим к методу прямого прохода feedForward.
bool CNeuronDiffusion::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cAddNoise.FeedForward(NeuronOCL)) return false;
В параметрах метода мы получаем указатель на объект исходных данных, который сразу передаем в одноименный метод внутреннего слоя добавления шума.
Зашумленные данные мы передаем в первый блок внимания.
if(!cAttention[0].FeedForward(cAddNoise.AsObject())) return false;
После чего изменяем размерность данных и передаем их объекту шеи.
if(!cMergeSplit[0].FeedForward(cAttention[0].AsObject())) return false; if(!cNeck.FeedForward(cMergeSplit[0].AsObject())) return false;
Полученные от шеи результаты поступают на вход второго блока внимания.
if(!cAttention[1].FeedForward(cNeck)) return false;
После чего мы восстанавливаем размерность данных до уровня исходных и суммируем с зашумленными.
if(!cMergeSplit[1].FeedForward(cAttention[1].AsObject())) return false; if(!SumAndNormilize(cAddNoise.getOutput(), cMergeSplit[1].getOutput(), cResidual.getOutput(), 1, true, 0, 0, 0, 1)) return false;
И в завершении работы метода мы возвращаем данные в подпространство исходного распределения.
if(!cRevIn.FeedForward(cResidual.AsObject())) return false; //--- return true; }
После чего нам остается лишь вернуть логический результат выполнения операций вызывающей программе.
Думаю, алгоритм метода прямого прохода не вызвал особой сложности. Но не все так просто с методами распределения градиента ошибки calcInputGradients. Именно здесь мы вспоминаем, что работаем с диффузионной моделью.
bool CNeuronDiffusion::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!prevLayer) return false;
В параметрах метода, как и в случае прямого прохода, мы получаем указатель на объект исходных данных. Только сейчас нам предстоит передать в него градиент ошибки в соответствии с влиянием исходных данных на результат работы модели. И мы сразу проверяем актуальность полученного указателя, так как в противном случае все дальнейшие операции теряют смысл.
Далее я хочу напомнить, что в процессе инициализации мы намеренно не осуществили подмену указателей на буфер градиентов ошибки. И на данный момент градиент ошибки, полученный от последующего слоя находится только в соответствующем буфере интерфейса. Это позволяет нам решить вторую нашу задачу — обучение диффузионной модели. Как было сказано в теоретической части нашей статьи, диффузионная модель обучается восстанавливать из шума исходные данные. Поэтому мы определим отклонение данных, полученных на выходе слоя при прямом проходе от полученных на вход данных без шума.
float error = 1; if(!cRevIn.calcOutputGradients(prevLayer.getOutput(), error) || !SumAndNormilize(cRevIn.getGradient(), Gradient, cRevIn.getGradient(), 1, false, 0, 0, 0, 1)) return false;
Но в своей работе мы хотим настроить фильтр, способный выделить значимые структуры в контексте решения основной задачи. Поэтому к полученному градиенту ошибки восстановления данных мы добавим градиент ошибки, полученный по основной магистрали, который указывает на погрешность работы основной модели.
Далее мы спускаем суммарный градиент ошибки до уровня слоя остаточных связей.
if(!cResidual.calcHiddenGradients(cRevIn.AsObject())) return false;
На этом этапе мы уже эксплуатируем подмену буферов данных и переходим к передаче градиента ошибки до уровня второго блока внимания.
if(!cAttention[1].calcHiddenGradients(cMergeSplit[1].AsObject())) return false;
И далее мы передаем градиент ошибки по цепочке: шея, слой понижения размерности, первый блок внимания, объект добавления шума.
if(!cNeck.calcHiddenGradients(cAttention[1].AsObject())) return false; if(!cMergeSplit[0].calcHiddenGradients(cNeck.AsObject())) return false; if(!cAttention[0].calcHiddenGradients(cMergeSplit[0].AsObject())) return false; if(!cAddNoise.calcHiddenGradients(cAttention[0].AsObject())) return false;
Здесь необходимо остановиться и добавить градиент ошибки остаточных связей.
if(!SumAndNormilize(cAddNoise.getGradient(), cResidual.getGradient(), cAddNoise.getGradient(), 1, false, 0, 0, 0, 1)) return false;
А затем передаем градиент ошибки на уровень исходных данных и завершаем работу метода, предварительно вернув логический результат выполнения операций вызывающей программе.
if(!prevLayer.calcHiddenGradients(cAddNoise.AsObject())) return false; //--- return true; }
На этом мы завершаем рассмотрение алгоритмов построения методов нашего класса фреймворка направленной диффузии. Вы можете ознакомиться с полным кодом всех методов данного класса в приложении. Там же находятся программы для взаимодействия с окружающей средой и обучения моделей, которые были перенесены из предыдущей работы без изменений.
Архитектуры моделей также были заимствованы из предыдущей статьи. Единственное изменение — мы заменили слой адаптивного представления графов в Энкодере окружающей среды на слой обучаемой направленной диффузии.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronDiffusion; descr.count = HistoryBars; descr.window = BarDescr; descr.window_out = BarDescr; descr.layers=2; descr.step=3; { int temp[] = {4}; // Heads if(ArrayCopy(descr.heads, temp) < (int)temp.Size()) return false; } descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Полную архитектуру обучаемых моделей вы найдете во вложении.
А мы переходим к заключительному этапу нашей работы — проверке эффективности реализованных подходов на реальных данных.
3. Тестирование
Мы провели значительную работу по имплементации подходов направленной диффузии средствами MQL5. И настал момент проверить их эффективность для решения задач трейдинга. Мы обучим модели с использованием предложенных подходов на реальных данных инструмента EURUSD за 2023 год. Во время обучения использовались исторические данные таймфрейма H1.
Как и прежде, мы применяем офлайн обучение моделей с регулярным обновлением обучающего набора данных, с целью поддержания его соответствие текущей политике Актера.
Ранее мы отмечали, что новая модель Энкодера состояния окружающей практически полностью заимствована из предыдущей статьи. И для сравнения результатов мы тестировали новую модель, полностью сохранив параметры тестирования базовой модели. Результаты тестирования за первые три месяца 2024 года приведены ниже.
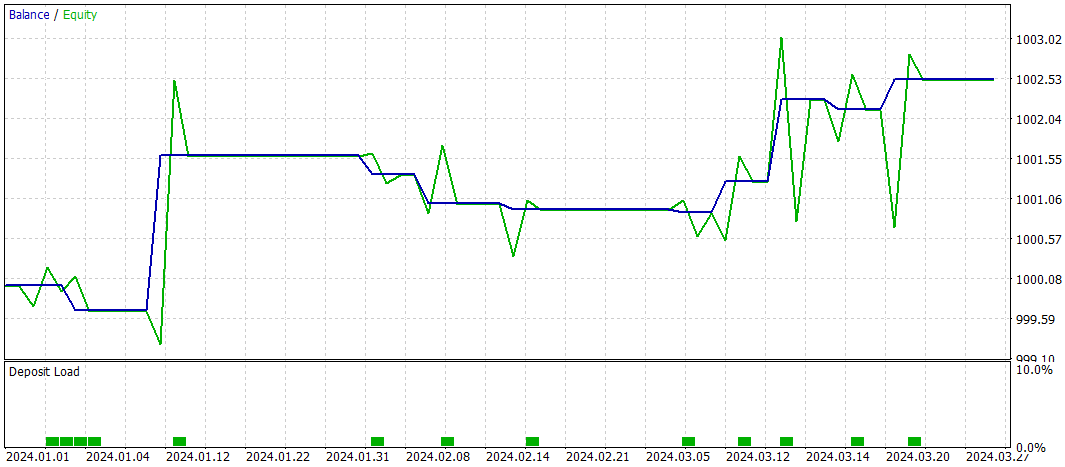
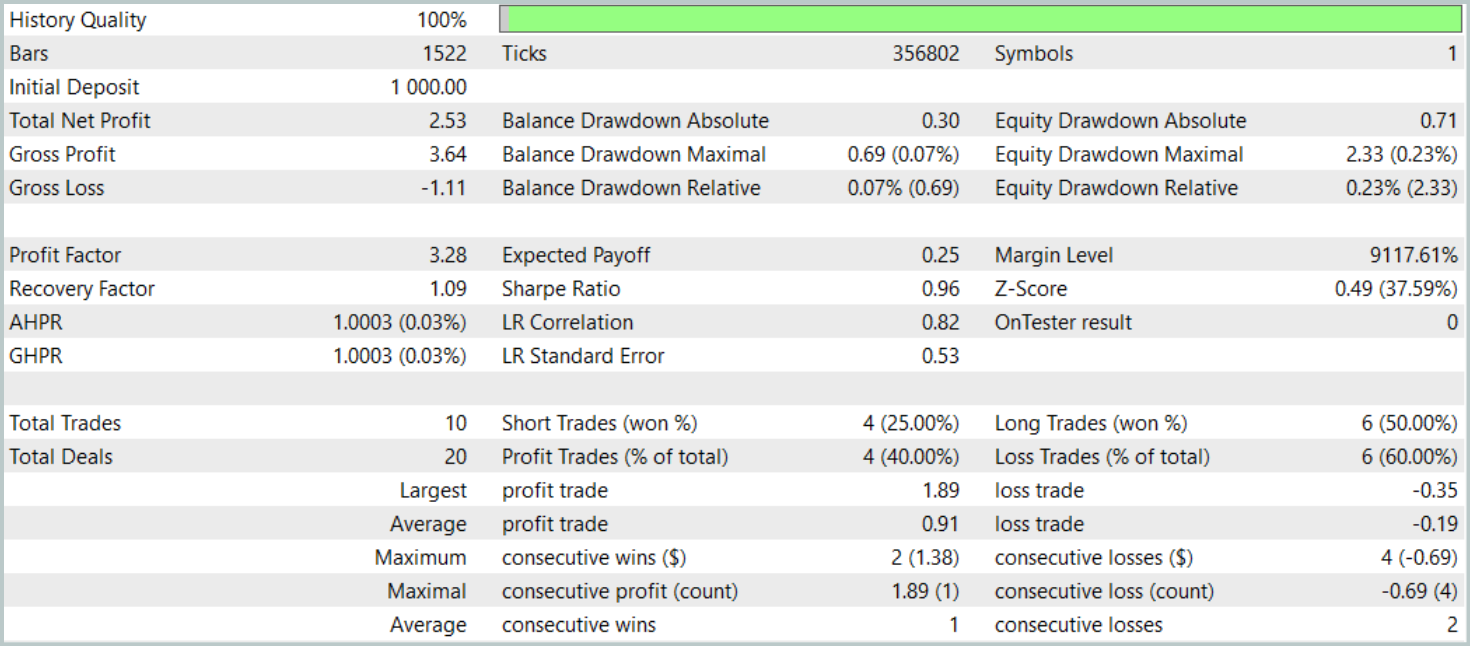
За период тестирования модель совершила только 10 торговых операций. И это очень мало. Более того, всего 4 из них было закрыто с прибылью. Не очень впечатляющий результат. Однако средняя и максимальная прибыльная сделка в 5 раз превышают аналогичные показатели убыточных операций. Что позволило модели зафиксировать профит фактор на уровне 3.28.
В целом модель показала хорошее соотношение прибыль/убыток, но слишком низкое количество торговых операций заставляет искать пути повышения частоты их совершения. Желательно без потери качества сделок.
Заключение
Направленные диффузионные модели (Directional diffusion model — DDM) представляют собой перспективный инструмент для анализа и представления рыночных данных в трейдинге. Учитывая, что финансовые рынки часто демонстрируют анизотропные и направленные паттерны из-за сложных структурных взаимосвязей и внешних факторов, традиционные диффузионные модели с изотропными процессами не всегда способны эффективно захватывать эти особенности. DDM, с их способностью адаптироваться к направленности данных через использование направленного шума, позволяют лучше выявлять важные закономерности и тренды, даже в условиях высокого уровня рыночного шума и волатильности.
В практической части мы реализовали свое видение предложенных подходов средствами MQL5. Обучили модели на реальных исторических данных и провели их тестирование за рамками обучающей выборки. Исходя из результатов проведенных экспериментов, можно сделать вывод о существующем потенциале DDM. Однако созданная нами модель требует дополнительной оптимизации.
Ссылки
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Research.mq5 | Советник | Советник сбора примеров |
| 2 | ResearchRealORL.mq5 | Советник | Советник сбора примеров методом Real-ORL |
| 3 | Study.mq5 | Советник | Советник обучения Моделей |
| 4 | Test.mq5 | Советник | Советник для тестирования модели |
| 5 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы |
| 6 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 7 | NeuroNet.cl | Библиотека | Библиотека кода программы OpenCL |
 Разработка системы репликации (Часть 55): Модуль управления
Разработка системы репликации (Часть 55): Модуль управления
 Возможности SQLite в MQL5: Пример интерактивной панели с торговой статистикой в разрезе символов и магиков
Возможности SQLite в MQL5: Пример интерактивной панели с торговой статистикой в разрезе символов и магиков
 Анализ влияния погоды на валюты аграрных стран с использованием Python
Анализ влияния погоды на валюты аграрных стран с использованием Python
 Методы оптимизации библиотеки Alglib (Часть II)
Методы оптимизации библиотеки Alglib (Часть II)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
