Funcionalidades do assistente MQL5 que você precisa conhecer (Parte 10): RBM não convencional

Introdução

As máquinas de Boltzmann restritas (RBM) são uma forma de rede neural que, apesar de sua estrutura simples, são bastante populares por suas capacidades de descobrir propriedades e funções ocultas em conjuntos de dados. A rede neural aprende os pesos em uma dimensão menor a partir dos dados de entrada de maior dimensão. Esses pesos são frequentemente chamados de distribuições de probabilidade. Como sempre, mais informações podem ser encontradas aqui, mas a estrutura da rede pode ser ilustrada na imagem abaixo:

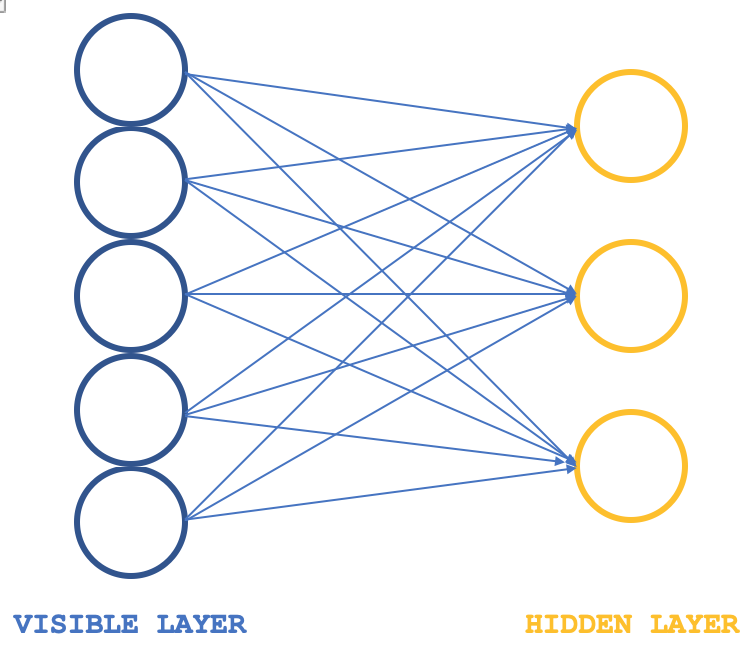
Normalmente, as RBM são compostas por duas camadas (eu digo "normalmente" porque há algumas redes que as integram em transformadores), especificamente uma camada visível e uma camada oculta, sendo que a camada visível é maior (tem mais neurônios) do que a camada oculta. Cada neurônio na camada visível é conectado a cada neurônio na camada oculta durante a chamada fase positiva. Durante esta fase, como é típico para a maioria das redes neurais, os valores de entrada na camada visível são multiplicados pelos valores dos pesos nas conexões dos neurônios, e a soma desses produtos é adicionada ao viés para determinar os valores dos neurônios ocultos correspondentes. A seguir vem a fase negativa. Através de várias conexões neuronais, ela restaura os dados de entrada ao estado original, começando pelos valores calculados na camada oculta.

Assim, nos primeiros ciclos, como esperado, os dados de entrada restaurados não corresponderão aos dados de entrada iniciais, já que muitas vezes a RBM é inicializada com pesos aleatórios. Isso significa que os pesos precisam ser ajustados para aproximar os dados de saída restaurados aos de entrada. Esta é uma fase adicional que seguirá cada ciclo. O resultado final e o objetivo desta fase positiva do ciclo, seguida pela fase negativa e ajuste de pesos, é obter os pesos que conectam os neurônios e que, quando aplicados aos dados de entrada, podem nos dar valores "intuitivos" dos neurônios na camada oculta. Esses valores dos neurônios na camada oculta representam o que é chamado de distribuição de probabilidades dos dados de entrada sobre os neurônios ocultos.

As fases positiva e negativa do ciclo da RBM são frequentemente chamadas juntas de amostragem de Gibbs.. Para alcançar uma correspondência precisa da distribuição de probabilidade dos dados, os pesos de ligação são ajustados usando o chamado contraste de divergência (Contrastive Divergence). Então, se tivéssemos uma classe simples ilustrando isso em MQL5, nossa interface poderia parecer da seguinte forma:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Crbm
{
protected:

... 

public:

   bool                             init;

   matrix                           weights_v_to_h;
   matrix                           weights_h_to_v;
   vector                           bias_v_to_h;
   vector                           bias_h_to_v;

   matrix                           old_visible;
   matrix                           old_hidden;
   matrix                           new_hidden;
   matrix                           new_visible;

   matrix                           output;

   void                             GibbsSample(matrix &Input);
   void                             ContrastiveDivergence();

   Crbm(int Visible, int Hidden, int Sample, double LearningRate, ENUM_LOSS_FUNCTION Loss);
   ~Crbm();
};

As variáveis notáveis aqui são as matrizes que registram os pesos durante a propagação da camada visível para a oculta e vice-versa. Elas são chamadas de weights_v_to_h e weights_h_to_v, respectivamente. Além disso, devem ser incluídos vetores que registram os erros sistemáticos e, o mais importante, 4 conjuntos de neurônios usados na amostragem de Gibbs para armazenar os valores dos neurônios em cada amostra - 2 para a camada visível e 2 para a camada oculta. A amostragem de Gibbs para as fases positiva e negativa pode ser definida da seguinte maneira:

//+------------------------------------------------------------------+
//| Feed through network using Gibbs Sampling                        |
//+------------------------------------------------------------------+
void Crbm::GibbsSample(matrix &Input)
{  old_visible.Fill(0.0);
   old_visible.Copy(Input);
   //old_hidden = old_visible * weights_v_to_h;
   //new_hidden = Sigmoid(old_hidden) + bias_v_to_h;
   for (int GibbsStep = 0; GibbsStep < sample; GibbsStep++)
   {  // Positive phase... Upward pass with biases
      for (int j = 0; j < hidden; j++)
      {  old_hidden[GibbsStep][j] = 0.0;
         for (int i = 0; i < visible; i++)
         {  old_hidden[GibbsStep][j] += (old_visible[GibbsStep][i] * weights_v_to_h[i][j]);
         }
         new_hidden[GibbsStep][j] = 1.0 / (1.0 + exp(-(old_hidden[GibbsStep][j] + bias_v_to_h[j])));
      }
   }
   //new_visible = new_hidden * weights_h_to_v;
   //output = Sigmoid(new_visible) + bias_v_to_h;
   for (int GibbsStep = 0; GibbsStep < sample; GibbsStep++)
   {  // Negative phase... Downward pass with biases
      for (int i = 0; i < visible; i++)
      {  new_visible[GibbsStep][i] = 0.0;
         for (int j = 0; j < hidden; j++)
         {  new_visible[GibbsStep][i] += (new_hidden[GibbsStep][j] * weights_h_to_v[j][i]);
         }
         output[GibbsStep][i] = 1.0 / (1.0 + exp(-(new_visible[GibbsStep][i] + bias_h_to_v[i])));
      }
   }
}

Similarmente, a atualização dos pesos e dos vieses dos neurônios pode ser implementada usando a função abaixo:

//+------------------------------------------------------------------+
//| Update weights using Contrastive Divergence                      |
//+------------------------------------------------------------------+
void Crbm::ContrastiveDivergence()
{  // Update weights based on the difference between positive and negative phase
   matrix _weights_v_to_h_update;
   _weights_v_to_h_update.Init(visible, hidden);
   _weights_v_to_h_update.Fill(0.0);
   matrix _weights_h_to_v_update;
   _weights_h_to_v_update.Init(hidden, visible);
   _weights_h_to_v_update.Fill(0.0);
   for (int i = 0; i < visible; i++)
   {  for (int j = 0; j < hidden; j++)
      {  _weights_v_to_h_update[i][j] = learning_rate * (
                                           (old_visible[0][i] * weights_v_to_h[i][j]) - old_hidden[0][j]
                                        );
         _weights_h_to_v_update[j][i] = learning_rate * (
                                           (new_hidden[0][j] * weights_h_to_v[j][i]) -
                                           new_visible[0][i]
                                        );
      }
   }
   // Apply weight updates
   for (int i = 0; i < visible; i++)
   {  for (int j = 0; j < hidden; j++)
      {  weights_v_to_h[i][j] += _weights_v_to_h_update[i][j];
         weights_h_to_v[j][i] += _weights_h_to_v_update[j][i];
      }
   }
   // Bias updates
   vector _bias_v_to_h_update;
   _bias_v_to_h_update.Init(hidden);
   vector _bias_h_to_v_update;
   _bias_h_to_v_update.Init(visible);
// Compute bias updates
   for (int j = 0; j < hidden; j++)
   {  _bias_v_to_h_update[j] = learning_rate * ((old_hidden[0][j] + bias_v_to_h[j]) - new_hidden[0][j]);
   }
   for (int i = 0; i < visible; i++)
   {  _bias_h_to_v_update[i] = learning_rate * ((new_visible[0][i] + bias_h_to_v[i]) - output[0][i]);
   }
// Apply bias updates
   for (int i = 0; i < visible; ++i)
   {  bias_h_to_v[i] += _bias_h_to_v_update[i];
   }
   for (int j = 0; j < hidden; ++j)
   {  bias_v_to_h[j] += _bias_v_to_h_update[j];
   }
}

Embora a estrutura antiga da RBM ilustrada mostre esquematicamente apenas 2 camadas, o código contém valores de neurônios para 5 camadas, pois os valores dos neurônios das fases negativa e positiva são registrados após cada multiplicação e após cada ativação. Assim, a antiga camada visível registra os valores brutos dos dados de entrada, a antiga camada oculta registra o primeiro produto dos dados de entrada e os pesos, e a nova camada oculta registra os valores sigmoidais ativados desse produto. A nova camada visível registra o segundo produto da nova camada oculta e os pesos negativos da fase, e, finalmente, a camada "de saída" registra a ativação do produto.

Essa abordagem tradicional para RBM é apresentada aqui apenas para fins de pesquisa na forma em que foi compilada, mas não verificada, já que este artigo se concentra na abordagem alternativa para projetar e treinar RBM. No entanto, para fins de análise, o resultado chave da função de amostragem de Gibbs serão os valores dos neurônios no primeiro e segundo "camadas ocultas". Os valores duplos desses dois conjuntos de neurônios fixarão as propriedades dos dados de entrada após a rede estar suficientemente treinada.

Então, que tipo de RBM não convencional é capaz de manter os princípios básicos, mas com uma estrutura diferente? Um Perceptron de três camadas, cuja camada de entrada e de saída têm o mesmo tamanho, enquanto a única camada oculta é menor que essas duas camadas externas. Como garantir que o treinamento ainda será não supervisionado, considerando que os perceptrons geralmente são treinados de forma supervisionada? A questão é que cada linha de dados de entrada também serve como saída alvo, que é essencialmente o que a amostragem de Gibbs realiza em cada ciclo, de modo que nosso objetivo de obter pesos para todas as conexões para a camada oculta pode ser alcançado, como de costume, através da retropropagação do erro. Assim, a estrutura da nossa RBM se assemelhará à imagem abaixo:

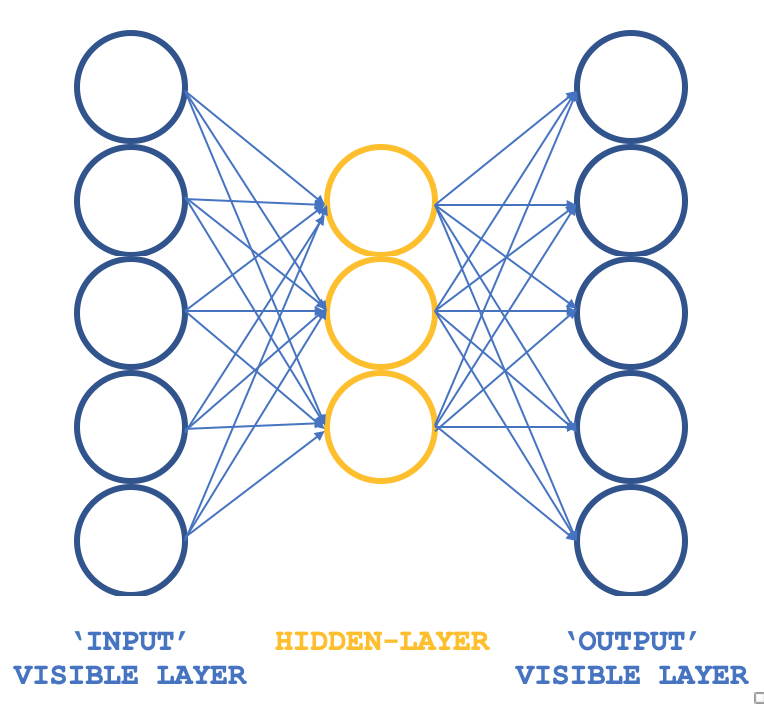
Essa abordagem, ao usar classes ALGLIB, garante uma maneira compacta e eficiente de testar a RBM em vez de escrever todo o código do zero. Uma vez que surjam ideias viáveis, podemos considerar a personalização e, possivelmente, escrever o código do zero.

Lembrando que o objetivo do treinamento é obter os pesos da rede que possam representar com precisão as características dos dados de entrada na camada oculta. Eles serão extraídos e usados na próxima etapa do modelo e, para nossos fins, podem ser considerados como um formato normalizado dos dados de entrada.

Origem da RBM

Em um artigo no site deeplearning.net, que infelizmente não está mais disponível, as RBMs são frequentemente definidas como modelos baseados em energia devido à sua capacidade de associar energia escalar a cada configuração do conjunto de dados de interesse. O treinamento é realizado alterando essa função de energia para que sua forma possua as propriedades desejadas. "Função de energia" é um termo informal para a função envolvida na transformação de um conjunto de dados de entrada em outro formato (transitório) e, finalmente, de volta aos dados de entrada, de modo que a "energia" represente a diferença entre o conjunto de dados de entrada e os dados de saída. Assim, o objetivo do treinamento da RBM é obter configurações de "baixa energia" desejadas, nas quais a diferença entre os dados de entrada iniciais e os dados de saída finais seja minimizada. Modelos probabilísticos baseados em energia definirão a distribuição de probabilidade, obtida por meio dessa função de energia, como um vetor de neurônios ocultos na forma de uma fração da soma dos valores dos neurônios ocultos para todos os dados de entrada selecionados.

Normalmente, os modelos baseados em energia são treinados executando a descida de gradiente estocástica no logaritmo negativo da verossimilhança dos dados de treinamento. Em geral, as máquinas de Boltzmann não possuem camadas ocultas e todos os neurônios estão interconectados.

Portanto, o primeiro passo para simplificar os cálculos é estimar a expectativa matemática usando um número fixo de amostras do modelo. As amostras usadas para estimar o gradiente da fase positiva são chamadas de  pesos, e o produto desses pesos matriciais e do vetor do conjunto de dados de entrada deve fornecer um vetor de valores dos neurônios (ou seja, ao usar Monte Carlo). Estamos quase com um algoritmo estocástico prático para treinar a RBM. O único ingrediente faltante é o que permitiria extrair esses pesos. Embora a literatura estatística seja rica em métodos de amostragem, os métodos de Monte Carlo com cadeias de Markov são especialmente adequados para modelos como as máquinas de Boltzmann (BM).

As máquinas de Boltzmann são uma forma particular de campo aleatório de Markov log-linear (log-linear Markov Random Field, MRF), para o qual a função de energia é linear em relação aos seus parâmetros livres. Para torná-las suficientemente poderosas para representar distribuições complexas (isto é, transitar de uma configuração paramétrica restrita para uma não paramétrica), consideramos que algumas variáveis nunca são observadas (elas são chamadas de ocultas, como mencionado acima). Tendo mais variáveis ocultas (também chamadas de unidades ocultas), podemos aumentar a capacidade de modelagem da Máquina de Boltzmann. As máquinas de Boltzmann restritas resultantes limitam ainda mais as máquinas de Boltzmann, eliminando conexões visível-visível e oculto-oculto, como mostrado na imagem introdutória acima.

Assim, na prática, fica claro que nem todos os aspectos do conjunto de dados são facilmente "visíveis", ou precisamos introduzir algumas variáveis não observáveis para aumentar o poder expressivo do modelo. Isso pode ser visto como uma suposição de que alguns aspectos do conjunto de dados de entrada são desconhecidos e, portanto, requerem aprendizado. Essa suposição implica um gradiente em relação a esses desconhecidos. O gradiente é a mudança ou diferença entre os dados conhecidos e os dados desconhecidos, ou seja, os dados "ocultos".

O gradiente terá duas fases - positiva e negativa. Os termos "positivo" e "negativo" refletem seu impacto na densidade de probabilidade ou nos desconhecidos exibidos, determinados pelo modelo. A fase positiva, conhecida como primeira fase, aumenta a probabilidade dos dados de treinamento (reduzindo a energia livre correspondente), e a segunda fase diminui a probabilidade de retorno das amostras geradas pelo modelo ao conjunto de dados amostrado.

Resumindo: quando o tamanho dos conjuntos de dados conhecidos e ocultos não é definido, como nas máquinas de Boltzmann não restritas, geralmente é difícil determinar esse gradiente analiticamente, pois requer muitos cálculos. É por isso que as RBMs, ao definir previamente a quantidade de dados conhecidos e desconhecidos, podem realmente determinar a distribuição de probabilidade.

Arquitetura da rede e treinamento

Nossa estrutura de três camadas, mostrada acima, será implementada com camadas de entrada e saída de tamanho 5 e uma camada oculta de tamanho 3. Os dados de entrada para os 5 valores dos neurônios serão os valores atuais dos indicadores. O leitor pode substituí-los, pois todas as fontes estão anexadas, mas neste artigo usamos os valores dos indicadores de média móvel, MACD, oscilador estocástico, faixa percentual de Williams e índice de vigor relativo (Relative Vigor Index). A saída normalizada, como mencionado anteriormente, fixa os valores dos neurônios dos valores do primeiro e do segundo camada oculta, o que significa que o tamanho desse vetor de saída é o dobro do tamanho de nossa camada oculta.

Todos os produtos de pesos e ativações são processados pelas classes ALGLIB, e eles são ajustados para cada neurônio. O código correspondente foi publicado no artigo anterior. Neste artigo, usamos os valores padrão, que certamente precisarão de ajustes se avançarmos mais um passo, mas por enquanto, eles podem servir para ilustrar a obtenção da distribuição de probabilidade dos dados.

Portanto, as conexões nesta rede lembram uma borboleta, em vez de uma seta, como mostrado no esquema acima.

A retropropagação do erro em uma rede neural comum ajusta os pesos das conexões através da descida de gradiente, utilizando a regra da cadeia multivariada (multivariate chain rule). Isso é diferente da divergência contrastiva e não só exige cálculos mais intensivos, como também pode resultar em pesos (distribuições de probabilidade) completamente diferentes em comparação com os obtidos em uma RBM comum. Nós a utilizamos para testes nesta matéria e, como o código fonte completo é compartilhado, as alterações neste estágio podem ser ajustadas.

Como mencionado acima, a retropropagação do erro é normalmente supervisionada, pois são necessários valores-alvo para obter os gradientes e, no nosso caso, como os dados de entrada servem como alvo, nossa RBM modificada ainda se qualifica como não supervisionada.

Durante o treinamento, nossa rede ajustará os pesos de modo que a saída seja o mais próxima possível da entrada. Com isso, qualquer novo conjunto de dados que entre na rede fornecerá informações cruciais para os neurônios da camada oculta. Essas informações, vindas dos neurônios, têm formato de array, como esperado. No entanto, o tamanho desse array é o dobro do número de neurônios na camada oculta. No formato que estamos adaptando para teste, temos três neurônios na camada oculta, o que significa que nosso array de saída, que fixa as propriedades dos cinco indicadores que estamos buscando, tem tamanho 6.

Esses valores dos neurônios ocultos podem ser vistos como uma forma de normalização dos cinco valores dos indicadores. Nesse caso, não temos uma redução de dimensionalidade, já que o vetor de propriedades tem tamanho 6, e ainda usamos 5 valores de entrada dos indicadores. No entanto, se utilizássemos mais indicadores, digamos 8, e mantivéssemos o número de neurônios na camada oculta em 3, teríamos uma redução.

Então, como podemos usar esses valores? Se mantivermos a visão de que eles representam apenas uma normalização dos valores dos indicadores, eles podem servir como um vetor de classificação, que pode ser útil ao comparar se agora os usarmos em outro modelo onde adicionamos um supervisor na forma de uma possível mudança de preço após cada conjunto de valores dos indicadores. Assim, tudo o que fazemos é comparar o vetor dos valores atuais, cujo possível movimento de preço é desconhecido, com outros vetores cujas mudanças são conhecidas, e uma média ponderada, onde a semelhança cosseno entre esses vetores pode atuar como um peso, fornece a previsão média da próxima mudança.

Desenvolvimento da rede no MQL5

O interface para implementar nossa RBM pode ser como mostrado abaixo:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Crbm
{
protected:

   int                              visible;
   int                              hidden;
   int                              sample;
   double                           loss;
   string                           file;

public:

   bool                             init;

... 

   CArrayDouble                     losses;

   void                             Train(matrix &W);
   void                             Process(matrix &W, matrix &XY, bool Compare = false);

   bool                             ReadWeights();
   bool                             WriteWeights();
   bool                             Writer();

   Crbm(int Visible, int Hidden, int Sample, double Loss, string File);
   ~Crbm();
};

No interface, declaramos e utilizamos as classes mínimas básicas que precisaremos para rodar o perceptron, como fizemos em artigos anteriores. A única adição notável é o array duplo `losses`, que nos ajuda a rastrear a diferença entre as camadas de entrada e saída, além de indicar, ao longo do caminho, quais redes obtêm seus parâmetros exportáveis registrados em um arquivo, pois, como já destacado anteriormente, os perceptrons devem ser testados com a capacidade de exportar parâmetros ajustáveis para que, ao implantar ou mover o EA para um ambiente de produção, os pesos obtidos possam ser facilmente usados, em vez de treinar novamente com base em pesos aleatórios iniciais.

Assim, o array `losses` simplesmente registra a similaridade cosseno entre os conjuntos de dados de entrada e saída para cada linha de dados em cada barra de preço. No final do teste, os pesos da rede ou os parâmetros exportáveis são gravados em um arquivo se o número de correspondências do cosseno abaixo do limite de entrada (o valor padrão é 0,9, mas pode ser ajustado) for menor do que o registrado na última vez que o arquivo foi gravado. Esse parâmetro de limiar é marcado como `loss`.

A sintaxe usada para multiplicação de pesos e valores de entrada provavelmente é mais complexa do que deveria, considerando que `matrix` e `vector` agora são tipos de dados embutidos no MQL5. Multiplicá-los de forma simples, monitorando a associação e os tamanhos correspondentes de linhas e colunas, pode levar ao mesmo resultado com menos memória e, portanto, menos recursos computacionais.

A função da rede utiliza classes ALGLIB para inicialização, treinamento e processamento de conjuntos de dados. Ajustes adicionais usando um perceptron codificado manualmente podem resultar em maior eficiência durante os testes e a implantação, já que o código ALGLIB é bastante complexo e "confuso", pois, sendo uma biblioteca, tende a atender a uma gama mais ampla de cenários. No entanto, mesmo com uma implementação pronta, alguns ajustes básicos, como ativação e vieses, podem ter um impacto significativo no desempenho da rede. Isso pode ser útil na fase inicial de testes, que estamos explorando aqui.

Assim, com esta configuração de teste, treinamos nossa RBM não convencional em cada nova barra ou sempre que recebemos um novo ponto de preço, implicando que os pesos, dos quais dependemos para classificar cada ponto de dados de entrada, são refinados e ajustados a cada passagem. Também é possível explorar abordagens alternativas para ajuste de pesos, como ajustar os pesos uma vez por trimestre ou duas vezes por ano, desde que a rede tenha sido treinada por vários anos antes do uso. Isso não é abordado no artigo, mas é mencionado como possíveis caminhos que o leitor pode seguir. As funções de treinamento e processo são definidas conforme abaixo:

//+------------------------------------------------------------------+
//|   Train Data Matrix                                              |
//+------------------------------------------------------------------+
void Crbm::Train(matrix &W)
{  for(int s = 0; s < sample; s++)
   {  for(int i = 0; i < visible; i++)
      {  xy.Set(s, i, W[s][i]);
         xy.Set(s, i + visible, W[s][i]);
      }
   }
   train.MLPTrainLM(model, xy, sample, 0.001, 2, info, report);
}

O código é bastante simples, pois as classes ALGLIB cuidam da sua criação. A função `process` é codificada da seguinte forma:

//+------------------------------------------------------------------+
//|   Process New Vector                                             |
//+------------------------------------------------------------------+
void Crbm::Process(matrix &W, matrix &XY, bool Compare = false)
{  for(int w = 0; w < int(W.Rows()); w++)
   {  CRowDouble _x = CRowDouble(W.Row(w)), _y;
      base.MLPProcess(model, _x, _y);
      for(int i = 6; i < visible + 7; i++)
      {  XY[w][i - 6] = model.m_neurons[i];
      }
      //Comparison
      vector _input = _x.ToVector();
      vector _output = _y.ToVector();
      if(Compare)
      {  for(int i = 0; i < int(_input.Size()); i++)
         {  printf(__FUNCSIG__ +
                   " at: " + IntegerToString(i) +
                   " we've input: " + DoubleToString(_input[i]) +
                   " & y: " + DoubleToString(_y[i])
                  );
         }
         //Loss
         printf(__FUNCSIG__ +
                " loss is: " + DoubleToString(_output.Loss(_input, LOSS_COSINE))
               );
      }
      losses.Add(_output.Loss(_input, LOSS_COSINE));
   }
}

Essa função é, de certa forma, o "ingrediente secreto" do algoritmo, pois mostra como extraímos os valores dos neurônios ocultos do perceptron para cada valor de entrada. Extraímos esses pesos em cada barra como uma amostra. Portanto, os exportamos em formato matricial, onde a linha de entrada nos dá um vetor de pesos.

Os pesos extraídos para cada ponto de dados de entrada servem como formas normalizadas dos cinco valores dos indicadores, e a comparação de vetores ponderados mencionada acima pode ser implementada da seguinte maneira:

//+------------------------------------------------------------------+
//| RBM Output.                                                      |
//+------------------------------------------------------------------+
double CSignalRBM::GetOutput(void)
   {
      m_close.Refresh(-1);
      
      MA.Refresh(-1);
      MACD.Refresh(-1);
      STOCH.Refresh(-1);
      WPR.Refresh(-1);
      RVI.Refresh(-1);
      
      double _output = 0.0;
      
      int _i=StartIndex();
      
      matrix _w; _w.Init(m_sample,__VISIBLE);
      
      matrix _xy; _xy.Init(m_sample,7);
      
      if(RBM.init)
      {
         for(int s=0;s<m_sample;s++)
         {
            for(int i=0;i<5;i++)
            {
               if(i==0){ _w[s][i] = MA.GetData(0,_i+s); }
               else if(i==1){ _w[s][i] = MACD.GetData(0,_i+s); }
               else if(i==2){ _w[s][i] = WPR.GetData(0,_i+s); }
               else if(i==3){ _w[s][i] = STOCH.GetData(0,_i+s); }
               else if(i==4){ _w[s][i] = RVI.GetData(0,_i+s); }
            }
            
            if(s>0){ _xy[s][2*__HIDDEN] = m_close.GetData(_i+s)-m_close.GetData(_i+s+1); }

         }
         
         RBM.Train(_w);
         RBM.Process(_w,_xy);
         
         double _w=0.0,_w_sum=0.0;
         
         vector _x0=_xy.Row(0); _x0.Resize(6);
         
         for(int s=1;s<m_sample;s++)
         {
            vector _x=_xy.Row(s); _x.Resize(6);
            double _weight=fabs(1.0+_x.Loss(_x0,LOSS_COSINE));
            
            _w+=(_weight*_xy[s][6]);
            _w_sum+=_weight;
         }
         
         if(_w_sum>0.0){ _w/=_w_sum; }
         
         _output=_w;
      }
      
      return(_output);
   }

Com o último loop `for`, obtemos a previsão média provável, baseada no coeficiente de similaridade cosseno com outros pontos de dados que têm um Y conhecido (possível alteração de preço).

Nós otimizamos esta instância ajustada da classe de sinais do EA para GBPUSD H4 de 01/07/2023 a 01/10/2023, usando um teste passo a passo de 01/10/2023 a 25/12/2023 e obtivemos os seguintes relatórios.

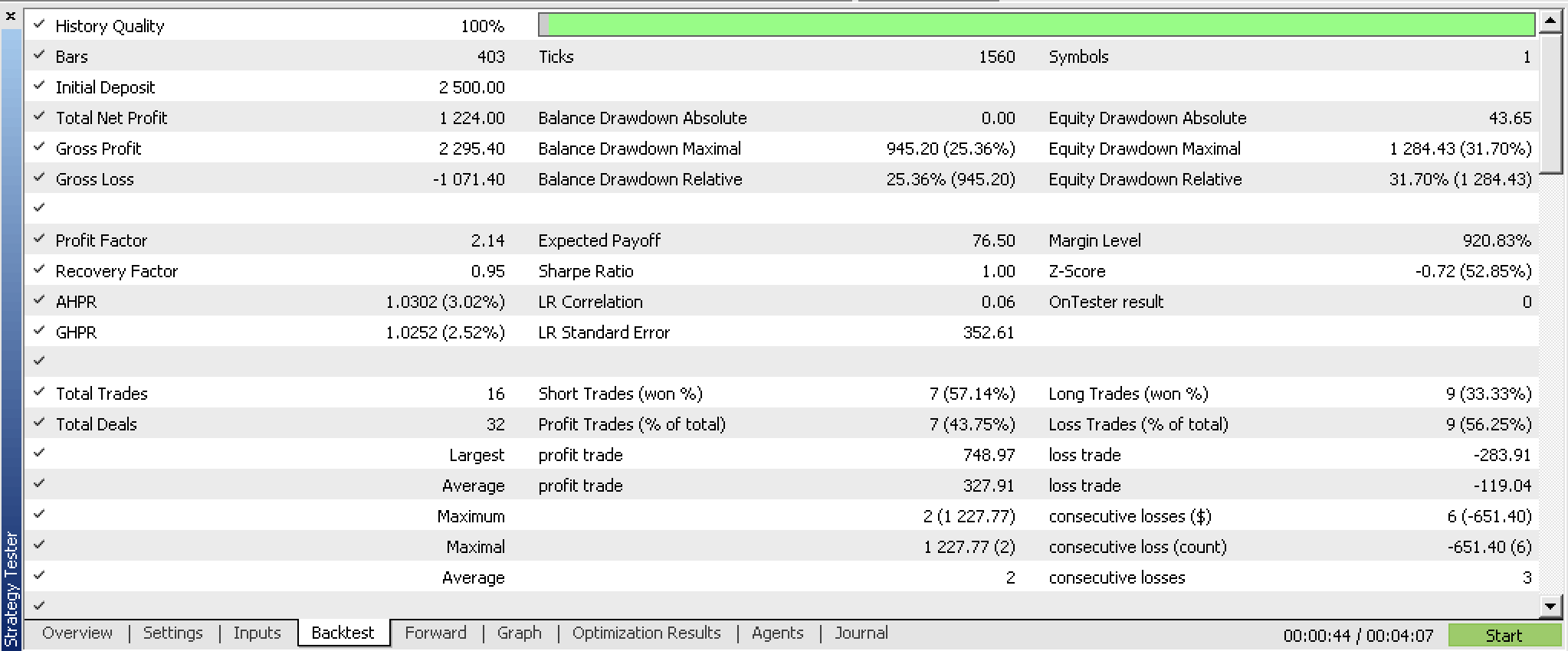
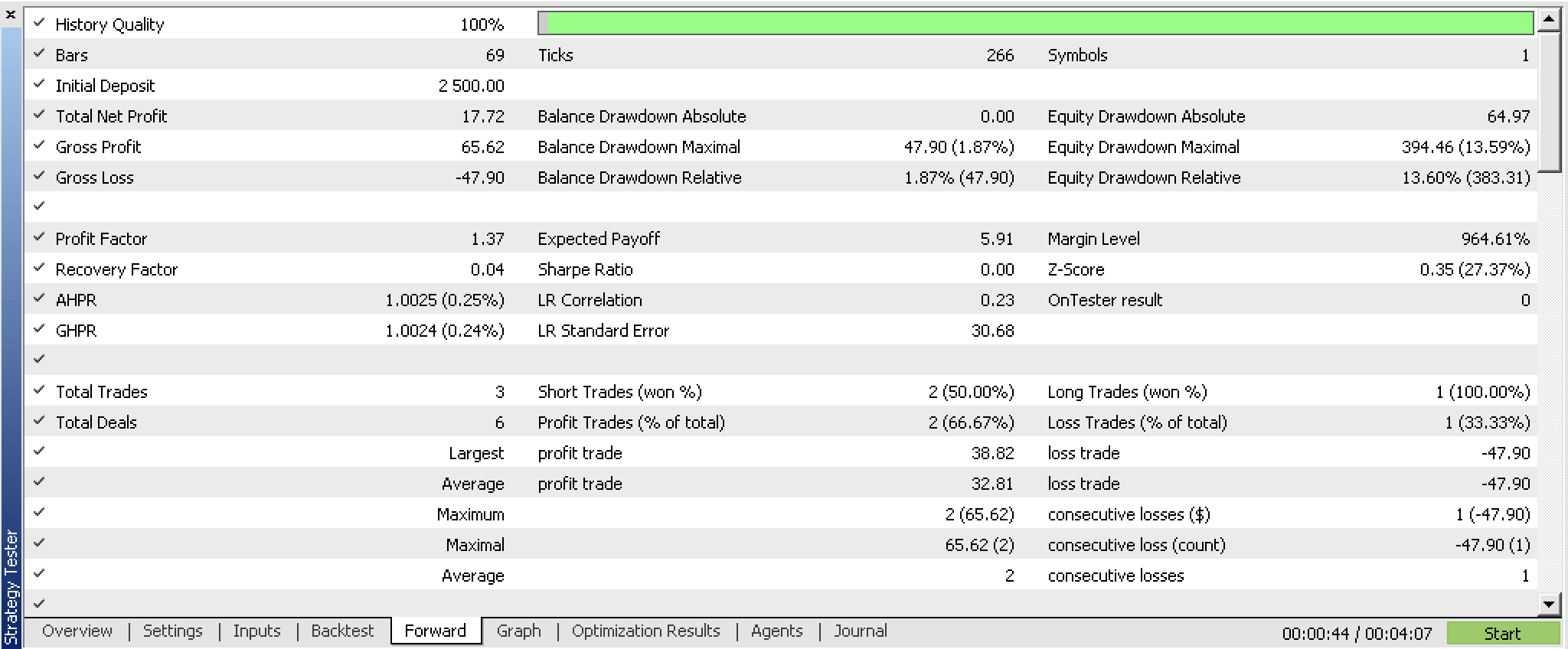
Os resultados são potencialmente bons. Idealmente, o teste normal deve ser realizado com os ticks reais da corretora com o qual você pretende negociar. E, idealmente, isso deve acontecer após fazer as devidas alterações e ajustes não apenas nas fontes de dados de entrada, mas possivelmente também na construção e eficiência do perceptron. Este último ponto é importante porque resultados confiáveis de teste devem ser obtidos ao longo de longos períodos de dados históricos, e com o código-fonte ALGLIB "out of the box", essa tarefa pode ser complicada.

Considerações finais

Analisamos a definição tradicional da rede RBM e como ela pode ser implementada no MQL5. Mais importante, exploramos uma variante não convencional dessa rede, que é estruturada e treinada de forma semelhante a um perceptron multicamadas simples, e consideramos se podemos usar a "distribuição de probabilidades", que chamamos de pesos de saída, ao construir outra instância personalizada da classe de sinal do EA. Os resultados dos testes diretos e reversos mostram que existe um potencial de uso do sistema, desde que sejam realizados testes mais rigorosos e, possivelmente, um ajuste fino na seleção dos dados de entrada.

Notas

O código anexado pode ser usado após ser compilado com o Assistente MQL5. Já descrevi como isso pode ser feito em artigos anteriores desta série. Este artigo também pode servir como um guia para aqueles que não estão familiarizados com o Assistente.