Algoritmos de otimização populacional: Mudamos a forma e deslocamos as distribuições de probabilidade e testamos com o "Cabeçudinho Inteligente" (Smart Cephalopod, SC)

Conteúdo:

1. Introdução
2. Bancada de teste para verificar distribuições
3. Geração de números aleatórios com a lei de distribuição requerida
4. Modelo para o algoritmo de otimização: "Cabeçudinho Inteligente"
5. Considerações finais

1. Introdução

A teoria das probabilidades é uma teoria matemática que estuda fenômenos aleatórios e determina o quão provável é sua ocorrência. Ela permite descrever e analisar processos aleatórios. Seus principais conceitos são: probabilidade, variável aleatória, distribuição de probabilidades, esperança matemática, variância.

Probabilidade é uma característica numérica que determina a chance de ocorrência de um determinado evento.

Variável aleatória é uma função que associa a cada resultado de um experimento aleatório um determinado número.

Distribuição de probabilidades é uma função que determina a probabilidade de ocorrência de cada um dos possíveis valores da variável aleatória.

Esperança matemática é o valor médio da variável aleatória, obtido através da repetição do experimento diversas vezes.

Variância é uma medida da dispersão dos valores da variável aleatória em relação à sua esperança matemática.

Momento é uma característica numérica da variável aleatória que descreve sua distribuição. Os momentos são usados para determinar o centro da distribuição (esperança matemática) e sua dispersão (variância e desvio padrão), bem como para analisar a forma da distribuição (assimetria e curtose). O primeiro momento (n=1) é a esperança matemática, que define o centro da distribuição da variável aleatória. O segundo momento (n=2) é a variância, que descreve a dispersão da variável aleatória em relação à sua esperança matemática. O terceiro momento (n=3) é uma medida da assimetria da distribuição, e o quarto momento (n=4) é uma medida da curtose (curvatura) da distribuição.

As distribuições de probabilidades desempenham um papel importante na modelagem de fenômenos aleatórios e na análise de dados, bem como na estatística para estimar parâmetros e testar hipóteses. Elas permitem descrever as propriedades probabilísticas de variáveis aleatórias e eventos, bem como determinar a probabilidade de diferentes resultados.

A teoria das probabilidades e a otimização são duas disciplinas científicas importantes que encontram ampla aplicação em várias áreas da ciência e da tecnologia, como economia, finanças, engenharia, biologia, medicina e muitas outras. O desenvolvimento dessas áreas e a aplicação de seus métodos de pesquisa e otimização permitem resolver problemas complexos e criar novas tecnologias, aumentando a performance e a qualidade do trabalho em diversas esferas de atividade. Um exemplo pode ser o desenvolvimento de tecnologias modernas para criar computadores quânticos, meios de comunicação seguros e ultrarrápidos, redes neurais generativas e inteligência artificial. 

Os cálculos probabilísticos, baseados na teoria das probabilidades, desempenham um papel fundamental na modelagem de fenômenos aleatórios e na análise de dados. A otimização, por sua vez, visa encontrar soluções ótimas em várias tarefas e permite encontrar as melhores soluções entre várias opções possíveis. Entretanto, em problemas reais, existe incerteza e aleatoriedade, e é aí que as distribuições de probabilidades entram em jogo. Elas permitem levar em conta a aleatoriedade e a incerteza nas tarefas de otimização.

As distribuições de probabilidades também são amplamente utilizadas em algoritmos evolutivos e populacionais. Nesses algoritmos, a geração aleatória de novos estados no espaço de busca é modelada com distribuições probabilísticas apropriadas. Isso permite explorar o espaço de parâmetros e encontrar soluções ótimas considerando a aleatoriedade e a diversidade na população.

Métodos de otimização mais complexos utilizam distribuições probabilísticas para modelar incertezas e aproximar funções complexas. Eles permitem explorar de forma eficaz o espaço de parâmetros e encontrar soluções ótimas considerando a aleatoriedade e o ruído nos dados.

Neste artigo, examinaremos vários tipos de distribuições probabilísticas, suas propriedades e sua implementação prática na forma de funções correspondentes no código. Ao gerar números aleatórios com diferentes tipos de distribuições na prática, podem surgir diversos problemas, como infinitude de caudas, deslocamento de probabilidades ao definir limites de variância, além da necessidade frequente de deslocar probabilidades em relação à esperança matemática ao projetar e criar algoritmos de otimização. O objetivo deste artigo é resolver esses problemas e criar funções de trabalho para lidar com probabilidades para sua posterior aplicação em algoritmos de otimização.

2. Bancada de teste para verificar distribuições

Para testar e visualizar distribuições de variáveis aleatórias, é necessário um banco de testes que permita ver claramente a forma das distribuições. Isso é importante ao projetar algoritmos de otimização, pois a representação visual e o entendimento de como a probabilidade da variável aleatória deve ser deslocada ajudam a alcançar os melhores resultados.

Para construir uma distribuição de probabilidades, é necessário criar algo semelhante a uma série de caixas onde os números aleatórios serão colocados. As caixas são essencialmente contadores. Por exemplo, temos uma situação com uma linha numérica, limitada à esquerda por "min" e à direita por "max" e com "in" no meio, podemos representar isso da seguinte forma:

min|-----|-----|-----|-----|-----|-----|in|--|--|--|--|--|--|max

Podemos ver que o valor "in" está deslocado na linha numérica mais próximo de "max". Se gerarmos números aleatórios no intervalo [min;max], o número de ocorrências de números aleatórios no intervalo [min;in] será maior do que no intervalo [in;max], criando assim um desequilíbrio, mas precisamos que o número de ocorrências à esquerda e à direita seja em média igual. Para isso, é necessário mudar a forma da distribuição sem deslocar as probabilidades. Para isso, o número de caixas à esquerda e à direita deve ser igual (no exemplo esquemático acima, são 6 caixas à esquerda e 6 à direita).

Assim, o banco de testes para construir distribuições é bastante simples. A essência por trás de seu funcionamento é a seguinte:

• criamos um objeto CCanvas para trabalhar com a tela
• geramos um número aleatório com a distribuição escolhida nas configurações
• verificamos em qual área da caixa correspondente o número aleatório ocorreu e adicionamos 1 à caixa
  
• contamos a quantidade mínima e máxima de ocorrências entre todas as caixas
• desenhamos círculos na tela para cada caixa, correspondendo ao número de números aleatórios que ocorreram nas caixas
• colorimos os círculos de azul (raro) a vermelho (frequente)
  

O objetivo geral do código é visualizar a distribuição probabilística na tela usando um gráfico, onde cada círculo representa a quantidade de números aleatórios nas caixas, normalizada pelo valor mínimo/máximo em todas as caixas.

#property script_show_inputs
#include <Canvas\Canvas.mqh>

enum E_Distribution
{
  uniform = 0,
  gauss   = 1,
  power   = 2,
  levi    = 3
};

//--- input parameters
input double         MinP       = -100.0;
input double         InpP       =  0;
input double         MaxP       =  100.0;
input int            CNT        =  1000000;
input int            Size       =  1000;
input double         SigmaP     =  3;       //Sigma for "Gauss" distribution
input double         PowerP     =  2;       //Power for "Power law" distribution
input double         LeviPowerP =  2;       //Power for "Levy flights" distribution
input E_Distribution Distr_P    = gauss;    //Distribution type

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  CCanvas Canvas;

  int W = 750;
  int H = 400;
  int O = 10;

  int CountL [];
  int CountR [];

  ArrayResize     (CountL, Size);
  ArrayInitialize (CountL, 0);

  ArrayResize     (CountR, Size);
  ArrayInitialize (CountR, 0);

  string canvasName = "Test_Probability_Distribution_Canvas";
  if (!Canvas.CreateBitmapLabel (canvasName, 5, 30, W, H, COLOR_FORMAT_ARGB_RAW))
  {
    Print ("Error creating Canvas: ", GetLastError ());
    return;
  }

  ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN,     false);
  ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true);

  Canvas.Erase (COLOR2RGB (clrWhite));
  Canvas.Rectangle (1, 1, W - 1, H - 1, COLOR2RGB (clrBlack));

  int    ind = 0;
  double X   = 0.0;

  for (int i = 0; i < CNT; i++)
  {
    switch (Distr_P)
    {
    case uniform:
      X = UniformDistribution (InpP, MinP, MaxP);
      break;
    case gauss:
      X = GaussDistribution (InpP, MinP, MaxP, SigmaP);
      break;
    case power:
      X = PowerDistribution (InpP, MinP, MaxP, PowerP);
      break;
    case levi:
      X = LeviDistribution (InpP, MinP, MaxP, LeviPowerP);
      break;
    }

    if (X < InpP)
    {
      ind = (int)Scale (X, MinP, InpP,
                        0,    Size, false);
      if (ind >= Size) ind = Size - 1;
      if (ind < 0)     ind = 0;
      CountL [ind] += 1;
    }
    else
    {
      ind = (int)Scale (X, InpP, MaxP,
                        0,    Size, false);
      if (ind >= Size) ind = Size - 1;
      if (ind < 0)     ind = 0;
      CountR [ind] += 1;
    }
  }

  int minCNT = CNT;
  int maxCNT = 0;

  for (int i = 0; i < Size; i++)
  {
    if (CountL [i] > maxCNT) maxCNT = CountL [i];
    if (CountR [i] > maxCNT) maxCNT = CountR [i];

    if (CountL [i] < minCNT) minCNT = CountL [i];
    if (CountR [i] < minCNT) minCNT = CountR [i];
  }

  int x = 0.0;
  int y = 0.0;
  color clrF;
  int centre = 0;
  int stepL  = 0;
  int stH_L  = 0;
  int stepR  = 0;
  int stH_R  = 0;

  centre = (int)Scale (InpP, MinP, MaxP, 10, W - 11, false);

  stepL = (centre - O) / Size;
  stH_L = stepL / 2;
  if (stH_L == 0) stH_L = 1;

  stepR = (W - O - centre) / Size;
  stH_R = stepR / 2;
  if (stH_R == 0) stH_R = 1;

  for (int i = 0; i < Size; i++)
  {
    x = (int)Scale (i,          0, Size - 1, O, centre - stH_L, false);
    y = (int)Scale (CountL [i], 0, maxCNT,   O, H - O,  true);

    clrF = DoubleToColor (CountL [i], minCNT, maxCNT, 0, 255);

    Canvas.Circle (x, y, 2, COLOR2RGB (clrF));
    Canvas.Circle (x, y, 3, COLOR2RGB (clrF));


    x = (int)Scale (i,          0, Size - 1, centre + stH_R, W - O, false);
    y = (int)Scale (CountR [i], 0, maxCNT,   O,      H - O, true);

    clrF = DoubleToColor (CountR [i], minCNT, maxCNT, 0, 255);

    Canvas.Circle (x, y, 2, COLOR2RGB (clrF));
    Canvas.Circle (x, y, 3, COLOR2RGB (clrF));
  }

  Canvas.Update ();
}
//——————————————————————————————————————————————————————————————————————————————

3. Geração de números aleatórios com a lei de distribuição requerida

Distribuição uniforme (uniform distribution)

A distribuição uniforme é uma distribuição de probabilidade onde todos os valores da variável aleatória em um intervalo definido têm igual probabilidade. A distribuição uniforme é amplamente utilizada para modelar variáveis aleatórias que podem assumir valores igualmente prováveis em um intervalo definido.

Figura 1. Distribuição uniforme de números sem deslocamento.

A distribuição uniforme é a mais simples de implementar entre todas. A única coisa a considerar aqui é que não podemos simplesmente gerar números no intervalo [min;max]; portanto, geramos um número aleatório à esquerda de In ou à direita de In, dependendo de um número aleatório previamente gerado no intervalo [0.0;1.0]. Portanto, a quantidade de números gerados à esquerda e à direita é igualmente provável para qualquer posição de In em relação a [min;max]. Aqui, não há problemas com saída de intervalo ou artefatos na distribuição.

Podemos usar a distribuição uniforme em todos os casos onde é necessário gerar um número em um intervalo definido com igual probabilidade em todo o intervalo.

//——————————————————————————————————————————————————————————————————————————————
double UniformDistribution (const double In, const double outMin, const double outMax)
{
  double rnd = RNDfromCI (0.0, 1.0);

  if (rnd >= 0.5) return RNDfromCI (In, outMax);
  else            return RNDfromCI (outMin, In);
}
//——————————————————————————————————————————————————————————————————————————————

Distribuição normal (Gaussian distribution)

A distribuição normal é uma distribuição de probabilidade que descreve muitos fenômenos aleatórios na natureza, economia e outras áreas. Ela é caracterizada por uma forma de sino e simetria em relação ao valor médio. O valor médio e a variância da distribuição normal a definem completamente.

Uma das propriedades chave da distribuição normal é sua simetria em relação ao valor médio. Isso significa que a probabilidade de a variável aleatória assumir o valor médio é a maior, e a probabilidade de assumir um valor diferente do valor médio diminui à medida que se afasta do valor médio. Essa propriedade torna a distribuição normal especialmente útil para modelagem e análise de dados, pois permite descrever e prever fenômenos aleatórios que têm um valor médio e desvios dele.

A distribuição normal também possui várias propriedades matemáticas, que a tornam conveniente para uso em métodos e modelos estatísticos. Por exemplo, se as variáveis aleatórias forem independentes e tiverem uma distribuição normal, a soma dessas variáveis também seguirá uma distribuição normal. Essa propriedade permite usar a distribuição normal para modelar e analisar sistemas complexos compostos por várias variáveis aleatórias. A distribuição normal tem muitas aplicações em estatística, física, economia, finanças e outras áreas. Ela é a base para muitos métodos e modelos estatísticos, como a regressão linear e a análise de séries temporais.

Para algoritmos de otimização, a distribuição normal pode ser útil em situações em que queremos focar em um determinado ponto na reta numérica. Nesse caso, podemos precisar apenas de uma parte da curva que forma a distribuição. Por exemplo, queremos usar a distribuição apenas dentro de três desvios padrão; tudo que ultrapassar esses limites não podemos simplesmente retornar aos valores das bordas. Se fizermos isso, teremos uma frequência nas bordas maior do que a frequência no valor médio. Esse problema é demonstrado na Fig. 2 e será resolvido na descrição abaixo.

Para gerar uma variável aleatória com distribuição normal, podemos usar o método Box-Muller.

• Primeiro, é necessário gerar dois números aleatórios uniformemente distribuídos u1 (0, 1] e u2 [0, 1].
• Em seguida, precisamos calcular a variável aleatória z0, usando a fórmula:

z0 = sqrt(-2 * ln(u1)) * cos(2 * pi * u2)   

• A variável aleatória z0 obtida terá uma distribuição normal padrão.
  

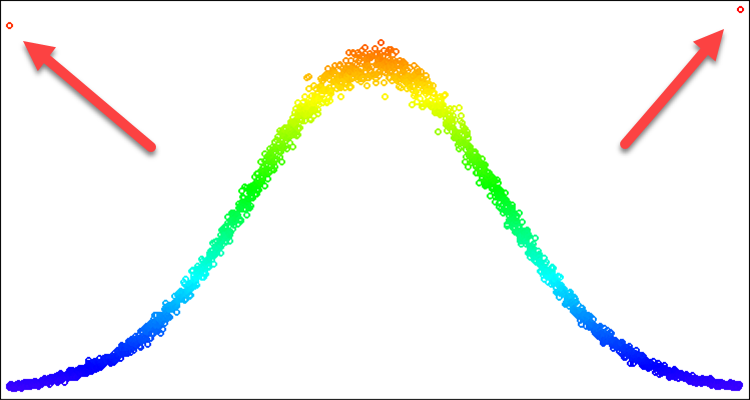
Figura 2. Distribuição normal com sigma=3 e artefatos ao tentar cortar tudo além de 3 sigmas.

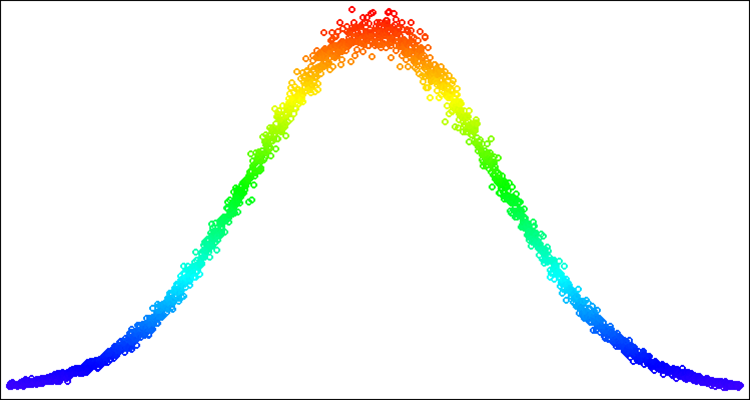
Figura 3. Distribuição normal com sigma=3 com problema de artefatos resolvido (saída dos limites da distribuição).

Vamos escrever a implementação da função GaussDistribution, que gera valores aleatórios com distribuição normal em relação ao valor médio "in":

• Definimos os parâmetros da função: valor de entrada (in), valores mínimo e máximo do intervalo de saída (outMin e outMax), desvio padrão (sigma).
• Calculamos o logaritmo natural de u1, que é gerado aleatoriamente no intervalo de 0 a 1.
• Se u1 for menor ou igual a 0, o logN recebe o valor 0.000000000000001; caso contrário, logN será igual a u1.
• Calculamos o valor de z0 usando a fórmula da distribuição normal.
• Verificamos o valor de entrada "sigma" para ver se está fora do intervalo máximo permitido para o desvio padrão, que é 8.583864105157389.
  
• Se z0 for maior ou igual a sigmaN, então z0 recebe um valor aleatório no intervalo de 0 a sigmaN; caso contrário, se z0 for menor ou igual a -sigmaN, então z0 recebe um valor aleatório no intervalo de -sigmaN a 0.0.
• Se z0 for maior ou igual a 0, retornamos o valor calculado usando a função Scale para o intervalo de 0 a sigmaN e o intervalo de saída de "in" a "outMax"; caso contrário, retornamos o valor calculado usando a função Scale para o intervalo de -sigmaN a 0 e o intervalo de saída de "outMin" a in.
  

A solução destacada em amarelo aborda o problema da frequência de ocorrências nos limites de um desvio padrão específico. Dessa forma, redistribuímos a probabilidade que excede os limites para dentro da curva de distribuição correspondente. Isso mantém a forma da distribuição intacta.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_SC::GaussDistribution (const double In, const double outMin, const double outMax, const double sigma)
{
  double logN = 0.0;
  double u1   = RNDfromCI (0.0, 1.0);
  double u2   = RNDfromCI (0.0, 1.0);

  logN = u1 <= 0.0 ? 0.000000000000001 : u1;

  double z0 = sqrt (-2 * log (logN)) * cos (2 * M_PI * u2);

  double sigmaN = sigma > 8.583864105157389 ? 8.583864105157389 : sigma;

  if (z0 >=  sigmaN) z0 = RNDfromCI (0.0,     sigmaN);
  if (z0 <= -sigmaN) z0 = RNDfromCI (-sigmaN, 0.0);

  if (z0 >= 0.0) z0 =  Scale (z0,        0.0, sigmaN, 0.0, outMax - In, false);
  else           z0 = -Scale (fabs (z0), 0.0, sigmaN, 0.0, In - outMin, false);
  
  return In + z0;
}
//——————————————————————————————————————————————————————————————————————————————

Abaixo, um exemplo de números aleatórios com distribuição normal na Fig. 4. Neste exemplo e nos seguintes, as distribuições estão centradas no valor alvo "50" no intervalo de "-100" a "100" [-100;50;100].

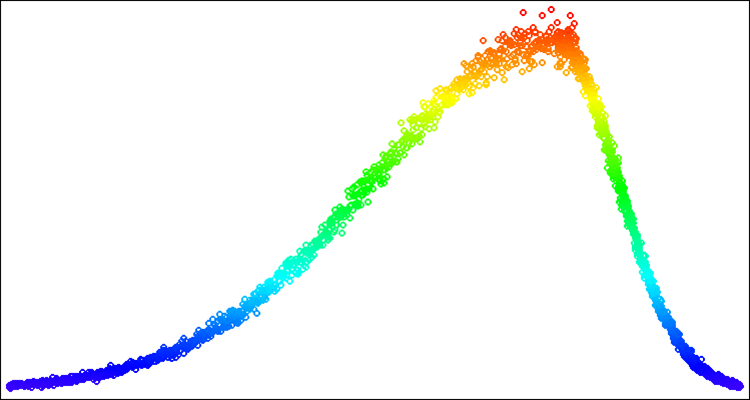
Figura 4. Distribuição normal com sigma=3, [-100;50;100].

Distribuição de lei de potência (Power law distribution)

A distribuição de lei de potência é uma distribuição de probabilidade que descreve variáveis aleatórias cuja probabilidade de assumir valores muito altos decresce conforme uma lei de potência. Essa distribuição também é conhecida como lei de Pareto ou lei de Zipf. Ela é utilizada em várias áreas da ciência e da engenharia. Por exemplo, na física, ela modela a distribuição de massas e energia em sistemas com muitas partículas, como aglomerados estelares e galáxias. Também é usada na economia e sociologia para analisar a distribuição de renda e riqueza.

A distribuição de lei de potência possui várias propriedades interessantes. Primeiro, ela tem caudas pesadas, o que significa que a probabilidade de uma variável aleatória assumir valores muito altos não é nula. Segundo, ela não tem uma expectativa matemática finita, o que significa que o valor médio da variável pode ser infinito.

A distribuição de lei de potência é muito útil, em alguns casos, para uso em algoritmos de otimização. Ela permite concentrar a densidade de números aleatórios em áreas do espaço de busca que requerem atenção especial. No entanto, em sua forma pura, ela não é adequada para aplicação quando queremos delimitar claramente os limites dos números aleatórios, pois possui caudas de comprimento infinito que não podem ser simplesmente "recolhidas" como na distribuição normal.

Para a implementação clássica da lei de potência, é necessário usar a função inversa; no entanto, para eliminar a infinidade nas caudas da distribuição, que atrapalha na geração de valores em limites conhecidos, podemos usar uma variável uniformemente distribuída elevada a uma potência. Embora isso não seja uma maneira rigorosa de definir a lei de potência, permite eliminar a infinidade nas caudas da distribuição, mantendo a forma da distribuição suficientemente próxima da teórica. Para algoritmos estocásticos de otimização, isso é mais do que suficiente.

A função PowerDistribution recebe quatro valores do tipo double: "in", "outMin", "outMax" e "power". Ela gera um número aleatório "rnd" no intervalo de [-1.0;1.0], calcula o valor "r", que é o resultado de elevar à potência "power", e depois escala esse valor do intervalo [0.0;1.0] para o intervalo de valores definido usando a função Scale. Se "rnd" for um número negativo, a escala é feita no intervalo [outMin; in], caso contrário, no intervalo [in; outMax]. O resultado da execução da função é retornado como um valor do tipo double.

• Se "power" for menor que 1, a maioria dos valores na distribuição gerada ficará concentrada perto de zero, e a cauda da distribuição será fortemente cortada. Essa distribuição lembrará uma parábola.
• Se "power" for igual a 1, a distribuição resultante será uniforme.
• Se "power" for maior que 1, a maioria dos valores na distribuição gerada ficará distante de zero, e a cauda da distribuição será longa. Essa distribuição terá uma cauda pesada e lembrará a distribuição de Pareto ou a lei de potência.
• Se "power" tender ao infinito, a distribuição resultante lembrará uma função delta, concentrada em zero.

Dessa forma, temos uma gama adicional de possibilidades ao utilizar diferentes valores de "power", o que proporciona mais opções de pesquisa para escolher a distribuição ideal para obter o melhor resultado no algoritmo de otimização, no contexto de resolver uma tarefa específica de otimização.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_SC::PowerDistribution (const double In, const double outMin, const double outMax, const double power)
{
  double rnd = RNDfromCI (-1.0, 1.0);
  double r   = pow (fabs (rnd), power);

  if (rnd >= 0.0) return In + Scale (r, 0.0, 1.0, 0.0, outMax - In, false);
  else            return In - Scale (r, 0.0, 1.0, 0.0, In - outMin, false);
}
//——————————————————————————————————————————————————————————————————————————————

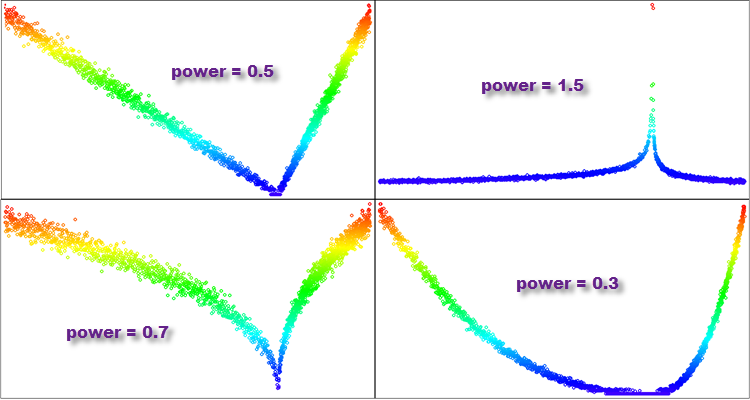
Figura 5. Exemplos de distribuições da função "PowerDistribution" com diferentes graus de "power".

Distribuição de Lévy (Levy distribution)

Os voos de Lévy são caminhadas aleatórias em que o comprimento de cada passo é determinado pela distribuição de Lévy.

A distribuição de Lévy é um exemplo de distribuição com momentos ilimitados. Ela descreve variáveis aleatórias com caudas pesadas, o que significa que a probabilidade de ocorrência de valores muito grandes é significativa. Na distribuição de Lévy, os momentos podem ser infinitos ou inexistentes, tornando-a especial e distinta das distribuições com momentos limitados, como a distribuição normal.

As caudas pesadas da distribuição de Lévy e seus momentos ilimitados a tornam útil para modelar fenômenos que podem ter valores extremos ou alta variabilidade. Os voos de Lévy têm muitas aplicações em várias áreas, incluindo física, matemática financeira, análise de riscos, ecologia, economia e engenharia. Por exemplo, eles podem ser usados para modelar processos aleatórios na física, como difusão, turbulência e transporte em plasma. Eles também podem ser usados para modelar estratégias de busca de animais e populações, bem como para otimizar parâmetros na engenharia e finanças.

A distribuição de Lévy foi introduzida pelo matemático francês Paul Lévy em 1925 e encontrou muitas aplicações em várias áreas da ciência e da engenharia.

Quando falamos de incrementos a partir de um valor específico de parâmetro na otimização, nos voos de Lévy cada incremento é escolhido a partir da distribuição de Lévy, e a direção é escolhida aleatoriamente. Isso leva a que, nos voos de Lévy, alguns passos possam ser muito longos, permitindo explorar o espaço de parâmetros mais rapidamente do que nas caminhadas aleatórias com comprimento de passo fixo.

A forma da distribuição dos Voos de Lévy é semelhante à da distribuição de lei de potência, mas em alguns casos, pode ser mais eficiente usar uma ou outra distribuição. Assim como no caso da lei de potência, precisaremos eliminar as caudas pesadas; no entanto, faremos isso de uma maneira mais adequada para esta distribuição. Foi descoberto experimentalmente que o intervalo [1.0;20.0] é ideal para números aleatórios uniformemente distribuídos usados na geração. É necessário calcular o valor mínimo no final da distribuição para os números aleatórios elevados à potência "power", o que servirá como limite para escalar o número gerado no intervalo [0.0;1.0].

A função LeviDistribution recebe quatro valores do tipo double: "in", "outMin", "outMax" e "power", e executa os seguintes passos:

• Primeiro, a função determina o valor mínimo "min" com base no parâmetro "power", que é o valor mínimo possível da função para a posterior escala.
  
• Em seguida, são gerados dois números aleatórios "r1" e "r2" de uma distribuição uniforme nos intervalos [0.0;1.0] e [1.0;20.0], respectivamente.
• O valor "y" é calculado elevando "r2" à potência negativa de "power" e escalando-o do intervalo [min, 1.0] para [0.0;1.0] usando a função Scale.
  
• Finalmente, a função retorna o valor gerado, escalado para o intervalo [outMin, outMax], dependendo do valor de "r1". Se r1 >= 0.5, o valor é escalado para o intervalo [in, outMax]; caso contrário, para o intervalo [outMin, in].
  

//——————————————————————————————————————————————————————————————————————————————
double C_AO_SC::LeviDistribution (const double In, const double outMin, const double outMax, const double power)
{
  double min = pow (20.0, -power);
  double r1 = RNDfromCI (0.0, 1.0);
  double r2 = RNDfromCI (1.0, 20.0);
  
  double y = pow (r2, -power);
  y = Scale (y, min, 1.0, 0.0, 1.0, false);
 
  if (r1 >= 0.5) return In + Scale (y, 0.0, 1.0, 0.0, outMax - In, false);
  else           return In - Scale (y, 0.0, 1.0, 0.0, In - outMin, false);
}
//——————————————————————————————————————————————————————————————————————————————

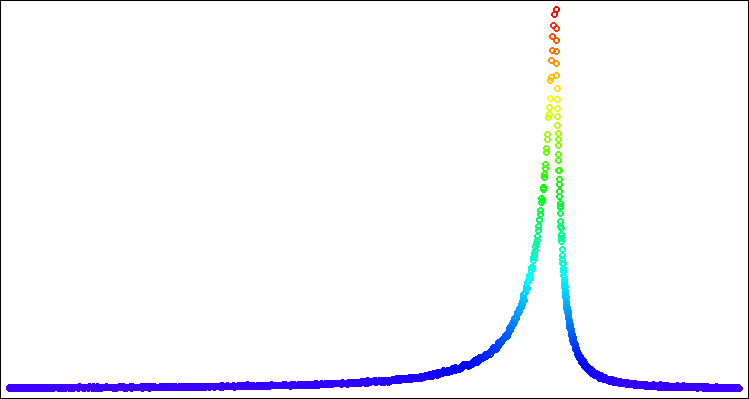
Figura 6. Distribuição de Lévy com power = 1.0.

4. Modelo para o algoritmo de otimização: "Cabeçudinho Inteligente"

Agora vamos para a parte mais interessante de nossa pesquisa! Vamos testar todas as distribuições em um algoritmo de otimização criado especificamente para isso, chamado... Hum, como vamos chamá-lo?

Vamos examinar a ideia por trás desse algoritmo. Imagine um cefalópode inteligente que está procurando o lugar mais saboroso, então presumimos que sua cabeça está no epicentro da comida e está comendo algo. Enquanto isso, seus tentáculos se espalham constantemente em busca de novas fontes de alimento. Assim que um dos tentáculos encontra um lugar saboroso, a cabeça se move. Talvez não seja uma má ideia para um algoritmo inspirado em criaturas marinhas. Então já sabemos como chamá-lo, será o cabeçudinho inteligente!

Estou certo de que será um experimento empolgante que nos permitirá entender melhor como funcionam as diferentes distribuições e como elas podem nos ajudar a resolver problemas complexos de otimização. Então, vamos começar e ver o que podemos descobrir nesta interessante pesquisa!

Faz sentido definir as propriedades das pernas do cabeçudinho de acordo com as leis de distribuição. Assim, o código para tatear novos lugares com as pernas do cabeçudinho ficará assim:

//----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      double X   = 0.0;
      double in  = cB [c];
      double min = rangeMin [c];
      double max = rangeMax [c];
      
      switch (distr)
      {
      case uniformDistr: X = UniformDistribution (in, min, max);         break;
      case gaussDistr:   X = GaussDistribution   (in, min, max, powers); break;
      case powerDistr:   X = PowerDistribution   (in, min, max, powers); break;
      case leviDistr:    X = LeviDistribution    (in, min, max, powers); break;
      }

      a [i].c [c] = SeInDiSp  (X, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

Este código consiste em dois laços aninhados que percorrem cada agente no array "a" de tamanho popSize, e para cada elemento, geram um novo valor de coordenada. A geração de um novo valor é feita escolhendo um dos quatro tipos de distribuições e aplicando a função de distribuição correspondente (UniformDistribution, GaussDistribution, PowerDistribution ou LeviDistribution) ao valor atual "in", que é retirado do array "cB", que representa a melhor solução até o momento (o lugar onde a cabeça está atualmente). Em seguida, o novo valor "X" é normalizado usando a função SeInDiSp com os valores de rangeMin, rangeMax e rangeStep para o elemento específico. O valor resultante é salvo no array "a" para o agente e coordenada correspondente.

Trabalhar neste artigo e nos métodos específicos da classe para gerar números aleatórios com as distribuições desejadas, adequadas para a construção de algoritmos de otimização, nos fez entender que a função Rastrigin tem várias desvantagens sérias que não eram óbvias no momento da escolha dessa função de teste, e decidi abandoná-la. O bom e velho Rastrigin será substituído pela função Peaks (uma justificativa mais completa será dada no próximo artigo).

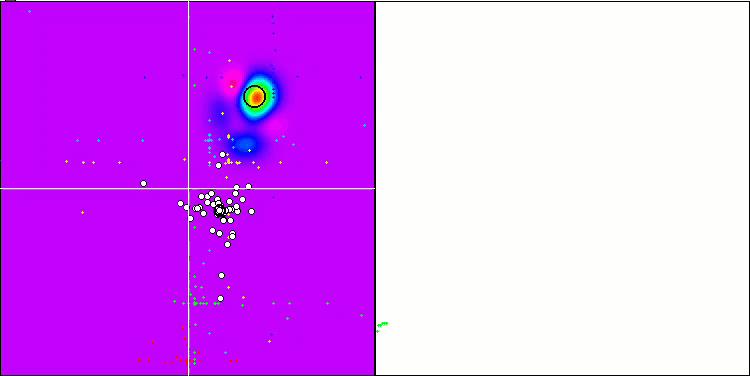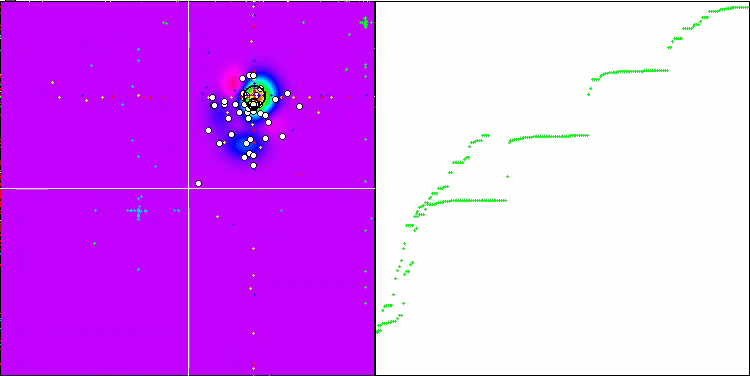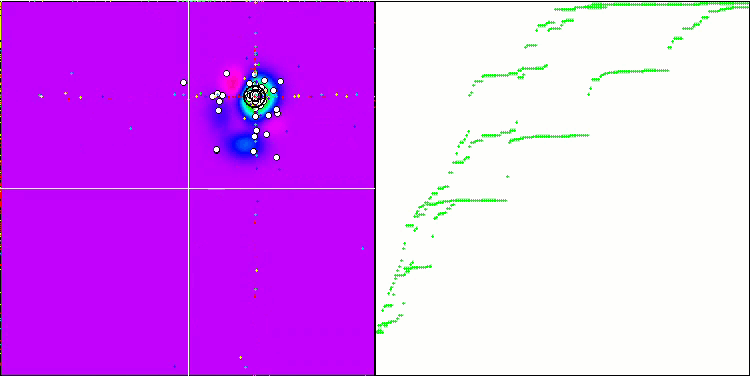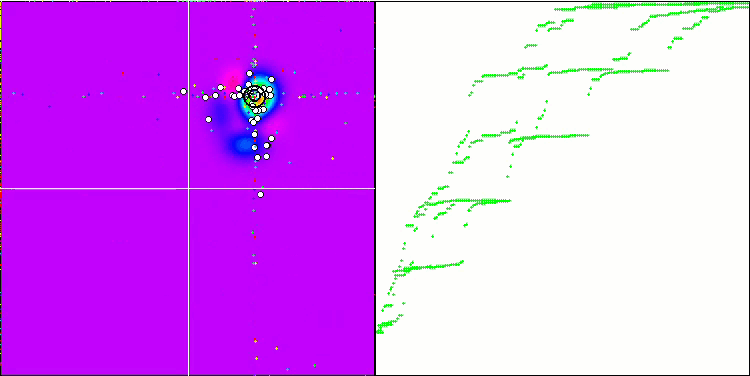
O "Cabeçudinho Inteligente" em ação.

5. Considerações finais

Concluindo, nosso experimento com o "Cabeçudinho Inteligente" trouxe resultados interessantes. A animação mostra como o algoritmo aleatório, aplicando uma determinada distribuição, executa a tarefa com sucesso. Não vou revelar qual distribuição e quais configurações foram usadas, mas ofereço a você a oportunidade de realizar seus próprios experimentos com o conjunto completo de ferramentas deste artigo. Ficarei feliz se você compartilhar seus sucessos nos comentários.

O "Cabeçudinho Inteligente" não será considerado na tabela de classificação, pois é apenas um experimento que nos ajudará a abordar a otimização de maneira mais consciente.

Minhas conclusões gerais são que a aplicação de distribuições de probabilidade e a escolha da estratégia de busca desempenham um papel importante na tarefa de otimização, pois permitem considerar fatores estocásticos e explorar mais eficazmente o espaço de soluções, descobrindo áreas com alta probabilidade de encontrar as melhores soluções.

Contudo, aplicar apenas distribuições de probabilidade não é suficiente. É igualmente importante considerar a escolha e as características da estratégia de busca. Diferentes estratégias de busca podem ter vantagens e desvantagens dependendo da tarefa de otimização.

Daí que, para alcançar resultados ainda melhores no design de algoritmos de otimização, tanto em tarefas específicas quanto de forma geral, é necessário usar conjuntamente a distribuição de probabilidade e a escolha da estratégia de busca. Esses elementos devem trabalhar em conjunto para garantir os resultados desejados no desenvolvimento do algoritmo de otimização (AO). Em geral, os resultados deste experimento destacam a importância de uma abordagem consciente à otimização. Por exemplo, aplicar distribuições de probabilidade e escolher a estratégia de busca apropriada pode ser útil na área de aprendizado de máquina, onde é necessário otimização e busca de soluções ideais.

Uma dos recursos mais importantes das ferramentas apresentadas neste artigo é a capacidade de deslocar distribuições em um intervalo de valores especificado. Você não encontrará recursos de deslocamento de distribuições em bibliotecas especializadas voltadas para tarefas gerais. Isso permite que os pesquisadores gerenciem e ajustem distribuições de probabilidade de acordo com as características exigidas pelo algoritmo de otimização. A regulação e controle do deslocamento das probabilidades, juntamente com os elementos da estratégia de busca, realmente permitem alcançar resultados incríveis!