Algoritmos de otimização populacionais: Colônia artificial de abelhas (Artificial Bee Colony, ABC)

MetaTrader 5 — Exemplos | 16 fevereiro 2023, 09:37

327

Andrey Dik

Conteúdo:

1. Introdução

Os insetos sociais são altamente evoluídos e executam tarefas complexas que muitos insetos isolados não conseguem realizar. As abelhas, em particular, demonstram uma série de comportamentos que permitem que elas prosperem em colônias sociais, incluindo comunicação, construção de colmeias complexas, controle ambiental, proteção e divisão de trabalho.
Além disso, as abelhas são representantes do enxame e têm habilidades notáveis para encontrar soluções ótimas. Na natureza, elas encontram cachos de flores para coletar néctar e pólen perto da colmeia, às vezes voando vários quilômetros para isso, e relatam a localização desses recursos às outras abelhas usando uma dança improvisada.

À primeira vista, pode parecer impossível, mas as abelhas são capazes de transmitir informações sobre a posição geográfica umas às outras por meio de movimentos rítmicos. Conforme a intensidade da dança das abelhas aumenta, elas conseguem tirar conclusões sobre o número de flores e a quantidade de néctar em uma determinada área. Esse fenômeno incomum foi descoberto pelo pesquisador de insetos Karl Frisch, na década de 1950.

Por muitos anos, apenas biólogos científicos exploraram os métodos de busca das abelhas. Entretanto, com o crescente interesse no comportamento de enxame na natureza para criar novos algoritmos de otimização, em 2005, o professor Dervis Karaboga ficou interessado nos resultados da pesquisa. Ele publicou um artigo científico e foi o primeiro a descrever um modelo de inteligência de enxame inspirado nas danças das abelhas. Esse modelo ficou conhecido como colônia artificial de abelhas (Artificial Bee Colony).

2. Descrição do algoritmo

O algoritmo de colônia artificial de abelhas possui inúmeras implementações que diferem apenas no gerenciamento das abelhas na colmeia, nas regras para explorar áreas. E neste artigo falarei sobre minha interpretação da versão clássica do algoritmo.

A ideia do algoritmo é inspirada no comportamento das abelhas ao procurar locais com o máximo de néctar possível. Inicialmente, todas as abelhas voam para fora da colmeia em direções aleatórias, atuando como batedoras que procuram áreas com néctar. Em seguida, elas retornam à colmeia e comunicam às demais abelhas onde encontraram néctar e em que quantidade.

As abelhas operárias são enviadas para as áreas encontradas, e quanto mais néctar for encontrado nesta área, mais abelhas voam nesta direção. Enquanto isso, as abelhas batedoras continuam a explorar novas áreas próximas às áreas já encontradas. Assim, as abelhas são divididas em dois tipos: as operárias que coletam néctar e as batedoras que exploram novas áreas. Cada área de coleta de néctar tem um valor correspondente à quantidade de néctar contida nela. Além disso, existe uma regra pela qual as regiões com menor valor de coleta de néctar são deslocadas em relação às regiões com valores mais altos ao longo de uma linha que passa pelos centros das regiões.

Vejamos a distribuição das operárias por região:

ABCarea

Figura 1. Número de abelhas em diferentes áreas dependendo de sua classificação.

Aqui a área 1 tem a maior classificação, já que contém mais néctar, logo mais abelhas tendem a voar para lá. Já a área 4 tem a menor classificação, porque, como podemos ver, o número de abelhas é menor. As informações sobre o valor de cada área da abelha são comunicadas através de uma dança específica. É importante destacar que cada colmeia tem a sua própria dança, na qual é codificada a direção e a quantidade de néctar da área.

Imagine agora que a área com a maior quantidade de néctar é a localização do extremo global e que essa é a única área com néctar abundante. As abelhas não vivem em um plano, onde apenas duas coordenadas são necessárias para determinar a localização de uma área, mas, sim, em um espaço multidimensional onde cada coordenada representa um parâmetro da função que precisa ser otimizada. A quantidade de néctar encontrada é o valor da função objetivo neste ponto. Se estamos procurando um máximo global, basta maximizar a função objetivo, mas se estamos procurando um mínimo global, basta multiplicar a função objetivo por -1.

Como as áreas de coleta de néctar têm um determinado valor, apenas a área com maior classificação tem o direito de se mover (deslocamento do centro) para o ponto de maior concentração de néctar. As áreas de coleta de néctar têm um determinado valor, então somente a área com a maior classificação tem permissão para se mover (deslocando o centro) em direção ao ponto de maior concentração de néctar. As áreas de classificação inferior serão deslocadas para o centro de maior concentração, mas serão verificadas na interseção com uma área de classificação superior. Isso evita que as abelhas se concentrem em áreas estreitas e reduz a possibilidade de esgotar a fonte de alimento. Em termos de otimização, isso elimina ou minimiza a possibilidade de ficar preso em extremos locais. Depois que as áreas são dispersas e deslocadas ao longo da cadeia de classificação em direção aos seus ótimos, suas vizinhanças serão adicionalmente investigadas por batedores.

Muitos apicultores recomendam o envio de abelhas exploradoras para áreas aleatórias do espaço de busca, mas minha experiência mostra que o valor prático de tal "exploração" é próximo de zero e só é útil em uma e duas dimensões. Quando se trata de espaços multidimensionais, os graus de liberdade aumentam geometricamente, e é incrivelmente difícil tropeçar acidentalmente em uma fonte de néctar mais valiosa, desperdiçando assim os recursos da colmeia. É muito mais útil enviar batedores para áreas de busca já conhecidas, mas não exatamente nelas, mas fora, limitadas pelo raio de reconhecimento. Dessa forma, as coordenadas não estão dispersas, mas concentradas especificamente nas zonas de possíveis fontes de néctar.

Quando as áreas se cruzam, é necessário deslocar o centro para que as áreas toquem apenas nas bordas, como ilustrado na Figura 2.

ABCcrossArea

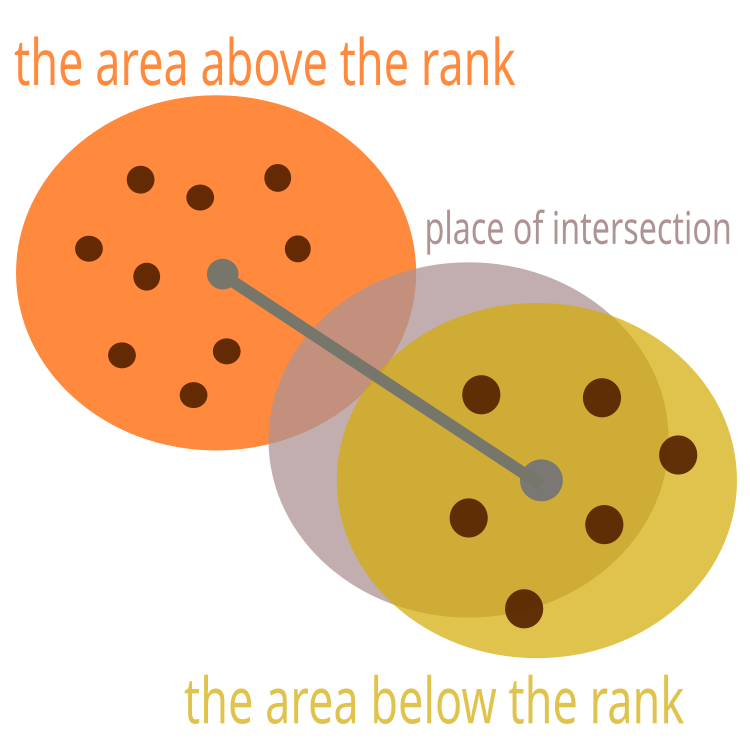
Figura 2. Área abaixo da classificação sendo deslocada

A classificação das áreas não é definida de forma rígida, mas é formada dinamicamente à medida que as abelhas batedoras descobrem novas fontes de néctar. Se uma fonte mais valiosa é encontrada, o centro da área será deslocado para essa nova localização, tornando-se assim o novo melhor centro de coleta de néctar. As demais áreas serão deslocadas em relação a ela ao longo da cadeia de classificação. Dessa forma, o algoritmo se adapta continuamente às mudanças no ambiente, permitindo que as abelhas encontrem as fontes de néctar mais valiosas de forma eficiente e evitando o esgotamento das fontes de alimento.

O método de transmissão de informações, conhecido como a "dança das abelhas", é um elemento crucial na estratégia da colmeia. É necessário distribuir os recursos disponíveis da colmeia de maneira racional para as áreas de processamento, e, portanto, o número de abelhas enviadas deve ser proporcional ao valor da área. Dessa forma, um número equivalente de abelhas será enviado para áreas de valor semelhante.

Vejamos o algoritmo em si. As etapas de execução estão listadas abaixo:

Todas as abelhas voam aleatoriamente pelo espaço de busca como batedoras.
Medimos a quantidade de néctar recebido de cada abelha.
Classificamos as abelhas.
Atribuímos áreas de acordo com as informações sobre a quantidade de néctar das abelhas.
Enviamos abelhas operárias para a área, quanto mais néctar na área, mais abelhas serão enviadas.
Enviamos abelhas batedoras nas proximidades de uma área selecionada aleatoriamente.
Medimos a quantidade de néctar recebido de cada abelha.
Classificamos as áreas pela quantidade de néctar.
Repetimos a etapa 4 até que o critério de parada seja atendido.

Para ver o cenário de maneira simples, vamos fazer um diagrama de blocos do algoritmo, Figura 3.

ABCsceme

Figura 3. Diagrama de blocos do algoritmo.

Vamos descrever com mais detalhes o código do algoritmo de colônia de abelhas.

A unidade lógica elementar e básica do algoritmo é uma abelha, pode ser descrita por uma estrutura. Lembramos que a localização da abelha é dada tanto pelas coordenadas da área em que o néctar foi coletado quanto pela quantidade de néctar. As abelhas da colmeia são representadas por um array, cada uma podendo ser acessada pelo seu índice.

//——————————————————————————————————————————————————————————————————————————————
struct S_Bee
{
  double c []; //coordinates
  int    aInd; //area index
  double n;    //nectar
};
//——————————————————————————————————————————————————————————————————————————————

A segunda unidade lógica principal é a área de coleta de néctar, que é definida pelo centro e pelo ponto de maior concentração de néctar, sendo que a quantidade de néctar presente determina o valor da área. Na região com a classificação mais alta (a primeira da lista), as coordenadas do centro e do ponto de maior concentração de néctar coincidem. No entanto, para as áreas de classificação inferior na lista, eles podem não corresponder, já que foram deslocados. O processo de inicialização da área consiste em zerar o indicador da quantidade de néctar e distribuir as coordenadas para o número correspondente de parâmetros da função que está sendo otimizada.

//——————————————————————————————————————————————————————————————————————————————
struct S_Area
{
  void Init (int coordinatesNumber)
  {
    n = -DBL_MAX;

    ArrayResize (cC, coordinatesNumber);
    ArrayResize (cB, coordinatesNumber);
  }

  double cC   []; //center coordinates
  double cB   []; //best coordinates
  double n;       //nectarAmount
};
//——————————————————————————————————————————————————————————————————————————————

Vamos descrever a dança das abelhas como uma estrutura, cujo array corresponderá ao número de áreas.

//——————————————————————————————————————————————————————————————————————————————
struct S_BeeDance
{
  double start;
  double end;
};
//——————————————————————————————————————————————————————————————————————————————

Vamos descrever a colmeia como uma classe. Nela, serão definidas as áreas de busca, as abelhas, as melhores coordenadas encontradas em todas as iterações e a maior quantidade de néctar encontrada. Além disso, serão definidos todos os métodos necessários para classificar abelhas e áreas (cada uma com sua própria classificação), mover abelhas entre áreas e mover áreas em relação umas às outras. Aqui podemos observar as funções que já são conhecidas pelos algoritmos anteriores: gerar números aleatórios distribuídos uniformemente, escalonar para um intervalo e selecionar um número dentro de um intervalo com um passo.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ABC //Bees Hive
{
  //============================================================================
  public: S_Area areas     []; //nectar collection areas
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: S_Bee  bees      []; //all the bees of the hive
  public: double cB        []; //best coordinates
  public: double nB;           //nectar of the best coordinates

  public: void InitHive (const int    coordinatesP,      //number of opt. parameters
                         const int    beesNumberP,       //bees number
                         const int    workerBeesNumberP, //worker bees number
                         const int    areasNumberP,      //areas number
                         const double collectionRadiusP, //collection radius
                         const double scoutAreaRadiusP); //scout area radius

  public: void TasksForBees ();
  public: void CollectingNectar ();

  //============================================================================
  private: void   BeeFlight      (double &cC [] , S_Bee &bee);
  private: void   ScoutBeeFlight (double &cC [] , S_Bee &bee);
  private: void   MarkUpAreas    ();
  private: void   SortingBees    ();
  private: void   SortingAreas   ();
  private: double SeInDiSp       (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI      (double Min, double Max);
  private: double Scale          (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool Revers);

  private: int    coordinates;      //coordinates number
  private: int    beesNumber;       //the number of all bees
  private: int    workerBeesNumber; //worker bees number
  private: int    areasNumber;      //areas number
  private: S_Bee  beesT       [];   //temporary, for sorting
  private: S_Area areasT      [];   //temporary, for sorting
  private: int    indA        [];   //array for indexes when sorting
  private: double valA        [];   //array for nectar values when sorting
  private: int    indB        [];   //array for indexes when sorting
  private: double valB        [];   //array for nectar values when sorting
  private: double areasRadius [];   //radius for each coordinate
  private: double scoutRadius [];   //scout radius for each coordinate

  private: double collectionRadius;   //collection radius
  private: double scoutAreaRadius;    //scout area radius
  private: double hypersphereRadius;  //hypersphere radius
  private: double distHyperspCenters; //distance hyperspheres centers
  private: double scoutHyperspRadius; //scout hypersphere radius
  private: bool   scouting;           //scouting flag

  private: S_BeeDance beeDance [];    //bee dance
};
//——————————————————————————————————————————————————————————————————————————————

Cada nova otimização deve necessariamente começar com a inicialização da classe, que consiste em redefinir o valor da quantidade de néctar para toda a colmeia e para as abelhas individuais, bem como para as áreas.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::InitHive (const int    coordinatesP,      //number of opt. parameters
                         const int    beesNumberP,       //bees number
                         const int    workerBeesNumberP, //worker bees number
                         const int    areasNumberP,      //areas number
                         const double collectionRadiusP, //collection radius
                         const double scoutAreaRadiusP)  //scout area radius
{
  MathSrand (GetTickCount ());
  scouting = false;
  nB       = -DBL_MAX;

  coordinates      = coordinatesP;
  beesNumber       = beesNumberP;
  workerBeesNumber = workerBeesNumberP;
  areasNumber      = areasNumberP < 3 ? 3 : areasNumberP;

  collectionRadius = collectionRadiusP; //collection radius
  scoutAreaRadius  = scoutAreaRadiusP;  //scout area radius

  ArrayResize (areas,  areasNumber);
  ArrayResize (areasT, areasNumber);
  for (int i = 0; i < areasNumber; i++)
  {
    areas  [i].Init (coordinates);
    areasT [i].Init (coordinates);
  }

  ArrayResize (beeDance, areasNumber);

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);
  ArrayResize (cB,        coordinates);

  ArrayResize (indA, areasNumber);
  ArrayResize (valA, areasNumber);

  ArrayResize (areasRadius, coordinates);
  ArrayResize (scoutRadius, coordinates);
  for (int i = 0; i < coordinates; i++)
  {
    areasRadius [i] = (rangeMax [i] - rangeMin [i]) * collectionRadius;
    scoutRadius [i] = (rangeMax [i] - rangeMin [i]) * scoutAreaRadius;
  }

  double sqr = 0.0;
  for (int i = 0; i < coordinates; i++) sqr += areasRadius [i] * areasRadius [i];
  hypersphereRadius  = MathSqrt (sqr) * collectionRadius;

  distHyperspCenters = hypersphereRadius * 2.0;

  sqr = 0.0;
  for (int i = 0; i < coordinates; i++) sqr += scoutRadius [i] * scoutRadius [i];
  scoutHyperspRadius = MathSqrt (sqr) * scoutAreaRadius;

  ArrayResize (indB, beesNumber);
  ArrayResize (valB, beesNumber);

  ArrayResize (bees,  beesNumber);
  ArrayResize (beesT, beesNumber);
  for (int i = 0; i < beesNumber; i++)
  {
    ArrayResize (bees  [i].c, coordinates);
    ArrayResize (beesT [i].c, coordinates);
    bees  [i].n = -DBL_MAX;
    beesT [i].n = -DBL_MAX;
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método de classe mais simples e aberto é a distribuição de tarefas entre as abelhas. O processo é bastante simples: se as áreas ainda não foram exploradas, o valor do néctar é redefinido para toda a colmeia e as áreas são marcadas. Este método é chamado em cada época até que o valor da função de adaptação seja alcançado.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::TasksForBees ()
{
  if (!scouting)
  {
    nB = -DBL_MAX;
  }
  MarkUpAreas ();
}
//——————————————————————————————————————————————————————————————————————————————

O segundo método público é chamado em cada época para obter o valor da função de adaptação. Se ainda não tivermos explorado todas as áreas, classificamos as abelhas pelo valor do néctar e copiamos as coordenadas e a quantidade de néctar da primeira abelha da lista para as áreas correspondentes em ordem. Se já tivermos explorado as áreas, então copiamos as coordenadas e a quantidade de néctar para a área de onde o néctar foi coletado, desde que os resultados tenham melhorado. Também atualizamos os melhores resultados para toda a colmeia.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::CollectingNectar ()
{
  if (!scouting)
  {
    SortingBees ();

    for (int a = 0; a <areasNumber; a++)
    {
      ArrayCopy (areas [a].cB, bees [a].c, 0, 0, WHOLE_ARRAY);
      areas [a].n = bees [a].n;
    }

    scouting = true;
  }
  else
  {
    //transfer the nectar to the hive---------------------------------------------
    for (int b = 0; b < beesNumber; b++)
    {
      if (bees [b].n > areas [bees [b].aInd].n)
      {
        ArrayCopy (areas [bees [b].aInd].cB, bees [b].c, 0, 0, WHOLE_ARRAY);
        areas [bees [b].aInd].n = bees [b].n;
      }

      if (bees [b].n > nB)
      {
        ArrayCopy (cB, bees [b].c, 0, 0, WHOLE_ARRAY);
        nB = bees [b].n;
      }
    }

    SortingAreas ();
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método MarkUpAreas () é digno de ser considerado em detalhes, vamos esmiuçar o código em partes.

Antes que as áreas sejam exploradas e sem informações sobre locais para coletar néctar, as abelhas de toda a colmeia serão enviadas em busca, realizando um reconhecimento preliminar. Nessa fase, todas as abelhas desempenham o papel de batedoras. Como não há informações sobre a localização do néctar, enviamos as batedoras em direções aleatórias, gerando números aleatórios distribuídos uniformemente no intervalo de coordenadas.

//if the areas is not scouting - send all the bees to scouting----------------
if (!scouting)
{
  for (int b = 0; b < beesNumber; b++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      bees [b].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      bees [b].c [c] = SeInDiSp  (bees [b].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

Após explorar as áreas, é necessário obter as coordenadas da concentração máxima de néctar e mover a área para esse local. No entanto, é importante garantir que a área não se sobreponha a uma classificação superior, o que pode ser verificado medindo a distância entre seus centros. Se a distância for menor que dois raios, as áreas se cruzam e a área é movida para um ponto a uma distância de dois raios. É importante ressaltar que as coordenadas da concentração máxima de néctar permanecem no mesmo local. Esse processo permite que as áreas estejam em constante movimento, o que pode levar a uma fonte de alimento mais rica. Posteriormente, ocorre a triagem no próximo método para determinar as melhores áreas.

for (int s = 0; s < areasNumber; s++)
{
  //move the center of the area to the best point in with more nectar-------
  ArrayCopy (areas [s].cC, areas [s].cB, 0, 0, WHOLE_ARRAY);

  //ordinary area-----------------------------------------------------------
  if (s != 0)
  {
    //check if there is no intersection of a region with a region of higher rank
    //measure the distance from the centers of the regions
    double centersDistance = 0.0;

    for (int c = 0; c < coordinates; c++) centersDistance += pow (areas [s].cC [c] - areas [s - 1].cC [c], 2.0);
    centersDistance = MathSqrt (centersDistance);

    //the areas intersect, then need to move the current area
    if (centersDistance < distHyperspCenters)
    {
      double incrementFactor = (distHyperspCenters - centersDistance) / centersDistance;
      double coordDistance   = 0.0;

      for (int c = 0; c < coordinates; c++)
      {
        coordDistance = areas [s].cC [c] - areas [s - 1].cC [c];
        areas [s].cC [c] = areas [s].cC [c] + (coordDistance * incrementFactor);

        areas [s].cC [c] = SeInDiSp (areas [s].cC [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }
}

Aqui é onde ocorre a dança das abelhas. Com base nas informações sobre a direção e a quantidade de néctar em cada região, utilizamos um componente aleatório para marcar a área de distribuição. Essa marcação é realizada de forma que a probabilidade de uma abelha escolher determinada área na próxima iteração seja proporcional à quantidade de néctar presente nessa área. De maneira mais simples, podemos representar a distribuição em uma linha numérica, na qual são plotados segmentos de comprimento proporcional à diferença entre o valor de néctar de cada área em relação à área com a menor quantidade de néctar.

//send bees to the marked areas-----------------------------------------------
double r = 0.0;

beeDance [0].start = bees [0].n;
beeDance [0].end   = beeDance [0].start + (bees [0].n - bees [areasNumber - 1].n);

for (int a = 1; a < areasNumber; a++)
{
  if (a != areasNumber - 1)
  {
    beeDance [a].start = beeDance [a - 1].end;
    beeDance [a].end   = beeDance [a    ].start + (bees [a].n - bees [areasNumber - 1].n);
  }
  else
  {
    beeDance [a].start = beeDance [a - 1].end;
    beeDance [a].end   = beeDance [a    ].start + (bees [a - 1].n - bees [a].n) * 0.1;
  }
}

Nesta etapa do método, ocorre a seleção aleatória da área com base na probabilidade transmitida pelas danças das abelhas, para as abelhas operárias. Isso é feito gerando um número aleatório em um intervalo determinado pela dança, que é marcada na linha numérica. Para os batedores, as danças não importam, pois eles voam com a mesma probabilidade para as proximidades de todas as áreas, expandindo assim as capacidades de busca da estratégia de abelhas da colmeia como um todo. Assim como na natureza, cada participante da colmeia desempenha um papel importante e possui um valor específico.

for (int b = 0; b < beesNumber; b++)
{
  if (b < workerBeesNumber)
  {
    r = RNDfromCI(beeDance [0].start, beeDance [areasNumber - 1].end);
        
    for (int a = 0; a < areasNumber; a++)
    {
      if (beeDance [a].start <= r && r < beeDance [a].end)
      {
        bees [b].aInd = a;
        break;
      }
    }

    BeeFlight (areas [bees [b].aInd].cC, bees [b]);
  }
  else
  {
    //choose the area to send the bees there
    r = RNDfromCI (0.0, areasNumber - 1);

    bees [b].aInd = (int)r; //area index

    ScoutBeeFlight (areas [bees [b].aInd].cC, bees [b]);
  }
}

Esse método privado implementa o voo de uma abelha, que é simples, apesar de parecer complicado à primeira vista. A abelha voa em direção a uma área com um deslocamento de probabilidade cúbica mais próximo do centro, em que a probabilidade diminui do centro em direção às bordas da região. Vale ressaltar que esse centro é o centro da área, e não a melhor posição encontrada anteriormente. Essa simples ação ilustra a estratégia da abelha em busca contínua de novas fontes de alimento, o que garante uma busca eficiente e contínua por recursos.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::BeeFlight (double &cC [] , S_Bee &bee)
{
  double r = 0.0;

  for (int c = 0; c < coordinates; c++)
  {
    r  = RNDfromCI (0.0, 1.0);
    r  = r * r * r;
    r = Scale (r, 0.0, 1.0, 0.0, areasRadius [c], false);
    r *= RNDfromCI (0.0, 1.0) > 0.5 ? 1.0 : -1.0;

    bee.c [c] = SeInDiSp  (cC [c] + r, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Ao contrário do método anterior, neste método descrevemos o voo de uma abelha exploradora. A abelha voa para fora da área dentro do raio especificado nas configurações do algoritmo. Embora a configuração seja a mesma, os raios são calculados antecipadamente quando a classe é inicializada, pois as áreas podem ter faixas de coordenadas diferentes, portanto os raios serão ajustados de acordo. Para lançar uma abelha exploradora em voo, é necessário gerar um número aleatório no intervalo de um raio de área até a soma do raio de área e o raio de exploração e, em seguida, adicionar simplesmente o valor resultante ao centro da área. Dessa forma, a abelha exploradora estará nas proximidades da área por acaso, enquanto as coordenadas não se espalham pelo espaço de busca. Essa estratégia permite que a colmeia busque além das áreas já conhecidas, aumentando as chances de encontrar novas fontes de alimento.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::ScoutBeeFlight (double &cC [] , S_Bee &bee)
{
  double r = 0.0;

  for (int c = 0; c < coordinates; c++)
  {
    r  = RNDfromCI (areasRadius [c], areasRadius [c] + scoutRadius [c]);
    r *= RNDfromCI (0.0, 1.0) > 0.5 ? 1.0 : -1.0;

    bee.c [c] = SeInDiSp  (cC [c] + r, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Existem dois métodos específicos no algoritmo - a classificação de abelhas e a classificação de área. Embora sejam simples, esses métodos são cruciais para a otimização da estratégia da colmeia. O método de classificação de bolha é amplamente utilizado em algoritmos de otimização por sua simplicidade e facilidade de adaptação a diferentes tarefas. Além disso, esse método oferece uma das melhores velocidades entre todos os métodos de classificação.

//——————————————————————————————————————————————————————————————————————————————
//Sorting of bees
void C_AO_ABC::SortingBees ()
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//Sorting of areas
void C_AO_ABC::SortingAreas ()
//——————————————————————————————————————————————————————————————————————————————

Com o código completo, é hora de compilar o algoritmo. Ao executar o banco de testes, é possível observar as animações que mostram o comportamento das abelhas em áreas separadas e deslocadas. As abelhas são claramente observadas em áreas separadas, é claro como as áreas são deslocadas, substituindo-se umas às outras. A precisão e a quantidade de "enxames" peculiares podem ser ajustadas de acordo com as configurações do algoritmo.

Skin

ABC na função de teste Skin.

Forest

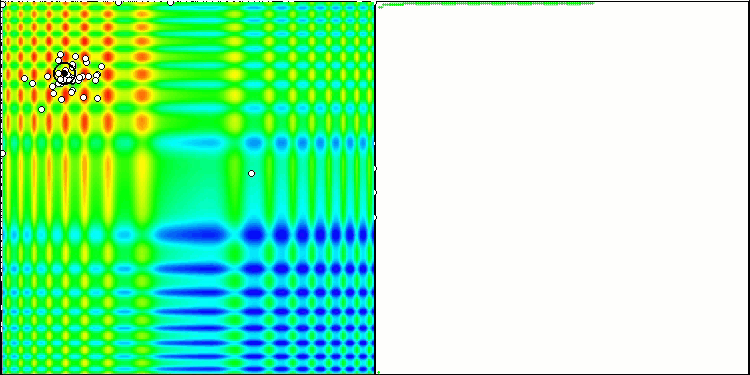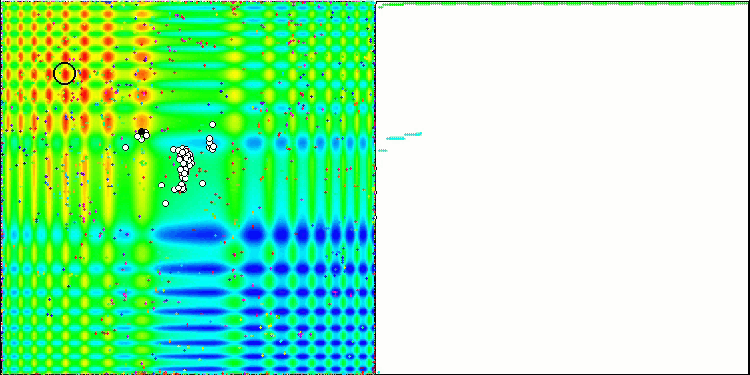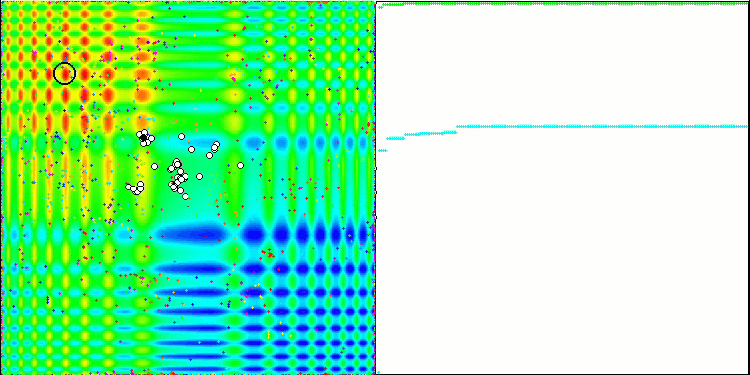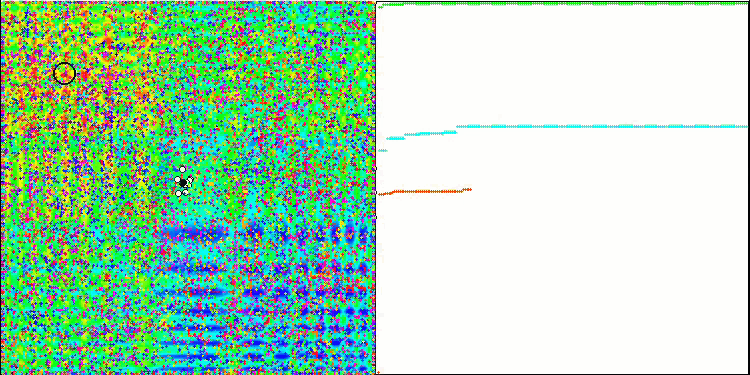
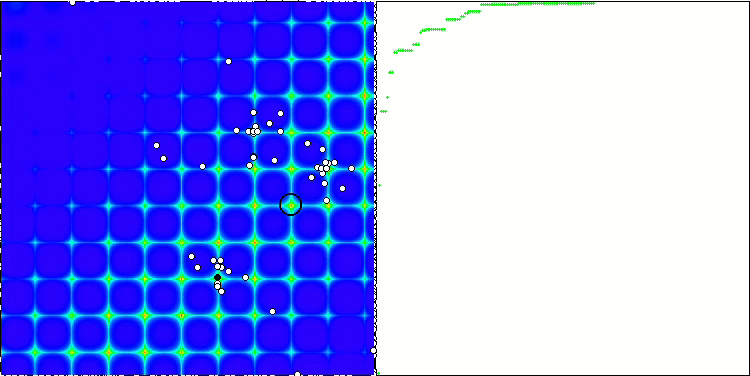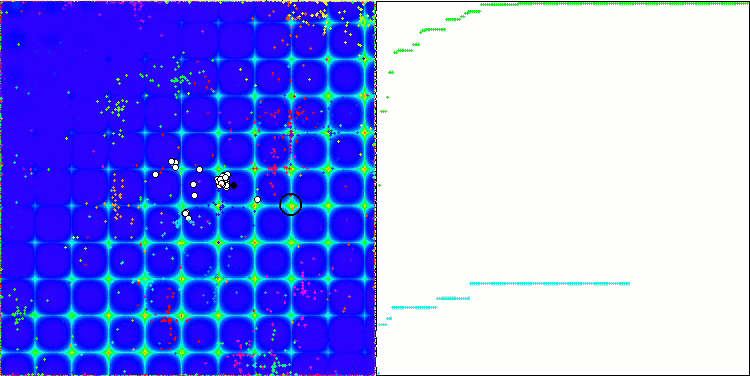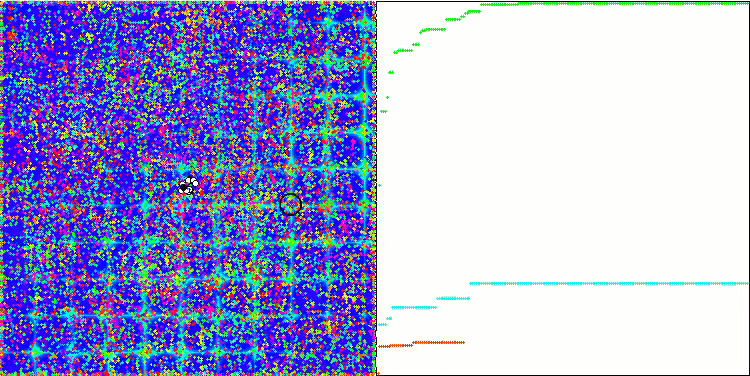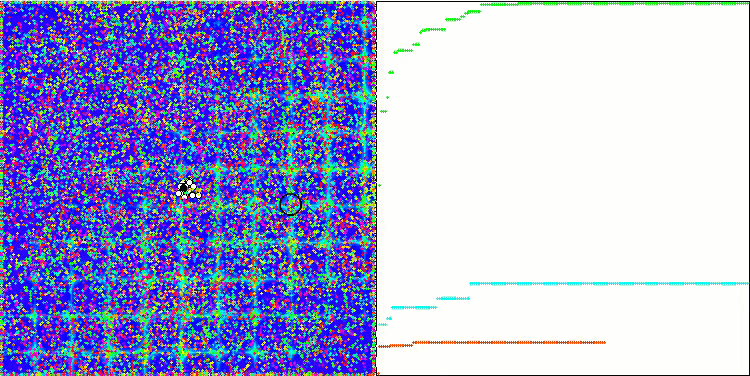
ABC na função de teste Forest.

Magacity

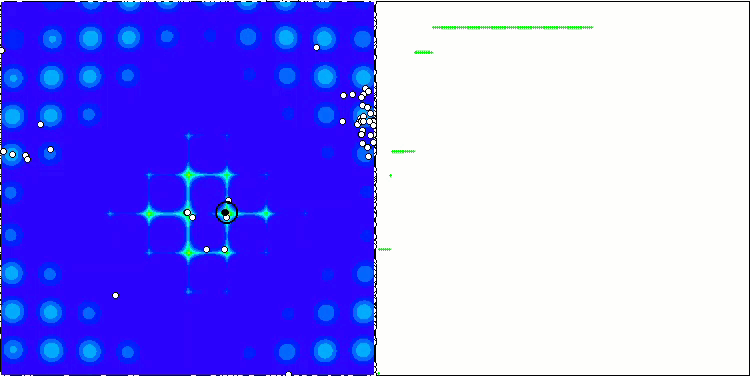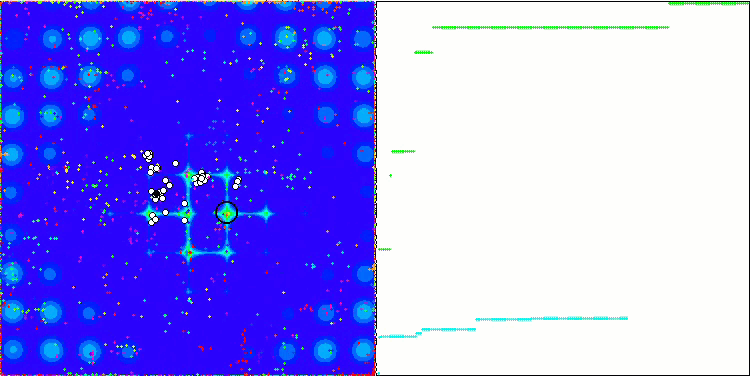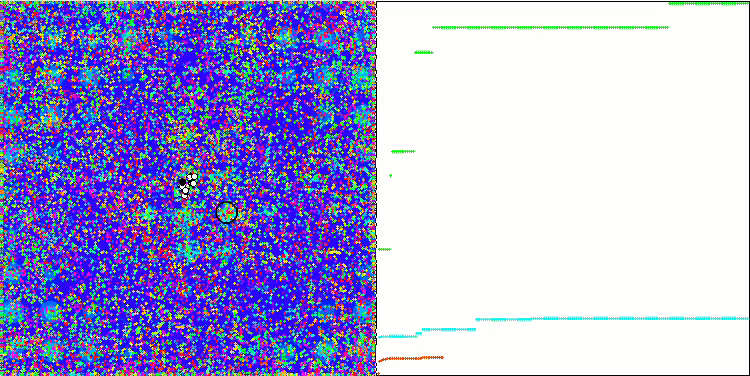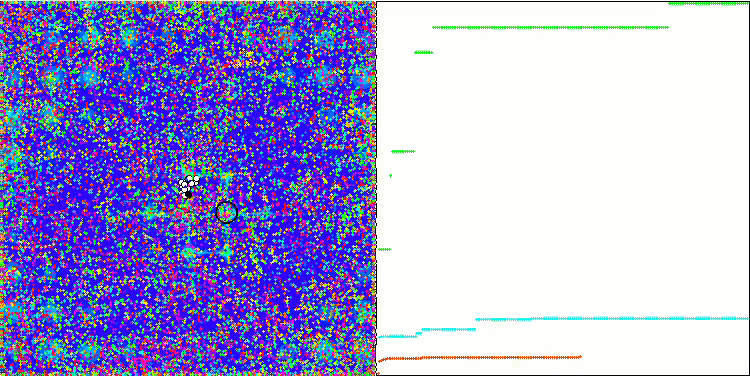
ACO na função de teste Megacity.

Aqui estão nossos resultados do algoritmo em funções de teste:

2022.11.21 13:14:06.669    Test_AO_ABC1 (EURUSD,M1)    =============================
2022.11.21 13:14:28.483    Test_AO_ABC1 (EURUSD,M1)    1 Skin's; Func runs 1000 result: 14.018634225602678; Func runs 10000 result: 14.06060189007221
2022.11.21 13:14:28.483    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.99772; Score2: 1.00000
2022.11.21 13:14:50.310    Test_AO_ABC1 (EURUSD,M1)    20 Skin's; Func runs 1000 result: 7.459929501115262; Func runs 10000 result: 8.320771456653533
2022.11.21 13:14:50.310    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.64085; Score2: 0.68769
2022.11.21 13:15:30.049    Test_AO_ABC1 (EURUSD,M1)    500 Skin's; Func runs 1000 result: 4.69267387794685; Func runs 10000 result: 4.838631770950824
2022.11.21 13:15:30.049    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.49029; Score2: 0.49823
2022.11.21 13:15:30.049    Test_AO_ABC1 (EURUSD,M1)    =============================
2022.11.21 13:15:51.880    Test_AO_ABC1 (EURUSD,M1)    1 Forest's; Func runs 1000 result: 15.063567301715784; Func runs 10000 result: 15.912087696850861
2022.11.21 13:15:51.880    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.94435; Score2: 0.99755
2022.11.21 13:16:13.721    Test_AO_ABC1 (EURUSD,M1)    20 Forest's; Func runs 1000 result: 3.0207584941876133; Func runs 10000 result: 4.1918977577943295
2022.11.21 13:16:13.721    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.18937; Score2: 0.26279
2022.11.21 13:17:01.467    Test_AO_ABC1 (EURUSD,M1)    500 Forest's; Func runs 1000 result: 1.2004991531402736; Func runs 10000 result: 1.288357831462411
2022.11.21 13:17:01.467    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.07526; Score2: 0.08077
2022.11.21 13:17:01.467    Test_AO_ABC1 (EURUSD,M1)    =============================
2022.11.21 13:17:23.227    Test_AO_ABC1 (EURUSD,M1)    1 Megacity's; Func runs 1000 result: 10.4; Func runs 10000 result: 15.0
2022.11.21 13:17:23.227    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.69333; Score2: 1.00000
2022.11.21 13:17:44.936    Test_AO_ABC1 (EURUSD,M1)    20 Megacity's; Func runs 1000 result: 1.5499999999999998; Func runs 10000 result: 2.31
2022.11.21 13:17:44.936    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.10333; Score2: 0.15400
2022.11.21 13:18:29.588    Test_AO_ABC1 (EURUSD,M1)    500 Megacity's; Func runs 1000 result: 0.6180000000000001; Func runs 10000 result: 0.6568
2022.11.21 13:18:29.588    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.04120; Score2: 0.04379
2022.11.21 13:18:29.588    Test_AO_ABC1 (EURUSD,M1)    =============================
2022.11.21 13:18:29.588    Test_AO_ABC1 (EURUSD,M1)    All score for C_AO_ABC: 0.49447371765340953

A partir da impressão dos resultados, é possível observar que o algoritmo convergiu a 100% para as duas funções de teste com duas variáveis, o que é um excelente indicador de convergência. No entanto, é preciso analisar os demais resultados antes de tirar conclusões definitivas. Para tanto, é recomendável inserir os resultados em uma tabela e compará-los com os obtidos por outros algoritmos de otimização.

3. Versão modificada

Gostaria de falar sobre um aspecto interessante. Ao desenvolver e projetar qualquer algoritmo de otimização, surge sempre a dúvida: "O algoritmo está funcionando conforme o planejado ou há um erro em algum lugar no código?". O processo de busca estocástica é aleatório por natureza, tornando difícil determinar se os resultados da otimização foram gerados pelo algoritmo ou se algum erro fez com que os resultados fossem não aleatórios. Durante o desenvolvimento do algoritmo da colônia de abelhas, encontrei um fenômeno semelhante. No decorrer do primeiro teste de um conjunto de cinco, o algoritmo ficou preso nos locais iniciais de busca, sem tentar convergir. O interessante é que o problema foi resolvido de uma forma surpreendentemente lógica. Foi suficiente inicializar a classe colmeia uma segunda vez adicional na primeira época, mesmo que a classe já tivesse sido pré-inicializada antes do início das épocas (p. 142 no arquivo Test_AO_ABC.mq5). Se alguém puder explicar esse mistério, ficarei feliz em ouvir a solução nos comentários do artigo.

Parte dos resultados insatisfatórios dos primeiros testes e, também, dos problemas já mencionados, me levaram a repensar a estratégia de busca das abelhas. Na versão original do algoritmo, as abelhas se moviam proporcionalmente ao valor da área, o que foi alterado para que houvesse um número fixo de abelhas em cada área. Em outras palavras, independentemente do nível de classificação da área, cada uma delas sempre teria o mesmo número de abelhas. Isso transformou logicamente a área no conceito de "enxame de abelhas".

Agora, em vez da estrutura da área, teremos essa estrutura:

//——————————————————————————————————————————————————————————————————————————————
struct S_BeesSwarm
{
  void Init (int coordinatesNumber, int beesNumber)
  {
    ArrayResize (bees, beesNumber);

    for (int i = 0; i < beesNumber; i++)
    {
      ArrayResize (bees [i].c, coordinatesNumber);
      bees [i].n = -DBL_MAX;
    }

    n = -DBL_MAX;

    ArrayResize     (cC, coordinatesNumber);
    ArrayInitialize (cC, -DBL_MAX);
  }

  S_Bee  bees []; //bees
  double cC   []; //center coordinates
  double cB   []; //best coordinates
  double n;       //nectarAmount
};
//——————————————————————————————————————————————————————————————————————————————

Essa estrutura também possui uma função de inicialização, mas adicionalmente existe um array de abelhas bees[].

Em geral, o restante do código é bastante similar à versão clássica e, portanto, não deve ser o foco principal. O código será anexado ao artigo no arquivo para consulta. No entanto, é importante prestar atenção especial às diferenças na lógica dos algoritmos. O passo a passo da implementação do algoritmo modificado pode ser descrito da seguinte maneira:

Criar um centro para o primeiro enxame e posicionar as abelhas nas proximidades do centro.
Criar um centro para os enxames subsequentes e verificar se a distância do centro para os enxames anteriores é maior ou igual a 2R (dois raios), posicionar as abelhas nas proximidades do centro.
Enviar abelhas exploradoras para cada enxame de forma que cada abelha esteja mais distante dos outros enxames por uma distância maior ou igual a R (raio).
Obter o valor da função de aptidão para todas as abelhas.
Classificar os enxames.
Posicionar as abelhas nas proximidades do centro de cada enxame.
Repetir a partir do passo 4 até que um critério de parada seja atendido.

É possível notar uma diferença fundamental na estratégia de busca adotada. Enquanto na versão clássica cada área pode ter um número diferente de abelhas, na nova versão todas as áreas são exploradas por enxames de tamanho igual. Essa mudança visa garantir que as áreas sejam exploradas a fundo mesmo quando a fonte de alimento se esgota, ampliando a exploração da superfície no hiperespaço. Os testes realizados confirmaram a efetividade dessa abordagem, já que os resultados melhoraram consideravelmente. As abelhas batedoras, assim como na versão clássica, não voam próximas às áreas exploradas e sim em áreas ainda não exploradas. É importante notar que na versão clássica, as abelhas batedoras não se comportam de acordo com as regras de áreas, pois se espalham aleatoriamente, sem se preocupar em entrar em áreas já exploradas, o que prejudica sua função básica de pesquisa. O último enxame na matriz é o enxame batedor, no qual a regra de não invadir o espaço de outras abelhas é aplicada individualmente às abelhas batedoras.

Prints dos resultados da versão modificada:

2022.11.21 21:53:19.695    Test_AO_ABCm (EURUSD,M1)    =============================
2022.11.21 21:53:25.104    Test_AO_ABCm (EURUSD,M1)    1 Skin's; Func runs 1000 result: 14.009060385607679; Func runs 10000 result: 14.060603974847265
2022.11.21 21:53:25.104    Test_AO_ABCm (EURUSD,M1)    Score1: 0.99720; Score2: 1.00000
2022.11.21 21:53:30.452    Test_AO_ABCm (EURUSD,M1)    20 Skin's; Func runs 1000 result: 7.826824877236677; Func runs 10000 result: 8.735832346695558
2022.11.21 21:53:30.452    Test_AO_ABCm (EURUSD,M1)    Score1: 0.66082; Score2: 0.71028
2022.11.21 21:53:40.060    Test_AO_ABCm (EURUSD,M1)    500 Skin's; Func runs 1000 result: 4.645933304640949; Func runs 10000 result: 4.844246724239038
2022.11.21 21:53:40.060    Test_AO_ABCm (EURUSD,M1)    Score1: 0.48774; Score2: 0.49853
2022.11.21 21:53:40.060    Test_AO_ABCm (EURUSD,M1)    =============================
2022.11.21 21:53:45.363    Test_AO_ABCm (EURUSD,M1)    1 Forest's; Func runs 1000 result: 15.44507700105064; Func runs 10000 result: 15.662273922787355
2022.11.21 21:53:45.363    Test_AO_ABCm (EURUSD,M1)    Score1: 0.96827; Score2: 0.98188
2022.11.21 21:53:50.697    Test_AO_ABCm (EURUSD,M1)    20 Forest's; Func runs 1000 result: 3.6397442648278924; Func runs 10000 result: 4.759146560755886
2022.11.21 21:53:50.697    Test_AO_ABCm (EURUSD,M1)    Score1: 0.22818; Score2: 0.29836
2022.11.21 21:54:01.111    Test_AO_ABCm (EURUSD,M1)    500 Forest's; Func runs 1000 result: 1.2349621811342104; Func runs 10000 result: 1.4191098624570897
2022.11.21 21:54:01.111    Test_AO_ABCm (EURUSD,M1)    Score1: 0.07742; Score2: 0.08897
2022.11.21 21:54:01.112    Test_AO_ABCm (EURUSD,M1)    =============================
2022.11.21 21:54:06.434    Test_AO_ABCm (EURUSD,M1)    1 Megacity's; Func runs 1000 result: 12.0; Func runs 10000 result: 15.0
2022.11.21 21:54:06.434    Test_AO_ABCm (EURUSD,M1)    Score1: 0.80000; Score2: 1.00000
2022.11.21 21:54:11.768    Test_AO_ABCm (EURUSD,M1)    20 Megacity's; Func runs 1000 result: 1.7; Func runs 10000 result: 2.35
2022.11.21 21:54:11.768    Test_AO_ABCm (EURUSD,M1)    Score1: 0.11333; Score2: 0.15667
2022.11.21 21:54:22.235    Test_AO_ABCm (EURUSD,M1)    500 Megacity's; Func runs 1000 result: 0.572; Func runs 10000 result: 0.67
2022.11.21 21:54:22.235    Test_AO_ABCm (EURUSD,M1)    Score1: 0.03813; Score2: 0.04467
2022.11.21 21:54:22.235    Test_AO_ABCm (EURUSD,M1)    =============================
2022.11.21 21:54:22.235    Test_AO_ABCm (EURUSD,M1)    All score for C_AO_ABCm: 0.508357869056105

Ao analisar os resultados obtidos com o algoritmo modificado, pode-se notar que ele obteve sucesso novamente nas duas funções com duas variáveis, apresentando uma taxa de convergência de 100%. De maneira geral, houve uma melhoria nos resultados, com a pontuação final chegando a 0.50836. Entretanto, é importante ressaltar que ainda não foi alcançada uma melhoria significativa em problemas de convergência com um grande número de variáveis, os quais apresentaram resultados comparáveis à versão clássica da implementação do algoritmo.

A propósito, não foi identificado nenhum erro que exigisse a reinicialização da colmeia na versão modificada.

4. Resultado dos testes

AO	Runs	Skin			Forest			Megacity (discrete)			Final result
AO	Runs	2 params (1 F)	40 params (20 F)	1000 params (500 F)	2 params (1 F)	40 params (20 F)	1000 params (500 F)	2 params (1 F)	40 params (20 F)	1000 params (500 F)	Final result
ACOm	1000	0,99502	0,69826	0,50498	0,99087	0,22374	0,08408	0,78667	0,11667	0,04224	0,54688
ACOm	10000	0,99599	0,86403	0,58800	0,99302	0,65571	0,17442	0,78667	0,26133	0,08208	0,54688
RND	1000	0,98744	0,61852	0,49408	0,89582	0,19645	0,14042	0,77333	0,19000	0,14283	0,51254
RND	10000	0,99977	0,69448	0,50188	0,98181	0,24433	0,14042	0,88000	0,20133	0,14283	0,51254
ABCm	1000	0,99720	0,66082	0,48774	0,96827	0,22818	0,07742	0,80000	0,11333	0,03813	0,50836
ABCm	10000	1,00000	0,71028	0,49853	0,98188	0,29836	0,08897	1,00000	0,15667	0,04467	0,50836
ABC	1000	0,99772	0,64085	0,49029	0,94435	0,18937	0,07526	0,69333	0,10333	0,04120	0,49447
ABC	10000	1,00000	0,68769	0,49823	0,99755	0,26279	0,08077	1,00000	0,15400	0,04379	0,49447
PSO	1000	0,98436	0,72243	0,65483	0,71122	0,15603	0,08727	0,53333	0,08000	0,04085	0,47695
PSO	10000	0,99836	0,72329	0,65483	0,97615	0,19640	0,09219	0,82667	0,10600	0,04085	0,47695

Vamos fazer um resumo do que foi apresentado. O algoritmo da colônia de abelhas mostrou surpreendentes 100% de convergência em todos os cinco testes realizados em duas funções de teste: Smooth Skin e Discrete Megacity. Esse resultado demonstra uma velocidade e qualidade de convergência fenomenais, porém, é importante notar que isso se aplica apenas a funções com duas variáveis. Quando se trata de escalabilidade, o algoritmo se mostra inferior em relação aos outros algoritmos avaliados na tabela. Funções com muitas variáveis apresentam dificuldade para serem resolvidas com uma colônia de abelhas, o que é evidenciado tanto na animação da bancada de testes quanto nos resultados da tabela.

O algoritmo ABC requer que o usuário ajuste várias parâmetros, incluindo o tamanho do enxame, o número de batedores e os raios de busca das áreas. Se essas configurações não forem definidas adequadamente para um aplicativo específico, o algoritmo pode convergir precocemente ou falhar em convergir. Além disso, o ABC apresenta desvantagens, como convergência lenta em funções complexas, captura de soluções locais e baixa qualidade na busca.

Prós:
1. Relativamente rápido.
2. Convergência fenomenal para funções suaves e discretas com poucas variáveis.

Contras:
1. Forte influência dos parâmetros do algoritmo no resultado.
2. Não universal.
3. Bloqueio em extremos locais.
4. Escalabilidade média.

Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/11736

Arquivos anexados |

Baixar como ZIP

94_The_world_of_AO_qABCn.zip (44.93 KB)

Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.

Outros artigos do autor

Ir para discussão

Aprendendo a construindo um Expert Advisor que opera de forma automática (Parte 15): Automação (VII)

Para coroar esta sequencia de automação. Vamos complementar o que foi visto no artigo anterior. Este definitivamente mostra como tudo irá se encaixar, fazendo o Expert Advisor, funcionar como um relógio.

DoEasy. Controles (Parte 26): Apurando o objeto WinForms "ToolTip" e desenvolvendo o "ProgressBar".

Neste artigo vamos completar o desenvolvimento do controle ToolTip e começar a desenvolver o objeto WinForms ProgressBar. Ao trabalharmos nesses objetos, desenvolveremos uma funcionalidade versátil para animar os controles e seus componentes.

Algoritmos de otimização populacionais: Otimizador lobo-cinzento (GWO)

Vamos falar sobre um dos algoritmos de otimização mais recentes e modernos: o "Packs of grey wolves" (manada de lobos-cinzentos). Devido ao seu comportamento distinto em funções de teste, este algoritmo se torna um dos mais interessantes em comparação com outros considerados anteriormente. Ele é um dos principais candidatos para treinamento de redes neurais e para otimizar funções suaves com muitas variáveis.

Redes neurais de maneira fácil (Parte 32): Aprendizado Q distribuído

Em um dos artigos desta série, já nos iniciamos no método aprendizado Q, que calcula a média da recompensa para cada ação. Em 2017, foram apresentados 2 trabalhos simultâneos, que tiveram sucesso quanto ao estudo da função de distribuição de recompensas. Vamos considerar a possibilidade de usar essa tecnologia para resolver nossos problemas.