
Algoritmo de otimização baseado em ecossistema artificial — Artificial Ecosystem-based Optimization (AEO)
Conteúdo
Introdução
No campo da otimização e da inteligência artificial, há uma busca constante por métodos novos e mais eficazes para resolver problemas complexos. Uma dessas abordagens inovadoras é o algoritmo de otimização baseado em ecossistema artificial (Artificial Ecosystem-based Optimization, AEO), desenvolvido em 2019. Inspirado em ecossistemas naturais, esse método imita interações e processos complexos que ocorrem no ambiente natural.
O algoritmo AEO se baseia em vários princípios fundamentais observados na natureza. Assim como há muitas espécies em um ecossistema, cada uma adaptada ao seu nicho ecológico, o AEO utiliza uma população de soluções diversas. Nesse contexto, cada solução pode ser vista como uma espécie distinta, com características únicas e capacidade de adaptação.
Na natureza, a energia é transferida de um organismo para outro por meio das cadeias alimentares. No AEO, isso é modelado por meio da interação entre diferentes tipos de "agentes", que vão desde "grama" até "onívoros". Aqui, a informação, análoga à energia, é transferida entre as soluções, contribuindo para a melhoria da qualidade geral da população. Os ecossistemas são caracterizados tanto pela competição por recursos quanto por relações simbióticas. O algoritmo AEO reflete esses processos por meio de estratégias de atualização das soluções, nas quais os agentes podem "competir" pelas melhores posições ou "colaborar", trocando informações.
Alterações cíclicas também estão presentes nos ecossistemas naturais e no AEO. O processo iterativo de otimização inclui fases alternadas de consumo e decomposição, permitindo que o algoritmo se adapte à dinâmica da tarefa. Na natureza, eventos aleatórios, como mutações e catástrofes naturais, coexistem com processos determinísticos, como a seleção natural. O AEO utiliza tanto elementos estocásticos (por exemplo, distribuição de Lévy) quanto regras determinísticas para a atualização das soluções, garantindo um equilíbrio entre a exploração de novas regiões e a exploração das já descobertas.
Para entender melhor como os processos naturais se refletem no algoritmo AEO, vejamos alguns exemplos concretos. Na savana africana, a energia se desloca da grama para as zebras (herbívoros), depois para os leões (predadores) e, por fim, para as hienas (necrófagos). No AEO, a informação sobre as melhores soluções é transferida da "grama" (a pior solução) para os "herbívoros" (soluções intermediárias) e "predadores" (melhores soluções), contribuindo para a melhoria da qualidade geral da população.
Quando os organismos morrem, eles se decompõem, devolvendo nutrientes ao ecossistema. Por exemplo, folhas caídas em uma floresta se decompõem, enriquecendo o solo e servindo de alimento para novas plantas. No AEO, a etapa de decomposição do algoritmo imita esse processo. Após a fase de consumo (atualização das soluções), segue-se a fase de decomposição, na qual a informação dos indivíduos atuais "se decompõe" e se espalha por todo o espaço de busca. Isso permite que o algoritmo explore novas regiões e evite ficar preso em ótimos locais. No algoritmo, isso é implementado por meio da aplicação da distribuição gaussiana às soluções atuais em relação à melhor solução global (que atua como o decompositor), o que pode ser interpretado como "decomposição" e "redistribuição" da informação no espaço de busca.
Assim, o algoritmo AEO representa uma síntese elegante entre os princípios naturais e a otimização matemática. Ele não só oferece um método eficaz para resolver problemas complexos, como também proporciona uma nova perspectiva sobre a conexão entre os processos naturais e a inteligência artificial. A seguir, examinaremos em detalhes a estrutura e os mecanismos de funcionamento desse algoritmo para compreender melhor seu potencial e aplicação.
Implementação do algoritmo
Todo o ecossistema é composto por organismos numerados simbolicamente de 1 até Xn. O número 1 representa a "grama", que possui a energia máxima (valor mínimo da função de fitness), enquanto o número Xn representa um saprófago, que cumpre a função de decomposição (energia mínima, valor máximo da função de fitness). Na figura, as setas indicam as direções da alimentação: a grama (número 1) pode usar apenas os produtos da atividade dos saprófagos, os herbívoros (número 2) se alimentam da grama,
e os organismos numerados como 2, 4 e 5 podem ser herbívoros (consomem apenas grama), carnívoros (se alimentam apenas de organismos cuja energia seja inferior à sua) ou onívoros (consomem tanto grama quanto organismos com energia superior). No topo do ecossistema estão os saprófagos, que decompõem todos os organismos ao final de seu ciclo de vida.
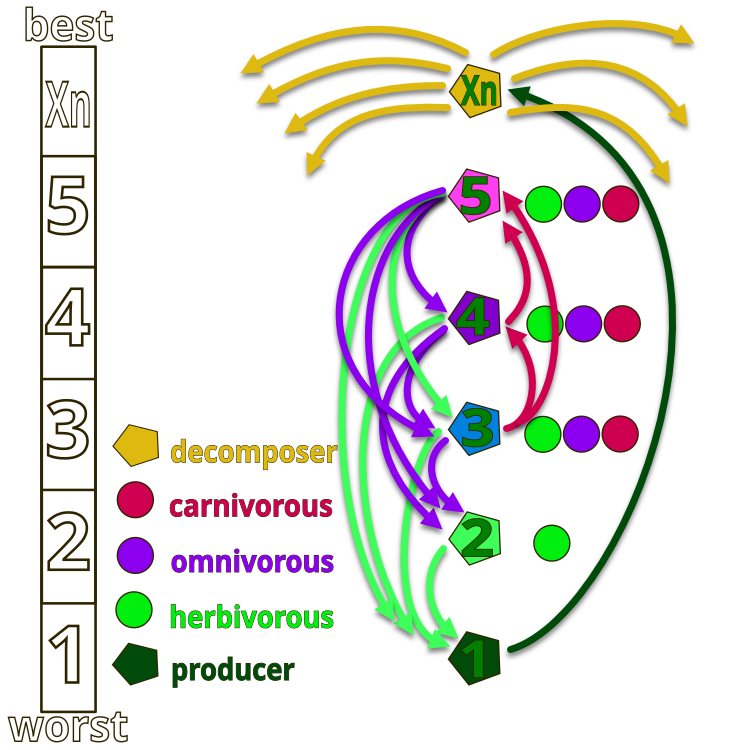
Figura 1. Hierarquia dos organismos em um ecossistema artificial do algoritmo AEO
A ideia central do algoritmo é modelar as interações entre os componentes de um ecossistema para resolver problemas de otimização. Ele se baseia em três princípios fundamentais observados na natureza:
1. Produção – na natureza, os produtores, como as plantas, transformam energia solar em compostos orgânicos.
2. Consumo – os consumidores (herbívoros, predadores, onívoros) utilizam a energia produzida por outros, especialmente pelas plantas.
3. Decomposição – os saprófagos decompõem substâncias orgânicas complexas em formas simples, o que é modelado no algoritmo como a decomposição das soluções.
Princípios de funcionamento do algoritmo:
1. Inicialização – é criada uma população inicial de soluções, representando o ecossistema.
2. Produção – a cada iteração, a pior solução é atualizada considerando a melhor e um fator aleatório.
3. Consumo – as demais soluções são atualizadas utilizando três estratégias:
- Herbívoros: são atualizados com base no produtor.
- Predadores: são atualizados com base em uma melhor solução escolhida aleatoriamente.
- Onívoros: são atualizados com base tanto no produtor quanto em uma solução aleatória.
4. Decomposição – todas as soluções passam por um processo de "decomposição", o que melhora a busca global.
5. Seleção – apenas as soluções melhoradas são mantidas, garantindo a melhoria gradual da população.
Assim, o algoritmo se apoia no mecanismo de transferência de energia entre organismos vivos, o que ajuda a manter a estabilidade das espécies por meio de três operadores: produção, consumo e decomposição.
1. Produção – o pior indivíduo da população "X1" é atualizado com base no melhor "Xn", somado a uma coordenada aleatória "Xrand" gerada dentro de um intervalo definido, criando um novo indivíduo por meio do operador de produção. Representação matemática: X1 (t + 1) = (1 - a) * Xn (t) + a * Xrand (t), onde a = (1 - t / T) * r1 (t é a época atual, T é o número total de épocas), r1 é um número aleatório [0; 1]. Neste caso, o componente "r1" pode ser omitido, pois já estamos utilizando uma coordenada aleatória na fórmula.
2. Consumo – um consumidor escolhido aleatoriamente pode "consumir" o produtor para obter energia. O fator de consumo C é definido como: C = 1/2 * (v1 / |v2|), onde v1 e v2 são números aleatórios uniformemente distribuídos no intervalo [0; 1].
- Herbívoros: Xi (t + 1) = Xi (t) + C * (Xi (t) - X1 (t)).
- Predadores: Xi (t + 1) = Xi (t) + C * (Xi (t) - Xj (t)).
- Onívoros: Xi (t + 1) = Xi (t) + C * (r2 * Xi (t) + (1 - r2) * Xj (t)).
3. Decomposição – o saprófago decompõe os restos dos indivíduos mortos, fornecendo nutrientes para os produtores. A atualização da posição dos indivíduos após a ação do saprófago é descrita como:
Xi (t + 1) = Xn (t) + D * (e * Xn (t) - h * Xi (t)), onde D = 3u, u ~ N (0, 1), e = r3 * rand(i), h = 2 * r3 - 1 (r3 é um número aleatório no intervalo [0; 1]).
Inicialmente, é gerada uma população aleatória, e a posição do primeiro indivíduo é atualizada a cada iteração utilizando a equação do item 1. As posições dos demais indivíduos são atualizadas escolhendo-se, com probabilidade igual, entre as equações do item 2. Na fase de decomposição, cada indivíduo atualiza sua posição utilizando a equação do item 3, e esse processo continua até que um critério satisfatório de parada seja alcançado. Por fim, o passo final retorna o melhor indivíduo encontrado até aquele momento.
Agora podemos compor o pseudocódigo do algoritmo AEO:
Algoritmo AEO (Artificial Ecosystem-based Optimization)
Inicialização:
Definir o tamanho da população (popSize)
Definir o número de épocas (epochs)
Definir o parâmetro da distribuição de Lévy (levisPower)
Inicializar a população com soluções aleatórias dentro do intervalo especificado
Avaliar a função de fitness para cada solução
Encontrar a melhor solução global cB
Para cada época de 1 até epochs:
// Fase de consumo
Para cada agente i na população:
Se i == 0:
Aplicar distribuição gaussiana à solução atual
Caso contrário, se i == popSize - 1:
Aplicar o comportamento da grama (GrassBehavior)
Caso contrário:
Escolher aleatoriamente um comportamento:
- Comportamento de herbívoro (HerbivoreBehavior)
- Comportamento de carnívoro (CarnivoreBehavior)
- Comportamento de onívoro (OmnivoreBehavior)
// Fase de decomposição
Para cada agente i na população:
Para cada coordenada c:
Escolher aleatoriamente um agente j
Calcular a distância D entre cB[c] e a[j].c[c]
Atualizar a[i].c[c] utilizando distribuição gaussiana
// Revisão
Avaliar a função de fitness de cada agente
Atualizar a melhor solução pessoal de cada agente
Atualizar a melhor solução global cB
Ordenar a população de acordo com o valor da função de fitness
Retornar a melhor solução encontrada cB
Sub-rotinas:
GrassBehavior (agente):
α = (1 - época_atual / total_de_épocas)
Para cada coordenada c:
Xr = valor aleatório no intervalo [min[c], max[c]]
Xn = cB[c]
X1 = Xn + α * (Xn - Xr)
agente.c[c] = X1 (respeitando os limites)
HerbivoreBehavior (agente, indice_coordenada):
Xi = agente.cB[indice_coordenada]
X1 = pior solução da população para essa coordenada
C = número aleatório gerado pela distribuição de Lévy (levisPower)
Xi = Xi + C * (Xi - X1)
agente.c[indice_coordenada] = Xi (respeitando os limites)
CarnivoreBehavior (agente, indice_agente, indice_coordenada):
Xi = agente.cB[coordenada]
j = índice aleatório < indice_agente
Xj = a[j].cB[indice_coordenada]
C = número aleatório gerado pela distribuição de Lévy (levisPower)
Xi = Xi + C * (Xj - Xi)
agente.c[indice_coordenada] = Xi (respeitando os limites)
OmnivoreBehavior (agente, indice_agente, indice_coordenada):
Xi = agente.cB[coordenada]
X1 = pior solução da população para essa coordenada
j = índice aleatório > indice_agente
Xj = a[j].cB[indice_coordenada]
C = número aleatório gerado pela distribuição de Lévy (levisPower)
r = número aleatório entre 0 e 1
Xi = Xi + C * r * (Xi - X1) + (1 - r) * (Xi - Xj)
agente.c[indice_coordenada] = Xi (respeitando os limites)
Após a descrição detalhada e a análise do algoritmo, passamos à implementação em código.
O algoritmo utiliza a distribuição de Lévy para gerar saltos extremamente longos, porém raros, no espaço de busca. Já usamos anteriormente essa distribuição de números aleatórios, por exemplo, no algoritmo "Busca com Cuco", mas sem nos aprofundarmos em suas particularidades. A questão é que a geração correta da distribuição de Lévy requer o uso de quatro números aleatórios uniformemente distribuídos, o que já é custoso por si só. Além disso, a distribuição de Lévy possui uma cauda infinitamente longa (ela é assimétrica, com uma única cauda), o que dificulta seu uso prático em algoritmos de otimização, especialmente quando existem restrições de limite. Também é necessário fazer verificações de borda durante a geração, como checar se o valor é 0 antes de calcular o logaritmo natural e evitar divisões por 0.
Segue o código de geração de números aleatórios com distribuição de Lévy, no qual faltam as verificações descritas acima e que não inclui a explicação da lógica do código:
double LevyFlight() { const double epsilon = 1e-10; // Малое значение для избежания деления на ноль const double maxValue = 1e10; // Максимальное допустимое значение double log1 = MathMax (RNDprobab(), epsilon); double log2 = MathMax (RNDprobab(), epsilon); double cos1 = MathCos (2 * M_PI * RNDprobab()); double cos2 = MathCos (2 * M_PI * RNDprobab()); double U = MathSqrt (-2.0 * MathLog (log1)) * cos1; double v = MathSqrt (-2.0 * MathLog (log2)) * cos2; double l = 0.5 * MathAbs(U) / MathMax(MathAbs(v), epsilon); return l; }
Para eliminar as desvantagens da geração de números com distribuição de Lévy, vamos escrever nossa própria função "LevyFlightDistribution", com uma distribuição aproximada, e incluí-la no nosso conjunto padrão de funções "C_AO_Utilities" para uso em algoritmos de otimização. Vamos analisá-la:
1. O parâmetro "levisPower" é o expoente que define o formato da distribuição. Quanto maior o valor de "levisPower", mais "esparsa" será a distribuição.
2. Cálculo do valor mínimo – é calculado o valor mínimo que será usado para escalonamento. Ele depende de "levisPower" e é calculado como 20^levisPower.
3. Geração de um número aleatório "r" utilizando a função "RNDfromCI", no intervalo de 1 a 20.
4. Aplicação da potência – o número gerado "r" é elevado à potência "-levisPower", o que altera sua distribuição.
5. Escalonamento do resultado – o valor obtido "r" é escalonado para o intervalo [0, 1]. Isso é feito subtraindo o valor mínimo e dividindo pela diferença entre 1 e o valor mínimo. Assim, o resultado sempre estará dentro do intervalo [0, 1].
6. Retorno do resultado – a função retorna o valor gerado "r", que agora apresenta uma distribuição próxima da distribuição de Lévy, com deslocamento para 0.
Como podemos ver, a função gera números aleatórios estritamente dentro do intervalo [0, 1], o que é muito conveniente para uso prático, pois esse intervalo sempre pode ser expandido para qualquer escala aplicando o fator de multiplicação apropriado. Essa função é significativamente mais rápida e produz uma distribuição bastante próxima da desejada (parte direita da distribuição em relação ao pico).
//------------------------------------------------------------------------------ //A distribution function close to the Levy Flight distribution. //The function generates numbers in the range [0.0;1.0], with the distribution shifted to 0.0. double C_AO_Utilities :: LevyFlightDistribution (double levisPower) { double min = pow (20, -levisPower); //calculate the minimum possible value double r = RNDfromCI (1.0, 20); //generating a number in the range [1; 20] r = pow (r, -levisPower); //we raise the number r to a power r = (r - min) / (1 - min); //we scale the resulting number to [0; 1] return r; }
Vamos agora à descrição do código principal do algoritmo. A classe "C_AO_AEO" deriva da classe "C_AO" e implementa o algoritmo. Vamos analisar em detalhes sua estrutura, membros e métodos.
Construtor:
- Define os valores padrão para o tamanho da população e o expoente de Lévy.
- Cria o array de parâmetros "params" e o inicializa com os valores definidos.
Métodos:
- Define os parâmetros "popSize" e "levisPower" a partir do array "params".
- Init() – inicializa o algoritmo com os intervalos de busca e número de épocas definidos. O método retorna "bool", permitindo verificar se a inicialização foi bem-sucedida.
- Moving() – processa o movimento dos agentes na época atual, atualizando suas coordenadas.
- Revision() – atualiza as informações dos agentes e suas melhores soluções.
Membros e variáveis privadas:
- levisPower – parâmetro utilizado na distribuição de Lévy.
- epochs – número total de épocas.
- epochNow – época atual.
- consModel – estágio (consumo ou decomposição).
S_AO_Agent aT[]<² — array temporário de agentes, usado para ordenação da população.
Métodos privados:
- GrassBehavior() – trata o comportamento do agente "grama".
- HerbivoreBehavior() – trata o comportamento do agente herbívoro, que "se alimenta" da grama (o pior agente).
- CarnivoreBehavior() – trata o comportamento do agente carnívoro, que "se alimenta" de agentes com valor de função de fitness mais alto.
- OmnivoreBehavior() – trata o comportamento do agente onívoro, que combina o comportamento do herbívoro com a capacidade de consumir qualquer um com adaptabilidade inferior.
A classe "C_AO_AEO" implementa o algoritmo de otimização baseado em ecossistema artificial, utilizando diferentes tipos de agentes e suas interações para encontrar soluções ótimas. Cada método é responsável por aspectos específicos do algoritmo, como a inicialização, o movimento dos agentes e a atualização de seus estados.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_AEO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_AEO () { } C_AO_AEO () { ao_name = "AEOm"; ao_desc = "Artificial Ecosystem-based Optimization Algorithm"; ao_link = "https://www.mql5.com/ru/articles/16058"; popSize = 50; // population size levisPower = 2; ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "levisPower"; params [1].val = levisPower; } void SetParams () { popSize = (int)params [0].val; levisPower = params [1].val; } bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // step search const int epochsP = 0); // number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double levisPower; private: //------------------------------------------------------------------- int epochs; int epochNow; int consModel; // consumption model; S_AO_Agent aT []; void GrassBehavior (S_AO_Agent &animal); void HerbivoreBehavior (S_AO_Agent &animal, int indCoord); void CarnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord); void OmnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord); }; //——————————————————————————————————————————————————————————————————————————————
Vamos analisar detalhadamente o código do método "Init" da classe "C_AO_AEO". O método "Init" retorna um valor do tipo "bool", o que permite verificar se a inicialização foi bem-sucedida. A inicialização padrão é verificada por meio da chamada ao método "StandardInit", que executa a configuração básica dos parâmetros passados para o método. Se "StandardInit" retornar "false", isso significa que a inicialização falhou, e o método "Init" também retorna "false".
Configuração das variáveis:
- epochs – define o número total de épocas, obtido a partir do parâmetro "epochsP".
- epochNow – inicializa a época atual com o valor 0, indicando que o algoritmo acabou de começar.
- consModel – define o valor do modelo como 0, para permitir alternância entre os estágios nas etapas seguintes.
Redimensionamento do array temporário de agentes "aT" para o tamanho "popSize".
Retorno do resultado: se todas as operações anteriores forem concluídas com sucesso, o método retorna "true", sinalizando que a inicialização foi realizada corretamente.
O método "Init" da classe "C_AO_AEO" é responsável pela configuração inicial do algoritmo. Ele verifica os parâmetros padrão, define os valores para as épocas e o estágio inicial, e prepara o array de agentes para o funcionamento. Se todas as etapas forem bem-sucedidas, o método retorna "true", indicando que o algoritmo está pronto para ser executado.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_AEO::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; consModel = 0; ArrayResize (aT, popSize); return true; } //——————————————————————————————————————————————————————————————————————————————
Vamos agora examinar o código do método "Moving" da classe "C_AO_AEO". Estrutura geral do método: "Moving" é responsável por atualizar o estado da população de agentes (indivíduos), dependendo da época atual e do modelo de consumo. Ele é dividido em vários blocos lógicos:
1. Incremento da época: "epochNow++" aumenta o contador da época atual.
2. Inicialização inicial:
- Se "revision" for igual a "false", ocorre a inicialização das coordenadas dos agentes na população. As coordenadas são escolhidas aleatoriamente dentro do intervalo especificado e depois arredondadas para o valor mais próximo, respeitando o passo definido.
- Após isso, "revision" é definido como "true", e o método encerra a execução.
3. Modelo de consumo:
- Se "consModel" for igual a "0", ocorre a atualização das coordenadas dos agentes com base em seus comportamentos.
- Para o primeiro agente (índice 0), são utilizadas distribuições gaussianas para a inicialização das coordenadas.
- Para os demais agentes, o comportamento depende de seu índice: o último agente (índice "popSize - 1") chama a função "GrassBehavior". Para o penúltimo e anteriores (índices "popSize - 2" e inferiores), o comportamento é determinado aleatoriamente: pode ser herbívoro, carnívoro ou onívoro.
4. Decomposição: se "consModel" for diferente de "0", ocorre a decomposição, onde para cada agente suas coordenadas são atualizadas com base em valores aleatórios e distribuição gaussiana. Para cada coordenada, é escolhido aleatoriamente o índice de outro agente, e a partir desse valor são calculadas novas coordenadas, respeitando os limites mínimo e máximo.
O método "Moving" implementa a lógica relacionada à mudança das coordenadas dos agentes em função de seus comportamentos e da época atual. Ele abrange tanto a inicialização inicial quanto a atualização dos estados dos agentes com base em seus modelos de consumo.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEO::Moving () { epochNow++; //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } // Consumption --------------------------------------------------------------- if (consModel == 0) { double r = 0.0; for (int i = 0; i < popSize; i++) { if (i == 0) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.GaussDistribution (a [i].c [c], rangeMin [c], rangeMax [c], 8); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } continue; } if (i == popSize - 1) GrassBehavior (a [i]); else { if (i >= popSize - 2) { for (int c = 0; c < coords; c++) { r = u.RNDprobab (); if (r < 0.333) HerbivoreBehavior (a [i], c); else { if (r < 0.667) { CarnivoreBehavior (a [i], i, c); } else { OmnivoreBehavior (a [i], i, c); } } } } else { for (int c = 0; c < coords; c++) { r = u.RNDprobab (); if (r < 0.5) CarnivoreBehavior (a [i], i, c); else OmnivoreBehavior (a [i], i, c); } } } } consModel++; return; } // Decomposition ------------------------------------------------------------- int j = 0; double D = 0.0; double min = 0.0; double max = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { j = u.RNDminusOne (popSize); D = 3.0 * (cB [c] - a [j].c [c]); // * u.RNDprobab (); min = cB [c] - D; max = cB [c] + D; if (min < rangeMin [c]) min = u.RNDfromCI (rangeMin [c], cB [c]); if (max > rangeMax [c]) min = u.RNDfromCI (cB [c], rangeMax [c]); a [i].c [c] = u.GaussDistribution (cB [c], min, max, 1); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } consModel = 0; } //——————————————————————————————————————————————————————————————————————————————
O método "Revision" da classe "C_AO_AEO" é responsável por atualizar as informações dos melhores agentes da população. Ele implementa a lógica que permite rastrear e armazenar as melhores soluções encontradas durante a execução do algoritmo. Estrutura do método:
1. Busca pelo melhor agente:
- Iteramos por todos os agentes da população.
- Comparamos seu fitness (valor de "f") com o fitness atual considerado o melhor, "fB".
- Se for encontrado um agente com melhor fitness, atualizamos "fB" e registramos seu índice.
2. Cópia das coordenadas do melhor agente: se um melhor agente foi encontrado (índice diferente de -1), suas coordenadas são copiadas para o array "cB", que armazena as melhores coordenadas atuais.
3. Atualização dos melhores fitness pessoais dos agentes: iteramos novamente por todos os agentes e verificamos se seu fitness atual é melhor que seu fitness pessoal ("fB"). Se for, atualizamos seu melhor fitness e copiamos suas coordenadas atuais para "cB".
4. Ordenação dos agentes: ao final, chamamos a função de ordenação para organizar os agentes com base em seus melhores valores individuais de adaptabilidade.
O método "Revision" é um componente fundamental do algoritmo, pois assegura o rastreamento e a preservação das melhores soluções descobertas ao longo da execução.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEO::Revision () { //---------------------------------------------------------------------------- int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } u.Sorting_fB (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
O método "GrassBehavior" da classe "C_AO_AEO" implementa o comportamento dos agentes baseado na ideia de "grama", simbolizando a busca por novas soluções no espaço de busca. Estrutura do método:
1. Cálculo do coeficiente "α", definido como "(1.0 - (double) epochNow / epochs)", o que significa que ele diminui conforme o número da época aumenta. Isso permite que o algoritmo explore o espaço de forma mais intensa no início e, posteriormente, foque em melhorar as soluções encontradas.
2. Inicialização das variáveis:
- X1 – coordenada atual do agente herbívoro.
- Xn – coordenada atual do saprófago.
- Xr – coordenada aleatória escolhida dentro do intervalo definido.
3. Laço pelas coordenadas. Para cada coordenada do agente:
- Um valor aleatório "Xr" é gerado dentro do intervalo especificado "[Xmin, Xmax]".
- A coordenada atual "Xn" é extraída do array "cB", que armazena as melhores coordenadas globais atuais (a posição do saprófago no espaço).
- Uma nova coordenada "X1" é calculada com a fórmula "X1 = Xn + α * (Xn - Xr)", o que permite misturar o valor atual com um valor aleatório, reduzindo o impacto da aleatoriedade conforme o número de épocas aumenta.
- Por fim, a nova coordenada é limitada dentro do intervalo permitido por meio da função "SeInDiSp".
//—————————————————————————————————————————————————————————————————————————————— // Трава // (Худший) X1 X2 X3 ...... Xn (Лучший) // X1(t+1) = (1 - α) * Xn(t) + α * Xrnd (t) // α = (1 - t / T) * rnd [0.0; 1.0] // Xrnd = rnd [Xmin; Xmax] void C_AO_AEO::GrassBehavior (S_AO_Agent &animal) { //0) (1 - α) * Xn + α * Xrnd //1) Xn - α * Xn + α * Xrnd //2) Xn + α * (Xrnd - Xn) double α = (1.0 - (double)epochNow / epochs); double X1 = 0.0; double Xn = 0.0; double Xr = 0.0; for (int c = 0; c < coords; c++) { Xr = u.RNDfromCI (rangeMin [c], rangeMax [c]); Xn = cB [c]; //X1 = Xn + α * (Xr - Xn); X1 = Xn + α * (Xn - Xr); animal.c [c] = u.SeInDiSp (X1, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
O método "HerbivoreBehavior" da classe "C_AO_AEO" implementa o comportamento do agente herbívoro. Estrutura do método:
1. Inicialização das variáveis:
- Xi – coordenada atual do agente que será atualizada.
- X1 – coordenada do pior agente da população, que representa a energia máxima (ou menor valor de fitness).
- C – valor aleatório gerado utilizando a distribuição de Lévy.
2. Atualização da coordenada: a coordenada "Xi" é atualizada pela fórmula: Xi(t+1) = Xi(t) + C * (Xi(t) - X1(t)). Essa fórmula indica que o agente altera sua coordenada com base na diferença entre sua posição atual e a do pior agente. Isso permite ao herbívoro "se alimentar" do pior agente, ou seja, explorar até mesmo regiões menos promissoras do espaço de busca.
3. Restrição da coordenada: após a atualização de "Xi", a nova coordenada é limitada dentro do intervalo definido usando a função "SeInDiSp", que recebe como argumentos o novo valor, os limites mínimo e máximo e o passo.
O método "HerbivoreBehavior" demonstra como os agentes herbívoros podem se adaptar "se alimentando" dos piores indivíduos da população.
//—————————————————————————————————————————————————————————————————————————————— // Травоядный // (Худший) X1 X2 X3 ...... Xn (Лучший) // Xi(t+1) = Xi(t) + C * (Xi(t) - X1(t)) для i ∈ [2, n] // Травоядный ест только того, у кого энергия максимальна (ест того, у кого самый худший ФФ) void C_AO_AEO::HerbivoreBehavior (S_AO_Agent &animal, int indCoord) { double Xi = animal.c [indCoord]; double X1 = a [popSize - 1].c [indCoord]; double C = u.LevyFlightDistribution (levisPower); Xi = Xi + C * (Xi - X1); animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]); } //——————————————————————————————————————————————————————————————————————————————
O método "CarnivoreBehavior" da classe "C_AO_AEO" implementa o comportamento do agente carnívoro dentro do algoritmo. Estrutura do método:
1. Inicialização das variáveis:
- Xi – coordenada atual do agente carnívoro que será atualizada.
- j – índice de um agente aleatório escolhido como presa (o carnívoro "consome" agentes com menor energia, ou seja, melhor fitness).
- Xj – coordenada da presa, que será utilizada na atualização da coordenada do carnívoro.
- C – valor aleatório gerado utilizando a distribuição de Lévy.
2. Atualização da coordenada: a coordenada "Xi" é atualizada pela fórmula: Xi(t+1) = Xi(t) + C * (Xj(t) - Xi(t)). Essa fórmula significa que o agente carnívoro altera sua coordenada com base na diferença entre a coordenada da presa e sua coordenada atual. Isso permite ao carnívoro "se alimentar" da presa, melhorando suas próprias características.
3. Restrição da coordenada: após a atualização da coordenada "Xi", ela é limitada dentro do intervalo definido usando a função "SeInDiSp".
O método "CarnivoreBehavior" mostra como os agentes carnívoros podem se adaptar "alimentando-se" de presas com menor energia. Isso lhes permite melhorar suas características, aproximando-se de soluções mais otimizadas.
//—————————————————————————————————————————————————————————————————————————————— // Плотоядный // (Худший) X1 X2 X3 ...... Xn (Лучший) // Xi(t+1) = Xi(t) + C * (Xi(t) - Xj(t)) для i ∈ [3, n] // Плотоядный ест тех, у кого энергии меньше (ест того, у кого выше ФФ) void C_AO_AEO::CarnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord) { //double Xi = animal.c [indCoord]; double Xi = animal.cB [indCoord]; int j = u.RNDminusOne (indAnimal); //double Xj = a [j].c [indCoord]; double Xj = a [j].cB [indCoord]; double C = u.LevyFlightDistribution (levisPower); //Xi = Xi + C * (Xi - Xj); Xi = Xi + C * (Xj - Xi); animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]); } //——————————————————————————————————————————————————————————————————————————————
O método "OmnivoreBehavior" da classe "C_AO_AEO" descreve o comportamento do agente onívoro no contexto do algoritmo evolutivo. Estrutura do método:
1. Inicialização das variáveis:
- Xi – coordenada atual do agente onívoro, que deve ser atualizada.
- X1 – coordenada do pior agente (com maior energia).
- j – índice aleatório de outro agente da população, que será usado para atualizar a coordenada.
- Xj – coordenada do agente aleatório selecionado.
- C – valor aleatório gerado utilizando a distribuição de Lévy.
- r – probabilidade aleatória que será usada para mesclar a atualização das coordenadas.
2. Atualização da coordenada: a coordenada "Xi" é atualizada com a fórmula: Xi(t+1) = Xi(t) + C * r * (Xi(t) - X1(t)) + (1 - r) * (Xi(t) - Xj(t)). Essa fórmula permite que o agente onívoro se adapte "alimentando-se" tanto do pior agente (com maior energia) quanto de outro agente aleatório com menor adaptabilidade, o que torna seu comportamento mais flexível.
3. Restrição da coordenada: após a atualização, a coordenada "Xi" é ajustada dentro dos limites especificados utilizando a função "SeInDiSp".
O método "OmnivoreBehavior" demonstra como agentes onívoros podem se adaptar e tirar proveito de múltiplas fontes de energia, incluindo os piores agentes e outros agentes aleatórios com menor adaptabilidade.
//—————————————————————————————————————————————————————————————————————————————— // Всеядный // (Худший) X1 X2 X3 ...... Xn (Лучший) // Xi(t+1) = Xi(t) + C * r2 * (Xi(t) - X1(t)) + (1 - r2) * (Xi(t) - Xj(t)) для i ∈ [3, n] // Всеядный есть всех, у кого энергии больше (траву и мелких животных, тоесть тех, у кого ФФ хуже) void C_AO_AEO::OmnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord) { //double Xi = animal.c [indCoord]; double Xi = animal.cB [indCoord]; //double X1 = a [popSize - 1].c [indCoord]; double X1 = a [popSize - 1].cB [indCoord]; int j = u.RNDintInRange (indAnimal + 1, popSize - 1); //double Xj = a [j].c [indCoord]; double Xj = a [j].cB [indCoord]; double C = u.LevyFlightDistribution (levisPower); double r = u.RNDprobab (); Xi = Xi + C * r * (Xi - X1) + (1.0 - r) * (Xi - Xj); animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]); } //——————————————————————————————————————————————————————————————————————————————
Agora que escrevemos o código do algoritmo, finalmente podemos iniciar os testes nas nossas funções de avaliação.
AEO|Artificial Ecosystem-based Optimization Algorithm|50.0|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.6991675795357223
25 Hilly's; Func runs: 10000; result: 0.34855292688850514
500 Hilly's; Func runs: 10000; result: 0.253085011547826
=============================
5 Forest's; Func runs: 10000; result: 0.6907505745478882
25 Forest's; Func runs: 10000; result: 0.23365521509528495
500 Forest's; Func runs: 10000; result: 0.1558073538195803
=============================
5 Megacity's; Func runs: 10000; result: 0.5430769230769231
25 Megacity's; Func runs: 10000; result: 0.20676923076923082
500 Megacity's; Func runs: 10000; result: 0.1004461538461546
=============================
All score: 3.23131 (35.90%)
O algoritmo obteve cerca de 36% nos testes, porém esse é um resultado mediano. Para esse algoritmo, decidi revisar o método "Moving", e eis o que foi implementado:
Lógica modificada do deslocamento dos agentes considerando diferentes modelos de comportamento (produção, consumo e decomposição) no método "Moving":
1. A inicialização da população permaneceu inalterada.
2. Atualização do coeficiente "α", que agora é calculado como uma função da época atual, diminuindo conforme o valor de "epochNow" aumenta. Esse coeficiente foi movido para fora de um método privado e agora é processado diretamente.
3. Produção (consModel == 0) – nesta parte, os agentes atualizam suas coordenadas utilizando uma fórmula baseada no estado anterior e em um valor aleatório. Isso permite que eles "produzam" novos estados.
4. Consumo (consModel == 1). Aqui, os agentes são divididos em três grupos de acordo com um valor aleatório:
- Herbívoros.
- Carnívoros.
- Onívoros.
5. Decomposição: nesta etapa, os agentes interagem entre si, alterando suas coordenadas com base em valores aleatórios e interações com outros agentes.
6. Reinício do modelo de consumo: ao final do método, "consModel" é redefinido para "0", iniciando assim um novo ciclo.
Como se pode ver, a principal mudança na lógica do algoritmo foi isolar a "Produção" como uma fase independente. Uma época foi dedicada exclusivamente a ela, permitindo uma reestruturação mais intensa da população de organismos. Isso também impactou o comportamento visual do AEO: agora é possível observar "piscadas", ou seja, as fases individuais do ecossistema artificial se tornam visíveis.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEO::Moving () { epochNow++; //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double α = (1.0 - (double)epochNow / epochs); double Xi = 0.0; double Xb = 0.0; double Xr = 0.0; double Xj = 0.0; double C = 0.0; int j = 0; double r = 0.0; // Production ---------------------------------------------------------------- Производство // X(t + 1) = (1 - α) * Xb(t) + α * Xrnd (t) // α = (1 - t / T) * rnd [0.0; 1.0] // Xrnd = rnd [Xmin; Xmax] if (consModel == 0) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { Xb = cB [c]; Xr = u.RNDfromCI (rangeMin [c], rangeMax [c]); //Xi = Xb + α * (Xr - Xb); Xi = Xb + α * (Xb - Xr); a [i].c [c] = u.SeInDiSp (Xi, rangeMin [c], rangeMax [c], rangeStep [c]); } } consModel++; return; } // Consumption --------------------------------------------------------------- Потребление if (consModel == 1) { for (int i = 0; i < popSize; i++) { if (i > 1) { for (int c = 0; c < coords; c++) { r = u.RNDprobab (); // Herbivore behavior ------------------------------------------------ Травоядный //Xi (t + 1) = Xi (t) + C * (Xi (t) - Xb (t)); if (r < 0.333) { C = u.LevyFlightDistribution (levisPower); Xb = cB [c]; //Xi = a [i].c [c]; Xi = a [i].cB [c]; //Xi = Xi + C * (Xi - Xb); Xi = Xi + C * (Xb - Xi); } else { // Carnivore behavior ---------------------------------------------- Плотоядный //Xi (t + 1) = Xi (t) + C * (Xi (t) - Xj (t)); if (r < 0.667) { C = u.LevyFlightDistribution (levisPower); j = u.RNDminusOne (i); //Xj = a [j].c [c]; Xj = a [j].cB [c]; //Xi = a [i].c [c]; Xi = a [i].cB [c]; //Xi = Xi + C * (Xi - Xj); Xi = Xi + C * (Xj - Xi); } // Omnivore behavior ----------------------------------------------- Всеядный //Xi (t + 1) = Xi (t) + C * r2 * (Xi (t) - Xb (t)) + // (1 - r2) * (Xi (t) - Xj (t)); else { C = u.LevyFlightDistribution (levisPower); Xb = cB [c]; j = u.RNDminusOne (i); //Xj = a [j].c [c]; Xj = a [j].cB [c]; //Xi = a [i].c [c]; Xi = a [i].cB [c]; r = u.RNDprobab (); //Xi = Xi + C * r * (Xi - Xb) + // (1 - r) * (Xi - Xj); Xi = Xi + C * r * (Xb - Xi) + (1 - r) * (Xj - Xi); } } a [i].c [c] = u.SeInDiSp (Xi, rangeMin [c], rangeMax [c], rangeStep [c]); } } } consModel++; return; } // Decomposition ------------------------------------------------------------- double D = 0.0; double h = 0.0; for (int i = 0; i < popSize; i++) { D = 3 * u.RNDprobab (); h = u.RNDprobab () * (u.RNDprobab () < 0.5 ? 1 : -1); C = u.LevyFlightDistribution (levisPower); j = u.RNDminusOne (popSize); for (int c = 0; c < coords; c++) { double x = a [i].cB [c] + D * (C * a [i].cB [c] - h * a [j].c [c]); a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); } } consModel = 0; } //——————————————————————————————————————————————————————————————————————————————
Resultados dos testes
Agora podemos testar novamente o algoritmo com as alterações feitas na lógica.
AEO|Artificial Ecosystem-based Optimization Algorithm|50.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9137986747745103
25 Hilly's; Func runs: 10000; result: 0.4671288391599192
500 Hilly's; Func runs: 10000; result: 0.2647022528159094
=============================
5 Forest's; Func runs: 10000; result: 0.9022293417142482
25 Forest's; Func runs: 10000; result: 0.4370486099190667
500 Forest's; Func runs: 10000; result: 0.2139965996985526
=============================
5 Megacity's; Func runs: 10000; result: 0.6615384615384616
25 Megacity's; Func runs: 10000; result: 0.30799999999999994
500 Megacity's; Func runs: 10000; result: 0.28563076923076974
=============================
All score: 4.45407 (49.49%)
Chama a atenção a ausência de grande dispersão nos resultados. O algoritmo consegue evitar armadilhas locais com sucesso, embora a precisão de convergência permaneça medianamente baixa. Também é visível o "piscamento" durante a alternância entre estágios, conforme mencionado anteriormente. O comportamento do algoritmo é particularmente incomum na função discreta Megacity, pois ele destaca grupos de coordenadas em linhas verticais e diagonais separadas, que passam por regiões significativas da superfície. Isso também se refletiu nos resultados ao lidar com essa função discreta — foram os melhores da tabela de classificação para uma função discreta com 1000 variáveis.
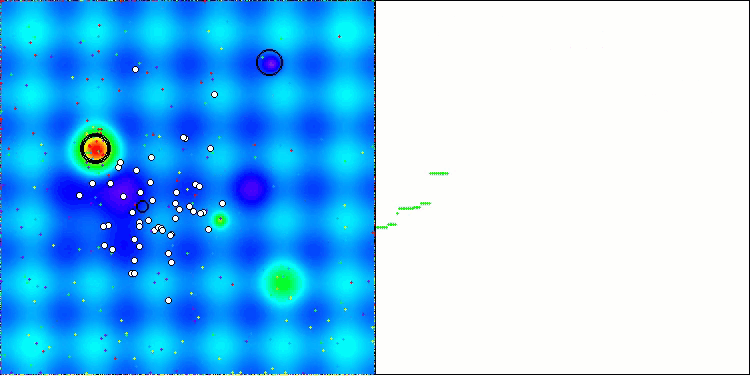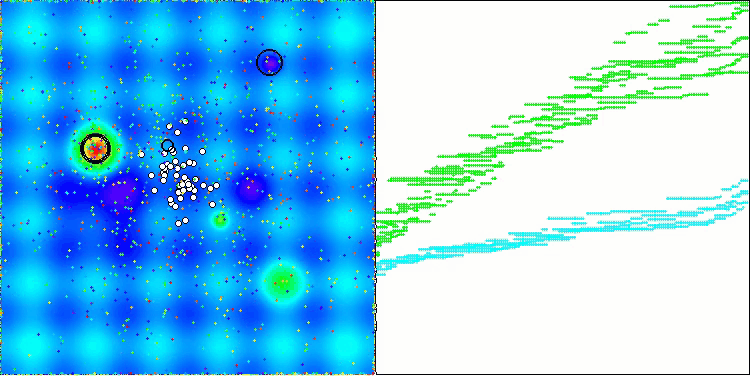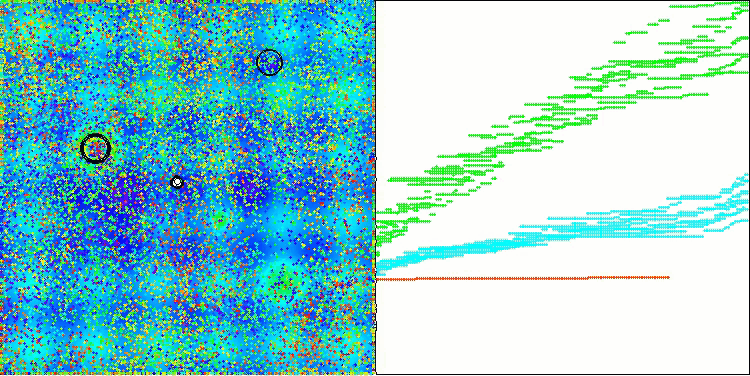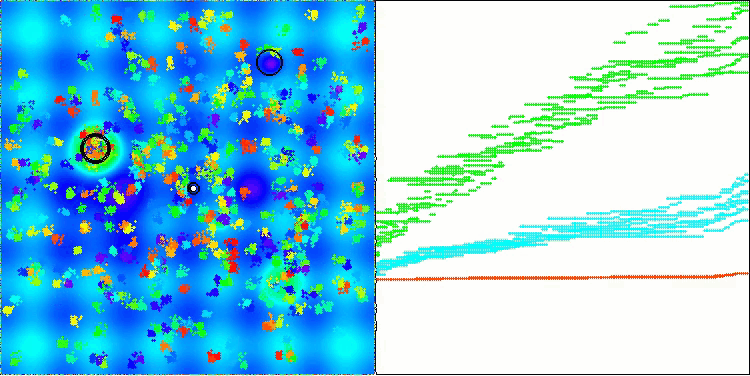
AEO na função de teste Hilly
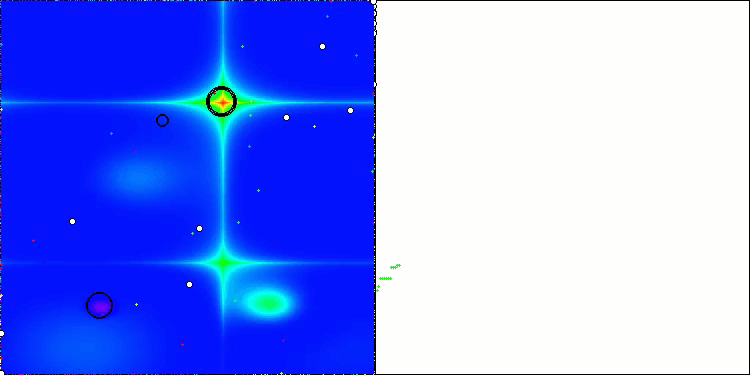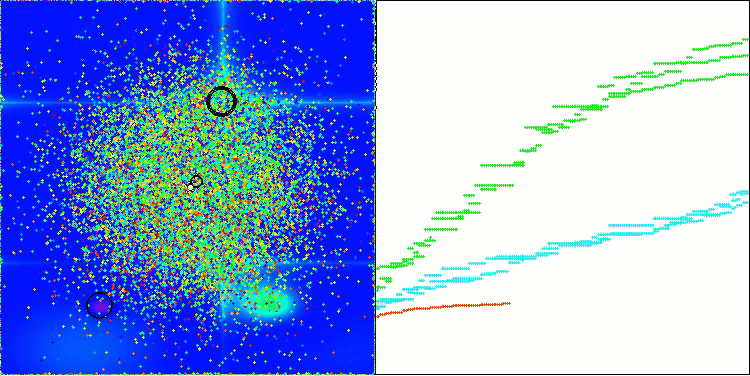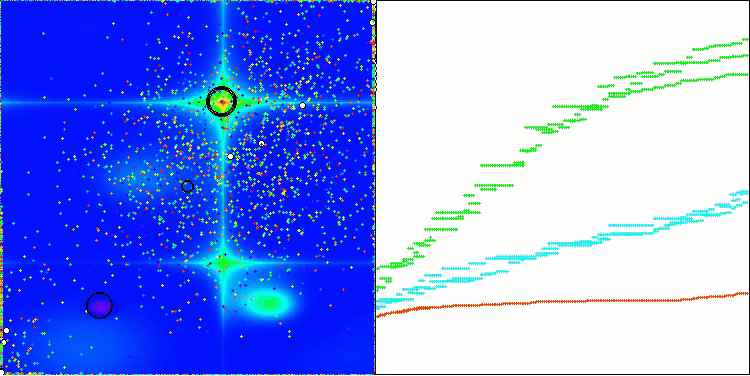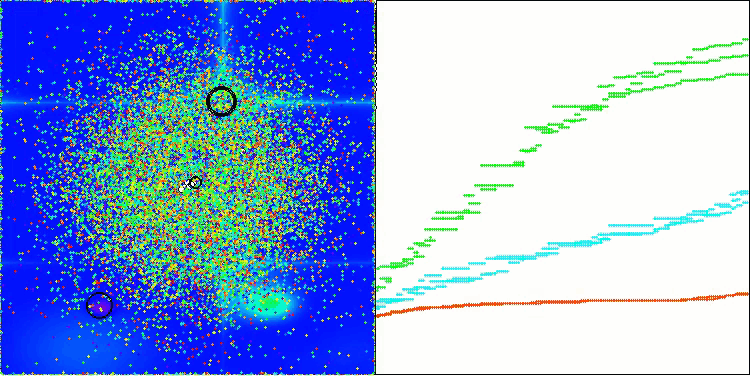
AEO na função de teste Forest
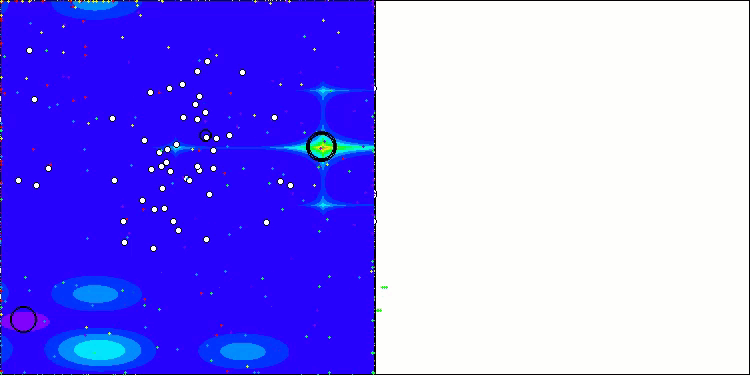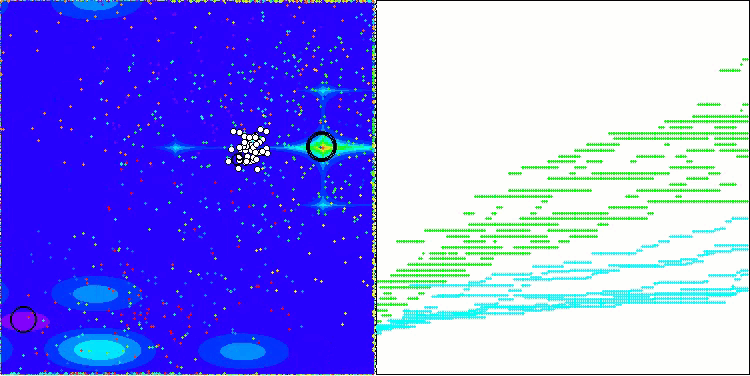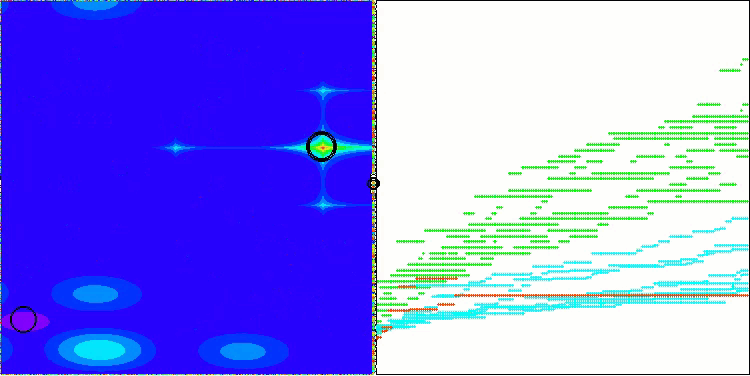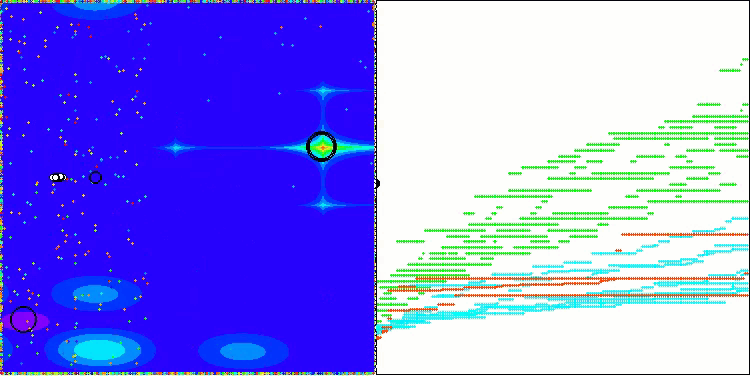
AEO na função de teste Megacity
Como podemos notar, o algoritmo melhorou significativamente seu desempenho em comparação com a versão original e agora alcança cerca de 50% do máximo possível. Esse é um resultado realmente impressionante! Na tabela de classificação, o algoritmo ocupa a 25ª posição, o que também é bastante respeitável. O mais impressionante é que o AEO estabeleceu um novo recorde na tabela para a função discreta Megacity, melhorando o resultado com 1000 parâmetros em nada menos que 5%!
№ | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration optimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 8 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 10 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 11 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 12 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 13 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 14 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 15 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 16 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 17 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 18 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 19 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 20 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 21 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 22 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 23 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 24 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 25 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 26 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 27 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 28 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 29 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 30 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 31 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 32 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 33 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 34 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 35 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 36 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 37 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 38 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 39 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 40 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 41 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 42 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 43 | AAA | algae adaptive algorithm | 0,50007 | 0,32040 | 0,25525 | 1,07572 | 0,37021 | 0,22284 | 0,16785 | 0,76089 | 0,27846 | 0,14800 | 0,09755 | 0,52402 | 2,361 | 26,23 |
| 44 | SA | simulated annealing | 0,55787 | 0,42177 | 0,31549 | 1,29513 | 0,34998 | 0,15259 | 0,05023 | 0,55280 | 0,31167 | 0,10033 | 0,02883 | 0,44083 | 2,289 | 25,43 |
| 45 | IWDm | intelligent water drops M | 0,54501 | 0,37897 | 0,30124 | 1,22522 | 0,46104 | 0,14704 | 0,04369 | 0,65177 | 0,25833 | 0,09700 | 0,02308 | 0,37842 | 2,255 | 25,06 |
Considerações finais
Características e vantagens do algoritmo:
1. Equilíbrio entre exploração e aproveitamento. O AEO proporciona um bom equilíbrio entre a exploração global do espaço de soluções (por meio da produção e do consumo) e o aproveitamento local (por meio da decomposição).
2. Adaptabilidade. O algoritmo se adapta ao relevo do problema por meio de diferentes estratégias de atualização das soluções.
3. Simplicidade. Apesar da metáfora biológica, o algoritmo é relativamente simples de implementar e entender.
4. Excelente desempenho em funções discretas de alta dimensionalidade.
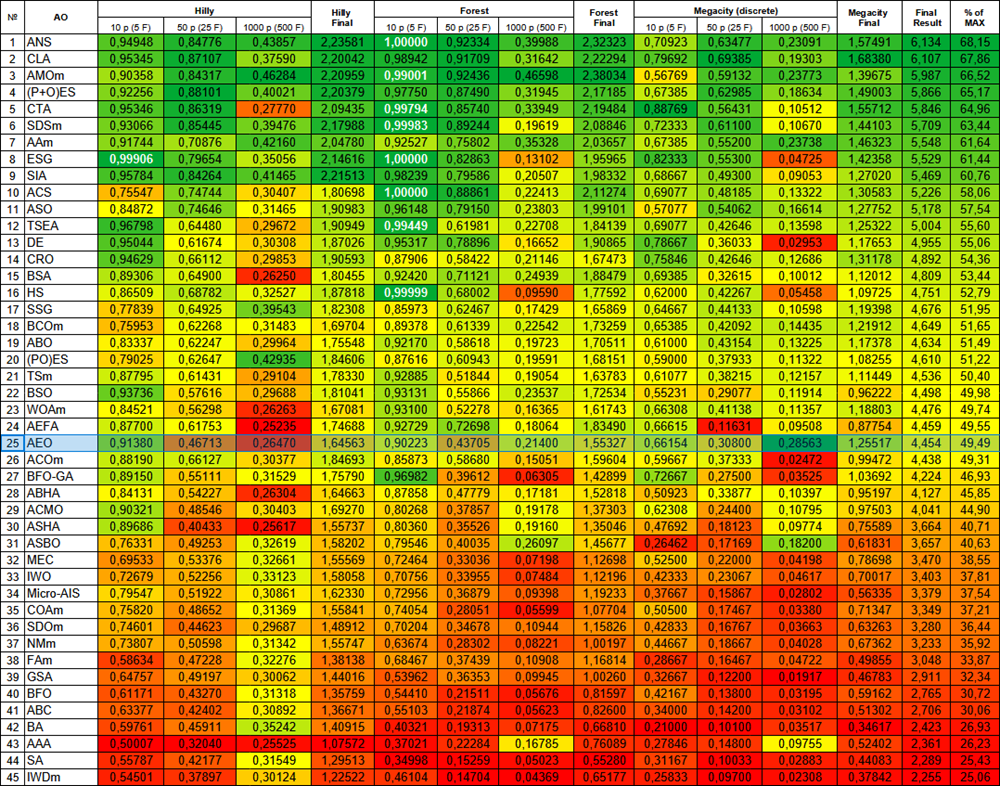
Figura 2. Gradação de cores dos algoritmos conforme os testes correspondentes. Resultados iguais ou superiores a 0.99 destacados em branco

Figura 3. Histograma dos resultados de teste dos algoritmos (em escala de 0 a 100, quanto maior, melhor,
onde 100 é o resultado teórico máximo possível, no arquivo o script para cálculo da tabela de classificação)
Pontos fortes e fracos do algoritmo AEO:
Vantagens:
- Apenas um único parâmetro externo (além do tamanho da população).
- Obteve bom desempenho em função discreta.
Desvantagens:
- A precisão de convergência não é das mais altas.
O artigo é acompanhado por um arquivo compactado com as versões atuais dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar as capacidades de busca. As conclusões e opiniões apresentadas nos artigos são baseadas nos resultados dos experimentos realizados.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/16058
 Do básico ao intermediário: Estruturas (III)
Do básico ao intermediário: Estruturas (III)
 Redes neurais em trading: Segmentação guiada (Conclusão)
Redes neurais em trading: Segmentação guiada (Conclusão)
 Simulação de mercado (Parte 15): Sockets (IX)
Simulação de mercado (Parte 15): Sockets (IX)
 De Novato a Especialista: A Jornada Essencial no Comércio MQL5
De Novato a Especialista: A Jornada Essencial no Comércio MQL5
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso