
Algoritmo do Campo Elétrico Artificial — Artificial Electric Field Algorithm (AEFA)
Introdução
O Algoritmo do Campo Elétrico Artificial é uma criação impressionante que incorpora a harmonia entre tecnologia e natureza. Inspirado na Lei de Coulomb da força eletrostática, esse algoritmo chama a atenção por sua capacidade única de simular fenômenos elétricos para resolver tarefas complexas de otimização. No contexto de algoritmos já conhecidos e descritos anteriormente em artigos baseados em leis da natureza, como o Charged System Search (CSS), ElectroMagnetism-like algorithm (EM), Gravitational Search Algorithm (GSA) e outros, o Campo Elétrico Artificial representa uma novidade empolgante que certamente despertará o interesse de qualquer pesquisador. E eu não consegui ignorá-lo...
O Algoritmo do Campo Elétrico Artificial é inspirado na Lei de Coulomb, que afirma que a força eletrostática (atração ou repulsão) entre duas partículas carregadas é diretamente proporcional ao produto de suas cargas e inversamente proporcional ao quadrado da distância entre elas. No algoritmo proposto, os agentes são considerados partículas carregadas, e sua força é medida de acordo com suas cargas. Todas essas partículas podem atrair ou repelir umas às outras pela força eletrostática, e, devido a ela, os objetos se movem pelo espaço de busca. Por isso, as cargas são usadas como uma forma direta de comunicação por meio da força eletrostática, e a posição da carga corresponde à solução do problema. As cargas são definidas como uma função da adaptabilidade da solução candidata e da adaptabilidade da população. No algoritmo proposto, consideramos apenas a atração da força eletrostática, de modo que a partícula carregada com a maior carga (o "melhor" indivíduo) atrai todas as outras partículas com cargas menores e se move lentamente no espaço de busca.
Dessa forma, o AEFA pode ser visto como um sistema isolado de cargas que obedece à primeira lei da eletrostática de Coulomb sobre força eletrostática e à lei do movimento: partículas com cargas de mesmo sinal se repelem, enquanto partículas com cargas de sinais opostos se atraem; e à segunda lei de Coulomb da eletrostática: a força de atração entre partículas com cargas opostas ou a força de repulsão entre partículas com cargas iguais é diretamente proporcional ao produto de suas cargas e inversamente proporcional ao quadrado da distância entre os centros das cargas, além da lei do movimento: a velocidade atual de qualquer carga é igual à soma das frações de sua velocidade anterior e das variações de velocidade. A variação de velocidade ou aceleração de qualquer carga é igual à força atuante sobre o sistema dividida pela massa da partícula.
Os autores do algoritmo AEFA (Artificial Electric Field Algorithm) são:
1. Anita — do Departamento de Ciências e Ciências Humanas, Instituto Nacional de Tecnologia de Uttarakhand, Srinagar, Índia.
2. Anupam Yadav — do Departamento de Matemática, Instituto Nacional de Tecnologia Dr. B.R. Ambedkar, Jalandhar, Índia.
O algoritmo AEFA foi proposto em 2019 e publicado na revista "Swarm and Evolutionary Computation". Os autores do artigo destacam que o conceito de campo elétrico e partículas carregadas nos fornece uma teoria sólida para o funcionamento da força de atração ou repulsão entre duas partículas carregadas. Assim, o AEFA utiliza princípios da força eletrostática para desenvolver um algoritmo de otimização populacional.
Implementação do algoritmo
O algoritmo AEFA é rico em fórmulas diversas e, antes de nos aprofundarmos nelas, vamos destacar seus pontos-chave:
- Os agentes do algoritmo (soluções) são representados como partículas carregadas, que se movimentam sob a ação da força eletrostática.
- A carga da partícula depende de seu melhor resultado pessoal e dos melhores e piores resultados atuais na população (não os melhores resultados alcançados ao longo da otimização, mas sim os atuais da população).
- A força que atua sobre a partícula depende das cargas das partículas e da distância entre elas.
- A constante de Coulomb K(t) diminui com o avanço das iterações, controlando o equilíbrio entre a busca global e a otimização local.
Vamos agora formalizar o algoritmo e analisar mais detalhadamente as fórmulas utilizadas nele.
Seja a posição da i-ésima partícula no d-dimensional espaço de busca denotada por X_i = (x_1, x_2, ..., x_d), onde i = 1, 2, ..., N, sendo N o tamanho da população.
A melhor posição encontrada pela i-ésima partícula é denotada por P_i, e a melhor posição global é denotada por P_best.
1. Fórmula de Coulomb para a força eletrostática: F_ij = K * Q_i * Q_j / R^2, onde:
- F_ij — magnitude da força eletrostática entre dois objetos carregados i e j
- K — constante de Coulomb
- Q_i e Q_j — cargas dos objetos i e j, respectivamente
- R — distância entre as duas cargas Q_i e Q_j
2. Fórmula do campo elétrico ao redor da carga Q_i: E_i = F_ij / Q_i, onde:
- E_i — campo elétrico ao redor da carga Q_i
- F_ij — força atuando sobre a carga Q_i
3. Fórmula da aceleração da partícula conforme a segunda lei de Newton: a_i = F_ij / M, onde:
- a_i — aceleração da i-ésima partícula
- F_ij — força atuando sobre a partícula
- M — massa da partícula
4. Fórmula da aceleração da partícula por meio do campo elétrico: a_i = E_i * Q_i / M, onde:
- a_i — aceleração da i-ésima partícula
- E_i — campo elétrico ao redor da partícula
- Q_i — carga da partícula
- M — massa da partícula
5. Fórmula de atualização da melhor posição da partícula: p_di (t+1) = {p_di (t) e X_i (t+1) = X_i (t)}, se f (X_i (t+1)) > f (X_i (t)), onde:
- p_di (t) — valor da adaptabilidade da i-ésima partícula no instante t
- p_di (t+1) — valor da adaptabilidade da i-ésima partícula no instante (t+1)
- X_i (t) — posição da i-ésima partícula no instante t
- X_i (t+1) — nova posição da i-ésima partícula no instante (t+1)
- f(X_i (t)) — valor da função objetivo na posição anterior da i-ésima partícula no instante t
- f(X_i (t+1)) — valor da função objetivo na nova posição da i-ésima partícula no instante (t+1)
6. Fórmula da força atuando sobre a i-ésima partícula por parte da j-ésima partícula: F_dij (t) = K (t) * (Q_i (t) * Q_j (t) * (p_dj (t) - X_di (t))) / (R_ij (t)^2 + ε), onde:
- F_dij (t) — força atuando sobre a i-ésima partícula pela j-ésima partícula no instante t
- K (t) — constante de Coulomb no instante t
- Q_i (t) e Q_j (t) — cargas das partículas i e j no instante t
- p_dj (t) — melhor posição da j-ésima partícula no instante t
- X_di (t) — posição da i-ésima partícula no instante t
- R_ij (t) — distância euclidiana entre as partículas i e j no instante t
- ε — pequena constante positiva usada para evitar divisão por 0
7. Fórmula da distância euclidiana entre as partículas i e j: R_ij (t) = (X_i (t) - X_j (t))^2
8. Fórmula da constante de Coulomb: K (t) = K_0 * exp (-α * t / maxiter), onde:
- K_0 — valor inicial da constante de Coulomb
- α — parâmetro externo
- t — instante atual (época)
- maxiter — número máximo de iterações
9. Fórmula da força total atuando sobre a i-ésima partícula: F_di (t) = Σ (rand () * F_dij (t)), j=(de 1 até N), j≠i, onde:
- F_di (t) — força total atuando sobre a i-ésima partícula no instante t
- rand () — número aleatório no intervalo [0, 1]
- N — número de partículas no espaço de busca
10. Fórmula do campo elétrico atuando sobre a i-ésima partícula: E_di (t) = F_di (t) / Q_i (t), onde:
- E_di (t) — campo elétrico atuando sobre a i-ésima partícula no instante t
- F_di (t) — força total atuando sobre a i-ésima partícula
- Q_i (t) — carga da i-ésima partícula no instante t
11. Fórmula que atualiza a velocidade da partícula i no instante t+1: V_i (t+1) = rand () * V_i (t) + a_i (t), onde:
- V_i(t) — velocidade anterior
- a_i(t) — aceleração atuando sobre a partícula
- rand () — número aleatório no intervalo [0, 1]
12. Fórmula que atualiza a posição da partícula i no instante t+1: X_i (t+1) = X_i (t) + V_i (t+1), onde:
- V_i (t+1) — nova velocidade
13. Fórmula que define que a carga de todas as partículas na população é a mesma e igual, Q_i (t) = Q_j (t) para todos i, j = 1, 2,..., N
14. Fórmula que calcula a carga relativa q_i (t) de cada partícula i no instante t: q_i (t) = exp ((fit_p_i (t) - worst (t)) / (best (t) - worst (t))), onde:
- fit_p_i (t) — valor da adaptabilidade da melhor posição pessoal da partícula
- fit_best (t) — valor da adaptabilidade da melhor posição global
- fit_worst(t) — valor da adaptabilidade da pior partícula na população
15. Fórmula: Q_i (t) = q_i (t) / Σ_j=1...N q_j (t).
Essa fórmula normaliza as cargas relativas q_i (t) de todas as partículas para que sua soma seja igual a 1. Assim, obtêm-se as cargas normalizadas Q_i (t) de cada partícula.
16. Fórmula: best (t) = max (fit_j (t)) para j = 1, 2,..., N
Essa fórmula calcula o valor atual da melhor adaptabilidade — best (t) — na população no instante t como o maior entre os valores de adaptabilidade de todas as partículas.
17. Fórmula: worst (t) = min (fit_j (t)) para j = 1, 2,..., N
Essa fórmula calcula o valor atual da pior adaptabilidade — worst (t) — na população no instante t como o menor entre os valores de adaptabilidade de todas as partículas.
Agora que conhecemos as fórmulas das leis de movimento das partículas no algoritmo, podemos montar o pseudocódigo que nos ajudará posteriormente a escrever o código do algoritmo AEFA em MQL5.
Pseudocódigo do algoritmo AEFA:
Passo 1: Inicialização
Inicializar aleatoriamente as posições das partículas.
Calcular os valores da função objetivo para cada partícula.
Definir a iteração atual t = 0.
Passo 2: Atualização das posições das partículas enquanto a condição de parada não for atendida:
1. Calcular a constante de Coulomb K(t) usando a fórmula (8)
2. Calcular os valores da função objetivo fit_best (t) e fit_worst(t) na iteração atual
3. Para cada partícula i = 1, 2, ..., N:
a. Calcular a carga da partícula Q_i (t) pela fórmula (14)
b. Calcular a força que atua sobre a partícula i vinda da partícula j pela fórmula (6)
c. Calcular a força total que atua sobre a partícula i pela fórmula (9)
d. Calcular a aceleração da partícula i pela fórmula (4)
e. Atualizar a velocidade pela fórmula (11) e a posição da partícula i pela fórmula (12)
4. Incrementar o contador de iterações t = t + 1
Passo 3: Condição de parada. Verificar a condição de parada (por exemplo, alcançar o número máximo de iterações). Se a condição não for atendida, retornar ao Passo 2.
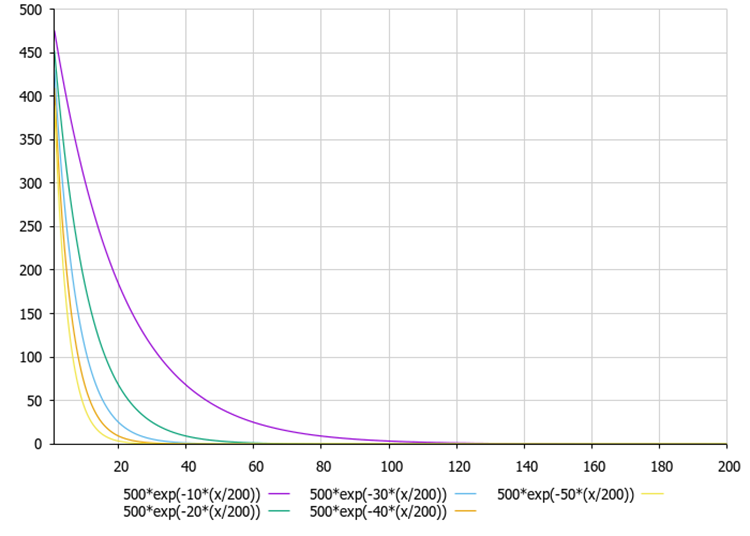
Figura 1. Dependência da força eletrostática segundo a fórmula de Coulomb em relação ao coeficiente α (parâmetro externo).
Finalmente, terminamos a parte de descrição, fórmulas e pseudocódigo do algoritmo. Agora é necessário partir para a criação do código.
Vamos escrever a estrutura "S_AEFA_Agent", que serve para descrever os agentes no algoritmo. Essa estrutura contém os seguintes campos:
- best_fitness — variável que representa a melhor adaptabilidade do agente.
- best_position[] — array de coordenadas da melhor posição do agente no espaço de busca.
- velocity[] — array que representa o vetor de velocidade de movimento da partícula.
- charge — carga do agente.
- relative_charge — carga relativa da partícula.
Também está definida na estrutura a função "Init", que inicializa a partícula (agente). Ela recebe o parâmetro "coords", que indica a quantidade de coordenadas do agente, e ajusta os tamanhos dos arrays "best_position" e "velocity" conforme necessário. Depois disso, define "best_fitness" com o menor valor possível do tipo double "-DBL_MAX", e as variáveis "charge" e "relative_charge" com o valor 0.
Esse código representa a base para a descrição dos agentes no algoritmo do campo elétrico artificial e os prepara para o funcionamento posterior nesse contexto.
//—————————————————————————————————————————————————————————————————————————————— struct S_AEFA_Agent { double best_fitness; double best_position []; double velocity []; double charge; double relative_charge; void Init (int coords) { ArrayResize (best_position, coords); ArrayResize (velocity, coords); best_fitness = -DBL_MAX; charge = 0; relative_charge = 0; } }; //——————————————————————————————————————————————————————————————————————————————
Vamos descrever a classe "C_AO_AEFA", que herda da classe "C_AO". Dentro da classe estão definidos os seguintes métodos e variáveis:
- C_AO_AEFA — construtor onde são definidos os valores das variáveis e dos parâmetros.
- SetParams — método que define os parâmetros com base nos valores armazenados no array "params".
- Init — método que recebe um conjunto de valores e executa a inicialização.
- "Moving" e "Revision" — métodos que executam a lógica principal do algoritmo.
- Diversas variáveis do tipo "double", como "K0", "alpha", "particleMass", "epsilon", além do array "agent" e outras variáveis privadas.
- Métodos privados "CalculateK", "UpdateCharges", "CalculateForces", "CalculateDistance", "UpdateVelocityAndPosition" realizam operações de movimentação das partículas no espaço de busca.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_AEFA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_AEFA () { } C_AO_AEFA () { ao_name = "AEFA"; ao_desc = "Artificial Electric Field Algorithm"; ao_link = ""; //"https://www.mql5.com/ru/articles/15162"; popSize = 50; K0 = 500.0; alpha = 20.0; particleMass = 1.0; ArrayResize (params, 4); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "K0"; params [1].val = K0; params [2].name = "alpha"; params [2].val = alpha; params [3].name = "particleMass"; params [3].val = particleMass; } void SetParams () { popSize = (int)params [0].val; K0 = params [1].val; alpha = params [2].val; particleMass = params [3].val; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0); void Moving (); void Revision (); //---------------------------------------------------------------------------- double K0; double alpha; double particleMass; double epsilon; S_AEFA_Agent agent []; private: //------------------------------------------------------------------- int epochs; int epochNow; double K; double CalculateK (int t); void UpdateCharges (double best, double worst); void CalculateForces (); double CalculateDistance (const double &x1 [], const double &x2 []); void UpdateVelocityAndPosition (int i); }; //——————————————————————————————————————————————————————————————————————————————
A seguir, passamos à implementação do método "Init" da classe "C_AO_AEFA". Neste método, é realizada a inicialização do algoritmo AEFA com os parâmetros fornecidos.
Parâmetros de entrada do método "Init":
- rangeMinP — array de valores dos limites mínimos do intervalo.
- rangeMaxP — array de valores dos limites máximos do intervalo.
- rangeStepP — array de valores dos passos do intervalo.
- epochsP — número de épocas (por padrão igual a 0).
Ações realizadas no método "Init":
1. O método "StandardInit" é chamado com os arrays "rangeMinP", "rangeMaxP" e "rangeStepP" como parâmetros. Se o método "StandardInit" retornar "false", então o método "Init" também retorna "false".
2. Os valores das variáveis "epochs" e "epochNow" são definidos com os valores dos parâmetros "epochsP" e "0", respectivamente.
3. O tamanho do array "agent" é ajustado para o valor "popSize".
4. Um laço inicializa cada elemento do array "agent" com a chamada do método "Init", passando o array "coords".
5. A variável "epsilon" é definida com o valor "1e-10".
6. O método retorna "true".
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_AEFA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; ArrayResize (agent, popSize); for (int i = 0; i < popSize; i++) agent [i].Init (coords); epsilon = 1e-10; return true; } //——————————————————————————————————————————————————————————————————————————————
Passamos agora para o método "Moving()" da classe C_AO_AEFA. Nesse método ocorre a atualização das posições das partículas no algoritmo de otimização. Aqui está um resumo do que acontece:
1. O valor da variável "epochNow" é incrementado.
2. Se a variável "revision" for "false", então é feita a inicialização das posições iniciais das partículas. Cada coordenada da partícula recebe um valor aleatório dentro do intervalo definido e, em seguida, esse valor é convertido de acordo com o passo estabelecido.
3. Se a variável "revision" for "true", então são calculados o valor de "K", as melhores e piores avaliações da função para cada partícula, os carregamentos são atualizados, as forças são calculadas, e a velocidade e posição de cada partícula são atualizadas.
A ideia geral deste método é atualizar as posições das partículas no algoritmo de otimização utilizando métodos específicos para calcular as fórmulas das leis de movimento das partículas.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEFA::Moving () { epochNow++; //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- K = CalculateK (epochNow); double best = -DBL_MAX; double worst = DBL_MAX; for (int i = 0; i < popSize; i++) { if (a [i].f > best) best = a [i].f; if (a [i].f < worst) worst = a [i].f; } UpdateCharges (best, worst); CalculateForces (); for (int i = 0; i < popSize; i++) { UpdateVelocityAndPosition (i); } } //——————————————————————————————————————————————————————————————————————————————
No método "CalculateK()" da classe "C_AO_AEFA", é calculado o valor do parâmetro "K" com base no tempo "t" (número da época atual) e nos demais parâmetros "K0", "alpha" e "epochs". Veja o que acontece nesse método:
1. O método recebe como entrada o parâmetro "t", que representa o número da época atual no algoritmo.
2. Em seguida, é feito o cálculo do valor de "K".
3. O resultado do cálculo pela fórmula é retornado como valor do método.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_AEFA::CalculateK (int t) { return K0 * MathExp (-alpha * t / epochs); } //——————————————————————————————————————————————————————————————————————————————
No método "UpdateCharges()" da classe "C_AO_AEFA", os carregamentos das partículas são atualizados com base nos valores de melhor e pior adaptabilidade. Resumo das ações do método:
1. Uma variável "sum_q" é criada e inicializada com "0".
2. Em seguida, é feito um laço sobre todas as partículas, do índice "0" até "popSize".
3. Dentro do laço, para cada partícula, calcula-se a carga relativa usando a fórmula.
4. O valor da carga relativa é somado à variável "sum_q".
5. Depois, ocorre um segundo laço sobre todas as partículas, em que a cada uma é atribuído um valor de carga igual à carga relativa dividida por "sum_q".
Dessa forma, esse método atualiza as cargas das partículas com base em sua adaptabilidade, de modo que elas reflitam sua qualidade relativa em comparação com os melhores e piores valores de adaptabilidade.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEFA::UpdateCharges (double best, double worst) { double sum_q = 0; for (int i = 0; i < popSize; i++) { agent [i].relative_charge = MathExp ((a [i].f - worst) / (best - worst)); sum_q += agent [i].relative_charge; } for (int i = 0; i < popSize; i++) { agent [i].charge = agent [i].relative_charge / sum_q; } } //——————————————————————————————————————————————————————————————————————————————
Apresentamos agora os métodos "CalculateForces()" e "CalculateDistance()" da classe "C_AO_AEFA".
O método "CalculateDistance()" recebe dois arrays "x1[]" e "x2[]", representando as coordenadas de duas partículas, e calcula a distância entre elas no espaço. Para isso, realiza-se uma iteração por todas as coordenadas dos arrays, e para cada coordenada calcula-se o quadrado da diferença entre os elementos correspondentes dos arrays, depois esses quadrados são somados. Em seguida, extrai-se a raiz quadrada da soma obtida, e esse valor é retornado como a distância entre os dois pontos no espaço (distância Euclidiana).
O método "CalculateForces()" calcula as forças que atuam sobre cada partícula. Para cada partícula, é calculado um vetor de forças em relação a todas as outras partículas. Para cada par de partículas, exceto quando i == j, calcula-se a distância entre elas utilizando o método "CalculateDistance()". Em seguida, para cada coordenada do espaço, calcula-se a força que atua sobre a partícula, usando uma fórmula que inclui as cargas das partículas, suas posições e a distância entre elas. Os resultados são somados para cada coordenada, e então as forças obtidas são divididas pela carga da partícula, para considerar sua influência sobre a velocidade da partícula.
Dessa forma, os métodos realizam os cálculos das forças que atuam entre as partículas no algoritmo e das distâncias entre elas no espaço, respectivamente.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEFA::CalculateForces () { double force []; ArrayResize (force, coords); for (int i = 0; i < popSize; i++) { ArrayInitialize (force, 0); for (int j = 0; j < popSize; j++) { if (i != j) { double R = CalculateDistance (a [i].c, a [j].c); for (int d = 0; d < coords; d++) { force [d] += u.RNDprobab () * K * (agent [i].charge * agent [j].charge * (agent [j].best_position [d] - a [i].c [d])) / (R * R + epsilon); } } } for (int d = 0; d < coords; d++) { agent [i].velocity [d] = force [d] / agent [i].charge; } } } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— double C_AO_AEFA::CalculateDistance (const double &x1 [], const double &x2 []) { double sum = 0; for (int d = 0; d < coords; d++) { sum += (x1 [d] - x2 [d]) * (x1 [d] - x2 [d]); } return MathSqrt (sum); } //——————————————————————————————————————————————————————————————————————————————
Apresentamos agora o método "UpdateVelocityAndPosition()" da classe "C_AO_AEFA". Esse método atualiza a velocidade e a posição da partícula com índice "i". Para cada coordenada da partícula no espaço, ocorre o seguinte:
1. Calcula-se a aceleração, que depende da carga da partícula, da sua velocidade atual e da massa da partícula.
2. A velocidade da partícula é atualizada adicionando-se um componente aleatório multiplicado pela velocidade atual, mais a aceleração.
3. A posição da partícula é atualizada somando à posição atual a nova velocidade. Em seguida, a nova posição é limitada dentro dos valores mínimos e máximos definidos para cada coordenada usando o método "u.SeInDiSp()".
Assim, o método "UpdateVelocityAndPosition()" atualiza a velocidade e a posição da partícula no algoritmo de otimização, considerando a aceleração, fatores aleatórios e restrições sobre a posição no espaço.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEFA::UpdateVelocityAndPosition (int i) { for (int d = 0; d < coords; d++) { double acceleration = (agent [i].charge * agent [i].velocity [d]) / particleMass; agent [i].velocity [d] = (u.RNDfromCI (0, 1)) * agent [i].velocity [d] + acceleration; a [i].c [d] += agent [i].velocity [d]; a [i].c [d] = u.SeInDiSp (a [i].c [d], rangeMin [d], rangeMax [d], rangeStep [d]); } } //——————————————————————————————————————————————————————————————————————————————
Para concluir, o método "Revision()" da classe C_AO_AEFA. Neste método, ocorre a atualização das informações sobre as melhores posições das partículas e seus melhores valores de adaptabilidade, bem como a melhor solução global "fB". O método executa as seguintes ações:
1. Uma variável "ind" é criada como uma flag e índice da posição no array da melhor solução, sendo inicializada com "-1".
2. Em seguida, é feito um laço sobre todas as partículas, do índice "0" até "popSize".
3. Dentro do laço, verifica-se se o valor da função de adaptabilidade da partícula é maior que o valor de "fB". Se for, "fB" é atualizado e a variável "ind" recebe o valor "i".
4. Depois, verifica-se se a adaptabilidade da partícula é maior que a melhor adaptabilidade que essa partícula já teve ao longo de todas as épocas (armazenada em agent[i].best_fitness). Se for, o melhor valor é atualizado, assim como a melhor posição.
5. Por fim, se "ind" for diferente de "-1", a posição "cB" é atualizada copiando a posição da partícula com índice "ind".
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEFA::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } if (a [i].f > agent [i].best_fitness) { agent [i].best_fitness = a [i].f; ArrayCopy (agent [i].best_position, a [i].c, 0, 0, WHOLE_ARRAY); } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
3. Resultados dos testes
Impressão da execução do algoritmo AEFA em um ambiente de testes com funções de benchmark:
AEFA|Artificial Electric Field Algorithm|20.0|1000.0|10.0|100.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8769988087850553
25 Hilly's; Func runs: 10000; result: 0.617530930198765
500 Hilly's; Func runs: 10000; result: 0.2523539056281608
=============================
5 Forest's; Func runs: 10000; result: 0.927287032866128
25 Forest's; Func runs: 10000; result: 0.7269761843712702
500 Forest's; Func runs: 10000; result: 0.18063577020760296
=============================
5 Megacity's; Func runs: 10000; result: 0.6661538461538462
25 Megacity's; Func runs: 10000; result: 0.11630769230769236
500 Megacity's; Func runs: 10000; result: 0.0950769230769239
=============================
All score: 4.45932 (49.55%)
Analisando a execução do algoritmo, é possível tirar as seguintes conclusões: os resultados de um teste para outro variam bastante. Além disso, o algoritmo demonstra capacidades de busca muito fracas ao lidar com funções de alta dimensionalidade, o que também é confirmado pela forma como os resultados de sua execução são apresentados. Foram identificados problemas específicos ao lidar com funções discretas.
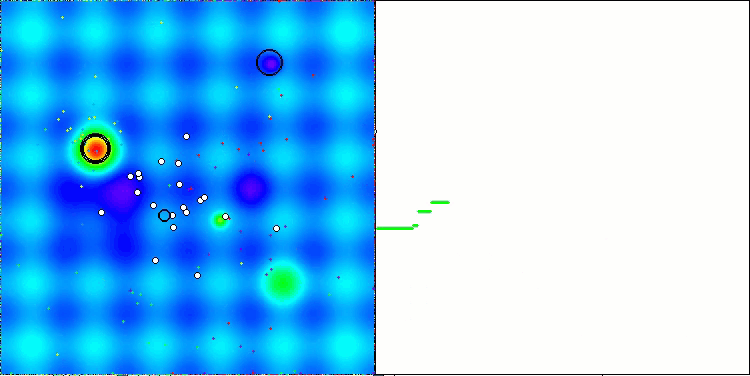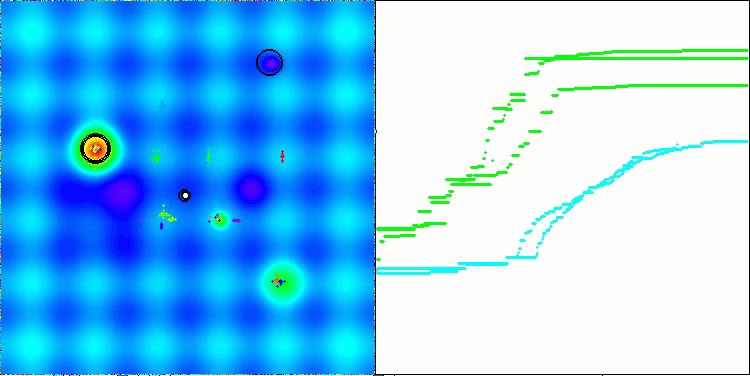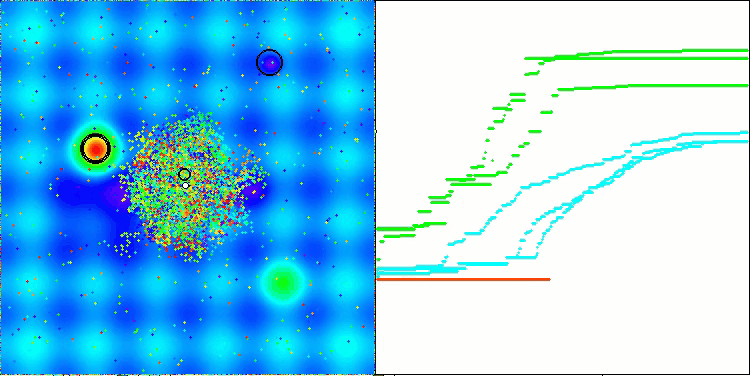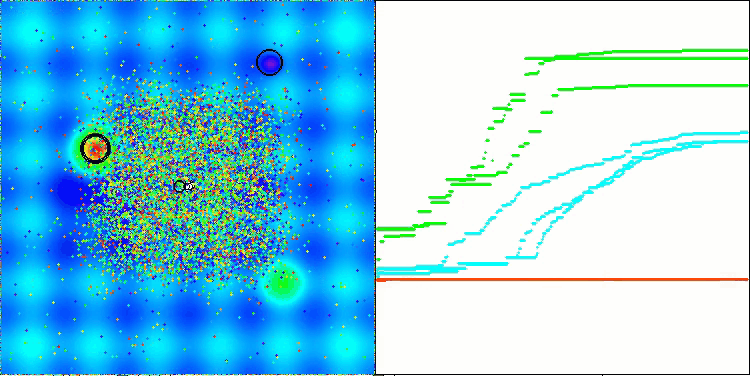
AEFA na função de teste Hilly.
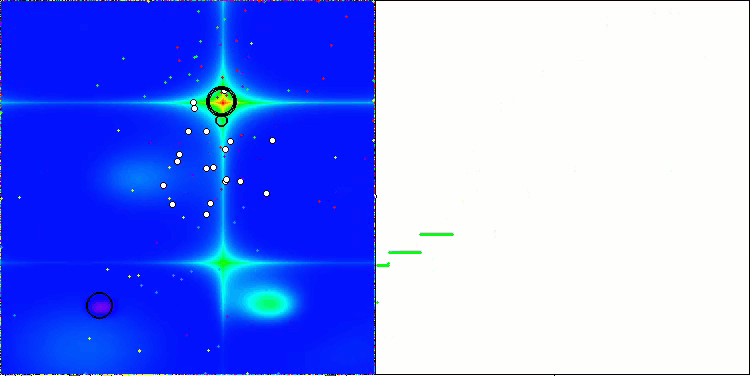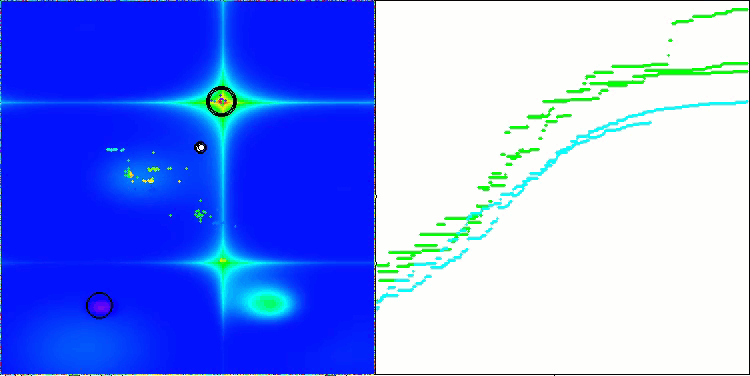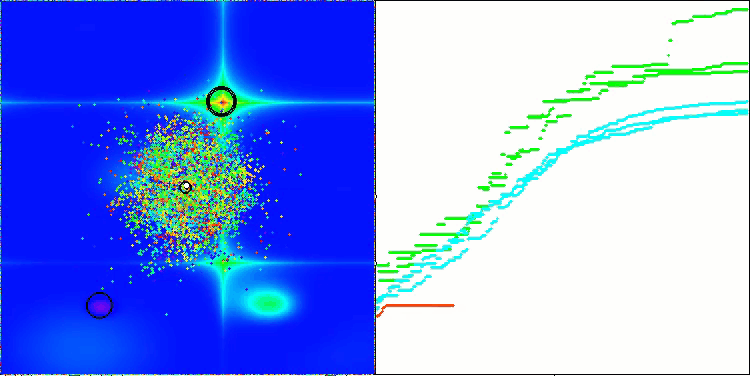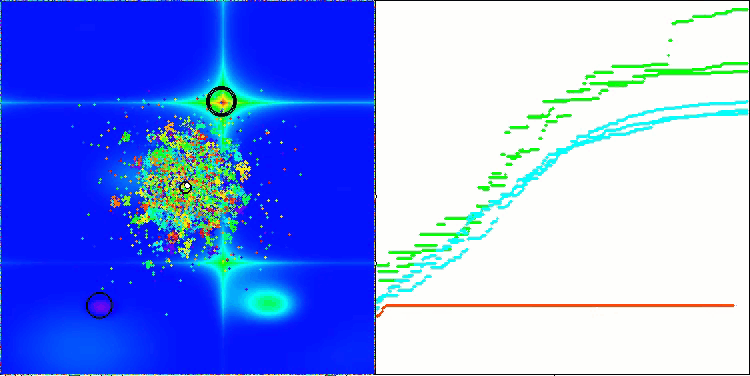
AEFA na função de teste Forest.
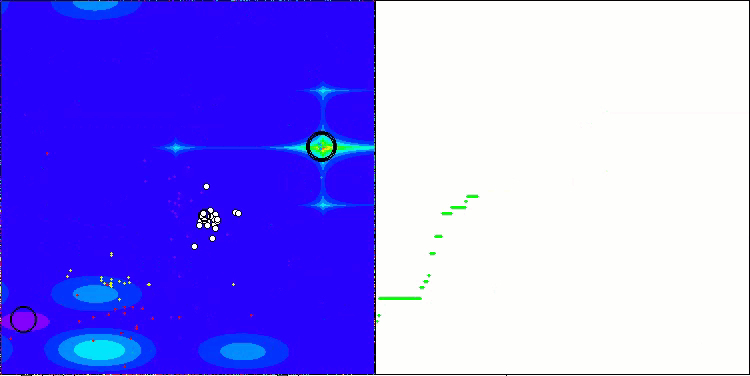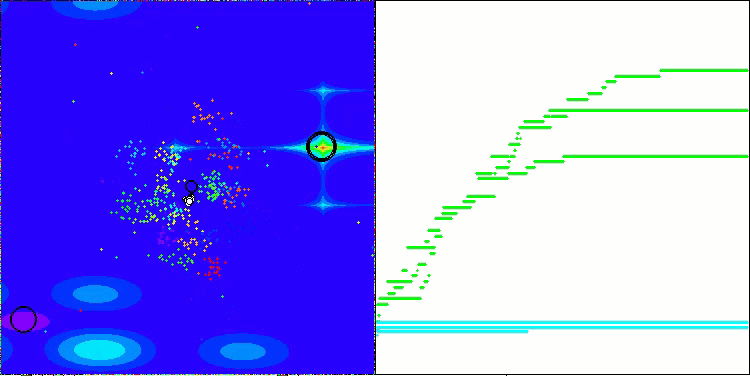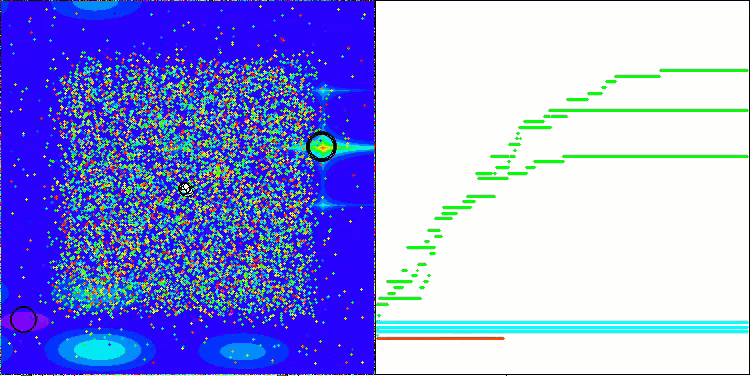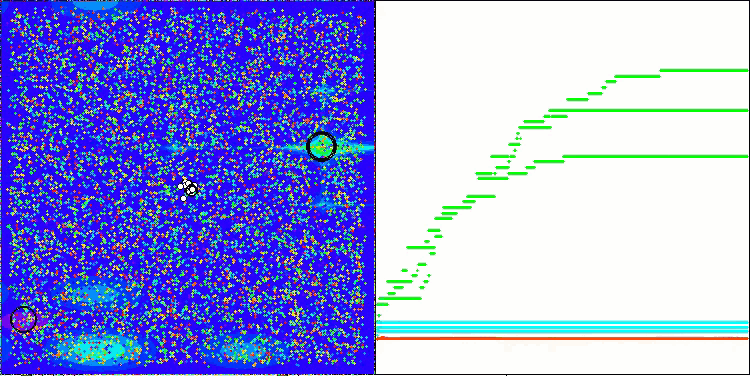
AEFA na função de teste Megacity.
Gostaria de destacar um aspecto importante do algoritmo AEFA. Após realizar os experimentos padrão com 10.000 execuções da função de adaptabilidade, decidimos realizar um experimento adicional, aumentando o número de execuções para 100.000, e o resultado superou minhas expectativas. Em muitas funções com pequeno número de parâmetros, o algoritmo atingiu 100% de convergência com o aumento no número de execuções da função de adaptabilidade. É importante observar que nem todos os algoritmos do ranking, mesmo os que ocupam as primeiras posições, conseguem atingir 100% de convergência com esse aumento, pois acabam presos em mínimos locais. Neste caso, o algoritmo mostra resistência a esse tipo de estagnação. No entanto, ele ainda enfrenta as mesmas dificuldades ao buscar soluções em espaços de alta dimensionalidade, o que é particularmente evidente em funções discretas.
Impressão da execução do algoritmo AEFA em um ambiente de testes com 100.000 execuções de funções de benchmark:
SDSm|Stochastic Diffusion Search M|100.0|100.0|0.05|
=============================
5 Hilly's; Func runs: 100000; result: 0.9874670077970368
25 Hilly's; Func runs: 100000; result: 0.9355482229513405
500 Hilly's; Func runs: 100000; result: 0.5943074120378588
=============================
5 Forest's; Func runs: 100000; result: 0.994126703499673
25 Forest's; Func runs: 100000; result: 0.9627011069578397
500 Forest's; Func runs: 100000; result: 0.5628894538341265
=============================
5 Megacity's; Func runs: 100000; result: 0.9015384615384615
25 Megacity's; Func runs: 100000; result: 0.7264615384615385
500 Megacity's; Func runs: 100000; result: 0.37464615384615396
=============================
All score: 7.03969 (78.22%)
Você pode observar essa característica de convergência do algoritmo nas imagens abaixo para as respectivas funções.
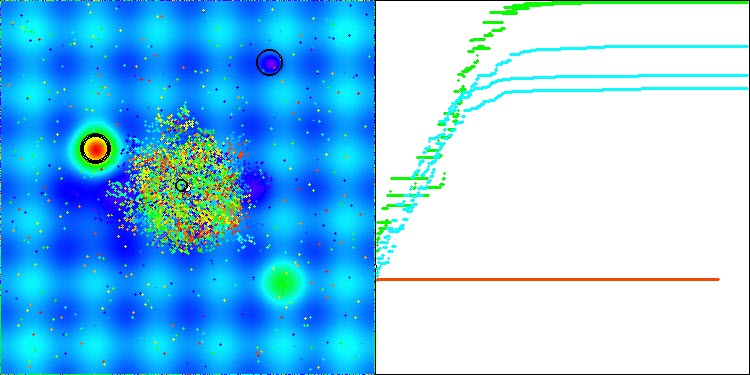
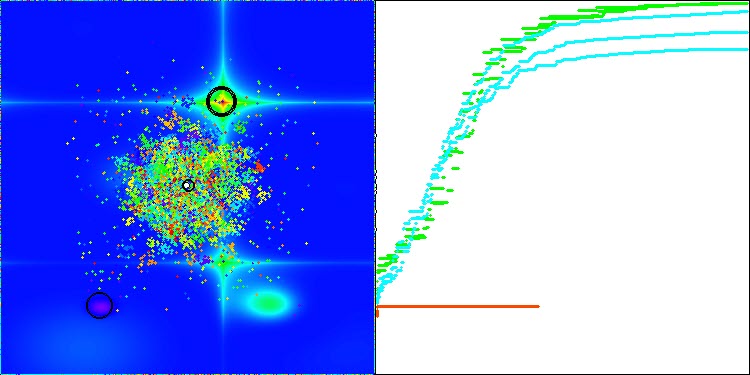
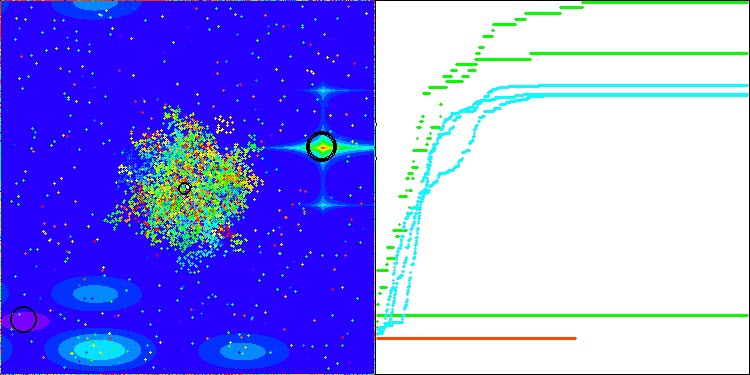
Tabela de classificação de algoritmos de otimização populacionais:
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | BGA | binary genetic algorithm | 0,99989 | 0,99518 | 0,42835 | 2,42341 | 0,96153 | 0,96181 | 0,32027 | 2,24360 | 0,91385 | 0,95908 | 0,24220 | 2,11512 | 6,782 | 75,36 |
| 2 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 3 | CLA | code lock algorithm | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | ESG | evolution of social groups | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 8 | SIA | simulated isotropic annealing | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 9 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 10 | TSEA | turtle shell evolution algorithm | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 11 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 12 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 13 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 14 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 15 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 16 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 17 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 18 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 19 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 20 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 21 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 22 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 23 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 24 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 25 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 26 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 27 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 28 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 29 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 30 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 31 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 32 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 33 | SA | simulated annealing | 0,55787 | 0,42177 | 0,31549 | 1,29513 | 0,34998 | 0,15259 | 0,05023 | 0,55280 | 0,31167 | 0,10033 | 0,02883 | 0,44083 | 2,289 | 25,43 |
| 34 | IWDm | intelligent water drops M | 0,54501 | 0,37897 | 0,30124 | 1,22522 | 0,46104 | 0,14704 | 0,04369 | 0,65177 | 0,25833 | 0,09700 | 0,02308 | 0,37842 | 2,255 | 25,06 |
| 35 | PSO | particle swarm optimisation | 0,59726 | 0,36923 | 0,29928 | 1,26577 | 0,37237 | 0,16324 | 0,07010 | 0,60572 | 0,25667 | 0,08000 | 0,02157 | 0,35823 | 2,230 | 24,77 |
| 36 | Boids | boids algorithm | 0,43340 | 0,30581 | 0,25425 | 0,99346 | 0,35718 | 0,20160 | 0,15708 | 0,71586 | 0,27846 | 0,14277 | 0,09834 | 0,51957 | 2,229 | 24,77 |
| 37 | MA | monkey algorithm | 0,59107 | 0,42681 | 0,31816 | 1,33604 | 0,31138 | 0,14069 | 0,06612 | 0,51819 | 0,22833 | 0,08567 | 0,02790 | 0,34190 | 2,196 | 24,40 |
| 38 | SFL | shuffled frog-leaping | 0,53925 | 0,35816 | 0,29809 | 1,19551 | 0,37141 | 0,11427 | 0,04051 | 0,52618 | 0,27167 | 0,08667 | 0,02402 | 0,38235 | 2,104 | 23,38 |
| 39 | FSS | fish school search | 0,55669 | 0,39992 | 0,31172 | 1,26833 | 0,31009 | 0,11889 | 0,04569 | 0,47467 | 0,21167 | 0,07633 | 0,02488 | 0,31288 | 2,056 | 22,84 |
| 40 | RND | random | 0,52033 | 0,36068 | 0,30133 | 1,18234 | 0,31335 | 0,11787 | 0,04354 | 0,47476 | 0,25333 | 0,07933 | 0,02382 | 0,35648 | 2,014 | 22,37 |
| 41 | GWO | grey wolf optimizer | 0,59169 | 0,36561 | 0,29595 | 1,25326 | 0,24499 | 0,09047 | 0,03612 | 0,37158 | 0,27667 | 0,08567 | 0,02170 | 0,38403 | 2,009 | 22,32 |
| 42 | CSS | charged system search | 0,44252 | 0,35454 | 0,35201 | 1,14907 | 0,24140 | 0,11345 | 0,06814 | 0,42299 | 0,18333 | 0,06300 | 0,02322 | 0,26955 | 1,842 | 20,46 |
| 43 | EM | electroMagnetism-like algorithm | 0,46250 | 0,34594 | 0,32285 | 1,13129 | 0,21245 | 0,09783 | 0,10057 | 0,41085 | 0,15667 | 0,06033 | 0,02712 | 0,24412 | 1,786 | 19,85 |
Considerações finais
Com base nos resultados da execução do algoritmo Artificial Electric Field Algorithm (AEFA) em funções de teste com diferentes dimensionalidades, podemos tirar as seguintes conclusões:
1. O AEFA apresenta resultados satisfatórios em várias funções de teste, incluindo Hilly, Forest e Megacity. No entanto, os resultados na função discreta Megacity são inferiores em comparação com as demais funções.
2. O algoritmo demonstra bom desempenho com um grande número de execuções da função (100.000), o que permite melhorar a precisão da convergência até alcançar 100% em problemas de baixa dimensionalidade.
3. O AEFA apresenta uma pontuação geral de 4.45932 (49,55%) e ocupa a 19ª posição na tabela de classificação, situando-se em uma posição intermediária entre os algoritmos populacionais de otimização.
Embora o algoritmo AEFA não tenha apresentado os melhores resultados em nosso conjunto padrão de testes com funções de diferentes dimensionalidades, ele possui uma vantagem adicional: à medida que o número de execuções da função de adaptabilidade aumenta, ele atinge um resultado geral impressionante de 7.03969 (78,22%), o que o torna uma opção interessante para problemas de baixa dimensionalidade, especialmente aqueles com superfícies suaves.
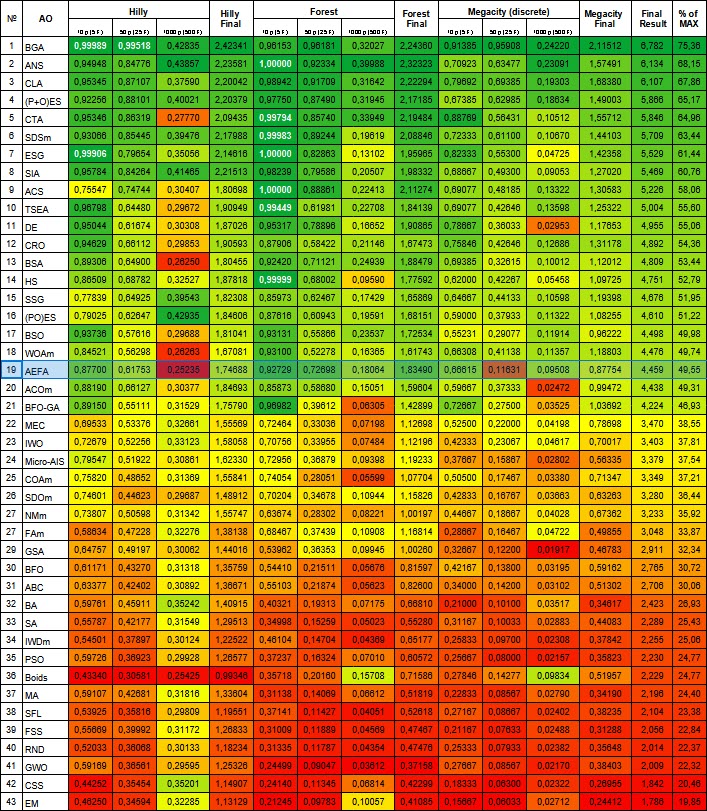
Figura 2. Gradiente de cores dos algoritmos de acordo com os respectivos testes. Branco destaca resultados maiores ou iguais a 0.99
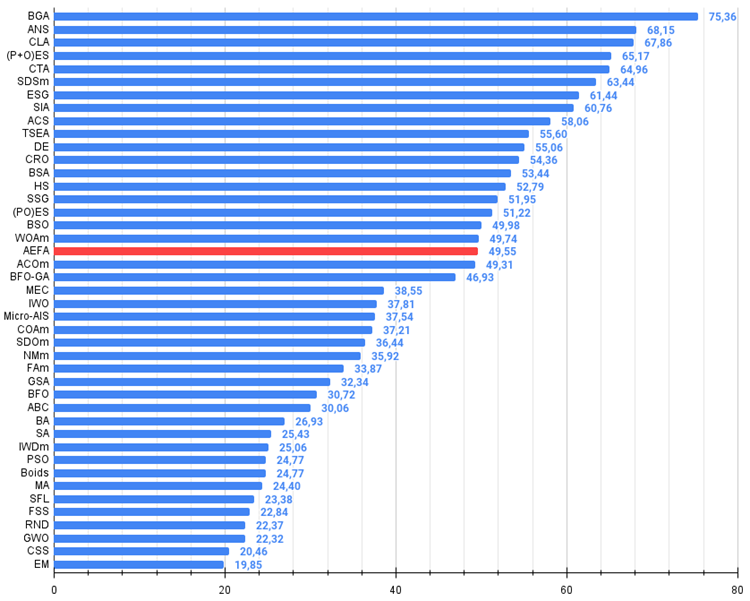
Figura 3. Histograma dos resultados dos testes dos algoritmos (em escala de 0 a 100, quanto maior, melhor,
onde 100 representa o resultado teórico máximo possível; o script para cálculo da tabela de classificação está no arquivo)
Pontos positivos e negativos do algoritmo do campo elétrico artificial (AEFA):
Prós:
- Excelente convergência em funções suaves de baixa dimensionalidade, quando há número suficiente de execuções da função de adaptabilidade.
- Número relativamente pequeno de parâmetros externos.
Contras:
- Grande variação nos resultados em funções do nosso teste padrão.
- Desempenho fraco em funções discretas.
- Escalabilidade muito baixa.
- Implementação complexa.
O artigo inclui um arquivo com as versões atualizadas dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar suas capacidades de busca. As conclusões e opiniões apresentadas nos artigos são baseadas nos resultados dos experimentos realizados.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/15162
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Do básico ao intermediário: Indicador (III)
Do básico ao intermediário: Indicador (III)
 Redes neurais em trading: Modelo de dupla atenção para previsão de tendências
Redes neurais em trading: Modelo de dupla atenção para previsão de tendências
 Simulação de mercado (Parte 13): Sockets (VII)
Simulação de mercado (Parte 13): Sockets (VII)
 Técnicas do MQL5 Wizard que você deve conhecer (Parte 33): Kernels de Processos Gaussianos
Técnicas do MQL5 Wizard que você deve conhecer (Parte 33): Kernels de Processos Gaussianos
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso