Redes neurais de maneira fácil (Parte 56): Utilização da norma nuclear para estimular a pesquisa

Introdução

O aprendizado por reforço é baseado no paradigma da exploração independente do ambiente realizada pelo Agente. Com suas ações, o Agente afeta o ambiente, levando à sua mudança. Em troca, o Agente recebe uma certa recompensa.

E aqui se destacam os dois principais problemas do aprendizado por reforço: a exploração do ambiente e a função de recompensa. Uma função de recompensa bem estruturada incentiva o Agente a explorar o ambiente e buscar as estratégias de comportamento mais ótimas.

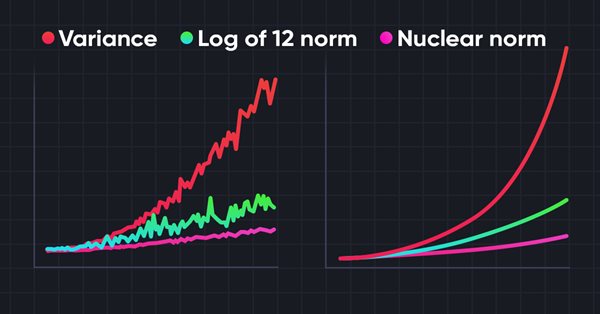
No entanto, ao resolver a maioria das tarefas práticas, nos deparamos com recompensas externas esparsas. Para superar essa barreira, foi proposto o uso das chamadas recompensas internas. Elas permitem que o Agente adquira novas habilidades que podem ser úteis para obter recompensas externas no futuro. Contudo, as recompensas internas podem ser ruidosas devido à estocasticidade do ambiente. A aplicação direta de valores preditivos ruidosos para observações pode impactar negativamente na eficácia do treinamento da política do Agente. Além disso, muitos métodos usam a norma L2 ou a variância para medir a novidade da pesquisa, o que intensifica o ruído por causa da operação de elevação ao quadrado.

Para resolver o problema indicado, no artigo "Nuclear Norm Maximization Based Curiosity-Driven Learning" foi proposto o uso de um novo algoritmo para estimular a curiosidade do Agente baseado na maximização da norma nuclear (Nuclear Norm Maximization - NNM). Tal recompensa interna pode avaliar mais precisamente a novidade da pesquisa do ambiente. Ao mesmo tempo, permite garantir alta resistência ao ruído e às anomalias.

1. Norma nuclear e sua aplicação

As normas matriciais, incluindo a norma nuclear, são amplamente utilizadas na análise e métodos computacionais de álgebra linear. A norma nuclear desempenha um papel importante no estudo das propriedades das matrizes, tarefas de otimização, avaliação de condições e muitas outras áreas da matemática e ciências aplicadas.

A norma nuclear de uma matriz é uma característica numérica que define o "tamanho" da matriz. Ela é um caso particular da norma de Schatten e é igual à soma dos valores singulares da matriz.

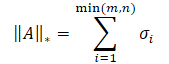
onde σi são os elementos do vetor de valores singulares da matriz A.

Por sua essência, a norma nuclear representa a envoltória convexa da função de postos para um conjunto de matrizes com a mesma norma espectral. Isso permite seu uso na resolução de várias tarefas de otimização.

A ideia principal do método de maximização da norma nuclear (NNM) consiste em uma avaliação precisa da novidade usando a norma nuclear da matriz ao visitar um estado, mitigando o impacto do ruído e várias anomalias. A matriz de tamanho n*m consiste em n estados codificados do ambiente. Cada estado tem dimensão m. A matriz combina o estado atual s e seus (n 1) vizinhos mais próximos. Aqui, s representa um estado abstrato, mapeando a observação multidimensional original para um espaço abstrato de baixa dimensão. Como cada linha da matriz S representa um estado codificado, o(s) posto(s) pode(m) ser usado(s) para representar a diversidade dentro da matriz. Uma maior classificação da matriz S indica uma maior distância linear entre os estados codificados. Os autores do método abordam criativamente a tarefa e aplicam a maximização do posto da matriz para aumentar a diversidade da pesquisa. Isso incentiva o Agente de nosso modelo a visitar estados mais diversos com alta variedade.

Existem duas abordagens para o uso do máximo posto da matriz: como uma função de perda ou como uma recompensa. Maximizar o posto da matriz diretamente é uma tarefa bastante difícil devido à sua função não convexa. Por isso, não o utilizaremos como uma função de perda. No entanto, o valor do posto da matriz é discreto e não pode refletir precisamente a novidade dos estados. Consequentemente, usar o valor bruto do posto da matriz como recompensa para guiar o treinamento do modelo também não é eficaz.

Matematicamente, o cálculo do posto da matriz é geralmente substituído por sua norma nuclear. Assim, a novidade pode ser suportada pela maximização aproximada da norma nuclear. Comparada ao posto, a norma nuclear possui várias propriedades boas. Primeiramente, a convexidade da norma nuclear permite o desenvolvimento de algoritmos de otimização rápidos e convergentes. Em segundo lugar, a norma nuclear é uma função contínua, o que é importante para muitas tarefas de treinamento.

Os autores do método NNM propõem definir a recompensa interna pela fórmula

onde:
      λ    — peso para ajustar o intervalo de valores da norma nuclear;
      ‖S‖⋆ — a norma nuclear da matriz de estados;
      ‖S‖F — a norma de Frobenius da matriz de estados.

Já conhecemos a norma nuclear da matriz, e a norma de Frobenius é calculada como a raiz quadrada da soma dos quadrados de todos os elementos da matriz.

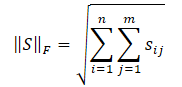
A desigualdade de Cauchy-Schwarz nos permite fazer as seguintes transformações.

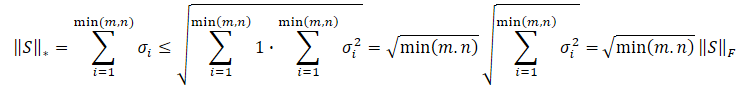
Obviamente, a raiz quadrada da soma dos quadrados dos valores será sempre menor ou igual à soma dos próprios valores. Consequentemente, a norma nuclear da matriz será sempre maior ou igual à norma de Frobenius da mesma matriz. E podemos derivar as seguintes desigualdades.

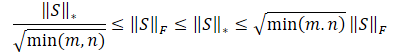
Esta desigualdade mostra que a norma nuclear e a norma de Frobenius se limitam mutuamente. Se a norma nuclear aumenta, então a norma de Frobenius tende a aumentar também.

Além disso, a norma de Frobenius possui outra propriedade útil para nós — ela é estritamente oposta à entropia em monotonicidade. Seu aumento é equivalente à diminuição da entropia. Como resultado, os efeitos da norma nuclear podem ser divididos em duas partes:

1. Alta diversidade.
2. Baixa entropia.

Necessitamos estimular o Agente a visitar estados mais novos, e nosso objetivo é a diversidade. No entanto, a redução da entropia significa um aumento na agregação dos estados. Isto é, uma maior semelhança entre os estados. Então, buscamos incentivar o primeiro efeito e reduzir a influência do segundo. Para isso, dividimos a norma nuclear da matriz pela sua norma de Frobenius.

Dividindo as desigualdades apresentadas acima pela norma de Frobenius, obtemos.

É óbvio que o uso direto de tal escala de recompensas pode prejudicar o desempenho do treinamento do modelo. Além disso, a raiz quadrada da menor dimensão da matriz de estados pode variar em diferentes ambientes ou com diferentes arquiteturas de modelos treináveis. Por isso, é bom reescalar nossa escala de recompensas. E, uma vez que min(m, n) ≤ max(m, n), obtemos:

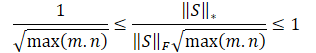
As exposições matemáticas acima nos permitem definir automaticamente o coeficiente de ajuste do intervalo de valores da norma nuclear da matriz λ, como

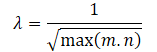
Assim, a fórmula da recompensa interna assume a forma:

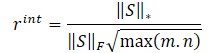
Abaixo está a visualização autoral do método de maximização da norma nuclear.

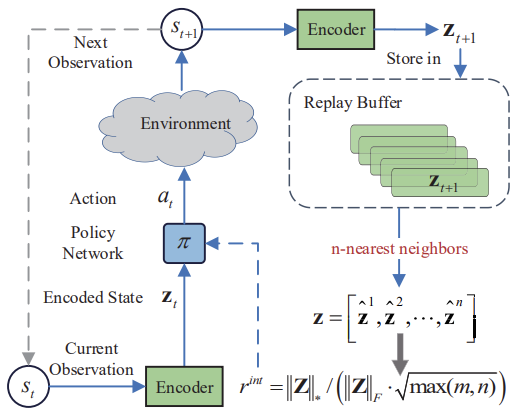
Os resultados dos testes apresentados no artigo do autor demonstram a superioridade do método proposto sobre outros algoritmos de exploração do ambiente. Incluindo o Módulo de Curiosidade Intrínseca e a Self-Supervised Exploration via Disagreement que já examinamos. Além disso, chama a atenção o fato de que o método mostra melhores resultados quando adicionado ruído aos dados de entrada. Sugiro que passemos à parte prática de nosso artigo para avaliar as capacidades do método na resolução de nossas tarefas.

2. Implementação com MQL5

Antes de começarmos a implementação do método Nuclear Norm Maximization (NNM), vamos destacar sua principal inovação — a nova fórmula de recompensa interna. Graças a isso, essa abordagem pode ser implementada como um complemento a praticamente qualquer algoritmo de aprendizado por reforço previamente examinado.

É importante notar também que o algoritmo utiliza um codificador para converter os estados do ambiente em uma representação comprimida. E também utiliza o algoritmo k-vizinhos mais próximos para formar a matriz de representações comprimidas do estado do ambiente.

Na minha opinião subjetiva, a solução mais simples parece ser a implementação da recompensa interna proposta no algoritmo RE3. Nele, também é utilizado um codificador para converter os estados do ambiente em uma representação comprimida. Para esses fins, no RE3, usamos um codificador convolutivo aleatório. Isso permite reduzir os custos de treinamento do codificador.

Além disso, no RE3, também são usados estados k-vizinhos mais próximos do ambiente para formar a recompensa interna. Mas esta recompensa é formada de maneira diferente.

A direção das nossas ações é clara e começamos a trabalhar. Primeiro, copiaremos todos os arquivos do diretório "...\Experts\RE3\" para "...\Experts\NNM\". Lembro que lá se encontram 4 arquivos:

• Trajectory.mqh — biblioteca de constantes comuns, estruturas e métodos.
• Research.mq5 — Expert Advisor para interação com o ambiente e coleta de amostras de treinamento.
• Study.mq5 — Expert Advisor para o treinamento direto dos modelos.
• Test.mq5 — Expert Advisor para testar os modelos treinados.

Também usaremos a recompensa decomposta. A estrutura do vetor de recompensas terá o seguinte formato.

//+------------------------------------------------------------------+
//| Rewards structure                                                |
//|   0     -  Delta Balance                                         |
//|   1     -  Delta Equity ( "-" Drawdown / "+" Profit)             |
//|   2     -  Penalty for no open positions                         |
//|   3     -  NNM                                                   |
//+------------------------------------------------------------------+

No arquivo "...\NNM\Trajectory.mqh", aumentaremos os tamanhos da representação comprimida do estado do ambiente e da camada totalmente conectadas interna dos nossos modelos.

#define                    EmbeddingSize   16            
#define                    LatentCount    512

Neste mesmo arquivo está o método para descrever a arquitetura dos modelos usados, CreateDescriptions. Hoje vamos usar 3 modelos de redes neurais: Ator, Crítico e Codificador. Como o último, usaremos um codificador convolucional aleatório.

bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic, CArrayObj *convolution)
  {
//---
   CLayerDescription *descr;
//---
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!critic)
     {
      critic = new CArrayObj();
      if(!critic)
         return false;
     }
   if(!convolution)
     {
      convolution = new CArrayObj();
      if(!convolution)
         return false;
     }

No corpo do método, criamos uma variável local para armazenar o ponteiro para o objeto de descrição de uma camada neural CLayerDescription e, se necessário, inicializamos arrays dinâmicos para descrever as soluções arquitetônicas dos modelos usados.

Primeiro, criaremos a descrição da arquitetura do Ator, que consiste em 2 blocos: pré-processamento dos dados de entrada e tomada de decisão.

Os dados históricos do movimento de preço do instrumento analisado e os indicadores são fornecidos à entrada do bloco de pré-processamento dos dados de entrada. Como se pode observar, diferentes indicadores têm diferentes gamas de valores. Isso tem um impacto negativo na eficácia do treinamento dos modelos. Portanto, os dados obtidos são normalizados usando a camada de normalização em lote CNeuronBatchNormOCL.

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1000;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Os dados normalizados são passados por 2 camadas convolucionais, para buscar padrões individuais dos indicadores.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = BarDescr;
   descr.window = HistoryBars;
   descr.step = HistoryBars;
   int prev_wout=descr.window_out = HistoryBars/2;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = prev_count;
   descr.window = prev_wout;
   descr.step = prev_wout;
   descr.window_out = 8;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Os dados resultantes são processados por camadas neurais totalmente conectadas.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.optimization = ADAM;
   descr.activation = LReLU;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Nesta etapa do bloco de pré-processamento dos dados de entrada, esperamos obter alguma representação latente dos dados históricos do instrumento analisado. Isso pode ser suficiente para determinar a direção de abertura ou manutenção de uma posição, mas não suficiente para implementar funções de gerenciamento de dinheiro. Complementaremos os dados com informações sobre o estado da conta.

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = prev_count;
   descr.step = AccountDescr;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Segue-se o bloco de tomada de decisões composto por camadas totalmente conectadas, que termina com uma camada estocástica de representação latente de um autocodificador variacional. Como antes, usamos este tipo de camada na saída do modelo para implementar a política estocástica do Ator.

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 2 * NActions;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 10
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronVAEOCL;
   descr.count = NActions;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Descrevemos completamente a arquitetura do Ator. Com isso, construímos um modelo para implementar uma política estocástica, destacando a possibilidade de usar o método Nuclear Norm Maximization para tais soluções. Além disso, nosso Ator trabalhará em um espaço de ação contínuo. No entanto, isso não limita o escopo de uso do método NNM.

A próxima etapa será criar a descrição da arquitetura do Crítico. Aqui, utilizaremos uma abordagem já testada e excluiremos o bloco de pré-processamento de dados. Como dados de entrada, tomaremos a representação latente do estado dos dados históricos do instrumento e do estado da conta dos camadas neurais internas do Ator. Ao mesmo tempo, combinamos a representação interna do estado do ambiente e o tensor de ações gerado pelo Ator.

//--- Critic
   critic.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = LatentCount;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = prev_count;
   descr.step = NActions;
   descr.optimization = ADAM;
   descr.activation = LReLU;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }

Os dados obtidos são processados por camadas totalmente conectadas do nosso Crítico e é gerado um vetor de valores preditivos no contexto da decomposição da nossa função de recompensa.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = NRewards;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }

Já descrevemos a arquitetura de 2 modelos. E nos resta criar a arquitetura do Codificador. Aqui, voltamos à parte teórica e observamos que o método NNM prevê o mapeamento dos estados do ambiente após a transição St+1. Claramente, o método foi desenvolvido para treinamento online. Mas falaremos mais sobre isso um pouco mais tarde. Na etapa de formação da arquitetura dos modelos, é importante entender que o codificador processará os dados históricos do instrumento analisado e os indicadores do estado da conta. Criaremos uma camada de dados de entrada de tamanho suficiente.

//--- Convolution
   convolution.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = (HistoryBars * BarDescr) + AccountDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }

Observe que não usamos nem a camada de normalização de dados nem a fusão de dois tensores de dados. Isso ocorre porque não planejamos treinar este modelo. Ele é usado apenas para adaptar a representação multidimensional do ambiente em algum espaço comprimido aleatório. No qual mediremos a distância entre os estados. Mas usaremos uma camada totalmente conectada, que permitirá representar os dados de uma forma comparável.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 1024;
   descr.window = prev_count;
   descr.step = NActions;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }

Segue-se um bloco de camadas convolucionais para reduzir a dimensionalidade dos dados.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = 1024 / 16;
   descr.window = 16;
   descr.step = 16;
   prev_wout = descr.window_out = 4;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = (prev_count * prev_wout) / 8;
   descr.window = 8;
   descr.step = 8;
   prev_wout = descr.window_out = 4;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = (prev_count * prev_wout) / 4;
   descr.window = 4;
   descr.step = 4;
   prev_wout = descr.window_out = 2;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }

E, finalmente, reduzimos a dimensionalidade dos dados para o tamanho especificado usando uma camada totalmente conectada.

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = EmbeddingSize;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

O uso de camadas totalmente conectadas na entrada e saída do Codificador nos permite configurar a arquitetura das camadas convolucionais sem vinculação aos tamanhos dos dados de entrada e do incorporação da representação comprimida.

Com isso, concluímos o trabalho com a arquitetura dos modelos e voltamos à questão da descrição do estado futuro. No processo de treinamento online, não teríamos dificuldades nesta questão. No entanto, o treinamento online tem suas desvantagens. Mas, ao usar o buffer de reprodução de experiência, não temos questões sobre os dados históricos do movimento de preços do instrumento analisado e indicadores. A influência das ações do Ator é tão insignificante que pode ser negligenciada. Outra questão é o estado da conta. Ele depende diretamente da direção e do volume da posição aberta. E precisamos prever o estado da conta dependendo do vetor de ações gerado pelo Ator, com base na análise do estado atual. E essa funcionalidade implementaremos na função ForecastAccount.

Nos parâmetros do método, passaremos:

• prev_account — array descrevendo o estado atual da conta (antes das ações do agente);
• actions          — vetor de ações do Ator;
• prof_1l          — lucro por 1 lote de uma posição longa;
• time_label    — carimbo de tempo do barra previsto.

É possível notar a "diversidade" dos tipos de parâmetros. Isso está relacionado à fonte de obtenção dos dados. A descrição do estado atual da conta e o carimbo de tempo da barra prevista obtemos do buffer de reprodução de experiência, onde os dados são armazenados em arrays dinâmicos do tipo float.

As ações do Ator obtemos como resultado da propagação direta do modelo, em forma de vetor. 

vector<float> ForecastAccount(float &prev_account[],
                              vector<float> &actions,
                              double prof_1l,
                              float time_label
                             )
  {
   vector<float> account;
   double min_lot = SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN);
   double step_lot = SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_STEP);
   double stops = MathMax(SymbolInfoInteger(_Symbol,SYMBOL_TRADE_STOPS_LEVEL), 1) * Point();
   double margin_buy,margin_sell;
   if(!OrderCalcMargin(ORDER_TYPE_BUY,_Symbol,1.0,SymbolInfoDouble(_Symbol,SYMBOL_ASK),margin_buy) ||
      !OrderCalcMargin(ORDER_TYPE_SELL,_Symbol,1.0,SymbolInfoDouble(_Symbol,SYMBOL_BID),margin_sell))
      return vector<float>::Zeros(prev_account.Size());

No corpo da função, realizamos um pequeno trabalho preparatório. Determinamos o lote mínimo do instrumento e o passo de alteração do volume da posição. Solicitamos os atuais níveis de stop. E o tamanho da margem por negociação. Aqui é importante notar que não introduzimos um parâmetro adicional para a identificação do instrumento analisado. Usamos o instrumento do gráfico no qual o programa é executado. Por isso, ao treinar modelos, é muito importante manter a consistência entre a ferramenta de coleta de dados de entrada da amostra de treinamento e o gráfico ao qual o programa de treinamento dos modelos é anexado.

Em seguida, ajustamos o vetor de ações do Ator para selecionar negociações apenas em uma direção, com base na diferença de volumes. Operações semelhantes são realizadas também nos Expert Advisors para interação com o ambiente. Manter regras uniformes em todos os programas do processo de treinamento de modelos é muito importante para alcançar o resultado desejado.

Verificamos também a suficiência de fundos na conta para abrir uma posição.

   account.Assign(prev_account);
//---
   if(actions[0] >= actions[3])
     {
      actions[0] -= actions[3];
      actions[3] = 0;
      if(actions[0]*margin_buy >= MathMin(account[0],account[1]))
         actions[0] = 0;
     }
   else
     {
      actions[3] -= actions[0];
      actions[0] = 0;
      if(actions[3]*margin_sell >= MathMin(account[0],account[1]))
         actions[3] = 0;
     }

E, com base no vetor de ações ajustado, prevemos o estado da conta. Primeiramente, verificamos as posições longas. Se necessário fechar a posição, transferimos o lucro acumulado para o saldo da conta. Após isso, zeramos o volume da posição aberta e o lucro acumulado.

Ao manter uma posição aberta, verificamos a necessidade de fechamento parcial ou de aumento da posição. No fechamento parcial de uma posição, dividimos o lucro acumulado proporcionalmente entre a parte que está sendo fechada e a parte que permanece. E transferimos a parte da posição que está sendo fechada do lucro acumulado para o saldo da conta.

Se necessário, ajustamos o volume da posição aberta e alteramos o tamanho do lucro/perda acumulado proporcionalmente ao volume da posição mantida.

//--- buy control
   if(actions[0] < min_lot || (actions[1] * MaxTP * Point()) <= stops || 
      (actions[2] * MaxSL * Point()) <= stops)
     {
      account[0] += account[4];
      account[2] = 0;
      account[4] = 0;
     }
   else
     {
      double buy_lot = min_lot + MathRound((double)(actions[0] - min_lot) / step_lot) * step_lot;
      if(account[2] > buy_lot)
        {
         float koef = (float)buy_lot / account[2];
         account[0] += account[4] * (1 - koef);
         account[4] *= koef;
        }
      account[2] = (float)buy_lot;
      account[4] += float(buy_lot * prof_1l);
     }

Repetimos operações semelhantes para posições curtas.

//--- sell control
   if(actions[3] < min_lot || (actions[4] * MaxTP * Point()) <= stops || 
      (actions[5] * MaxSL * Point()) <= stops)
     {
      account[0] += account[5];
      account[3] = 0;
      account[5] = 0;
     }
   else
     {
      double sell_lot = min_lot + MathRound((double)(actions[3] - min_lot) / step_lot) * step_lot;
      if(account[3] > sell_lot)
        {
         float koef = float(sell_lot / account[3]);
         account[0] += account[5] * (1 - koef);
         account[5] *= koef;
        }
      account[3] = float(sell_lot);
      account[5] -= float(sell_lot * prof_1l);
     }

Em seguida, ajustamos o volume total de lucro/perda acumulado em ambas as direções e o capital líquido da conta.

   account[6] = account[4] + account[5];
   account[1] = account[0] + account[6];

Com base nos valores previstos obtidos, preparamos um vetor que descreve o estado da conta no formato usado para o fornecimento de dados ao modelo. E retornamos o resultado das operações ao programa chamador.

   vector<float> result = vector<float>::Zeros(AccountDescr);
   result[0] = (account[0] - prev_account[0]) / prev_account[0];
   result[1] = account[1] / prev_account[0];
   result[2] = (account[1] - prev_account[1]) / prev_account[1];
   result[3] = account[2];
   result[4] = account[3];
   result[5] = account[4] / prev_account[0];
   result[6] = account[5] / prev_account[0];
   result[7] = account[6] / prev_account[0];
   double x = (double)time_label / (double)(D'2024.01.01' - D'2023.01.01');
   result[8] = (float)MathSin(2.0 * M_PI * x);
   x = (double)time_label / (double)PeriodSeconds(PERIOD_MN1);
   result[9] = (float)MathCos(2.0 * M_PI * x);
   x = (double)time_label / (double)PeriodSeconds(PERIOD_W1);
   result[10] = (float)MathSin(2.0 * M_PI * x);
   x = (double)time_label / (double)PeriodSeconds(PERIOD_D1);
   result[11] = (float)MathSin(2.0 * M_PI * x);
//--- return result
   return result;
  }

Com isso, concluímos o trabalho preparatório e passamos para a atualização dos programas de interação com o ambiente e treinamento de modelos. Lembro que o método NNM introduz alterações na função de recompensa interna. E esta funcionalidade não afeta o processo de interação com o ambiente. Assim, os Expert Advisors "...\NNM\Research.mq5" e "...\NNM\Test.mq5" permaneceram inalterados. Seu código pode ser encontrado no anexo. E a descrição dos algoritmos é dada nos artigos anteriores.

Mas vamos nos aprofundar mais no Expert Advisor de treinamento de modelos "...\NNM\Study.mq5". Antes de mais nada, é importante dizer que o método NNM foi desenvolvido principalmente para o treinamento online. E isso é indicado pelo mapeamento dos sucessivos estados. Claro, podemos gerar estados previstos por bastante tempo. Mas a falta deles na base de comparação de estados pode ter um impacto negativo no treinamento como um todo. Pois, na ausência deles, o modelo perceberá os estados como novos e estimulará sua revisitação, sem saber de suas visitas anteriores durante o treinamento.
Teoricamente, existem 2 opções para resolver esta questão:

1. Adicionar estados previstos à base de exemplos.
2. Reduzir as iterações do ciclo de treinamento.

Ambas as abordagens têm suas desvantagens. Ao adicionar estados previstos à base de exemplos, estamos preenchendo-a com dados não confiáveis e incompletos. Sim, realizamos um cálculo matemático com base em nosso conhecimento a priori e uma série de suposições. No entanto, ainda admitimos a presença de uma certa margem de erro neles. Além disso, não temos valores de recompensa atuais para essas ações para treinar o modelo. Por isso, escolhemos o segundo método, embora ele implique um aumento do trabalho manual em termos de mais coletas de dados de treinamento e treinamento de modelos.

Reduzimos o número de iterações do ciclo de treinamento.

//+------------------------------------------------------------------+
//| Input parameters                                                 |
//+------------------------------------------------------------------+
input int                  Iterations     = 10000;
input float                Tau            = 0.001f;

Durante o treinamento, usaremos um Ator, 2 Críticos e seus modelos-alvo. Bem como um codificador convolucional aleatório. Todos os modelos dos Críticos terão a mesma arquitetura, mas diferentes parâmetros, que são formados durante o treinamento.

CNet                 Actor;
CNet                 Critic1;
CNet                 Critic2;
CNet                 TargetCritic1;
CNet                 TargetCritic2;
CNet                 Convolution;

Vamos treinar o Ator e os 2 Críticos. Os modelos-alvo dos Críticos serão suavemente atualizados a partir dos parâmetros do Crítico correspondente com o parâmetro Tau. O Codificador não é treinado.

No método de inicialização do Expert Advisor OnInit, carregamos os dados de entrada previamente coletados. E, na impossibilidade de carregar modelos pré-treinados, inicializamos novos de acordo com a arquitetura especificada. Este processo permaneceu inalterado e você pode se familiarizar com ele no anexo. Agora, vamos direto ao método de treinamento dos modelos, Train.

Neste método, primeiro determinamos o número de trajetórias armazenadas no buffer de reprodução de experiência e contabilizamos o total de estados neles.

Preparamos matrizes para gravar o incorporação dos estados e as respectivas recompensas externas.

//+------------------------------------------------------------------+
//| Train function                                                   |
//+------------------------------------------------------------------+
void Train(void)
  {
   int total_tr = ArraySize(Buffer);
   uint ticks = GetTickCount();
//---
   int total_states = Buffer[0].Total;
   for(int i = 1; i < total_tr; i++)
      total_states += Buffer[i].Total;
   vector<float> temp, next;
   Convolution.getResults(temp);
   matrix<float> state_embedding = matrix<float>::Zeros(total_states,temp.Size());
   matrix<float> rewards = matrix<float>::Zeros(total_states,NRewards);

Em seguida, executamos o sistema de 2 laços aninhados, no corpo dos quais configuramos a codificação de todos os estados do buffer de reprodução de experiência. Com os dados obtidos, preenchemos as matrizes de incorporação dos estados e das respectivas recompensas. Observe que armazenamos as recompensas por uma transição individual para um novo estado, sem considerar os valores acumulados até o final da passagem. Assim, queremos tornar comparáveis os estados semelhantes em "espírito", mas separados no tempo.

   int state = 0;
   for(int tr = 0; tr < total_tr; tr++)
     {
      for(int st = 0; st < Buffer[tr].Total; st++)
        {
         State.AssignArray(Buffer[tr].States[st].state);
         float PrevBalance = Buffer[tr].States[MathMax(st,0)].account[0];
         float PrevEquity = Buffer[tr].States[MathMax(st,0)].account[1];
         State.Add((Buffer[tr].States[st].account[0] - PrevBalance) / PrevBalance);
         State.Add(Buffer[tr].States[st].account[1] / PrevBalance);
         State.Add((Buffer[tr].States[st].account[1] - PrevEquity) / PrevEquity);
         State.Add(Buffer[tr].States[st].account[2]);
         State.Add(Buffer[tr].States[st].account[3]);
         State.Add(Buffer[tr].States[st].account[4] / PrevBalance);
         State.Add(Buffer[tr].States[st].account[5] / PrevBalance);
         State.Add(Buffer[tr].States[st].account[6] / PrevBalance);
         double x = (double)Buffer[tr].States[st].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
         State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_MN1);
         State.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_W1);
         State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_D1);
         State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         if(!Convolution.feedForward(GetPointer(State),1,false,NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            ExpertRemove();
            return;
           }
         Convolution.getResults(temp);
         state_embedding.Row(temp,state);
         temp.Assign(Buffer[tr].States[st].rewards);
         next.Assign(Buffer[tr].States[st + 1].rewards);
         rewards.Row(temp - next * DiscFactor,state);
         state++;
         if(GetTickCount() - ticks > 500)
           {
            string str = StringFormat("%-15s %6.2f%%", "Embedding ", 
                                      state * 100.0 / (double)(total_states));
            Comment(str);
            ticks = GetTickCount();
           }
        }
     }
   if(state != total_states)
     {
      rewards.Resize(state,NRewards);
      state_embedding.Reshape(state,state_embedding.Cols());
      total_states = state;
     }

Após a preparação do incorporação dos estados, passamos diretamente para a configuração do laço de treinamento dos modelos. Como de costume, o número de iterações do ciclo é definido por um parâmetro externo e adicionamos uma verificação para o evento de término do programa pelo usuário.

No corpo do ciclo, selecionamos aleatoriamente uma trajetória e um estado específico nela do buffer de reprodução de experiência.

   vector<float> rewards1, rewards2;
   int bar = (HistoryBars - 1) * BarDescr;
   for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++)
     {
      int tr = (int)((MathRand() / 32767.0) * (total_tr - 1));
      int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2));
      if(i < 0)
        {
         iter--;
         continue;
        }
      vector<float> reward, target_reward = vector<float>::Zeros(NRewards);
      reward.Assign(Buffer[tr].States[i].rewards);

Preparamos vetores para registrar as recompensas.

Em seguida, preparamos a descrição do próximo estado. Note que preparamos isso independentemente da necessidade de usar os modelos-alvo. Afinal, precisaremos dele de qualquer forma para formar a recompensa interna pelo método NNM.

      //--- Target
      TargetState.AssignArray(Buffer[tr].States[i + 1].state);

Mas a vetor de descrição do estado subsequente e a propagação direta dos modelos-alvo são realizadas apenas se necessário.

      if(iter >= StartTargetIter)
        {
         float PrevBalance = Buffer[tr].States[i].account[0];
         float PrevEquity = Buffer[tr].States[i].account[1];
         Account.Clear();
         Account.Add((Buffer[tr].States[i + 1].account[0] - PrevBalance) / PrevBalance);
         Account.Add(Buffer[tr].States[i + 1].account[1] / PrevBalance);
         Account.Add((Buffer[tr].States[i + 1].account[1] - PrevEquity) / PrevEquity);
         Account.Add(Buffer[tr].States[i + 1].account[2]);
         Account.Add(Buffer[tr].States[i + 1].account[3]);
         Account.Add(Buffer[tr].States[i + 1].account[4] / PrevBalance);
         Account.Add(Buffer[tr].States[i + 1].account[5] / PrevBalance);
         Account.Add(Buffer[tr].States[i + 1].account[6] / PrevBalance);
         double x = (double)Buffer[tr].States[i + 1].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
         Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_MN1);
         Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_W1);
         Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_D1);
         Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         //---
         if(Account.GetIndex() >= 0)
            Account.BufferWrite();
         if(!Actor.feedForward(GetPointer(TargetState), 1, false, GetPointer(Account)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         //---
         if(!TargetCritic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) ||
            !TargetCritic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         TargetCritic1.getResults(rewards1);
         TargetCritic2.getResults(rewards2);
         if(rewards1.Sum() <= rewards2.Sum())
            target_reward = rewards1;
         else
            target_reward = rewards2;
         for(ulong r = 0; r < target_reward.Size(); r++)
            target_reward -= Buffer[tr].States[i + 1].rewards[r];
         target_reward *= DiscFactor;
        }

Em seguida, procede-se ao treinamento dos Críticos. Neste bloco, primeiro preparamos os dados do estado atual do ambiente.

      //--- Q-function study
      State.AssignArray(Buffer[tr].States[i].state);
      float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0];
      float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];
      Account.Clear();
      Account.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance);
      Account.Add(Buffer[tr].States[i].account[1] / PrevBalance);
      Account.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity);
      Account.Add(Buffer[tr].States[i].account[2]);
      Account.Add(Buffer[tr].States[i].account[3]);
      Account.Add(Buffer[tr].States[i].account[4] / PrevBalance);
      Account.Add(Buffer[tr].States[i].account[5] / PrevBalance);
      Account.Add(Buffer[tr].States[i].account[6] / PrevBalance);
      double x = (double)Buffer[tr].States[i].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
      Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_MN1);
      Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_W1);
      Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_D1);
      Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      if(Account.GetIndex() >= 0)
         Account.BufferWrite();

E realizamos a propagação direta do Ator.

      if(!Actor.feedForward(GetPointer(State), 1, false, GetPointer(Account)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

Aqui é importante notar que para o treinamento dos Críticos, usamos as ações reais do Ator ao interagir com o ambiente e a recompensa efetivamente obtida. No entanto, ainda realizamos a propagação direta do Ator com o objetivo de utilizar seu bloco de pré-processamento de dados, que foi excluído da arquitetura do Crítico.

Preparamos o buffer de ações do Ator do buffer de reprodução de experiência e realizamos a propagação direta de ambos os Críticos.

      Actions.AssignArray(Buffer[tr].States[i].action);
      if(Actions.GetIndex() >= 0)
         Actions.BufferWrite();
      //---
      if(!Critic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions)) ||
         !Critic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

Após a propagação direta, precisamos realizar a retropropagação e atualizar os parâmetros dos modelos. Mas lembro que usamos uma função de recompensa decomposta. E para a otimização dos gradientes, aplica-se o método CAGrad. Obviamente, apesar de um objetivo comum, os gradientes de erro para cada Crítico serão diferentes. E realizamos a atualização dos modelos sequencialmente. Primeiro, ajustamos os gradientes de erro e realizamos a retropropagação do Crítico 1.

      Critic1.getResults(rewards1);
      Result.AssignArray(CAGrad(reward + target_reward - rewards1) + rewards1);
      if(!Critic1.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) ||
         !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

Depois, repetimos as operações para o Crítico 2. E, claro, controlamos o processo de execução das operações a cada etapa.

      Critic2.getResults(rewards2);
      Result.AssignArray(CAGrad(reward + target_reward - rewards2) + rewards2);
      if(!Critic2.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) ||
         !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

Os modelos dos Críticos são treinados para avaliar corretamente as ações do Ator em um estado específico do ambiente. Como resultado do trabalho dos modelos do Crítico, esperamos obter uma recompensa prevista correta. Isso é, por assim dizer, a ponta do iceberg. Mas há também sua parte submersa. No processo de treinamento, o Crítico aproxima a função Q e estabelece certas dependências entre as ações do Ator e a recompensa.

Nosso objetivo é maximizar a recompensa externa. Mas ela não depende diretamente da qualidade do treinamento do Crítico. Ao contrário, a recompensa é alcançada pelas ações do Ator. E para a correção das ações do Ator, usaremos a função Q aproximada. O gradiente de erro entre a avaliação do Crítico das ações do Ator e a recompensa obtida indicará a direção para a correção das ações do Ator. A probabilidade de ações superestimadas diminuirá, enquanto a das subestimadas aumentará.

Para treinar o Ator, usaremos o Crítico com o menor erro médio móvel de previsão, o que potencialmente nos dá uma avaliação mais precisa das ações do Ator.

      CNet *critic = NULL;
      if(Critic1.getRecentAverageError() <= Critic2.getRecentAverageError())
         critic = GetPointer(Critic1);
      else
         critic = GetPointer(Critic2);

A propagação direta do Ator já foi realizada e, para avaliar as ações escolhidas, precisamos realizar a propagação direta do Crítico selecionado. Mas antes, vamos preparar o vetor de valores-alvo de recompensa. A tarefa não é trivial. Precisamos de alguma forma prever a recompensa externa do ambiente e complementá-la com uma recompensa interna para estimular o potencial exploratório do Ator.

E, por mais estranho que pareça, começaremos com a recompensa interna, que definiremos pelo método NNM. Foi descrito anteriormente que para determinar a recompensa interna precisamos obter a representação codificada do estado subsequente. Os dados históricos do estado subsequente já foram adicionados ao buffer TargetState. Obtemos o estado previsto da conta usando a função previamente descrita ForecastAccount.

      Actor.getResults(rewards1);
      double cl_op = Buffer[tr].States[i + 1].state[bar];
      double prof_1l = SymbolInfoDouble(_Symbol, SYMBOL_TRADE_TICK_VALUE_PROFIT) * cl_op /
                       SymbolInfoDouble(_Symbol, SYMBOL_POINT);
      vector<float> forecast = ForecastAccount(Buffer[tr].States[i].account,rewards1,
                                               prof_1l,Buffer[tr].States[i + 1].account[7]);
      TargetState.AddArray(forecast);

Concatenamos 2 tensores e realizamos a propagação direta de 2 modelos. O Crítico, para avaliar as ações do Ator. E o Codificador, para obter a representação comprimida do estado previsto.

      if(!critic.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) ||
         !Convolution.feedForward(GetPointer(TargetState)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

Em seguida, passamos para a formação do vetor de recompensa. Lembro que o vetor target_reward contém o desvio da avaliação das ações do Ator pelo Crítico-alvo do acúmulo real de recompensa obtido ao interagir com o ambiente. Essencialmente, este vetor representa a influência da mudança de política no resultado geral.

Como a recompensa externa alvo da ação atual do Ator, usaremos as recompensas reais dos k-vizinhos mais próximos, ajustadas pela distância entre os vetores. Aqui partimos do pressuposto de que a recompensa por uma ação é inversamente proporcional à distância para o vizinho correspondente.

A escolha dos k- vizinhos mais próximos e a formação da recompensa interna são realizadas na função KNNReward, cujo algoritmo veremos um pouco mais adiante.

Mas aqui precisamos prestar atenção em mais um ponto. Na matriz de recompensas dos estados codificados, salvamos a recompensa externa apenas para a última transição, sem o total acumulado. Assim, para obtermos metas comparáveis, precisamos adicionar ao target_reward as recompensas acumuladas obtidas até a conclusão da passagem atual do buffer de reprodução de experiência.

      next.Assign(Buffer[tr].States[i + 1].rewards);
      target_reward+=next;
      Convolution.getResults(rewards1);
      target_reward=KNNReward(7,rewards1,state_embedding,rewards) + next * DiscFactor;
      if(forecast[3] == 0.0f && forecast[4] == 0.0f)
         target_reward[2] -= (Buffer[tr].States[i + 1].state[bar + 6] / PrevBalance) / DiscFactor;
      critic.getResults(reward);
      reward += CAGrad(target_reward - reward);

O desvio dos valores-alvo das recompensas da avaliação do Crítico ajustaremos pelo método Conflict-Averse Gradient Descent e os valores obtidos adicionaremos aos valores previstos pelo Crítico. Assim, obtemos um vetor de valores-alvo, ajustado com a decomposição da recompensa. E usamos isso para a retropropagação e atualização dos parâmetros do Ator. Desativamos previamente o modo de treinamento do Crítico para não ajustar seus parâmetros às metas corrigidas.

      Result.AssignArray(reward);
      critic.TrainMode(false);
      if(!critic.backProp(Result, GetPointer(Actor)) ||
         !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         critic.TrainMode(true);
         break;
        }
      critic.TrainMode(true);

Após a atualização bem-sucedida dos parâmetros do Ator, retornamos o modelo do Crítico ao modo de treinamento e atualizamos os modelos-alvo de ambos os Críticos.

      //--- Update Target Nets
      TargetCritic1.WeightsUpdate(GetPointer(Critic1), Tau);
      TargetCritic2.WeightsUpdate(GetPointer(Critic2), Tau);

Com isso, concluem-se as iterações do ciclo de treinamento dos modelos. Resta apenas informar o usuário sobre o processo de execução das operações.

      if(GetTickCount() - ticks > 500)
        {
         string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic1", 
                                    iter * 100.0 / (double)(Iterations), Critic1.getRecentAverageError());
         str += StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic2", 
                                    iter * 100.0 / (double)(Iterations), Critic2.getRecentAverageError());
         Comment(str);
         ticks = GetTickCount();
        }
     }

Após a conclusão bem-sucedida de todas as iterações do ciclo de treinamento, limpamos a área de comentários do gráfico. Exibimos no log os resultados do treinamento dos modelos e iniciamos a conclusão do trabalho do Expert Advisor.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, 
               "Critic1", Critic1.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, 
               "Critic2", Critic2.getRecentAverageError());
   ExpertRemove();
//---
  }

E agora, para uma compreensão completa do funcionamento do algoritmo de treinamento dos modelos, vamos olhar para a função de formação de recompensa KNNReward. É importante dizer que é exatamente nesta função que estão contidas as principais características do método considerado de Nuclear Norm Maximization.

Nos parâmetros, a função recebe o número de vizinhos mais próximos analisados, o incorporação do estado analisado, as matrizes de incorporação dos estados e as respectivas recompensas do buffer de reprodução de experiência.

vector<float> KNNReward(ulong k, 
                        vector<float> &embedding, 
                        matrix<float> &state_embedding, 
                        matrix<float> &rewards
	               )
  {
   if(embedding.Size() != state_embedding.Cols())
     {
      PrintFormat("%s -> %d Inconsistent embedding size", __FUNCTION__, __LINE__);
      return vector<float>::Zeros(0);
     }

No corpo do método, realizamos uma verificação da dimensão do incorporação do estado atual e dos estados do buffer de reprodução de experiência. Na implementação atual, essa verificação pode parecer redundante. Afinal, obtemos todas as incorporações usando um único codificador nesse EA. No entanto, ela pode ser muito útil se você decidir gerar a incorporação dos estados no processo de interação com o ambiente e salvar no buffer de reprodução de experiência, como recomendado no artigo original do método RE3.

Em seguida, realizaremos um pequeno trabalho preparatório, definindo algumas constantes em variáveis locais. E então, se necessário, reduziremos o número de vizinhos mais próximos para o número de estados no buffer de reprodução de experiência. A probabilidade de tal necessidade é bastante baixa. Mas esse detalhe torna nosso código mais universal e protegido contra erros durante a execução.

   ulong size = embedding.Size();
   ulong states = state_embedding.Rows();
   k = MathMin(k,states);
   ulong rew_size = rewards.Cols();
   matrix<float> temp = matrix<float>::Zeros(states,size);

O próximo passo é definir a distância entre o vetor do estado analisado e os estados no buffer de reprodução de experiência. Os valores obtidos são salvos no vetor distance.

   for(ulong i = 0; i < size; i++)
      temp.Col(MathPow(state_embedding.Col(i) - embedding[i],2.0f),i);
   vector<float> distance = MathSqrt(temp.Sum(1));

Agora, precisamos identificar os k-vizinhos mais próximos. Seus parâmetros salvaremos nas matrizes k_embeding e k_rewards. Observe que na matriz k_embeding criamos uma linha a mais. Nela, registraremos a incorporação do estado analisado.

Os dados para as matrizes serão transferidos em um ciclo percorrendo o número de vetores procurados. No corpo do ciclo, com a operação vetorial ArgMin, determinamos a posição do valor mínimo no vetor de distâncias. Este será nosso vizinho mais próximo. Transferimos seus dados para as linhas correspondentes de nossas matrizes. E no vetor de distâncias, definimos nessa posição a constante máxima possível. Assim, após a transferência dos dados, mudamos a distância mínima para o valor máximo. E na próxima iteração do ciclo, a operação ArgMin nos dará a posição do próximo vizinho.

Note que ao transferir o vetor de recompensas, ajustamos seus valores pelo coeficiente inverso à distância entre os vetores de estados.

   matrix<float> k_rewards = matrix<float>::Zeros(k,rew_size);
   matrix<float> k_embeding = matrix<float>::Zeros(k + 1,size);
   for(ulong i = 0; i < k; i++)
     {
      ulong pos = distance.ArgMin();
      k_rewards.Row(rewards.Row(pos) * (1 - MathLog(distance[pos] + 1)),i);
      k_embeding.Row(state_embedding.Row(pos),i);
      distance[pos] = FLT_MAX;
     }
   k_embeding.Row(embedding,k);

Esse algoritmo possui uma série de vantagens:

• O número de iterações não depende do tamanho do buffer de reprodução de experiência, o que é conveniente ao usar grandes bases de dados;
• Não é necessária a ordenação dos dados, que muitas vezes requer muitos recursos;
• Copiamos os dados de cada vizinho apenas uma vez, outros dados não são copiados.

Após a transferência dos dados de todos os vizinhos necessários, na última linha da matriz k_embeding adicionamos o estado atual.

Em seguida, para determinar a norma nuclear da matriz k_embeding e implementar o método NNM, precisamos encontrar os valores singulares da matriz. Para isso, utilizaremos a operação matricial SVD.

   matrix<float> U,V;
   vector<float> S;
   k_embeding.SVD(U,V,S);

Agora, os valores singulares da matriz estão armazenados no vetor S e para determinar a norma nuclear, basta somar seus valores. Mas antes, geramos o vetor de recompensas externas como um vetor dos valores médios das colunas da matriz de recompensas selecionadas k_rewards.

A recompensa interna é determinada pelo método NNM, como a relação da norma nuclear da matriz de incorporações de estados com sua norma de Frobenius, e ajustada pelo coeficiente de escala da norma nuclear. O valor obtido é registrado no elemento correspondente do vetor de recompensas e retornado ao programa que chama.

   vector<float> result = k_rewards.Mean(0);
   result[rew_size - 1] = S.Sum() / (MathSqrt(MathPow(k_embeding,2.0f).Sum() * MathMax(k + 1,size)));
//---
   return (result);
  }

Com isso, concluímos o trabalho de implementação do método Nuclear Norm Maximization com ferramentas MQL5. O código completo de todos os programas usados no artigo pode ser consultado no anexo.

3. Teste

Realizamos um trabalho considerável na implementação da integração do método Nuclear Norm Maximization no algoritmo RE3. E chegou a hora de avançar para a fase de teste do trabalho realizado. Como sempre, o treinamento e teste dos modelos são realizados nos dados históricos do EURUSD com timeframe H1 de 1 a 5 meses de 2023. Os parâmetros de todos os indicadores são usados por padrão.

Ao criar o EA de treinamento "...\NNM\Study.mq5", já falamos sobre as características desse método e o problema da ausência de estados gerados no buffer de reprodução de experiência. Então, decidimos reduzir o número de iterações de um ciclo de treinamento. Obviamente, isso também afeta todo o processo de aprendizado.

Não reduzimos o buffer de reprodução da experiência como um todo. Mas, ao mesmo tempo, é preciso considerar que, para realizar 10 mil iterações de atualização dos parâmetros do modelo, não há necessidade de um banco de dados de 1,3 milhão de estados. Sim, um banco de dados maior permite um melhor ajuste do modelo. Porém, quando há mais de 100 estados por 1 iteração de atualização, não conseguimos trabalhar com todos eles. Por isso, preencheremos o buffer de reprodução da experiência gradualmente. Na primeira iteração, executamos o Expert Advisor para coletar dados de treinamento para apenas 50 execuções. No intervalo histórico especificado, isso já nos dá cerca de 120 mil estados para modelos de treinamento.

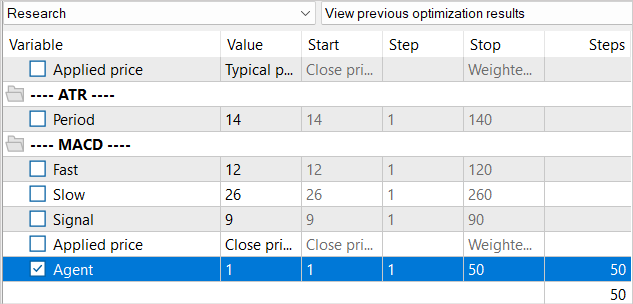
E após a primeira iteração do treinamento do modelo, aumentamos a base de exemplos para mais 50 passagens. Dessa forma, preenchemos gradualmente o buffer de reprodução da experiência com novos estados que correspondem às ações do Ator dentro da política treinada.

Sim, essa abordagem aumenta significativamente o trabalho manual envolvido na execução de EAs. Mas ela nos permite manter o banco de dados de exemplos relativamente atualizado. E as recompensas intrínsecas que geramos guiarão o Ator a explorar novos estados do ambiente.

No treinamento dos modelos, conseguimos obter um modelo capaz de gerar lucros na amostra de treinamento e generalizar esse aprendizado para as condições ambientais posteriores. Assim, no testador de estratégia, o modelo treinado por nós foi capaz de gerar um lucro de 1% durante um mês após a amostra de treinamento. Durante o período de teste, o modelo fez 133 operações, e dessas, 42% foram fechadas com lucro. O lucro máximo por operação é quase duas vezes maior do que o lucro máximo por operação perdida. E o lucro médio por negociação excede a perda média em 40% por cento. Tudo isso junto permitiu obter o fator de lucro no nível de 1,02.

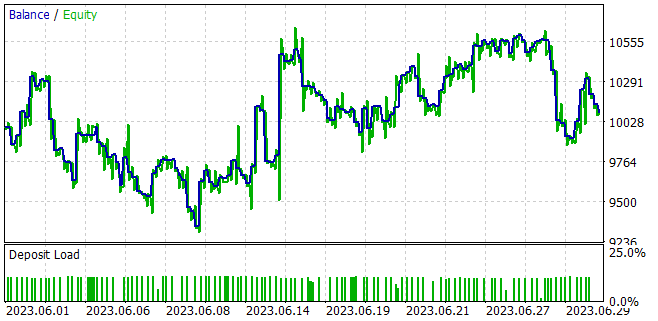
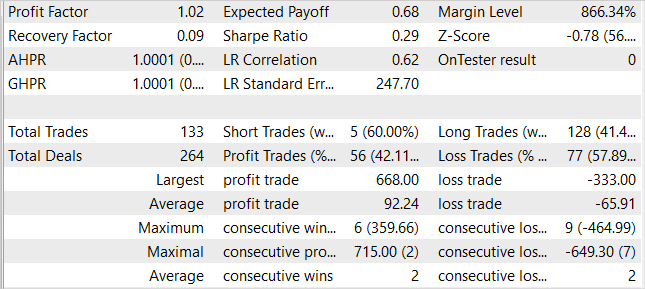
Conclusão

Neste artigo, aprendemos uma nova abordagem para estimular a exploração no aprendizado por reforço com base na maximização da norma nuclear. Esse método avalia com eficácia a novidade da pesquisa ambiental, pois considera informações históricas e oferece alta resistência a ruídos e emissões. 

Na parte prática deste documento, integramos o método de maximização da norma nuclear ao algoritmo RE3. Treinamos o modelo e o testamos no testador de estratégia MetaTrader 5. Com base nos resultados do teste, podemos dizer que o método proposto diversificou significativamente o comportamento do Ator, em comparação com os resultados do treinamento do modelo usando o método puro RE3. Entretanto, obtivemos uma negociação mais caótica. O que pode indicar a necessidade de trabalhar o equilíbrio entre a exploração e o aproveitamento, introduzindo coeficientes de influência adicionais nas funções de recompensa.

Referências

• Nuclear Norm Maximization Based Curiosity-Driven Learning
• Redes neurais de maneira fácil (Parte 53): decomposição de recompensa
• Redes neurais de maneira fácil (Parte 54): usando o codificador aleatório para exploração eficiente (RE3)

Programas usados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	EA	EA para coleta de exemplos
2	Study.mq5	EA	EA de treinamento do agente
3	Test.mq5	EA	EA para testar o modelo
4	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema
5	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de rede neural
6	NeuroNet.cl	Biblioteca	Biblioteca de código do programa OpenCL