
Redes neurais de maneira fácil (Parte 53): decomposição de recompensa
Introdução
Continuamos a explorar métodos de aprendizado por reforço. Como você sabe, todos os algoritmos de treinamento de modelos desta área do aprendizado de máquina são baseados no paradigma de maximização da recompensa do ambiente. E a função de recompensa desempenha um papel crucial no processo de treinamento dos modelos. Seus sinais raramente são unívocos.
Na tentativa de estimular o Agente ao comportamento desejado, introduzimos prêmios e penalidades adicionais na função de recompensa. Por exemplo, frequentemente complicamos a função de recompensa na tentativa de estimular o Agente a explorar o ambiente e introduzimos penalidades por inatividade. No entanto, a arquitetura do modelo e a função de recompensa permanecem como produtos de considerações subjetivas do arquiteto do modelo.
No processo de aprendizado, o modelo pode enfrentar várias dificuldades e desafios, mesmo com uma abordagem cuidadosa no design. O Agente pode não alcançar os resultados desejados por uma variedade de razões, e a busca dessas razões pode se tornar uma "adivinhação nas borras de café". Mas como entender se o Agente está interpretando corretamente nossos sinais na função de recompensa? Na tentativa de responder a essa questão, surge o desejo de dividir a recompensa em componentes individuais. Usar recompensas decompostas e analisar o impacto de cada componente pode ser muito útil na busca por maneiras de otimizar o processo de treinamento do modelo. Isso ajudará a entender melhor como diferentes aspectos afetam o comportamento do Agente; identificar as causas dos problemas e ajustar efetivamente a arquitetura do modelo, o processo de aprendizado ou a função de recompensa.
1. A necessidade de decomposição da recompensa
A decomposição dos valores da função de recompensa é um método simples e amplamente aplicável que pode resolver uma série de desafios. No aprendizado por reforço, o Agente recebe uma recompensa, que muitas vezes consiste na soma de vários componentes. Cada um deles se destina a codificar algum aspecto do comportamento desejado do Agente. A partir dessa recompensa composta, o Agente aprende uma única função de valor complexa. Usando a decomposição de valores, o Agente aprende funções de valor para cada componente da recompensa. E qualquer uma dessas funções isoladamente provavelmente terá uma forma mais simples.
Para fins de otimização de estratégia, a função de valor composta é reconstruída através da soma ponderada das funções de valor dos componentes.
A decomposição de recompensas pode ser incorporada a uma ampla gama de métodos, incluindo a família de métodos Ator-Crítico que estamos considerando.
No entanto, as capacidades diagnósticas e de treinamento adicionais da decomposição da função de recompensa vêm com um preço na forma de uma tarefa de previsão mais complexa: em vez de treinar uma única função de valor, é necessário treinar várias funções. A análise do impacto desse fator no desempenho do Agente é discutida no artigo "Value Function Decomposition for Iterative Design of Reinforcement Learning Agents". Os autores do artigo descobriram que, ao adicionar a decomposição da função de recompensa ao algoritmo Soft Actor-Critic, os resultados do treinamento do modelo foram inferiores ao algoritmo original. No entanto, os autores propuseram variantes para melhorar o código. Isso permitiu não apenas corresponder ao algoritmo original Soft Actor-Critic, mas às vezes superar seu desempenho. Essas melhorias podem ser aplicadas à decomposição da função de recompensa e a outros algoritmos da família Ator-Crítico.
Uma ampla gama de algoritmos de aprendizado por reforço pode ser adaptada para usar a decomposição da função de recompensa seguindo o seguinte padrão:
- Modificamos o modelo de funções Q para que a saída do modelo gere um elemento para cada componente da função de recompensa.
- Usamos o algoritmo básico de treinamento da função Q para atualizar cada componente.
Este padrão funciona para algoritmos de treinamento de modelos com espaços de ação discretos e contínuos.
A ideia é bastante simples. Mas, como mencionado anteriormente, os autores do artigo descobriram ineficiências na "solução direta" ao usar a decomposição de recompensas no contexto do algoritmo Soft Actor-Critic. Relembro as fórmulas de otimização da função Q neste algoritmo.
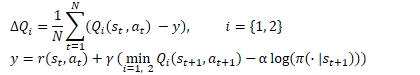
Aqui, vemos o uso da estimativa mínima do estado futuro de 2 modelos-alvo dos Críticos. Conforme indicado no ponto 2 do padrão, para atualizar os parâmetros de cada componente da função Q, usamos o algoritmo básico. No entanto, a prática mostrou que o uso do valor mínimo por componente leva ao desequilíbrio do modelo. É mais eficiente usar um modelo com a menor avaliação geral. E usar suas avaliações de componentes para treinar os modelos.
Em geral, presume-se que a função de recompensa do modelo é uma função linear de seus componentes.
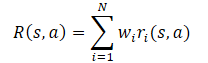
Aplicando a linearidade da expectativa matemática, descobrimos que a função Q herda a estrutura linear da função de recompensa.
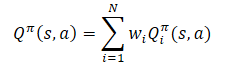
A menos que indicado de outra forma, assumimos que Wi=1 para todos i. E como os pesos dos componentes são removidos da função Q, eles podem ser alterados sem alterar a previsão alvo do componente. Isso permite avaliar a política para qualquer combinação de pesos.
O segundo ponto a ser observado é que a otimização da função de recompensa decomposta é a otimização do modelo em muitos critérios. E possui problemas típicos da otimização multiobjetivo: gradientes conflitantes, alta curvatura e grandes diferenças nos tamanhos dos gradientes. Para minimizar o impacto negativo desse fator, os autores do método sugerem o uso do algoritmo Conflict-Averse Gradient Descent (CAGrad), desenvolvido para o ambiente de aprendizado por reforço multi-tarefa. Este método visa mitigar os problemas mencionados da otimização multiobjetivo. A ideia principal é substituir o gradiente da função objetivo multitarefa por uma soma ponderada dos gradientes para cada tarefa individual. Para isso, resolve-se a seguinte tarefa de otimização:
![]()
onde d é o vetor de atualização,
g₀ é o gradiente médio,
c é o coeficiente de taxa de convergência no intervalo [0, 1).
A solução desta tarefa de otimização permite considerar o impacto de cada componente na otimização e focar na melhoria da pior avaliação a cada etapa.
2. Implementação usando MQL5
2.1 Criação de uma nova classe de modelo
Implementaremos nossa própria versão da decomposição da função de recompensa com base no algoritmo SAC+DICE. Devido às peculiaridades da implementação dos algoritmos, não herdaremos da classe CNet_SAC_DICE criada no artigo anterior. No entanto, ainda utilizaremos os trabalhos anteriores como base. Criaremos uma nova classe, CNet_SAC_D_DICE, cuja estrutura é apresentada abaixo.
class CNet_SAC_D_DICE : protected CNet { protected: CNet cActorExploer; CNet cCritic1; CNet cCritic2; CNet cTargetCritic1; CNet cTargetCritic2; CNet cZeta; CNet cNu; CNet cTargetNu; vector<float> fLambda; vector<float> fLambda_m; vector<float> fLambda_v; int iLatentLayer; float fCAGrad_C; int iCAGrad_Iters; int iUpdateDelay; int iUpdateDelayCount; //--- float fLoss1; float fLoss2; vector<float> fZeta; vector<float> fQWeights; //--- vector<float> GetLogProbability(CBufferFloat *Actions); vector<float> CAGrad(vector<float> &grad); public: //--- CNet_SAC_D_DICE(void); ~CNet_SAC_D_DICE(void) {} //--- bool Create(CArrayObj *actor, CArrayObj *critic, CArrayObj *zeta, CArrayObj *nu, int latent_layer = -1); //--- virtual bool Study(CArrayFloat *State, CArrayFloat *SecondInput, CBufferFloat *Actions, vector<float> &Rewards, CBufferFloat *NextState, CBufferFloat *NextSecondInput, float discount, float tau); virtual void GetLoss(float &loss1, float &loss2) { loss1 = fLoss1; loss2 = fLoss2; } virtual bool TargetsUpdate(float tau); //--- virtual void SetQWeights(vector<float> &weights) { fQWeights=weights; } virtual void SetCAGradC(float c) { fCAGrad_C=c; } virtual void SetLambda(vector<float> &lambda) { fLambda=lambda; fLambda_m=vector<float>::Zeros(lambda.Size()); fLambda_v=fLambda_m; } virtual void TargetsUpdateDelay(int delay) { iUpdateDelay=delay; iUpdateDelayCount=delay; } //--- virtual bool Save(string file_name, bool common = true); bool Load(string file_name, bool common = true); };
Na estrutura da classe apresentada, vemos objetos de modelos emprestados. Mas, em vez de variáveis para armazenar o coeficiente de Lagrange e suas médias, usaremos vetores, cujo tamanho é igual ao número de componentes da função de recompensa. Também adicionaremos o vetor fQWeights para armazenar os pesos de cada componente. A variável fCAGrad_C será usada para registrar o coeficiente de taxa de convergência do método CAGrad.
Naturalmente, essas mudanças são refletidas no construtor da classe. No estágio inicial, inicializamos todos os vetores com comprimento unitário.
CNet_SAC_D_DICE::CNet_SAC_D_DICE(void) : fLoss1(0), fLoss2(0), fCAGrad_C(0.5f), iCAGrad_Iters(15), iUpdateDelay(100), iUpdateDelayCount(100) { fLambda = vector<float>::Full(1, 1.0e-5f); fLambda_m = vector<float>::Zeros(1); fLambda_v = vector<float>::Zeros(1); fZeta = vector<float>::Zeros(1); fQWeights = vector<float>::Ones(1); }
O método de inicialização da classe e a criação de modelos aninhados são quase inteiramente recuperados do último artigo. As alterações são feitas apenas em termos de mudança nos tamanhos dos vetores.
bool CNet_SAC_D_DICE::Create(CArrayObj *actor, CArrayObj *critic, CArrayObj *zeta, CArrayObj *nu, int latent_layer = -1) { ResetLastError(); //--- if(!cActorExploer.Create(actor) || !CNet::Create(actor)) { PrintFormat("Error of create Actor: %d", GetLastError()); return false; } //--- if(!opencl) { Print("Don't opened OpenCL context"); return false; } //--- if(!cCritic1.Create(critic) || !cCritic2.Create(critic)) { PrintFormat("Error of create Critic: %d", GetLastError()); return false; } //--- if(!cZeta.Create(zeta) || !cNu.Create(nu)) { PrintFormat("Error of create function nets: %d", GetLastError()); return false; } //--- if(!cTargetCritic1.Create(critic) || !cTargetCritic2.Create(critic) || !cTargetNu.Create(nu)) { PrintFormat("Error of create target models: %d", GetLastError()); return false; } //--- cActorExploer.SetOpenCL(opencl); cCritic1.SetOpenCL(opencl); cCritic2.SetOpenCL(opencl); cZeta.SetOpenCL(opencl); cNu.SetOpenCL(opencl); cTargetCritic1.SetOpenCL(opencl); cTargetCritic2.SetOpenCL(opencl); cTargetNu.SetOpenCL(opencl); //--- if(!cTargetCritic1.WeightsUpdate(GetPointer(cCritic1), 1.0) || !cTargetCritic2.WeightsUpdate(GetPointer(cCritic2), 1.0) || !cTargetNu.WeightsUpdate(GetPointer(cNu), 1.0)) { PrintFormat("Error of update target models: %d", GetLastError()); return false; } //--- cZeta.getResults(fZeta); ulong size = fZeta.Size(); fLambda = vector<float>::Full(size,1.0e-5f); fLambda_m = vector<float>::Zeros(size); fLambda_v = vector<float>::Zeros(size); fQWeights = vector<float>::Ones(size); iLatentLayer = latent_layer; //--- return true; }
Observe que aqui inicializamos o vetor de pesos fQWeights com valores unitários. Se a sua função de recompensa requer coeficientes diferentes, você deve usar o método SetQWeights. No entanto, ele deve ser chamado após a inicialização da classe com o método Create, caso contrário, seus coeficientes serão substituídos por valores unitários.
O algoritmo Conflict-Averse Gradient Descent foi transferido para um método separado, CAGrad. Este método recebe um vetor de gradientes como parâmetros e retorna um vetor ajustado.
No corpo do método, primeiro realizaremos um pequeno trabalho preparatório, no qual:
- definimos o valor médio do gradiente;
- escalamos os gradientes para aumentar a estabilidade dos cálculos;
- preparamos variáveis locais e vetores.
vector<float> CNet_SAC_D_DICE::CAGrad(vector<float> &grad) { matrix<float> GG = grad.Outer(grad); GG.ReplaceNan(0); if(MathAbs(GG).Sum() == 0) return grad; float scale = MathSqrt(GG.Diag() + 1.0e-4f).Mean(); GG = GG / MathPow(scale,2); vector<float> Gg = GG.Mean(1); float gg = Gg.Mean(); vector<float> w = vector<float>::Zeros(grad.Size()); float c = MathSqrt(gg + 1.0e-4f) * fCAGrad_C; vector<float> w_best = w; float obj_best = FLT_MAX; vector<float> moment = vector<float>::Zeros(w.Size());
Após a conclusão do trabalho preparatório, realizamos um ciclo para resolver a tarefa de otimização. No corpo do ciclo, resolvemos iterativamente a tarefa de encontrar o vetor de atualização ótimo usando o método de descida de gradiente.
for(int i = 0; i < iCAGrad_Iters; i++) { vector<float> ww; w.Activation(ww,AF_SOFTMAX); float obj = ww.Dot(Gg) + c * MathSqrt(ww.MatMul(GG).Dot(ww) + 1.0e-4f); if(MathAbs(obj) < obj_best) { obj_best = MathAbs(obj); w_best = w; } if(i < (iCAGrad_Iters - 1)) { float loss = -obj; vector<float> derev = Gg + GG.MatMul(ww) * c / (MathSqrt(ww.MatMul(GG).Dot(ww) + 1.0e-4f) * 2) + ww.MatMul(GG) * c / (MathSqrt(ww.MatMul(GG).Dot(ww) + 1.0e-4f) * 2); vector<float> delta = derev * loss; ulong size = delta.Size(); matrix<float> ident = matrix<float>::Identity(size, size); vector<float> ones = vector<float>::Ones(size); matrix<float> sm_der = ones.Outer(ww); sm_der = sm_der.Transpose() * (ident - sm_der); delta = sm_der.MatMul(delta); if(delta.Ptp() != 0) delta = delta / delta.Ptp(); moment = delta * 0.8f + moment * 0.5f; w += moment; if(w.Ptp() != 0) w = w / w.Ptp(); } }
Após a conclusão das iterações do ciclo, ajustamos os gradientes de erro usando os coeficientes de peso ótimos. O resultado obtido é retornado ao programa de chamada.
w_best.Activation(w,AF_SOFTMAX); float gw_norm = MathSqrt(w.MatMul(GG).Dot(w) + 1.0e-4f); float lmbda = c / (gw_norm + 1.0e-4f); vector<float> result = ((w * lmbda + 1.0f / (float)grad.Size()) * grad) / (1 + MathPow(fCAGrad_C,2)); //--- return result; }
Todo o processo de treinamento, assim como na classe CNet_SAC_DICE, é estruturado no método CNet_SAC_D_DICE::Study. No entanto, apesar da unidade de abordagens e semelhanças externas, há muitas diferenças no algoritmo e na estrutura do método. E as primeiras mudanças que fizemos foram nos parâmetros do método. Aqui substituímos a variável de recompensa reward por um vetor de recompensas decompostas Rewards.
Além disso, excluímos o vetor de logaritmos de probabilidades de ações ActionsLogProbab. Como você sabe, no algoritmo Soft Actor-Critic, o componente entrópico é incluído na função de recompensa para estimular o Agente a repetir ações com baixa probabilidade. E a decomposição da função de recompensa destaca um elemento separado para cada componente. Assim, os logaritmos de probabilidade já estão presentes no vetor de recompensas decompostas Rewards e não há necessidade de duplicá-los em um vetor separado.
bool CNet_SAC_D_DICE::Study(CArrayFloat *State, CArrayFloat *SecondInput, CBufferFloat *Actions, vector<float> &Rewards, CBufferFloat *NextState, CBufferFloat *NextSecondInput, float discount, float tau) { //--- if(!Actions) return false;
No corpo do método, verificamos a atualidade do ponteiro para o buffer de ações executadas. E com isso concluímos o bloco de controle do nosso método.
Passando para a próxima etapa, deve-se mencionar que, durante o processo de treinamento do modelo, foi observado um crescimento bastante grande e injustificado nas avaliações dos estados subsequentes pelos modelos-alvo. Tais avaliações excediam em muito as recompensas reais, levando a uma adaptação mútua do modelo e ser treinado ua cópia-alvo sem considerar as recompensas reais do ambiente.
Para minimizar esse efeito, decidiu-se treinar o modelo inicialmente usando a recompensa cumulativa real. A completa renúncia ao uso de modelos-alvo também tem um efeito negativo. Afinal, no buffer de reprodução de experiência, a avaliação cumulativa é limitada aos períodos de treinamento. Ela pode variar significativamente para estados e ações semelhantes, dependendo da distância até o final do conjunto de treinamento. Isso é suavizado pelo modelo-alvo. Além disso, o modelo-alvo ajuda a avaliar os estados levando em conta as ações da política atual. Com o aumento do número de iterações de atualização dos parâmetros do Agente, a política atual vai se diferenciando cada vez mais da política no buffer de reprodução de experiência, o que não pode ser ignorado. Mas é necessário um modelo-alvo com avaliações adequadas. Portanto, precisamos de dois modos de operação do método: com o uso de modelos-alvo e sem.
Na elaboração do algoritmo do método, seguimos as seguintes considerações:
- Quando necessário o uso de modelos-alvo, o usuário passa os ponteiros para os futuros estados nos parâmetros. No vetor Rewards, contém-se a recompensa decomposta apenas pela ação realizada no estado atual.
- Ao recusar o uso de modelos-alvo, o usuário não passa os ponteiros para os futuros estados (as variáveis dos parâmetros contêm NULL). No vetor Rewards, contém-se a recompensa acumulada decomposta.
Consequentemente, verificamos o ponteiro para o estado futuro e, se necessário, determinamos a ação no estado futuro levando em conta a política atual. E avaliamos o par estado-ação.
if(!!NextState) if(!CNet::feedForward(NextState, 1, false, NextSecondInput)) return false; if(!cTargetCritic1.feedForward(GetPointer(this), iLatentLayer, GetPointer(this), layers.Total() - 1) || !cTargetCritic2.feedForward(GetPointer(this), iLatentLayer, GetPointer(this), layers.Total() - 1)) return false; //--- if(!cTargetNu.feedForward(GetPointer(this), iLatentLayer, GetPointer(this), layers.Total() - 1)) return false;
Em seguida, realizamos a propagação da política conservadora no estado atual. Substituímos as ações e realizamos a propagação dos modelos do bloco DICE.
if(!CNet::feedForward(State, 1, false, SecondInput)) return false; CBufferFloat *output = ((CNeuronBaseOCL*)((CLayer*)layers.At(layers.Total() - 1)).At(0)).getOutput(); output.AssignArray(Actions); output.BufferWrite(); if(!cNu.feedForward(GetPointer(this), iLatentLayer, GetPointer(this))) return false; if(!cZeta.feedForward(GetPointer(this), iLatentLayer, GetPointer(this))) return false;
Após isso, determinamos os valores das funções de perda dos modelos do bloco Distribution Correction Estimation. Esta etapa foi detalhadamente descrita no artigo anterior artigo. Apenas enfatizo que, no caso de recusa ao uso do modelo-alvo, o vetor de avaliação do próximo estado next_nu é preenchido com valores nulos.
vector<float> nu, next_nu, zeta, ones; cNu.getResults(nu); cZeta.getResults(zeta); if(!!NextState) cTargetNu.getResults(next_nu); else next_nu = vector<float>::Zeros(nu.Size()); ones = vector<float>::Ones(zeta.Size()); vector<float> log_prob = GetLogProbability(output); int shift = (int)(Rewards.Size() - log_prob.Size()); if(shift < 0) return false; float policy_ratio = 0; for(ulong i = 0; i < log_prob.Size(); i++) policy_ratio += log_prob[i] - Rewards[shift + i] / LogProbMultiplier; policy_ratio = MathExp(policy_ratio / log_prob.Size()); vector<float> bellman_residuals = (next_nu * discount + Rewards) * policy_ratio - nu; vector<float> zeta_loss = MathPow(zeta, 2.0f) / 2.0f - zeta * (MathAbs(bellman_residuals) - fLambda) ; vector<float> nu_loss = zeta * MathAbs(bellman_residuals) + MathPow(nu, 2.0f) / 2.0f; vector<float> lambda_los = fLambda * (ones - zeta);
Então, atualizamos o vetor de coeficientes de Lagrange usando o método de otimização Adam.
Observe que o vetor de gradientes de erro é corrigido usando o método CAGrad mencionado anteriormente. E o uso de operações vetoriais nos permite trabalhar com vetores tão facilmente quanto com variáveis simples.
Os valores corrigidos serão salvos no vetor correspondente.
vector<float> grad_lambda = CAGrad((ones - zeta) * (lambda_los * (-1.0f))); fLambda_m = fLambda_m * b1 + grad_lambda * (1 - b1); fLambda_v = fLambda_v * b2 + MathPow(grad_lambda, 2) * (1.0f - b2); fLambda += fLambda_m * lr / MathSqrt(fLambda_v + lr / 100.0f);
A próxima etapa é atualizar os parâmetros dos modelos v, ζ. O algoritmo dessas operações permanece o mesmo. Apenas substituímos as variáveis por vetores e usamos operações vetoriais.
CBufferFloat temp; temp.BufferInit(MathMax(Actions.Total(), SecondInput.Total()), 0); temp.BufferCreate(opencl); //--- update nu int last_layer = cNu.layers.Total() - 1; CLayer *layer = cNu.layers.At(last_layer); if(!layer) return false; CNeuronBaseOCL *neuron = layer.At(0); if(!neuron) return false; CBufferFloat *buffer = neuron.getGradient(); if(!buffer) return false; vector<float> nu_grad = CAGrad(nu_loss * (zeta * bellman_residuals / MathAbs(bellman_residuals) - nu)); if(!buffer.AssignArray(nu_grad) || !buffer.BufferWrite()) return false; if(!cNu.backPropGradient(output, GetPointer(temp))) return false;
Os vetores de gradientes de erro são obrigatoriamente corrigidos usando o algoritmo Conflict-Averse Gradient Descent no método CNet_SAC_D_DICE::CAGrad.
//--- update zeta last_layer = cZeta.layers.Total() - 1; layer = cZeta.layers.At(last_layer); if(!layer) return false; neuron = layer.At(0); if(!neuron) return false; buffer = neuron.getGradient(); if(!buffer) return false; vector<float> zeta_grad = CAGrad(zeta_loss * (zeta - MathAbs(bellman_residuals) + fLambda) * (-1.0f)); if(!buffer.AssignArray(zeta_grad) || !buffer.BufferWrite()) return false; if(!cZeta.backPropGradient(output, GetPointer(temp))) return false;
Neste estágio, finalizamos o trabalho com os objetos do bloco Distribution Correction Estimation e passamos para o procedimento de treinamento de nossos modelos Críticos. Primeiro, realizamos sua propagação. A propagação do Ator já foi realizada anteriormente.
//--- feed forward critics if(!cCritic1.feedForward(GetPointer(this), iLatentLayer, output) || !cCritic2.feedForward(GetPointer(this), iLatentLayer, output)) return false;
A próxima etapa é determinar o vetor de valores de referência para a atualização dos parâmetros dos Críticos. Há dois pontos a considerar aqui. Ambos estão relacionados aos modelos-alvo. Primeiro, verificamos a necessidade de usá-los para avaliar o próximo estado e ação. Para isso, verificamos o ponteiro para o próximo estado do sistema.
Se usarmos modelos-alvo para avaliar o próximo par estado-ação, precisamos escolher o Crítico-alvo com a menor avaliação cumulativa. A avaliação cumulativa é facilmente obtida multiplicando-se o vetor de coeficientes de peso dos componentes da função de recompensa pelo vetor de recompensa prevista decomposta, obtido na propagação dos modelos-alvo. Em seguida, basta escolher a menor avaliação e salvar o vetor de valores previstos do modelo selecionado.
Se optarmos por não avaliar os próximos estados, o vetor de valores previstos é preenchido com zeros.
vector<float> result; if(fZeta.CompareByDigits(vector<float>::Zeros(fZeta.Size()),8) == 0) fZeta = MathAbs(zeta); else fZeta = fZeta * 0.9f + MathAbs(zeta) * 0.1f; zeta = MathPow(MathAbs(zeta), 1.0f / 3.0f) / (MathPow(fZeta, 1.0f / 3.0f) * 10.0f); vector<float> target = vector<float>::Zeros(Rewards.Size()); if(!!NextState) { cTargetCritic1.getResults(target); cTargetCritic2.getResults(result); if(fQWeights.Dot(result) < fQWeights.Dot(target)) target = result; }
As previsões são ajustadas pelo coeficiente de desconto e somadas com a recompensa do estado atual.
target = (target * discount + Rewards); ulong total = log_prob.Size(); for(ulong i = 0; i < total; i++) target[shift + i] = log_prob[i] * LogProbMultiplier;
No vetor resultante, ajustamos o logaritmo da probabilidade das ações na política atual. É importante notar que os logaritmos das probabilidades das ações, armazenados no buffer de reprodução de experiência, já estão contidos no vetor de recompensas. Substituímos seus valores pelos logaritmos da política atual para treinar o crítico com uma avaliação que considera a política atual.
Após determinar os valores-alvo, calculamos o erro de previsão do primeiro Crítico e o gradiente do erro para cada componente da função Q. Os gradientes obtidos são corrigidos usando o algoritmo Conflict-Averse Gradient Descent.
//--- update critic1 cCritic1.getResults(result); vector<float> loss = zeta * MathPow(result - target, 2.0f); if(fLoss1 == 0) fLoss1 = MathSqrt(fQWeights.Dot(loss) / fQWeights.Sum()); else fLoss1 = MathSqrt(0.999f * MathPow(fLoss1, 2.0f) + 0.001f * fQWeights.Dot(loss) / fQWeights.Sum()); vector<float> grad = CAGrad(loss * zeta * (target - result) * 2.0f);
Os gradientes de erro corrigidos são transferidos para o buffer correspondente do Crítico1 e realizamos a retropropagação do modelo.
last_layer = cCritic1.layers.Total() - 1; layer = cCritic1.layers.At(last_layer); if(!layer) return false; neuron = layer.At(0); if(!neuron) return false; buffer = neuron.getGradient(); if(!buffer) return false; if(!buffer.AssignArray(grad) || !buffer.BufferWrite()) return false; if(!cCritic1.backPropGradient(output, GetPointer(temp)) || !backPropGradient(SecondInput, GetPointer(temp), iLatentLayer)) return false;
Aqui também realizamos uma retropropagação parcial do Ator para ajustar o bloco de pré-processamento de dados.
Repetimos as operações para o segundo Crítico.
//--- update critic2 cCritic2.getResults(result); loss = zeta * MathPow(result - target, 2.0f); if(fLoss2 == 0) fLoss2 = MathSqrt(fQWeights.Dot(loss) / fQWeights.Sum()); else fLoss2 = MathSqrt(0.999f * MathPow(fLoss2, 2.0f) + 0.001f * fQWeights.Dot(loss) / fQWeights.Sum()); grad = CAGrad(loss * zeta * (target - result) * 2.0f); last_layer = cCritic2.layers.Total() - 1; layer = cCritic2.layers.At(last_layer); if(!layer) return false; neuron = layer.At(0); if(!neuron) return false; buffer = neuron.getGradient(); if(!buffer) return false; if(!buffer.AssignArray(grad) || !buffer.BufferWrite()) return false; if(!cCritic2.backPropGradient(output, GetPointer(temp)) || !backPropGradient(SecondInput, GetPointer(temp), iLatentLayer)) return false;
Na próxima seção do nosso método, realizaremos a atualização das políticas. Lembre-se de que o algoritmo SAC+DICE prevê o treinamento de duas políticas de Atores: conservadora e otimista. Primeiro, atualizamos a política conservadora. A propagação para este modelo já foi realizada anteriormente.
Para treinar os Atores, usaremos o Crítico com o menor erro médio. Determinamos esse modelo e salvamos um ponteiro para ele em uma variável local.
vector<float> mean; CNet *critic = NULL; if(fLoss1 <= fLoss2) { cCritic1.getResults(result); cCritic2.getResults(mean); critic = GetPointer(cCritic1); } else { cCritic1.getResults(mean); cCritic2.getResults(result); critic = GetPointer(cCritic2); }
Carregamos então as avaliações previstas de cada um dos Críticos. Em seguida, determinamos os valores de referência para a retropropagação dos modelos usando a fórmula.
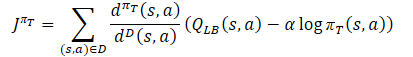
Neste processo, certamente corrigimos o vetor de gradientes de erro usando o método Conflict-Averse Gradient Descent.
vector<float> var = MathAbs(mean - result) / 2.0f; mean += result; mean /= 2.0f; target = mean; for(ulong i = 0; i < log_prob.Size(); i++) target[shift + i] = discount * log_prob[i] * LogProbMultiplier; target = CAGrad(zeta * (target - var * 2.5f) - result) + result;
Em seguida, transferimos os dados obtidos para o buffer e realizamos a retropropagação do Crítico e do Ator. Para evitar ajustes mútuos nos modelos, desativamos o modo de treinamento do Crítico antes de começar as operações. Neste caso, usamos o Crítico apenas para transmitir o gradiente de erro ao Ator.
CBufferFloat bTarget; bTarget.AssignArray(target); critic.TrainMode(false); if(!critic.backProp(GetPointer(bTarget), GetPointer(this)) || !backPropGradient(SecondInput, GetPointer(temp))) { critic.TrainMode(true); return false; }
O modelo do Ator otimista, ao contrário do conservador, ainda não foi utilizado. Portanto, antes de começar a atualizar seus parâmetros, precisamos realizar sua propagação com o estado atual do ambiente.
//--- update exploration policy if(!cActorExploer.feedForward(State, 1, false, SecondInput)) { critic.TrainMode(true); return false; } output = ((CNeuronBaseOCL*)((CLayer*)cActorExploer.layers.At(layers.Total() - 1)).At(0)).getOutput(); output.AssignArray(Actions); output.BufferWrite();
Como no caso do Ator conservador, realizamos a substituição do vetor de ações e obtemos os logaritmos das probabilidades, mas agora considerando a política otimista.
cActorExploer.GetLogProbs(log_prob);
E determinamos o vetor de valores de referência para a retropropagação dos modelos, mas agora usando a fórmula da política otimista.
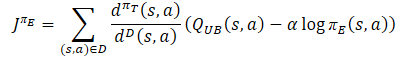
O vetor de gradientes de erros é corrigido pelo método Conflict-Averse Gradient Descent.
target = mean; for(ulong i = 0; i < log_prob.Size(); i++) target[shift + i] = discount * log_prob[i] * LogProbMultiplier; target = CAGrad(zeta * (target + var * 2.0f) - result) + result;
Depois disso, realizamos a retropropagação dos modelos e retornamos o Crítico ao modo de treinamento.
bTarget.AssignArray(target); if(!critic.backProp(GetPointer(bTarget), GetPointer(cActorExploer)) || !cActorExploer.backPropGradient(SecondInput, GetPointer(temp))) { critic.TrainMode(true); return false; } critic.TrainMode(true);
Finalmente, resta-nos atualizar os modelos-alvo. E aqui eu fiz mais adições para evitar distorções nas avaliações dos estados futuros e na adaptação dos modelos dos Críticos aos valores de suas cópias-alvo.
As atualizações dos parâmetros dos modelos-alvo em cada iteração são feitas somente se seu uso for descartado para a estimativa de estado subsequente. Se os modelos-alvo são usados no processo de treinamento, a atualização deles é feita com um atraso.
Portanto, primeiro verificamos a necessidade de atualizar os modelos e só então realizamos as operações.
if(!!NextState) { if(iUpdateDelayCount > 0) { iUpdateDelayCount--; return true; } iUpdateDelayCount = iUpdateDelay; } if(!cTargetCritic1.WeightsUpdate(GetPointer(cCritic1), tau) || !cTargetCritic2.WeightsUpdate(GetPointer(cCritic2), tau) || !cTargetNu.WeightsUpdate(GetPointer(cNu), tau)) { PrintFormat("Error of update target models: %d", GetLastError()); return false; } //--- return true; }
Após a conclusão bem-sucedida de todas as iterações do método, concluímos seu trabalho com o resultado true.
A decomposição das recompensas e o uso de vetores trouxeram mudanças em outros métodos. Isso inclui os métodos de trabalho com arquivos. Mas não vamos nos deter neles agora. Você pode se familiarizar com eles, bem como com o código completo de todos os métodos da nova classe, no arquivo anexado "MQL5\Experts\SAC-D&DICE\Net_SAC_D_DICE.mqh".
2.2 Ajustando as estruturas de armazenamento de dados
Continuamos e passamos para o trabalho no arquivo "MQL5\Experts\SAC-D&DICE\Trajectory.mqh". Se antes alterávamos a arquitetura dos modelos aqui, agora a deixamos praticamente inalterada. Precisamos apenas mudar o número de neurônios na saída do Crítico. Deve haver o suficiente para a decomposição da função de recompensa. Mas antes de especificar o número deles, vamos definir a estrutura da recompensa decomposta.
No primeiro elemento com índice "0", indicaremos a mudança relativa do saldo. Como você sabe, nosso objetivo principal é maximizar os lucros no mercado.
No parâmetro com índice "1", indicaremos a mudança relativa do Equity. Um valor negativo indica uma rebaixamento indesejado, enquanto um valor positivo indica lucro não realizado.
Designaremos outro elemento para penalidades por falta de posições abertas.
Em seguida, adicionaremos os logaritmos das probabilidades das ações. Como você sabe, o comprimento do vetor de logaritmos de probabilidades é igual ao vetor de ações.
//+------------------------------------------------------------------+ //| Rewards structure | //| 0 - Delta Balance | //| 1 - Delta Equity ( "-" Drawdown / "+" Profit) | //| 2 - Penalty for no open positions | //| 3... - LogProbs vector | //+------------------------------------------------------------------+
Assim, o tamanho da camada de neurônios de resultados do Crítico é 3 elementos maior do que o número de ações.
#define NActions 6 //Number of possible Actions #define NRewards 3+NActions //Number of rewards
bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; } //--- Actor ........ ........ //--- Critic critic.Clear(); //--- Input layer ........ ........ //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NRewards; descr.optimization = ADAM; descr.activation = None; if(!critic.Add(descr)) { delete descr; return false; } //--- return true; }
Além disso, é importante notar que a decomposição da recompensa também mudou a estrutura de armazenamento de dados no buffer de reprodução de experiência. Agora, uma única variável para registrar a recompensa não é suficiente. Precisamos de um array de dados. Ao mesmo tempo, incluímos a componente entrópica no array de recompensas, portanto, não precisamos de um array separado para registrar novamente esses valores. Consequentemente, na estrutura de descrição do estado, substituiremos o array log_prob por rewards. E ajustaremos os métodos de cópia da estrutura e trabalho com arquivos.
struct SState { float state[HistoryBars * BarDescr]; float account[AccountDescr - 4]; float action[NActions]; float rewards[NRewards]; //--- SState(void); //--- bool Save(int file_handle); bool Load(int file_handle); //--- overloading void operator=(const SState &obj) { ArrayCopy(state, obj.state); ArrayCopy(account, obj.account); ArrayCopy(action, obj.action); ArrayCopy(rewards, obj.rewards); } };
Na estrutura da trajetória STrajectory, removemos o array de recompensas Rewards, pois agora descreveremos a recompensa na estrutura do estado SState. E fazemos ajustes pontuais nos métodos da estrutura.
struct STrajectory { SState States[Buffer_Size]; int Total; float DiscountFactor; bool CumCounted; //--- STrajectory(void); //--- bool Add(SState &state); void CumRevards(void); //--- bool Save(int file_handle); bool Load(int file_handle); };
O código completo das estruturas mencionadas e seus métodos pode ser consultado no anexo.
2.3 Criação de EAs para o treinamento do modelo
Avançamos para o trabalho nos EAs de treinamento do modelo. No processo de treinamento, como antes, usamos 3 EAs:
- Research — coleta de base de exemplos
- Study — treinamento dos modelos
- Test — verificação dos resultados obtidos
Nas atividades dos EAs Research e Test, as mudanças afetaram apenas a preparação da estrutura de descrição do estado do ambiente e da recompensa obtida no final do método OnTick. Se antes somávamos recompensas e penalidades, agora cada componente é inserido em seu próprio elemento do array. É importante manter a estrutura de dados mencionada acima. Cada elemento do array deve ser preenchido em uma ordem obrigatória. Se um valor de componente estiver ausente, registramos "0" no elemento correspondente do array. Essa abordagem nos dará confiança na correção dos dados utilizados.
void OnTick() { //--- ........ ........ //--- sState.rewards[0] = bAccount[0]; sState.rewards[1] = 1.0f-bAccount[1]; vector<float> log_prob; Actor.GetLogProbs(log_prob); if((buy_value + sell_value) == 0) sState.rewards[2] -= (float)(atr / PrevBalance); else sState.rewards[2] = 0; for(ulong i = 0; i < NActions; i++) { sState.action[i] = ActorResult[i]; sState.rewards[i + 3] = log_prob[i] * LogProbMultiplier; } if(!Base.Add(sState)) ExpertRemove(); }
O código completo dos EAs pode ser consultado no anexo.
O treinamento dos modelos é realizado, como de costume, no EA Study. Como mencionado anteriormente, dividimos o processo de treinamento dos modelos em duas etapas:
- Treinamento com recompensa acumulativa real (sem modelos-alvo),
- Treinamento com o uso de modelos-alvo.
A duração da primeira etapa é determinada por uma constante.
#define StartTargetIteration 20000
É importante notar que o treinamento sem o uso de modelos-alvo é realizado apenas na primeira execução do EA Study, quando não há modelos previamente treinados.
Se o EA de treinamento conseguir carregar modelos previamente treinados ao ser iniciado, os modelos-alvo são usados desde a primeira iteração de treinamento.
Esse controle é implementado no método OnInit do EA.
int OnInit() { //--- ResetLastError(); if(!LoadTotalBase()) { PrintFormat("Error of load study data: %d", GetLastError()); return INIT_FAILED; } //--- load models if(!Net.Load(FileName, true)) { CArrayObj *actor = new CArrayObj(); CArrayObj *critic = new CArrayObj(); if(!CreateDescriptions(actor, critic)) { delete actor; delete critic; return INIT_FAILED; } if(!Net.Create(actor, critic, critic, critic, LatentLayer)) { delete actor; delete critic; return INIT_FAILED; } delete actor; delete critic; StartTargetIter = StartTargetIteration; } else StartTargetIter = 0; //--- if(!EventChartCustom(ChartID(), 1, 0, 0, "Init")) { PrintFormat("Error of create study event: %d", GetLastError()); return INIT_FAILED; } //--- return(INIT_SUCCEEDED); }
Como se pode notar, ao criar novos modelos, gravamos na variável StartTargetIter o valor da constante StartTargetIteration. Se, no entanto, modelos previamente treinados são carregados, salvamos "0" na variável de atraso.
As iterações de treinamento são estruturadas no método Train. No início do método, como de costume, determinamos o número de trajetórias armazenadas no buffer de reprodução de experiência. E realizamos um ciclo de treinamento com o número de iterações definido no parâmetro externo do EA.
void Train(void) { int total_tr = ArraySize(Buffer); uint ticks = GetTickCount(); //--- for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) { int tr = (int)((MathRand() / 32767.0) * (total_tr - 1)); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2)); if(i < 0) { iter--; continue; }
No corpo do ciclo, amostramos aleatoriamente um estado em uma das trajetórias armazenadas. Em seguida, transferimos as informações sobre o estado selecionado para os buffers de dados e para o vetor.
//--- bState.AssignArray(Buffer[tr].States[i].state); float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; bAccount.Clear(); bAccount.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[1] / PrevBalance); bAccount.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); bAccount.Add(Buffer[tr].States[i].account[2]); bAccount.Add(Buffer[tr].States[i].account[3]); bAccount.Add(Buffer[tr].States[i].account[4] / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[5] / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[6] / PrevBalance); double x = (double)Buffer[tr].States[i].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_MN1); bAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_W1); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_D1); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); //--- bActions.AssignArray(Buffer[tr].States[i].action); vector<float> rewards; rewards.Assign(Buffer[tr].States[i].rewards);
Note que nesta fase preparamos informações apenas sobre o estado selecionado. Para não realizar trabalho extra, as informações sobre o próximo estado serão geradadas apenas se necessário.
Verificamos a necessidade de usar modelos-alvo para avaliar o próximo estado comparando a iteração atual de treinamento com o valor da variável StartTargetIter. Se o número de iterações ainda não atingiu o valor limite, realizamos o treinamento com valores cumulativos. Mas há um ponto importante aqui. Ao salvar dados no buffer de reprodução de experiência, calculamos o total cumulativo dos valores de todos os componentes da recompensa. No entanto, a componente entrópica é necessária sem o total cumulativo. Portanto, realizamos um ciclo e removemos os valores acumulados apenas da componente entrópica da função de recompensa.
//--- if(iter < StartTargetIter) { ulong start = rewards.Size() - bActions.Total(); for(ulong r = start; r < rewards.Size(); r++) rewards[r] -= Buffer[tr].States[i + 1].rewards[r] * DiscFactor; if(!Net.Study(GetPointer(bState), GetPointer(bAccount), GetPointer(bActions), rewards, NULL, NULL, DiscFactor, Tau)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } }
E então chamamos o método de treinamento da nossa nova classe. Aqui indicamos "NULL" nos parâmetros do próximo estado.
Após atingir o valor limite para o uso de modelos-alvo, primeiro preparamos as informações sobre o próximo estado do sistema.
else { //--- Target bNextState.AssignArray(Buffer[tr].States[i + 1].state); PrevBalance = Buffer[tr].States[i].account[0]; PrevEquity = Buffer[tr].States[i].account[1]; if(PrevBalance == 0) { iter--; continue; } bNextAccount.Clear(); bNextAccount.Add((Buffer[tr].States[i + 1].account[0] - PrevBalance) / PrevBalance); bNextAccount.Add(Buffer[tr].States[i + 1].account[1] / PrevBalance); bNextAccount.Add((Buffer[tr].States[i + 1].account[1] - PrevEquity) / PrevEquity); bNextAccount.Add(Buffer[tr].States[i + 1].account[2]); bNextAccount.Add(Buffer[tr].States[i + 1].account[3]); bNextAccount.Add(Buffer[tr].States[i + 1].account[4] / PrevBalance); bNextAccount.Add(Buffer[tr].States[i + 1].account[5] / PrevBalance); bNextAccount.Add(Buffer[tr].States[i + 1].account[6] / PrevBalance); x = (double)Buffer[tr].States[i + 1].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); bNextAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_MN1); bNextAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_W1); bNextAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_D1); bNextAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
Em seguida, removemos os valores acumulados de todos os componentes da função de recompensa, deixando apenas as recompensas do estado atual.
for(ulong r = 0; r < rewards.Size(); r++) rewards[r] -= Buffer[tr].States[i + 1].rewards[r] * DiscFactor; if(!Net.Study(GetPointer(bState), GetPointer(bAccount), GetPointer(bActions), rewards, GetPointer(bNextState), GetPointer(bNextAccount), DiscFactor, Tau)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } }
E chamamos o método de treinamento do modelo da nossa classe. Desta vez, indicamos os objetos com dados do próximo estado.
Ao finalizar a iteração do ciclo, exibimos uma mensagem para informar o usuário e passamos para a próxima iteração.
//--- if(GetTickCount() - ticks > 500) { float loss1, loss2; Net.GetLoss(loss1, loss2); string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic1", iter * 100.0 / (double)(Iterations), loss1); str += StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic2", iter * 100.0 / (double)(Iterations), loss2); Comment(str); ticks = GetTickCount(); } }
Após a conclusão bem-sucedida de todas as iterações do ciclo, limpamos o campo de comentários no gráfico. Realizamos uma atualização forçada dos modelos-alvo. Registramos o resultado do treinamento no log do MetaTrader 5 e iniciamos o processo de encerramento do trabalho do EA.
Comment(""); //--- float loss1, loss2; Net.GetLoss(loss1, loss2); Net.TargetsUpdate(Tau); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic1", loss1); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic2", loss2); ExpertRemove(); //--- }
Com isso, concluímos o trabalho com os EAs de treinamento do modelo. Você pode consultar o código completo de todos os programas usados no artigo no anexo.
3. Testando
A versão proposta para implementar a abordagem de decomposição da função de recompensa com base no algoritmo SAC+DICE foi apresentada e agora podemos avaliar na prática os resultados do trabalho realizado. Como antes, o treinamento dos modelos foi realizado com dados históricos do instrumento EURUSD, timeframe H1, durante os primeiros 5 meses de 2023. Todos os parâmetros dos indicadores são usados por padrão. Saldo inicial de 10.000 USD.
O processo de treinamento do modelo é iterativo, alternando entre as fases de coleta de exemplos no buffer de experiência acumulada e a atualização dos parâmetros do modelo.
No primeiro estágio, criamos uma base primária de exemplos usando modelos de Atores preenchidos com parâmetros aleatórios. Como resultado, obtemos uma série de passagens aleatórias que geram conjuntos de dados "Estado → Ação → Novo Estado → Recompensa" não relacionados por política.
Diferentemente de todos os algoritmos anteriormente considerados, neste caso, coletamos dados decompostos sobre recompensas do ambiente para as ações realizadas pelo Agente.
Após a coleta de exemplos, realizamos o treinamento inicial do nosso modelo. Para isso, executamos o EA "..\SAC-D&DICE\Study.mq5".
Devo dizer que, no treinamento inicial sem o uso de modelos-alvo, observamos uma tendência estável de redução do erro de ambos os Críticos. No entanto, ao usar modelos-alvo para avaliar o próximo estado, observamos picos caóticos (embora infrequentes) no erro de previsão. Após esses picos, é possível observar um retorno suave ao nível anterior de erro.
Na segunda etapa, reiniciamos o EA de coleta de dados de treinamento no modo de otimização do testador de estratégias com a varredura completa dos parâmetros. Desta vez, em todas as passagens, usamos o Ator otimista treinado na primeira etapa. A variação nos resultados das passagens individuais é menor do que na coleta de dados inicial e é causada pela estocasticidade da política do Ator.
O processo de coleta de exemplos e treinamento do modelo é repetido várias vezes até obter o resultado desejado ou atingir um mínimo local, quando a próxima iteração de coleta de exemplos e treinamento do modelo não traz progresso nos resultados.
Durante o processo de treinamento do modelo, obtivemos uma política do Ator capaz de gerar um pequeno lucro durante o período de treinamento.
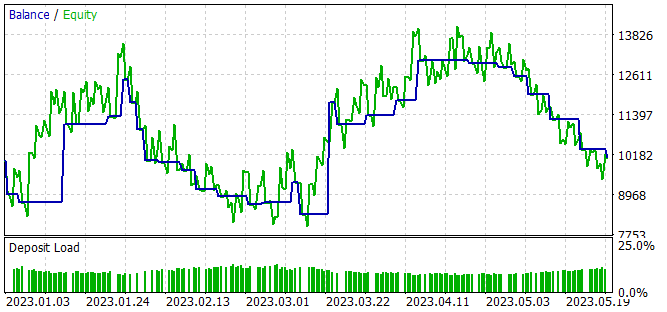
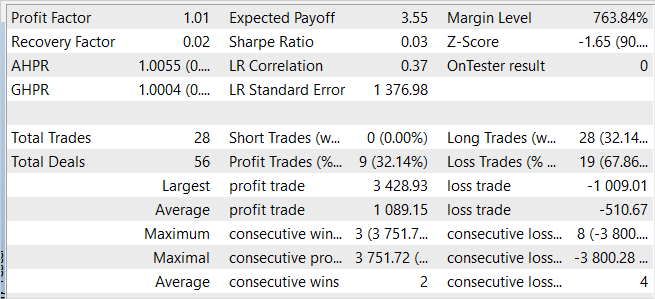
Apesar do lucro obtido, a política aprendida está longe de nossos desejos. No gráfico de balanço, observamos um movimento ondulatório com amplitude relativamente grande. De 28 negociações, apenas 32% foram fechadas com lucro. O lucro total foi alcançado graças ao tamanho da operação lucrativa superar o da perda. Assim, o lucro médio por negociação é duas vezes maior que a perda média. E o lucro máximo em uma única operação é quase 3,5 vezes maior que a maior perda. Como resultado, o fator de lucro é ligeiramente superior a 1.
Em defesa do modelo, pode-se dizer que em novos dados o EA também demonstrou lucro. Em um mês após o período de treinamento, o modelo conseguiu quase 20% de retorno, que é superior ao resultado na amostra de treinamento. No entanto, a estatística dos resultados é comparável aos dados da amostra de treinamento. Durante o teste, foram realizadas apenas 4 operações, e apenas uma delas foi fechada com lucro. Mas o lucro desta negociação foi 12,8 vezes maior do que a maior perda entre as transações perdedoras.
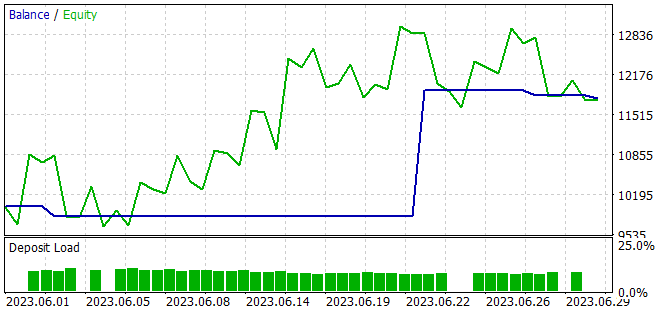
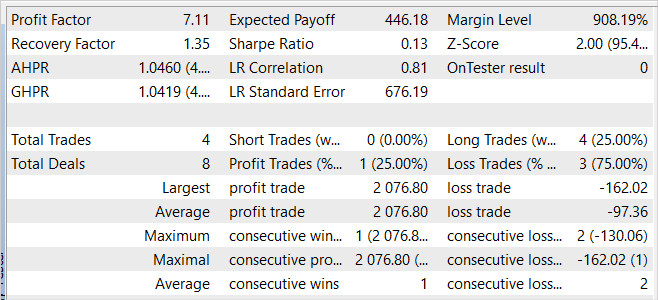
Comparando os resultados da amostra de treinamento com o período subsequente, podemos supor que em novos dados estamos vendo o início de uma onda de rentabilidade. Onda essa que pode ser seguida por um declínio no futuro previsível.
No geral, o modelo é capaz de gerar lucro, mas requer otimização adicional.
Considerações finais
Neste artigo, exploramos a abordagem de decomposição da função de recompensa, que permite treinar Agentes de maneira mais eficiente. A decomposição da recompensa permite analisar o impacto de diferentes componentes nas decisões tomadas pelo Agente.
Implementamos o algoritmo usando MQL5 e integramos a decomposição da função de recompensa no método SAC+DICE.
Durante os testes práticos do algoritmo implementado, conseguimos obter um modelo capaz de gerar lucro tanto na amostra de treinamento quanto fora dela, o que demonstra a capacidade de generalização do algoritmo.
No entanto, os resultados obtidos estão longe do ideal. Ao mesmo tempo, a decomposição da função de recompensa permite analisar o impacto de componentes individuais no resultado do treinamento. Eu sugiro que você experimente incluir e excluir componentes individuais e avalie o impacto deles nos resultados do treinamento.
Referências
- Conflict-Averse Gradient Descent para Aprendizado Multi-tarefa
- Value Function Decomposition for Iterative Design of Reinforcement Learning Agents
- Redes neurais de maneira fácil (Parte 52): exploração com otimização e correção de distribuição
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | EA | EA para coleta de exemplos |
| 2 | Study.mq5 | EA | EA para treinamento do agente |
| 3 | Test.mq5 | EA | EA para teste do modelo |
| 4 | Trajectory.mqh | Biblioteca de classe | Estrutura de descrição do estado do sistema |
| 5 | Net_SAC_D_DICE.mqh | Biblioteca de classe | Classe do modelo |
| 6 | NeuroNet.mqh | Biblioteca de classe | Biblioteca de classes para criação de redes neurais |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/13098
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Desenvolvendo um sistema de Replay (Parte 41): Iniciando a segunda fase (II)
Desenvolvendo um sistema de Replay (Parte 41): Iniciando a segunda fase (II)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Obrigado, Dmitry, cliquei em seu perfil de vendedor na esperança de encontrar alguns EAs de nn que eu pudesse testar.
Fiz um curso MQL5 da udemy sobre nn e agora estou tentando me aprofundar. Estou começando com sua série de artigos.