Algoritmi di ottimizzazione della popolazione: Algoritmo della scimmia (MA)

Contenuti:

1. Introduzione
2. L’Algoritmo
3. Risultati del test

1. Introduzione

L'algoritmo della scimmia (MA) è un algoritmo di ricerca meta-euristico. Questo articolo descrive i componenti principali dell'algoritmo e presenta le soluzioni per la salita (movimento verso l'alto), il salto locale e il salto globale. L'algoritmo è stato proposto da R. Zhao e W. Tang nel 2007. L'algoritmo simula il comportamento del movimento e del salto delle scimmie sulle montagne in cerca di cibo. Si presume che le scimmie derivino dal fatto che più alta è la montagna, più cibo c'è sulla sua cima.

L'area esplorata dalle scimmie è un paesaggio di funzioni di fitness, quindi la montagna più alta corrisponde alla soluzione del problema (consideriamo il problema di massimizzazione globale). Dalla sua posizione attuale, ogni scimmia sale fino a raggiungere la cima della montagna. Il processo di scalata è progettato per migliorare gradualmente il valore della funzione obiettivo. Poi, la scimmia effettua una serie di salti locali in una direzione casuale nella speranza di trovare una montagna più alta e il movimento verso l'alto viene ripetuto. Dopo aver eseguito un certo numero di salite e salti locali, la scimmia ritiene di aver esplorato sufficientemente il paesaggio nelle vicinanze della sua posizione iniziale.

Per esplorare una nuova area dello spazio di ricerca, la scimmia esegue un lungo salto globale. I passaggi precedenti vengono ripetuti un numero specifico di volte nei parametri dell'algoritmo. La soluzione del problema è dichiarata essere il più alto dei vertici trovati dalla popolazione di scimmie. Tuttavia, la MA spende un tempo computazionale significativo nella ricerca di soluzioni ottimali locali nel processo di scalata. Il processo di salto globale può accelerare il tasso di convergenza dell'algoritmo. Lo scopo di questo processo è forzare le scimmie a trovare nuove opportunità di ricerca per non cadere nella ricerca locale. L'algoritmo presenta vantaggi quali una struttura semplice, un'affidabilità relativamente elevata e una buona ricerca di soluzioni ottimali locali.

Il MA è un nuovo tipo di algoritmo evolutivo che può risolvere molti problemi di ottimizzazione complessi caratterizzati da non linearità, non differenziabilità e alta dimensionalità. La differenza rispetto agli altri algoritmi è che il tempo impiegato da MA è dovuto principalmente all'uso del processo di scalata per trovare soluzioni ottimali locali. Nella prossima sezione descriverò i componenti principali dell'algoritmo, le soluzioni presentate, l'inizializzazione, la salita, l'osservazione e il salto.

2. L’Algoritmo

Per facilitare la comprensione dell'algoritmo della scimmia, è ragionevole iniziare con uno pseudocodice.

Pseudocodice dell'algoritmo MA:

1. Distribuire le scimmie in modo casuale nello spazio di ricerca.
2. Misurare l'altezza della posizione della scimmia.
3. Eseguire salti locali per un numero fisso di volte.
4. Se il nuovo vertice ottenuto al punto 3 è il più alto, allora i salti locali devono essere effettuati da questo punto.
5. Se il limite del numero di salti locali è esaurito e non viene trovato un nuovo vertice, si effettua un salto globale.
6. Dopo il punto 5, ripetere il punto 3
7. Ripetere dal punto 2 fino a quando non viene soddisfatto il criterio di arresto.

Analizziamo ogni punto dello pseudocodice in modo più dettagliato.

1. All'inizio dell'ottimizzazione, lo spazio di ricerca è sconosciuto alle scimmie. Gli animali si trovano casualmente in un terreno inesplorato, poiché la posizione del cibo è ugualmente probabile in qualsiasi luogo.

2. Il processo di misurazione dell'altezza della posizione della scimmia è l'adempimento del compito della funzione di fitness.

3. Quando si effettuano salti locali, c’è un limite al loro numero specificato nei parametri dell'algoritmo. Ciò significa che la scimmia sta cercando di migliorare la sua posizione attuale facendo piccoli salti locali nell'area del cibo. Se la nuova fonte di cibo è migliore, passare al punto 4.

4. È stata trovata una nuova fonte di cibo, il conteggio dei salti locali viene azzerato. Ora la ricerca di una nuova fonte di cibo sarà effettuata da questo punto.

5. Se i salti locali non portano alla scoperta di una fonte di cibo migliore, la scimmia conclude che l'area attuale è stata completamente esplorata ed è ora di cercare un nuovo posto più lontano. A questo punto sorge la domanda sulla direzione degli ulteriori salti. L'idea dell'algoritmo è quella di utilizzare il centro delle coordinate di tutte le scimmie, fornendo così qualche comunicazione - comunicazione tra le scimmie di un branco: le scimmie possono urlare ad alta voce e avendo un buon udito, sono in grado di determinare la posizione esatta dei loro simili. Allo stesso tempo, conoscendo la posizione dei loro simili (i simili non saranno in luoghi dove non c'è cibo), è possibile calcolare approssimativamente la nuova posizione ottimale del cibo, quindi è necessario fare un salto in questa direzione.

Nell'algoritmo originale, la scimmia effettua un salto globale lungo una linea che passa per il centro delle coordinate di tutte le scimmie e la posizione attuale dell'animale. La direzione del salto può essere o verso il centro delle coordinate o in direzione opposta al centro. Un salto nella direzione opposta rispetto al centro contraddice la logica stessa della ricerca del cibo con coordinate approssimate per tutte le scimmie, che è stato confermato dai miei esperimenti con l'algoritmo - infatti, si tratta di una probabilità del 50% che ci sia una distanza dall'optimum globale.

La pratica ha dimostrato che è più redditizio saltare oltre il centro delle coordinate che non saltare o saltare nella direzione opposta. La concentrazione di tutte le scimmie in un unico punto non si verifica, sebbene a prima vista tale logica lo rende inevitabile. Infatti, le scimmie, avendo esaurito il limite dei salti locali, saltano più in là del centro, ruotando così la posizione di tutte le scimmie della popolazione. Se immaginiamo mentalmente le scimmie superiori che obbediscono a questo algoritmo, vedremo un branco di animali che di volta in volta salta sul centro geometrico del branco, mentre il branco stesso si sposta verso una fonte di cibo più ricca. Questo effetto di "movimento del branco" può essere chiaramente visto nell'animazione dell'algoritmo (l'algoritmo originale non ha questo effetto e i risultati sono peggiori).

6. Avendo compiuto un salto globale, la scimmia inizia a specificare la posizione della fonte di cibo nel nuovo luogo. Il processo continua finché non viene soddisfatto il criterio di arresto.

L'intera idea dell'algoritmo può essere facilmente adattata in un singolo diagramma. Nella Figura 1, il movimento della scimmia è indicato da cerchi con numeri. Ogni numero rappresenta una nuova posizione per la scimmia. I piccoli cerchi gialli rappresentano i tentativi di salto locale falliti. Il numero 6 indica la posizione in cui il limite dei salti locali è stato raggiunto e non è stata trovata una nuova posizione migliore. I cerchi senza numeri rappresentano le posizioni del resto del branco. Il centro geometrico del branco è indicato da un piccolo cerchio con coordinate (x,y).

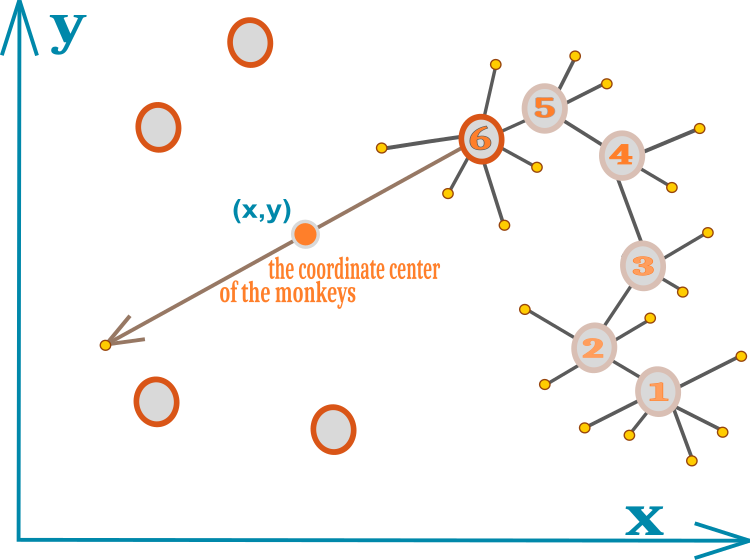
Figura 1. Rappresentazione schematica del movimento di una scimmia in un branco

Diamo un'occhiata al codice MA.

È conveniente descrivere una scimmia in un branco con la struttura S_Monkey. La struttura contiene l'array c [] con le coordinate correnti, l'array cB [] con le coordinate del cibo migliore (è dalla posizione con queste coordinate che si verificano i salti locali), h e hB - il valore dell'altezza del punto corrente e il valore del punto più alto, rispettivamente. lCNT — contatore dei salti locali che limita il numero di tentativi di migliorare una posizione.

//——————————————————————————————————————————————————————————————————————————————
struct S_Monkey
{
  double c  []; //coordinates
  double cB []; //best coordinates
  double h;     //height of the mountain
  double hB;    //best height of the mountain
  int    lCNT;  //local search counter
};
//——————————————————————————————————————————————————————————————————————————————

La classe dell’algoritmo C_AO_MA non è diversa dagli algoritmi discussi in precedenza. Un branco di scimmie è rappresentato nella classe come un array di strutture m[]. Le dichiarazioni dei metodi e dei membri della classe sono piccole in termini di volume di codice. Poiché l'algoritmo è conciso, non c'è alcun ordinamento qui, a differenza di molti altri algoritmi di ottimizzazione. Avremo bisogno di array per impostare il massimo, il minimo e il passo dei parametri ottimizzati, come anche di variabili costanti per passare loro i parametri esterni dell'algoritmo. Passiamo alla descrizione dei metodi che contengono la logica principale di MA.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_MA
{
  //----------------------------------------------------------------------------
  public: S_Monkey m       []; //monkeys
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //minimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double hB;           //best height of the mountain

  public: void Init (const int    coordNumberP,     //coordinates number
                     const int    monkeysNumberP,   //monkeys number
                     const double bCoefficientP,    //local search coefficient
                     const double vCoefficientP,    //jump coefficient
                     const int    jumpsNumberP);    //jumps number

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordNumber;       //coordinates number
  private: int    monkeysNumber;     //monkeys number

  private: double b [];              //local search coefficient
  private: double v [];              //jump coefficient
  private: double bCoefficient;      //local search coefficient
  private: double vCoefficient;      //jump coefficient
  private: double jumpsNumber;       //jumps number
  private: double cc [];             //coordinate center

  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Il metodo pubblico Init() serve a inizializzare l'algoritmo. Qui si imposta la dimensione degli array. Inizializziamo la qualità del miglior territorio trovato dalla scimmia con il minimo valore 'double' possibile, e faremo lo stesso con le variabili corrispondenti degli array della struttura MA.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_MA::Init (const int    coordNumberP,    //coordinates number
                    const int    monkeysNumberP,  //monkeys number
                    const double bCoefficientP,   //local search coefficient
                    const double vCoefficientP,   //jump coefficient
                    const int    jumpsNumberP)    //jumps number
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  hB       = -DBL_MAX;
  revision = false;

  coordNumber   = coordNumberP;
  monkeysNumber = monkeysNumberP;
  bCoefficient  = bCoefficientP;
  vCoefficient  = vCoefficientP;
  jumpsNumber   = jumpsNumberP;

  ArrayResize (rangeMax,  coordNumber);
  ArrayResize (rangeMin,  coordNumber);
  ArrayResize (rangeStep, coordNumber);
  ArrayResize (b,         coordNumber);
  ArrayResize (v,         coordNumber);
  ArrayResize (cc,        coordNumber);

  ArrayResize (m, monkeysNumber);

  for (int i = 0; i < monkeysNumber; i++)
  {
    ArrayResize (m [i].c,  coordNumber);
    ArrayResize (m [i].cB, coordNumber);
    m [i].h    = -DBL_MAX;
    m [i].hB   = -DBL_MAX;
    m [i].lCNT = 0;
  }

  ArrayResize (cB, coordNumber);
}
//——————————————————————————————————————————————————————————————————————————————

Il primo metodo pubblico Moving(), che deve essere eseguito a ogni iterazione, implementa la logica del salto della scimmia. Alla prima iterazione, quando il flag "revision" è "false", è necessario inizializzare gli agenti con valori casuali nell'intervallo di coordinate dello spazio studiato, che equivale alla posizione casuale delle scimmie nell'habitat del branco. Per ridurre le operazioni ripetute, come il calcolo dei coefficienti dei salti globali e locali, memorizziamo i valori delle coordinate corrispondenti (ciascuna delle coordinate può avere una propria dimensione) negli array v [] e b []. Azzeriamo il contatore dei salti locali di ogni scimmia. 

//----------------------------------------------------------------------------
if (!revision)
{
  hB = -DBL_MAX;

  for (int monk = 0; monk < monkeysNumber; monk++)
  {
    for (int c = 0; c < coordNumber; c++)
    {
      m [monk].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      m [monk].c [c] = SeInDiSp  (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      m [monk].h     = -DBL_MAX;
      m [monk].hB    = -DBL_MAX;
      m [monk].lCNT  = 0;
    }
  }

  for (int c = 0; c < coordNumber; c++)
  {
    v [c] = (rangeMax [c] - rangeMin [c]) * vCoefficient;
    b [c] = (rangeMax [c] - rangeMin [c]) * bCoefficient;
  }

  revision = true;
}

Per calcolare il centro delle coordinate di tutte le scimmie, utilizziamo l'array cc [] la cui dimensione corrisponde al numero di coordinate. L'idea qui è di sommare le coordinate delle scimmie e dividere la somma risultante per la dimensione della popolazione. Pertanto, il centro delle coordinate è la media aritmetica delle coordinate.

//calculate the coordinate center of the monkeys----------------------------
for (int c = 0; c < coordNumber; c++)
{
  cc [c] = 0.0;

  for (int monk = 0; monk < monkeysNumber; monk++)
  {
    cc [c] += m [monk].cB [c];
  }

  cc [c] /= monkeysNumber;
}

Secondo lo pseudocodice, se il limite di salti locali non viene raggiunto, la scimmia salterà dalla sua posizione in tutte le direzioni con la stessa probabilità. Il raggio del cerchio dei salti locali è regolato dal coefficiente dei salti locali, che viene ricalcolato in base alla dimensione delle coordinate dell'array b[].

//local jump--------------------------------------------------------------
if (m [monk].lCNT < jumpsNumber) //local jump
{
  for (int c = 0; c < coordNumber; c++)
  {
    m [monk].c [c] = RNDfromCI (m [monk].cB [c] - b [c], m [monk].cB [c] + b [c]);      
    m [monk].c [c] = SeInDiSp (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

Passiamo a una parte molto importante della logica MA - le prestazioni dell'algoritmo dipendono in larga misura dall'implementazione dei salti globali. Diversi autori affrontano questo problema da angolazioni diverse, proponendo ogni sorta di soluzione. Secondo la ricerca, i salti locali hanno un effetto minimo sulla convergenza dell'algoritmo. Sono i salti globali a determinare la capacità dell'algoritmo di "saltare" dagli estremi locali. I miei esperimenti con i salti globali hanno rivelato solo un approccio valido per questo particolare algoritmo, che migliora i risultati.

In precedenza, abbiamo discusso l'opportunità di saltare verso il centro delle coordinate, ed è meglio se il punto finale si trova dietro il centro e non tra il centro e le coordinate attuali. Questo approccio applica le equazioni di volo di Levy che abbiamo descritto in dettaglio nell'articolo sull'algoritmo di ottimizzazione del Cuculo (COA).

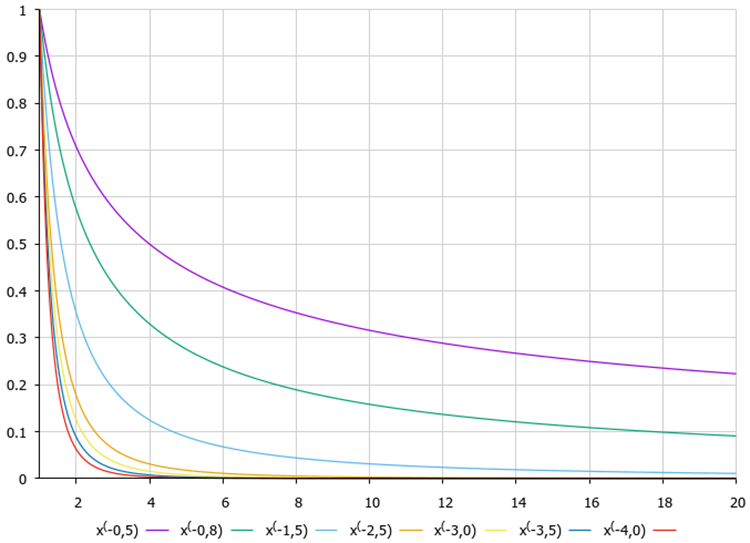
Figure 2. Grafici della funzione del volo di Levy a seconda del grado dell'equazione

Le coordinate della scimmia sono calcolate utilizzando la seguente equazione:

m [monk].c [c] = cc [c] + v [c] * pow (r2, -2.0);

dove:

cc [c] — coordinata del centro delle coordinate,

v [c] — coefficiente del raggio di salto ricalcolato sulla dimensione dello spazio di ricerca,

r2 — numero nell'intervallo da 1 a 20.

Applicando il volo di Levy in questa operazione, otteniamo un’alta probabilità che la scimmia colpisca in prossimità del centro delle coordinate e una bassa probabilità di trovarsi oltre il centro. In questo modo, garantiamo un equilibrio tra ricerca e sfruttamento della ricerca, scoprendo nuove fonti di cibo. Se la coordinata ricevuta supera il limite inferiore dell'intervallo consentito, la coordinata viene trasferita alla distanza corrispondente al limite superiore dell'intervallo. Lo stesso avviene quando si supera il limite superiore. Al termine dei calcoli delle coordinate, si verifica che il valore ottenuto sia conforme ai confini e alla fase di ricerca.

//global jump-------------------------------------------------------------
for (int c = 0; c < coordNumber; c++)
{
  r1 = RNDfromCI (0.0, 1.0);
  r1 = r1 > 0.5 ? 1.0 : -1.0;
  r2 = RNDfromCI (1.0, 20.0);

  m [monk].c [c] = cc [c] + v [c] * pow (r2, -2.0);
          
  if (m [monk].c [c] < rangeMin [c]) m [monk].c [c] = rangeMax [c] - (rangeMin [c] - m [monk].c [c]);
  if (m [monk].c [c] > rangeMax [c]) m [monk].c [c] = rangeMin [c] + (m [monk].c [c] - rangeMax [c]);
          
  m [monk].c [c] = SeInDiSp (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
}

Dopo aver effettuato salti locali/globali, aumentare di uno il contatore dei salti.

m [monk].lCNT++;

Revision() è il secondo metodo pubblico chiamato ad ogni iterazione dopo il calcolo della funzione di fitness. Questo metodo aggiorna la soluzione globale se ne viene trovata una migliore. Le logiche di elaborazione dei risultati dopo i salti locali e globali differiscono tra loro. Nel caso di un salto locale, è necessario controllare se la posizione corrente è migliorata e aggiornarla (nelle iterazioni successive, i salti vengono effettuati da questa nuova posizione), mentre nel caso di salti globali, non c'è alcun controllo dei miglioramenti - i nuovi salti verranno effettuati da questa posizione in ogni caso.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_MA::Revision ()
{
  for (int monk = 0; monk < monkeysNumber; monk++)
  {
    if (m [monk].h > hB)
    {
      hB = m [monk].h;
      ArrayCopy (cB, m [monk].c, 0, 0, WHOLE_ARRAY);
    }

    if (m [monk].lCNT <= jumpsNumber) //local jump
    {
      if (m [monk].h > m [monk].hB)
      {
        m [monk].hB = m [monk].h;
        ArrayCopy (m [monk].cB, m [monk].c, 0, 0, WHOLE_ARRAY);
        m [monk].lCNT = 0;
      }
    }
    else //global jump
    {
      m [monk].hB = m [monk].h;
      ArrayCopy (m [monk].cB, m [monk].c, 0, 0, WHOLE_ARRAY);
      m [monk].lCNT = 0;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Possiamo notare la somiglianza degli approcci di questo algoritmo con un gruppo di algoritmi di intelligenza a sciame, come lo sciame di particelle (PSO) e altri con una logica di strategia di ricerca simile.

3. Risultati del test

Risultati del banco di prova MA:

2023.02.22 19:36:21.841    Test_AO_MA (EURUSD,M1)    C_AO_MA:50;0.01;0.9;50
2023.02.22 19:36:21.841    Test_AO_MA (EURUSD,M1)    =============================
2023.02.22 19:36:26.877    Test_AO_MA (EURUSD,M1)    5 Rastrigin's; Func cicli 10000 risultato: 64.89788419898215
2023.02.22 19:36:26.878    Test_AO_MA (EURUSD,M1)    Punteggio: 0.80412
2023.02.22 19:36:36.734    Test_AO_MA (EURUSD,M1)    25 Rastrigin's; Func cicli 10000 risultato: 55.57339368461394
2023.02.22 19:36:36.734    Test_AO_MA (EURUSD,M1)    Punteggio: 0.68859
2023.02.22 19:37:34.865    Test_AO_MA (EURUSD,M1)    500 Rastrigin's; Func cicli 10000 risultato: 41.41612351844293
2023.02.22 19:37:34.865    Test_AO_MA (EURUSD,M1)    Punteggio: 0.51317
2023.02.22 19:37:34.865    Test_AO_MA (EURUSD,M1)    =============================
2023.02.22 19:37:39.165    Test_AO_MA (EURUSD,M1)    5 Forest's; Func cicli 10000 risultato: 0.4307085210424681
2023.02.22 19:37:39.165    Test_AO_MA (EURUSD,M1)    Punteggio: 0.24363
2023.02.22 19:37:49.599    Test_AO_MA (EURUSD,M1)    25 Forest's; Func cicli 10000 risultato: 0.19875891413613866
2023.02.22 19:37:49.599    Test_AO_MA (EURUSD,M1)    Punteggio: 0.11243
2023.02.22 19:38:47.793    Test_AO_MA (EURUSD,M1)    500 Forest's; Func cicli 10000 risultato: 0.06286212143582881
2023.02.22 19:38:47.793    Test_AO_MA (EURUSD,M1)    Punteggio: 0.03556
2023.02.22 19:38:47.793    Test_AO_MA (EURUSD,M1)    =============================
2023.02.22 19:38:53.947    Test_AO_MA (EURUSD,M1)    5 Megacity's; Func cicli 10000 risultato: 2.8
2023.02.22 19:38:53.947    Test_AO_MA (EURUSD,M1)    Punteggio: 0.23333
2023.02.22 19:39:03.336    Test_AO_MA (EURUSD,M1)    25 Megacity's; Func cicli 10000 risultato: 0.96
2023.02.22 19:39:03.336    Test_AO_MA (EURUSD,M1)    Punteggio: 0.08000
2023.02.22 19:40:02.068    Test_AO_MA (EURUSD,M1)    500 Megacity's; Func cicli 10000 risultato: 0.34120000000000006
2023.02.22 19:40:02.068    Test_AO_MA (EURUSD,M1)    Punteggio: 0.02843

Prestando attenzione alla visualizzazione dell'algoritmo sulle funzioni di test, va notato che non ci sono schemi nel comportamento, ovvero è molto simile a quello dell'algoritmo RND. C'è una piccola concentrazione di agenti negli estremi locali, che indica i tentativi di affinare la soluzione da parte dell'algoritmo, ma non ci sono inceppamenti evidenti.

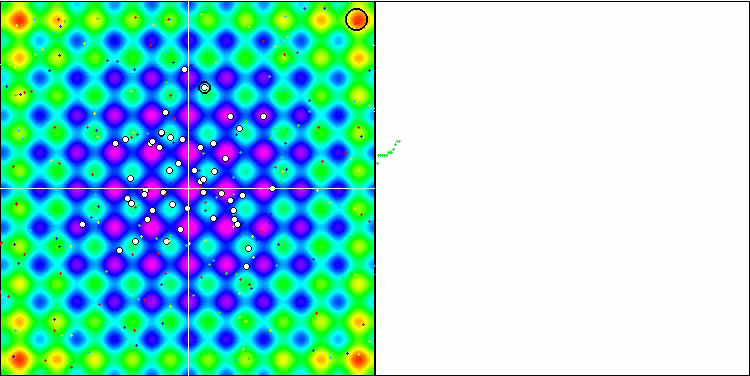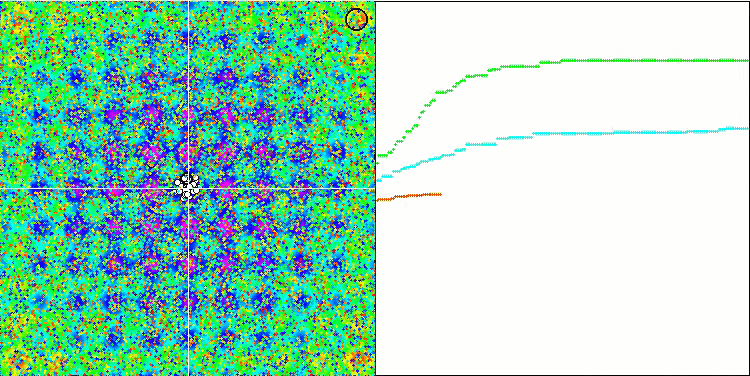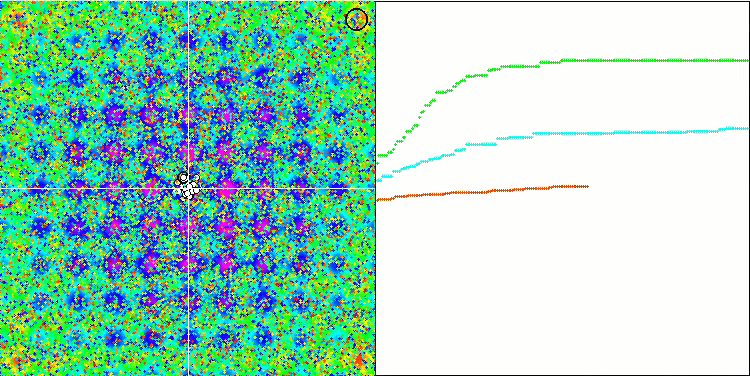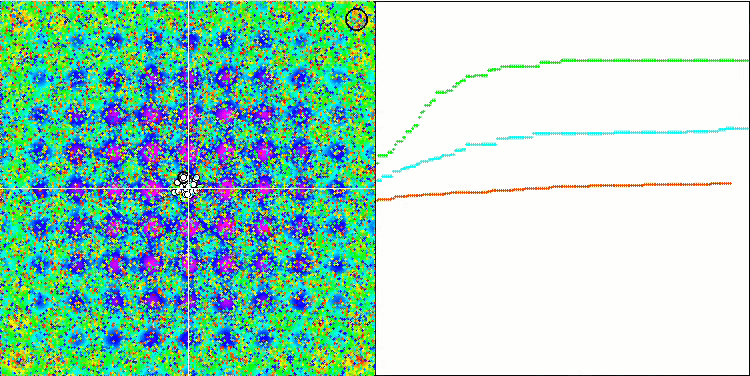
  MA sulla funzione di test Rastrigin.

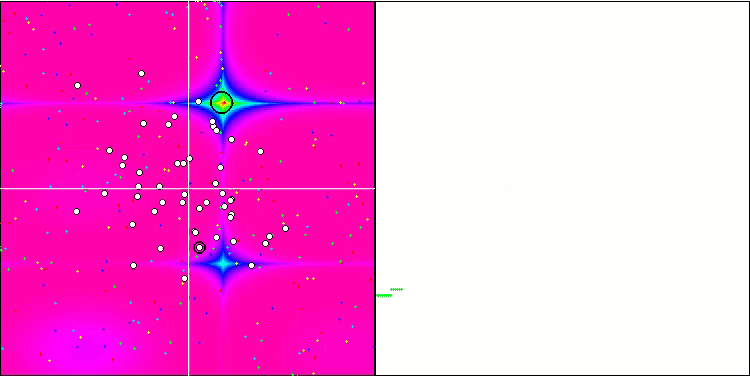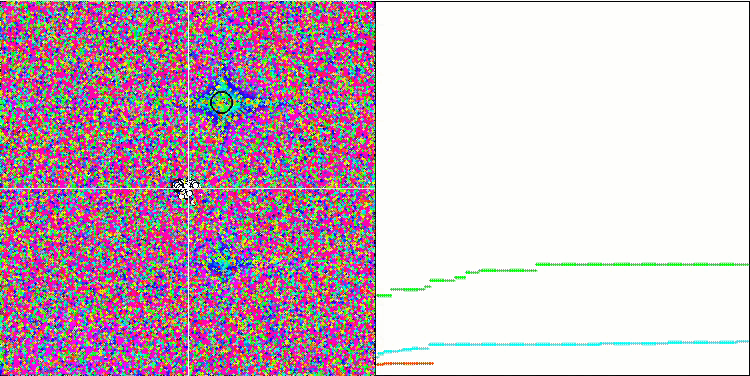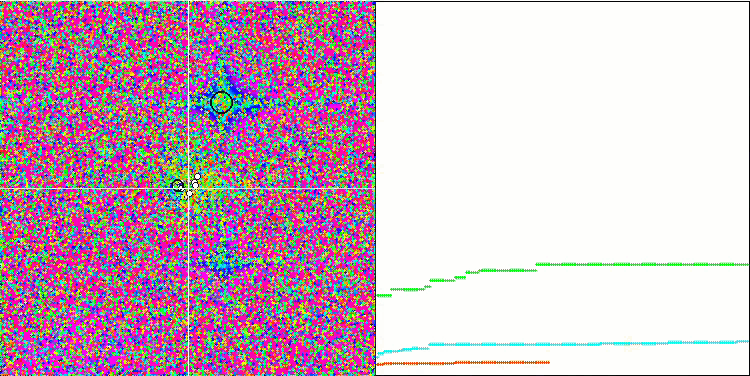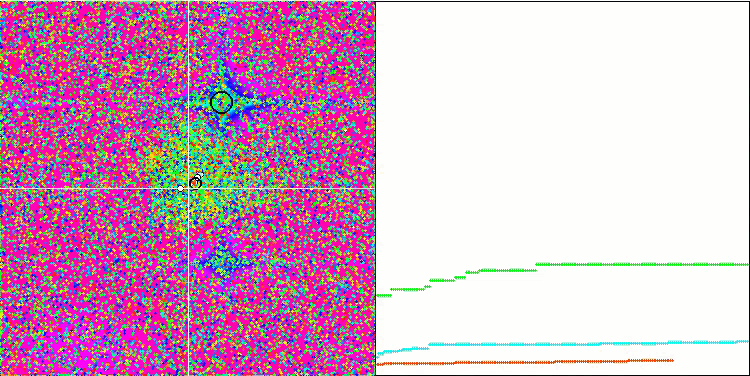
  MA sulla funzione di test Forest.

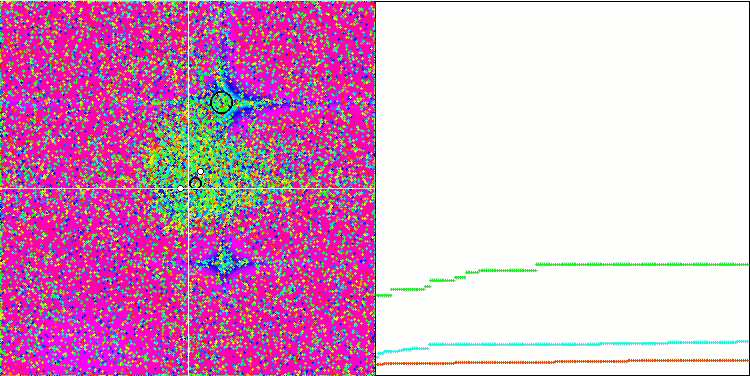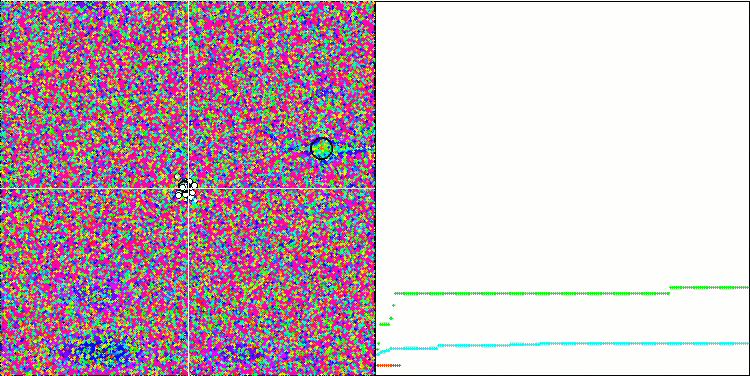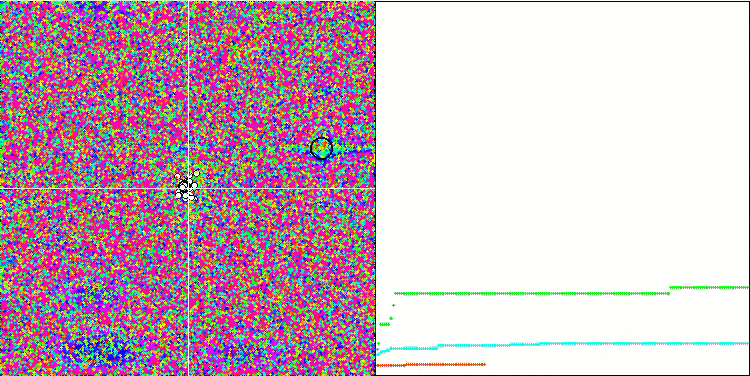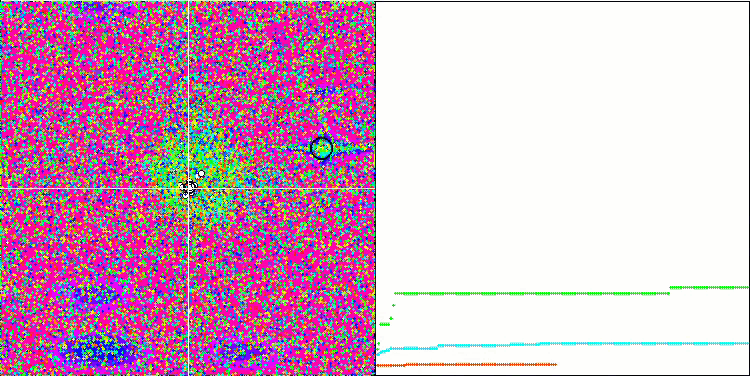
  MA sulla funzione di test Megacity.

Passiamo all'analisi dei risultati dei test. In base ai risultati del punteggio, l'algoritmo MA si colloca in fondo alla classifica tra GSA e FSS. Poiché il test degli algoritmi si basa sul principio dell'analisi comparativa, in cui i punteggi dei risultati sono valori relativi tra il migliore e il peggiore, l'emergere di un algoritmo con risultati eccezionali in un test e scarsi in altri, provoca talvolta una modifica dei parametri degli altri partecipanti al test.

Ma i risultati di MA non hanno causato un ricalcolo dei risultati degli altri partecipanti al test nella tabella. MA non ha un singolo risultato di test che sia il peggiore, anche se ci sono algoritmi con zero risultati relativi e una valutazione più alta (ad esempio, GSA). Pertanto, sebbene l'algoritmo si comporti in modo piuttosto modesto e la capacità di ricerca non sia sufficientemente espressa, l'algoritmo mostra risultati stabili, il che è una qualità positiva per gli algoritmi di ottimizzazione.

AO	Descrizione	Rastrigin			Finale Rastrigin	Forest			Finale Forest	Megacity (discreta)			Finale Megacity	Risultato finale
		10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)		10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)		10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)
HS	Ricerca dell'armonia	1.00000	1.00000	0.57048	2.57048	1.00000	0.98931	0.57917	2.56848	1.00000	1.00000	1.00000	3.00000	100.000
ACOm	Ottimizzazione della colonia di formiche M	0.34724	0.18876	0.20182	0.73782	0.85966	1.00000	1.00000	2.85966	1.00000	0.88484	0.13497	2.01981	68.094
IWO	Ottimizzazione delle piante infestanti	0.96140	0.70405	0.35295	2.01840	0.68718	0.46349	0.41071	1.56138	0.75912	0.39732	0.80145	1.95789	67.087
COAm	Algoritmo di ottimizzazione del cuculo M	0.92701	0.49111	0.30792	1.72604	0.55451	0.34034	0.21362	1.10847	0.67153	0.30326	0.41127	1.38606	50.422
FAm	Algoritmo della lucciola M	0.60020	0.35662	0.20290	1.15972	0.47632	0.42299	0.64360	1.54291	0.21167	0.25143	0.84884	1.31194	47.816
BA	Algoritmo del pipistrello	0.40658	0.66918	1.00000	2.07576	0.15275	0.17477	0.33595	0.66347	0.15329	0.06334	0.41821	0.63484	39.711
ABC	Colonia di api artificiali	0.78424	0.34335	0.24656	1.37415	0.50591	0.21455	0.17249	0.89295	0.47444	0.23609	0.33526	1.04579	38.937
BFO	Ottimizzazione del foraggiamento batterico	0.67422	0.32496	0.13988	1.13906	0.35462	0.26623	0.26695	0.88780	0.42336	0.30519	0.45578	1.18433	37.651
GSA	Algoritmo di ricerca gravitazionale	0.70396	0.47456	0.00000	1.17852	0.26854	0.36416	0.42921	1.06191	0.51095	0.32436	0.00000	0.83531	35.937
MA	Algoritmo della scimmia	0.33300	0.35107	0.17340	0.85747	0.03684	0.07891	0.11546	0.23121	0.05838	0.00383	0.25809	0.32030	14.848
FSS	Ricerca del banco di pesci	0.46965	0.26591	0.13383	0.86939	0.06711	0.05013	0.08423	0.20147	0.00000	0.00959	0.19942	0.20901	13.215
PSO	Ottimizzazione dello sciame di particelle	0.20515	0.08606	0.08448	0.37569	0.13192	0.10486	0.28099	0.51777	0.08028	0.21100	0.04711	0.33839	10.208
RND	Casuale	0.16881	0.10226	0.09495	0.36602	0.07413	0.04810	0.06094	0.18317	0.00000	0.00000	0.11850	0.11850	5.469
GWO	Ottimizzazione del lupo grigio	0.00000	0.00000	0.02672	0.02672	0.00000	0.00000	0.00000	0.00000	0.18977	0.03645	0.06156	0.28778	1.000

Riepilogo

L'algoritmo MA classico consiste fondamentalmente nell'utilizzare il processo di scalata per trovare soluzioni ottimali locali. Il passo di salita gioca un ruolo decisivo nell'accuratezza dell'approssimazione della soluzione locale. Più piccolo è il passo di salita per i salti locali, maggiore è l'accuratezza della soluzione, ma sono necessarie più iterazioni per trovare l'optimum globale. Per ridurre il tempo di calcolo riducendo il numero di iterazioni, molti ricercatori raccomandano di utilizzare altri metodi di ottimizzazione nelle fasi iniziali dell'ottimizzazione, come ABC, COA, IWO, e di utilizzare MA per affinare la soluzione globale. Non sono d'accordo con questo approccio. Credo sia più opportuno utilizzare immediatamente gli algoritmi descritti invece di MA, anche se MA ha un potenziale di sviluppo che lo rende un buon oggetto per ulteriori esperimenti e studi. 

L'Algoritmo della Scimmia è un algoritmo basato sulla popolazione che affonda le sue radici nella natura. Come molti altri algoritmi meta-euristici, questo algoritmo è evolutivo ed è in grado di risolvere una serie di problemi di ottimizzazione, tra cui la non linearità, la non differenziabilità e l'elevata dimensionalità dello spazio di ricerca con un alto tasso di convergenza. Un altro vantaggio dell'algoritmo della scimmia è che questo algoritmo è controllato da un numero ridotto di parametri, il che lo rende abbastanza facile da implementare. Nonostante la stabilità dei risultati, il basso tasso di convergenza non consente di raccomandare l'algoritmo della scimmia per la risoluzione di problemi ad alta complessità computazionale, poiché richiede un numero significativo di iterazioni. Esistono molti altri algoritmi che svolgono lo stesso lavoro in un tempo più breve (numero di iterazioni).

Nonostante i miei numerosi esperimenti, la versione classica dell'algoritmo non riusciva a superare la terza riga dal basso della tabella di valutazione, si bloccava agli estremi locali e funzionava in modo estremamente male sulle funzioni discrete. Non avevo particolare voglia di scrivere un articolo a riguardo, quindi ho fatto dei tentativi per migliorarlo. Uno di questi tentativi ha mostrato alcuni miglioramenti negli indicatori di convergenza e ha aumentato la stabilità dei risultati utilizzando il bias di probabilità nei salti globali, oltre a rivedere il principio dei salti globali stessi. Molti ricercatori MA sottolineano la necessità di modernizzare l'algoritmo, per cui sono state apportate molte modifiche all'algoritmo della scimmia. Non era mia intenzione prendere in considerazione tutti i tipi di modifiche di MA, perché l'algoritmo in sé non è eccezionale, piuttosto è una variazione dello sciame di particelle (PSO). Il risultato degli esperimenti è stata la versione finale dell'algoritmo riportata in questo articolo senza il segno aggiuntivo "m" (modificato).

Di seguito è riportato l'istogramma dei risultati del test dell'algoritmo.

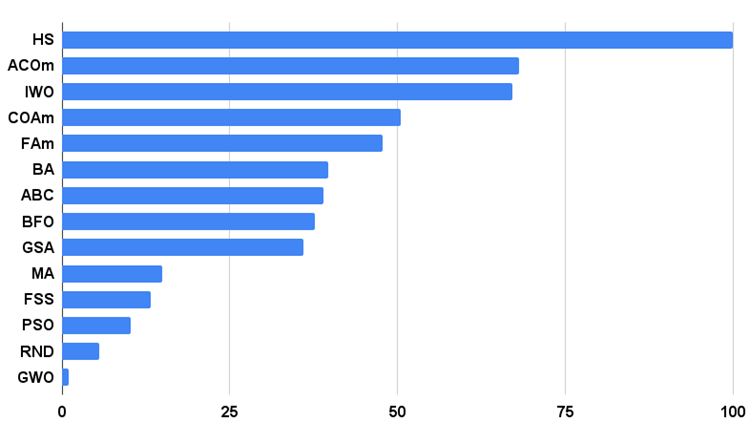
Figura 3. Istogramma dei risultati dei test degli algoritmi

Pro e contro di MA:

Pro:
1. Facile implementazione.
2. Buona scalabilità nonostante il basso tasso di convergenza.
3. Buone prestazioni sulle funzioni discrete.
4. Numero ridotto di parametri esterni.

Contro:
1. Basso tasso di convergenza.
2. Richiede un numero elevato di iterazioni per una ricerca.
3. Bassa efficienza complessiva.

Ogni articolo presenta un archivio che contiene le versioni aggiornate dei codici degli algoritmi per tutti gli articoli precedenti. L'articolo si basa sull'esperienza accumulata dall'autore e rappresenta la sua opinione personale. Le conclusioni e i giudizi si basano sugli esperimenti.