Algoritmi di ottimizzazione della popolazione: Colonia di api artificiali (ABC)

Contenuto

1. Introduzione
2. Descrizione dell'algoritmo
3. Versione modificata
4. Risultati del test
   

1. Introduzione

Gli insetti sociali sono creature altamente evolute che svolgono molti compiti complessi non eseguiti da singoli insetti. La comunicazione, la complessa costruzione del nido, il controllo dell'ambiente, la protezione e la divisione del lavoro sono solo alcuni dei comportamenti che le api mellifere hanno evoluto per prosperare nelle colonie sociali.
Le api appartengono agli esseri dello sciame e dimostrano abilità straordinarie nel trovare soluzioni ottimali. In natura, trovano gruppi di fiori per raccogliere nettare e polline vicino all'alveare. A volte il raggio di ricerca può aumentare fino a diversi chilometri. Le api di ritorno riferiscono le loro scoperte con una danza improvvisata.

A prima vista, questo sembra sia impossibile, ma sono in grado di trasmettere informazioni sulla posizione geografica alle altre attraverso movimenti ritmici. In base all'intensità della danza delle loro sorelle, le api traggono conclusioni sul numero di fiori e sulla quantità stimata di nettare in un determinato punto. Più il cibo è potenziale, più la danza si svolge attivamente. Questo insolito fenomeno è stato scoperto a metà del XX secolo dallo studioso di insetti Karl von Frisch.

Per molti anni, i metodi di ricerca delle api sono stati studiati esclusivamente dai biologi. Tuttavia, l'interesse per l'applicazione del comportamento degli sciami nello sviluppo di nuovi algoritmi di ottimizzazione stava crescendo. Nel 2005, il professor Dervis Karaboga si è interessato ai risultati della ricerca. Ha pubblicato un articolo scientifico ed è stato il primo a descrivere il modello di intelligenza dello sciame ispirato principalmente alla danza delle api. Il modello è stato chiamato colonia artificiale di api.

2. Descrizione dell'algoritmo

Esistono molte implementazioni di una colonia artificiale di api, che differiscono nei principi di gestione delle api in un alveare e nelle regole di esplorazione dell’area. In questo articolo parlerò della mia interpretazione della versione classica dell'algoritmo.

L'idea dell'algoritmo si basa sul comportamento delle api nella ricerca di luoghi dove ottenere il maggior quantitativo possibile di nettare. Per prima cosa, tutte le api volano fuori dall'alveare in una direzione casuale, agendo come esploratori provando a cercare aree dove c'è del nettare. Dopodiché, le api tornano all'alveare e, in modo particolare, dicono alle altre dove e quanto nettare hanno trovato.

Le api operaie vengono inviate nelle aree scoperte. Più si suppone che in quest'area si trovi del nettare, più api volano in quella direzione. I ricognitori si allontanano nuovamente per cercare altre aree, ma già nelle vicinanze delle aree trovate. Pertanto, tutte le api si dividono in due tipi: le api operaie che raccolgono il nettare e le api esploratrici che esplorano nuove aree. Le aree di raccolta del nettare hanno un valore corrispondente alla quantità di nettare presente in esse. Le regioni di rango inferiore sono spostate rispetto a una regione di rango superiore lungo una linea che passa per i centri delle regioni.

La distribuzione delle api operaie per regione può essere visualizzata in modo schematico nella Figura 1.

Fig. 1. Il numero di api nelle aree dipende dalla classificazione dell'area

L'area 1 ha un rango più alto, contiene più nettare e quindi più api tendono a volare lì. In base al numero di api, possiamo determinare visivamente che l'area 4 ha il rango (valore) più basso. Le informazioni sul valore di ogni area sono riportate dalle api sotto forma di una speciale danza. Ogni alveare ha una propria danza, in cui viene programmata la direzione e la quantità di nettare nell'area.

Supponiamo che la posizione dell'estremo globale sia l'area dove c'è più nettare e che ci sia solo un'area di questo tipo. Il nettare è presente in altri luoghi, anche se in quantità minore. Le api vivono in uno spazio multidimensionale, dove ogni coordinata rappresenta un parametro della funzione che necessita di essere ottimizzata. La quantità di nettare trovata è il valore della funzione obiettivo a questo punto, se stiamo cercando un massimo globale. Se stiamo cercando un minimo globale, è sufficiente moltiplicare la funzione obiettivo per -1.

Poiché le aree di raccolta del nettare hanno un determinato valore, solo l'area con il rango più alto ha il diritto di spostarsi (spostamento centrale) verso il punto con la maggiore concentrazione di nettare. Le aree di rango inferiore saranno spostate al centro della concentrazione più alta e controllate per intersezione con un'area di rango superiore. In questo modo, la concentrazione delle api in un'area ristretta non è consentita e lo spazio di ricerca viene servito dalle api operaie nel modo più efficiente possibile, evitando così l'esaurimento della fonte di cibo. In termini di ottimizzazione, questo elimina o minimizza il blocco negli estremi locali. Dopo che le aree sono state disperse e spostate l'una rispetto all'altra lungo la catena di rango verso il loro optimum, i loro dintorni saranno ulteriormente indagati dalle api esploratrici.

Molti apicoltori consigliano di inviare api esploratrici in aree casuali dello spazio di ricerca, ma la mia esperienza dimostra che il valore pratico di tale "esplorazione" è prossimo allo zero ed è utile solo per una e due dimensioni. In altre parole, se parliamo di spazi multidimensionali, i gradi di libertà aumentano geometricamente ed è incredibilmente difficile imbattersi accidentalmente in una fonte di nettare più preziosa. Le risorse dell'alveare andranno solo sprecate. È molto più utile mandare le esploratrici nelle vicinanze delle aree di ricerca già note, in modo che le coordinate non siano disperse, ma siano concentrate specificamente nelle zone di possibili fonti di nettare.

Se le aree si intersecano, è necessario spostare il centro in modo che le aree tocchino solo i bordi. Questo è mostrato in Fig. 2.

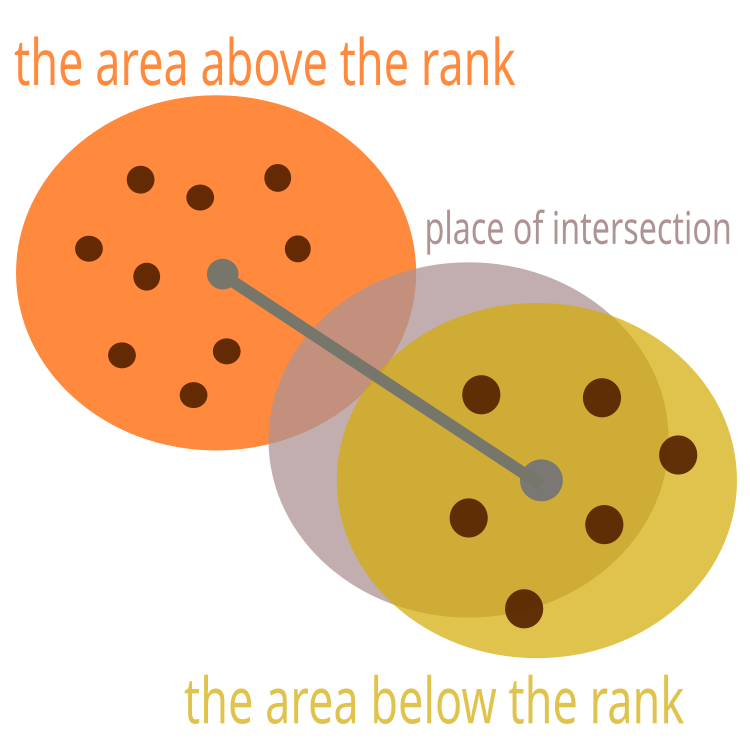
Figura 2. L'area che ha un rango inferiore dovrebbe essere spostata

Il rango delle aree non è impostato rigidamente, ma si forma dinamicamente. I ritrovamenti delle api esploratrici saranno assegnati all'area, in prossimità della quale hanno volato. Nel caso in cui venga scoperta una fonte di cibo più preziosa, il centro dell'area verrà spostato lì. Potrebbe anche diventare il nuovo miglior centro di raccolta del nettare. Le aree rimanenti saranno ora spostate rispetto ad essa. In altre parole, saranno spostati rispetto ad essa lungo la catena di rango.

Il metodo di trasmissione delle informazioni, chiamato danza delle api, è un elemento essenziale della strategia dell'alveare nel suo complesso. È necessario distribuire nel modo più razionale possibile le risorse disponibili dell'alveare per le aree di lavorazione, così che il numero di api inviate deve essere proporzionale al valore dell'area. Ciò significa che un numero uguale di api sarà inviato in aree di pari valore.

Passiamo all'algoritmo stesso. Le fasi di esecuzione sono elencate di seguito:

1. Tutte le api volano a caso lungo lo spazio di ricerca come esploratrici.
2. Misurare la quantità di nettare ricevuto da ciascuna ape.
3. Smistamento delle api.
4. Assegnare le aree in base alle informazioni sulla quantità di nettare ottenute dalle api.
5. Invio delle api operaie nella zona. Più nettare c'è nell'area, più api saranno inviate.
6. Invio di api esploratrici nelle vicinanze di un'area selezionata a caso.
   
7. Misurare la quantità di nettare ricevuta da ogni ape.
8. Classificare le aree in base alla quantità di nettare.
   
9. Ripetere p. 4 fino al raggiungimento del criterio di arresto.

Per facilitare la percezione visiva, facciamo un diagramma a blocchi dell'algoritmo in Figura 3.

Fig. 3. Diagramma a blocchi dell'algoritmo

Descriviamo il codice dell'algoritmo Bee Colony in modo più dettagliato.

Un'ape è un'unità logica elementare e di base dell'algoritmo. Può essere descritto da una struttura. Come potrai ricordare, la posizione di un'ape viene stabilita in base alle coordinate, all'appartenenza all'area in cui è stato raccolto il nettare e alla quantità di nettare. Le api dell'alveare saranno quindi rappresentate da un array. Ognuno di essi è accessibile tramite il suo indice.

//——————————————————————————————————————————————————————————————————————————————
struct S_Bee
{
  double c []; //coordinates
  int    aInd; //area index
  double n;    //nectar
};
//——————————————————————————————————————————————————————————————————————————————

La seconda e più grande unità logica è l'area di raccolta del nettare. È definita dal centro e dal punto di maggiore concentrazione di nettare e dalla quantità di nettare che determina il valore dell'area. Nell'area di rango più elevato (la prima dell'elenco), le coordinate del centro e della massima concentrazione di nettare coincidono. Per le aree del secondo e dei ranghi inferiori dell'elenco, potrebbero non corrispondere, poiché sono state spostate. L'inizializzazione dell'area si conclude con il ripristino dell'indicatore della quantità di nettare e la distribuzione delle coordinate al numero corrispondente di parametri della funzione ottimizzata.

//——————————————————————————————————————————————————————————————————————————————
struct S_Area
{
  void Init (int coordinatesNumber)
  {
    n = -DBL_MAX;

    ArrayResize (cC, coordinatesNumber);
    ArrayResize (cB, coordinatesNumber);
  }

  double cC   []; //center coordinates
  double cB   []; //best coordinates
  double n;       //nectarAmount
};
//——————————————————————————————————————————————————————————————————————————————

Descriviamo la danza delle api come una struttura, il cui array corrisponderà al numero di aree.

//——————————————————————————————————————————————————————————————————————————————
struct S_BeeDance
{
  double start;
  double end;
};
//——————————————————————————————————————————————————————————————————————————————

Descriverò l'alveare come una classe che imposta le aree di ricerca, le api, le coordinate migliori e la maggiore quantità di nettare trovata in tutte le iterazioni. Inoltre, verranno definiti tutti i metodi necessari per ordinare le api e le aree, nonché per spostare le api e le relative aree l'una rispetto all'altra. Qui possiamo vedere le dichiarazioni di funzioni già note per gli algoritmi precedenti: generazione di numeri casuali uniformemente distribuiti, ridimensionamento in un intervallo e scelta di un numero da un intervallo con un passo.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ABC //Bees Hive
{
  //============================================================================
  public: S_Area areas     []; //nectar collection areas
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: S_Bee  bees      []; //all the bees of the hive
  public: double cB        []; //best coordinates
  public: double nB;           //nectar of the best coordinates

  public: void InitHive (const int    coordinatesP,      //number of opt. parameters
                         const int    beesNumberP,       //bees number
                         const int    workerBeesNumberP, //worker bees number
                         const int    areasNumberP,      //areas number
                         const double collectionRadiusP, //collection radius
                         const double scoutAreaRadiusP); //scout area radius

  public: void TasksForBees ();
  public: void CollectingNectar ();

  //============================================================================
  private: void   BeeFlight      (double &cC [] , S_Bee &bee);
  private: void   ScoutBeeFlight (double &cC [] , S_Bee &bee);
  private: void   MarkUpAreas    ();
  private: void   SortingBees    ();
  private: void   SortingAreas   ();
  private: double SeInDiSp       (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI      (double Min, double Max);
  private: double Scale          (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool Revers);

  private: int    coordinates;      //coordinates number
  private: int    beesNumber;       //the number of all bees
  private: int    workerBeesNumber; //worker bees number
  private: int    areasNumber;      //areas number
  private: S_Bee  beesT       [];   //temporary, for sorting
  private: S_Area areasT      [];   //temporary, for sorting
  private: int    indA        [];   //array for indexes when sorting
  private: double valA        [];   //array for nectar values when sorting
  private: int    indB        [];   //array for indexes when sorting
  private: double valB        [];   //array for nectar values when sorting
  private: double areasRadius [];   //radius for each coordinate
  private: double scoutRadius [];   //scout radius for each coordinate

  private: double collectionRadius;   //collection radius
  private: double scoutAreaRadius;    //scout area radius
  private: double hypersphereRadius;  //hypersphere radius
  private: double distHyperspCenters; //distance hyperspheres centers
  private: double scoutHyperspRadius; //scout hypersphere radius
  private: bool   scouting;           //scouting flag

  private: S_BeeDance beeDance [];    //bee dance
};
//——————————————————————————————————————————————————————————————————————————————

Ogni nuova ottimizzazione deve necessariamente iniziare con l'inizializzazione della classe. Il valore della quantità di nettare viene azzerato per l'intero alveare e per le singole api, come per le aree.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::InitHive (const int    coordinatesP,      //number of opt. parameters
                         const int    beesNumberP,       //bees number
                         const int    workerBeesNumberP, //worker bees number
                         const int    areasNumberP,      //areas number
                         const double collectionRadiusP, //collection radius
                         const double scoutAreaRadiusP)  //scout area radius
{
  MathSrand (GetTickCount ());
  scouting = false;
  nB       = -DBL_MAX;

  coordinates      = coordinatesP;
  beesNumber       = beesNumberP;
  workerBeesNumber = workerBeesNumberP;
  areasNumber      = areasNumberP < 3 ? 3 : areasNumberP;

  collectionRadius = collectionRadiusP; //collection radius
  scoutAreaRadius  = scoutAreaRadiusP;  //scout area radius

  ArrayResize (areas,  areasNumber);
  ArrayResize (areasT, areasNumber);
  for (int i = 0; i < areasNumber; i++)
  {
    areas  [i].Init (coordinates);
    areasT [i].Init (coordinates);
  }

  ArrayResize (beeDance, areasNumber);

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);
  ArrayResize (cB,        coordinates);

  ArrayResize (indA, areasNumber);
  ArrayResize (valA, areasNumber);

  ArrayResize (areasRadius, coordinates);
  ArrayResize (scoutRadius, coordinates);
  for (int i = 0; i < coordinates; i++)
  {
    areasRadius [i] = (rangeMax [i] - rangeMin [i]) * collectionRadius;
    scoutRadius [i] = (rangeMax [i] - rangeMin [i]) * scoutAreaRadius;
  }

  double sqr = 0.0;
  for (int i = 0; i < coordinates; i++) sqr += areasRadius [i] * areasRadius [i];
  hypersphereRadius  = MathSqrt (sqr) * collectionRadius;

  distHyperspCenters = hypersphereRadius * 2.0;

  sqr = 0.0;
  for (int i = 0; i < coordinates; i++) sqr += scoutRadius [i] * scoutRadius [i];
  scoutHyperspRadius = MathSqrt (sqr) * scoutAreaRadius;

  ArrayResize (indB, beesNumber);
  ArrayResize (valB, beesNumber);

  ArrayResize (bees,  beesNumber);
  ArrayResize (beesT, beesNumber);
  for (int i = 0; i < beesNumber; i++)
  {
    ArrayResize (bees  [i].c, coordinates);
    ArrayResize (beesT [i].c, coordinates);
    bees  [i].n = -DBL_MAX;
    beesT [i].n = -DBL_MAX;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Il metodo più semplice e aperto è la distribuzione dei compiti alle api. Qui tutto è semplice. Se le aree non sono ancora state esplorate, si azzera il valore del nettare per l'intero alveare e si avvia la marcatura delle aree. Il metodo viene richiamato ad ogni periodo fino ad ottenere il valore della funzione di fitness.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::TasksForBees ()
{
  if (!scouting)
  {
    nB = -DBL_MAX;
  }
  MarkUpAreas ();
}
//——————————————————————————————————————————————————————————————————————————————

Il secondo metodo pubblico viene chiamato ad ogni periodo. Il lancio deve essere eseguito dopo aver ottenuto il valore della funzione di fitness. In questo caso, se l'esplorazione non è ancora stata effettuata, ordiniamo le api in base al valore del nettare e copiamo le coordinate e la quantità di nettare delle prime api in elenco nelle aree corrispondenti. Se l'esplorazione è già avvenuta, copiamo le coordinate e la quantità di nettare nell'area in cui è stato raccolto, a condizione che i risultati siano migliorati. Inoltre, aggiorniamo i risultati migliori per l'intero alveare.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::CollectingNectar ()
{
  if (!scouting)
  {
    SortingBees ();

    for (int a = 0; a <areasNumber; a++)
    {
      ArrayCopy (areas [a].cB, bees [a].c, 0, 0, WHOLE_ARRAY);
      areas [a].n = bees [a].n;
    }

    scouting = true;
  }
  else
  {
    //transfer the nectar to the hive---------------------------------------------
    for (int b = 0; b < beesNumber; b++)
    {
      if (bees [b].n > areas [bees [b].aInd].n)
      {
        ArrayCopy (areas [bees [b].aInd].cB, bees [b].c, 0, 0, WHOLE_ARRAY);
        areas [bees [b].aInd].n = bees [b].n;
      }

      if (bees [b].n > nB)
      {
        ArrayCopy (cB, bees [b].c, 0, 0, WHOLE_ARRAY);
        nB = bees [b].n;
      }
    }

    SortingAreas ();
  }
}
//——————————————————————————————————————————————————————————————————————————————

Il metodo MarkUpAreas () merita di essere considerato in dettaglio. Suddividiamo il codice in parti.

Prima che le aree vengano esplorate e non ci sono informazioni sulla ricerca di fiori per raccogliere il nettare, invieremo tutte le api ad eseguire un'esplorazione preliminare. In questa fase, tutte le api svolgono il ruolo di esploratrici. Poiché non ci sono informazioni sul nettare, inviamo le esploratrici in una direzione casuale, generando numeri casuali distribuiti uniformemente nell'intervallo di coordinate.

//if the areas is not scouting - send all the bees to scouting----------------
if (!scouting)
{
  for (int b = 0; b < beesNumber; b++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      bees [b].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      bees [b].c [c] = SeInDiSp  (bees [b].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

Dopo aver esplorato le aree, è necessario copiare le coordinate della massima concentrazione di nettare al centro dell'area. In altre parole, è necessario spostare l'area in un luogo migliore. Dopo aver eseguito questa azione, dobbiamo assicurarci che l'area non intersechi l'area di rango superiore. Possiamo verificare l'intersezione delle aree misurando la distanza tra i loro centri. Le aree si intersecano se la distanza tra i centri è inferiore ai due raggi (uno dei parametri dell'algoritmo). Se viene rilevata un'intersezione, l'area viene trasferita in un punto a una distanza di due raggi, mentre le coordinate del miglior risultato ottenuto (le coordinate della massima concentrazione di nettare) rimangono nello stesso punto. Pertanto, le aree sono costantemente in movimento. Le aree migliori costringono le altre a spostarsi. Le aree di riposo, pur spostandosi, possono arrivare a una fonte di cibo più ricca, diventando le migliori dopo la cernita, che avviene nel metodo successivo.

for (int s = 0; s < areasNumber; s++)
{
  //move the center of the area to the best point in with more nectar-------
  ArrayCopy (areas [s].cC, areas [s].cB, 0, 0, WHOLE_ARRAY);

  //ordinary area-----------------------------------------------------------
  if (s != 0)
  {
    //check if there is no intersection of a region with a region of higher rank
    //measure the distance from the centers of the regions
    double centersDistance = 0.0;

    for (int c = 0; c < coordinates; c++) centersDistance += pow (areas [s].cC [c] - areas [s - 1].cC [c], 2.0);
    centersDistance = MathSqrt (centersDistance);

    //the areas intersect, then need to move the current area
    if (centersDistance < distHyperspCenters)
    {
      double incrementFactor = (distHyperspCenters - centersDistance) / centersDistance;
      double coordDistance   = 0.0;

      for (int c = 0; c < coordinates; c++)
      {
        coordDistance = areas [s].cC [c] - areas [s - 1].cC [c];
        areas [s].cC [c] = areas [s].cC [c] + (coordDistance * incrementFactor);

        areas [s].cC [c] = SeInDiSp (areas [s].cC [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }
}

È qui che si svolge la danza delle api. Utilizzando le informazioni sulla direzione e sulla quantità di nettare nelle regioni e applicando una componente casuale, contrassegniamo l'area di distribuzione di un numero casuale in modo tale che la probabilità che un'ape scelga un'area all'iterazione successiva sia proporzionale alla quantità di nettare in quest'area. In parole povere, sulla linea dei numeri si tracciano i segmenti la cui lunghezza corrisponde alla differenza tra il valore del nettare di ogni area e quello dell'area peggiore.

//send bees to the marked areas-----------------------------------------------
double r = 0.0;

beeDance [0].start = bees [0].n;
beeDance [0].end   = beeDance [0].start + (bees [0].n - bees [areasNumber - 1].n);

for (int a = 1; a < areasNumber; a++)
{
  if (a != areasNumber - 1)
  {
    beeDance [a].start = beeDance [a - 1].end;
    beeDance [a].end   = beeDance [a    ].start + (bees [a].n - bees [areasNumber - 1].n);
  }
  else
  {
    beeDance [a].start = beeDance [a - 1].end;
    beeDance [a].end   = beeDance [a    ].start + (bees [a - 1].n - bees [a].n) * 0.1;
  }
}

In questa parte di codice del metodo, si verifica una selezione casuale dell'area con la probabilità trasmessa dalla danza delle api operaie. Per fare ciò, generiamo un numero casuale nell'intervallo fatto contrassegnando la linea dei numeri con una danza. Per le esploratrici, la danza non ha importanza, poiché volano con lo stesso grado di probabilità in prossimità di qualsiasi area, ampliando così le capacità di ricerca della strategia delle api. Come in natura, ogni partecipante dell'alveare ha un certo valore mentre svolge un ruolo.

for (int b = 0; b < beesNumber; b++)
{
  if (b < workerBeesNumber)
  {
    r = RNDfromCI(beeDance [0].start, beeDance [areasNumber - 1].end);
        
    for (int a = 0; a < areasNumber; a++)
    {
      if (beeDance [a].start <= r && r < beeDance [a].end)
      {
        bees [b].aInd = a;
        break;
      }
    }

    BeeFlight (areas [bees [b].aInd].cC, bees [b]);
  }
  else
  {
    //choose the area to send the bees there
    r = RNDfromCI (0.0, areasNumber - 1);

    bees [b].aInd = (int)r; //area index

    ScoutBeeFlight (areas [bees [b].aInd].cC, bees [b]);
  }
}

Questo metodo privato implementa il volo di un'ape. Qui tutto è semplice, anche se a prima vista sembra incomprensibile e complicato. L'ape vola verso un'area con uno spostamento di probabilità cubico più vicino al centro. Pertanto, la probabilità diminuisce dal centro dell'area ai suoi confini. Tenete presente che questo è il centro dell'area e non la posizione migliore trovata in precedenza. Anche in questa semplice azione, la strategia delle api può essere tracciata, garantendo una continua ricerca di nuove fonti di cibo.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::BeeFlight (double &cC [] , S_Bee &bee)
{
  double r = 0.0;

  for (int c = 0; c < coordinates; c++)
  {
    r  = RNDfromCI (0.0, 1.0);
    r  = r * r * r;
    r = Scale (r, 0.0, 1.0, 0.0, areasRadius [c], false);
    r *= RNDfromCI (0.0, 1.0) > 0.5 ? 1.0 : -1.0;

    bee.c [c] = SeInDiSp  (cC [c] + r, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

A differenza del metodo precedente, qui viene descritto il volo dell'ape esploratrice. L'ape vola fuori dall'area entro il raggio specificato nelle impostazioni dell'algoritmo. Nonostante l'impostazione sia la stessa, i raggi vengono calcolati prima, quando la classe viene inizializzata, perché gli intervalli delle coordinate possono essere diversi e quindi i raggi devono essere appropriati. Per lanciare un'ape esploratrice in volo, dobbiamo generare un numero casuale nell'intervallo compreso tra il raggio dell'area e la somma del raggio dell'area e del raggio di esplorazione, e poi aggiungere semplicemente il valore risultante al centro dell'area. In questo semplice modo, l'ape esploratrice si troverà per caso nelle vicinanze dell'area, mentre le coordinate non saranno disperse nello spazio di ricerca.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::ScoutBeeFlight (double &cC [] , S_Bee &bee)
{
  double r = 0.0;

  for (int c = 0; c < coordinates; c++)
  {
    r  = RNDfromCI (areasRadius [c], areasRadius [c] + scoutRadius [c]);
    r *= RNDfromCI (0.0, 1.0) > 0.5 ? 1.0 : -1.0;

    bee.c [c] = SeInDiSp  (cC [c] + r, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

L'algoritmo prevede due metodi specifici - l'ordinamento per api e l'ordinamento per aree. Non ha senso descriverli, è solo un semplice ordinamento a bolla. Lo uso in quasi tutti gli algoritmi di ottimizzazione (quando è richiesto l'ordinamento), perché questo metodo è semplice e facilmente modificabile per compiti specifici, pur fornendo una delle migliori velocità tra tutti i metodi di ordinamento.

//——————————————————————————————————————————————————————————————————————————————
//Sorting of bees
void C_AO_ABC::SortingBees ()
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//Sorting of areas
void C_AO_ABC::SortingAreas ()
//——————————————————————————————————————————————————————————————————————————————

È il momento di raccogliere tutto il codice considerato e compilarlo. Dopo aver eseguito il banco di prova, possiamo vedere le seguenti animazioni, che mostrano il comportamento dell'algoritmo delle api. Le api sono chiaramente osservate in aree separate. Possiamo vedere come le aree si spostano sostituendosi l'una all'altra. La precisione e il numero di "sciami" particolari dipendono dalle impostazioni dell'algoritmo.

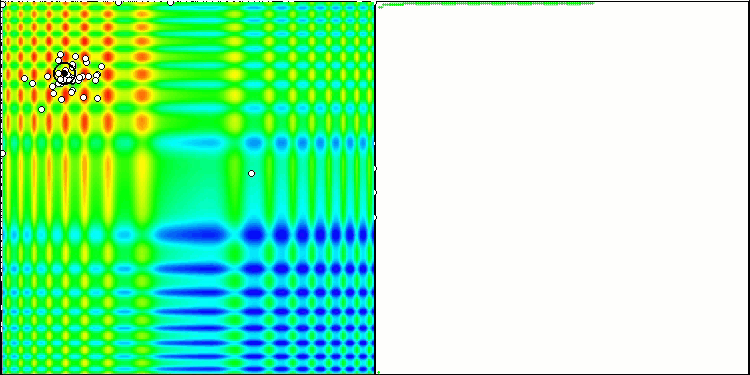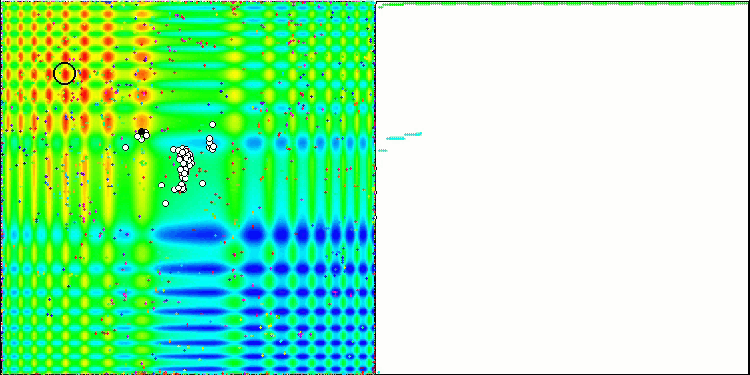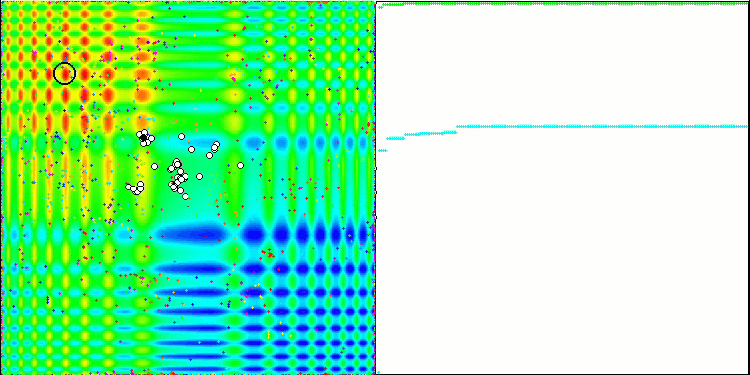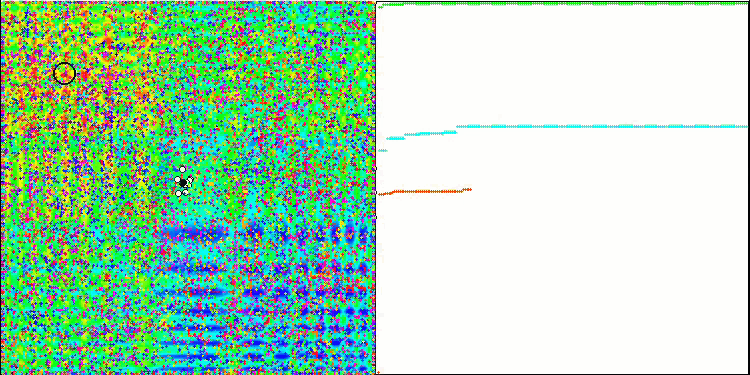
ABC sulla funzione test Skin .

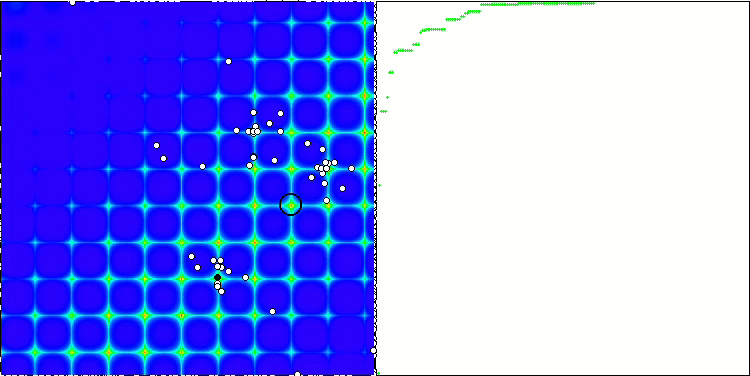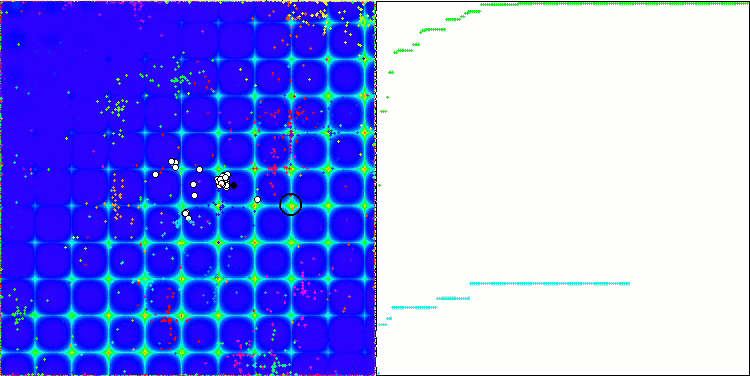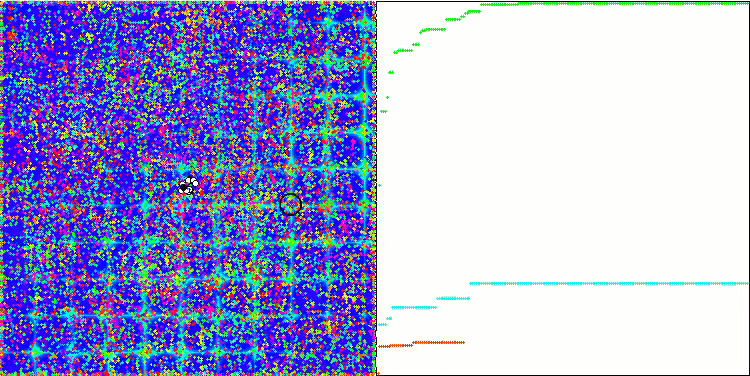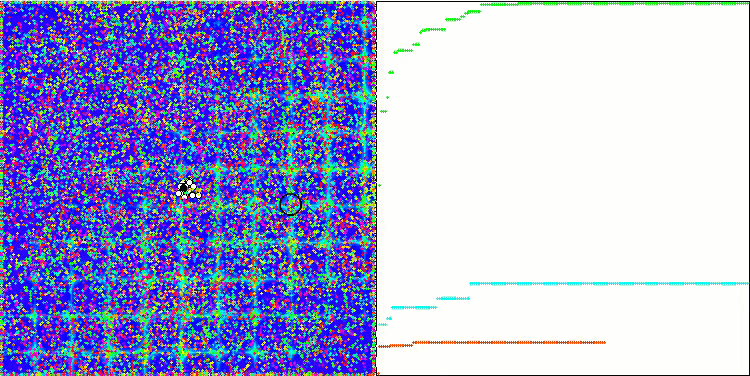
ABC sulla funzione di test Forest .

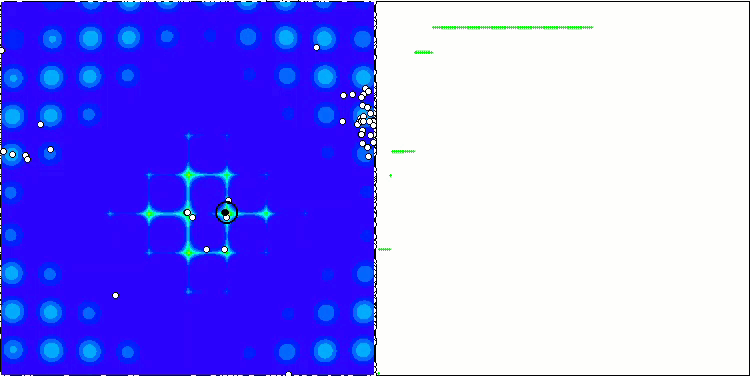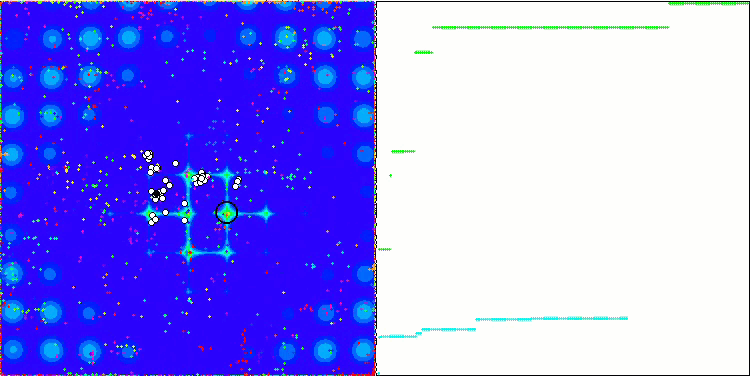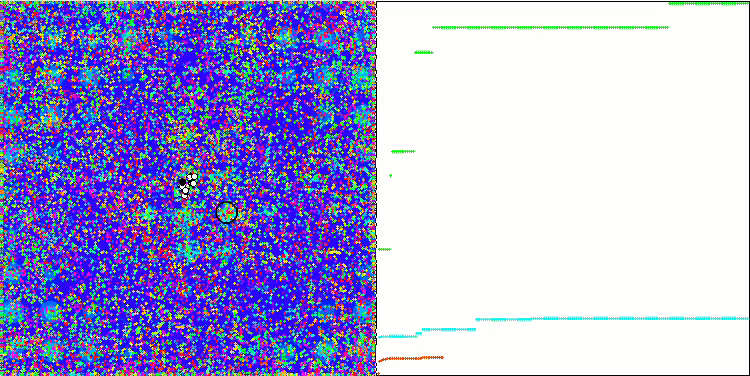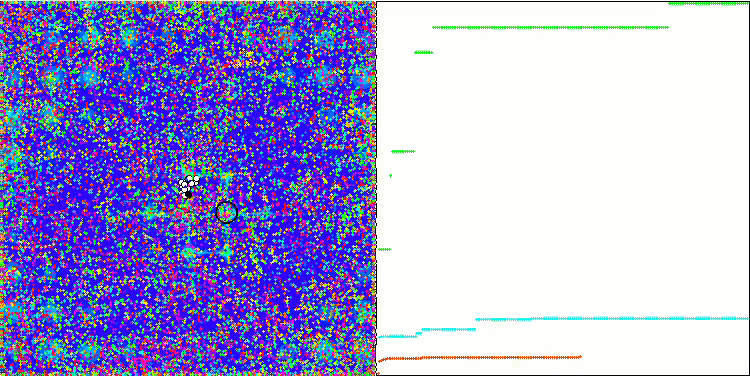
ABC sulla funzione di test Megacity .

Ecco i risultati dell'algoritmo sulle funzioni test:

2022.11.21 13:14:06.669 Test_AO_ABC1 (EURUSD,M1) =============================
2022.11.21 13:14:28.483 Test_AO_ABC1 (EURUSD,M1) 1 Skin's; Func cicli 1000 risultati: 14.018634225602678; Func cicli 10000 risultati: 14.06060189007221
2022.11.21 13:14:28.483 Test_AO_ABC1 (EURUSD,M1) Punteggio1: 0.99772; Punteggio2: 1.00000
2022.11.21 13:14:50.310 Test_AO_ABC1 (EURUSD,M1) 20 Skin; Func cicli 1000 risultati: 7.459929501115262; Func cicli 10000 risultati: 8.320771456653533
2022.11.21 13:14:50.310 Test_AO_ABC1 (EURUSD,M1) Punteggio1: 0.64085; Punteggio2: 0.68769
2022.11.21 13:15:30.049 Test_AO_ABC1 (EURUSD,M1) 500 Skin's; Func cicli 1000 risultati: 4.69267387794685; Func cicli 10000 risultati: 4.838631770950824
2022.11.21 13:15:30.049 Test_AO_ABC1 (EURUSD,M1) Punteggio1: 0.49029; Punteggio2: 0.49823
2022.11.21 13:15:30.049 Test_AO_ABC1 (EURUSD,M1) =============================
2022.11.21 13:15:51.880 Test_AO_ABC1 (EURUSD,M1) 1 Forest; Func cicli 1000 risultati: 15.063567301715784; Func cicli 10000 risultati: 15.912087696850861
2022.11.21 13:15:51.880 Test_AO_ABC1 (EURUSD,M1) Punteggio1: 0.94435; Punteggio2: 0.99755
2022.11.21 13:16:13.721 Test_AO_ABC1 (EURUSD,M1) 20 Forest; Func cicli 1000 risultati: 3.0207584941876133; Func cicli 10000 risultati: 4.1918977577943295
2022.11.21 13:16:13.721 Test_AO_ABC1 (EURUSD,M1) Punteggio1: 0.18937; Punteggio2: 0.26279
2022.11.21 13:17:01.467 Test_AO_ABC1 (EURUSD,M1) 500 Forest; Func cicli 1000 risultati: 1.2004991531402736; Func cicli 10000 risultati: 1.288357831462411
2022.11.21 13:17:01.467 Test_AO_ABC1 (EURUSD,M1) Punteggio1: 0.07526; Punteggio2: 0.08077
2022.11.21 13:17:01.467 Test_AO_ABC1 (EURUSD,M1) =============================
2022.11.21 13:17:23.227 Test_AO_ABC1 (EURUSD,M1) 1 Megacity's; Func cicli 1000 risultati: 10.4; Func cicli 10000 risultati: 15.0
2022.11.21 13:17:23.227 Test_AO_ABC1 (EURUSD,M1) Punteggio1: 0.69333; Punteggio2: 1.00000
2022.11.21 13:17:44.936 Test_AO_ABC1 (EURUSD,M1) 20 Megacity's; Func cicli 1000 risultati: 1.54999999999998; Func cicli 10000 risultati: 2.31
2022.11.21 13:17:44.936 Test_AO_ABC1 (EURUSD,M1) Punteggio1: 0.10333; Punteggio2: 0.15400
2022.11.21 13:18:29.588 Test_AO_ABC1 (EURUSD,M1) 500 Megacity's; Func cicli 1000 risultati: 0.6180000000000001; Func cicli 10000 risultati: 0.6568
2022.11.21 13:18:29.588 Test_AO_ABC1 (EURUSD,M1) Punteggio1: 0.04120; Punteggio2: 0.04379
2022.11.21 13:18:29.588 Test_AO_ABC1 (EURUSD,M1) =============================
2022.11.21 13:18:29.588 Test_AO_ABC1 (EURUSD,M1) Tutti i punteggi per C_AO_ABC: 0.49447371765340953

L'algoritmo è completamente convergente per le due funzioni test a due variabili, il che è un ottimo indicatore di convergenza. La valutazione dei restanti risultati sarebbe prematura. È meglio mettere i risultati in una tabella e trarre conclusioni comparando altri algoritmi di ottimizzazione.

3. Versione modificata

Quando si sviluppa e si progetta un qualsiasi algoritmo di ottimizzazione, sorge sempre la domanda: "L'algoritmo funziona come previsto o c'è un errore da qualche parte nel codice?". Il processo di ricerca stocastica è casuale per sua natura, quindi non è chiaro se i risultati dell'ottimizzazione sono stati ottenuti dall'algoritmo o se c'è stato un errore da qualche parte e il risultato è davvero non casuale? Quando ho sviluppato l'algoritmo della colonia di api, ho riscontrato un fenomeno simile. Durante il primo test su cinque dell'insieme di prova, l'algoritmo si è ovviamente bloccato nei punti da cui aveva iniziato la ricerca, non cercando di convergere affatto. Questo bug è stato risolto in modo del tutto incredibile dal punto di vista della logica. Tutto ciò che ho dovuto fare è stato inizializzare la classe hive una seconda volta oltre al primo periodo, nonostante la classe fosse già stata preinizializzata prima dell'inizio dei periodi (stringa 142 in Test_AO_ABC.mq5). Se qualcuno riesce a svelare questo mistero, sarò lieto di ascoltare la soluzione nei commenti.

In parte a causa di quanto sopra e in parte a causa dei risultati non del tutto soddisfacenti dei primi test (anche se in seguito è risultato chiaro che dovevo sperimentare con le impostazioni dell'algoritmo), mi è venuta l'idea di cambiare la strategia di ricerca delle api. Nella versione originale, le api volano in proporzione al valore dell'area. Il nuovo algoritmo prevede un numero fisso di api in ogni area. In altre parole, indipendentemente dal rango dell'area, ognuna di esse ha sempre lo stesso numero di api. Pertanto, l'area è stata logicamente trasformata nel concetto di "Sciame di api".

Ora, invece della struttura ad aree, ci sarà la seguente struttura:

//——————————————————————————————————————————————————————————————————————————————
struct S_BeesSwarm
{
  void Init (int coordinatesNumber, int beesNumber)
  {
    ArrayResize (bees, beesNumber);

    for (int i = 0; i < beesNumber; i++)
    {
      ArrayResize (bees [i].c, coordinatesNumber);
      bees [i].n = -DBL_MAX;
    }

    n = -DBL_MAX;

    ArrayResize     (cC, coordinatesNumber);
    ArrayInitialize (cC, -DBL_MAX);
  }

  S_Bee  bees []; //bees
  double cC   []; //center coordinates
  double cB   []; //best coordinates
  double n;       //nectarAmount
};
//——————————————————————————————————————————————————————————————————————————————

Anche questa struttura ha una funzione di inizializzazione, ma in aggiunta c'è l'array bees[].

In generale, il resto del codice è molto simile alla versione classica e non ci si deve concentrare troppo su di esso. Il codice è allegato nell'archivio sottostante. Vale la pena prestare particolare attenzione alle differenze nella logica degli algoritmi. In forma progressiva, si presenta così:

1. Creare un centro per il primo sciame e posizionare le api intorno al centro.
2. Creare un centro per gli sciami successivi e verificare che la distanza dal centro agli sciami precedenti sia maggiore o uguale a R*2 (due raggi), posizionare le api in prossimità del centro.
3. Inviare le api esploratrici in modo che ognuna di esse sia più lontana degli altri sciami di una distanza maggiore o uguale a R (raggio).
4. Ottenere il valore della funzione fitness per tutte le api.
5. Smistare gli sciami.
6. Posizionare le api al centro di ogni sciame.
7. Ripetere da p. 4 fino a quando non viene soddisfatto il criterio di arresto.

Come avrete notato, c'è una differenza fondamentale nella strategia di ricerca. Mentre nella versione classica ogni area può avere un numero differente di api, qui gli sciami sono sempre della stessa dimensione. Questo per garantire che le aree continuino a essere esplorate anche se la fonte di cibo si esaurisce, garantendo così un'esplorazione più approfondita della superficie nell'iperspazio. I test confermano la legittimità di questo approccio. I risultati stanno migliorando. Le api esploratrici non volano in prossimità delle aree, ma cadono in aree libere dello spazio, peraltro seguendo le regole delle aree, come nella versione classica. Nella versione classica delle api, le esploratrici non si comportano come descritto, perché si disperdono in una direzione completamente casuale senza curarsi di poter entrare in aree precedentemente esplorate, perdendo così l'esplorazione più elementare. L'ultimo sciame dell'array è lo sciame esploratore. Per questo sciame vale anche la regola "non entrare nello spazio altrui", ma non per lo sciame nel suo complesso, bensì per le api esploratrici personalmente.

Di seguito sono riportati i risultati della versione modificata:

2022.11.21 21:53:19.695 Test_AO_ABCm (EURUSD,M1) =============================
2022.11.21 21:53:25.104 Test_AO_ABCm (EURUSD,M1) 1 Skin's; Func cicli 1000 risultati: 14.009060385607679; Func cicli 10000 risultati: 14.060603974847265
2022.11.21 21:53:25.104 Test_AO_ABCm (EURUSD,M1) Punteggio1: 0.99720; Punteggio2: 1.00000
2022.11.21 21:53:30.452 Test_AO_ABCm (EURUSD,M1) 20 Skin; Func cicli 1000 risultati: 7.826824877236677; Func cicli 10000 risultati: 8.735832346695558
2022.11.21 21:53:30.452 Test_AO_ABCm (EURUSD,M1) Punteggio1: 0.66082; Punteggio2: 0.71028
2022.11.21 21:53:40.060 Test_AO_ABCm (EURUSD,M1) 500 Skin's; Func cicli 1000 risultati: 4.645933304640949; Func cicli 10000 risultati: 4.844246724239038
2022.11.21 21:53:40.060 Test_AO_ABCm (EURUSD,M1) Punteggio1: 0.48774; Punteggio2: 0.49853
2022.11.21 21:53:40.060 Test_AO_ABCm (EURUSD,M1) =============================
2022.11.21 21:53:45.363 Test_AO_ABCm (EURUSD,M1) 1 Forest's; Func cicli 1000 risultati: 15.44507700105064; Func cicli 10000 risultati: 15.662273922787355
2022.11.21 21:53:45.363 Test_AO_ABCm (EURUSD,M1) Punteggio1: 0.96827; Punteggio2: 0.98188
2022.11.21 21:53:50.697 Test_AO_ABCm (EURUSD,M1) 20 Forest's; Func cicli 1000 risultati: 3.6397442648278924; Func cicli 10000 risultati: 4.759146560755886
2022.11.21 21:53:50.697 Test_AO_ABCm (EURUSD,M1) Punteggio1: 0.22818; Punteggio2: 0.29836
2022.11.21 21:54:01.111 Test_AO_ABCm (EURUSD,M1) 500 Forest; Func cicli 1000 risultati: 1.2349621811342104; Func cicli 10000 risultati: 1.4191098624570897
2022.11.21 21:54:01.111 Test_AO_ABCm (EURUSD,M1) Punteggio1: 0.07742; Punteggio2: 0.08897
2022.11.21 21:54:01.112 Test_AO_ABCm (EURUSD,M1) =============================
2022.11.21 21:54:06.434 Test_AO_ABCm (EURUSD,M1) 1 Megacity's; Func cicli 1000 risultati: 12.0; Func cicli 10000 risultati: 15.0
2022.11.21 21:54:06.434 Test_AO_ABCm (EURUSD,M1) Punteggio1: 0.80000; Punteggio2: 1.00000
2022.11.21 21:54:11.768 Test_AO_ABCm (EURUSD,M1) 20 Megacity's; Func cicli 1000 risultati: 1.7; Func cicli 10000 risultati: 2.35
2022.11.21 21:54:11.768 Test_AO_ABCm (EURUSD,M1) Punteggio1: 0.11333; Punteggio2: 0.15667
2022.11.21 21:54:22.235 Test_AO_ABCm (EURUSD,M1) 500 Megacity's; Func cicli 1000 risultati: 0.572; Func cicli 10000 risultati: 0.67
2022.11.21 21:54:22.235 Test_AO_ABCm (EURUSD,M1) Punteggio1: 0.03813; Punteggio2: 0.04467
2022.11.21 21:54:22.235 Test_AO_ABCm (EURUSD,M1) =============================
2022.11.21 21:54:22.235 Test_AO_ABCm (EURUSD,M1) Tutti i punteggi per C_AO_ABCm: 0.508357869056105

Possiamo notare che l'algoritmo modificato ha avuto successo su due funzioni a due variabili, mostrando una convergenza del 100%. In generale, i risultati sono migliorati, il punteggio finale è diventato più alto: 0.50836. Sfortunatamente non si tratta di un miglioramento significativo dei risultati. I problemi di convergenza su funzioni con un numero elevato di variabili sono paragonabili alla versione classica dell'implementazione dell'algoritmo.

A proposito, nella versione modificata non c'è alcun bug che richieda la reinizializzazione dell'alveare.

4. Risultati del test

AO	Cicli	Skin			Forest			Megacity (discreta)			Risultato finale
		2 parametri (1 F)	40 parametri (20 F)	1000 parametri (500 F)	2 parametri (1 F)	40 parametri (20 F)	1000 parametri (500 F)	2 parametri (1 F)	40 parametri (20 F)	1000 parametri (500 F)
ACOm	1000	0.99502	0.69826	0.50498	0.99087	0.22374	0.08408	0.78667	0.11667	0.04224	0.54688
	10.000	0.99599	0.86403	0.58800	0.99302	0.65571	0.17442	0.78667	0.26133	0.08208
RND	1000	0.98744	0.61852	0.49408	0.89582	0.19645	0.14042	0.77333	0.19000	0.14283	0.51254
	10.000	0.99977	0.69448	0.50188	0.98181	0.24433	0.14042	0.88000	0.20133	0.14283
ABCm	1000	0.99720	0.66082	0.48774	0.96827	0.22818	0.07742	0.80000	0.11333	0.03813	0.50836
	10.000	1.00000	0.71028	0.49853	0.98188	0.29836	0.08897	1.00000	0.15667	0.04467
ABC	1000	0.99772	0.64085	0.49029	0.94435	0.18937	0.07526	0.69333	0.10333	0.04120	0.49447
	10.000	1.00000	0.68769	0.49823	0.99755	0.26279	0.08077	1.00000	0.15400	0.04379
PSO	1000	0.98436	0.72243	0.65483	0.71122	0.15603	0.08727	0.53333	0.08000	0.04085	0.47695
	10.000	0.99836	0.72329	0.65483	0.97615	0.19640	0.09219	0.82667	0.10600	0.04085

Riassumiamo. Sorprendentemente, l'algoritmo della colonia di api ha mostrato una convergenza del 100% in tutti e cinque i test su due funzioni di prova, la regolare Skin e la discreta Megacity, dimostrando così una velocità e una qualità di convergenza fenomenali. Tuttavia, questo vale solo per le funzioni con due variabili. In termini di scalabilità, l'algoritmo è inferiore ad altri membri della tabella di valutazione. Le funzioni con più variabili non sono certo il punto di forza di una colonia di api. Ciò è visibile sia nell'animazione del banco di prova sia nei risultati riportati nella tabella.

L'algoritmo ABC richiede all'utente di regolare diverse impostazioni parametriche, come la dimensione dello sciame, il numero di esploratrici e i raggi dell'area. Se queste impostazioni non vengono scelte in modo appropriato per una particolare applicazione, l'algoritmo può convergere prematuramente o non convergere affatto. Inoltre, l'ABC presenta svantaggi quali la lentezza della convergenza su funzioni complesse, la cattura di soluzioni locali e proprietà di ricerca mediocri.

Pro:
1. Relativamente veloce.
2. Convergenza fenomenale per funzioni regolari e discrete con poche variabili.

Contro:
1. Forte influenza dei parametri dell'algoritmo sul risultato.
2. Non universalità.
3. Rimanere bloccati negli estremi locali.
4. Scalabilità media.