Popülasyon optimizasyon algoritmaları: Maymun algoritması (Monkey Algorithm, MA)

İçindekiler:

1. Giriş
2. Algoritma
3. Test sonuçları

1. Giriş

Maymun algoritması (Monkey Algorithm, MA) bir metasezgisel arama algoritmasıdır. Bu makale, algoritmanın ana bileşenlerini açıklayacak ve tırmanma (yukarı doğru hareket), yerel atlama ve global atlama şeklinde çözümler sunacaktır. Algoritma 2007 yılında R. Zhao ve W. Tang tarafından önerilmiştir. Algoritma, maymunların yiyecek aramak için dağlar üzerinde hareket etme ve zıplama davranışlarını simüle etmektedir. Dağ ne kadar yüksekse, tepesinde o kadar fazla yiyecek olduğu varsayılmaktadır.

Maymunlar tarafından keşfedilen alan bir uygunluk fonksiyonu sahasıdır, bu nedenle en yüksek dağ problemin çözümüne karşılık gelir (global maksimizasyon problemini ele alıyoruz). Maymunların her biri bulunduğu konumdan dağın tepesine ulaşana kadar yukarı doğru hareket eder. Tırmanma süreci, amaç fonksiyonun değerini kademeli olarak iyileştirmek üzere tasarlanmıştır. Ardından maymun daha yüksek bir dağ bulma umuduyla rastgele bir yönde bir dizi yerel sıçrama yapar ve yukarı doğru hareket tekrarlanır. Belirli sayıda tırmanış ve yerel sıçrama gerçekleştirdikten sonra maymun, başlangıç konumunun çevresindeki sahayı yeterince keşfettiğine inanır.

Arama uzayının yeni bir alanını keşfetmek için maymun uzun bir global sıçrama gerçekleştirir. Yukarıdaki adımlar algoritma parametrelerinde belirtilen sayıda tekrarlanır. Problemin çözümü, maymun popülasyonu tarafından bulunan en yüksek tepe noktası olarak ilan edilir. Ancak MA, tırmanma süreci boyunca yerel optimum çözümleri aramak için önemli bir hesaplama zamanı harcar. Global atlama süreci, algoritmanın yakınsama hızını artırabilir. Bu sürecin amacı, maymunları yerel aramaya düşmemeleri için yeni arama fırsatları bulmaya zorlamaktır. Algoritma basit yapı, nispeten yüksek güvenilirlik ve yerel optimum çözümler için iyi arama gibi avantajlara sahiptir.

MA, lineer olmama, türevlenememe ve yüksek boyutluluk ile karakterize edilen birçok karmaşık optimizasyon problemini çözebilen yeni bir evrimsel algoritma türüdür. Diğer algoritmalardan farkı, MA tarafından harcanan zamanın esas olarak yerel optimum çözümleri bulmak için tırmanma sürecinin kullanılmasından kaynaklanmasıdır. Bir sonraki bölümde, algoritmanın ana bileşenlerini, sunulan çözümleri, başlatmayı, tırmanmayı, gözlemeyi ve sıçramayı açıklayacağız.

2. Algoritma

Maymun algoritmasını anlamayı kolaylaştırmak için yalancı kod ile başlamak mantıklıdır.

MA algoritmasının yalancı kodu:

1. Maymunları arama uzayına rastgele dağıt.
2. Maymun konumunun yüksekliğini ölç.
3. Sabit sayıda yerel atlama gerçekleştir.
4. Üçüncü adımda elde edilen yeni tepe noktası daha yüksekse, bu yerden yerel atlamalar yapılmalıdır.
5. Yerel atlama sayısı sınırı tükenirse ve yeni bir tepe noktası bulunmazsa, global bir atlama yap.
6. Üçüncü adımı tekrarla.
7. Durma kriteri karşılanana kadar 2. adımdan itibaren tekrarla.

Yalancı kodun her bir maddesini daha ayrıntılı olarak analiz edelim.

1. Optimizasyonun en başında, arama uzayı maymunlar tarafından bilinmemektedir. Hayvanlar keşfedilmemiş araziye rastgele yerleştirilir, çünkü yiyeceklerin konumu her yerde eşit derecede olasıdır.

2. Maymun konumunun yüksekliğini ölçme süreci, uygunluk fonksiyonu görevinin yerine getirilmesidir.

3. Yerel atlamalar yapılırken, algoritma parametrelerinde belirtilen bir sayı sınırı vardır. Bu da maymunun yiyeceğin bulunduğu alanda küçük yerel sıçramalar yaparak mevcut konumunu iyileştirmeye çalıştığı anlamına gelir. Yeni bulunan besin kaynağı daha iyiyse, 4. adıma geçilir.

4. Yeni bir besin kaynağı bulunduğunda yerel atlama sayacı sıfırlanır. Şimdi yeni bir besin kaynağı arayışı buradan yapılacaktır.

5. Yerel sıçramalar daha iyi bir besin kaynağının keşfedilmesine yol açmazsa, maymun mevcut alanın tamamen keşfedildiği ve daha uzakta yeni bir yer aramanın zamanının geldiği sonucuna varır. Bu noktada, daha ileri sıçramaların yönü hakkında bir soru ortaya çıkıyor? Algoritmanın fikri, tüm maymunların koordinat merkezini kullanmak ve böylece sürüdeki maymunlar arasında bir iletişim sağlamaktır: maymunlar yüksek sesle bağırabilir ve iyi uzamsal işitme duyusuna sahip olarak türdeşlerinin tam konumunu belirleyebilirler. Aynı zamanda, türdeşlerinin konumunu bilerek (türdeşler yiyecek bulunmayan yerlerde olmayacaktır), en uygun yeni besin konumunu yaklaşık olarak hesaplamak mümkündür, bu nedenle bu yönde bir sıçrama yapmak gerekir.

Orijinal algoritmada maymun, tüm maymunların koordinat merkezinden ve hayvanın mevcut konumundan geçen bir çizgi boyunca global bir sıçrama yapar. Sıçramanın yönü koordinatların merkezine doğru ya da merkezin tersi yönde olabilir. Merkezden ters yönde bir sıçrama, tüm maymunlar için yaklaşık koordinatlarla yiyecek bulma mantığıyla çelişiyor ve bu da algoritmayla yaptığım deneylerle doğrulandı - aslında bu, global optimumdan uzaklaşma olasılığının %50 olduğu anlamına geliyor.

Yapılan denemeler, koordinat merkezinin ötesine atlamanın, atlamamaktan veya ters yönde atlamaktan daha kârlı olduğunu göstermiştir. Tüm maymunların bir noktada toplanması, ilk bakışta böyle bir mantık bunu kaçınılmaz kılsa da gerçekleşmez. Aslında, yerel zıplama sınırını tüketen maymunlar merkezden daha uzağa zıplar ve böylece popülasyondaki tüm maymunların konumunu değiştirir. Yüksek maymunların bu algoritmaya uyduğunu zihinsel olarak hayal edersek, sürünün kendisi daha zengin bir besin kaynağına doğru hareket ederken, zaman zaman sürünün geometrik merkezinin üzerinden atlayan bir hayvan sürüsü göreceğiz. "Sürü hareketinin" bu etkisi, algoritmanın animasyonunda görsel olarak açıkça görülebilir (orijinal algoritmada bu etki yoktur ve sonuçlar daha kötüdür).

6. Global bir sıçrama yapan maymun, yeni yerdeki besin kaynağının konumunu belirlemeye başlar. Süreç, durma kriteri karşılanana kadar devam eder.

Algoritmanın tüm fikri tek bir diyagrama kolayca sığabilir. Maymunun hareketi Şekil 1'de üzerinde sayılar bulunan dairelerle gösterilmiştir. Her sayı maymun için yeni bir konumdur. Küçük sarı daireler başarısız yerel atlama denemelerini temsil etmektedir. 6 sayısı, yerel sıçrama sınırının tükendiği ve yeni bir en iyi konumun bulunamadığı konumu gösterir. Numarasız daireler sürünün geri kalanının konumlarını temsil etmektedir. Sürünün geometrik merkezi (x,y) koordinatlarına sahip küçük bir daire ile gösterilir.

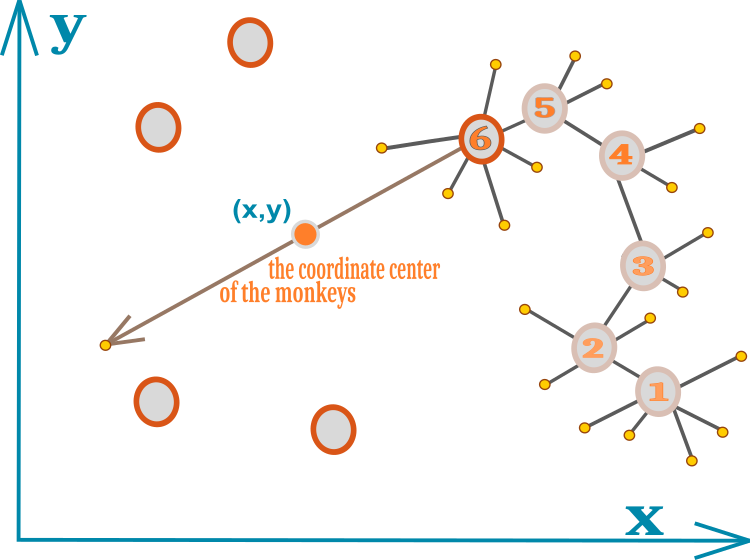
Şekil 1. Bir maymunun sürü içindeki hareketinin şematik gösterimi

Şimdi MA kodunu incelemeye geçelim.

Sürüdeki bir maymunu S_Monkey yapısı ile tanımlamak uygundur. Yapı, mevcut koordinatları içeren c[] dizisini, en iyi besin koordinatlarını içeren cB[] dizisini (yerel atlamalar bu koordinatlara sahip konumdan gerçekleşir), sırasıyla mevcut noktanın yükseklik değeri ve en yüksek noktanın değeri olan h ve hB’yi ve konumu iyileştirme girişimlerinin sayısını sınırlayan yerel atlama sayacı olan lCNT’yi içerir.

//——————————————————————————————————————————————————————————————————————————————
struct S_Monkey
{
  double c  []; //coordinates
  double cB []; //best coordinates
  double h;     //height of the mountain
  double hB;    //best height of the mountain
  int    lCNT;  //local search counter
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_MA maymun algoritması sınıfı daha önce tartışılan algoritmalardan farklı değildir. Bir maymun sürüsü, sınıfta m[] yapılarının dizisi olarak temsil edilir. Metotlar ve üyeler sınıfındaki bildirimler kod hacmi açısından küçüktür. Algoritma özlü olduğu için, diğer birçok optimizasyon algoritmasının aksine burada sıralama yoktur. Optimize edilen parametrelerin maksimum, minimum ve adımını ayarlamak için dizilere ve algoritmanın harici parametrelerini aktarmak için sabit değişkenlere ihtiyacımız olacaktır. MA'nın ana mantığını içeren metotların açıklamasına geçelim.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_MA
{
  //----------------------------------------------------------------------------
  public: S_Monkey m       []; //monkeys
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //minimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double hB;           //best height of the mountain

  public: void Init (const int    coordNumberP,     //coordinates number
                     const int    monkeysNumberP,   //monkeys number
                     const double bCoefficientP,    //local search coefficient
                     const double vCoefficientP,    //jump coefficient
                     const int    jumpsNumberP);    //jumps number

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordNumber;       //coordinates number
  private: int    monkeysNumber;     //monkeys number

  private: double b [];              //local search coefficient
  private: double v [];              //jump coefficient
  private: double bCoefficient;      //local search coefficient
  private: double vCoefficient;      //jump coefficient
  private: double jumpsNumber;       //jumps number
  private: double cc [];             //coordinate center

  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Public Init() metodu algoritmayı başlatmak içindir. Burada dizilerin boyutunu ayarlıyoruz. Maymun tarafından bulunan en iyi bölgenin kalitesini mümkün olan en düşük 'double' türündeki değerle başlatıyoruz ve aynı şeyi MA yapı dizilerinin ilgili değişkenleri için de yapacağız.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_MA::Init (const int    coordNumberP,    //coordinates number
                    const int    monkeysNumberP,  //monkeys number
                    const double bCoefficientP,   //local search coefficient
                    const double vCoefficientP,   //jump coefficient
                    const int    jumpsNumberP)    //jumps number
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  hB       = -DBL_MAX;
  revision = false;

  coordNumber   = coordNumberP;
  monkeysNumber = monkeysNumberP;
  bCoefficient  = bCoefficientP;
  vCoefficient  = vCoefficientP;
  jumpsNumber   = jumpsNumberP;

  ArrayResize (rangeMax,  coordNumber);
  ArrayResize (rangeMin,  coordNumber);
  ArrayResize (rangeStep, coordNumber);
  ArrayResize (b,         coordNumber);
  ArrayResize (v,         coordNumber);
  ArrayResize (cc,        coordNumber);

  ArrayResize (m, monkeysNumber);

  for (int i = 0; i < monkeysNumber; i++)
  {
    ArrayResize (m [i].c,  coordNumber);
    ArrayResize (m [i].cB, coordNumber);
    m [i].h    = -DBL_MAX;
    m [i].hB   = -DBL_MAX;
    m [i].lCNT = 0;
  }

  ArrayResize (cB, coordNumber);
}
//——————————————————————————————————————————————————————————————————————————————

Her yinelemede çalıştırılması gereken ilk public metot Moving(), maymun atlama mantığını uygular. İlk yinelemede, 'revision' bayrağı 'false' olduğunda, temsilcileri, çalışılan uzayın koordinatları aralığında rastgele değerlerle başlatmak gerekir; bu, maymunların sürü habitatı içindeki rastgele konumlarına eşdeğerdir. Global ve yerel sıçramaların katsayılarının hesaplanması gibi çok sayıda tekrarlanan işlemi azaltmak için, ilgili koordinatların değerlerini (koordinatların her biri kendi boyutuna sahip olabilir) v[] ve b[] dizilerinde saklarız. Her maymunun yerel sıçrama sayacını sıfırlayalım. 

//----------------------------------------------------------------------------
if (!revision)
{
  hB = -DBL_MAX;

  for (int monk = 0; monk < monkeysNumber; monk++)
  {
    for (int c = 0; c < coordNumber; c++)
    {
      m [monk].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      m [monk].c [c] = SeInDiSp  (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      m [monk].h     = -DBL_MAX;
      m [monk].hB    = -DBL_MAX;
      m [monk].lCNT  = 0;
    }
  }

  for (int c = 0; c < coordNumber; c++)
  {
    v [c] = (rangeMax [c] - rangeMin [c]) * vCoefficient;
    b [c] = (rangeMax [c] - rangeMin [c]) * bCoefficient;
  }

  revision = true;
}

Tüm maymunların koordinat merkezini hesaplamak için, boyutu koordinat sayısına karşılık gelen cc[] dizisini kullanalım. Buradaki fikir, maymunların koordinatlarını toplamak ve elde edilen toplamı popülasyonun büyüklüğüne bölmektir. Dolayısıyla, koordinatların merkezi koordinatların aritmetik ortalamasıdır.

//calculate the coordinate center of the monkeys----------------------------
for (int c = 0; c < coordNumber; c++)
{
  cc [c] = 0.0;

  for (int monk = 0; monk < monkeysNumber; monk++)
  {
    cc [c] += m [monk].cB [c];
  }

  cc [c] /= monkeysNumber;
}

Yalancı koda göre, yerel sıçrama sınırına ulaşılmazsa, maymun bulunduğu yerden her yöne eşit olasılıkla sıçrayacaktır. Yerel atlama çemberinin yarıçapı, b[] dizisinin koordinatlarının boyutuna göre yeniden hesaplanan yerel atlama katsayısı tarafından düzenlenir.

//local jump--------------------------------------------------------------
if (m [monk].lCNT < jumpsNumber) //local jump
{
  for (int c = 0; c < coordNumber; c++)
  {
    m [monk].c [c] = RNDfromCI (m [monk].cB [c] - b [c], m [monk].cB [c] + b [c]);      
    m [monk].c [c] = SeInDiSp (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

MA mantığının çok önemli bir kısmına geçelim - algoritmanın performansı büyük ölçüde global sıçramaların uygulanmasına bağlıdır. Farklı yazarlar bu konuya farklı açılardan yaklaşarak çeşitli çözümler sunmaktadır. Araştırmalara göre, yerel sıçramaların algoritmanın yakınsaması üzerinde çok az etkisi vardır. Algoritmanın yerel ekstremumlardan "sıçrama" yeteneğini belirleyen global sıçramalardır. Global sıçramalarla yaptığım deneyler, bu algoritma için sonuçları iyileştiren tek bir etkili yaklaşım ortaya çıkardı.

Yukarıda, koordinatların merkezine doğru atlamanın tavsiye edilebilirliğini tartıştık ve varış noktasının merkez ile mevcut koordinatlar arasında olması yerine merkezin arkasında olması daha iyidir. Bu yaklaşım, guguk kuşu optimizasyon algoritması (COA) ile ilgili makalede ayrıntılı olarak açıkladığımız Levy uçuşu denklemlerini uygular.

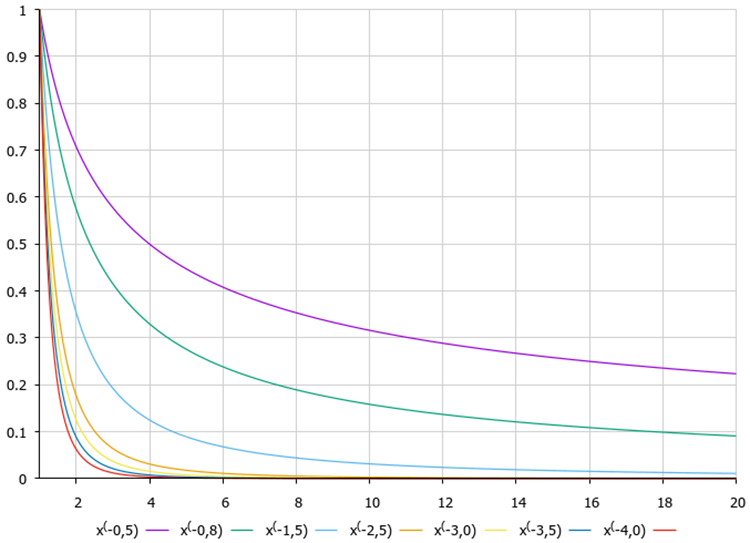
Şekil 2. Denklem derecesine bağlı olarak Levy uçuşu fonksiyonunun grafikleri

Maymun koordinatları aşağıdaki denklem kullanılarak hesaplanır:

m[monk].c[c] = cc[c] + v[c] * pow(r2, -2.0)

Burada:

cc[c] - koordinatların merkezinin koordinatı,

v[c] - arama uzayının boyutuna göre yeniden hesaplanan atlama yarıçapının katsayısı,

r2 - 1 ila 20 aralığında sayı.

Bu işlemde Levy uçuşunu uygulayarak, maymunun koordinat merkezinin yakınına isabet etme olasılığını daha yüksek, merkezin uzağına düşme olasılığını ise daha düşük hale getiriyoruz. Bu şekilde, yeni besin kaynakları keşfederken araştırma ve sömürü arasında bir denge sağlıyoruz. Elde edilen koordinat izin verilen aralığın alt sınırının ötesindeyse, koordinat aralığın üst sınırına karşılık gelen mesafeye aktarılır. Aynı şey üst sınırın ötesine geçildiğinde de yapılır. Koordinat hesaplamalarının sonunda, elde edilen değerin sınırlara ve araştırma adımına uygunluğunu kontrol ederiz.

//global jump-------------------------------------------------------------
for (int c = 0; c < coordNumber; c++)
{
  r1 = RNDfromCI (0.0, 1.0);
  r1 = r1 > 0.5 ? 1.0 : -1.0;
  r2 = RNDfromCI (1.0, 20.0);

  m [monk].c [c] = cc [c] + v [c] * pow (r2, -2.0);
          
  if (m [monk].c [c] < rangeMin [c]) m [monk].c [c] = rangeMax [c] - (rangeMin [c] - m [monk].c [c]);
  if (m [monk].c [c] > rangeMax [c]) m [monk].c [c] = rangeMin [c] + (m [monk].c [c] - rangeMax [c]);
          
  m [monk].c [c] = SeInDiSp (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
}

Yerel/global zıplamalar yaptıktan sonra, zıplama sayacını 1 artırırız.

m [monk].lCNT++;

Revision(), uygunluk fonksiyonu hesaplandıktan sonra her yinelemede çağrılan ikinci public yöntemdir. Bu metot, daha iyi bir çözüm bulunursa global çözümü günceller. Yerel ve global sıçramalardan sonra sonuçların işlenme mantığı birbirinden farklıdır. Yerel bir sıçrama durumunda, mevcut konumun iyileşip iyileşmediğini kontrol etmek ve güncellemek gerekir (sonraki yinelemelerde, sıçramalar bu yeni yerden yapılır), global sıçramalar durumunda ise, iyileşmeler için herhangi bir kontrol yoktur - her durumda bu yerden yeni sıçramalar yapılacaktır.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_MA::Revision ()
{
  for (int monk = 0; monk < monkeysNumber; monk++)
  {
    if (m [monk].h > hB)
    {
      hB = m [monk].h;
      ArrayCopy (cB, m [monk].c, 0, 0, WHOLE_ARRAY);
    }

    if (m [monk].lCNT <= jumpsNumber) //local jump
    {
      if (m [monk].h > m [monk].hB)
      {
        m [monk].hB = m [monk].h;
        ArrayCopy (m [monk].cB, m [monk].c, 0, 0, WHOLE_ARRAY);
        m [monk].lCNT = 0;
      }
    }
    else //global jump
    {
      m [monk].hB = m [monk].h;
      ArrayCopy (m [monk].cB, m [monk].c, 0, 0, WHOLE_ARRAY);
      m [monk].lCNT = 0;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Bu algoritmanın yaklaşımlarının, parçacık sürüsü (PSO) ve benzer arama stratejisi mantığına sahip diğerleri gibi grup sürü zekası algoritmalarıyla benzerliğini fark edebiliriz.

3. Test sonuçları

MA test ortamı sonuçları:

2023.02.22 19:36:21.841    Test_AO_MA (EURUSD,M1)    C_AO_MA:50;0.01;0.9;50
2023.02.22 19:36:21.841    Test_AO_MA (EURUSD,M1)    =============================
2023.02.22 19:36:26.877    Test_AO_MA (EURUSD,M1)    5 Rastrigin's; Func runs 10000 result: 64.89788419898215
2023.02.22 19:36:26.878    Test_AO_MA (EURUSD,M1)    Score: 0.80412
2023.02.22 19:36:36.734    Test_AO_MA (EURUSD,M1)    25 Rastrigin's; Func runs 10000 result: 55.57339368461394
2023.02.22 19:36:36.734    Test_AO_MA (EURUSD,M1)    Score: 0.68859
2023.02.22 19:37:34.865    Test_AO_MA (EURUSD,M1)    500 Rastrigin's; Func runs 10000 result: 41.41612351844293
2023.02.22 19:37:34.865    Test_AO_MA (EURUSD,M1)    Score: 0.51317
2023.02.22 19:37:34.865    Test_AO_MA (EURUSD,M1)    =============================
2023.02.22 19:37:39.165    Test_AO_MA (EURUSD,M1)    5 Forest's; Func runs 10000 result: 0.4307085210424681
2023.02.22 19:37:39.165    Test_AO_MA (EURUSD,M1)    Score: 0.24363
2023.02.22 19:37:49.599    Test_AO_MA (EURUSD,M1)    25 Forest's; Func runs 10000 result: 0.19875891413613866
2023.02.22 19:37:49.599    Test_AO_MA (EURUSD,M1)    Score: 0.11243
2023.02.22 19:38:47.793    Test_AO_MA (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.06286212143582881
2023.02.22 19:38:47.793    Test_AO_MA (EURUSD,M1)    Score: 0.03556
2023.02.22 19:38:47.793    Test_AO_MA (EURUSD,M1)    =============================
2023.02.22 19:38:53.947    Test_AO_MA (EURUSD,M1)    5 Megacity's; Func runs 10000 result: 2.8
2023.02.22 19:38:53.947    Test_AO_MA (EURUSD,M1)    Score: 0.23333
2023.02.22 19:39:03.336    Test_AO_MA (EURUSD,M1)    25 Megacity's; Func runs 10000 result: 0.96
2023.02.22 19:39:03.336    Test_AO_MA (EURUSD,M1)    Score: 0.08000
2023.02.22 19:40:02.068    Test_AO_MA (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.34120000000000006
2023.02.22 19:40:02.068    Test_AO_MA (EURUSD,M1)    Score: 0.02843

Algoritmanın test fonksiyonları üzerindeki görselleştirmesine dikkat edildiğinde, RND algoritmasına çok benzeyen davranışta herhangi bir kalıp olmadığı belirtilmelidir. Algoritma tarafından çözümü iyileştirme girişimlerini gösteren yerel ekstremumlarda bazı küçük temsilci yoğunlaşmaları vardır, ancak bariz bir sıkışma yoktur.

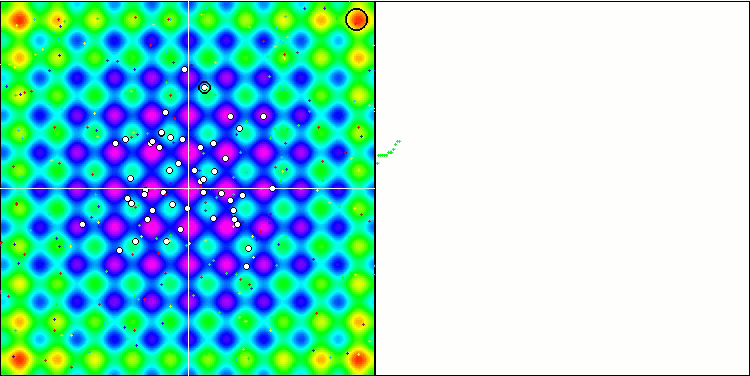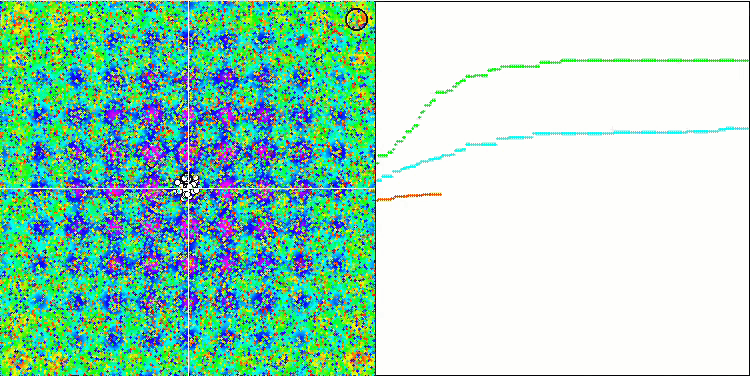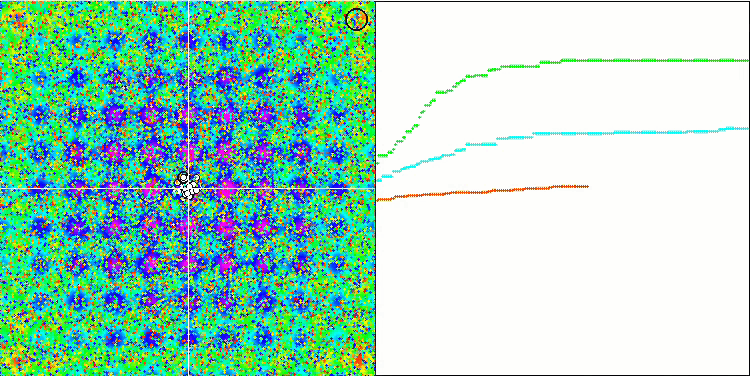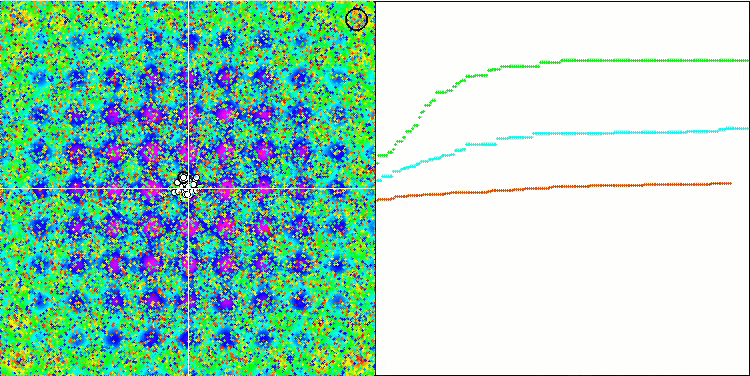
  Rastrigin test fonksiyonu üzerinde MA

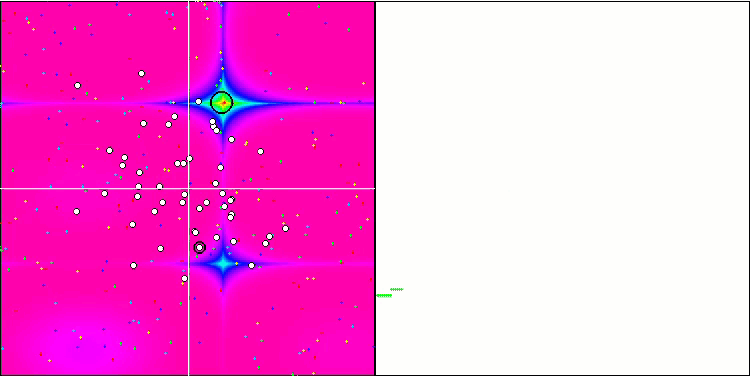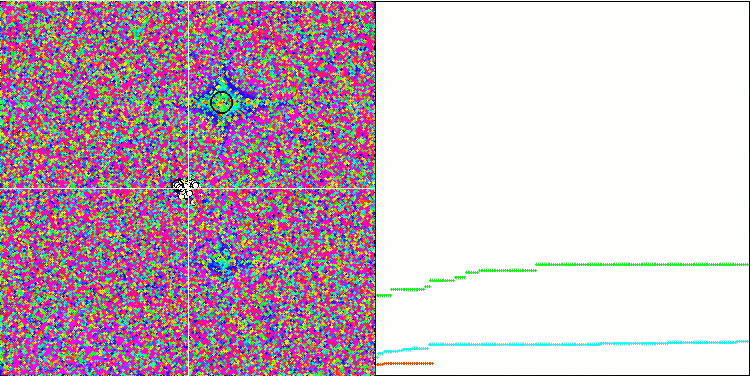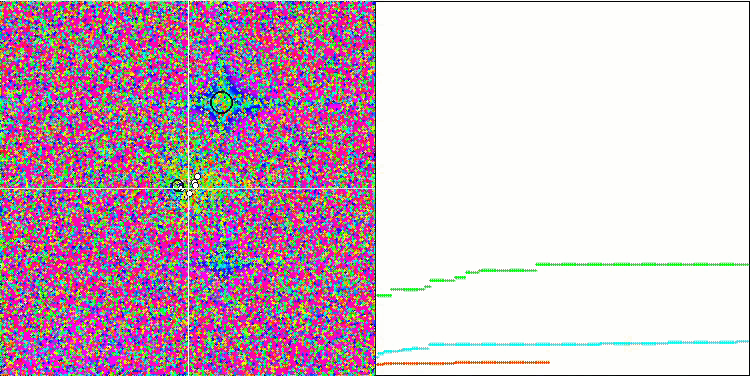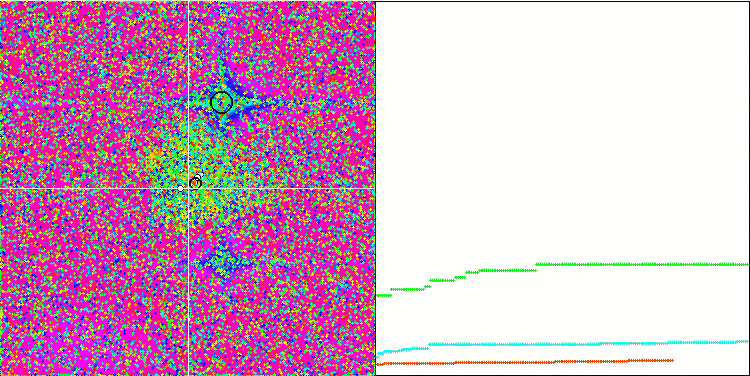
  Forest test fonksiyonu üzerinde MA

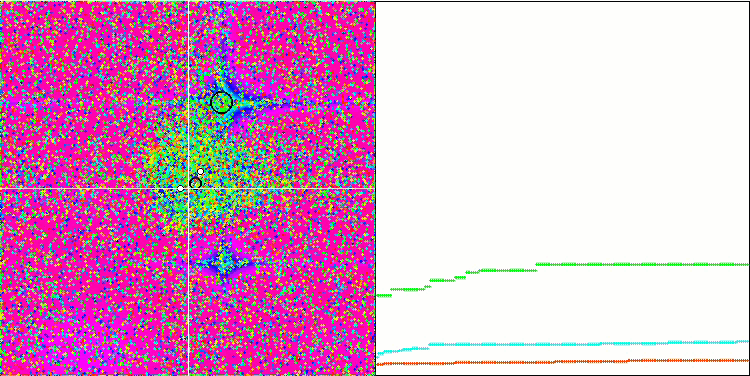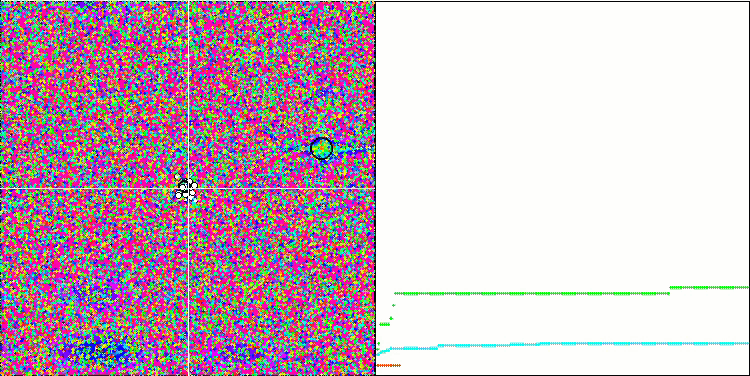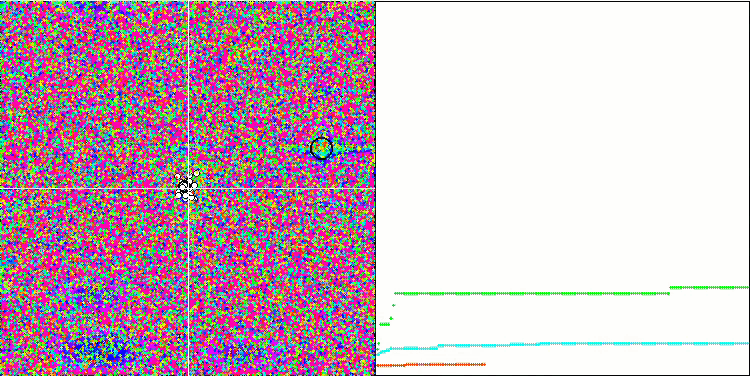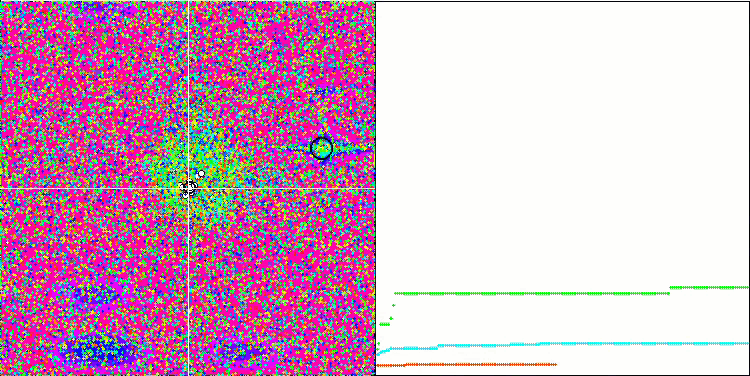
  Megacity test fonksiyonu üzerinde MA

Test sonuçlarının analizine geçelim. Puanlama sonuçlarına göre MA algoritması, GSA ve FSS arasında en alt sırada yer almaktadır. Algoritmaların test edilmesi, sonuçların puanlarının en iyi ve en kötü arasındaki göreceli değerler olduğu karşılaştırmalı analiz ilkesine dayandığından, bir testte olağanüstü sonuçlar veren ve diğerlerinde kötü sonuçlar veren bir algoritmanın ortaya çıkması bazen diğer test katılımcılarının puanlarında değişikliğe neden olur.

Ancak MA'nın sonuçları, tablodaki diğer test katılımcılarının sonuçlarının herhangi birinin yeniden hesaplanmasına neden olmamıştır. MA'nın en kötü olabilecek tek bir test sonucu yoktur, ancak sıfır göreceli sonuçlara ve daha yüksek bir derecelendirmeye sahip algoritmalar vardır (örneğin, GSA). Bu nedenle, algoritma oldukça mütevazı davranmasına ve arama yeteneği yeterince iyi ifade edilmemesine rağmen, algoritma optimizasyon algoritmaları için olumlu bir nitelik olan istikrarlı sonuçlar göstermektedir.

AO	Açıklama	Rastrigin			Rastrigin için nihai sonuç	Forest			Forest için nihai sonuç	Megacity (ayrık)			Megacity için nihai sonuç	Nihai sonuç
		10 parametre (5 F)	50 parametre (25 F)	1000 parametre (500 F)		10 parametre (5 F)	50 parametre (25 F)	1000 parametre (500 F)		10 parametre (5 F)	50 parametre (25 F)	1000 parametre (500 F)
HS	Armoni araması	1.00000	1.00000	0.57048	2.57048	1.00000	0.98931	0.57917	2.56848	1.00000	1.00000	1.00000	3.00000	100.000
ACOm	Karınca kolonisi optimizasyonu (m)	0.34724	0.18876	0.20182	0.73782	0.85966	1.00000	1.00000	2.85966	1.00000	0.88484	0.13497	2.01981	68.094
IWO	İstilacı yabancı ot optimizasyonu	0.96140	0.70405	0.35295	2.01840	0.68718	0.46349	0.41071	1.56138	0.75912	0.39732	0.80145	1.95789	67.087
COAm	Guguk kuşu optimizasyon algoritması (m)	0.92701	0.49111	0.30792	1.72604	0.55451	0.34034	0.21362	1.10847	0.67153	0.30326	0.41127	1.38606	50.422
FAm	Ateş böceği algoritması (m)	0.60020	0.35662	0.20290	1.15972	0.47632	0.42299	0.64360	1.54291	0.21167	0.25143	0.84884	1.31194	47.816
BA	Yarasa algoritması	0.40658	0.66918	1.00000	2.07576	0.15275	0.17477	0.33595	0.66347	0.15329	0.06334	0.41821	0.63484	39.711
ABC	Yapay arı kolonisi	0.78424	0.34335	0.24656	1.37415	0.50591	0.21455	0.17249	0.89295	0.47444	0.23609	0.33526	1.04579	38.937
BFO	Bakteri yiyecek arama optimizasyonu	0.67422	0.32496	0.13988	1.13906	0.35462	0.26623	0.26695	0.88780	0.42336	0.30519	0.45578	1.18433	37.651
GSA	Yerçekimsel arama algoritması	0.70396	0.47456	0.00000	1.17852	0.26854	0.36416	0.42921	1.06191	0.51095	0.32436	0.00000	0.83531	35.937
MA	Maymun algoritması	0.33300	0.35107	0.17340	0.85747	0.03684	0.07891	0.11546	0.23121	0.05838	0.00383	0.25809	0.32030	14.848
FSS	Balık sürüsü arama	0.46965	0.26591	0.13383	0.86939	0.06711	0.05013	0.08423	0.20147	0.00000	0.00959	0.19942	0.20901	13.215
PSO	Parçacık sürüsü optimizasyonu	0.20515	0.08606	0.08448	0.37569	0.13192	0.10486	0.28099	0.51777	0.08028	0.21100	0.04711	0.33839	10.208
RND	Rastgele	0.16881	0.10226	0.09495	0.36602	0.07413	0.04810	0.06094	0.18317	0.00000	0.00000	0.11850	0.11850	5.469
GWO	Gri kurt optimizasyonu	0.00000	0.00000	0.02672	0.02672	0.00000	0.00000	0.00000	0.00000	0.18977	0.03645	0.06156	0.28778	1.000

Özet

Klasik MA algoritması temel olarak yerel optimum çözümleri bulmak için tırmanma sürecini kullanmaktan ibarettir. Tırmanma adımı, yerel çözüme yaklaşma doğruluğunda belirleyici bir rol oynar. Yerel sıçramalar için tırmanma adımı ne kadar küçük olursa, çözümün doğruluğu o kadar yüksek olur, ancak global optimumun bulunması için daha fazla yineleme gerekir. Yineleme sayısını azaltarak hesaplama süresini kısaltmak için, birçok araştırmacı optimizasyonun ilk aşamalarında ABC, COA, IWO gibi diğer optimizasyon yöntemlerinin kullanılmasını ve global çözümü iyileştirmek için MA’nın kullanılmasını önermektedir. Ben bu yaklaşıma katılmıyorum. MA yerine belirtilen algoritmaları hemen kullanmanın daha uygun olduğuna inanıyorum, ancak MA'nın gelişme potansiyeli onu daha fazla deney ve çalışma için iyi bir nesne haline getirmektedir. 

Maymun algoritması, kökleri doğada olan popülasyon tabanlı bir algoritmadır. Diğer birçok metasezgisel algoritma gibi, bu algoritma da evrimseldir ve lineer olmama, türevlenememe ve arama uzayının yüksek boyutluluğu da dahil olmak üzere bir dizi optimizasyon problemini yüksek bir yakınsama oranıyla çözebilir. Maymun algoritmasının bir diğer avantajı, bu algoritmanın az sayıda parametre ile kontrol edilmesi ve bu sayede uygulanmasının oldukça kolay olmasıdır. Sonuçların istikrarına rağmen, düşük yakınsama oranı, önemli sayıda yineleme gerektirdiğinden, maymun algoritmasının yüksek hesaplama karmaşıklığına sahip problemleri çözmek için önerilmesine izin vermez. Aynı işi daha kısa sürede (yineleme sayısı) yapan başka birçok algoritma vardır.

Sayısız denememe rağmen, algoritmanın klasik versiyonu derecelendirme tablosunun alttan üçüncü sırasından daha yükseğe çıkamadı, yerel ekstremumlarda takıldı ve ayrık fonksiyonlarda son derece kötü çalıştı. Bu konuda bir makale yazmak için özel bir isteğim yoktu, bu yüzden onu geliştirmek için girişimlerde bulundum. Bu girişimlerden biri, yakınsama göstergelerinde bazı iyileşmeler göstermiş ve global sıçramalarda olasılık yanlılığı kullanarak ve global sıçramaların ilkesini gözden geçirerek sonuçların istikrarını artırmıştır. Birçok MA araştırmacısı algoritmanın modernize edilmesi gerektiğine işaret etmektedir, bu nedenle maymun algoritmasında birçok değişiklik yapılmıştır. Niyetim MA'nın her türlü modifikasyonunu ele almak değildi, çünkü algoritmanın kendisi olağanüstü değil, daha ziyade parçacık sürüsünün (PSO) bir varyasyonudur. Deneylerin sonucu, bu makalede verilen algoritmanın ek 'm' (değiştirilmiş) işareti içermeyen son haliydi.

Algoritma test sonuçlarının histogramı aşağıda verilmiştir.

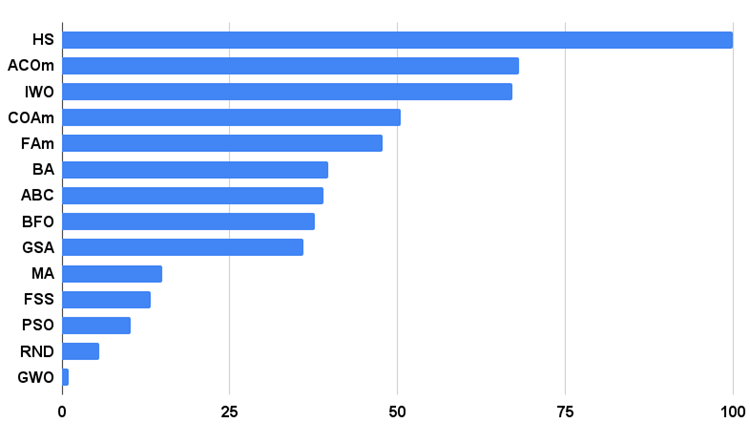
Şekil 3. Algoritmaların test sonuçlarının histogramı

MA’nın avantajları ve dezavantajları:

Avantajları:
1. Kolay uygulama.
2. Düşük yakınsama oranına rağmen iyi ölçeklenebilirlik.
3. Ayrık fonksiyonlarda iyi performans.
4. Az sayıda harici parametre.

Dezavantajları:
1. Düşük yakınsama oranı.
2. Bir arama için çok sayıda yineleme gerektirir.
3. Düşük genel verimlilik.

Her makale, önceki tüm makalelerdeki algoritma kodlarının güncellenmiş sürümlerini içeren bir arşive sahiptir. Makale, yazarın birikmiş deneyimlerine dayanmaktadır ve kişisel görüşünü temsil etmektedir. Sonuçlar ve yargılar deneylere dayanmaktadır.