Le modèle de régression de Sultonov (SRM) - qui prétend être un modèle mathématique du marché.
recherche de modèles, description des principaux modèles
Toutes les hypothèses de base de la théorie de la corrélation et de la régression reposent sur l'hypothèse que les données étudiées sont normalement distribuées. Vos intrants (prix) ont-ils une distribution normale ?
Toutes les hypothèses de base de la théorie de la corrélation et de la régression reposent sur l'hypothèse que les données étudiées sont normalement distribuées. Vos intrants (prix) ont-ils une distribution normale ?
n'a pas compris
En principe, je montrerai que RMS détecte tout motif intégré dans une série de chiffres, y compris les séries temporelles (RT), je pense, quelle que soit la nature de l'apparition de ces chiffres dans la série. Toutes ces subtilités et d'autres encore seront discutées à l'aide d'exemples concrets, notamment l'analyse de séries aléatoires.
RMS trouvera un modèle valide ou fictif, mais en raison du manque de normalité de la distribution, la valeur prédictive du modèle sera de 0. Ce ne sont pas des subtilités, c'est la base.
Qu'est-ce que tu n'as pas compris, exactement ?
RMS trouvera un modèle réel ou imaginaire, mais en raison de l'absence de normalité de la distribution, la valeur prédictive du modèle sera de 0. Ce n'est pas de la subtilité, c'est la base.
RMS trouvera la dépendance la plus adéquate, plutôt qu'une dépendance dérivée. Et au sujet de l'absence ou de la présence de la normalité de la distribution des données initiales, ouvrons une discussion séparée et laissons les experts de cette base parler ici en parallèle.
Je l'ai eu..... Et à droite - oublie ça, la normalité ! C'est juste un obstacle.
P.S. la valeur prédictive du modèle sera proche de 0
Commençons par une fonction linéaire.
Imaginons qu'une série soit donnée par les nombres Yi = a+bxi :
xi Yi
0,00000001 10,0000
1,00000001 15,0000
2,00000001 20,0000
3,00000001 25,0000
4,00000001 30,0000
5,00000001 35,0000
6,00000001 40,0000
7,00000001 45,0000
8,00000001 50,0000
9,00000001 55,0000
10,00000001 60,0000
11,00000001 65,0000
12,00000001 70,0000
13,00000001 75,0000
14,00000001 80,0000
15,00000001 85,0000
16,00000001 90,0000
17,00000001 95,0000
18,00000001 100,0000
Voici un graphique des valeurs réelles et calculées, l'erreur du modèle est de 2.78163E-14% :
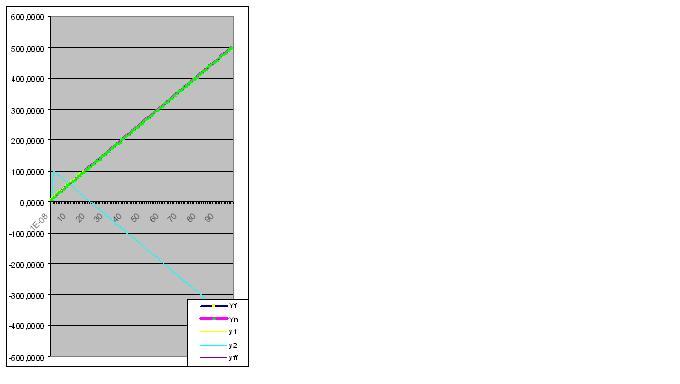
Je l'ai eu..... Et à juste titre - au diable la normalité ! Ça ne fait qu'entraver les choses.
P.S. la valeur prédictive du modèle sera proche de 0
En raison de votre persistance, je dois commencer par démontrer la capacité prédictive du modèle en analysant la fonction Y=tg(0,1x)+2 et en introduisant les 8 premières paires de chiffres :
xi Yi
0,00000001 2,0000
1,00000001 2,1003
2,00000001 2,2027
3,00000001 2,3093
4,00000001 2,4228
5,00000001 2,5463
6,00000001 2,6841
7,00000001 2,8423
Erreur 0.427140953% :
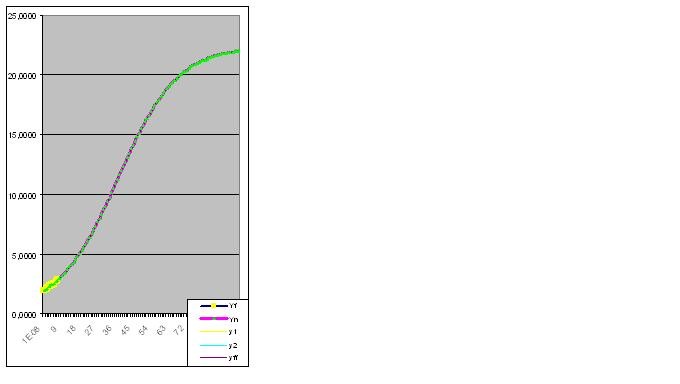
Cependant, dès que la neuvième paire de chiffres est saisie, le modèle prédit immédiatement le comportement "étrange" de l'objet dans le futur :
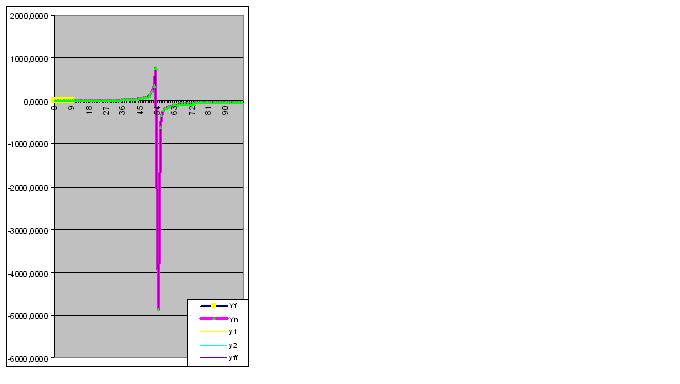
Une nouvelle saisie de données rapproche l'"anomalie" prédite des données d'origine :
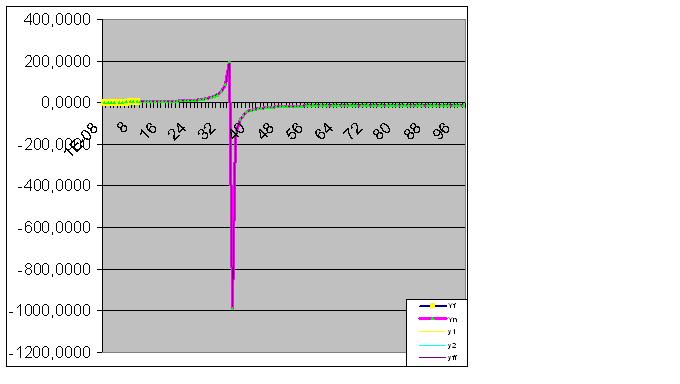
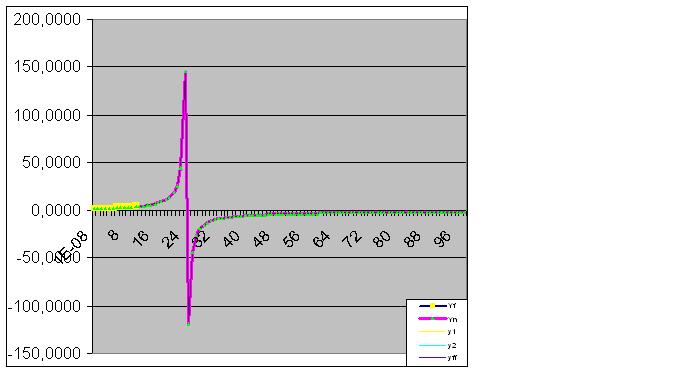
Ici, les données brutes ont également commencé à effectuer la "feinte" prédite :
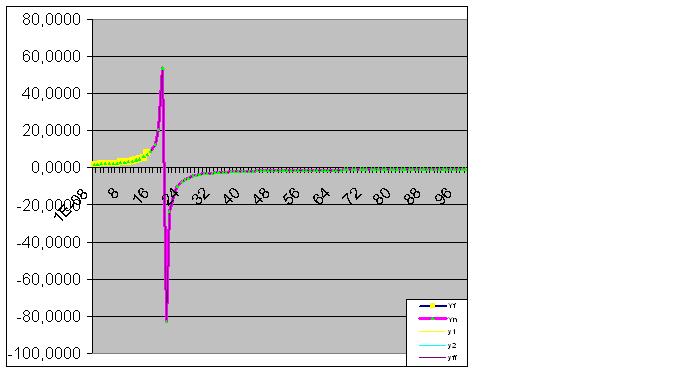
Finalement, la prédiction se réalise parfaitement :
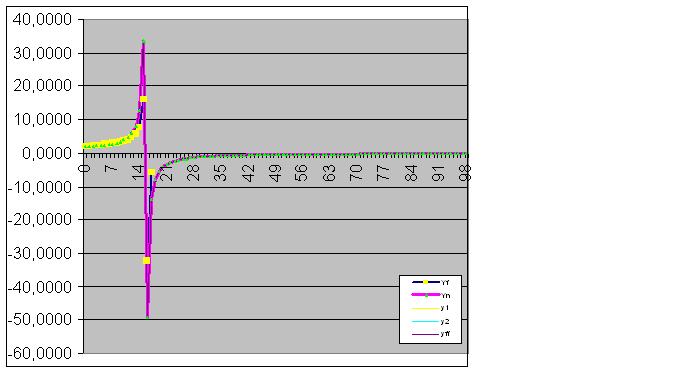
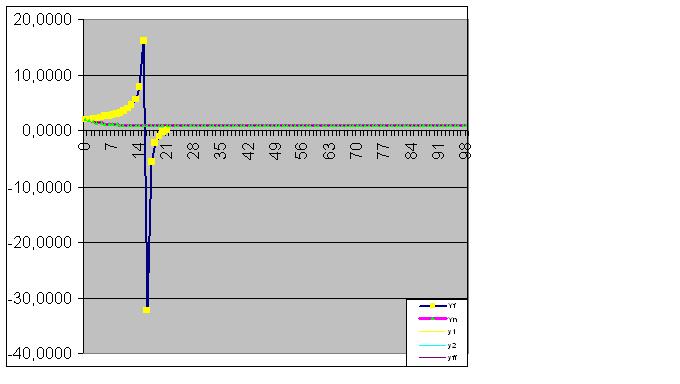
Ensuite, le modèle capture parfaitement l'état final de l'objet, de sorte que la somme des valeurs réelles de la fonction est égale à la valeur efficace calculée, avec une précision informatique.
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation
Chers membres du forum, ce n'est pas un secret que la question de trouver les dépendances qui décrivent les modèles de base du marché est importante. Nous tenterons ici d'aborder cette question par tous les moyens d'analyse disponibles, y compris les diverses propositions des participants sur cette question et le matériel théorique et pratique accumulé à ce jour de toutes les sources possibles. Grâce à ce travail, si nous nous attardons ne serait-ce que sur une partie de cette fonction, je pense que nous considérerons que le temps et les efforts n'ont pas été dépensés en vain.
Je commencerai par démontrer les capacités de RMS à l'aide d'exemples simples de descriptions de motifs bien connus : linéaire, parabole, hyperbole, exposant, sinus, cosinus, tangente, cotangente et autres, ainsi que leur combinaison, qui sont certainement présents sur le marché. Veuillez me soutenir dans cette impulsion par des suggestions constructives et des critiques saines si nécessaire.