Redes neuronales: así de sencillo (Parte 37): Atención dispersa (Sparse Attention)

Introducción

En el artículo anterior, examinamos los modelos relacionales que usan mecanismos de atención en su arquitectura. Asimismo, utilizamos ese modelo para crear un asesor experto que ha ofrecido buenos resultados. Sin embargo, observamos que la tasa de aprendizaje del modelo disminuía en comparación con experimentos anteriores: esto se debe a que la unidad del Transformer utilizada en el modelo ya es en sí misma una solución arquitectónica bastante compleja que realiza un gran número de operaciones. El número de dichas operaciones crece en progresión cuadrática a medida que aumenta el tamaño de la secuencia analizada, lo cual conlleva un aumento del consumo de memoria y del tiempo de entrenamiento del modelo.

No obstante, entendemos que los recursos disponibles para mejorar el modelo son limitados. Por ello, deberemos optimizar el modelo intentando que las pérdidas en la calidad de su funcionamiento sean mínimas.

1. Atención dispersa

Cuando hablamos de optimizar el rendimiento de un modelo, lo primero a lo que debemos prestar atención es a sus hiperparámetros. Su elección debe ser óptima en cuanto a los recursos consumidos y la calidad del rendimiento del modelo. Aumentar el número de neuronas de una capa a partir de un determinado umbral casi no mejora la calidad del rendimiento del modelo, y lo mismo podemos decir del número de capas de neuronas. No obstante, la determinación de los hiperparámetros óptimos depende del problema específico y de su complejidad.

Todo esto se aplica también al número de cabezas de atención en un bloque de auto-atención con varias cabezas. A veces bastan dos cabezas para obtener buenos resultados, pero no es el valor óptimo para todas las tareas. Todos los hiperparámetros deben seleccionarse de forma experimental para cada tarea específica y la arquitectura de modelo.

Este artículo analizará enfoques arquitectónicos para reducir el número de operaciones en el bloque de auto-atención. Sin embargo, antes de pasar a la optimización del algoritmo, debemos recordar cómo funciona el bloque auto-atención.

Primero se calculan las 3 entidades: Query, Key y Value para cada elemento de la secuencia. Para ello, multiplicaremos el vector que describe el elemento de la secuencia por la matriz de coeficientes de peso correspondiente. A continuación, multiplicaremos la matriz Query por la matriz Key transpuesta para obtener los coeficientes de las dependencias entre los elementos de la secuencia. Después normalizaremos estos coeficientes usando la función SoftMax.

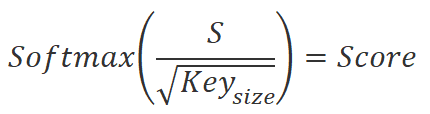
Tras normalizar los coeficientes de dependencia, los multiplicaremos por la matriz de entidades Value para obtener los valores de salida de cada elemento de la secuencia. Estos valores de salida son sumas ponderadas de los valores de los elementos que tienen en cuenta la importancia de cada elemento en el contexto de la tarea.

Un aumento en el número de elementos de la secuencia conlleva un aumento de la complejidad computacional de las operaciones en los algoritmos que usan mecanismos de atención. Esto se debe a que en cada paso se realizan las operaciones de cálculo de entidades, multiplicación de matrices y normalización de coeficientes de dependencia para cada elemento de la secuencia.

Si tenemos un gran número de elementos en la secuencia, esto puede suponer un aumento significativo del tiempo de cálculo y de los recursos informáticos. Para optimizar el algoritmo y reducir el número de cálculos en cada paso, podemos usar varios métodos, incluida la atención dispersa. Este método fue propuesto por Rewon Child en el artículo "Generating Long Sequences with Sparse Transformers", publicado en abril de 2019.

La atención dispersa es una técnica que permite optimizar el mecanismo de atención para reducir la cantidad de cálculos necesarios para procesar los elementos de la secuencia.

La esencia del método consiste en considerar solo los elementos más importantes de la secuencia a la hora de calcular los coeficientes de atención entre ellos. Así, en lugar de calcular los coeficientes de atención para todos los pares de elementos de una secuencia, seleccionaremos solo los pares más destacados.

Una de las ventajas del método de atención dispersa es que puede reducir significativamente el número de cálculos necesarios para procesar los elementos de una secuencia. Esto resulta especialmente importante al procesar grandes secuencias en las que el número de cálculos puede ser muy elevado.

Además, la atención dispersa puede ayudar a combatir el problema de la "atención a todo" (attention on everything), en el que el mecanismo de atención distribuye la atención uniformemente a todos los elementos de una secuencia, lo cual provoca un uso ineficiente de los recursos y ralentiza el algoritmo.

A la hora de aplicar la atención dispersa pueden usarse distintos enfoques. Uno consiste en dividir la secuencia en bloques y calcular la atención solo entre los elementos de cada bloque y entre los elementos de bloques diferentes. Para reducir el número de cálculos, solo consideran los elementos más próximos según la distancia.

Otro enfoque consiste en seleccionar los elementos más importantes de una secuencia en función de sus similitudes. Para ello, se pueden usar varios métodos de clusterización.

Un tercer enfoque consiste en usar diversas heurísticas y algoritmos para seleccionar los elementos más importantes de una secuencia, por ejemplo, según su frecuencia, importancia o contexto.

Los autores señalan que, para que la atención dispersa funcione de forma eficaz, debemos utilizar un algoritmo para asignar los elementos de la secuencia en bloques que ofrezca una estructura de bloques diferente para cada cabeza de atención. Este enfoque determinará mejor el impacto de cada elemento de la secuencia y mejorará la eficacia del algoritmo.

La atención dispersa encuentra aplicaciones en diversas áreas del aprendizaje automático y el procesamiento del lenguaje natural, tales como la traducción automática, la generación de textos, el análisis tonal y muchas otras. En su artículo, los autores del método presentan el resultado del algoritmo para textos, imágenes y grabaciones de audio.

Además, la atención dispersa puede combinarse eficazmente con otras técnicas de optimización de mecanismos de atención para conseguir resultados más precisos en el procesamiento de secuencias.

A pesar de su eficacia, el método de atención dispersa tiene sus desventajas. Una de ellas es que la selección de los elementos más importantes de una secuencia puede resultar errónea, lo que puede provocar una pérdida de información. Por ello, se debe elegir un método adecuado para cada tarea específica y ajustar cuidadosamente los parámetros del algoritmo.

Creo que el método de atención dispersa puede resultar útil para resolver problemas de análisis de los mercados financieros. Al analizar la historia de cambios en las cotizaciones de los instrumentos financieros, debemos analizar datos con una profundidad considerable, y a menudo solo algunos elementos de esta historia influyen en la situación actual. El uso del método de atención dispersa reducirá la cantidad de recursos computacionales destinados a la selección de bloques significativos de los datos investigados. El método también ayudará a excluir elementos insignificantes de las operaciones posteriores, lo cual aumentará la eficacia del análisis de los mercados financieros.

Sin embargo, las cotizaciones de los mercados financieros tienen una estructura cambiante que no permite trabajar con bloques fijos de elementos en la secuencia analizada. En este sentido, para acelerar el proceso de aprendizaje del modelo, podemos usar la heurística de la regla 80/20 de Pareto, en la que solo tomamos el 20% de los elementos más significativos de la secuencia global. La determinación de la importancia de los elementos se basa en los coeficientes de dependencia entre los mismos, calculados con la ayuda de las dos primeras fórmulas descritas anteriormente. Ya después de la primera iteración, antes de normalizar los datos, resulta posible identificar con precisión los elementos más significativos de la secuencia y excluir los restantes de las operaciones posteriores. Esto reduce el número de operaciones en la fase de normalización y determinación de resultados del bloque de auto-atención.

Como cada cabeza de atención utiliza sus propias matrices únicas para definir Query y Key, es probable que los elementos seleccionados sean diferentes en cada cabeza de atención.

Una vez determinadas las direcciones principales de la optimización del algoritmo, podemos proceder a su implementación usando el lenguaje MQL5.

2. Implementación usando MQL5

Para implementar el método propuesto, crearemos una nueva clase de capa neuronal CNeuronMLMHSparseAttention. Obviamente, no recrearemos todos los métodos de la clase. En su lugar, usaremos la herencia de la clase CNeuronMLMHAttentionOCL existente. Y aquí vamos a analizar qué métodos de clase y kernels del programa OpenCL necesitamos modificar para implementar la optimización propuesta.

Como ya hemos mencionado, nuestro primer cambio en el algoritmo se referirá al bloque de determinación del coeficiente de dependencia. Estos valores proceden de una pasada directa en el kernel MHAttentionScore. Para nuestra implementación, sustituiremos el kernel especificado por MHSparseAttentionScore.

En los parámetros del kernel de la clase padre, hemos transmitido punteros a 2 búferes de datos: un tensor concatenado de entidades Query, Key y Value como datos de entrada y un búfer para registrar los resultados de las operaciones en forma de coeficientes de dependencia. Además de los búferes de datos, se transmitía al kernel la dimensionalidad de las entidades internas. A los parámetros ya mencionados, añadiremos el factor de reducción sparse. En él transmitiremos un valor en el rango de 0 a 1, que indicará la proporción de elementos de la secuencia seleccionados con una máxima influencia sobre el elemento analizado.

__kernel void MHSparseAttentionScore(__global float *qkv,    ///<[in] Matrix of Querys, Keys, Values
                                     __global float *score,  ///<[out] Matrix of Scores
                                     int dimension,          ///< Dimension of Key
                                     float sparse            ///< less than 1.0 coefficient of sparse
                                    )
  {
   int q = get_global_id(0);
   int h = get_global_id(1);
   int units = get_global_size(0);
   int heads = get_global_size(1);
//---

El nuevo kernel, al igual que el kernel de la clase padre, se ejecutará en un espacio de tareas bidimensional. La primera dimensión indicará el número de secuencia del elemento secuencial analizado, mientras que la segunda se corresponderá con la cabeza de atención utilizada. En el cuerpo del kernel, guardaremos directamente los identificadores globales del hilo ejecutado en las variables locales.

A continuación, realizaremos un pequeño trabajo preparatorio en el que declararemos las variables locales necesarias y definiremos el desplazamiento en los búferes de datos hasta los elementos analizados.

   int shift_q = dimension * (h + 3 * q * heads);
   int shift_s = units * (h + q * heads);
   int active_units = (int)max((float)(units * sparse), min((float)units, 3.0f));
//---
   float koef = sqrt((float)dimension);
   if(koef < 1)
      koef = 1;
   float sum = 0.0f;
   float min_s = 0.0f;
   float max_s = 0.0f;

Aquí será también donde determinaremos el valor absoluto de los elementos seleccionados. Obsérvese que, al determinar el número de elementos importantes seleccionados de la secuencia, hemos limitado el límite inferior de este valor a un número de tres elementos. Esto nos ayudará a evitar la desconexión no deseada de la unidad de atención al usar secuencias pequeñas. Al fin y al cabo, no supone ningún secreto que la máxima relación de dependencia la generarán casi siempre los elementos analizados para la propia Key.

A continuación, organizaremos un ciclo en el que multiplicaremos el vector Query del elemento de secuencia analizado por la matriz Key. En el cuerpo de este ciclo, también determinaremos los valores máximo y mínimo del vector resultante.

   for(int k = 0; k < units; k++)
     {
      float result = 0;
      int shift_k = dimension * (h + heads * (3 * k + 1));
      for(int i = 0; i < dimension; i++)
        {
         if((dimension - i) > 4)
           {
            result += dot((float4)(qkv[shift_q + i], qkv[shift_q + i + 1], qkv[shift_q + i + 2], qkv[shift_q + i + 3]),
                          (float4)(qkv[shift_k + i], qkv[shift_k + i + 1], qkv[shift_k + i + 2], qkv[shift_k + i + 3]));
            i += 3;
           }
         else
            result += (qkv[shift_q + i] * qkv[shift_k + i]);
        }
      score[shift_s + k] = result;
      if(k == 0)
         min_s = max_s = result;
      else
        {
         max_s = max(max_s, result);
         min_s = min(min_s, result);
        }
     }

Para preservar las dependencias entre los valores obtenidos y los elementos correspondientes de la secuencia, no clasificaremos el vector para seleccionar los elementos más significativos. En su lugar, aumentaremos iterativamente el límite inferior del rango de significación de los coeficientes de dependencia hasta obtener el número necesario de elementos de secuencia "importantes". Implementaremos esta funcionalidad en el próximo ciclo.

   int count = units;
   float temp = max_s;
   while(count > active_units)
     {
      count = 0;
      for(int k = 0; k < units; k++)
        {
         float value = score[shift_s + k];
         if(value < min_s)
            continue;
         count++;
         if(value < temp && value > min_s)
            temp = value;
        }
      if(count > active_units)
         min_s = temp;
     }

Una vez determinado el rango de significación, pasaremos a la siguiente etapa, la normalización de los datos, que constará de dos pasos. En el primer paso, calcularemos los valores exponenciales de los niveles de dependencia obtenidos en el paso anterior. A continuación, dividiremos estos valores por la suma total. Pero es importante recordar que hemos definido un intervalo de significación y que para los elementos que se encuentran fuera de este intervalo simplemente pondremos a cero los coeficientes de dependencia y los excluiremos de operaciones posteriores. Esto se refiere tanto al cálculo de los valores exponenciales como a la etapa de normalización.

   if(max_s == 0.0f)
      max_s = 1.0f;
   for(int k = 0; k < units; k++)
     {
      float value = score[shift_s + k];
      if(value < min_s)
        {
         score[shift_s + k] = 0.0f;
         continue;
        }
      value = exp(value / max_s / koef);
      score[shift_s + k] = value;
      sum += value;
     }

   for(int k = 0; (k < units && sum > 1); k++)
     {
      temp = score[shift_s + k];
      if(temp == 0.0f)
         continue;
      score[shift_s + k] = temp / sum;
     }
  }

Como resultado de las operaciones de kernel anteriores, obtendremos solo un pequeño número de coeficientes de dependencia distintos de cero para los elementos seleccionados de la secuencia analizada, con los que seguiremos trabajando. Al hacerlo, excluiremos los elementos de la secuencia con coeficientes de dependencia cero de las operaciones posteriores de pasada directa e inversa.

El siguiente paso consistirá en obtener la salida del bloque de atención. Para ello, según el algoritmo de auto-atención, deberemos multiplicar la matriz normalizada de coeficientes de dependencia Score por la matriz de entidades Value. Esta operación se realizará en el kernel MHSparseAttentionOut. En él, también organizaremos las comprobaciones del coeficiente de dependencia cero para reducir el número de operaciones realizadas.

En los parámetros del kernel, transmitiremos los punteros a 3 búferes de datos. El tensor concatenado de entidades Query, Key y Value junto con la matriz de coeficientes de dependencia Score son los datos de entrada para las operaciones realizadas, mientras que escribiremos el resultado de las operaciones en el búfer Out. También en los parámetros, transmitiremos la dimensionalidad del vector Key de un elemento de la secuencia. Recordemos que en la clase de atención multi-cabeza, utilizamos vectores de la misma dimensionalidad para las entidades internas Query, Key y Value.

__kernel void MHSparseAttentionOut(__global float *scores, ///<[in] Matrix of Scores
                                   __global float *qkv,    ///<[in] Matrix of Values
                                   __global float *out,    ///<[out] Output tensor
                                   int dimension           ///< Dimension of Value
                                  )
  {
   int u = get_global_id(0);
   int units = get_global_size(0);
   int h = get_global_id(1);
   int heads = get_global_size(1);

Este kernel, al igual que el anterior, se llamará en el espacio de tareas bidimensional para realizar la separación en hilos de operaciones independientes según los elementos de la secuencia y las cabezas de atención. Al principio del kernel, almacenaremos los identificadores de los hilos en las variables locales.

A continuación, definiremos los desplazamientos en los búferes de datos.

   int shift_s = units * (h + heads * u);
   int shift_out = dimension * (h + heads * u);

Después, organizaremos un sistema de ciclos anidados de multiplicación del vector de coeficientes de dependencia por la matriz de valores. Aquí insertaremos una comprobación sobre el coeficiente de dependencia cero para eliminar operaciones redundantes.

   for(int d = 0; d < dimension; d++)
     {
      float result = 0;
      for(int v = 0; v < units; v ++)
        {
         float cur_score = scores[shift_s + v];
         if(cur_score == 0)
            continue;
         int shift_v = dimension * (h + heads * (3 * v + 2)) + d;
         result += cur_score * qkv[shift_v];
        }
      out[shift_out + d] = result;
     }
  }

Con esto podemos dar por finalizado el trabajo con los kernels de pasada directa de nuestra nueva clase: ahora veremos el alcance de los cambios en la parte de la pasada inversa.

Hemos organizado la pasada inversa del bloque de auto-atención de la clase padre en el kernel MHAttentionInsideGradients. El algoritmo para construir este se ha construido de tal forma que permita añadir los puntos de control necesarios a lo largo de un kernel existente sin crear un duplicado del mismo. Le proponemos examinar el algoritmo construido y los puntos de control añadidos.

En los parámetros del kernel, transmitiremos los punteros a 5 búferes de datos:

• Un tensor concatenado de entidades Query, Key y Value (qkv)
• Un tensor concatenado para registrar los gradientes de error de las entidades Query, Key y Value (qkv_g)
• Un matriz de coeficientes de dependencia (scores)
• Una matriz para registrar los gradientes de error a nivel de la matriz de coeficientes de dependencia (scores_g)
• Un tensor de gradientes de error al nivel de salida de bloque de la cabeza de atención actual.

__kernel void MHAttentionInsideGradients(__global float *qkv, __global float *qkv_g,
                                         __global float *scores, __global float *scores_g,
                                         __global float *gradient, int dimension)
  {
   int u = get_global_id(0);
   int h = get_global_id(1);
   int units = get_global_size(0);
   int heads = get_global_size(1);
   float koef = sqrt((float)dimension);
   if(koef < 1)
      koef = 1;

Llamaremos kernel de distribución del gradiente del error en el espacio bidimensional del problema, como hicimos en los dos casos discutidos anteriormente. Una dimensión identificará el elemento de secuencia analizado, mientras que la segunda dimensión señalará a la cabeza de atención actual. Son estos identificadores los que nos ayudarán a determinar el desplazamiento en los búferes de datos hacia los elementos necesarios. Así que al principio del kernel, almacenaremos estos identificadores de hilos en las variables locales.

Además, el algoritmo del kernel se dividirá convencionalmente en 2 bloques. En el primero, definiremos el gradiente de error a nivel de la matriz de coeficientes de dependencia. Aquí, organizaremos un ciclo para recopilar los gradientes en el vector de coeficientes de dependencia del elemento de secuencia analizado. Debemos decir que, como los elementos de secuencia no seleccionados con coeficientes de dependencia nulos no han influido en el resultado final, el gradiente de error para ellos debería ser cero. Por ello, en el cuerpo del ciclo, primero comprobaremos el coeficiente de dependencia actual, y cuando se detecte un valor nulo, simplemente pasaremos al siguiente elemento.

Resulta importante señalar que acceder a la memoria global, que contiene los elementos de todos nuestros búferes de datos, es una operación relativamente cara, y el vector de gradientes de error en el nivel de la matriz de coeficientes de la secuencia supone un almacenamiento temporal y no se utilizará en otros kernels. Entonces ni siquiera escribiremos un valor nulo en él, ya que sería una operación innecesaria sin carga útil.

//--- Calculating score's gradients
   uint shift_s = units * (h + u * heads);
   for(int v = 0; v < units; v++)
     {
      float s = scores[shift_s + v];
      if(s <= 0)
         continue;
      float sg = 0;
      int shift_v = dimension * (h + heads * (3 * v + 2));
      int shift_g = dimension * (h + heads * v);
      for(int d = 0; d < dimension; d++)
         sg += qkv[shift_v + d] * gradient[shift_g + d];
      scores_g[shift_s + v] = sg * (s < 1 ? s * (1 - s) : 1) / koef;
     }
   barrier(CLK_GLOBAL_MEM_FENCE);

En el siguiente paso, realizaremos la distribución del gradiente de error hasta las entidades internas Query, Key y Value. En él, primero definiremos el desplazamiento en los búferes de datos, y, a continuación, organizaremos el sistema de ciclos para recopilar los gradientes de error de la forma correspondiente.

Aquí, dentro del ciclo anidado, comprobaremos la relación de dependencia, y si se encuentra un valor cero, simplemente pasaremos al siguiente elemento. Así se eliminarán operaciones innecesarias.

//--- Calculating gradients for Query, Key and Value
   uint shift_qg = dimension * (h + 3 * u * heads);
   uint shift_kg = dimension * (h + (3 * u + 1) * heads);
   uint shift_vg = dimension * (h + (3 * u + 2) * heads);
   for(int d = 0; d < dimension; d++)
     {
      float vg = 0;
      float qg = 0;
      float kg = 0;
      for(int l = 0; l < units; l++)
        {
         float sg = scores[shift_s + l];
         if(sg <= 0)
            continue;
         uint shift_q = dimension * (h + 3 * l * heads) + d;
         uint shift_k = dimension * (h + (3 * l + 1) * heads) + d;
         uint shift_g = dimension * (h + heads * l) + d;
         //---
         vg += gradient[shift_g] * sg;
         sg = scores_g[shift_s + l];
         kg += sg * qkv[shift_q];
         qg += sg * qkv[shift_k];
        }
      qkv_g[shift_qg + d] = qg;
      qkv_g[shift_kg + d] = kg;
      qkv_g[shift_vg + d] = vg;
     }
  }

Tras finalizar completamente las iteraciones de este kernel, obtendremos los gradientes de error en los niveles de entidad Query, Key y Value, que se distribuirán posteriormente a las correspondientes matrices de pesos y a la capa neuronal anterior.

Esto completa nuestro trabajo sobre los kernels del programa OpenCL, así que pasaremos a trabajar en el código del programa principal. Arriba hemos añadido dos kernels. Por lo tanto, tendremos que añadir una llamada al kernel en el programa principal. En primer lugar, crearemos las constantes para recurrir a los kernels.

Tenga en cuenta que estamos creando constantes para trabajar con 2 kernels y sólo una constante de parámetro. Luego crearemos kernels basados en los ya existentes y replicaremos casi por completo la estructura de los parámetros de los kernels básicos. Por lo tanto, podemos usar las constantes existentes en el proceso de uso de los kernels. Solo crearemos una constante para especificar el parámetro de descarga.

#define def_k_MHSparseAttentionScore    44 ///< Index of the kernel of the multi-heads sparse attention neuron 
                                           //   to calculate score matrix (#MHSparseAttentionScore)
#define def_k_mhas_sparse                3  ///< less than 1.0 coefficient of sparse
//---
#define def_k_MHSparseAttentionOut      45 ///< Index of the kernel of the multi-heads sparse attention neuron 
                                           //   to calculate multi-heads out matrix (#MHSparseAttentionOut)

A continuación, deberemos organizar la creación de kernels en el contexto de OpenCL. Para ello, tendremos que aumentar el número total de kernels activos en el contexto hasta 46 y llamar a los métodos de creación de kernels.

   opencl.SetKernelsCount(46);

   if(!opencl.KernelCreate(def_k_MHSparseAttentionScore, "MHSparseAttentionScore"))
     {
      PrintFormat("Error of create kernell: %d line %d", GetLastError(), __LINE__);
      return false;
     }
   if(!opencl.KernelCreate(def_k_MHSparseAttentionOut, "MHSparseAttentionOut"))
     {
      PrintFormat("Error of create kernell: %d line %d", GetLastError(), __LINE__);
      return false;
     }

Aquí hay que decir que las anteriores operaciones de creación de kernels en el contexto de OpenCL tendremos que repetirlas en los tres métodos de la clase gestión de la red neuronal CNet. Sí, estoy de acuerdo en que no es precisamente cómodo. En el futuro, planeo poner estas operaciones en un método aparte.

   bool              Create(CArrayObj *Description);
   bool              Load(string file_name, float &error, float &undefine, float &forecast, datetime &time, 
                          bool common = true);
   ///< Load method. @param[in] file_name File name to save @param[out] error Average error 
   ///< @param[out] undefine Undefined percent @param[out] Forecast percent 
   ///< @param[out] time Last study time @param[in] common Common flag
   virtual bool      Load(const int file_handle);

En la siguiente etapa de nuestro trabajo, pasaremos directamente a crear los métodos de nuestra nueva clase. La funcionalidad de nuestra nueva clase de red neuronal CNeuronMLMHSparseAttention resulta muy similar a la de la clase padre CNeuronMLMMHAttentionOCL. Por lo tanto, en la mayoría de los casos también usaremos métodos heredados. Las principales diferencias estarán relacionadas con la creación de la dispersión de la atención. En esta parte, crearemos una nueva variable interna m_dSparse para almacenar el nivel de dispersión.

Hemos decidido no complicar el trabajo reescribiendo métodos innecesariamente, así que hemos dejado el constructor y el destructor de la clase vacíos. Después de todo, en la nueva clase no estamos creando nuevos objetos, sino creando métodos Sparse sobrecargados para trabajar con el parámetro de dispersión. La posibilidad de sobrecargar métodos permite usar métodos con el mismo nombre para funcionalidades distintas: con el valor especificado en los parámetros, transmitiremos el valor del parámetro al método; sin especificar los parámetros, el método retornará el valor almacenado previamente.

class CNeuronMLMHSparseAttention  : public CNeuronMLMHAttentionOCL
  {
protected:
   float             m_dSparse;
   //---
   virtual bool      AttentionScore(CBufferFloat *qkv, CBufferFloat *scores, bool mask = true);
   ///< \brief Multi-heads attention scores method of calling kernel ::MHAttentionScore().
   virtual bool      AttentionOut(CBufferFloat *qkv, CBufferFloat *scores, CBufferFloat *out);
   ///< \brief Multi-heads attention out method of calling kernel ::MHAttentionOut().

public:
                     CNeuronMLMHSparseAttention(void)   :  m_dSparse(0.3f) {};
                    ~CNeuronMLMHSparseAttention(void) {};
   //---
   void              Sparse(float value)  { m_dSparse = value;}
   float             Sparse(void)         { return m_dSparse; }
   virtual int       Type(void)   const   {  return defNeuronMLMHSparseAttentionOCL;   }
                     ///< Identificatory of class.@return Type of class
   //--- methods for working with files
   virtual bool      Save(int const file_handle);  
                     ///< Save method @param[in] file_handle handle of file @return logical result of operation
   virtual bool      Load(int const file_handle);  
                     ///< Load method @param[in] file_handle handle of file @return logical result of operation
  };

No se olvide de redefinir el método virtual para identificar el objeto Type.

Además, entre los métodos públicos, los métodos de gestión de archivos Save y Load deben ser sobrescritos. El algoritmo de estos métodos es bastante simple. En ellos, primero llamaremos a los métodos homónimos de la clase padre, donde ya están definidos todos los puntos de control y organizados los algoritmos para guardar y cargar las variables, así como los objetos heredados. Solo tendremos que comprobar el resultado lógico de la ejecución de los métodos llamados, y después de ejecutar con éxito el método de la clase padre, guardaremos o leeremos el valor del parámetro Sparse, dependiendo de la funcionalidad del método de ejecución.

bool CNeuronMLMHSparseAttention::Save(const int file_handle)
  {
   if(!CNeuronMLMHAttentionOCL::Save(file_handle))
      return false;
   if(FileWriteFloat(file_handle, m_dSparse) < sizeof(float))
      return false;
//---
   return true;
  }

Bien, ya hemos terminado con los métodos públicos de ayuda a la nueva clase, pero la funcionalidad principal de la clase consiste en crear un algoritmo para la capa neuronal, y aquí volvemos a las pasadas directa e inversa. Para esta funcionalidad hemos actualizado los kernels de programas OpenCL.

Nos desviaremos un poco de la estructura habitual del análisis de métodos al describir la funcionalidad de las redes neuronales: empezaremos con las pasadas inversas, en lugar de directas. Arriba no hemos creado nuevos kernels de funcionalidad de pasada inversa. Acabamos de hacer cambios en el kernel existente utilizado por la clase padre. Heredando la funcionalidad de la clase padre, también hemos obtenido los algoritmos para llamar al kernel MHAttentionInsideGradients discutido anteriormente, lo cual significa que ahora podemos usar el método calcInputGradients de la clase padre para distribuir los gradientes de error. En cuanto a la funcionalidad de actualización de los parámetros entrenados, no hemos realizado ningún cambio y también podemos utilizar el método de la clase padre updateInputWeights.

Veamos ahora los métodos de pasada directa. Al construir el algoritmo de pasada directa de la clase padre, no hemos combinado todo el algoritmo ramificado en el cuerpo de un único método. En su lugar, hemos creado un método de gestión estructurado feedForward en el que los métodos para ejecutar funcionalidades individuales se llaman secuencialmente, según el algoritmo de auto-atención. Gracias a este enfoque, ahora no necesitaremos reescribir completamente el método de pasada directa. Todo lo que deberemos hacer es sobrescribir los métodos para llamar a los dos nuevos kernels. Hablamos de los métodos AttentionScore y AttentionOut.

bool CNeuronMLMHAttentionOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(CheckPointer(NeuronOCL) == POINTER_INVALID)
      return false;
//---
   for(uint i = 0; (i < iLayers && !IsStopped()); i++)
     {
      //--- Calculate Queries, Keys, Values
      CBufferFloat *inputs = (i == 0 ? NeuronOCL.getOutput() : FF_Tensors.At(6 * i - 4));
      CBufferFloat *qkv = QKV_Tensors.At(i * 2);
      if(IsStopped() || !ConvolutionForward(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)),
                                            inputs, qkv, iWindow, 3 * iWindowKey * iHeads, None))
         return false;
      //--- Score calculation
      CBufferFloat *temp = S_Tensors.At(i * 2);
      if(IsStopped() || !AttentionScore(qkv, temp, true))
         return false;
      //--- Multi-heads attention calculation
      CBufferFloat *out = AO_Tensors.At(i * 2);
      if(IsStopped() || !AttentionOut(qkv, temp, out))
         return false;
      //--- Attention out calculation
      temp = FF_Tensors.At(i * 6);
      if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), 
                                            out, temp, iWindowKey * iHeads, iWindow, None))
         return false;
      //--- Sum and normilize attention
      if(IsStopped() || !SumAndNormilize(temp, inputs, temp))
         return false;
      //--- Feed Forward
      inputs = temp;
      temp = FF_Tensors.At(i * 6 + 1);
      if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), 
                                            inputs, temp, iWindow, 4 * iWindow, LReLU))
         return false;
      out = FF_Tensors.At(i * 6 + 2);
      if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), 
                                            temp, out, 4 * iWindow, iWindow, activation))
         return false;
      //--- Sum and normilize out
      if(IsStopped() || !SumAndNormilize(out, inputs, out))
         return false;
     }
//---
   return true;
  }

Para preservar las reglas de herencia, hemos dado a ambos métodos parámetros similares a los de la clase padre. Esto resulta vital, porque cambiar los parámetros del método crearía métodos sobrecargados, mientras que nosotros necesitamos sobrescribir los métodos de la clase padre. Cuando se sobrecargan métodos, el sistema selecciona uno de ellos según los parámetros especificados al llamar al método, mientras que al sobrescribir los métodos, el sistema sigue la jerarquía de herencia y utiliza el último método sobrescrito. Por lo tanto, solo en el caso de los métodos redefinidos, al llamar desde el método heredado feedForward, el sistema hará referencia a los métodos redefinidos de nuestra clase.

El método AttentionScore obtiene en los parámetros el puntero a los objetos de dos búferes: el tensor concatenado de entidades Query, Key, Value y la matriz de coeficientes de dependencia. Además, en los parámetros del método transmitiremos la bandera mask. Esta bandera no la utilizaremos nosotros, la dejaremos en los parámetros por las razones mencionadas anteriormente.

En el cuerpo del método, comprobaremos inmediatamente la relevancia de los punteros recibidos. Aquí es también donde comprobamos la relevancia del objeto de trabajo con el contexto OpenCL. Además de los propios punteros a los objetos, comprobaremos la existencia de los búferes de datos creados en el contexto OpenCL. Solo después de transmitir con éxito todos los puntos de control anteriores podremos organizar el proceso de colocación del kernel en la cola de ejecución.

Recordemos que todos los kernels que hemos creado se han planificado para su uso en un espacio de tareas bidimensional, y ahora tendremos que crear arrays que describan el espacio de tareas global_work_size y el desplazamiento en el espacio de tareas global_work_offset. La dimensionalidad de ambos arrays deberá corresponderse con el espacio de tareas. Para crear un espacio de tareas bidimensional, crearemos ambos arrays de 2 elementos.

En los elementos del primer array, especificaremos el número total de elementos de la secuencia analizada y el número de cabezas de atención. La posición del elemento en el array indicará la dimensión, mientras que su valor indicará el número de hilos. De esta forma, cada elemento de la secuencia para cada cabeza de atención tendrá su propio hilo independiente para realizar las operaciones, y, en general, las operaciones sobre todos los elementos de la secuencia se realizarán simultáneamente (en la medida en que sea técnicamente posible) en hilos paralelos.

Luego llenaremos los elementos del segundo array con valores nulos, ya que no estamos suponiendo un desplazamiento en el espacio de tareas.

bool CNeuronMLMHSparseAttention::AttentionScore(CBufferFloat *qkv, CBufferFloat *scores, bool mask = true)
  {
   if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(qkv) == POINTER_INVALID ||
      CheckPointer(scores) == POINTER_INVALID)
      return false;
//---
   if(qkv.GetIndex() < 0)
      return false;
   if(scores.GetIndex() < 0)
      return false;
//---
   uint global_work_offset[2] = {0, 0};
   uint global_work_size[2];
   global_work_size[0] = iUnits;
   global_work_size[1] = iHeads;
   OpenCL.SetArgumentBuffer(def_k_MHSparseAttentionScore, def_k_mhas_qkv, qkv.GetIndex());
   OpenCL.SetArgumentBuffer(def_k_MHSparseAttentionScore, def_k_mhas_score, scores.GetIndex());
   OpenCL.SetArgument(def_k_MHSparseAttentionScore, def_k_mhas_dimension, (int)iWindowKey);
   OpenCL.SetArgument(def_k_MHSparseAttentionScore, def_k_mhas_sparse, (float)m_dSparse);
   if(!OpenCL.Execute(def_k_MHSparseAttentionScore, 2, global_work_offset, global_work_size))
     {
      string error;
      CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error);
      printf("Error of execution kernel %s: %s", __FUNCSIG__, error);
      return false;
     }
//---
   return true;
  }

Los siguientes pasos consistirán en transmitir los parámetros al kernel. Para ello, utilizaremos los métodos SetArgumentBuffer y SetArgument. El primero se usa para transmitir los punteros a los búferes de datos. El segundo para transmitir valores discretos. En los parámetros del método, especificaremos el identificador del kernel, el número de secuencia del parámetro transmitido (se corresponde con la secuencia de parámetros del kernel en el programa OpenCL que comienza con un valor "0") y el valor transmitido directamente.

Aquí, deberemos tener cuidado con el tipo de valores transmitidos y el tipo de parámetro especificado en el kernel. Si los tipos no coinciden, podría producirse un error de ejecución del kernel.

Tras realizar el trabajo preparativo, llamaremos al método Execute para enviar el kernel a la cola de ejecución. En los parámetros del método, especificaremos el ID del kernel, la dimensionalidad del espacio de tareas y los arrays de descripción del espacio de tareas creados anteriormente,

e inmediatamente comprobaremos el resultado de la ejecución del método de colocación del kernel en la cola. Si se produce un error de colocación en la cola, solicitaremos información sobre el error y la mostramos en el registro del terminal.

Una vez que el kernel se haya colocado en la cola con éxito para su ejecución, finalizaremos el método con el resultado true.

Repetiremos el mismo algoritmo en el método AttentionOut para llamar al segundo kernel.

bool CNeuronMLMHSparseAttention::AttentionOut(CBufferFloat *qkv, CBufferFloat *scores, CBufferFloat *out)
  {
   if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(qkv) == POINTER_INVALID || 
      CheckPointer(scores) == POINTER_INVALID || CheckPointer(out) == POINTER_INVALID)
      return false;
   uint global_work_offset[2] = {0, 0};
   uint global_work_size[2];
   global_work_size[0] = iUnits;
   global_work_size[1] = iHeads;
   if(qkv.GetIndex() < 0)
      return false;
   if(scores.GetIndex() < 0)
      return false;
   if(out.GetIndex() < 0)
      return false;
//---
   OpenCL.SetArgumentBuffer(def_k_MHSparseAttentionOut, def_k_mhao_qkv, qkv.GetIndex());
   OpenCL.SetArgumentBuffer(def_k_MHSparseAttentionOut, def_k_mhao_score, scores.GetIndex());
   OpenCL.SetArgumentBuffer(def_k_MHSparseAttentionOut, def_k_mhao_out, out.GetIndex());
   OpenCL.SetArgument(def_k_MHSparseAttentionOut, def_k_mhao_dimension, (int)iWindowKey);
   if(!OpenCL.Execute(def_k_MHSparseAttentionOut, 2, global_work_offset, global_work_size))
     {
      string error;
      CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error);
      printf("Error of execution kernel %s: %s", __FUNCSIG__, error);
      return false;
     }
//---
   return true;
  }

Con esto concluiremos nuestro trabajo con la nueva clase de red neuronal, pero queda un detalle más. Necesitaremos añadir el procesamiento de nuestra nueva clase a los métodos de gestión de la organización del modelo.

En primer lugar, añadiremos el bloque para crear un nuevo tipo de capa neuronal en el método CNet::Create,

            case defNeuronMLMHSparseAttentionOCL:
               neuron_sparseattention = new CNeuronMLMHSparseAttention();
               if(CheckPointer(neuron_sparseattention) == POINTER_INVALID)
                 {
                  delete temp;
                  return false;
                 }
               if(!neuron_sparseattention.Init(outputs, 0, opencl, desc.window, desc.window_out, desc.step, 
                                                               desc.count, desc.layers, desc.optimization, desc.batch))
                 {
                  delete neuron_sparseattention;
                  delete temp;
                  return false;
                 }
               neuron_sparseattention.SetActivationFunction(desc.activation);
               neuron_sparseattention.Sparse(desc.probability);
               if(!temp.Add(neuron_sparseattention))
                 {
                  delete neuron_mlattention_ocl;
                  delete temp;
                  return false;
                 }
               neuron_sparseattention = NULL;
               break;

y añadiremos el nuevo tipo de capa al método CLayer::CreateElement.

         case  defNeuronMLMHSparseAttentionOCL:
            if(CheckPointer(OpenCL) == POINTER_INVALID)
               return false;
            temp_mlat_ocl = new CNeuronMLMHSparseAttention();
            if(CheckPointer(temp_mlat_ocl) == POINTER_INVALID)
               result = false;
            if(temp_mlat_ocl.Init(iOutputs, index, OpenCL, 1, 1, 1, 1, 0, ADAM, 1))
              {
               m_data[index] = temp_mlat_ocl;
               return true;
              }
            break;

Además, introduciremos el nuevo tipo en el método de gestión de la pasada directa de la clase básica de la red neuronal,

bool CNeuronBaseOCL::FeedForward(CObject *SourceObject)
  {
   if(CheckPointer(SourceObject) == POINTER_INVALID)
      return false;
//---
   CNeuronBaseOCL *temp = NULL;
   switch(SourceObject.Type())
     {
      case defNeuronBaseOCL:
      case defNeuronProofOCL:
      case defNeuronConvOCL:
      case defNeuronAttentionOCL:
      case defNeuronMHAttentionOCL:
      case defNeuronMLMHAttentionOCL:
      case defNeuronMLMHSparseAttentionOCL:
      case defNeuronDropoutOCL:
      case defNeuronBatchNormOCL:
      case defNeuronVAEOCL:
      case defNeuronLSTMOCL:
      case defNeuronSoftMaxOCL:
         temp = SourceObject;
         return feedForward(temp);
         break;
     }
//---
   return false;
  }

y repetiremos la operación en el método similar de pasada inversa CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject).

      case defNeuronMLMHAttentionOCL:
      case defNeuronMLMHSparseAttentionOCL:
         mlat = TargetObject;
         if(!bTrain && !mlat.TrainMode())
            return true;
         temp = GetPointer(this);
         return mlat.calcInputGradients(temp);

El código completo con todas las clases y su método se puede encontrar en el archivo adjunto.

3. Simulación

Una vez finalizada la nueva clase de la capa neuronal, podremos probar el algoritmo construido en el simulador de estrategias comerciales de la plataforma MetaTrader 5. El simulador de estrategias comerciales nos permite probar el funcionamiento de los asesores e indicadores comerciales con datos históricos. Para probar el funcionamiento del algoritmo construido, crearemos un pequeño asesor comercial que entrenará el modelo directamente en el proceso de pasada por los datos históricos. Ya hemos creado asesores expertos similares al probar los algoritmos discutidos anteriormente. Ahora simplemente tomaremos el asesor del artículo anterior como base y reemplazaremos la capa neuronal de atención multi-cabeza en la arquitectura de su modelo con la capa de atención dispersa recién creada.

Recordemos que en el artículo anterior probamos un modelo de aprendizaje por refuerzo relacional que utilizaba un algoritmo de función cuantílica totalmente parametrizado con el uso de un bloque de curiosidad interno. Para implementar ese modelo, crearemos una combinación de 3 modelos: Model, Forward y Inverse. El bloque de atención lo utilizamos en el primer modelo. En su arquitectura introduciremos las modificaciones. La arquitectura de los otros 2 modelos permanecerá inalterada.

La arquitectura de los modelos se describe en la función CreateDescriptions. Debemos decir que, para aligerar el modelo, hemos decidido abandonar los bloques LSTM recursivos; su lugar lo ocupan ahora las capas totalmente conectadas. Así, el modelo entrenado ha obtenido la siguiente arquitectura.

A la entrada del modelo hay una capa de datos iniciales que consta de 12 elementos para describir cada barra, la historia analizada, y 9 elementos para describir el estado actual de la cuenta.

//--- Model
   Description.Clear();
   CLayerDescription *descr;
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (int)(HistoryBars * 12 + 9);
   descr.window = 0;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!Description.Add(descr))
     {
      delete descr;
      return false;
     }

A esto le sigue una capa de normalización de datos.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1000;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!Description.Add(descr))
     {
      delete descr;
      return false;
     }

A continuación, vienen dos bloques consecutivos de capas convolucionales y totalmente conectadas.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = prev_count - 2;
   descr.window = 3;
   descr.step = 1;
   descr.window_out = 6;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!Description.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 100;
   descr.optimization = ADAM;
   if(!Description.Add(descr))
     {
      delete descr;
      return false;
     }

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = 50;
   descr.window = 2;
   descr.step = 2;
   descr.window_out = 4;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!Description.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 100;
   descr.optimization = ADAM;
   if(!Description.Add(descr))
     {
      delete descr;
      return false;
     }

Los datos comprimidos son analizados por la unidad de atención. Aquí estamos usando una nueva capa de atención dispersa. Luego dividiremos toda la secuencia de datos comprimidos en 20 bloques de 5 elementos cada uno. Cada bloque representa un elemento de la secuencia analizada. Para analizar los datos utilizaremos 4 cabezas de atención con una selección del 30% de los elementos de la secuencia más significativos en cada cabeza de atención. El análisis se realizará en 2 capas consecutivas con parámetros similares. Especificaremos esto en el parámetro layers.  

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMLMHSparseAttentionOCL;
   descr.count = 20;
   descr.window = 5;
   descr.step = 4;
   descr.window_out = 8;
   descr.layers = 2;
   descr.probability = 0.3f;
   descr.optimization = ADAM;
   if(!Description.Add(descr))
     {
      delete descr;
      return false;
     }

La decisión de realizar una operación por parte del asesor experto se tomará en el bloque de la función cuantil totalmente parametrizada. El asesor puede decidir una de estas 4 acciones:

• comprar, 
• vender, 
• cerrar todas las transacciones
• no realizar ninguna transacción comercial.

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFQF;
   descr.count = 4;
   descr.window_out = 32;
   descr.optimization = ADAM;
   if(!Description.Add(descr))
     {
      delete descr;
      return false;
     }

El código completo del Asesor Experto "SparseRL-learning.mq5" se encuentra en el archivo adjunto.

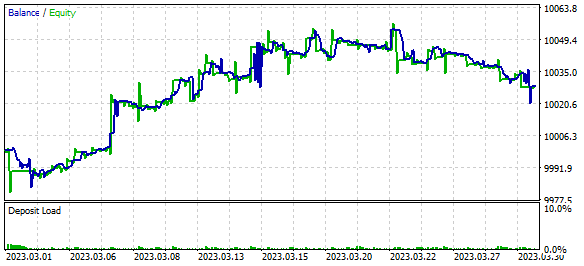
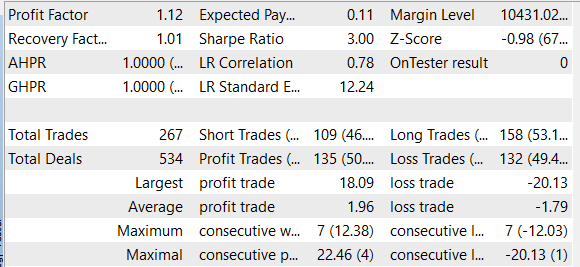
Entrenamos el modelo y probamos el asesor experto con datos históricos de EURUSD con el marco temporal H1 para marzo de 2023. Hemos obtenido beneficios en el periodo de prueba durante el entrenamiento. Cabe señalar que el beneficio se ha logrado gracias a que el tamaño de la transacción media rentable ha sido superior al tamaño de la transacción media perdedora. Al mismo tiempo, el número de posiciones ganadoras y perdedoras ha sido prácticamente el mismo. Como resultado, el factor de beneficio ha sido de 1,12, mientras que el factor de recuperación ha sido de 1,01.

Conclusión

En este artículo, hemos estudiado el mecanismo de atención dispersa y añadido su algoritmo a nuestra biblioteca de clases para después probarlo con datos históricos. Como resultado de las pruebas, el modelo ha generado beneficios, lo cual indica que es posible usar dicha arquitectura para construir soluciones comerciales. No obstante, debemos señalar que el modelo presentado en el artículo solo sirve para familiarizarse con el tema y realizar pruebas.

Para utilizar este modelo en condiciones comerciales reales, deberemos hacer un análisis más detallado de su eficacia y resistencia a los cambios del mercado. También requerirá un ajuste más cuidadoso de los hiperparámetros del modelo para obtener los resultados más óptimos.

Además, hay que tener en cuenta que el uso de cualquier modelo para comerciar en los mercados financieros siempre implica el riesgo de sufrir pérdidas. Por lo tanto, antes de utilizar cualquier modelo para el comercio real, deberemos estudiar cuidadosamente los principios de su funcionamiento y evaluar los posibles riesgos.

A pesar de ello, el mecanismo de atención dispersa puede ser una herramienta útil para construir patrones comerciales.

Enlaces

1. Generating Long Sequences with Sparse Transformers
2. Attention Is All You Need
3. Redes neuronales: así de sencillo (Parte 8): Mecanismos de atención
4. Redes neuronales: así de sencillo (Parte 10): Multi-Head Attention (atención multi-cabeza)
5. Redes neuronales: así de sencillo (Parte 11): Variaciones de GTP
6. Redes neuronales: así de sencillo (Parte 35): Módulo de curiosidad intrínseca (Intrinsic Curiosity Module)
7. Redes neuronales: así de sencillo (Parte 36): Modelos relacionales de aprendizaje por refuerzo (Relational Reinforcement Learning)

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	SparseRL-learning.mq5	Asesor	Asesor para el entrenamiento de modelos
2	ICM.mqh	Biblioteca de clases	Biblioteca de clases para organizar el modelo
3	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
4	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL