Características del Wizard MQL5 que debe conocer (Parte 31): Selección de la función de pérdida

Introducción

El asistente MQL5 (MQL5 Wizard) puede ser un banco de pruebas para una gran variedad de ideas, como hemos tratado hasta ahora en esta serie. Y de vez en cuando, uno se encuentra con una señal personalizada que tiene más de una forma de implementarse. Ya vimos este escenario en los 2 artículos sobre las tasas de aprendizaje, así como en el último artículo sobre la normalización por lotes. Cada uno de esos aspectos del aprendizaje automático presentaba más de una posible señal personalizada, como ya se ha comentado. La pérdida , también por tener múltiples formatos, se encuentra en una situación similar.

La forma de comparar el resultado de una prueba con su objetivo no tiene un método único. Si consideramos las enumeraciones disponibles en ENUM_LOSS_FUNCTION enumeración en MQL5, son 14, y esta lista ni siquiera es exhaustiva. ¿Significa esto que cada uno de ellos ofrece una forma distinta de formarse en aprendizaje automático? Probablemente no, pero la cuestión es que hay diferencias, algunas matizadas, y estas diferencias a menudo pueden implicar que es necesario seleccionar cuidadosamente la función de pérdida dependiendo de la naturaleza de la red o del algoritmo que se esté entrenando.

Además de la función de pérdida, se podría considerar el uso de ENUM_REGRESSION_METRIC pero esto, que está más relacionado con la estadística, sería inapropiado ya que sirve mejor como una métrica post-entrenamiento para evaluar el rendimiento de un algoritmo de aprendizaje automático. Esta enumeración métrica sería muy útil, sobre todo en los casos en los que el resultado final tiene más de una dimensión. Sin embargo, este artículo se centra en la función objetivo.

Y la selección de la medida de pérdida adecuada es vital porque, en principio, las redes neuronales (nuestro algoritmo de aprendizaje automático para este artículo) podrían pertenecer a la categoría de regresores frente a clasificadores, o al tipo de supervisados frente a no supervisados. Además, paradigmas como el aprendizaje por refuerzo podrían requerir un enfoque polifacético a la hora de utilizar y aplicar la función de pérdida.

Así pues, las funciones de pérdida pueden aplicarse de diversas maneras, no sólo porque existen muchos formatos, sino también porque hay una gran variedad de "problemas" (tipos de redes neuronales) que resolver. En la resolución de estos problemas o en el entrenamiento, la función de pérdida cuantifica principalmente lo alejados que están los parámetros probados del objetivo previsto, un proceso que también se conoce como aprendizaje supervisado.

Sin embargo, aunque con la función de pérdida siempre parece intuitivo que están pensadas para el entrenamiento supervisado; la cuestión de la función de pérdida ideal para el aprendizaje no supervisado podría parecer fuera de lugar. Sin embargo, incluso en entornos no supervisados, como los mapas de Kohonen o la agrupación, siempre es necesario disponer de una métrica estandarizada para medir los huecos o la distancia entre datos multidimensionales, y la función de pérdida llenaría este vacío.

Resumen de las funciones de pérdidas

Así, MQL5 ofrece hasta 14 métodos diferentes para cuantificar la función de pérdida, y tocaremos todos ellos antes de considerar los casos de aplicación. Para nuestro propósito, la pérdida se utiliza para implicar el gradiente de pérdida y los resultados esperados de esto son vectores, no valores escalares. Además, el código MQL5 que implementa estas fórmulas no se compartirá porque TODOS se ejecutan desde funciones vectoriales incorporadas. A continuación se ofrece un sencillo script para probar las distintas funciones de pérdida:

#property  script_show_inputs
input ENUM_LOSS_FUNCTION __loss = LOSS_HUBER;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
      vector _a = {1.0, 2.0, 4.0};
      vector _b = {4.0, 12.0, 36.0 };
      
      vector _loss = _a.LossGradient(_b,__loss); 
      
      printf(__FUNCSIG__+" for: "+EnumToString(__loss));
      Print(" loss gradient is: ",_loss);
      PrintFormat(" while loss is: %.5f. ",_a.Loss(_b,__loss));
  }
//+------------------------------------------------------------------+

En primer lugar, el error cuadrático medio de pérdida. Se trata de una función de pérdida muy utilizada cuyo objetivo es medir la diferencia al cuadrado entre los valores previstos y los deseados, poniendo así un número a la cantidad de error. Asegura que el error sea siempre positivo (centrándose en la magnitud) y penaliza enormemente los errores mayores debido al cuadrado. La interpretación también es más fluida ya que el error siempre está en las unidades al cuadrado de la variable objetivo. Su fórmula se presenta a continuación:

Donde:

• 'n' es el tamaño de la dimensión de la variable objetivo y comparada. Normalmente, estas variables están en formato vectorial.
• 'i' es un índice intra dentro del espacio vectorial
• 'y^' es un vector de salida o predicho
• 'y' es el vector objetivo

Sus ventajas podrían ser la sensibilidad a grandes errores y una adaptabilidad adecuada a los métodos de optimización de descenso de gradiente debido a su gradiente suave. Las desventajas serían la sensibilidad a los valores atípicos.

A continuación, la función de pérdida de error absoluto medio. Ésta, al igual que el MSE anterior, es otra función de pérdida común que, al igual que el MSE, se centra en el error de magnitud sin tener en cuenta la dirección. La diferencia con el MSE anterior es que no otorga ponderación extra a los valores grandes, ya que no implica ningún cuadrado. Como no se utiliza el cuadrado, las unidades de error coinciden con las del vector objetivo y, por lo tanto, la interpretación es más sencilla que con MSE. Su fórmula, que es similar a la que tenemos arriba, se da de la siguiente manera:

Donde:

• 'n', 'i', 'y' e 'y^' representan los mismos valores que en MSE anterior

Sus principales ventajas son su menor sensibilidad a los valores atípicos y a los errores importantes, ya que no realiza ninguna cuadratura, así como su sencillez a la hora de mantener las unidades objetivo, lo que facilita la interpretación. Sin embargo, el comportamiento de su gradiente no es tan suave como el de MSE, ya que en la diferenciación la salida es +1,0, -1,0 o cero. La alternancia entre estos valores no ayuda a que el proceso de entrenamiento converja tan suavemente como lo hace con el MSE, y particularmente en entornos de regresión esto podría ser un problema. Además, el tratamiento de todos los errores como iguales va en contra del proceso de convergencia hasta cierto punto.

Esto nos lleva a la entropía cruzada categórica. Mide, en un espacio estrictamente multidimensional, la diferencia entre la distribución de probabilidad prevista y la distribución de probabilidad real. Así, mientras que estamos utilizando MAE, y MSE como salidas vectoriales en el algoritmo de la función de pérdida MQL5 (ya que las diferencias individuales no se suman), que fácilmente podría ser escalares como sus fórmulas indican. Por otro lado, la Entropía Cruzada Categórica (Categorical Cross Entropy, CCE) siempre produce un resultado multidimensional. La fórmula viene dada por:

Donde:

• 'N' es el número de clases o el tamaño del vector de puntos de datos
• 'y' es el valor real o objetivo
• 'p' es el valor de salida previsto o de la red
• y 'log' es el logaritmo natural

CCE es inherentemente un clasificador, no un regresor, y es particularmente adecuado cuando se utiliza más de una clase para categorizar un conjunto de datos durante el entrenamiento. Las principales aplicaciones de esto son en gráficos y procesamiento de imágenes, pero, por supuesto, como siempre, esto no nos impide buscar formas de aplicarlo a los traders. Sin embargo, es digno de mención que CCE funciona mejor combinado con la activación Soft-Max, que normalmente también genera un vector de valores con el agregado de que todos ellos suman uno. Esto contribuye al objetivo de encontrar distribuciones de probabilidad de las clases analizadas para un punto de datos determinado. El componente logarítmico penaliza más severamente los pronósticos confiables pero incorrectos que los menos confiables, y esto se debe principalmente a la práctica de la codificación one-hot. Los valores objetivo o verdaderos siempre se normalizan de modo que solo la clase correcta recibe una ponderación completa (que normalmente es 1,0) y a todo lo demás se le asigna un cero. CCE proporciona gradientes suaves durante la optimización y alienta a los modelos a confiar en sus pronósticos debido al efecto penalizador mencionado anteriormente sobre los pronósticos incorrectos. Al entrenar con poblaciones desequilibradas en distintas clases, se pueden implementar ajustes de ponderación para nivelar el campo de juego. Sin embargo, existe el peligro de sobreajuste cuando se presentan demasiadas clases, por lo que se deben tomar precauciones al determinar la cantidad de clases que un modelo debe evaluar.

A continuación se muestra la entropía cruzada binaria (Binary Cross Entropy, BCE) que puede considerarse un primo del CCE mencionado anteriormente. También cuantifica la brecha entre el pronóstico y el objetivo en configuraciones de 2 clases, a diferencia de CCE que es más adecuado para manejar múltiples clases. Su salida está limitada en un rango de 0,0 a 1,0 y está guiada por la siguiente fórmula:

Donde:

• 'N' como en otras funciones de pérdida anteriores es el tamaño de la muestra
• 'y' es el valor predicho
• 'p' es la predicción
• y 'log' es el logaritmo natural

En la jerga de BCE, las dos clases consideradas suelen denominarse clase positiva y clase negativa. Entonces, en esencia, la salida BCE siempre se entiende como una fuente de probabilidad en la medida en que un punto de datos esté en la clase positiva y este valor esté en el rango de 0,0 a 1,0 con una función de activación emparejable adecuada que es la función sigmoidea dura. La salida vectorial de las funciones de activación MQL5 integradas en el tipo de datos vectorial genera un vector que debe incluir 2 probabilidades para la clase positiva y la clase negativa.

La divergencia de Kullback-Leibler es otro algoritmo de función de pérdida interesante, similar a los métodos de brecha vectorial que hemos visto anteriormente. Su fórmula viene dada por:

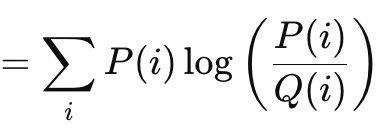
Donde:

• 'P' es la probabilidad que se pronostica
• 'Q' es la probabilidad real

Sus salidas van desde 0, que indicaría que no hay divergencia, hasta infinito. Estos valores sólo positivos son un claro indicador de lo lejos que está una previsión de la "verdad". Como se muestra en la fórmula anterior, la suma sólo es relevante cuando se apunta a una salida escalar. La implementación vectorial incorporada de esto en MQL5 proporciona una salida vectorial que es más adecuada y necesaria en el cálculo de deltas y eventualmente gradientes al realizar propagaciones hacia atrás. La divergencia de Kullback-Liebler se fundamenta en la teoría de la información y ha encontrado algunas aplicaciones en el aprendizaje por refuerzo, dada su destreza, así como en los autocodificadores variacionales. Sus contras son la asimetría, la sensibilidad a los valores cero y las dificultades de interpretación, dada la naturaleza no consolidada de sus resultados. La sensibilidad cero es importante porque si a una clase se le da una probabilidad de cero, la otra tiene automáticamente un valor infinito, pero la asimetría no sólo dificulta la interpretación adecuada de la probabilidad dada, sino que dificulta el aprendizaje por transferencia. (La probabilidad de P dada K no es inversa a la de K dada P). La suma de las probabilidades de avance y retroceso no es un valor predefinido. A veces es infinito, a veces no.

Esto nos lleva a la similitud del coseno, que a diferencia de las medidas de brecha vectorial que hemos visto hasta ahora, sí tiene en cuenta la dirección. Su fórmula se da como sigue:

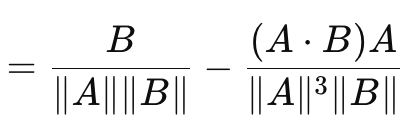
Donde:

• A.B es el producto escalar de dos vectores
• ||A|| y ||B|| son sus magnitudes o normas

La fórmula anterior es para el gradiente de pérdida con respecto al vector A. La fórmula con respecto al vector B es una fórmula inversa separada y cuando se suma al coseno de A a B no da como resultado una constante fija o arbitraria. Para este fin, la similitud del coseno no es una métrica verdadera ya que no satisface el triángulo de desigualdad. (La similitud del coseno de A con B más la similitud del coseno de B con C no siempre es mayor o igual que la similitud del coseno de A con C). Sus ventajas son la invariancia de escala ya que el valor que proporciona es independiente de la magnitud de los vectores en cuestión, lo que puede ser importante cuando lo importante es la dirección y no la magnitud. Además, requiere menos esfuerzo computacional que otros métodos, lo que es una consideración clave cuando se trabaja con redes muy profundas o transformadores o ambos. Se ha encontrado una gran aplicabilidad para datos de alta dimensión, como incrustaciones de texto de modelos de lenguaje grandes, donde la dirección inferida (¿significado?) es una métrica más relevante que las magnitudes individuales de cada valor vectorial. Sus desventajas son que no es adecuado para todas las tareas, especialmente en situaciones donde la magnitud de los vectores durante el entrenamiento es importante. Además, en el caso de que uno de los vectores tenga una norma de cero (donde todos los valores son cero) entonces la similitud del coseno sería indefinida. Finalmente, ya se menciona la incapacidad de ser una métrica por no cumplir la regla del triángulo de desigualdad. Los ejemplos de casos en los que esto es crucial pueden ser un poco complicados, pero incluyen: aprendizaje profundo geométrico, redes neuronales basadas en gráficos y pérdida contrastiva de redes siamesas. En cada uno de estos casos de uso, la magnitud es más importante que la dirección. Sin embargo, al aplicar la similitud del coseno en MQL5, es importante tener en cuenta que lo que se utiliza y se devuelve es la proximidad del coseno, ya que es más pertinente para el aprendizaje automático. Es la distancia equivalente al coseno del ángulo, y se obtiene restando la semejanza del coseno a uno.

La función de pérdidas de regresión de Poisson es adecuada para modelar datos contables o discretos. Es como si las funciones de pérdida mencionadas anteriormente se implementaran a través de las funciones integradas del tipo de datos vectorial. Su fórmula viene dada por:

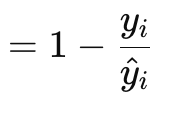
Donde:

• 'y' es el valor del vector de destino (en el índice 'i')
• 'y^' es el valor pronosticado

Los valores de gradiente se devuelven en formato vectorial porque esto facilita mucho el proceso de retropropagación. También son derivadas de primer orden de la fórmula escalar de retorno de la función Poisson original, que es:

Donde:

• Representaciones mucho más precisas que la fórmula del gradiente.

El tipo de datos discretos que los comerciantes podrían alimentar a una red neuronal en este caso podría incluir tipos de velas de barras de precios, o si las barras anteriores son alcistas, bajistas o planas. Sin embargo, sus casos de uso cubren escenarios de conteo de datos, por lo que, por ejemplo, una red neuronal que toma varios patrones de barras de precios de velas que serían del historial reciente podría entrenarse para devolver la cantidad de un tipo de vela específico que debería esperarse de una muestra estándar de, digamos, 10 barras de precios futuras. Sus coeficientes son fáciles de interpretar ya que son razones de tasa logarítmica, y se alinean bien con la regresión de Poisson, lo que significa que el análisis posterior al entrenamiento se puede realizar fácilmente con la regresión de Poisson. También garantiza que los pronósticos de recuento sean siempre positivos (no negativos). No es así, por lo que entre los rasgos positivos se incluye la suposición de varianza, en la que siempre se supone que la media y la varianza tienen valores iguales o casi similares. Si claramente este no es el caso, entonces la función de pérdida no funcionará bien. Es sensible a valores atípicos, especialmente aquellos con recuentos altos en los datos de entrada; el uso del logaritmo natural presenta el potencial de producir NaN o resultados no válidos. Además, su aplicación está restringida a datos contables positivos, lo que significa que no se utilizaría en casos en que son necesarios pronósticos negativos continuos, como cuando se pronostican cambios de precios.

La función de pérdida de Huber concluye nuestra muestra de lo que MQL5 tiene para ofrecer dentro del tipo de datos vectoriales. Existen otras funciones de pérdida que no hemos analizado, como el logaritmo del coseno hiperbólico, la bisagra categórica, la bisagra cuadrática, la bisagra estándar, el error cuadrático medio logarítmico y el error porcentual absoluto medio. No son fundamentales para determinar si una red neuronal es un regresor o un clasificador, lo que forma parte de nuestro objetivo, por lo que las omitimos. La pérdida de Huber, sin embargo, viene dada por la fórmula:

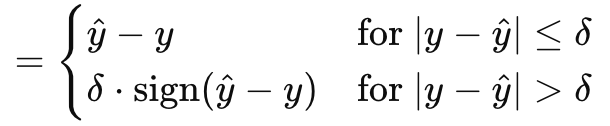
Donde:

• 'y^' es el valor pronosticado
• 'y' es el objetivo
• Delta es un valor de entrada de pérdida en el que la relación cambia de lineal a cuadrática.

El gradiente, al igual que la pérdida de Huber original, puede calcularse de dos maneras, dependiendo de cómo se compare el valor real o el valor objetivo con la previsión. Se trata de una función en parte lineal y en parte cuadrática que es una cartografía de la diferencia entre los valores objetivo y los valores previstos a medida que se ajustan los parámetros de entrada. Es predominante con la regresión robusta, ya que combina lo mejor de MAE y MSE y es menos sensible a valores atípicos a la vez que más estable que MAE para errores pequeños. Al ser totalmente diferenciable, es ideal para el descenso de gradientes y es adaptable gracias al delta, donde un delta más pequeño lo hace actuar como MAE mientras que un delta más grande lo hace actuar más como MSE. Esto permite controlar el equilibrio entre robustez y sensibilidad. Sin embargo, en el lado negativo, la pérdida de Huber es relativamente más compleja, no solo porque su fórmula es fragmentaria (como se muestra arriba), sino que el cálculo y la determinación del delta ideal suelen ser un ejercicio oneroso. Con este fin, la implementación en MQL5, que creo que se basa en una biblioteca de matrices y vectores estándar a la que no he hecho referencia, no revela cómo se calcula su valor delta para las funciones integradas de pérdida de Huber y gradiente de pérdida de Huber. Aunque se puede combinar con una variedad de funciones de activación, a menudo se recomienda la activación lineal como la más adecuada.

Funciones de pérdida para modelos de regresión

Entonces, ¿cuál de estos algoritmos de pérdida sería el más adecuado para las redes de regresión? La respuesta, MSE, MAE y Huber. Aquí está el por qué. Las redes de regresión se caracterizan por su objetivo de pronosticar valores numéricos continuos en lugar de etiquetas categóricas o datos discretos. Esto implica que la capa de salida de estas redes generalmente produce números de valor real que pueden abarcar un amplio rango. La naturaleza de las tareas de regresión requiere minimizar la necesidad de medir desviaciones de amplio alcance entre los valores predichos y los verdaderos, en su optimización, a diferencia de las redes de clasificación donde los resultados que deben enumerarse son a menudo pocos y conocidos en número de antemano.

Esto nos lleva entonces a MSE. Como se observó anteriormente, tiene grandes penalizaciones cuadráticas para errores grandes, lo que implica desde el principio que guía el descenso del gradiente y la optimización hacia desviaciones más estrechas, lo cual es importante para que las redes de regresión funcionen de manera eficiente. Además, la suavidad y facilidad de diferenciación lo convierten en una opción natural para los datos continuos manejados por redes de regresión.

Las redes de regresión también son muy susceptibles a los valores atípicos, por lo que se necesita una función de pérdida que sea un poco robusta para manejarlos. Ahí es donde entra MAE. A diferencia de MSE, que impone penalizaciones cuadráticas a sus errores, MAE impone penalizaciones lineales y esto lo hace menos sensible a los valores atípicos en comparación con MSE. Además, su medida de error es un error promedio robusto, que puede ser útil en datos ruidosos.

Por último, se argumenta que las redes de regresión, además de lo mencionado anteriormente, necesitan un mecanismo de equilibrio o compensación entre la sensibilidad a pequeños errores y la robustez. Estas son dos propiedades que proporciona la función de pérdida de Huber y, además, ofrecen suavidad que ayuda en la diferenciación durante todo el proceso de optimización.

Con las tres funciones de pérdida "ideales" a cero, ¿cuál sería la paleta ideal de funciones de activación a tener en cuenta al utilizarlas en una red de regresión? Oficialmente, las recomendaciones son para la activación lineal y la activación de identidad, siendo esta última la que implica que las salidas de la red se conservan en su magnitud con el fin de capturar la mayor parte posible de la variabilidad de los datos. Los principales argumentos a favor de estas dos son que la naturaleza no ligada de sus resultados garantiza que no haya pérdida de datos a través de los procesos de alimentación y entrenamiento de la red. Personalmente, soy partidario de los resultados acotados, por lo que preferiría optar por Soft-Sign y TANH, ya que capturan tanto números reales negativos como positivos, pero están acotados de -1,0 a +1,0. Creo que las salidas acotadas son importantes porque evitan los problemas de explosión y gradientes evanescentes durante la retropropagación, que son una fuente importante de quebraderos de cabeza.

Funciones de pérdida para modelos de clasificación

¿Y las redes neuronales de clasificación? ¿Cómo sería la elección de las funciones de pérdida y activación? El proceso de elección no difiere mucho: nos fijamos esencialmente en las características clave de la red, que guían nuestra elección.

Las redes de clasificación están pensadas para pronosticar etiquetas de clase discretas a partir de un conjunto de posibles categorías predefinidas. Estas redes emiten probabilidades que indican la probabilidad de cada clase, con el objetivo principal de maximizar la precisión de estas predicciones mediante la minimización de la pérdida. Por tanto, la elección de la función de pérdida desempeña un papel clave en el entrenamiento de la red para distinguir e identificar las clases. Basándonos en estas características clave, el consenso es para la entropía cruzada categórica y la entropía cruzada binaria como las dos funciones de pérdida clave más adecuadas para las redes de clasificación de la enumeración proporcionada por MQL5.

BCE (Binary Cross Entropy) clasifica a partir de dos categorías posibles, pero el número de predicciones que hay que hacer puede ser a menudo superior a dos y el tamaño de este lote determina la norma del vector gradiente. Así, el valor en cada índice del vector gradiente sería una derivada parcial de la función de pérdida BCE como se ha destacado anteriormente en la fórmula compartida y estos valores se utilizarían en la retropropagación. Sin embargo, los valores de salida de la red serían probabilidades a la clase positiva como se mencionó anteriormente, y serían para cada valor proyectado en el vector de salida.

La BCE es adecuada para las redes de clasificación porque las probabilidades son fácilmente interpretables, ya que apuntan a la clase positiva. Es sensible a las distintas probabilidades de cada valor de salida, ya que se centra en maximizar la log-verosimilitud de las clases correctas del lote. Dado que puede diferenciarse no como una constante, sino como una variable, esto facilita enormemente un cálculo suave y eficiente del gradiente en la retropropagación.

La CCE (Categorical Cross Entropy) amplía la BCE (Binary Cross Entropy) al permitir clasificar más de 2 categorías, y la norma o tamaño del vector de salida es siempre el número de clases para las que se da una probabilidad para cada una. A diferencia de la BCE, en la que podríamos hacer previsiones de hasta 5 valores y todos los valores de cada uno son verdaderos o falsos. Con CCE, el tamaño de salida lleva un prefijo que coincide con el número de clase. La codificación en caliente, como ya se ha mencionado, es útil para normalizar los vectores objetivo antes de medir los desfases con respecto a la previsión.

La forma ideal de activación para emparejar con esto, se deduce, sería cualquier función que outbounds en el rango de 0,0 a +1,0. Esto incluye Soft-Max, Sigmoide y Sigmoide Duro.

Pruebas

Por tanto, realizamos 2 conjuntos de pruebas, uno para un MLP regresivo y otro para un clasificador. El propósito de esta prueba es demostrar la implementación en formato MQL5 y el Expert Advisor (EA) con las ideas de función de pérdida y activación analizadas en este artículo. Estos resultados de prueba presentados no son una justificación para implementar y usar el código adjunto en cuentas reales, sino una invitación al lector a realizar su propia diligencia probando con datos reales de su bróker durante períodos prolongados, si considera adecuado el(los) sistema(s) de trading. El despliegue en entornos reales, como siempre, sólo debería ser ideal después de haber realizado una validación cruzada o pruebas de avance que arrojen resultados satisfactorios.

Por lo tanto, vamos a probar GBPCHF en el marco de tiempo diario durante el último año, 2023. Para obtener una red regresiva haremos referencia a la clase 'Cmlp' que introdujimos en el último artículo y como nuestros datos de entrada serán porcentajes de cambio de precio (no puntos) podemos probar con la activación TANH y la función de pérdida de Huber para ver cómo de negociable podría ser nuestro sistema. Las condiciones personalizadas de señal larga y corta se implementan en MQL5 de la siguiente manera:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalRegr::LongCondition(void)
{  int result = 0;
   vector _out;
   GetOutput(_out);
   m_close.Refresh(-1);
   if(_out[0] > 0.0)
   {  result = int(round(100.0*(fabs(_out[0])/(fabs(_out[0])+fabs(m_close.GetData(StartIndex()) - m_close.GetData(StartIndex()+1))))));
   }
//printf(__FUNCSIG__ + " output is: %.5f,  and result is: %i", _out[0],  result);return(0);
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalRegr::ShortCondition(void)
{  int result = 0;
   vector _out;
   GetOutput(_out);
   m_close.Refresh(-1);
   if(_out[0] < 0.0)
   {  result = int(round(100.0*(fabs(_out[0])/(fabs(_out[0])+fabs(m_close.GetData(StartIndex()) - m_close.GetData(StartIndex()+1))))));
   }
//printf(__FUNCSIG__ + " output is: %.5f,  and result is: %i", _out[0],  result);return(0);
   return(result);
}

También realizamos pruebas simultáneas del Experto en datos históricos con el entrenamiento de la red, ambos en cada nueva barra de precios. Se trata de otra decisión clave que puede modificarse fácilmente y en la que el entrenamiento se realiza una vez cada 6 meses u otro periodo más largo predeterminado para evitar el sobreajuste de la red a la acción a corto plazo. Esta red regresora tiene un tamaño de 3 capas 4-7-1 (donde los números representan el tamaño de las capas), lo que implica que 4 cambios de precios recientes sirven de entrada y la única salida es el siguiente cambio de precios.

La realización de pruebas en GBPCHF para el año 2023 en el diario nos da el siguiente informe:

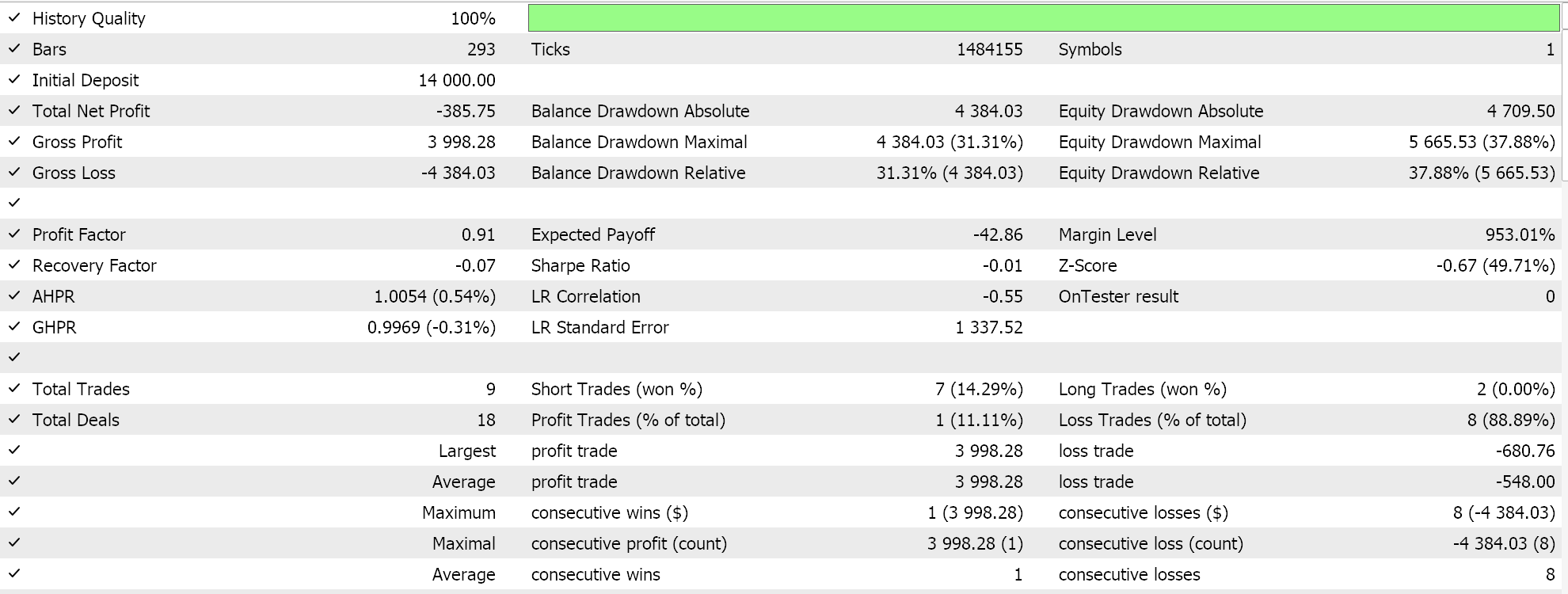
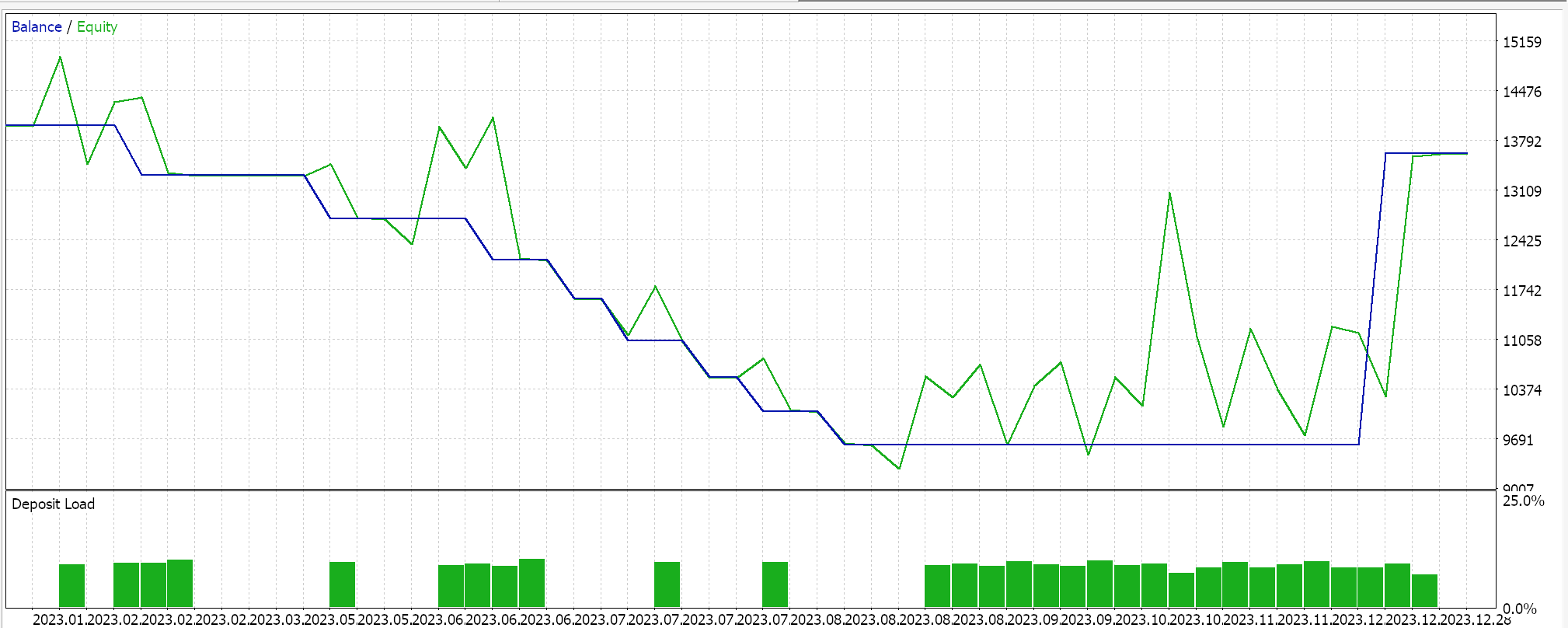
Para la red clasificadora seguimos utilizando la clase 'Cmlp' como base y nuestros datos de entrada serán las clasificaciones de los últimos 3 puntos de precio. Esto alimentará una red MLP simple 3-6-3, también de sólo 3 capas, en la que, dado que estamos considerando 3 posibles clasificaciones y nuestra función de pérdida es CCE, la capa de salida final también debe tener un tamaño de 3 para que sirva como distribución de probabilidad. La generación de condiciones largas y cortas se implementa en MQL5 de la siguiente manera:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalClas::LongCondition(void)
{  int result = 0;
   vector _out;
   GetOutput(_out);
   m_close.Refresh(-1);
   if(_out[2] > _out[1] && _out[2] > _out[0])
   {  result = int(round(100.0 * _out[2]));
   }
//printf(__FUNCSIG__ + " output is: %.5f,  and result is: %i", _out[2],  result);return(0);
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalClas::ShortCondition(void)
{  int result = 0;
   vector _out;
   GetOutput(_out);
   m_close.Refresh(-1);
   if(_out[0] > _out[1] && _out[0] > _out[2])
   {  result = int(round(100.0 * _out[0]));
   }
//printf(__FUNCSIG__ + " output is: %.5f,  and result is: %i", _out[0],  result);return(0);
   return(result);
}

Ejecuciones de pruebas similares para el Asesor Experto del clasificador nos arrojan los siguientes resultados:

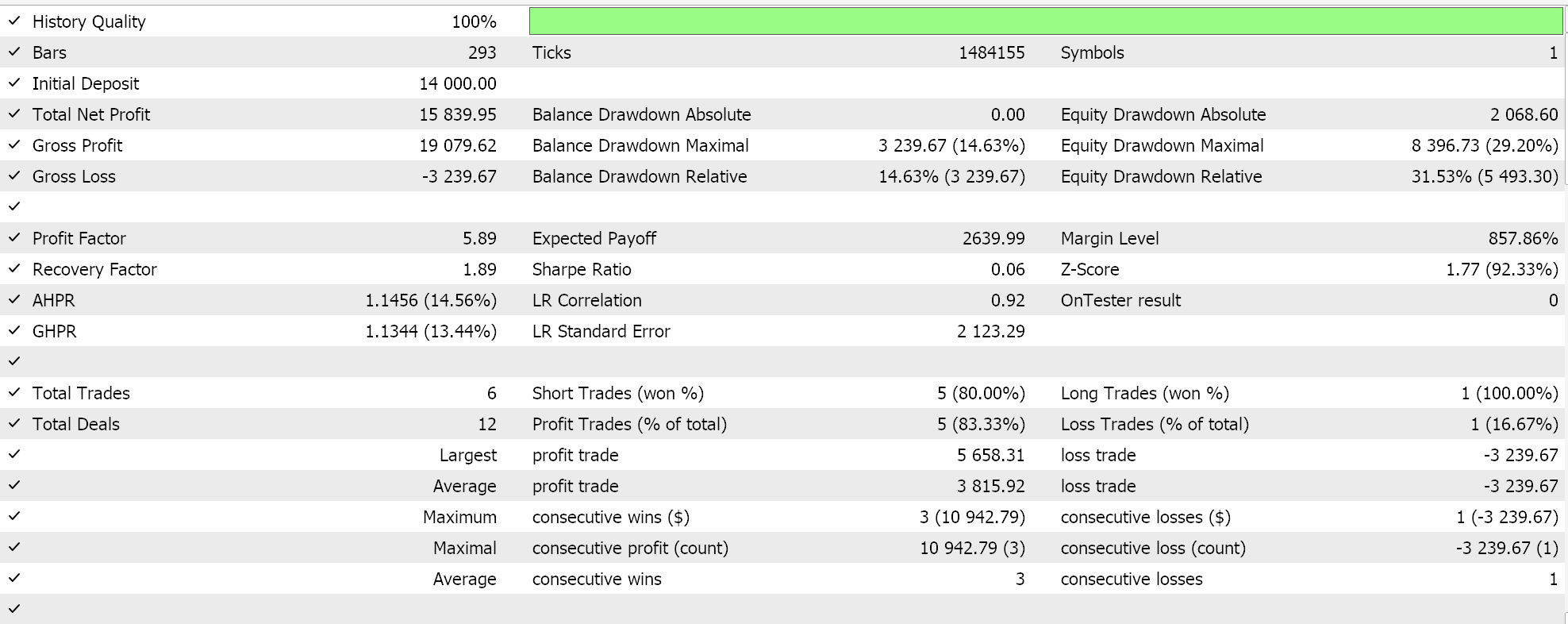
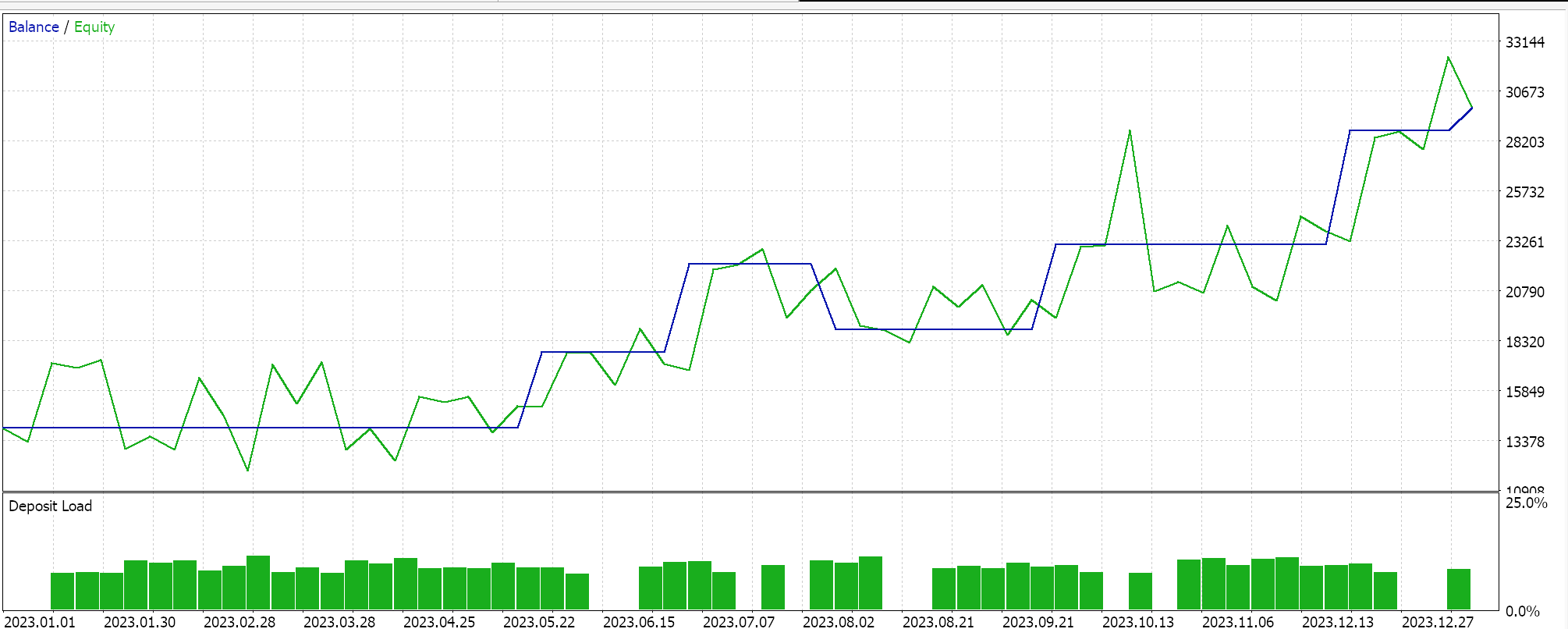
El código adjunto se utiliza a través del ensamblaje del asistente para generar Asesores Expertos, para lo cual existen las guías aquí y aquí.

Conclusión

En resumen, hemos recorrido el itinerario de posibles funciones de pérdida disponibles en MQL5 a la hora de desarrollar algoritmos de aprendizaje automático como las redes neuronales. Hay una lista muy larga que, irónicamente, ni siquiera es exhaustiva, sin embargo, hemos hecho hincapié en algunas claves que funcionan bien con determinadas funciones de activación que hemos cubierto en artículos anteriores, haciendo hincapié en evitar la explosión / gradientes de fuga y la eficiencia. Muchas de las funciones de pérdida disponibles no serían necesariamente adecuadas para las redes típicas de regresión y clasificación, no sólo porque sus resultados no están vinculados, sino porque no abordan los requisitos característicos clave de estas redes, como hemos destacado, razón por la cual las funciones de pérdida consideradas fueron un número menor de las disponibles.