Integrating Hidden Markov Models in MetaTrader 5

Introduction

It is well known that one of the fundamental characteristics of financial time series is that they exhibit memory. In the context of time series analysis, memory refers to the dependency structure within data, where past values influence current and future values. Understanding the memory structure helps in choosing the appropriate model for the time series. In this article, we discuss a different kind of memory: the type that takes the form of a Hidden Markov Model (HMM). We will explore the fundamentals of HMMs and demonstrate how to build an HMM using Python's hmmlearn module. Finally, we will present code in Python and MQL5 that enables the export of HMMs for use in MetaTrader 5 programs.

Understanding Hidden Markov Models

Hidden Markov Models are a powerful statistical tool used for modeling time series data, where the system being modeled is characterized by unobservable (hidden) states. A fundamental premise of HMMs is that the probability of being in a given state at a particular time depends on the process's state at the previous time slot. This dependence represents the memory of an HMM.

In the context of financial time series, the states could represent whether a series is trending upwards, trending downwards, or oscillating within a specific range. Anyone who has used any financial indicator is familiar with the whipsaw effect caused by the noise inherent in financial time series. An HMM can be employed to filter out these false signals, providing a clearer understanding of the underlying trends.

To build a HMM, we need observations that capture the totality of the behaviour defining the process. This sample of data is used to learn the parameters of the appropriate HMM. This dataset would be made up of various features of the process being modeled. For example, if we were studying the close prices of a financial asset, we could also include other aspects related to the close price, like various indicators that ideally, help in defining the hidden states we are interested in.

The process of learning the model parameters is carried out under the assumption that the series being modeled will always be in one of two or more states. The states are simply labeled 0 to S-1. For these states, we must assign a set of probabilities that capture the likelihood of the process switching from one state to another. These probabilities are usually referred to as the transition matrix. The first observation has a special set of initial probabilities for being in each possible state. If an observation is in a particular state, it is expected to follow a specific distribution associated with that state.

An HMM is therefore fully defined by four properties:

• The number of states to assume
• The initial probabilities for the first observation being in any one of the states
• The transition matrix of probabilities
• The probability density functions for each state.
  

At the beginning, we have the observations and the assumed number of states. We want to find the parameters of an HMM that fit the dataset before us. This is done by observing likelihood using a statistical technique called maximum likelihood estimation. In this context, maximum likelihood estimation is the process of searching for the model properties that most likely correspond to our data samples. This is achieved by calculating the likelihood of each sample being in a particular state at a specific time. This is done using the forward and backward algorithms, which traverse through all samples, forwards and backwards in time, respectively.

The forward algorithm

We start with the first observation in our dataset before calculating likelihoods for subsequent samples. For the first sample, we use the initial state probabilities, which, at this time, are considered to be trial parameters for a candidate HMM. If nothing is known about the process being modeled, it is perfectly acceptable to set all the initial state probabilities to 1/S, where S represents the total number of assumed states. Applying Bayes Theorem we have the following general equation:

Where "lk" is the likelihood of a sample at time "t" being in state  "i" , and   "p"  is the probability of being in state  "i"  at time  "t"  given the samples up until time  "t" . "O" is an individual sample, a single row in the dataset.

The likelihood of the first sample is calculated according to the conditional probability rule,  P(A) = P(A|B)P(B). Therefore, for the first sample, the likelihood of being in state i is computed by multiplying the initial state probability for being in state i with the probability density function of the first sample.

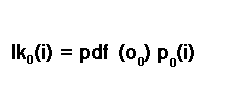
This is another trial parameter of the candidate HMM. In literature, it is sometimes referred to as an emission probability. We will go into more detail about emission probabilities later in the text. For now, just be aware that it is another trial parameter at this stage.We must not forget that we are not certain of the state we are in. We have to account for the possibility that we could be in any one of all possible states. This results in the final initial likelihood being the summation of all likelihoods of all possible states.

 

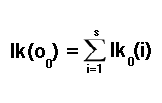
To calculate the likelihoods for subsequent observations, we have to consider the possibility of transitioning to a particular state from any one of the possible states in the previous time slot. This is where transition probabilities come into effect, which is another trial parameter at this point. The probability of arriving at a specific state in the next time slot, given that we have calculated the probability for the current time slot, is estimated by multiplying the currently known state probability with the corresponding transition probability.

This is as good a time as any to talk about transition probabilities or the transition matrix.

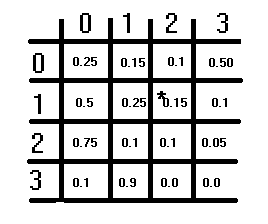
The illustration above shows a hypothetical transition matrix. It has an S×S structure, with S being the number of assumed states. Each element represents a probability, and the probabilities in each row should sum up to 1. This condition does not apply to the columns. To obtain the corresponding transition probability for switching from one state to another, you refer to the rows first and then the columns. The current state being switched from corresponds to the row index, and the state being switched to corresponds to the column index. The value at these indices is the corresponding transition probability. The diagonal of the matrix depicts the probabilities of the state not changing.

Returning to the task of calculating likelihoods for the rest of the observations in our chosen data sample, we were multiplying a state probability with a transition probability. However, to get the full picture, we must consider the possibility of transitioning to any one of all possible states. We do this by adding up all the possibilities, in accordance with the following equation:

            

This concludes the calculation of individual likelihoods for each sample in our dataset. These individual likelihoods can be combined through multiplication to obtain the likelihood for the entire dataset. The computation just described is called the forward algorithm, due to the method's temporal forward recursion. This is in contrast to the backward algorithm, which we will discuss in the next section.

The backward algorithm

It is also possible to calculate the individual likelihoods moving backwards in time, starting from the last data sample to the first. We begin by setting the likelihood for all states to 1 for the last data sample. For each data sample, if in a specific state, we calculate the likelihood of the subsequent set of samples, considering that we can transition to any of the states. We do this by computing the weighted sum of the likelihoods of each state: the probability of being in that state multiplied by the probability density function of the sample being in the same state. The result of this calculation is then adjusted by using the probability of transitioning from the current state to the next as a weighting factor. This is all encapsulated in the formula below:

The probability density functions

In the discussions about the forward and backward algorithms, there was mention of probability density functions (pdf) as parameters of an HMM. A question then arises: What distribution are we assuming? As previously mentioned, the pdf parameters of an HMM are usually called the emission probabilities. They are referred to as probabilities when the data being modeled consists of discrete or categorical values. When dealing with continuous variables, we use the pdf.

In this text, we demonstrate HMMs that model datasets of continuous variables following a multivariate normal distribution. It is possible to implement other distributions; in fact, the Python module we will look at later on has HMM implementations for different distributions of the data being modeled. By extension, the parameters of the assumed distribution become one of the parameters of the HMM. In the case of the multivariate normal distribution, its parameters are the means and covariances.

The Baum-Welch algorithm

The Baum-Welch algorithm is an expectation-maximization technique used to trial different parameters for candidate HMMs to arrive at the optimal one. The value being maximized in this optimization procedure is the likelihood for the entire dataset of samples. The Baum-Welch algorithm is known for being efficient and dependable, but it does have its flaws. One glaring drawback is its non-convex nature. Non-convex functions in relation to optimization are functions with numerous local minima or maxima.

This means that when convergence is achieved, the global maximum or minimum of the parameter space may not have been found. The function is basically not guaranteed to converge at the optimal point. The best way to mitigate this flaw is to trial parameters that have a large likelihood compared to others in the parameter space. To do so, we would have to trial numerous random parameter values to find the best initial parameter space to start the optimization process from.

Calculating state probabilities

Once we have the optimal HMM and its parameters, we can use it to calculate the state probabilities for unseen data samples. The result of such a calculation would be a set of probabilities, one for each state, indicating the probability of being in each state. The individual likelihoods from the forward algorithm are multiplied by the likelihoods from the backward algorithm, resulting in the likelihood of a particular state. According to Bayes rule, the probability that an observation is in a particular state, is calculated as :

Calculating State Probabilities Using the Viterbi Algorithm

As well as the state probabilities, we can also infer the likely state an observation is in by using the Viterbi algorithm. The calculation starts from the first observation, whose state probabilities are calculated using the initial state probabilities multiplied by the emission probabilities.

For each observation from the second to the last, each state probability is calculated using the previous state probability, the corresponding transition probability, and its emission probability. The most probable state will be the one with the highest probability.

We have looked at all the components of a Hidden Markov Model. We now delve into its practical implementation. We begin by looking at a Python-based implementation of HMMs provided in the hmmlearn package. We will discuss the use of hmmlearn's Gaussian HMM implementation before switching to MQL5 code to demonstrate how to integrate a model trained in Python using hmmlearn into MetaTrader 5 applications.

Python's hmmlearn package

The hmmlearn library in Python provides tools for working with hidden Markov models. The tools for training HMMs are found in the `hmm` namespace. Within `hmm`, several special classes are declared for working with processes of different distributions. Namely:

• MultinomialHMM: Models HMMs where the observations are discrete and follow a multinomial distribution
• GMMHMM: Models HMMs where the observations are generated from a mixture of Gaussian distributions
• PoissonHMM: Models HMMs where the observations are assumed to follow a Poisson distribution
• Lastly, we have the GaussianHMM class that handles datasets that tend to follow a multivariate Gaussian (normal) distribution. This is the class we will demonstrate and whose resulting model we will link with MetaTrader 5.

To install the package, you can use the following command:

pip install hmmlearn

After installing the package, you can import the `GaussianHMM` class using the following import statement:

from hmmlearn.hmm import GaussianHMM

Alternatively, you can import the `hmm` module, which contains all the classes listed above along with other useful utilities. If this method is used, then class names have to be prefixed by `hmm`, like so:

from hmmlearn import hmm

You can initialize a GaussianHMM object with several parameters:

model = GaussianHMM(n_components=3, covariance_type='diag', n_iter=100, tol=0.01)

where:

• "n_components": Number of states in the model
• "covariance_type": Type of covariance parameters to use ('spherical', 'diag', 'full', 'tied'). The covariance type used relates to the features of the dataset. A spherical covariance should be chosen if the features or variables in the dataset being modeled have similar variance with no possibility of being correlated. Otherwise, if the variables have contrasting variances, the best option is to choose a diagonal covariance type. If the variables are correlated, then either a full or tied covariance type should be chosen. Selecting full covariance provides the most flexibility but can also be computationally expensive. It's the safest choice that limits the number of assumptions made about the process being modeled. Tied covariance makes the additional assumption that states share a similar covariance structure. It's a little more efficient relative to full covariance
• "n_iter": Maximum number of iterations to perform during training
• "tol": Convergence threshold.

To explore all the parameters that specify a model, you can refer to the documentation for the hmmlearn library. This documentation provides detailed information on the various parameters and their usage. You can access it online at the hmmlearn library's official website or through the documentation included with the library's installation, through Python's built in help utility.

help(GaussianHMM)

To train a model, we call the "fit()" method. It expects at least one 2-dimensional array as input.

model.fit(data)

After training is completed, we can get the hidden states of a dataset by calling either "predict()" or "decode()". Both expect a 2-dimensional array with the same number of features as the dataset used to train the model. The "predict()" method returns an array of calculated hidden states, while "decode()" returns the log likelihood in conjunction with the array of hidden states enclosed in a tuple.

Calling "score_samples()" returns the log likelihood as well as the state probabilities for the dataset provided as input. Again, the data should have the same number of features as the data used to train the model.

Exporting a hidden Markov model

Exporting a model trained in Python using the hmmlearn package for use in MetaTrader 5 involves implementing two custom components:

• Python Component: This component is responsible for saving the parameters of a trained model in a format readable from a MetaTrader application. It involves exporting the model parameters to a file format that can be parsed by MetaTrader 5 applications
• MQL5 Component: The MQL5 component comprises code written in MQL5. This component should include functionality to read the HMM parameters exported by the Python component. Additionally, it needs to implement the forward, backward, and Viterbi algorithms to calculate the hidden states and state probabilities for a dataset based on a specified HMM.
  

Implementing these components involves careful consideration of data serialization formats, file input and output operations, and algorithmic implementations in both Python and MQL5. It's essential to ensure compatibility between the Python and MQL5 implementations to accurately transfer the trained model and perform inference tasks in MetaTrader 5.

The hmmlearn package provides the ability to save a trained HMM using the pickle module. The problem is that pickled files are not easy to work with outside of Python. So, a better option would be to use the json format. The HMM parameter will be written to a structured JSON file that can be read using MQL5 code. This functionality is implemented in the Python function below.

def hmm2json(hmm_model, filename):
    """
    function save a GaussianHMM model to json format 
    readable from MQL5 code.
    param: hmm_model should an instance of GaussianHMM
    param: string. filename or path to file where HMM 
    parameters will be written to
    """
    if hmm_model.__class__.__name__ != 'GaussianHMM':
        raise TypeError(f'invalid type supplied')
    if len(filename) < 1 or not isinstance(filename,str):
        raise TypeError(f'invalid filename supplied')
    jm  = {
            "numstates":hmm_model.n_components,
            "numvars":hmm_model.n_features,
            "algorithm":str(hmm_model.algorithm),
            "implementation":str(hmm_model.implementation), 
            "initprobs":hmm_model.startprob_.tolist(),
            "means":hmm_model.means_.tolist(),
            "transitions":hmm_model.transmat_.tolist(),
            "covars":hmm_model.covars_.tolist()
          }
    with open(filename,'w') as file:
        json.dump(jm,file,indent=None,separators=(',', ':')) 
    return 

This function takes an instance of the GaussianHMM class and a file name as input, and it writes the HMM parameters to a JSON file in a structured format that can be read using MQL5 code.

In the MQL5 code, the functionality for reading HMM models saved in JSON format is enclosed in hmmlearn.mqh. The file includes the definition of the HMM class.

//+------------------------------------------------------------------+
//|                                                     hmmlearn.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<Math\Alglib\dataanalysis.mqh>
#include<Math\Stat\Uniform.mqh>
#include<Math\Stat\Math.mqh>
#include<JAson.mqh>
#include<Files/FileTxt.mqh>
#include<np.mqh>

//+------------------------------------------------------------------+
//|Markov model estimation method                                    |
//+------------------------------------------------------------------+
enum ENUM_HMM_METHOD
  {
   MODE_LOG=0,
   MODE_SCALING
  };
//+------------------------------------------------------------------+
//| state sequence decoding algorithm                                |
//+------------------------------------------------------------------+
enum ENUM_DECODE_METHOD
  {
   MODE_VITERBI=0,
   MODE_MAP
  };
//+------------------------------------------------------------------+
//| Hidden Markov Model class                                        |
//+------------------------------------------------------------------+
class HMM
  {
private:
   ulong m_samples ;       // Number of cases in dataset
   ulong m_vars ;        // Number of variables in each case
   ulong m_states ;      // Number of states
   vector            m_initprobs;   // vector of probability that first case is in each state
   matrix            m_transition;  // probability matrix
   matrix m_means ;                 //state means
   matrix m_covars[] ;              // covariances
   matrix densities ;              // probability densities
   matrix alpha ;       // result of forward algorithm
   matrix beta ;        // result of backward algorithm
   matrix m_stateprobs ; // probabilities of state
   double likelihood ;  //  log likelihood
   matrix            trial_transition;
   bool              trained;
   double            m_mincovar;
   ENUM_HMM_METHOD   m_hmm_mode;
   ENUM_DECODE_METHOD m_decode_mode;
   //+------------------------------------------------------------------+
   //| normalize array so sum(exp(a)) == 1                              |
   //+------------------------------------------------------------------+
   matrix            log_normalize(matrix &in)
     {
      matrix out;
      if(in.Cols()==1)
         out = matrix::Zeros(in.Rows(), in.Cols());
      else
         out = logsumexp(in);
      return in-out;
     }
   //+------------------------------------------------------------------+
   //| log of the sum of exponentials of input elements                 |
   //+------------------------------------------------------------------+
   matrix            logsumexp(matrix &in)
     {
      matrix out;

      vector amax = in.Max(1);

      for(ulong i = 0; i<amax.Size(); i++)
         if(fpclassify(MathAbs(amax[i])) == FP_INFINITE)
            amax[i] = 0.0;

      matrix ama(amax.Size(),in.Cols());
      for(ulong i=0; i<ama.Cols();i++)
         ama.Col(amax,i);

      matrix tmp = exp(in - ama);

      vector s = tmp.Sum(1);

      out.Init(s.Size(),in.Cols());
      for(ulong i=0; i<out.Cols();i++)
         out.Col(log(s),i);

      out+=ama;

      return out;
     }

   //+------------------------------------------------------------------+
   //| normarlize vector                                                |
   //+------------------------------------------------------------------+
   vector            normalize_vector(vector &in)
     {
      double sum = in.Sum();
      return in/sum;
     }
   //+------------------------------------------------------------------+
   //|  normalize matrix                                                |
   //+------------------------------------------------------------------+
   matrix            normalize_matrix(matrix &in)
     {
      vector sum = in.Sum(1);

      for(ulong i = 0; i<sum.Size(); i++)
         if(sum[i] == 0.0)
            sum[i] = 1.0;

      matrix n;
      n.Init(sum.Size(), in.Cols());
      for(ulong i =0; i<n.Cols(); i++)
         n.Col(sum,i);

      return in/n;
     }
   //+------------------------------------------------------------------+
   //|   Set up model from JSON object                                  |
   //+------------------------------------------------------------------+
   bool              fromJSON(CJAVal &jsonmodel)
     {

      if(jsonmodel["implementation"].ToStr() == "log")
         m_hmm_mode = MODE_LOG;
      else
         m_hmm_mode = MODE_SCALING;

      if(jsonmodel["algorithm"].ToStr() == "Viterbi")
         m_decode_mode = MODE_VITERBI;
      else
         m_decode_mode = MODE_MAP;

      m_states = (ulong)jsonmodel["numstates"].ToInt();
      m_vars = (ulong)jsonmodel["numvars"].ToInt();


      if(!m_initprobs.Resize(m_states) || !m_means.Resize(m_states,m_vars) ||
         !m_transition.Resize(m_states,m_states) || ArrayResize(m_covars,int(m_states))!=int(m_states))
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }

      for(uint i = 0; i<m_covars.Size(); i++)
        {
         if(!m_covars[i].Resize(m_vars,m_vars))
           {
            Print(__FUNCTION__, " error ", GetLastError());
            return false;
           }

         for(int k = 0; k<int(m_covars[i].Rows()); k++)
            for(int j = 0; j<int(m_covars[i].Cols()); j++)
               m_covars[i][k][j] = jsonmodel["covars"][i][k][j].ToDbl();
        }

      for(int i =0; i<int(m_initprobs.Size()); i++)
        {
         m_initprobs[i] = jsonmodel["initprobs"][i].ToDbl();
        }

      for(int i=0; i<int(m_states); i++)
        {
         for(int j = 0; j<int(m_vars); j++)
            m_means[i][j] = jsonmodel["means"][i][j].ToDbl();
        }

      for(int i=0; i<int(m_states); i++)
        {
         for(int j = 0; j<int(m_states); j++)
            m_transition[i][j] = jsonmodel["transitions"][i][j].ToDbl();
        }

      return true;
     }

   //+------------------------------------------------------------------+
   //|  Multivariate Normal Density function                            |
   //+------------------------------------------------------------------+
   double            mv_normal(ulong nv,vector &x, vector &mean, matrix &in_covar)
     {
      matrix cv_chol;
      vector vc = x-mean;

      if(!in_covar.Cholesky(cv_chol))
        {
         matrix ncov = in_covar+(m_mincovar*matrix::Eye(nv,nv));
         if(!ncov.Cholesky(cv_chol))
           {
            Print(__FUNCTION__,": covars matrix might not be symmetric positive-definite, error ", GetLastError());
            return EMPTY_VALUE;
           }
        }

      double cv_log_det = 2.0 * (MathLog(cv_chol.Diag())).Sum();
      vector cv_sol = cv_chol.Solve(vc);

      return -0.5*((nv*log(2.0 * M_PI)) + (pow(cv_sol,2.0)).Sum() + cv_log_det);

     }


   //+------------------------------------------------------------------+
   //|logadd exp                                                        |
   //+------------------------------------------------------------------+
   double            logaddexp(double a, double b)
     {
      return a==-DBL_MIN?b:b==-DBL_MIN?a:MathMax(a,b)+log1p(exp(-1.0*MathAbs(b-a)));
     }
   //+------------------------------------------------------------------+
   //| scaled trans calculation                                         |
   //+------------------------------------------------------------------+
   matrix            compute_scaling_xi_sum(matrix &trans, matrix &dens,matrix &alf, matrix &bta)
     {
      matrix logdens = exp(dens).Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      matrix out;
      out.Resize(nc,nc);
      out.Fill(0.0);

      for(ulong t =0; t<ns-1; t++)
        {
         for(ulong i = 0; i<nc; i++)
           {
            for(ulong j = 0; j<nc; j++)
              {
               out[i][j] += alf[t][i] * trans[i][j] * logdens[t+1][j]*bta[t+1][j];
              }
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| log trans calculation                                            |
   //+------------------------------------------------------------------+
   matrix            compute_log_xi_sum(matrix &trans, matrix &dens,matrix &alf, matrix &bta)
     {
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      vector row = alf.Row(ns-1);
      double logprob = (log(exp(row-row[row.ArgMax()]).Sum()) + row[row.ArgMax()]);

      matrix out;
      out.Init(nc,nc);

      out.Fill(-DBL_MIN);

      for(ulong t = 0 ; t<ns-1; t++)
        {
         for(ulong i =0; i<nc; i++)
           {
            for(ulong j =0; j<nc; j++)
              {
               double vl = alf[t][i] + logtrans[i][j]+ logdens[t+1][j]+bta[t+1][j] - logprob;
               out[i][j] = logaddexp(out[i][j], vl);
              }
           }
        }

      return out;

     }
   //+------------------------------------------------------------------+
   //| forward scaling                                                  |
   //+------------------------------------------------------------------+
   double            forwardscaling(vector &startp, matrix &trans, matrix &dens,matrix &out, vector&outt)
     {
      double minsum = 1.e-300;
      vector gstartp = startp;
      matrix gtrans = trans;
      matrix gdens = exp(dens).Transpose();

      ulong ns = gdens.Rows();
      ulong nc = gdens.Cols();

      if(out.Cols()!=nc || out.Rows()!=ns)
         out.Resize(ns,nc);

      if(outt.Size()!=ns)
         outt.Resize(ns);

      out.Fill(0.0);

      double logprob = 0.0;

      for(ulong i = 0; i<nc; i++)
         out[0][i] = gstartp[i]*gdens[0][i];

      double sum  = (out.Row(0)).Sum();

      if(sum<minsum)
         Print("WARNING: forward pass failed with underflow consider using log implementation ");

      double scale = outt[0] = 1.0/sum;
      logprob -= log(scale);

      for(ulong i=0; i<nc; i++)
         out[0][i] *=scale;

      for(ulong t =1; t<ns; t++)
        {
         for(ulong j=0; j<nc; j++)
           {
            for(ulong i=0; i<nc; i++)
              {
               out[t][j]+=out[t-1][i] * gtrans[i][j];
              }
            out[t][j]*=gdens[t][j];
           }
         sum = (out.Row(t)).Sum();
         if(sum<minsum)
            Print("WARNING: forward pass failed with underflow consider using log implementation ");

         scale = outt[t] = 1.0/sum;
         logprob -= log(scale);
         for(ulong j = 0; j<nc; j++)
            out[t][j] *= scale;

        }
      return logprob;
     }
   //+------------------------------------------------------------------+
   //|backward scaling                                                  |
   //+------------------------------------------------------------------+
   matrix            backwardscaling(vector &startp, matrix &trans, matrix &dens,vector &scaling)
     {
      vector gstartp = startp;
      vector scaled = scaling;
      matrix gtrans = trans;
      matrix gdens =  exp(dens).Transpose();

      ulong ns = gdens.Rows();
      ulong nc = gdens.Cols();

      matrix out;
      out.Init(ns,nc);

      out.Fill(0.0);
      for(ulong i = 0; i<nc; i++)
         out[ns-1][i] = scaling[ns-1];

      for(long t = long(ns-2); t>=0; t--)
        {
         for(ulong i=0; i<nc; i++)
           {
            for(ulong j =0; j<nc; j++)
              {
               out[t][i]+=(gtrans[i][j]*gdens[t+1][j]*out[t+1][j]);
              }
            out[t][i]*=scaling[t];
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| forward log                                                      |
   //+------------------------------------------------------------------+
   double            forwardlog(vector &startp, matrix &trans, matrix &dens,matrix &out)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      if(out.Cols()!=nc || out.Rows()!=ns)
         out.Resize(ns,nc);

      vector buf;
      buf.Init(nc);

      for(ulong i =0; i<nc; i++)
         out[0][i] = logstartp[i] + logdens[0][i];

      for(ulong t =1; t<ns; t++)
        {
         for(ulong j =0; j<nc; j++)
           {
            for(ulong i =0; i<nc; i++)
              {
               buf[i] = out[t-1][i] + logtrans[i][j];
              }
            out[t][j] = logdens[t][j] + (log(exp(buf-buf[buf.ArgMax()]).Sum()) + buf[buf.ArgMax()]);
           }
        }

      vector row = out.Row(ns-1);

      return (log(exp(row-row[row.ArgMax()]).Sum()) + row[row.ArgMax()]);
     }
   //+------------------------------------------------------------------+
   //|  backwardlog                                                     |
   //+------------------------------------------------------------------+
   matrix            backwardlog(vector &startp, matrix &trans, matrix &dens)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      matrix out;
      out.Init(ns,nc);

      vector buf;
      buf.Init(nc);

      for(ulong i =0; i<nc; i++)
         out[ns-1][i] = 0.0;

      for(long t = long(ns-2); t>=0; t--)
        {
         for(long i =0; i<long(nc); i++)
           {
            for(long j =0; j<long(nc); j++)
              {
               buf[j] = logdens[t+1][j] + out[t+1][j] + logtrans[i][j];
              }
            out[t][i] = (log(exp(buf-buf[buf.ArgMax()]).Sum()) + buf[buf.ArgMax()]);
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| compute posterior state probabilities scaling                    |
   //+------------------------------------------------------------------+
   matrix            compute_posteriors_scaling(matrix &alf, matrix &bta)
     {
      return normalize_matrix(alf*bta);
     }
   //+------------------------------------------------------------------+
   //| compute posterior state probabilities log                        |
   //+------------------------------------------------------------------+
   matrix            compute_posteriors_log(matrix &alf, matrix &bta)
     {
      return exp(log_normalize(alf+bta));
     }
   //+------------------------------------------------------------------+
   //|calculate the probability of a state                              |
   //+------------------------------------------------------------------+
   double            compute_posteriors(matrix &data, matrix &result, ENUM_HMM_METHOD use_log=MODE_LOG)
     {
      matrix alfa,bt,dens;
      double logp=0.0;
      dens = find_densities(m_vars,m_states,data,m_means,m_covars);
      if(use_log == MODE_LOG)
        {
         logp = forwardlog(m_initprobs,m_transition,dens,alfa);
         bt = backwardlog(m_initprobs,m_transition,dens);
         result = compute_posteriors_log(alfa,bt);
        }
      else
        {
         vector scaling_factors;
         logp = forwardscaling(m_initprobs,m_transition,dens,alfa,scaling_factors);
         bt = backwardscaling(m_initprobs,m_transition,dens,scaling_factors);
         result = compute_posteriors_scaling(alfa,bt);
        }
      return logp;
     }
   //+------------------------------------------------------------------+
   //| map  implementation                                              |
   //+------------------------------------------------------------------+
   double            map(matrix &data,vector &out, ENUM_HMM_METHOD use_log=MODE_LOG)
     {
      matrix posteriors;
      double lp = compute_posteriors(data,posteriors,use_log);
      lp = (posteriors.Max(1)).Sum();
      out = posteriors.ArgMax(1);
      return lp;
     }
   //+------------------------------------------------------------------+
   //| viterbi implementation                                           |
   //+------------------------------------------------------------------+
   double            viterbi(vector &startp, matrix &trans, matrix &dens, vector &out)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      double logprob = 0;
      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      if(out.Size()<ns)
         out.Resize(ns);

      matrix vit(ns,nc);
      for(ulong i = 0; i<nc; i++)
         vit[0][i] = logstartp[i] + logdens[0][i];

      for(ulong t = 1; t<ns; t++)
        {
         for(ulong i =0; i<nc; i++)
           {
            double max = -DBL_MIN;
            for(ulong j = 0; j<nc; j++)
              {
               max = MathMax(max,vit[t-1][j]+logtrans[j][i]);
              }
            vit[t][i] = max+logdens[t][i];
           }
        }
      out[ns-1] = (double)(vit.Row(ns-1)).ArgMax();
      double prev = out[ns-1];
      logprob = vit[ns-1][long(prev)];
      for(long t = long(ns-2); t>=0; t--)
        {
         for(ulong i =0; i<nc; i++)
           {
            prev = ((vit[t][i]+logtrans[i][long(prev)])>=-DBL_MIN && i>=0)?double(i):double(0);
           }
         out[t] = prev;
        }
      return logprob;
     }
   //+------------------------------------------------------------------+
   //| Calculate the probability density function                       |
   //+------------------------------------------------------------------+
   matrix              find_densities(ulong variables,ulong states,matrix &mdata,matrix &the_means, matrix &covs[])
     {
      matrix out;
      out.Resize(states,mdata.Rows());

      for(ulong state=0 ; state<states ; state++)
        {
         for(ulong i=0 ; i<mdata.Rows() ; i++)
            out[state][i] = mv_normal(variables, mdata.Row(i), the_means.Row(state), covs[state]) ;
        }

      return out;
     }
   //+------------------------------------------------------------------+
   //| Forward algorithm                                                |
   //+------------------------------------------------------------------+

   double            forward(matrix &_transitions)
     {
      double sum, denom, log_likelihood;

      denom = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
        {
         alpha[0][i] = m_initprobs[i] * densities[i][0] ;
         denom += alpha[0][i] ;
        }

      log_likelihood = log(denom) ;
      for(ulong i=0 ; i<m_states ; i++)
         alpha[0][i] /= denom ;


      for(ulong t=1 ; t<m_samples ; t++)
        {
         denom = 0.0 ;
         for(ulong i=0 ; i<m_states ; i++)
           {
            ulong trans_ptr = i;
            sum = 0.0 ;
            for(ulong j=0 ; j<m_states ; j++)
              {
               sum += alpha[t-1][j] * _transitions.Flat(trans_ptr);
               trans_ptr += m_states ;
              }
            alpha[t][i] = sum * densities[i][t] ;
            denom += alpha[t][i] ;
           }
         log_likelihood += log(denom) ;
         for(ulong i=0 ; i<m_states ; i++)
            alpha[t][i] /= denom ;
        }

      return log_likelihood ;

     }
   //+------------------------------------------------------------------+
   //| Backward algorithm                                               |
   //+------------------------------------------------------------------+
   double            backward(void)
     {
      double sum, denom, log_likelihood ;

      denom = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
        {
         beta[(m_samples-1)][i] = 1.0 ;
         denom += beta[(m_samples-1)][i] ;
        }

      log_likelihood = log(denom) ;
      for(ulong i=0 ; i<m_states ; i++)
         beta[(m_samples-1)][i] /= denom ;

      for(long t=long(m_samples-2) ; t>=0 ; t--)
        {
         denom = 0.0 ;
         for(ulong i=0 ; i<m_states ; i++)
           {
            sum = 0.0 ;
            for(ulong j=0 ; j<m_states ; j++)
               sum += m_transition[i][j] * densities[j][t+1] * beta[(t+1)][j] ;
            beta[t][i] = sum ;
            denom += beta[t][i] ;
           }
         log_likelihood += log(denom) ;
         for(ulong i=0 ; i<m_states ; i++)
            beta[t][i] /= denom ;
        }

      sum = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
         sum += m_initprobs[i] * densities[i][0] * beta[0][i] ;

      return log(sum) + log_likelihood ;
     }

public:
   //+------------------------------------------------------------------+
   //| constructor                                                      |
   //+------------------------------------------------------------------+

                     HMM(void)
     {
      trained =false;

      m_hmm_mode = MODE_LOG;
      m_decode_mode = MODE_VITERBI;
      m_mincovar = 1.e-7;
     }
   //+------------------------------------------------------------------+
   //| desctructor                                                      |
   //+------------------------------------------------------------------+

                    ~HMM(void)
     {

     }

   //+------------------------------------------------------------------+
   //| Load model data from regular file                                |
   //+------------------------------------------------------------------+
   bool               load(string file_name)
     {
      trained = false;
      CFileTxt modelFile;
      CJAVal js;
      ResetLastError();

      if(modelFile.Open(file_name,FILE_READ|FILE_COMMON,0)==INVALID_HANDLE)
        {
         Print(__FUNCTION__," failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         if(!js.Deserialize(modelFile.ReadString()))
           {
            Print("failed to read from ",file_name,".Error -",::GetLastError());
            return false;
           }
         trained = fromJSON(js);
        }
      return trained;
     }
   //+------------------------------------------------------------------+
   //|Predict the state given arbitrary input variables                 |
   //+------------------------------------------------------------------+

   matrix            predict_state_probs(matrix &inputs)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__, " Call fit() to estimate the model parameters");
         matrix::Zeros(1, m_states);
        }

      if(inputs.Rows()<2 || inputs.Cols()<m_vars)
        {
         Print(__FUNCTION__, " invalid matrix size ");
         matrix::Zeros(1, m_states);
        }

      matrix probs;
      compute_posteriors(inputs,probs,m_hmm_mode);

      return probs;
     }
   //+------------------------------------------------------------------+
   //|Predict the state sequence of arbitrary input variables           |
   //+------------------------------------------------------------------+
   vector            predict_state_sequence(matrix &inputs, ENUM_DECODE_METHOD decoder=WRONG_VALUE)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__, " Call fit() to estimate the model parameters");
         matrix::Zeros(1, m_states);
        }

      if(inputs.Rows()<2 || inputs.Cols()<m_vars)
        {
         Print(__FUNCTION__, " invalid matrix size ");
         vector::Zeros(1);
        }

      vector seq = vector::Zeros(inputs.Rows());
      ENUM_DECODE_METHOD decm;
      if(decoder!=WRONG_VALUE)
         decm = decoder;
      else
         decm = m_decode_mode;

      switch(decm)
        {
         case MODE_VITERBI:
           {
            matrix d = find_densities(m_vars,m_states,inputs,m_means,m_covars);
            viterbi(m_initprobs,m_transition,d,seq);
            break;
           }
         case MODE_MAP:
           {
            map(inputs,seq,m_hmm_mode);
            break;
           }
        }

      return seq;
     }
   //+------------------------------------------------------------------+
   //| get the loglikelihood of the model                             |
   //+------------------------------------------------------------------+

   double            get_likelihood(matrix &data)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return EMPTY_VALUE;
        }

      matrix dens = find_densities(m_vars,m_states,data,m_means,m_covars);
      matrix alfa;
      vector sc;

      switch(m_hmm_mode)
        {
         case MODE_LOG:
            likelihood = forwardlog(m_initprobs,m_transition,dens,alfa);
            break;
         case MODE_SCALING:
            likelihood = forwardscaling(m_initprobs,m_transition,dens,alfa,sc);
            break;
        }

      return likelihood;
     }
   //+------------------------------------------------------------------+
   //| get the initial state probabilities of the model          |
   //+------------------------------------------------------------------+

   vector            get_init_probs(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return vector::Zeros(1);
        }
      return m_initprobs;
     }
   //+------------------------------------------------------------------+
   //| get the probability transition matrix                            |
   //+------------------------------------------------------------------+

   matrix            get_transition_matrix(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_transition;
     }
   //+------------------------------------------------------------------+
   //|get the state means matrix                                        |
   //+------------------------------------------------------------------+

   matrix            get_means(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_means;
     }

   //+------------------------------------------------------------------+
   //| get the covariance matrix for a particular state                 |
   //+------------------------------------------------------------------+

   matrix            get_covar_matrix_for_state_at(ulong state_index)
     {
      if(!trained || state_index>m_states)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_covars[state_index];
     }
   //+------------------------------------------------------------------+
   //|  get the number of features for the model                |
   //+------------------------------------------------------------------+
   ulong             get_num_features(void)
     {
      return m_vars;
     }
  };


//+------------------------------------------------------------------+

After creating an instance of the HMM class, we would call the "load()" method with a specific filename.

//---declare object
   HMM hmm;
//--load exampleHMM model from json file
   if(!hmm.load("exampleHMM.json"))
     {
      Print("error loading model");
      return;
     }

If the model parameters are successfully read, the method would return true.

Once a model has been loaded, we can obtain the hidden states and state probabilities for a particular set of observations. However, it's important to note that the implementation of all algorithms described earlier in the text is slightly different. Instead of raw likelihoods, the code uses the log of the raw values to ensure numerical stability. Therefore, we have log-likelihoods instead of likelihoods. This also means that anywhere multiplication is called for, we have to use addition since we are dealing with the log of the values.

The HMM method `get_likelihood()` returns the log likelihood for a set of observations based on the loaded model parameters. It is calculated using the forward algorithm. The "predict_state_probs()" method calculates the state probabilities for each observation provided as input. This method returns a matrix where each row represents the state probabilities for an observation.

On the other hand, the "predict_state_sequence()" method returns a vector representing the state for each sample provided as input. By default, it uses the Viterbi algorithm to calculate the most probable state sequence. However, it is also possible to select the simple "map" technique, mimicking the behavior of the GaussianHMM's "decode()" method.

The "HMM" class provides getter methods for extracting the parameters of a loaded model:

• "get_means()": Returns the matrix of means used to determine the probability densities
• "get_covar_matrix_for_state_at()": Gets the full covariance matrix for a particular state
• "get_transition_matrix()": Returns the transition probabilities as a matrix
• "get_init_probs()": Returns a vector of the initial state probabilities of the model
• "get_num_features()": Returns an unsigned long value representing the number of variables expected as input for the model. This means that for any matrix supplied as input to "predict_state_probs()", "predict_state_sequence()", and "get_likelihood()", it should have this number of columns and at least 2 rows.

The saveHMM.py script trains a HMM based on a random dataset. It includes the definition of the function "hmm2json()" which is responsible for saving the final model parameters to a json file. The data consists fo 10 rows and 5 columns. An instance of the GaussianHMM class is created and the HMM is trained on the random data. After fitting a mode,l "hmm2json()" is called to save the model parameters to a json file. Then, the log likelihood, hidden states and state probabilities are printed.

# Copyright 2024, MetaQuotes Ltd.
# https://www.mql5.com
from hmmlearn import hmm
import numpy as np
import pandas as pd
import json 


assumed_states = 2 #number of states of process
maxhmm_iters = 10000 #maximum number of iterations for optimization procedure

def hmm2json(hmm_model, filename):
    """
    function save a GaussianHMM model to json format 
    readable from MQL5 code.
    param: hmm_model should an instance of GaussianHMM
    param: string. filename or path to file where HMM 
    parameters will be written to
    """
    if hmm_model.__class__.__name__ != 'GaussianHMM':
        raise TypeError(f'invalid type supplied')
    if len(filename) < 1 or not isinstance(filename,str):
        raise TypeError(f'invalid filename supplied')
    jm  = {
            "numstates":hmm_model.n_components,
            "numvars":hmm_model.n_features,
            "algorithm":str(hmm_model.algorithm),
            "implementation":str(hmm_model.implementation), 
            "initprobs":hmm_model.startprob_.tolist(),
            "means":hmm_model.means_.tolist(),
            "transitions":hmm_model.transmat_.tolist(),
            "covars":hmm_model.covars_.tolist()
          }
    with open(filename,'w') as file:
        json.dump(jm,file,indent=None,separators=(',', ':')) 
    return 
#dataset to train model on    
dataset = np.array([[0.56807844,0.67179966,0.13639585,0.15092627,0.17708295],
                   [0.62290044,0.15188847,0.91947761,0.29483647,0.34073613],
                   [0.47687505,0.06388765,0.20589139,0.16474974,0.64383775],
                   [0.25606858,0.50927144,0.49009671,0.0284832,0.37357852],
                   [0.95855305,0.93687549,0.88496015,0.48772751,0.10256193],
                   [0.36752403,0.5283874 ,0.52245909,0.77968798,0.88154157],
                   [0.35161822,0.50672902,0.7722671,0.56911901,0.98874104],
                   [0.20354888,0.82106204,0.60828044,0.13380222,0.4181293,],
                   [0.43461371,0.60170739,0.56270993,0.46426138,0.53733481],
                   [0.51646574,0.54536398,0.03818231,0.32574409,0.95260478]])  
#instantiate an HMM and train on dataset
model = hmm.GaussianHMM(assumed_states,n_iter=maxhmm_iters,covariance_type='full',random_state=125, verbose=True).fit(dataset)  
#save the model to the common folder of Metatrader 5 install
hmm2json(model,r'C:\Users\Zwelithini\AppData\Roaming\MetaQuotes\Terminal\Common\Files\exampleHMM.json')
#get the state probabilities and log likelihood
result = model.score_samples(dataset)
print("log_likelihood " ,result[0]) #print the loglikelihood
print("state sequence ", model.decode(dataset)[1]) #print the state sequence of dataset
print("state probs ", result[1]) #print the state probabilities 

The corresponding MetaTrader 5 script testHMM.mq5 is designed to load the json file created by saveHMM.py. The idea is to reproduce the log likelihood, hidden states and state probabilities  output by saveHMM.py.

//+------------------------------------------------------------------+
//|                                                      TestHMM.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<hmmlearn.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- random dataset equal to that used in corresponding python script saveHMM.py
   matrix dataset =
     {
        {0.56807844,0.67179966,0.13639585,0.15092627,0.17708295},
        {0.62290044,0.15188847,0.91947761,0.29483647,0.34073613},
        {0.47687505,0.06388765,0.20589139,0.16474974,0.64383775},
        {0.25606858,0.50927144,0.49009671,0.0284832,0.37357852},
        {0.95855305,0.93687549,0.88496015,0.48772751,0.10256193},
        {0.36752403,0.5283874,0.52245909,0.77968798,0.88154157},
        {0.35161822,0.50672902,0.7722671,0.56911901,0.98874104},
        {0.20354888,0.82106204,0.60828044,0.13380222,0.4181293},
        {0.43461371,0.60170739,0.56270993,0.46426138,0.53733481},
        {0.51646574,0.54536398,0.03818231,0.32574409,0.95260478}
     };
//---declare object
   HMM hmm;
//--load exampleHMM model from json file
   if(!hmm.load("exampleHMM.json"))
     {
      Print("error loading model");
      return;
     }
//--get the log likelihood of the model
   double lk = hmm.get_likelihood(dataset);
   Print("LL ", lk);
//-- get the state probabilities for a dataset
   matrix probs = hmm.predict_state_probs(dataset);
   Print("state probs ", probs);
//---get the hidden states for the provided dataset
   vector stateseq = hmm.predict_state_sequence(dataset);
   Print("state seq ", stateseq);
  }
//+------------------------------------------------------------------+

The results of running both scripts are shown below.

Output from saveHMM.py.

KO      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   log_likelihood  47.90226114316213
IJ      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   state sequence  [0 1 1 1 1 0 0 1 0 0]
ED      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   state probs  [[1.00000000e+000 1.32203104e-033]
RM      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
JR      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
RH      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
JM      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
LS      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 5.32945369e-123]
EH      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 8.00195599e-030]
RN      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
HS      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 1.04574121e-027]
RD      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [9.99999902e-001 9.75116254e-008]]

The saved JSON file contents.

{"numstates":2,"numvars":5,"algorithm":"viterbi","implementation":"log","initprobs":[1.0,8.297061845628157e-28],"means":[[0.44766002665812865,0.5707974904960126,0.406402863181157,0.4579477485782787,0.7074610252191268],[0.5035892002511225,0.4965970189510691,0.6217412486192438,0.22191983002481444,0.375768737249644]],"transitions":[[0.4999999756220927,0.5000000243779074],[0.39999999999999913,0.6000000000000008]],"covars":[[[0.009010166768420797,0.0059122234200326374,-0.018865453701221935,-0.014521967883281419,-0.015149047353550696],[0.0059122234200326374,0.0055414217505728725,-0.0062874071503534424,-0.007643976931274206,-0.016093347935464856],[-0.018865453701221935,-0.0062874071503534424,0.0780495488091017,0.044115693492388836,0.031892068460887116],[-0.014521967883281419,-0.007643976931274206,0.044115693492388836,0.04753113728071052,0.045326684356283],[-0.015149047353550696,-0.016093347935464856,0.031892068460887116,0.045326684356283,0.0979523557527634]],[[0.07664631322010616,0.01605057520615223,0.042602194598462206,0.043095659393111246,-0.02756159799208612],[0.01605057520615223,0.12306893856632573,0.03943267795353822,0.019117932498522734,-0.04009804834113386],[0.042602194598462206,0.03943267795353822,0.07167474799610704,0.030420143149584727,-0.03682040884824712],[0.043095659393111246,0.019117932498522734,0.030420143149584727,0.026884283954788642,-0.01676189860422705],[-0.02756159799208612,-0.04009804834113386,-0.03682040884824712,-0.01676189860422705,0.03190589647162701]]]}

Output from testHMM.mq5.

HD      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   LL 47.90226114316213
EO      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   state probs [[1,1.322031040402482e-33]
KP      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KO      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KF      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KM      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
EJ      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,5.329453688054051e-123]
IP      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,8.00195599043147e-30]
KG      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
ES      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,1.045741207369424e-27]
RQ      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0.999999902488374,9.751162535898832e-08]]
QH      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   state seq [0,1,1,1,1,0,0,1,0,0]

Conclusion

HMMs are powerful statistical tools for modeling and analyzing sequential data. Their ability to capture the underlying hidden states driving observed sequences makes them valuable for tasks involving time series such as financial data. Despite their strengths, HMMs are not without limitations. They rely on the first order Markov assumption, which can be overly simplistic for complex dependencies. The computational demands of training and inference especially for large state spaces, and the potential for overfitting are significant challenges. Moreover, selecting the optimal number of states and initializing the model parameters require careful consideration and can impact performance. Nonetheless, HMMs remain a foundational method in sequence modeling, offering a robust framework for many practical applications. With ongoing advancements and hybrid approaches that combine HMMs with more flexible models, their utility continues to evolve. For practitioners, understanding both the capabilites and limitations of HMMs is essential for effectively leveraging their potential in automated trading development.

All the code described in the article is attached below. Each of the source code files are described in the table.

File	Description
Mql5\Python\script\saveHMM.py	demonstrates training and saving a hidden Markov model, contains the definition of hmm2json() function
Mql5\include\hmmlearn.mqh	contains definition of HMM class that enables the import of HMMs trained in Python to be used in MQL5
Mql5\script\testHMM.mq5	MT5 script demonstrating how to load a saved HMM