Integration von Hidden-Markov-Modellen in MetaTrader 5

Einführung

Es ist allgemein bekannt, dass eines der grundlegenden Merkmale von Finanzzeitreihen darin besteht, dass sie ein Gedächtnis aufweisen. Im Zusammenhang mit der Zeitreihenanalyse bezieht sich das Gedächtnis auf die Abhängigkeitsstruktur innerhalb der Daten, bei der vergangene Werte aktuelle und zukünftige Werte beeinflussen. Das Verständnis der Speicherstruktur hilft bei der Wahl des geeigneten Modells für die Zeitreihe. In diesem Artikel geht es um eine andere Art von Gedächtnis: die Form eines Hidden Markov Models (HMM). Wir werden die Grundlagen von HMMs erforschen und demonstrieren, wie man ein HMM mit dem Python-Modul hmmlearn erstellt. Schließlich werden wir einen Code in Python und MQL5 vorstellen, der den Export von HMMs zur Verwendung in MetaTrader 5-Programmen ermöglicht.

Hidden Markov Modelle verstehen

Hidden-Markov-Modelle sind ein leistungsfähiges statistisches Instrument zur Modellierung von Zeitreihendaten, bei denen das modellierte System durch nicht beobachtbare (verborgene) Zustände gekennzeichnet ist. Eine grundlegende Prämisse von HMMs ist, dass die Wahrscheinlichkeit, sich zu einem bestimmten Zeitpunkt in einem bestimmten Zustand zu befinden, vom Zustand des Prozesses im vorherigen Zeitfenster abhängt. Diese Abhängigkeit stellt das Gedächtnis eines HMM dar.

Im Zusammenhang mit finanziellen Zeitreihen könnten die Zustände darstellen, ob eine Reihe aufwärts oder abwärts tendiert oder innerhalb einer bestimmten Spanne schwankt. Jeder, der schon einmal mit einem Finanzindikator gearbeitet hat, kennt den „Whipsaw“-Effekt, der durch das Rauschen in den Finanzzeitreihen verursacht wird. Ein HMM kann eingesetzt werden, um diese falschen Signale herauszufiltern und ein klareres Verständnis der zugrunde liegenden Trends zu ermöglichen.

Um ein HMM zu erstellen, benötigen wir Beobachtungen, die die Gesamtheit des Verhaltens erfassen, das den Prozess definiert. Diese Datenprobe wird verwendet, um die Parameter des entsprechenden HMM zu lernen. Dieser Datensatz würde sich aus verschiedenen Merkmalen des zu modellierenden Prozesses zusammensetzen. Wenn wir zum Beispiel die Schlusskurse eines finanziellen Vermögenswerts untersuchen, könnten wir auch andere Aspekte einbeziehen, die mit dem Schlusskurs zusammenhängen, wie verschiedene Indikatoren, die idealerweise dazu beitragen, die verborgenen Zustände zu definieren, an denen wir interessiert sind.

Der Prozess des Lernens der Modellparameter erfolgt unter der Annahme, dass sich die modellierte Reihe immer in einem von zwei oder mehr Zuständen befindet. Die Zustände werden einfach mit 0 bis S-1 bezeichnet. Für diese Zustände müssen wir eine Reihe von Wahrscheinlichkeiten zuordnen, die die Wahrscheinlichkeit erfassen, dass der Prozess von einem Zustand in einen anderen wechselt. Diese Wahrscheinlichkeiten werden gewöhnlich als Übergangsmatrix bezeichnet. Die erste Beobachtung hat einen speziellen Satz von Anfangswahrscheinlichkeiten für jeden möglichen Zustand. Befindet sich eine Beobachtung in einem bestimmten Zustand, so wird erwartet, dass sie einer bestimmten Verteilung folgt, die mit diesem Zustand verbunden ist.

Ein HMM ist also durch vier Eigenschaften vollständig definiert:

• Die Anzahl der anzunehmenden Zustände
• Die anfänglichen Wahrscheinlichkeiten, dass die erste Beobachtung in einem der Zustände
• Die Übergangsmatrix der Wahrscheinlichkeiten
• Die Wahrscheinlichkeitsdichtefunktionen für jeden Zustand.
  

Zu Beginn haben wir die Beobachtungen und die angenommene Anzahl der Zustände. Wir wollen die Parameter eines HMMs finden, die zu dem vor uns liegenden Datensatz passen. Dies geschieht durch Beobachtung der Wahrscheinlichkeit (likelihood) mit Hilfe einer statistischen Technik, die als Maximum-Likelihood-Schätzung bezeichnet wird. In diesem Zusammenhang ist die Maximum-Likelihood-Schätzung der Prozess der Suche nach den Modelleigenschaften, die am ehesten mit unseren Datenproben übereinstimmen. Dazu wird die Wahrscheinlichkeit berechnet, dass sich jede Probe zu einem bestimmten Zeitpunkt in einem bestimmten Zustand befindet. Dies geschieht mit Hilfe des Vorwärts- und des Rückwärtsalgorithmus, die alle Stichproben vorwärts bzw. rückwärts in der Zeit durchlaufen.

Der Vorwärtsalgorithmus

Wir beginnen mit der ersten Beobachtung in unserem Datensatz, bevor wir die Wahrscheinlichkeiten für die nachfolgenden Stichproben berechnen. Für die erste Stichprobe verwenden wir die anfänglichen Zustandswahrscheinlichkeiten, die zu diesem Zeitpunkt als Versuchsparameter für ein Kandidaten-HMM betrachtet werden. Wenn nichts über den zu modellierenden Prozess bekannt ist, ist es durchaus akzeptabel, alle Anfangszustandswahrscheinlichkeiten auf 1/S zu setzen, wobei S die Gesamtzahl der angenommenen Zustände darstellt. Unter Anwendung des Satzes von Bayes ergibt sich die folgende allgemeine Gleichung:

Dabei ist „lk“ die Wahrscheinlichkeit, dass sich eine Stichprobe zum Zeitpunkt „t“ im Zustand „i“ befindet, und „p“ ist die Wahrscheinlichkeit, dass sie sich zum Zeitpunkt „t“ im Zustand „i“ befindet, wenn man die Stichproben bis zum Zeitpunkt „t“ betrachtet. „O“ ist eine einzelne Probe, eine einzelne Zeile im Datensatz.

Die Wahrscheinlichkeit der ersten Stichprobe wird nach der bedingten Wahrscheinlichkeitsregel P(A) = P(A|B)P(B) berechnet. Daher wird für die erste Stichprobe die Wahrscheinlichkeit, sich im Zustand i zu befinden, berechnet, indem die Wahrscheinlichkeit des Ausgangszustands, sich im Zustand i zu befinden, mit der Wahrscheinlichkeitsdichtefunktion der ersten Stichprobe multipliziert wird.

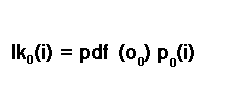
Dies ist ein weiterer Versuchsparameter des Kandidaten-HMM. In der Literatur wird sie manchmal auch als Emissionswahrscheinlichkeit bezeichnet. Auf die Emissionswahrscheinlichkeiten werden wir später im Text noch genauer eingehen. Wir dürfen nicht vergessen, dass wir nicht sicher sind, in welchem Zustand wir uns befinden. Wir müssen die Möglichkeit in Betracht ziehen, dass wir uns in irgendeinem der möglichen Zustände befinden könnten. Dies führt dazu, dass die endgültige Anfangswahrscheinlichkeit die Summe aller Wahrscheinlichkeiten aller möglichen Zustände ist.

 

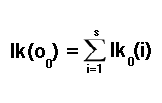
Um die Wahrscheinlichkeiten für nachfolgende Beobachtungen zu berechnen, müssen wir die Möglichkeit des Übergangs zu einem bestimmten Zustand aus einem der möglichen Zustände im vorherigen Zeitfenster berücksichtigen. Hier kommen Übergangswahrscheinlichkeiten zum Tragen, die an dieser Stelle ein weiterer Versuchsparameter sind. Die Wahrscheinlichkeit, im nächsten Zeitfenster einen bestimmten Zustand zu erreichen, wird durch Multiplikation der aktuell bekannten Zustandswahrscheinlichkeit mit der entsprechenden Übergangswahrscheinlichkeit geschätzt, wenn man die Wahrscheinlichkeit für das aktuelle Zeitfenster berechnet hat.

Dies ist ein guter Zeitpunkt, um über Übergangswahrscheinlichkeiten oder die Übergangsmatrix zu sprechen.

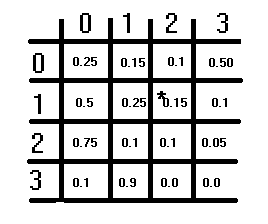
Die obige Abbildung zeigt eine hypothetische Übergangsmatrix. Sie hat eine S×S-Struktur, wobei S die Anzahl der angenommenen Zustände ist. Jedes Element stellt eine Wahrscheinlichkeit dar, und die Wahrscheinlichkeiten in jeder Zeile sollten sich zu 1 summieren. Diese Bedingung gilt nicht für die Spalten. Um die entsprechende Übergangswahrscheinlichkeit für den Wechsel von einem Zustand zum anderen zu erhalten, beziehen Sie sich zuerst auf die Zeilen und dann auf die Spalten. Der aktuelle Zustand, von dem aus umgeschaltet wird, entspricht dem Zeilenindex, und der Zustand, in den umgeschaltet wird, entspricht dem Spaltenindex. Der Wert bei diesen Indizes ist die entsprechende Übergangswahrscheinlichkeit. Die Diagonale der Matrix stellt die Wahrscheinlichkeiten dar, dass sich der Zustand nicht ändert.

Bei der Berechnung der Wahrscheinlichkeiten für den Rest der Beobachtungen in der von uns gewählten Datenstichprobe haben wir eine Zustandswahrscheinlichkeit mit einer Übergangswahrscheinlichkeit multipliziert. Um jedoch ein vollständiges Bild zu erhalten, müssen wir die Möglichkeit des Übergangs in einen beliebigen der möglichen Zustände berücksichtigen. Wir tun dies, indem wir alle Möglichkeiten gemäß der folgenden Gleichung zusammenzählen:

            

Damit ist die Berechnung der individuellen Wahrscheinlichkeiten für jede Stichprobe in unserem Datensatz abgeschlossen. Diese individuellen Wahrscheinlichkeiten können durch Multiplikation kombiniert werden, um die Wahrscheinlichkeit für den gesamten Datensatz zu erhalten. Die soeben beschriebene Berechnung wird aufgrund der zeitlichen Vorwärtsrekursion der Methode als Vorwärtsalgorithmus bezeichnet. Dies steht im Gegensatz zum Rückwärtsalgorithmus, den wir im nächsten Abschnitt erörtern werden.

Der Rückwärtsalgorithmus

Es ist auch möglich, die einzelnen Wahrscheinlichkeiten zu berechnen, indem man rückwärts in der Zeit geht, beginnend mit der letzten Datenprobe. Wir beginnen damit, dass wir für die letzte Datenstichprobe die Wahrscheinlichkeit für alle Zustände auf 1 setzen. Für jede Datenprobe, die sich in einem bestimmten Zustand befindet, berechnen wir die Wahrscheinlichkeit für den nachfolgenden Satz von Proben, wobei wir davon ausgehen, dass wir in jeden der Zustände übergehen können. Dazu berechnen wir die gewichtete Summe der Wahrscheinlichkeiten jedes Zustands: die Wahrscheinlichkeit, sich in diesem Zustand zu befinden, multipliziert mit der Wahrscheinlichkeitsdichtefunktion, dass sich die Stichprobe in demselben Zustand befindet. Das Ergebnis dieser Berechnung wird dann angepasst, indem die Wahrscheinlichkeit des Übergangs vom aktuellen Zustand zum nächsten als Gewichtungsfaktor verwendet wird. Dies alles ist in der folgenden Formel zusammengefasst:

Die Wahrscheinlichkeitsdichtefunktionen

In den Diskussionen über die Vorwärts- und Rückwärtsalgorithmen wurde die Wahrscheinlichkeitsdichtefunktion (probability density functions, pdf) als Parameter eines HMM erwähnt. Dann stellt sich eine Frage: Von welcher Verteilung gehen wir aus? Wie bereits erwähnt, werden die pdf-Parameter eines HMM gewöhnlich als Emissionswahrscheinlichkeiten bezeichnet. Sie werden als Wahrscheinlichkeiten bezeichnet, wenn die zu modellierenden Daten aus diskreten oder kategorialen Werten bestehen. Bei kontinuierlichen Variablen verwenden wir das pdf.

In diesem Text zeigen wir HMMs, die Datensätze mit kontinuierlichen Variablen modellieren, die einer multivariaten Normalverteilung folgen. Es ist möglich, andere Verteilungen zu implementieren; das Python-Modul, das wir uns später ansehen werden, verfügt über HMM-Implementierungen für verschiedene Verteilungen der zu modellierenden Daten. Durch die Erweiterung werden die Parameter der angenommenen Verteilung zu einem der Parameter des HMM. Im Falle der multivariaten Normalverteilung sind ihre Parameter die Mittelwerte und Kovarianzen.

Der Baum-Welch-Algorithmus

Der Baum-Welch-Algorithmus ist ein Verfahren zur Erwartungsmaximierung, mit dem verschiedene Parameter für HMM-Kandidaten ausprobiert werden, um den optimalen Parameter zu finden. Der Wert, der bei diesem Optimierungsverfahren maximiert wird, ist die Wahrscheinlichkeit für den gesamten Datensatz der Stichproben. Der Baum-Welch-Algorithmus ist dafür bekannt, dass er effizient und zuverlässig ist, aber er hat auch seine Schwächen. Ein eklatanter Nachteil ist, dass sie nicht konvex ist. Nicht-konvexe Funktionen im Zusammenhang mit der Optimierung sind Funktionen mit zahlreichen lokalen Minima oder Maxima.

Dies bedeutet, dass bei Erreichen der Konvergenz das globale Maximum oder Minimum des Parameterraums möglicherweise noch nicht gefunden wurde. Grundsätzlich ist nicht garantiert, dass die Funktion am optimalen Punkt konvergiert. Der beste Weg, um diesen Fehler abzuschwächen, ist die Erprobung von Parametern, die eine große Wahrscheinlichkeit im Vergleich zu anderen im Parameterraum haben. Dazu müssten wir zahlreiche zufällige Parameterwerte ausprobieren, um den besten Ausgangs-Parameterraum zu finden, von dem aus wir den Optimierungsprozess starten können.

Berechnung von Zustandswahrscheinlichkeiten

Sobald wir das optimale HMM und seine Parameter haben, können wir es zur Berechnung der Zustandswahrscheinlichkeiten für ungesehene Datenproben verwenden. Das Ergebnis einer solchen Berechnung wäre eine Reihe von Wahrscheinlichkeiten, eine für jeden Zustand, die die Wahrscheinlichkeit angibt, in jedem Zustand zu sein. Die einzelnen Wahrscheinlichkeiten aus dem Vorwärtsalgorithmus werden mit den Wahrscheinlichkeiten aus dem Rückwärtsalgorithmus multipliziert, was die Wahrscheinlichkeit eines bestimmten Zustands ergibt. Nach der Bayes-Regel wird die Wahrscheinlichkeit, dass sich eine Beobachtung in einem bestimmten Zustand befindet, wie folgt berechnet:

Berechnung von Zustandswahrscheinlichkeiten mit dem Viterbi-Algorithmus

Neben den Zustandswahrscheinlichkeiten können wir auch den wahrscheinlichen Zustand einer Beobachtung mit Hilfe des Viterbi-Algorithmus ableiten. Die Berechnung beginnt mit der ersten Beobachtung, deren Zustandswahrscheinlichkeiten anhand der mit den Emissionswahrscheinlichkeiten multiplizierten Anfangszustandswahrscheinlichkeiten berechnet werden.

Für jede Beobachtung, von der zweiten bis zur letzten, wird die Wahrscheinlichkeit jedes Zustands anhand der Wahrscheinlichkeit des vorherigen Zustands, der entsprechenden Übergangswahrscheinlichkeit und der Emissionswahrscheinlichkeit berechnet. Der wahrscheinlichste Zustand ist derjenige mit der höchsten Eintrittswahrscheinlichkeit.

Wir haben uns alle Komponenten eines Hidden-Markov-Modells angesehen. Wir wollen uns nun mit der praktischen Umsetzung befassen. Wir beginnen mit einer Python-basierten Implementierung von HMMs, die im Paket hmmlearn bereitgestellt wird. Wir werden die Verwendung der Gaußschen HMM-Implementierung von hmmlearn besprechen, bevor wir zu MQL5-Code wechseln, um zu demonstrieren, wie man ein in Python mit hmmlearn trainiertes Modell in MetaTrader 5-Anwendungen integriert.

Das hmmlearn-Paket von Python

Die hmmlearn-Bibliothek in Python bietet Werkzeuge für die Arbeit mit verdeckten Markov-Modellen. Die Werkzeuge für das Training von HMMs befinden sich im Namensraum „hmm“. Innerhalb von „hmm“ sind mehrere spezielle Klassen deklariert, um mit Prozessen verschiedener Verteilungen zu arbeiten. Nämlich:

• MultinomialHMM: Modelle von HMMs, bei denen die Beobachtungen diskret sind und einer Multinomialverteilung folgen
• GMMHMM: Modelle von HMMs, bei denen die Beobachtungen aus einer Mischung von Gaußschen Verteilungen erzeugt werden
• PoissonHMM: Modelle von HMMs, bei denen davon ausgegangen wird, dass die Beobachtungen einer Poisson-Verteilung folgen
• Schließlich gibt es noch die Klasse GaussianHMM, die sich mit Datensätzen befasst, die einer multivariaten Gaußschen (normalen) Verteilung folgen. Dies ist die Klasse, die wir demonstrieren und deren Modell wir mit MetaTrader 5 verknüpfen werden.

Um das Paket zu installieren, können Sie den folgenden Befehl verwenden:

pip install hmmlearn

Nach der Installation des Pakets können Sie die Klasse „GaussianHMM“ mit der folgenden Import-Anweisung importieren:

from hmmlearn.hmm import GaussianHMM

Alternativ können Sie auch das Modul „hmm“ importieren, das alle oben genannten Klassen sowie weitere nützliche Dienstprogramme enthält. Wenn diese Methode verwendet wird, muss den Klassennamen ein „hmm“ vorangestellt werden, etwa so:

from hmmlearn import hmm

Sie können ein GaussianHMM-Objekt mit mehreren Parametern initialisieren:

model = GaussianHMM(n_components=3, covariance_type='diag', n_iter=100, tol=0.01)

wobei:

• „n_components“: Anzahl der Zustände im Modell.
• „covariance_type“: Art der zu verwendenden Kovarianzparameter ('sphärisch', 'diag', 'vollständig', 'gebunden'). Der verwendete Kovarianztyp bezieht sich auf die Merkmale des Datensatzes. Eine sphärische Kovarianz sollte gewählt werden, wenn die Merkmale oder Variablen in dem zu modellierenden Datensatz eine ähnliche Varianz aufweisen und nicht korreliert sein können. Andernfalls, wenn die Variablen unterschiedliche Varianzen aufweisen, ist es am besten, einen diagonalen Kovarianztyp zu wählen. Wenn die Variablen korreliert sind, sollte entweder ein Typ mit vollständiger oder gebundener Kovarianz gewählt werden. Die Auswahl der vollständigen Kovarianz bietet die größte Flexibilität, kann aber auch sehr rechenintensiv sein. Es ist die sicherste Wahl, die die Anzahl der Annahmen über den zu modellierenden Prozess begrenzt. Bei der gebundenen Kovarianz wird zusätzlich davon ausgegangen, dass die Zustände eine ähnliche Kovarianzstruktur aufweisen. Im Vergleich zur vollständigen Kovarianz ist sie etwas effizienter.
• „n_iter“: Maximale Anzahl von Iterationen, die während des Trainings durchgeführt werden.
• „tol“: Konvergenzschwelle.

Alle Parameter, die ein Modell spezifizieren, können Sie in der Dokumentation der hmmlearn-Bibliothek nachlesen. Diese Dokumentation enthält detaillierte Informationen zu den verschiedenen Parametern und ihrer Verwendung. Sie können online auf die offizielle Website zugreifen oder über die Dokumentation, die bei der Installation der Bibliothek mitgeliefert wird, über das in Python integrierte Hilfsprogramm.

help(GaussianHMM)

Um ein Modell zu trainieren, rufen wir die Methode „fit()“ auf. Er erwartet mindestens ein 2-dimensionales Array als Eingabe.

model.fit(data)

Nachdem das Training abgeschlossen ist, können wir die verdeckten Zustände eines Datensatzes durch den Aufruf von „predict()“ oder „decode()“ ermitteln. Beide erwarten ein 2-dimensionales Array mit der gleichen Anzahl von Merkmalen wie der zum Trainieren des Modells verwendete Datensatz. Die Methode „predict()“ gibt ein Array von berechneten verdeckten Zuständen zurück, während „decode()“ den Logarithmus der Wahrscheinlichkeiten (log likelihood) in Verbindung mit dem Array von verdeckten Zuständen in einem Tupel zurückgibt.

Der Aufruf von „score_samples()“ liefert den Logarithmus der Wahrscheinlichkeiten sowie die Zustandswahrscheinlichkeiten für den als Eingabe angegebenen Datensatz. Auch hier sollten die Daten die gleiche Anzahl von Merkmalen aufweisen wie die Daten, die zum Trainieren des Modells verwendet wurden.

Exportieren eines verborgenen Markov-Modells

Der Export eines in Python mit dem hmmlearn-Paket trainierten Modells zur Verwendung in MetaTrader 5 erfordert die Implementierung zweier nutzerdefinierter Komponenten:

• Python-Komponente: Diese Komponente ist für die Speicherung der Parameter eines trainierten Modells in einem von einer MetaTrader-Anwendung lesbaren Format verantwortlich. Es geht darum, die Modellparameter in ein Dateiformat zu exportieren, das von den MetaTrader 5-Anwendungen geparst werden kann.
• MQL5-Komponente: Die MQL5-Komponente umfasst in MQL5 geschriebenen Code. Diese Komponente sollte Funktionen zum Lesen der von der Python-Komponente exportierten HMM-Parameter enthalten. Außerdem müssen die Vorwärts-, Rückwärts- und Viterbi-Algorithmen implementiert werden, um die verborgenen Zustände und Zustandswahrscheinlichkeiten für einen Datensatz auf der Grundlage eines bestimmten HMM zu berechnen.
  

Die Implementierung dieser Komponenten erfordert eine sorgfältige Prüfung der Daten-Serialisierungsformate, der Dateieingabe- und -ausgabeoperationen und der algorithmischen Implementierungen sowohl in Python als auch in MQL5. Es ist wichtig, die Kompatibilität zwischen den Python- und MQL5-Implementierungen sicherzustellen, um das trainierte Modell genau zu übertragen und Inferenzaufgaben in MetaTrader 5 durchzuführen.

Das hmmlearn-Paket bietet die Möglichkeit, ein trainiertes HMM mit Hilfe des Moduls „pickle“ zu speichern. Das Problem ist, dass es nicht einfach ist, mit „gepickelten“ Dateien außerhalb von Python zu arbeiten. Eine bessere Option wäre also die Verwendung des json-Formats. Der HMM-Parameter wird in eine strukturierte JSON-Datei geschrieben, die mit MQL5-Code gelesen werden kann. Diese Funktionalität ist in der folgenden Python-Funktion implementiert.

def hmm2json(hmm_model, filename):
    """
    function save a GaussianHMM model to json format 
    readable from MQL5 code.
    param: hmm_model should an instance of GaussianHMM
    param: string. filename or path to file where HMM 
    parameters will be written to
    """
    if hmm_model.__class__.__name__ != 'GaussianHMM':
        raise TypeError(f'invalid type supplied')
    if len(filename) < 1 or not isinstance(filename,str):
        raise TypeError(f'invalid filename supplied')
    jm  = {
            "numstates":hmm_model.n_components,
            "numvars":hmm_model.n_features,
            "algorithm":str(hmm_model.algorithm),
            "implementation":str(hmm_model.implementation), 
            "initprobs":hmm_model.startprob_.tolist(),
            "means":hmm_model.means_.tolist(),
            "transitions":hmm_model.transmat_.tolist(),
            "covars":hmm_model.covars_.tolist()
          }
    with open(filename,'w') as file:
        json.dump(jm,file,indent=None,separators=(',', ':')) 
    return 

Diese Funktion nimmt eine Instanz der Klasse GaussianHMM und einen Dateinamen als Eingabe und schreibt die HMM-Parameter in eine JSON-Datei in einem strukturierten Format, das mit MQL5-Code gelesen werden kann.

Im MQL5-Code ist die Funktionalität zum Lesen von HMM-Modellen, die im JSON-Format gespeichert sind, in hmmlearn.mqh enthalten. Die Datei enthält die Definition der HMM-Klasse.

//+------------------------------------------------------------------+
//|                                                     hmmlearn.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<Math\Alglib\dataanalysis.mqh>
#include<Math\Stat\Uniform.mqh>
#include<Math\Stat\Math.mqh>
#include<JAson.mqh>
#include<Files/FileTxt.mqh>
#include<np.mqh>

//+------------------------------------------------------------------+
//|Markov model estimation method                                    |
//+------------------------------------------------------------------+
enum ENUM_HMM_METHOD
  {
   MODE_LOG=0,
   MODE_SCALING
  };
//+------------------------------------------------------------------+
//| state sequence decoding algorithm                                |
//+------------------------------------------------------------------+
enum ENUM_DECODE_METHOD
  {
   MODE_VITERBI=0,
   MODE_MAP
  };
//+------------------------------------------------------------------+
//| Hidden Markov Model class                                        |
//+------------------------------------------------------------------+
class HMM
  {
private:
   ulong m_samples ;       // Number of cases in dataset
   ulong m_vars ;        // Number of variables in each case
   ulong m_states ;      // Number of states
   vector            m_initprobs;   // vector of probability that first case is in each state
   matrix            m_transition;  // probability matrix
   matrix m_means ;                 //state means
   matrix m_covars[] ;              // covariances
   matrix densities ;              // probability densities
   matrix alpha ;       // result of forward algorithm
   matrix beta ;        // result of backward algorithm
   matrix m_stateprobs ; // probabilities of state
   double likelihood ;  //  log likelihood
   matrix            trial_transition;
   bool              trained;
   double            m_mincovar;
   ENUM_HMM_METHOD   m_hmm_mode;
   ENUM_DECODE_METHOD m_decode_mode;
   //+------------------------------------------------------------------+
   //| normalize array so sum(exp(a)) == 1                              |
   //+------------------------------------------------------------------+
   matrix            log_normalize(matrix &in)
     {
      matrix out;
      if(in.Cols()==1)
         out = matrix::Zeros(in.Rows(), in.Cols());
      else
         out = logsumexp(in);
      return in-out;
     }
   //+------------------------------------------------------------------+
   //| log of the sum of exponentials of input elements                 |
   //+------------------------------------------------------------------+
   matrix            logsumexp(matrix &in)
     {
      matrix out;

      vector amax = in.Max(1);

      for(ulong i = 0; i<amax.Size(); i++)
         if(fpclassify(MathAbs(amax[i])) == FP_INFINITE)
            amax[i] = 0.0;

      matrix ama(amax.Size(),in.Cols());
      for(ulong i=0; i<ama.Cols();i++)
         ama.Col(amax,i);

      matrix tmp = exp(in - ama);

      vector s = tmp.Sum(1);

      out.Init(s.Size(),in.Cols());
      for(ulong i=0; i<out.Cols();i++)
         out.Col(log(s),i);

      out+=ama;

      return out;
     }

   //+------------------------------------------------------------------+
   //| normarlize vector                                                |
   //+------------------------------------------------------------------+
   vector            normalize_vector(vector &in)
     {
      double sum = in.Sum();
      return in/sum;
     }
   //+------------------------------------------------------------------+
   //|  normalize matrix                                                |
   //+------------------------------------------------------------------+
   matrix            normalize_matrix(matrix &in)
     {
      vector sum = in.Sum(1);

      for(ulong i = 0; i<sum.Size(); i++)
         if(sum[i] == 0.0)
            sum[i] = 1.0;

      matrix n;
      n.Init(sum.Size(), in.Cols());
      for(ulong i =0; i<n.Cols(); i++)
         n.Col(sum,i);

      return in/n;
     }
   //+------------------------------------------------------------------+
   //|   Set up model from JSON object                                  |
   //+------------------------------------------------------------------+
   bool              fromJSON(CJAVal &jsonmodel)
     {

      if(jsonmodel["implementation"].ToStr() == "log")
         m_hmm_mode = MODE_LOG;
      else
         m_hmm_mode = MODE_SCALING;

      if(jsonmodel["algorithm"].ToStr() == "Viterbi")
         m_decode_mode = MODE_VITERBI;
      else
         m_decode_mode = MODE_MAP;

      m_states = (ulong)jsonmodel["numstates"].ToInt();
      m_vars = (ulong)jsonmodel["numvars"].ToInt();


      if(!m_initprobs.Resize(m_states) || !m_means.Resize(m_states,m_vars) ||
         !m_transition.Resize(m_states,m_states) || ArrayResize(m_covars,int(m_states))!=int(m_states))
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }

      for(uint i = 0; i<m_covars.Size(); i++)
        {
         if(!m_covars[i].Resize(m_vars,m_vars))
           {
            Print(__FUNCTION__, " error ", GetLastError());
            return false;
           }

         for(int k = 0; k<int(m_covars[i].Rows()); k++)
            for(int j = 0; j<int(m_covars[i].Cols()); j++)
               m_covars[i][k][j] = jsonmodel["covars"][i][k][j].ToDbl();
        }

      for(int i =0; i<int(m_initprobs.Size()); i++)
        {
         m_initprobs[i] = jsonmodel["initprobs"][i].ToDbl();
        }

      for(int i=0; i<int(m_states); i++)
        {
         for(int j = 0; j<int(m_vars); j++)
            m_means[i][j] = jsonmodel["means"][i][j].ToDbl();
        }

      for(int i=0; i<int(m_states); i++)
        {
         for(int j = 0; j<int(m_states); j++)
            m_transition[i][j] = jsonmodel["transitions"][i][j].ToDbl();
        }

      return true;
     }

   //+------------------------------------------------------------------+
   //|  Multivariate Normal Density function                            |
   //+------------------------------------------------------------------+
   double            mv_normal(ulong nv,vector &x, vector &mean, matrix &in_covar)
     {
      matrix cv_chol;
      vector vc = x-mean;

      if(!in_covar.Cholesky(cv_chol))
        {
         matrix ncov = in_covar+(m_mincovar*matrix::Eye(nv,nv));
         if(!ncov.Cholesky(cv_chol))
           {
            Print(__FUNCTION__,": covars matrix might not be symmetric positive-definite, error ", GetLastError());
            return EMPTY_VALUE;
           }
        }

      double cv_log_det = 2.0 * (MathLog(cv_chol.Diag())).Sum();
      vector cv_sol = cv_chol.Solve(vc);

      return -0.5*((nv*log(2.0 * M_PI)) + (pow(cv_sol,2.0)).Sum() + cv_log_det);

     }


   //+------------------------------------------------------------------+
   //|logadd exp                                                        |
   //+------------------------------------------------------------------+
   double            logaddexp(double a, double b)
     {
      return a==-DBL_MIN?b:b==-DBL_MIN?a:MathMax(a,b)+log1p(exp(-1.0*MathAbs(b-a)));
     }
   //+------------------------------------------------------------------+
   //| scaled trans calculation                                         |
   //+------------------------------------------------------------------+
   matrix            compute_scaling_xi_sum(matrix &trans, matrix &dens,matrix &alf, matrix &bta)
     {
      matrix logdens = exp(dens).Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      matrix out;
      out.Resize(nc,nc);
      out.Fill(0.0);

      for(ulong t =0; t<ns-1; t++)
        {
         for(ulong i = 0; i<nc; i++)
           {
            for(ulong j = 0; j<nc; j++)
              {
               out[i][j] += alf[t][i] * trans[i][j] * logdens[t+1][j]*bta[t+1][j];
              }
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| log trans calculation                                            |
   //+------------------------------------------------------------------+
   matrix            compute_log_xi_sum(matrix &trans, matrix &dens,matrix &alf, matrix &bta)
     {
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      vector row = alf.Row(ns-1);
      double logprob = (log(exp(row-row[row.ArgMax()]).Sum()) + row[row.ArgMax()]);

      matrix out;
      out.Init(nc,nc);

      out.Fill(-DBL_MIN);

      for(ulong t = 0 ; t<ns-1; t++)
        {
         for(ulong i =0; i<nc; i++)
           {
            for(ulong j =0; j<nc; j++)
              {
               double vl = alf[t][i] + logtrans[i][j]+ logdens[t+1][j]+bta[t+1][j] - logprob;
               out[i][j] = logaddexp(out[i][j], vl);
              }
           }
        }

      return out;

     }
   //+------------------------------------------------------------------+
   //| forward scaling                                                  |
   //+------------------------------------------------------------------+
   double            forwardscaling(vector &startp, matrix &trans, matrix &dens,matrix &out, vector&outt)
     {
      double minsum = 1.e-300;
      vector gstartp = startp;
      matrix gtrans = trans;
      matrix gdens = exp(dens).Transpose();

      ulong ns = gdens.Rows();
      ulong nc = gdens.Cols();

      if(out.Cols()!=nc || out.Rows()!=ns)
         out.Resize(ns,nc);

      if(outt.Size()!=ns)
         outt.Resize(ns);

      out.Fill(0.0);

      double logprob = 0.0;

      for(ulong i = 0; i<nc; i++)
         out[0][i] = gstartp[i]*gdens[0][i];

      double sum  = (out.Row(0)).Sum();

      if(sum<minsum)
         Print("WARNING: forward pass failed with underflow consider using log implementation ");

      double scale = outt[0] = 1.0/sum;
      logprob -= log(scale);

      for(ulong i=0; i<nc; i++)
         out[0][i] *=scale;

      for(ulong t =1; t<ns; t++)
        {
         for(ulong j=0; j<nc; j++)
           {
            for(ulong i=0; i<nc; i++)
              {
               out[t][j]+=out[t-1][i] * gtrans[i][j];
              }
            out[t][j]*=gdens[t][j];
           }
         sum = (out.Row(t)).Sum();
         if(sum<minsum)
            Print("WARNING: forward pass failed with underflow consider using log implementation ");

         scale = outt[t] = 1.0/sum;
         logprob -= log(scale);
         for(ulong j = 0; j<nc; j++)
            out[t][j] *= scale;

        }
      return logprob;
     }
   //+------------------------------------------------------------------+
   //|backward scaling                                                  |
   //+------------------------------------------------------------------+
   matrix            backwardscaling(vector &startp, matrix &trans, matrix &dens,vector &scaling)
     {
      vector gstartp = startp;
      vector scaled = scaling;
      matrix gtrans = trans;
      matrix gdens =  exp(dens).Transpose();

      ulong ns = gdens.Rows();
      ulong nc = gdens.Cols();

      matrix out;
      out.Init(ns,nc);

      out.Fill(0.0);
      for(ulong i = 0; i<nc; i++)
         out[ns-1][i] = scaling[ns-1];

      for(long t = long(ns-2); t>=0; t--)
        {
         for(ulong i=0; i<nc; i++)
           {
            for(ulong j =0; j<nc; j++)
              {
               out[t][i]+=(gtrans[i][j]*gdens[t+1][j]*out[t+1][j]);
              }
            out[t][i]*=scaling[t];
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| forward log                                                      |
   //+------------------------------------------------------------------+
   double            forwardlog(vector &startp, matrix &trans, matrix &dens,matrix &out)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      if(out.Cols()!=nc || out.Rows()!=ns)
         out.Resize(ns,nc);

      vector buf;
      buf.Init(nc);

      for(ulong i =0; i<nc; i++)
         out[0][i] = logstartp[i] + logdens[0][i];

      for(ulong t =1; t<ns; t++)
        {
         for(ulong j =0; j<nc; j++)
           {
            for(ulong i =0; i<nc; i++)
              {
               buf[i] = out[t-1][i] + logtrans[i][j];
              }
            out[t][j] = logdens[t][j] + (log(exp(buf-buf[buf.ArgMax()]).Sum()) + buf[buf.ArgMax()]);
           }
        }

      vector row = out.Row(ns-1);

      return (log(exp(row-row[row.ArgMax()]).Sum()) + row[row.ArgMax()]);
     }
   //+------------------------------------------------------------------+
   //|  backwardlog                                                     |
   //+------------------------------------------------------------------+
   matrix            backwardlog(vector &startp, matrix &trans, matrix &dens)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      matrix out;
      out.Init(ns,nc);

      vector buf;
      buf.Init(nc);

      for(ulong i =0; i<nc; i++)
         out[ns-1][i] = 0.0;

      for(long t = long(ns-2); t>=0; t--)
        {
         for(long i =0; i<long(nc); i++)
           {
            for(long j =0; j<long(nc); j++)
              {
               buf[j] = logdens[t+1][j] + out[t+1][j] + logtrans[i][j];
              }
            out[t][i] = (log(exp(buf-buf[buf.ArgMax()]).Sum()) + buf[buf.ArgMax()]);
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| compute posterior state probabilities scaling                    |
   //+------------------------------------------------------------------+
   matrix            compute_posteriors_scaling(matrix &alf, matrix &bta)
     {
      return normalize_matrix(alf*bta);
     }
   //+------------------------------------------------------------------+
   //| compute posterior state probabilities log                        |
   //+------------------------------------------------------------------+
   matrix            compute_posteriors_log(matrix &alf, matrix &bta)
     {
      return exp(log_normalize(alf+bta));
     }
   //+------------------------------------------------------------------+
   //|calculate the probability of a state                              |
   //+------------------------------------------------------------------+
   double            compute_posteriors(matrix &data, matrix &result, ENUM_HMM_METHOD use_log=MODE_LOG)
     {
      matrix alfa,bt,dens;
      double logp=0.0;
      dens = find_densities(m_vars,m_states,data,m_means,m_covars);
      if(use_log == MODE_LOG)
        {
         logp = forwardlog(m_initprobs,m_transition,dens,alfa);
         bt = backwardlog(m_initprobs,m_transition,dens);
         result = compute_posteriors_log(alfa,bt);
        }
      else
        {
         vector scaling_factors;
         logp = forwardscaling(m_initprobs,m_transition,dens,alfa,scaling_factors);
         bt = backwardscaling(m_initprobs,m_transition,dens,scaling_factors);
         result = compute_posteriors_scaling(alfa,bt);
        }
      return logp;
     }
   //+------------------------------------------------------------------+
   //| map  implementation                                              |
   //+------------------------------------------------------------------+
   double            map(matrix &data,vector &out, ENUM_HMM_METHOD use_log=MODE_LOG)
     {
      matrix posteriors;
      double lp = compute_posteriors(data,posteriors,use_log);
      lp = (posteriors.Max(1)).Sum();
      out = posteriors.ArgMax(1);
      return lp;
     }
   //+------------------------------------------------------------------+
   //| viterbi implementation                                           |
   //+------------------------------------------------------------------+
   double            viterbi(vector &startp, matrix &trans, matrix &dens, vector &out)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      double logprob = 0;
      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      if(out.Size()<ns)
         out.Resize(ns);

      matrix vit(ns,nc);
      for(ulong i = 0; i<nc; i++)
         vit[0][i] = logstartp[i] + logdens[0][i];

      for(ulong t = 1; t<ns; t++)
        {
         for(ulong i =0; i<nc; i++)
           {
            double max = -DBL_MIN;
            for(ulong j = 0; j<nc; j++)
              {
               max = MathMax(max,vit[t-1][j]+logtrans[j][i]);
              }
            vit[t][i] = max+logdens[t][i];
           }
        }
      out[ns-1] = (double)(vit.Row(ns-1)).ArgMax();
      double prev = out[ns-1];
      logprob = vit[ns-1][long(prev)];
      for(long t = long(ns-2); t>=0; t--)
        {
         for(ulong i =0; i<nc; i++)
           {
            prev = ((vit[t][i]+logtrans[i][long(prev)])>=-DBL_MIN && i>=0)?double(i):double(0);
           }
         out[t] = prev;
        }
      return logprob;
     }
   //+------------------------------------------------------------------+
   //| Calculate the probability density function                       |
   //+------------------------------------------------------------------+
   matrix              find_densities(ulong variables,ulong states,matrix &mdata,matrix &the_means, matrix &covs[])
     {
      matrix out;
      out.Resize(states,mdata.Rows());

      for(ulong state=0 ; state<states ; state++)
        {
         for(ulong i=0 ; i<mdata.Rows() ; i++)
            out[state][i] = mv_normal(variables, mdata.Row(i), the_means.Row(state), covs[state]) ;
        }

      return out;
     }
   //+------------------------------------------------------------------+
   //| Forward algorithm                                                |
   //+------------------------------------------------------------------+

   double            forward(matrix &_transitions)
     {
      double sum, denom, log_likelihood;

      denom = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
        {
         alpha[0][i] = m_initprobs[i] * densities[i][0] ;
         denom += alpha[0][i] ;
        }

      log_likelihood = log(denom) ;
      for(ulong i=0 ; i<m_states ; i++)
         alpha[0][i] /= denom ;


      for(ulong t=1 ; t<m_samples ; t++)
        {
         denom = 0.0 ;
         for(ulong i=0 ; i<m_states ; i++)
           {
            ulong trans_ptr = i;
            sum = 0.0 ;
            for(ulong j=0 ; j<m_states ; j++)
              {
               sum += alpha[t-1][j] * _transitions.Flat(trans_ptr);
               trans_ptr += m_states ;
              }
            alpha[t][i] = sum * densities[i][t] ;
            denom += alpha[t][i] ;
           }
         log_likelihood += log(denom) ;
         for(ulong i=0 ; i<m_states ; i++)
            alpha[t][i] /= denom ;
        }

      return log_likelihood ;

     }
   //+------------------------------------------------------------------+
   //| Backward algorithm                                               |
   //+------------------------------------------------------------------+
   double            backward(void)
     {
      double sum, denom, log_likelihood ;

      denom = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
        {
         beta[(m_samples-1)][i] = 1.0 ;
         denom += beta[(m_samples-1)][i] ;
        }

      log_likelihood = log(denom) ;
      for(ulong i=0 ; i<m_states ; i++)
         beta[(m_samples-1)][i] /= denom ;

      for(long t=long(m_samples-2) ; t>=0 ; t--)
        {
         denom = 0.0 ;
         for(ulong i=0 ; i<m_states ; i++)
           {
            sum = 0.0 ;
            for(ulong j=0 ; j<m_states ; j++)
               sum += m_transition[i][j] * densities[j][t+1] * beta[(t+1)][j] ;
            beta[t][i] = sum ;
            denom += beta[t][i] ;
           }
         log_likelihood += log(denom) ;
         for(ulong i=0 ; i<m_states ; i++)
            beta[t][i] /= denom ;
        }

      sum = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
         sum += m_initprobs[i] * densities[i][0] * beta[0][i] ;

      return log(sum) + log_likelihood ;
     }

public:
   //+------------------------------------------------------------------+
   //| constructor                                                      |
   //+------------------------------------------------------------------+

                     HMM(void)
     {
      trained =false;

      m_hmm_mode = MODE_LOG;
      m_decode_mode = MODE_VITERBI;
      m_mincovar = 1.e-7;
     }
   //+------------------------------------------------------------------+
   //| desctructor                                                      |
   //+------------------------------------------------------------------+

                    ~HMM(void)
     {

     }

   //+------------------------------------------------------------------+
   //| Load model data from regular file                                |
   //+------------------------------------------------------------------+
   bool               load(string file_name)
     {
      trained = false;
      CFileTxt modelFile;
      CJAVal js;
      ResetLastError();

      if(modelFile.Open(file_name,FILE_READ|FILE_COMMON,0)==INVALID_HANDLE)
        {
         Print(__FUNCTION__," failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         if(!js.Deserialize(modelFile.ReadString()))
           {
            Print("failed to read from ",file_name,".Error -",::GetLastError());
            return false;
           }
         trained = fromJSON(js);
        }
      return trained;
     }
   //+------------------------------------------------------------------+
   //|Predict the state given arbitrary input variables                 |
   //+------------------------------------------------------------------+

   matrix            predict_state_probs(matrix &inputs)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__, " Call fit() to estimate the model parameters");
         matrix::Zeros(1, m_states);
        }

      if(inputs.Rows()<2 || inputs.Cols()<m_vars)
        {
         Print(__FUNCTION__, " invalid matrix size ");
         matrix::Zeros(1, m_states);
        }

      matrix probs;
      compute_posteriors(inputs,probs,m_hmm_mode);

      return probs;
     }
   //+------------------------------------------------------------------+
   //|Predict the state sequence of arbitrary input variables           |
   //+------------------------------------------------------------------+
   vector            predict_state_sequence(matrix &inputs, ENUM_DECODE_METHOD decoder=WRONG_VALUE)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__, " Call fit() to estimate the model parameters");
         matrix::Zeros(1, m_states);
        }

      if(inputs.Rows()<2 || inputs.Cols()<m_vars)
        {
         Print(__FUNCTION__, " invalid matrix size ");
         vector::Zeros(1);
        }

      vector seq = vector::Zeros(inputs.Rows());
      ENUM_DECODE_METHOD decm;
      if(decoder!=WRONG_VALUE)
         decm = decoder;
      else
         decm = m_decode_mode;

      switch(decm)
        {
         case MODE_VITERBI:
           {
            matrix d = find_densities(m_vars,m_states,inputs,m_means,m_covars);
            viterbi(m_initprobs,m_transition,d,seq);
            break;
           }
         case MODE_MAP:
           {
            map(inputs,seq,m_hmm_mode);
            break;
           }
        }

      return seq;
     }
   //+------------------------------------------------------------------+
   //| get the loglikelihood of the model                             |
   //+------------------------------------------------------------------+

   double            get_likelihood(matrix &data)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return EMPTY_VALUE;
        }

      matrix dens = find_densities(m_vars,m_states,data,m_means,m_covars);
      matrix alfa;
      vector sc;

      switch(m_hmm_mode)
        {
         case MODE_LOG:
            likelihood = forwardlog(m_initprobs,m_transition,dens,alfa);
            break;
         case MODE_SCALING:
            likelihood = forwardscaling(m_initprobs,m_transition,dens,alfa,sc);
            break;
        }

      return likelihood;
     }
   //+------------------------------------------------------------------+
   //| get the initial state probabilities of the model          |
   //+------------------------------------------------------------------+

   vector            get_init_probs(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return vector::Zeros(1);
        }
      return m_initprobs;
     }
   //+------------------------------------------------------------------+
   //| get the probability transition matrix                            |
   //+------------------------------------------------------------------+

   matrix            get_transition_matrix(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_transition;
     }
   //+------------------------------------------------------------------+
   //|get the state means matrix                                        |
   //+------------------------------------------------------------------+

   matrix            get_means(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_means;
     }

   //+------------------------------------------------------------------+
   //| get the covariance matrix for a particular state                 |
   //+------------------------------------------------------------------+

   matrix            get_covar_matrix_for_state_at(ulong state_index)
     {
      if(!trained || state_index>m_states)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_covars[state_index];
     }
   //+------------------------------------------------------------------+
   //|  get the number of features for the model                |
   //+------------------------------------------------------------------+
   ulong             get_num_features(void)
     {
      return m_vars;
     }
  };


//+------------------------------------------------------------------+

Nachdem wir eine Instanz der HMM-Klasse erstellt haben, rufen wir die Methode „load()“ mit einem bestimmten Dateinamen auf.

//---declare object
   HMM hmm;
//--load exampleHMM model from json file
   if(!hmm.load("exampleHMM.json"))
     {
      Print("error loading model");
      return;
     }

Wenn die Modellparameter erfolgreich gelesen wurden, gibt die Methode true zurück.

Sobald ein Modell geladen ist, können wir die verborgenen Zustände und Zustandswahrscheinlichkeiten für einen bestimmten Satz von Beobachtungen erhalten. Es ist jedoch wichtig zu beachten, dass die Implementierung aller zuvor im Text beschriebenen Algorithmen leicht unterschiedlich ist. Anstelle von Rohwahrscheinlichkeiten verwendet der Code den Logarithmus der Rohwerte, um numerische Stabilität zu gewährleisten. Daher haben wir den Logarithmus der Wahrscheinlichkeiten anstelle von Wahrscheinlichkeiten selbst. Das bedeutet auch, dass wir überall dort, wo eine Multiplikation erforderlich ist, die Addition verwenden müssen, da es sich um den Logarithmus der Werte handelt.

Die HMM-Methode „get_likelihood()“ liefert Wahrscheinlichkeiten für eine Reihe von Beobachtungen auf der Grundlage der geladenen Modellparameter. Sie wird mit Hilfe des Vorwärtsalgorithmus berechnet. Die Methode „predict_state_probs()“ berechnet die Zustandswahrscheinlichkeiten für jede als Eingabe bereitgestellte Beobachtung. Diese Methode gibt eine Matrix zurück, in der jede Zeile die Zustandswahrscheinlichkeiten für eine Beobachtung darstellt.

Andererseits gibt die Methode „predict_state_sequence()“ einen Vektor zurück, der den Zustand für jede als Eingabe bereitgestellte Probe darstellt. Standardmäßig wird der Viterbi-Algorithmus zur Berechnung der wahrscheinlichsten Zustandsfolge verwendet. Es ist jedoch auch möglich, die einfache „Map“-Technik zu wählen, die das Verhalten der Methode „decode()“ des GaussianHMM nachahmt.

Die Klasse „HMM“ bietet Getter-Methoden zum Extrahieren der Parameter eines geladenen Modells:

• „get_means()“: Gibt die Matrix der Mittelwerte zurück, die zur Bestimmung der Wahrscheinlichkeitsdichten verwendet wurden.
• „get_covar_matrix_for_state_at()“: Ermittelt die vollständige Kovarianzmatrix für einen bestimmten Zustand.
• „get_transition_matrix()“: Gibt die Übergangswahrscheinlichkeiten als Matrix zurück.
• „get_init_probs()“: Gibt einen Vektor der Anfangszustandswahrscheinlichkeiten des Modells zurück.
• „get_num_features()“: Gibt einen Long-Wert ohne Vorzeichen zurück, der die Anzahl der Variablen angibt, die als Eingabe für das Modell erwartet werden. Das bedeutet, dass jede Matrix, die als Eingabe für „predict_state_probs()“, „predict_state_sequence()“ und „get_likelihood()“ dient, diese Anzahl von Spalten und mindestens 2 Zeilen haben sollte.

Das Skript saveHMM.py trainiert ein HMM auf der Grundlage eines zufälligen Datensatzes. Sie enthält die Definition der Funktion „hmm2json()“, die für die Speicherung der endgültigen Modellparameter in einer json-Datei verantwortlich ist. Die Daten bestehen aus 10 Zeilen und 5 Spalten. Es wird eine Instanz der Klasse GaussianHMM erstellt und das HMM wird auf den Zufallsdaten trainiert. Nach der Anpassung eines Modus wird „hmm2json()“ aufgerufen, um die Modellparameter in einer json-Datei zu speichern. Anschließend werden die Logarithmen der Wahrscheinlichkeiten, die verborgenen Zustände und die Zustandswahrscheinlichkeiten ausgedruckt.

# Copyright 2024, MetaQuotes Ltd.
# https://www.mql5.com
from hmmlearn import hmm
import numpy as np
import pandas as pd
import json 


assumed_states = 2 #number of states of process
maxhmm_iters = 10000 #maximum number of iterations for optimization procedure

def hmm2json(hmm_model, filename):
    """
    function save a GaussianHMM model to json format 
    readable from MQL5 code.
    param: hmm_model should an instance of GaussianHMM
    param: string. filename or path to file where HMM 
    parameters will be written to
    """
    if hmm_model.__class__.__name__ != 'GaussianHMM':
        raise TypeError(f'invalid type supplied')
    if len(filename) < 1 or not isinstance(filename,str):
        raise TypeError(f'invalid filename supplied')
    jm  = {
            "numstates":hmm_model.n_components,
            "numvars":hmm_model.n_features,
            "algorithm":str(hmm_model.algorithm),
            "implementation":str(hmm_model.implementation), 
            "initprobs":hmm_model.startprob_.tolist(),
            "means":hmm_model.means_.tolist(),
            "transitions":hmm_model.transmat_.tolist(),
            "covars":hmm_model.covars_.tolist()
          }
    with open(filename,'w') as file:
        json.dump(jm,file,indent=None,separators=(',', ':')) 
    return 
#dataset to train model on    
dataset = np.array([[0.56807844,0.67179966,0.13639585,0.15092627,0.17708295],
                   [0.62290044,0.15188847,0.91947761,0.29483647,0.34073613],
                   [0.47687505,0.06388765,0.20589139,0.16474974,0.64383775],
                   [0.25606858,0.50927144,0.49009671,0.0284832,0.37357852],
                   [0.95855305,0.93687549,0.88496015,0.48772751,0.10256193],
                   [0.36752403,0.5283874 ,0.52245909,0.77968798,0.88154157],
                   [0.35161822,0.50672902,0.7722671,0.56911901,0.98874104],
                   [0.20354888,0.82106204,0.60828044,0.13380222,0.4181293,],
                   [0.43461371,0.60170739,0.56270993,0.46426138,0.53733481],
                   [0.51646574,0.54536398,0.03818231,0.32574409,0.95260478]])  
#instantiate an HMM and train on dataset
model = hmm.GaussianHMM(assumed_states,n_iter=maxhmm_iters,covariance_type='full',random_state=125, verbose=True).fit(dataset)  
#save the model to the common folder of Metatrader 5 install
hmm2json(model,r'C:\Users\Zwelithini\AppData\Roaming\MetaQuotes\Terminal\Common\Files\exampleHMM.json')
#get the state probabilities and log likelihood
result = model.score_samples(dataset)
print("log_likelihood " ,result[0]) #print the loglikelihood
print("state sequence ", model.decode(dataset)[1]) #print the state sequence of dataset
print("state probs ", result[1]) #print the state probabilities 

Das entsprechende MetaTrader 5-Skript testHMM.mq5 dient dazu, die von saveHMM.py erstellte json-Datei zu laden. Die Idee ist, die Logarithmen der Wahrscheinlichkeiten, die verdeckten Zustände und die Zustandswahrscheinlichkeiten zu reproduzieren, die von saveHMM.py ausgegeben werden.

//+------------------------------------------------------------------+
//|                                                      TestHMM.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<hmmlearn.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- random dataset equal to that used in corresponding python script saveHMM.py
   matrix dataset =
     {
        {0.56807844,0.67179966,0.13639585,0.15092627,0.17708295},
        {0.62290044,0.15188847,0.91947761,0.29483647,0.34073613},
        {0.47687505,0.06388765,0.20589139,0.16474974,0.64383775},
        {0.25606858,0.50927144,0.49009671,0.0284832,0.37357852},
        {0.95855305,0.93687549,0.88496015,0.48772751,0.10256193},
        {0.36752403,0.5283874,0.52245909,0.77968798,0.88154157},
        {0.35161822,0.50672902,0.7722671,0.56911901,0.98874104},
        {0.20354888,0.82106204,0.60828044,0.13380222,0.4181293},
        {0.43461371,0.60170739,0.56270993,0.46426138,0.53733481},
        {0.51646574,0.54536398,0.03818231,0.32574409,0.95260478}
     };
//---declare object
   HMM hmm;
//--load exampleHMM model from json file
   if(!hmm.load("exampleHMM.json"))
     {
      Print("error loading model");
      return;
     }
//--get the log likelihood of the model
   double lk = hmm.get_likelihood(dataset);
   Print("LL ", lk);
//-- get the state probabilities for a dataset
   matrix probs = hmm.predict_state_probs(dataset);
   Print("state probs ", probs);
//---get the hidden states for the provided dataset
   vector stateseq = hmm.predict_state_sequence(dataset);
   Print("state seq ", stateseq);
  }
//+------------------------------------------------------------------+

Die Ergebnisse der Ausführung beider Skripte sind unten dargestellt.

Ausgabe von saveHMM.py.

KO      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   log_likelihood  47.90226114316213
IJ      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   state sequence  [0 1 1 1 1 0 0 1 0 0]
ED      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   state probs  [[1.00000000e+000 1.32203104e-033]
RM      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
JR      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
RH      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
JM      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
LS      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 5.32945369e-123]
EH      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 8.00195599e-030]
RN      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
HS      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 1.04574121e-027]
RD      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [9.99999902e-001 9.75116254e-008]]

Der Inhalt der gespeicherten JSON-Datei.

{"numstates":2,"numvars":5,"algorithm":"viterbi","implementation":"log","initprobs":[1.0,8.297061845628157e-28],"means":[[0.44766002665812865,0.5707974904960126,0.406402863181157,0.4579477485782787,0.7074610252191268],[0.5035892002511225,0.4965970189510691,0.6217412486192438,0.22191983002481444,0.375768737249644]],"transitions":[[0.4999999756220927,0.5000000243779074],[0.39999999999999913,0.6000000000000008]],"covars":[[[0.009010166768420797,0.0059122234200326374,-0.018865453701221935,-0.014521967883281419,-0.015149047353550696],[0.0059122234200326374,0.0055414217505728725,-0.0062874071503534424,-0.007643976931274206,-0.016093347935464856],[-0.018865453701221935,-0.0062874071503534424,0.0780495488091017,0.044115693492388836,0.031892068460887116],[-0.014521967883281419,-0.007643976931274206,0.044115693492388836,0.04753113728071052,0.045326684356283],[-0.015149047353550696,-0.016093347935464856,0.031892068460887116,0.045326684356283,0.0979523557527634]],[[0.07664631322010616,0.01605057520615223,0.042602194598462206,0.043095659393111246,-0.02756159799208612],[0.01605057520615223,0.12306893856632573,0.03943267795353822,0.019117932498522734,-0.04009804834113386],[0.042602194598462206,0.03943267795353822,0.07167474799610704,0.030420143149584727,-0.03682040884824712],[0.043095659393111246,0.019117932498522734,0.030420143149584727,0.026884283954788642,-0.01676189860422705],[-0.02756159799208612,-0.04009804834113386,-0.03682040884824712,-0.01676189860422705,0.03190589647162701]]]}

Ausgabe von testHMM.mq5.

HD      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   LL 47.90226114316213
EO      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   state probs [[1,1.322031040402482e-33]
KP      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KO      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KF      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KM      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
EJ      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,5.329453688054051e-123]
IP      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,8.00195599043147e-30]
KG      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
ES      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,1.045741207369424e-27]
RQ      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0.999999902488374,9.751162535898832e-08]]
QH      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   state seq [0,1,1,1,1,0,0,1,0,0]

Schlussfolgerung

HMMs sind leistungsstarke statistische Werkzeuge für die Modellierung und Analyse von sequentiellen Daten. Ihre Fähigkeit, die zugrundeliegenden verborgenen Zustände zu erfassen, die die beobachteten Sequenzen antreiben, macht sie wertvoll für Aufgaben, die Zeitreihen wie Finanzdaten betreffen. Trotz ihrer Stärken sind HMMs nicht ohne Einschränkungen. Sie stützen sich auf die Markov-Annahme erster Ordnung, die für komplexe Abhängigkeiten zu vereinfachend sein kann. Der Rechenaufwand für das Training und die Inferenz, insbesondere bei großen Zustandsräumen, und die Möglichkeit der Überanpassung stellen eine große Herausforderung dar. Auch die Auswahl der optimalen Anzahl von Zuständen und die Initialisierung der Modellparameter erfordern sorgfältige Überlegungen und können die Leistung beeinträchtigen. Nichtsdestotrotz bleiben HMMs eine grundlegende Methode der Sequenzmodellierung und bieten einen robusten Rahmen für viele praktische Anwendungen. Mit den laufenden Fortschritten und hybriden Ansätzen, die HMMs mit flexibleren Modellen kombinieren, entwickelt sich ihr Nutzen weiter. Für Praktiker ist es wichtig, sowohl die Möglichkeiten als auch die Grenzen von HMMs zu verstehen, um ihr Potenzial für die Entwicklung des automatisierten Handels effektiv nutzen zu können.

Der gesamte in dem Artikel beschriebene Code ist unten angefügt. Die einzelnen Quellcodedateien sind in der Tabelle beschrieben.

Datei	Beschreibung
Mql5\Python\script\saveHMM.py	demonstriert das Trainieren und Speichern eines Hidden-Markov-Modells und enthält die Definition der Funktion hmm2json().
Mql5\include\hmmlearn.mqh	enthält die Definition einer HMM-Klasse, die den Import von in Python trainierten HMMs zur Verwendung in MQL5 ermöglicht.
Mql5\script\testHMM.mq5	MT5-Skript, das das Laden eines gespeicherten HMM demonstriert.