Pattern Recognition Using Dynamic Time Warping in MQL5

Introduction

Pattern recognition has always been a valuable tool for traders. Whether it's identifying unique combinations of candlesticks or drawing imaginary lines on a chart, these patterns have become an integral part of technical analysis. Humans have always excelled at finding and recognizing patterns—so much so that it is often said we sometimes see patterns where there are none. Therefore, it would benefit us to apply more objective techniques when identifying potentially profitable patterns in financial time series. In this article, we discuss the application of Dynamic Time Warping (DTW) as an objective technique for finding unique patterns in price data. We will explore its origins, how it works, and its application to financial time series analysis. Additionally, we will present the implementation of the algorithm in pure MQL5 and demonstrate its use through a practical example.

Dynamic time warping

Dynamic time warping is a sophisticated algorithm designed to measure the similarity between two sequences of data that evolve over time, even when their speeds or rhythms vary. Unlike traditional methods that require strict alignment between data points, DTW offers a more flexible approach by allowing for warping or stretching of time to find the optimal match between the sequences. Imagine two people walking through a forest on different paths. They both start at the same place and end at the same place, but one might walk faster than the other and make arbitrary stops for whatever reason. DTW helps figure out the best way to match the steps of both, even though they took different paths. DTW can effectively account for differences in walking speed, acceleration, or deceleration, providing a measure of similarity. This versatility makes it applicable to a wide range of data types, including audio, video, and graphics. Any data that can be transformed into a sequential format is a potential candidate for DTW analysis.

DTW was initially developed for speech recognition by Vintsyuk in 1968 and later refined by researchers like Sakoe and Chiba in 1978. The method gained traction in various fields due to its ability to compare sequences of different lengths by warping the time dimension to align similar patterns. DTW has since found applications in diverse areas such as bioinformatics, and gait analysis. Financial markets are characterized by non-linear and non-stationary time series data. Traditional distance measures like Euclidean distance may fail to capture the complexities and distortions in such data. DTW, however, excels in identifying similarities between time series with temporal distortions, making it a suitable tool for analyzing financial markets. By aligning sequences based on their shape rather than their temporal alignment, DTW can uncover unique patterns in financial data.

How it works

When applying the DTW algorithm, the goal is to determine whether a candidate sequence is similar to a predefined reference sequence. The final metric produced by the algorithm indicates the similarity between the candidate and the reference sequence—the lower this value, the more similar the sequences are. If the sequences are the same, this value would be 0. To find the optimal alignment between a candidate sequence and a reference dataset, the DTW algorithm adheres to specific principles. Every point in the candidate sequence must correspond to at least one data point in the reference sequence, and vice versa. The beginning of one sequence must align with the beginning of the other, and the end of one must align with the end of the other. Additionally, when traversing the sequences, the corresponding points must progress forward only. This ensures that no point in one sequence can align with a point that comes before it in the other sequence, preventing any possibility of alignment to previous points.

The process begins by constructing a distance matrix that captures the pairwise distances between elements of the two sequences. Each element of this matrix represents the distance between a point in the first sequence and a corresponding point in the second sequence. At this stage, any of the traditional spatial distance measures can be employed. Spatial distance measures are mathematical methods used to quantify the distance or dissimilarity between data points within a given space. The choice of distance measure depends on the specific characteristics of the data and the task at hand. The table below lists the most common spatial distance measures and brief descriptions of each.

Distance Metric	Description
Euclidean Distance	Euclidean distance is the straight-line distance between two points in Euclidean space. It is the most intuitive and widely used distance measure.
Manhattan Distance	Manhattan distance, also known as taxicab or city block distance, measures the distance between two points by summing the absolute differences of their coordinates.
Minkowski Distance	Minkowski distance is a generalized form of both Euclidean and Manhattan distances. It includes a parameter that can be adjusted to switch between different distance measures.
Chebyshev Distance	Chebyshev distance, also known as maximum or chessboard distance, measures the most significant difference between coordinates of a pair of points.
Cosine Similarity	Cosine similarity measures the cosine of the angle between two non-zero vectors, representing their directional similarity rather than magnitude.

The choice of spatial distance measure depends on the nature of the data and the specific requirements of the task. Understanding the differences and applications of these measures helps in selecting the most appropriate one for meaningful analysis.

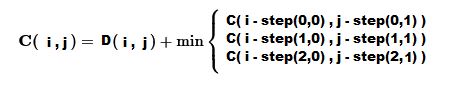
In the next step, the distance matrix is used to calculate the cumulative cost matrix, where each element represents the minimal cost of aligning the sequences. This alignment process involves transforming the candidate sequence so that it closely resembles the reference sequence. The cumulative cost matrix quantifies how much individual points in the candidate sequence need to be altered to best match the reference values. A larger cost indicates a more significant transformation, signifying greater dissimilarity between the sequences. These cumulative cost matrix values are used to determine the optimal warping path, which represents the sequence of alignments that map one time series to another while minimizing the distance between them. Essentially, the warping path illustrates how parts of a sequence are stretched or compressed to align as closely as possible with another sequence.

To find the warping path, we imagine the sequences placed on a grid, with one sequence along the x-axis and the other along the y-axis. Each point on this grid represents a possible match between an element from the first sequence and an element from the second sequence. The warping path is the route through this grid that results in the best alignment between the two sequences. The path starts in the bottom-left corner of the grid, corresponding to the first elements of both sequences, and ends in the top-right corner, corresponding to the last elements of both sequences. As the path progresses, it can move in three directions: diagonally, which matches elements from both sequences; horizontally, which repeats an element from the first sequence; or vertically, which repeats an element from the second sequence. This movement ensures that the alignment process always moves forward in time and does not skip any elements in the sequences.

The warping path is chosen to minimize the cumulative distance or cost between the aligned elements of the two sequences. To achieve this, the distance matrix values are overlaid on the grid that will be used to align the points. The cost at each point on the grid is calculated by adding the corresponding distance metric to the minimum value of adjacent cumulative distances from previous points, following the three possible directions (diagonal, horizontal, or vertical) that can be taken when moving forward in time. Since each grid point is associated with the distance metric of corresponding sequence values, the minimum value represents the operation required to transform the candidate sequence to match the reference sequence. If the minimum cumulative distance lies diagonally to the current point, it represents a matching operation. If the smallest cumulative distance from previous points is horizontal to the current point, it indicates an insertion operation, where a value from the reference sequence is effectively inserted into the candidate sequence. Conversely, if the minimum cumulative distance is vertical to the current point, it signifies a deletion operation, where a value from the candidate sequence is removed. The choice of prior cumulative distance values considered to find the minimum is governed by a specific step pattern.

Step patterns determine the allowable moves or transitions between points in the sequences during alignment. They specify the number of points in any of the valid directions (diagonal, horizontal, vertical) considered when calculating the minimum cumulative distance. The choice of step pattern significantly influences the alignment process and the overall distance calculation. Various step patterns exist, each tailored for specific applications. Practitioners can also create custom step patterns, provided they adhere to the principles of forward motion and continuity. In this text, we will focus on the most common and generic step patterns, which have proven effective across different domains. For those interested in exploring other step patterns, the papers by Sakoe-Chiba, Rabiner-Juang, and Rabiner-Myers offer in-depth insights.

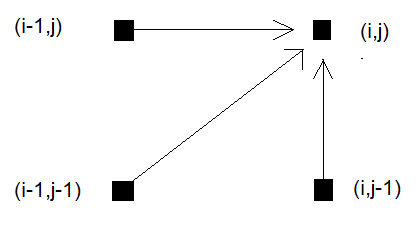
The most commonly applied step pattern is the standard step pattern, also known as the symmetric or classic step pattern. Its main advantage is that it ensures both time series are fully traversed. This pattern considers only the immediate values above, to the right, and diagonal to the current point, allowing for diagonal, horizontal, and vertical single-step movements on the grid.

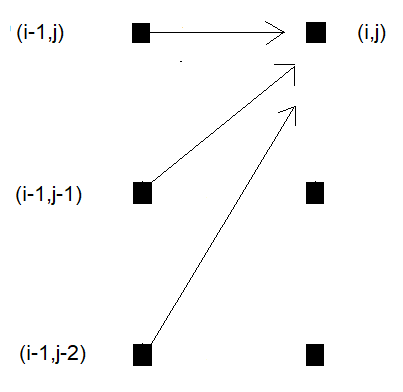
Another popular step pattern is the classic asymmetric pattern. Similar to the standard step pattern, it defines transitions in three directions but introduces a bias toward one sequence. This pattern allows the algorithm to move diagonally, but if a point is skipped, it favors progressing forward in one sequence more than the other. It is often used alongside additional constraints that limit the algorithm's movements on the grid. In the case of the asymmetric step pattern, an additional slope constraint is applied, restricting the steepness or flatness of the warping path. This constraint is useful when the sequences are expected to be similar in length and shift, as it prevents one sequence from being overly stretched or compressed relative to the other.

Additional constraints can be applied to prevent alignments that are technically perfect but meaningless, which may result in overfitting the data. These constraints ensure that the alignment makes logical sense within the context of the data being analyzed, preventing excessive stretching or compression of the sequences. Such constraints are known as global constraints and enhance the effectiveness and interpretability of the DTW algorithm in practical applications. Two common global constraints are the Sakoe-Chiba band and the Itakura parallelogram.

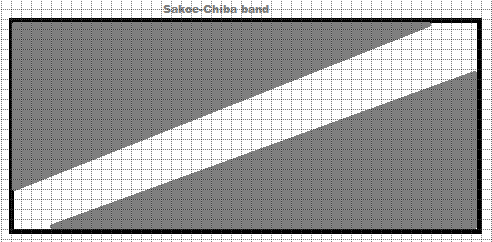
The Sakoe-Chiba band restricts the warping path to stay within a fixed band around the diagonal of the alignment matrix. This prevents the alignment from deviating too far from the original timing or shift, which is useful in tasks where slight timing differences are expected, but large deviations are not.

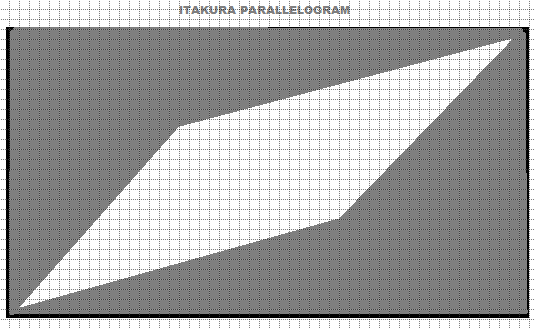
The Itakura parallelogram constraint defines a parallelogram-shaped region within which the warping path must remain. It is narrower at the ends and wider in the middle, which is particularly useful when sequences are expected to align more closely at the beginning and end, but allow for some flexibility in the middle. Global constraints are essential to the DTW for controlling the warping process and ensuring that the resulting alignment is relevant to the specific task. It is important to select the most appropriate constraints based on the characteristics of the datasets and the goals of the analysis.

Once the cumulative cost matrix is completed, it is used to determine the optimal warping path. The algorithm traces back from the last element of the cumulative cost matrix to the first, identifying the path that minimizes the total alignment cost. This path represents the best alignment between the sequences. The final value in the cumulative cost matrix provides the overall distance score, which is also used to calculate the normalized distance score. The warping path will list the paired indices that represent aligned points in both sequences. To assess the alignment procedure, it is common to plot the optimal warping path. A satisfactory result should yield a roughly diagonal plot. This diagonal plot indicates that the sequences are well-aligned, with a perfectly straight diagonal line corresponding to two identical sequences. In the following section we will discuss a MQL5 native implementation of dynamic time warping.

MQL5 implementation

The DTW MQL5 implementation is presented in the include file dtw.mqh. It does not offer complete or extensive coverage of all aspects of dynamic time warping. Later on, we will look at a Python implementation of the DTW that offers a lot more features. The goal in creating this library is to provide the basic functionality for calculating the distance score. The library is a partial fork of the dtw-python module.

The code starts by defining enumerations for step patterns and various distance measures and global constraints.

//+------------------------------------------------------------------+
//|  step patterns                                                   |
//+------------------------------------------------------------------+
enum ENUM_STEP_PATTERN
  {
   STEP_SYMM1=0,//symmetric1
   STEP_SYMM2,//symmetric2
   STEP_ASYMM//asymmetric
  };

ENUM_STEP_PATTERN: Defines a set of enumerations that restrict permissible transition patterns during the path search phase of the DTW algorithm. These patterns guide the warping process and influence the allowed alignments between the time series.

//+------------------------------------------------------------------+
//|  distance metric                                                 |
//+------------------------------------------------------------------+
enum ENUM_DIST_METRIC
  {
   DIST_EUCLIDEAN=0,//euclidean
   DIST_CITYBLOCK,//city block
   DIST_COSINE,//cosine
   DIST_CORRELATION,//correlation
   DIST_CHEBYSHEV,//chebyshev
   DIST_SQEUCLIDEAN//squared euclidean
  };

ENUM_DIST_METRIC: Provides a collection of enumerations corresponding to supported distance metrics. These metrics quantify the dissimilarity between data points in the time series, with options like Euclidean distance, City Block distance, and more.

//+------------------------------------------------------------------+
//|   window function                                                |
//+------------------------------------------------------------------+
enum ENUM_GLOBAL_CONSTRAINT
  {
   CONSTRAINT_NONE=0,// no constrains applied
   CONSTRAINT_SAKOECHIBA,// sakoe chiba
   CONSTRAINT_SLATEDBAND,// slated band
   CONSTRAINT_ITAKURA// itakura
  };

ENUM_GLOBAL_CONSTRAINT: Encompasses different global restrictions that impose constraints during path search. These can influence the warping flexibility and potentially improve alignment accuracy.

//+------------------------------------------------------------------+
//| lists the transitions allowed while searching                    |
//|for the minimum-distance path                                     |
//+------------------------------------------------------------------+
class CStepPattern
  {
private:
   matrix            m_mx,m_stepsMatrix;
   ENUM_HINT         m_stephint;
public:
                     CStepPattern(matrix &mx, matrix &stepmatrix, ENUM_HINT hint=HINT_NA)
     {
      m_mx = mx;
      m_stepsMatrix = stepmatrix;
      m_stephint = hint;
     }
                    ~CStepPattern(void)
     {

     }
   matrix            getStepMatrix(void)
     {
      return m_stepsMatrix;
     }
   ulong             getNRows(void)
     {
      return m_mx.Rows();
     }
   int               getNPatterns(void)
     {
      vector vec = m_mx.Col(0);
      return (int(vec.Max()));
     }

   CStepPattern*     T(void)
     {
      ulong cols[] = {0, 2, 1, 3};

      matrix cpy = np::selectMatrixCols(m_mx,cols);
      ENUM_HINT hint = m_stephint;

      if(m_stephint == HINT_N)
         hint = HINT_M;
      else
         if(m_stephint == HINT_M)
            hint = HINT_N;

      CStepPattern* out = new CStepPattern(cpy,m_stepsMatrix,hint);

      return out;
     }

   matrix            extractPattern(vector &sn)
     {
      vector col  =  m_mx.Col(0);
      matrix out = matrix::Ones(1,1);
      for(ulong i = 0; i<m_mx.Rows(); i++)
        {
         for(ulong j = 0; j<col.Size(); j++)
           {
            if(col[j] == sn[j])
              {
               if(!out.Resize(out.Rows()+1,m_mx.Cols()-1,100))
                 {
                  Print(__FUNCTION__, " error ", GetLastError());
                  return matrix::Zeros(1,1);
                 }
               vector v = m_mx.Row(j);
               vector vv = np::sliceVector(v,1);
               if(!out.Row(vv,out.Rows()-1))
                 {
                  Print(__FUNCTION__, " error ", GetLastError());
                  return matrix::Zeros(1,1);
                 }
              }
           }
        }

      if(!np::reverseMatrixRows(out))
        {
         Print(__FUNCTION__, " Reverse Matrix failure ");
         return matrix::Zeros(1,1);
        }
      return out;
     }

   matrix            mkDIrDeltas(void)
     {
      matrix out = matrix::Zeros(1,1);
      vector col = m_mx.Col(3);
      for(ulong i = 0; i<m_mx.Rows(); i++)
        {
         for(ulong j = 0; j<col.Size(); j++)
           {
            if(col[j] == -1.0)
              {
               if(!out.Resize(out.Rows()+1,m_mx.Cols(),100))
                 {
                  Print(__FUNCTION__, " error ", GetLastError());
                  return matrix::Zeros(1,1);
                 }
               vector v = m_mx.Row(j);
               if(!out.Row(v,out.Rows()-1))
                 {
                  Print(__FUNCTION__, " error ", GetLastError());
                  return matrix::Zeros(1,1);
                 }
              }
           }
        }

      return np::sliceMatrixCols(out,1,3);
     }

   matrix             getP(void)
     {
      ulong sel[] = {0, 2, 1, 3};
      matrix s = np::selectMatrixCols(m_mx,sel);
      return s;
     }

   matrix            getMx(void)
     {
      return m_mx;
     }
  };

CStepPattern is a class designed to handle different step patterns by managing matrices that define the allowed transitions and operations. It provides methods to extract patterns based on specific sequences and to manipulate matrices for directional deltas, essential for DTW computations.

//+------------------------------------------------------------------+
//| Global constraints                                               |
//+------------------------------------------------------------------+
class CConstraint
  {
public:
                     CConstraint(void)
     {

     }
                    ~CConstraint(void)
     {

     }

   static matrix       noConstraint(ulong iw,ulong jw)
     {
      matrix mats[];

      np::indices(iw,jw,mats);

      for(ulong i = 0; i<mats[0].Rows(); i++)
        {
         for(ulong j = 0; j<mats[0].Cols(); j++)
           {
            long value = long(mats[0][i][j]);
            mats[0][i][j] = (double)(value|1);
            if(mats[0][i][j]==0.0)
               mats[0][i][j] = double("inf");
           }
        }

      return mats[0];
     }

   static matrix       sakoeChibaConstraint(ulong iw,ulong jw, ulong qsize, ulong refsize, ulong winsize)
     {
      matrix mats[];

      np::indices(iw,jw,mats);

      matrix abs = MathAbs(mats[1]-mats[0]);

      for(ulong i = 0; i<abs.Rows(); i++)
        {
         for(ulong j = 0; j<abs.Cols(); j++)
           {
            if(ulong(abs[i][j])<=winsize)
               abs[i][j] = (double)(1);
            else
               abs[i][j] = double("inf");
           }
        }

      return abs;
     }

   static matrix       itakuraConstraint(ulong iw,ulong jw, ulong qsize, ulong refsize)
     {
      matrix mats[];

      np::indices(iw,jw,mats);

      long a,b,c,d;

      for(ulong i = 0, k = 0; i<mats[0].Rows() && k<mats[1].Rows(); i++,k++)
        {
         for(ulong j = 0; j<mats[0].Cols(); j++)
           {
            a = long(mats[1][k][j]) < (2*long(mats[0][i][j]))?1:0;
            b = long(mats[0][i][j]) <=(2*long(mats[1][k][j]))?1:0;
            c = long(mats[0][i][j]) >=(long(qsize)-1-2*(long(refsize)-long(mats[1][k][j])))?1:0;
            d = long(mats[1][k][j]) > (long(refsize)-1-2*(long(qsize)-long(mats[0][i][j])))?1:0;
            mats[0][i][j] = double(ulong(a&b&c&d));
            if(mats[0][i][j]==0.0)
               mats[0][i][j] = double("inf");
           }
        }

      return mats[0];
     }

   static matrix       slantedBandConstraint(ulong iw,ulong jw, ulong qsize, ulong refsize,ulong winsize)
     {

      matrix mats[];

      np::indices(iw,jw,mats);

      matrix  diagj = (mats[0]*refsize/qsize);

      matrix abs = MathAbs(mats[1]-diagj);


      for(ulong i = 0; i<abs.Rows(); i++)
        {
         for(ulong j = 0; j<abs.Cols(); j++)
           {
            if(ulong(abs[i][j])<=winsize)
               abs[i][j] = (double)(1);
            else
               abs[i][j] = double("inf");
           }
        }

      return abs;

     }

  };

The CConstraint class includes static methods for effecting different types of constraints, such as Sakoe-Chiba, Itakura, and Slanted Band. These help constrain the DTW alignment to improve computational efficiency and relevance by limiting the search space based on predefined criteria.

• The noConstraint() method: Generates a matrix filled with ones, signifying the absence of any constraints.

• The sakoeChibaConstraint() method: Imposes a Sakoe-Chiba constraint based on the specified window size and the lengths of the time series.

• The itakuraWindow() method: Enforces an Itakura constraint using the lengths of the time series.

• The slantedBandConstraint() method: Implements a Slanted Band constraint based on the window size and the lengths of the time series.
  

The Cdtw class is the core class responsible for DTW calculations.

   //+------------------------------------------------------------------+
   //|     main interface method for dtw                                |
   //+------------------------------------------------------------------+

   bool              dtw(matrix&x, matrix&y, ENUM_DIST_METRIC dist_method,ENUM_STEP_PATTERN step_pattern=STEP_SYMM2, ENUM_GLOBAL_CONSTRAINT win_type=CONSTRAINT_NONE,ulong winsize=0)
     {
      if(y.Cols()!=x.Cols())
        {
         Print(__FUNCTION__, " invalid input parameters, size containers donot match. ");
         return false;
        }

      if(CheckPointer(m_stepPattern)==POINTER_DYNAMIC)
         delete m_stepPattern;

      switch(step_pattern)
        {
         case STEP_SYMM1:
            m_stepPattern = new CStepPattern(_symmetric1,Symmetric);
            m_stephint = HINT_NA;
            break;

         case STEP_SYMM2:
            m_stepPattern = new CStepPattern(_symmetric2,Symmetric,HINT_NM);
            m_stephint = HINT_NM;
            break;

         case STEP_ASYMM:
            m_stepPattern = new CStepPattern(_asymmetric,Asymmetric,HINT_N);
            m_stephint = HINT_N;
            break;
        }

      if(CheckPointer(m_stepPattern)==POINTER_INVALID)
        {
         Print(__FUNCTION__," failed step pointer initialization ", GetLastError());
         return false;
        }

      matrix stepsMatrix = m_stepPattern.getStepMatrix();
      m_query = x;
      m_qlen = x.Rows();
      m_ref = y;
      m_reflen = y.Rows();
      m_distMetric = dist_method;
      m_winMethod = win_type;
      m_winsize = winsize;

      if(y.Rows())
        {
         if(!m_distance.Resize(m_qlen,m_reflen))
           {
            Print(__FUNCTION__," resize error ", GetLastError());
            return false;
           }
         for(ulong i = 0; i<m_qlen; i++)
            for(ulong j =0; j<m_reflen; j++)
               m_distance[i][j]=dist(m_query.Row(i),m_ref.Row(j));
        }
      else
         m_distance = m_query;

      ulong n,m;
      n=m_distance.Rows();
      m=m_distance.Cols();
      matrix wm;
      if(m_winMethod == CONSTRAINT_NONE)
         wm = matrix::Ones(m_distance.Rows(), m_distance.Cols());
      else
        {
         switch(m_winMethod)
           {
            case CONSTRAINT_ITAKURA:
               wm = CConstraint::itakuraConstraint(n,m,m_qlen,m_reflen);
               break;
            case CONSTRAINT_SAKOECHIBA:
               wm = CConstraint::sakoeChibaConstraint(n,m,m_qlen,m_reflen,m_winsize);
               break;
            case CONSTRAINT_SLATEDBAND:
               wm = CConstraint::slantedBandConstraint(n,m,m_qlen,m_reflen,m_winsize);
               break;
            default:
               wm = CConstraint::noConstraint(n,m);
               break;
           }
        }

      if(m_winMethod!=CONSTRAINT_NONE)
        {
         for(ulong i = 0; i<wm.Rows(); i++)
            for(ulong j = 0; j<wm.Cols(); j++)
               if((i+j)>0 && wm[i][j] != 1.0)
                  m_distance[i][j] = wm[i][j];
        }


      m_costMatrix = matrix::Zeros(m_distance.Rows()+ulong(stepsMatrix.Col(0).Max()),m_distance.Cols()+ulong(stepsMatrix.Col(1).Max()));
      m_costMatrix.Fill(double("inf"));
      m_costMatrix[ulong(stepsMatrix.Col(0).Max())][ulong(stepsMatrix.Col(1).Max())] = m_distance[0][0];

      m_dirMatrix = matrix::Zeros(m_costMatrix.Rows(),m_costMatrix.Cols());
      m_dirMatrix.Fill(double(INT_MIN));
      for(ulong i = 0; i<m_dirMatrix.Cols(); i++)
         m_dirMatrix[0][i] = double(1);
      for(ulong i = 0; i<m_dirMatrix.Rows(); i++)
         m_dirMatrix[i][0] = double(2);

      if(!calCM(m_distance,stepsMatrix,m_costMatrix,m_dirMatrix))
        {
         Print(__FUNCTION__, " computeCM() failed ");
         return false;
        }

      m_jmin = m_costMatrix.Cols() - 1;

      return true;
     }

It provides the dtw() method as the primary function for performing DTW. Note that the method is overloaded to cater for univariate (vectors) and multivariate (matrices) time series. It takes two time series (represented as matrices or vectors), distance metric, step pattern, a global constraint, and window size as input arguments. On invocation, the method begins by performing various checks on the validity of input data and the chosen step pattern. This is followed by the calculation of the distance matrix based on the selected distance metric. If a global constraint is specified, the cost and direction matrices used during the DTW algorithm are prepared accordingly. The calCM() function is then invoked to compute the accumulated cost matrix. Finally, the dtw() function returns a boolean value indicating success or failure. 

   //+------------------------------------------------------------------+
   //|    Get the optimal path: corresponding points from both series   |
   //+------------------------------------------------------------------+

   matrix            warpPath(bool openEnd=false)
     {
      matrix stmatrix = m_stepPattern.getStepMatrix();
      return backtrack(m_dirMatrix,stmatrix,openEnd,openEnd?long(m_costMatrix.Row(m_costMatrix.Rows()-1).ArgMin()):-1);
     }

The warpPath() method retrieves the optimal path (corresponding points) identified from both time series based on an optional 'openEnd' argument that controls path termination (open or closed).

   //+------------------------------------------------------------------+
   //|     Get the accumulated cost matrix                              |
   //+------------------------------------------------------------------+

   matrix            costMatrix(void)
     {
      return m_costMatrix;
     }

The costMatrix() method provides access to the accumulated cost matrix, a key output of the DTW algorithm.

   //+------------------------------------------------------------------+
   //|       Get the cost matrix                                        |
   //+------------------------------------------------------------------+

   matrix            localCostMatrix(void)
     {
      return m_distance;
     }

The localCostMatrix() method returns the local distance matrix, representing the pairwise distances between data points in the time series.

   //+------------------------------------------------------------------+
   //|        Get the direction matrix                                  |
   //+------------------------------------------------------------------+

   matrix            directionMatrix(void)
     {
      return m_dirMatrix;
     }

The directionMatrix() method grants access to the direction matrix, which plays a role in guiding the path search process during DTW.

   //+------------------------------------------------------------------+
   //|  private method implementing accumulated cost calculation        |
   //+------------------------------------------------------------------+

   bool              calCM(matrix &distMatrix,matrix &stepMatrix,matrix &costMatrix,matrix &dirMatrix)
     {
      ulong max0,max1;
      max0 = ulong(stepMatrix.Col(0).Max());
      max1 = ulong(stepMatrix.Col(1).Max());
      double curCost,curd;

      for(ulong i = max0; i<costMatrix.Rows(); i++)
        {
         for(ulong j = max1; j<costMatrix.Cols(); j++)
           {
            for(ulong k = 0; k<stepMatrix.Rows(); k++)
              {
               curd = costMatrix[i-ulong(stepMatrix[k][0])][j-ulong(stepMatrix[k][1])];
               curCost = curd + distMatrix[i-max0][j-max1];
               if(curCost<costMatrix[i][j])
                 {
                  costMatrix[i][j] = curCost;
                  dirMatrix[i][j] = double(k);
                 }
              }
           }
        }
      costMatrix = np::sliceMatrix(costMatrix,max0,END,1,max1);
      dirMatrix  = np::sliceMatrix(dirMatrix,max0,END,1,max1);
      return true;

     }

The calCM() private method calculates the accumulated cost matrix, a core component of the DTW algorithm. It utilizes the distance matrix, step pattern, cost matrix, and direction matrix as input.

   //+------------------------------------------------------------------+
   //|  distance metric calculation                                     |
   //+------------------------------------------------------------------+


   double            dist(vector &u,vector &v)
     {
      switch(m_distMetric)
        {
         case DIST_EUCLIDEAN:
            return euclidean(u,v);
         case DIST_CITYBLOCK:
            return cityblock(u,v);
         case DIST_CHEBYSHEV:
            return chebyshev(u,v);
         case DIST_CORRELATION:
            return correlation(u,v);
         case DIST_COSINE:
            return cosine(u,v);
         case DIST_SQEUCLIDEAN:
            return sqeuclidean(u,v);
         default:
            Print(__FUNCTION__, " invalid parameter ");
            return EMPTY_VALUE;
        }
     }

The dist() private function calculates the distance between two data points based on a chosen distance metric.

Testing the Cdtw class

In this section, we will demonstrate the capabilities of the Cdtw class by comparing its output relative to that produced by a Python-based implementation of the DTW. The module, dtw-python, is one of a number of DTW implementations in Python. We will run a simple script in Python and see if the results can be reproduced by our MQL5 implementation. We begin by listing the Python script.

import numpy as np
import matplotlib.pyplot as plt
import dtw

len = 10
add_noise = True
noise = np.random.uniform(size=len)if add_noise else np.zeros((len,))
arx = np.linspace(start = 1, stop = 6.28,num = len)
query = np.sin(arx) + noise
ref = np.cos(arx)

alignment =  dtw.dtw(query,ref,dist_method='cosine',step_pattern='symmetric2', window_type=None,keep_internals=True)
print( f'Accumulated Cost Matrix is {alignment.costMatrix}')
print(f'Distance is {alignment.distance}, \n normalize distance is {alignment.normalizedDistance}')
print(f'Warp Path is {alignment.index1[:]}:{alignment.index2[:]}')
plt.plot(alignment.index1,alignment.index2)
plt.show()

This script demonstrates how to align two time series using the DTW algorithm and visualize the alignment. The code begins by importing necessary libraries: 'numpy' for numerical operations, 'matplotlib.pyplot' for plotting, and 'dtw' for implementing the DTW algorithm. The length of the time series is set to 10, and an array arx of 10 evenly spaced values between 1 and 6.28 is created. A time series 'query' is generated by taking the sine of 'arx' and adding some random noise, while the reference time series ref is generated by taking the cosine of 'arx'. The DTW alignment is then performed between the 'query' and 'ref' series. The distance between the time series is measured using the cosine distance method, and a symmetric step pattern is applied to the warping path. No windowing constraint is used, and internal details like the cost matrix and warping path are retained.

The code then prints the accumulated cost matrix, the total alignment distance, the normalized distance, and the indices of the warping path between the two series. Finally, the warping path is visualized by plotting the alignment indices, showing how the indices of the two time series align, and the plot is displayed. This approach allows for a detailed comparison of two time series that may be out of phase or have different lengths, enabling the observation of how one series warps to align with the other.

The MQL5 equivalent of the Python code just described is given below.

//+------------------------------------------------------------------+
//|                                                      dtwTest.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Math\Stat\Uniform.mqh>
#include<dtw.mqh>
//---
input ulong series_len = 10;
input bool  AddRandomNoise = false;
input ENUM_DIST_METRIC AppliedDistanceMetric = DIST_EUCLIDEAN;
input ENUM_STEP_PATTERN AppliedStepPattern = STEP_SYMM2;
input ENUM_GLOBAL_CONSTRAINT AppliedGlobalConstraint = CONSTRAINT_NONE;
input ulong GlobalConstraintWinSize = 0;
input bool WarpPathConstraint = false;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   if(series_len<10)
     {
      Alert(" Invalid input for series_len parameter. Should be >=10 ");
      return;
     }
//---
   vector arg = np::linspace(1.0,6.28,series_len);
   vector noise = vector::Zeros(series_len);

   if(AddRandomNoise)
     {
      double array[];
      if(!MathRandomUniform(0.0,1.0,int(series_len),array))
        {
         Print(__LINE__, " MathRandomUniform() failed ", GetLastError());
         return;
        }

      if(!noise.Assign(array))
        {
         Print(__LINE__, " vector assignment failure ", GetLastError());
         return;
        }
     }

   vector q = sin(arg) + noise; // candidate sequence
   vector rf =  cos(arg);       // reference sequence

   Cdtw cdtw;

   cdtw.dtw(q,rf,AppliedDistanceMetric,AppliedStepPattern,AppliedGlobalConstraint,GlobalConstraintWinSize);

   Print(" local cm ", cdtw.localCostMatrix());
   Print(" final cm ", cdtw.costMatrix());
   Print(" direction matrix \n", cdtw.directionMatrix());
   matrix path = cdtw.warpPath();
   Print(" Warp path \n", cdtw.warpPath());
   Print(" Distance metric ", cdtw.distance());
   Print(" Normalized Distance metric ", cdtw.normalizedDistance());

   vector xx = path.Col(0);
   vector yy = path.Col(1);

   CGraphic *g = np::plotXY(xx,yy,"Warp Plot", " Query ", " Reference ");

   Sleep(20000);
   g.Destroy();
   ChartRedraw();
   delete g;
  }
//+------------------------------------------------------------------+

The output from the Python script:

KQ      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily) Accumulated Cost Matrix is [[ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
RD      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
FH      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
JL      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
NQ      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
GD      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 2.  0.  0.  0.  0.  0.  0.  2.  4.  6.]
QH      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 4.  0.  0.  0.  0.  0.  0.  2.  4.  6.]
KL      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 6.  0.  0.  0.  0.  0.  0.  2.  4.  6.]
GS      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 6.  2.  2.  2.  2.  2.  2.  0.  0.  0.]
PJ      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 6.  4.  4.  4.  4.  4.  4.  0.  0.  0.]]
LJ      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily) Distance is 0.0, 
MM      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  normalize distance is 0.0
CH      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily) Warp Path is [0 1 2 3 4 5 5 5 5 6 7 8 8 9]:[0 0 0 0 0 1 2 3 4 5 6 7 8 9]

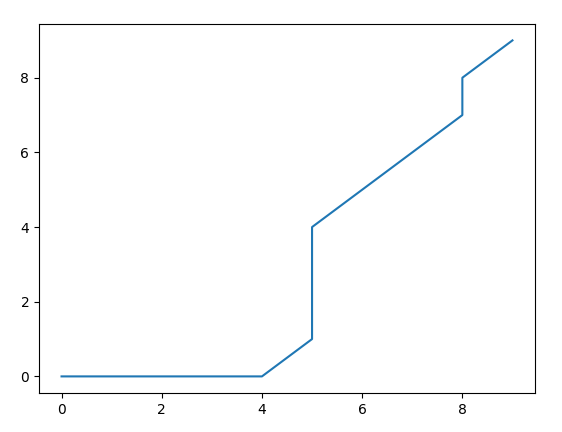
The output from the MQL5 script:

NE      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         local cm [[0,2,2,2,2,2,2,0,0,0]
LH      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
FR      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
HE      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
RL      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
DF      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [2,2.220446049250313e-16,0,0,2.220446049250313e-16,0,0,2,2,2]
ND      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,2,2,2]
FR      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,2.220446049250313e-16,2,2,2]
RS      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
OH      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]]
ML      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         final cm [[0,2,4,6,8,10,12,12,12,12]
JR      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,4,6,8,10,12,12,12,12]
JH      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,4,6,8,10,12,12,12,12]
JN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,4,6,8,10,12,12,12,12]
JD      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,4,6,8,10,12,12,12,12]
EI      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,4.440892098500626e-16,4.440892098500626e-16,4.440892098500626e-16,2,4,6]
CP      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [4,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2,4,6]
EH      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,4.440892098500626e-16,2,4,6]
IN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,2,2,2,2,2,2,4.440892098500626e-16,4.440892098500626e-16,4.440892098500626e-16]
HS      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,4,4,4,4,4,4,4.440892098500626e-16,4.440892098500626e-16,4.440892098500626e-16]]
MO      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         direction matrix 
QK      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)        [[-2147483648,1,1,1,1,1,1,1,1,1]
GN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,0,0,0]
QQ      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,0,0,0]
CK      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,0,0,0]
MR      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,0,0,0]
OE      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,1,1,1,1,1,1,1,1]
HO      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2,0,0,0,1,1,1,0,0]
MF      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2,0,0,0,0,0,0,0,0]
CH      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2,0,0,0,0,0,0,1,1]
LN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2,0,0,0,0,0,2,0,0]]
PK      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         Warp path 
HM      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)        [[9,9]
GJ      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [8,8]
HS      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [8,7]
DK      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [7,6]
HP      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,5]
QI      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,4]
GQ      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [5,3]
RN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [5,2]
MG      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [5,1]
CO      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [4,0]
LD      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [3,0]
EL      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0]
JE      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [1,0]
DO      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,0]]
LD      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         Distance metric 4.440892098500626e-16
NR      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         Normalized Distance metric 2.2204460492503132e-17

Comparing the output from both scripts confirms that the code seems to be working well enough. We can therefore use it for something more practical. This brings us to how the DTW may be put to use in strategy development.

Applying dynamic time warping

The DTW can be utilized in automated strategy development by enabling flexible pattern recognition and comparison techniques of financial time series. For instance, DTW allows for the identification of recurring price patterns, even when they occur at different scales or with varying time dynamics. By aligning these patterns with historical data, it becomes possible to detect subtle shifts and anomalies that may precede significant market movements.

In back testing, DTW can be applied to compare the performance of different strategies across varying market conditions by aligning their respective time series outcomes. This approach helps in assessing how well a strategy adapts to changes in market behavior, providing a more in-depth understanding of its robustness. Additionally, DTW can be used to cluster similar trading signals or market states, which can then be analyzed to identify high-probability trading opportunities. By recognizing these clusters, a strategy can be fine-tuned to exploit recurring market behaviors more effectively.

Furthermore, in the optimization of algorithmic strategies, DTW can assist in matching the most promising parameter sets with historical market conditions that closely resemble current market dynamics. This enables the strategy to adapt more dynamically to evolving market conditions. By leveraging DTW, automated strategies can thus become more adaptive, context-aware, and capable of recognizing complex temporal relationships in financial data. Whilst the DTW may be a useful tool, it is no magic wand. It can be difficult to work with, especially for inexperienced users.

One of the biggest problems with DTW relates to the configuration of its operating parameters. The right combination of global and local constraints is crucial for getting the most out of the method. DTW is prone to producing spurious matches, and achieving the best results often requires a lot of trial and error. This is demonstrated in the MQL5 script below.

//+------------------------------------------------------------------+
//|                                             dtwPatternSearch.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#resource "\\Indicators\\LogReturns.ex5"
#property script_show_inputs
#include<dtw.mqh>
#include<ErrorDescription.mqh>
enum ENUM_PRICE
  {
   CLOSE=0,//close price
   MEDIAN,//median price
   TYPICAL//typical price
  };

enum ENUM_TRANSFORM_TYPE
  {
   PERCENT_DIFF=0,//percent difference
   LOG_DIFF//log difference
  };
//--- input parameters
input string   Pattern = "0.0469,0.0093,0.0697,-0.0699";
input string   SymbolName="BTCUSD";
input datetime SearchStartDate=D'2024.06.01';
input datetime SearchStopDate=D'2018.04.22';
input double   NormalizedDistanceThreshold=0.01;
input ENUM_TIMEFRAMES      TimeFrame=PERIOD_D1;
input ENUM_DIST_METRIC AppliedDistanceMetric = DIST_EUCLIDEAN;
input ENUM_STEP_PATTERN AppliedStepPattern = STEP_SYMM2;
input ENUM_GLOBAL_CONSTRAINT AppliedGlobalConstraint = CONSTRAINT_NONE;
input ulong GlobalConstraintWinSize = 0;
input ENUM_PRICE AppliedPrice=CLOSE;
input ENUM_TRANSFORM_TYPE AppliedTransform=LOG_DIFF;
input int Lag = 1;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   string pattern_values[];
//---
   int len = StringSplit(Pattern,StringGetCharacter(",",0),pattern_values);
   if(pattern_values[len-1]=="")
      len--;
//---
   if(len<3)
     {
      Alert("Pattern sequence is inadequately defined");
      return;
     }
//---
   vector pattern(len);
   for(ulong i = 0; i<pattern.Size(); i++)
      pattern[i]=StringToDouble(pattern_values[i]);
//---set prices handle
   int handle = INVALID_HANDLE;
   handle=iCustom(SymbolName!=""?SymbolName:NULL,TimeFrame,"::Indicators\\LogReturns.ex5",AppliedPrice,AppliedTransform,1);
   if(handle==INVALID_HANDLE)
     {
      Print("invalid handle ",ErrorDescription(GetLastError()));
      return;
     }
//---
   vector searchBuffer;
   if(!searchBuffer.CopyIndicatorBuffer(handle,0,SearchStartDate,SearchStopDate))
     {
      Print("History loading error ",ErrorDescription(GetLastError()));
      return;
     }
//---
   ulong stop = searchBuffer.Size()-pattern.Size();
   vector subv;
   Cdtw cdtw;
   ulong counter=0;
   for(ulong i = 0; i<stop; i++)
     {
      subv = np::sliceVector(searchBuffer,i,i+pattern.Size());

      if(!cdtw.dtw(subv,pattern,AppliedDistanceMetric,AppliedStepPattern,AppliedGlobalConstraint,GlobalConstraintWinSize))
        {
         Print(" dtw failed ");
         return;
        }

      if(cdtw.normalizedDistance()<NormalizedDistanceThreshold)
        {
         counter++;
         Print(" pattern found  ", datetime(SearchStopDate+(PeriodSeconds(TimeFrame)*(i+pattern.Size()-1))));
        }
     }
//---
   Print(" SearchBuffer size ", searchBuffer.Size());
   Print(" Reference pattern found ", counter, " times.");
  }
//+------------------------------------------------------------------+

The script allows a user to define an arbitrary pattern made up from a sequence of log returns, calculated by the indicator, 'LogReturns.ex5'. The script is designed to search for a specific pattern within the price data of a financial instrument, using Dynamic Time Warping (DTW) for comparison. It includes the necessary libraries, such as dtw.mqh for the DTW algorithm and ErrorDescription.mqh for handling error descriptions. The script defines two enumerations: ENUM_PRICE, which specifies the type of price to use (close, median, or typical), and ENUM_TRANSFORM_TYPE, which determines how the price data will be transformed (percent difference or logarithmic difference).

The input parameters allow the user to specify details for the search, including the pattern to be matched, the symbol name (e.g., "BTCUSD"), the date range for the search, a threshold for the normalized distance, the time frame of the data, the distance metric, the step pattern, the global constraint, the window size for the constraint, the type of price to be used, the type of transformation to apply, and a lag value. When the script starts, it first splits the input pattern string into an array of values, ensuring that the pattern is adequately defined with at least three values. If the pattern is valid, it is converted into a vector format for further processing. The script then attempts to load the price data by using the iCustom function to call a custom indicator (LogReturns.ex5) that applies the selected price type and transformation to the data. If the handle returned by iCustom is invalid, an error message is printed, and the script exits.

Assuming the price data is loaded successfully, it is stored in a 'searchBuffer' vector. The script then iterates through the 'searchBuffer', slicing it into smaller sub-vectors of the same size as the pattern and comparing each sub-vector to the pattern using the DTW algorithm. The DTW comparison uses the specified distance metric, step pattern, and global constraint. For each comparison, if the normalized distance between the sub-vector and the pattern is less than the specified threshold, the script considers the pattern to be found at that point in the price data. It prints a message indicating the timestamp where the pattern was found and increments a counter. Finally, the script prints the size of the 'searchBuffer' and the total number of times the pattern was found within the specified date range. This script allows for the automated detection of specific patterns in historical price data, which can be useful in developing trading strategies based on pattern recognition.

The default sequence describes the pattern illustrated below.

Running the script with different constraints applied produces a varying number of matches. This is the output using the default settings.

RN      0       22:00:09.210    dtwPatternSearch (BTCUSD,D1)    Chosen Parameters
IJ      0       22:00:09.210    dtwPatternSearch (BTCUSD,D1)    Distance Threshold 0.01
CS      0       22:00:09.210    dtwPatternSearch (BTCUSD,D1)    DIST_EUCLIDEAN
ND      0       22:00:09.211    dtwPatternSearch (BTCUSD,D1)    STEP_SYMM2
CN      0       22:00:09.211    dtwPatternSearch (BTCUSD,D1)    CONSTRAINT_NONE
HG      0       22:00:09.211    dtwPatternSearch (BTCUSD,D1)     WinSize 0
OO      0       22:00:09.211    dtwPatternSearch (BTCUSD,D1)     pattern found  2018.04.25 00:00:00
NJ      0       22:00:09.221    dtwPatternSearch (BTCUSD,D1)     pattern found  2019.04.28 00:00:00
KD      0       22:00:09.222    dtwPatternSearch (BTCUSD,D1)     pattern found  2019.07.01 00:00:00
QO      0       22:00:09.230    dtwPatternSearch (BTCUSD,D1)     pattern found  2020.04.27 00:00:00
II      0       22:00:09.234    dtwPatternSearch (BTCUSD,D1)     pattern found  2020.10.26 00:00:00
PD      0       22:00:09.237    dtwPatternSearch (BTCUSD,D1)     pattern found  2021.02.06 00:00:00
RN      0       22:00:09.250    dtwPatternSearch (BTCUSD,D1)     pattern found  2024.01.29 00:00:00
DH      0       22:00:09.250    dtwPatternSearch (BTCUSD,D1)     SearchBuffer size 2197
PQ      0       22:00:09.250    dtwPatternSearch (BTCUSD,D1)     Reference pattern found 7 times.

The 'NormalizedDistanceThreshold' parameter obviously plays a significant role in determining whether a match exists. Still, varying constraints can lead to considerably different results. It’s not just the constraints; users also have to choose the appropriate distance metric. Clearly, significant domain knowledge is essential when employing the DTW algorithm.

Conclusion

Dynamic Time Warping offers a sophisticated approach to pattern recognition in financial time series analysis, but it also comes with several disadvantages that should be considered. First, DTW is computationally intensive, especially when dealing with long time series or large datasets. The algorithm involves comparing each point in one time series to every point in another, which can result in significant processing time and memory usage. This becomes particularly problematic when attempting to analyze high-frequency financial data or perform real-time analysis. Second, DTW is sensitive to noise and outliers in financial data.

Financial time series are often noisy due to market volatility, and small fluctuations or anomalies can cause the DTW algorithm to produce misleading alignments. This sensitivity may lead to false positives in pattern recognition, where patterns are identified that do not hold significant predictive power. Finally, DTW can struggle with interpretability. While it provides a measure of similarity between time series, the warping path and the resulting distance metric can be difficult to interpret in a meaningful way, especially in the context of financial analysis where clear and actionable insights are crucial. These challenges suggest that while DTW can be a useful tool for pattern recognition in financial time series, it should be applied carefully and often in combination with other analytical methods that can address its limitations.

File	Description
Mql5\include\np.mqh	header file of various vector and matrix utility functions
Mql5\include\dtw.mqh	include file containing the MQL5 implementation of the Dynamic time warping algorithm
Mql5\indicators\LogReturns.mq5	indicator of log returns of a price series
Mql5\scripts\dwTest.mq5	script used to test and demonstrate use of the MQL5 implementation of DTW
Mql5\scripts\dtwPatternSearch.mq5	script used to search for an arbitrary pattern in a sample of data
Mql5\scripts\DTW.py	a Python script that uses the dtw-python module to align two series using the DTW algorithm