
Eigenvectors and eigenvalues: Exploratory data analysis in MetaTrader 5
Introduction
Principal Component Analysis (PCA) is widely known for its role in dimensionality reduction during data exploration. However, its potential extends far beyond reducing large datasets. At the core of PCA are eigenvalues and eigenvectors, which play a crucial role in uncovering hidden relationships within data. In this article, we will explore techniques that leverage eigenstructure to reveal these hidden relationships.
We will start with factor analysis, demonstrating how eigenstructure helps identify latent variables, offering a more comprehensive understanding of the data's underlying structure. By identifying latent variables, we can expose redundancies among seemingly independent variables, showing how multiple variables might simply reflect the same underlying factor. Additionally, we will examine how eigenvectors and eigenvalues can be used to assess the relationships between variables over time. By analyzing the eigenstructure of data collected at different intervals, we can gain valuable insights into the dynamic relationships between variables. Allowing us to identify variables that move in tandem or exhibit contrasting behaviour over time.
Latent Variables in Data: Principal Factor Analysis
Factor analysis is a methodology aimed at uncovering hidden factors that explain the interrelations among observed variables in data. It represents measured variables as combinations of latent factors, which signify constructs that are known to have an effect but are difficult to measure or quantify. For instance, consider the indicators a trader uses to evaluate market behavior. Factor analysis could reveal that these indicators are influenced by underlying factors such as investor sentiment or risk appetite. While it may be straightforward to compute technical indicators, quantifying market sentiment or risk appetite is more challenging. It's like observing ripples on the surface of a murky body of water. The ripples represent what we see, while the underlying cause remains hidden. Factor analysis aims to uncover these hidden causes.
Factor analysis is often mistaken for an alternative to principal components analysis (PCA). Both techniques reduce the dimensionality of data but differ in how the reduced variables relate to the original set. PCA reduces a large set of variables into a smaller set of uncorrelated or orthogonal variables called principal components. These components capture the maximum variance of the original data. Imagine a dense dataset with hundreds of variables. Conducting PCA might reveal that only three variables represent more than 99% of the data's information. These three principal components correspond to distinct properties inherent in the observed data, explained by combining bits of the original data. Each principal component is influenced by the dense set of variables. In contrast, factor analysis theorizes that latent variables influence the observed variables. In this text we focus on computing these hidden dimensions and the unique perspectives they provide on the observed variables, rather than on dimensionality reduction.
Eigenvalues and eigenvectors are fundamental mathematical concepts crucial for understanding this article. If matrix A is a p by p matrix, x is a column vector of length p, and E is a scalar, then x is an eigenvector of A with eigenvalue E if Ax=Ex. The eigenvector's direction is significant, not its length, and it's typically normalized to unit length. Geometrically, multiplying a vector by a matrix generally rotates it, but eigenvectors remain directionally unchanged when multiplied by the matrix. This direction is key to their relevance. In a standardized multivariate normal distribution, the covariance matrix is the correlation matrix R. Let V be a p by m matrix. The new random vector y=V'x has a covariance matrix C=V'RV.
The matrix V has desirable properties that translate to y. For m=1, V is a single column, and C is the variance of y. Normalizing V so that its components sum to one yields the eigenvector of R corresponding to the largest eigenvalue. Extending this to m=2, the second column of V, orthogonal to the first, is the eigenvector of R corresponding to the second-largest eigenvalue. This process continues for all p columns, making the eigenvectors of R the transformation matrix for mapping x variables to independent y variables that capture the most variance.
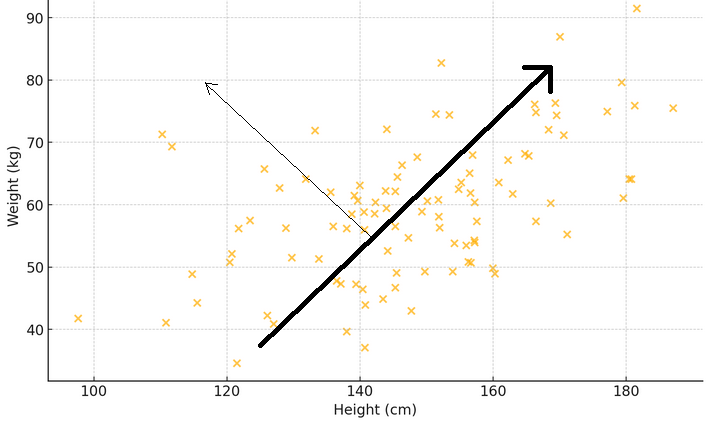
To illustrate what the previous two paragraphs mean, consider a scatter plot where the x-axis measures the weight and the y-axis represents the height of a sample of people. If a line is drawn through the dots that best matches the spread of the measurements, this line will depict the main pattern: taller people tend to be heavier. Now, think of an eigenvector as an arrow that points in this main direction, showing the biggest trend or the dominat pattern. The corresponding eigenvalue tells you how strong this phenomenon is. If another arrow is drawn perpendicular to the first, it shows a secondary pattern, like how some people might be heavier or lighter than usual for their height.
The goal is to determine how each observed variable relates to the eigenvalues of the correlation matrix. This involves computing the correlations between the eigenvalues and the observed variables. These correlations form a special matrix called the factor loading matrix, derived by multiplying each eigenvector by the square root of its corresponding eigenvalue. By examining how variables correlate with certain eigenvalues, we can hypothesize about the effects on the observed variables. This analysis helps us understand which variables are most relevant to the factors and provides clues about the appropriate number of factors influencing the observed variables.
Example: Principal Factor Analysis on Financial Indicators
In this section, we will demonstrate Principal Factor Analysis (PFA) on a dataset of financial indicators. We will use MQL5 to implement all the steps involved in calculating the factor loading matrix. We start by collecting the data of interest. Which in this context, will consist of a few indicators, sampled within a specified range of window lengths. For demonstration purposes we will use two common indicators, the Moving Average (MA) indicator , which provides information about the trend, and the Average True Range (ATR) , which provides a basic measure of volatility. Several window lengths of these indicators will be collected over a period of time.
Since most of the analysis involves the examination of potentially large matrices, simply printing them to the terminal's experts tab is inadequate due to their size. Given the objective to perform all the analyses within MetaTrader 5 without switching to other platforms like Python or R, a graphical user interface was incorporated in the application that implements PFA. Below is a graphic showing the data set we will be working with in this example. Each column contains the values for an indicator for a particular window length as given by the column header. "ATR_2" referrs to the ATR indicator with a window lenght of 2. The zero index points to the oldest value in time, in the period 2019.12.31 to 2022.12.31 based on daily prices of BitCoin (BTCUSD).
Before attempting to extract the principal factors, it would be prudent to assess whether a dataset is amenable to factor analysis. There are two statistical tests that can be done on a dataset to determine if the variables are likely to be explained by latent factors. The first is the Kaiser-Meyer-Olkin (KMO) test. The KMO criterion is a statistic that measures the adequacy of sample data for factor analysis. It quantifies the degree of correlation among variables and evaluates the proportion of variance among variables that might be common variance, that which can be attributed to underlying factors. The KMO measure compares the magnitude of observed correlation coefficients to the magnitude of partial correlation coefficients. It ranges from 0 to 1, where:
- Values close to 1 indicate that the data is highly suitable for factor analysis.
- Values below 0.6 generally indicate that the data is not suitable for factor analysis.
Mathematically, the KMO statistic is defined as:
Where:
- r(ij) is the correlation coefficient between variables i and j.
- p(ij) is the partial correlation coefficient between variables i and j.
Below is a MQL5 implementation of the KMO test. The function 'kmo()' requires a three input parameters. The matrix 'in' should be supplied with the dataset of variables being studied. The results of the test will be output to the second and third input parameters, respectively. The vector 'kmo_per_item' will contain the KMO values for each variable ( corresponding to each column of 'in' matrix) and 'kmo_total' is the overall KMO statistic for the combined variables.
//+---------------------------------------------------------------------------+ //| Calculate the Kaiser-Meyer-Olkin criterion | //| In general, a KMO < 0.6 is considered inadequate. | //+---------------------------------------------------------------------------+ void kmo(matrix &in, vector &kmo_per_item, double &kmo_total) { matrix partial_corr = partial_correlations(in); matrix x_corr = (stdmat(in)).CorrCoef(false); np::fillDiagonal(x_corr,0.0); np::fillDiagonal(partial_corr,0.0); partial_corr = pow(partial_corr,2.0); x_corr = pow(x_corr,2.0); vector partial_corr_sum = partial_corr.Sum(0); vector corr_sum = x_corr.Sum(0); kmo_per_item = corr_sum/(corr_sum+partial_corr_sum); double corr_sum_total = x_corr.Sum(); double partial_corr_sum_total = partial_corr.Sum(); kmo_total = corr_sum_total/(corr_sum_total + partial_corr_sum_total); return; }
An alternetive or additional test that can be done to assess a dataset is Bartlett’s Test of Sphericity, (BTS). It is a statistical test used to examine whether a correlation matrix is an identity matrix, which would indicate that the variables are unrelated and unsuitable for structure detection methods such as factor analysis. Essentially, it tests if the observed correlation matrix diverges significantly from the identity matrix, where all diagonal elements are 1 ,indicating that variables perfectly correlate with themselves, and off-diagonal elements are 0, indicating no correlation between different variables. The test is based on the Chi-square test, whose test statistic is calculated using the following formula:
where :
- n is the number of observations.
- p is the number of variables.
-|R| is the determinant of the correlation matrix R.
The test statistic follows a Chi-square distribution with (p(p-1))/2 degrees of freedom. If the Bartlett’s test statistic is large and the associated p-value is small , typically p-value < 0.05, we reject the null hypothesis. This suggests that the correlation matrix significantly differs from an identity matrix, indicating that the variables are related and suitable for factor analysis. Otherwise, if the p-value is large, we fail to reject the null hypothesis, suggesting that the correlation matrix is close to an identity matrix, and the variables are not significantly correlated.
The code below defines the 'bartlet_sphericity()' function which implements BTS. The function ouputs its results to the last two input parameters. Both of which are scalar values. 'statistic' is the Chi-square statistic and 'p_value' is the computed probability value.
//+------------------------------------------------------------------+ //| Compute the Bartlett sphericity test. | //+------------------------------------------------------------------+ void bartlet_sphericity(matrix &in, double &statistic, double &p_value) { long n,p; n = long(in.Rows()); p = long(in.Cols()); matrix x_corr = (stdmat(in)).CorrCoef(false); double corr_det = x_corr.Det(); double neg = -log(corr_det); statistic = (corr_det>0.0)?neg*(double(n)-1.0-(2.0*double(p)+5.0)/6.0):DBL_MAX; double degrees_of_freedom = double(p)*(double(p)-1.0)/2.0; int error; p_value = 1.0 - MathCumulativeDistributionChiSquare(statistic,degrees_of_freedom,error); if(error) Print(__FUNCTION__, " MathCumulativeDistributionChiSquare() error ", error); return; }
If one of or both of the tests provide encouraging results we can move forward with principal factor extraction. Using the data set of indicators we can see that both tests show the variables are suitable for factor extraction.
The next step involves a little preprocessing, where the dataset is standardized. Standardizing the data ensures that each indicator contributes equally to the analysis, regardless of its scale.
//+------------------------------------------------------------------+ //| standardize a matrix | //+------------------------------------------------------------------+ matrix stdmat(matrix &in) { vector mean = in.Mean(0); vector std = in.Std(0); std+=1e-10; matrix out = in; for(ulong row =0; row<out.Rows(); row++) if(!out.Row((in.Row(row)-mean)/std,row)) { Print(__FUNCTION__, " error ", GetLastError()); return matrix::Zeros(in.Rows(), in.Cols()); } return out; }
The correlation matrix is calculated from the standardized data.
m_data = stdmat(in);
m_corrmat = m_data.CorrCoef(false); Then we calculate the eigenvalues and eigenvectors of the correlation matrix. We opted use the eigenvector decompostion implementation provide by the Aglib library due to a problem encountered whilst using the "Eig()" method for native matrices.
CMatrixDouble cdata(m_corrmat); CMatrixDouble vects; CRowDouble vals; if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Cols(),1,true,vals,vects)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; }
The problem is best illustrated through an example. The code below defines a script that decomposes the eigenvectors and values of a symmetric matrix.
//+------------------------------------------------------------------+ //| TestEigenDecompostion.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include<Math\Alglib\linalg.mqh> //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- matrix dataset = { {1,0.5,-0.2}, {0.5,1,-0.8}, {-0.2,-0.8,1} }; matrix evectors; vector evalues; dataset.Eig(evectors,evalues); Print("Eigen decomposition of \n", dataset); Print(" EVD using built in Eig() \n", evectors); Print(evalues); CMatrixDouble data(dataset); CMatrixDouble vects; CRowDouble vals; CEigenVDetect::SMatrixEVD(data,data.Rows(),1,true,vals,vects); Print(" EVD using Alglib implementation \n", vects.ToMatrix()); Print(vals.ToVector()); } //+------------------------------------------------------------------+
The output of the script is given next.
It shows the difference in how the eigenvectors and values are presented. The Alglib implementation sorts the vectors and values in ascending order, which is more convenient. The MQL5 native method "Eig()" does not provide any ordering but this is not the main reason for disparaging it. Looking at the last eigenvector (column) we notice that the signs of the individual values are the exact opposit to those of the corresponding values output from the Alglib code. It is not clear why this is the case. To confirm whether this was an anomaly, the same decompostion was performed using Python's Numpy and the Alglib results were replicated. Its obvious the factor loadings will be sensitive to the sign of eigenvector member values. Seeing as that the loadings are defined as correlations, the sign of the value has significant meaning.
The factor loading matrix is derived by multiplying each eigenvector by the square root of its corresponding eigenvalue. To prevent the possibility of getting invalid numbers, we first replace any eigenvalues less that zero with 0. This effectively discards the associated dimension (eigenvector) in the factor loading matrix.
m_structmat = m_eigvectors; vector copyevals = m_eigvalues; if(!copyevals.Clip(0.0,DBL_MAX)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } for(ulong i = 0; i<m_structmat.Cols(); i++) if(!m_structmat.Col(m_eigvectors.Col(i)*sqrt(copyevals[i]),i)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } if(!m_structmat.Clip(-1.0,1.0)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; }
The code snippets we have seen so far were extracted from the Cpfa class, for conducting Principal Factor Analysis (PFA) in MetaTrader 5. The full class is shown below, followed by a table that documents its public methods.
//+------------------------------------------------------------------+ //| Principal factor extraction | //+------------------------------------------------------------------+ class Cpfa { private: bool m_fitted; //flag showing if principal factors were extracted matrix m_corrmat, //correlation matrix m_data, //standardized data is here m_eigvectors, //matrix of eigen vectors of correlation matrix m_structmat; //factor loading matrix vector m_eigvalues, //vector of eigen values m_cumeigvalues; //eigen values sorted in descending order long m_indices[];//original order of column indices in input data matrix public: //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ Cpfa(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ ~Cpfa(void) { } //+------------------------------------------------------------------+ //| fit() called with input matrix and extracts principal factors | //+------------------------------------------------------------------+ bool fit(matrix &in) { m_fitted = false; m_data = stdmat(in); m_corrmat = m_data.CorrCoef(false); CMatrixDouble cdata(m_corrmat); CMatrixDouble vects; CRowDouble vals; if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Cols(),1,true,vals,vects)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } m_eigvectors = vects.ToMatrix(); m_eigvalues = vals.ToVector(); double sum = 0.0; double total = m_eigvalues.Sum(); if(!np::reverseVector(m_eigvalues) || !np::reverseMatrixCols(m_eigvectors)) return m_fitted; m_cumeigvalues = m_eigvalues; for(ulong i=0 ; i<m_cumeigvalues.Size() ; i++) { sum += m_eigvalues[i] ; m_cumeigvalues[i] = 100.0 * sum/total; } m_structmat = m_eigvectors; vector copyevals = m_eigvalues; if(!copyevals.Clip(0.0,DBL_MAX)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } for(ulong i = 0; i<m_structmat.Cols(); i++) if(!m_structmat.Col(m_eigvectors.Col(i)*sqrt(copyevals[i]),i)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } if(!m_structmat.Clip(-1.0,1.0)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } m_fitted = true; return m_fitted; } //+------------------------------------------------------------------+ //| returns factor loading matrix | //+------------------------------------------------------------------+ matrix get_factor_loadings(void) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return matrix::Zeros(1,1); } return m_structmat; } //+------------------------------------------------------------------+ //| get the eigenvector and values of correlation matrix | //+------------------------------------------------------------------+ bool get_eigen_structure(matrix &out_eigvectors, vector &out_eigvalues) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return false; } out_eigvalues = m_eigvalues; out_eigvectors = m_eigvectors; return true; } //+------------------------------------------------------------------+ //| returns variance contributions for each factor as a percent | //+------------------------------------------------------------------+ vector get_cum_var_contributions(void) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return vector::Zeros(1); } return m_cumeigvalues; } //+------------------------------------------------------------------+ //| get the correlation matrix of the dataset | //+------------------------------------------------------------------+ matrix get_correlation_matrix(void) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return matrix::Zeros(1,1); } return m_corrmat; } //+------------------------------------------------------------------+ //| returns the rotated factor loadings | //+------------------------------------------------------------------+ matrix rotate_factorloadings(ENUM_FACTOR_ROTATION factor_rotation_type) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return matrix::Zeros(1,1); } CRotator rotator; if(!rotator.fit(m_structmat,factor_rotation_type,4,true)) return matrix::Zeros(1,1); else return rotator.get_transformed_loadings(); } };
| Method | Description | Return Type |
|---|---|---|
| fit | Extracts principal factors from the input matrix `in`. This function standardizes the input data, computes the correlation matrix, and performs eigen decomposition. It also computes the factor loading matrix and cumulative eigenvalues. This is the method that should be called first after object instantiation. | bool |
| get_factor_loadings | Returns the factor loading matrix if principal factors have been extracted; otherwise, returns a zero matrix. The loadings will be sorted in descending order relative to the largest eigenvalue. After 'fit()' completes successfully , this and other methods can be called to retrieve properties of the analysis. | matrix |
| get_eigen_structure | Returns the eigenvectors and eigenvalues of the correlation matrix. Optionally sorts them. | matrix, vector |
| get_cum_var_contributions | Returns the cumulative variance contributions of each factor as a percentage, if principal factors have been extracted; otherwise, returns a zero vector. | vector |
| get_correlation_matrix | Returns the correlation matrix of the dataset if principal factors have been extracted; otherwise, returns a zero matrix. | matrix |
| rotate_factorloadings | Returns the rotated factor loadings matrix using the specified rotation type if principal factors have been extracted; otherwise, returns a zero matrix. | matrix |
We now know how to get the factor loadings, in the next section we will see what these correlations convey.
Interpreting factor loadings
Factor loadings represent the correlation between the observed variables and the underlying latent factors. They indicate the extent to which a variable is associated with a factor. To facilitate interpretation, the eigenvectors are arranged in descending order according to the magnitude of their corresponding eigenvalues. This ensures that the first eigenvector corresponds to the largest eigenvalue, which references the latent factor with the highest influence on the observed variables. The rows of the factor loading matrix follow the same order as the columns of the original dataset, meaning each row corresponds to a variable. The columns depict the factors arranged in descending order of explained variance. Correlations above 0.4 or below -0.4 are considered significant. Any variable with loadings within the range of -0.4 to 0.4 indicates that the corresponding factor has little impact on that variable.
| Variables | Factor 1 | Factor 2 | Factor 3 |
|---|---|---|---|
| X1 | 0.8 | 0.3 | 0.1 |
| X2 | -0.3 | -0.93 | 0.00002 |
| X3 | 0.0 | 0.342 | -1 |
| X4 | 0.5 | 0.1 | -0.38 |
| X5 | 0.5 | -0.33 | 0.44 |
Data sets with a simple factor structure have variables that load highly on one factor and low on others. The table above represents the factor loadings of a hypothetical dataset. Variables X1 to X4 show that they are loading significantly onto distinct factors whilst variable X5 gives mixed signals due to it loading mildly to two factors simultaneously. Characteristics of the meaured variable in conjuction with its factor loadings can provide clues as to the nature of the underlying factor. For instance, if several economic indicators load highly on a single factor, this factor might represent an underlying economic trend or market sentiment. Conversely, if a variable loads moderately on multiple factors, it may suggest that the variable is influenced by several underlying factors, each contributing to a different aspect of the variable’s behaviour.
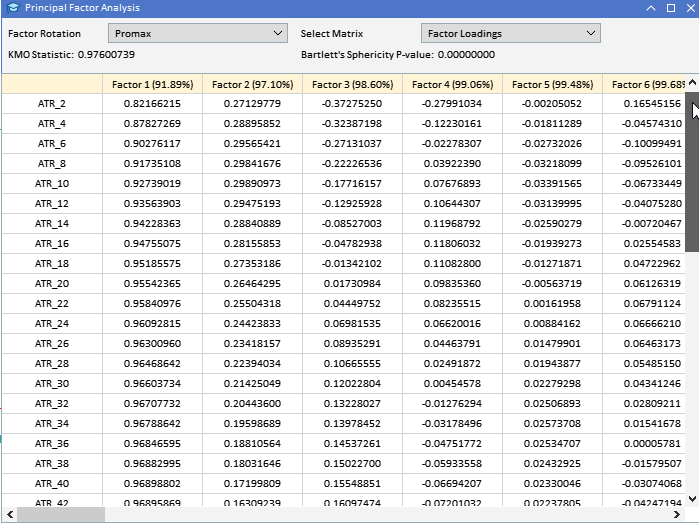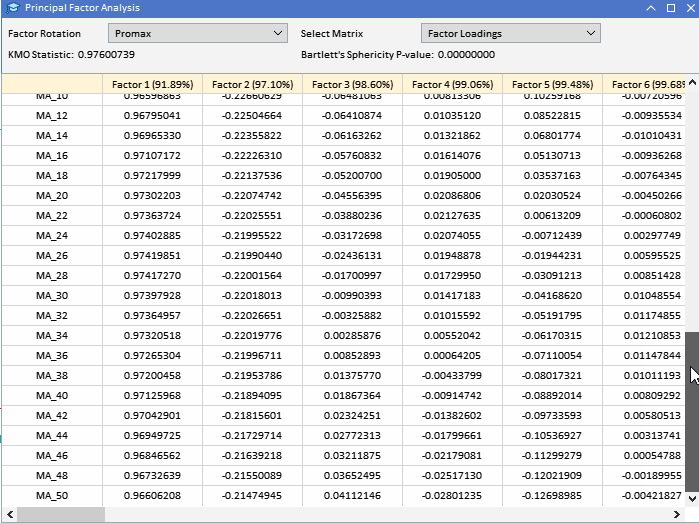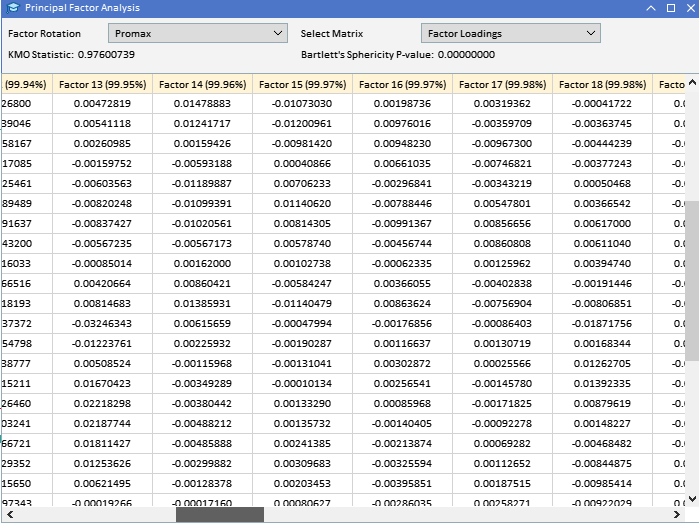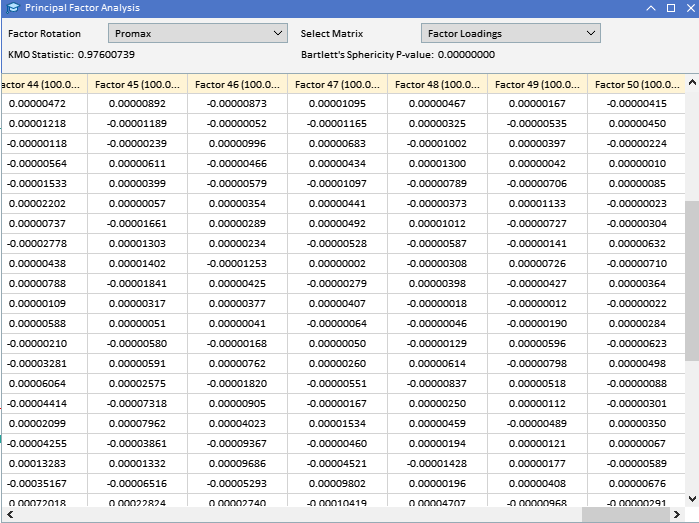
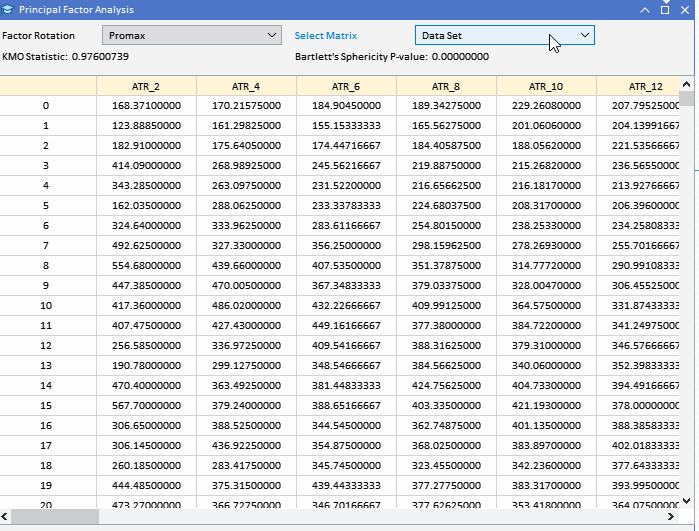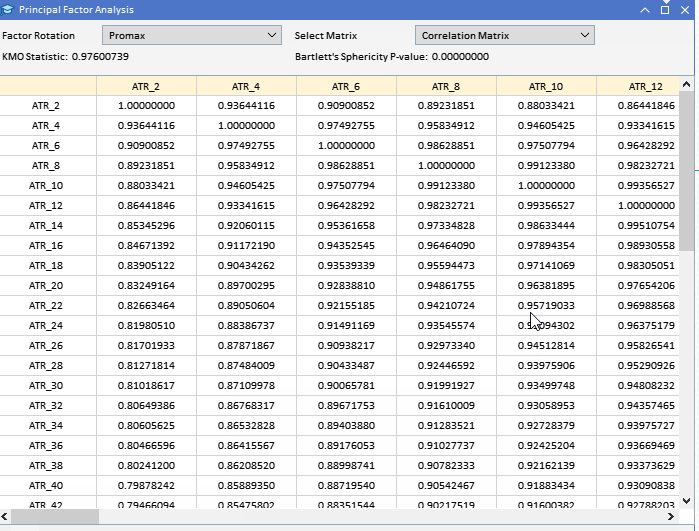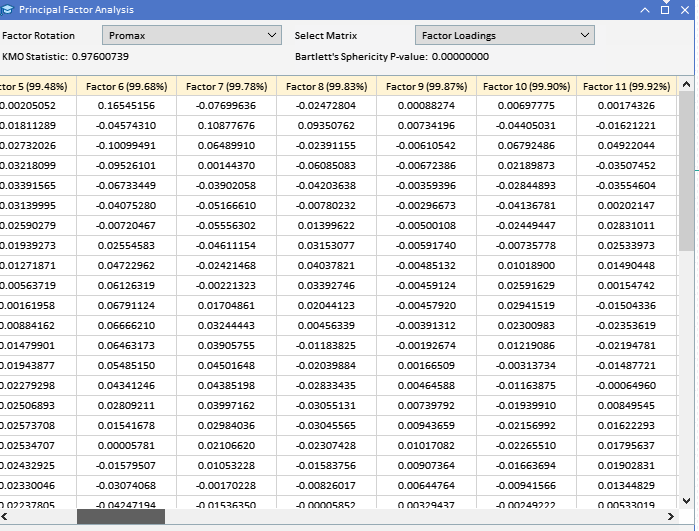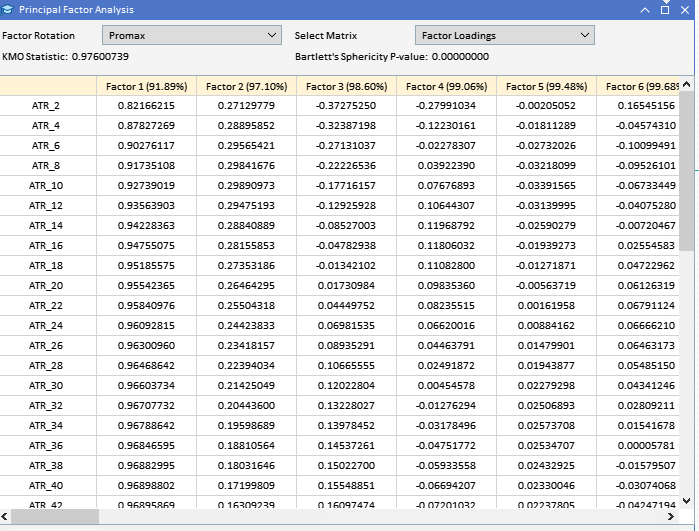
Looking at the factor loadings of the ATR variables collected earlier, we can see that most variables have high loadings on Factor 1, suggesting that these variables are primarily influenced by this factor. Factor 1 explains a significant portion of the variance in these variables, with a percentage of variance explained indicated by the number in parentheses (91.89%). Although Factor 1 appears dominant, some variables also have notable loadings on other factors. ATR_4, ATR_6, ATR_10, ATR_14, and others have moderate loadings on Factor 2, indicating a secondary influence. ATR_2, ATR_4, ATR_6, ATR_8, have smaller but significant loadings on Factor 3. Factors 4 and beyond have smaller loadings across various variables, suggesting they account for less variance in the data set compared to the first three factors.
If the factor loadings are too difficult to interpret due to a complex factor structure, it is possible to simplify the loadings by transforming them to enhance interpretability. This kind of transformation is called factor rotation. There are two types of rotations that can be applied to the factor loadings matrix. Orthogonal rotations maintain the independence of factors. Examples include varimax and equamax rotations. Orthogonal rotations should be applied if the factors are believed to be independent. Oblique rotations allow for some dependence among factors. Examples include promax and oblimin rotations. Oblique rotations are appropriate if the factors are suspected to be interrelated. Transforming the correlations through rotation drives the raw correlations of the factor structure matrix to extreme values (-1,0,1) so as to make interpretation of the correlations easier , amplifying the effects on the observed variables.
To facilitate rotations we introduce the CRotator class which implements promax and varimax rotations.
//+------------------------------------------------------------------+ //| class implementing factor rotations | //| implements varimax and promax rotations | //+------------------------------------------------------------------+ class CRotator { private: bool m_normalize, //normalization flag m_done; //rotation flag int m_power, //exponent to which to raise the promax loadings m_maxIter; //maximum number of iterations. Used for 'varimax' double m_tol; //convergence threshold. Used for 'varimax' matrix m_loadings, //the rotated factor loadings m_rotation_mtx, //the rotation matrix m_phi; //factor correlations matrix. ENUM_FACTOR_ROTATION m_rotation_type; //rotation method employed //+------------------------------------------------------------------+ //| implements varimax rotation | //+------------------------------------------------------------------+ bool varimax(matrix &in) { ulong rows,cols; rows = in.Rows(); cols = in.Cols(); matrix X = in; vector norm_mat(X.Rows()); if(m_normalize) { for(ulong i = 0; i<X.Rows(); i++) norm_mat[i]=sqrt((pow(X.Row(i),2.0)).Sum()); X = X.Transpose()/np::repeat_vector_as_rows_cols(norm_mat,X.Rows()); X = X.Transpose(); } m_rotation_mtx = matrix::Eye(cols,cols); double d = 0,old_d; matrix diag,U,V,transformed,basis; vector S,ones; for(int i =0; i< m_maxIter; i++) { old_d = d; basis = X.MatMul(m_rotation_mtx); ones = vector::Ones(rows); diag.Diag(ones.MatMul(pow(basis,2.0))); transformed = X.Transpose().MatMul(pow(basis,3.0) - basis.MatMul(diag)/double(rows)); if(!transformed.SVD(U,V,S)) { Print(__FUNCTION__, " error ", GetLastError()); return false; } m_rotation_mtx = U.Inner(V); d = S.Sum(); if(d<old_d*(1.0+m_tol)) break; } X = X.MatMul(m_rotation_mtx); if(m_normalize) { matrix xx = X.Transpose(); X = xx * np::repeat_vector_as_rows_cols(norm_mat,xx.Rows()); } else X = X.Transpose(); m_loadings = X.Transpose(); return true; } //+------------------------------------------------------------------+ //| implements promax rotation | //+------------------------------------------------------------------+ bool promax(matrix &in) { ulong rows,cols; rows = in.Rows(); cols = in.Cols(); matrix X = in; matrix weights,h2; h2.Init(1,1); if(m_normalize) { matrix array = X; matrix m = array.MatMul(array.Transpose()); vector dg = m.Diag(); h2.Resize(dg.Size(),1); h2.Col(dg,0); weights = array/np::repeat_vector_as_rows_cols(sqrt(dg),array.Cols(),false); } else weights = X; if(!varimax(weights)) return false; X = m_loadings; ResetLastError(); matrix Y = X * pow(MathAbs(X),double(m_power-1)); matrix coef = (((X.Transpose()).MatMul(X)).Inv()).MatMul(X.Transpose().MatMul(Y)); vector diag_inv = ((coef.Transpose()).MatMul(coef)).Inv().Diag(); if(GetLastError()) { diag_inv = ((coef.Transpose()).MatMul(coef)).PInv().Diag(); ResetLastError(); } matrix D; D.Diag(sqrt(diag_inv)); coef = coef.MatMul(D); matrix z = X.MatMul(coef); if(m_normalize) z = z * np::repeat_vector_as_rows_cols(sqrt(h2).Col(0),z.Cols(),false); m_rotation_mtx = m_rotation_mtx.MatMul(coef); matrix coef_inv = coef.Inv(); m_phi = coef_inv.MatMul(coef_inv.Transpose()); m_loadings = z; return true; } public: //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CRotator(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ ~CRotator(void) { } //+------------------------------------------------------------------+ //| performs rotation on supplied factor loadings passed to /in/ | //+------------------------------------------------------------------+ bool fit(matrix &in, ENUM_FACTOR_ROTATION rot_type=MODE_VARIMX, int power = 4, bool normalize = true, int maxiter = 500, double tol = 1e-05) { m_rotation_type = rot_type; m_power = power; m_maxIter = maxiter; m_tol = tol; m_done=false; if(in.Cols()<2) { m_loadings = in; m_rotation_mtx = matrix::Zeros(in.Rows(), in.Cols()); m_phi = matrix::Zeros(in.Rows(),in.Cols()); m_done = true; return true; } switch(m_rotation_type) { case MODE_VARIMX: m_done = varimax(in); break; case MODE_PROMAX: m_done = promax(in); break; default: return m_done; } return m_done; } //+------------------------------------------------------------------+ //| get the rotated loadings | //+------------------------------------------------------------------+ matrix get_transformed_loadings(void) { if(m_done) return m_loadings; else return matrix::Zeros(1,1); } //+------------------------------------------------------------------+ //| get the rotation matrix | //+------------------------------------------------------------------+ matrix get_rotation_matrix(void) { if(m_done) return m_rotation_mtx; else return matrix::Zeros(1,1); } //+------------------------------------------------------------------+ //| get the factor correlation matrix | //+------------------------------------------------------------------+ matrix get_phi(void) { if(m_done && m_rotation_type==MODE_PROMAX) return m_phi; else return matrix::Zeros(1,1); } };
Here’s an overview of its public methods:
| Method | Description | Parameters | Return Type |
|---|---|---|---|
| fit | Performs the specified rotation (varimax or promax) on the provided factor loadings matrix. | in: The factor loadings matrix to be rotated | bool |
| get_transformed_loadings | Returns the rotated factor loadings matrix | None | matrix |
| get_rotation_matrix | Returns the rotation matrix used in the transformation. | None | matrix |
| get_phi | Returns the factor correlation matrix (only for promax rotation). | None | matrix |
Applying the rotation to the factor loadings matrix.
CRotator rotator; if(!rotator.fit(m_structmat,MODE_PROMAX,4,false)) return; Print(" Rotated Loadings Matrix ", rotator.get_transformed_loadings());
The promax rotated factor loadings make clear the effects that Factor 1 and Factor 2 have on the two classes of variables. Factor 1 is the dominant influence on MA variables.
Factor 2 captures additional influence on ATR variables. The minimal impact of other Factors is greatly amplified by capturing less significant patterns within the data. This rotated solution provides a clearer understanding of the underlying structure of the dataset, facilitating better interpretation. While factor rotation can greatly enhance the interpretability of factor loadings, there are several disadvantages and limitations to consider:
- Rotation might oversimplify the underlying structure by forcing variables to load highly on a single factor, potentially masking more complex interrelationships.
- The choice between orthogonal and oblique rotations depends on theoretical assumptions about factor independence, which may not always be clear or justified.
- In some cases, rotation can lead to a slight loss of explained variance, as the goal of rotation is interpretability rather than maximizing explained variance.
- With a large number of variables and factors, the interpretation of rotated loadings can still be challenging, especially if there is no clear simple structure.
- Rotations, especially iterative ones like varimax, can be computationally expensive for large datasets, potentially affecting performance in real-time applications.
This concludes our discussion on principal factor extraction. Next, we will explore redundancy in variables based on latent factors, examining how latent factors can reveal hidden relationships.
Redundancy in variables based on latent factors
When dealing with a large number of variables, it's useful to identify sets of variables that are significantly redundant. This means some variables give similar information, and we might not need to consider all of them. Usually, the important information comes from the redundancy itself, as it can indicate a common effect impacting multiple variables. By identifying groups of highly redundant variables, we can simplify our analysis by focusing on a few representative variables or a single factor that correlates well with the group.
One popular method to spot redundant variables is by using scatterplots on principal or rotated orthogonal axes. Variables that cluster together on the plot are likely redundant. However, this method has its limitations. Firstly, it's subjective, and its usually practical to only handle two dimensions at a time to conduct effective analysis. An intuitive method to detect redundancy involves considering unobservable underlying factors. For example, if we have three factors (V1, V2, V3) giving rise to observed variables (X1, X2, X3), and we find that one factor (V3) is just noise, then X1 and X2 might be redundant when V3 is ignored. In other words, if X2 is just a scaled version of X1, they are redundant in terms of the important factors (V1 and V2).
To measure redundancy rigorously, we consider the observed variables as vectors in a space defined by the underlying factors. When we have observed variables, we can represent them as vectors in a multidimensional space where each dimension corresponds to an underlying factor. These vectors show how each variable relates to the factors. The angle between these vectors indicates how similar the variables are in terms of the information they carry about the underlying factors. A smaller angle means the vectors point in almost the same direction, indicating high redundancy. In other words, the variables provide similar information.
To quantify this redundancy, we can use the dot product of normalized vectors (vectors with length 1). This dot product ranges from -1 to 1, where a dot product of 1 means the vectors are identical, indicating perfect redundancy. Whilst a dot product of -1 means the vectors are in opposite directions, which can also be considered redundant since knowing one gives you the negative of the other. A dot product of 0 means the vectors are orthogonal (independent), indicating no redundancy.
The coefficients for computing observed variables from underlying factors can be found using principal components. Dominant principal components (with large eigenvalues) usually contain most of the useful information, while components with small eigenvalues are often noise. The factor loading matrix, which shows the correlation of factors with variables, can be used to compute standardized observed variables from principal components. For practical purposes, we often take the absolute value of the dot product to measure redundancy, recognizing that opposite vectors also indicate redundancy. Normalizing the vectors ensures that their lengths are 1, allowing the dot product to be a direct measure of the cosine of the angle between them.
To calculate the degree to which two variables are related in terms of a hidden factor, we usually first have to determine the number of principal components we deem important. The clustering computations will focus on the data in the first of these columns of the factor loading matrix. Each row in these columns will be rescaled so they all add up to 1. The degree of similarity between the two variables becomes the absolute value of the dot product of the two corresponding rows of the transformed factor loading matrix.
The next step is to group this data into sets that constitute variables that are very similar based on their relation to a latent factor. One of the better clustering algorithms, known for being adept at producing good results, is hierarchical clustering. In hierarchical clustering, also known as agglomerative hierarchical clustering (AHC), grouping begins by assigning each variable to a group with one member. Every possible pair of groups is tested to find the two that are nearest. These groups are combined into one group. This process repeats until there is either one group left or the degree of similarity becomes overly small.
Implementation of AHC is provided in the MQL5 port of the Alglib library. It is especially suited for our purposes because it supports the ability to implement a custom distance metric. This functionality is provided through three Alglib classes. To use Alglib's hierarchical agglomerative clustering implementation, we need an instance of the CAHCReport structure to store the results of the operation.CAHCReport m_rep;
The CClusterizerState class encapsulates the clusterization engine. Clustering cannot be done without it.
CClusterizerState m_cs;
The process begins by initializing the clusterization engine, through a call to the static method 'ClusterizerCreate()' of the CClustering class.
CClustering::ClusterizerCreate(m_cs);
After initialization we can set the parameters of the clusterization process, using other static methods of CClustering. All require an initialized clusterization engine.
CClustering::ClusterizerSetPoints(m_cs,pp,pp.Rows(),pp.Cols(),dist<22?dist:DIST_EUCLIDEAN); CClustering::ClusterizerSetDistances(m_cs,pd,pd.Cols(),true); CClustering::ClusterizerSetAHCAlgo(m_cs,linkage);
Finally 'ClusterizerRunAHC()' triggers the actual operation.
CClustering::ClusterizerRunAHC(m_cs,m_rep);
The results can be accessed through the CAHCReport instance properties.
As mentioned earlier, we will be implementing a custom distance metric for the operation. This is accomplished by providing a matrix with initial distances for each variable (row in the factor loadings). The code snippet below shows how the initial distances are calculated from the provided loadings.
for(int i=0 ; i<nvars ; i++) { length = 0.0 ; for(int j=0 ; j<ndim ; j++) length += structure[i][j] * structure[i][j] ; length = 1.0 / sqrt(length) ; for(int j=0 ; j<ndim ; j++) out[0][i][j] = length * structure[i][j] ; }
We first normalize the loadings with respect to the number dimensions taken into consideration.
for(int irow1=0 ; irow1<nvars-1 ; irow1++) { for(int irow2=irow1+1 ; irow2<nvars ; irow2++) { dotprod = 0.0 ; for(int i=0 ; i<ndim ; i++) dotprod += out[0][irow1][i] * out[0][irow2][i] ; out[1][irow1][irow2] = fabs(dotprod) ; } }
And these are used to calculate the distances. Also, the normalized loadings are the ones passed to the clusterizer. Not the raw factor loadings. All the code that implements clustering is given in the CCluster class.
//+------------------------------------------------------------------+ //| cluster a set of points | //+------------------------------------------------------------------+ class CCluster { private: CClusterizerState m_cs; CAHCReport m_rep; matrix m_pd[]; //+------------------------------------------------------------------+ //| Preprocesses input matrix before clusterization | //+------------------------------------------------------------------+ bool customDist(matrix &structure, ulong num_factors, matrix& out[], bool calculate_custom_distances = true) { int nvars; double dotprod, length; nvars = int(structure.Rows()); int ndim = (num_factors && num_factors<=structure.Cols())?int(num_factors):int(structure.Cols()); if(out.Size()<2) if(out.Size()<2 && (ArrayResize(out,2)!=2 || !out[0].Resize(nvars,ndim) || !out[1].Resize(nvars,nvars))) { Print(__FUNCTION__, " error ", GetLastError()); return false; } if(calculate_custom_distances) { for(int i=0 ; i<nvars ; i++) { length = 0.0 ; for(int j=0 ; j<ndim ; j++) length += structure[i][j] * structure[i][j] ; length = 1.0 / sqrt(length) ; for(int j=0 ; j<ndim ; j++) out[0][i][j] = length * structure[i][j] ; } out[1].Fill(0.0); for(int irow1=0 ; irow1<nvars-1 ; irow1++) { for(int irow2=irow1+1 ; irow2<nvars ; irow2++) { dotprod = 0.0 ; for(int i=0 ; i<ndim ; i++) dotprod += out[0][irow1][i] * out[0][irow2][i] ; out[1][irow1][irow2] = fabs(dotprod) ; } } } else { out[0] = np::sliceMatrixCols(structure,0,ndim); } return true; } public: //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CCluster(void) { CClustering::ClusterizerCreate(m_cs); } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ ~CCluster(void) { } //+------------------------------------------------------------------+ //| cluster a set | //+------------------------------------------------------------------+ bool cluster(matrix &in_points, ulong factors=0, ENUM_LINK_METHOD linkage=MODE_COMPLETE, ENUM_DIST_CRIT dist = DIST_CUSTOM) { if(!customDist(in_points,factors,m_pd,dist==DIST_CUSTOM)) return false; CMatrixDouble pp(m_pd[0]); CMatrixDouble pd(m_pd[1]); CClustering::ClusterizerSetPoints(m_cs,pp,pp.Rows(),pp.Cols(),dist<22?dist:DIST_EUCLIDEAN); if(dist==DIST_CUSTOM) CClustering::ClusterizerSetDistances(m_cs,pd,pd.Cols(),true); CClustering::ClusterizerSetAHCAlgo(m_cs,linkage); CClustering::ClusterizerRunAHC(m_cs,m_rep); return m_rep.m_terminationtype==1; } //+------------------------------------------------------------------+ //| output clusters to vector array | //+------------------------------------------------------------------+ bool get_clusters(vector &out[]) { if(m_rep.m_terminationtype!=1) { Print(__FUNCTION__, " no cluster information available"); return false; } if(ArrayResize(out,m_rep.m_pz.Rows())!=m_rep.m_pz.Rows()) { Print(__FUNCTION__, " error ", GetLastError()); return false; } for(int i = 0; i<m_rep.m_pm.Rows(); i++) { int zz = 0; for(int j = 0; j<m_rep.m_pm.Cols()-2; j+=2) { int from = m_rep.m_pm.Get(i,j); int to = m_rep.m_pm.Get(i,j+1); if(!out[i].Resize((to-from)+zz+1)) { Print(__FUNCTION__, " error ", GetLastError()); return false; } for(int k = from; k<=to; k++,zz++) out[i][zz] = m_rep.m_p[k]; } } return true; } };
The 'cluster()' function performs hierarchical clustering on a given set of input points. It takes four parameters: a reference to a matrix of input points, the number of factors to consider, the linkage method to be used, and the distance criterion. First, it calculates a custom distance matrix if the specified distance criterion is custom. If the distance calculation fails, the function returns false. Next, it initializes two matrices, pp and pd , from the computed distance data. The function then sets the points for clustering using the distance criterion, defaulting to Euclidean if the criterion is not set to the custom option. If the distance criterion is custom, it sets the distances for clustering accordingly.After setting up the distance and points, the function configures the hierarchical clustering algorithm with the specified linkage method. It runs the agglomerative hierarchical clustering algorithm and checks the termination type of the clustering process. The function returns true if the termination type is 1, indicating successful clustering, otherwise it returns false.
The ' get_clusters()' function extracts and outputs clusters from the results of a hierarchical clustering process. It takes one parameter: an array of vectors out[] , which will be populated with the clusters. The function first checks if the termination type of the clustering process is 1, indicating successful clustering. If not, it prints an error message and returns false. Then, the function iterates through each row of the matrix m_rep.m_pm , which contains the clustering information. For each row, it initializes a variable zz to track the index in the output vector. It then iterates through the columns of the current row, processing pairs of columns (representing the start and end indices of clusters). For each pair, it calculates the range of indices ( from to to ) and resizes the current output vector to accommodate the cluster elements. If resizing fails, it prints an error message and returns false. Finally, the function populates the current output vector with the elements of the cluster, iterating from from to to and incrementing zz for each element. If the process completes successfully, the function returns true, indicating that the clusters have been successfully extracted and stored in the out array.
The code snippet below shows how to use the CCluster class.
vector clusters[]; CCluster fc; if(!fc.cluster(fld,Num_Dimensions,AppliedClusterAlgorithm,AppliedDistanceCriterion)) return; if(!fc.get_clusters(clusters)) return; for(uint i =0; i<clusters.Size(); i++) { Print("cluster at ", i, "\n variable indices ", clusters[i]); }MetaTrader 5 lacks tools for visualizing the results of Agglomerative Hierarchical Clustering (AHC) directly. While the terminal's console can display some output, it is not user-friendly for viewing complex results like those from AHC. AHC results are best visualized through dendrograms, which show the hierarchical structure of the data groupings. A dendrogram illustrates how clusters are formed by merging data points or clusters step by step. Below is a dendrogram drawn manually that shows the groupings from our dataset of indicators.
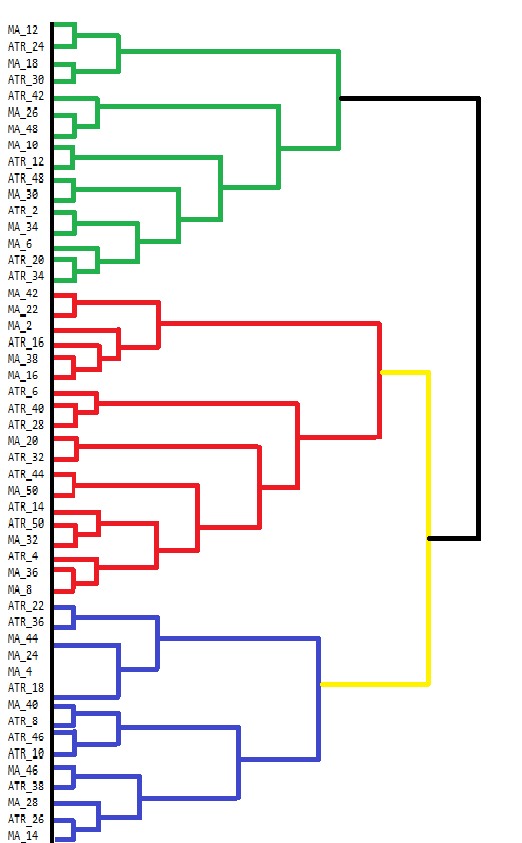
The dendrogram shows clusters of variables that are more similar to each other. Variables that merge at lower levels (closer to the bottom of the dendrogram) are more similar to each other than those that merge higher up. For example, MA_12 and MA_24 are more similar to each other compared to ATR_18. The dendrogram uses different colors to indicate different clusters. The clusters in green, red, blue, and yellow highlight groups of variables that are closely related. Each color represents a set of variables that exhibit high similarity or redundancy.
The height at which two clusters merge provides an indication of the dissimilarity between them. The lower the height, the more similar the clusters. Clusters that merge at higher levels, such as the black merge at the top, indicate larger differences between these clusters. This hierarchical clustering can inform decisions on variable selection. By analyzing the clusters, one might decide to focus on certain representative variables within each cluster for further analysis, thus simplifying the dataset without losing significant information.
The MQL5 code used to collect and analyze the dataset of indicators is contained in the script EDA.mq5. It makes use of all the code tools described in the article, which are defined in pfa.mqh.
//+------------------------------------------------------------------+ //| EDA.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #resource "\\Indicators\\Slope.ex5" #resource "\\Indicators\\CMMA.ex5" #include<pfa.mqh> #include<ErrorDescription.mqh> #property script_show_inputs //+------------------------------------------------------------------+ //|indicator type | //+------------------------------------------------------------------+ enum SELECT_INDICATOR { CMMA=0,//CMMA SLOPE//SLOPE }; //--- input parameters input uint period_inc=2;//lookback increment input uint max_lookback=50; input ENUM_MA_METHOD AppliedMA = MODE_SMA; input datetime SampleStartDate=D'2019.12.31'; input datetime SampleStopDate=D'2022.12.31'; input string SetSymbol="BTCUSD"; input ENUM_TIMEFRAMES SetTF = PERIOD_D1; input ENUM_FACTOR_ROTATION AppliedFactorRotation = MODE_PROMAX; input ENUM_DIST_CRIT AppliedDistanceCriterion = DIST_CUSTOM; input ENUM_LINK_METHOD AppliedClusterAlgorithm = MODE_COMPLETE; input ulong Num_Dimensions = 10; //---- string csv_header=""; //csv file header int size_sample, //training set size size_observations, //size of of both training and testing sets combined maxperiod, //maximum lookback indicator_handle=INVALID_HANDLE; //long moving average indicator handle //--- vector indicator[]; //indicator indicator values; //--- matrix feature_matrix; //full matrix of features; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //---get relative shift of sample set int samplestart,samplestop,num_features; samplestart=iBarShift(SetSymbol!=""?SetSymbol:NULL,SetTF,SampleStartDate); samplestop=iBarShift(SetSymbol!=""?SetSymbol:NULL,SetTF,SampleStopDate); num_features = int((max_lookback/period_inc)*2); //---check for errors from ibarshift calls if(samplestart<0 || samplestop<0) { Print(ErrorDescription(GetLastError())); return; } //---set the size of the sample sets size_observations=(samplestart - samplestop) + 1 ; maxperiod=int(max_lookback); //---check for input errors if(size_observations<=0 || maxperiod<=0) { Print("Invalid inputs "); return; } //---allocate memory if(ArrayResize(indicator,num_features)<num_features) { Print(ErrorDescription(GetLastError())); return; } //----get the full collection of indicator values int period_len; int k=0; //--- for(SELECT_INDICATOR select_indicator = 0; select_indicator<2; select_indicator++) { for(int iperiod=0; iperiod<int(indicator.Size()/2); iperiod++) { period_len=int((iperiod+1) * period_inc); int try=10; while(try) { switch(select_indicator) { case CMMA: indicator_handle=iCustom(SetSymbol!=""?SetSymbol:NULL,SetTF,"\\Indicators\\CMMA.ex5",AppliedMA,period_len); break; case SLOPE: indicator_handle=iCustom(SetSymbol!=""?SetSymbol:NULL,SetTF,"\\Indicators\\Slope.ex5",period_len); break; } if(indicator_handle==INVALID_HANDLE) try--; else break; } if(indicator_handle==INVALID_HANDLE) { Print("Invalid indicator handle ",EnumToString(select_indicator)," ", GetLastError()); return; } Comment("copying data to buffer for indicator ",period_len); try = 0; while(!indicator[k].CopyIndicatorBuffer(indicator_handle,0,samplestop,size_observations) && try<10) { try++; Sleep(5000); } if(try<10) ++k; else { Print("error copying to indicator buffers ",GetLastError()); Comment(""); return; } if(indicator_handle!=INVALID_HANDLE && IndicatorRelease(indicator_handle)) indicator_handle=INVALID_HANDLE; } } //---resize matrix if(!feature_matrix.Resize(size_observations,indicator.Size())) { Print(ErrorDescription(GetLastError())); Comment(""); return; } //---copy collected data to matrix for(ulong i = 0; i<feature_matrix.Cols(); i++) if(!feature_matrix.Col(indicator[i],i)) { Print(ErrorDescription(GetLastError())); Comment(""); return; } //--- Comment(""); //---test dataset for principal factor analysis suitability //---kmo test vector kmo_vect; double kmo_stat; kmo(feature_matrix,kmo_vect,kmo_stat); Print("KMO test statistic ", kmo_stat); //---Bartlett sphericity test double bs_stat,bs_pvalue; bartlet_sphericity(feature_matrix,bs_stat,bs_pvalue); Print("Bartlett sphericity test p_value ", bs_pvalue); //---Extract the principal factors Cpfa fa; //--- if(!fa.fit(feature_matrix)) return; //--- matrix fld = fa.get_factor_loadings(); //--- matrix rotated_fld = fa.rotate_factorloadings(AppliedFactorRotation); //--- Print(" factor loading matrix ", fld); //--- Print("\n rotated factor loading matrix ", rotated_fld); //--- matrix egvcts; vector egvals; fa.get_eigen_structure(egvcts,egvals,false); Print("\n vects ", egvcts); Print("\n evals ", egvals); //--- vector clusters[]; CCluster fc; if(!fc.cluster(fld,Num_Dimensions,AppliedClusterAlgorithm,AppliedDistanceCriterion)) return; if(!fc.get_clusters(clusters)) return; for(uint i =0; i<clusters.Size(); i++) { Print("cluster at ", i, "\n variable indices ", clusters[i]); } } //+------------------------------------------------------------------+
Coherence in Time Series
When analyzing variables over time, their relationships can change unexpectedly. Normally related variables might suddenly diverge, signaling a potential issue. For example, temperature changes can impact electricity demand, which then affects natural gas prices. If their usual pattern changes, it might indicate something unusual is happening. Similarly, variables that typically behave independently might suddenly move together, such as when different sectors of a stock market rise simultaneously due to positive economic news.
Measuring coherence involves quantifying how related a set of time-series variables are within a moving time window. One basic method is to check how much variance is captured by the largest eigenvalue. However, this method can be limiting as it only considers one dimension. A more comprehensive approach involves summing the largest eigenvalues, particularly when multiple relationships exist among the variables. This approach provides a more accurate picture of the overall coherence in a system with complex interrelationships, but it requires knowing before hand which are the most relevant factors. Something that may not be possible or is simply too subjective.
A more general approach is needed for scenarios where the number of relationships is unknown or fluctuates over time, especially with a large number of variables. In scenarios with unknown dimensionality, we can visualize the sorted eigenvalues from largest to smallest, as members of an orchestra. The key to producing beautiful music is to regulate the different instruments accordingly in a uniform manner. If individual orchestra members are not able to follow in union at the correct level, the resulting music will be terrible. Cohesion will be poor. Imagine the sound output of each orchestra member as a weighted value contributing to the music audiences hear. The imbalance in these values represents the coherence. We calculate a weighted sum, with weights denoting the volume an instrument can produce.
If each instrument (variable) is playing its own tune independently, the overall sound is disorganized and chaotic, representing zero coherence. However, when the instruments are perfectly synchronized, playing in harmony, they produce a cohesive and beautiful piece of music, representing full coherence. Coherence in this analogy is like the harmony of the orchestra, indicating how well the instruments (variables) are playing together. If the harmony suddenly changes, it suggests that something unusual is happening with the instruments or the composition.
Consider two extremes. If the variables are completely independent. The correlation matrix of these variables will be an identity matrix, and all eigenvalues will be equal (1.0). The weighted sum (due to symmetrical weights) will be zero, reflecting zero coherence. Alternatively, if there is perfect correlation between variables Only one non-zero eigenvalue exists, equal to the number of variables. The weighted sum becomes the number of variables, which after normalization (dividing by the number of variables) results in a coherence of 1.0, reflecting perfect correlation.This method offers a 0-1 measure of coherence based on the imbalance in the eigenvalue distribution, without making any assumptions about dimensionality.
To illustrate coherence we will produce an indicator that measures the coherence of close prices of different symbols within a time window. This indicator will be called Coherence.mq5. Users will be able to measure cohesion amongst numerous symbols by adding them as a comma separated list of instrument names. The indicator employs a different approach to calculating the correlations between multiple variables. This time around we use Spearmans non parametric correlation coefficient.
covar[0][0] = 1.0 ; for(int i=1 ; i<npred ; i++) { for(int j=0 ; j<i ; j++) { for(int k=0 ; k<lookback ; k++) { nonpar1[k] = iClose(stringbuffer[i],PERIOD_CURRENT,ibar+k); nonpar2[k] = iClose(stringbuffer[j],PERIOD_CURRENT,ibar+k); } if(!MathCorrelationSpearman(nonpar1,nonpar2,covar[i][j])) Print(" MathCorrelationSpearman failed ", GetLastError(), " :", ibar); } covar[i][i] = 1.0 ; }
Since we are using Aglib's EVD implementation we donot need to define the full matrix of correations, we just need to construct the upper or lower triangle. We donot need the eigenvectors, only eigenvalues are needed.
CMatrixDouble cdata(covar); if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Rows(),0,false,evals,evects)) { Print(" EVD failed ", GetLastError(), " :", ibar); coherenceBuffer[ibar]=0.0; continue; }
In order to get the distribution of eigenvalues in the right orientation, we have to reverse the vector.
vector eval = evals.ToVector(); if(!np::reverseVector(eval)) Print(" failed vecter reversal operation : ", ibar);
The cohesion is calculated using the eigenvalues.
double center = 0.5 * (npred - 1) ; double sum = 0.0; for(ulong i=0 ; i<eval.Size() ; i++) { sum += (center - i) * eval[i] / center ; } coherenceBuffer[ibar] = sum / eval.Sum();
The complete code is attached at the end of the article. Lets see what the indicator looks like a different window lengths, by measuring coherence amongst crypto currencies BTCUSD,DOGUSD and XRPUSD.
Looking at the 60 day plot of Coherence, it managed to dispel personal preconceptions that, these symbols move with notable coherence. What is surprising is how much it fluctuates. With values varying across the full spectrum of possible values.
As we move up to higher window lengths we start to see periods of stability in coherence, but again the nature of this coherence is unexpected. There are significant periods of time where there is almost zero coherence.
Conclusion
The use of eigenvalues and eigenvectors in these advanced techniques underscores their versatility and fundamental importance in data science. They provide a robust framework for dimensionality reduction, pattern recognition, and the discovery of latent structures within complex datasets. By moving beyond PCA, we unlock a richer set of tools that offer nuanced insights. This text demonstrates that eigenvectors and eigenvalues are far more than mathematical abstractions; they are the cornerstones of sophisticated analytical techniques that modern traders can leverage to gain an edge. All code demonstrated in the article is attached in the compressed archive file. The table below lists the files available for download.| File | Description |
|---|---|
| Mql5\Include\np.mqh | include file that contains various matrix and vector function utilities |
| Mql5\Include\pfa.mqh | pfa.mqh provides the definition of the Cpfa class, CCluster class and CRotator class. As well as the function definition for the KMO and BTS test implementations |
| Mql5\Scripts\EDA.mq5 | The script demonstrates the use of all the code tools described in the article by collecting a dataset of custom indicators for Principal factor analysis |
| Mql5\Scripts\TestEigenDecomposition.mq5 | This script reproduces the problems alluded to, with regards to the built in 'Eig()' matrix method |
| Mql5\Indicators\Coherence.mq5 | This is the Coherence indicator applied to 3 symbols |
| Mql5\Experts\PrincipalFactors.mq5 | The is the source code for the application referenced for viewing large matrices. The code depends on the venerable Easy and Fast GUI library which can be found in the MQL5 codebase |
| Mql5\Experts\PrincipalFactors.ex5 | This is a compiled version of the above listing |
 Using PatchTST Machine Learning Algorithm for Predicting Next 24 Hours of Price Action
Using PatchTST Machine Learning Algorithm for Predicting Next 24 Hours of Price Action
 How to Integrate Smart Money Concepts (BOS) Coupled with the RSI Indicator into an EA
How to Integrate Smart Money Concepts (BOS) Coupled with the RSI Indicator into an EA
 MQL5 Wizard Techniques you should know (Part 27): Moving Averages and the Angle of Attack
MQL5 Wizard Techniques you should know (Part 27): Moving Averages and the Angle of Attack
 Creating a Daily Drawdown Limiter EA in MQL5
Creating a Daily Drawdown Limiter EA in MQL5
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use