Algorithmen zur Optimierung mit Populationen: Differenzielle Evolution (DE)

Inhalt

1. Einführung
2. Der Algorithmus
3. Testergebnisse

1. Einführung

Metaheuristische Optimierungsmethoden sind eine Klasse von Algorithmen, die heuristische Ansätze zur Lösung komplexer Optimierungsprobleme verwenden. Sie unterscheiden sich von numerischen Optimierungsverfahren, die in der Regel auf mathematischer Analyse beruhen und die Kenntnis des Gradienten oder der Ableitung der Zielfunktion erfordern. Der Hauptunterschied zwischen metaheuristischen Methoden ist ihre Fähigkeit, große Räume zu erforschen und globale Optima zu finden, auch wenn die Funktion viele lokale Optima hat oder nicht kontinuierlich differenzierbar ist. Der Vorteil metaheuristischer Methoden ist, dass sie mit einer „Black Box“ arbeiten können - einer Funktion, für die es keine analytische Lösung gibt. Sie beruhen auf stochastischen probabilistischen Prinzipien und bieten eine gute Lösungsqualität.

Evolutionäre Algorithmen (EA) sind eine eigene Klasse von metaheuristischen Optimierungsmethoden, die den Prozess der natürlichen Evolution simulieren, um komplexe Optimierungsprobleme zu lösen. Sie beruhen auf den Prinzipien der Vererbung, der Mutation, der Kreuzung und der natürlichen Selektion. Der Evolutionsprozess in evolutionären Algorithmen ist der natürlichen Selektion nachempfunden, bei der die fittesten Lösungen mit größerer Wahrscheinlichkeit überleben und ihre Eigenschaften an die nächste Generation weitergeben. So konvergiert die Population allmählich zur optimalen Lösung. Einige der bekanntesten evolutionären Algorithmen sind: genetische Algorithmen (GA), evolutionäre Programmierung (EP), evolutionäre Strategien (ES) und genetische Programmierung (GP). Jeder dieser Algorithmen hat seine eigenen Merkmale und wird in verschiedenen Bereichen eingesetzt.

Im Allgemeinen sind evolutionäre Algorithmen ein leistungsfähiges Werkzeug zur Lösung komplexer Optimierungsprobleme, insbesondere in Fällen, in denen kein Zugang zu einem analytischen Funktionsausdruck oder Gradienten besteht. Sie ermöglichen es, den Suchraum zu erkunden und optimale Lösungen zu finden, indem sie Informationen aus verschiedenen Einzellösungen kombinieren.

Die differentielle Evolution (DE) ist eine der metaheuristischen Optimierungsmethoden. Sie unterscheidet sich von anderen Methoden durch ihre Einfachheit und Effizienz. DE verwendet eine Population von Vektoren, die mutieren und sich kreuzen, um neue Lösungen zu schaffen. Es erfordert keine Kenntnis des Gradienten und ist in der Lage, globale Optima zu finden.

Der DE-Algorithmus wurde in den 90er Jahren von Storn und Price entwickelt (veröffentlicht in „Differential Evolution - A Simple and Efficient Heuristic for global Optimization over Continuous Spaces“) und hat sich seitdem zu einer der beliebtesten Optimierungsmethoden entwickelt, die eine Population von Parametervektoren verwendet, um die optimale Lösung zu finden.

2. Der Algorithmus

Die Idee der differentiellen Evolution ist eine Kombination aus Einfachheit und Effizienz. Der Algorithmus der differentiellen Evolution verwendet eine Population von Vektoren, die potenzielle Lösungen darstellen. Jeder Vektor besteht aus Komponenten, die die Werte der Variablen des Optimierungsproblems darstellen.

In DE übernimmt ein Vektor die Rolle des Suchagenten. Der Algorithmus beginnt mit der Erstellung einer zufälligen Population von Vektoren. Anschließend findet ein iterativer Prozess statt, bei dem jeder Vektor mutiert und sich mit anderen Vektoren in der Population kreuzt. Die Mutation erfolgt durch Addition der Differenz zwischen zwei zufällig ausgewählten Vektoren aus der Population zu einem dritten Vektor. So entsteht ein neuer Vektor, der eine mögliche Lösung für das Problem darstellt.

Nach der Mutation wird der mutierte Vektor mit dem ursprünglichen Vektor gekreuzt. Die Kreuzung ermöglicht es, Informationen aus zwei Vektoren zu kombinieren und neue Lösungen zu schaffen. Das erzielte Ergebnis wird mit der aktuell besten Lösung in der Population verglichen. Wenn der neue Vektor besser ist, ersetzt er den alten und wird Teil der Population. Die Mutation ermöglicht die Erkundung des Suchraums, während die Kreuzung die Kombination von Informationen aus verschiedenen Vektoren und die Schaffung neuer Lösungen ermöglicht.

Mutation, Kreuzung und Ersetzung werden über mehrere Iterationen wiederholt, bis eine Stop-Bedingung erreicht ist, wie z. B. eine bestimmte Anzahl von Iterationen oder das Erreichen der erforderlichen Lösungsgenauigkeit (in unserem Fall das Erreichen von 10.000 Fitnessfunktionsläufen).

DE ist einer der evolutionären Algorithmen, die häufig zur Lösung von Optimierungsproblemen eingesetzt werden. Der Differenzialalgorithmus verwendet den Differenzierungsoperator, um neue Kandidaten auf der Grundlage der aktuellen Population zu erstellen. Hier sind die grundlegenden Gleichungen, die im Differentialalgorithmus verwendet werden:

1. Gleichung zur Erstellung eines neuen Kandidaten (Differenzierung):

r = r1 + F * (r2 - r3)

wobei:

• v - neue Vektorkomponente
• r1, r2 und r3 - Komponenten von zufällig ausgewählten Vektoren (individuelle Lösungen aus der Grundgesamtheit)
• F - Differenzierungsverhältnis, das den Grad der Variabilität der Lösung steuert (Streuung der erhaltenen Werte). Der Standardbereich ist (0.0;1.0]
  

2. Gleichung der Kreuzung (crossover):

u = Kreuzung (x, v)

Die Gleichung beschreibt den Kreuzung zwischen der aktuellen Lösung x und dem neuen Kandidaten v. Der Kreuzungsoperator bestimmt, welche Komponenten der Lösung aus dem neuen Kandidaten übernommen werden. Dies ist die Wahrscheinlichkeit, dass eine neue Vektorkomponente verwendet wird, ansonsten bleibt die Komponente unverändert. Es werden die Werte (0.0;1.0] verwendet.

Schreiben wir einen Pseudocode für den DE-Algorithmus, der aufgrund der Einfachheit des Algorithmus selbst einfach und verständlich ist (tatsächlich wird der Code nur ein wenig komplexer sein als sein Pseudocode):

1. Erstelle eine zufälligen Population von Vektoren
   
2. Berechne die Fitnessfunktion
3. Aktualisiere die beste Lösung
4. Aktualisiere die Population (Ersetzen von Vektoren durch bessere Mutanten)
5. Erstelle eine mutierte Vektorkomponente oder belasse sie, je nachdem, was besser ist.
   
6. Wiederhole den Vorgang ab S. 2.

Um einen Vektor im DE-Algorithmus zu beschreiben, schreiben wir eine Struktur und nennen sie S_Vector, die ein Vektor im n-dimensionalen Raum ist. Die Struktur hat die folgenden Felder:

•  Init (int coords): Die Funktion initialisiert den angegebenen Längenvektor „coords“. Es werden zwei Arrays erstellt - „c“ und „cPrev“ -, die die Koordinaten des Vektors bzw. seine vorherigen Koordinaten darstellen. Auch die Anfangswerte für f und fPrev werden auf -DBL_MAX gesetzt. 
• c []: Array mit Vektorkoordinaten
• cPrev []: Array mit den Vektorkoordinaten der vorherigen Iteration 
• f: Wert der Fitnessfunktion für den aktuellen Vektor 
• fPrev: Wert der Vektor-Fitnessfunktion bei der vorherigen Iteration

//——————————————————————————————————————————————————————————————————————————————
struct S_Vector
{
  void Init (int coords)
  {
    ArrayResize (c,     coords);
    ArrayResize (cPrev, coords);
    f        = -DBL_MAX;
    fPrev    = -DBL_MAX;
  }

  double c     []; //coordinates
  double cPrev []; //previous coordinates
  double f;        //fitness
  double fPrev;    //previous fitness
};
//——————————————————————————————————————————————————————————————————————————————

Die Klassenbeschreibung für einen so elementaren Algorithmus wie DE ist ebenfalls sehr einfach. Lassen Sie uns die Klasse C_AO_DE deklarieren. Die Felder der Klasse C_AO_DE enthalten Informationen über den aktuellen Zustand des Algorithmus und seiner Parameter, und die Methoden führen verschiedene Operationen im Zusammenhang mit der Optimierung der Funktion aus.

Die Klasse hat die folgenden Felder und Methoden:

• cB []: Array mit den besten vom Algorithmus gefundenen Koordinaten
• fB: Wert der Fitnessfunktion für die besten Koordinaten
• v []: Array von S_Vector-Strukturen, die eine Population von Vektoren darstellen
• rangeMax[]: das Array speichert die Höchstwerte für jede Vektorkoordinate
• rangeMin[]: das Array speichert die Tiefstwerte für jede Vektorkoordinate
• rangeStep[]: Array speichert Schrittwerte für jede Vektorkoordinate
• Init (int coordsP, int popSizeP, double diffWeightP, double crossProbabP): Die Funktion initialisiert die Algorithmusparameter. Er nimmt die Anzahl der Koordinaten „coordsP“, die Populationsgröße „popSizeP“, die differentielle Gewichtung „diffWeightP“ und die Kreuzungswahrscheinlichkeit „crossProbabP“.
• Moving (): die Funktion führt einen Schritt des Algorithmus der differentiellen Evolution aus
• Revision (): die Funktion führt eine Revision der Vektorpopulation durch
• SeInDiSp (double In, double InMin, double InMax, double Step): die Methode berechnet einen neuen Koordinatenwert in einem bestimmten Bereich mit einem bestimmten Schritt
• RNDfromCI (double min, double max): die Funktion erzeugt eine Zufallszahl im Bereich [min, max]

//——————————————————————————————————————————————————————————————————————————————
class C_AO_DE
{
  //----------------------------------------------------------------------------
  public: double cB  []; //best coordinates
  public: double fB;     //FF of the best coordinates
  public: S_Vector v []; //vector

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,       //coordinates number
                     const int    popSizeP,      //population size
                     const double diffWeightP,   //differential weight
                     const double crossProbabP); //crossover robability

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;       //coordinates number
  private: int    popSize;      //population size

  private: double diffWeight;   //differential weight
  private: double crossProbab;  //crossover robability

  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

Die Init-Methode der Klasse C_AO_DE initialisiert die Parameter des differentiellen Evolutionsalgorithmus. Die Methode benötigt vier Parameter:

• coordsP - Anzahl der Koordinaten,
• popSizeP - Größe der Population,
• diffWeightP - Differentialgewicht
• crossProbabP - Kreuzungswahrscheinlichkeit.

Zu Beginn verwendet die Methode die Funktion MathSrand, um den Zufallszahlengenerator zurückzusetzen. Dadurch wird sichergestellt, dass der Algorithmus bei jedem Start eine neue Folge von Zufallszahlen verwendet.

Anschließend initialisiert die Methode die Variablen „fB“ und „revision“. Die Variable „fB“ enthält den besten vom Algorithmus gefundenen Wert der Fitnessfunktion. Anfänglich ist er auf „-DBL_MAX“, d.h. auf eine sehr kleine Zahl, eingestellt. Die Variable „revision“ ist auf „false“ gesetzt, was bedeutet, dass die Vektorpopulation noch nicht überarbeitet wurde.

Die Methode initialisiert dann die Variablen „coords“, „popSize“, „diffWeight“ und „crossProbab“ mit den als Parameter übergebenen Werten.

Die Methode erstellt dann ein Array „v“ der Größe „popSize“, das eine Population von Vektoren enthält.

Als Nächstes erstellt die Methode drei Arrays: „rangeMax“, „rangeMin“ und „rangeStep“ mit jeweils der Größe „coords“ (Anzahl der Koordinaten).

Schließlich erstellt die Methode das Array „cB“ mit der Größe „coords“, das die besten vom Algorithmus gefundenen Koordinaten enthält.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_DE::Init  (const int    coordsP,      //coordinates number
                     const int    popSizeP,     //population size
                     const double diffWeightP,  //differential weight
                     const double crossProbabP) //crossover robability
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords  = coordsP;
  popSize = popSizeP;

  diffWeight  = diffWeightP;
  crossProbab = crossProbabP;

  ArrayResize (v, popSize);
  for (int i = 0; i < popSize; i++) v [i].Init (coords);

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);
}
//——————————————————————————————————————————————————————————————————————————————

Um die Lösungsvektoren im Suchraum zu ändern, schreiben wir die Methode Moving der Klasse C_AO_DE. Die Methode wendet Mutations- und Crossover-Operatoren an, um neue Kandidatenvektoren zu erzeugen, und wählt die beste Lösung auf der Grundlage der Fitnessfunktion aus.

Der erste Codeblock, der mit der Bedingung „if (!revision)“ beginnt, wird nur bei der ersten Ausführung der Methode „Moving“ oder nach dem Aufruf der Methode Init ausgeführt. Es initialisiert die Anfangspopulation von Vektoren mit Zufallswerten innerhalb der angegebenen Grenzen und mit dem im Array „rangeStep“ angegebenen Schritt.

Die Methode verwendet dann die „for“-Schleife, um jeden Vektor in der Population zu aktualisieren. Für jeden Vektor wählt die Methode drei verschiedene Zufallsvektoren aus der Population (r1, r2, r3), die nicht mit dem aktuellen Vektor (i) identisch sind, und wendet die Operatoren Mutation und Crossover an, um einen neuen Kandidatenvektor zu erhalten. Der Mutationsoperator berechnet die Differenz zwischen den Vektoren „r2“ und „r3“ multipliziert mit der Differenzgewichtung „diffWeight“ und fügt das Ergebnis dem Vektor „r1“ hinzu. Der Crossover-Operator wählt eine Vektorkoordinate aus und ersetzt sie durch die entsprechende Koordinate eines neuen Kandidatenvektors mit der crossProbab-Wahrscheinlichkeit. Ist die Kreuzungswahrscheinlichkeit nicht gegeben, so bleibt die aktuelle Vektorkoordinate unverändert.

Wenn Sie den nachstehenden Code analysieren, werden Sie feststellen, dass die Methode „Moving“ zum Ändern von Vektoren keine anderen Koordinaten im Raum erzeugt, als die, die aus den vorhandenen Koordinaten gewonnen werden können. Die Stochastizität des Algorithmus liegt also nur in der Auswahl der zu kreuzenden Vektoren, nicht aber in der Erzeugung neuer, origineller Vektoren. Dieses Merkmal hat weitreichende Folgen, die wir weiter unten erörtern werden.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_DE::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        v [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
        v [i].c [c] = SeInDiSp (v [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double rnd = 0.0;
  int    r   = 0;
  int    r1  = 0;
  int    r2  = 0;
  int    r3  = 0;

  for (int i = 0; i < popSize; i++)
  {
    do
    {
      r = (int)RNDfromCI (0, popSize);
      if (r >= popSize) r = popSize - 1;

      r1 = r;
    }
    while (r1 == i);

    do
    {
      r = (int)RNDfromCI (0, popSize);
      if (r >= popSize) r = popSize - 1;

      r2 = r;
    }
    while (r2 == i || r2 == r1);

    do
    {
      r = (int)RNDfromCI (0, popSize);
      if (r >= popSize) r = popSize - 1;

      r3 = r;
    }
    while (r3 == i || r3 == r1 || r3 == r2);

    for (int c = 0; c < coords; c++)
    {
      rnd = RNDfromCI (0, 1.0);

      if (rnd < crossProbab)
      {
        v [i].c [c] = v [r1].cPrev [c] + diffWeight * (v [r2].cPrev [c] - v [r3].cPrev [c]);
        v [i].c [c] = SeInDiSp (v [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
      else
      {
        v [i].c [c] = v [i].cPrev [c];
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Schließlich benötigen wir die Revisionsmethode der Klasse C_AO_DE, die die beste Lösung in der Population aktualisiert und die vorherigen Werte der Fitnessfunktion und der Vektorkoordinaten speichert.

Zunächst initialisiert die Methode die Variable „ind“ mit dem Wert „-1“. Anschließend wird die „for“-Schleife verwendet, um alle Vektoren der Grundgesamtheit zu durchlaufen. Wenn die Fitnessfunktion des aktuellen Vektors größer ist als „fB“ (die beste bisher gefundene Fitnessfunktion), wird der Index dieses Vektors in der Variablen „ind“ gespeichert.

Wenn „ind“ ungleich „-1“ ist, aktualisiert die Methode den Wert von „fB“ auf den Wert der Fitnessfunktion des Vektors mit dem Index „ind“ und speichert seine Koordinaten in dem Array „cB“.

Die Methode verwendet dann eine weitere „for“-Schleife, um alle Vektoren der Population zu durchlaufen. Wenn die Fitnessfunktion des aktuellen Vektors größer ist als sein vorheriger Wert, speichert die Methode den aktuellen Wert der Fitnessfunktion und die Vektorkoordinaten in den entsprechenden Feldern v[i].fPrev und v[i].cPrev.

Mit dieser Methode kann die Klasse C_AO_DE die beste Lösung in der Population und die vorherigen Werte der Fitnessfunktion und der Vektorkoordinaten speichern, um sie später für die Optimierung der Fitnessfunktion zu verwenden.

Wir sehen, dass sich die Population nicht weiter im Suchraum bewegt, bis ein Vektor gefunden wird, der besser ist als seine ursprüngliche (Eltern-)Version. Dieser Punkt ergänzt alles, was oben gesagt wurde.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_DE::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (v [i].f > fB) ind = i;
  }

  if (ind != -1)
  {
    fB = v [ind].f;
    ArrayCopy (cB, v [ind].c, 0, 0, WHOLE_ARRAY);
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (v [i].f > v [i].fPrev)
    {
      v [i].fPrev = v [i].f;
      ArrayCopy (v [i].cPrev, v [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Testergebnisse

Die Testergebnisse von DE:

C_AO_DE:50;0.2;0.8
=============================
5 Rastrigin's; Func runs 10000 result: 80.30183306326985
Score: 0.99498
25 Rastrigin's; Func runs 10000 result: 76.15178282331799
Score: 0.94356
500 Rastrigin's; Func runs 10000 result: 52.17316317703311
Score: 0.64645
=============================
5 Forest's; Func runs 10000 result: 1.7348423083855402
Score: 0.98131
25 Forest's; Func runs 10000 result: 1.28572746338484
Score: 0.72727
500 Forest's; Func runs 10000 result: 0.20833645141168078
Score: 0.11785
=============================
5 Megacity's; Func runs 10000 result: 9.640000000000002
Score: 0.80333
25 Megacity's; Func runs 10000 result: 3.9199999999999995
Score: 0.32667
500 Megacity's; Func runs 10000 result: 0.3548
Score: 0.02957
=============================
All score: 5.57100

Anhand der Ausgabewerte des Algorithmus sehen wir ausgezeichnete Testergebnisse.

Wir können die phänomenale Konvergenz des Algorithmus sehen, aber wir können auch die Eigenschaft bemerken, die oben in der Beschreibung der Methoden von Moving und Revision erwähnt wurde. Bei der Erstellung der Visualisierung habe ich nach mehreren Versuchen gezielt die erfolgreichsten ausgewählt. In der Tat sind die Ergebnisse nicht immer so hervorragend. Dies wird durch die Degeneration der Population erklärt, wenn die gesamte Population, jeder einzelne Vektor, zu einem einzigen Extremwert konvergiert. Aber das ist vielleicht gar nicht das globale Optimum. Wie bereits erwähnt, verfügt der Algorithmus nicht über Mechanismen, um den Suchraum weiter zu erkunden und neue eindeutige Vektoren zu erzeugen. Der DE-Algorithmus erzeugt keine neuen Vektoren, sondern generiert nur Kombinationen aus bestehenden Vektoren. Dies erklärt die vollständige Degeneration. Es wird kein „neues Blut“ geschaffen, um den „Genpool“ der Bevölkerung zu diversifizieren.

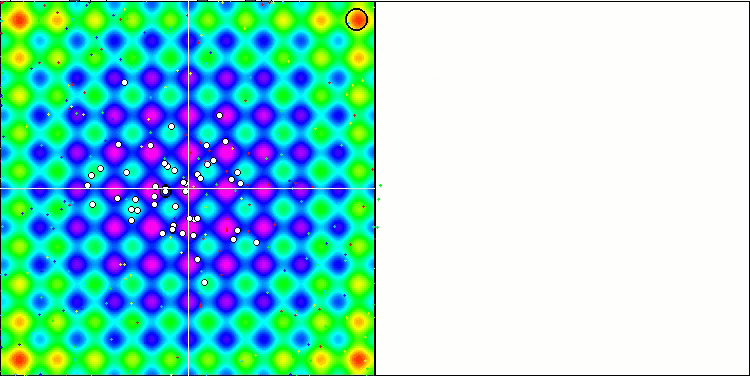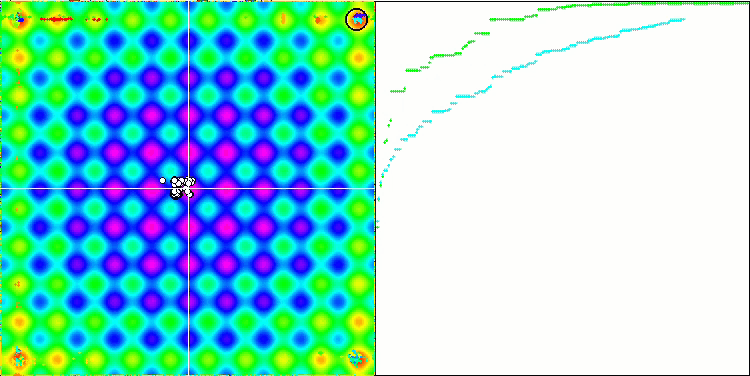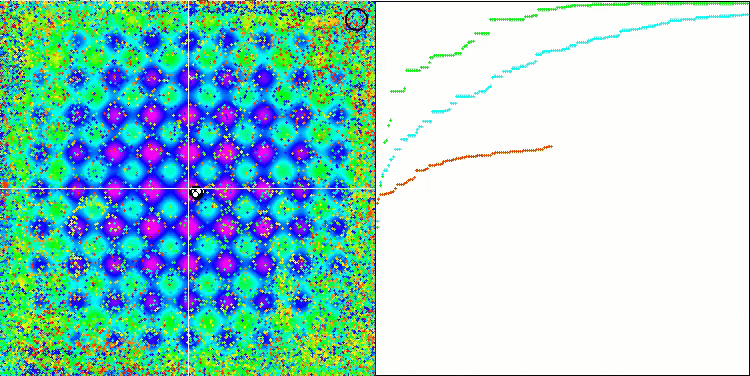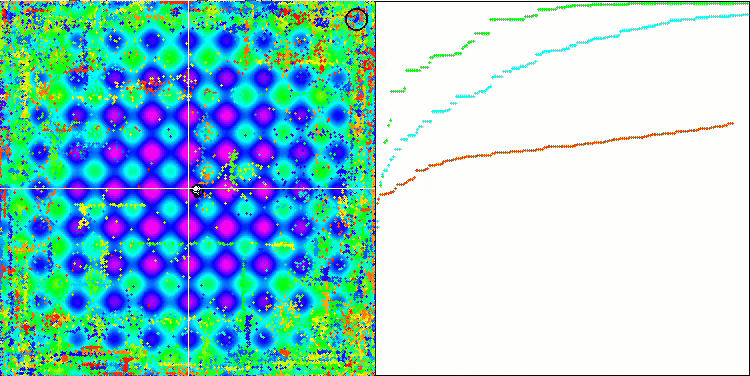
  DE mit der Testfunktion Rastrigin.

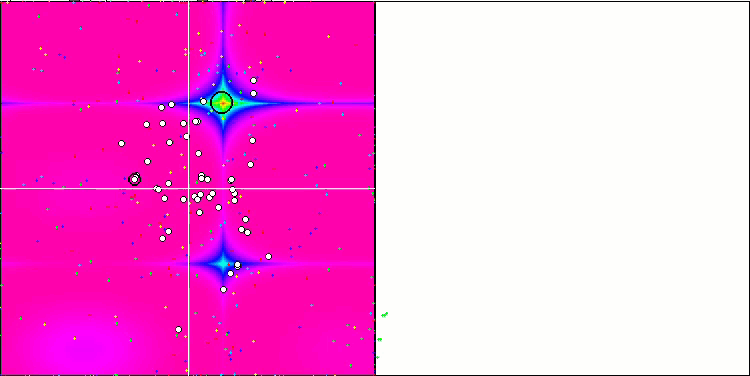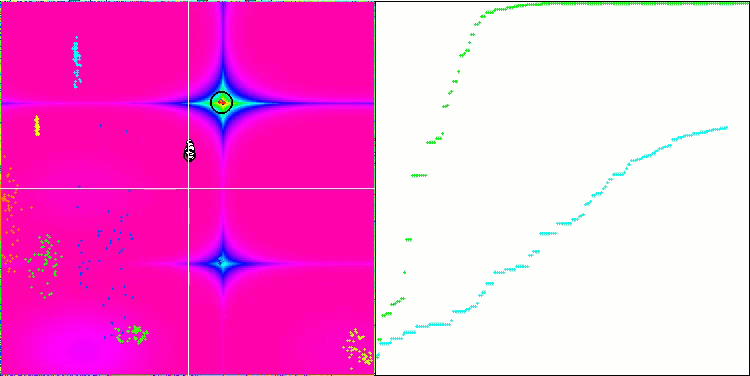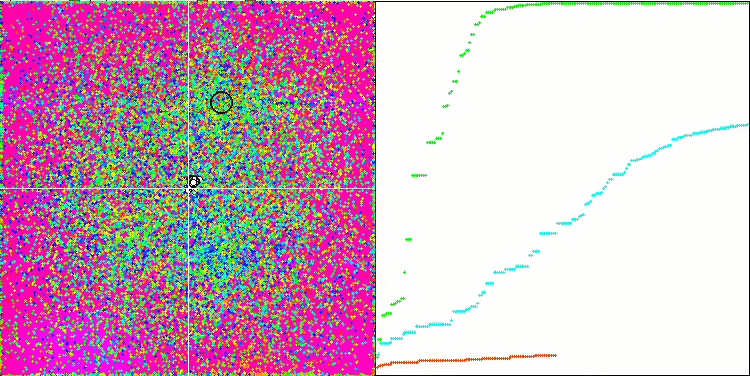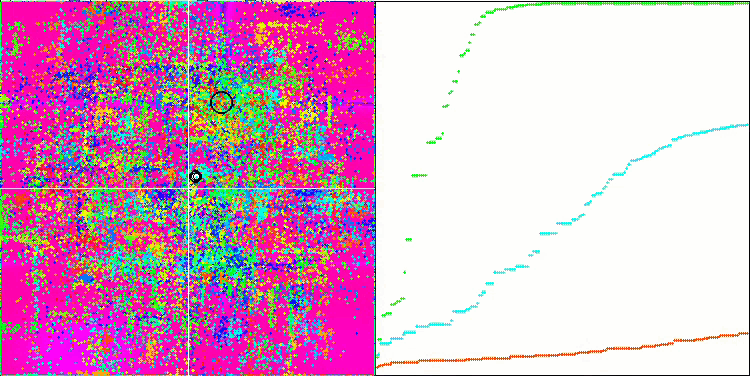
  DE mit der Testfunktion Forest.

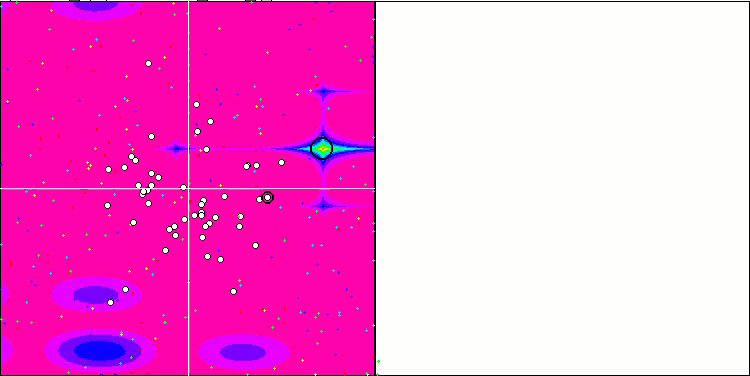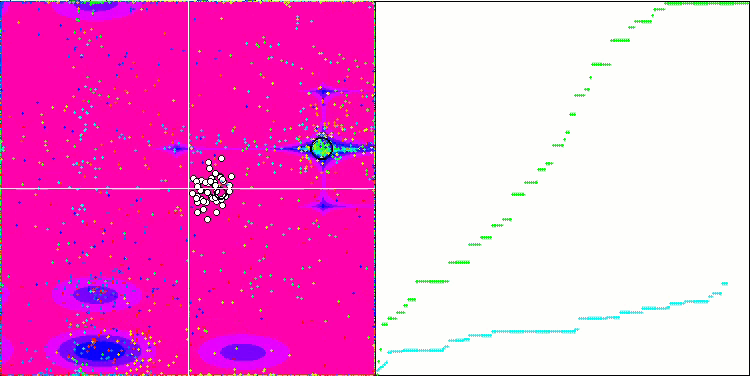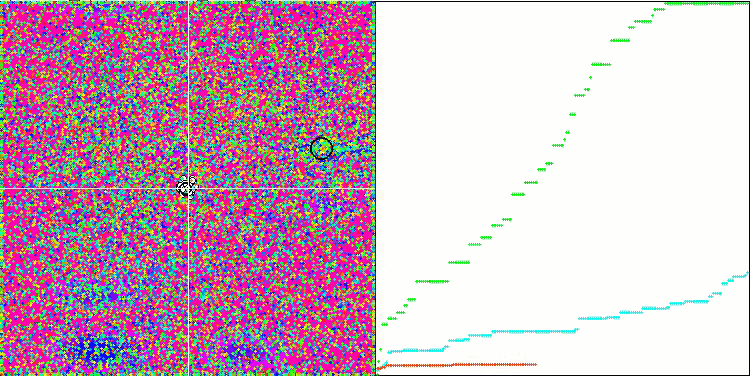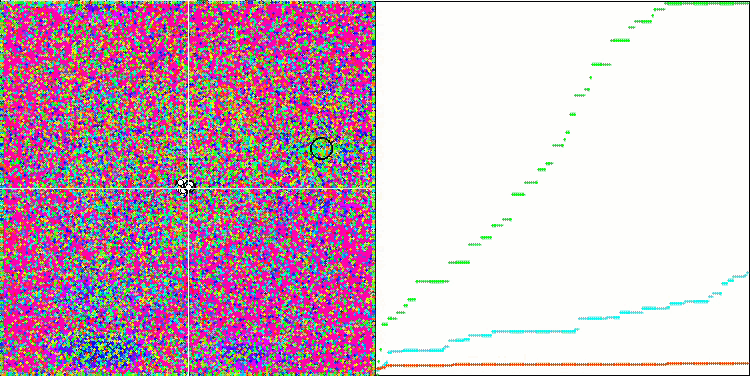
  DE mit der Testfunktion Megacity.

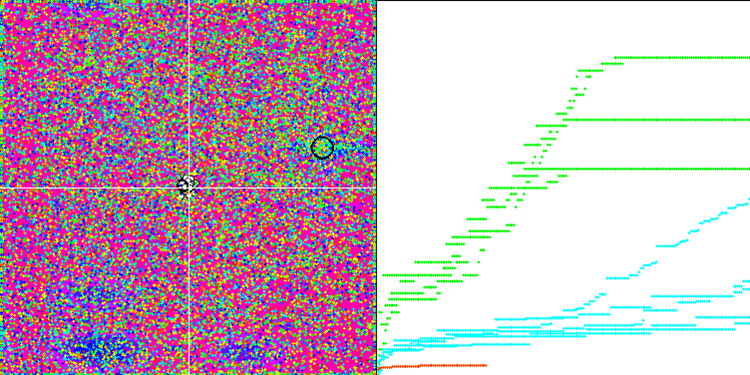
Enorme Verbreiterung der Konvergenz. Besonders auffällig ist das bei den Funktionen Forest und Megacity.

Betrachten wir nun die abschließende Wertungstabelle mit dem neuen Teilnehmer - DE. Der Algorithmus konnte dem derzeitigen Spitzenreiter SDSm im Forest-Test mit 10 Variablen den Spitzenplatz wegschnappen. Die Ergebnisse der anderen Tests sind ebenfalls sehr gut, und DE belegt nach der SSG den vierten Platz. Es ist anzumerken, dass ich anstelle des üblichen 5-fachen Testlaufs für jede der Testfunktionen den 10-fachen Test durchführen musste, da die Ergebnisse für die Funktionen Forest und Megacity stark streuten. Bei der glatten Rastrigin-Funktion ist die Streuung der Ergebnisse weniger auffällig. 

#	AO	Beschreibung	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (diskret)			Megacity final	Final result
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	SDSm	stochastische Diffusionssuche M	0.99809	1.00000	0.69149	2.68958	0.99265	1.00000	1.00000	2.99265	1.00000	1.00000	1.00000	3.00000	100.000
2	SDS	stochastische Diffusionssuche	0.99737	0.97322	0.58904	2.55963	0,96067	0.93572	0.79649	2.69288	0.78696	0.93815	0.71804	2.44315	88.201
3	SSG	Setzen, Säen und Wachsen	1.00000	0.92761	0.51630	2.44391	0.72120	0.65201	0.83760	2.21081	0.54782	0.61841	0.99522	2.16146	77.683
4	DE	differentielle Evolution	0.98295	0.89236	0.51375	2.38906	1.00000	0.84602	0.65510	2.50112	0.90000	0.52237	0.12031	1.54268	73.099
5	HS	Harmoniesuche	0.99676	0.88385	0.44686	2.32747	0.99148	0.68242	0.37529	2.04919	0.71739	0.71842	0.41338	1.84919	70.623
6	IWO	Optimierung mit invasiven Unkräutern	0.95828	0.62227	0.27647	1.85703	0.70170	0.31972	0.26613	1.28755	0.57391	0.30527	0.33130	1.21048	48.250
7	ACOm	Ameisen-Kolonie-Optimierung M	0.34611	0.16683	0.15808	0.67103	0.86147	0.68980	0.64798	2.19925	0.71739	0.63947	0.05579	1.41265	47.387
8	MEC	Evolutionäre Berechnung des Geistes	0.99270	0.47345	0.21148	1.67763	0.60244	0.28046	0.21324	1.09615	0.66957	0.30000	0.26045	1.23002	44.049
9	SDOm	Optimierung der Spiraldynamik M	0.69840	0.52988	0.33168	1.55996	0.59818	0.38766	0.37600	1.36183	0.35653	0.15262	0.25842	0.76758	40.289
10	COAm	Kuckuck-Optimierungsalgorithmus M	0.92400	0.43407	0.24120	1.59927	0.57881	0.23477	0.13842	0.95200	0.52174	0.24079	0.17001	0.93254	37.830
11	FAm	Firefly-Algorithmus M	0.59825	0.31520	0.15893	1.07239	0.50637	0.29178	0.41704	1.21519	0.24783	0.20526	0.35090	0.80398	33.139
12	ABC	Künstliches Bienenvolk (Artificial Bee Colony, ABC)	0.78170	0.30347	0.19313	1.27829	0.53379	0.14799	0.11177	0.79355	0.40435	0.19474	0.13859	0.73768	29.766
13	BA	Fledermaus-Algorithmus	0.40526	0.59145	0.78330	1.78002	0.20664	0.12056	0.21769	0.54488	0.21305	0.07632	0.17288	0.46225	29.499
14	CSS	Suche geladener Systeme	0.56605	0.68683	1.00000	2.25289	0.13961	0.01853	0.13638	0.29452	0.07392	0.00000	0.03465	0.10856	27.930
15	GSA	Algorithmus für die Schwerkraftsuche	0.70167	0.41944	0.00000	1.12111	0.31390	0.25120	0.27812	0.84322	0.42609	0.25525	0.00000	0.68134	27.807
16	BFO	Optimierung der bakteriellen Futtersuche	0.67203	0.28721	0.10957	1.06881	0.39364	0.18364	0.17298	0.75026	0.37392	0.24211	0.18841	0.80444	27.542
17	EM	elektromagnetismusähnlicher Algorithmus	0.12235	0.42928	0.92752	1.47915	0.00000	0.02413	0.29215	0.31628	0.00000	0.00527	0.10872	0.11399	19.002
18	SFL	schlurfender Froschsprung	0.40072	0.22021	0.24624	0.86717	0.19981	0.02861	0.02221	0.25063	0.19565	0.04474	0.06607	0.30646	13.200
19	MA	Affen-Algorithmus	0.33192	0.31029	0.13582	0.77804	0.09927	0.05443	0.07482	0.22852	0.15652	0.03553	0.10669	0.29874	11.777
20	FSS	Fischschulsuche	0.46812	0.23502	0.10483	0.80798	0.12730	0.03458	0.05458	0.21647	0.12175	0.03947	0.08244	0.24366	11.332
21	IWDm	intelligente Wassertropfen M	0.26459	0.13013	0.07500	0.46972	0.28358	0.05445	0.05112	0.38916	0.22609	0.05659	0.05054	0.33322	10.423
22	PSO	Partikelschwarmoptimierung	0.20449	0.07607	0.06641	0.34696	0.18734	0.07233	0.18207	0.44175	0.16956	0.04737	0.01947	0.23641	8.426
23	RND	zufällig	0.16826	0.09038	0.07438	0.33302	0.13381	0.03318	0.03949	0.20648	0.12175	0.03290	0.04898	0.20363	5.054
24	GWO	Grauer-Wolf-Optimierung	0.00000	0.00000	0.02093	0.02093	0.06514	0.00000	0.00000	0.06514	0.23478	0.05789	0.02545	0.31812	1.000

Zusammenfassung

Der Algorithmus der differentiellen Evolution (DE) ist in der Lage, sehr schnell globale Optima zu finden und weist eine ausgezeichnete Konvergenz auf, wenn man die sehr mittelmäßigen Ergebnisse in den einzelnen Tests bedenkt. DE ist in verschiedenen Bereichen weit verbreitet, z. B. bei der Optimierung von Modellparametern, der Abstimmung neuronaler Netze, der Optimierung von Funktionen in Physik und Wirtschaft und vielen anderen. Ich würde empfehlen, mehrere Optimierungsläufe mit diesem Algorithmus durchzuführen, da die Ergebnisse stark von der Ausgangspopulation in der ersten Iteration abhängen. Eine Erhöhung der Populationsgröße bei gleichzeitiger Erhöhung der Anzahl der Iterationen kann von Vorteil sein.

Trotz seiner Einfachheit und Arbeitsgeschwindigkeit hat der Algorithmus der differentiellen Evolution offensichtliche Nachteile, wie die Degeneration der Population und das Verharren in lokalen Extrema. Dies muss bei der Auswahl von DE für Ihre Optimierungsprobleme berücksichtigt werden.

Der in diesem Artikel besprochene DE-Algorithmus ist eine Art Vorlage, mit der verschiedene Änderungen vorgenommen werden können. Meine Vorschläge zur Verbesserung des Algorithmus der differentiellen Evolution (DE) lauten wie folgt:

1. Verwendung von Methoden der adaptiven Parametersteuerung: Bei DE gibt es mehrere Parameter, die aufgrund ihrer erheblichen Auswirkungen auf die Ergebnisse angepasst werden müssen.

Der von den Autoren empfohlene Parameter für das Differentialgewicht ist „0,2“. Dieser Wert ist der Standardwert, den ich in das DE-Testskript übernommen habe. Dieser Parameter hat einen erheblichen Einfluss auf die Vielfalt der Population. Wählt man einen Wert kleiner als „0,2“, kann man eine noch bessere Konvergenz des Algorithmus erreichen, muss aber gleichzeitig mit einer noch größeren Streuung der Ergebnisse rechnen. Erhöht man dagegen den Wert dieses Parameters, so wird der Algorithmus resistent gegen Populationsdegeneration und das Verharren in lokalen Extrema, aber gleichzeitig nimmt die Qualität der Konvergenz über die durch Tests begrenzte Anzahl von Iterationen rapide ab, und dementsprechend steigt die Suchzeit unweigerlich an.

Die Kreuzungswahrscheinlichkeit (Crossover probability) wirkt sich auch auf die Qualität der Optimierung aus. Der Autor empfiehlt den Wert „0,9“. Meine Experimente zeigen jedoch, dass „0,8“ besser geeignet ist. 

In Anbetracht der obigen Ausführungen erscheint es ratsam, adaptive Methoden zur Steuerung und dynamischen Änderung von Parametern zu verwenden, sodass der Algorithmus automatisch an die jeweilige Aufgabe angepasst werden kann.

2. Verwendung verschiedener Mutations- und Kreuzungsstrategien.

3. Einsatz von Hybridmethoden: DE kann mit anderen Optimierungsmethoden kombiniert werden, z. B. mit genetischen Algorithmen, gradientenbasierten Optimierungsmethoden, Partikelschwarm-Optimierungsmethoden usw. Dies kann die Leistung des Algorithmus verbessern und dazu beitragen, die Effizienz des Algorithmus als Ganzes zu steigern.

4. Verbesserung der Konvergenz: Anwendung zusätzlicher Zufallsvektoren zur Erhöhung der Diversität in einer Population.

5. Verwendung verschiedener Strategien zur Auswahl von Individuen für die Mutation: Dieser Algorithmus berücksichtigt eine völlig zufällige Methode zur Auswahl von Individuen für die Kreuzung. Diese Methode kann jedoch auch durch andere Strategien zur Auswahl von Individuen für Crossover/Mutation ergänzt oder vollständig ersetzt werden, z. B. durch die Strategie der Auswahl von Individuen auf der Grundlage ihrer Eignung. Dies kann dazu beitragen, die Populationsvielfalt zu erhöhen und die Resistenz des Algorithmus gegen das Hängenbleiben deutlich zu verbessern.

Insgesamt vermittelt der DE-Algorithmus einen sehr guten Eindruck von seiner Leistungsfähigkeit, aber es ist notwendig, entweder die Eigenschaften dieses interessanten Algorithmus im Auge zu behalten oder einige Versuche zu unternehmen, die differentielle Evolution durch die Anwendung einer Kombination verschiedener Strategien und Methoden zu verbessern. DE hat überzeugend bewiesen, dass Algorithmen sehr effizient sein können und dennoch unglaublich einfach und schnell sind. Der differentielle Evolutionsalgorithmus kann für die Lösung komplexer Optimierungsprobleme mit hohen Dimensionen empfohlen werden, da die Auswirkungen der Abnahme der Diversität während der Evolution bei einer großen Anzahl optimierter Parameter weniger ausgeprägt sind.

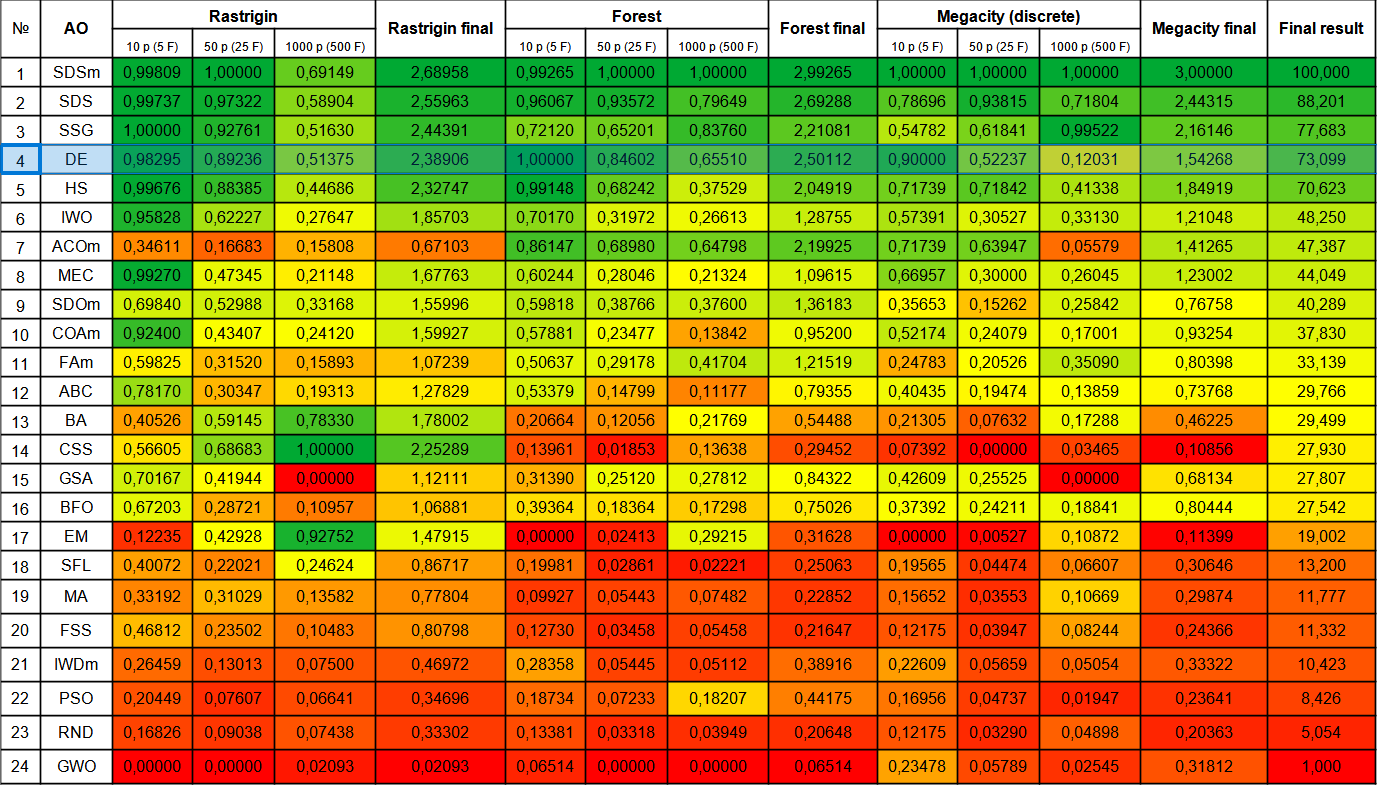
Bild 1. Farbabstufung der Algorithmen gemäß den einschlägigen Tests

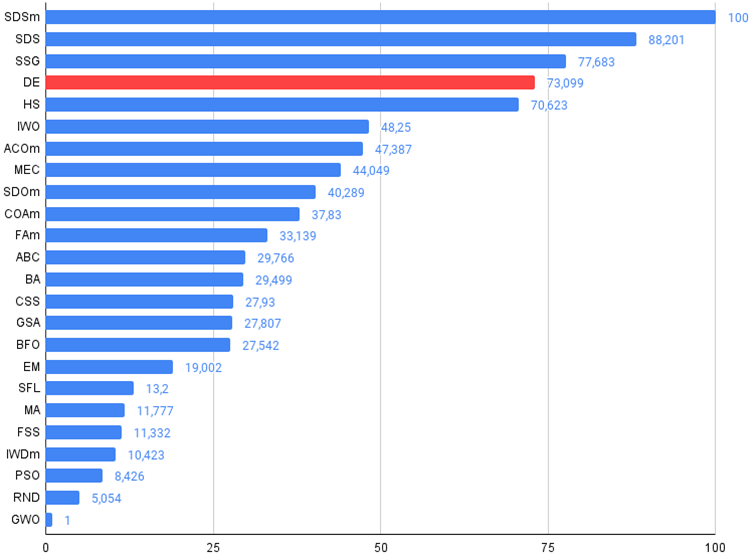
Bild 2. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, je mehr, desto besser,

das Archiv enthält das Skript zur Berechnung der Bewertungstabelle nach der im Artikel angewandten Methode).

Vor- und Nachteile des Algorithmus der differentiellen Evolution (DE)

Vorteile:

1. Eine kleine Anzahl von externen Parametern.
2. Einfache Umsetzung.
3. Operationsgeschwindigkeit.
4. Gute Skalierbarkeit.
5. Sehr gute Leistung bei verschiedenen Arten von Funktionen (unter Berücksichtigung der Nachteile).

Nachteile:

1. Hohe Streuung der Ergebnisse.
2. Tendenz, in lokalen Extrema stecken zu bleiben.

Dem Artikel ist ein Archiv mit aktualisierten Versionen der in früheren Artikeln beschriebenen Algorithmuscodes beigefügt. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.