
Algorithmen zur Optimierung mit Populationen: Nelder-Mead- oder Simplex-Suchverfahren (NM)
Inhalt
1. Einführung
2. Der Algorithmus
3. Testergebnisse
1. Einführung
Die Nelder-Mead-Methode wurde 1965 von John Nelder und Roger Mead entwickelt. Sie waren auf der Suche nach einer Optimierungsmethode, die mit Funktionen arbeiten konnte, die keine Ableitungen oder keine analytischen Gleichungen für Ableitungen besaßen. Außerdem wollten sie eine Methode entwickeln, die einfach zu implementieren und auf den damaligen Computern effizient zu nutzen war. Dabei kamen sie auf die Idee, ein Simplex zu verwenden - ein Polyeder im Raum der Funktionsparameter.
Die Entwicklungsgeschichte dieser Methode begann mit der Arbeit von John Nelder und seinen Kollegen am Computing Laboratory in Oxford. Sie sahen sich mit dem Problem konfrontiert, Funktionen zu optimieren, die keine analytischen Ableitungen besaßen oder zu komplex zu berechnen waren. Traditionelle Optimierungsmethoden wie Gradientenmethoden waren in solchen Fällen nicht anwendbar. Stattdessen schlugen Nelder und Mead eine neue Methode vor, die auf der iterativen Suche nach der optimalen Lösung im Raum der Funktionsparameter beruht.
Die Nelder-Mead-Methode wurde „Simplex-Methode“ genannt und 1965 in dem Artikel „A Simplex Method for Function Minimization“ in The Computer Journal veröffentlicht. Diese Methode ist in der wissenschaftlichen Gemeinschaft anerkannt und wird in verschiedenen Bereichen, in denen eine Funktionsoptimierung erforderlich ist, häufig eingesetzt.
Ein Simplex ist eine Menge von Punkten, die ein Polyeder bilden, wobei jeder Punkt eine Menge von Parameterwerten der zu optimierenden Funktion darstellt. Die Idee ist, ein Simplex im Parameterraum zu verändern und zu verschieben, um den optimalen Wert der Funktion zu finden.
Das Nelder-Mead-Verfahren (Nelder-Mead-Simplex-Verfahren) gehört zur Klasse der unbedingten Optimierungsalgorithmen. Es handelt sich um einen deterministischen Algorithmus, der keine Funktionsableitungen erfordert und mit Funktionen arbeiten kann, die mehrere lokale Minima haben.
2. Der Algorithmus
Die Nelder-Mead-Methode ist keine Populationsmethode, da nur ein Optimierungsagent verwendet wird, der ein Simplex darstellt, das wiederum aus einer Menge von Punkten im Suchraum besteht, die selbst als Population betrachtet werden kann. Wir werden jedoch mehrere Agenten verwenden, von denen jeder sein eigenes Simplex hat, sodass diese Implementierung durchaus als Populationsalgorithmus eingestuft werden kann.
Nehmen wir also zum besseren Verständnis an, dass zwei variable Funktionen optimiert werden müssen. Mit anderen Worten, die Dimension des Raums ist z = 2, dann besteht das Simplex aus z + 1 = 3 Scheitelpunkten. Die Änderung des Simplex ist eine Operation am schlechtesten dieser drei Punkte. Bezeichnen wir diese Punkte als „Best“, „Good“, „Worst“, (bester, guter, schlechtester) wobei „Good“ der zweite Punkt nach „Worst“ ist (wenn die Dimension größer als zwei ist, dann ist Good immer der zweite Punkt nach „Worst“ in der sortierten Liste der Scheitelpunkte).
Als Nächstes müssen wir diese drei Scheitelpunkte verwenden, um „Worst“ im Verhältnis zu den übrigen Scheitelpunkten zu berechnen und anzupassen. Wir bewegen „Worst“ relativ zum geometrischen Mittelpunkt der Scheitelpunkte mit Ausnahme von sich selbst, d. h. wir berechnen den Schwerpunkt und bewegen „Worst“ relativ zum Schwerpunkt.
Bei jeder Iteration der Nedler-Mead-Methode führen wir die folgenden Schritte durch:
1. Sortierung der Scheitelpunkte des Simplex nach den Werten der Zielfunktion, d.h.
f(P0) ⩾ f(P1) ⩾ ... ⩾ f(P(n-1))
wobei:
- P0, P1 ... P(n-1) - Simplexpunkte
- n - Anzahl der Simplex-Scheitelpunkte
2. Berechnung des Schwerpunkts: Berechnung des Durchschnittswerts über die entsprechenden Koordinaten aller Scheitelpunkte des Simplex, mit Ausnahme des schlechtesten Scheitelpunkts. Der Vektor Xo sei der Schwerpunkt aller Scheitelpunkte außer X(n-1), dann:
Xo = (X0 + X1 + ... + X(n-2)) / (n-1)
wobei:
- X0, X1 ... X(n-2) - entsprechende Koordinatenvektoren aller Scheitelpunkte außer dem schlechtesten
3. Reflection: Spiegelung des schlechtesten Scheitelpunkts relativ zum Schwerpunkt. Der Vektor Xr des neuen reflektierten Scheitelpunkts wird wie folgt berechnet:
Xr = Xo + α (Xo - Xw)
wobei:
- Xw - schlechtester Scheitelpunktvektor, entspricht dem Scheitelpunkt P(n-1)
- α - Reflexionsverhältnis, in der Regel gleich 1
4. Bewertung eines neuen Scheitelpunkts: Der Wert der Zielfunktion wird an diesem Punkt berechnet. Wenn ein neuer Knoten einen besseren Zielfunktionswert hat als der schlechteste Knoten des Simplex, dann kann er diesen ersetzen, d.h. die Spiegelung ersetzt das Original. Die Reflexionsoperation ermöglicht es uns, eine neue Region des Parameterraums zu erkunden, indem wir vom Simplexschwerpunkt aus reflektieren.
5. Expansion: wird verwendet, um den Parameterraum weiter zu erforschen, wenn eine Reflexionsoperation einen Scheitelpunkt erzeugt hat, der besser als der beste ist, unter der Annahme, dass eine weitere Bewegung in der Reflexionsrichtung seine Position weiter verbessert. Die Expansionsoperation ermöglicht es uns, einen noch größeren Bereich des Parameterraums zu untersuchen als die Reflexionsoperation. Sie vergrößert den Abstand zwischen dem Schwerpunkt und dem reflektierten Punkt, was dazu beitragen kann, neue lokale Minima der Zielfunktion zu finden. Der Expansionsvektor Xe kann wie folgt berechnet werden:
Xe = Xo + γ(Xr - Xo)
wobei:
- γ - Expansionsverhältnis, in der Regel größer als 1, Standardwert ist 2
5.1. Wenn die Expansionsoperation durchgeführt wurde: Die Fitnessfunktion für den Xe-Eckpunkt wird berechnet. Wenn er besser ist als der Scheitelpunkt Xr, kann er den schlechtesten Simplex-Scheitelpunkt Xw ersetzen. Nach Abschluss der Erweiterung wird mit Schritt 1 fortgefahren.
Achten Sie darauf, das Ausdehnungsverhältnis γ sorgfältig zu wählen. Wenn es zu groß ist, kann es dazu führen, dass sich das Simplex über einen großen Bereich des Parameterraums ausbreitet, was die Konvergenz verlangsamen oder zum Verlust von Informationen über lokale Extrema führen kann. Wenn es sich als zu klein erweist, kann es sein, dass neue Regionen des Parameterraums nicht ausreichend erforscht werden.
6. Contraction: Die Kontraktion wird verwendet, um den Scheitelpunkt Xc zu berechnen, wenn die Spiegelungsoperation einen Scheitelpunkt erzeugt hat, der schlechter als oder gleich dem guten Punkt Xb ist (der zweite nach dem schlechtesten), d.h. wir versuchen, eine bessere Position innerhalb des Simplex zu finden. Die Gleichung lautet wie folgt:
Xc = Xo + β(Xw - Xo)
wobei:
- β - Kontraktionsverhältnis, normalerweise zwischen 0 und 1, Standardwert 0,5
6.1. Wenn eine Kontraktion durchgeführt wurde: Es wird der Wert der Zielfunktion Xc für den Scheitelpunkt berechnet. Wenn ein neuer Knoten einen besseren Zielfunktionswert hat als der schlechteste Knoten des Simplex, dann kann er den schlechtesten ersetzen. Nach Abschluss der Erweiterung wird mit Schritt 1 fortgefahren.
Die Kontraktion ermöglicht es uns, das Simplex näher an den schlechtesten Punkt heranzuführen, was bei der Erkundung der Umgebung dieses Punktes hilfreich sein kann. Wie bei der Expansion ist es wichtig, das Kontraktionsverhältnis β sorgfältig zu wählen. Wenn es zu groß ist, kann es dazu führen, dass das Simplex zu stark komprimiert wird, was zu einem Verlust von Informationen über lokale Minimums führt. Wenn es zu klein ist, reicht die Kompression möglicherweise nicht aus, um die Umgebung des schlechtesten Punktes zu erkunden.
7. Shrinkage: Die letzte Operation, die Schrumpfung, der Nelder-Mead-Methode wird durchgeführt, wenn keine der vorangegangenen Operationen (Spiegelung, Expansion, Kontraktion) zu einer Verbesserung des Zielfunktionswertes führt. Die Schrumpfung reduziert die Größe des Simplex, um den Suchbereich einzugrenzen und sich auf den Sweet Spot zu konzentrieren.
Wie wir sehen können, haben die Autoren vier Operationen mit dem Simplex. Um mit der Optimierung beginnen zu können, müssen wir die Fitnessfunktion für alle Simplexpunkte berechnen. Die Anzahl der Simplexpunkte ist gleich „z+1“, wobei z die Dimension des Suchraums ist. Wenn wir zum Beispiel eine Suchdimension von 1000 haben, dann sollten wir die Fitnessfunktion 1001 Mal auswerten, um mit den Simplex-Operationen zu beginnen. Während ein typischer Populationsalgorithmus mit einer Population von 50 Agenten 20 Epochen durchläuft, wird dieser Algorithmus nur eine Epoche durchlaufen und den Großteil seiner begrenzten Anzahl von Iterationen verbrauchen.
Bei der Schrumpfung werden alle Punkte auf den besten Punkt verschoben. Danach ist es notwendig, die Fitnessfunktion 1000 Mal zu berechnen. Mit anderen Worten: Die Schrumpfung ist sehr ressourcenintensiv. Nach der Idee der Autoren sollte diese Operation aufgerufen werden, wenn der Algorithmus nicht mehr weiterkommt und das Verschieben des schlechtesten Punktes des Simplexes keine Verbesserung der Lösung bringt. Meine Experimente haben jedoch gezeigt, dass dieser Vorgang im verhältnismäßig viel Rechenressourcen verwendet und außerdem für den Optimierungsalgorithmus sinnlos und selbstmörderisch ist, da die Konvergenz aller Punkte des Simplex-Agenten zu einem lokalen Extremum bedeuten würde, dass er stecken bleibt und die Erkundung des Suchraums abbricht. Daher habe ich beschlossen, bei der praktischen Umsetzung des Algorithmus auf die Schrumpfung zu verzichten.
Wir werden die ersten drei Operationen mit dem Simplex anwenden. Zur besseren Übersichtlichkeit sind sie in Abbildung 1 dargestellt:
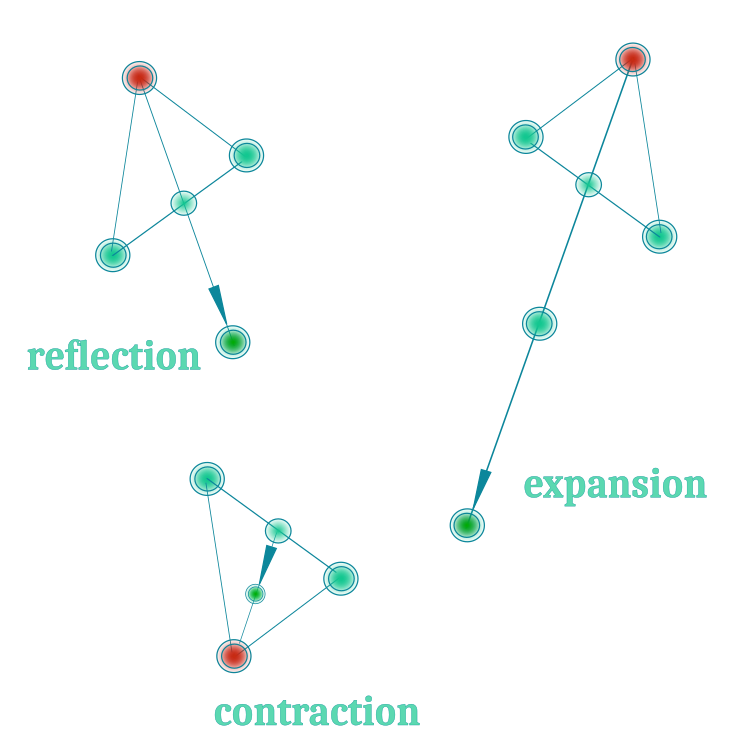
Bild 1. Drei Hauptoperationen der Nelder-Mead-Methode
Da die Simplex-Suchmethode aufgrund ihres deterministischen Charakters eine schlechte Auswahl der Anfangspunkte haben kann, kann ihr Optimierungsergebnis unbefriedigend sein. Experimente mit diesem Algorithmus bestätigten nur die Befürchtungen: Er funktioniert nur in einem begrenzten Koordinatenraum akzeptabel.
Aufgrund von Konvergenzproblemen werden die Scheitelpunkte des Simplexes einfach um einen festen Wert verschoben. Stellen Sie sich vor, Sie stehen auf Stelzen und versuchen, sich auf einer Bank zu setzen. Sie ist zu niedrig, um dies zu tun. Genau die gleiche Situation ergibt sich bei einem wechselnden Simplex. Damit der Algorithmus perfekt funktioniert, müssen wir viel Glück haben, damit die Anfangspunkte des Simplexes an der richtigen Stelle landen. Das ist ähnlich wie bei den Stelzen - um sicher sitzen zu können, brauchen wir eine hohe Bank. Der Algorithmus konvergiert relativ gut bei glatten monoextremalen Funktionen, zum Beispiel bei einer Parabel. Unsere praktischen Probleme sind jedoch sehr viel komplexer und in der Regel voller lokaler „Fallen“, insbesondere bei Handelsproblemen, die diskreter Natur sind.
Dann stellt sich die Frage. Was ist zu tun, wenn das Simplex „für immer“ an einem lokalen Extremum hängen bleibt? Die Logik des Nelder-Mead-Algorithmus bietet keine Möglichkeit, dieser „Falle“ zu entkommen. Nach jeder Operation, sei es Kontraktion oder Expansion, kehrt der Algorithmus zur Reflexion zurück und versucht, den schlechtesten Punkt zu überwinden. Optisch sieht dies wie ein „Blinken“ aus. Um dieses Problem zu lösen, habe ich versucht, dem Simplex die Möglichkeit zu geben, die lokale „Falle“ zu verlassen und in neuen Bereichen des Raums weiterzusuchen. Um dies zu erreichen, habe ich die Levy Flights eingesetzt, die in einigen Fällen dazu beigetragen haben, die Bevölkerung „wiederzubeleben“, wie in früheren Artikeln beschrieben. Es ist jedoch anzumerken, dass die Levy Flights nicht immer nützlich sind und ihre Anwendung von der Logik des Optimierungsalgorithmus abhängt. In unserem Fall handelte es sich um ein Experiment, und eine Verbesserung der Ergebnisse war nicht garantiert.
Kommen wir nun zum interessantesten Teil - dem Schreiben des Codes.
Nach jeder Iteration muss man wissen, welche Operation am schlechtesten Knotenpunkt des Simplexes durchgeführt wurde. Der Enumerator wird für diese Aufgabe sehr nützlich sein. Zusätzlich zu den drei Hauptoperationen mit dem Scheitelpunkt eines Simplexes habe ich eine weitere hinzugefügt - „none“, für den Fall, dass ich mich entscheide, den Algorithmus irgendwie zu ergänzen. Nennen wir den Enumerator E_SimplexOperation. Sie umfasst die Felder:
- none: keine Operationen
- reflection (Reflexion)
- expansion (Erweiterung)
- contraction (Kontraktion)
//—————————————————————————————————————————————————————————————————————————————— enum E_SimplexOperation { none = 0, reflection = 1, expansion = 2, contraction = 3 }; //——————————————————————————————————————————————————————————————————————————————Um den Simplexpunkt zu beschreiben, benötigen wir die Struktur S_Point, die folgende Felder enthält:
- Init(int coords): Punktinitialisierung, übernimmt das Argument „coords“
- c[]: das Koordinatenfeld eines Punktes im mehrdimensionalen Raum; die Größe des Feldes wird mit der Init-Methode bestimmt
- f: Wert der Scheitelfitnessfunktion
//—————————————————————————————————————————————————————————————————————————————— struct S_Point { void Init (int coords) { ArrayResize (c, coords); f = -DBL_MAX; } double c []; double f; }; //——————————————————————————————————————————————————————————————————————————————
Für das Simplex wird die Struktur S_Simplex verwendet, die ein einfaches Simplex für jeden Agenten darstellt und die folgenden Felder enthält:
- Init(int coords): Simplex-Initialisierung, nimmt das Argument „coords“ - Anzahl der Koordinaten
- S_Point p[]: Array von Simplex-Scheitelpunkten, Arraygröße wird in der Init-Methode bestimmt
- c[]: das Array der Simplex-Schwerpunktkoordinaten; die Größe des Arrays wird in der Init-Methode festgelegt.
- S_Point Xr: Reflexionspunkt
- S_Point Xe: Expansionspunkt
- S_Point Xc: Kontraktionspunkt
- indG: Guter Punkt Index im Simplex
- indW: Index des schlechtesten Punktes im Simplex
- E_SimplexOperation: Simplex-Operationstyp
//—————————————————————————————————————————————————————————————————————————————— struct S_Simplex { void Init (int coords) { ArrayResize (p, coords + 1); for (int i = 0; i <= coords; i++) { p [i].Init (coords); } ArrayResize (c, coords); Xr.Init (coords); Xe.Init (coords); Xc.Init (coords); operation = none; } S_Point p []; double c []; //centroid S_Point Xr; //reflection point S_Point Xe; //expansion point S_Point Xc; //expansion point int indG; //index of good point int indW; //index of worst point E_SimplexOperation operation; //type of simplex operation }; //——————————————————————————————————————————————————————————————————————————————
Definieren der Struktur S_Agent für den Optimierungsagenten. Die Struktur enthält folgende Felder:
- Init (int coords): Methode zur Initialisierung des Agenten, die mit dem Argument „coords“ die Anzahl der Koordinaten angibt. Die Methode ändert die Größe des Arrays „c“ in „coords“ unter Verwendung der Funktion ArrayResize. Das Feld „f“ wird dann auf -DBL_MAX gesetzt, was der Anfangswert für die Agentenbewertungsfunktion ist. Als Nächstes wird die Init-Methode für das Feld „s“ aufgerufen, das das Agenten-Simplex darstellt.
- c[]: das Feld der Koordinaten des Agenten im mehrdimensionalen Raum für den Austausch mit einem externen Programm. Die Größe des Arrays wird in der Methode Init festgelegt.
- f: Wert der Fitnessfunktion des Agenten
- s: Agenten-Simplex, dargestellt durch die Struktur S_Simplex. Das Simplex wird durch den Aufruf der Init-Methode für das Feld „s“ initialisiert.
//—————————————————————————————————————————————————————————————————————————————— struct S_Agent { void Init (int coords) { ArrayResize (c, coords); f = -DBL_MAX; s.Init (coords); } double c []; //coordinates double f; //fitness S_Simplex s; //agent simplex }; //——————————————————————————————————————————————————————————————————————————————
Definieren des Simplex-Suchalgorithmus der Klasse C_AO_NMm, der die folgenden Felder enthält:
- cB[]: Array der besten Koordinaten.
- fB: Wert der Fitnessfunktion für die besten Koordinaten.
- a[]: die durch die S_Agent-Struktur repräsentierte Agentengruppe.
- rangeMax[]: Array der maximalen Suchbereichswerte für jede Koordinate.
- rangeMin[]: Array der minimalen Suchbereichswerte für jede Koordinate.
- rangeStep[]: Array von Suchschritten für jede Koordinate.
- Init(const int coordsP, const int popSizeP, const double reflectionCoeffP, const double expansionCoeffP, const double contractionCoeffP): Die Methode zur Initialisierung des Algorithmus, nimmt Argumente entgegen, die die Anzahl der Koordinaten, die Größe der Grundgesamtheit und die Verhältnisse für Reflexions-, Expansions- und Kompressionsoperationen festlegen; die Methode führt die Initialisierung aller Klassenfelder durch.
- Moving(): Die Methode führt die Bewegung der Agenten im Algorithmus durch.
- Revision(): die Methode führt die Bewegung der Agenten im Algorithmus durch.
- Sorting, CalcCentroid, Reflection, Expansion, Contraction, Flying: zum Durchführung von Operationen mit Simplexen. Die Methoden
- SeInDiSp, RNDfromCI und Scale werden ausgeführt, um Werte zu erzeugen und in gültige Bereiche mit einem bestimmten Schritt umzuwandeln.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_NMm { //---------------------------------------------------------------------------- public: double cB []; //best coordinates public: double fB; //FF of the best coordinates public: S_Agent a []; //agent public: double rangeMax []; //maximum search range public: double rangeMin []; //manimum search range public: double rangeStep []; //step search public: void Init (const int coordsP, //coordinates number const int popSizeP, //population size const double reflectionCoeffP, //Reflection coefficient const double expansionCoeffP, //Expansion coefficient const double contractionCoeffP); //Contraction coefficient public: void Moving (); public: void Revision (); //---------------------------------------------------------------------------- private: int coords; //coordinates number private: int popSize; //population size private: int simplexPoints; //simplex points private: double reflectionCoeff; //Reflection coefficient private: double expansionCoeff; //Expansion coefficient private: double contractionCoeff; //Contraction coefficient private: bool revision; private: S_Point pTemp []; private: int ind []; private: double val []; private: void Sorting (S_Point &p []); private: void CalcCentroid (S_Simplex &s, int indW); private: void Reflection (S_Agent &agent, int indW); private: void Expansion (S_Agent &agent); private: void Contraction (S_Agent &agent, int indW); private: void Flying (S_Agent &agent, int indW); private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double min, double max); private: double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool revers); }; //——————————————————————————————————————————————————————————————————————————————
Um den Algorithmus zu initialisieren, verwenden wir die Init-Methode der Klasse C_AO_NMm, die alle Felder der Klasse initialisiert und die notwendigen Arrays erstellt, damit der Optimierungsalgorithmus funktioniert.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_NMm::Init (const int coordsP, //coordinates number const int popSizeP, //population size const double reflectionCoeffP, //reflection coefficient const double expansionCoeffP, //expansion coefficient const double contractionCoeffP) //contraction coefficient { MathSrand ((int)GetMicrosecondCount ()); // reset of the generator fB = -DBL_MAX; revision = false; coords = coordsP; popSize = popSizeP; simplexPoints = coords + 1; reflectionCoeff = reflectionCoeffP; expansionCoeff = expansionCoeffP; contractionCoeff = contractionCoeffP; ArrayResize (pTemp, simplexPoints); ArrayResize (ind, simplexPoints); ArrayResize (val, simplexPoints); ArrayResize (a, popSize); for (int i = 0; i < popSize; i++) { a [i].Init (coords); } ArrayResize (rangeMax, coords); ArrayResize (rangeMin, coords); ArrayResize (rangeStep, coords); ArrayResize (cB, coords); } //——————————————————————————————————————————————————————————————————————————————
Normalerweise verwenden wir die Moving-Methode, um Agenten im Suchraum zu bewegen, aber für den NM-Algorithmus belassen wir nur die Funktion der anfänglichen zufälligen Platzierung der Scheitelpunkte der Agenten-Simplexe im Suchraum.
Um einen zufälligen Scheitelpunkt von Simplexen zu erzeugen, verwenden wir RNDfromCI und bringen ihn mit der SeInDiSp-Methode in den erforderlichen Bereich mit dem erforderlichen Schritt.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_NMm::Moving () { if (!revision) { int cnt = 0; for (int i = 0; i < popSize; i++) { for (int p = 0; p < simplexPoints; p++) { cnt++; for (int c = 0; c < coords; c++) { a [i].s.p [p].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]); a [i].s.p [p].c [c] = SeInDiSp (a [i].s.p [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } } } //——————————————————————————————————————————————————————————————————————————————
Die Hauptlogik für das Verschieben der Eckpunkte der Simplexe der Agenten wird in der Revisionsmethode ausgeführt.
Wenn die Revision noch nicht durchgeführt wurde „if (!revision)“, dann ist es notwendig, die Scheitelpunkte im Simplex zu sortieren, einen Schwerpunkt zu konstruieren und die Reflexion für die schlechtesten Scheitelpunkte der Simplexe der Agenten durchzuführen. Dies ist die allererste Operation mit Scheitelpunkten, und sie ist immer „Spiegelung“. Hier können wir die globale Lösung aktualisieren, da wir zu diesem Zeitpunkt den Fitnesswert für jeden Eckpunkt kennen. Setzen des Wertes der Variablen „revision“ auf „true“ und Beenden der Methode.
Ab der nächsten Iteration kennen wir die Fitnessfunktion nicht mehr für die Scheitelpunkte von Simplexen, sondern für bestimmte Optimierungsagenten. In Übereinstimmung mit den durchgeführten Operationen auf Simplexen werden wir bekannte Lösungen von Agenten ihren entsprechenden Simplexpunkten zuordnen. Wir müssen die globale Lösung mit den besten Fitnesswerten der Agenten aktualisieren.
Als Nächstes wird geprüft, welche Operation bei der vorherigen Iteration an den Scheitelpunkten durchgeführt wurde. Wir meinen, dass die Scheitelpunkte von Simplexen Vektoren sind.
Wenn die Operation der „Reflektion“ (reflection) durchgeführt wurde, dann:
- weise den Fitnesswert des Agenten dem Vektor Xr zu,
- vergleiche die Fitness des Vektors Xr mit der von Xw, wenn der Wert besser ist, wird der Vektor Xw aktualisiert,
- vergleiche die Fitness des Vektors Xr mit der von Xb, wenn der Wert besser ist, dann führen die „Erweiterung“ durch,
- vergleiche den Fitnessvektor Xr mit dem von Xg (dem zweiten Wert nach dem schlechtesten Scheitelpunkt) und, wenn der Wert schlechter ist, führe eine „Komprimierung“ durch.
- wenn es eine Verbesserung des Scheitelpunkts gab, führe eine „Reflexion“ mit Vorsortierung und Konstruktion des Schwerpunkts durch. Andernfalls führe das „Flying“ aus.
Wenn die „Erweiterung“ (extension) durchgeführt wurde, dann:
- weise den Fitnesswert des Agenten dem Vektor Xe zu,
- vergleiche die Fitness des Vektors Xe mit der von Xw, wenn der Wert besser ist, wird der Vektor Xw aktualisiert,
- führe eine „Reflexion“ mit Vorsortierung und Konstruktion des Schwerpunkts durch.
Wenn die „Kontraktion“ (contraction) durchgeführt wurde, dann:
- weise den Fitnesswert des Agenten dem Vektor Xс zuordnen und
- vergleiche die Fitness des Vektors Xс mit des von Xw, wenn der Wert besser ist, wird der Vektor Xw aktualisiert, andernfalls führe „Flying“ aus,
- wenn es eine Verbesserung im Scheitelpunkt gab, dann führe „Reflexion“ (reflection) mit Vorsortierung und Konstruktion des Schwerpunkts durch.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_NMm::Revision () { //---------------------------------------------------------------------------- if (!revision) { //sort agent simplex points by FF value and assign BGW for (int i = 0; i < popSize; i++) { Sorting (a [i].s.p); } //calculate the simplex centroid for (int i = 0; i < popSize; i++) { a [i].s.indG = simplexPoints - 2; a [i].s.indW = simplexPoints - 1; CalcCentroid (a [i].s, a [i].s.indW); } //assign the next type of operation - reflection for (int i = 0; i < popSize; i++) { Reflection (a [i], a [i].s.indW); a [i].s.operation = reflection; } //save the best point of the agents’ simplexes as a global solution for (int i = 0; i < popSize; i++) { if (a [i].s.p [0].f > fB) { fB = a [i].s.p [0].f; ArrayCopy (cB, a [i].s.p [0].c, 0, 0, WHOLE_ARRAY); } } revision = true; return; } //---------------------------------------------------------------------------- if (revision) { int pos = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) pos = i; } if (pos != -1) { fB = a [pos].f; ArrayCopy (cB, a [pos].c, 0, 0, WHOLE_ARRAY); } } //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { //++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ //if there was reflection ++++++++++++++++++++++++++++++++++++++++++++ if (a [i].s.operation == reflection) { a [i].s.Xr.f = a [i].f; bool needUpd = false; //------------------------------------------------------------------------ if (a [i].s.Xr.f > a [i].s.p [a [i].s.indW].f) //Xr > Xw |---w--Xr--g----------b---| { a [i].s.p [a [i].s.indW] = a [i].s.Xr; //replace Xw with Xr needUpd = true; } //------------------------------------------------------------------------ if (a [i].s.Xr.f > a [i].s.p [0].f) //if Xr > Xb |---w----g----------b---Xr| { Expansion (a [i]); //perform expansion continue; } //------------------------------------------------------------------------ if (a [i].s.Xr.f <= a [i].s.p [a [i].s.indG].f) //if Xr < Xg |---w---Xr--g----------b--| { Contraction (a [i], a [i].s.indG); //perform contraction continue; } if (needUpd) { Sorting (a [i].s.p); a [i].s.indG = simplexPoints - 2; a [i].s.indW = simplexPoints - 1; CalcCentroid (a [i].s, a [i].s.indW); Reflection (a [i], a [i].s.indW); } else Flying (a [i], a [i].s.indW); continue; } //++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ //if there was expansion +++++++++++++++++++++++++++++++++++++++++++++ if (a [i].s.operation == expansion) { a [i].s.Xe.f = a [i].f; if (a [i].s.Xe.f > a [i].s.Xr.f) a [i].s.p [a [i].s.indW] = a [i].s.Xe; else a [i].s.p [a [i].s.indW] = a [i].s.Xr; Sorting (a [i].s.p); a [i].s.indG = simplexPoints - 2; a [i].s.indW = simplexPoints - 1; CalcCentroid (a [i].s, a [i].s.indW); Reflection (a [i], a [i].s.indW); continue; } //++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ //if there was contraction +++++++++++++++++++++++++++++++++++++++++++ if (a [i].s.operation == contraction) { a [i].s.Xc.f = a [i].f; if (a [i].s.Xc.f > a [i].s.p [a [i].s.indW].f) { a [i].s.p [a [i].s.indW] = a [i].s.Xc; Sorting (a [i].s.p); a [i].s.indG = simplexPoints - 2; a [i].s.indW = simplexPoints - 1; CalcCentroid (a [i].s, a [i].s.indW); Reflection (a [i], a [i].s.indW); } else Flying (a [i], a [i].s.indW); continue; } } } //——————————————————————————————————————————————————————————————————————————————
Um den Centroid zu berechnen, schreiben wir die Methode CalcCentroid. Sie berechnet den Mittelwert der Koordinaten im angegebenen Simplex „s“ bis zum angegebenen indW-Index.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_NMm::CalcCentroid (S_Simplex &s, int indW) { double summ = 0.0; for (int c = 0; c < coords; c++) { summ = 0.0; for (int p = 0; p < simplexPoints; p++) { if (p != indW) summ += s.p [p].c [c]; } s.c [c] = summ / coords; } } //——————————————————————————————————————————————————————————————————————————————
Die Operation „Reflexion“ wird von der Methode „Reflexion“ für den Indexpunkt „indW“ des Simplex „Agent“ durchgeführt.
Innerhalb der Schleife wird der reflektierter Wert Xr anhand der Gleichung Xr = Xo + reflectionCoeff * (Xo - Xw) berechnet. Dabei ist reflectionCoeff ein Reflexionsverhältnis, das den Grad der Abweichung des reflektierten Scheitelpunkts vom ursprünglichen Scheitelpunkt bestimmt.
Wenden Sie dann SeInDiSp auf Xr an, um sicherzustellen, dass es innerhalb des gültigen BereichsMin[c] und BereichMax[c] mit dem Schritt von rangeStep[c] liegt. Das Ergebnis wird in agent.s.Xr.c[c] gespeichert.
Die Konfiguration der Operation „Reflexion“ für den agent.s.operation agent, die anzeigt, dass die Operation „Reflexion“ für diesen agent durchgeführt wurde.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_NMm::Reflection (S_Agent &agent, int indW) { double Xo; double Xr; double Xw; for (int c = 0; c < coords; c++) { Xo = agent.s.c [c]; Xw = agent.s.p [indW].c [c]; //Xr = Xo + RNDfromCI (0.0, reflectionCoeff) * (Xo - Xw); Xr = Xo + reflectionCoeff * (Xo - Xw); agent.s.Xr.c [c] = SeInDiSp (Xr, rangeMin [c], rangeMax [c], rangeStep [c]); agent.c [c] = agent.s.Xr.c [c]; } agent.s.operation = reflection; } //——————————————————————————————————————————————————————————————————————————————
Der Vorgang „Expansion“ wird von der Methode „Expansion“ für den „Agenten“ durchgeführt.
Innerhalb der Schleife wird der erweiterte Wert von Xe anhand der Gleichung Xe = Xo + expansionCoeff * (Xr - Xo) berechnet. Dabei ist expansionCoeff das Expansionsverhältnis, das den Grad der Zunahme der Abweichung des erweiterten Scheitelpunkts vom ursprünglichen Scheitelpunkt bestimmt.
Wenden Sie anschließend SeInDiSp auf Xe an, um sicherzustellen, dass es innerhalb des gültigen Bereichs rangeMin[c] und rangeMax[c] mit der Schrittweite rangeStep[c] liegt. Das Ergebnis wird in agent.s.Xe.c[c] gespeichert.
Die Einstellungen der Operation „Expansion“ für den agent.s.operation agent, die anzeigt, dass die Operation „Expansion“ für diesen Agenten durchgeführt wurde.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_NMm::Expansion (S_Agent &agent) { double Xo; double Xr; double Xe; for (int c = 0; c < coords; c++) { Xo = agent.s.c [c]; Xr = agent.s.Xr.c [c]; //Xe = Xo + RNDfromCI (0.0, expansionCoeff) * (Xr - Xo); Xe = Xo + expansionCoeff * (Xr - Xo); agent.s.Xe.c [c] = SeInDiSp (Xe, rangeMin [c], rangeMax [c], rangeStep [c]); agent.c [c] = agent.s.Xe.c [c]; } agent.s.operation = expansion; } //——————————————————————————————————————————————————————————————————————————————
Die Operation „Kontraktion“ wird von der Methode „Kontraktion“ für den Indexpunkt indW des Simplexes „Agent“ durchgeführt.
Berechnen Sie innerhalb der Schleife den komprimierten Wert von Xc anhand der Gleichung Xc = Xo + contractionCoeff * (Xw - Xo) . Dabei ist contractionCoeff das Kontraktionsverhältnis, das den Grad der Abweichung des komprimierten Scheitelpunkts vom ursprünglichen Scheitelpunkt angibt.
Wenden Sie dann SeInDiSp auf Xc an, um sicherzustellen, dass es innerhalb des gültigen BereichsMin[c] und BereichMax[c] mit dem Schritt von rangeStep[c] liegt. Das Ergebnis wird in agent.s.Xc.c[c] gespeichert.
Die Konfiguration der Operation „contraction“ für den agent.s.operation des Agenten, die anzeigt, dass die Kontraktion für diesen Agenten durchgeführt wurde.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_NMm::Contraction (S_Agent &agent, int indW) { double Xo; double Xw; double Xc; for (int c = 0; c < coords; c++) { Xo = agent.s.c [c]; Xw = agent.s.p [indW].c [c]; //Xc = Xo + RNDfromCI (0.0, contractionCoeff) * (Xw - Xo); Xc = Xo + contractionCoeff * (Xw - Xo); agent.s.Xc.c [c] = SeInDiSp (Xc, rangeMin [c], rangeMax [c], rangeStep [c]); agent.c [c] = agent.s.Xc.c [c]; } agent.s.operation = contraction; } //——————————————————————————————————————————————————————————————————————————————
Für Levy Flights wenden wir die Flying-Methode an, die eine „fliegende“ Operation für den „Agenten“ durchführt, mit dem Ziel, den Scheitelpunkt des Simplex an neue Orte im Suchraum mit einer Zufallsverteilung zu schieben, die die Wahrscheinlichkeit näher an die beste globale Lösung konzentriert, wobei die Wahrscheinlichkeit in Richtung der Grenzen des untersuchten Raums bis auf 0 abnimmt.
Nach der Anwendung der Flying-Methode legen Sie für agent.s.operation die Operation „reflection“ fest, sodass in den nachfolgenden Iterationen die Logik des Algorithmus so ausgeführt wird, als ob die Operation „reflection“ durchgeführt worden wäre.
Wenden Sie SeInDiSp auf Xr an, um sicherzustellen, dass es innerhalb des gültigen BereichsMin[c] und BereichMax[c] mit dem Schritt von rangeStep[c] liegt. Das Ergebnis wird in agent.s.Xr.c[c] gespeichert.
Die Flying-Methode führt also eine „Flug“-Operation mit dem Agenten durch, bei der seine Koordinaten auf der Grundlage der aktuellen Koordinaten der global besten Lösung und zufällig generierter Werte geändert werden. Dies ermöglicht es dem Agenten, neue Bereiche des Lösungsraums zu erkunden und möglicherweise weitere optimale Lösungen zu finden.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_NMm::Flying (S_Agent &agent, int indW) { for (int c = 0; c < coords; c++) { double r1 = RNDfromCI (-1.0, 1.0); r1 = r1 > 0.5 ? 1.0 : -1.0; double r2 = RNDfromCI (1.0, 20.0); r2 = pow (r2, -2.0); if (r1 > 0.0) Xr = cB [c] + Scale (r2, 0.0, 1.0, 0.0, rangeMax [c] - cB [c], false); else Xr = cB [c] - Scale (r2, 0.0, 1.0, 0.0, cB [c] - rangeMin [c], false); //Xr = RNDfromCI (rangeMin [c], rangeMax [c]); agent.s.Xr.c [c] = SeInDiSp (Xr, rangeMin [c], rangeMax [c], rangeStep [c]); agent.c [c] = agent.s.Xr.c [c]; } agent.s.operation = reflection; } //——————————————————————————————————————————————————————————————————————————————
3. Testergebnisse
Ergebnisse des NM-Testergebnisse:
C_AO_NMm:5;1.0;2.0;0.5
=============================
5 Rastrigin's; Func runs 10000 result: 77.96849465506082
Score: 0.96607
25 Rastrigin's; Func runs 10000 result: 61.68192953373487
Score: 0.76427
500 Rastrigin's; Func runs 10000 result: 50.62713783555849
Score: 0.62730
=============================
5 Forest's; Func runs 10000 result: 0.9552378700292385
Score: 0.54033
25 Forest's; Func runs 10000 result: 0.45877475613538293
Score: 0.25951
500 Forest's; Func runs 10000 result: 0.09902427974784639
Score: 0.05601
=============================
5 Megacity's; Func runs 10000 result: 5.6
Score: 0.46667
25 Megacity's; Func runs 10000 result: 2.304
Score: 0.19200
500 Megacity's; Func runs 10000 result: 0.40280000000000005
Score: 0.03357
=============================
All score: 3.90573
Anhand der Ergebnisse des Algorithmus können wir feststellen, dass die glatte Rastrigin-Funktion recht anständige Ergebnisse liefert.
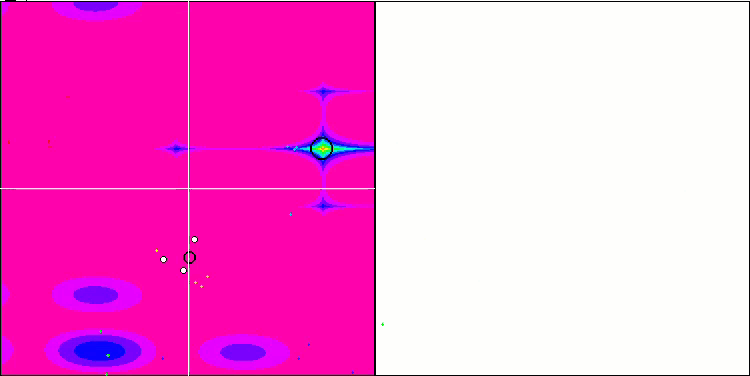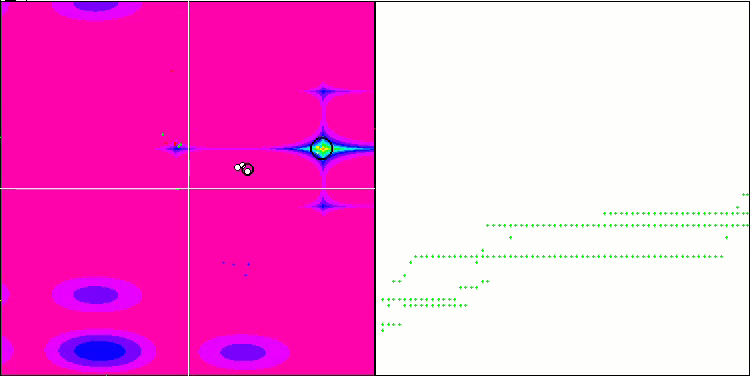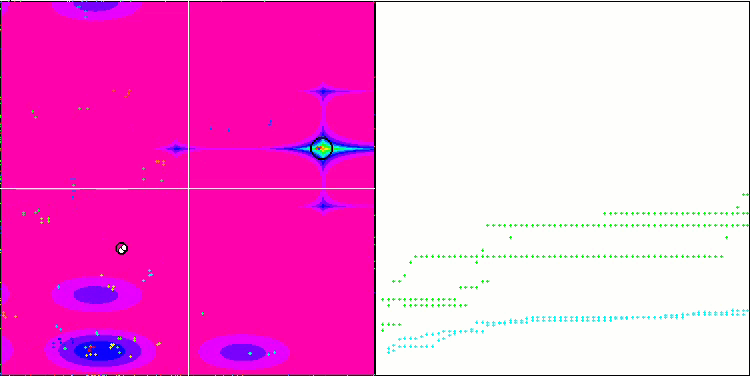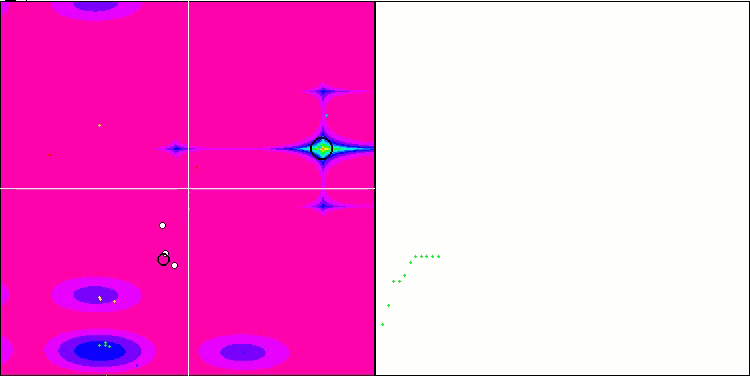
Die Visualisierung zeigt Anzeichen für die Degeneration der Population und die Konzentration der Erreger an einem Ort. Die Situation wird durch den Einsatz von Levy-Flügen etwas verbessert. Dies macht sich an einzelnen Punkten der entsprechenden Koordinaten bemerkbar. Die Konvergenzkurven sind nicht sehr stabil. Ich habe nur die ersten beiden Tests für jede Funktion visualisiert, weil der dritte Test mit 1000 Variablen so lange dauert, dass es nicht möglich ist, ihn in einem GIF darzustellen.
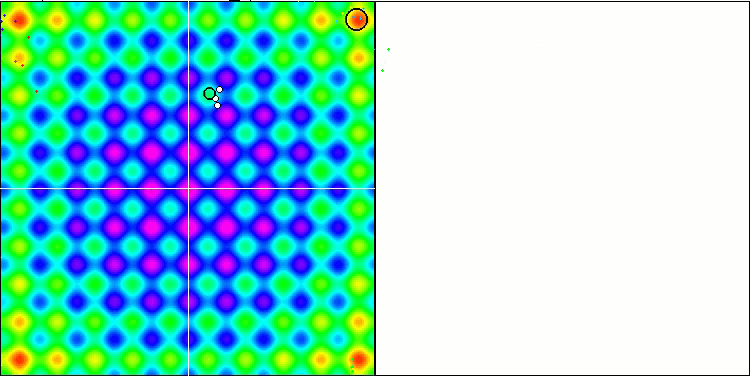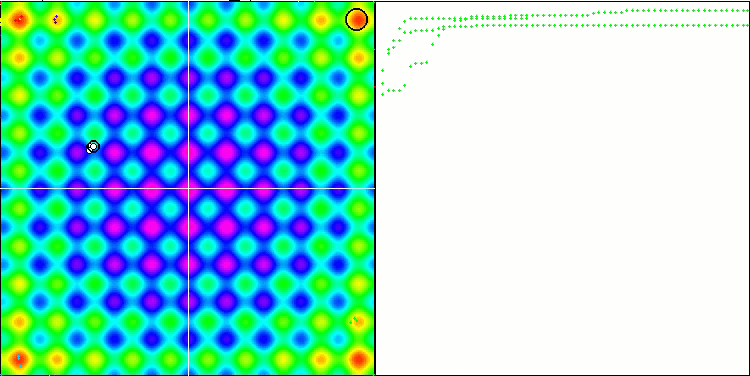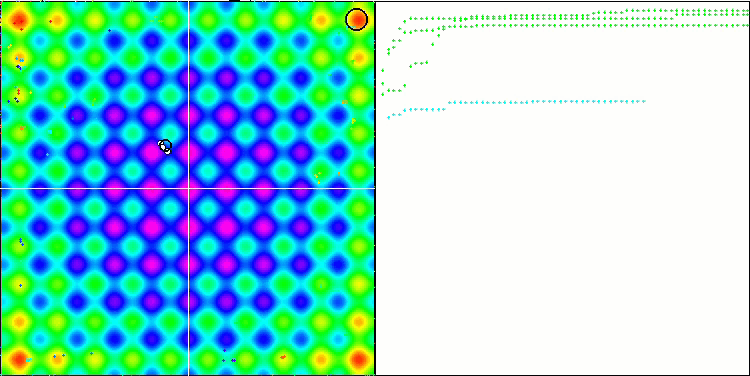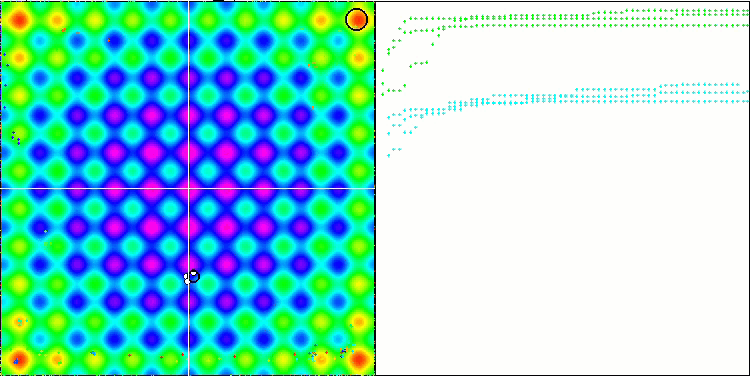
NMm mit der Testfunktion Rastrigin.
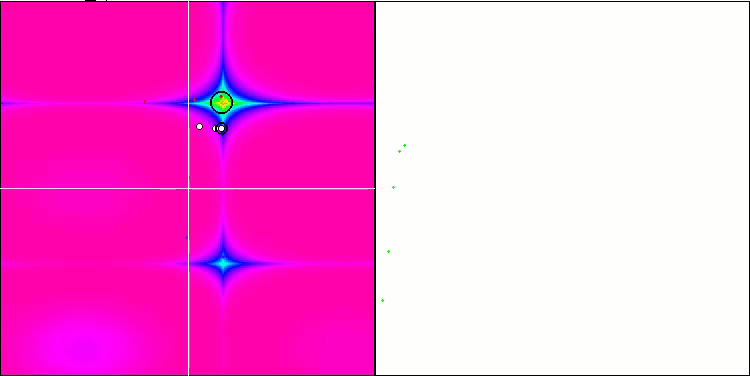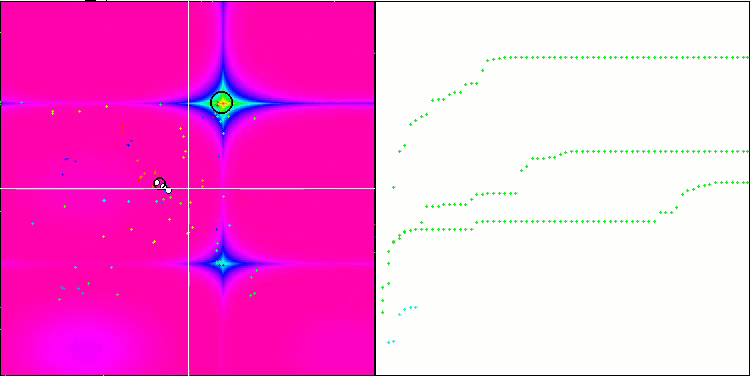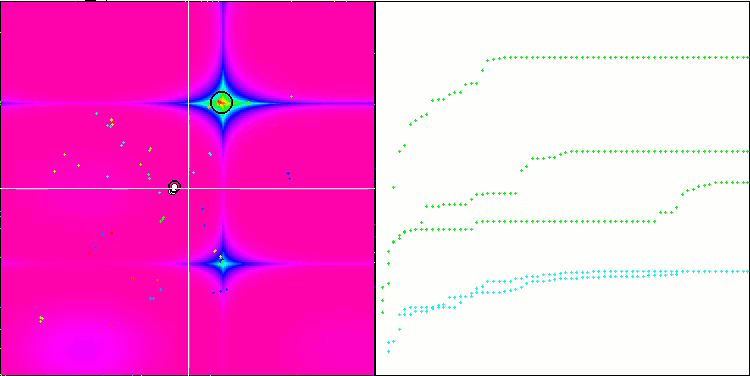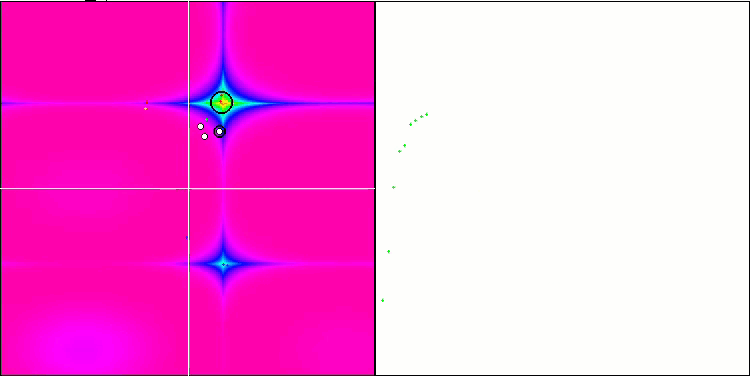
NMm mit der Testfunktion Forest.
NMm mit der Testfunktion Megacity.
Trotz seiner vielen Unzulänglichkeiten landete der Algorithmus der Nelder-Mead-Methode auf Platz 9.
| # | AO | Beschreibung | Rastrigin | Rastrigin final | Forest | Forest final | Megacity (diskret) | Megacity final | Final result | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | |||||||
| 1 | SDSm | stochastische Diffusionssuche M | 0.99809 | 1.00000 | 0.69149 | 2.68958 | 0.99265 | 1.00000 | 1.00000 | 2.99265 | 1.00000 | 1.00000 | 1.00000 | 3.00000 | 100.000 |
| 2 | SSG | Setzen, Säen und Wachsen | 1.00000 | 0.92761 | 0.51630 | 2.44391 | 0.72120 | 0.65201 | 0.83760 | 2.21081 | 0.54782 | 0.61841 | 0.99522 | 2.16146 | 77.683 |
| 3 | DE | differentielle Evolution | 0.98295 | 0.89236 | 0.51375 | 2.38906 | 1.00000 | 0.84602 | 0.65510 | 2.50112 | 0.90000 | 0.52237 | 0.12031 | 1.54268 | 73.099 |
| 4 | HS | Harmoniesuche | 0.99676 | 0.88385 | 0.44686 | 2.32747 | 0.99148 | 0.68242 | 0.37529 | 2.04919 | 0.71739 | 0.71842 | 0.41338 | 1.84919 | 70.623 |
| 5 | IWO | Optimierung mit invasiven Unkräutern | 0.95828 | 0.62227 | 0.27647 | 1.85703 | 0.70170 | 0.31972 | 0.26613 | 1.28755 | 0.57391 | 0.30527 | 0.33130 | 1.21048 | 48.250 |
| 6 | ACOm | Ameisen-Kolonie-Optimierung M | 0.34611 | 0.16683 | 0.15808 | 0.67103 | 0.86147 | 0.68980 | 0.64798 | 2.19925 | 0.71739 | 0.63947 | 0.05579 | 1.41265 | 47.387 |
| 7 | MEC | Evolutionäre Berechnung des Geistes | 0.99270 | 0.47345 | 0.21148 | 1.67763 | 0.60244 | 0.28046 | 0.21324 | 1.09615 | 0.66957 | 0.30000 | 0.26045 | 1.23002 | 44.049 |
| 8 | SDOm | Optimierung der Spiraldynamik M | 0.69840 | 0.52988 | 0.33168 | 1.55996 | 0.59818 | 0.38766 | 0.37600 | 1.36183 | 0.35653 | 0.15262 | 0.25842 | 0.76758 | 40.289 |
| 9 | NMm | Nelder-Mead-Verfahren M | 0.88433 | 0.48306 | 0.45945 | 1.82685 | 0.46155 | 0.24379 | 0.21903 | 0.92437 | 0.46088 | 0.25658 | 0.16810 | 0.88555 | 39.660 |
| 10 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.92400 | 0.43407 | 0.24120 | 1.59927 | 0.57881 | 0.23477 | 0.13842 | 0.95200 | 0.52174 | 0.24079 | 0.17001 | 0.93254 | 37.830 |
| 11 | FAm | Firefly-Algorithmus M | 0.59825 | 0.31520 | 0.15893 | 1.07239 | 0.50637 | 0.29178 | 0.41704 | 1.21519 | 0.24783 | 0.20526 | 0.35090 | 0.80398 | 33.139 |
| 12 | ABC | Künstliches Bienenvolk (Artificial Bee Colony, ABC) | 0.78170 | 0.30347 | 0.19313 | 1.27829 | 0.53379 | 0.14799 | 0.11177 | 0.79355 | 0.40435 | 0.19474 | 0.13859 | 0.73768 | 29.766 |
| 13 | BA | Fledermaus-Algorithmus | 0.40526 | 0.59145 | 0.78330 | 1.78002 | 0.20664 | 0.12056 | 0.21769 | 0.54488 | 0.21305 | 0.07632 | 0.17288 | 0.46225 | 29.499 |
| 14 | CSS | Suche geladener Systeme | 0.56605 | 0.68683 | 1.00000 | 2.25289 | 0.13961 | 0.01853 | 0.13638 | 0.29452 | 0.07392 | 0.00000 | 0.03465 | 0.10856 | 27.930 |
| 15 | GSA | Algorithmus für die Schwerkraftsuche | 0.70167 | 0.41944 | 0.00000 | 1.12111 | 0.31390 | 0.25120 | 0.27812 | 0.84322 | 0.42609 | 0.25525 | 0.00000 | 0.68134 | 27.807 |
| 16 | BFO | Optimierung der bakteriellen Futtersuche | 0.67203 | 0.28721 | 0.10957 | 1.06881 | 0.39364 | 0.18364 | 0.17298 | 0.75026 | 0.37392 | 0.24211 | 0.18841 | 0.80444 | 27.542 |
| 17 | EM | elektromagnetismusähnlicher Algorithmus | 0.12235 | 0.42928 | 0.92752 | 1.47915 | 0.00000 | 0.02413 | 0.29215 | 0.31628 | 0.00000 | 0.00527 | 0.10872 | 0.11399 | 19.002 |
| 18 | SFL | schlurfender Froschsprung | 0.40072 | 0.22021 | 0.24624 | 0.86717 | 0.19981 | 0.02861 | 0.02221 | 0.25063 | 0.19565 | 0.04474 | 0.06607 | 0.30646 | 13.200 |
| 19 | MA | Affen-Algorithmus | 0.33192 | 0.31029 | 0.13582 | 0.77804 | 0.09927 | 0.05443 | 0.07482 | 0.22852 | 0.15652 | 0.03553 | 0.10669 | 0.29874 | 11.777 |
| 20 | FSS | Fischschulsuche | 0.46812 | 0.23502 | 0.10483 | 0.80798 | 0.12730 | 0.03458 | 0.05458 | 0.21647 | 0.12175 | 0.03947 | 0.08244 | 0.24366 | 11.332 |
| 21 | IWDm | intelligente Wassertropfen M | 0.26459 | 0.13013 | 0.07500 | 0.46972 | 0.28358 | 0.05445 | 0.05112 | 0.38916 | 0.22609 | 0.05659 | 0.05054 | 0.33322 | 10.423 |
| 22 | PSO | Partikelschwarmoptimierung | 0.20449 | 0.07607 | 0.06641 | 0.34696 | 0.18734 | 0.07233 | 0.18207 | 0.44175 | 0.16956 | 0.04737 | 0.01947 | 0.23641 | 8.426 |
| 23 | RND | zufällig | 0.16826 | 0.09038 | 0.07438 | 0.33302 | 0.13381 | 0.03318 | 0.03949 | 0.20648 | 0.12175 | 0.03290 | 0.04898 | 0.20363 | 5.054 |
| 24 | GWO | Grauer-Wolf-Optimierung | 0.00000 | 0.00000 | 0.02093 | 0.02093 | 0.06514 | 0.00000 | 0.00000 | 0.06514 | 0.23478 | 0.05789 | 0.02545 | 0.31812 | 1.000 |
Zusammenfassung
Der Nelder-Mead-Algorithmus ist für moderne schwere Optimierungsprobleme wenig geeignet, da er die Berechnung der Fitnessfunktion für jeden Simplexpunkt in der Anfangsphase erfordert, was seine Eignung für mehrdimensionale Suchräume zunichte macht, sodass der Algorithmus trotz seiner relativ guten Ergebnisse und seines Platzes in der Bewertungstabelle nicht empfohlen werden kann.
Der SDS-Algorithmus wurde aus der Tabelle gestrichen und nur seine modifizierte Version blieb übrig.
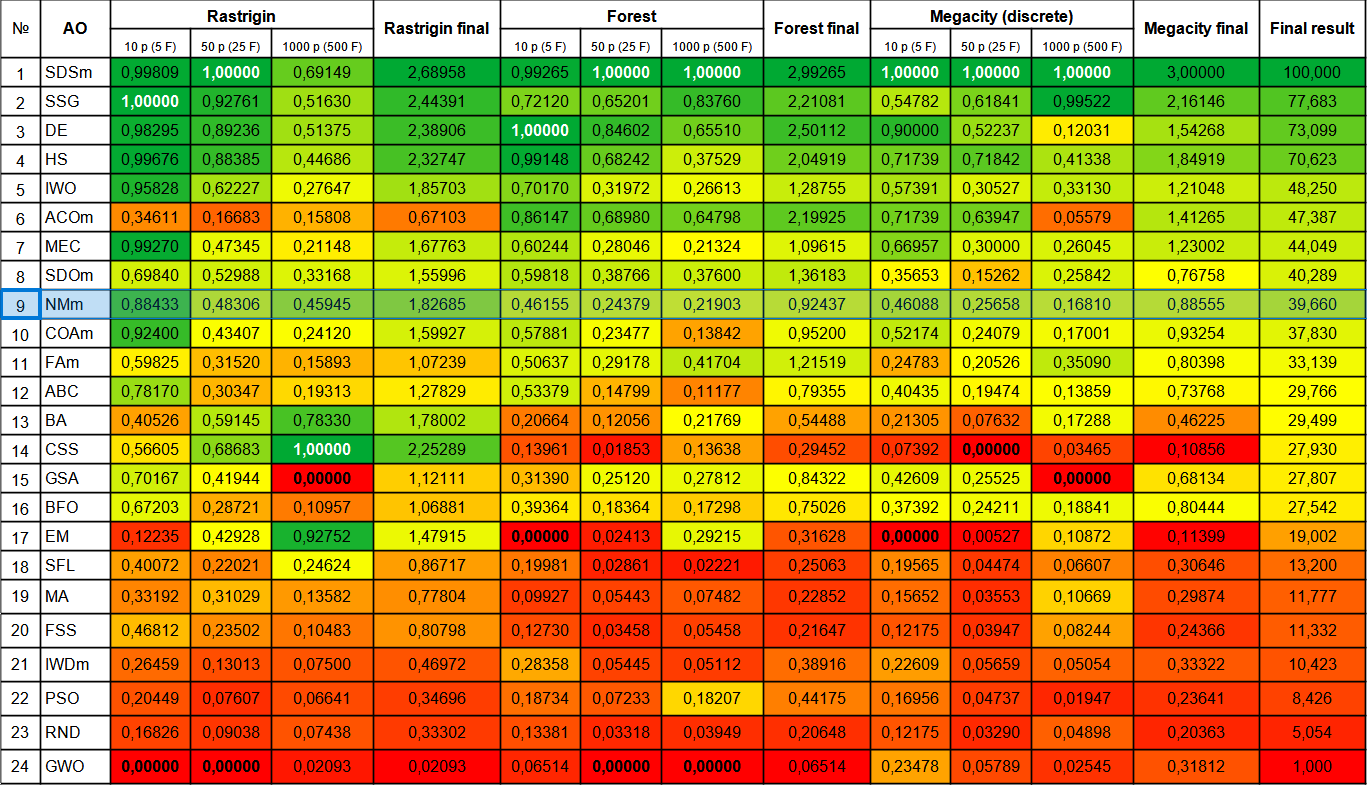
Bild 2. Farbabstufung der Algorithmen gemäß den einschlägigen Tests
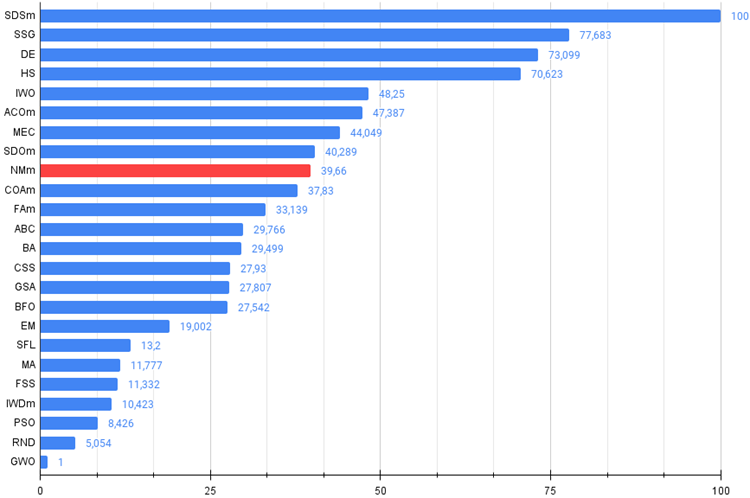
Abb. 3. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, größer ist besser,
das Archiv enthält das Skript zur Berechnung der Bewertungstabelle nach der im Artikel angewandten Methode).
Vor- und Nachteile des modifizierten Nelder-Mead-Algorithmus (NMm):
Vorteile:
- Eine kleine Anzahl externer Parameter.
- Gute Ergebnisse bei glatten Funktionen mit einer kleinen Anzahl von Variablen.
Nachteile
- Komplexe Umsetzung.
- Die Verwendung mit Anwendungen von Drittanbietern ist schwierig, da die Fitness für alle Simplex-Eckpunkte im Voraus berechnet werden muss.
- Niedrige Ausführungsgeschwindigkeit.
- Sehr schlechte Skalierbarkeit.
- Hohe Streuung der Ergebnisse.
- Tendenz, in lokalen Extrema stecken zu bleiben.
Bitte beachten Sie, dass sich die Vor- und Nachteile speziell auf die modifizierte Version der Simplex-Suche beziehen. Es macht keinen Sinn, die reguläre NM-Version in die Tabelle aufzunehmen, da die Ergebnisse sehr schwach sind.
Dem Artikel ist ein Archiv mit aktualisierten Versionen der in früheren Artikeln beschriebenen Algorithmuscodes beigefügt. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/13805
 Neuronale Netze leicht gemacht (Teil 67): Nutzung früherer Erfahrungen zur Lösung neuer Aufgaben
Neuronale Netze leicht gemacht (Teil 67): Nutzung früherer Erfahrungen zur Lösung neuer Aufgaben
 Quantitative Analyse in MQL5: Implementierung eines vielversprechenden Algorithmus
Quantitative Analyse in MQL5: Implementierung eines vielversprechenden Algorithmus
 Neuronale Netze leicht gemacht (Teil 66): Explorationsprobleme beim Offline-Lernen
Neuronale Netze leicht gemacht (Teil 66): Explorationsprobleme beim Offline-Lernen
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.