Algorithmen zur Populationsoptimierung Optimierung mit invasiven Unkräutern (IWO)

Inhalt

1. Einführung
2. Beschreibung des Algorithmus
3. Testergebnisse

1. Einführung

Der metaheuristische Algorithmus der invasiven Unkräuter ist ein populationsbasierter Optimierungsalgorithmus, der das Gesamtoptimum der optimierten Funktion findet, indem er die Kompatibilität und Zufälligkeit einer Unkrautkolonie simuliert.
Der Algorithmus zur Unkrautoptimierung bezieht sich auf von der Natur inspirierte Populationsalgorithmen und spiegelt das Verhalten von Unkraut in einem begrenzten Gebiet im Kampf ums Überleben für eine begrenzte Zeit wider.

Unkräuter sind mächtige Gräser, die mit ihrem offensiven Wachstum eine ernsthafte Bedrohung für die Kulturpflanzen darstellen. Sie sind sehr widerstandsfähig und können sich an Umweltveränderungen anpassen. Unter Berücksichtigung ihrer Eigenschaften haben wir einen leistungsstarken Optimierungsalgorithmus. Dieser Algorithmus versucht, die Robustheit, Anpassungsfähigkeit und Zufälligkeit der Unkrautgemeinschaft in der Natur zu imitieren.

Was macht Unkraut so besonders? Unkräuter sind in der Regel die ersten, die sich durch eine Vielzahl von Mechanismen überall ausbreiten. Daher fallen sie nur selten unter die Kategorie der gefährdeten Arten.
Im Folgenden werden acht Anpassungs- und Überlebensstrategien von Unkräutern in der Natur kurz beschrieben:

1. Universeller Genotyp. Die Studien haben die evolutionären Veränderungen bei Unkräutern als Reaktion auf den Klimawandel aufgezeigt.

2. Lebenszyklusstrategien, Fruchtbarkeit. Unkräuter weisen eine breite Palette von Lebenszyklusstrategien auf. Wenn sich die Bodenbearbeitungssysteme ändern, werden Unkräuter, die früher in einem bestimmten Anbausystem kein großes Problem darstellten, widerstandsfähiger. So verursachen beispielsweise reduzierte Bodenbearbeitungssysteme das Auftreten von mehrjährigen Unkräutern mit unterschiedlichen Lebenszyklusstrategien. Darüber hinaus beginnt der Klimawandel, neue Nischen für Unkrautarten oder Genotypen zu schaffen, deren Lebensweise besser an die veränderten Bedingungen angepasst ist. Als Reaktion auf die erhöhten Kohlendioxidemissionen werden Unkräuter höher, größer und stärker, was bedeutet, dass sie mehr Samen produzieren und diese aufgrund der aerodynamischen Eigenschaften von höheren Pflanzen weiter verbreiten können. Ihre Fruchtbarkeit ist enorm. Die Mais-Saatdistel zum Beispiel produziert bis zu 19.000 Samen.

3. Rasche Entwicklung (Keimung, anspruchsloses Wachstum, Wettbewerbsfähigkeit, Zuchtsystem, Saatguterzeugung und Vertriebsmerkmale). Die erhöhte Fähigkeit zur Verbreitung von Samen, die damit einhergehende Ausbreitung und die Anspruchslosigkeit des Wachstums bieten Überlebenschancen. Unkräuter sind äußerst anspruchslos in Bezug auf die Bodenbeschaffenheit und halten starke Temperatur- und Feuchtigkeitsschwankungen standhaft aus.

4. Epigenetik. Zusätzlich zur schnellen Evolution haben viele invasive Pflanzen die Fähigkeit, durch Änderung ihrer Genexpression schnell auf veränderte Umweltfaktoren zu reagieren. In einer sich ständig verändernden Umwelt müssen Pflanzen flexibel sein, um Stressfaktoren wie Schwankungen bei Licht, Temperatur, Wasserverfügbarkeit und Salzgehalt des Bodens standhalten zu können. Um flexibel zu sein, sind Pflanzen in der Lage, selbständig epigenetische Veränderungen vorzunehmen.

5. Hybridisierung. Hybride Unkrautarten weisen häufig eine hybride Wuchskraft auf, die auch als Heterosis bezeichnet wird. Die Nachkommenschaft weist im Vergleich zu beiden Elternarten eine verbesserte biologische Funktion auf. Eine Hybride zeigt in der Regel ein aggressiveres Wachstum mit einer verbesserten Fähigkeit, sich in neue Gebiete auszubreiten und innerhalb der eroberten Gebiete zu konkurrieren.

6. Resistenz und Toleranz gegenüber Herbiziden. In den letzten Jahrzehnten hat die Herbizidresistenz bei den meisten Unkräutern stark zugenommen.

7. Co-Evolution von Unkräutern in Verbindung mit menschlichen Aktivitäten. Durch Unkrautbekämpfungsmaßnahmen wie Herbizideinsatz und Unkrautbekämpfung haben Unkräuter Resistenzmechanismen entwickelt. Im Vergleich zu Kulturpflanzen werden sie bei der Bodenbearbeitung weniger stark von außen beschädigt. Im Gegenteil, diese Schäden sind oft sogar nützlich für die Vermehrung von vegetativ vermehrten Unkräutern (z. B. solche, die sich über Teile der Wurzel oder Rhizome vermehren).

8. Die immer häufigeren klimatischen Veränderungen bieten Unkräutern die Möglichkeit, sich im Vergleich zu den im Gewächshaus angebauten Pflanzen besser zu behaupten. Unkräuter fügen der Landwirtschaft großen Schaden zu. Da sie weniger Ansprüche an die Wachstumsbedingungen stellen, übertreffen sie die Kulturpflanzen in Wachstum und Entwicklung. Unkräuter absorbieren Feuchtigkeit, Nährstoffe und Sonnenlicht und führen zu erheblichen Ertragseinbußen, erschweren die Ernte und das Dreschen von Feldfrüchten und verschlechtern die Produktqualität.

2. Beschreibung des Algorithmus

Der Algorithmus für invasives Unkraut ist vom Wachstumsprozess des Unkrauts in der Natur inspiriert. Diese Methode wurde von Mehrabian und Lucas im Jahr 2006 eingeführt. Natürlich ist das Unkraut stark gewachsen, und dieses starke Wachstum stellt eine ernsthafte Bedrohung für die Nutzpflanzen dar. Eine wichtige Eigenschaft von Unkräutern ist ihre Widerstandsfähigkeit und hohe Anpassungsfähigkeit in der Natur, was die Grundlage für die Optimierung des IWO-Algorithmus ist. Dieser Algorithmus kann als Grundlage für effiziente Optimierungsansätze verwendet werden.

IWO ist ein kontinuierlicher stochastischer numerischer Algorithmus, der das Kolonisierungsverhalten von Unkraut nachahmt. Zunächst wird die Ausgangspopulation nach dem Zufallsprinzip über den gesamten Suchraum verteilt. Dieses Unkraut wird schließlich wachsen und weitere Schritte des Algorithmus ausführen. Der Algorithmus besteht aus sieben Schritten, die als Pseudocode dargestellt werden können:

1. Saatgut wahllos aussäen
2. FF berechnen
3. Aussaat der Unkrautsamen
4. FF berechnen
5. Untergeordnete Unkräuter mit übergeordneten Unkräutern zusammenführen
6. Alle Unkräuter sortieren
7. Wiederholen ab Schritt 3, bis die Stoppbedingung erfüllt.

Das Blockdiagramm zeigt die Funktionsweise des Algorithmus bei einer Iteration. IWO beginnt seine Arbeit mit dem Initialisierungsprozess des Saatguts. Die Samen werden zufällig und gleichmäßig auf dem "Feld" des Suchraums verstreut. Danach gehen wir davon aus, dass die Samen gekeimt sind und erwachsene Pflanzen gebildet haben, die mit der Fitnessfunktion bewertet werden sollten.

Im nächsten Schritt können wir, wenn wir die Fitness jeder Pflanze kennen, dem Unkraut erlauben, sich durch Samen zu vermehren, wobei die Anzahl der Samen proportional zur Fitness ist. Danach kombinieren wir die gekeimten Samen mit den Mutterpflanzen und sortieren sie. Im Allgemeinen kann der Algorithmus für invasives Unkraut als einfach zu programmieren, zu ändern und in Verbindung mit Anwendungen von Drittanbietern zu verwenden angesehen werden.

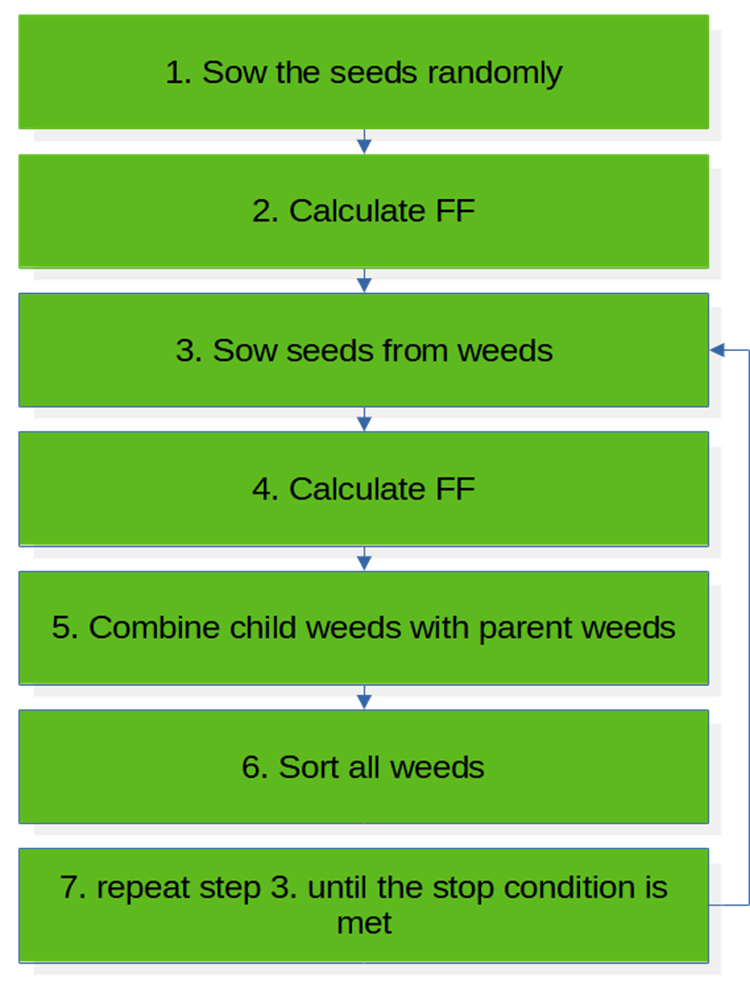
Abb. 1. Blockdiagramm des IWO-Algorithmus

Kommen wir nun zur Betrachtung der Merkmale des Unkrautalgorithmus. Es weist viele der extremen Überlebensfähigkeiten von Unkraut auf. Ein besonderes Merkmal einer Unkrautkolonie ist, im Gegensatz zu Algorithmen wie Genetik, Bienen und einigen anderen, die garantierte Aussaat von Samen durch alle Pflanzen der Kolonie ohne Ausnahme. Dadurch ist es möglich, dass selbst die am schlechtesten angepassten Pflanzen Nachkommen hinterlassen, da die Wahrscheinlichkeit, dass die schlechteste Pflanze dem globalen Extrem am nächsten kommt, immer ungleich Null ist.

Wie ich bereits sagte, produziert jedes Unkraut Samen in einem Bereich zwischen der kleinstmöglichen und der größtmöglichen Menge (externe Parameter des Algorithmus). Unter solchen Bedingungen, wenn jede Pflanze mindestens einen oder mehrere Samen hinterlässt, gibt es natürlich mehr Kinderpflanzen als Elternpflanzen - diese Funktion ist interessanterweise im Code implementiert und wird weiter unten besprochen. Der Algorithmus im Allgemeinen wird in Abbildung 2 visuell dargestellt. Die Elternpflanzen streuen die Samen im Verhältnis zu ihrer Fitness.

Die beste Pflanze auf Platz 1 hat also 6 Samen ausgesät, die Pflanze auf Platz 6 nur einen Samen (den garantierten). Aus gekeimten Samen entstehen Pflanzen, die anschließend zusammen mit den Elternpflanzen sortiert werden. Dies ist eine Imitation des Überlebens. Aus der gesamten sortierten Gruppe werden neue Elternpflanzen ausgewählt, und der Lebenszyklus wird bei der nächsten Iteration wiederholt. Der Algorithmus verfügt über einen Mechanismus zur Lösung der Probleme der "Überbevölkerung" und der unvollständigen Realisierung der Aussaatfähigkeit.

Nehmen wir als Beispiel an, die Anzahl der Samen, einer der Parameter des Algorithmus, sei 50 und die Anzahl der Elternpflanzen sei 5, die minimale Anzahl der Samen sei 1 und die maximale Anzahl sei 6. In diesem Fall ist 5 * 6 = 30, was weniger als 50 ist. Wie wir an diesem Beispiel sehen können, werden die Möglichkeiten der Aussaat nicht voll ausgeschöpft. In diesem Fall geht das Recht, einen Nachkommen zu behalten, auf den nächsten in der Liste über, bis die zulässige Höchstzahl von Nachkommen in allen Elternpflanzen erreicht ist. Wenn das Ende der Liste erreicht ist, geht das Recht auf den ersten auf der Liste über, und es wird erlaubt, mehr Nachkommen als das Limit auszusäen. 

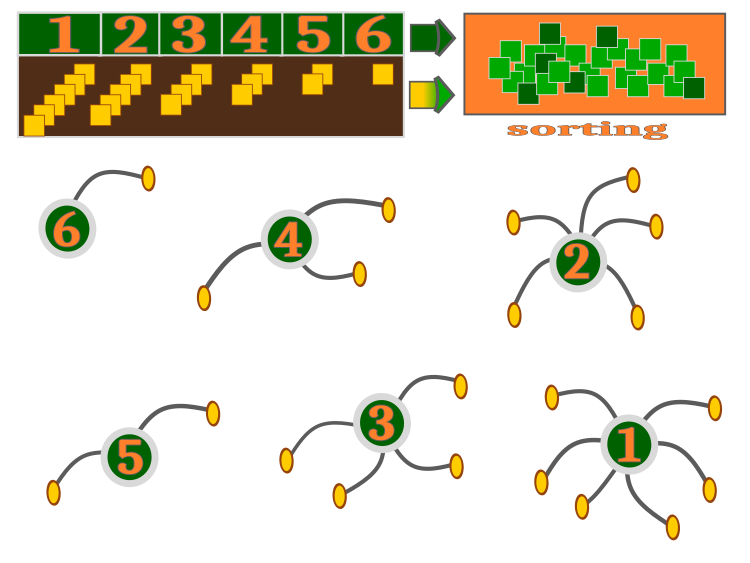
Abb. 2. Arbeitsweise des IWO-Algorithmus. Die Anzahl der Nachkommen ist proportional zur Fitness des Elternteils

Der nächste Punkt, auf den man achten muss, ist die Streuung des Saatguts. Die Saatgutverteilung im Algorithmus ist eine linear abnehmende Funktion proportional zur Anzahl der Iterationen. Die externen Verteilungsparameter sind die untere und obere Grenze der Saatgutverteilung. Mit zunehmender Anzahl von Iterationen verringert sich also der Saatgutradius und die gefundenen Extrema werden verfeinert. Nach der Empfehlung der Autoren des Algorithmus sollte die normalverteilte Saatgutverteilung verwendet werden, aber ich habe die Berechnungen vereinfacht und die kubische Funktion verwendet. Die Verteilungsfunktion der Anzahl der Iterationen ist in Abbildung 3 zu sehen.

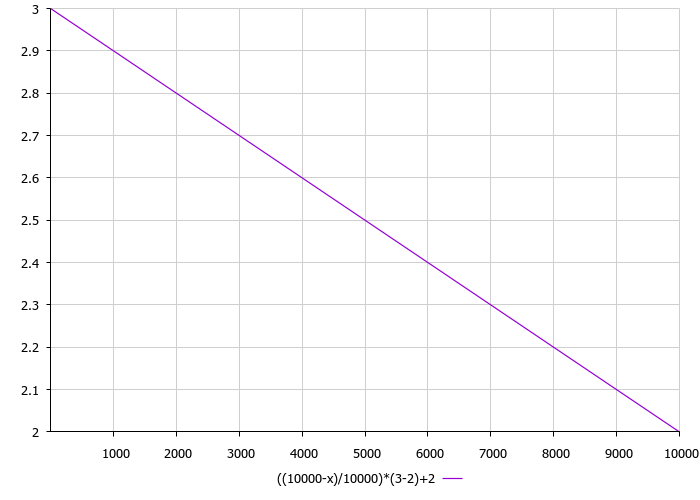
Abb. 3. Die Abhängigkeit der Verteilung von der Anzahl der Iterationen, wobei 3 die Höchstgrenze und 2 die Mindestgrenze ist

Kommen wir nun zum IWO-Code. Der Code ist einfach und schnell in der Ausführung.

Die einfachste Einheit (Agent) des Algorithmus ist das "Unkraut". Sie beschreibt auch die Samen des Unkrauts. So können wir dieselbe Art von Daten für spätere Sortierungen verwenden. Die Struktur besteht aus einem Array von Koordinaten, einer Variablen zur Speicherung des Werts der Fitnessfunktion und einem Zähler für die Anzahl der Samen (Nachkommen). Dieser Zähler ermöglicht es uns, die minimale und maximale Anzahl der Samen für jede Pflanze zu kontrollieren.

//——————————————————————————————————————————————————————————————————————————————
struct S_Weed
{
  double c []; //coordinates
  double f;    //fitness
  int    s;    //number of seeds
};
//——————————————————————————————————————————————————————————————————————————————

Wir brauchen eine Struktur, um die Wahrscheinlichkeitsfunktion für die Auswahl der Eltern im Verhältnis zu ihrer Fitness zu implementieren. In diesem Fall wird das Roulette-Prinzip angewendet, das wir bereits beim Bienenvolk-Algorithmus gesehen haben. Die Variablen "start" und "end" sind für den Anfang und das Ende des Wahrscheinlichkeitsfeldes verantwortlich.

//——————————————————————————————————————————————————————————————————————————————
struct S_WeedFitness
{
  double start;
  double end;
};
//——————————————————————————————————————————————————————————————————————————————

Deklarieren wir die Klasse des Unkrautalgorithmus. Darin deklarieren wir alle notwendigen Variablen, die wir benötigen - die Grenzen und den Schritt der zu optimierenden Parameter, das Array, das die Unkräuter beschreibt, sowie das Array der Samen, das Array der besten globalen Koordinaten und den besten Wert der Fitnessfunktion, der vom Algorithmus erreicht wurde. Außerdem benötigen wir das Flag „sowing“ (Aussaat) der ersten Iteration und konstante Variablen der Algorithmusparameter.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_IWO
{
  //============================================================================
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: S_Weed weeds     []; //weeds
  public: S_Weed weedsT    []; //temp weeds
  public: S_Weed seeds     []; //seeds
  public: double cB        []; //best coordinates
  public: double fB;           //fitness of the best coordinates

  public: void Init (const int    coordinatesP,      //Number of coordinates
                     const int    numberSeedsP,      //Number of seeds
                     const int    numberWeedsP,      //Number of weeds
                     const int    maxNumberSeedsP,   //Maximum number of seeds per weed
                     const int    minNumberSeedsP,   //Minimum number of seeds per weed
                     const double maxDispersionP,    //Maximum dispersion
                     const double minDispersionP,    //Minimum dispersion
                     const int    maxIterationP);    //Maximum iterations

  public: void Sowing      (int iter);
  public: void Germination ();

  //============================================================================
  private: void   Sorting        ();
  private: double SeInDiSp       (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI      (double Min, double Max);
  private: double Scale          (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool Revers);

  private: double vec [];            //Vector
  private: int    ind [];
  private: double val [];
  private: S_WeedFitness wf [];      //Weed fitness
  private: bool   sowing;            //Sowing
  private: int    coordinates;       //Coordinates number
  private: int    numberSeeds;       //Number of seeds
  private: int    numberWeeds;       //Number of weeds
  private: int    totalNumWeeds;     //Total number of weeds
  private: int    maxNumberSeeds;    //Maximum number of seeds
  private: int    minNumberSeeds;    //Minimum number of seeds
  private: double maxDispersion;     //Maximum dispersion
  private: double minDispersion;     //Minimum dispersion
  private: int    maxIteration;      //Maximum iterations
};
//——————————————————————————————————————————————————————————————————————————————

In der offenen Methode der Initialisierungsfunktion weisen wir konstanten Variablen einen Wert zu und überprüfen die Eingabeparameter des Algorithmus auf gültige Werte, sodass das Produkt aus Elternpflanzen und dem kleinstmöglichen Wert der Samen die Gesamtzahl der Samen nicht überschreiten kann. Die Summe der Elternpflanzen und Samen wird benötigt, um das Feld für die Sortierung zu bestimmen.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_IWO::Init (const int    coordinatesP,      //Number of coordinates
                     const int    numberSeedsP,      //Number of seeds
                     const int    numberWeedsP,      //Number of weeds
                     const int    maxNumberSeedsP,   //Maximum number of seeds per weed
                     const int    minNumberSeedsP,   //Minimum number of seeds per weed
                     const double maxDispersionP,    //Maximum dispersion
                     const double minDispersionP,    //Minimum dispersion
                     const int    maxIterationP)     //Maximum iterations
{
  MathSrand (GetTickCount ());
  sowing = false;
  fB     = -DBL_MAX;

  coordinates    = coordinatesP;
  numberSeeds    = numberSeedsP;
  numberWeeds    = numberWeedsP;
  maxNumberSeeds = maxNumberSeedsP;
  minNumberSeeds = minNumberSeedsP;
  maxDispersion  = maxDispersionP;
  minDispersion  = minDispersionP;
  maxIteration   = maxIterationP;


  if (minNumberSeeds < 1) minNumberSeeds = 1;
  if (numberWeeds * minNumberSeeds > numberSeeds) numberWeeds = numberSeeds / minNumberSeeds;
  else numberWeeds = numberWeedsP;

  totalNumWeeds  = numberWeeds + numberSeeds;

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);
  ArrayResize (vec,       coordinates);
  ArrayResize (cB,        coordinates);

  ArrayResize (weeds,  totalNumWeeds);
  ArrayResize (weedsT, totalNumWeeds);
  ArrayResize (seeds,  numberSeeds);

  for (int i = 0; i < numberWeeds; i++)
  {
    ArrayResize (weeds  [i].c, coordinates);
    ArrayResize (weedsT [i].c, coordinates);
    weeds [i].f = -DBL_MAX;
    weeds [i].s = 0;
  }
  for (int i = 0; i < numberSeeds; i++)
  {
    ArrayResize (seeds [i].c, coordinates);
    seeds [i].s = 0;
  }

  ArrayResize (ind, totalNumWeeds);
  ArrayResize (val, totalNumWeeds);

  ArrayResize (wf, numberWeeds);
}
//——————————————————————————————————————————————————————————————————————————————

Die erste öffentliche Methode, die bei jeder Iteration von Sowing() aufgerufen wird. Sie enthält die Hauptlogik des Algorithmus. Der Einfachheit halber werde ich die Methode in mehrere Teile unterteilen.

Wenn sich der Algorithmus in der ersten Iteration befindet, ist es notwendig, Samen im gesamten Suchraum auszusäen. Dies geschieht in der Regel willkürlich und gleichmäßig. Nach der Generierung von Zufallszahlen im Bereich der akzeptablen Werte der optimierten Parameter werden die erhaltenen Werte auf Überschreitung des Bereichs geprüft und die durch die Algorithmusparameter festgelegte Diskretion eingestellt. Hier werden wir auch einen Verteilungsvektor zuweisen, den wir später im Code für die Aussaat benötigen. Wir initialisieren die Fitnesswerte der Samen auf den minimalen doppelten Wert und setzen den Saatgutzähler zurück (aus Samen werden Pflanzen, die den Saatgutzähler verwenden).

//the first sowing of seeds---------------------------------------------------
if (!sowing)
{
  fB = -DBL_MAX;

  for (int s = 0; s < numberSeeds; s++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      seeds [s].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      seeds [s].c [c] = SeInDiSp (seeds [s].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);

      vec [c] = rangeMax [c] - rangeMin [c];
    }

    seeds [s].f = -DBL_MAX;
    seeds [s].s = 0;
  }

  sowing = true;
  return;
}

In diesem Abschnitt des Codes wird die Verteilung in Abhängigkeit von der aktuellen Iteration berechnet. Die bereits erwähnte garantierte Mindestanzahl der Samen für jedes Elternkraut wird hier umgesetzt. Die Mindestanzahl an Samen wird durch zwei Schleifen gewährleistet, wobei in der ersten Schleife die Elternpflanzen sortiert werden und in der zweiten Schleife tatsächlich neue Samen erzeugt werden, wobei der Samenzähler erhöht wird. Wie man sehen kann, besteht der Sinn der Erstellung eines neuen Nachkommens darin, eine Zufallszahl mit der Verteilung einer kubischen Funktion mit der zuvor berechneten Streuung zur übergeordneten Koordinate zu inkrementieren. Prüfen wir den erhaltenen Wert der neuen Koordinate auf akzeptable Werte und weisen die Abstände zu.

//guaranteed sowing of seeds by each weed-------------------------------------
int    pos = 0;
double r   = 0.0;
double dispersion = ((maxIteration - iter) / (double)maxIteration) * (maxDispersion - minDispersion) + minDispersion;

for (int w = 0; w < numberWeeds; w++)
{
  weeds [w].s = 0;

  for (int s = 0; s < minNumberSeeds; s++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      r = RNDfromCI (-1.0, 1.0);
      r = r * r * r;

      seeds [pos].c [c] = weeds [w].c [c] + r * vec [c] * dispersion;
      seeds [pos].c [c] = SeInDiSp (seeds [pos].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }

    pos++;
    weeds [w].s++;
  }
}

Mit diesem Code werden wir Wahrscheinlichkeitsfelder für jede der Elternpflanzen im Verhältnis zur Fitness nach dem Roulette-Prinzip erstellen. Der obige Code garantierte eine bestimmte Anzahl von Samen für jede der Pflanzen zu einem Zeitpunkt, zu dem die Anzahl der Samen einem Zufallsgesetz folgt, d. h. je besser das Unkraut angepasst ist, desto mehr Samen kann es hinterlassen und umgekehrt. Je weniger angepasst die Pflanze ist, desto weniger Samen wird sie produzieren.

//============================================================================
//sowing seeds in proportion to the fitness of weeds--------------------------

//the distribution of the probability field is proportional to the fitness of weeds
wf [0].start = weeds [0].f;
wf [0].end   = wf [0].start + (weeds [0].f - weeds [numberWeeds - 1].f);

for (int f = 1; f < numberWeeds; f++)
{
  if (f != numberWeeds - 1)
  {
    wf [f].start = wf [f - 1].end;
    wf [f].end   = wf [f].start + (weeds [f].f - weeds [numberWeeds - 1].f);
  }
  else
  {
    wf [f].start = wf [f - 1].end;
    wf [f].end   = wf [f].start + (weeds [f - 1].f - weeds [f].f) * 0.1;
  }
}

Auf der Grundlage der ermittelten Wahrscheinlichkeitsfelder wählen wir die Elternpflanze aus, die das Recht hat, einen Nachkommen zu hinterlassen. Wenn der Zähler für das Saatgut den maximal zulässigen Wert erreicht hat, geht das Recht auf das nächste in der sortierten Liste über. Wenn das Ende der Liste erreicht ist, geht das Recht nicht zum nächsten, sondern zum ersten in der Liste. Dann wird eine Tochterplanze nach der oben beschriebenen Regel mit der berechneten Verteilung gebildet.

bool seedingLimit = false;
int  weedsPos = 0;

for (int s = pos; s < numberSeeds; s++)
{
  r = RNDfromCI (wf [0].start, wf [numberWeeds - 1].end);

  for (int f = 0; f < numberWeeds; f++)
  {
    if (wf [f].start <= r && r < wf [f].end)
    {       
      weedsPos = f;
      break;
    }
  }

  if (weeds [weedsPos].s >= maxNumberSeeds)
  {
    seedingLimit = false;
    while (!seedingLimit)
    {
      weedsPos++;
      if (weedsPos >= numberWeeds)
      {
        weedsPos = 0;
        seedingLimit = true;
      }
      else
      {
        if (weeds [weedsPos].s < maxNumberSeeds)
        {
          seedingLimit = true;
        }
      }
    }
  }

  for (int c = 0; c < coordinates; c++)
  {
    r = RNDfromCI (-1.0, 1.0);
    r = r * r * r;

    seeds [s].c [c] = weeds [weedsPos].c [c] + r * vec [c] * dispersion;
    seeds [s].c [c] = SeInDiSp (seeds [s].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }

  seeds [s].s = 0;
  weeds [weedsPos].s++;
}

Die zweite offene Methode muss bei jeder Iteration ausgeführt werden und wird nach der Berechnung der Fitnessfunktion für jedes untergeordnete Unkraut benötigt. Bevor die Sortierung durchgeführt wird, werden die gekeimten Samen in das gemeinsame Feld mit den Elternpflanzen am Ende der Liste eingefügt, wodurch die vorherige Generation ersetzt wird, die sowohl Nachkommen als auch Eltern aus der vorherigen Iteration enthalten kann. So vernichten wir schwach angepasste Unkräuter, wie es in der Natur geschieht. Danach wird sortiert. Das erste Unkraut in der daraus resultierenden Liste ist es wert, die global erreichte beste Lösung zu aktualisieren, wenn es wirklich besser ist.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_IWO::Germination ()
{
  for (int s = 0; s < numberSeeds; s++)
  {
    weeds [numberWeeds + s] = seeds [s];
  }

  Sorting ();

  if (weeds [0].f > fB) fB = weeds [0].f;
}
//——————————————————————————————————————————————————————————————————————————————

3. Testergebnisse

Die Ergebnisse des Prüfstands sehen wie folgt aus:

2023.01.13 18:12:29.880    Test_AO_IWO (EURUSD,M1)    C_AO_IWO:50;12;5;2;0.2;0.01
2023.01.13 18:12:29.880    Test_AO_IWO (EURUSD,M1)    =============================
2023.01.13 18:12:32.251    Test_AO_IWO (EURUSD,M1)    5 Rastrigins; Funktionsdurchläufe10000 Ergebnis: 79.71791976868334
2023.01.13 18:12:32.251    Test_AO_IWO (EURUSD,M1)    Score: 0.98775
2023.01.13 18:12:36.564    Test_AO_IWO (EURUSD,M1)    25 Rastrigins; Funktionsdurchläufe10000 Ergebnis: 66.60305588198622
2023.01.13 18:12:36.564    Test_AO_IWO (EURUSD,M1)    Score: 0.82525
2023.01.13 18:13:14.024    Test_AO_IWO (EURUSD,M1)    500 Rastrigins; Funktionsdurchläufe10000 Ergebnis: 45.4191288396659
2023.01.13 18:13:14.024    Test_AO_IWO (EURUSD,M1)    Score: 0.56277
2023.01.13 18:13:14.024    Test_AO_IWO (EURUSD,M1)    =============================
2023.01.13 18:13:16.678    Test_AO_IWO (EURUSD,M1)    5 Forests; Funktionsdurchläufe10000 Ergebnis: 1.302934874807614
2023.01.13 18:13:16.678    Test_AO_IWO (EURUSD,M1)    Score: 0.73701
2023.01.13 18:13:22.113    Test_AO_IWO (EURUSD,M1)    25 Forests; Funktionsdurchläufe10000 Ergebnis: 0.5630336066477166
2023.01.13 18:13:22.113    Test_AO_IWO (EURUSD,M1)    Score: 0.31848
2023.01.13 18:14:05.092    Test_AO_IWO (EURUSD,M1)    500 Forests; Funktionsdurchläufe10000 Ergebnis: 0.11082098547471195
2023.01.13 18:14:05.092    Test_AO_IWO (EURUSD,M1)    Score: 0.06269
2023.01.13 18:14:05.092    Test_AO_IWO (EURUSD,M1)    =============================
2023.01.13 18:14:09.102    Test_AO_IWO (EURUSD,M1)    5 Megacities; Funktionsdurchläufe10000 Ergebnis: 6.640000000000001
2023.01.13 18:14:09.102    Test_AO_IWO (EURUSD,M1)    Score: 0.55333
2023.01.13 18:14:15.191    Test_AO_IWO (EURUSD,M1)    25 Megacities; Funktionsdurchläufe10000 Ergebnis: 2.6
2023.01.13 18:14:15.191    Test_AO_IWO (EURUSD,M1)    Score: 0.21667
2023.01.13 18:14:55.886    Test_AO_IWO (EURUSD,M1)    500 Megacities; Funktionsdurchläufe10000 Ergebnis: 0.5668
2023.01.13 18:14:55.886    Test_AO_IWO (EURUSD,M1)    Score: 0.04723

Ein kurzer Blick genügt, um die guten Ergebnisse des Algorithmus bei den Testfunktionen zu erkennen. Es gibt eine deutliche Präferenz für die Arbeit mit glatten Funktionen, obwohl bisher keiner der betrachteten Algorithmen bei diskreten Funktionen eine bessere Konvergenz als bei glatten Funktionen gezeigt hat, was sich durch die Komplexität der Forest- und Megacity-Funktionen für ausnahmslos alle Algorithmen erklärt. Es ist möglich, dass wir irgendwann einen Algorithmus für Tests bekommen werden, der diskrete Funktionen besser löst als glatte Funktionen.

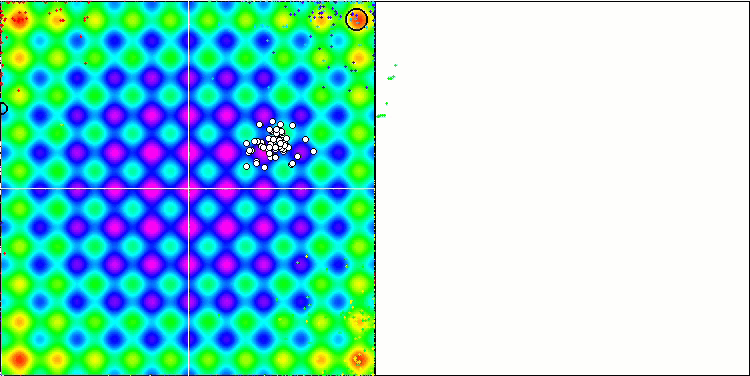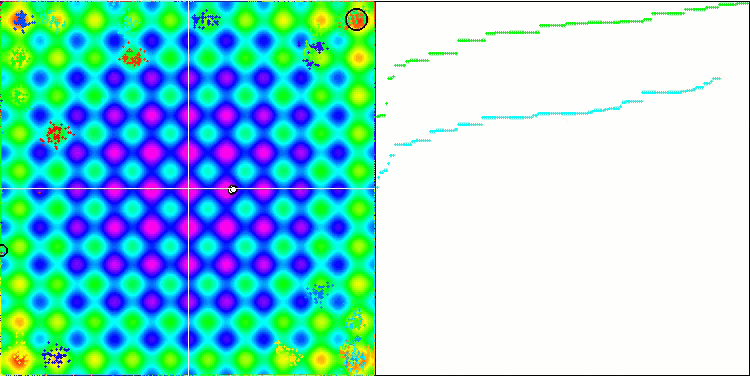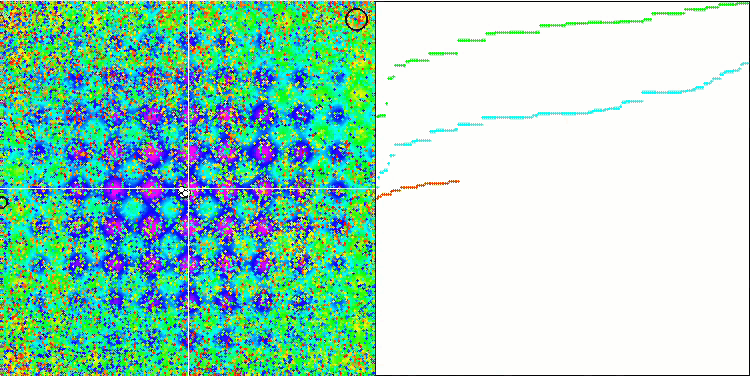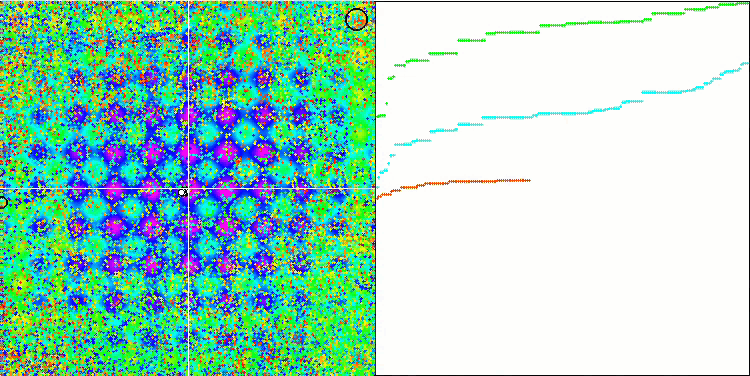
  IWO mit der Rastrigin-Testfunktion

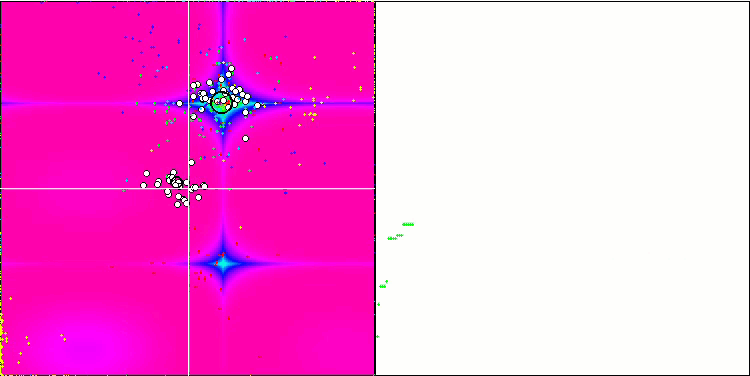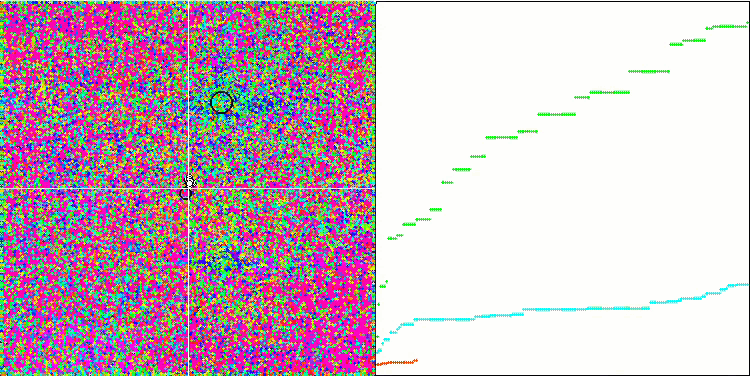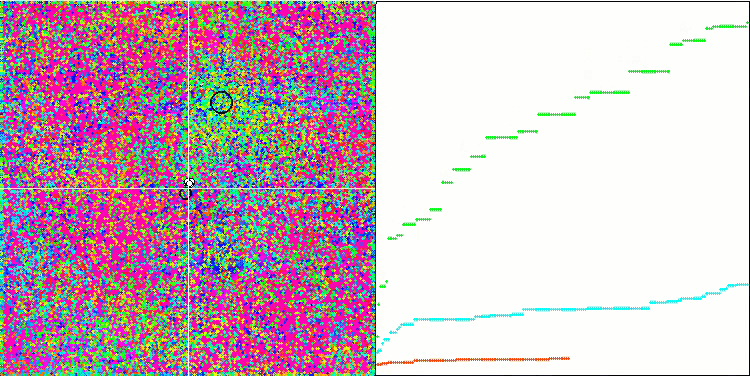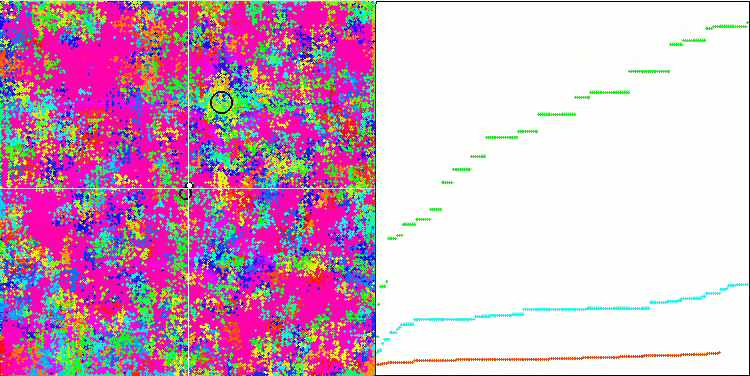
IWO mit der Forest-Testfunktion

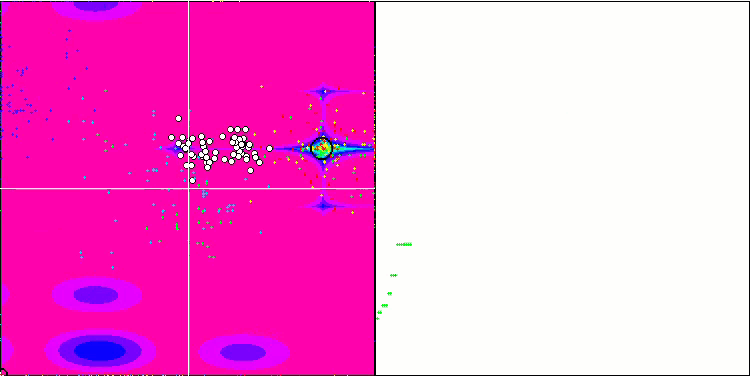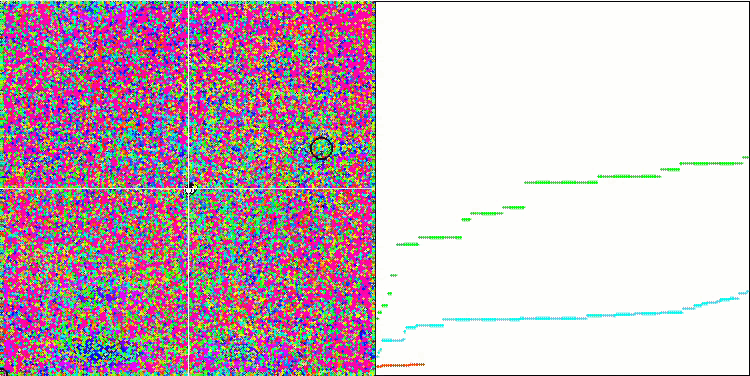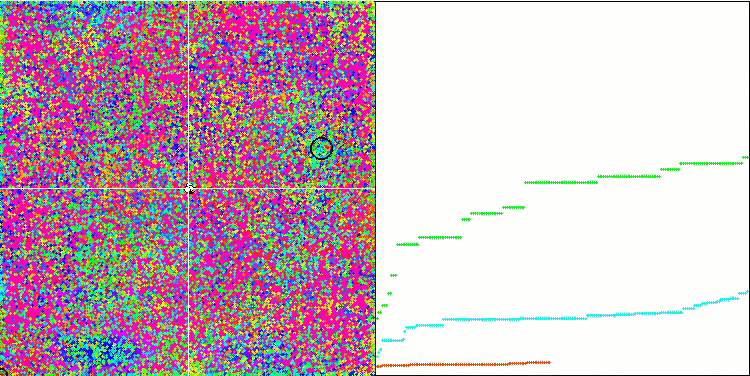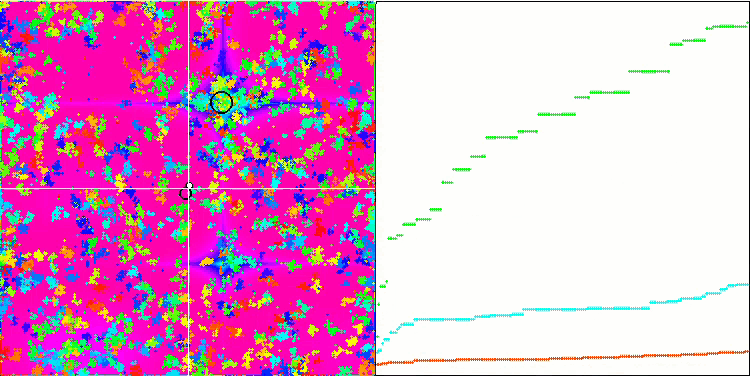
IWO mit der Megacity-Testfunktion

Der invasive Unkraut-Algorithmus zeigte bei den meisten Tests beeindruckende Ergebnisse, insbesondere bei der glatten Rastrigin-Funktion mit 10 und 50 Parametern. Lediglich bei dem Test mit 1000 Parametern ist die Leistung leicht gesunken, was im Allgemeinen auf eine gute Leistung bei glatten Funktionen hindeutet. Dadurch kann ich den Algorithmus für komplexe glatte Funktionen und neuronale Netze empfehlen. Bei den Forest-Funktionen zeigte der Algorithmus im ersten Test mit 10 Parametern gute Ergebnisse, aber insgesamt nur durchschnittliche Ergebnisse. Bei der diskreten Funktion Megacity schnitt der Algorithmus für invasive Unkräuter überdurchschnittlich gut ab und zeigte insbesondere beim Test mit 1000 Variablen eine hervorragende Skalierbarkeit. Er verlor seinen ersten Platz nur an den Firefly-Algorithmus, übertraf ihn aber bei den Tests mit 10 und 50 Parametern deutlich.

Obwohl der Algorithmus für invasive Unkräuter eine relativ große Anzahl von Parametern hat, sollte dies nicht als Nachteil angesehen werden, da die Parameter sehr intuitiv sind und leicht konfiguriert werden können. Außerdem wirkt sich die Feinabstimmung des Algorithmus im Allgemeinen nur auf die Ergebnisse der Tests einer diskreten Funktion aus, während die Ergebnisse bei einer glatten Funktion gut bleiben.

Bei der Visualisierung der Testfunktionen ist die Fähigkeit des Algorithmus, bestimmte Teile des Suchraums zu isolieren und zu erforschen, deutlich sichtbar, genau wie beim Bienenalgorithmus und einigen anderen. In mehreren Veröffentlichungen wird jedoch darauf hingewiesen, dass der Algorithmus dazu neigt, stecken zu bleiben, und nur über schwache Suchfunktionen verfügt. Obwohl der Algorithmus keinen Verweis auf das globale Extremum und keine Mechanismen zum "Herausspringen" aus lokalen Fallen hat, gelingt es IWO irgendwie, bei so komplexen Funktionen wie Forest und Megacity angemessen zu arbeiten. Bei der Arbeit an einer diskreten Funktion gilt: je mehr optimierte Parameter, desto stabiler die Ergebnisse.

Da die Saatgutverteilung mit jeder Iteration linear abnimmt, nimmt die Extremwertverfeinerung gegen Ende der Optimierung weiter zu. Meiner Meinung nach ist dies nicht ganz optimal, weil die Erkundungsfähigkeiten des Algorithmus ungleichmäßig über die Zeit verteilt sind, was man an der Visualisierung der Testfunktionen als konstantes weißes Rauschen erkennen kann. Auch die Ungleichmäßigkeit der Suche kann anhand der Konvergenzkurven im rechten Teil des Prüfstandsfensters beurteilt werden. Zu Beginn der Optimierung ist eine gewisse Beschleunigung der Konvergenz zu beobachten, was für fast alle Algorithmen typisch ist. Nach einem steilen Start verlangsamt sich die Konvergenz für den größten Teil der Optimierung. Eine deutliche Beschleunigung der Konvergenz ist erst gegen Ende zu erkennen. Die dynamische Veränderung der Verteilung ist ein Grund für weitere detaillierte Studien und Experimente. Da wir sehen können, dass die Konvergenz wieder aufgenommen werden könnte, wenn die Anzahl der Iterationen größer wäre. Um Objektivität und praktische Gültigkeit zu gewährleisten, gibt es jedoch Einschränkungen bei den Vergleichstests. 

Kommen wir nun zur endgültigen Bewertungstabelle. Die Tabelle zeigt, dass IWO derzeit führend ist. Der Algorithmus hat in zwei von neun Tests die besten Ergebnisse erzielt, während die Ergebnisse in den übrigen Tests weit über dem Durchschnitt liegen, sodass das Endergebnis 100 Punkte beträgt. An zweiter Stelle steht der modifizierte Ameisenkolonie-Algorithmus (ACOm). Er bleibt in 5 von 9 Tests der Beste.

AO	Beschreibung	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (diskret)			Megacity final	Endergebnis
		10 Parameter (5 F)	50 Parameter (25 F)	1000 Parameter (500 F)		10 Parameter (5 F)	50 Parameter (25 F)	1000 Parameter (500 F)		10 Parameter (5 F)	50 Parameter (25 F)	1000 Parameter (500 F)
IWO	Optimierung mit invasiven Unkräutern	1.00000	1.00000	0.33519	2.33519	0.79937	0.46349	0.41071	1.67357	0.75912	0.44903	0.94088	2.14903	100.000
ACOm	Ameisen-Kolonie-Optimierung M	0.36118	0.26810	0.17991	0.80919	1.00000	1.00000	1.00000	3.00000	1.00000	1.00000	0.10959	2.10959	95.996
COAm	Kuckuck-Optimierungsalgorithmus M	0.96423	0.69756	0.28892	1.95071	0.64504	0.34034	0.21362	1.19900	0.67153	0.34273	0.45422	1.46848	74.204
FAm	Firefly-Algorithmus M	0.62430	0.50653	0.18102	1.31185	0.55408	0.42299	0.64360	1.62067	0.21167	0.28416	1.00000	1.49583	71.024
BA	Fledermaus-Algorithmus	0.42290	0.95047	1.00000	2.37337	0.17768	0.17477	0.33595	0.68840	0.15329	0.07158	0.46287	0.68774	59.650
ABC	Künstliches Bienenvolk (Artificial Bee Colony, ABC)	0.81573	0.48767	0.22588	1.52928	0.58850	0.21455	0.17249	0.97554	0.47444	0.26681	0.35941	1.10066	57.237
FSS	Fischschulsuche	0.48850	0.37769	0.11006	0.97625	0.07806	0.05013	0.08423	0.21242	0.00000	0.01084	0.18998	0.20082	20.109
PSO	Partikelschwarmoptimierung	0.21339	0.12224	0.05966	0.39529	0.15345	0.10486	0.28099	0.53930	0.08028	0.02385	0.00000	0.10413	14.232
RND	zufällig	0.17559	0.14524	0.07011	0.39094	0.08623	0.04810	0.06094	0.19527	0.00000	0.00000	0.08904	0.08904	8.142
GWO	Grauer-Wolf-Optimierung	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	0.18977	0.04119	0.01802	0.24898	1.000

Der Algorithmus für invasives Unkraut eignet sich hervorragend für die globale Suche. Dieser Algorithmus zeigt eine gute Leistung, obwohl das beste Mitglied der Population nicht verwendet wird und es keine Mechanismen zum Schutz vor einem möglichen Verharren in lokalen Extremen gibt. Es besteht kein Gleichgewicht zwischen Forschung und Nutzung des Algorithmus, was sich jedoch nicht negativ auf die Genauigkeit und Geschwindigkeit des Algorithmus auswirkt. Dieser Algorithmus hat aber auch andere Nachteile. Die ungleichmäßige Leistung der Suche während der gesamten Optimierung deutet darauf hin, dass die Leistung der IWO potenziell höher sein könnte, wenn die oben genannten Probleme gelöst werden könnten.

Histogramm der Algorithmus-Testergebnisse in Abbildung 4

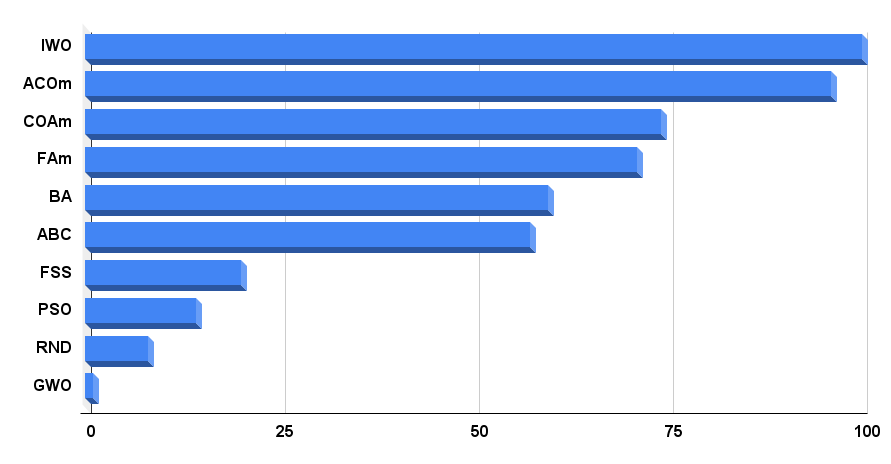
Abb. 4. Histogramm der Endergebnisse der Testalgorithmen

Schlussfolgerungen zu den Eigenschaften des Algorithmus zur Optimierung mit invasiven Unkräutern (IWO):

Vorteile:
1. Hohe Geschwindigkeit.
2. Der Algorithmus funktioniert gut mit verschiedenen Arten von Funktionen, sowohl glatten als auch diskreten.
3. Gute Skalierbarkeit.

Nachteile
1. Zahlreiche Parameter (obwohl sie selbsterklärend sind).