Algorithmen zur Optimierung mit Populationen: Spiralförmige Dynamische Optimization (SDO) Algorithmus

Inhalt

1. Einführung
2. Der Algorithmus
3. Testergebnisse

1. Einführung

In der wissenschaftlichen Literatur findet sich eine Vielzahl von metaheuristischen Optimierungsalgorithmen, die auf verschiedenen Aspekten der Natur und der Populationen basieren. Diese Algorithmen werden in verschiedene Kategorien eingeteilt, zum Beispiel: Schwarmintelligenz, Physik, Chemie, soziales menschliches Verhalten, Pflanzen, Tiere und andere. Es gibt viele metaheuristische Optimierungsalgorithmen, die auf Schwarmintelligenz basieren. Algorithmen, die auf physikalischen Phänomenen beruhen, werden ebenfalls häufig vorgeschlagen und in verschiedenen Bereichen erfolgreich eingesetzt.

Algorithmen, die auf Schwarmintelligenz beruhen, beziehen Elemente der Intelligenz in den Prozess der Suche nach der optimalen Lösung ein. Sie modellieren das Verhalten eines Schwarms oder einer Kolonie, in der einzelne Agenten Informationen austauschen und zusammenarbeiten, um ein gemeinsames Ziel zu erreichen. Diese Algorithmen können bei Problemen, die eine globale Suche und Anpassungsfähigkeit an veränderte Bedingungen erfordern, effizient sein.

Physikbasierte Algorithmen hingegen stützen sich bei der Lösung von Optimierungsproblemen auf die Gesetze und Prinzipien der Physik. Sie simulieren physikalische Phänomene wie Schwerkraft, Elektromagnetismus oder Thermodynamik und nutzen diese Prinzipien, um die optimale Lösung zu finden. Einer der Hauptvorteile physikbasierter Algorithmen ist ihre leichte Interpretierbarkeit. Sie können die Dynamik im gesamten Suchbereich genau und konsistent anzeigen.

Darüber hinaus verwenden einige physikbasierte Algorithmen den Goldenen Schnitt, ein mathematisches und natürliches Verhältnis, das besondere Eigenschaften aufweist und dazu beiträgt, schnell und effizient zu einer optimalen Lösung zu konvergieren. Der Goldene Schnitt wurde in verschiedenen Bereichen untersucht und angewandt, u. a. bei der Optimierung künstlicher neuronaler Netze und der Ressourcenzuweisung.

Somit bieten physikbasierte metaheuristische Optimierungsalgorithmen ein leistungsstarkes Werkzeug zur Lösung komplexer Optimierungsprobleme. Ihre Präzision und die Anwendung grundlegender physikalischer Prinzipien machen sie für verschiedene Bereiche attraktiv, in denen eine effiziente Suche nach optimalen Lösungen erforderlich ist.

Die Spiralförmige Dynamische Optimierung (Spiral Dynamics Optimization, SDO) ist einer der einfachsten physikalischen Algorithmen, der 2011 von Tamura und Yasuda vorgeschlagen und anhand des logarithmischen Spiralphänomens in der Natur entwickelt wurde. Der Algorithmus ist einfach und hat nur wenige Kontrollparameter. Darüber hinaus verfügt der Algorithmus über eine hohe Rechengeschwindigkeit, lokale Suchmöglichkeiten, Diversifizierung in einem frühen Stadium und Intensivierung in einem späteren Stadium.

In der Natur gibt es viele Spiralen, wie Galaxien, Polarlichter, Tierhörner, Tornados, Muscheln, Schnecken, Ammoniten, Chamäleonschwänze oder Seepferdchen. Spiralen sind auch in der antiken Kunst zu sehen, die von der Menschheit zu Beginn ihrer Existenz geschaffen wurde. Im Laufe der Jahre haben mehrere Forscher Anstrengungen unternommen, um die Abläufe und die Komplexität von Spiralen zu verstehen und Spiralgleichungen und Algorithmen zu entwickeln. Ein in der Natur häufig vorkommendes Spiralphänomen ist die logarithmische Spirale, die in Galaxien und tropischen Wirbelstürmen zu beobachten ist. Diskrete logarithmische Spiralgenerierungsprozesse wurden als effizientes Suchverhalten in Metaheuristiken implementiert, was die Entwicklung eines spiralförmigen dynamischen Optimierungsalgorithmus inspirierte.

In der Natur vorkommende Muster, so genannte sichtbare Spiralsequenzen, stellen Pflanzen, Bäume, Wellen und viele andere Formen dar. Visuelle Muster in der Natur können mit Hilfe der Chaostheorie, Fraktalen, Spiralen und anderen mathematischen Konzepten modelliert werden. In einigen natürlichen Mustern sind Spiralen und Fraktale eng miteinander verwandt. Die Fibonacci-Spirale zum Beispiel ist eine Variante der logarithmischen Spirale, die auf dem Goldenen Schnitt und den Fibonacci-Zahlen basiert. Da sie logarithmisch ist, sieht die Kurve in jedem Maßstab gleich aus und kann auch als Fraktal betrachtet werden.

Die oben erwähnten Muster haben die Forscher zur Entwicklung von Optimierungsalgorithmen inspiriert. Es gibt verschiedene Arten von Spiraltrajektorien, hier sind die wichtigsten:

• Archimedische Spirale
• Zykloidenspirale
• Epitrochoide Spirale
• Hypotrochoide Spirale
• Logarithmische Spirale
• Rosenspirale
• Fermatsche Spirale

Jede dieser Arten von Spiralen hat ihre eigenen einzigartigen Eigenschaften und kann zur Modellierung verschiedener natürlicher Muster verwendet werden. Besonderes Augenmerk liegt dabei auf der Darstellung verschiedener von der Natur inspirierter Optimierungsalgorithmen, die auf dem Konzept der Spiralpfade basieren. Im Laufe der Jahre haben Forscher verschiedene neue Optimierungsalgorithmen entwickelt, die sich die Spiralbewegung zunutze machen.

Zusätzlich kann das Verhalten von nicht-spiralen Algorithmen durch die Verwendung von Spiralpfaden als Überbau oder Ergänzung verändert werden, um die Genauigkeit der optimalen Lösung zu verbessern.

Der von Tamura und Yasuda vorgeschlagene zweidimensionale Spiraloptimierungsalgorithmus ist ein metaheuristisches Mehrpunkt-Suchverfahren für zweidimensionale kontinuierliche Optimierungsprobleme. Tamura und Yasuda schlugen dann eine n-dimensionale Optimierung vor, die auf der Philosophie der zweidimensionalen Optimierung basiert.

2. Der Algorithmus

Der von den Autoren beschriebene SDO-Algorithmus für die Suche in mehrdimensionalen Räumen hat Einschränkungen und Nachteile:

• Unanwendbarkeit für eindimensionale und andere Optimierungsprobleme mit ungeraden Dimensionen.
• Die paarweise Verknüpfung von Koordinaten durch den Algorithmus kann die Qualität der Lösung bei bestimmten Problemen beeinträchtigen und bei synthetischen Tests zu falsch-positiven Ergebnissen führen.

Die Konstruktion von Spiralbahnen im mehrdimensionalen Raum ist mit gewissen Schwierigkeiten verbunden. Wenn sich das Problem also auf einen eindimensionalen Raum beschränkt, kann eine Spirale nicht im üblichen Sinne konstruiert werden, da eine Spirale eine Bewegung in mindestens zwei Dimensionen erfordert. In diesem Fall können wir eine einfache Funktion verwenden, um den Koordinatenwert über die Zeit zu ändern, ohne eine Spirale zu verwenden. Wenn es sich um ein eindimensionales Optimierungsproblem handelt, dann wird die Spirale nicht verwendet, da es keine zusätzlichen Dimensionen für die Bewegung entlang der Spirale gibt.

Im mehrdimensionalen Raum können für jedes Koordinatenpaar Spiralen konstruiert werden, aber für die eine verbleibende Koordinate kann keine Spirale definiert werden. Im Falle eines 13-dimensionalen Raums ist es zum Beispiel möglich, Spiralen für 6 Koordinatenpaare zu konstruieren, aber eine Koordinate wird sich ohne Spiralkomponente bewegen.

Um Spiralen im mehrdimensionalen Raum zu konstruieren, können wir die Methode der „mehrdimensionalen Spirale“ oder „Hyperspirale“ verwenden. Bei dieser Methode werden zusätzliche virtuelle Koordinaten eingeführt und die Spiralform in jeder Dimension definiert. Um eine Hyperspirale zu konstruieren, können wir Rotationsmatrizen und Algorithmen verwenden, die auf der Geometrie mehrdimensionaler Räume basieren. Dieser Ansatz erfordert jedoch komplexere Berechnungen und kann bei praktischen Optimierungsproblemen schwierig umzusetzen sein.

Da in den Artikeln mehrdimensionale Funktionen in Form von mehrfach duplizierten zweidimensionalen Funktionen verwendet werden, kann die ursprüngliche SDO unangemessen hohe Ergebnisse liefern, da sie eine paarweise Koordinatenbindung verwendet. Daher wird der Spiralalgorithmus bei anderen mehrdimensionalen Problemen, bei denen die Koordinaten in keiner Beziehung zueinander stehen, schlechte Ergebnisse liefern. Mit anderen Worten: In diesem Fall schaffen wir ungewollt perfekte Bedingungen für den Spiralalgorithmus bei duplizierten Funktionen.

Um die oben genannten Probleme mit dem Spiralalgorithmus zu vermeiden, schlage ich einen Ansatz vor, der auf der Projektion einer zweidimensionalen Spirale auf eine Koordinatenachse beruht. Wenn wir die Bewegung eines Punktes auf einer zweidimensionalen Spirale als die Bewegung eines Pendels betrachten, dann entspricht die Projektion der Punktbewegung auf jede der beiden Koordinaten der Projektion der Pendelbewegung auf jede der Koordinaten. So können wir die Projektion der Pendelpunktbewegung auf jede der Achsen im mehrdimensionalen Raum verwenden, um die Punktspiralbewegung im zweidimensionalen Raum zu simulieren.

Bei der Methode, Spiralen zu konstruieren, die das Verhalten eines Pendels an jeder Koordinate in einem mehrdimensionalen Raum simulieren, kann der Radius jeder „virtuellen“ Spirale unterschiedlich sein. Dies kann sich positiv auf die Qualität der Optimierung auswirken, da einige Koordinaten möglicherweise näher an bekannten Optima liegen und nicht wesentlich verändert werden müssen.

Wir können jedes Gesetz der harmonischen Schwingungen mit Dämpfung als Projektion einer zweidimensionalen Spirale auf eine eindimensionale Achse betrachten. Ich habe einen einfachen gedämpften harmonischen Oszillator (die Abhängigkeit der Punktposition von der Zeit) mit der folgenden Gleichung gewählt:

x(t) = A*e^(-γt)*cos(ωt + φ)

wobei:

• A - Amplitude der Schwingungen
• γ - Dämpfungsverhältnis
• ω - Eigenfrequenz des Oszillators
• φ - Anfangsphase der Schwingungen

Die Gleichung macht deutlich, dass das Dämpfungsverhältnis, die Frequenz und die Anfangsphase Konstanten sind und als Algorithmus-Eingaben verwendet werden können, aber wir werden nicht drei, sondern zwei Parameter verwenden. Die Anfangsphase der Schwingungen wird bei jeder Iteration als Zufallskomponente verwendet (jede Koordinate wird gegenüber den anderen Koordinaten leicht phasenverschoben), ansonsten ist der Algorithmus vollständig deterministisch und hängt nur von der anfänglichen Platzierung der Punkte im Raum ab.

Die Idee ist, dass, sobald ein neues bestes globales Extremum entdeckt wird, eine neue Amplitude für alle Punkte berechnet wird, die die Differenz zwischen der Koordinate des globalen Extremums und der entsprechenden Koordinate des Punktes ist. Ab diesem Zeitpunkt sind die Amplituden entlang der Koordinaten individuell und werden im Speicher jedes Punktes abgelegt, bis ein neues besseres Extremum entdeckt und neue Amplituden bestimmt werden.

Nach der Bestimmung der Amplituden beginnt jeder Punkt mit der Abschwächung zu schwingen, wobei die Symmetrieachse der Schwingungen die bekannte Koordinate des globalen Optimums ist. Anhand der Abbildungen 1 und 2 lässt sich der Einfluss von Dämpfungsverhältnis und Frequenz (externe Parameter) visuell gut beurteilen.

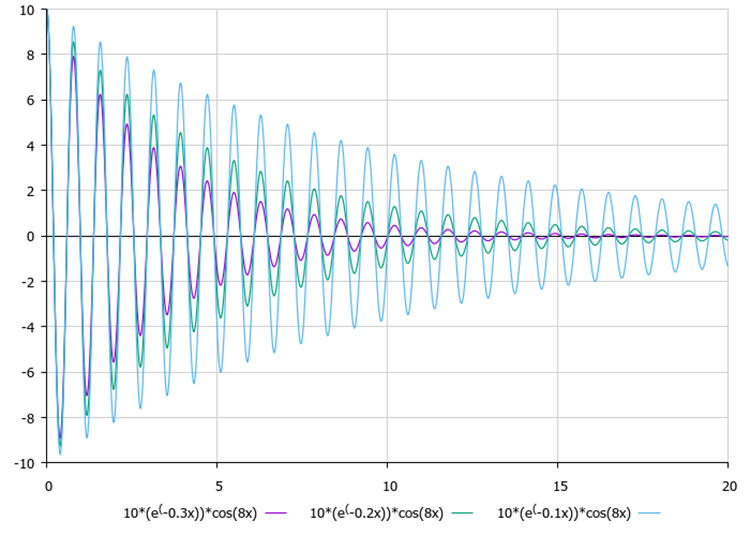
Bild 1. Der Einfluss der Amplitude auf die Art der Schwingungen

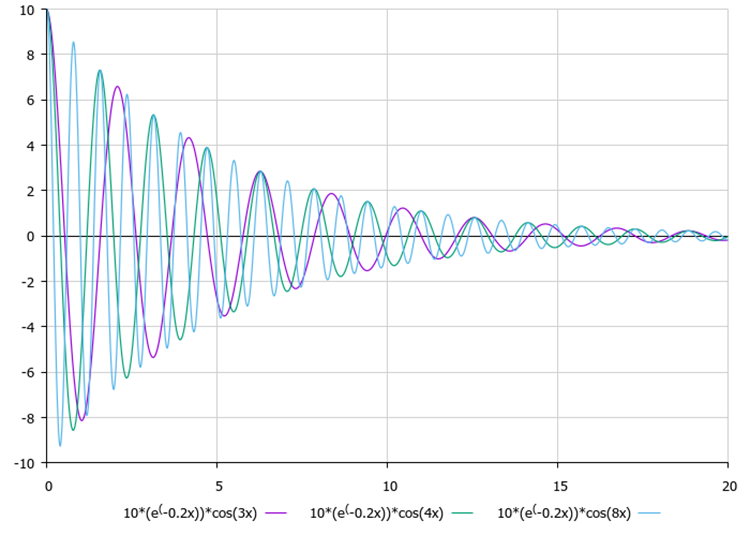
Bild 2. Der Einfluss der Frequenz auf die Art der Schwingungen

Obwohl in unserem Algorithmus alle Koordinaten absolut unabhängig sind, gibt es, wie bereits erwähnt, keine paarweisen Kombinationen und Verbindungen zwischen ihnen in der Logik zur Konstruktion von Spiralen. Würde man die Bewegung eines Punktes auf einer zweidimensionalen Ebene konstruieren, so ergäbe sich eine Spirale der folgenden Art, wie in Abbildung 3 dargestellt.

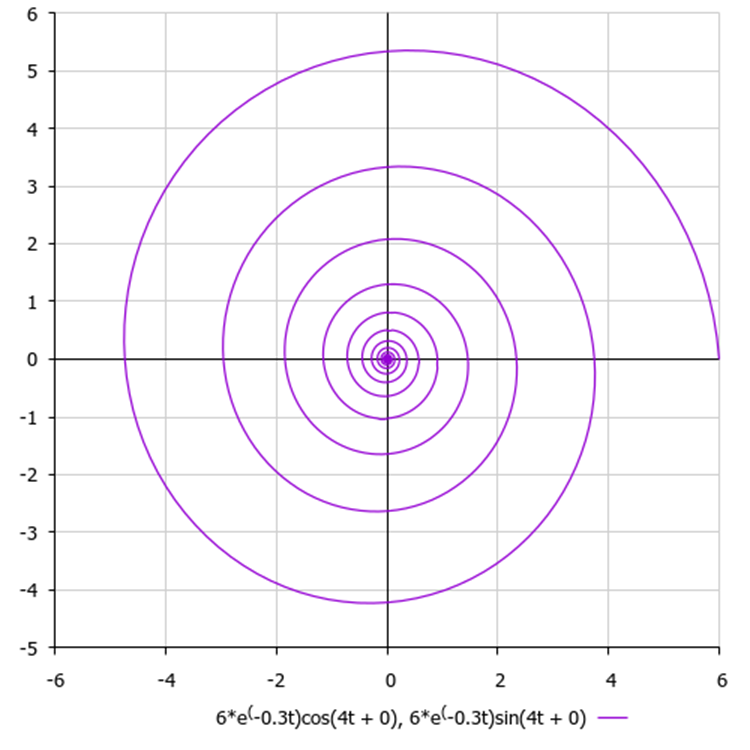
Abb. 3. Eine hypothetische Spirale mit Standard-Algorithmusparametern, wobei 6 der Amplitudenwert, 0,3 das Dämpfungsverhältnis und 4 die Frequenz ist.

Bei realen Problemen wie auch bei Testfunktionen müssen die Amplituden entlang der einzelnen Koordinaten nicht gleich sein (im Gegensatz zum ursprünglichen Algorithmus). Der Unterschied in den Amplituden führt zu abgeflachten Spiralen. Bei einer kleineren Amplitude wird die entsprechende Koordinate schneller verfeinert, da sie näher am bekannten besten Wert liegt.

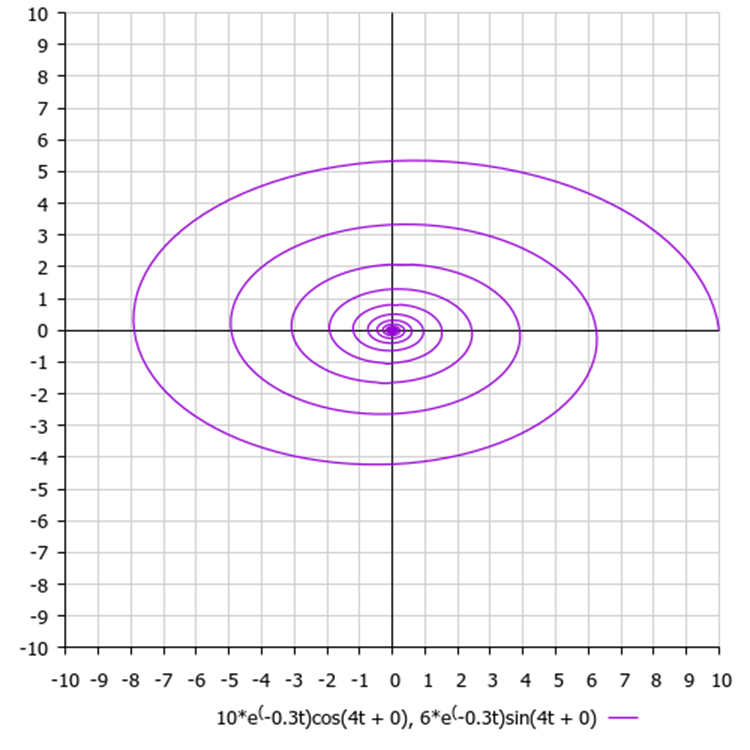
Abb. 4. Der Wert des Punktes entlang der Y-Koordinate liegt näher am bekannten Wert und seine Schwingungsamplitude ist kleiner als die des Punktes entlang der X-Achse.

Alle Darstellungen in den Diagrammen beziehen sich auf den Wert Null, da wir die Differenz zum Wert des bekannten Optimums betrachten, d. h. die Verschiebung von Null ist ein Inkrement.

Kommen wir nun zur Beschreibung des Codes. Zunächst müssen wir die Struktur des Algorithmus festlegen und einen Pseudocode erstellen:

1. Initialisierung der Punktpopulation.
2. Berechnung des Wertes der Fitnessfunktion.
3. Berechnung der Amplitude für jede Punktkoordinate, wenn ein neues bestes Optimum erscheint.
4. Wenn ein neues Optimum auftaucht, wird der beste Punkt in eine zufällige Richtung „ausgeworfen“.
   
5. Berechnung der neuen Position der Punkte mit Hilfe der Gleichung der gedämpften harmonischen Schwingungen.
6. Wiederholung des Vorgang ab S. 2.

Punkt 4 wurde eigens hinzugefügt und soll einen erhöhten Widerstand gegen das Steckenbleiben bieten, sodass die Punkte nicht in einer „Spirale“ zu einem lokalen Extremwert konvergieren und dort stecken bleiben. Die Autoren des Algorithmus gehen auf dieses Thema nicht ein.

Zur Beschreibung einer Belastung (Partikel, Punkt) eignet sich die Struktur S_Particle mit den folgenden Variablen:

• c [] - Array von Partikelkoordinaten
  
• cD [] - Array der Partikelgeschwindigkeiten
• t - Iterationsschritt, spielt die Rolle der „Zeit“ in der Gleichung
  
• f - Wert der Partikelfitnessfunktion
  

Die Struktur definiert auch die Funktion Init, die zur Initialisierung von Strukturvariablen verwendet wird. Der Parameter coords gibt die Anzahl der Partikelkoordinaten an.

//——————————————————————————————————————————————————————————————————————————————
struct S_Particle
{
  void Init (int coords)
  {
    ArrayResize (c,    coords);
    ArrayResize (cD,   coords);
    t = 0;
    f = -DBL_MAX;
  }

  double c  []; //coordinates
  double cD []; //coordinates
  int    t;     //iteration (time)
  double f;     //fitness
};
//——————————————————————————————————————————————————————————————————————————————

Definieren wir die Klasse des SDOm-Algorithmus - C_AO_SDOm. Die Klasse enthält die folgenden Variablen und Methoden:

• cB [] - Array der besten Koordinaten
• fB - Wert der Fitnessfunktion für die besten Koordinaten
• p [] - Array von Partikeln, Datentyp - S_Particle
• rangeMax [] - Array der maximalen Suchbereichswerte
  
• rangeMin [] - Array der minimalen Suchbereichswerte
  
• rangeStep [] - Array von Suchschritten
  
• Init - Methode zur Initialisierung der Klassenparameter, akzeptiert folgende Parameter: coordinatesNumberP - Anzahl der Koordinaten, populationSize - Größe der Population, dampingFactorP - Dämpfungsverhältnis, frequencyP - Frequenz, precisionP - Präzision.
• Moving - Methode zum Bewegen von Partikeln im Suchraum
• Revision - Methode zur Überarbeitung und Aktualisierung der besten Koordinaten
• coords - Anzahl der Koordinaten
• popSiz - Größe der Population
• A, e, γ, ω, φ - Komponenten der gedämpften harmonischen Schwingungsgleichung
  
• precision, revision - private Variablen, die innerhalb der Klasse verwendet werden
• SeInDiSp - Berechnung eines neuen Koordinatenwertes in einem bestimmten Bereich mit einem bestimmten Schritt
  
• RNDfromCI - Methode erzeugt eine Zufallszahl in einem bestimmten Bereich

Der Code beschreibt die Klasse C_AO_SDOm, die eine Implementierung des Algorithmus mit zusätzlichen Funktionen zur Überarbeitung und Aktualisierung der besten Koordinaten darstellt.

Die ersten drei Variablen der Klasse sind das cB-Array, das die besten Koordinaten speichert, die fB-Variable, die den Wert der Fitnessfunktion der besten Koordinaten speichert, und das p-Array, das die Kandidaten (Partikel) der Population speichert.

Die nächsten drei Klassenvariablen sind die Arrays rangeMax, rangeMin und rangeStep, in denen die Höchst- und Mindestwerte des Suchbereichs bzw. der Suchschritte gespeichert werden.

Darüber hinaus enthält die Klasse drei öffentliche Methoden: Init, Moving und Revision. Init wird verwendet, um Klassenparameter zu initialisieren und eine Anfangspopulation von Partikeln zu erzeugen. Moving wird verwendet, um die Partikel im Suchraum zu bewegen. Revision wird angewandt, um die besten Koordinaten zu überarbeiten und ihre Werte zu aktualisieren.

Die Klasse enthält auch mehrere private Variablen, die innerhalb der Klasse verwendet werden. Dies sind die Variablen coords und popSize, die die Anzahl der Koordinaten bzw. die Größe der Population speichern. Die Variable „A“, die in der Methode „Moving“ verwendet wird, die Variable „precision“, die den Präzisionswert speichert, und die Variable „revision“, die dafür verantwortlich ist, dass die besten Koordinaten überarbeitet werden müssen.

Die Klasse enthält mehrere private Methoden: Research, SeInDiSp und RNDfromCI. Research dient der Untersuchung neuer Partikelkoordinaten, während SeInDiSp und RNDfromCI zur Berechnung von Zufallswerten in einem bestimmten Bereich verwendet werden.

„Präzision“ ist ein externer Parameter des Algorithmus, der für die Diskretion der Bewegung entlang der Trajektorie einer gedämpften Schwingung verantwortlich ist. Je größer der Wert ist, desto genauer wird die Trajektorie wiedergegeben, und kleinere Werte führen zu einer „Zerklüftung“ der Trajektorie (dies bedeutet nicht, dass das Ergebnis negativ beeinflusst wird, es hängt von der Aufgabe ab). Die Standardeinstellung hat sich nach einer Reihe von Experimenten als optimal erwiesen.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SDOm
{
  //----------------------------------------------------------------------------
  public: double     cB []; //best coordinates
  public: double     fB;    //FF of the best coordinates
  public: S_Particle p  []; //particles

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const double dampingFactorP,       //damping factor
                     const double frequencyP,           //frequency
                     const double precisionP);          //precision

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;   //coordinates number
  private: int    popSize;  //population size

  private: double A;
  private: double e;
  private: double γ;
  private: double ω;
  private: double φ;
  private: double precision;

  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

Die Init-Methode der Klasse C_AO_SDOm wird verwendet, um die Klassenparameter zu initialisieren und eine Anfangspopulation von Partikeln zu erstellen.

Zunächst wird MathSrand verwendet, um den Zufallszahlengenerator zurückzusetzen, und die Funktion GetMicrosecondCount wird zur Initialisierung des Generators verwendet.

Als Nächstes setzt die Methode Anfangswerte für die Variablen „fB“ und „revision“ und weist konstanten Variablen, die an der gedämpften Schwingungsgleichung beteiligt sind, Werte zu.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDOm::Init (const int    coordinatesNumberP,   //coordinates number
                      const int    populationSizeP,      //population size
                      const double dampingFactorP,       //damping factor
                      const double frequencyP,           //frequency
                      const double precisionP)           //precision
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords  = coordinatesNumberP;
  popSize = populationSizeP;

  e = M_E;
  γ = dampingFactorP;
  ω = frequencyP;
  φ = 0.0;
  precision = precisionP;

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);

  ArrayResize (p, popSize);

  for (int i = 0; i < popSize; i++)
  {
    p [i].Init (coords);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Wir werden die Moving-Methode verwenden, um die Partikel im Suchraum zu bewegen.

Der erste Codeblock (if (!revision)) wird nur bei der ersten Iteration ausgeführt und dient dazu, die Partikel zufällig im Suchraum zu platzieren. Die Methode setzt dann den Wert von „revision“ auf „true“, sodass beim nächsten Mal der normale Codeblock verwendet wird.

Der nächste Teil des Methodencodes ist für die Bewegung der Populationsteilchen zuständig. Wenn der Fitnesswert des aktuellen Partikels gleich dem Fitnesswert der besten Koordinaten ist (p[i].f == fB), dann werden die Partikelkoordinaten auf die gleiche Weise wie im ersten Codeblock aktualisiert. Das bedeutet, dass das Teilchen aus seiner Position in eine zufällige Richtung geschleudert wird, um zu verhindern, dass alle Teilchen in einem einzigen Punkt zusammenlaufen.

Andernfalls verwendet die Methode die Variable t, um die aktuelle Zeit für jedes Partikel mit Hilfe des Iterationszählers zu simulieren (der zurückgesetzt wird, wenn die beste globale Lösung aktualisiert wird). Anschließend werden die Koordinaten der einzelnen Teilchen mit Hilfe der Gleichung der gedämpften harmonischen Schwingungen berechnet.

Der auskommentierte Teil des Codes fügt dem durch die Gleichung berechneten Koordinatenwert eine zufällige Erhöhung hinzu und kann verwendet werden, um einen schönen visuellen Feuerwerkseffekt zu erzeugen. Dieser Effekt hat jedoch keinen praktischen Wert und verbessert die Ergebnisse nicht, weshalb der Code auskommentiert wird.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDOm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        p [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
        p [i].c [c] = SeInDiSp (p [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  int t = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    if  (p [i].f == fB)
    {
      for (int c = 0; c < coords; c++)
      {
        p [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
        p [i].c [c] = SeInDiSp (p [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }

      continue;
    }

    p [i].t++;
    t = p [i].t;

    for (int c = 0; c < coords; c++)
    {
      A = p [i].cD [c];
      φ = RNDfromCI (0.0, 2.0);

      p [i].c [c] = p [i].c [c] + A * pow (e, -γ * t / precision) * cos (ω * t / (precision) + φ);// + RNDfromCI (-0.01, 0.01) * (rangeMax [c] - rangeMin [c]);
      p [i].c [c] = SeInDiSp (p [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode der Klasse Revision wird verwendet, um die besten Koordinaten zu aktualisieren und die Differenz zwischen den Partikelkoordinaten und der bekannten besten Lösung zu berechnen. Diese Differenz dient als Anfangsamplitude, und sobald eine neue, bessere Lösung gefunden ist, beginnen die Teilchen um die am besten bekannten Koordinaten zu schwingen, die im Zentrum dieser Bewegungen liegen.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDOm::Revision ()
{
  //----------------------------------------------------------------------------
  bool flag = false;
  for (int i = 0; i < popSize; i++)
  {
    if (p [i].f > fB)
    {
      flag = true;
      fB = p [i].f;
      ArrayCopy (cB, p [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  if (flag)
  {
    for (int i = 0; i < popSize; i++)
    {
      p [i].t = 0;

      for (int c = 0; c < coords; c++)
      {
        p [i].cD [c] = (cB [c] - p [i].c [c]);

      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Testergebnisse

Die Ergebnisse auf dem Prüfstand scheinen gut zu sein:

C_AO_SDOm:100;0.3;4.0;10000.0
=============================
5 Rastrigin's; Func runs 10000 result: 76.22736727464056
Score: 0.94450
25 Rastrigin's; Func runs 10000 result: 64.5695106264092
Score: 0.80005
500 Rastrigin's; Func runs 10000 result: 47.607500083305425
Score: 0.58988
=============================
5 Forest's; Func runs 10000 result: 1.3265635010116805
Score: 0.75037
25 Forest's; Func runs 10000 result: 0.5448141810532924
Score: 0.30817
500 Forest's; Func runs 10000 result: 0.12178250603909949
Score: 0.06889
=============================
5 Megacity's; Func runs 10000 result: 5.359999999999999
Score: 0.44667
25 Megacity's; Func runs 10000 result: 1.552
Score: 0.12933
500 Megacity's; Func runs 10000 result: 0.38160000000000005
Score: 0.03180
=============================
All score: 4.06967

Die Visualisierung des SDOm-Algorithmus zeigt einige Besonderheiten: Der Konvergenzgraph für alle Testfunktionen ist instabil, die Art der Konvergenzkurve ändert sich während aller Iterationen. Dies trägt nicht dazu bei, das Vertrauen in die Ergebnisse zu stärken. Die Visualisierung der Megacity-Funktion zeigt speziell mehrere wiederholte Tests (normalerweise wird nur einer im Video angezeigt, damit das GIF nicht zu groß wird), um die Instabilität der Ergebnisse von Test zu Test zu zeigen. Die Streuung der Ergebnisse ist sehr groß.

Es wurden keine Besonderheiten in der Art der Partikelbewegung festgestellt, mit Ausnahme des „sharp Forest“ und diskreten „Megacity, wo sich die Koordinaten der Partikel in deutlich sichtbaren Linien aneinanderreihen. Es ist schwer zu beurteilen, ob dies gut oder schlecht ist. Im Falle des ACOm-Algorithmus war dies beispielsweise ein Zeichen für qualitative Konvergenz, aber im Falle von SDOm ist dies wahrscheinlich nicht der Fall.

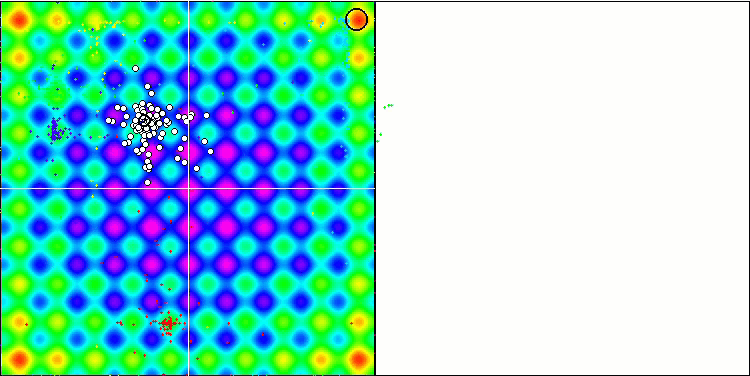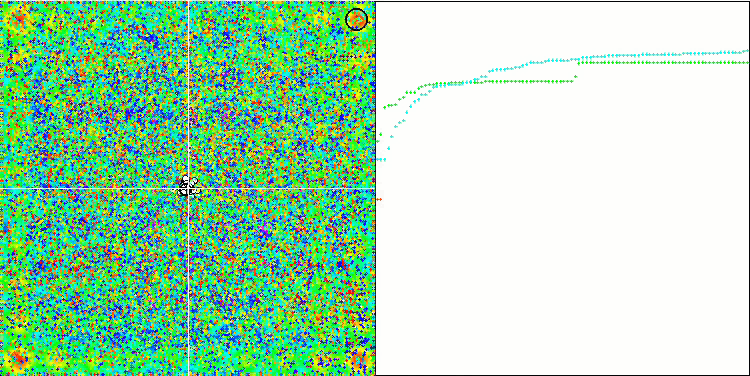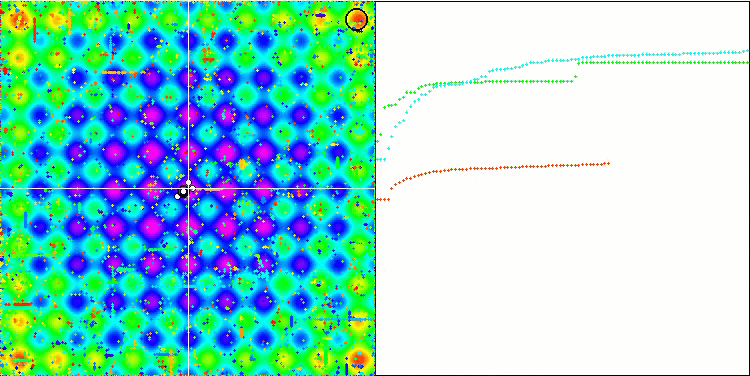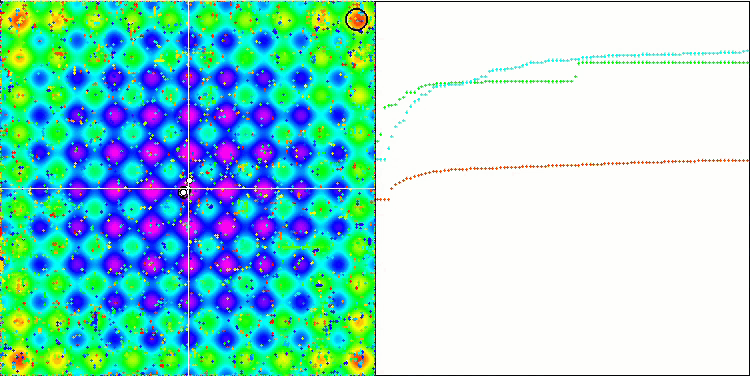
  SDOm mit der Testfunktion Rastrigin.

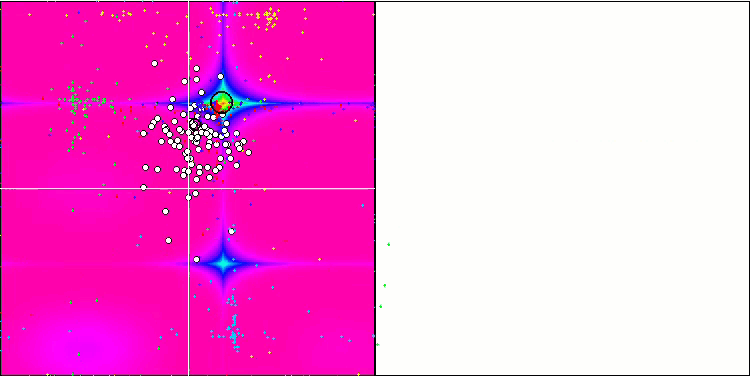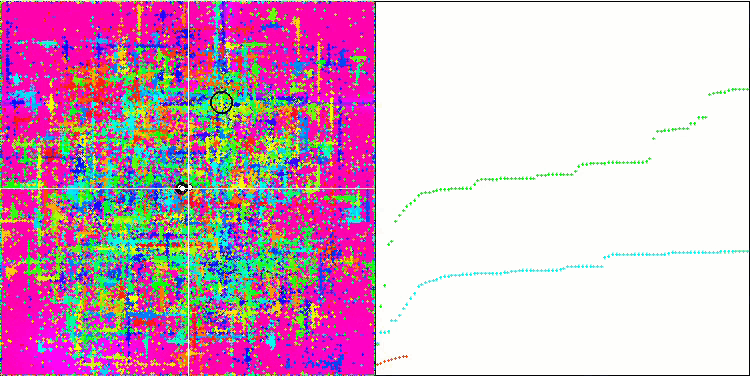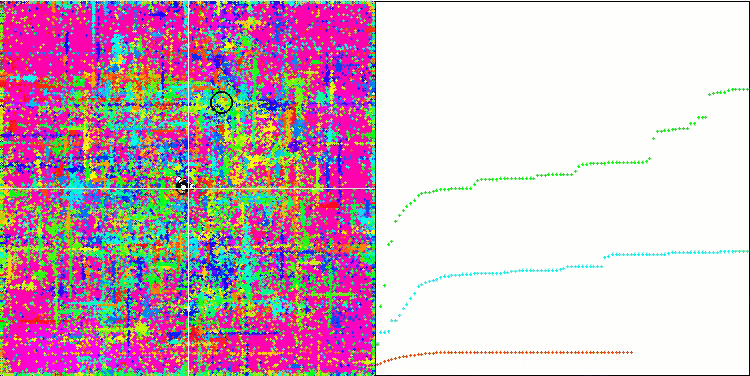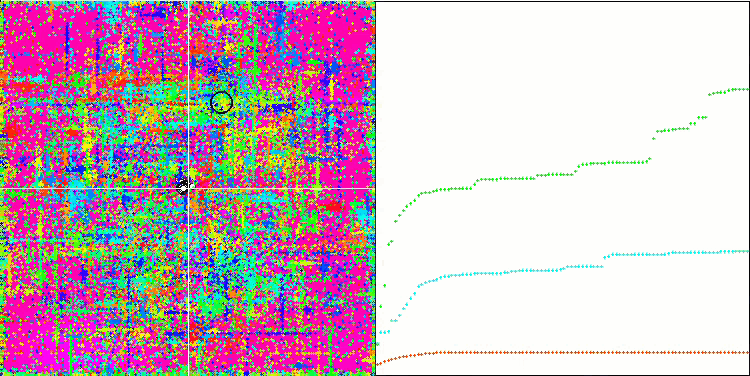
  SDOm mit der Testfunktion Forest.

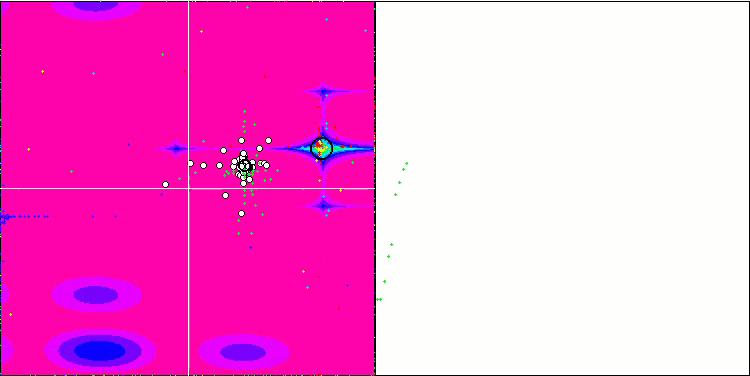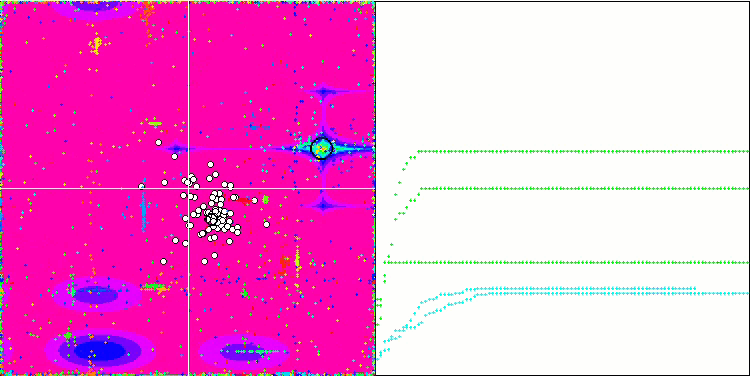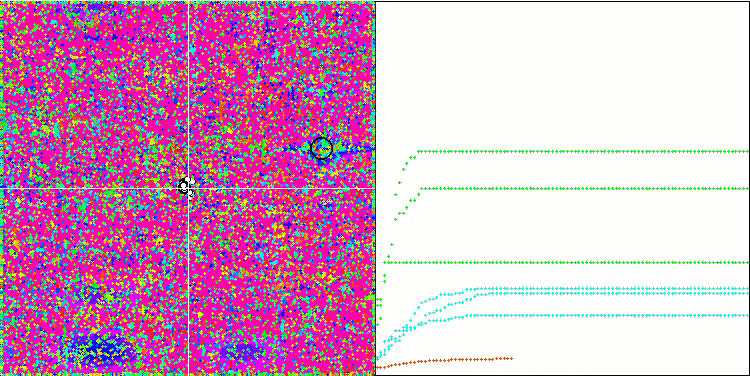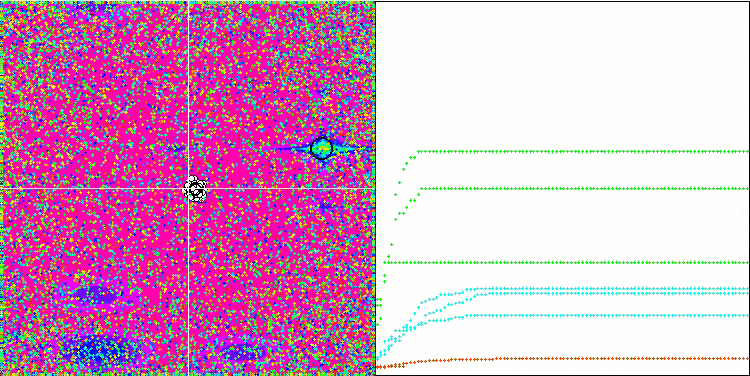
  SDOm mit der Testfunktion Megacity.

Bei Verwendung des in der Moving-Methode auskommentierten Codes, der für das Hinzufügen von Zufallsrauschen zur Teilchenkoordinate verantwortlich ist, tritt ein interessantes Phänomen auf, das einem Feuerwerk ähnelt, während die zufällige Änderung der Phase der Schwingungen nicht verwendet wird. Ich nehme an, dass die Teilchen nach der Massenkonvergenz zu einer bekannten Lösung in verschiedene Richtungen geschleudert werden, und dies ist der Grund für den schönen Effekt, der den Moment zeigt, in dem der Algorithmus feststeckt. Dies lässt sich daran erkennen, dass die Explosion des Feuerwerks mit dem Beginn des horizontalen Abschnitts der Konvergenzkurve zusammenfällt.

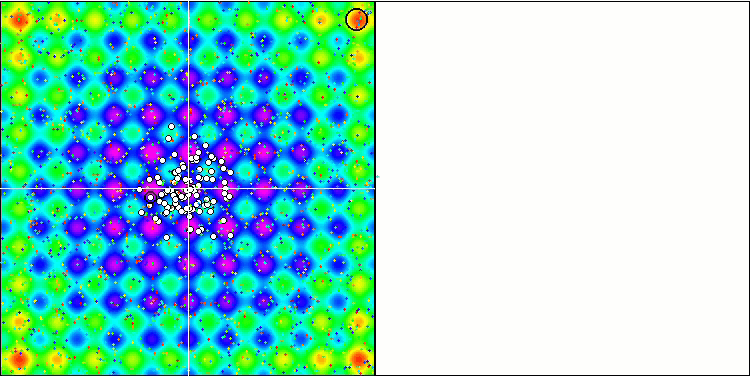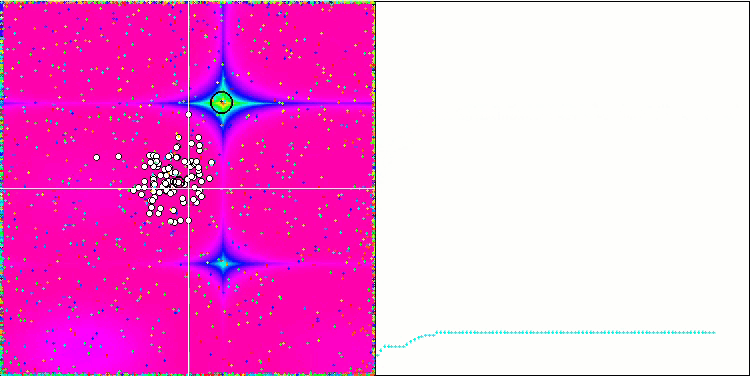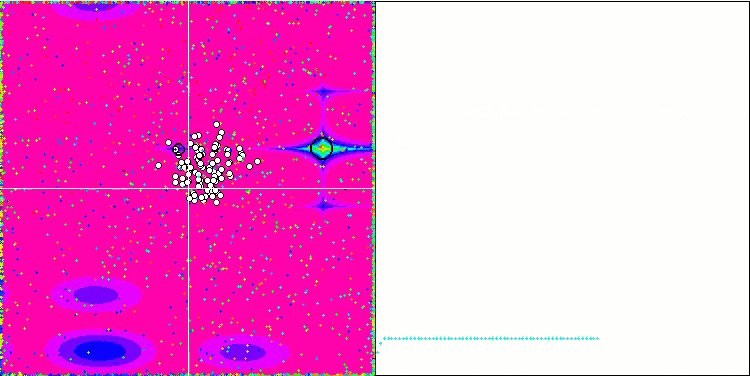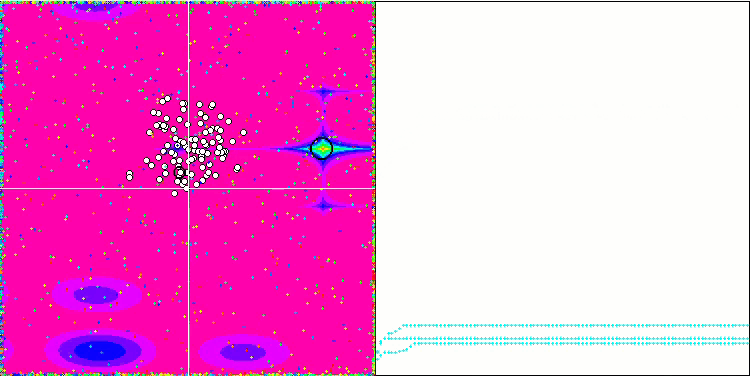
Demonstration eines nutzlosen, aber schönen Feuerwerkseffekts.

Der SDOm-Algorithmus hat insgesamt recht gute Ergebnisse erzielt und wurde in der Bewertungstabelle auf Platz 8 von 23 teilnehmenden Algorithmen gesetzt. SDOm zeigt deutlich bessere Ergebnisse bei der glatten Rastrigin-Funktion. Die Tendenz, stecken zu bleiben, beeinträchtigt die Ergebnisse der komplexen Funktionen Forest und Megacity.

#	AO	Beschreibung	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (diskret)			Megacity final	Final result
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	SDSm	stochastische Diffusionssuche M	0.99809	1.00000	0.69149	2.68958	1.00000	1.00000	1.00000	3.00000	1.00000	1.00000	1.00000	3.00000	100000
2	SDS	stochastische Diffusionssuche	0.99737	0.97322	0.58904	2.55963	0.96778	0.93572	0.79649	2.69999	0.78696	0.93815	0.71804	2.44315	88.208
3	SSG	Setzen, Säen und Wachsen	1.00000	0.92761	0.51630	2.44391	0.72654	0.65201	0.83760	2.21615	0.54782	0.61841	0.99522	2.16146	77.678
4	HS	Harmoniesuche	0.99676	0.88385	0.44686	2.32747	0.99882	0.68242	0.37529	2.05653	0.71739	0.71842	0.41338	1.84919	70.647
5	IWO	Optimierung mit invasiven Unkräutern	0.95828	0.62227	0.27647	1.85703	0.70690	0.31972	0.26613	1.29275	0.57391	0.30527	0.33130	1.21048	48.267
6	ACOm	Ameisen-Kolonie-Optimierung M	0.34611	0.16683	0.15808	0.67103	0.86785	0.68980	0.64798	2.20563	0.71739	0.63947	0.05579	1.41265	47.419
7	MEC	Evolutionäre Berechnung des Geistes	0.99270	0.47345	0.21148	1.67763	0.60691	0.28046	0.21324	1.10061	0.66957	0.30000	0.26045	1.23002	44.061
8	SDOm	Optimierung der Spiraldynamik M	0.81076	0.56474	0.35334	1.72884	0.72333	0.30644	0.30985	1.33963	0.43479	0.13289	0.14695	0.71463	41.370
9	COAm	Kuckuck-Optimierungsalgorithmus M	0.92400	0.43407	0.24120	1.59927	0.58309	0.23477	0.13842	0.95629	0.52174	0.24079	0.17001	0.93254	37.845
10	FAm	Firefly-Algorithmus M	0.59825	0.31520	0.15893	1.07239	0.51012	0.29178	0.41704	1.21894	0.24783	0.20526	0.35090	0.80398	33.152
11	ABC	Künstliches Bienenvolk (Artificial Bee Colony, ABC)	0.78170	0.30347	0.19313	1.27829	0.53774	0.14799	0.11177	0.79750	0.40435	0.19474	0.13859	0.73768	29.784
12	BA	Fledermaus-Algorithmus	0.40526	0.59145	0.78330	1.78002	0.20817	0.12056	0.21769	0.54641	0.21305	0.07632	0.17288	0.46225	29.488
13	CSS	Suche geladener Systeme	0.56605	0.68683	1.00000	2.25289	0.14065	0.01853	0.13638	0.29555	0.07392	0.00000	0.03465	0.10856	27.914
14	GSA	Algorithmus für die Schwerkraftsuche	0.70167	0.41944	0.00000	1.12111	0.31623	0.25120	0.27812	0.84554	0.42609	0.25525	0.00000	0.68134	27.807
15	BFO	Optimierung der bakteriellen Futtersuche	0.67203	0.28721	0.10957	1.06881	0.39655	0.18364	0.17298	0.75317	0.37392	0.24211	0.18841	0.80444	27.549
16	EM	elektromagnetismusähnlicher Algorithmus	0.12235	0.42928	0.92752	1.47915	0.00000	0.02413	0.29215	0.31628	0.00000	0.00527	0.10872	0.11399	18.981
17	SFL	schlurfender Froschsprung	0.40072	0.22021	0.24624	0.86717	0.20129	0.02861	0.02221	0.25211	0.19565	0.04474	0.06607	0.30646	13.201
18	MA	Affen-Algorithmus	0.33192	0.31029	0.13582	0.77804	0.10000	0.05443	0.07482	0.22926	0.15652	0.03553	0.10669	0.29874	11.771
19	FSS	Fischschulsuche	0.46812	0.23502	0.10483	0.80798	0.12825	0.03458	0.05458	0.21741	0.12175	0.03947	0.08244	0.24366	11.329
20	IWDm	intelligente Wassertropfen M	0.26459	0.13013	0.07500	0.46972	0.28568	0.05445	0.05112	0.39126	0.22609	0.05659	0.05054	0.33322	10.434
21	PSO	Partikelschwarmoptimierung	0.20449	0.07607	0.06641	0.34696	0.18873	0.07233	0.18207	0.44313	0.16956	0.04737	0.01947	0.23641	8.431
22	RND	zufällig	0.16826	0.09038	0.07438	0.33302	0.13480	0.03318	0.03949	0.20747	0.12175	0.03290	0.04898	0.20363	5.056
23	GWO	grey wolf optimizer	0.00000	0.00000	0.02093	0.02093	0.06562	0.00000	0.00000	0.06562	0.23478	0.05789	0.02545	0.31812	1.000

Zusammenfassung

Der ursprüngliche Ansatz für die Implementierung der modifizierten Version ermöglichte es, schwere Matrixberechnungen wie im ursprünglichen Algorithmus des Autors zu vermeiden, und machte es auch möglich, ihn ohne Bezug auf die Beziehungen zwischen den Koordinaten für den n-dimensionalen Raum universell zu machen.

Ich habe versucht, das Konzept der „Masse“ in der Gleichung für gedämpfte harmonische Schwingungen zu verwenden, um das Verhalten der Teilchen individuell von ihrer Fitness abhängig zu machen. Die Idee war, die Amplitude und Häufigkeit von Teilchen mit einer größeren Masse (mit einem besseren Wert der Fitnessfunktion) zu verringern, während leichtere Teilchen Bewegungen mit größerer Amplitude und höherer Frequenz ausführen müssten. Dies könnte einen höheren Verfeinerungsgrad der bekannten besten Lösungen ermöglichen und gleichzeitig die Suchmöglichkeiten aufgrund der „breiten“ Bewegungen der leichten Teilchen erhöhen. Leider hat diese Idee nicht die erwartete Verbesserung der Ergebnisse gebracht.

Die physikalische Simulation von Partikelbahnen im Algorithmus legt die Möglichkeit nahe, physikalische Konzepte wie Geschwindigkeit, Beschleunigung und Trägheit zu verwenden. Dies ist eine Frage der weiteren Forschung.

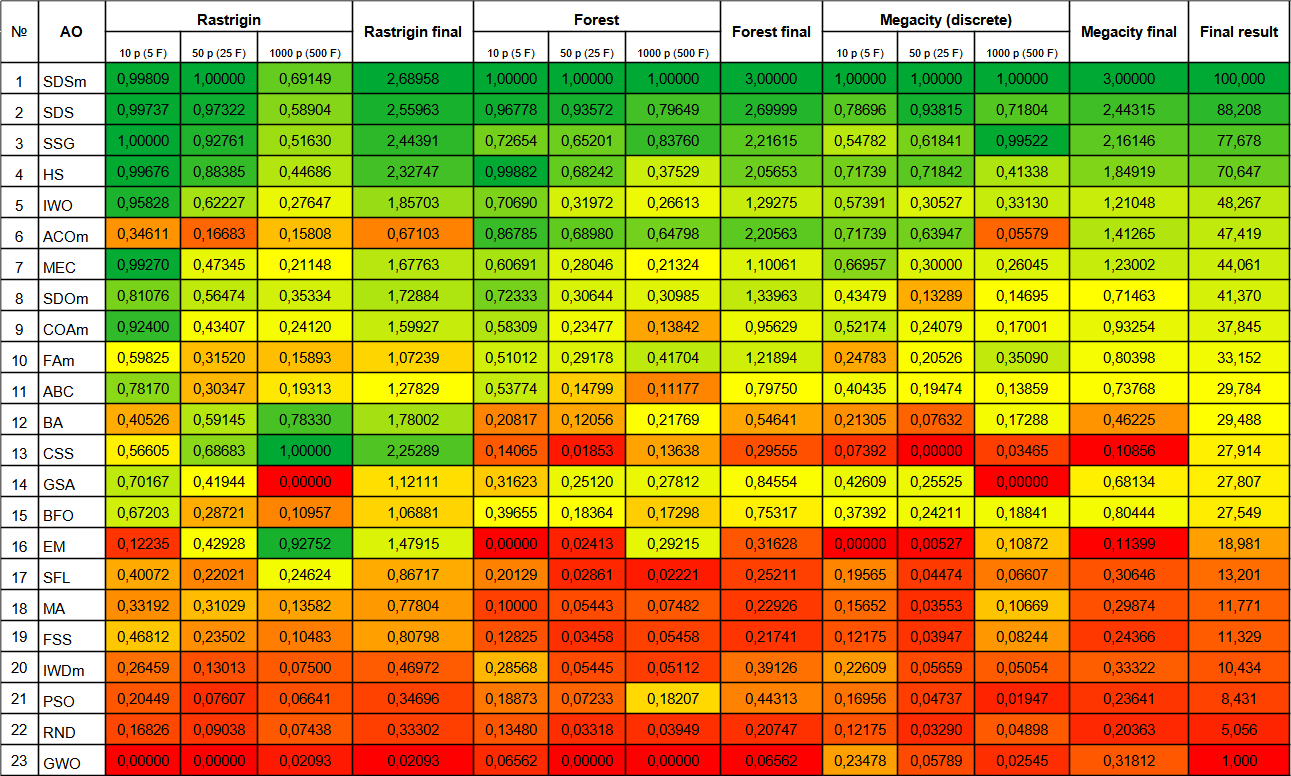
Abbildung 5. Farbabstufung der Algorithmen gemäß den einschlägigen Tests

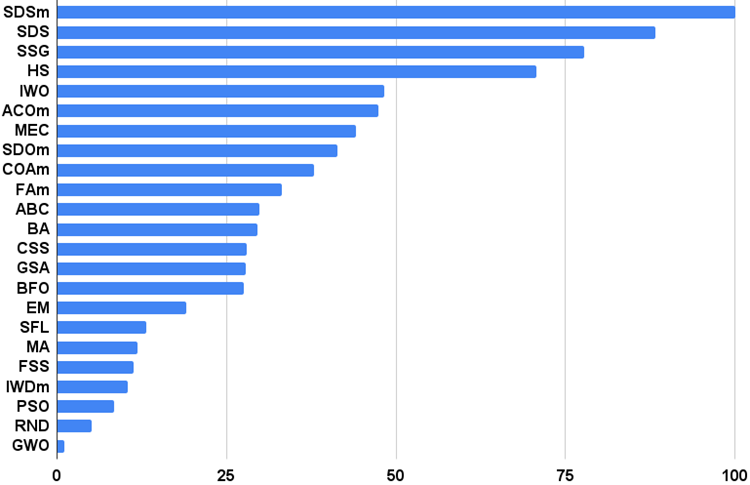
Abbildung 6. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, je mehr, desto besser,

das Archiv enthält das Skript zur Berechnung der Bewertungstabelle nach der im Artikel verwendeten Methode).

Vor- und Nachteile des modifizierten Spiral Dynamics Optimization (SDOm) Algorithmus:

Vorteile:
1. Eine kleine Anzahl von externen Parametern.
2. Einfache Umsetzung.
3. Ausführungsgeschwindigkeit.

Nachteile
1. Hohe Streuung der Ergebnisse.
2. Tendenz, in lokalen Extremen stecken zu bleiben.

Dem Artikel ist ein Archiv mit aktualisierten Versionen der in früheren Artikeln beschriebenen Algorithmuscodes beigefügt. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.