
Nachbarschaftsübergreifende Suche (ANS)
1. Einführung
In der heutigen Welt spielt die Entwicklung effizienter Optimierungsmethoden eine wichtige Rolle bei der Lösung einer Vielzahl von Problemen, die von technischen Anwendungen bis hin zur wissenschaftlichen Forschung auf dem Gebiet des maschinellen Lernens und der künstlichen Intelligenz reichen. In diesem Zusammenhang stellen metaheuristische, evolutionäre Algorithmen leistungsstarke Werkzeuge für die Lösung komplexer Optimierungsprobleme dar. Um ihre Leistung und Effizienz weiter zu verbessern, ist jedoch eine kontinuierliche Weiterentwicklung und Änderung der bestehenden Methoden sowie die Entwicklung neuer Algorithmen erforderlich.
In diesem Artikel werde ich einen Optimierungsalgorithmus namens Across Neighborhood Search (ANS) vorstellen, der 2014 von Guohua Wu vorgeschlagen wurde und auf der Populationssuche für numerische Optimierung basiert. Der entwickelte ANS-Algorithmus stellt einen bedeutenden Fortschritt auf dem Gebiet der Optimierung dar und verspricht, verschiedene Probleme in der realen Welt mit hoher Effizienz und Genauigkeit zu lösen. Wir werden im Folgenden prüfen, ob dies der Fall ist. Die Grundidee von ANS besteht darin, das Verhalten eines Multi-Agenten-Systems zu modellieren, bei dem sich jeder Agent durch einen Lösungsraum bewegt, mit seinen Nachbarn interagiert und Informationen austauscht. Dieser Ansatz ermöglicht eine hervorragende Erkundung des Suchraums durch die Kombination von lokaler und globaler Optimierung.
Wir werden uns mit einer detaillierten Beschreibung der Struktur des ANS-Algorithmus und den Prinzipien seiner Funktionsweise vertraut machen und eine vergleichende Analyse mit bestehenden Optimierungsmethoden durchführen. Der entwickelte ANS-Algorithmus öffnet das Feld der Optimierung und ermöglicht es uns, ein breites Spektrum von Problemen mit hoher Leistung zu lösen. Im Zusammenhang mit der Entwicklung der künstlichen Intelligenz ist es außerdem wichtig festzustellen, dass der ANS-Algorithmus einen wichtigen Schritt zur Schaffung flexiblerer und intelligenterer Optimierungsmethoden darstellt, die die Besonderheiten des Problems und die Dynamik der Umgebung berücksichtigen können.
2. Implementierung des Algorithmus
Der Algorithmus Across Neighborhood Search (ANS) ist eine Optimierungsmethode, die Ideen aus dem Bereich der evolutionären Algorithmen und Metaheuristiken verwendet und darauf ausgelegt ist, optimale Lösungen im Raum der Problemparameter zu finden.
Lassen Sie uns die wichtigsten Merkmale von ANS festhalten:
- Nachbarschaftssuche - Agenten erforschen die Nachbarschaft aktueller Lösungen, was es ihnen ermöglicht, lokale Optima effizienter zu finden.
- Verwendung der Normalverteilung - ANS verwendet die Normalverteilung, um neue Parameterwerte zu erzeugen.
- Kollektion von Lösungen - ANS verwendet Kollektionen der besten Lösungen, die dem Algorithmus helfen, sich in mehrere vielversprechende Richtungen gleichzeitig zu orientieren.
Bei ANS sucht eine Gruppe von Personen gemeinsam einen Lösungsraum, um das betrachtete Optimierungsproblem optimal zu lösen. Die Grundidee des Algorithmus besteht darin, eine Kollektion hervorragender Lösungen, die bisher von einzelnen Personen gefunden wurden, zu pflegen und dynamisch zu aktualisieren. In jeder Generation sucht das Individuum direkt in der Nachbarschaft nach mehreren unterschiedlichen Lösungen gemäß der normalen Wahrscheinlichkeitsverteilung. Auf diese Weise wird die Idee ausgenutzt, mehrere potenziell gute Lösungen gleichzeitig zu haben, da nicht im Voraus bekannt ist, welche von ihnen die beste sein wird.
Im Folgenden wird eine vollständige Beschreibung des ANS-Algorithmus mit Gleichungen und Stufen nach dem Konzept des Autors gegeben. ANS führt die folgenden Schritte durch:
1. Initialisierung der Parameter:
- Größe der Population m
- Kollektion der besten Lösungen Menge c
- Standardabweichung einer Gaußschen Verteilung sigma
- Dimensionalität des Suchraums D
- Maximale Anzahl von Generationen MaxG
2. Initialisierung der Population. Zufällige Initialisierung der Position jedes Individuums der Population im Suchraum.
3. Aktualisierung der besten Lösungen. Jedes Individuum in der Population aktualisiert seine aktuelle Position, indem es die Nachbarschaft der besten Lösungen aus der Kollektion unter Verwendung der Normalverteilung erkundet.
4. Auswahl der Koordinaten für die Suche. Die Zufallszahlenauswahl n (suchübergreifender Grad) bestimmt die aktuelle Koordinate der Position des Individuums im Lösungsraum.
5. Aktualisierung der Position eines Individuums. Aktualisierung der Position einer Person i gemäß dem vorherigen Schritt.
Gleichungen und Operationen:
1. Aktualisierung der Position pos_i des Individuums i (Erkundung der Nachbarschaft einer Lösung aus einer Kollektion):
- Die Position des Individuums i wird anhand einer Gaußschen Verteilung aktualisiert: pos_i = r_g + G (r_g - pos_i), wobei:
- G - Zufallswert aus einer Gaußschen Verteilung
- r_g - Position der besten Lösung aus der Kollektion
2. Aktualisierung der Position pos_i des Individuums i (Erkundung der Nachbarschaft der eigenen besten Lösung):
- Die Position des Individuums i wird anhand einer Gaußschen Verteilung aktualisiert: pos_i = r_i + G (r_i - pos_i), wobei:
- G - Zufallswert aus einer Gaußschen Verteilung
- r_i - Position der besten Lösung des Einzelnen
3. Aktualisierung einer Reihe der besten Lösungen:
- Die Kollektion der besten Lösungen wird auf der Grundlage neuer Positionen von Einzelpersonen aktualisiert.
Die Gleichungen spiegeln also den Mechanismus der Suche nach dem Individuum i in der Nachbarschaft seiner besten Lösung r_i sowie in der Nachbarschaft anderer bester Lösungen r_g aus der Kollektion R wider. Diese Schritte des Algorithmus stellen die grundlegende Logik der ANS-Methode (Across Neighbourhood Search, nachbarschaftsübergreifende Suche) zur Lösung von Optimierungsproblemen dar. Es umfasst die Initialisierung der Parameter, die zufällige Initialisierung der einzelnen Positionen, die Aktualisierung der einzelnen Positionen anhand der Nachbarschaften der besten Lösungen und die Aktualisierung der Kollektion der besten Lösungen. Der Algorithmus läuft weiter, bis die Stopp-Bedingung erfüllt ist.
Die Suche auf der Grundlage der besten Lösungen oder Individuen ist eine gängige und häufig verwendete Suchmethode in Populationsstrategiealgorithmen, obwohl die Prozesse zur Umsetzung eines solchen Suchmechanismus für verschiedene Optimierungsalgorithmen unterschiedlich sein können. In diesem Fall wird zusätzlich zur Hauptpopulation der Agenten eine neue Population eingeführt - eine Kollektion der besten Lösungen (potenzielle Suchrichtungen). Die Größe der Kollektion wird in den externen Parametern des Algorithmus festgelegt und kann entweder kleiner oder größer als die Größe der Hauptpopulation eingestellt werden.
Die Suchstrategie im ANS-Algorithmus beginnt mit dem Füllen der Kollektion der besten Lösungen und geht dann zur Suche in der Nachbarschaft der besten Lösungen der Kollektion und der besten individuellen Lösungen jedes Agenten über. Die Größe der Standardabweichung sigma spielt bei dem Algorithmus eine Schlüsselrolle. Ein niedriger Sigma-Wert ermöglicht eine breitere Erkundung des Suchraums, während höhere Werte eine Verfeinerung der Lösungen durch Eingrenzung ihrer Umgebung ermöglichen. Dieser Algorithmusparameter ist für das Gleichgewicht zwischen Suchintensivierung und Diversifizierung verantwortlich. Einige Algorithmen binden dieses Gleichgewicht an die aktuelle Epochenzahl, um dynamische Änderungen des Gleichgewichts zwischen Exploration und Verfeinerung zu ermöglichen, aber in diesem Fall haben die Autoren die Anpassung des Gleichgewichts als einen externen Parameter von ANS definiert.
Der ANS-Algorithmus kombiniert also die Nutzung der besten gefundenen Lösungen (durch die Suche in ihren Nachbarschaften) und die Erkundung des Lösungsraums (durch die Suche in den Nachbarschaften der eigenen besten Lösungen der Individuen). Dies sollte theoretisch ein gutes Gleichgewicht zwischen Suchintensivierung und Diversifizierung bieten.
Nun geht es an das Schreiben und Parsen des Algorithmus-Codes von ANS. Wir definieren die Struktur S_ANS_Agent, die zur Darstellung von Agenten im ANS-Algorithmus verwendet werden soll. Die Felder der Struktur:
- c - Array zur Speicherung der Koordinaten des Agenten.
- cBest - Array zur Speicherung der besten Agentenkoordinaten.
- f - Fitnesswert des Agenten.
- fBest - bester Fitnesswert des Agenten.
- Init(int coords) - Initialisierungsmethode, die die Größen der Arrays c und cBest sowie die Anfangswerte von f und fBest festlegt.
Dieser Teil des Codes stellt die Grundstruktur eines Agenten dar. Die Gruppe der Agenten stellt die Hauptpopulation im ANS-Algorithmus dar.
//—————————————————————————————————————————————————————————————————————————————— struct S_ANS_Agent { double c []; //coordinates double cBest []; //best coordinates double f; //fitness double fBest; //best fitness void Init (int coords) { ArrayResize (c, coords); ArrayResize (cBest, coords); f = -DBL_MAX; fBest = -DBL_MAX; } }; //—————————————————————————————————————————————————————————————————————————————
Um eine Kollektion der besten Lösungen zu beschreiben, legen wir die Struktur S_Collection fest, die zur Speicherung von Informationen über die besten Koordinaten im Suchraum und den entsprechenden Fitnesswert verwendet wird. Die Struktur enthält folgende Felder:
- c - Array zum Speichern von Koordinaten.
- f - Fitnesswert für eine bestimmte Lösung eines Problems in der Kollektion.
- Init(int coords) - Die Initialisierungsmethode setzt die Größe der c-Arrays und den anfänglichen f-Wert auf den kleinstmöglichen Wert vom Typ double.
//—————————————————————————————————————————————————————————————————————————————— struct S_Collection { double c []; //coordinates double f; //fitness void Init (int coords) { ArrayResize (c, coords); f = -DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
Wir deklarieren die Klasse C_AO_ANS, die ein Erbe der Basisklasse C_AO ist und den Algorithmus Across Neighbourhood Search (ANS) implementiert. Hier sind einige wichtige Punkte:
- ao_name, ao_desc, ao_link - Eigenschaften zur Beschreibung des ANS-Algorithmus.
- popSize - Größe der Population.
- collectionSize, sigma, range, collChoiceProbab - Parameter des ANS-Algorithmus.
- SetParams() - Methode zum Setzen von Parametern.
- Init(), Moving(), Revision() - Methoden zum Initialisieren, Verschieben von Agenten und Aktualisieren der Population und Lösungskollektion.
- S_ANS_Agent, S_Collection - Strukturen zur Speicherung von Agentendaten und Kollektionen.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ANS : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ANS () { } C_AO_ANS () { ao_name = "ANS"; ao_desc = "Across Neighbourhood Search"; ao_link = "https://www.mql5.com/de/articles/15049"; popSize = 50; //population size collectionSize = 20; //Best solutions collection sigma = 3.0; //Form of normal distribution range = 0.5; //Range of values dispersed collChoiceProbab = 0.8; //Collection choice probab ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "collectionSize"; params [1].val = collectionSize; params [2].name = "sigma"; params [2].val = sigma; params [3].name = "range"; params [3].val = range; params [4].name = "collChoiceProbab"; params [4].val = collChoiceProbab; } void SetParams () { popSize = (int)params [0].val; collectionSize = (int)params [1].val; sigma = params [2].val; range = params [3].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- int collectionSize; //Best solutions collection double sigma; //Form of normal distribution double range; //Range of values dispersed double collChoiceProbab; //Collection choice probab S_ANS_Agent agent []; private: //------------------------------------------------------------------- S_Collection coll []; S_Collection collTemp []; }; //——————————————————————————————————————————————————————————————————————————————
Die Methode Init initialisiert die Parameter des ANS-Algorithmus.
- rangeMinP, rangeMaxP, rangeStepP - Arrays, die das Minimum, das Maximum und den Schritt des Suchbereichs darstellen.
- epochsP - Anzahl der Epochen (Generationen).
Innerhalb der Methode:
- Die erfolgreiche Initialisierung der Standardparameter wird mit StandardInit überprüft.
- Es werden Arrays von Agent (agent) und Kollektion (coll) erstellt (zweite Population für die Speicherung der besten Lösungen), sowie collTemp (ein temporäres Array für die Sortierung der Collection).
- Für jeden Agenten und jede Kollektion wird die Methode Init aufgerufen, um die Anfangswerte festzulegen.
Diese Methode spielt eine wichtige Rolle bei der Vorbereitung des ANS-Algorithmus zur Durchführung der Optimierung. Es ist wichtig zu beachten, dass die Arrays coll und collTemp mit der doppelten Größe relativ zum Parameter collectionSize initialisiert werden. Dies geschieht, damit neu hinzukommende Agenten in der zweiten Hälfte des Arrays landen. Anschließend wird die gesamte Kollektion sortiert, und nur die erste Hälfte, die die besten Bearbeiter enthält, wird für die weitere Arbeit verwendet.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ANS::Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0) //number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (agent, popSize); for (int i = 0; i < popSize; i++) agent [i].Init (coords); ArrayResize (coll, collectionSize * 2); ArrayResize (collTemp, collectionSize * 2); for (int i = 0; i < collectionSize * 2; i++) { coll [i].Init (coords); collTemp [i].Init (coords); } return true; } //——————————————————————————————————————————————————————————————————————————————
Die Methode Moving führt die Bewegung (Verschiebung) der Agenten im ANS-Algorithmus durch. Schauen wir uns diesen Code einmal genauer an:
1. Initialisierung (wenn revision gleich false ist):
- Wenn dies der erste Schritt (erste Epoche) ist, dann für jeden Agenten:
- Der Zufallswert val wird im Bereich von rangeMin[c] bis rangeMax[c] erzeugt.
- Der Operator SeInDiSp wird angewendet, um den SchrittbereichStep[c] zu berücksichtigen.
- Der Wert val wird den Koordinaten des Agenten agent[i].c[c] zugewiesen.
- Der Wert val wird auch den besten Koordinaten des Agenten agent[i].cBest[c] zugewiesen (in diesem Stadium sind die Fitnesswerte der Agenten unbekannt, sodass die besten Koordinaten den aktuellen Anfangswerten entsprechen).
- Der Wert val wird dem Agenten-Array a[i].c[c] zugewiesen.
2. Agentenbewegungen (wenn revision gleich true ist):
- Für jeden Agenten und jede Koordinate:
- Ist die Zufallszahl kleiner als collChoiceProbab, wird eine Zufallslösung aus der Kollektion ausgewählt:
- Der Zufallsindex ind wird aus der Kollektion ausgewählt (bis eine nicht leere Lösung gefunden wird).
- Der p-Wert wird von den aktuellen Koordinaten des Agenten übernommen.
- Der r-Wert wird der ausgewählten Lösung aus der Kollektion entnommen.
- Andernfalls werden die besten Agentenkoordinaten verwendet:
- Der p-Wert wird von den aktuellen Koordinaten des Agenten übernommen.
- Der r-Wert wird von den Koordinaten des besten Agenten übernommen.
- Für die Bewegung werden die Distanz und der (minimale und maximale) Bereich berechnet.
- Die Mindest- und Höchstwerte sind auf die Bereiche rangeMin[c] und rangeMax[c] beschränkt.
- Die Normalverteilung mit den Parametern r, min, max und sigma.
- Der Wert val wird den Koordinaten des Agenten agent[i].c[c] zugewiesen.
- Der Wert val wird auch dem Agenten-Array a[i].c[c] zugewiesen.
Dieser Code aktualisiert die Koordinaten der Agenten im ANS-Algorithmus, wobei die besten Koordinaten der Agenten und Lösungen in der Kollektion berücksichtigt werden.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ANS::Moving () { double val = 0.0; //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { val = u.RNDfromCI (rangeMin [c], rangeMax [c]); val = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); agent [i].c [c] = val; agent [i].cBest [c] = val; a [i].c [c] = val; } } revision = true; return; } //---------------------------------------------------------------------------- double min = 0.0; double max = 0.0; double dist = 0.0; int ind = 0; double r = 0.0; double p = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { if (u.RNDprobab () < collChoiceProbab) { do ind = u.RNDminusOne (collectionSize); while (coll [ind].f == -DBL_MAX); p = agent [i].c [c]; r = coll [ind].c [c]; } else { p = agent [i].c [c]; r = agent [i].cBest [c]; } dist = fabs (p - r) * range; min = r - dist; max = r + dist; if (min < rangeMin [c]) min = rangeMin [c]; if (max > rangeMax [c]) max = rangeMax [c]; val = u.GaussDistribution (r, min, max, sigma); val = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); agent [i].c [c] = val; a [i].c [c] = val; } } } //——————————————————————————————————————————————————————————————————————————————
Die Revisionsmethode führt die Revision (Aktualisierung) von Bearbeitern und Kollektionen im ANS-Algorithmus durch. Hier sind die wichtigsten Punkte:
- Der erste Teil der Methode: sucht nach einem Agenten, dessen Fitness besser ist als die globale Lösung mit der Fitness fB und speichert seine Koordinaten in der Matrix cB.
- Der zweite Teil der Methode: aktualisiert die besten Koordinaten der Agenten agent[i].cBest auf der Grundlage ihrer aktuellen Fitness a[i].f.
- Der dritte Teil der Methode: aktualisiert die KollKollektion auf der Grundlage der besten Koordinaten der Agenten.
- Sortieren der Kollektion.
Diese Methode spielt eine wichtige Rolle bei der Aktualisierung von Agenten und der Lösungskollektion während der Ausführung des Algorithmus. Die Agentenpopulation wird in den zweiten Teil der Kollektion gelegt, die Kollektion wird sortiert, und die erste Hälfte der Kollektion, die die besten Lösungen enthält, wird dann verwendet.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ANS::Revision () { //---------------------------------------------------------------------------- int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (a [i].f > agent [i].fBest) { agent [i].fBest = a [i].f; ArrayCopy (agent [i].cBest, a [i].c, 0, 0, WHOLE_ARRAY); } } //---------------------------------------------------------------------------- int cnt = 0; for (int i = collectionSize; i < collectionSize * 2; i++) { if (cnt < popSize) { coll [i].f = agent [cnt].fBest; ArrayCopy (coll [i].c, agent [cnt].cBest, 0, 0, WHOLE_ARRAY); cnt++; } else break; } u.Sorting (coll, collTemp, collectionSize * 2); } //——————————————————————————————————————————————————————————————————————————————
3. Testergebnisse
ANS-Testergebnisse:
ANS|Across Neighbourhood Search|50.0|100.0|8.0|1.0|0.6|
=============================
5 Hilly's; Func runs: 10000; result: 0.9494753644543816
25 Hilly's; Func runs: 10000; result: 0.8477633752716718
500 Hilly's; Func runs: 10000; result: 0.43857039929159747
=============================
5 Forest's; Func runs: 10000; result: 0.9999999999988883
25 Forest's; Func runs: 10000; result: 0.9233446583489741
500 Forest's; Func runs: 10000; result: 0.3998822848099108
=============================
5 Megacity's; Func runs: 10000; result: 0.709230769230769
25 Megacity's; Func runs: 10000; result: 0.6347692307692309
500 Megacity's; Func runs: 10000; result: 0.2309076923076936
=============================
All score: 6.13394 (68.15%)
ANS zeigt bei allen Testfunktionen beeindruckende Ergebnisse. Werfen wir einen Blick auf die Visualisierung der Funktionsweise dieses Algorithmus auf dem Prüfstand. Die Ergebnisse von ANS sind wirklich erstaunlich, aber bei der Visualisierung stellen sich einige Fragen. Besonders auffällig ist das Verhalten der Population - sie scheint aus dem Blickfeld zu verschwinden. Der Lösungsraum wird geleert und die Funktionslandschaft bleibt ohne Agenten. Das kann nur eines bedeuten: Trotz der hervorragenden Ergebnisse des Algorithmus ist die Population anfällig für Degeneration. Die Kollektion hervorragender Lösungen wird durch sehr ähnliche Lösungen unübersichtlich, und neue Lösungen können einfach nicht geschaffen werden, da alle Lösungen Ableitungen der bereits vorhandenen sind.
Eine solche Populationsdynamik kann ein Hinweis auf die Notwendigkeit sein, die Mechanismen zur Erhaltung der Vielfalt in der Population zu verbessern. Es könnte sich lohnen, einen Mutationsoperator hinzuzufügen oder andere Mechanismen einzuführen, die dazu beitragen, eine größere Vielfalt an Lösungen während der Optimierung zu erhalten. Dies trägt dazu bei, eine Degeneration der Population zu vermeiden und einen stabileren Betrieb des Algorithmus zu gewährleisten.
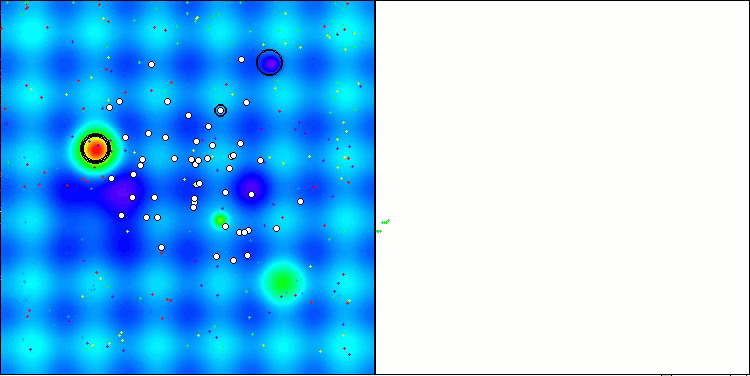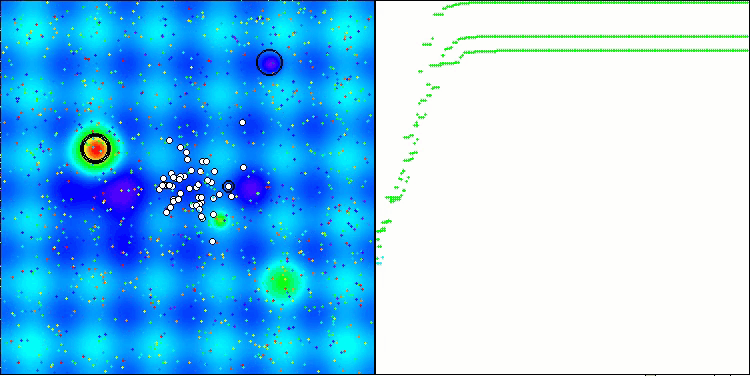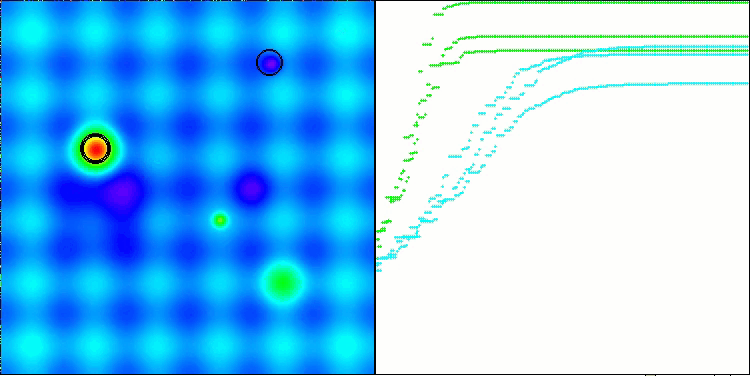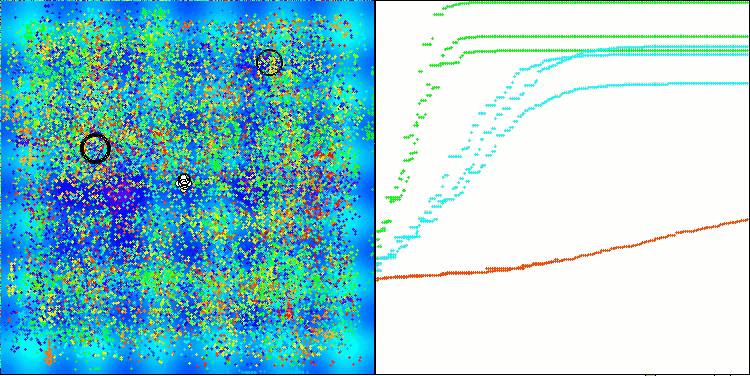
ANS mit der Testfunktion Hilly
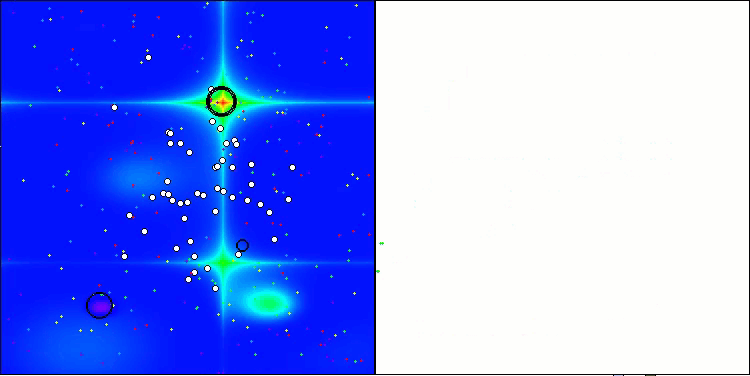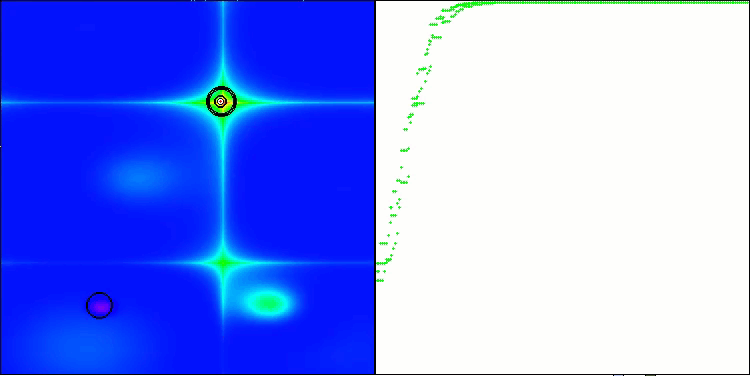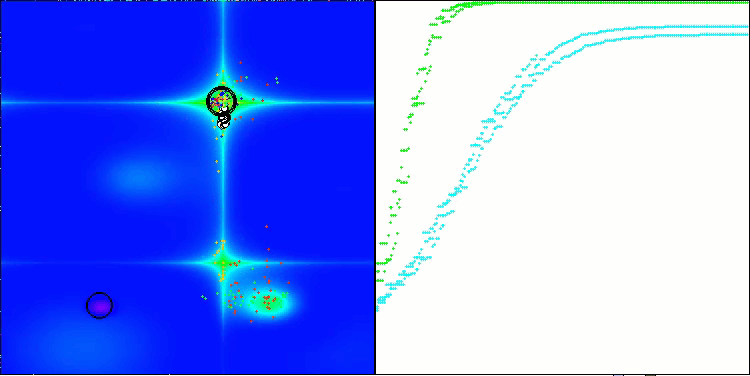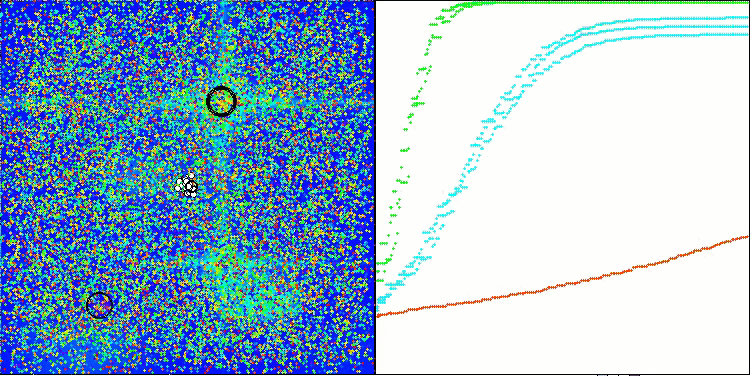
ANS mit der Testfunktion Forest
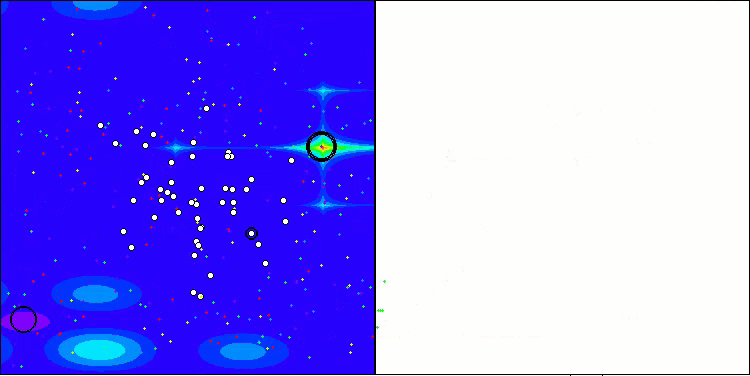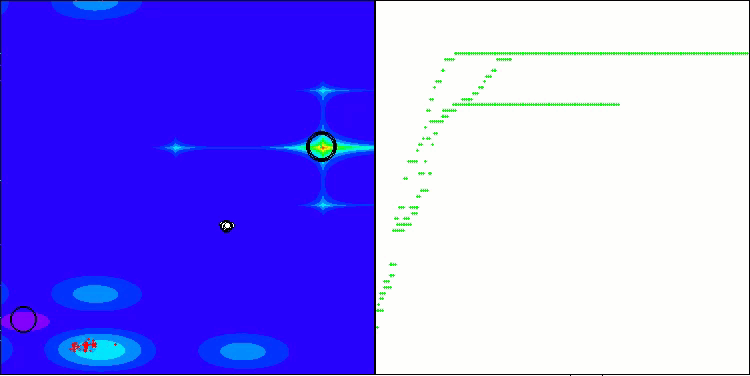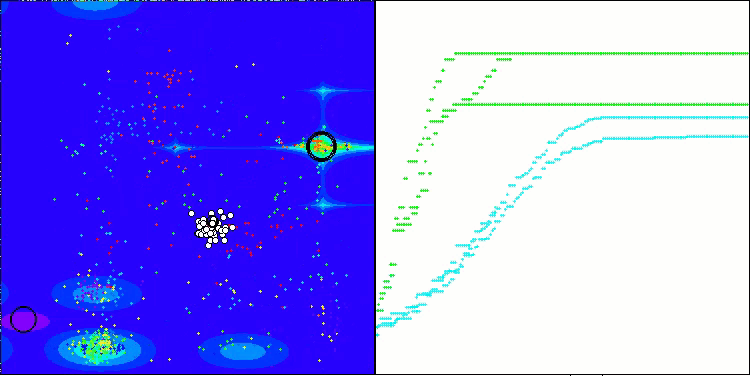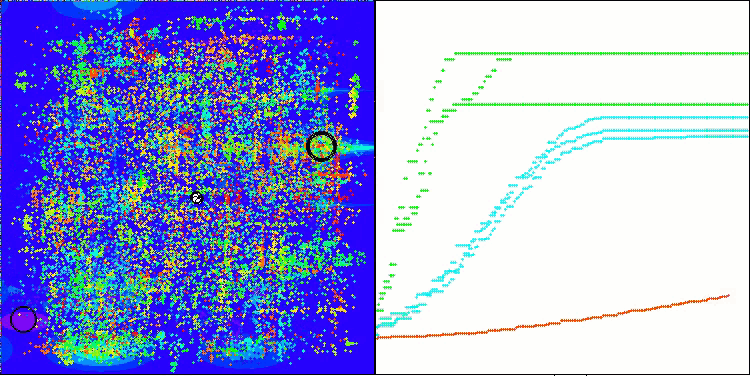
ANS mit der Testfunktion Megacity
Der in diesem Artikel betrachtete Algorithmus belegte souverän den zweiten Platz in der Bewertungstabelle. Der Algorithmus zeigt eine beeindruckende Skalierbarkeit, da er auch bei großdimensionalen Problemen die Fähigkeit zur Suche beibehält.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | BGA | binärer genetischer Algorithmus | 0.99989 | 0.99518 | 0.42835 | 2.42341 | 0.96153 | 0.96181 | 0.32027 | 2.24360 | 0.91385 | 0.95908 | 0.24220 | 2.11512 | 6.782 | 75.36 |
| 2 | ANS | Nachbarschaftsübergreifende Suche | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 3 | CLA | Zahlenschloss-Algorithmus | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 4 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | ESG | Entwicklung der sozialen Gruppen | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 8 | SIA | Simuliertes isotropes Abkühlen | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 9 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 10 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 11 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 12 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 13 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 14 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 15 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 16 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 17 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 18 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 19 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 20 | BFO-GA | Optimierung der bakteriellen Futtersuche - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 21 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 22 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 23 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 24 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 25 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 26 | NMm | Nelder-Mead-Verfahren M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 27 | FAm | Firefly-Algorithmus M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 28 | GSA | Algorithmus für die Schwerkraftsuche | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 29 | BFO | Optimierung der bakteriellen Futtersuche | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 30 | ABC | Künstliches Bienenvolk (Artificial Bee Colony, ABC) | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 31 | BA | Fledermaus-Algorithmus | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 32 | SA | simuliertes Abkühlen | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
| 33 | IWDm | intelligente Wassertropfen M | 0.54501 | 0.37897 | 0.30124 | 1.22522 | 0.46104 | 0.14704 | 0.04369 | 0.65177 | 0.25833 | 0.09700 | 0.02308 | 0.37842 | 2.255 | 25.06 |
| 34 | PSO | Partikelschwarmoptimierung | 0.59726 | 0.36923 | 0.29928 | 1.26577 | 0.37237 | 0.16324 | 0.07010 | 0.60572 | 0.25667 | 0.08000 | 0.02157 | 0.35823 | 2.230 | 24.77 |
| 35 | Gebote | Boids-Algorithmus | 0.43340 | 0.30581 | 0.25425 | 0.99346 | 0.35718 | 0.20160 | 0.15708 | 0.71586 | 0.27846 | 0.14277 | 0.09834 | 0.51957 | 2.229 | 24.77 |
| 36 | MA | Affen-Algorithmus | 0.59107 | 0.42681 | 0.31816 | 1.33604 | 0.31138 | 0.14069 | 0.06612 | 0.51819 | 0.22833 | 0.08567 | 0.02790 | 0.34190 | 2.196 | 24.40 |
| 37 | SFL | schlurfender Froschsprung | 0.53925 | 0.35816 | 0.29809 | 1.19551 | 0.37141 | 0.11427 | 0.04051 | 0.52618 | 0.27167 | 0.08667 | 0.02402 | 0.38235 | 2.104 | 23.38 |
| 38 | FSS | Fischschulsuche | 0.55669 | 0.39992 | 0.31172 | 1.26833 | 0.31009 | 0.11889 | 0.04569 | 0.47467 | 0.21167 | 0.07633 | 0.02488 | 0.31288 | 2.056 | 22.84 |
| 39 | RND | zufällig | 0.52033 | 0.36068 | 0.30133 | 1.18234 | 0.31335 | 0.11787 | 0.04354 | 0.47476 | 0.25333 | 0.07933 | 0.02382 | 0.35648 | 2.014 | 22.37 |
| 40 | GWO | Grauer-Wolf-Optimierung | 0.59169 | 0.36561 | 0.29595 | 1.25326 | 0.24499 | 0.09047 | 0.03612 | 0.37158 | 0.27667 | 0.08567 | 0.02170 | 0.38403 | 2.009 | 22.32 |
| 41 | CSS | Suche geladener Systeme | 0.44252 | 0.35454 | 0.35201 | 1.14907 | 0.24140 | 0.11345 | 0.06814 | 0.42299 | 0.18333 | 0.06300 | 0.02322 | 0.26955 | 1.842 | 20.46 |
| 42 | EM | elektromagnetismusähnlicher Algorithmus | 0.46250 | 0.34594 | 0.32285 | 1.13129 | 0.21245 | 0.09783 | 0.10057 | 0.41085 | 0.15667 | 0.06033 | 0.02712 | 0.24412 | 1.786 | 19.85 |
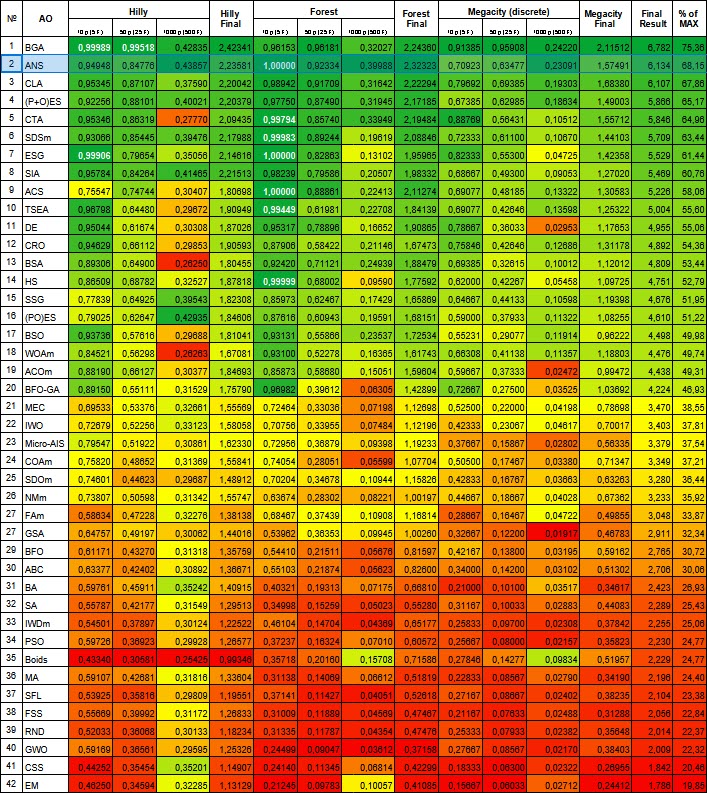
Abbildung 1. Die farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben
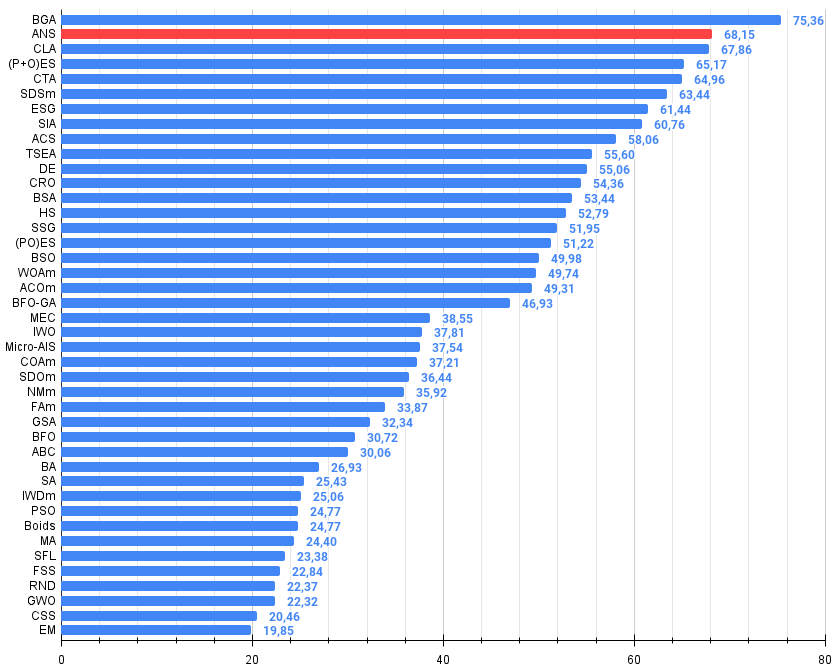
Abbildung 2. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, je mehr, desto besser,
wobei 100 das maximal mögliche theoretische Ergebnis ist; das Archiv enthält ein Skript zur Berechnung der Bewertungstabelle)
Weiter oben in diesem Artikel haben wir die Tendenz der ANS-Algorithmenpopulation zur Degenerierung festgestellt. Um diesen großen Nachteil zu beheben, habe ich beschlossen, den Algorithmus durch Hinzufügen eines Mutationsoperators zu ändern. In diesem Fall ist die Mutation eine Gaußsche Wahrscheinlichkeit, eine neue Koordinate zu erhalten, die in der Nähe der besten Lösung des Agenten, aber im Bereich zwischen dem minimalen und dem maximalen akzeptablen Wert für die entsprechende Koordinate liegt. Zu diesem Zweck müssen wir einige Änderungen an der Methode „Moving“ vornehmen.
Sehen wir uns an, welche Änderungen am Code vorgenommen wurden, und beschreiben wir kurz die Logik der Methode:
- Wenn die Zufallszahl kleiner als 0,005 ist, findet eine Mutation unter Verwendung einer Normalverteilung statt.
- Andernfalls wird eine zufällige Lösung aus der Kollektion ausgewählt, oder es werden die besten Agentenkoordinaten verwendet.
- Der Abstand und der Bereich für eine Normalverteilung werden berechnet.
- Die Normalverteilung wird verwendet, um neue Koordinatenwerte zu erhalten.
//---------------------------------------------------------------------------- double min = 0.0; double max = 0.0; double dist = 0.0; int ind = 0; double r = 0.0; double p = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { if (u.RNDprobab () < 0.005) { val = u.GaussDistribution (agent [i].cBest [c], rangeMin [c], rangeMax [c], sigma); val = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); } else { if (u.RNDprobab () < collChoiceProbab) { do ind = u.RNDminusOne (collectionSize); while (coll [ind].f == -DBL_MAX); p = agent [i].c [c]; r = coll [ind].c [c]; } else { p = agent [i].c [c]; r = agent [i].cBest [c]; } dist = fabs (p - r) * range; min = r - dist; max = r + dist; if (min < rangeMin [c]) min = rangeMin [c]; if (max > rangeMax [c]) max = rangeMax [c]; val = u.GaussDistribution (r, min, max, sigma); val = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); } agent [i].c [c] = val; a [i].c [c] = val; } }
Nach dem Hinzufügen des Mutationsoperators fährt der Algorithmus fort, den Suchraum für eine beliebige Anzahl von Epochen zu erkunden, wie in Abbildung 3 (ein Screenshot der Algorithmusvisualisierung) gezeigt wird.
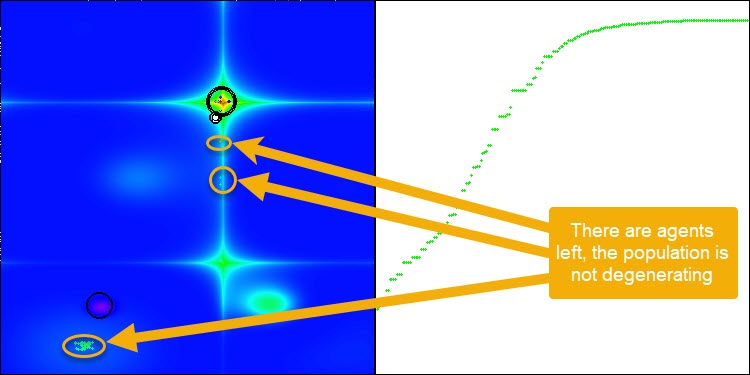
Abbildung 3. Es sind Agenten übergeblieben, die Population degeneriert nicht (Parameter mut = 0,005)
- Der Mutationsoperator mit Mut 0,1 hat einen negativen Einfluss auf das Gesamtergebnis. Bei einer so großen Mutationsrate (10 % der Gesamtzahl der Operationen auf jeder Koordinate) ist eine Verschlechterung der Algorithmusleistung zu beobachten. Deshalb habe ich beschlossen, diesen Parameter schrittweise zu reduzieren. Eine Verringerung des Parameterwerts verbesserte die Ergebnisse, und ich entschied mich für einen Wert von 0,005. Dieses Verhältnis erwies sich als ausreichend, um eine Degeneration der Population zu verhindern und gleichzeitig die Leistung des Algorithmus zu verbessern, wie unten dargestellt.
Ergebnisse der Algorithmusoperation mit Mutationswahrscheinlichkeit mut = 0,1:
=============================
All score: 6.05103 (67.23%)
ANS|Across Neighbourhood Search|50.0|100.0|8.0|1.0|0.6|
=============================
5 Hilly's; Func runs: 10000; result: 0.9534829314854332
25 Hilly's; Func runs: 10000; result: 0.8136803288623282
500 Hilly's; Func runs: 10000; result: 0.31144979106165716
=============================
5 Forest's; Func runs: 10000; result: 0.9996561274415626
25 Forest's; Func runs: 10000; result: 0.81670393859872
500 Forest's; Func runs: 10000; result: 0.25620559379918284
=============================
5 Megacity's; Func runs: 10000; result: 0.8753846153846153
25 Megacity's; Func runs: 10000; result: 0.5778461538461539
500 Megacity's; Func runs: 10000; result: 0.13375384615384744
=============================
All score: 5.73816 (63.76%)
Ergebnisse der Algorithmusoperation mit Mutationswahrscheinlichkeit mut = 0,01:
=============================
5 Hilly's; Func runs: 10000; result: 0.9073657389037575
25 Hilly's; Func runs: 10000; result: 0.871278233418226
500 Hilly's; Func runs: 10000; result: 0.3960769225373809
=============================
5 Forest's; Func runs: 10000; result: 0.989394440004635
25 Forest's; Func runs: 10000; result: 0.9513150500729907
500 Forest's; Func runs: 10000; result: 0.35407610928209116
=============================
5 Megacity's; Func runs: 10000; result: 0.7492307692307691
25 Megacity's; Func runs: 10000; result: 0.6387692307692309
500 Megacity's; Func runs: 10000; result: 0.19352307692307838
=============================
All score: 6.05103 (67.23%)
Ergebnisse der Algorithmusoperation mit Mutationswahrscheinlichkeit mut = 0,005:
ANS|Across Neighbourhood Search|50.0|100.0|8.0|1.0|0.6|
=============================
5 Hilly's; Func runs: 10000; result: 0.949632264944664
25 Hilly's; Func runs: 10000; result: 0.871206955779846
500 Hilly's; Func runs: 10000; result: 0.40738389742274217
=============================
5 Forest's; Func runs: 10000; result: 0.9924803131691761
25 Forest's; Func runs: 10000; result: 0.9493489251290264
500 Forest's; Func runs: 10000; result: 0.3666276564633121
=============================
5 Megacity's; Func runs: 10000; result: 0.8061538461538461
25 Megacity's; Func runs: 10000; result: 0.6732307692307691
500 Megacity's; Func runs: 10000; result: 0.20844615384615534
=============================
All score: 6.22451 (69.16%)
Zusammenfassung
Nachdem wir nun die Ergebnisse der Zusammenarbeit mit dem Mutationsoperator betrachtet haben, können wir folgende Schlussfolgerungen ziehen:
1. Einfachheit und Leichtigkeit der Umsetzung.
2. Gleichgewicht zwischen Erkundung und Ausbeutung.
3. Effizienz bei der Lösung verschiedener Arten von Problemen.
4. Anpassungsfähigkeit an verschiedene Aufgaben.
5. Potenzial für weitere Verbesserungen.
ANS ist also ein einfacher, aber effektiver Optimierungsalgorithmus, der bei einem breiten Spektrum von Problemen wettbewerbsfähige Ergebnisse liefert und Potenzial für weitere Entwicklungen hat.
ANS allgemeine Vor- und Nachteile:
Vorteile:
- Gute Konvergenz bei verschiedenen Arten von Funktionen.
- Sehr schneller EA.
- Einfache Umsetzung.
- Ausgezeichnete Skalierbarkeit.
Nachteile
- Bleibt manchmal in lokalen Extremen stecken.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Algorithmuscodes begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15049
 Wie Smart-Money-Konzepte (SMC) zusammen mit dem Fibonacci-Indikator einen optimalen Handelseinstieg signalisieren.
Wie Smart-Money-Konzepte (SMC) zusammen mit dem Fibonacci-Indikator einen optimalen Handelseinstieg signalisieren.
 Neuronale Netze leicht gemacht (Teil 96): Mehrskalige Merkmalsextraktion (MSFformer)
Neuronale Netze leicht gemacht (Teil 96): Mehrskalige Merkmalsextraktion (MSFformer)
 Nachrichtenhandel leicht gemacht (Teil 4): Leistungsverbesserung
Nachrichtenhandel leicht gemacht (Teil 4): Leistungsverbesserung
 MetaTrader 5 unter macOS
MetaTrader 5 unter macOS
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.