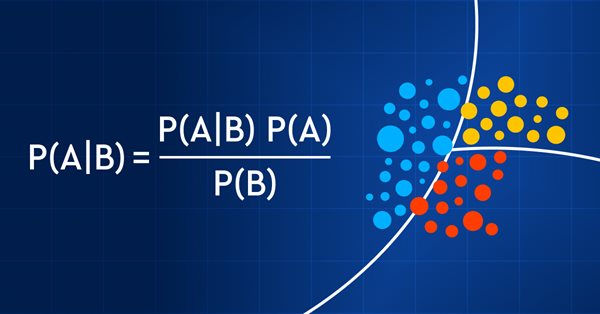
Datenwissenschaft und maschinelles Lernen (Teil 11): Naïve Bayes, Wahrscheinlichkeitsrechnung im Handel
Vierter Hauptsatz der Thermodynamik: Wenn die Erfolgswahrscheinlichkeit nicht fast eins ist, dann ist sie verdammt nahe null.
David J. Rose
Einführung
Der Naïve Bayes-Klassifikator ist ein probabilistischer Algorithmus, der beim maschinellen Lernen für Klassifizierungsaufgaben verwendet wird. Sie basiert auf dem Bayes-Theorem, mit dem die Wahrscheinlichkeit einer Hypothese anhand der verfügbaren Beweise berechnet wird. Dieser probabilistische Klassifikator ist ein einfacher, aber effektiver Algorithmus für verschiedene Situationen. Dabei wird davon ausgegangen, dass die für die Klassifizierung verwendeten Merkmale unabhängig voneinander sind. Zum Beispiel: Wenn Sie möchten, dass dieses Modell Menschen (männlich und weiblich) anhand von Größe, Fußgröße, Gewicht und Schulterlänge klassifiziert, behandelt dieses Modell alle diese Variablen als unabhängig voneinander. In diesem Fall geht es nicht einmal davon aus, dass Fußgröße und Größe bei einem Menschen zusammenhängen.
Da sich dieses Modell nicht darum kümmert, die Muster zwischen den unabhängigen Variablen zu verstehen, denke ich, dass wir einen Versuch wagen sollten, es zu nutzen, um fundierte Handelsentscheidungen zu treffen. Ich glaube, dass im Handelsbereich ohnehin niemand die Muster vollständig versteht, also schauen wir mal, wie sich Naïve Bayes schlägt.

Rufen wir also kurzerhand die Modellinstanz auf und verwenden sie sofort. Wir werden später erörtern, woraus dieses Modell besteht.
Vorbereiten der Trainingsdaten
Für dieses Beispiel habe ich 5 Indikatoren ausgewählt, die meisten von ihnen sind Oszillatoren und Volumina, da ich denke, dass sie gute Klassifizierungsvariablen darstellen. Außerdem haben sie eine endliche Menge, was sie gut für die Normalverteilung macht, die eine der Ideen im Kern dieses Algorithmus ist. Sie sind jedoch nicht auf diese Indikatoren beschränkt, Sie können also auch andere Indikatoren und Daten verwenden, die Sie bevorzugen.
Das Wichtigste zuerst:
matrix Matrix(TrainBars, 6); int handles[5]; double buffer[]; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Preparing Data handles[0] = iBearsPower(Symbol(),TF, bears_period); handles[1] = iBullsPower(Symbol(),TF, bulls_period); handles[2] = iRSI(Symbol(),TF,rsi_period, rsi_price); handles[3] = iVolumes(Symbol(),TF,VOLUME_TICK); handles[4] = iMFI(Symbol(),TF,mfi_period,VOLUME_TICK ); //--- vector col_v; for (ulong i=0; i<5; i++) //Independent vars { CopyBuffer(handles[i],0,0,TrainBars, buffer); col_v = matrix_utils.ArrayToVector(buffer); Matrix.Col(col_v, i); } //-- Target var vector open, close; col_v.Resize(TrainBars); close.CopyRates(Symbol(),TF, COPY_RATES_CLOSE,0,TrainBars); open.CopyRates(Symbol(),TF, COPY_RATES_OPEN,0,TrainBars); for (int i=0; i<TrainBars; i++) { if (close[i] > open[i]) //price went up col_v[i] = 1; else col_v[i] = 0; } Matrix.Col(col_v, 5); //Adding independent variable to the last column of matrix //---
Die Variablen TF, bears_period usw. sind durch die Eingabe definierte Variablen, die sich oben im obigen Code befinden:
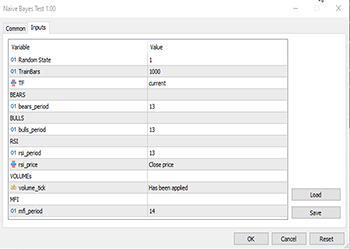
Da es sich um überwachtes Lernen handelt, musste ich die Zielvariable erfinden, die Logik ist einfach. Wenn der Schlusskurs über dem Eröffnungskurs lag, wird die Zielvariable auf die Klasse 1 gesetzt, andernfalls ist die Klasse 0. Auf diese Weise wurde die Zielvariable festgelegt. Nachfolgend finden Sie einen Überblick über das Aussehen der Matrix mit den Daten:
CS 0 13:21:15.457 Naive Bayes Test (EURUSD,H1) "Bears" "Bulls" "Rsi" "Volumes" "MFI" "Target Var" CS 0 13:21:15.457 Naive Bayes Test (EURUSD,H1) [-3.753148029472797e-06,0.008786246851970603,67.65238281791684,13489,55.24611392389958,0] CS 0 13:21:15.457 Naive Bayes Test (EURUSD,H1) [-0.002513216984025402,0.005616783015974569,50.29835423473968,12226,49.47293811405203,1] CS 0 13:21:15.457 Naive Bayes Test (EURUSD,H1) [-0.001829900272021678,0.0009700997279782353,47.33479153312328,7192,46.84320886771249,1] CS 0 13:21:15.457 Naive Bayes Test (EURUSD,H1) [-0.004718485947447171,-0.0001584859474472733,39.04848493977027,6267,44.61564654651691,1] CS 0 13:21:15.457 Naive Bayes Test (EURUSD,H1) [-0.004517273669240485,-0.001367273669240276,45.4127802340401,3867,47.8438816641815,0]
Ich beschloss dann, die Daten in Verteilungsdiagrammen zu visualisieren, um zu sehen, ob sie der Wahrscheinlichkeitsverteilung folgen:
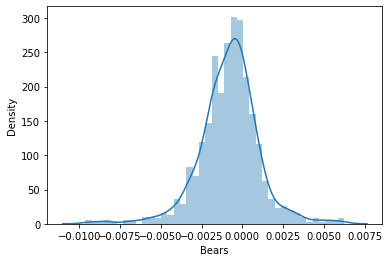
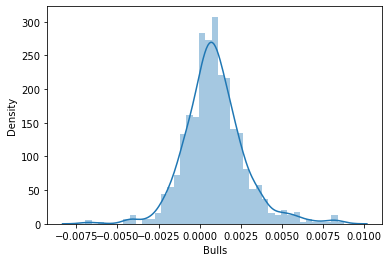
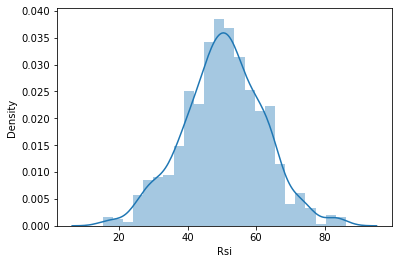
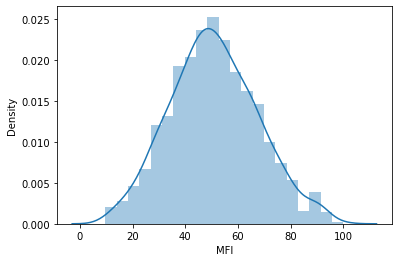
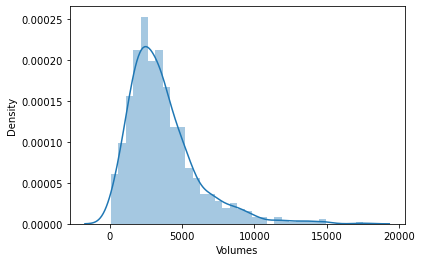
Für diejenigen, die die verschiedenen Arten von Wahrscheinlichkeitsverteilungen verstehen wollen, gibt es einen ganzen Artikel, der hier verlinkt ist.
Wenn man sich die Korrelationskoeffizientenmatrix aller unabhängigen Variablen genauer ansieht:
string header[5] = {"Bears","Bulls","Rsi","Volumes","MFI"}; matrix vars_matrix = Matrix; //Independent variables only matrix_utils.RemoveCol(vars_matrix, 5); //remove target variable ArrayPrint(header); Print(vars_matrix.CorrCoef(false));
Ausgabe:
CS 0 13:21:15.481 Naive Bayes Test (EURUSD,H1) "Bears" "Bulls" "Rsi" "Volumes" "MFI" CS 0 13:21:15.481 Naive Bayes Test (EURUSD,H1) [[1,0.7784600081627714,0.8201955846987788,-0.2874457184671095,0.6211980865273238] CS 0 13:21:15.481 Naive Bayes Test (EURUSD,H1) [0.7784600081627714,1,0.8257210032763984,0.2650418244580489,0.6554288778228361] CS 0 13:21:15.481 Naive Bayes Test (EURUSD,H1) [0.8201955846987788,0.8257210032763984,1,-0.01205084357067248,0.7578863565293196] CS 0 13:21:15.481 Naive Bayes Test (EURUSD,H1) [-0.2874457184671095,0.2650418244580489,-0.01205084357067248,1,0.0531475992791923] CS 0 13:21:15.481 Naive Bayes Test (EURUSD,H1) [0.6211980865273238,0.6554288778228361,0.7578863565293196,0.0531475992791923,1]]
Sie werden feststellen, dass mit Ausnahme der Volumina Korrelation zum Rest, alle Variablen sind stark miteinander korreliert, einige zufällig zum Beispiel RSI gegen beide Bullen und Bären mit einer Korrelation von etwa 82%. Auch Volumen und MFI haben etwas gemeinsam, woraus sie bestehen, nämlich Volumen, sodass sie zu 62% korreliert sind. Da Gaussian Naïve Bayes sich nicht um all diese Dinge kümmert, sollten wir weitermachen, aber ich hielt es für eine gute Idee, die Variablen zu überprüfen und zu analysieren.
Training des Modells
Das Training des Gaussian Naïve Bayes ist einfach und dauert nur sehr kurz. Sehen wir uns zunächst an, wie man es richtig macht:
Print("\n---> Training the Model\n"); matrix x_train, x_test; vector y_train, y_test; matrix_utils.TrainTestSplitMatrices(Matrix,x_train,y_train,x_test,y_test,0.7,rand_state); //--- Train gaussian_naive = new CGaussianNaiveBayes(x_train,y_train); //Initializing and Training the model vector train_pred = gaussian_naive.GaussianNaiveBayes(x_train); //making predictions on trained data vector c= gaussian_naive.classes; //Classes in a dataset that was detected by mode metrics.confusion_matrix(y_train,train_pred,c); //analyzing the predictions in confusion matrix //---
Die Funktion TrainTestSplitMatrices teilt die Daten in x Trainings- und x Testmatrizen und ihre jeweiligen Zielvektoren auf. Genau wie train_test_split in sklearn python. Die Funktion geht im Kern folgendermaßen:
void CMatrixutils::TrainTestSplitMatrices(matrix &matrix_,matrix &x_train,vector &y_train,matrix &x_test, vector &y_test,double train_size=0.7,int random_state=-1)
Standardmäßig werden 70 Prozent der Daten als Trainingsdaten und der Rest als Testdaten verwendet. Lesen Sie mehr über diese Aufteilung.
Was Viele wohl in dieser Funktion verwirrend finden, ist die Variable random_state. Menschen der Python ML-Community entscheiden sich oft für random_state = 42, obwohl jede Zahl gewählt werden könnte. Sie soll nur sicherstellen, dass bei jeder Generierung der randomisierten / gemischt Matrix jedes Mal die gleiche erstellt wird, damit so das Debuggen einfacher ist, da so Random-Seed für die Generierung von Zufallszahlen für das Mischen der Zeilen in einer Matrix setzt festlegt.
Sie werden bemerken, dass die von dieser Funktion erhaltenen Ausgabematrizen nicht in der Standardreihenfolge sind, die sie hatten. Es gibt mehrere Diskussionen über die Wahl dieser 42 Nummer.
Nachfolgend sehen Sie die Ausgabe dieses Codeblocks:
CS 0 14:33:04.001 Naive Bayes Test (EURUSD,H1) ---> Training the Model CS 0 14:33:04.001 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.002 Naive Bayes Test (EURUSD,H1) ---> GROUPS [0,1] CS 0 14:33:04.002 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.002 Naive Bayes Test (EURUSD,H1) ---> Prior_proba [0.5457142857142857,0.4542857142857143] Evidence [382,318] CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) Confusion Matrix CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) [[236,146] CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) [145,173]] CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) Classification Report CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) _ Precision Recall Specificity F1 score Support CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) 0.0 0.62 0.62 0.54 0.62 382.0 CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) 1.0 0.54 0.54 0.62 0.54 318.0 CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) Accuracy 0.58 CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) Average 0.58 0.58 0.58 0.58 700.0 CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) W Avg 0.58 0.58 0.58 0.58 700.0 CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1)
Das trainierte Modell ist laut dem Klassifizierungsbericht der Konfusionsmatrix zu 58% genau. Aus diesem Bericht lässt sich vieles ablesen, z. B. die Genauigkeit, die angibt, wie genau jede Klasse klassifiziert wurde (mehr darüber hier). Grundsätzlich schien die Klasse 0 besser klassifiziert zu werden als die Klasse 1, was sinnvoll ist, weil das Modell sie besser vorhergesagt hat als die andere Klasse 1, ganz zu schweigen von der Prioritätswahrscheinlichkeit, die die Primärwahrscheinlichkeit oder die Wahrscheinlichkeit auf den ersten Blick im Daten ist. In diesen Daten sind die vorherigen Wahrscheinlichkeiten:
Prior_proba [0.5457142857142857,0.4542857142857143] Evidence [382,318]. Diese Vorabwahrscheinlichkeit wird wie folgt berechnet:
Prior Proba = Evidence/ Gesamtzahl der Ereignisse/Ergebnisse
In diesem Fall Prior Proba [382/700, 318/700]. Erinnern Sie sich: 700 ist die Größe der Trainingsdaten, den wir haben, nachdem wir 70% der 1000 Daten als Trainingsdaten verwenden.
Das Gaußsche Naïve-Bayes-Modell betrachtet zunächst die Wahrscheinlichkeiten des Auftretens von Klassen in den Daten und verwendet diese dann, um zu erraten, was in der Zukunft passieren könnte, was auf der Grundlage von Evidenz berechnet wird. Die Klasse mit der höheren Evidenz, die zu einer höheren Wahrscheinlichkeit führt als die andere, wird vom Algorithmus beim Trainieren und Testen bevorzugt. Das macht doch Sinn, oder? Dies ist einer der Nachteile dieses Algorithmus, denn wenn eine Klasse in den Trainingsdaten nicht vorkommt, geht das Modell davon aus, dass diese Klasse nicht existiert, sodass es ihr eine Wahrscheinlichkeit von Null gibt, was bedeutet, dass sie in den Testdaten oder irgendwann in der Zukunft nicht vorhergesagt werden wird.
Prüfung des Modells
Auch das Testen des Modells ist einfach. Sie müssen lediglich die neuen Daten in die Funktion GaussianNaiveBayes einfügen, die zu diesem Zeitpunkt bereits über die Parameter des trainierten Modells verfügt.
//--- Test Print("\n---> Testing the model\n"); vector test_pred = gaussian_naive.GaussianNaiveBayes(x_test); //giving the model test data to predict and obtain predictions to a vector metrics.confusion_matrix(y_test,test_pred, c); //analyzing the tested model
Ausgaben:
CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) ---> Testing the model CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) Confusion Matrix CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) [[96,54] CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) [65,85]] CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) Classification Report CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) _ Precision Recall Specificity F1 score Support CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) 0.0 0.60 0.64 0.57 0.62 150.0 CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) 1.0 0.61 0.57 0.64 0.59 150.0 CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) Accuracy 0.60 CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) Average 0.60 0.60 0.60 0.60 300.0 CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) W Avg 0.60 0.60 0.60 0.60 300.0
Großartig, also hat das Modell mit den Testdaten etwas besser abgeschnitten, mit einer Genauigkeit von 60%, 2% mehr als mit den Trainingsdaten, das sind gute Nachrichten.
Das Gaußsche Naïve-Bayes-Modell im Strategy Tester
Die Verwendung von Modellen des maschinellen Lernens auf dem Strategietester erbringt oft keine guten Leistungen, nicht weil sie keine Vorhersagen machen könnten, sondern weil wir uns in der Regel das Gewinndiagramm auf dem Strategietester ansehen. Wenn ein maschinelles Lernmodell erahnen kann, wohin sich der Markt als Nächstes bewegt, bedeutet das nicht zwangsläufig, dass man damit Geld verdienen kann, vor allem nicht mit der einfachen Logik, die ich bei der Sammlung und Aufbereitung unserer Daten verwendet habe. Die Datensätze wurden auf jedem Balken mit TF, gemäß der Eingabe gleich PERIOD_H1 (eine Stunde) gesammelt.
close.CopyRates(Symbol(),TF, COPY_RATES_CLOSE,0,TrainBars); open.CopyRates(Symbol(),TF, COPY_RATES_OPEN,0,TrainBars);
Ich habe 1000 Balken des einstündigen Zeitrahmen gesammelt und ihre Indikatorwerte als unabhängige Variablen gelesen. Ich habe dann die Zielvariablen erstellt, indem ich geschaut habe, ob es eine Aufwärtskerze war, dann setzt unser EA setzt die Klasse 1, ansonsten die Klasse 0. Als ich die Funktion für den Handel entwickelt habe, habe ich dies berücksichtigt. Da unser Modell die nächste Kerze vorhersagen wird, habe ich bei jeder neuen Kerze Positionen eröffnet und die vorherigen geschlossen. Im Grunde wird unser EA bei jedem Signal in jedem Balken handeln.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { if (!train_state) TrainTest(); train_state = true; //--- vector v_inputs(5); //5 independent variables double buff[1]; //current indicator value for (ulong i=0; i<5; i++) //Independent vars { CopyBuffer(handles[i],0,0,1, buff); v_inputs[i] = buff[0]; } //--- MqlTick ticks; SymbolInfoTick(Symbol(), ticks); int signal = -1; double min_volume = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN); if (isNewBar()) { signal = gaussian_naive.GaussianNaiveBayes(v_inputs); Comment("SIGNAL ",signal); CloseAll(); if (signal == 1) { if (!PosExist()) m_trade.Buy(min_volume, Symbol(), ticks.ask, 0 , 0,"Naive Buy"); } else if (signal == 0) { if (!PosExist()) m_trade.Sell(min_volume, Symbol(), ticks.bid, 0 , 0,"Naive Sell"); } } }
Damit diese Funktion sowohl im Live-Handel als auch im Strategietester funktioniert, musste ich die Logik ein wenig ändern. Das Abrufen der Indikatorwerte mit CopyBuffer() und das Training befinden sich jetzt innerhalb der Funktion TrainTest(). Diese Funktion wird einmal bei der Funktion OnTick ausgeführt. Sie können sie öfter ausführen lassen, um das Modell sehr oft zu trainieren, aber das überlasse ich Ihnen zur Übung.
Da die Funktion Init nicht die geeignete Funktion für all diese Methoden CopyBuffer und CopyRates ist (sie geben beim Strategy Tester Nullwerte zurück, wenn sie auf diese Weise verwendet werden), wird nun alles in die Funktion TrainTest() verschoben .
int OnInit() { handles[0] = iBearsPower(Symbol(),TF, bears_period); handles[1] = iBullsPower(Symbol(),TF, bulls_period); handles[2] = iRSI(Symbol(),TF,rsi_period, rsi_price); handles[3] = iVolumes(Symbol(),TF,VOLUME_TICK); handles[4] = iMFI(Symbol(),TF,mfi_period,VOLUME_TICK ); //--- m_trade.SetExpertMagicNumber(MAGIC_NUMBER); m_trade.SetTypeFillingBySymbol(Symbol()); m_trade.SetMarginMode(); m_trade.SetDeviationInPoints(slippage); return(INIT_SUCCEEDED); }
Einzeltest: Zeitrahmen 1 Stunde
Ich habe einen Test über zwei Monate vom 1. Januar 2023 bis zum 14. Februar 2023 (gestern) durchgeführt:
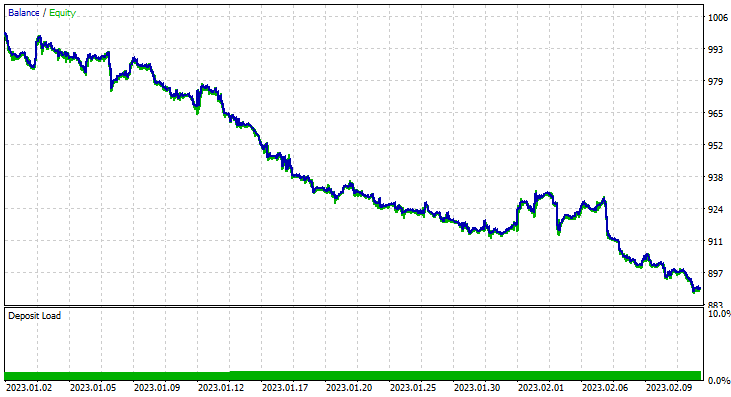
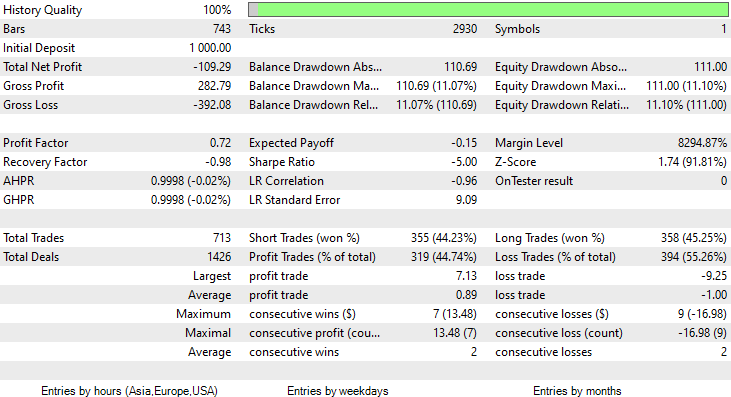
Ich habe mich für einen Test über einen so kurzen Zeitraum (2 Monate) entschieden, weil 1000 einstündige Takte keine so lange Trainingszeit sind, fast 41 Tage, damit die Trainingszeit kurz ist und die Tests auch. Da die Funktion TrainTest() wurde auch auf dem Tester ausgeführt. Die Kerzen, mit denen das Modell trainiert wurde, sind 700 Balken.
Was ist schief gelaufen?
Das Modell hinterließ beim Strategietester einen ersten Eindruck, indem es eine beeindruckende Genauigkeit von 60% bei den Trainingsdaten erzielte.
CS 0 08:30:13.816 Tester initial deposit 1000.00 USD, leverage 1:100 CS 0 08:30:13.818 Tester successfully initialized CS 0 08:30:13.818 Network 80 Kb of total initialization data received CS 0 08:30:13.819 Tester Intel Core i5 660 @ 3.33GHz, 6007 MB CS 0 08:30:13.900 Symbols EURUSD: symbol to be synchronized CS 0 08:30:13.901 Symbols EURUSD: symbol synchronized, 3720 bytes of symbol info received CS 0 08:30:13.901 History EURUSD: history synchronization started .... .... .... CS 0 08:30:14.086 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 ---> Training the Model CS 0 08:30:14.086 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 CS 0 08:30:14.086 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 ---> GROUPS [0,1] CS 0 08:30:14.086 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 CS 0 08:30:14.086 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 ---> Prior_proba [0.4728571428571429,0.5271428571428571] Evidence [331,369] CS 0 08:30:14.377 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 Confusion Matrix CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 [[200,131] CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 [150,219]] CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 Classification Report CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 _ Precision Recall Specificity F1 score Support CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 0.0 0.57 0.60 0.59 0.59 331.0 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 1.0 0.63 0.59 0.60 0.61 369.0 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 Accuracy 0.60 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 Average 0.60 0.60 0.60 0.60 700.0 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 W Avg 0.60 0.60 0.60 0.60 700.0
Allerdings konnte er keine profitablen Geschäfte mit der versprochenen Genauigkeit oder auch nur annähernd so genau abschließen. Im Folgenden finden Sie meine Beobachtungen:
- Die Logik ist irgendwie blind, sie tauscht Quantität gegen Qualität. 713 Abschlüsse im Laufe von zwei Monaten. Kommen Sie, das ist eine ganze Menge an Geschäften. Dies muss in sein Gegenteil umgewandelt werden. Wir müssen dieses Modell auf einem höheren Zeitrahmen trainieren und auf höheren Zeitrahmen handeln, was zu wenigen Qualitätspositionen führt.
- Die Trainingsbalken müssen für diesen Test reduziert werden, ich möchte das Modell mit aktuellen Daten trainieren.
Um diese zu erreichen, führte ich die Optimierung mit dem Zeitrahmen 6H durch, und kam zu Train Bars = 80, TF = 12 Stunden, um so einen Test laufen zu lassen (2 Monate mit den neuen Parametern). Sehen Sie sich alle Parameter in der *set-Datei an, die am Ende dieses Artikels verlinkt ist.
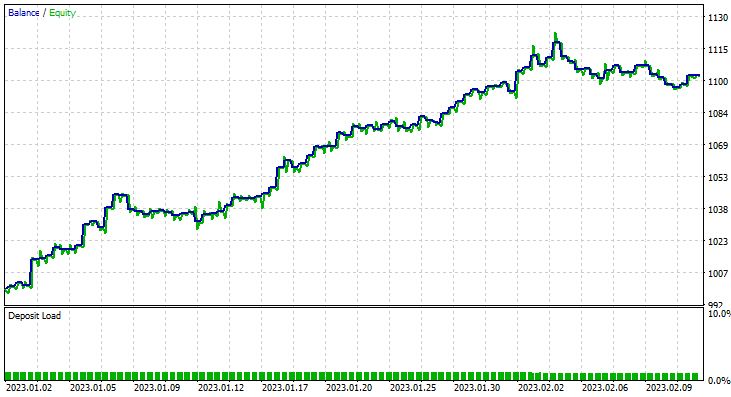
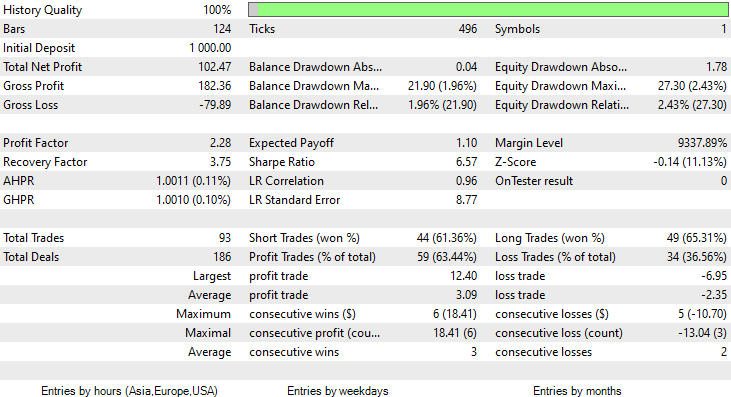
Diesmal lag die Trainingsgenauigkeit des Gaußsche Naïve-Bayes-Modells bei 58%.
93 Positionen im Laufe von 2 Monaten, das nenne ich eine gesunde Handelsaktivität, im Durchschnitt sind es 2,3 pro Tag. Dieses Mal hat der Gaussian Naïve Bayes EA 63% der Trades profitabel gemacht, ganz zu schweigen von einem Gewinn von etwa 10%.
Nachdem Sie nun gesehen haben, wie Sie das Gaussian-Naïve-Bayes-Modell nutzen können, um fundierte Handelsentscheidungen zu treffen, wollen wir uns ansehen, wie es funktioniert.
Naïve Bayes-Theorie
Nicht zu verwechseln mit dem Gaußschen Naïve Bayes.
Der Algorithmus heißt
- Naiv, weil er davon ausgeht, dass die Variablen/Merkmale unabhängig sind, was selten der Fall ist
-
Bayes, weil er auf dem Satz von Bayes beruht.
Die Formel für das Bayes-Theorem ist unten angegeben:
![]()
Wobei:
P(A|B) = die (bedingte) Wahrscheinlichkeit des Ereignisses A unter der Bedingung, dass B eingetreten ist,
P(B|A) = die (bedingte) Wahrscheinlichkeit des Ereignisses B unter der Bedingung, dass A eingetreten ist, In einfachen Worten: Wahrscheinlichkeit von B, wenn A wahr ist
P(A) = die A-priori-Wahrscheinlichkeit des Ereignisses A der Hypothese vor der Beobachtung einer Evidenz
P(B) = die A-priori-Wahrscheinlichkeit des Ereignisses B der Hypothese vor der Beobachtung einer Evidenz
Diese Begriffe in der Formel mögen auf den ersten Blick verwirrend erscheinen. Sie werden in der Praxis deutlich werden, also bleiben Sie bei mir.
Arbeiten mit dem Klassifikator
Werfen wir einen Blick auf ein einfaches Beispiel: Wetterdaten. Konzentrieren wir uns auf die erste Spalte Vorhersage. Sobald das verstanden ist, ist das Hinzufügen anderer Spalten als unabhängige Variablen genau derselbe Prozess.
| Vorhersage | Tennis spielen |
|---|---|
| Sonnig | No |
| Sonnig | No |
| Bedeckt | Ja |
| Regen | Ja |
| Regen | Ja |
| Regen | No |
| Bedeckt | Ja |
| Sonnig | No |
| Sonnig | Ja |
| Regen | Ja |
| Sonnig | Ja |
| Bedeckt | Ja |
| Bedeckt | Ja |
| Regen | No |
Nun wollen wir das Gleiche in MetaEditor tun:
void OnStart() { //--- matrix Matrix = matrix_utils.ReadCsvEncode("weather dataset.csv"); int cols[3] = {1,2,3}; matrix_utils.RemoveMultCols(Matrix, cols); //removing Temperature Humidity and Wind ArrayRemove(matrix_utils.csv_header,1,3); //removing column headers ArrayPrint(matrix_utils.csv_header); Print(Matrix); matrix x_matrix; vector y_vector; matrix_utils.XandYSplitMatrices(Matrix, x_matrix, y_vector); }
Beachten Sie, dass Naïve Bayes nur für diskrete/nicht-kontinuierliche Variablen geeignet ist. Nicht zu verwechseln mit dem Gaußschen Naïve Bayes-Modell, das wir oben in Aktion gesehen haben und das mit kontinuierlichen Variablen umgehen kann, ist der Fall bei diesem Naïve Bayes-Modell anders. Nachfolgend sehen Sie die Ausgabe des obigen Vorgangs
CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) "Outlook" "Play" CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [[0,0] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [0,0] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [1,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [2,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [2,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [2,0] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [1,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [0,0] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [0,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [2,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [0,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [1,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [1,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [2,0]]
Lassen Sie uns also die vorherige Wahrscheinlichkeit in unserem Naïve Bayes-Klassenkonstruktor ermitteln:
CNaiveBayes::CNaiveBayes(matrix &x_matrix, vector &y_vector) { XMatrix.Copy(x_matrix); YVector.Copy(y_vector); classes = matrix_utils.Classes(YVector); c_evidence.Resize((ulong)classes.Size()); n = YVector.Size(); if (n==0) { Print("--> n == 0 | Naive Bayes class failed"); return; } //--- vector v = {}; for (ulong i=0; i<c_evidence.Size(); i++) { v = matrix_utils.Search(YVector,(int)classes[i]); c_evidence[i] = (int)v.Size(); } //--- c_prior_proba.Resize(classes.Size()); for (ulong i=0; i<classes.Size(); i++) c_prior_proba[i] = c_evidence[i]/(double)n; #ifdef DEBUG_MODE Print("---> GROUPS ",classes); Print("Prior Class Proba ",c_prior_proba,"\nEvidence ",c_evidence); #endif }
Ausgaben:
CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) ---> GROUPS [0,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) Prior Class Proba [0.3571428571428572,0.6428571428571429] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) Evidence [5,9]
Die vorherige Wahrscheinlichkeit von [Nein, Ja] ist ungefähr [0,36, 0,64].
Angenommen, Sie wollen wissen, wie hoch die Wahrscheinlichkeit ist, dass eine Person an einem sonnigen Tag Tennis spielt, dann werden Sie Folgendes tun;
P(Ja | Sonnig) = P(Sonnig | Ja) * P(Ja) / P(Sonnig)
Mehr Details in einfacher Sprache:
Die Wahrscheinlichkeit, dass jemand an einem sonnigen Tag Tennis spielt = wie oft (als Wahrscheinlichkeitswert) war es sonnig und irgendein Idiot hat Tennis gespielt * wie oft (als Wahrscheinlichkeitswert) haben Menschen Tennis gespielt / wie oft (als Wahrscheinlichkeitswert) gab es einen sonniger Tag im Allgemeinen.
P(Sonnig | Ja) = 2/9
P(Ja) = 0,64
P(Sonnig ) = 5/14 = 0,357
also schließlich das P(Ja | Sonnig) = 0,333 x 0,64 / 0,357 = 0,4
Wie sieht es mit der Wahrscheinlichkeit von (Nein| Sonnig) aus: Wir können es berechnen, indem wir 1 - Wahrscheinlichkeit für Ja = 1 - 0,5972 = 0,4027 nehmen als Abkürzung, aber schauen wir uns das an:
P(Nein|Sonnig) = (3/5) x 0,36 / (0,357) = 0,6
Nachstehend finden Sie den entsprechenden Code:
vector CNaiveBayes::calcProba(vector &v_features) { vector proba_v(classes.Size()); //vector to return if (v_features.Size() != XMatrix.Cols()) { printf("FATAL | Can't calculate probability, features columns size = %d is not equal to XMatrix columns =%d",v_features.Size(),XMatrix.Cols()); return proba_v; } //--- vector v = {}; for (ulong c=0; c<classes.Size(); c++) { double proba = 1; for (ulong i=0; i<XMatrix.Cols(); i++) { v = XMatrix.Col(i); int count =0; for (ulong j=0; j<v.Size(); j++) { if (v_features[i] == v[j] && classes[c] == YVector[j]) count++; } proba *= count==0 ? 1 : count/(double)c_evidence[c]; //do not calculate if there isn't enough evidence' } proba_v[c] = proba*c_prior_proba[c]; } return proba_v; }
Der von dieser Funktion bereitgestellte Wahrscheinlichkeitsvektor für Sonnig ist:
2023.02.15 16:34:21.519 Naive Bayes theory script (EURUSD,H1) Probabilities [0.6,0.4]
Genau das, was wir erwartet haben, aber machen wir keinen Fehler, diese Funktion gibt uns keine Wahrscheinlichkeiten. Lassen Sie mich erklären. Wenn es nur zwei Klassen in dem Daten gibt, den wir in diesem Szenario vorherzusagen versuchen, ist das Ergebnis eine Wahrscheinlichkeit, aber ansonsten müssen die Ausgaben dieser Funktion in Wahrscheinlichkeitsbedingungen validiert werden. Das zu erreichen, ist einfach:
Nehmen wir die Summe des Vektors, der aus dieser Funktion hervorgegangen ist, und dividieren dann jedes Element durch die Gesamtsumme. Der verbleibende Vektor wird die realen Wahrscheinlichkeitswerte sein, die, wenn sie addiert werden, gleich eins sind.
probability_v = v[i]/probability_v.Sum()
Dieser kleine Prozess wird innerhalb der Funktion NaiveBayes() durchgeführt, die die Ergebnisklasse oder die Klasse mit der höchsten Wahrscheinlichkeit von allen vorhersagt:
int CNaiveBayes::NaiveBayes(vector &x_vector) { vector v = calcProba(x_vector); double sum = v.Sum(); for (ulong i=0; i<v.Size(); i++) //converting the values into probabilities v[i] = NormalizeDouble(v[i]/sum,2); vector p = v; #ifdef DEBUG_MODE Print("Probabilities ",p); #endif return((int)classes[p.ArgMax()]); }
Nun, das war's. Der Naïve Bayes ist ein einfacher Algorithmus. Nun wollen wir uns dem Gaußschen Naïve Bayes zuwenden, den wir zu Beginn dieses Artikels verwendet haben.
Gaußscher Naïve Bayes
Der Gaußsche Naïve Bayes geht davon aus, dass die Merkmale einer Normalverteilung folgen, d. h. wenn die Prädiktoren kontinuierliche statt diskrete Variablen annehmen, wird davon ausgegangen, dass diese Werte aus der Gaußschen Verteilung gezogen werden.
Eine kurze Wiederholung zur Normalverteilung
Die Normalverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die um ihren Mittelwert symmetrisch ist, wobei sich die meisten Beobachtungen um die zentrale Spitze gruppieren und die Wahrscheinlichkeiten für Werte, die weiter vom Mittelwert entfernt sind, in beide Richtungen gleichmäßig abnehmen. Extremwerte in beiden Enden der Verteilung sind ebenfalls unwahrscheinlich.
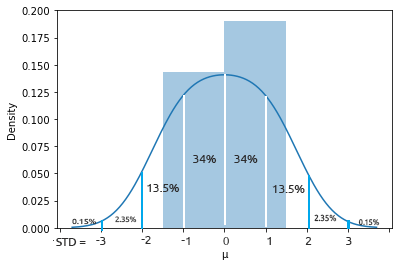
Diese glockenförmige Wahrscheinlichkeitskurve ist so aussagekräftig, dass sie zu den nützlichen statistischen Analyseinstrumenten gehört. Sie zeigt, dass die Wahrscheinlichkeit, etwas zu finden, das eine Standardabweichung vom Mittelwert abweicht, ungefähr 34% beträgt, und 34%, etwas auf der anderen Seite der Glockenkurve zu finden. Das bedeutet, dass die Wahrscheinlichkeit, einen Wert zu finden, der auf beiden Seiten zusammen einen Standard vom Mittelwert entfernt ist, etwa 68% beträgt. Diejenigen, die den Mathematikunterricht geschwänzt haben, sollten hier weiterlesen.
Aus dieser Normalverteilung/Gaußschen Verteilung wollen wir die Wahrscheinlichkeitsdichte ermitteln. Sie wird nach der folgenden Formel berechnet.
![]()
Wobei:
μ = Mittelwert
𝜎 = Standardabweichung
x = Eingabewert
Ok, da der Gaußsche Naïve Bayes davon abhängt, wollen wir ihn codieren.
class CNormDistribution { public: double m_mean; //Assign the value of the mean double m_std; //Assign the value of Variance CNormDistribution(void); ~CNormDistribution(void); double PDF(double x); //Probability density function }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ CNormDistribution::CNormDistribution(void) { } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ CNormDistribution::~CNormDistribution(void) { ZeroMemory(m_mean); ZeroMemory(m_std); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CNormDistribution::PDF(double x) { double nurm = MathPow((x - m_mean),2)/(2*MathPow(m_std,2)); nurm = exp(-nurm); double denorm = 1.0/(MathSqrt(2*M_PI*MathPow(m_std,2))); return(nurm*denorm); }
Erstellen des Gauß-Naïve-Bayes-Modells
Der Klassenkonstruktor von Gaussian Naïve Bayes sieht ähnlich aus wie der von Naïve Bayes. Der Konstruktorcode muss hier nicht gezeigt und erklärt werden. Im Folgenden finden Sie unsere Hauptfunktion, die für die Berechnung der Wahrscheinlichkeit zuständig ist.
vector CGaussianNaiveBayes::calcProba(vector &v_features) { vector proba_v(classes.Size()); //vector to return if (v_features.Size() != XMatrix.Cols()) { printf("FATAL | Can't calculate probability, features columns size = %d is not equal to XMatrix columns =%d",v_features.Size(),XMatrix.Cols()); return proba_v; } //--- vector v = {}; for (ulong c=0; c<classes.Size(); c++) { double proba = 1; for (ulong i=0; i<XMatrix.Cols(); i++) { v = XMatrix.Col(i); int count =0; vector calc_v = {}; for (ulong j=0; j<v.Size(); j++) { if (classes[c] == YVector[j]) { count++; calc_v.Resize(count); calc_v[count-1] = v[j]; } } norm_distribution.m_mean = calc_v.Mean(); //Assign these to Gaussian Normal distribution norm_distribution.m_std = calc_v.Std(); #ifdef DEBUG_MODE printf("mean %.5f std %.5f ",norm_distribution.m_mean,norm_distribution.m_std); #endif proba *= count==0 ? 1 : norm_distribution.PDF(v_features[i]); //do not calculate if there isn't enought evidence' } proba_v[c] = proba*c_prior_proba[c]; //Turning the probability density into probability #ifdef DEBUG_MODE Print(">> Proba ",proba," prior proba ",c_prior_proba); #endif } return proba_v; }
Sehen wir uns an, wie sich dieses Modell in der Praxis bewährt.
Verwendung des Genderdaten.
| Höhe(ft) | Gewicht (lbs) | Schuhgröße (Zoll) | Person(0 männlich, 1 weiblich) |
|---|---|---|---|
| 6 | 180 | 12 | 0 |
| 5.92 | 190 | 11 | 0 |
| 5.58 | 170 | 12 | 0 |
| 5.92 | 165 | 10 | 0 |
| 5 | 100 | 6 | 1 |
| 5.5 | 150 | 8 | 1 |
| 5.42 | 130 | 7 | 1 |
| 5.75 | 150 | 9 | 1 |
//--- Gaussian naive bayes Matrix = matrix_utils.ReadCsv("gender dataset.csv"); ArrayPrint(matrix_utils.csv_header); Print(Matrix); matrix_utils.XandYSplitMatrices(Matrix, x_matrix, y_vector); gaussian_naive = new CGaussianNaiveBayes(x_matrix, y_vector);
Ausgabe:
CS 0 18:52:18.653 Naive Bayes theory script (EURUSD,H1) ---> GROUPS [0,1] CS 0 18:52:18.653 Naive Bayes theory script (EURUSD,H1) CS 0 18:52:18.653 Naive Bayes theory script (EURUSD,H1) ---> Prior_proba [0.5,0.5] Evidence [4,4]
Da 4 von 8 Personen männlich und die restlichen 4 weiblich waren, besteht eine 50:50-Chance, dass das Modell in erster Linie einen Mann oder eine Frau vorhersagt.
Versuchen wir das Modell mit diesen neuen Daten einer Person mit einer Größe von 5,3, einem Gewicht von 140 und einer Fußgröße von 7,5. Wir beide wissen, dass diese Person höchstwahrscheinlich eine Frau ist.
vector person = {5.3, 140, 7.5}; Print("The Person is a ",gaussian_naive.GaussianNaiveBayes(person));
Ausgabe:
2023.02.15 19:14:40.424 Naive Bayes theory script (EURUSD,H1) The Person is a 1
Gut, es wurde richtig vorhergesagt, dass es sich um eine weibliche Person handelt.
Das Testen des Gaußschen Naïven Bayes-Modells ist relativ einfach. Übergeben wir einfach die Matrix, mit der es trainiert wurde, und messen die Genauigkeit der Vorhersagen anhand der Konfusionsmatrix.
CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) Confusion Matrix CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) [[4,0] CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) [0,4]] CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) Classification Report CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) _ Precision Recall Specificity F1 score Support CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) 0.0 1.00 1.00 1.00 1.00 4.0 CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) 1.0 1.00 1.00 1.00 1.00 4.0 CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) Accuracy 1.00 CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) Average 1.00 1.00 1.00 1.00 8.0 CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) W Avg 1.00 1.00 1.00 1.00 8.0
Ja, die Trainingsgenauigkeit beträgt 100%, unser Modell kann erkennen, ob eine Person männlich oder weiblich ist, wenn alle Daten als Trainingsdaten verwendet wurden.
Vorteile von Naïve & Gaussian Bayes Klassifikatoren
- Sie sind einer der einfachsten und schnellsten Algorithmen für maschinelles Lernen, die zur Klassifizierung von Datensätzen verwendet werden.
- Sie können sowohl für die binäre als auch für die Mehrklassen-Klassifizierung verwendet werden.
- So einfach sie auch sind, sie leisten oft gute Arbeit bei der Klassifizierung mehrerer Klassen, die die meisten Algorithmen
- Es ist die beliebteste Wahl für Textklassifizierungsprobleme
Nachteile dieser Klassifikatoren.
Naïve Bayes ist zwar ein einfacher und effektiver Algorithmus für maschinelles Lernen zur Klassifizierung, hat aber einige Einschränkungen und Nachteile, die berücksichtigt werden sollten.
Naïve Bayes.
- Vermutung der Unabhängigkeit: Naïve Bayes geht davon aus, dass alle Merkmale unabhängig voneinander sind, was in der Praxis nicht immer der Fall ist. Diese Annahme kann zu einer Verschlechterung der Klassifizierungsgenauigkeit führen, wenn die Merkmale stark voneinander abhängig sind.
- Zu wenig Daten: Naïve Bayes beruht auf dem Vorhandensein einer ausreichenden Anzahl von Trainingsbeispielen für jede Klasse, um die Klassenprioritäten und bedingten Wahrscheinlichkeiten genau zu schätzen. Wenn der Datensatz zu klein ist, können die Schätzungen ungenau sein und zu einer schlechten Klassifizierungsleistung führen.
- Empfindlichkeit gegenüber irrelevanten Merkmalen: Naïve Bayes behandelt alle Merkmale gleich, unabhängig von ihrer Relevanz für die Klassifizierungsaufgabe. Dies kann zu einer schlechten Klassifizierungsleistung führen, wenn irrelevante Merkmale in den Datensatz aufgenommen werden. Es ist eine unbestreitbare Tatsache, dass einige Merkmale in einem Datensatz wichtiger sind als andere.
- Unfähigkeit, mit kontinuierlichen Variablen umzugehen: Naïve Bayes geht davon aus, dass alle Merkmale diskret oder kategorisiert sind, und kann kontinuierliche Variablen nicht direkt verarbeiten. Um Naïve Bayes mit kontinuierlichen Variablen zu verwenden, müssen die Daten diskretisiert werden, was zu Informationsverlusten und einer geringeren Klassifizierungsgenauigkeit führen kann.
- Begrenzte Ausdruckskraft: Naïve Bayes kann nur lineare Entscheidungsgrenzen modellieren, was für komplexere Klassifizierungsaufgaben möglicherweise nicht ausreicht. Dies kann zu einer schlechten Leistung führen, wenn die Entscheidungsgrenze nicht linear ist.
- Ungleichgewicht der Klassen: Naïve Bayes kann schlecht funktionieren, wenn die Verteilung der Beispiele über die Klassen sehr unausgewogen ist, da es zu verzerrten Klassenprioritäten und einer schlechten Schätzung der bedingten Wahrscheinlichkeiten für die Minderheitsklasse führen kann. Wenn die Evidenz nicht ausreicht, wird die Klasse nicht vorhergesagt - Punkt.
Gaußsche Naïve Bayes.
Die Gaußsche Naïve Bayes-Methode teilt die oben genannten Nachteile aber noch zwei weitere:
- Empfindlich gegenüber Ausreißern: Der Gaußsche Naïve Bayes geht davon aus, dass die Merkmale normalverteilt sind, was bedeutet, dass Extremwerte oder Ausreißer einen erheblichen Einfluss auf die Schätzungen von Mittelwert und Varianz haben können. Dies kann zu einer schlechten Klassifizierungsleistung führen, wenn der Datensatz Ausreißer enthält.
- Nicht geeignet für Merkmale mit starken Rändern: Der Gaußsche Naïve Bayes geht davon aus, dass die Merkmale eine Normalverteilung mit endlicher Varianz haben. Wenn die Merkmale starke Rändern haben, wie z. B. eine Cauchy-Verteilung, kann der Algorithmus nicht gut funktionieren.
Schlussfolgerung
Damit ein Modell des maschinellen Lernens im Strategietester Ergebnisse liefert, muss man nicht nur das Modell trainieren, sondern auch die Leistung verbessern und gleichzeitig sicherstellen, dass man am Ende eine aufwärtsgerichtete Gewinnkurve erhält. Auch wenn Sie nicht unbedingt zum Strategietester gehen müssen, um ein maschinelles Lernmodell zu testen, weil einige Modelle zu rechenintensiv sind, um sie zu testen, werden Sie aus anderen Gründen wie der Optimierung Ihrer Handelsvolumina, Zeitrahmen usw. auf jeden Fall dorthin gehen müssen. Eine sorgfältige Analyse der Logik muss durchgeführt werden, bevor man sich entscheidet, mit einem beliebigen Modus in den Live-Handel einzusteigen.
Mit freundlichen Grüßen.
Verfolgen Sie die Entwicklung und Änderungen an diesem Algorithmus auf meinem GitHub Repo https://github.com/MegaJoctan/MALE5
| Datei | Inhalt & Verwendung |
|---|---|
| Naive Bayes.mqh | Enthält die Klassen der Naïve Bayes-Modelle |
| Naive Bayes theory script.mq5 | Ein Skript zum Testen der Bibliothek |
| Naive Bayes Test.mq5 | EA für den Handel mit den besprochenen Modellen |
| matrix_utils.mqh | Enthält zusätzliche Matrixfunktionen |
| metrics.mqh | Enthält die Funktionen zur Analyse der Leistung von ML-Modellen, wie die Konfusionsmatrix |
| naive bayes visualize.py | Python-Skript zum Zeichnen von Verteilungsdiagrammen für alle vom Modell verwendeten unabhängigen Variablen |
| gender datasets.csv & weather dataset.csv | In diesem Artikel als Beispiele verwendete Datensätze |
Haftungsausschluss: Dieser Artikel ist nur für Bildungszwecke, Handel ist ein riskantes Spiel hoffentlich wissen Sie, das Risiko mit ihm verbunden. Der Autor übernimmt keine Verantwortung für Verluste oder Schäden, die durch die Anwendung der in diesem Artikel beschriebenen Methoden verursacht werden können, denken Sie daran. Riskieren Sie das Geld, das Sie sich leisten können zu verlieren.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/12184
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.