Машинное обучение и Data Science (Часть 11): Наивный байесовский классификатор и теория вероятностей в трейдинге
Четвертый закон термодинамики: если вероятность успеха не близка к единице, она близка к нулю.
А. Кондрашов
Введение
Наивный байесовский классификатор — это вероятностный алгоритм, используемый в машинном обучении для задач классификации. Классификатор основан на теореме Байеса (или формуле Байеса), которая позволяет определить вероятность гипотезы при имеющихся доказательствах. Вероятностный классификатор — простой алгоритм, который тем не менее эффективен в различных ситуациях. Предполагается, что используемые для классификации признаки независимы друг от друга. Например, если вы хотите, чтобы модель классифицировала людей (мужчин и женщин) по росту, размеру стопы, весу и ширине плеч, модель будет рассматривать все эти переменные как независимые друг от друга. То есть, она даже не подумает, что размер ноги и человека рост взаимосвязаны.
Поскольку алгоритм не пытается понять закономерности между независимыми переменными, я думаю, стоит попытаться использовать его в работе для принятия торговых решений. Я считаю, что все равно в сфере трейдинга никто полностью не понимает закономерности, поэтому давайте посмотрим, как работает наивный байесовский алгоритм.

Без лишних слов давайте сразу же вызовем экземпляр модели и используем его. Позже мы обсудим, из чего состоит эта модель.
Подготовка обучающих данных
Для этого примера я выбрал 5 индикаторов, большинство из которых являются осцилляторами и индикаторами объемов. Думаю, они являются хорошими классификационными переменными, а также имеют конечное количество, что делает их подходящими для нормального распределения — а это, в свою очередь, является одной из идей, лежащих в основе этого алгоритма. Однако этот список не является эталонным, поэтому вы можете составить собственный набор и исследовать различные подходящие вам индикаторы и данные.
Пойдем по порядку:
matrix Matrix(TrainBars, 6); int handles[5]; double buffer[]; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Preparing Data handles[0] = iBearsPower(Symbol(),TF, bears_period); handles[1] = iBullsPower(Symbol(),TF, bulls_period); handles[2] = iRSI(Symbol(),TF,rsi_period, rsi_price); handles[3] = iVolumes(Symbol(),TF,VOLUME_TICK); handles[4] = iMFI(Symbol(),TF,mfi_period,VOLUME_TICK ); //--- vector col_v; for (ulong i=0; i<5; i++) //Независимые переменные { CopyBuffer(handles[i],0,0,TrainBars, buffer); col_v = matrix_utils.ArrayToVector(buffer); Matrix.Col(col_v, i); } //-- Целевые переменные vector open, close; col_v.Resize(TrainBars); close.CopyRates(Symbol(),TF, COPY_RATES_CLOSE,0,TrainBars); open.CopyRates(Symbol(),TF, COPY_RATES_OPEN,0,TrainBars); for (int i=0; i<TrainBars; i++) { if (close[i] > open[i]) //price went up col_v[i] = 1; else col_v[i] = 0; } Matrix.Col(col_v, 5); //Добавляем независимую переменную в последний столбец матрицы //---
Переменные TF, bears_period и прочие являются входными определенными переменными, они определены в верхней части кода выше.
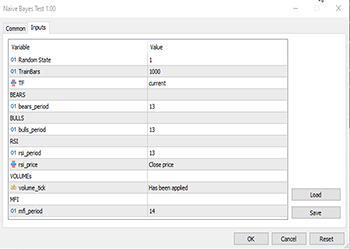
Поскольку мы имеем дело с обучением, пришлось ввести целевую переменную. Логика проста: если цена закрытия была выше цены открытия, целевой переменной присваивается класс 1, в противном случае класс равен 0. Так получаем значение целевой переменной. Ниже приведен обзор того, как выглядит матрица с набором данных:
CS 0 13:21:15.457 Naive Bayes Test (EURUSD,H1) "Bears" "Bulls" "Rsi" "Volumes" "MFI" "Target Var" CS 0 13:21:15.457 Naive Bayes Test (EURUSD,H1) [-3.753148029472797e-06,0.008786246851970603,67.65238281791684,13489,55.24611392389958,0] CS 0 13:21:15.457 Naive Bayes Test (EURUSD,H1) [-0.002513216984025402,0.005616783015974569,50.29835423473968,12226,49.47293811405203,1] CS 0 13:21:15.457 Naive Bayes Test (EURUSD,H1) [-0.001829900272021678,0.0009700997279782353,47.33479153312328,7192,46.84320886771249,1] CS 0 13:21:15.457 Naive Bayes Test (EURUSD,H1) [-0.004718485947447171,-0.0001584859474472733,39.04848493977027,6267,44.61564654651691,1] CS 0 13:21:15.457 Naive Bayes Test (EURUSD,H1) [-0.004517273669240485,-0.001367273669240276,45.4127802340401,3867,47.8438816641815,0]
Далее я решил визуализировать данные на графиках распределения, чтобы увидеть, соответствуют ли они распределению вероятностей:
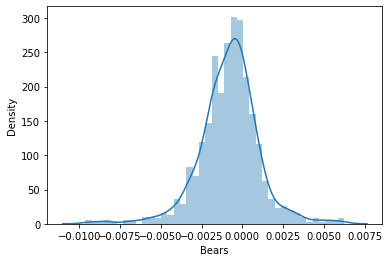
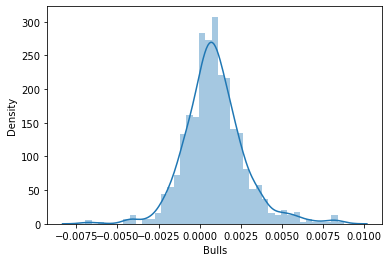
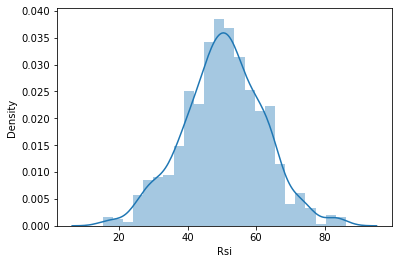
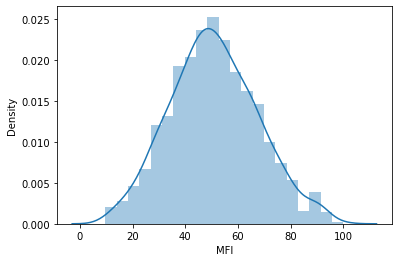
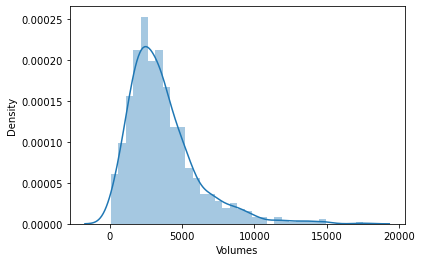
Если хотите узнать больше о различных видах распределения вероятностей, об этом написана целая статья по ссылке.
Посмотрим внимательнее на матрицу коэффициентов корреляции всех независимых переменных:
string header[5] = {"Bears","Bulls","Rsi","Volumes","MFI"}; matrix vars_matrix = Matrix; //Только независимые переменные matrix_utils.RemoveCol(vars_matrix, 5); //Удаляем целевую переменную ArrayPrint(header); Print(vars_matrix.CorrCoef(false));
Выводимая информация:
CS 0 13:21:15.481 Naive Bayes Test (EURUSD,H1) "Bears" "Bulls" "Rsi" "Volumes" "MFI" CS 0 13:21:15.481 Naive Bayes Test (EURUSD,H1) [[1,0.7784600081627714,0.8201955846987788,-0.2874457184671095,0.6211980865273238] CS 0 13:21:15.481 Naive Bayes Test (EURUSD,H1) [0.7784600081627714,1,0.8257210032763984,0.2650418244580489,0.6554288778228361] CS 0 13:21:15.481 Naive Bayes Test (EURUSD,H1) [0.8201955846987788,0.8257210032763984,1,-0.01205084357067248,0.7578863565293196] CS 0 13:21:15.481 Naive Bayes Test (EURUSD,H1) [-0.2874457184671095,0.2650418244580489,-0.01205084357067248,1,0.0531475992791923] CS 0 13:21:15.481 Naive Bayes Test (EURUSD,H1) [0.6211980865273238,0.6554288778228361,0.7578863565293196,0.0531475992791923,1]]
Можно заметить, что за исключением корреляции объемов с остальными, все переменные сильно коррелируют друг с другом. В некоторых случаях корреляция очень сильная, например, между RSI и Bulls и Bears корреляция составила около 82%. В основе индикаторов Объемов и MFI есть общие части — а именно, сами объемы, поэтому их корреляция в 62% совершенно объяснима. Поскольку гауссовский наивный байесовский метод не вдается в подробности таких причин, давайте двигаться дальше. Я просто подумал, что неплохо бы проверить и проанализировать переменные.
Обучение модели
Обучение для гауссовского наивного байесовского метода простое и быстрое. Давайте посмотрим, как проходит процесс:
Print("\n---> Training the Model\n"); matrix x_train, x_test; vector y_train, y_test; matrix_utils.TrainTestSplitMatrices(Matrix,x_train,y_train,x_test,y_test,0.7,rand_state); //--- Обучение gaussian_naive = new CGaussianNaiveBayes(x_train,y_train); //Инициализация и обучение модели vector train_pred = gaussian_naive.GaussianNaiveBayes(x_train); //делаем прогнозы на обученных данных vector c= gaussian_naive.classes; //определенные в наборе данных классы metrics.confusion_matrix(y_train,train_pred,c); //анализ предсказания в матрице путаницы //---
Функция TrainTestSplitMatrices разбивает данные на x обучающих и x тестовых матриц и соответствующие им целевые векторы. Аналогично функции train_test_split в sklearn python. Основная функция выглядит следующим образом:
void CMatrixutils::TrainTestSplitMatrices(matrix &matrix_,matrix &x_train,vector &y_train,matrix &x_test, vector &y_test,double train_size=0.7,int random_state=-1)
По умолчанию 70 процентов данных будут отнесены к обучающим данным, а остальные будут сохранены в качестве выборки для тестирования. Здесь можно почитать больше об этом разделении данных.
Что многих людей запутало в этой функции, так это параметр random_state. В коммьюнити Python ML люди часто устанавливают random_state = 42, хотя на самом деле подойдет любое число, поскольку этот параметр предназначен только для того, чтобы рандомизированная/перетасованная матрица каждый раз генерировалась одинаково, чтобы упростить отладку, поскольку для генерации случайных чисел для перетасовки строк в матрице используется Random seed.
Можно заметить, что выходные матрицы, полученные из этой функции, расположены не в том порядке, в котором они были по умолчанию. О выборе этого числа 42 можете почитать различные обсуждения, например здесь.
Вот что мы имеем на выходе из этого блока кода:
CS 0 14:33:04.001 Naive Bayes Test (EURUSD,H1) ---> Training the Model CS 0 14:33:04.001 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.002 Naive Bayes Test (EURUSD,H1) ---> GROUPS [0,1] CS 0 14:33:04.002 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.002 Naive Bayes Test (EURUSD,H1) ---> Prior_proba [0.5457142857142857,0.4542857142857143] Evidence [382,318] CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) Confusion Matrix CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) [[236,146] CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) [145,173]] CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) Classification Report CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) _ Precision Recall Specificity F1 score Support CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) 0.0 0.62 0.62 0.54 0.62 382.0 CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) 1.0 0.54 0.54 0.62 0.54 318.0 CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) Accuracy 0.58 CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) Average 0.58 0.58 0.58 0.58 700.0 CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) W Avg 0.58 0.58 0.58 0.58 700.0 CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1)
Согласно отчету о классификации матрицы путаницы, точность обученной модели составила 58%. Из этого отчета можно многое понять, например, точность, которая говорит, насколько точно каждый класс был классифицирован (подробности). В целом кажется, класс 0 классифицируется лучше, чем класс 1. Вообще это понятно, поскольку модель предсказала его больше, чем второй класс1, не говоря уже об априорной вероятности (основная первичная вероятность в выборке данных). В этом наборе данных имеем такие априорные вероятности:
Prior_proba [0.5457142857142857,0.4542857142857143] Evidence [382,318]. Априорная вероятность рассчитывается как:
Априорная вероятность = доказательство/общее количество событий/результатов
В нашем случае Prior Proba [382/700, 318/700]. Напомню, 700 — это размер обучающей выборки, получившейся в результате разбиения данных для выделения 70% под обучение из 1000 общей выборки.
Наивная гауссовская байесовская модель сначала ищет вероятности появления классов в наборе данных, а затем использует их, чтобы угадать, что может произойти в будущем на основе расчета по доказательствам (evidence). Класс с более высокими доказательствами будет иметь более высокую вероятность, чем другой класс, и поэтому будет предпочтительнее для алгоритма при обучении и тестировании. Вполне логично, не так ли? Это один из недостатков этого алгоритма, потому что, когда класс отсутствует в обучающих данных, модель предполагает, что этого класса не существует, поэтому она дает ему нулевую вероятность, а это означает, что для этого класса не будет предсказаний в тестовой выборке или когда-либо в будущем.
Тестирование модели
В тестировании модели также нет ничего сложного. Все, что нужно сделать, это добавить новые данные в функцию GaussianNaiveBayes, которая к этому моменту уже имеет параметры обученной модели.
//--- Test Print("\n---> Testing the model\n"); vector test_pred = gaussian_naive.GaussianNaiveBayes(x_test); //подаем на вход модели тестовые данные для прогнозирования и получения предсказаний в вектор metrics.confusion_matrix(y_test,test_pred, c); //анализ тестируемой модели
Результат
CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) ---> Testing the model CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) Confusion Matrix CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) [[96,54] CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) [65,85]] CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) Classification Report CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) _ Precision Recall Specificity F1 score Support CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) 0.0 0.60 0.64 0.57 0.62 150.0 CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) 1.0 0.61 0.57 0.64 0.59 150.0 CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) Accuracy 0.60 CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) Average 0.60 0.60 0.60 0.60 300.0 CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) W Avg 0.60 0.60 0.60 0.60 300.0
Что ж, модель показала себя немного лучше на тестовом выборке, показав точность в 60%, что на 2% больше, чем точность обучающих данных, так что это хорошие новости.
Наивная гауссовская байесовская модель в тестере стратегий
Использование моделей машинного обучения в тестере стратегий часто не дает хороших результатов не потому, что модели не способны делать прогнозы, а потому, что мы обычно смотрим на график прибыли в тестере стратегий. Модель машинного обучения способна угадать, куда рынок пойдет дальше, но это не обязательно означает, что вы заработаете на этом деньги, особенно с учетом простой логики, которую я использовал для сбора и подготовки нашего набора данных. Посмотрим выборки данных, которые были собраны на каждом баре для установленного в параметре таймфрейма, в данном случае PERIOD_H1 (часовой ТФ).
close.CopyRates(Symbol(),TF, COPY_RATES_CLOSE,0,TrainBars); open.CopyRates(Symbol(),TF, COPY_RATES_OPEN,0,TrainBars);
Мы собрали 1000 баров часового таймфрейма и прочитали значения их индикаторов в независимые переменные. Затем мы создали целевые переменные, в которых указывается, была ли свеча бычьей — в таком случае советник устанавливает класс 1. В противном случае он устанавливает класс 0. Эти значения учитываются в функции для торговли. Поскольку наша модель будет предсказывать следующую свечу, сделки открывались на каждой новой свече, при этом предыдущие сделки закрывались. По сути, мы позволили нашему советнику торговать по каждому сигналу на каждом баре.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { if (!train_state) TrainTest(); train_state = true; //--- vector v_inputs(5); //5 независимых переменных double buff[1]; //текущее значение индикатора for (ulong i=0; i<5; i++) //Независимые переменные { CopyBuffer(handles[i],0,0,1, buff); v_inputs[i] = buff[0]; } //--- MqlTick ticks; SymbolInfoTick(Symbol(), ticks); int signal = -1; double min_volume = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN); if (isNewBar()) { signal = gaussian_naive.GaussianNaiveBayes(v_inputs); Comment("SIGNAL ",signal); CloseAll(); if (signal == 1) { if (!PosExist()) m_trade.Buy(min_volume, Symbol(), ticks.ask, 0 , 0,"Naive Buy"); } else if (signal == 0) { if (!PosExist()) m_trade.Sell(min_volume, Symbol(), ticks.bid, 0 , 0,"Naive Sell"); } } }
Чтобы эта функция работала как в реальной торговле, так и в тестере стратегий, пришлось немного изменить логику. Функция CopyBuffer()и обучение теперь находятся внутри функции TrainTest(). Эта функция запускается один раз в функции OnTick. Можно сделать так, чтобы она запускалась чаще, при этом и модель будет обучаться чаще. Оставим это на ваше усмотрение.
Поскольку функция Init не подходит для всех этих методов copy buffer и copy rates (gри таком использовании они возвращают нулевые значения в тестере стратегий), теперь все перемещено в функцию TrainTest().
int OnInit() { handles[0] = iBearsPower(Symbol(),TF, bears_period); handles[1] = iBullsPower(Symbol(),TF, bulls_period); handles[2] = iRSI(Symbol(),TF,rsi_period, rsi_price); handles[3] = iVolumes(Symbol(),TF,VOLUME_TICK); handles[4] = iMFI(Symbol(),TF,mfi_period,VOLUME_TICK ); //--- m_trade.SetExpertMagicNumber(MAGIC_NUMBER); m_trade.SetTypeFillingBySymbol(Symbol()); m_trade.SetMarginMode(); m_trade.SetDeviationInPoints(slippage); return(INIT_SUCCEEDED); }
Одиночный тест: часовой таймфрейм
Я запускал тестирование на данных двух месяцев с 1 января 2023 года по 14 февраля 2023 года.
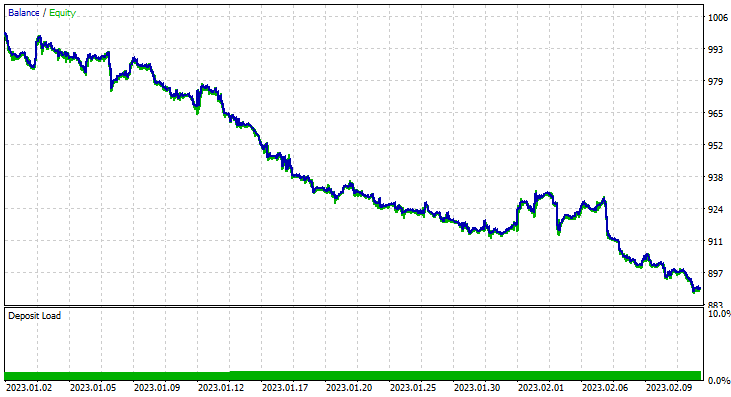
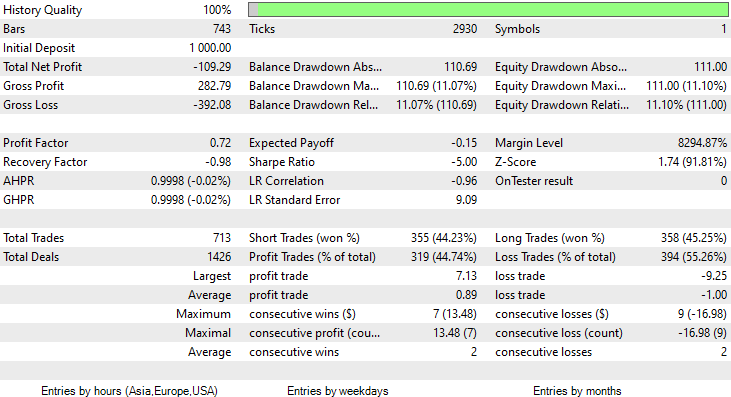
Я выбрал именно такой период для тестирования (2 месяца), потому что 1000 часовых баров — это не такой уж большой период обучения. Это почти 41 день, так что период обучения короткий, как и тестирование. Когда функция TrainTest() работала в тестере, у нас получилось тестирование на 700 барах.
Что случилось?
Модель произвела первое впечатление при тестировании в тестере стратегий, обеспечив впечатляющую 60-процентную точность обучающих данных.
CS 0 08:30:13.816 Tester initial deposit 1000.00 USD, leverage 1:100 CS 0 08:30:13.818 Tester successfully initialized CS 0 08:30:13.818 Network 80 Kb of total initialization data received CS 0 08:30:13.819 Tester Intel Core i5 660 @ 3.33GHz, 6007 MB CS 0 08:30:13.900 Symbols EURUSD: symbol to be synchronized CS 0 08:30:13.901 Symbols EURUSD: symbol synchronized, 3720 bytes of symbol info received CS 0 08:30:13.901 History EURUSD: history synchronization started .... .... .... CS 0 08:30:14.086 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 ---> Training the Model CS 0 08:30:14.086 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 CS 0 08:30:14.086 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 ---> GROUPS [0,1] CS 0 08:30:14.086 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 CS 0 08:30:14.086 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 ---> Prior_proba [0.4728571428571429,0.5271428571428571] Evidence [331,369] CS 0 08:30:14.377 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 Confusion Matrix CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 [[200,131] CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 [150,219]] CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 Classification Report CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 _ Precision Recall Specificity F1 score Support CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 0.0 0.57 0.60 0.59 0.59 331.0 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 1.0 0.63 0.59 0.60 0.61 369.0 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 Accuracy 0.60 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 Average 0.60 0.60 0.60 0.60 700.0 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 W Avg 0.60 0.60 0.60 0.60 700.0
Однако далее советник не смог совершать прибыльные сделки с обещанной точностью или близкой к ней. Ниже мои наблюдения:
- Логика получилась слепой, стратегия платит качеством за количество. Советник совершил 713 сделок за два месяца. Это очень много. Этот момент нужно поменять. Обучим модель на старшем таймфрейме и торговать также будем на старших таймфреймах, в итоге это уменьшит количество совершаемых сделок.
- В этот раз уменьшим бары для обучения — хочется обучить модель на последних данных.
Для этого мы запустили оптимизацию на шестичасовом таймфрейме и получили значения Train Bars = 80, TF = 12 hours. Тестирование проводилось на данных за два месяца с использованием новых параметров. Все параметры доступны в *set-файле, приложенном в конце статьи.
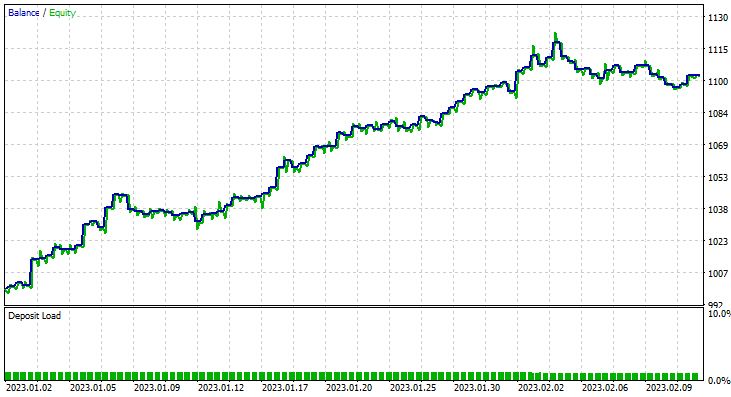
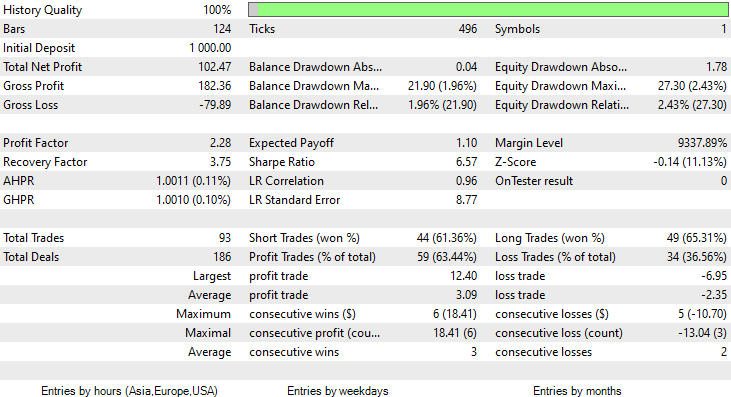
На этот раз точность обучения гауссовской наивной байесовской модели составила 58%.
93 сделки за период в 2 месяца — это можно называть здоровой торговой активностью. В среднем получилось 2,3 сделки в день. На этот раз 63% сделок, совершенных советником Gaussian Naïve Bayes, оказались прибыльными. Прибыль составила 10%.
Мы посмотрели, как можно использовать наивную гауссовскую байесовскую модель для принятия торговых решений. Теперь давайте посмотрим, как она работает.
Теория наивного Байеса
Не путайте с Гауссовским наивным байесовским метод.
Алгоритм называется
- Наивным, потому что он предполагает, что переменные/функции независимы, что в реальности бывает редко.
-
Байес, потому что он основан на теореме Байеса
Формула теоремы Байеса приведена ниже:
![]()
Где:
P(A|B) — апостериорная вероятность гипотезы (состояния) A при наблюдении события B
P(B|A) — вероятность наступления события при условия, что вероятность теории верна. Простыми словами, это вероятность B при условии, что A верно
P(A) — априорная (безусловная) вероятность A или вероятность гипотезы до наступления события
P(B) — предельная вероятность наступления события
Термины в этой формуле могут сначала показаться запутанными. Далее, по мере работы над нашим алгоритмом, все станет понятнее.
Работа с классификатором
Давайте рассмотрим простой пример с выборкой данных о погоде. Обратите внимание на первый столбец "Прогноз". Сначала поймем, что происходит в нем, а затем займемся добавлением других столбцов в качестве независимых переменных — это точно такой же процесс.
| Прогноз | Играть в теннис |
|---|---|
| Солнечно | Нет |
| Солнечно | Нет |
| Пасмурно | Да |
| Дождь | Да |
| Дождь | Да |
| Дождь | Нет |
| Пасмурно | Да |
| Солнечно | Нет |
| Солнечно | Да |
| Дождь | Да |
| Солнечно | Да |
| Пасмурно | Да |
| Пасмурно | Да |
| Дождь | Нет |
Теперь давайте сделаем то же самое в MetaEditor:
void OnStart() { //--- matrix Matrix = matrix_utils.ReadCsvEncode("weather dataset.csv"); int cols[3] = {1,2,3}; matrix_utils.RemoveMultCols(Matrix, cols); //удалим данные о температуре, влажности и ветре ArrayRemove(matrix_utils.csv_header,1,3); //удаление заголовков столбцов ArrayPrint(matrix_utils.csv_header); Print(Matrix); matrix x_matrix; vector y_vector; matrix_utils.XandYSplitMatrices(Matrix, x_matrix, y_vector); }
Обратите внимание, что Наивный Байес предназначен только для дискретных/прерывистых переменных. Не путайте наивной байесовской моделью Гаусса, которую мы видели в действии выше — она может работать с непрерывными переменными, в отличие от этой наивной байесовской модели. Вот почему в этом примере я решил использовать именно этот набор данных, который содержит дискретные значения. Ниже приведен результат отработки кода, показанного выше.
CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) "Outlook" "Play" CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [[0,0] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [0,0] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [1,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [2,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [2,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [2,0] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [1,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [0,0] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [0,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [2,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [0,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [1,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [1,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [2,0]]
Теперь найдем априорную вероятность в нашем конструкторе класса NaïveBayes:
CNaiveBayes::CNaiveBayes(matrix &x_matrix, vector &y_vector) { XMatrix.Copy(x_matrix); YVector.Copy(y_vector); classes = matrix_utils.Classes(YVector); c_evidence.Resize((ulong)classes.Size()); n = YVector.Size(); if (n==0) { Print("--> n == 0 | Naive Bayes class failed"); return; } //--- vector v = {}; for (ulong i=0; i<c_evidence.Size(); i++) { v = matrix_utils.Search(YVector,(int)classes[i]); c_evidence[i] = (int)v.Size(); } //--- c_prior_proba.Resize(classes.Size()); for (ulong i=0; i<classes.Size(); i++) c_prior_proba[i] = c_evidence[i]/(double)n; #ifdef DEBUG_MODE Print("---> GROUPS ",classes); Print("Prior Class Proba ",c_prior_proba,"\nEvidence ",c_evidence); #endif }
Результат
CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) ---> GROUPS [0,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) Prior Class Proba [0.3571428571428572,0.6428571428571429] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) Evidence [5,9]
Априорная вероятность [Yes, No] приблизительно равна [0.36, 0.64].
Теперь предположим, мы хотим узнать вероятность того, что человек будет играть в теннис в солнечный день. Для этого мы сделаем следующее:
P(Yes | Sunny) = P(Sunny | Yes) * P(Yes) / P(Sunny)
More details in simple English:
Вероятность того, что кто-то будет играть в солнечный день = сколько раз по вероятности было солнечно и кто-то играл в теннис * сколько раз с точки зрения вероятности люди играли в теннис / сколько раз с точки зрения вероятности это был солнечный день.
P(Sunny | Yes) = 2/9
P(Yes) = 0.64
P(Sunny) = 5/14 = 0.357
Итого получается P(Yes | Sunny) = 0.333 x 0.64 / 0.357 = 0.4
Что касается вероятности (No| Sunny), ее можно вычислить так: 1 - вероятность Yes = 1 - 0.5972 = 0.4027. Это так просто, но все же посмотрим и на эту часть.
P(No|Sunny) = (3/5) x 0.36 / (0.357) = 0.6
В коде это происходит так:
vector CNaiveBayes::calcProba(vector &v_features) { vector proba_v(classes.Size()); //вектор для возврата if (v_features.Size() != XMatrix.Cols()) { printf("FATAL | Can't calculate probability, features columns size = %d is not equal to XMatrix columns =%d",v_features.Size(),XMatrix.Cols()); return proba_v; } //--- vector v = {}; for (ulong c=0; c<classes.Size(); c++) { double proba = 1; for (ulong i=0; i<XMatrix.Cols(); i++) { v = XMatrix.Col(i); int count =0; for (ulong j=0; j<v.Size(); j++) { if (v_features[i] == v[j] && classes[c] == YVector[j]) count++; } proba *= count==0 ? 1 : count/(double)c_evidence[c]; //не считаем, если нет достаточно доказательств } proba_v[c] = proba*c_prior_proba[c]; } return proba_v; }
Вектор вероятности, предоставленный этой функцией для солнечной погоды:
2023.02.15 16:34:21.519 Naive Bayes theory script (EURUSD,H1) Probabilities [0.6,0.4]
Именно то, что мы ожидали. Но внимание, эта функция не дает нам вероятности. Я объясню. Когда в наборе данных для предсказания есть только два класса, в этом сценарии результат является вероятностью, но с другой стороны, выходные данные этой функции необходимо проверить с точки зрения вероятности. Это достаточно просто:
Берем сумму вектора, который получился в результате работы этой функции, затем разделим каждый элемент на общую сумму, а оставшийся вектор и будет реальными значениями вероятности, которые при суммировании будут равны единице.
probability_v = v[i]/probability_v.Sum()
Этот небольшой процесс выполняется внутри функции NaiveBayes(), которая предсказывает результат класса или класс с наибольшей вероятностью из всех:
int CNaiveBayes::NaiveBayes(vector &x_vector) { vector v = calcProba(x_vector); double sum = v.Sum(); for (ulong i=0; i<v.Size(); i++) //преобразуем значения в вероятности v[i] = NormalizeDouble(v[i]/sum,2); vector p = v; #ifdef DEBUG_MODE Print("Probabilities ",p); #endif return((int)classes[p.ArgMax()]); }
И это все. Наивный байесовский алгоритм настолько прост. Теперь сосредоточимся на гауссовском наивном байесовском алгоритме, который мы использовали в начале этой статьи.
Гауссовский наивный байесовский метод
Гауссовский наивный Байес предполагает, что признаки следуют нормальному распределению. Это означает, что если предикторы принимают непрерывные переменные вместо дискретных, то предполагается, что эти значения взяты из распределения Гаусса.
Вспомним о нормальном распределении
Нормальное распределение — это непрерывное распределение вероятностей, симметричное относительно своего среднего значения. Большинство наблюдений сосредоточено вокруг центрального пика, а вероятности значений, находящихся дальше от среднего значения, сужаются одинаково в обоих направлениях. Экстремальные значения в обоих хвостах распределения также маловероятны.
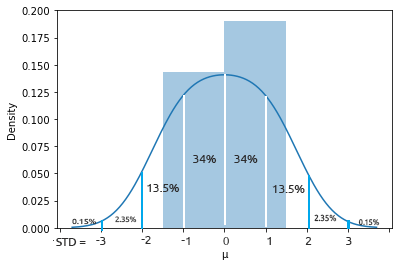
Эта колоколообразная кривая вероятности настолько эффективна, что считается одним из самых полезных инструментов статистического анализа. Она показывает, что существует приблизительная 34% вероятность найти что-то на одно стандартное отклонение от среднего и 34% найти что-то по другую сторону кривой нормального распределения. Это означает, что вероятность найти значение, которое находится на расстоянии одного стандартного отклонения от среднего значения с обеих сторон, составляет около 68%. Если хотите узнать об этом подробнее, рекомендую почитать здесь.
Из этого нормального распределения/распределения Гаусса нам нужно найти плотность вероятности. Он рассчитывается по следующей формуле.
![]()
где:
μ — среднее значение
𝜎 — стандартное отклонение
х — входное значение
Поскольку это часть гауссовского наивного байесовского алгоритма, напишем соответствующий код.
class CNormDistribution { public: double m_mean; //присваем значение среднего double m_std; //присваиваем значение дисперсии CNormDistribution(void); ~CNormDistribution(void); double PDF(double x); //функция плотности вероятности }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ CNormDistribution::CNormDistribution(void) { } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ CNormDistribution::~CNormDistribution(void) { ZeroMemory(m_mean); ZeroMemory(m_std); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CNormDistribution::PDF(double x) { double nurm = MathPow((x - m_mean),2)/(2*MathPow(m_std,2)); nurm = exp(-nurm); double denorm = 1.0/(MathSqrt(2*M_PI*MathPow(m_std,2))); return(nurm*denorm); }
Создание гауссовской наивной байесовской модели
Конструктор класса Gaussian Naïve Bayes похож на конструктор класса Naïve Bayes. Поэтому не буду показывать и объяснять код конструктора здесь. Ниже представлена наша основная функция, отвечающая за вычисление вероятности.
vector CGaussianNaiveBayes::calcProba(vector &v_features) { vector proba_v(classes.Size()); //вектор для возврата if (v_features.Size() != XMatrix.Cols()) { printf("FATAL | Can't calculate probability, features columns size = %d is not equal to XMatrix columns =%d",v_features.Size(),XMatrix.Cols()); return proba_v; } //--- vector v = {}; for (ulong c=0; c<classes.Size(); c++) { double proba = 1; for (ulong i=0; i<XMatrix.Cols(); i++) { v = XMatrix.Col(i); int count =0; vector calc_v = {}; for (ulong j=0; j<v.Size(); j++) { if (classes[c] == YVector[j]) { count++; calc_v.Resize(count); calc_v[count-1] = v[j]; } } norm_distribution.m_mean = calc_v.Mean(); //назначаем нормальному распределению Гаусса norm_distribution.m_std = calc_v.Std(); #ifdef DEBUG_MODE printf("mean %.5f std %.5f ",norm_distribution.m_mean,norm_distribution.m_std); #endif proba *= count==0 ? 1 : norm_distribution.PDF(v_features[i]); //не считаем, если нет достаточно доказательств } proba_v[c] = proba*c_prior_proba[c]; //превращение плотности вероятности в вероятность #ifdef DEBUG_MODE Print(">> Proba ",proba," prior proba ",c_prior_proba); #endif } return proba_v; }
Посмотрим, как эта модель поведет себя в действии.
Для примера используем выборку о гендерных данных.
| Высота (футы) | Вес (фунты) | Размер стопы (дюймы) | Пол (0 - мужчина, 1 - женщина) |
|---|---|---|---|
| 6 | 180 | 12 | 0 |
| 5.92 | 190 | 11 | 0 |
| 5.58 | 170 | 12 | 0 |
| 5.92 | 165 | 10 | 0 |
| 5 | 100 | 6 | 1 |
| 5.5 | 150 | 8 | 1 |
| 5.42 | 130 | 7 | 1 |
| 5.75 | 150 | 9 | 1 |
//--- гауссовский наивный байес Matrix = matrix_utils.ReadCsv("gender dataset.csv"); ArrayPrint(matrix_utils.csv_header); Print(Matrix); matrix_utils.XandYSplitMatrices(Matrix, x_matrix, y_vector); gaussian_naive = new CGaussianNaiveBayes(x_matrix, y_vector);
Выводимая информация:
CS 0 18:52:18.653 Naive Bayes theory script (EURUSD,H1) ---> GROUPS [0,1] CS 0 18:52:18.653 Naive Bayes theory script (EURUSD,H1) CS 0 18:52:18.653 Naive Bayes theory script (EURUSD,H1) ---> Prior_proba [0.5,0.5] Evidence [4,4]
Поскольку 4 из 8 были мужчинами, а остальные 4 были женщинами, вероятность того, что модель предскажет мужчину или женщину, составляет 50-50.
Давайте попробуем модель с новыми данными человека ростом 5,3, весом 140 и размером стопы 7,5. Мы с вами понимаем, что этот человек, скорее всего, женщина.
vector person = {5.3, 140, 7.5}; Print("The Person is a ",gaussian_naive.GaussianNaiveBayes(person));
Выводимая информация:
2023.02.15 19:14:40.424 Naive Bayes theory script (EURUSD,H1) The Person is a 1
Отлично, предсказание получилось верным — это женщина.
Тестирование гауссовой наивной байесовской модели тоже относительно простое. Просто передаем матрицу, на которой модель была обучена, и измерим точность прогнозов, используя матрицу путаницы.
CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) Confusion Matrix CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) [[4,0] CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) [0,4]] CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) Classification Report CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) _ Precision Recall Specificity F1 score Support CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) 0.0 1.00 1.00 1.00 1.00 4.0 CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) 1.0 1.00 1.00 1.00 1.00 4.0 CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) Accuracy 1.00 CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) Average 1.00 1.00 1.00 1.00 8.0 CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) W Avg 1.00 1.00 1.00 1.00 8.0
Точность обучения составляет 100%! Наша модель может классифицировать, является ли человек мужчиной или женщиной, при использовании всех данных в качестве обучающей выборки.
Преимущества наивных и гауссовых байесовских классификаторов
- Это одни из самых простых и быстрых алгоритмов машинного обучения, используемых для классификации наборов данных.
- Их можно использовать как для бинарной, так и для многоклассовой классификации.
- Несмотря на их простоту, они часто лучше справляются с многоклассовой классификацией, чем большинство других алгоритмов.
- Это самый популярный инструмент для решения задач классификации текста.
Недостатки этих классификаторов
Хотя наивный байесовский алгоритм является простым и эффективным алгоритмом машинного обучения для классификации, он имеет некоторые ограничения и недостатки, которые следует учитывать.
Наивный Байес
- Предположение о независимости. Наивный байесовский подход предполагает, что все функции независимы друг от друга, что не всегда может быть верным на практике. Это предположение может привести к снижению точности классификации, если признаки сильно зависят друг от друга.
- Разреженность данных. Наивный Байес полагается на наличие достаточного количества обучающих примеров для каждого класса для точной оценки априорных значений класса и условных вероятностей. Если выборка данных слишком мала, оценки могут быть неточными, а классификация неэффективной.
- Чувствительность к несущественным функциям. Наивный байесовский метод рассматривает все признаки одинаково, независимо от их значимости для задачи классификации. Это может привести худшей классификации, если в набор данных включены нерелевантные функции. При этом сложно спорить с тем, что некоторые функции в наборе данных более важны, чем другие.
- Неспособность обрабатывать непрерывные переменные. Наивный байесовский подход предполагает, что все функции являются дискретными или категориальными и не могут напрямую обрабатывать непрерывные переменные. Чтобы использовать Наивный Байес с непрерывными переменными, данные должны быть дискретизированы, что может привести к потере информации и снижению точности классификации.
- Ограниченная выразительность. Наивный байесовский алгоритм может моделировать только линейные границы решений, чего может быть недостаточно для более сложных задач классификации. Из-за этого показатели могут быть хуже, если граница решения нелинейна.
- Дисбаланс классов. Наивный байесовский метод может работать хуже, когда распределение примеров по классам сильно несбалансировано, поскольку это может привести к смещенным априорным оценкам класса и плохой оценке условных вероятностей для класса меньшинства. Если нет достаточных доказательств, класс вообще не будет предсказан.
Гауссовский наивный байесовский метод
Гауссовский наивный байесовский метод повторяет вышеуказанные недостатки и плюс имеет два дополнительных:
- Чувствительность к выбросам. Гауссовский наивный байесовский метод предполагает, что признаки нормально распределены, что означает, что экстремальные значения или выбросы могут оказывать значительное влияние на оценки среднего значения и дисперсии. Это может привести к снижению производительности классификации, если набор данных содержит выбросы.
- Не подходит для функций с тяжелыми хвостами. Гауссовский наивный байесовский метод предполагает, что признаки имеют нормальное распределение с конечной дисперсией. Если же есть тяжелые хвосты, такие как распределение Коши, алгоритм может работать плохо.
Заключение
Чтобы модель машинного обучения давала результаты в тестере стратегий, требуется больше, чем просто обучение модели. Приходится бороться за производительность, стараться получить растущий график прибыли. Иногда нам не нужно прогонять саму модель машинного обучения в тестере стратегий, потому что для некоторых моделей тестирование потребует слишком больших вычислительных ресурсов. Тем не менее, вам обязательно нужно будет использовать тестер по другим причинам, таким как оптимизация объемов торговли, таймфреймов и т.д. Необходимо провести тщательный анализ логики, прежде чем вы решите начать торговлю в реальном времени в любом режиме.
С наилучшими пожеланиями.
Следите за развитием темы в моем репозитории GitHub https://github.com/MegaJoctan/MALE5
| Файл | Содержание и использование |
|---|---|
| Naive Bayes.mqh | Содержит классы наивных байесовских моделей |
| Naive Bayes theory script.mq5 | Скрипт для тестирования библиотеки |
| Naive Bayes Test.mq5 | Советник для торговли по изученным моделям |
| matrix_utils.mqh | Содержит дополнительные матричные функции |
| metrics.mqh | Содержит функции для анализа производительности моделей машинного обучения, как матрица путаницы |
| naive bayes visualize.py | Скрипт Python для рисования графиков распределения по всем независимым переменным, используемым в модели |
| gender datasets.csv & weather dataset.csv | Выборки данных, используемые в качестве примеров в этой статье |
Внимание! Эта статья предназначена только для образовательных целей. Трейдинг — рискованное занятие, и вы должны осознавать все связанные с ним риски. Автор не несет ответственности за любые убытки или потери в результате использования моделей, обсуждаемых в этой статье. Никогда не рискуйте деньгами большими, чем вы можете себе позволить потерять без ущерба для себя!
Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/12184
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
всё хорошо и замечательно, но вот только взятые индикаторы не являются не то чтобы независимыми, они вообще взаимное переложение одного и того-же. По показаниям одного можно вывести остальные и формулы известны
Байес ничего не сделает
Просто скачать и запустить в тестере - какой-то слив. В статье не нашёл инструкции "чтобы обучить, нажмите X"
Опять что-то для академиков
всё хорошо и замечательно, но вот только взятые индикаторы не являются не то чтобы независимыми, они вообще взаимное переложение одного и того-же. По показаниям одного можно вывести остальные и формулы известны
Байес ничего не сделает
Как "оно" работает?
Просто скачать и запустить в тестере - какой-то слив. В статье не нашёл инструкции "чтобы обучить, нажмите X"
Опять что-то для академиков