Нейросети — это просто (Часть 74): Адаптивное прогнозирование траекторий

Введение

Построение торговой стратегии неотделимо от анализа рыночной ситуации с прогнозированием наиболее вероятного движения финансового инструмента. Которое довольно часто коррелируется с другими финансовыми активами и макроэкономическими показателями. Можно провести параллель с движением транспорта, где каждое транспортное средство следует к своей индивидуальной точке назначения. Тем не менее, их действия на дороге в определенной степени взаимосвязаны и строго регулируются правилами дорожного движения. При этом вследствие индивидуальности восприятия дорожной ситуации водителями транспортных средств на дорогах остается доля стохастичности.

Аналогично в мире финансов формирование цены подчиняется определенным правилам. Однако стохастичность спроса и предложения, создаваемых участниками рынка, приводит к стохастичности цены. Возможно, поэтому многие методы прогнозирования траекторий, применяемые в области навигации, показывают хорошие результаты при предсказании будущего ценового движения.

В данной статье я хочу познакомить Вас с методом для эффективного совместного прогнозирования траекторий всех агентов на сцене с динамическим обучением весов ADAPT, который был предложен для решения задач в области навигации автономных транспортных средств. Впервые метод был представлен в статье "ADAPT: Efficient Multi-Agent Trajectory Prediction with Adaptation".

1. Алгоритм ADAPT

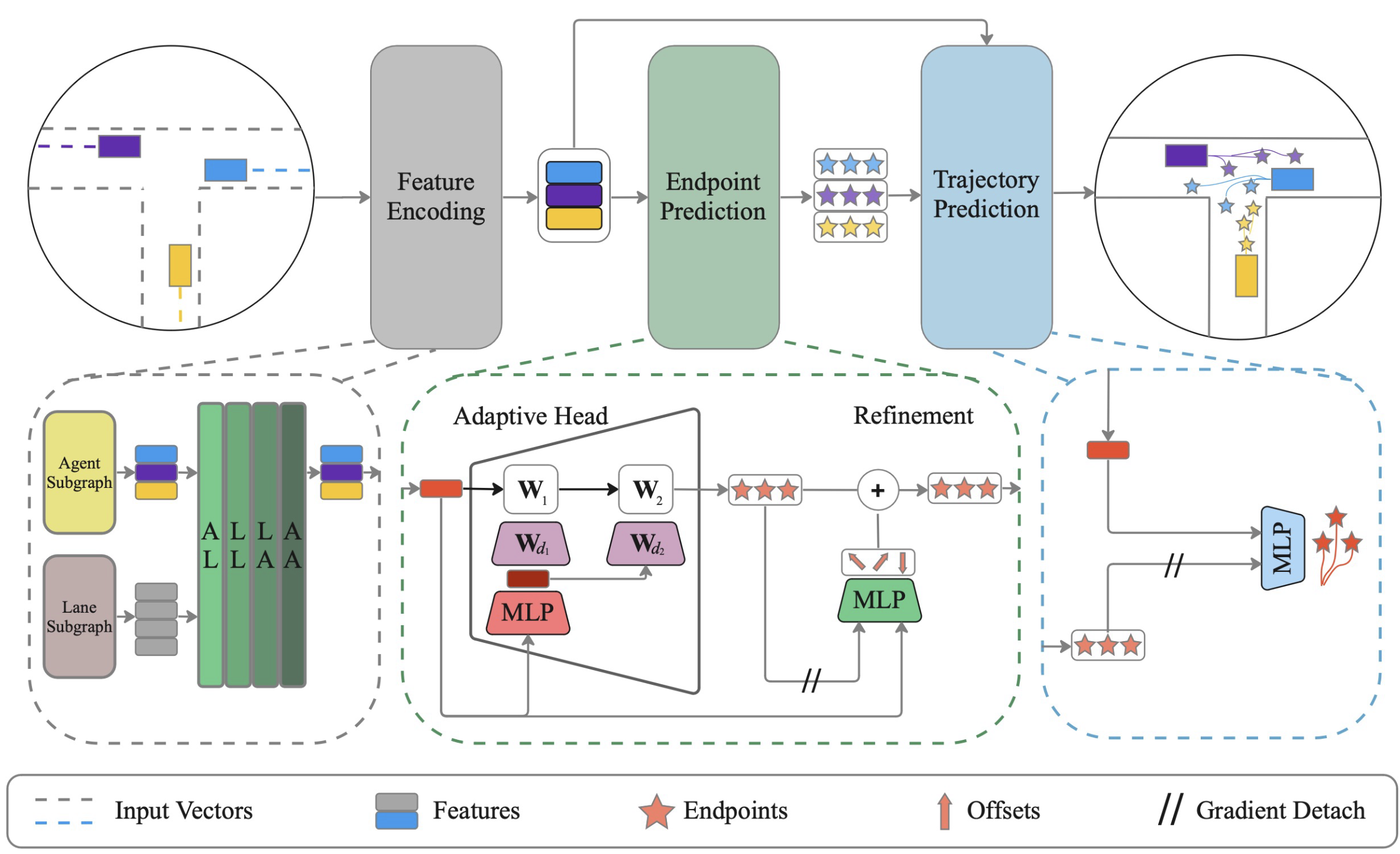
Метод ADAPT анализирует прошлые траектории всех агентов на карте сцены и прогнозирует их будущие траектории. В векторизованном представлении сцены моделируются различные типы взаимодействий между агентами и картой для получения максимально возможного представления об агентах. Аналогично подходам постановки целей, алгоритмом предусмотрено сначала прогнозирование возможного набора конечных точек. Затем каждая конечная точка уточняется с учетом смещение агента на сцене. После чего прогнозируется полная траектория, обусловленная на конечных точках.

Авторы метода стабилизируют обучение модели, разделяя прогнозирование конечной точки и траектории с отсоединением градиентов. Представленная авторами модель использует небольшие многослойные персептроны для прогнозирования конечных точек и траекторий, чтобы сохранить низкую сложность модели.

В предложенном авторами методе для кодирования карты и агентов используется векторизованное представление структурированным образом. Такое представление создает соединенный граф для каждого элемента сцены независимо, учитывая прошлые траектории агентов и карту сцены. При этом авторы метода предлагают использовать два отдельных подграфа для агентов и объектов карты.

ADAPT позволяет моделировать различные типы взаимодействий между элементами сцены. Авторами предложено моделировать четыре типа отношений: агент-полоса (AL), полоса-полоса (LL), полоса-агент (LA) и агент-агент (AA).

Для анализа взаимозависимостей используются блоки многоголового внимания, аналогично АвтоБотам. Однако, к блокам самовнимания (AA, LL) добавляются и блоки кросс-отношения (AL, LA) с использованием кодера кросс-внимания. Каждое взаимодействие моделируется последовательно и повторяем процесс L раз.

Таким образом, промежуточные признаки могут обновляться на каждой итерации, а затем обновленные признаки используются для вычисления внимания на следующей итерации. Каждый элемент сцены может быть информирован различными типами взаимодействий L раз.

Для прогнозирования конечной точки в случае использования агентоцентрической системы отсчета возможно использование MLP, что может быть предпочтительнее из-за ее преимуществ в прогнозировании для одного агента. Но при использовании сценоцентрической системы отсчета рекомендуется использовать адаптивную голову с динамическими весами, которая более эффективна в многоагентном прогнозировании конечных точек траекторий.

После получения конечной точки для каждого агента алгоритмом предусмотрена интерполяция будущих координат между начальной точкой и конечной с использованием MLP. При этом "отсоединяем" конечные точки, чтобы гарантировать, что обновления весов для полного прогнозирования траектории отделены от предсказания конечной точки. Аналогично прогнозируем вероятность для каждой траектории, используя отсоединенные конечные точки.

Для обучения моделей осуществляется прогнозирования K траекторий и применяются разнообразные функции потери для захвата многомодальных будущих сценариев. Обратный градиент ошибки передается только через наиболее точную траекторию. Поскольку полные траектории прогнозируются с условием на конечные точки, точность прогнозирования конечной точки является ключевой для полного прогнозирования траектории. Поэтому авторы метода применяют отдельную функцию потерь для улучшения прогнозирования конечной точки. Завершающим элементом авторской функции потерь является ошибка классификации для направления вероятностей, присвоенных траекториям.

Авторская визуализация метода представлена ниже.

2. Реализация средствами MQL5

Выше представлено довольно сжатое теоретическое описание метода ADAPT, что связано с большим объемом предстоящей работы и ограничениями формата статьи. Более детально некоторые аспекты будут обсуждены в ходе нашей реализации предложенных подходов. Сразу скажу, что наша реализация во многом будет отличаться от авторского метода. За что не судите строго.

И первое отличие — мы отказались от отдельных тензоров для кодирования агентов и полилиний. Агентами в нашем случае являются анализируемые признаки. Каждый признак у нас, можно сказать, характеризуется 2 параметрами: значение и время. И за анализируемый временной отрезок он осуществляет движение в некоторой траектории. При этом, хотя каждый индикатор имеет свой диапазон значений, практически же у нас нет карты сцены. Однако у нас есть срез сцены в отдельный момент времени со всеми агентами на ней. Технически мы можем заменить одну сущность на другую. А нужно ли нам для этого создавать отдельный тензор, ведь это взгляд на те же данные в другом измерении. Мы остановились на использовании одного тензора с разными акцентами.

2.1 Блок Кросс-Отношений

Далее, размышляя о способе реализации предложенных подходов я столкнулся с отсутствием реализации блока кросс-отношений. Ранее наши задачи больше носили авторегрессионный характер. И в них нас вполне удовлетворял блок самовнимания. Сейчас же нам понадобился анализ отношения различных сущностей, и мы приступаем к реализации нового нейронного слоя CNeuronMH2AttentionOCL. Алгоритмы реализации класса во многом заимствованы в блоке самовнимания, только сущности Query, Key и Value будут формироваться с различных измерений тензора исходных данных. Что потребовало не малых доработок. Поэтому было принято решение о создании нового класса, а не модернизации существующего.

class CNeuronMH2AttentionOCL       :  public CNeuronBaseOCL
  {
protected:
   uint              iHeads;                                      ///< Number of heads
   uint              iWindow;                                     ///< Input window size
   uint              iUnits;                                      ///< Number of units
   uint              iWindowKey;                                  ///< Size of Key/Query window
   //---
   CNeuronConvOCL    Q_Embedding;
   CNeuronConvOCL    KV_Embedding;
   CNeuronTransposeOCL Transpose;
   int               ScoreIndex;
   CNeuronBaseOCL    MHAttentionOut;
   CNeuronConvOCL    W0;
   CNeuronBaseOCL    AttentionOut;
   CNeuronConvOCL    FF[2];
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      attentionOut(void);
   //---
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual bool      AttentionInsideGradients(void);
public:
   /** Constructor */
                     CNeuronMH2AttentionOCL(void);
   /** Destructor */~CNeuronMH2AttentionOCL(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_key, uint heads, 
                          uint units_count, ENUM_OPTIMIZATION optimization_type, 
                          uint batch);
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);
   //---
   virtual int       Type(void)   const   {  return defNeuronMH2AttentionOCL;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   virtual CLayerDescription* GetLayerInfo(void);
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

В конструкторе класса мы лишь задаем начальные значения локальным переменным.

CNeuronMH2AttentionOCL::CNeuronMH2AttentionOCL(void)  :  iHeads(0),
                                                         iWindow(0),
                                                         iUnits(0),
                                                         iWindowKey(0)
  {
   activation = None;
  }

Деструктор класса остается пустым.

Инициализация объектов класса CNeuronMH2AttentionOCL осуществляется в методе Init. В начале метода мы вызываем аналогичный метод родительского класса, в котором проверяются данные, полученные от внешней программы и инициализируются унаследованные объекты.

bool CNeuronMH2AttentionOCL::Init(uint numOutputs, uint myIndex, 
                                  COpenCLMy *open_cl, uint window,
                                  uint window_key, uint heads, 
                                  uint units_count, 
                                  ENUM_OPTIMIZATION optimization_type, 
                                  uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count,
                                                       optimization_type, batch))
      return false;

Сохраним значения основных параметров.

   iWindow = fmax(window, 1);
   iWindowKey = fmax(window_key, 1);
   iUnits = fmax(units_count, 1);
   iHeads = fmax(heads, 1);
   activation = None;

Так как мы будем анализировать исходные данные в разных измерениях, нам потребуется транспонирование тензора исходных данных.

   if(!Transpose.Init(0, 0, OpenCL, iUnits, iWindow, optimization_type, batch))
      return false;
   Transpose.SetActivationFunction(None);

Для генерации сущностей Query, Key и Value мы будем использовать сверточные слои. Количество фильтров равно размерности вектора одной сущности. При этом Query мы будем генерировать с одного измерения тензора исходных данных, а Key и Value с другого. Поэтому мы создадим 2 слоя (по одному для каждого измерения).

   if(!Q_Embedding.Init(0, 0, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 
                                                                     optimization_type, batch))
      return false;
   Q_Embedding.SetActivationFunction(None);

   if(!KV_Embedding.Init(0, 0, OpenCL, iUnits, iUnits, 2 * iWindowKey * iHeads, iWindow, 
                                                                     optimization_type, batch))
      return false;
   KV_Embedding.SetActivationFunction(None);

Матрица коээфициентов зависимости нам потребуется только на стороне контекста OpenCL. И для экономии используемых ресурсов мы создаем буфер только в контексте. На стороне основной программы хранится лишь указатель на буфер.

   ScoreIndex = OpenCL.AddBuffer(sizeof(float) * iUnits * iWindow * iHeads, CL_MEM_READ_WRITE);
   if(ScoreIndex == INVALID_HANDLE)
      return false;

Далее следуют объекты, аналогичные блоку самовнимания. Здесь мы создаем слой выхода много-голового внимания.

//---
   if(!MHAttentionOut.Init(0, 0, OpenCL, iWindowKey * iUnits * iHeads, optimization_type, batch))
      return false;
   MHAttentionOut.SetActivationFunction(None);

Слой понижения размерности.

   if(!W0.Init(0, 0, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow, iUnits, 
                                                                      optimization_type, batch))
      return false;
   W0.SetActivationFunction(None);

На выходе блока внимания мы суммируем полученные результаты с исходными данными в отдельном слое.

   if(!AttentionOut.Init(0, 0, OpenCL, iWindow * iUnits, optimization_type, batch))
      return false;
   AttentionOut.SetActivationFunction(None);

За которым следует блок линейных MLP.

   if(!FF[0].Init(0, 0, OpenCL, iWindow, iWindow, 4 * iWindow, iUnits, optimization_type, batch))
      return false;
   if(!FF[1].Init(0, 0, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iUnits, optimization_type, 
                                                                                          batch))
      return false;
   for(int i = 0; i < 2; i++)
      FF[i].SetActivationFunction(None);

Чтобы при обратном проходе не осуществлять излишнее копирование градиентов ошибки из буфера родительского класса в буфер внутреннего слоя мы осуществим подмену указателей на объекты.

   Gradient.BufferFree();
   delete Gradient;
   Gradient = FF[1].getGradient();
//---
   return true;
  }

Переходя к описанию прямого прохода, стоит обратить внимание, что несмотря на большое количество внутренних слоев, которые уже организуют определенный функционал, непосредственно анализ взаимосвязей нам предстоит реализовать. И хотя математически данный функционал полностью идентичен блоку самовнимания, мы сталкиваемся с тем, что количество сущностей Query с большой долей вероятности будет отличаться от количества сущностей Key и Value, что приводит к прямоугольной матрице Score и нарушает логику созданных ранее кернелов. Поэтому мы приступаем к созданию новых кернелов.

Для прямого прохода мы создадим кернел MH2AttentionOut. В параметрах кернелу будем передавать 4 указателя на буферы данных и размерность вектора одного элемента сущности. Все наши сущности имеют одинаковый размер элементов.

__kernel void MH2AttentionOut(__global float *q,      ///<[in] Matrix of Querys
                              __global float *kv,     ///<[in] Matrix of Keys
                              __global float *score,  ///<[out] Matrix of Scores
                              __global float *out,    ///<[out] Matrix of Scores
                              int dimension           ///< Dimension of Key
                             )
  {
//--- init
   const int q_id = get_global_id(0);
   const int k = get_global_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int kunits = get_global_size(1);
   const int heads = get_global_size(2);

Запускать кернел мы будем в пространстве задач аж 3 измерений. Элементов Query, Key и голов внимания. При этом все потоки в рамках одного элемента Query и одной головы внимания мы объединим в группы, что связано с необходимостью нормализации матрицы Score функцией SoftMax в рамках указанных групп.

В теле кернела мы сначала идентифицируем каждый поток и определим смещение в глобальных буферах данных.

   const int shift_q = dimension * (q_id + qunits * h);
   const int shift_k = dimension * (k + kunits * h);
   const int shift_v = dimension * (k + kunits * (heads + h));
   const int shift_s = q_id * kunits * heads + h * kunits + k;

Тут же мы определим другие константы и объявим локальный массив.

   const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE);
   float koef = sqrt((float)dimension);
   if(koef < 1)
      koef = 1;
   __local float temp[LOCAL_ARRAY_SIZE];

Затем мы рассчитаем матрицу коэффициентов зависимости.

//--- sum of exp
   uint count = 0;
   if(k < ls)
      do
        {
         if((count * ls) < (kunits - k))
           {
            float sum = 0;
            for(int d = 0; d < dimension; d++)
               sum = q[shift_q + d] * kv[shift_k + d];
            sum = exp(sum / koef);
            if(isnan(sum))
               sum = 0;
            temp[k] = (count > 0 ? temp[k] : 0) + sum;
           }
         count++;
        }
      while((count * ls + k) < kunits);
   barrier(CLK_LOCAL_MEM_FENCE);

   count = min(ls, (uint)kunits);
//---
   do
     {
      count = (count + 1) / 2;
      if(k < ls)
         temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0);
      if(k + count < ls)
         temp[k + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

//--- score
   float sum = temp[0];
   float sc = 0;
   if(sum != 0)
     {
      for(int d = 0; d < dimension; d++)
         sc = q[shift_q + d] * kv[shift_k + d];
      sc = exp(sc / koef);
      if(isnan(sc))
         sc = 0;
     }
   score[shift_s] = sc;
   barrier(CLK_LOCAL_MEM_FENCE);

И рассчитаем новые значения сущности Query с учетом коэффициентов зависимости по каждому элементу вектора отдельно.

//--- out
   for(int d = 0; d < dimension; d++)
     {
      uint count = 0;
      if(k < ls)
         do
           {
            if((count * ls) < (kunits - k))
              {
               float sum = q[shift_q + d] * kv[shift_v + d] * 
                                (count == 0 ? sc : score[shift_s + count * ls]);
               if(isnan(sum))
                  sum = 0;
               temp[k] = (count > 0 ? temp[k] : 0) + sum;
              }
            count++;
           }
         while((count * ls + k) < kunits);
      barrier(CLK_LOCAL_MEM_FENCE);
      //---
      count = min(ls, (uint)kunits);
      do
        {
         count = (count + 1) / 2;
         if(k < ls)
            temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0);
         if(k + count < ls)
            temp[k + count] = 0;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);
      //---
      out[shift_q + d] = temp[0];
     }
  }

Далее мы создадим новый кернел для реализации функционала обратного прохода MH2AttentionInsideGradients. Данный кернел мы также будем запускать в 3 мерном пространстве задач.

В параметрах кернела мы будем передавать уже 6 указателей на буферы данных. Добавились буферы градиентов ошибок для всех сущностей.

__kernel void MH2AttentionInsideGradients(__global float *q, __global float *q_g,
                                          __global float *kv, __global float *kv_g,
                                          __global float *scores,
                                          __global float *gradient,
                                          int kunits)
  {
//--- init
   const int q_id = get_global_id(0); ошибок
   const int d = get_global_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int dimension = get_global_size(1);
   const int heads = get_global_size(2);

В теле кернела мы, как всегда, идентифицируем поток и создадим необходимые константы.

   const int shift_q = dimension * (q_id + qunits * h) + d;
   const int shift_k = dimension * (q_id + kunits * h) + d;
   const int shift_v = dimension * (q_id + kunits * (heads + h)) + d;
   const int shift_s = q_id * kunits * heads + h * kunits;
   const int shift_g = h * qunits * dimension + d;
   float koef = sqrt((float)dimension);
   if(koef < 1)
      koef = 1;

Вначале мы посчитаем градиенты ошибки для сущности Value. Для этого достаточно умножить вектор градиентов ошибки с выхода блока внимания на соответствующие коэффициенты зависимости.

//--- Calculating Value's gradients
   int step_score = q_id * kunits * heads;
   for(int v = q_id; v < kunits; v += qunits)
     {
      int shift_score = h * kunits + v;
      float grad = 0;
      for(int g = 0; g < qunits; g++)
         grad += gradient[shift_g + g * dimension] * scores[shift_score + g * step_score];
      kv_g[shift_v + v * dimension]=grad;
     }

Затем мы посчитаем градиенты ошибки для сущности Query. На этот раз нам предстоит сначала посчитать градиент ошибки на элементах матрицы коэффициентов зависимости с учетом производной функции SoftMax. И затем умножить его на соответствующий элемент тензора Key.

//--- Calculating Query's gradients
   float grad = 0;
   float out_g = gradient[shift_g + q_id * dimension];
   int shift_val = (heads + h) * kunits * dimension + d;
   int shift_key = h * kunits * dimension + d;
   for(int k = 0; k < kunits; k++)
     {
      float sc_g = 0;
      float sc = scores[shift_s + k];
      for(int v = 0; v < kunits; v++)
         sc_g += scores[shift_s + v] * out_g * kv[shift_val + v * dimension] * 
                                                        ((float)(k == v) - sc);
      grad += sc_g * kv[shift_key + k * dimension];
     }
   q_g[shift_q] = grad / koef;

Аналогично посчитаем градиент ошибки для сущности Key. Только на это раз мы считаем градиенты ошибки коэффициентов зависимости по соответствующему столбцу тензора.

//--- Calculating Key's gradients
   for(int k = q_id; k < kunits; k += qunits)
     {
      int shift_score = h * kunits + k;
      int shift_val = (heads + h) * kunits * dimension + d;
      grad = 0;
      float val = kv[shift_v];
      for(int scr = 0; scr < qunits; scr++)
        {
         float sc_g = 0;
         int shift_sc = scr * kunits * heads;
         float sc = scores[shift_sc + k];
         for(int v = 0; v < kunits; v++)
            sc_g += scores[shift_sc + v] * gradient[shift_g + scr * dimension] * val * 
                                                                ((float)(k == v) - sc);
         grad += sc_g * q[shift_q + scr * dimension];
        }
      kv_g[shift_k + k * dimension] = grad / koef;
     }
  }

После построения алгоритма на стороне контекста OpenCL мы возвращаемся к нашему классу для организации процесса на стороне основной программы. И первым мы рассмотрим метод прямого прохода feedForward. Аналогично одноименным методам других нейронных слоев, в параметрах мы  получаем указатель на предшествующий нейронный слой, который предоставляет нам исходные данные.

bool CNeuronMH2AttentionOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//---
   if(!Q_Embedding.FeedForward(NeuronOCL))
      return false;

Однако, мы не будем проверять актуальность полученного указателя. Вместо этого мы вызываем метод прямого прохода внутреннего слоя Q_Embedding для создания тензора сущностей Query, с передачей ему полученного указателя. В теле указанного метода уже реализованы все необходимы контроли и нам нет необходимости осуществлять их повторно.

Далее мы сгенерируем сущности Key и Value. Как было сказано ранее, для них мы используем другое измерение тензора исходных данных. Поэтому мы сначала транспонируем матрицу исходных данных, а потом вызываем метод прямого прохода соответствующего внутреннего слоя.

   if(!Transpose.FeedForward(NeuronOCL) || !KV_Embedding.FeedForward(NeuronOCL))
      return false;

Организацию вызова кернела MH2AttentionOut мы вынесем в отдельный метод attentionOut.

   if(!attentionOut())
      return false;

Тензор результатов много-голового внимания мы сжимаем до размера исходных данных.

   if(!W0.FeedForward(GetPointer(MHAttentionOut)))
      return false;

После чего полученные значения складываем с исходными данными и нормализуем их. Метод SumAndNormilize унаследован от родительского класса.

//---
   if(!SumAndNormilize(W0.getOutput(), NeuronOCL.getOutput(), AttentionOut.getOutput(), iWindow))
      return false;

В завершении блока внимания мы пропускаем данные через MLP.

   if(!FF[0].FeedForward(GetPointer(AttentionOut)))
      return false;
   if(!FF[1].FeedForward(GetPointer(FF[0])))
      return false;

Повторно суммируем и нормализуем.

   if(!SumAndNormilize(FF[1].getOutput(), AttentionOut.getOutput(), Output, iWindow))
      return false;
//---
   return true;
  }

Для "полноты картины" алгоритма прямого прохода рассмотрим метод attentionOut. Метод не получает параметров и работает только с внутренними объектами класса. Поэтому в теле метода мы проверяем только актуальность указателя на контекст OpenCL.

bool CNeuronMH2AttentionOCL::attentionOut(void)
  {
   if(!OpenCL)
      return false;

Затем создадим массивы пространства задач и смещения. Как обсуждалось при построении кернела, мы создаем 3 мерное пространство задач с локально группой по второму измерению.

   uint global_work_offset[3] = {0};
   uint global_work_size[3] = {iUnits, iWindow, iHeads};
   uint local_work_size[3] = {1, iWindow, 1};

Передаем необходимые параметры в кернел.

   ResetLastError();
   if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionOut, def_k_mh2ao_q, 
                                                       Q_Embedding.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, 
                                                            GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionOut, def_k_mh2ao_kv, 
                                                       KV_Embedding.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, 
                                                             GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionOut, def_k_mh2ao_score, ScoreIndex))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, 
                                                             GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionOut, def_k_mh2ao_out, 
                                                       MHAttentionOut.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, 
                                                              GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_MH2AttentionOut, def_k_mh2ao_dimension, (int)iWindowKey))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, 
                                                              GetLastError(), __LINE__);
      return false;
     }

После чего поставим кернел в очередь выполнения.

   if(!OpenCL.Execute(def_k_MH2AttentionOut, 3, global_work_offset, global_work_size, 
                                                                    local_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

Выше мы реализовали процесс прямого прохода как на стороне основной программы, так и на стороне контекста OpenCL. И далее нам предстоит организовать процесс обратного прохода. Напомню, для реализации алгоритма на стороне контекста OpenCL выше мы уже создали кернел MH2AttentionInsideGradients. И сейчас нам предстоит создать метод вызова данного кернела AttentionInsideGradients. В параметрах методу мы не будем ничего передавать, подобно аналогичному методу прямого прохода.

bool CNeuronMH2AttentionOCL::AttentionInsideGradients(void)
  {
   if(!OpenCL)
      return false;

В теле метода мы проверяем актуальность указателя на контекст OpenCL. После чего создадим массивы указания размерности пространства задач и смещения в нем.

   uint global_work_offset[3] = {0};
   uint global_work_size[3] = {iUnits, iWindowKey, iHeads};

Передадим необходимые кернелу праметры.

   ResetLastError();
   if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionInsideGradients, def_k_mh2aig_q, 
                                                            Q_Embedding.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), 
                                                                                 __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionInsideGradients, def_k_mh2aig_qg, 
                                                            Q_Embedding.getGradientIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), 
                                                                                 __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionInsideGradients, def_k_mh2aig_kv, 
                                                            KV_Embedding.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), 
                                                                                  __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionInsideGradients, def_k_mh2aig_kvg, 
                                                           KV_Embedding.getGradientIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), 
                                                                                  __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionInsideGradients, def_k_mh2aig_score, 
                                                                                ScoreIndex))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), 
                                                                                  __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionInsideGradients, def_k_mh2aig_outg,
                                                         MHAttentionOut.getGradientIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), 
                                                                                  __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_MH2AttentionInsideGradients, def_k_mh2aig_kunits, (int)iWindow))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), 
                                                                                  __LINE__);
      return false;
     }

И поставим кернел в очередь выполнения.

   if(!OpenCL.Execute(def_k_MH2AttentionInsideGradients, 3, global_work_offset, 
                                                             global_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

В целом это стандартный алгоритм для подобных задач. А весь алгоритм распределения градиента ошибки внутри нашего слоя описывается методом calcInputGradients. В параметрах метод получает указатель на объект предшествующего слоя, которому необходимо передать градиент ошибки.

bool CNeuronMH2AttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(!FF[1].calcInputGradients(GetPointer(FF[0])))
      return false;

В теле метода мы поочередно будем спускать градиент ошибки от выхода блока к предыдущему слою. Как вы помните, при инициализации класса мы подменили указатель на буфер градиента ошибки. И последующий слой записал градиент ошибки непосредственно в последний слой внутреннего MLP. С него мы и будем спускать градиент ошибки до уровня выхода блока внимания.

   if(!FF[0].calcInputGradients(GetPointer(AttentionOut)))
      return false;

На этом уровне мы складывали результаты блока внимания с исходными данными. Аналогично мы собираем градиент с 2 направлений.

   if(!SumAndNormilize(FF[1].getGradient(), AttentionOut.getGradient(), W0.getGradient(), 
                                                                           iWindow, false))
      return false;

Далее распределим градиент ошибки по головам внимания.

   if(!W0.calcInputGradients(GetPointer(MHAttentionOut)))
      return false;

И распределим градиент ошибки на сущности.

   if(!AttentionInsideGradients())
      return false;

Градиент ошибки от Key и Value передадим на слой транспонирования. При прямом проходе мы транспонировали матрицу исходных данных. С градиентом ошибки нам предстоит сделать обратную операцию.

   if(!KV_Embedding.calcInputGradients(GetPointer(Transpose)))
      return false;

И далее нам предстоит передать градиент ошибки от всех сущностей на предыдущий слой.

   if(!Q_Embedding.calcInputGradients(prevLayer))
      return false;

Но здесь надо понимать, что к предыдущему слою градиент ошибки идет с 4 потоков:

• Query
• Key
• Value
• В обход блока внимания.

Однако, методы наших внутренних слоев при передаче градиента ошибки удаляют ранее записанные данные. Поэтому, получив градиент ошибки от Query, мы складываем его с градиентом ошибки на выходе блока внимания в буфере внутреннего слоя.

   if(!SumAndNormilize(prevLayer.getGradient(), W0.getGradient(), AttentionOut.getGradient(), 
                                                                              iWindow, false))
      return false;

А после получения данных от Key и Value складываем все потоки.

   if(!Transpose.calcInputGradients(prevLayer))
      return false;
   if(!SumAndNormilize(prevLayer.getGradient(), AttentionOut.getGradient(), 
                                                      prevLayer.getGradient(), iWindow, false))
      return false;
//---
   return true;
  }

В методе обновления весовых коэффициентов все довольно просто. Мы просто вызываем аналогичные методы внутренних слоев.

bool CNeuronMH2AttentionOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!Q_Embedding.UpdateInputWeights(NeuronOCL))
      return false;
   if(!KV_Embedding.UpdateInputWeights(GetPointer(Transpose)))
      return false;
   if(!W0.UpdateInputWeights(GetPointer(MHAttentionOut)))
      return false;
   if(!FF[0].UpdateInputWeights(GetPointer(AttentionOut)))
      return false;
   if(!FF[1].UpdateInputWeights(GetPointer(FF[0])))
      return false;
//---
   return true;
  }

На этом мы завершаем рассмотрение методов организации процесса кросс-отношений. С полным кодом класса и всех его методов Вы можете самостоятельно ознакомиться во вложении. А мы переходим к построению советников обучения и тестирования моделей.

2.2 Архитектура моделей

Как можно было заметить из теоретического описания метода ADAPT, предложенный подход имеет довольно сложную иерархическую структуру. Для нас это выражается в большом количестве обучаемых моделей. Описание их архитектуры мы разделим на 2 метода. Вначале мы создадим 3 модели, которые связаны с процессом прогнозирования конечных точек.

bool CreateTrajNetDescriptions(CArrayObj *encoder, CArrayObj *endpoints, CArrayObj *probability)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
   if(!endpoints)
     {
      endpoints = new CArrayObj();
      if(!endpoints)
         return false;
     }
   if(!probability)
     {
      probability = new CArrayObj();
      if(!probability)
         return false;
     }

Энкодер состояния окружающей среды получает на вход сырые исходные данные описания 1 состояния.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

 Полученные данные мы, как всегда, нормализуем.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = MathMax(1000, GPTBars);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

И генерируем эмбединг, который добавляем в буфер накопления исторической последовательности.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronEmbeddingOCL;
     {
      int temp[] = {prev_count};
      ArrayCopy(descr.windows, temp);
     }
   prev_count = descr.count = GPTBars;
   int prev_wout = descr.window_out = EmbeddingSize;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Внедряем позиционное кодирование.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronPEOCL;
   descr.count = prev_count;
   descr.window = prev_wout;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

А далее идут блоки всестороннего внимания. И здесь для удобства управления архитектурой модели мы создадим цикл по числу итераций повторения блока.

   for(int l = 0; l < Lenc; l++)
     {
      //--- layer 4
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronTransposeOCL;
      descr.count = prev_count;
      descr.window = prev_wout;
      if(!encoder.Add(descr))
        {
         delete descr;
         return false;
        }

Согласно алгоритму, предложенному авторами метода ADAPT, сначала мы проверяем отношения между полилиниями (в нашем случае состояниями) и агентами. Перед применением нашего блока кросс-отношениий в данном направлении нам необходимо транспонировать получаемый объем информации. И затем добавляем наш новый слой.

      //--- layer 5
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronMH2AttentionOCL;
      descr.count = prev_wout;
      descr.window = prev_count;
      descr.step = 8;
      descr.window_out = 16;
      descr.optimization = ADAM;
      if(!encoder.Add(descr))
        {
         delete descr;
         return false;
        }

Затем идет блок самовнимания траекторий.

      //--- layer 6
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronMLMHAttentionOCL;
      descr.count = prev_wout;
      descr.window = prev_count;
      descr.step = 8;
      descr.window_out = 16;
      descr.layers = 1;
      descr.optimization = ADAM;
      if(!encoder.Add(descr))
        {
         delete descr;
         return false;
        }

Далее анализируем отношения в другой плоскости. Для этого мы транспонируем данные и повторяем блоки внимания.

      //--- layer 7
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronTransposeOCL;
      descr.count = prev_wout;
      descr.window = prev_count;
      if(!encoder.Add(descr))
        {
         delete descr;
         return false;
        }

      //--- layer 8
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronMH2AttentionOCL;
      descr.count = prev_count;
      descr.window = prev_wout;
      descr.step = 8;
      descr.window_out = 16;
      descr.layers = 1;
      descr.optimization = ADAM;
      if(!encoder.Add(descr))
        {
         delete descr;
         return false;
        }

      //--- layer 9
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronMLMHAttentionOCL;
      descr.count = prev_count;
      descr.window = prev_wout;
      descr.step = 8;
      descr.window_out = 16;
      descr.layers = 1;
      descr.optimization = ADAM;
      if(!encoder.Add(descr))
        {
         delete descr;
         return false;
        }
     }

Как уже было сказано выше, блок Энкодера мы обернули в цикл. А число итераций цикла мы вынесли в константы.

#define        Lenc                    3             //Number ADAPT Encoder blocks

Таким образом, изменение одной константы позволяет нам оперативно изменять количество блоков внимания в Энкодере.

Результаты Энкодера используются для прогнозирования нескольких наборов конечных точек. Количество таких наборов определяется константой NForecast.

#define        NForecast               5             //Number of forecast

В качестве модели прогнозирования конечных точек мы будем использовать простую MLP. В ней данные, полученные от Энкодера проходят через полносвязные слои.

//--- Endpoints
   endpoints.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = (prev_count * prev_wout);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!endpoints.Add(descr))
     {
      delete descr;
      return false;
     }

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!endpoints.Add(descr))
     {
      delete descr;
      return false;
     }

Латентное состояние состояния нормализуется функцией SoftMax.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   descr.count = LatentCount;
   descr.step = 1;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!endpoints.Add(descr))
     {
      delete descr;
      return false;
     }

И генерируем конечные точки в полносвязном слое.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 3 * NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!endpoints.Add(descr))
     {
      delete descr;
      return false;
     }

Модель прогнозирования вероятностей выбора траекторий также использует результаты работы Энкодера в качестве исходных данных.

//--- Probability
   probability.Clear();
//--- Input layer
   if(!probability.Add(endpoints.At(0)))
      return false;

Но в ней они анализируются с учетом прогнозируемых конечных точек.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = prev_count;
   descr.step = 3 * NForecast;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }

При этом работа с вероятностными величинами позволяет нам использовать слой SoftMax на выходе модели.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   descr.count = NForecast;
   descr.step = 1;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

А вот дальше, можно сказать, мы внесли кардинальные изменения в алгоритм метода ADAPT. Наши изменения продиктованы спецификой работы финансовых рынков. Однако, на мой взгляд, они абсолютно не противоречат предложенным авторами метода подходам.

Дело в том, что авторы метода предложили свой алгоритм для решения задач навигации автономных транспортных средств. И здесь качество прогнозирования траектории имеет большое значение. Ведь столкновение 2 и более транспортных средств на любом участке траектории может привести критическим последствиям.

В нашем же случае торговли на финансовых рынках больше внимания уделяется контрольным точкам. Для нас не столько важна траектория движения цены и её мелкие колебания в диапазоне общего тренда, сколько экстремумы максимально возможных прибыли и просадок в рамках этого движения.

Поэтому мы исключили блок прогнозирования траектории и заменили его моделью Актера, которая будет генерировать параметры совершаемой сделки. При этом мы сохранили общий подход к обучению моделей. Но об этом мы поговорим чуть позже.

Здесь надо сказать, что наш Актер для принятия решения использует 4 источника данных:

• Эмбединг состояния
• Описания состояния счета
• Наборы прогнозируемых конечных точек
• Вероятности каждого прогнозируемого набора конечных точек.

Ранее мы создали механизм объединения только 2 потоков информации. Для объединения 4 потоков мы построим каскад моделей.

bool CreateDescriptions(CArrayObj *actor, CArrayObj *end_encoder, CArrayObj *state_encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!end_encoder)
     {
      end_encoder = new CArrayObj();
      if(!end_encoder)
         return false;
     }
   if(!state_encoder)
     {
      state_encoder = new CArrayObj();
      if(!state_encoder)
         return false;
     }

Наборы прогнозируемых конечных точек и их вероятности мы объединим в эмбединг конечных точек.

//--- Endpoints Encoder
   end_encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = 3 * NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!end_encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = prev_count;
   descr.step = NForecast;
   descr.optimization = ADAM;
   descr.activation = LReLU;
   if(!end_encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Эмбединг состояния окружающей среды мы объединим с параметрами баланса и открытых позиций.

//--- State Encoder
   state_encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = GPTBars * EmbeddingSize;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!state_encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = prev_count;
   descr.step = AccountDescr;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!state_encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Результаты работы 2 указанных моделей мы передадим Актеру для принятия решения.

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = LatentCount;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = prev_count;
   descr.step = LatentCount;
   descr.optimization = ADAM;
   descr.activation = LReLU;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Внутри Актера мы используем полносвязные слои.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

И генерируем его стохастическое поведение.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 2 * NActions;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronVAEOCL;
   descr.count = NActions;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Как можно заметить, мы планируем использовать максимально простые архитектуры моделей. Что является одним из преимуществ метода ADAPT.

В рамках данной статьи я решил не останавливаться на подробном описании советников взаимодействия с окружающей средой. Структура собираемых данных не изменилась, как и методы взаимодействия с окружающей средой. Конечно, в них внесены изменения в части последовательности вызова моделей для принятия решений. Но с этим я предлагаю Вам познакомиться самостоятельно. Код советников Вы можете найти во вложении. А вот советник обучения моделей имеет несколько уникальных моментов.

2.3 Обучение моделей

В отличие от нескольких последних статей на это раз мы будем обучать все модели в рамках одного советника "...\Experts\ADAPT\Study.mq5". И это связано с передачей градиента ошибки почти от всех моделей в Энкодер состояния окружающей среды.

Метод инициализации советника построен по уже стандартной схеме. Сначала мы загружаем обучающую выборку.

int OnInit()
  {
//---
   ResetLastError();
   if(!LoadTotalBase())
     {
      PrintFormat("Error of load study data: %d", GetLastError());
      return INIT_FAILED;
     }

После чего в 2 этапа загружаем ранее созданные модели и, при необходимости, создаем новые.

//--- load models
   float temp;
   if(!ADAPTEncoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) ||
      !ADAPTEndpoints.Load(FileName + "Endp.nnw", temp, temp, temp, dtStudied, true) ||
      !ADAPTProbability.Load(FileName + "Prob.nnw", temp, temp, temp, dtStudied, true)
     )
     {
      CArrayObj *encoder = new CArrayObj();
      CArrayObj *endpoint = new CArrayObj();
      CArrayObj *prob = new CArrayObj();
      if(!CreateTrajNetDescriptions(encoder, endpoint, prob))
        {
         delete endpoint;
         delete prob;
         delete encoder;
         return INIT_FAILED;
        }
      if(!ADAPTEncoder.Create(encoder) ||
         !ADAPTEndpoints.Create(endpoint) ||
         !ADAPTProbability.Create(prob))
        {
         delete endpoint;
         delete prob;
         delete encoder;
         return INIT_FAILED;
        }
      delete endpoint;
      delete prob;
      delete encoder;
     }

   if(!StateEncoder.Load(FileName + "StEnc.nnw", temp, temp, temp, dtStudied, true) ||
      !EndpointEncoder.Load(FileName + "EndEnc.nnw", temp, temp, temp, dtStudied, true) ||
      !Actor.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true))
     {
      CArrayObj *actor = new CArrayObj();
      CArrayObj *endpoint = new CArrayObj();
      CArrayObj *encoder = new CArrayObj();
      if(!CreateDescriptions(actor, endpoint, encoder))
        {
         delete actor;
         delete endpoint;
         delete encoder;
         return INIT_FAILED;
        }
      if(!Actor.Create(actor) || 
         !StateEncoder.Create(encoder) || 
         !EndpointEncoder.Create(endpoint))
        {
         delete actor;
         delete endpoint;
         delete encoder;
         return INIT_FAILED;
        }
      delete actor;
      delete endpoint;
      delete encoder;
      //---
     }

Все модели переносим в единый контекст OpenCL.

   OpenCL = Actor.GetOpenCL();
   StateEncoder.SetOpenCL(OpenCL);
   EndpointEncoder.SetOpenCL(OpenCL);
   ADAPTEncoder.SetOpenCL(OpenCL);
   ADAPTEndpoints.SetOpenCL(OpenCL);
   ADAPTProbability.SetOpenCL(OpenCL);

И осуществляем минимальный контроль архитектуры моделей.

   Actor.getResults(Result);
   if(Result.Total() != NActions)
     {
      PrintFormat("The scope of the actor does not match the actions count (%d <> %d)", 
                                                                NActions, Result.Total());
      return INIT_FAILED;
     }
//---
   ADAPTEndpoints.getResults(Result);
   if(Result.Total() != 3 * NForecast)
     {
      PrintFormat("The scope of the Endpoints does not match forecat endpoints (%d <> %d)", 
                                                            3 * NForecast, Result.Total());
      return INIT_FAILED;
     }
//---
   ADAPTEncoder.GetLayerOutput(0, Result);
   if(Result.Total() != (HistoryBars * BarDescr))
     {
      PrintFormat("Input size of Encoder doesn't match state description (%d <> %d)", 
                                                Result.Total(), (HistoryBars * BarDescr));
      return INIT_FAILED;
     }

Создадим вспомогательный буфер.

   if(!bGradient.BufferInit(MathMax(AccountDescr, NForecast), 0) ||
      !bGradient.BufferCreate(OpenCL))
     {
      PrintFormat("Error of create buffers: %d", GetLastError());
      return INIT_FAILED;
     }

И генерируем пользовательское событие начала обучения моделей.

   if(!EventChartCustom(ChartID(), 1, 0, 0, "Init"))
     {
      PrintFormat("Error of create study event: %d", GetLastError());
      return INIT_FAILED;
     }
//---
   return(INIT_SUCCEEDED);
  }

Непосредственно процесс обучения организован ив методе Train.

void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);

В теле метода мы сначала создаем вектор вероятностей выбора траекторий из буфера воспроизведения опыта. После чего создаем необходимые нам локальные переменные.

   vector<float> result, target;
   matrix<float> targets, temp_m;
   bool Stop = false;
//---
   uint ticks = GetTickCount();

Обучение, как обычно, осуществляется в системе вложенных циклов. В теле внешнего цикла мы сэмплируем траекторию и пакет состояний обучения на ней.

   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++)
     {
      int tr = SampleTrajectory(probability);
      int batch = GPTBars + 48;
      int state = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * 
                             (Buffer[tr].Total - 2 - PrecoderBars - batch));
      if(state <= 0)
        {
         iter--;
         continue;
        }
      ADAPTEncoder.Clear();
      int end = MathMin(state + batch, Buffer[tr].Total - PrecoderBars);

Во вложенном цикле строится процесс обучения моделей на последовательности исторических данных.

      for(int i = state; i < end; i++)
        {
         bState.AssignArray(Buffer[tr].States[i].state);

Мы берем одно состояние окружающей среды и передаем его в Энкодер.

         //--- Trajectory
         if(!ADAPTEncoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, 
                                                              (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

После чего формируем наборы прогнозных конечных точек и их вероятности.

         if(!ADAPTEndpoints.feedForward((CNet*)GetPointer(ADAPTEncoder), -1, 
                                                             (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

         if(!ADAPTProbability.feedForward((CNet*)GetPointer(ADAPTEncoder), -1, 
                                               (CNet*)GetPointer(ADAPTEndpoints)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Далее для организации процесса обучения конечных точек нам предстоит сформировать целевые значения. Мы берем из буфера воспроизведения опыта последующие состояния на заданную глубину планирования.

         targets = matrix<float>::Zeros(PrecoderBars, 3);
         for(int t = 0; t < PrecoderBars; t++)
           {
            target.Assign(Buffer[tr].States[i + 1 + t].state);
            if(target.Size() > BarDescr)
              {
               matrix<float> temp(1, target.Size());
               temp.Row(target, 0);
               temp.Reshape(target.Size() / BarDescr, BarDescr);
               temp.Resize(temp.Rows(), 3);
               target = temp.Row(temp.Rows() - 1);
              }
            targets.Row(target, t);
           }

Но в них мы берем не последнее состояние, как можно подумать из определения конечных точек, а ищем ближайшие экстремумы. Сначала мы посчитаем накопительным итогом отклонение цены закрытия каждой свечи от анализируемого состояния. И к полученным значениям прибавим интервалы до High и Low каждого бара. Результаты расчетов сохраним в матрицу.

         target = targets.Col(0).CumSum();
         targets.Col(target, 0);
         targets.Col(target + targets.Col(1), 1);
         targets.Col(target + targets.Col(2), 2);

В полученной матрице мы находим ближайший экстремум.

         int extr = 1;
         if(target[0] == 0)
            target[0] = target[1];
         int direct = (target[0] > 0 ? 1 : -1);
         for(int i = 1; i < PrecoderBars; i++)
           {
            if((target[i]*direct) < 0)
               break;
            extr++;
           }

И формируем вектор из найденных ближайших экстремумов.

         targets.Resize(extr, 3);
         if(direct >= 0)
           {
            target = targets.Max(AXIS_HORZ);
            target[2] = targets.Col(2).Min();
           }
         else
           {
            target = targets.Min(AXIS_HORZ);
            target[1] = targets.Col(1).Max();
           }

Среди наборов прогнозируемых конечных точек определяем вектор с минимальным отклонением. И заменяем его целевыми значениями.

         ADAPTEndpoints.getResults(result);
         targets.Reshape(1, result.Size());
         targets.Row(result, 0);
         targets.Reshape(NForecast, 3);
         temp_m = targets;
         for(int i = 0; i < 3; i++)
            temp_m.Col(temp_m.Col(i) - target[i], i);
         temp_m = MathPow(temp_m, 2.0f);
         ulong pos = temp_m.Sum(AXIS_VERT).ArgMin();
         targets.Row(target, pos);

Полученную матрицу используем для обучения модели прогнозирования целевых точек.

         Result.AssignArray(targets);
         //---
         if(!ADAPTEndpoints.backProp(Result, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Градиент ошибки распространяем до модели Энкодера и обновляем её параметры.

         if(!ADAPTEncoder.backPropGradient((CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Тут же мы обучаем модель прогнозирования вероятностей траекторий. Только от неё градиент ошибки не передается другим моделям.

         bProbs.AssignArray(vector<float>::Zeros(NForecast));
         bProbs.Update((int)pos, 1);
         bProbs.BufferWrite();
         if(!ADAPTProbability.backProp(GetPointer(bProbs), GetPointer(ADAPTEndpoints)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

После обновления параметров моделей прогнозирования конечных точек мы переходим к обучению политики нашего Актера. И для осуществления операций прямого прохода нашего Актера на данном этапе нам не хватает только тензора описания состояния счета и открытых позиций. Его мы и сформируем.

         //--- Policy
         float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0];
         float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];
         bAccount.Clear();
         bAccount.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance);
         bAccount.Add(Buffer[tr].States[i].account[1] / PrevBalance);
         bAccount.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity);
         bAccount.Add(Buffer[tr].States[i].account[2]);
         bAccount.Add(Buffer[tr].States[i].account[3]);
         bAccount.Add(Buffer[tr].States[i].account[4] / PrevBalance);
         bAccount.Add(Buffer[tr].States[i].account[5] / PrevBalance);
         bAccount.Add(Buffer[tr].States[i].account[6] / PrevBalance);
         double time = (double)Buffer[tr].States[i].account[7];
         double x = time / (double)(D'2024.01.01' - D'2023.01.01');
         bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_MN1);
         bAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_W1);
         bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_D1);
         bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         if(bAccount.GetIndex() >= 0)
            bAccount.BufferWrite();

Далее мы осуществляем последовательный вызов методов прямого прохода нашего каскада моделей Актера.

         //--- State embedding
         if(!StateEncoder.feedForward((CNet *)GetPointer(ADAPTEncoder), -1, 
                                      (CBufferFloat*)GetPointer(bAccount)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

И здесь надо уточнить, что вместо прогнозных значений наборов конечных точек и их вероятностей мы используем тензоры целевых значений, которые использовали выше для обучения соответствующих моделей.

         //--- Endpoint embedding
         if(!EndpointEncoder.feedForward(Result, -1, false, (CBufferFloat*)GetPointer(bProbs)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

         //--- Actor
         if(!Actor.feedForward((CNet *)GetPointer(StateEncoder), -1, 
                                                          (CNet*)GetPointer(EndpointEncoder)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

После прямого прохода нам следует обновить параметры моделей. А для этого нам нужные целевые значения. Методом ADAPT предполагается обучение модели прогнозирования траекторий на реальных данных из буфера воспроизведения опыта. Мы могли бы как и ранее взять действия Агента из буфера воспроизведения опыта. Но в данном случае у нас нет механизма оценки и приоритезации таких действий.

В данной ситуации я решил использовать иной подход. Так как мы уже имеем целевые значения конечных точек, построенных на реальных данных последующего ценового движения из обучающей выборки. То почему бы нам не воспользоваться ими для генерации "оптимальной" сделки в анализируемых условиях. Мы определяем направление и торговые уровни "оптимальной" сделки. Объем позиции возьмем с учетом риска в 1% от Эквити на сделку.

         result = vector<float>::Zeros(NActions);
         double value = SymbolInfoDouble(_Symbol, SYMBOL_TRADE_TICK_VALUE_LOSS);
         double risk = AccountInfoDouble(ACCOUNT_EQUITY) * 0.01;
         if(direct > 0)
           {
            float tp = float(target[1] / _Point / MaxTP);
            result[1] = tp;
            int sl = int(MathMax(MathMax(target[1] / 3, -target[2]) / _Point, MaxSL/10));
            result[2] = float(sl) / MaxSL;
            result[0] = float(MathMax(risk / (value * sl), 0.01))+FLT_EPSILON;
           }
         else
           {
            float tp = float((-target[2]) / _Point / MaxTP);
            result[4] = tp;
            int sl = int(MathMax(MathMax((-target[2]) / 3, target[1]) / _Point, MaxSL/10));
            result[5] = float(sl) / MaxSL;
            result[3] = float(MathMax(risk / (value * sl), 0.01))+FLT_EPSILON;
           }

При расчёте объема позиции мы используем Эквити, так как на момент совершения операции по счету уже могут быть открытые позиции, прибыль (убыток) которых не учтены в Балансе счета.

Сгенерированная таким образом "оптимальная" позиция используется для обучения моделей Актера.

         Result.AssignArray(result);
         if(!Actor.backProp(Result, (CNet *)GetPointer(EndpointEncoder)) ||
            !StateEncoder.backPropGradient(GetPointer(bAccount), 
                                  (CBufferFloat *)GetPointer(bGradient)) ||
            !EndpointEncoder.backPropGradient(GetPointer(bProbs), 
                                  (CBufferFloat *)GetPointer(bGradient))
           )
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Градиент ошибки от обучения моделей Актера используем для обновления параметров Энкодера.

         if(!ADAPTEncoder.backPropGradient((CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Обратите внимание, что на данном этапе мы не обновляем параметры модели прогнозирования конечных точек. Такое ограничение вводится авторами метода ADAPT и призвано повысить стабильность обучения моделей.

После обновления параметров всех моделей нам остается проинформировать пользователя о ходе процесса обучения и перейти к следующей итерации системы циклов.

         //---
         if(GetTickCount() - ticks > 500)
           {
            double percent = (double(i - state) / ((end - state)) + iter) * 100.0 / (Iterations);
            string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", percent, 
                                                                  Actor.getRecentAverageError());
            str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Endpoints", percent, 
                                                         ADAPTEndpoints.getRecentAverageError());
            str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Probability", percent, 
                                                       ADAPTProbability.getRecentAverageError());
            Comment(str);
            ticks = GetTickCount();
           }
        }
     }

В завершении метода мы очищаем поле комментариев на графике. Выводим в журнал результаты обучения моделей. И инициируем завершение работы советника.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, 
                                                       "Actor", Actor.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, 
                                          "Endpoints", ADAPTEndpoints.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, 
                                      "Probability", ADAPTProbability.getRecentAverageError());
   ExpertRemove();
//---
  }

На этом мы завершаем описание реализации нашего видения алгоритма средствами MQL5. Полный код всех используемых в статье программ вы можете найти во вложении.

3.Тестирование

Выше была проделана довольно большая работа по реализации метода ADAPT средствами MQL5. Наша реализация далека от авторского алгоритма. Тем не менее она выдержана в духе предложенных подходов и эксплуатирует авторскую идею всестороннего анализа отношений между объектами анализируемой сцены. И теперь пришло время проверить результаты наших трудов на реальных исторических данных в тестере стратегий.

Обучение моделей осуществлялось на исторических данных первых 7 месяцев 2023 года инструмента EURUSD тайм-фрейм H1. Параметры всех анализируемых индикаторов используются по умолчанию.

Тестирование обученных моделей осуществлялось с полным соблюдением параметров обучения. Изменен лишь временной интервал исторических данных. На данном этапе мы использовали исторические данные за Август 2023 года.

Здесь я должен сказать, что так как структура данных, собираемых в процессе взаимодействия с окружающей средой, не изменилась. То в своем эксперименте я не осуществлял новый сбор обучающих данных. Для обучения моделей я использовать проходы, собранные при обучении предыдущих моделей. Более того, предложенный подход с расчетом "оптимальной сделки" позволяет нам отказаться от необходимости сбора дополнительных проходов, уточняющих и дополняющих пространство обучающих данных.

Тут может показаться, что достаточно одного прохода для обучения модели. Однако в процессе обучения нам необходимо предоставлять модели как можно больше разносторонней информации, включая информацию о состоянии счета и открытых позиций.

По результатам проведенных тестов могу сказать об эффективности рассмотренного метода. Простота моделей позволяет обучать модели довольно быстро. А эффективность предложенных подходов подтверждается результатами работы обученной модели. Которая позволяет генерировать прибыль как на обучающей, так и на тестовой выборке.

Заключение

Рассмотренный в данной статье метод ADAPT представляет собой инновационный подход к прогнозированию траекторий агентов в различных сложных сценариях. Данный подход эффективен, требует небольшого объема вычислительных ресурсов и обеспечивает высокое качество прогнозов для каждого агента на сцене.

Улучшения, внесенные в метод ADAPT, включают адаптивную голову, увеличивающую емкость модели без увеличения ее размера, а также использование динамического обучения весов для лучшей адаптации к индивидуальным ситуациям каждого агента. Эти инновации в значительной степени способствуют эффективному прогнозированию траекторий.

В практической части статьи мы реализовали свое видение предложенных подходов средствами MQL5. Провели обучение и тестирование моделей на реальных исторических данных. Полученные результаты позволяют сделать вывод об эффективности метода ADAPT и возможности использования его вариаций для построения модели и её эксплуатации в условиях финансовых рынков.

Однако, ещё раз напоминаю, что все программы, используемые при подготовке статьи, приведены только в качестве демонстрации возможности и не оптимизированы для реальной работы на финансовых рынках.

Ссылки

ADAPT: Efficient Multi-Agent Trajectory Prediction with Adaptation

Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Research.mq5	Советник	Советник сбора примеров
2	ResearchRealORL.mq5	Советник	Советник сбора примеров методом Real-ORL
3	Study.mq5	Советник	Советник обучения Моделей
4	Test.mq5	Советник	Советник для тестирования модели
5	Trajectory.mqh	Библиотека класса	Структура описания состояния системы
6	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
7	NeuroNet.cl	Библиотека	Библиотека кода программы OpenCL